Mechanisms of Adhesion Increase in Wet Sanded Wheel–Rail Contacts—A DEM-Based Analysis

Abstract

In railways, problems in braking and traction can be caused by so-called low-adhesion conditions. Adhesion is increased by sanding, where sand grains are blasted towards the wheel–rail contact. Despite the successful use of sanding in practice and extensive experimental studies, the physical mechanisms of adhesion increase are poorly understood. This study combines experimental work with a DEM model to aim at a deeper understanding of adhesion increase during sanding. The experimentally observed processes during sanding involve repeated grain breakage, varying sand fragment spread, formation of clusters of crushed sand powders, plastic deformation of the steel surfaces due to the high load applied and shearing of the compressed sand fragments. The developed DEM model includes all these processes. Two types of rail sand are analysed, which differ in adhesion increase in High-Pressure Torsion tests under wet contact conditions. This study shows that higher adhesion is achieved when a larger proportion of the normal load is transferred through sand–steel contacts. This is strongly influenced by the coefficient of friction between sand and steel. Adhesion is higher for larger sand grains, higher sand fragment spread, and higher steel hardness, resulting in less indentation, all leading to larger areas covered by sand.

1. Introduction

This work combines experiments and DEM modelling for the investigation of the adhesion-increasing effect of sanding in wheel–rail contacts. In railways, the large weight of the train is transferred from its wheels to the rail on small contact patches, resulting in extreme normal stresses up to 1 GPa and higher. Tangential stresses in the wheel–rail contact are also extremely high and are caused, for example, by traction and braking. Due to these high stresses, severe plastic shear deformations occur in the near-surface layers of wheels and rails [1,2,3]. These plastic deformations cause crack initiation at the surfaces, which results in wear. In some cases, initiated cracks grow deeper, leading to macroscopic cracks known, for example, as head checks on rails.

The transferable tangential force available for traction and braking is limited by the maximal adhesion coefficient (AC). Furthermore, the AC is also affected by third body layers (3BLs) embedded between wheels and rails [4,5,6,7]; both liquid (water, lubricants, etc.) and solid (wear debris, iron oxides, leaves, etc.) 3BLs exist. Such 3BLs can cause, under certain conditions, so-called low-adhesion conditions where the ACs between the wheel and rail are below 0.1 [8,9]. Low-adhesion conditions influence the traction and braking performance of railway vehicles in service. At worst, they can cause safety issues [9,10]. Typical causes for low-adhesion conditions are damp (wet) contact conditions or when the rail surface is contaminated with leaves [4].

Sanding of wheel–rail contacts has been used for many years to increase the AC and thus overcome low-adhesion conditions. The process is shown in Figure 1. Sand particles are sprayed from a nozzle towards the wheel–rail contact. Some particles are expelled and some are entrained into the contact. The entrained particles fracture repeatedly and influence the adhesion, also changing the roughness of the wheel and rail. While sanding does increase the AC under low-adhesion conditions, it can also lead to increased damage on both the wheel and rail [11].

There are many experimental studies in the field of wheel–rail sanding [13]. Adhesion coefficients (ACs) are measured under different contact conditions (dry, wet, …) [14,15], applying different sands or other particles [16,17,18], or studying the influence of wheel slip and rolling speed [19]. Some studies have investigated wheel–rail isolation or wear in contacts of sand [20,21,22]. Moreover, the efficiency of sanding systems, i.e., the number of particles entrained in wheel–rail contact in relation to the total amount of sand released, is studied in [23,24].

Modelling the wheel–rail contact, in general, is a complex and well-addressed topic in tribology. There are models based on classical theory [25,26,27,28,29,30,31,32,33,34,35], which assume purely elastic material behaviour, perfectly smooth surfaces (half-space theory) and tangential stresses being limited according to Coulomb’s law of friction. Most of these assumptions are not met in reality. Besides models based on classical theory, extended models can be found in the literature [36,37,38,39,40,41] in review articles as well as recent works. However, numerical models considering local effects in the wheel–rail contact region during sanding are very sparse in the literature and focus on electrical isolation, as this hinders train detection, potentially leading to safety problems [42,43] or particle entrainment efficiency [44,45].

Despite the active research in this field, the physical mechanisms causing the change in ACs under sanded conditions are not yet well understood. Simulation models can help to increase this understanding, when they include the relevant features of the sanding process. Sand grains entering the wheel–rail contact will fracture repeatedly, and some of their fragments will be expelled. During roll-over, the fragments may spread out or stay close together and they will solidify under the high load and form clusters [12]. Figure 2 shows two scenarios regarding possible mechanisms of load transfer: Figure 2a presents a sketch including descriptions and Figure 2b depicts a DEM modelling approach. In the upper part of Figure 2a, a larger number of sand fragments with a higher fragment spread could separate the wheel from the rail. In this scenario, the sand slides over metal, which can be expected to increase AC compared to the unsanded case of sliding wet metal surfaces. In a second scenario illustrated in the lower part of Figure 2a, the sand fragments show little spread, and the resulting compact cluster might indent deeper into wheel and rail surfaces (affecting roughness) [12]. The AC could be increased, for example, by form closure effects in combination with a high shear resistance of the compacted sand fragment cluster. The role of water is also unclear. This mentioned lack of understanding is caused by the fact that current experimental abilities do not allow for any monitoring of the aforementioned mechanisms in the contact zone during roll-over.

Two very recent and different approaches have emerged, aimed at modelling the wheel–rail sanding process using DEM.

In [46], a DEM model of sanded High-Pressure Torsion (HPT) tests under dry conditions is presented. A sand grain is modelled using bonds between equally sized spheres, which allow for breakage of the particle. The wheel and rail specimens are modelled as an undeformable plate and a regular grid of spheres, respectively. Contact between the wheel and rail specimens is ignored. Under dry conditions, experimental results show little difference in adhesion between the sanded and the unsanded cases. The simulation results are in good agreement with the measured adhesion. Furthermore, variations in bond parameters, in initial sand grain size and number of sand grains in the test, are shown. The bond parameters naturally influence the breakage behaviour, and the bond stiffness also has a strong influence on the simulated adhesion. With increasing initial sand grain size, the simulated adhesion decreased, while this effect could not be seen in the experimental results.

In [12,47,48], the authors started to build a DEM model of wheel–rail sanding. At first, for two types of rail sand, single-grain sand crushing tests were conducted under dry and wet contact conditions [12]. In initial breakage tests and high-loading tests under a realistic wheel–rail load of 900 MPa, the spread behaviour of sand fragments was investigated. High fragment spread can lead to the ejection of a certain amount of sand fragments from the wheel–rail contact; thus, a reduced number of fragments remains inside and potentially increases adhesion. Under dry contact conditions, a rail sand used in Great Britain, called GB sand, showed high fragment spread while it showed low spread under wet conditions. On the contrary, a rail sand used in Austria, called AT sand, showed low fragment spread both under dry and wet conditions. In the high-loading tests under wet conditions for both rail sands, large clusters of solidified sand fragments formed. High-resolution 3D scans of these sand clusters and the supporting steel plate showed indents in the steel plates caused by sand clusters in prior tests. This confirms that the form closure effects depicted schematically in Figure 2 might play a role in adhesion increase.

In [47], a DEM model of these sand crushing tests was developed and parametrised. Particle breakage is modelled via the replacement method. Sand grains and fragments are modelled as spheres with blocked rotation. A method from the literature [49] is adapted to achieve mass conservation during breakage and a different spread of fragments between both types of sand. After replacement, the fragments are placed with a high degree of overlapping to ensure mass conservation. Freezing steps allow dissipation of most of the artificial energy introduced by the fragments’ initial overlap. The definition of an appropriate condition for unfreezing, thus resuming the normal simulation, allows control of fragment spreading. The mechanism of the experimentally observed formation of clusters is modelled phenomenologically by including cohesion, where the cohesion coefficient is much greater than in normal cohesive materials. Under wet contact conditions, the spread of fragments was reduced [12], which can be modelled efficiently by adding a drag force following Stokes’ law to each particle. For both types of rail sand and both dry and wet contact conditions, a good agreement between experiments and simulations was achieved regarding the sand fragment spread and formation of clusters. As a first step, in [47], the steel plates were modelled as undeformable plate objects.

In [48], the DEM model was extended with the experimentally observed indentation of steel plates during crushing [12]. The starting point was the method presented in [50], which allows for the DEM simulation of plastic wear of a surface caused by an indenter sphere. The surface was modelled by a regular hexagonal grid of non-overlapping spheres, and the indenter sphere is several times larger than the surface spheres. When the stress at a surface sphere is higher than its given hardness H, then the surface sphere is moved vertically to ensure surface grid regularity. The method is similar to an ideal plastic material law. This model from the literature was adapted in [48] to allow the surface to be indented by a granular material under vertical loading. The representation of the surface using different overlapping and non-overlapping regular grids was investigated for two test cases with purely elastic and elastic–(ideal-)plastic behaviour. Experimental measurements on spherical indentation were conducted to calibrate the hardness parameter H. As a proof of concept, a sand grain is crushed and loaded up to 900 MPa between indentable steel plates by combining the developed models of [47,48].

This study continues the previously described works of the authors. In sanded HPT tests under wet conditions, both types of rail sand increase adhesion but to a different extent. The mechanisms of adhesion increase and the reasons for the observed differences between the sand types cannot be studied with current experimental availabilities. Hence, to enhance understanding of these processes, the developed DEM model is used to simulate crushing and shearing of both types of rail sands in an HPT test under wet conditions. In the DEM model, a variation in parameters, e.g., allows to change fragment spread during breakage or the coefficient of friction during sliding and to study the influence on the simulated adhesion coefficient. Moreover, the DEM model allows to study all particle and contact details, e.g., mobilised friction, area of the bottom specimen covered by sand, transfer of normal force through sand–steel or steel–steel contacts and so on. The knowledge gained is used to explain mechanisms and factors increasing the simulated adhesion and the differences between GB and AT sand. Simulation results will be compared qualitatively with existing and new measurements from HPT tests. Agreement with experimental findings increases trust in the DEM simulations and the conclusions drawn from them.

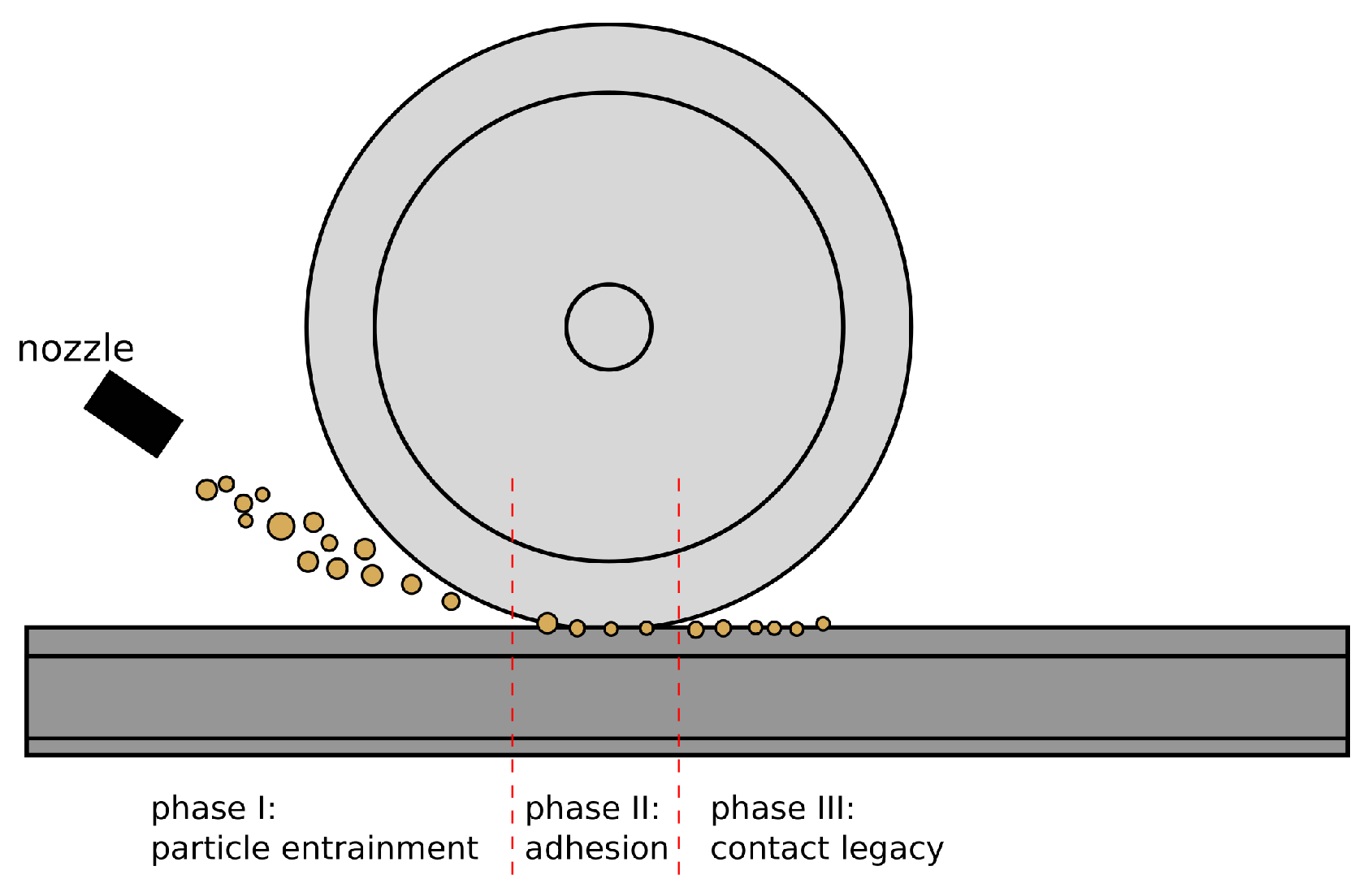
This work is organised as follows. In Section 2, experimental results of HPT tests under wet conditions are shown together with high-resolution 3D scans of the surfaces, showing the formation of clusters of sand fragments and their indents in the metal surface. Section 3 summarises the developed DEM model, including relevant mechanisms and parameters. Simulation results of unsanded and sanded HPT tests are shown in Section 4. Both types of rail sands are studied and parameter variations reveal factors influencing simulated adhesion. The final section contains conclusions and an outlook.

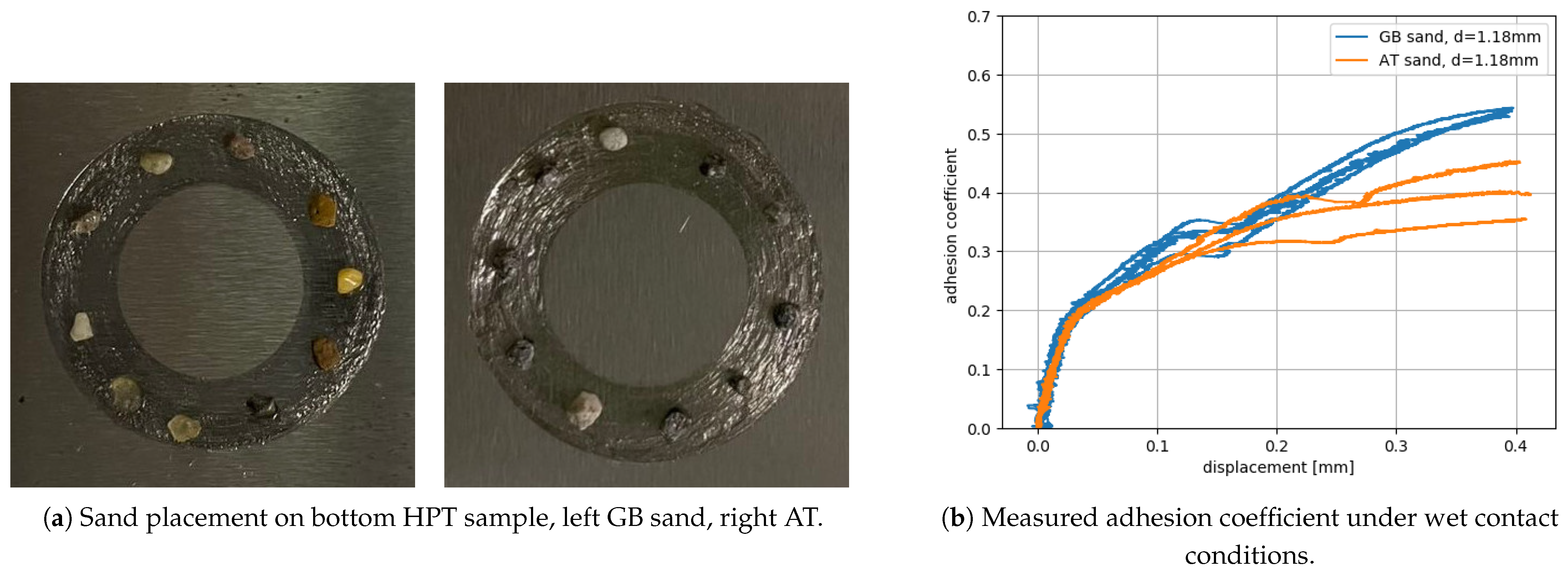
2. Experimental Results of High-Pressure Torsion (HPT) Tests

In this section, previously conducted HPT tests will be summarised, and new measurement results will be presented. Rail sands from Great Britain (GB) and Austria (AT) are used in this study. In [51], these rail sands were studied in detail, including particle characterisation and sanded HPT tests under dry, wet and contaminated (leaf layer) conditions.

The HPT test has previously been used as a laboratory model of the wheel–rail contact. The HPT rig compresses a square bottom plate onto a ring-shaped top specimen to create an annular contact. The annular contact has an inner diameter of 10.5 mm and an outer diameter of 18 mm. After the application of a specified normal load, corresponding to a contact pressure of 900 MPa, a torque is applied to the bottom plate and rotated at a low speed ($<1$ mm/s) for a set angle of rotation. A schematic of this device is shown in Figure 3a. Initially, the surface deforms elastically until part of the surface plastically deforms and the contact surfaces begin to slip against one another. To ensure repeatability and a realistic state of both the top and bottom specimens, they are run together to fully condition (shakedown) the surfaces. For wet contact conditions, 20 $\mathsf{\mu }$L of distilled water is added using a pipette. The sand particles are placed by hand, 0.025 g for each test; see Figure 3b for an example. Full details on the testing procedure are given in [51].

HPT measurements under wet conditions conducted in [51] are shown in Figure 3c. In these tests, the bottom plate was made of R260-grade rail, and the top specimen was made of R8T-grade wheel. The tests were conducted using medium-sized sand grains. For GB sand, $d_{50}=1.42$ mm, 0.025 g of weight resulted in four to five sand grains being placed. AT sand is smaller, $d_{50}=0.98$ mm; thus, about 19 sand grains were used to reach the same weight of 0.025 g. For both AT and GB sand, three measurements of the adhesion coefficient were conducted. Although some scattering can be seen in the measured adhesion, GB sand shows generally higher adhesion values than AT sand. For both types of sand, adhesion increases only slowly after a shear path of 0.2 mm. The final adhesion values range between 0.59 and 0.63 for GB sand and 0.48 and 0.55 for AT sand.

As the sizes of the used grains of AT and GB sand are expected to influence the measured adhesion, new HPT tests are conducted for this study using the same grain size for both types of rail sand, $d=1.18$ mm. Using the same weight of 0.025 g, 10 sand grains are placed for each test; see Figure 4a. The colour of the GB sand grains varies between black, grey, brown and yellow, possibly indicating different behaviour of the grains in the tests. The AT sand grains are much more homogeneous in their colour. For better comparison with the simulations presented later, both top and bottom specimens are made from R260-grade rail steel. Using the same procedure as before to run the surfaces together, for each type of sand, three measurements are conducted, and results are shown in Figure 4b. Comparing the tests in Figure 3c with those in Figure 4b, a noticeable change in the shape of the curves is apparent. This difference is most likely due to the different specimen materials being used in the test. In the tests shown in Figure 3c, an R260 steel (rail steel) bottom specimen and an R8T steel (wheel steel) top specimen were used, whilst the tests in Figure 4b used R260 for both top and bottom specimens. This difference in material matching may have influenced the run-in process: in the tests shown in Figure 3c, the softer R8T on the harder R260 conditioned the surfaces to the limit of their plasticity, whereas the tests in Figure 4b may have conditioned the surfaces beyond this limit of their plasticity. Matching surfaces have been found to result in higher friction values, and the higher friction values between both R260 samples may have caused the tangential force to be exerted in the contact to exceed this plasticity limit. While this makes it difficult to compare the tests in Figure 3c and Figure 4b, it can be observed that the relative differences between GB and AT sand remain broadly the same.

After the HPT tests, a non-contact imaging and measuring tool named Alicona InfiniteFocus SL is used to perform high-resolution 3D scans of the top and bottom specimens. Scans are taken directly after the tests, with crushed sand clusters sticking to the surfaces, and after cleaning, with the surfaces showing indentations under these clusters. The scans had a vertical resolution of 500 nm. Examples of these scans are shown in Figure 5, with different colours indicating the sample height in $\mathsf{\mu }$m. Note that the data created in the new measurements is publicly available at https://doi.org/10.5281/zenodo.15370620. For GB sand, Figure 5a,c show the state after the tests. Out of ten sand grains placed in the test, five formed smaller or larger clusters, while the remaining five grains had a higher fragment spread during crushing and/or shearing. After cleaning the metal surfaces, Figure 5b,d each show one larger indent formed under a sand cluster, and several small indents can be seen. From the three tests conducted with GB sand, the maximal indentation depth ranged between 80 $\mathsf{\mu }$m and 160 $\mathsf{\mu }$m. The difference in fragment spread of single grains of GB sand could be related to different mineral compositions, which could be the reason for the different colours of the grains.

The AT sand showed considerably less fragment spread and formed much larger clusters of sand fragments. It seems that almost every sand grain placed formed a cluster, which then covered the metal surfaces; see Figure 5e,g. At the cleaned top and bottom specimens, as shown in Figure 5f,h, there are ten indents, which will most likely belong to the ten sand grains placed in the test. The maximal indentation depths seen in the three tests conducted for AT sand were comparable to those from the tests with GB sand and ranged between 80 $\mathsf{\mu }$m and 160 $\mathsf{\mu }$m.

These results show the differences in the crushing and spread of fragments between both rail sands. For GB sand, fragment spread is higher, a lower number of large clusters form, and smaller numbers of sand fragments indent top and bottom specimens. For AT sand, each sand grain forms a cluster and indents over a larger area in the metal surfaces. The observed indentation depth is comparable for both types of sand. The differences in fragment spread between both sand types are consistent with previous experimental findings [12].

3. DEM Modelling of a Sanded Wheel–Rail Contact

The main objective of developing the DEM model was to include all the above-mentioned experimental observations. In Section 4, the DEM model will be used for shearing simulations, investigating the mechanisms of adhesion increase and differences between GB and AT sand. Involving all available experimental findings makes the DEM simulations and the conclusions drawn from them more reliable.

This section contains a summary of the DEM model developed in [47,48], which will be used for simulations of the HPT tests in the following section. The software used for all DEM simulations is YADE [53,54]. YADE is open-source and utilises the soft contact approach together with explicit time integration.

In [47], the focus was on modelling sand grain crushing and the resulting spread of fragments, which were observed in experimental works, [12]. The sand grains were crushed between steel plates, which were modelled as rigid plates in [47]. Experimental results from both single-grain crushing tests and HPT tests showed that the crushed sand fragments can indent in the steel surface. This effect was believed to play an important role in the shearing and adhesion-increasing mechanisms. Therefore, in [48], a DEM surface indentation model from the literature was extended such that a sand grain can be crushed between two indentable steel plates.

The sand fragments are modelled as spheres and using the Hertz–Mindlin contact law with viscous damping [55]. As real sand grains and their fragments are clearly non-spherical, it is necessary to restrict the sphere’s rolling in the DEM model. In the literature, rolling resistance models have been formulated and successfully applied to different applications, e.g., [56,57,58,59]. However, these models introduce at least one additional parameter to the DEM model, which can lead to ambiguous parameter combinations if no proper experimental data is available, even for cohesionless material without external load; see [60]. To avoid this problem, in [47], it was decided to block the spheres’ rotation completely.

The crushing of the sand grain was modelled via the particle replacement method [61,62,63]. If a sphere breaks, it is replaced by 20 fragments (with varying sphere diameters) of the same mass, which are placed with a high degree of overlapping in the volume of the broken sphere. This avoids the problem of mass loss due to repeated breakage but requires a special numerical treatment to avoid high overlaps, which lead to unrealistically high particle accelerations and velocities. In [47], a method was presented which avoids this problem and at the same time allows control of the spread of the newly created fragments. After the replacement of a broken particle, the system goes into a freezing mode. For a certain time period $t_0$, only the newly added particles and their neighbours are allowed to move. During this time, the initially high overlaps of the newly added fragments can reduce, and the system can tend towards equilibrium. The freezing mode is ended when the maximal velocity in the system is below a model parameter $V_b$, and the simulation proceeds. Higher or lower values of $V_b$ will result in higher or lower spread of fragments. To avoid infinite breakage of particles under the applied high load, a radius $R_{lim}$ is introduced in the model, below which particles are considered unbreakable.

The formation of clusters of sand fragments is mimicked in the DEM model by adding cohesion to the Hertz–Mindlin contact law. A simple cohesion model is that of Derjaguin–Muller–Toporov (DMT) [64], which uses $\gamma$ to represent a cohesion parameter. To model the observed change in the behaviour of the sand fragments from initially cohesionless to cohesive, the cohesive force is only activated if one of the contact partners has a radius below a parameter $R_{\gamma }$. It is important to note that the value of $\gamma$ used here is not in the same order as for natural cohesive granular materials. This is because the cohesion was used as a substitute to represent the observed behaviour of sand cluster formation.

In the experiments, under wet contact conditions, the spread of fragments was reduced compared to dry contact conditions. In the DEM model, an efficient way to model this effect is to add a drag force, $F_{drag}$, following Stokes’ law to each particle, given by

$$F_{drag}=6\pi \eta rv,$$

(1)

where r is the particle’s radius, v its velocity and $\eta$ the dynamic viscosity. As the assumptions for deriving Stokes’ law are not entirely given—e.g., Stokes’ law considers laminar flow—the parameter $\eta$ will be calibrated to experimental results.

All aforementioned parameters of the DEM model for both GB and AT sand can be found in

Table 1. Parameters of Hertz–Mindlin contact law for both GB and AT sand as well as steel.

Material	Young’s Modulus E [GPa]	Poisson Ratio $\mathit{\nu }$ [-]	Coeff. of Friction $\mathit{\mu }$ [-]	Density $\mathit{\rho }\left[\frac{\mathbf{kg}}{{\mathsf{m}}^3}\right]$	Coeff. of Restitution ${\mathit{e}}_{\mathit{n}}$ [-]
GB sand	86.5	0.3	0.5	2650	0.5
AT sand	79.1	0.3	0.7	2650	0.3
steel	200.0	0.28	0.2	7833

and

Table 2. Further parameters of developed DEM model for both GB and AT sand; see [47] for details.

Sand	${\mathit{V}}_{\mathit{b}}\left[\frac{\mathsf{m}}{\mathsf{s}}\right]$	$\mathit{\eta }$ [Pa s]	${\mathit{R}}_{\mathit{lim}}$ [$\mathsf{\mu }$m]	$\mathit{\gamma }\left[\frac{\mathsf{J}}{{\mathsf{m}}^2}\right]$	${\mathit{R}}_{\mathit{\gamma }}$ [$\mathsf{\mu }$m]
GB	0.12	0.012	64	800	100
AT	0.08	0.012	53	800	125

.

The steel plates are represented in the DEM model using the surface indentation model presented in [48]. The plates themselves are modelled as a regular hexagonal grid of overlapping spheres of radius $r_s$. The contacts to the sand fragments and the second steel plate are again realised using the Hertz–Mindlin law. These spheres can be vertically indented, when they are subjected to vertical stress higher than their hardness H. Spherical indentation tests were used in [48] to parametrise a DEM model. The same set-up will be used here: steel spheres have a radius of $r_s=0.15$ mm and an overlap of $ov=1.5$ (see [48] for the definition).

The developed DEM model involves all processes observed in HPT tests: sand grain crushing with different fragment spread behaviour between GB and AT sand, formation of solidified clusters under high load and indentation of these clusters into the steel surfaces. Simulation results are in qualitative agreement with the results of single-grain crushing tests and high-loading tests from [12].

4. HPT Test Simulation Under Wet Conditions

The DEM model described in the previous section will now be used to simulate wet HPT tests. After general comments, unsanded HPT tests are simulated for later comparison. Then, sanded HPT tests are simulated; split into the crushing and shearing phase. The shearing phase involves a detailed study on the influence of several parameters on simulated adhesion. Adhesion-increasing mechanisms as well as differences in adhesion increase between GB and AT sand are discussed in detail. Comparing simulation results with the experimental results from Section 2 shows qualitative agreement, which increases trust in DEM simulations and the conclusions drawn from them.

In the DEM model, the whole geometry of the HPT test specimen is not simulated; instead, only an area of 10 mm × 10 mm, which is roughly the area of the wheel–rail contact patch, is modelled. The model has no intrinsic restrictions on simulating this domain size or a single sand grain. A simulation of the whole HPT contact area with multiple sand grains is possible but would be computationally expensive. In the HPT tests, first the normal stress of 900 MPa (i.e., 90 kN normal force) is applied, and then, the specimen is sheared under constant normal stress. During the application of the normal load, the surface indentation model is active, such that the sand fragments can form indentations in the steel plates. It is assumed that no further surface indentation takes place during the shearing phase. Therefore, the surface indentation model is disabled before the shearing starts.

4.1. Unsanded HPT Test

As a first step, simulations of unsanded HPT tests under wet conditions are conducted. They will serve as a reference for the adhesion-increasing effect of the sanding process later on. The two steel plates, modelled as a regular hexagonal grid of overlapping spheres, were placed on top of each other, loaded normally and then sheared. The simulated adhesion coefficient was calculated as the sum of forces on the top plate in the shearing direction, divided by the applied normal load. In the first try, this approach led to huge variation in the simulated adhesion coefficient over the shear path. The values ranged between 0.0 and 0.5, when the steel–steel coefficient of friction was 0.2. As both steel plates are modelled as identical regular hexagonal grids of overlapping spheres and were placed exactly on top of each other, this leads to a strong variation in the number of contacts, causing the described variation in the adhesion coefficient due to geometrical effects (repeated interlocking of the two rough surfaces). This problem could be drastically reduced by generating the grid of the top steel plate with a rotation angle of ${10}^{\circ }$ around an axis perpendicular to the shear plane. This rotation reduces the mentioned geometric interlocking effect, thereby decreasing the variation in the number of contacts during shearing. As a result, the simulated adhesion coefficient ranges between 0.18 and 0.22, as shown in Figure 6.

4.2. Sanded HPT Tests: Crushing Phase

The first step of sanded HPT tests is the application of pure normal stress. This subsection deals with the simulation of the crushing of GB and AT sand grains under varied parameters. For both sand types, two sizes of the initial grain will be considered. Following the measured particle size distribution (PSD) curves for both sand types given in [51], sizes corresponding to 25%, 50% and 75% passing are chosen; see

Table 3. Variation in parameters in the crushing phase for both GB and AT sand.

Parameters	GB Sand	AT Sand
grain size [mm]	1.18 (S: 25%), 1.43 (M: 50%)	0.98 (M: 50%), 1.18 (L: 75%)
cohesion activ. radius $R_{\gamma }\left[\mathsf{\mu }\mathsf{m}\right]$	low: S: 77, M: 100, high: S&M: ${10}^6$	low: M: 125, L: 150, high: S&M: ${10}^6$
hardness H [GPa]	2.5, 10	2.5, 10

. The grain size corresponding to 25% passing will be noted as S, 50% passing as M and 75% passing as L. The cohesion activation radius $R_{\gamma }$ is also varied as it strongly influences fragment spread. For the different initial sand grain sizes considered, $R_{\gamma }$ is scaled linearly from values stated in [47]. This ensures similar spreading behaviour of the different initial sand grain sizes. Additionally, $R_{\gamma }$ is set to 1 m, meaning that all fragments are cohesive from the first breakage incident. In the first case, there will be a certain amount of scattering of the sand fragments, while in the second case, the sand fragments will stay together, forming one large cluster, which then indents deeper in the steel plates. The hardness of the steel plates will also be varied, to study the effect of indentation depth and possible form closure under shearing. These three influencing factors will be varied during the normal loading step with the fully loaded configuration saved.

For GB sand, the indented steel plates, as well as the formed sand clusters for the parameter combinations, are shown in Figure 7. Additionally, the maximal indentation, the indentation volume and an estimation of the area covered by sand fragments are given. For both grain sizes S and M, the effects of varying $R_{\gamma }$ and H show the same trend. While for $R_{\gamma }=77/100\mathsf{\mu }$m, there is some scattering of the sand fragments, in the case of $R_{\gamma }=1$ m, one large cluster of sand forms with only very few fragments spreading out; compare the given sand-covered area in the figure. The spread of fragments is linked to the maximal indentation of the steel plates for both hardness values. The case of spreading fragments shows considerably less (about half) maximal indentation than the case of one sand cluster forming. Regarding the indentation volume, also given in the figure, the effect is different. For the softer steel plates, $H=2.5$ GPa, the indentation volume is almost independent of $R_{\gamma }$, meaning that the sand fragments are fully enclosed and both steel plates are massively in contact. This will also be confirmed by later analysis. For the harder steel plates, $H=10$ GPa, simulations with high fragment spread show considerably less indentation volume than simulations with $R_{\gamma }=1$ m, where one large cluster forms.

For AT sand, the results of the parameter variations are shown in Figure 8. As AT sand is in general smaller than GB sand, here sand grain sizes M and L are considered; see Table 3. This will allow an interesting comparison between both sand types in later sections, as GB S and AT L have the same size. In experiments, AT sand showed less fragment spread than GB sand. This is reflected in the DEM model by parameters involved in the breakage phase, $R_{\gamma },V_b$, but also by the chosen friction coefficient for sand–sand particles, ${\mu }_{SaSa}$. Therefore, in Figure 8, the resulting sand areas for low and high $R_{\gamma }$ values differ less than for GB sand. The maximal indentation values are lower for simulations with more fragmentation spread, i.e., low $R_{\gamma }$ values. Thus, the same trend is seen as for GB sand. The indentation volume depends only on the steel hardness H and on the initial sand grain size. As $R_{\gamma }$ shows nearly no influence, it can be concluded that both steel plates are massively in contact and enclose the sand fragments. The reason is the smaller initial sand grain size and the reduced fragmentation spread, compared to GB sand.

4.3. Sanded HPT Tests: Shearing Phase

The saved configurations from the crushing simulations will be loaded and used as initial states for the shearing simulations. The next subsection investigates the variation in parameters in the shearing phase for two initial configurations of GB sand. In the second subsection, the results of shearing simulations for both types of sand for all initial configurations will be presented.

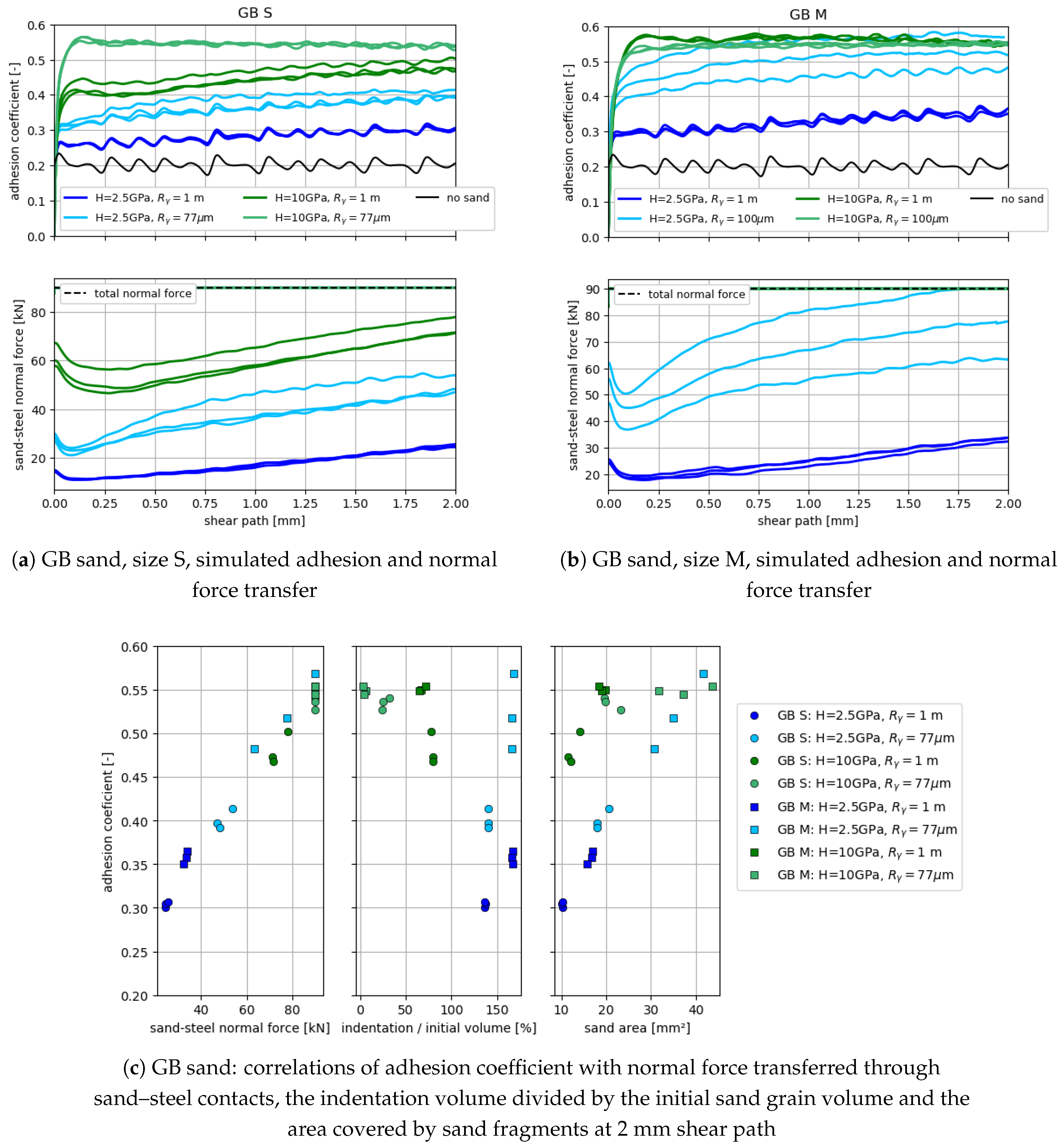
4.3.1. Parameter Variations in the Shearing Phase

For the shearing phase, the most influential parameters are expected to be the coefficients of friction between sand particles, ${\mu }_{SaSa}$, and between sand particles and steel, ${\mu }_{SaSt}$; see

Table 4. Variation in parameters in the shearing phase for GB sand.

Parameters	GB Sand
friction coefficient sand–steel ${\mu }_{SaSt}$ [-]	0.2, 0.5, 1.0
friction coefficient sand–sand ${\mu }_{SaSa}$ [-]	0.5, 1.0

. The friction coefficient for steel–steel contacts is always 0.2, as wet conditions are considered; see HPT test results in [51]. To study the effect of parameters during shearing, two initial configurations are chosen: GB S, $R_{\gamma }=77\mathsf{\mu }$m, $H=2.5$ GPa and $H=10$ GPa; see Figure 7a,b. In the case of $H=2.5$ GPa, the sand fragments indent deeper in the steel, resulting in contact between the two steel plates. In contrast, for $H=10$ GPa, steel indentation is much lower, and the steel plates are separated completely. Note that the case of fully separated steel surfaces, over a longer period of time, is very rare in practical wheel–rail sanding and could also lead to problems in train detection. However, in the chosen simulation setting, this case occurs.

For further analysis, it will be important to understand what proportion of the normal force of 90 kN is transferred through steel–steel and sand–steel contacts. Furthermore, the coefficient of mobilised friction in the different contact groups, steel–steel, sand–steel and sand–sand, will be important. Mobilised friction is calculated for each contact as the tangential force divided by the normal force and then averaged for each contact group, $m_F={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\displaystyle \frac{F_t^i}{F_n^i}}$. Thus, mobilised friction ranges between 0 (no tangential force transferred) and $\mu$ (meaning all contacts are sliding).

Figure 9 shows the simulation results for five combinations of friction coefficients. Figure 9a,b are structured as follows: The first subplot shows the adhesion coefficient over the shear path. The following two subplots have two y-axes. The second subplot shows, on the left y-axis, the coefficient of mobilised friction for steel–steel contacts and, on the right y-axis, the normal force transferred through steel–steel contacts. The third subplot shows the same information for the sand–steel contacts. In the fourth subplot, the coefficient of mobilised friction for sand–sand contacts can be seen. Also shown in Figure 9 are cuts through the initial and sheared samples. The considered friction coefficients are as follows: ${\mu }_{SaSa}=0.5$ in combination with ${\mu }_{SaSt}=0.2,0.5,1.0$ and additionally ${\mu }_{SaSa}=1.0$ in combination with ${\mu }_{SaSt}=0.5,1.0$.

It is easier to discuss Figure 9b first, as here the steel plates are separated and no steel–steel contacts occur. The simulated adhesion coefficients are similar for simulations with the same ${\mu }_{SaSt}$, while variations of ${\mu }_{SaSa}$ have little influence. For the lowest value of ${\mu }_{SaSt}=0.2$, the simulated adhesion is 0.23. Increasing ${\mu }_{SaSt}$ to 0.5 and 1.0 increases adhesion to 0.58 and values above 1, respectively. The sand–steel contacts transfer the complete normal load of 90 kN, and their mobilised friction (nearly all sand–steel contacts are sliding) is directly correlated with the adhesion values. In contrast, an increase in the mobilised friction values in sand–sand contacts for ${\mu }_{SaSa}=1.0$ results in little to no increase in the simulated adhesion values.

In all simulations with $H=10$ GPa, the simulated adhesion values are roughly 10% higher than the ${\mu }_{SaSt}$ friction coefficients. This could be caused by form closure effects introduced by the indentations or by the artificially introduced roughness from modelling the steel plates as a regular grid of spheres. This point will be addressed later. For visualisation, Figure 9d contains a cut through the initial and sheared samples. Indentations are relatively low due to the high hardness of 10 GPa. The separation of the steel plates remains during the shearing.

In the simulations shown in Figure 9a, steel–steel contacts are present, and the simulated adhesion values are mostly lower than in the case without steel–steel contacts. In all cases, steel–steel contacts are fully sliding as $m_F=0.2$. Mobilised friction values for both sand–steel and sand–sand contacts are similar to the case without steel–steel contacts. The applied normal load is constant, and as the normal force transferred through steel–steel contacts decreases with increasing shear path, it increases for sand–steel contacts. In general, simulated adhesion values are determined by the mobilised friction values between steel–steel and sand–steel contacts together with the fraction of normal force transferred in both contact groups. In all cases with steel–steel contacts, the transfer of normal force through steel–steel contacts reduces the simulated adhesion values in comparison to the case without steel–steel contact. Again, Figure 9c shows the cut through the initial and sheared sample for $H=2.5$ GPa. Due to the lower hardness, indentations are much larger compared to Figure 9d. What is more difficult to see might be the increase in sand–steel contacts/contact area during shearing, which causes the increase in simulated adhesion over the shear path.

In cases where the crushed sand grain fully separates the steel plates, as shown in Figure 9b, the reason for the adhesion coefficients being higher than the ${\mu }_{SaSt}$ friction coefficients needs to be found. Possible reasons would be form closure effects resulting from the indentations or the artificially introduced roughness from modelling the steel plates. For this investigation, the previous simulation of ${\mu }_{SaSa}={\mu }_{SaSt}=0.5$ and $H=10$ GPa is compared to a new simulation of ${\mu }_{SaSa}={\mu }_{SaSt}=0.5$ where the steel plates are undeformable, meaning that no indentations occur. From the results shown in Figure 10, it is quite clear that the artificial roughness of the steel plate causes the observed increase in adhesion above ${\mu }_{SaSt}$ values, and form closure effects are negligible. The roughness of wheel and rail specimens in the experiment and their modelling in the simulation need further investigation.

In the simulations conducted, adhesion ranged between 0.23 and 1.1 for the two initial configurations considered and the different values of coefficients of friction for ${\mu }_{SaSa}$ and ${\mu }_{SaSt}$. For both initial configurations, the simulated adhesion increased considerably with increasing ${\mu }_{SaSt}$ and slightly with increasing ${\mu }_{SaSa}$. To choose coefficients of friction for further simulations, a brief comparison of measured adhesion is performed, as shown in Figure 4b. The parameter combination closest to the experimental results is ${\mu }_{SaSt}=0.5$ and ${\mu }_{SaSa}=0.5$, and thus, these values will be used from now on.

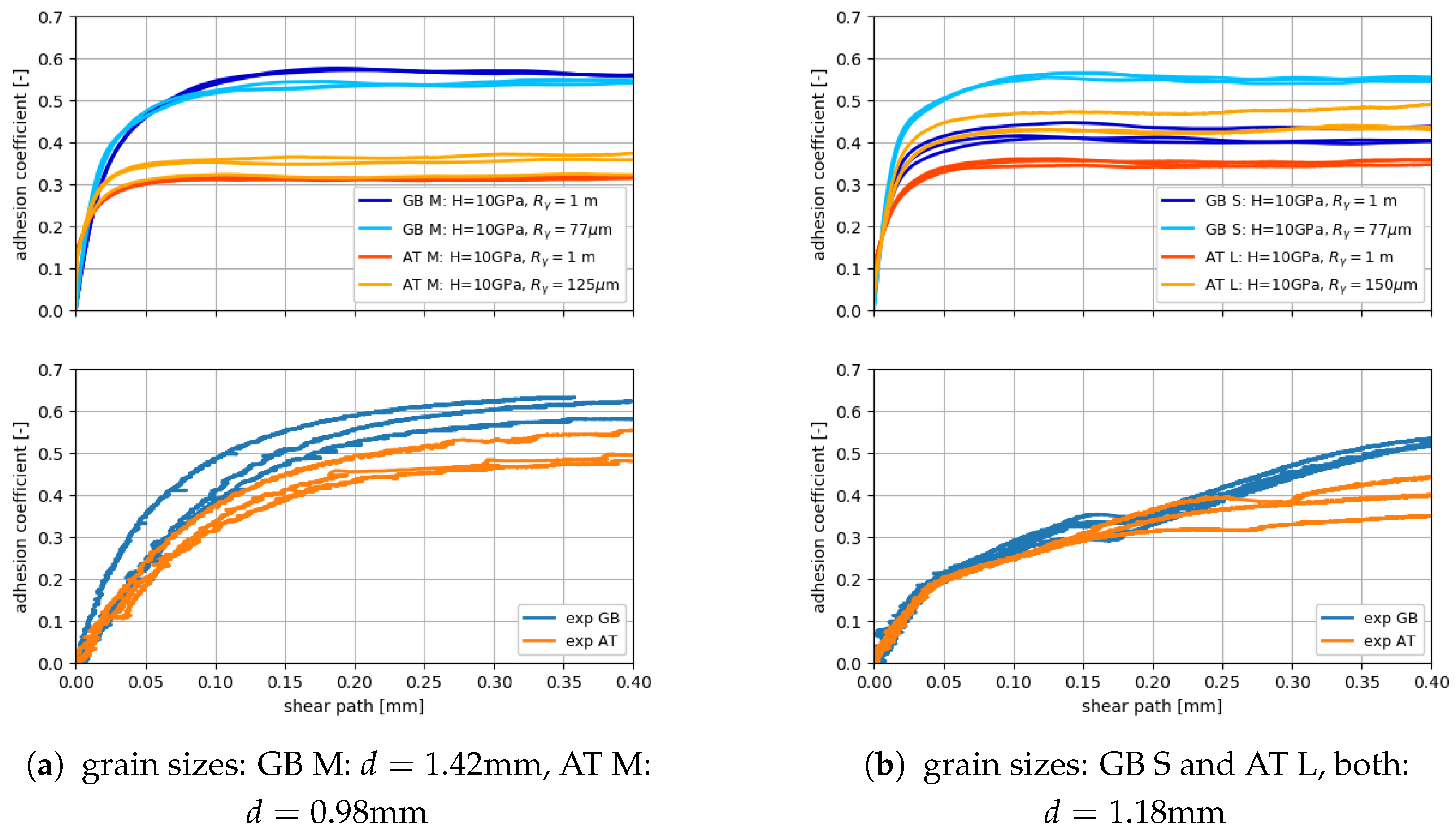
4.3.2. Shearing of GB and AT Sand

In this subsection, all results from the crushing simulations in Section 4.2 will now be sheared, and the influence on simulated adhesion will be studied; see Table 3. In all shearing simulations, friction coefficients between sand and steel particles are set as ${\mu }_{SaSt}=0.5$. Sand–sand friction coefficients remain unchanged from their values in [47]: GB sand ${\mu }_{SaSa}=0.5$ and AT sand ${\mu }_{SaSa}=0.7$.

Sand grain crushing, fragment spread and the resulting indentation of steel plates naturally involve a certain amount of randomness. The DEM simulations also involve randomness: after each breakage event, the broken particle is replaced by a set of fragment particles, which are rotated randomly. Therefore, for each parameter combination in Section 4.2 of sand grain size, hardness and $R_{\gamma }$, repeated simulations of sand grain crushing and shearing are conducted.

The simulation results for GB sand are shown in Figure 11. Here, Figure 11a,b show simulated adhesion and normal force transferred through sand–steel contacts over the shear path of 2 mm for both initial sand grain sizes. Figure 11c shows correlations of the adhesion coefficient with the normal force transferred through sand–steel contacts, the indentation volume divided by the initial sand grain volume and the area covered by sand fragments at the end of the simulations at 2 mm shear path. For the considered initial configurations, the adhesion coefficient ranges between 0.25 and 0.55 over the shear path of 2 mm. The main difference between the initial configurations is the amount of applied normal force transferred through sand–steel contacts. In Figure 11c, a strong linear correlation is seen between this normal force and the adhesion coefficient for all considered simulations. How normal force is transferred depends on the steel hardness H, the size of the sand grain and the spread of fragments during grain crushing, influenced by $R_{\gamma }$.

All simulations with $H=2.5$ GPa, with blue curves and symbols, show a higher relative indentation volume; see Figure 11c. Note that the relative indentation volume goes up to 165% because the crushed sand fragments form a polydisperse sphere packing; thus, the volume is higher than that of the initial sand grain. At the shear path of 2 mm, the area covered by sand is almost independent of H but strongly dependent on $R_{\gamma }$ and the initial sand grain size. Thus, for simulations with $H=2.5$ GPa and $R_{\gamma }=1$ m (dark blue), one sand cluster forms, with low values of sand-covered area and high relative indentation volumes. This leads to massive contact between the steel plates and low amounts of normal load transfer through sand–steel contacts, resulting in low adhesion values. As the larger sand grains have a higher sand-covered area, here adhesion is slightly higher than for the smaller grain size.

In simulations with $H=2.5$ GPa and low $R_{\gamma }$ values (light blue), the relative indentation volume is high, but there is more fragmentation spread and thus a larger sand-covered area. Depending on the initial sand grain size, this allows for a higher amount of normal force transferred by sand–steel contacts and results in increased adhesion coefficients compared to the previous case. These simulations show a higher variation in adhesion, which naturally stems from the possibility of fragment spread. For a small initial grain size, the adhesion values reach up to 0.4, while for the medium grain size, two out of three simulations reach (nearly) maximal adhesion values and (nearly) separate the metal surfaces.

The simulations of the harder steel plates, $H=10$ GPa, with green curves and symbols, show full separation of the steel surfaces and maximal adhesion values around 0.55 for medium-sized grains and for small grain sizes with low $R_{\gamma }$ values. The higher hardness leads to clearly reduced relative indentation volumes, while the sand-covered area is almost independent of H and depends only on $R_{\gamma }$ and the initial sand grain size. It can be seen that sand-covered areas above 18 ${\mathrm{mm}}^2$ combined with low relative indentation volume leads to steel surface separation; i.e., the entire normal force is transferred through sand–steel contacts and results in adhesion values around 0.55. For small initial sand grain size and $R_{\gamma }=1$ m, the sand clusters being formed have low values of sand-covered area, and despite the low relative indentation volume, steel surfaces are not separated. The resulting adhesion values range between 0.45 and 0.5 at the end of the simulation.

The same evaluation for AT sand can be found in Figure 12 for both initial sand grain sizes M and L. The simulated adhesion values for AT sand range between 0.22 and 0.52 and are in general lower than for GB sand. The lower adhesion values are accompanied by lower values of normal force transferred by sand–steel contacts. This force and simulated adhesion coefficients show, again, a strong linear correlation; see Figure 12c.

The simulations of softer steel plates, $H=2.5$ GPa (blue curves and markers), have high relative indentation volumes around 140%. As AT sand is smaller than GB sand and shows less fragment spread, the sand-covered area is clearly lower than for GB sand. It increases with sand grain size and decreasing $R_{\gamma }$ values. The combination of high relative indentation volume and low sand-covered area leads to a low amount of normal force being transferred through sand–steel contacts. This results in adhesion values below 0.32.

The simulations with $H=10$ GPa (green curves and markers) clearly have lower relative indentation volumes at around 80%. The sand-covered area shows the same dependencies on initial sand grain size and $R_{\gamma }$ as before, but values are often slightly higher for the harder steel plates than for the softer ones. In this combination, the amount of normal force transferred through sand–steel contacts is higher and results in higher adhesion values. As the relative indentation volume is nearly constant, adhesion increases with increasing sand-covered area.

With this simulation model, high adhesion values can be achieved with higher steel hardness, larger sand grains and some spread of fragments during crushing. Maximal adhesion values occur for fully separated steel plates.

4.4. Sanded HPT Test: Comparing Results for AT and GB Sand to Experiments

In this subsection, simulation results will be compared with the HPT tests presented in Section 2. A quantitative comparison is not possible for several reasons. The tests presented in Figure 3c were conducted using a different type of steel for the upper specimen. The steel discs were run in using a defined procedure, leaving the hardness of the steel plates unknown. The simulations contain only one sand grain in a computational domain of 10 ${\mathrm{mm}}^2$, which corresponds roughly to the contact area in a wheel–rail contact. From the simulations, it was seen that the coefficient of friction between sand and steel plates has a strong influence on simulated adhesion; see Figure 9. Also, the sand-covered area strongly influences simulated adhesion; see Figure 11 and Figure 12. In the DEM model, this value is strongly influenced by parameters $R_{\gamma },V_b$; see [47] for a discussion of problems with unique parametrisation.

Despite the described problems, simulation results can be compared qualitatively to experimental ones. From the simulations, high steel hardness, $H=10$ GPa, is considered, as the maximal indentations are closer to the experimental ones. Measured and simulated adhesion is plotted in Figure 13 over a shear path of 0.4 mm. At first, medium-sized GB and AT sands are compared, showing that AT grains are smaller than GB grains; see Figure 13a. The simulated adhesion curves increase very fast to their final values, which is in contrast to the experiments. For GB sand, parameter $R_{\gamma }$ has little influence, as the steel surfaces are fully separated due to the initial sand grain size. For AT sand, the steel surfaces are in contact, and higher fragment spread results in higher adhesion values. The final values of simulated adhesion are influenced by the previously mentioned factors. In both measurements and simulations, GB has higher adhesion values than AT sand. From the simulation evaluation in the previous section, this is related to the larger grain size of GB sand and higher sand-covered area due to sand grain size and fragment spread.

The HPT test results using equal-size sand grains for GB and AT are shown in Figure 13b for both measured and simulated adhesion. Here, the difference in initial slope between simulations and experiments is even higher. GB sand with low $R_{\gamma }=77\mathsf{\mu }$m shows high fragment spread, and steel surfaces are fully separated, resulting in high adhesion values. GB sand with $R_{\gamma }=1$ m results in similar adhesion values as AT sand with $R_{\gamma }=150\mathsf{\mu }$m. This is caused by other parameters in the simulations influencing fragment spread, $V_b,u_{SaSa}$, which result in similar indentation volume and sand-covered area. AT sand with $R_{\gamma }=1$ m clearly shows the highest indentation and lowest fragment spread, which result in the lowest adhesion values. It is helpful to compare the observed fragment spread and indentation depth in the experiments, as shown in Figure 5, with those in the simulations; see Figure 7 and Figure 8. For GB sand, the formation of larger clusters resulting in deep indentations was visible for two to three sand grains per test. The remaining grains formed smaller clusters with shallow indentations or showed very high fragment spread. Thus, the simulation results with $R_{\gamma }=1$ m are not realistic for GB sand. For AT sand, nearly all sand grains formed clusters in the experiments. In the simulations, both values of $R_{\gamma }$ resulted in sand cluster formation, which differed in their size and indentation depth. Thus, for GB sand, most realistic simulations are with high fragment spread, $R_{\gamma }=77\mathsf{\mu }$m, which yield clearly higher adhesion values than simulations of AT sand with both $R_{\gamma }$ values. To summarise, also in the case of the same particle size in both measurements and simulations, GB has higher adhesion values than AT sand.

Conducting crushing simulations with several grains of varying $R_{\gamma }$ would be an interesting point for future work, especially for GB sand.

5. Conclusions and Outlook

The combination of experimental work and DEM modelling allows to study the mechanisms that increase adhesion in sanded wheel–rail contacts under wet conditions. Experimental works on both GB and AT sand included the following: wet HPT tests showing differences in adhesion increase [51], single-grain crushing tests showing differences in sand fragment spread [12], and high-loading tests with 900 MPa contact pressure showing the formations of solidified clusters of sand powder which indent into the metal surfaces for both sand types [12]. In modelling, first, a DEM model was developed for the crushing tests that could reproduce the observed differences in fragment spread and the formation of sand fragment clusters under high load [47]. Second, this model was extended to allow surface indentations, i.e., the formed sand clusters indenting into the steel surface [48].

In continuation of these works, the present study now focuses on adhesion increase due to sanding in HPT tests under wet conditions.

Mechanisms of adhesion increase:

• The coefficient of friction between sand and steel strongly influences the maximal simulated adhesion.
• Associated with this, the higher the amount of normal force being transferred through sand–steel contacts, the higher the simulated adhesion (assuming that the coefficient of friction is higher for sand–steel contacts than for wet steel–steel contacts). A maximal value is reached for separated steel surfaces; thus, the complete normal force is transferred through sand–steel contacts.
• Larger sizes of the initial sand grain and higher fragment spread both result in a larger area covered by sand fragments.
• Higher steel hardness results in reduced indentation.
• Both effects lead to a higher amount of normal force being transferred through sand–steel contacts and thus promote separation of steel surfaces.
• Full surface separation happens very rarely in practical wheel–rail sanding and could lead to problems in train detection.

Results of comparing simulations with experiments:

• Two measurements of wet HPT tests are available: First, average-sized initial grains are used for GB and AT sands. Second, the same initial grain size is used. In both cases, GB sand shows higher measured adhesion than AT sand.
• A comparison between simulations and experiments is conducted qualitatively. For both cases, simulated adhesion is higher for GB sand. Thus, simulation and experimental results are in qualitative agreement.

In the developed DEM model, several points would benefit from additional measurements/modelling work. In general, the parametrisation of the model conducted in [12] was not unique. The coefficient of friction between sand fragments and steel surfaces has a high influence on simulated adhesion and would be interesting to measure. Indeed, first steps in this direction have already been taken using mini shear box tests. The obtained results for GB sand will be shown in [65].

In this work, only the crushing and shearing of one single sand grain is simulated. The DEM model can be used to simulate the crushing and shearing of several sand grains, with the limitation of high computational times. A speed up of the model would be needed for this purpose.

Currently, the sand fragments are modelled as spheres with blocked rotation. A comparison between simulations of free rotating spheres and spheres with blocked rotation will be discussed in [65]. These two cases of blocked/free rotation present the limiting cases. It would probably be most realistic to equip the spheres with a rolling resistance. This comes at the cost of an additional parameter which will make parametrisation of the model more difficult. Future work should involve the modelling of steel surfaces as a regular hexagonal grid of spheres. This would introduce a kind of artificial roughness, which could be compared to the roughness of the steel discs in use. In the current model, surface indentation is only considered during the application of the normal load. An extension to the shearing phase of the simulation might be of interest.

The conducted research could be a first step towards the optimisation of future sanding systems by addressing several open questions: Which size (distribution) of sand particles is a good trade-off between adhesion increase and wear/damage of wheel and rail? What fragment spread should used sand particles have? How much sand should be applied? As low-adhesion conditions are frequently caused by leaf layers, an extension of the model to include this case remains a task for future work.