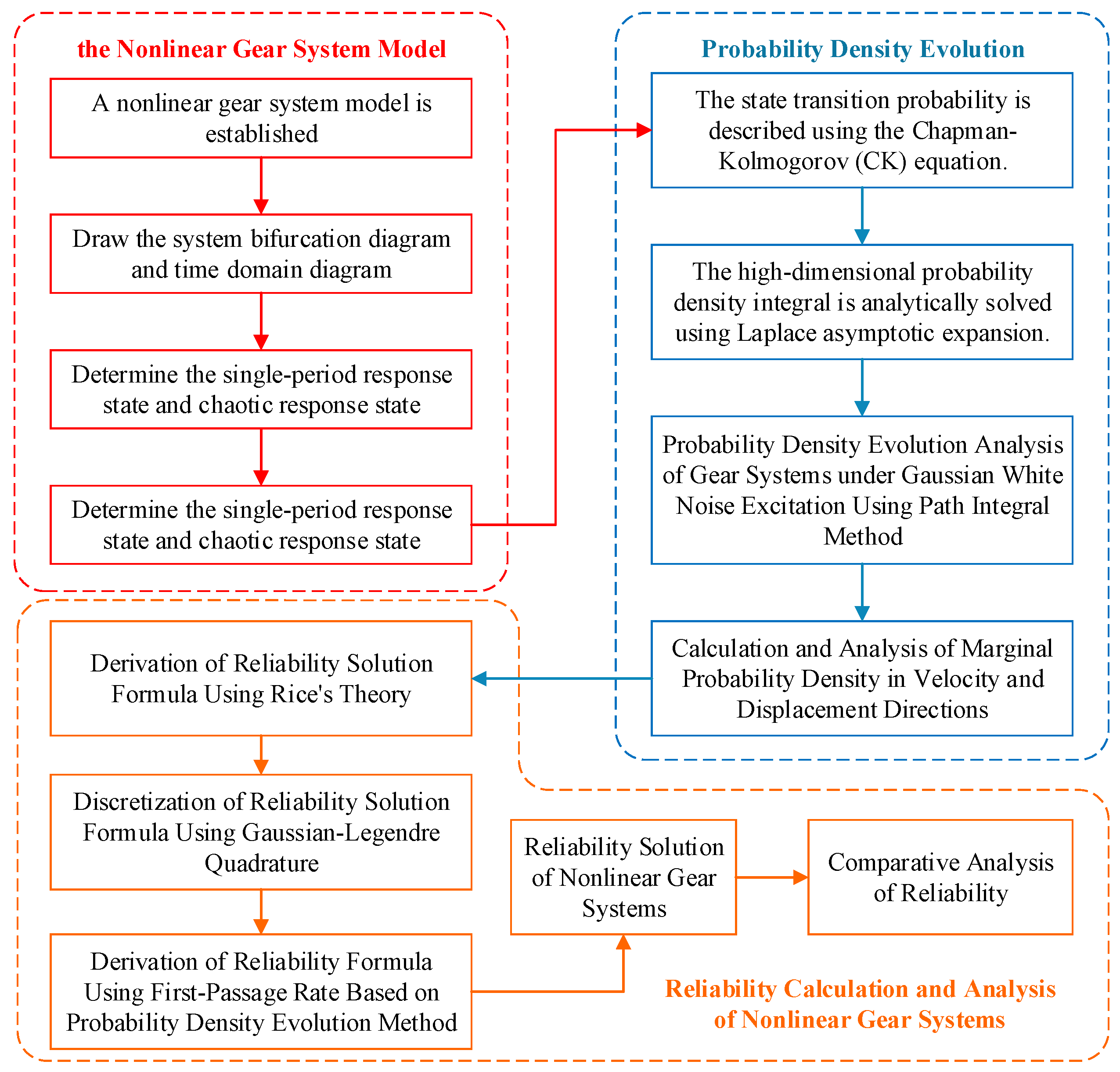
Probability Density Evolution and Reliability Analysis of Gear Transmission Systems Based on the Path Integration Method
Abstract
1. Introduction
2. Evolution Process of Probability Density Based on the Laplace Asymptotic Expansion Method
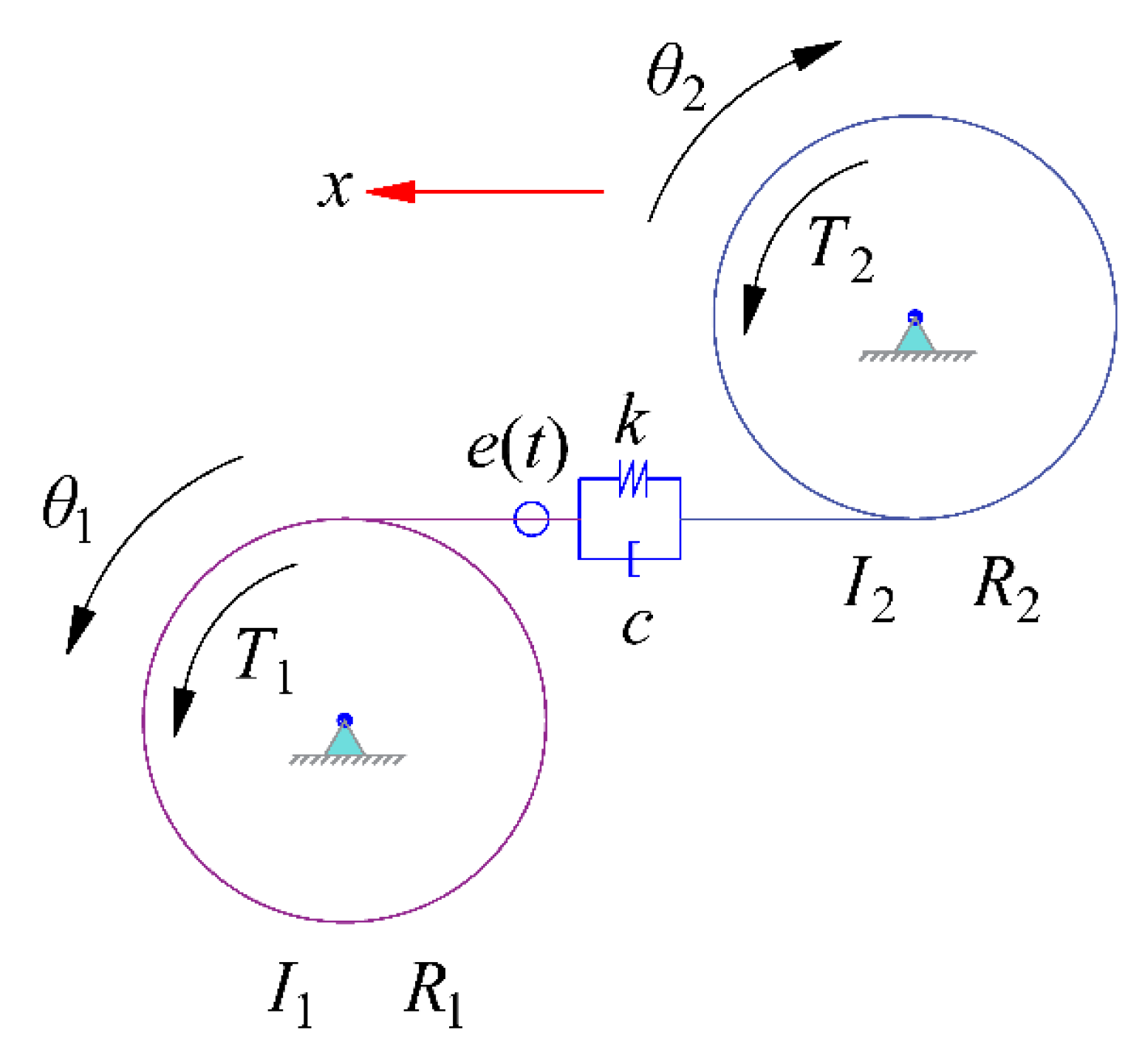
2.1. Establishment of the Dynamic Model of the Nonlinear Gear Systems
2.2. Solution of Probability Density Evolution
2.2.1. Markov Processes
2.2.2. Transition Probability Density Equation
2.3. Laplace Asymptotic Expansion Method
2.3.1. Laplace Asymptotic Expansion Method for Solving Joint Probability Density
2.3.2. Edge Probability Density
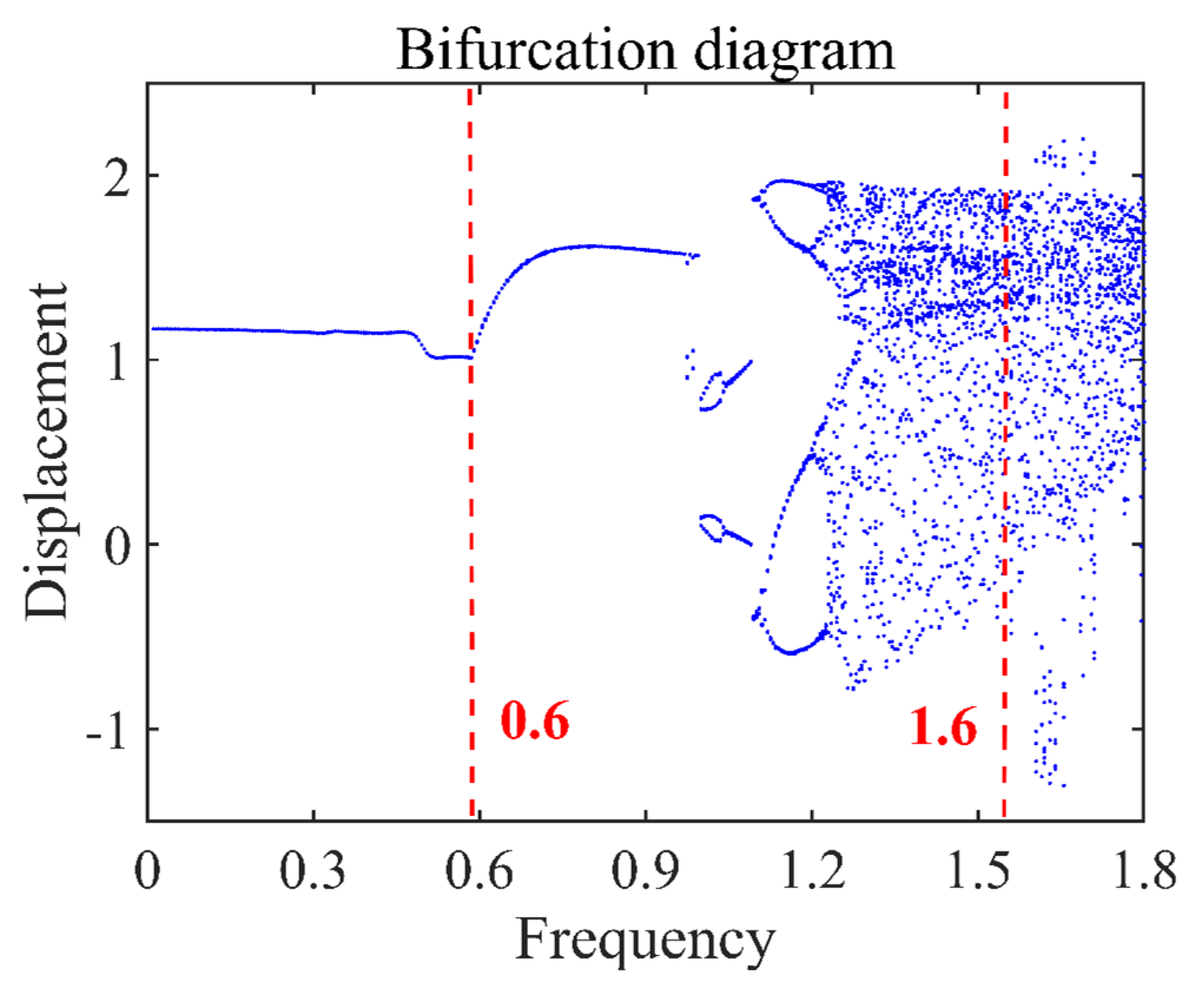
2.4. Evolution Process of Probability Density Under Different Response States
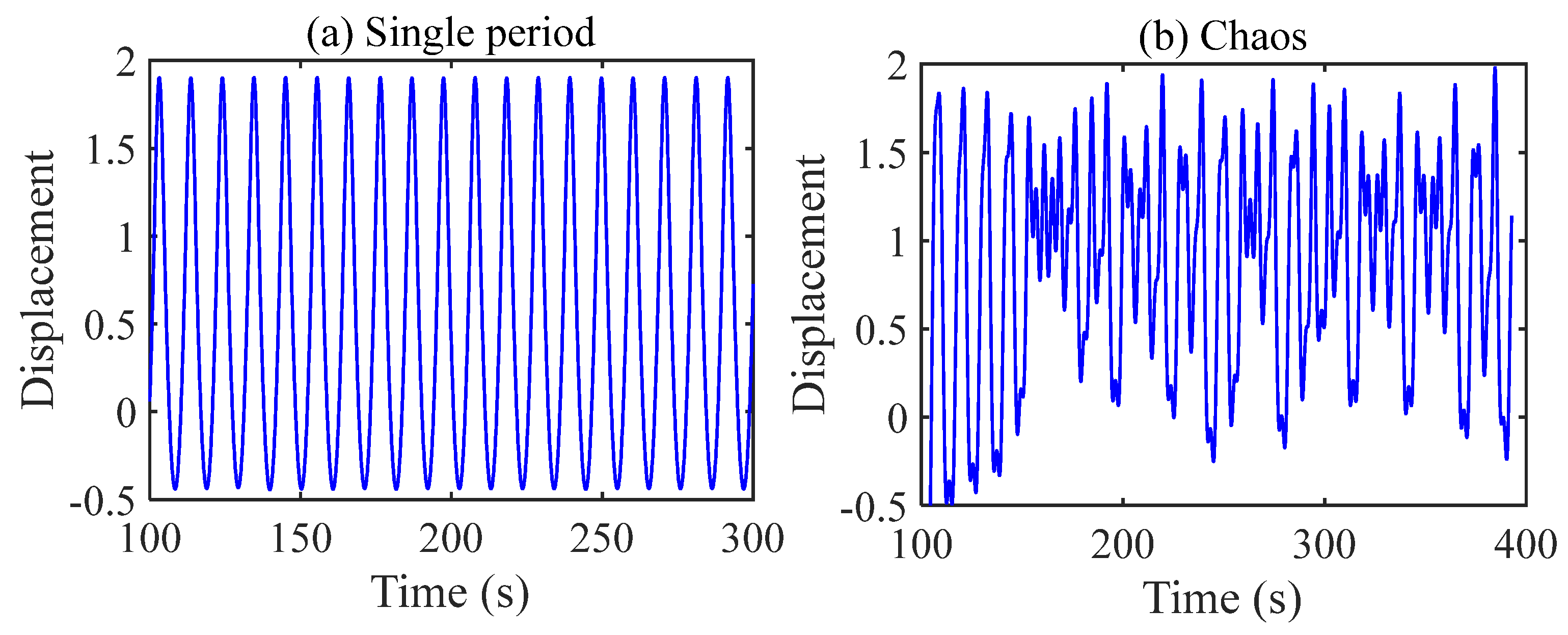
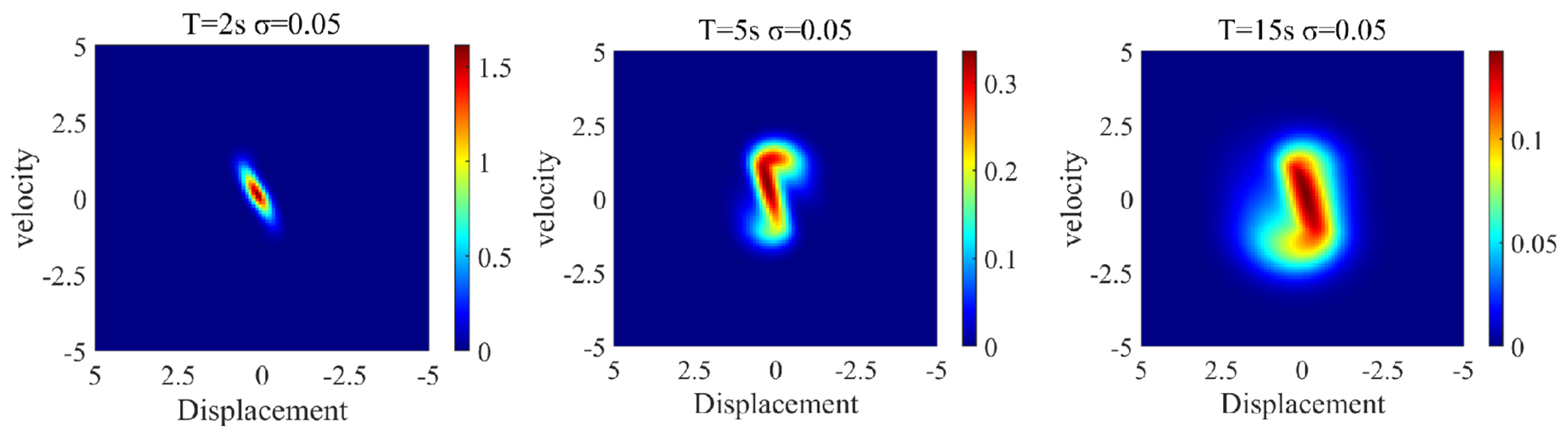
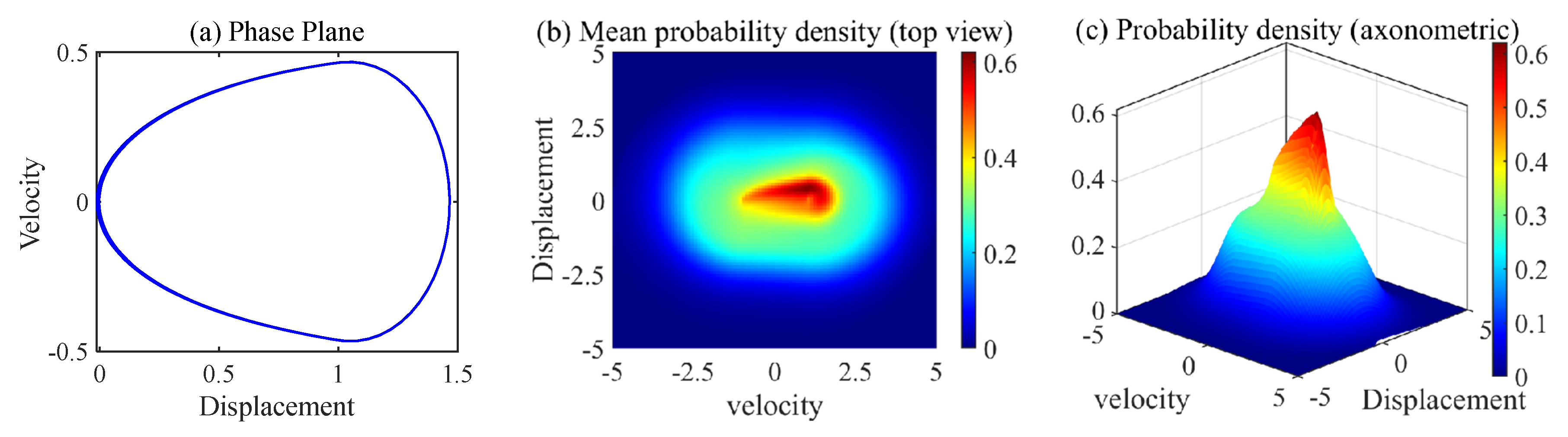
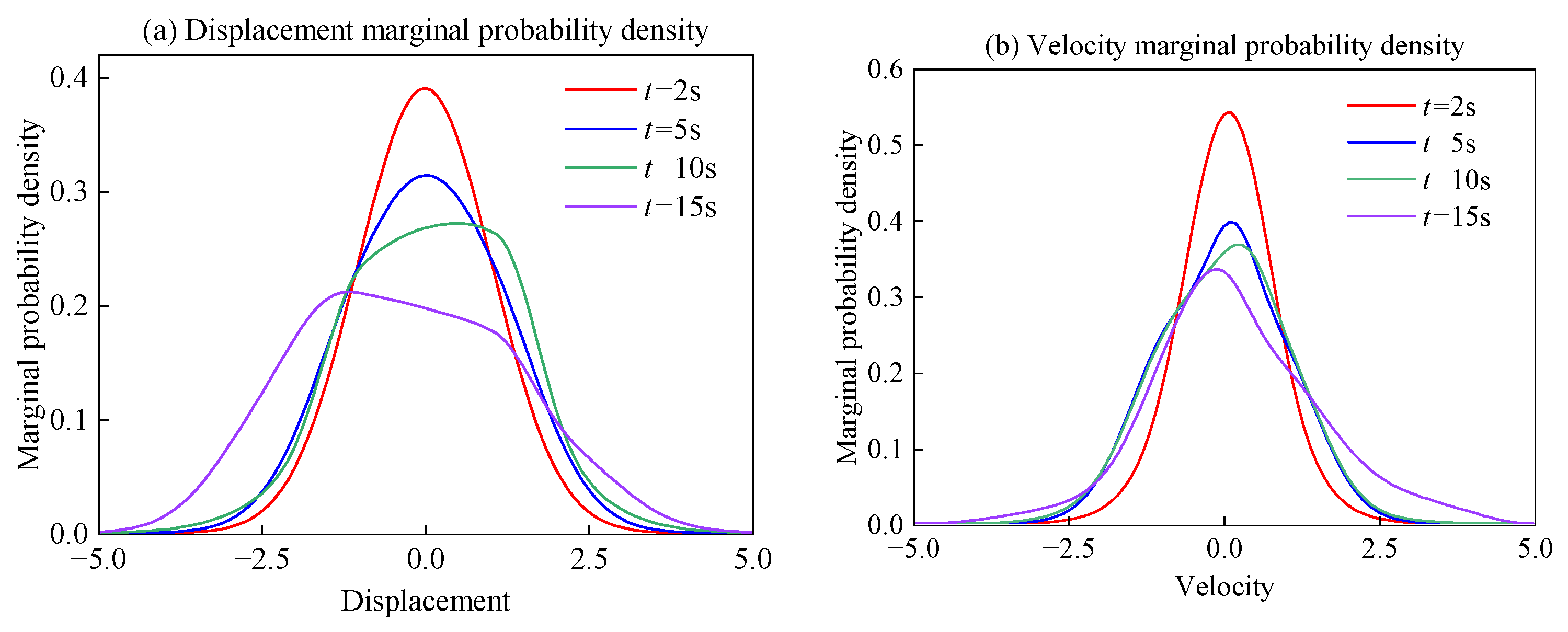
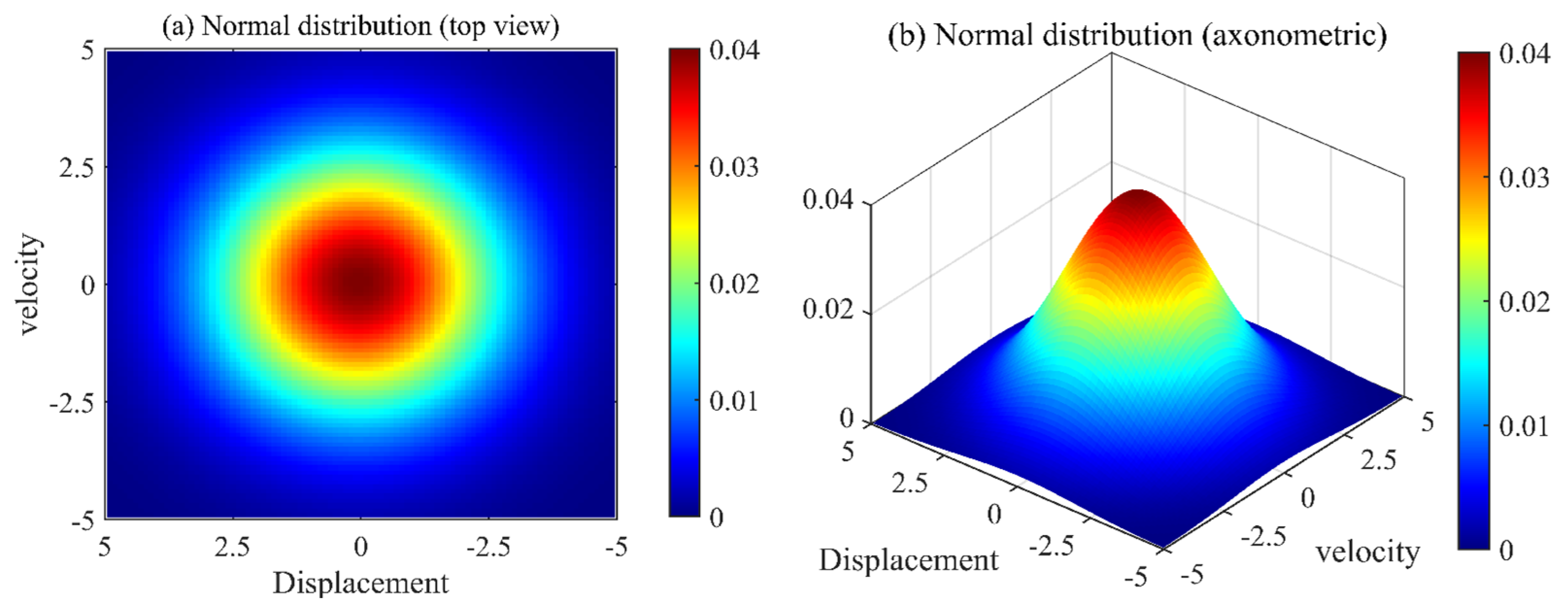
2.4.1. Probability Density Evolution Analysis of Nonlinear Gear Systems Under Periodic Response
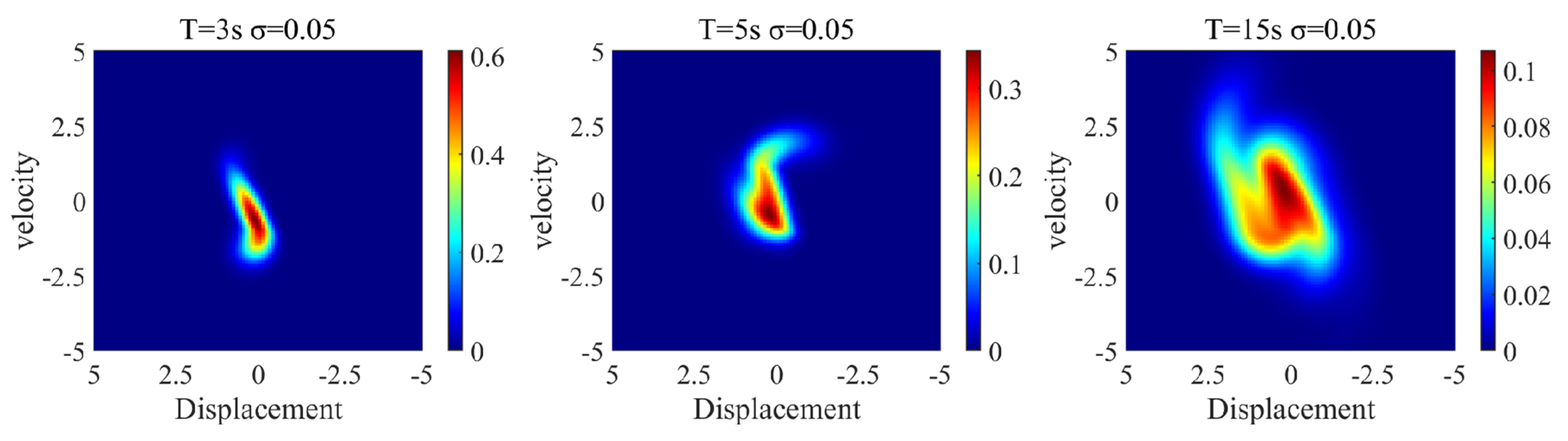
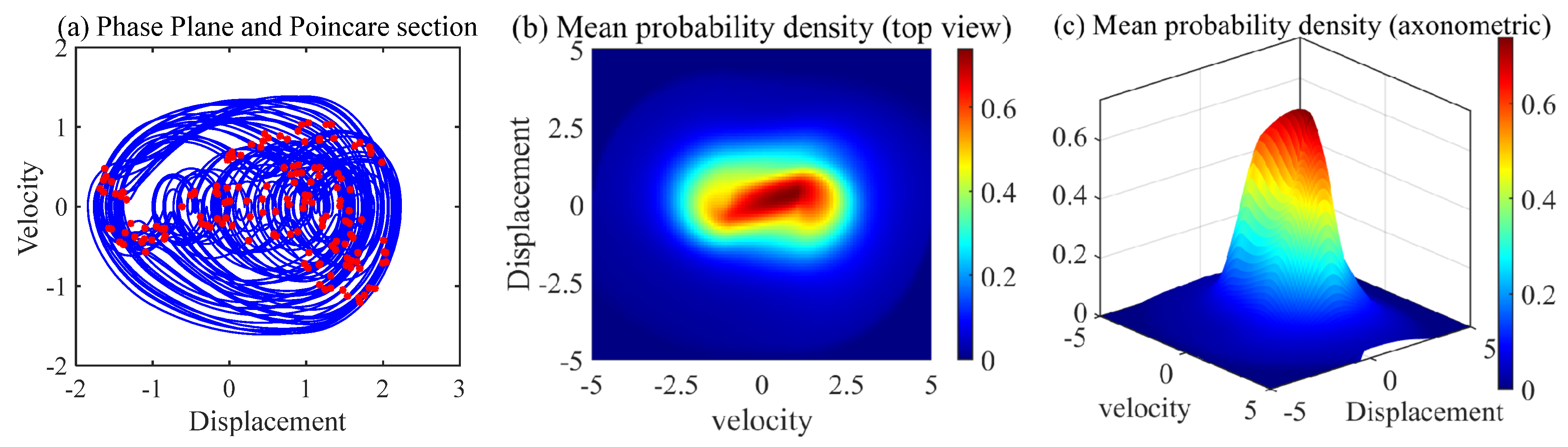
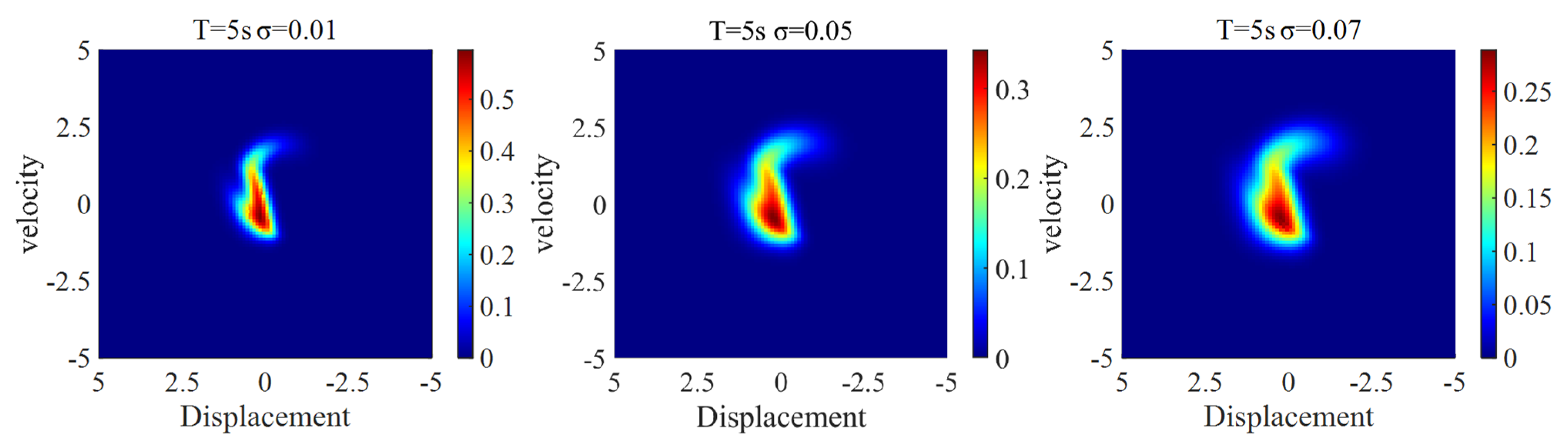
2.4.2. Probability Density Evolution of Nonlinear Gear Transmission Systems Under Chaotic Response
3. Reliability Analysis of Nonlinear Gear Systems
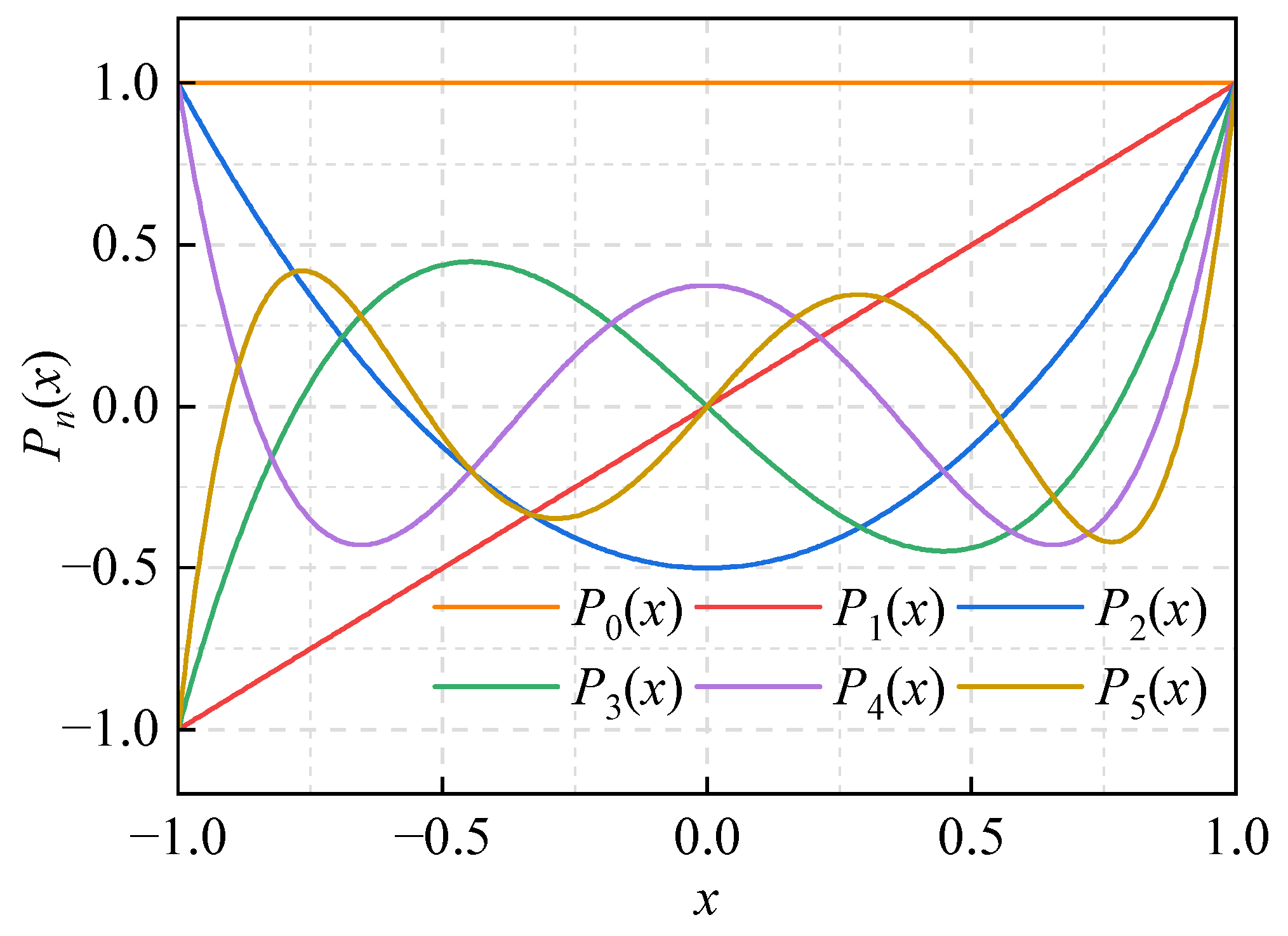
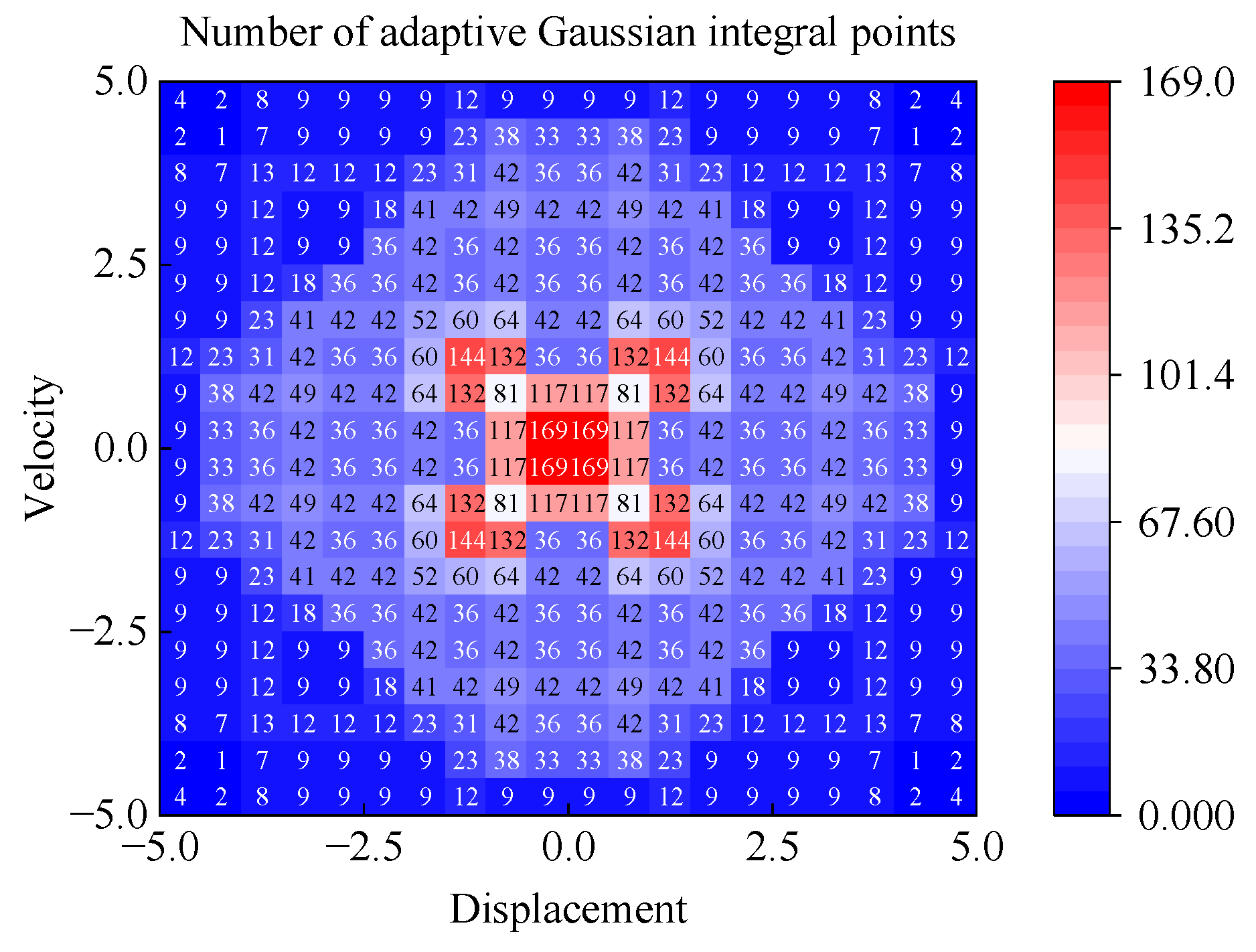
3.1. Adaptive Gauss–Legendre Method
3.1.1. Gauss–Legendre Product Formula
3.1.2. Adaptive Gauss–Legendre Integration Method
3.1.3. Two-Dimensional Adaptive Gauss–Legendre Integration Method
3.2. Reliability Indicators Based on Average Crossing Rate
3.2.1. Rice’s Theory and Average Crossing Rate
3.2.2. Reliability Theory and Reliability Indicators
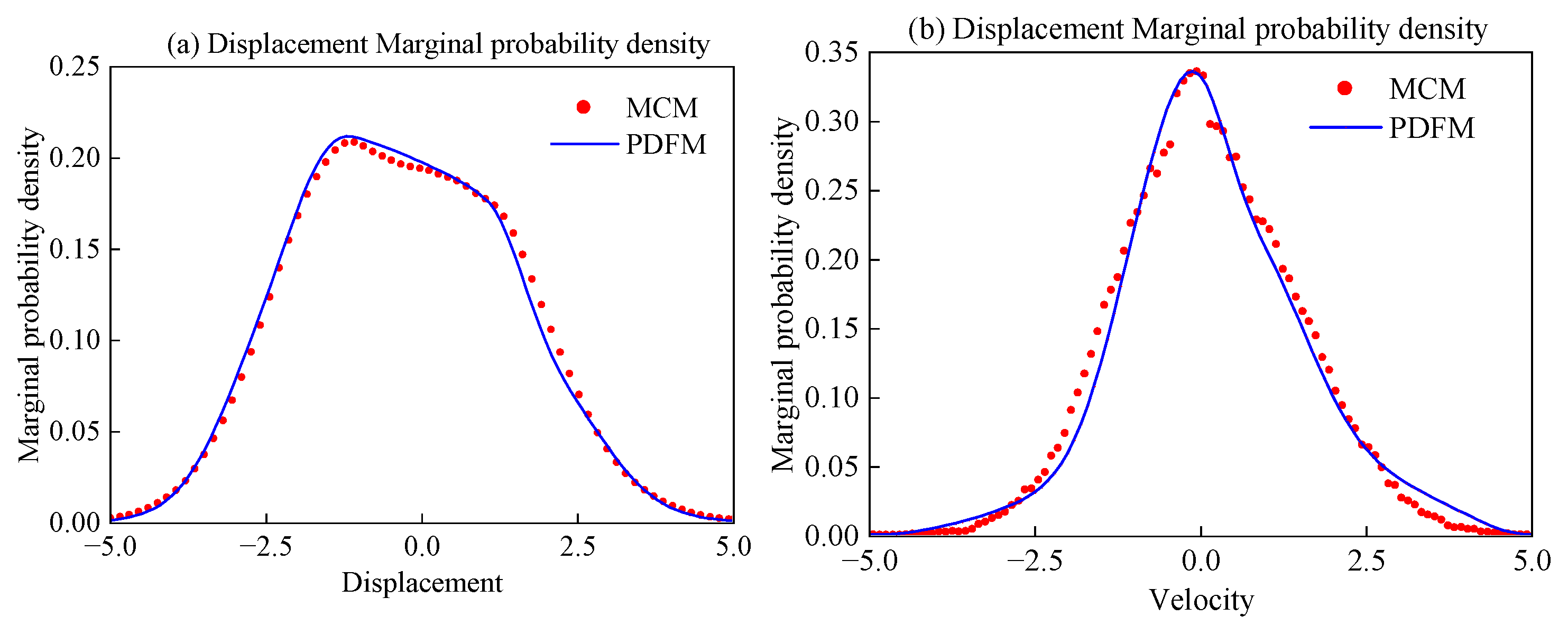
3.3. Gear Reliability Under Different Response States Based on the Evolution of Probability Density
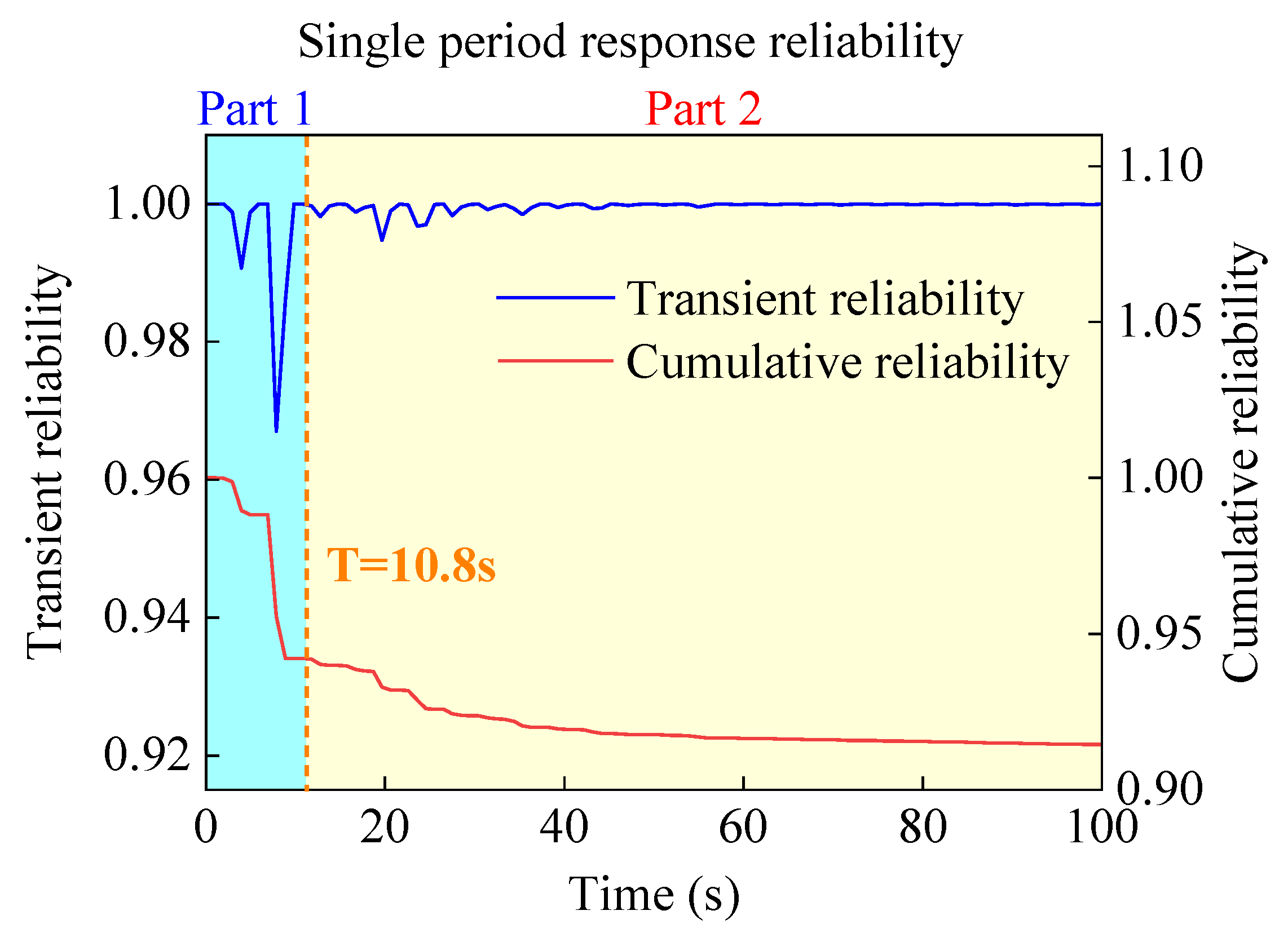
3.3.1. Nonlinear Gear Transmission Systems with Periodic Response
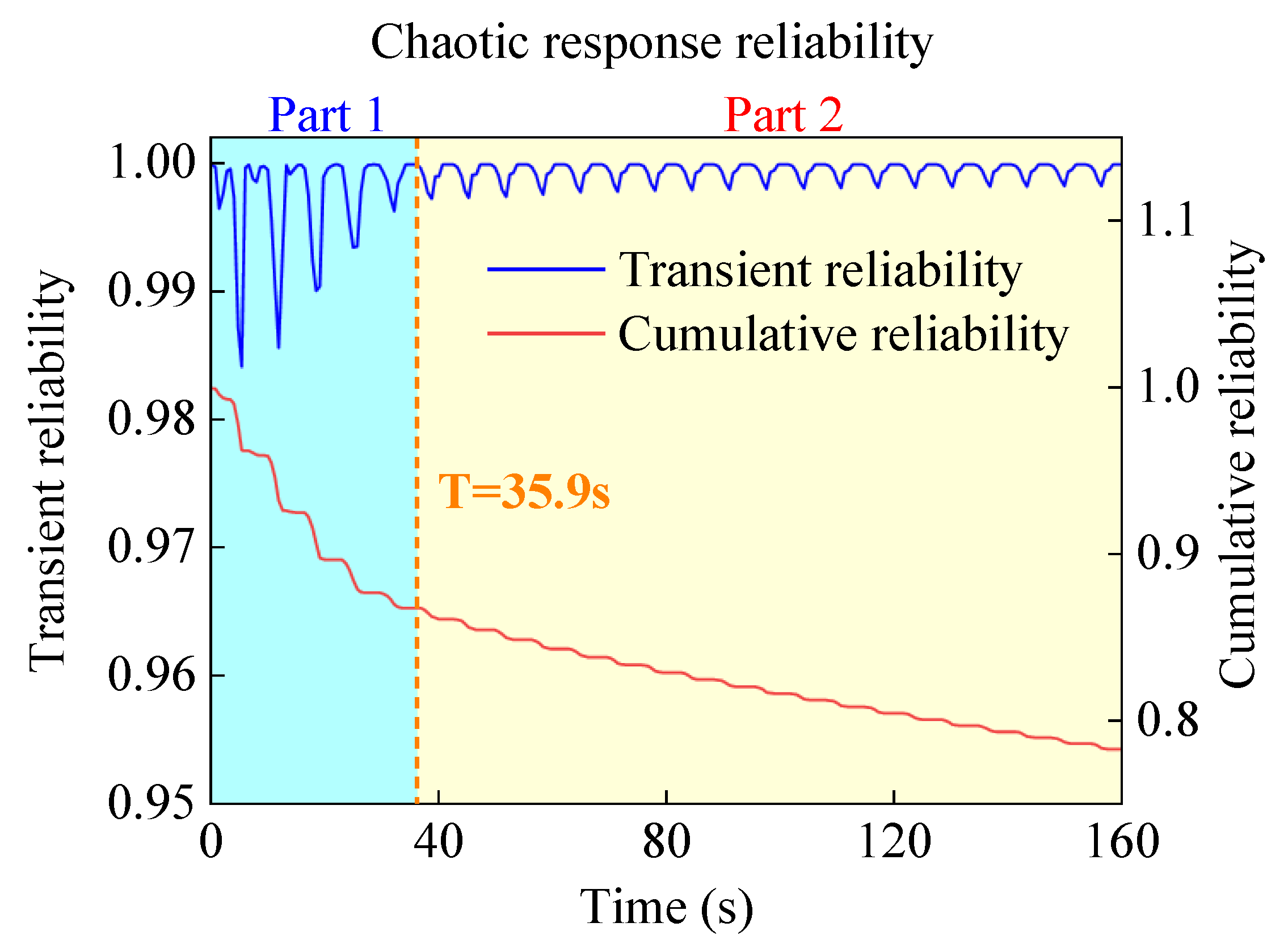
3.3.2. Nonlinear Gear Transmission Systems with Chaotic Responses
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, T.; Zhu, C.; Chen, J.; Liu, H. A review on gear scuffing studies: Theories, experiments and design. Tribol. Int. 2024, 196, 109741. [Google Scholar] [CrossRef]
- Tian, X.; Sun, Y.; Mu, W.; Xia, L.; Han, J. High-Speed and Low-Noise Gear Finishing by Gear Grinding and Honing: A Review. Chin. J. Mech. Eng. 2024, 37, 127. [Google Scholar] [CrossRef]
- Tian, H.; Ma, H.; Peng, Z.; Zhu, J.; Zhao, S.; Zhang, X. Study on rigid-flexible coupling modeling of planetary gear systems: Incorporation of the pass effect and random excitations. Mech. Mach. Theory 2024, 201, 105745. [Google Scholar] [CrossRef]
- Di Paola, M.; Santoro, R. Path integral solution for non-linear system enforced by Poisson white noise. Probabilistic Eng. Mech. 2008, 23, 164–169. [Google Scholar] [CrossRef]
- Ma, X.; Xu, F.; Liu, Z. A method for evaluation of the probability density function of white noise filtered non-Gaussian stochastic process. Mech. Syst. Signal Process. 2024, 211, 111242. [Google Scholar] [CrossRef]
- Mao, J.; Cao, Y.; Yang, J. A transmission error analysis method using Monte Carlo simulation. Adv. Sci. Lett. 2011, 4, 2474–2477. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, F. Statistical modification analysis of helical planetary gears based on response surface method and Monte Carlo simulation. Chin. J. Mech. Eng. 2015, 28, 1194–1203. [Google Scholar] [CrossRef]
- Lu, N.; Li, Y.F.; Huang, H.Z.; Mi, J.; Niazi, S.G. AGP-MCS+ D: An active learning reliability analysis method combining dependent Gaussian process and Monte Carlo simulation. Reliab. Eng. Syst. Saf. 2023, 240, 109541. [Google Scholar] [CrossRef]
- Sun, Z.; Yu, T.; Cui, W.; Song, B. Reliability analysis for close position accuracy of gear door mechanism based on importance sampling. In Proceedings of the 2011 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering, Xi’an, China, 17–19 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 168–172. [Google Scholar]
- Tang, Y.; Lu, H.; Zhu, Z.; Shi, Z.; Xu, B. Performance reliability evaluation of high-pressure internal gear pump. Qual. Reliab. Eng. Int. 2024, 40, 3465–3486. [Google Scholar] [CrossRef]
- Abdullatif, F.; Wang, D. Acceleration of source convergence in Monte Carlo criticality calculation with CMDF schemes. In Proceedings of the International Conference on Physics of Reactors, Pittsburgh, PA, USA, 15–20 May 2022; pp. 3479–3488. [Google Scholar]
- Lu, Y.; Lu, Z.; Feng, K.; Zhang, X. Meta model-based importance sampling combined with adaptive Kriging method for estimating failure probability function. Aerosp. Sci. Technol. 2024, 151, 109260. [Google Scholar] [CrossRef]
- Cui, D.; Wang, G.; Lu, Y.; Sun, K. Reliability design and optimization of the planetary gear by a GA based on the DEM and Kriging model. Reliab. Eng. Syst. Saf. 2020, 203, 107074. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.; Li, X.; Ren, Y. Global optimization of reliability design for large ball mill gear transmission based on the Kriging model and genetic algorithm. Mech. Mach. Theory 2013, 69, 321–336. [Google Scholar] [CrossRef]
- Qian, H.M.; Huang, T.; Wei, J.; Huang, H.-Z. Active learning strategy-based reliability assessment on the wear of spur gears. J. Mech. Sci. Technol. 2023, 37, 6467–6476. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, Y.; Zhang, R.; Zhang, P. Time-dependent reliability of spur gear system based on gradually wear process. Eksploat. I Niezawodn. Maint. Reliab. 2018, 20, 207–218. [Google Scholar] [CrossRef]
- Liang, M.; Wang, Y.; Zhao, T. Optimization on nonlinear dynamics of gear rattle in automotive transmission system. Shock Vib. 2019, 2019, 4056204. [Google Scholar] [CrossRef]
- Swain, S. Handbook of stochastic methods for physics, chemistry and the natural sciences. Opt. Acta Int. J. Opt. 1984, 31, 977–978. [Google Scholar] [CrossRef]
- Elgin, J. The Fokker-Planck equation: Methods of solution and applications. Opt. Acta Int. J. Opt. 1984, 31, 1206–1207. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhao, Y.; Li, P. A novel decoupled time-variant reliability-based design optimization approach by improved extreme value moment method. Reliab. Eng. Syst. Saf. 2023, 229, 108825. [Google Scholar] [CrossRef]
- Sektnan, A.; Vázquez, A.; Hauge, R.; Aarnes, I.; Skauvold, J.; Vevle, M.L. A Tree Representation of Pluri-Gaussian Truncation Rules. Math. Geosci. 2025, 57, 445–470. [Google Scholar] [CrossRef]
- Lyu, W.; Falzarano, J. Estimating the stationary distribution of pitch motion response for floating offshore wind platforms via the detailed balance method. Ships Offshore Struct. 2025, 1–12. [Google Scholar] [CrossRef]
- Xiao, Y.; Chen, L.; Duan, Z.; Sun, J.; Tang, Y. An efficient method for solving high-dimension stationary FPK equation of strongly nonlinear systems under additive and/or multiplicative white noise. Probabilistic Eng. Mech. 2024, 77, 103668. [Google Scholar] [CrossRef]
- Jia, W.; Luo, M.; Ni, F.; Hao, M.; Zan, W. Response and reliability of suspension system under stochastic and periodic track excitations by path integral method. Int. J. Non-Linear Mech. 2023, 157, 104544. [Google Scholar] [CrossRef]
- Han, J.; Lee, Y. Enhanced laplace approximation. J. Multivar. Anal. 2024, 202, 105321. [Google Scholar] [CrossRef]
- López, J.; Pagola, P.; Palacios, P. A generalization of the Laplace’s method for integrals. Appl. Math. Comput. 2024, 483, 128987. [Google Scholar] [CrossRef]
- Di Matteo, A.; Pirrotta, A. Efficient path integral approach via analytical asymptotic expansion for nonlinear systems under Gaussian white noise. Nonlinear Dyn. 2024, 112, 13995–14018. [Google Scholar] [CrossRef]
- Liu, P.; Lou, S. Applications of Symmetries to Nonlinear Partial Differential Equations. Symmetry 2024, 16, 1591. [Google Scholar] [CrossRef]
- Leblond, J.; Lebihain, M. An extended Bueckner-Rice theory for arbitrary geometric perturbations of cracks. J. Mech. Phys. Solids 2023, 172, 105191. [Google Scholar] [CrossRef]
- Jin, B.; Bian, Y.; Liu, X.; Gao, Z. Dynamic modeling and nonlinear analysis of a spur gear system considering a nonuniformly distributed meshing force. Appl. Sci. 2022, 12, 12270. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z. Nonlinear dynamic response of a multi-degree of freedom gear system dynamic model coupled with tooth surface characters: A case study on coal cutters. Nonlinear Dyn. 2016, 84, 271–286. [Google Scholar] [CrossRef]
- Tian, R.; Xu, Y. A modified Chebyshev collocation method for the generalized probability density evolution equation. Eng. Struct. 2024, 305, 117676. [Google Scholar] [CrossRef]
- Mi, W.; Qian, T. A new backward shift algorithm for system identification by a good choice of frequencies. Asian J. Control 2024, 26, 1364–1373. [Google Scholar] [CrossRef]



| Number of Nodes n | |||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Shi, Z.; Fu, G.; Cui, Y.; Shang, Z.; Huang, X. Probability Density Evolution and Reliability Analysis of Gear Transmission Systems Based on the Path Integration Method. Lubricants 2025, 13, 275. https://doi.org/10.3390/lubricants13060275
Cheng H, Shi Z, Fu G, Cui Y, Shang Z, Huang X. Probability Density Evolution and Reliability Analysis of Gear Transmission Systems Based on the Path Integration Method. Lubricants. 2025; 13(6):275. https://doi.org/10.3390/lubricants13060275
Chicago/Turabian StyleCheng, Hongchuan, Zhaoyang Shi, Guilong Fu, Yu Cui, Zhiwu Shang, and Xingbao Huang. 2025. "Probability Density Evolution and Reliability Analysis of Gear Transmission Systems Based on the Path Integration Method" Lubricants 13, no. 6: 275. https://doi.org/10.3390/lubricants13060275
APA StyleCheng, H., Shi, Z., Fu, G., Cui, Y., Shang, Z., & Huang, X. (2025). Probability Density Evolution and Reliability Analysis of Gear Transmission Systems Based on the Path Integration Method. Lubricants, 13(6), 275. https://doi.org/10.3390/lubricants13060275






