On the Non-Dimensional Modelling of Friction Hysteresis of Conformal Rough Contacts
Abstract
1. Introduction
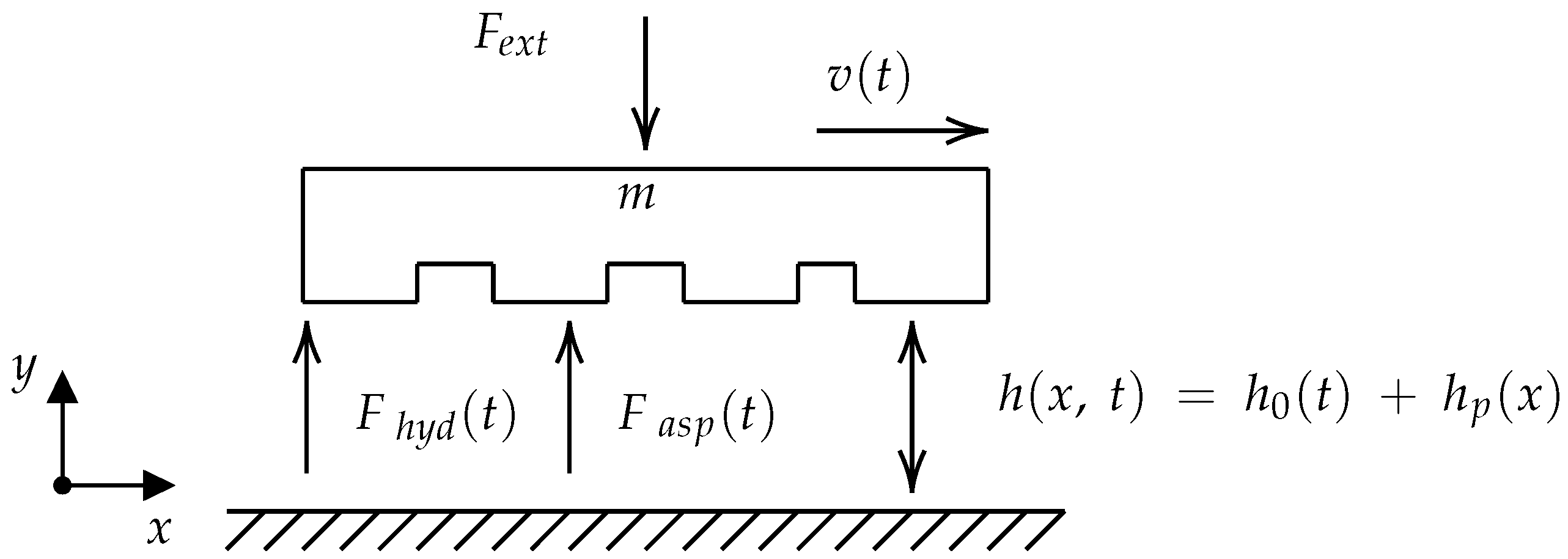
2. Non-Dimensional Model
2.1. Non-Dimensional Formulation
2.2. Limitations of Model
2.3. Discussion of Non-Dimensional Groups
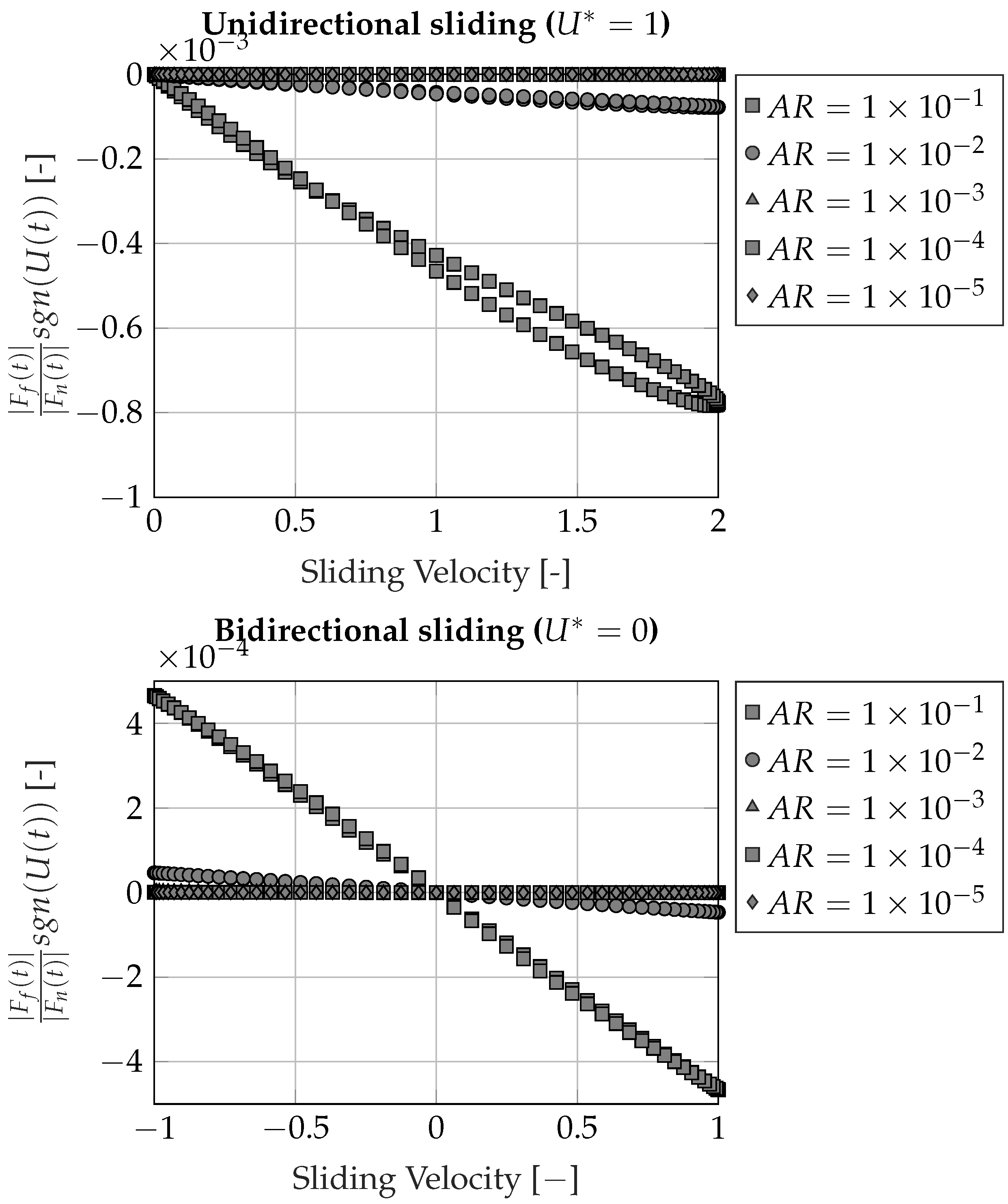
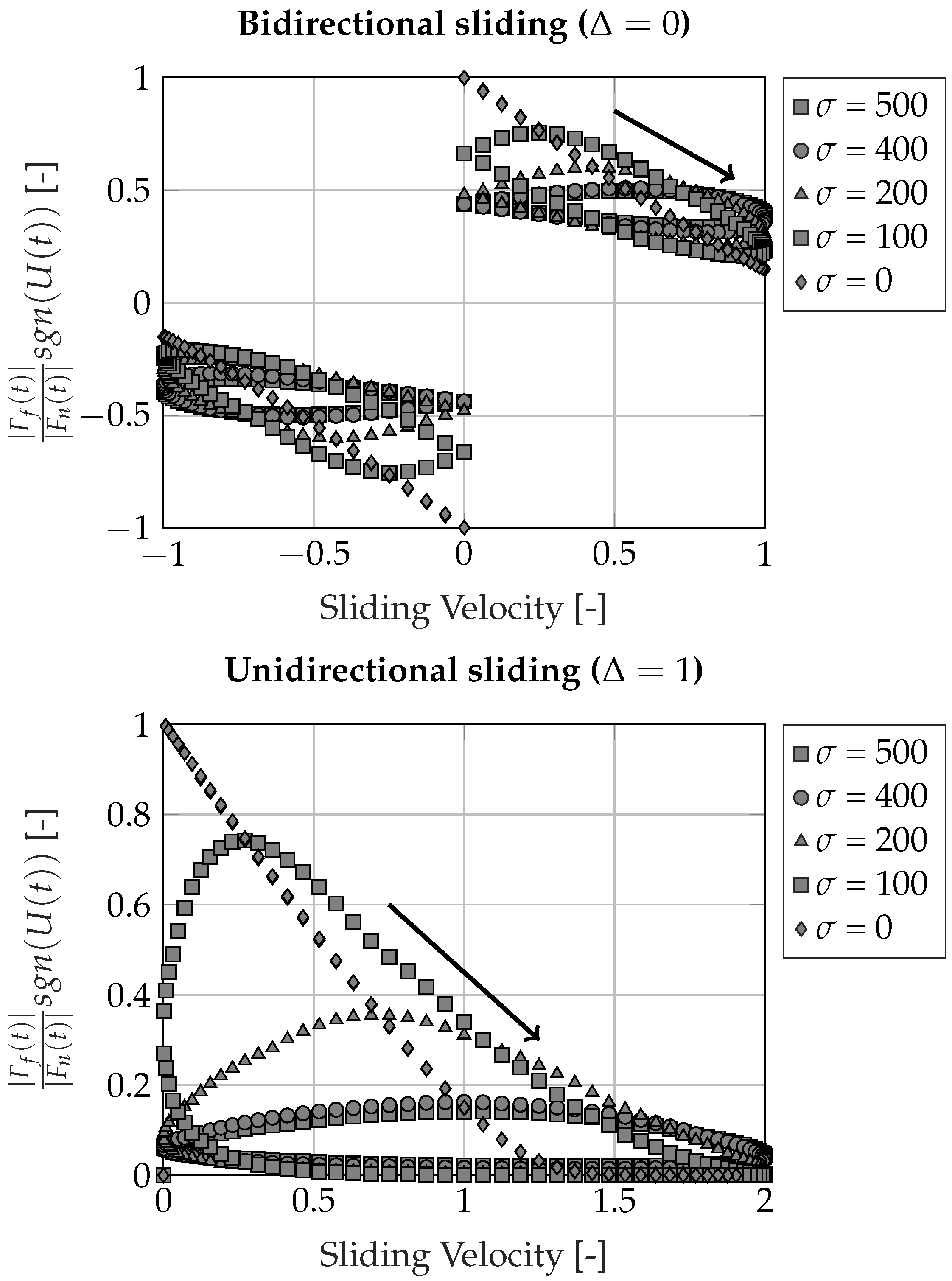
- The Velocity Ratio Parameter () is a measure of the average sliding velocity of the system, around which the sinusoidal perturbation is applied. Using the absolute value of this parameter, three different sliding regimes are distinguished: (i) , a pure sinusoidal sliding velocity is applied, (ii) , the sinusoidal motion can be seen as a perturbation around a mean value, and no motion reversal is occurring, (iii) , motion reversal is still occurring; however, the sliding distance is not equal for both sides of the oscillation.
- The Aspect Ratio parameter () is a measure of the clearance when subject to boundary lubrication relative to the length of the contact. Typical aspect ratios of non-conformal lightly loaded contacts are around 0.001 (Bearing dimensions in mm have typical roughness in m, and contacts in km scale have roughness in cm scale (i.e., roads)).
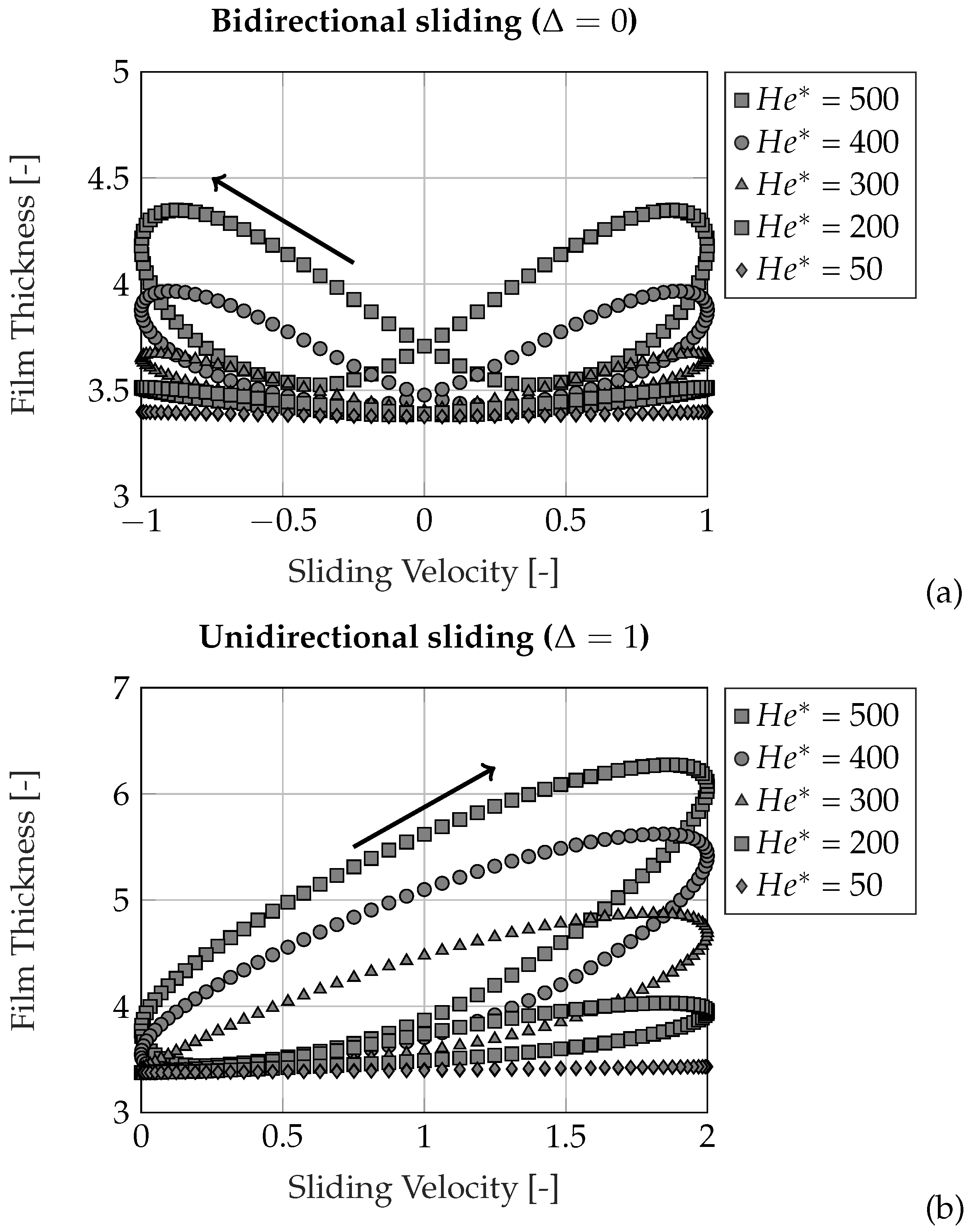
- The Bearing parameter () is equivalent to the Hersey number, rescaled with the aspect ratio, and expresses the relative importance of pressure to the viscosity contributions. The bearing parameter can be interpreted as the inverse of the Reynolds times the Euler number, indicating the magnitude of the pressure buildup w.r.t. the viscous lubricant flow. The parameter should be strictly positive to ensure hydrodynamic pressure build-up.
- The Squeeze parameter () is a measure for the squeeze contribution and is inversely proportional to the average pressure (external load divided by length) and proportional to the frequency. When the squeeze number equals zero, the contact reduces to steady-state operation.
- The Contact parameter () determines the maximum load carried by the asperities when the film thickness equals the minimal possible clearance.
- The Friction parameter () is a measure of the maximum friction force that can occur due to asperity contact and is used to normalized the resulting friction force (i.e., combining asperity and hydrodynamic contributions) of the system. Hence, it can be used to determine in which friction regime the contact is operating.
3. Results and Discussion
3.1. Parameter Study
3.2. Parameter Analysis
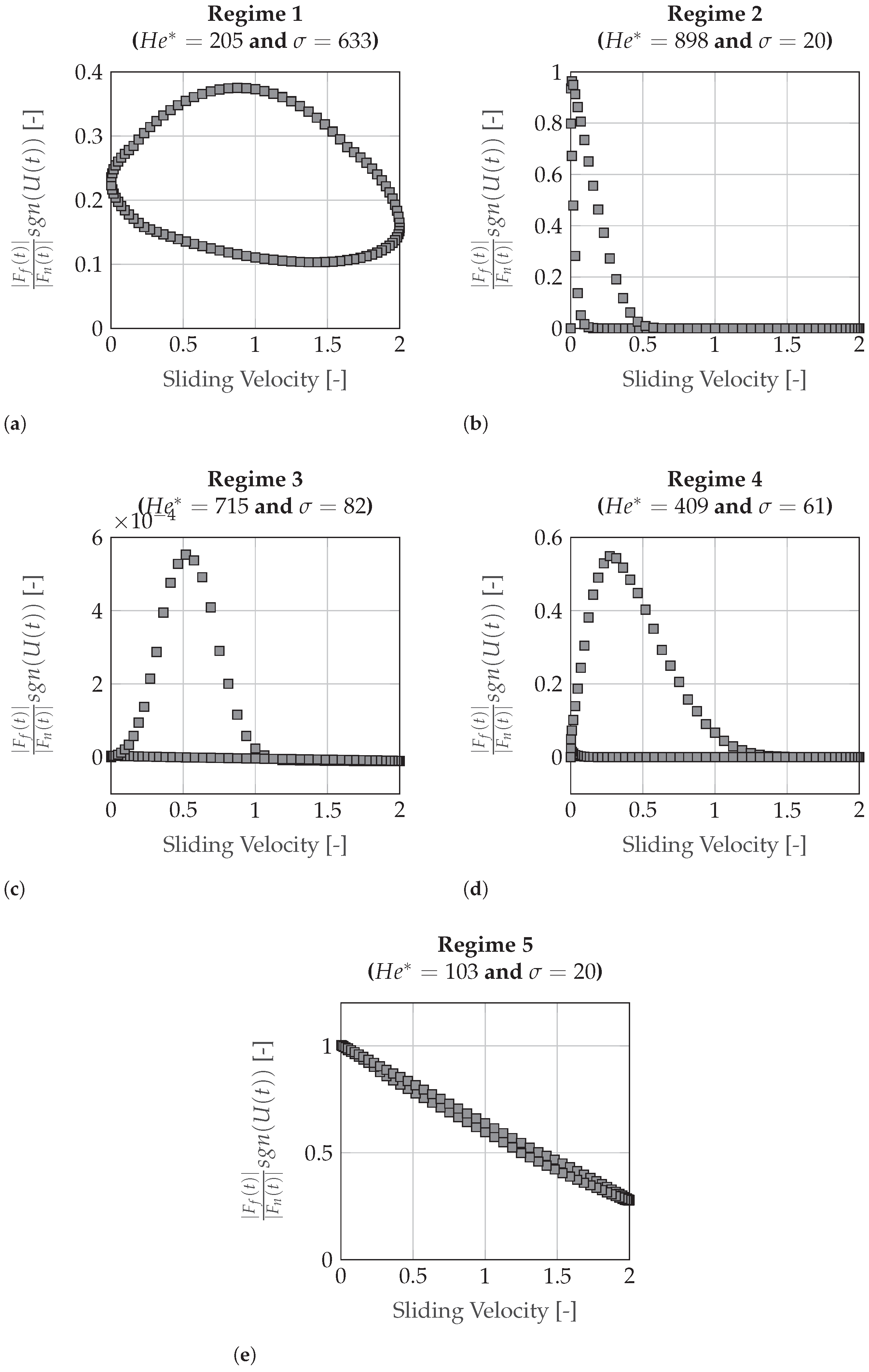
- Regime 1: Characterized by a quasi-circular friction hysteresis loop, where both acceleration and deceleration phases are in the mixed friction regime. A rather high squeeze value is present, leading to a quasi-circular friction loop and an overall lower friction value as compared with Regime 5, contributing to the observed loop.
- Regime 2: Represents a scenario where the upper branch is in the mixed lubrication regime, while the lower branch operates in the full film regime. The hysteresis loop exhibits symmetry and closely follows the Stribeck curve.
- Regime 3: Distinguished by extremely low friction values and a relatively small hysteresis loop. Both phases of the loop operate in the full friction regime, facilitated by elevated bearing and squeeze numbers.
- Regime 4: Occupies a transitional position where the upper branch is in the mixed regime, while the lower branch is entirely in the full regime. This results in highly asymmetric friction loops with substantial differences between both phases.
- Regime 5: In this regime, the contact operates in both acceleration and deceleration phases within the mixed friction regime. Additionally, this regime is subjected to relatively low values of the squeeze number. The outcome is narrow, quasi-straight hysteresis loops with a notably large coefficient of friction.
4. Conclusions
- Contact and Friction Parameters:
- -
- The contact and friction parameters exhibit limited influence on friction hysteresis loops, with variations within a 10% threshold.
- -
- The friction parameter, , serves as a scaling factor without a pronounced effect on the loops, reaffirming its role in boundary lubrication coefficient incorporation.
- Aspect Ratio Parameter:
- -
- The aspect ratio parameter, , demonstrates negligible influence on friction hysteresis loops, especially in non-conformal, lightly loaded scenarios. The Aspect Ratio (AR) primarily affects the fluid friction force but has minimal impact on the total friction force, which is the sum of both fluid and asperity friction forces.
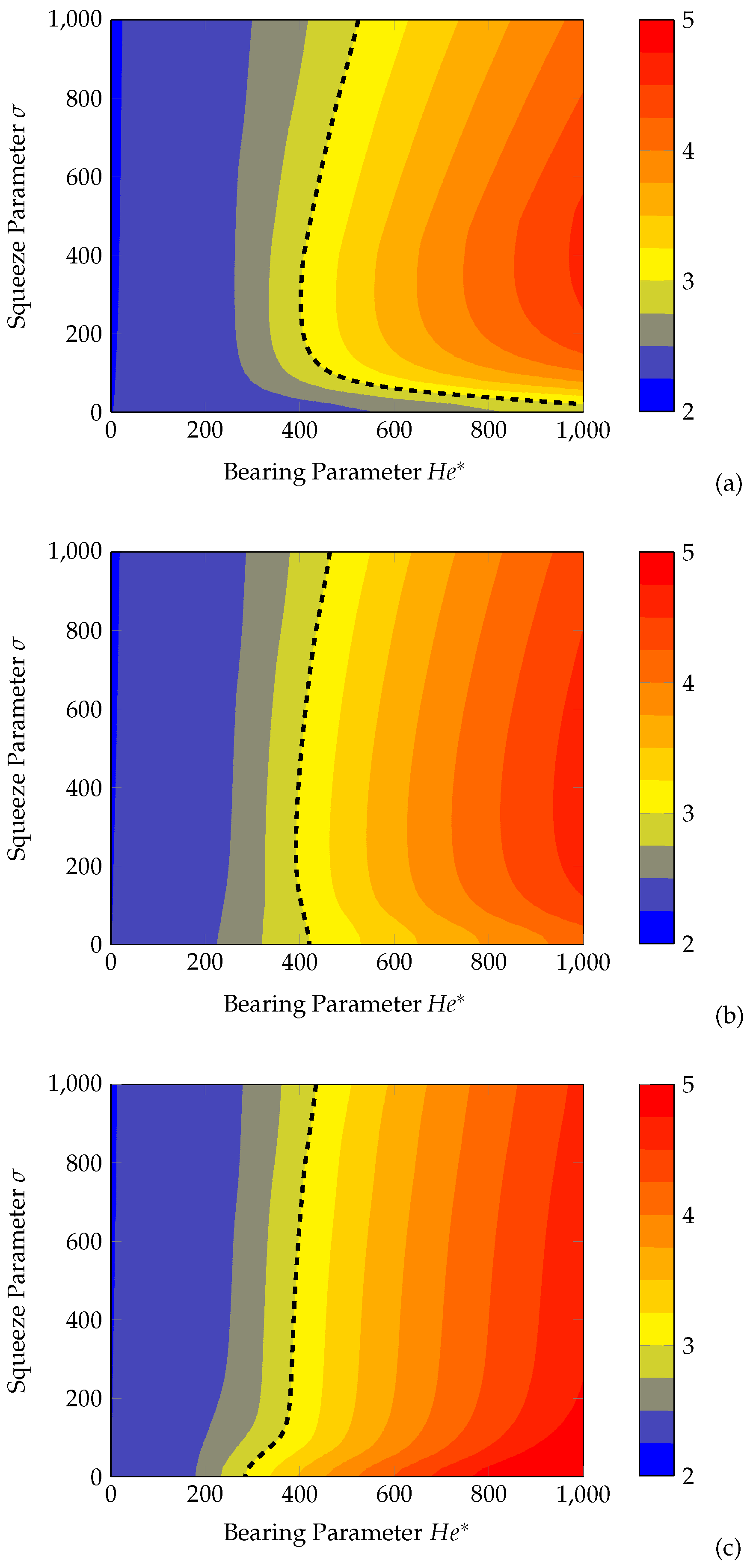
- Bearing, Squeeze, and Contact Parameters:
- -
- Bearing, squeeze, and contact parameters emerge as significant determinants, defining lubrication regimes for different loop phases.
- -
- Graphical analysis identifies five unique regions based on bearing and squeeze parameters, each associated with characteristic friction hysteresis loop profiles.
- Regime 1: Bulky friction hysteresis loop with both phases in the mixed friction regime, influenced by a high squeeze value.
- Regime 2: Symmetric loop with up-going phase in the mixed regime and down-going phase in the full film regime.
- Regime 3: Extremely low friction values with both phases operating in the full friction regime, characterized by high bearing and squeeze numbers.
- Regime 4: Transitional regime with asymmetric friction loops, where the up-going phase is in the mixed regime and the down-going phase is entirely in the full regime.
- Regime 5: Narrow, quasi-straight hysteresis loops with a large friction value, where both phases operate in the mixed friction regime with low squeeze values.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Armstrong-Hélouvry, B.; Dupont, P.; De Wit, C.C. A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Olsson, H. Control Systems with Friction. Ph.D. Thesis, Department of Automatic Control, New Jersey Institute of Technology, Newark, NJ, USA, 1996. [Google Scholar]
- Lampaert, V.; Al-Bender, F.; Swevers, J. Experimental Characterization of Dry Friction at Low Velocities on a Developed Tribometer Setup for Macroscopic Measurements. Tribol. Lett. 2004, 16, 95–105. [Google Scholar] [CrossRef]
- van Geffen, V. A Study of Friction Models and Friction Compensation; Technical Report for TU Eindhoven: Eindhoven, The Netherlands, 2009. [Google Scholar]
- De Moerlooze, K. Contributions to the Characterisation of Friction and Wear: Theoretical Modelling and Experimental Validation. Ph.D. Thesis, KU Leuven Faculteit Ingenieurswetenschappen, Leuven, Belgium, 2010. [Google Scholar]
- Rabinowicz, E. The Intrinsic Variables affecting the Stick-Slip Process. Proc. Phys. Soc. 1958, 71, 668–675. [Google Scholar] [CrossRef]
- Hess, D.P.; Soom, A. Friction at a Lubricated Line Contact Operating at Oscillating Sliding Velocities. J. Tribol. 1990, 112, 147–152. [Google Scholar] [CrossRef]
- Lu, X.; Khonsari, M.M. An Experimental Study of Grease-Lubricated Journal Bearings Undergoing Oscillatory Motion. J. Tribol. Trans. Asme 2007, 129. [Google Scholar] [CrossRef]
- Lu, X.; Khonsari, M.M. An Experimental Study of Oil-Lubricated Journal Bearings Undergoing Oscillatory Motion. J. Tribol. 2008, 130, 021702. [Google Scholar] [CrossRef]
- Zhai, X.; Needham, G.; Chang, L. On the Mechanism of Multi-Valued Friction in Unsteady Sliding Line Contacts Operating in the Regime of Mixed-Film Lubrication. J. Tribol. 1997, 119, 149–155. [Google Scholar] [CrossRef]
- Sojoudi, H.; Khonsari, M.M. On the Modeling of Quasi-Steady and Unsteady Dynamic Friction in Sliding Lubricated Line Contact. J. Tribol. 2009, 132, 012101. [Google Scholar] [CrossRef]
- Harnoy, A.; Friedland, B. Dynamic Friction Model of Lubricated Surfaces for Precise Motion Control. Tribol. Trans. 1994, 37, 608–614. [Google Scholar] [CrossRef]
- Sampson, J.B.; Morgan, F.; Reed, D.W.; Muskat, M. Studies in Lubrication: XII. Friction Behavior During the Slip Portion of the Stick-Slip Process. J. Appl. Phys. 1943, 14, 689–700. [Google Scholar] [CrossRef]
- Driesen, K.; Castagne, S.; Lauwers, B.; Fauconnier, D. On the Numerical Modeling of Friction Hysteresis of Conformal Rough Contacts. Lubricants 2023, 11, 326. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. London Ser. A. Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Chang, L.; Jeng, Y.R. Effects of Negative Skewness of Surface Roughness on the Contact and Lubrication of Nominally Flat Metallic Surfaces. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2012. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, D.; Tang, J.; Yi, J. A Comparative Study on Asperity Peak Modeling Methods. Chin. J. Mech. Eng. 2021. [Google Scholar] [CrossRef]
- Maaboudallah, F.; Najah, M.; Atalla, N. A Review on the Contact Mechanics Modeling of Rough Surfaces in the Elastic Regime: Fundamentals, Theories, and Numerical Implementations. In Tribology of Machine Elements; Pintaude, G., Cousseau, T., Rudawska, A., Eds.; IntechOpen: Rijeka, Croatia, 2022; Chapter 3. [Google Scholar] [CrossRef]
- Taylor, R.I. Rough Surface Contact Modelling—A Review. Lubricants 2022, 10, 98. [Google Scholar] [CrossRef]
- Ciavarella, M.; Delfine, V.; Demelio, G. A “re-vitalized” Greenwood and Williamson model of elastic contact between fractal surfaces. J. Mech. Phys. Solids 2006, 54, 2569–2591. [Google Scholar] [CrossRef]
- Ciavarella, M.; Greenwood, J.; Paggi, M. Inclusion of “interaction” in the Greenwood and Williamson contact theory. Wear 2008, 265, 729–734. [Google Scholar] [CrossRef]
- Müser, M.H.; Dapp, W.B.; Bugnicourt, R.; Sainsot, P.; Lesaffre, N.; Lubrecht, T.A.; Persson, B.N.J.; Harris, K.; Bennett, A.; Schulze, K.; et al. Meeting the Contact-Mechanics Challenge. Tribol. Lett. 2017, 65, 118. [Google Scholar] [CrossRef]
- Dapp, W.B.; Lücke, A.; Persson, B.N.J.; Müser, M.H. Self-Affine Elastic Contacts: Percolation and Leakage. Phys. Rev. Lett. 2012, 108, 244301. [Google Scholar] [CrossRef]
- Sahlin, F.; Almqvist, A.; Larsson, R.; Glavatskih, S. A cavitation algorithm for arbitrary lubricant compressibility. Tribol. Int. 2007, 40, 1294–1300. [Google Scholar] [CrossRef]
- Bertocchi, L.; Dini, D.; Giacopini, M.; Fowell, M.T.; Baldini, A. Fluid film lubrication in the presence of cavitation: A mass-conserving two-dimensional formulation for compressible, piezoviscous and non-Newtonian fluids. Tribol. Int. 2013, 67, 61–71. [Google Scholar] [CrossRef]
- Profito, F.; Giacopini, M.; Zachariadis, D.; Dini, D. A General Finite Volume Method for the Solution of the Reynolds Lubrication Equation with a Mass-Conserving Cavitation Model. Tribol. Lett. 2015, 60, 18. [Google Scholar] [CrossRef]
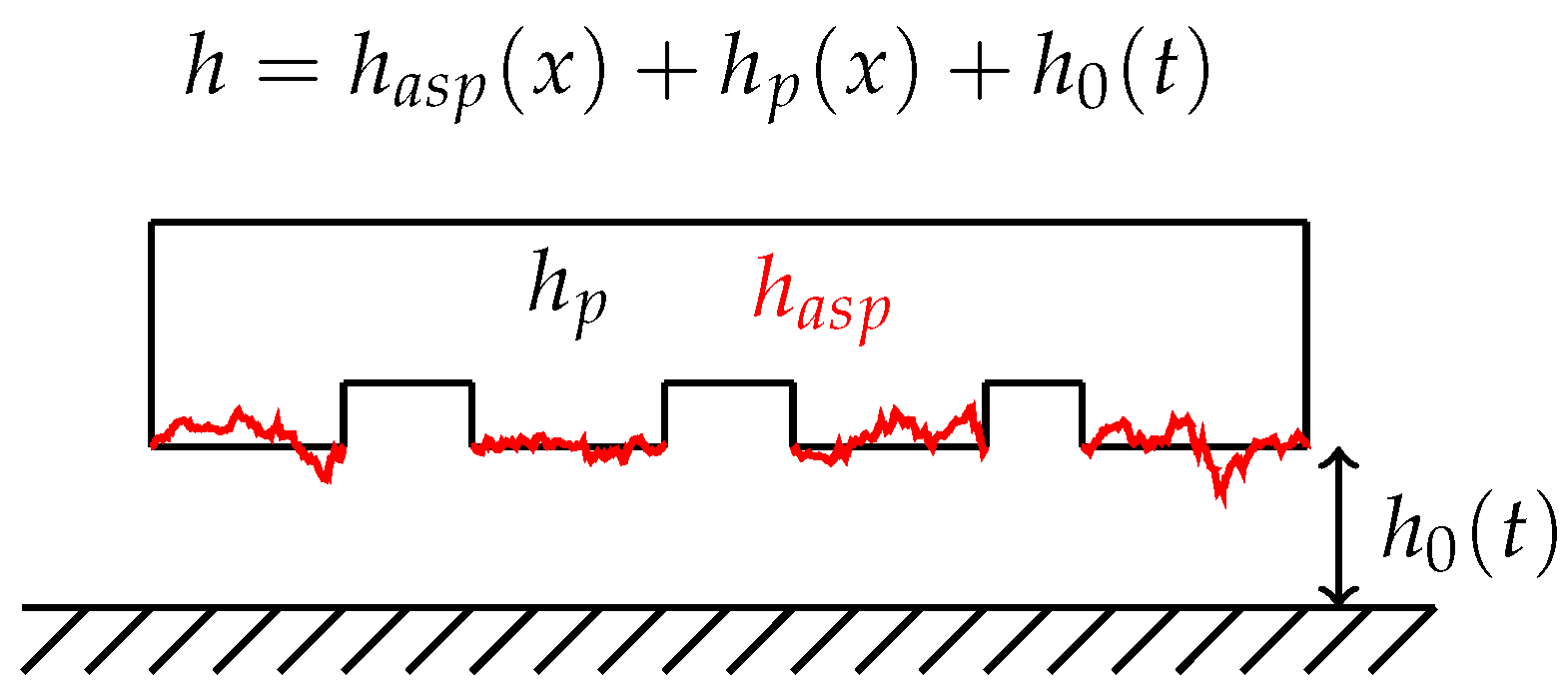




| Dimensionless Quantity | Symbol | Definition | Typical Value for Engineering Contacts |
|---|---|---|---|
| Velocity Ratio | |||
| Aspect Ratio | |||
| Bearing Parameter | – | ||
| Squeeze Parameter | – | ||
| Contact Parameter | – | ||
| Friction Parameter |
| Parameter | Value |
|---|---|
| 0.001 | |
| 500 | |
| 250 | |
| 1,120,000 | |
| 6300 | |
| 1 | |
| 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Driesen, K.; Castagne, S.; Lauwers, B.; Fauconnier, D. On the Non-Dimensional Modelling of Friction Hysteresis of Conformal Rough Contacts. Lubricants 2025, 13, 248. https://doi.org/10.3390/lubricants13060248
Driesen K, Castagne S, Lauwers B, Fauconnier D. On the Non-Dimensional Modelling of Friction Hysteresis of Conformal Rough Contacts. Lubricants. 2025; 13(6):248. https://doi.org/10.3390/lubricants13060248
Chicago/Turabian StyleDriesen, Kristof, Sylvie Castagne, Bert Lauwers, and Dieter Fauconnier. 2025. "On the Non-Dimensional Modelling of Friction Hysteresis of Conformal Rough Contacts" Lubricants 13, no. 6: 248. https://doi.org/10.3390/lubricants13060248
APA StyleDriesen, K., Castagne, S., Lauwers, B., & Fauconnier, D. (2025). On the Non-Dimensional Modelling of Friction Hysteresis of Conformal Rough Contacts. Lubricants, 13(6), 248. https://doi.org/10.3390/lubricants13060248






