Finite Element Analysis of Friction-Induced Stress Concentrations in Press Fits with Chamfer Hubs
Abstract
1. Introduction
2. Materials and Methods
Finite Elements Numerical Modeling
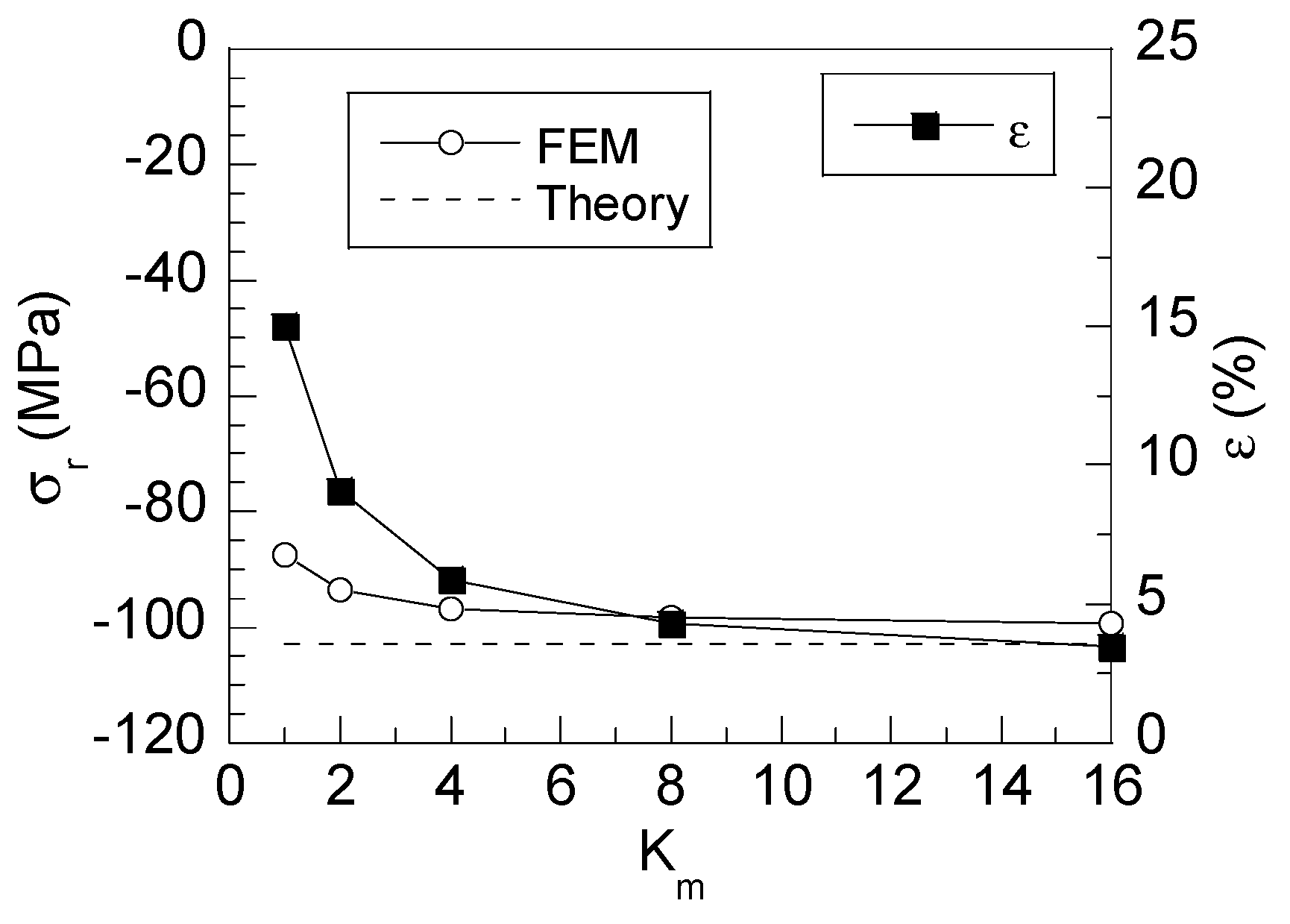
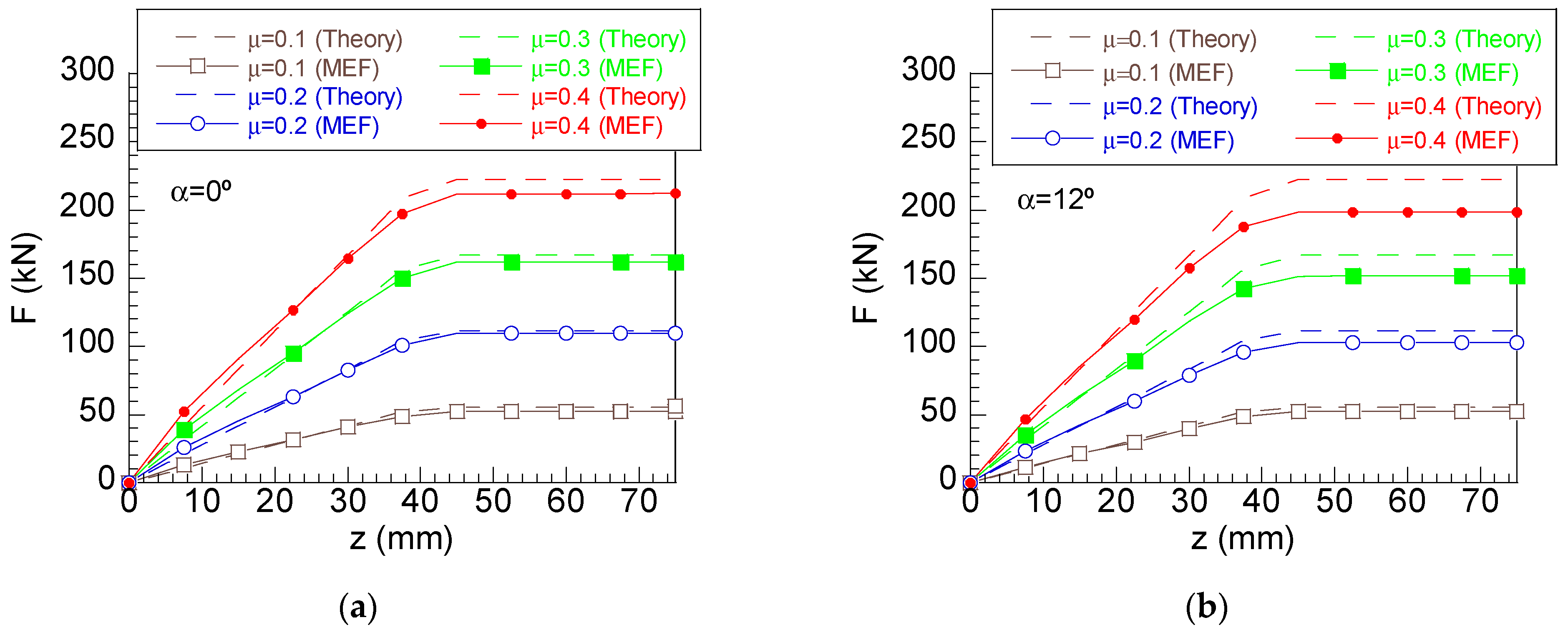
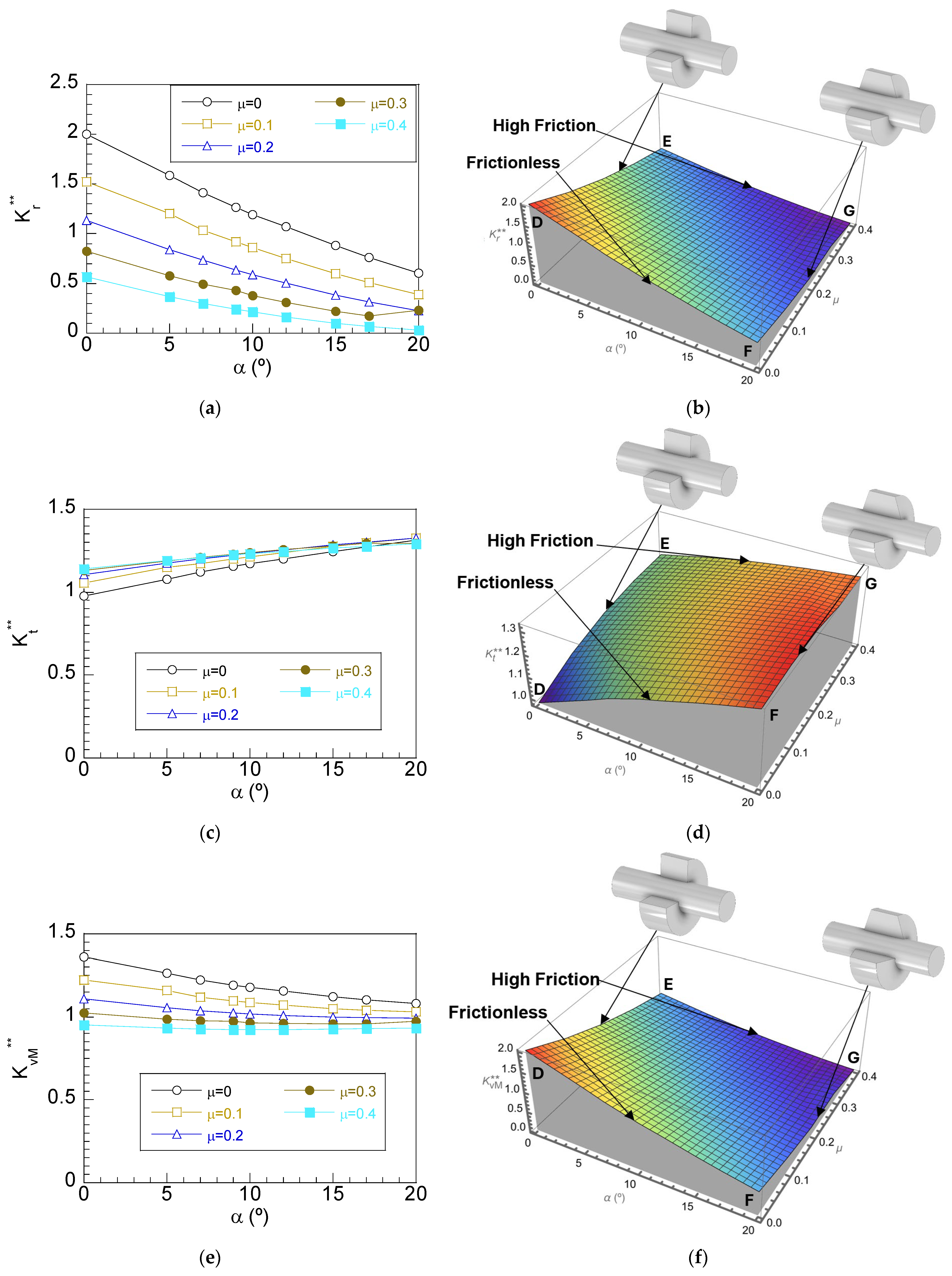
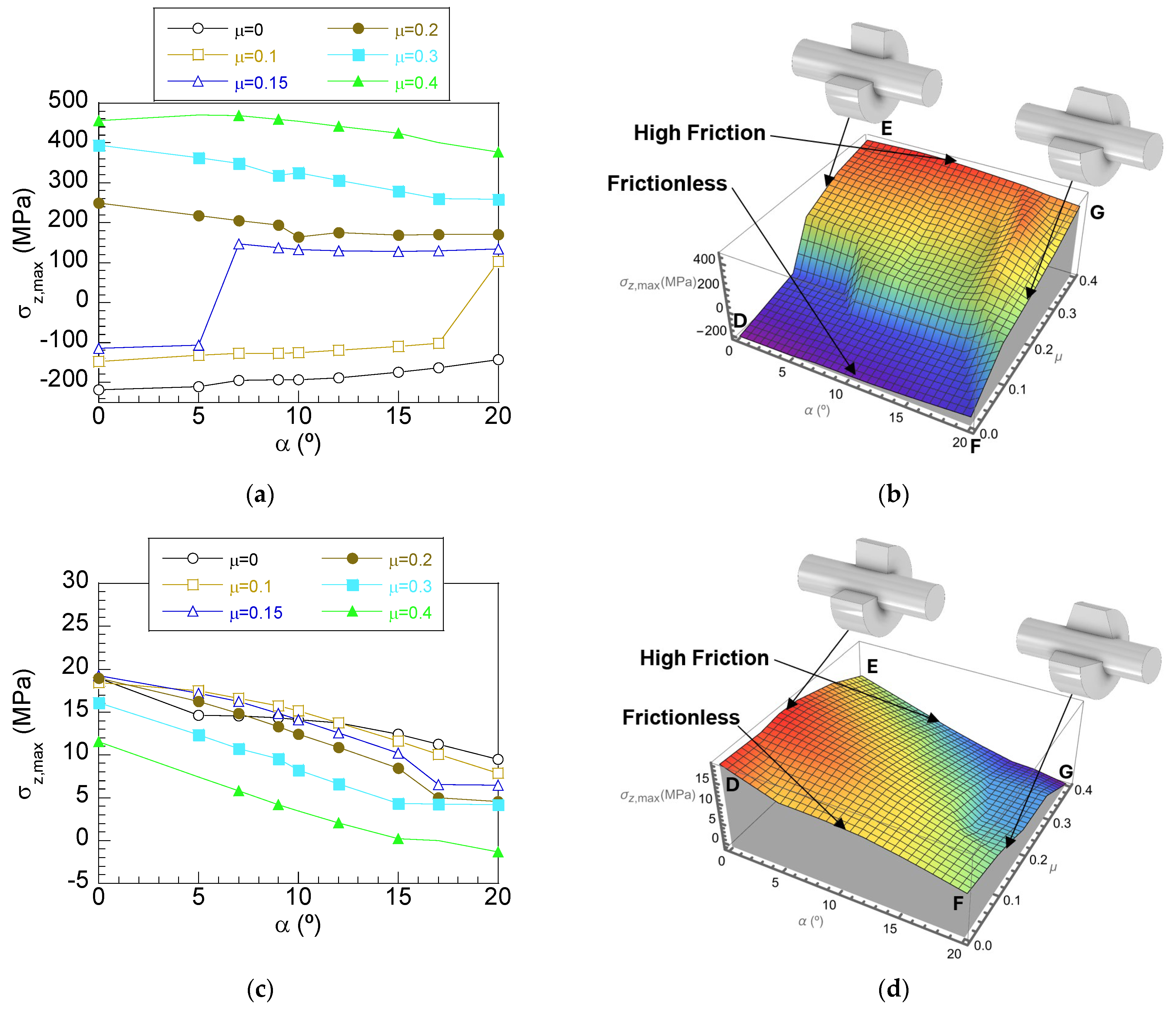
3. Results
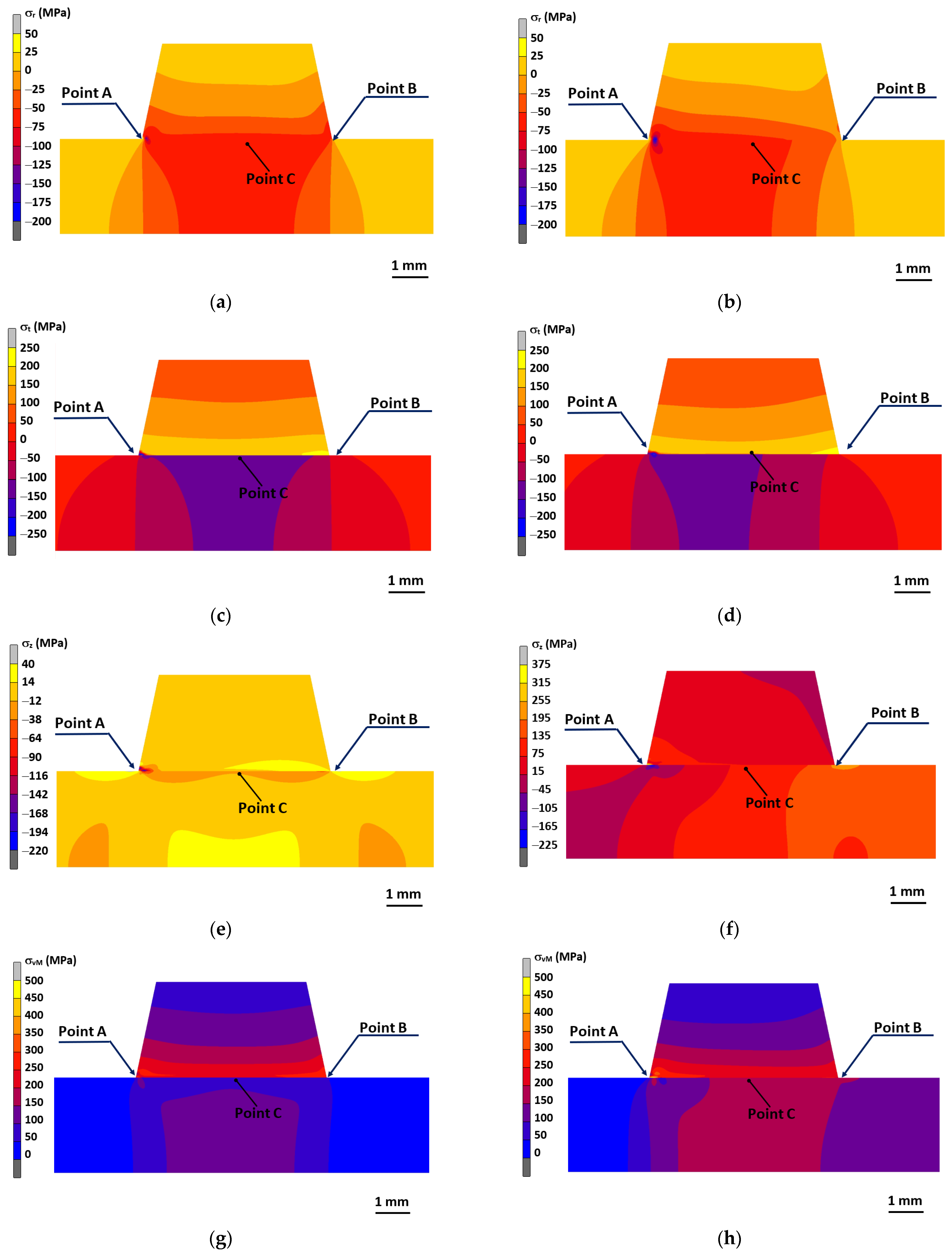
3.1. Shaft–Hub Interface Stress Distributions
3.2. Role of Friction in Stress Distributions at the Shaft–Hub Interface
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zdravecká, E.; Ondáč, M.; Tkáčová, J.; Vojtko, M.; Slota, J. Failure analysis of the pulleys during the press-fit assembling process. Case Stud. Eng. Fail. Anal. 2015, 3, 34–38. [Google Scholar] [CrossRef][Green Version]
- Chu, S.J.; Jeong, T.K.; Jung, E.H. Effect of radial interference on torque capacity of press-and shrink-fit gears. Int. J. Automot. Technol. 2016, 17, 763–768. [Google Scholar] [CrossRef]
- Shu, Y.; Yang, G.; Liu, Z. Experimental study on fretting damage in the interference fit area of high-speed train wheels and axles based on specimen. Eng. Fail. Anal. 2022, 141, 106619. [Google Scholar] [CrossRef]
- Murcinkova, Z.; Baron, P.; Pollak, M. Study of the press fit bearing-shaft joint dimensional parameters by analytical and numerical approach. Adv. Mater. Sci. Eng. 2018, 1, 2916068. [Google Scholar] [CrossRef]
- Wang, T.; Guo, H.; Qiao, J.; Liu, X.; Fan, Z. Experimental study on the relationship between the friction coefficient and interference in locomotive axle press-fitting. Int. J. Struct. Integr. 2021, 12, 878–893. [Google Scholar] [CrossRef]
- Wang, X.; Lou, Z.; Wang, X.; Xu, C. A new analytical method for press-fit curve prediction of interference fitting parts. J. Mater. Process. Technol. 2017, 250, 16–24. [Google Scholar] [CrossRef]
- Tohmyoh, H.; Yamanobe, K.; Saka, M.; Utsunomiba, J.; Nakamura, T.; Nakano, Y. Determination of the friction coefficient of a press fit pin in thin plating. JSME Int. Ser. Solid Mech. Mater. Eng. 2006, 49, 363–369. [Google Scholar] [CrossRef][Green Version]
- Levitas, V.I.; Idesman, A.V.; Nemirosvskii, A.B.; Nemirovskii, Y.B.; Zherebtsov, Y.V.; Stashkevich, I.E.; Gerovskoo, A.I. Numerical modelling of the process of press fitting dies into ring blocks with allowance for plastic deformation and frictional forces. Strength Mater. 1990, 22, 1675–1682. [Google Scholar] [CrossRef]
- Zehsaz, M.; Shahriary, P. The effects of friction coefficient and interference on the fretting fatigue strength of railway axle assembly. Int. Union Railw. 2013, 75, 71–84. [Google Scholar]
- Norton, R.L. Machine Design, 5th ed.; Prentice Hall: New York, NY, USA, 2013. [Google Scholar]
- Zhao, J.; Wang, J.X.; Yu, C.; Tang, S.Q.; Yao, J. Influence of radial interference on torque capacity of shrink-fit cam shaft. Adv. Mech. Eng. 2019, 11, 1687814018817640. [Google Scholar] [CrossRef]
- Nwe, T.; Pimsarn, M. Railway axle and wheel assembly press-fitting force characteristics and holding torque capacity. Appl. Sci. 2021, 11, 8862. [Google Scholar] [CrossRef]
- Baugher, J.W. Transmission of torque by means of press and shrink fits. Trans. ASME 1931, 53, 85–89. [Google Scholar] [CrossRef]
- Post, C.E.; Bitter, T.; Briscoe, A.; Verdonschot, N.; Janssen, D. A FE study on the effect of interference fit and coefficient of friction on the micromotions and interface gaps of a cementless PEEK femoral component. J. Biomech. 2022, 137, 310–322. [Google Scholar] [CrossRef]
- Loc, N.H.; Phong, L.V. Study of interference fit between steel and brass parts. EUREKA Phys. Eng. 2022, 5, 140–149. [Google Scholar] [CrossRef]
- Yang, G.M.; Coquille, J.C.; Fontaine, J.F.; Lambertin, M. Influence of roughness on characteristics of tight interference fit of a shaft and a hub. Int. J. Solids Struct. 2001, 38, 7691–7701. [Google Scholar] [CrossRef]
- Persson, B.N.J. Influence of surface roughness on press fits. Tribol. Lett. 2023, 71, 19. [Google Scholar] [CrossRef]
- Shigley, J.E.; Mischke, C.R. Standard Handbook of Machine Design, 11th ed.; McGraw Hill: New York, NY, USA, 1988. [Google Scholar]
- Campos, U.A.; Hall, D.E. Simplified Lamé’s equations to determine contact pressure and hoop stress in thin-walled press-fits. Thin Wall. Struct. 2019, 138, 199–207. [Google Scholar] [CrossRef]
- Strozzi, A.; Baldini, A.; Giacopini, M.; Bertocchi, E.; Bertocchi, L. Achievement of a uniform contact pressure in a shaft-hub press-fit. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 227, 405–419. [Google Scholar] [CrossRef]
- Irena, K.A.; Lemu, H.G.; Kedir, Y.A. Effect of interference size on contact pressure distribution of railway wheel axle press fitting. Designs 2023, 7, 119. [Google Scholar] [CrossRef]
- Wang, X.; Lou, Z.; Wang, X.; Hao, X.; Wang, Y. Prediction of stress distribution in press-fit process of interference fit with a new theoretical model. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 233, 2834–2846. [Google Scholar] [CrossRef]
- Prasad, N.S.; Sashikanth, P.; Ramamurti, V. Stress distribution in interference joints. Comput. Struct. 1994, 51, 535–540. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, Q.; Shao, H.; Wang, C.; Li, X.; Hong, Y. Stress-based optimization of assembly surface mechanical properties oriented to stress-uniform assembly. Precis. Eng. 2023, 82, 350–359. [Google Scholar] [CrossRef]
- Yamamoto, M.; Ishiduka, H. Stress concentration of transition groove induced by a press-fitted part in railway axles. Int. J. Fatigue 2017, 97, 48–55. [Google Scholar] [CrossRef]
- Song, C.; Liu, J.; Peng, J.; Zhang, L.; Zhou, Y.; Zhu, M. Effect of contact stress on rotating bending fretting fatigue life of railway axle steel. J. Mater. Eng. 2014, 1, 34–38. [Google Scholar] [CrossRef]
- Nwe, T.; Pimsarn, M. Effect of interference on the press fitting of railway wheel and axle assemblies. Mater. Sci. Eng. 2021, 1137, 012051. [Google Scholar] [CrossRef]
- Falter, J.; Binz, H.; Kreimeyer, M. Investigations on design limits and improved material utilization of press-fit connections using elastic-plastic design. Appl. Eng. Sci. 2023, 13, 100124. [Google Scholar] [CrossRef]
- You, B.; Luo, Y.; Wang, X.D. The application of computing methods for analysis of press-fit assembly in elasto-plastic field. J. Inf. Comput. Sci. 2014, 11, 3157–3166. [Google Scholar] [CrossRef]
- Zou, L.; Zeng, D.; Wang, J.; Lu, L.; Li, Y.; Zhang, Y. Effect of plastic deformation and fretting wear on the fretting fatigue of scaled railway axles. Int. J. Fatigue 2020, 132, 105371. [Google Scholar] [CrossRef]
- Hüyük, H.; Music, O.; Koç, A.; Karadogan, C.; Bayram, C. Analysis of elastic-plastic interference-fit joints. Proc. Eng. 2014, 81, 2030–2035. [Google Scholar] [CrossRef]
- Izard, E.; Garcia-Martín, R.; Rodríguez-Martín, M.; Lorenzo, M. Influence of the Friction Coefficient on the Stress Distributions and Contact Pressure in Press-Fits via Finite Element Analysis. Lubricants 2023, 11, 472. [Google Scholar] [CrossRef]
- Dieudonné, E.; Florence, O.; Joseph, N.A.; Valerya, N.A.C.; Achillea, N.P.A.; Nelson, Z.C. A study on the experimental investigation of low frequency vibration wave assisted disassembly of press-fit joints. J. Manuf. Process. 2020, 49, 70–81. [Google Scholar] [CrossRef]
- Dong, Y.; Zeng, D.; Zhao, H.; Wu, P.; Song, Y.; Li, X.; Lu, L. Fretting fatigue strength evaluation of scaled press-fitted railway axle containing a circumferential groove defect. Int. J. Fatigue 2025, 194, 108824. [Google Scholar] [CrossRef]
- Bian, X.; Wei, C.; Lui, Y. Research on the fretting contact fatigue strength of interference fit in high speed rail traction motor shafts. Eng. Fail. Anal. 2024, 157, 107875. [Google Scholar] [CrossRef]
- Zou, L.; Zeng, D.; Chen, X.; Li, J.; Zhao, H.; Lu, L. Experimental and numerical study on press-fitted railway axles: Competition between fretting and plain fatigue. Int. J. Fatigue 2024, 179, 108032. [Google Scholar] [CrossRef]
- Kowalski, S. The analysis of fretting fatigue in forced-in joint with the induction- hardened shaft. Tribol. Finn. J. Tribol. 2021, 38, 11–21. [Google Scholar] [CrossRef]
- Zou, L.; Lu, L.; Li, Y.; Yang, K.; Zhao, H.; Dong, Y.; Zeng, D. Experimental and numerical study on press-fitted railway axles: Fretting fatigue behaviour in the very high cycle regime. Int. J. Fatigue 2023, 166, 107243. [Google Scholar] [CrossRef]
- Pourheidar, A.; Regazzi, D.; Cervello, S.; Foletti, S.; Beretta, S. Fretting fatigue analysis of full-scale railway axles in presence of artificial micro-notches. Tribol. Int. 2020, 150, 106383. [Google Scholar] [CrossRef]
- Shu, Y.; Yang, G.; Liu, Z. Simulation research on fretting wear of train axles with interference fit based on press-fitted specimen. Wear 2023, 523, 204777. [Google Scholar] [CrossRef]
- Zou, L.; Zeng, D.; Dong, Y.; Li, J.; Chen, X.; Zhao, H.; Lu, L. Experimental and numerical study on the fretting wear-fatigue interaction evolution in press-fitted axles. Int. J. Fatigue 2023, 175, 107793. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, L.; Gong, Y.; Zhang, J.; Zeng, D. Fretting wear-induced evolution of surface damage in press-fitted shaft. Wear 2017, 384–385, 131–141. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, Y.; Xu, J. Slip damping of a press-fit joint under non uniform pressure distribution along the interface. J. Mech. Mater. Struct. 2020, 15, 307–323. [Google Scholar] [CrossRef]
- Xu, T.; Lu, L.; Zeng, D.; Zou, L. Fretting fatigue crack growth simulation and residual life assessment of railway press-fitted axle. Eng. Fract. Mech. 2023, 286, 109290. [Google Scholar] [CrossRef]
- Zou, L.; Zeng, D.; Zhang, Y.; Lu, L.; Zhao, H.; Xu, T.; Shi, G.; Chen, H. A coupled wear and crack initiation-propagation methodology for fretting fatigue life assessment in press-fitted axles. Int. J. Fatigue 2022, 159, 106817. [Google Scholar] [CrossRef]
- Gürer, G.; Gür, C.H. Failure analysis of fretting fatigue initiation and growth on railway axle press-fits. Eng. Fail. Anal. 2018, 84, 151–166. [Google Scholar] [CrossRef]
- Zou, L.; Zeng, D.; Tian, X.; Jiang, G.; Dong, Y.; Zhao, H.; Lu, L. Experimental and numerical study on the multi-site fretting fatigue crack initiation of press-fitted axles. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 473–490. [Google Scholar] [CrossRef]
- Dong, Y.; Zeng, D.; Wu, P.; Lu, L.; Zhao, H.; Li, Y.; Zou, L. Study on fretting fatigue crack initiation of scaled railway axles in consideration of fretting wear. Wear 2023, 512–513, 204545. [Google Scholar] [CrossRef]
- Ubando, A.T.; Gonzaga, J.; Arriola, E.; Moran, R.L.; Lim, N.R.E.; Mercado, J.P.; Belarmino, D. Analysis of the effects of geometry on the press fit application in automotive power modules. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1109, 012019. [Google Scholar] [CrossRef]
- Lorenzo, M.; Blanco, C.; Moreno, P.; Pérez-Cerdán, J.C. Influence of geometry on the stress peaks in interference fits with grooved hub. DYNA 2016, 91, 47–51. [Google Scholar] [CrossRef]
- Lee, D.H.; Choi, H.Y.; Song, C.Y.; Lee, B.G. Design of stress relief groove on a press-fitted assembly. Adv. Mater. Res. 2013, 753–755, 1339–1342. [Google Scholar] [CrossRef]
- Izard, E.; García-Martín, R.; Rodríguez-Martín, M.; Lorenzo, M. Finite element analysis of the influence of chamfer hub geometry on the stress concentrations of shrink fits. Appl. Sci. 2023, 13, 3606. [Google Scholar] [CrossRef]
- Pedersen, N.L. On optimization of interference fit assembly. Struct. Multidiscip. Optim. 2016, 54, 349–359. [Google Scholar] [CrossRef]
- Izard, E.; Garcia, R.; Rodriguez-Martín, M.; Lorenzo, M. Finite element analysis of the reduction in stress concentration factors in shrink fits by using contact rings. Appl. Sci. 2022, 12, 10037. [Google Scholar] [CrossRef]
- Güven, U. Stress distribution in shrink fit with elastic-plastic hub exhibiting variable thickness. Int. J. Mech. Sci. 1993, 35, 39–46. [Google Scholar] [CrossRef]
- Arslan, E.; Mack, W. Shrink fit with solid inclusion and functionally graded hub. Compos. Struct. 2015, 121, 217–224. [Google Scholar] [CrossRef]
- Apatay, T.; Arslan, E.; Mack, W. Effects of homogeneous and inhomogeneous heating on rotating shrink fits with annular inclusion and functionally graded hub. J. Therm. Stress. 2019, 42, 1458–1479. [Google Scholar] [CrossRef]
- Wang, R.; Xu, L. Mechanical behavior investigation of press-fit connector based on finite element simulation and its reliability evaluation. Microelectron. Reliab. 2021, 116, 114010. [Google Scholar] [CrossRef]
- Shu, Y.; Liu, Z.; Yang, G. Finite element simulation of fretting wear on railway axle press-fit specimens. Tribol. Int. 2023, 178, 108024. [Google Scholar] [CrossRef]
- Sarabandi, S.; Soleimani, H.; Mahmoudi, S. The 3-D finite-element analysis of press fitting process in railway wheel-set. Sci. Iran. 2019, 26, 367–374. [Google Scholar] [CrossRef]
- Gao, Z.; Meng, X.Y.; Guan, S. Simulation and analytical study of the process parameters of the press-fit method. Int. J. Nanomanuf. 2024, 19, 1–22. [Google Scholar] [CrossRef]
- ISO 286-1:2010; Geometrical Product Specifications (GPS)—ISO Code System for Tolerances on Linear Sizes—Part 1: Basis of Tolerances, Deviations and Fits. International Organization for Standardization: Geneve, Switzerland, 2010; p. 38.
- Maxim, D.I.; Marsavina, L.; Rusu, L. The effect of manufacturing on the press fit insertion force. IOP Conf. Ser. Mater. Sci. Eng. 2018, 416, 012050. [Google Scholar] [CrossRef]
- Wang, M.; Hou, B.; Wang, W. Deep-learning-coupled numerical optimization method for designing geometric structure and insertion-withdrawal force of press-fit connector. Acta Mech. Solida Sin. 2025, 38, 78–90. [Google Scholar] [CrossRef]




| Point A | Point B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| μ = 0 | μ = 0.1 | μ = 0.2 | μ = 0.3 | μ = 0.4 | μ = 0 | μ = 0.1 | μ = 0.2 | μ = 0.3 | μ = 0.4 | |
| σr (MPa) | −300.38 | −317.64 | −335.75 | −348.14 | −336.53 | −221.61 | −168.57 | −125.28 | −90.86 | −62.78 |
| σt (MPa) | −371.82 | −346.21 | −316. 68 | −292.52 | −268.84 | 203.43 | 209.19 | 211.62 | 211.52 | 210.72 |
| σz (MPa) | −219.36 | −147.81 | 248.99 | 394.33 | 454.58 | 26.54 | 34.35 | 35.71 | 33.77 | 30.48 |
| σvM (MPa) | 247.91 | 404.84 | 482.42 | 534.68 | 537.35 | 351.21 | 315.05 | 286.22 | 263.77 | 245.85 |
| Point A | Point B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| μ = 0 | μ = 0.1 | μ = 0.2 | μ = 0.3 | μ = 0.4 | μ = 0 | μ = 0.1 | μ = 0.2 | μ = 0.3 | μ = 0.4 | |
| σr (MPa) | −242 | −261.32 | −284.57 | 303.84 | 303.30 | 118.63 | 83.12 | 55.40 | 34.13 | 17.88 |
| σt (MPa) | −338.64 | 335.45 | 299.86 | 277.74 | 252.40 | 226.12 | 229.18 | 231.41 | 231.58 | 229.63 |
| σz (MPa) | −189.5 | −120.19 | 175.69 | 305.66 | 442.35 | 13.75 | 13.70 | 10.83 | 6.61 | 2.03 |
| σvM (MPa) | 315.35 | 364.28 | 427.58 | 485.49 | 534.89 | 298.02 | 276.22 | 260.13 | 251.27 | 242.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izard, E.; García-Martín, R.; Rodríguez-Martín, M.; Lorenzo, M. Finite Element Analysis of Friction-Induced Stress Concentrations in Press Fits with Chamfer Hubs. Lubricants 2025, 13, 231. https://doi.org/10.3390/lubricants13050231
Izard E, García-Martín R, Rodríguez-Martín M, Lorenzo M. Finite Element Analysis of Friction-Induced Stress Concentrations in Press Fits with Chamfer Hubs. Lubricants. 2025; 13(5):231. https://doi.org/10.3390/lubricants13050231
Chicago/Turabian StyleIzard, Eulalia, Roberto García-Martín, Manuel Rodríguez-Martín, and Miguel Lorenzo. 2025. "Finite Element Analysis of Friction-Induced Stress Concentrations in Press Fits with Chamfer Hubs" Lubricants 13, no. 5: 231. https://doi.org/10.3390/lubricants13050231
APA StyleIzard, E., García-Martín, R., Rodríguez-Martín, M., & Lorenzo, M. (2025). Finite Element Analysis of Friction-Induced Stress Concentrations in Press Fits with Chamfer Hubs. Lubricants, 13(5), 231. https://doi.org/10.3390/lubricants13050231







