An Approach for Predicting the Vibro-Impact Behavior of Angular Contact Ball Bearing Considering Variable Clearance
Abstract
1. Introduction
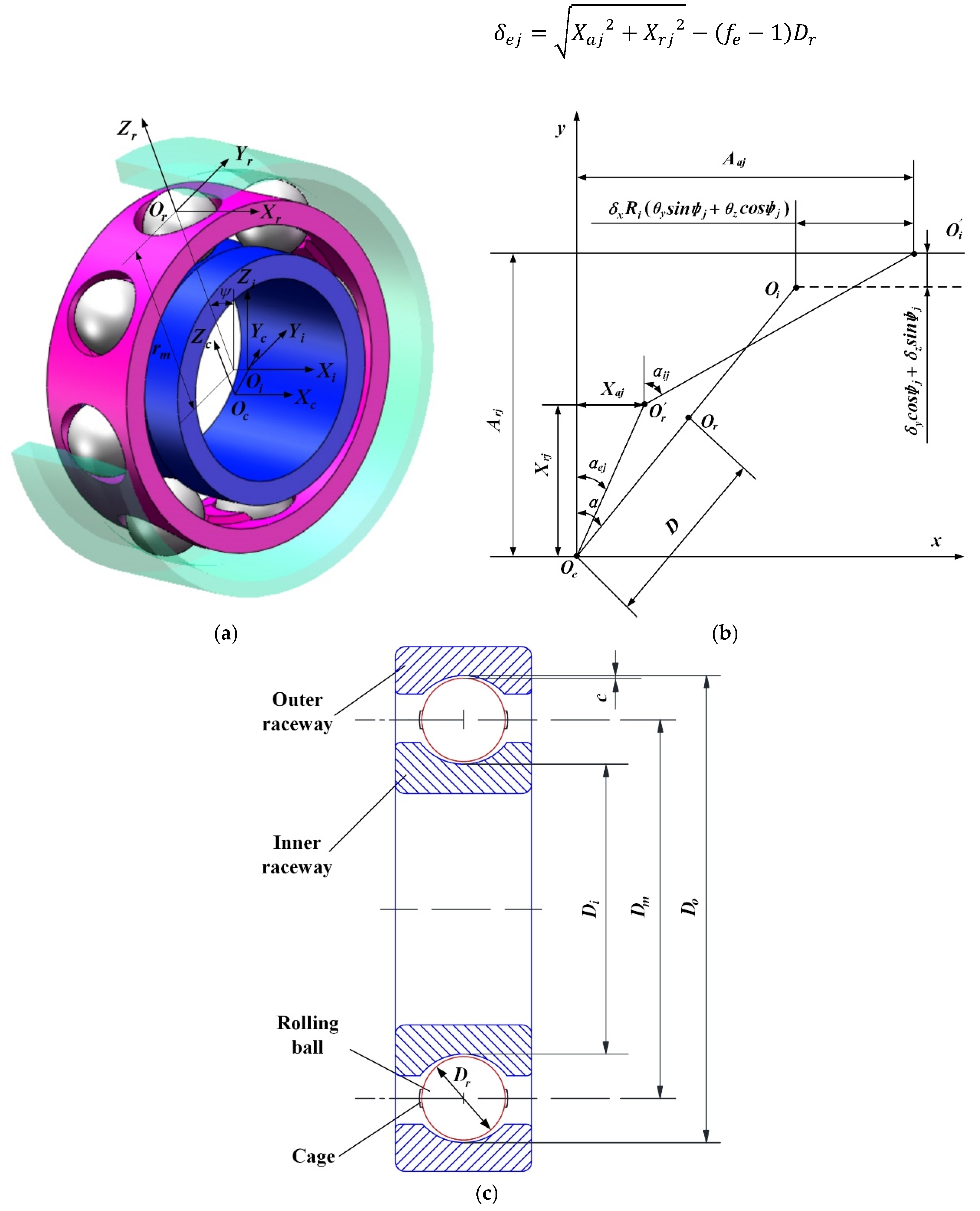
2. Theoretical Analysis of Ball Bearings
2.1. Geometric Relationship of Coordinate Systems
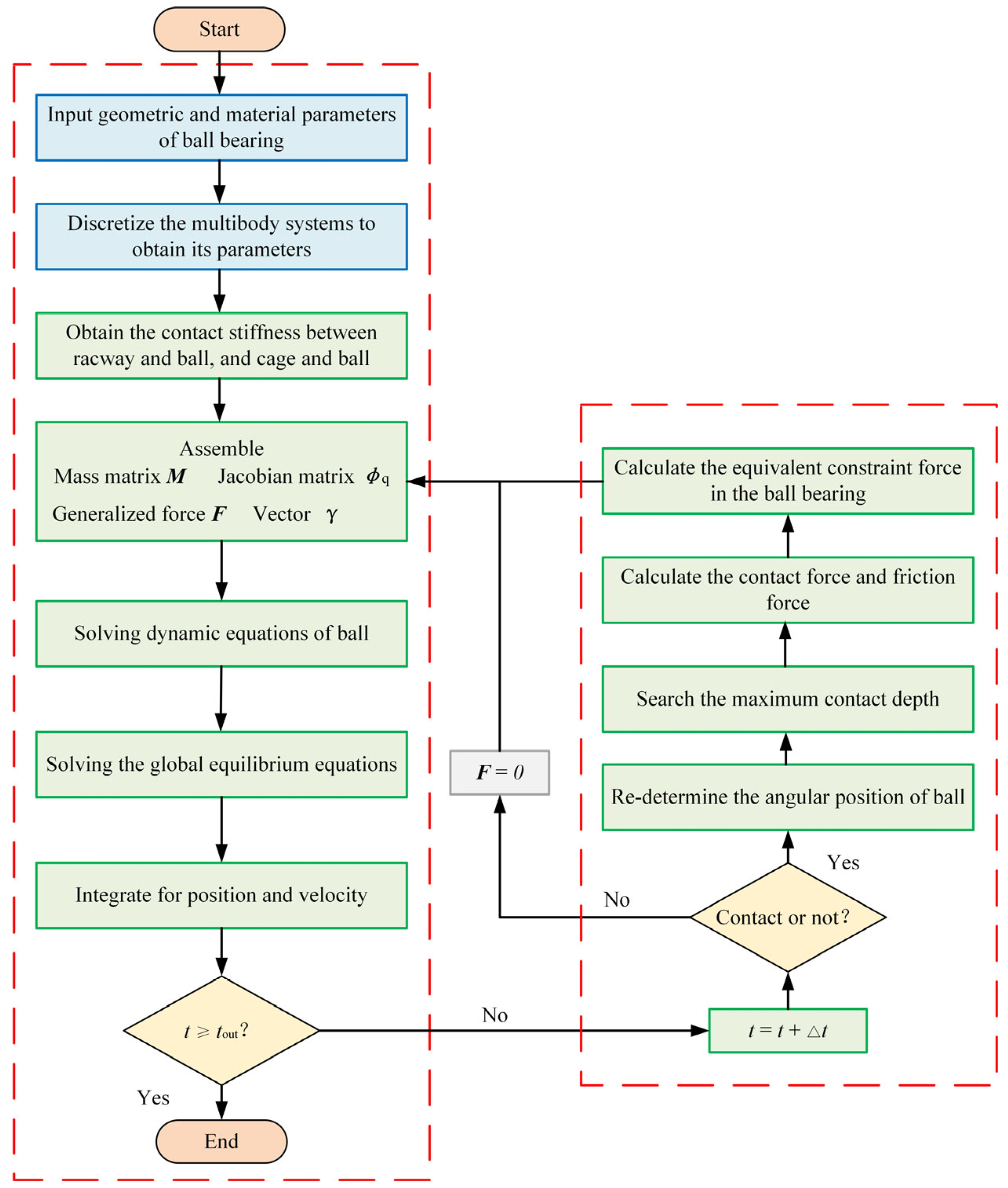
2.2. Equilibrium Constraint and Dynamic Motion
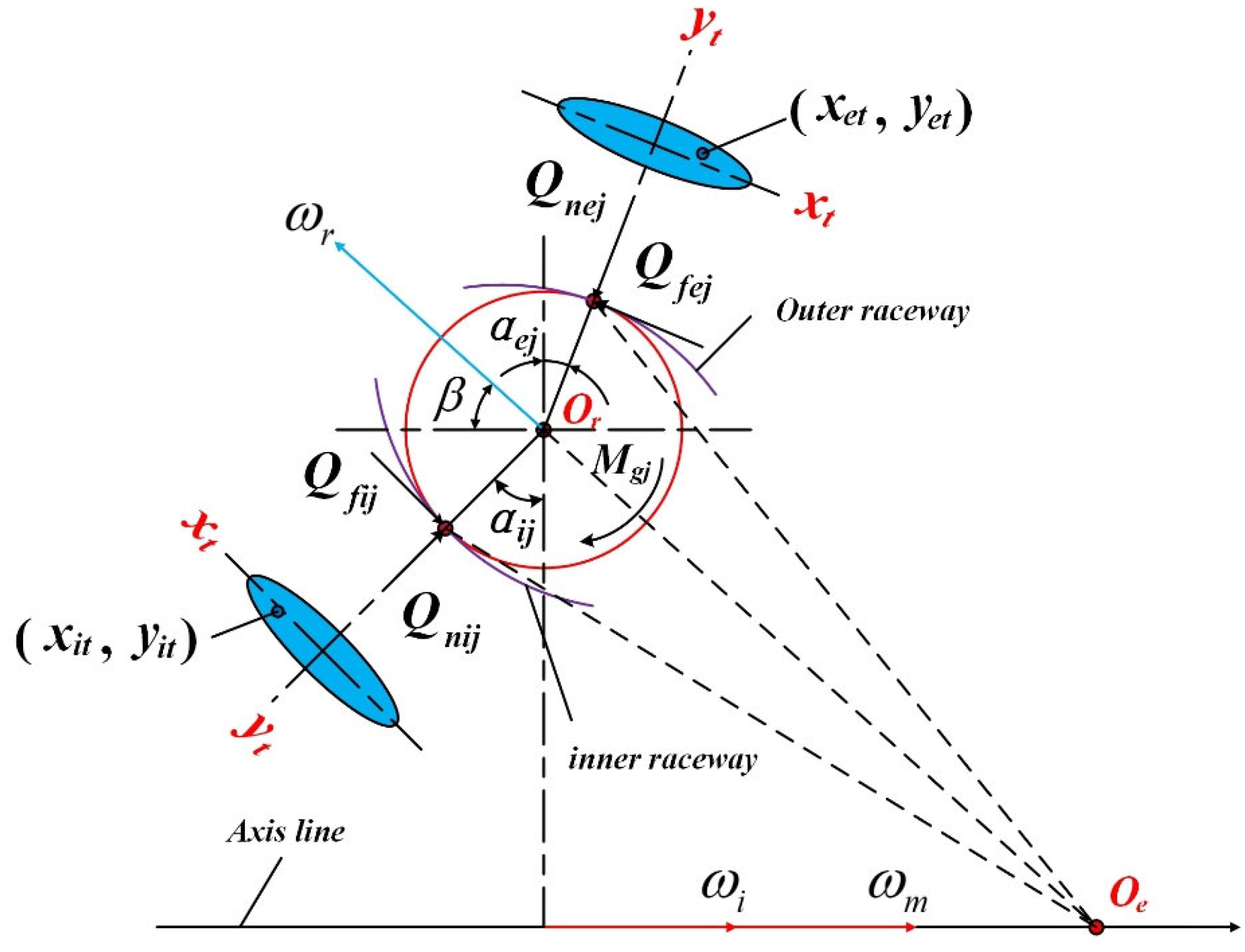
2.3. Interactive Force of Contact Elements
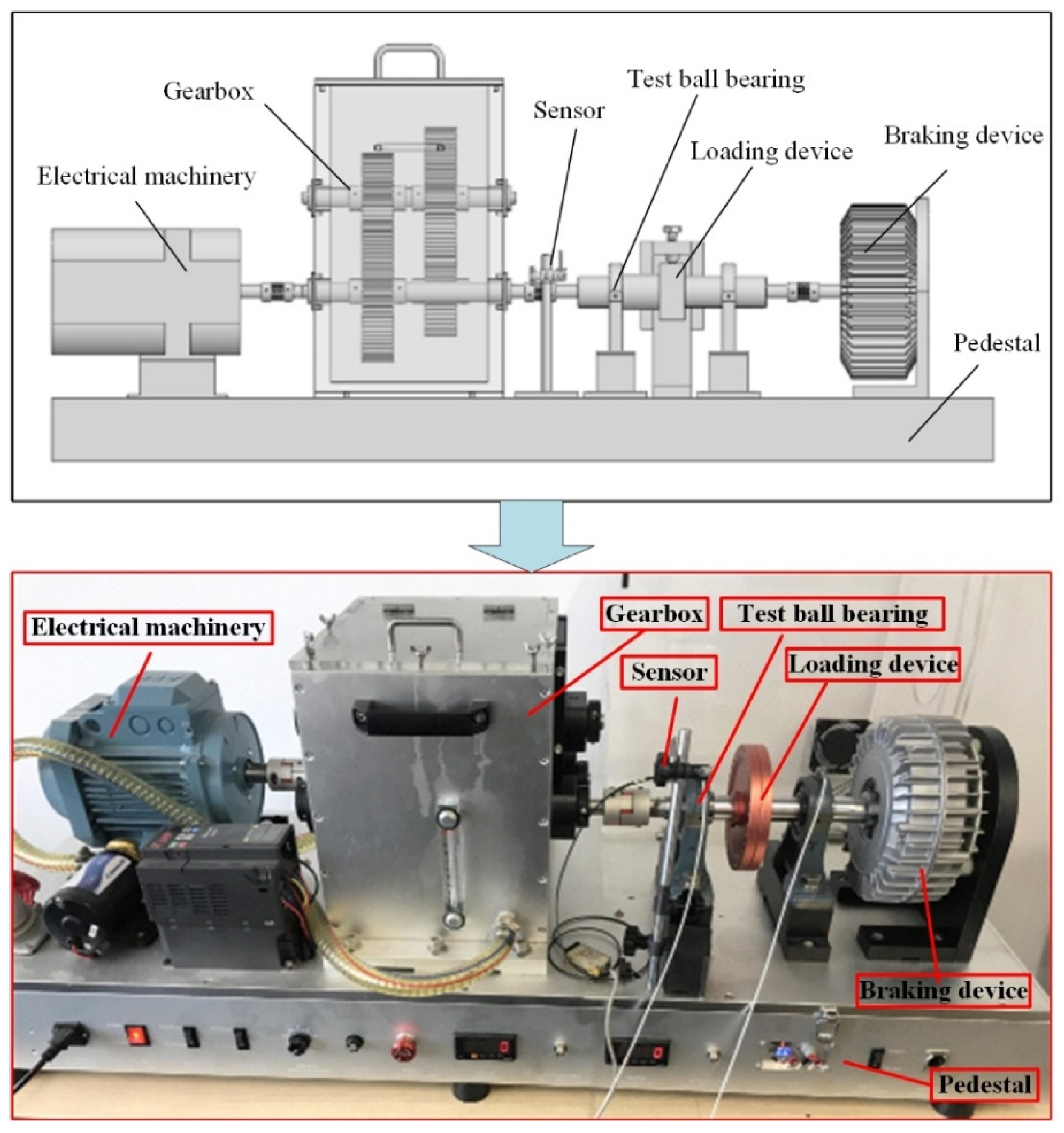
3. Solution and Experiment
4. Results and Discussion
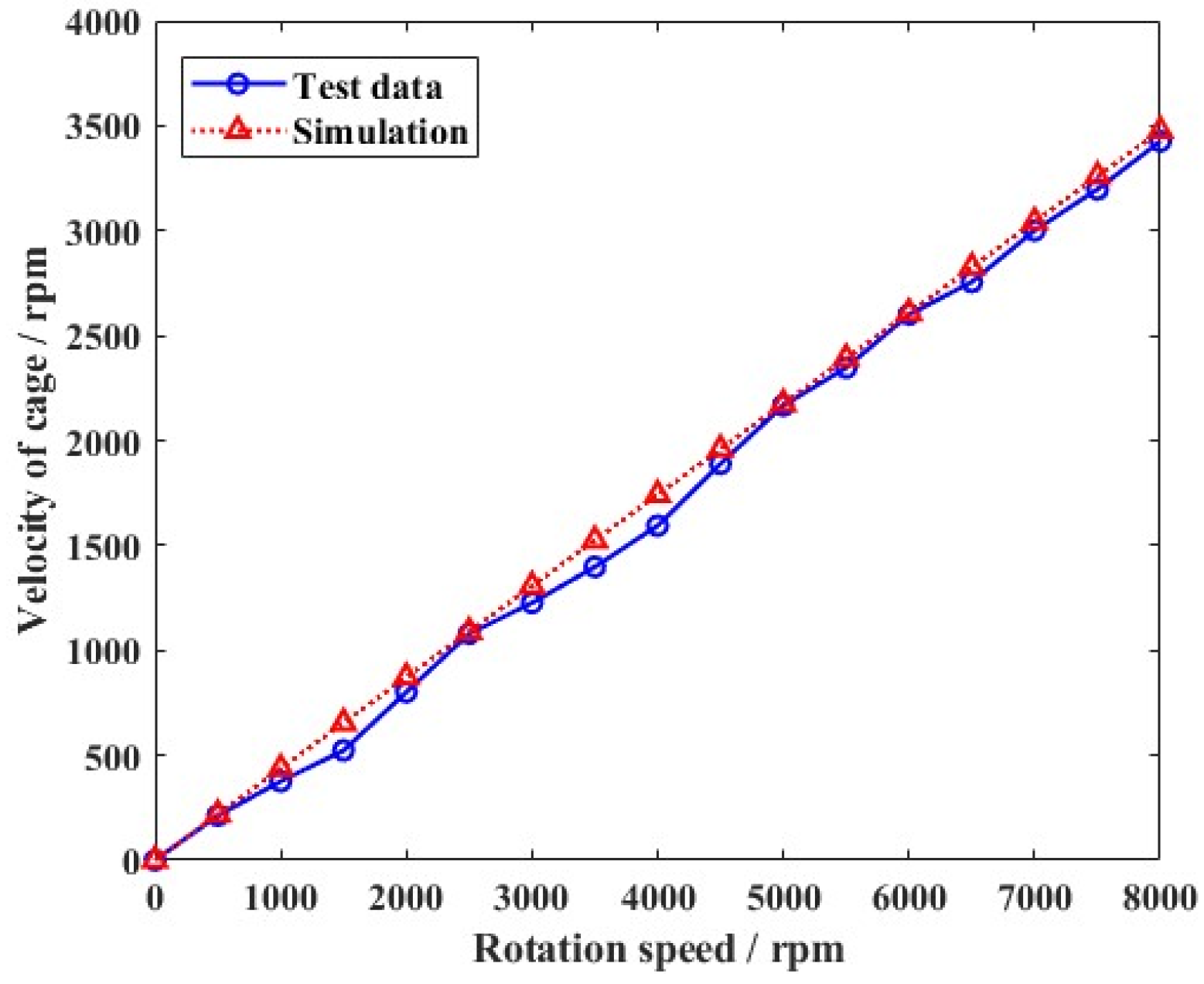
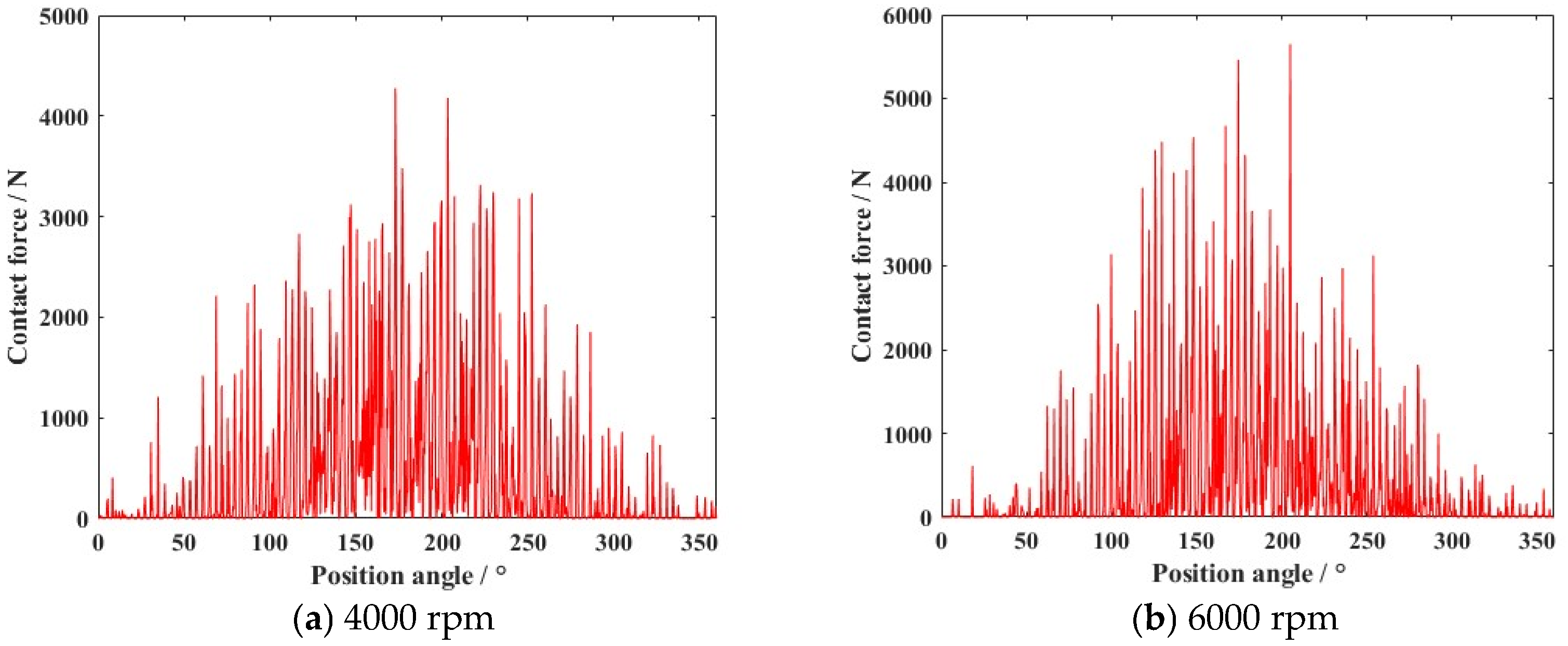
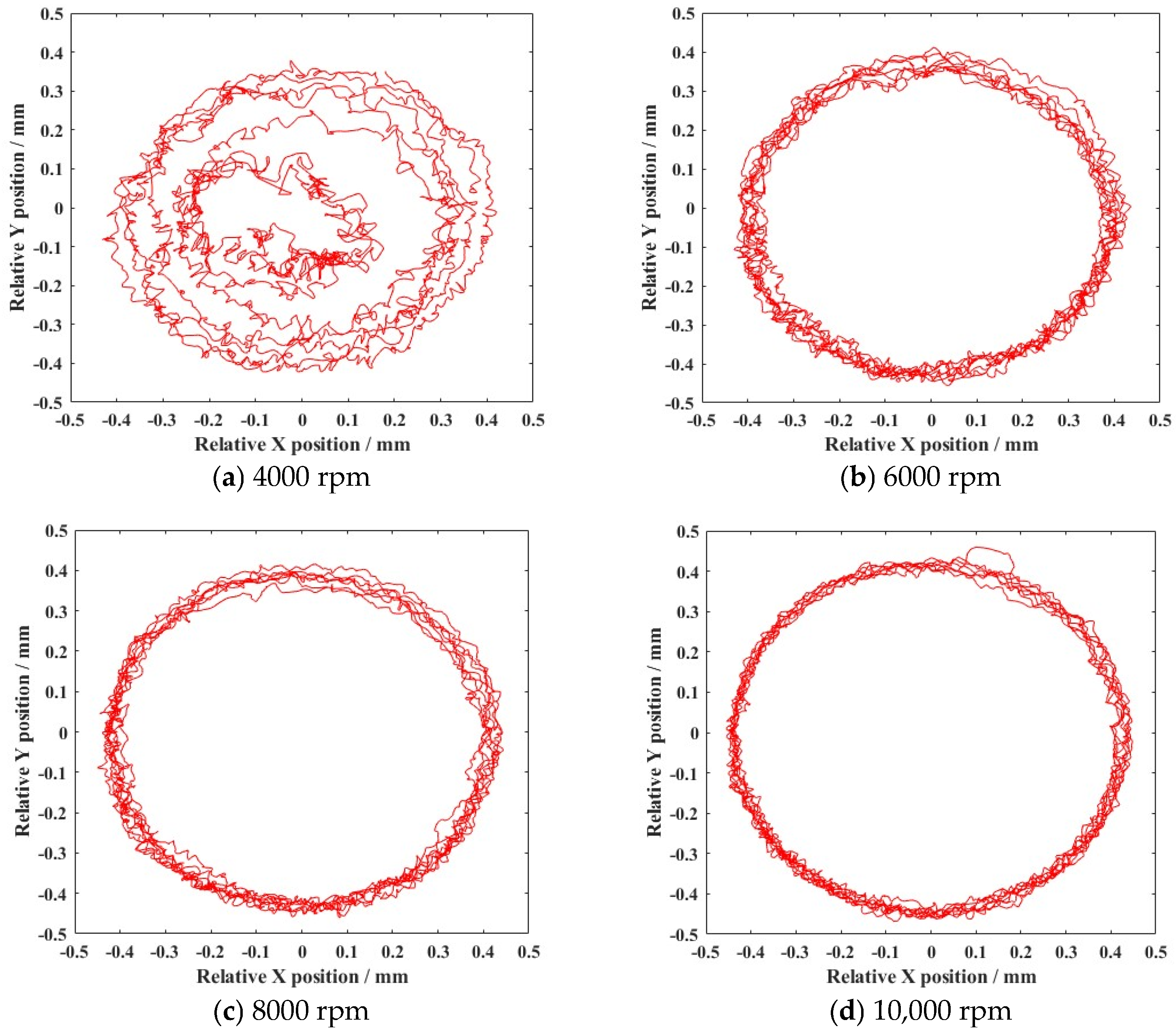
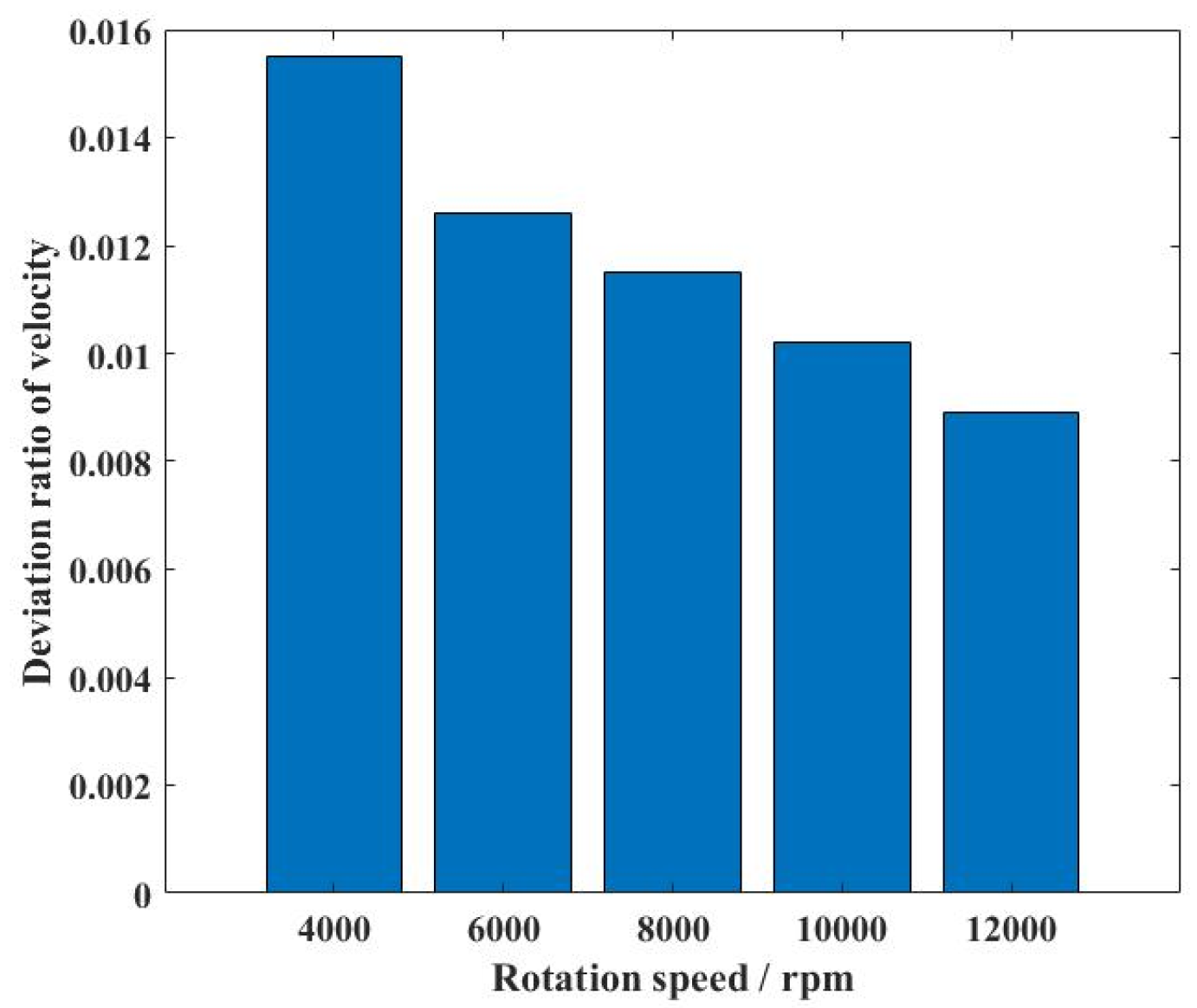
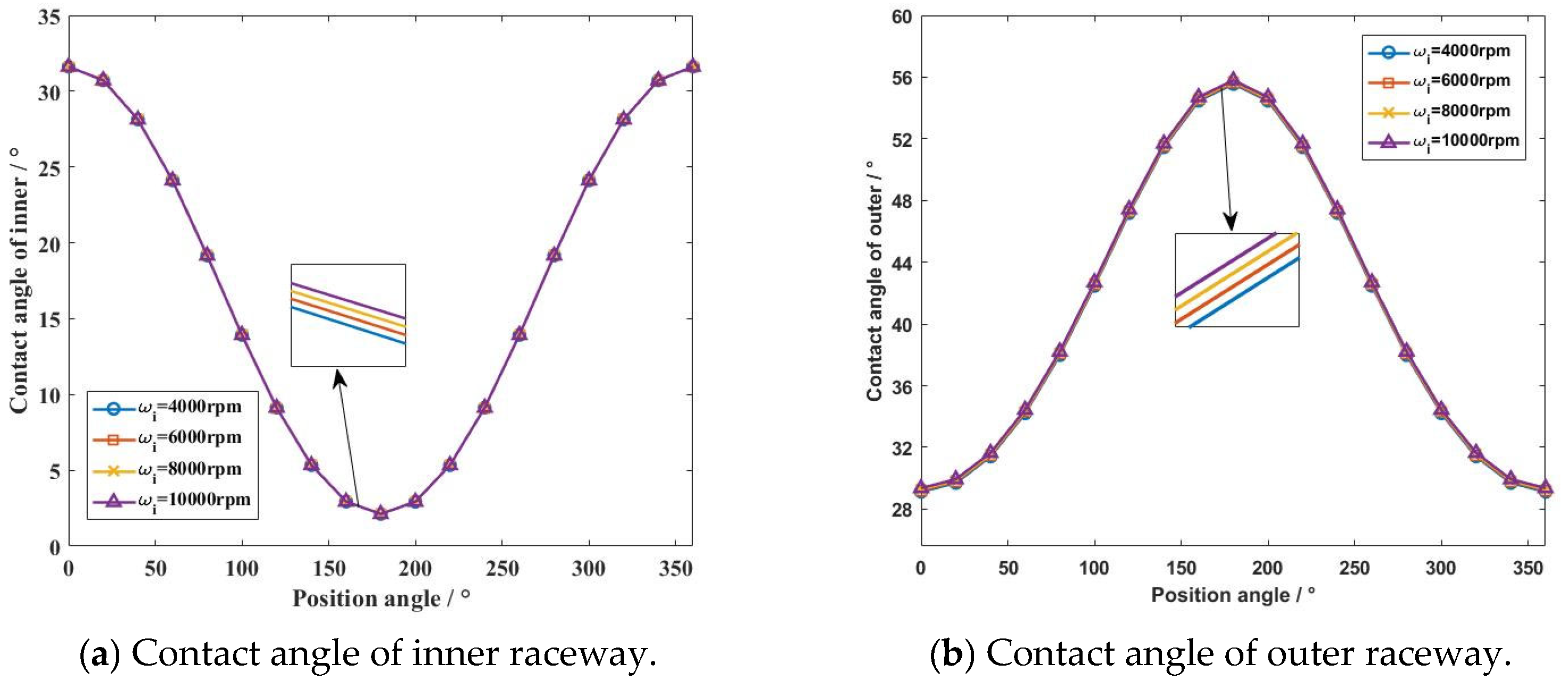
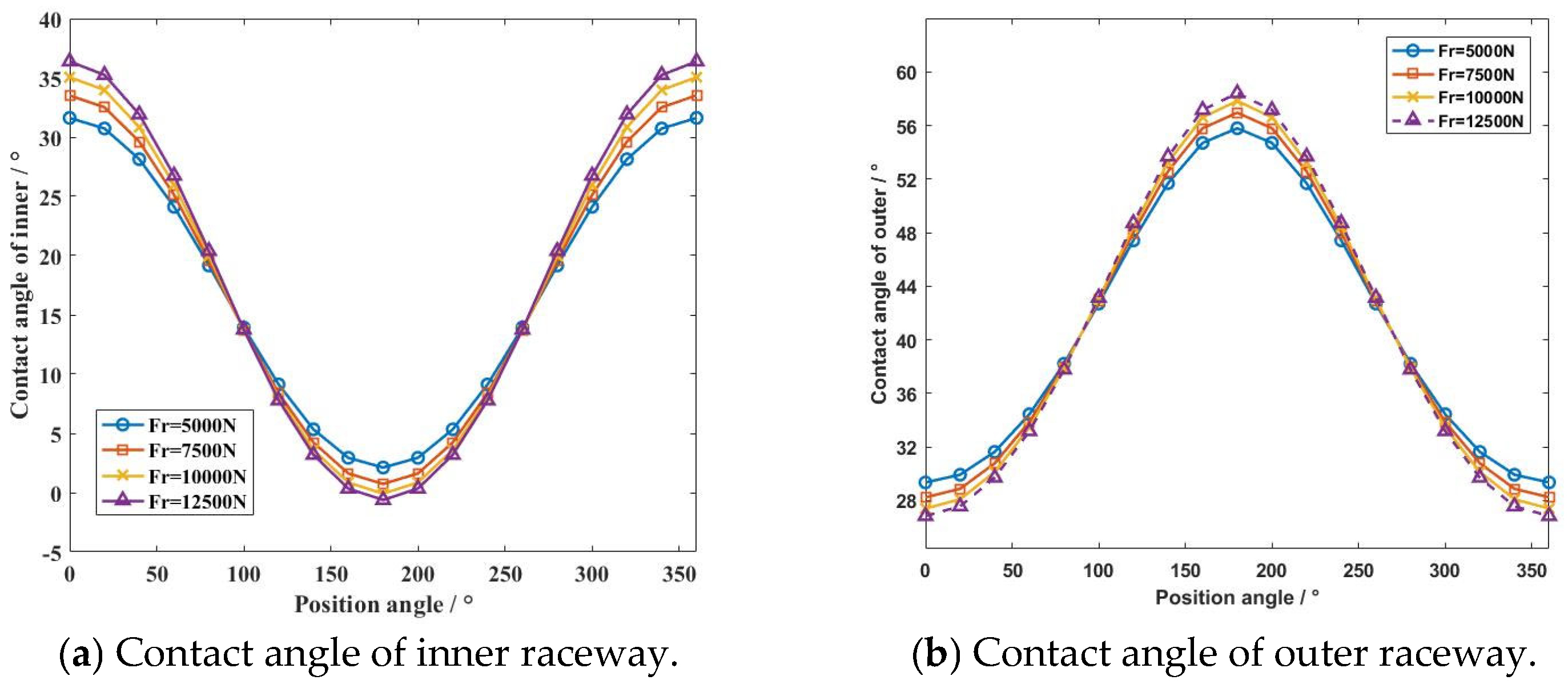
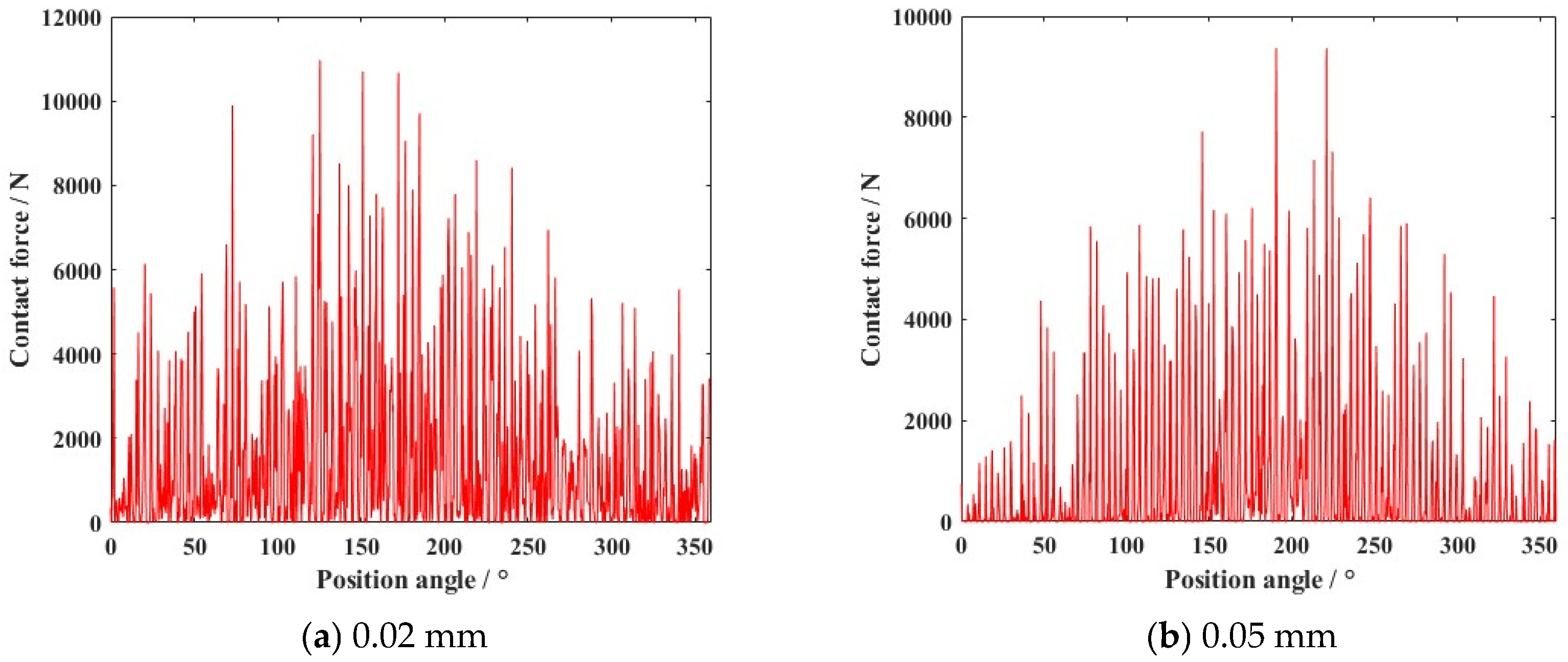
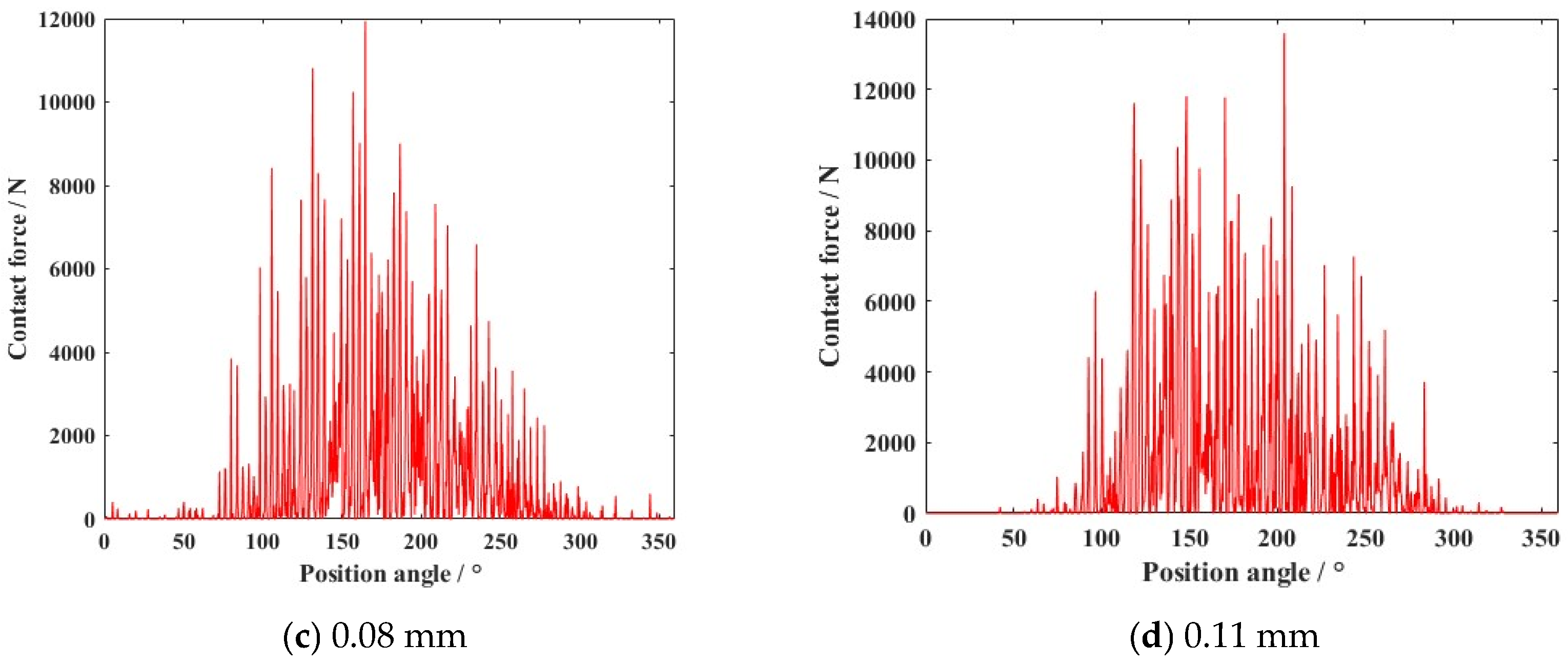
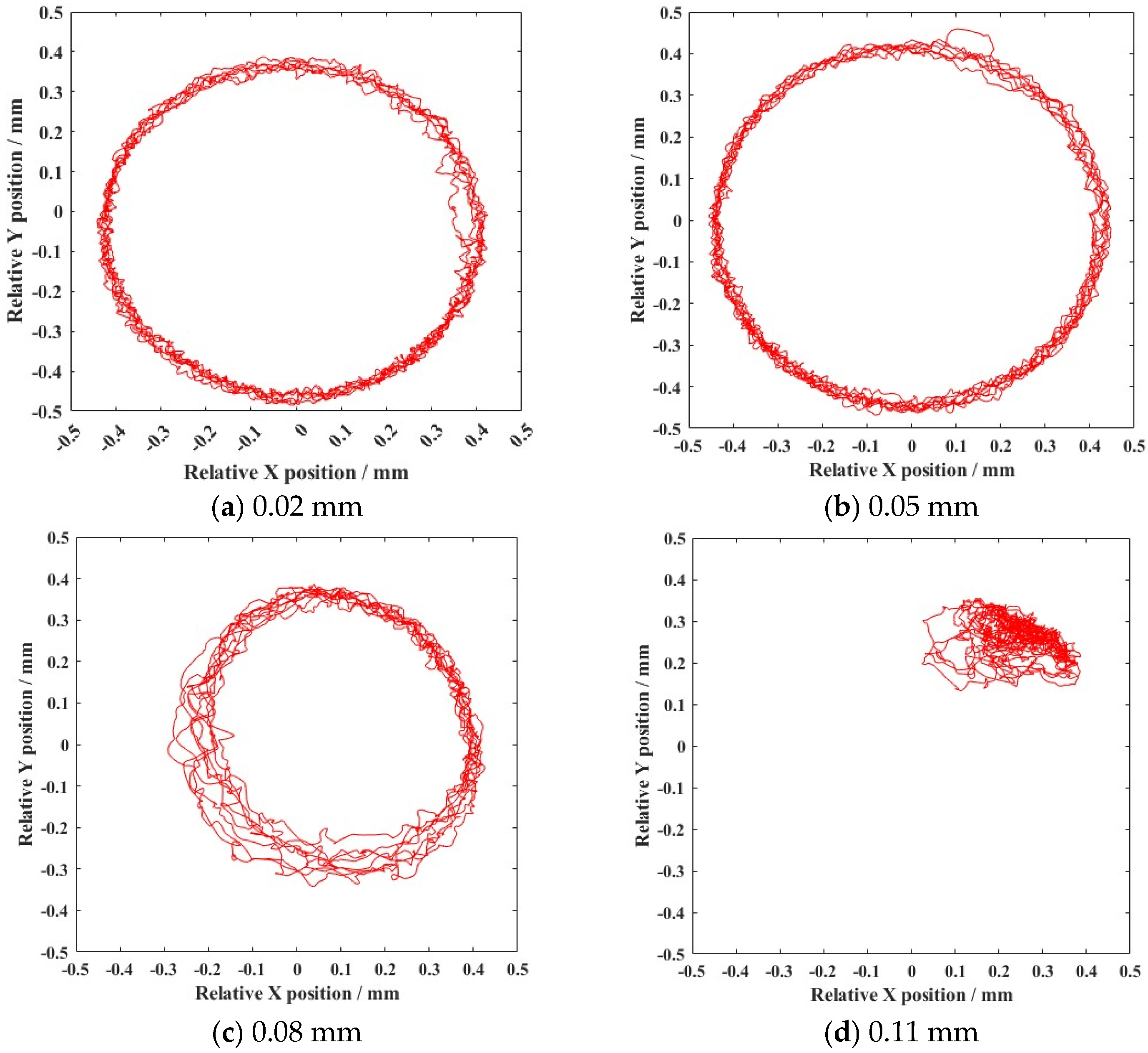
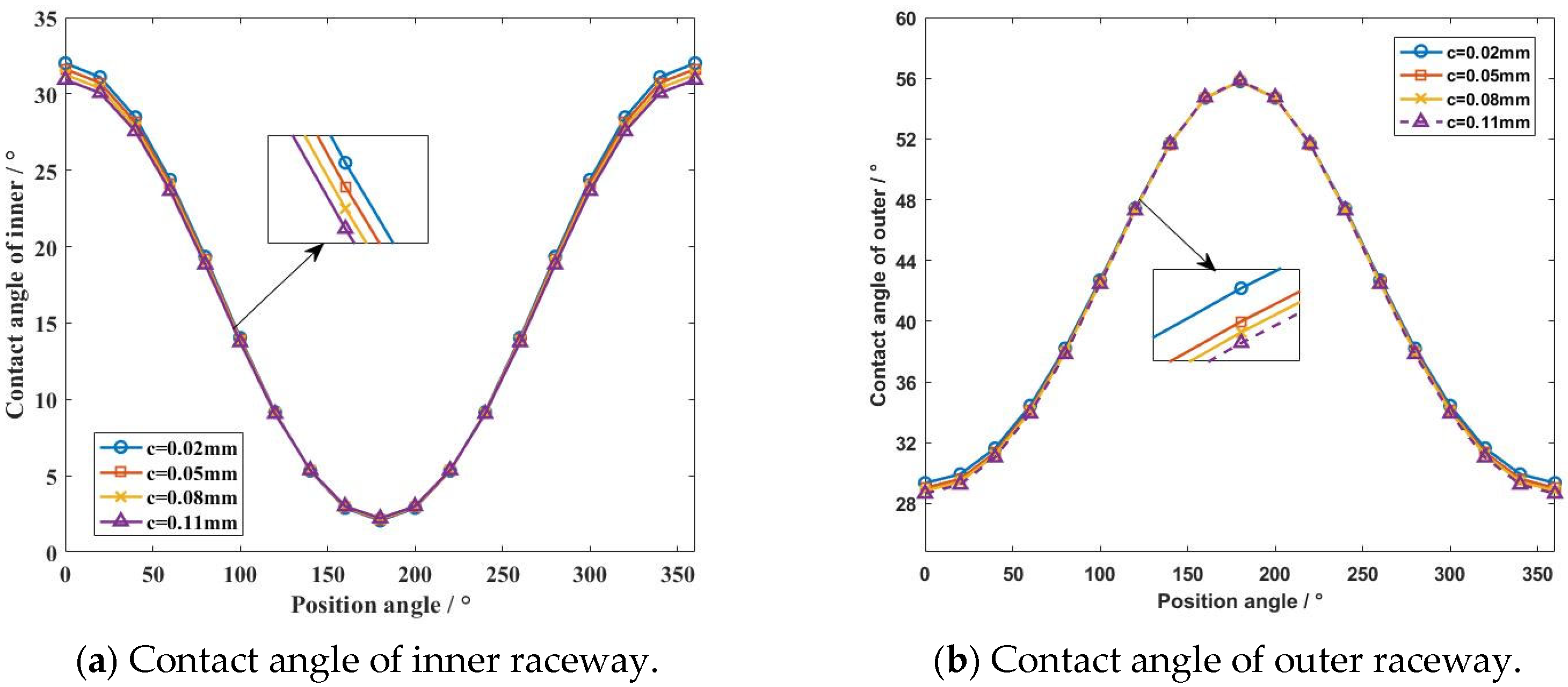
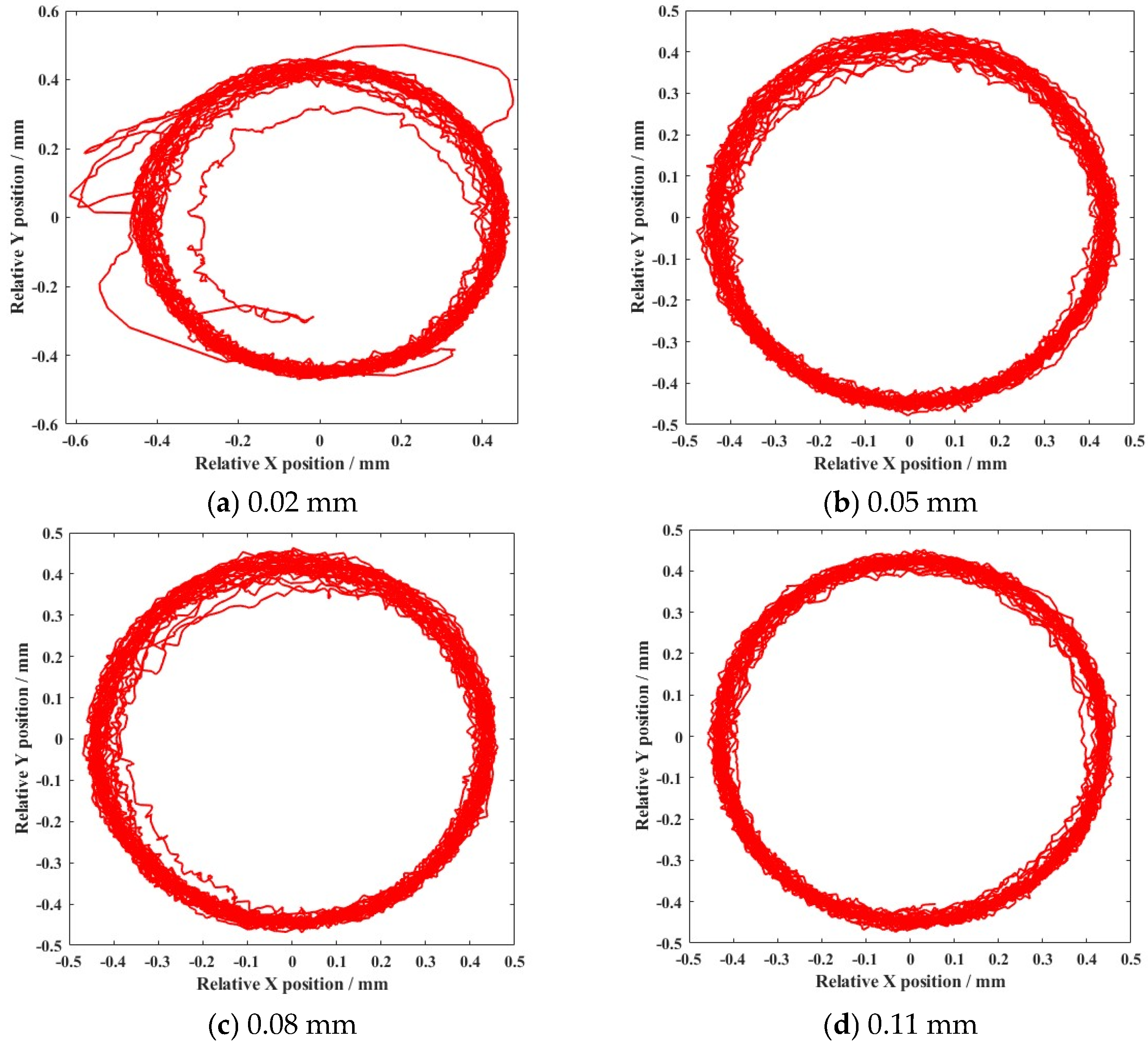
4.1. Dynamic Characteristics of the Ball Bearing Under a Uniform Motion State
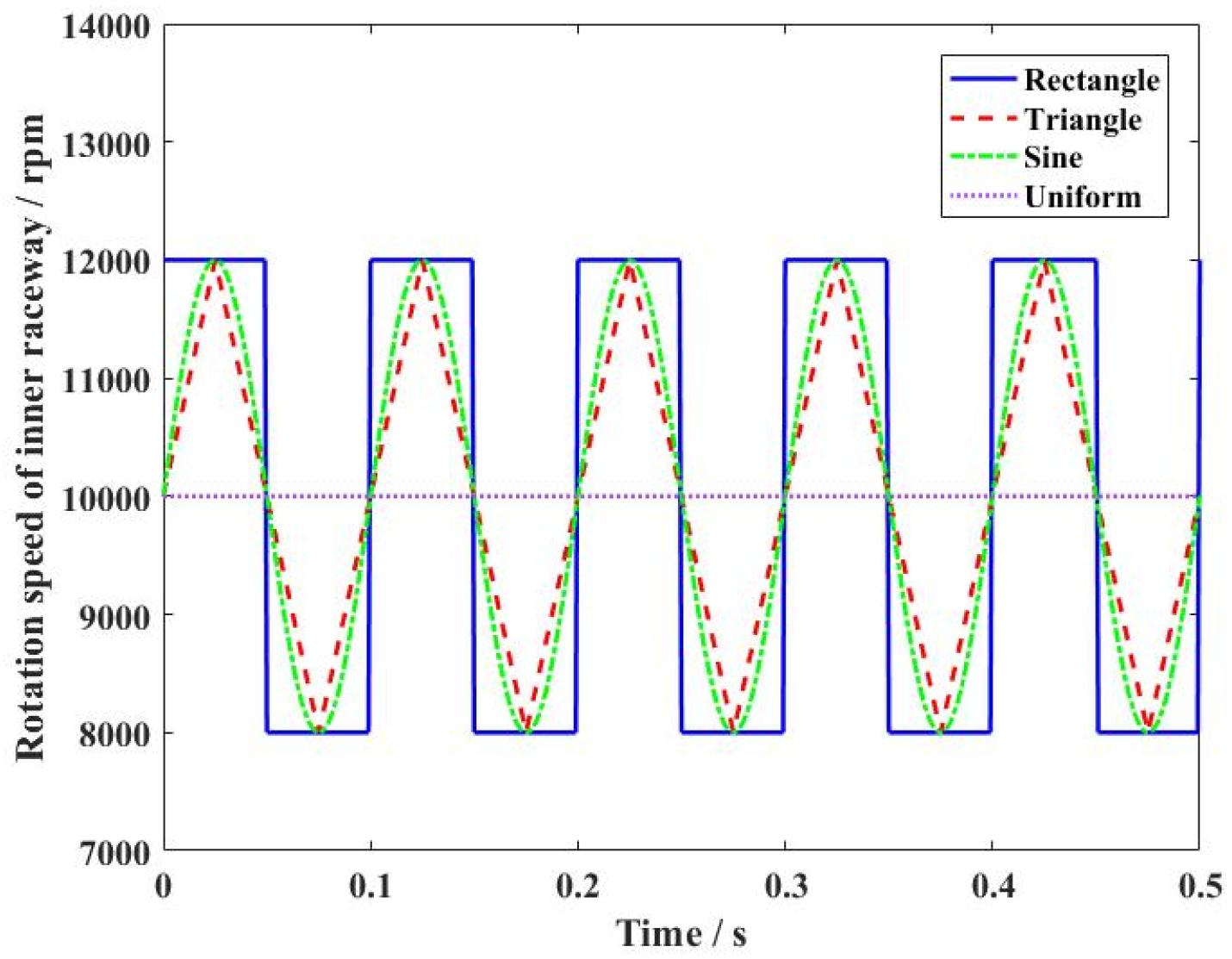
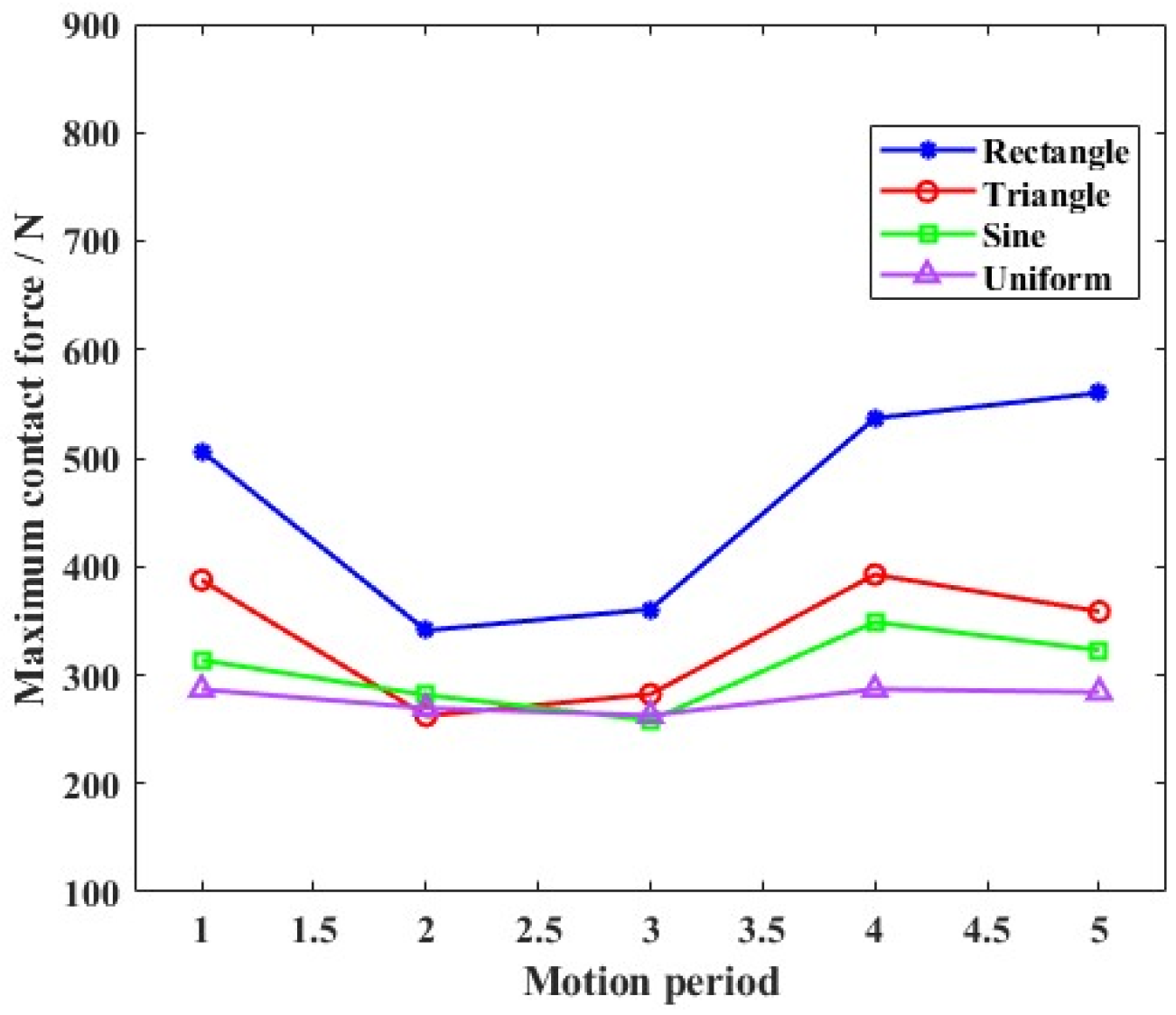
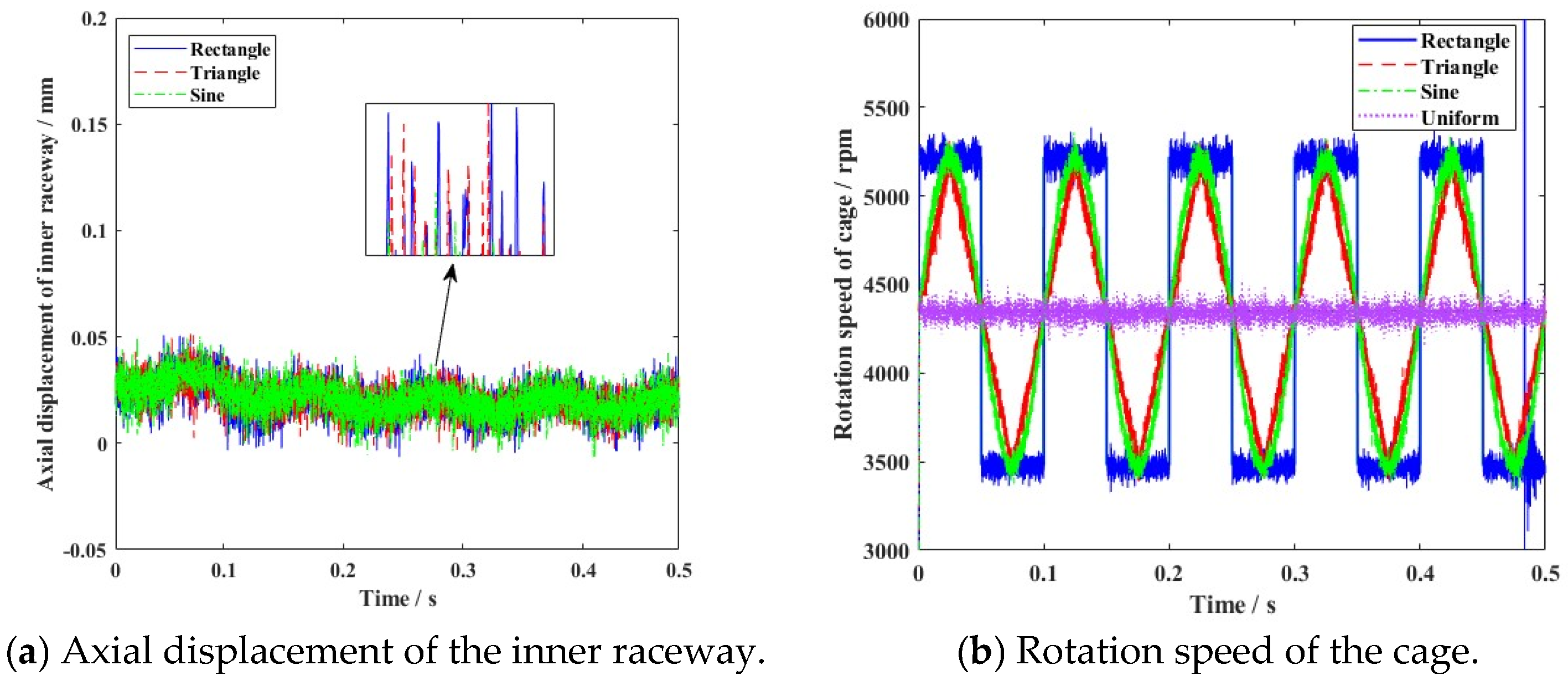
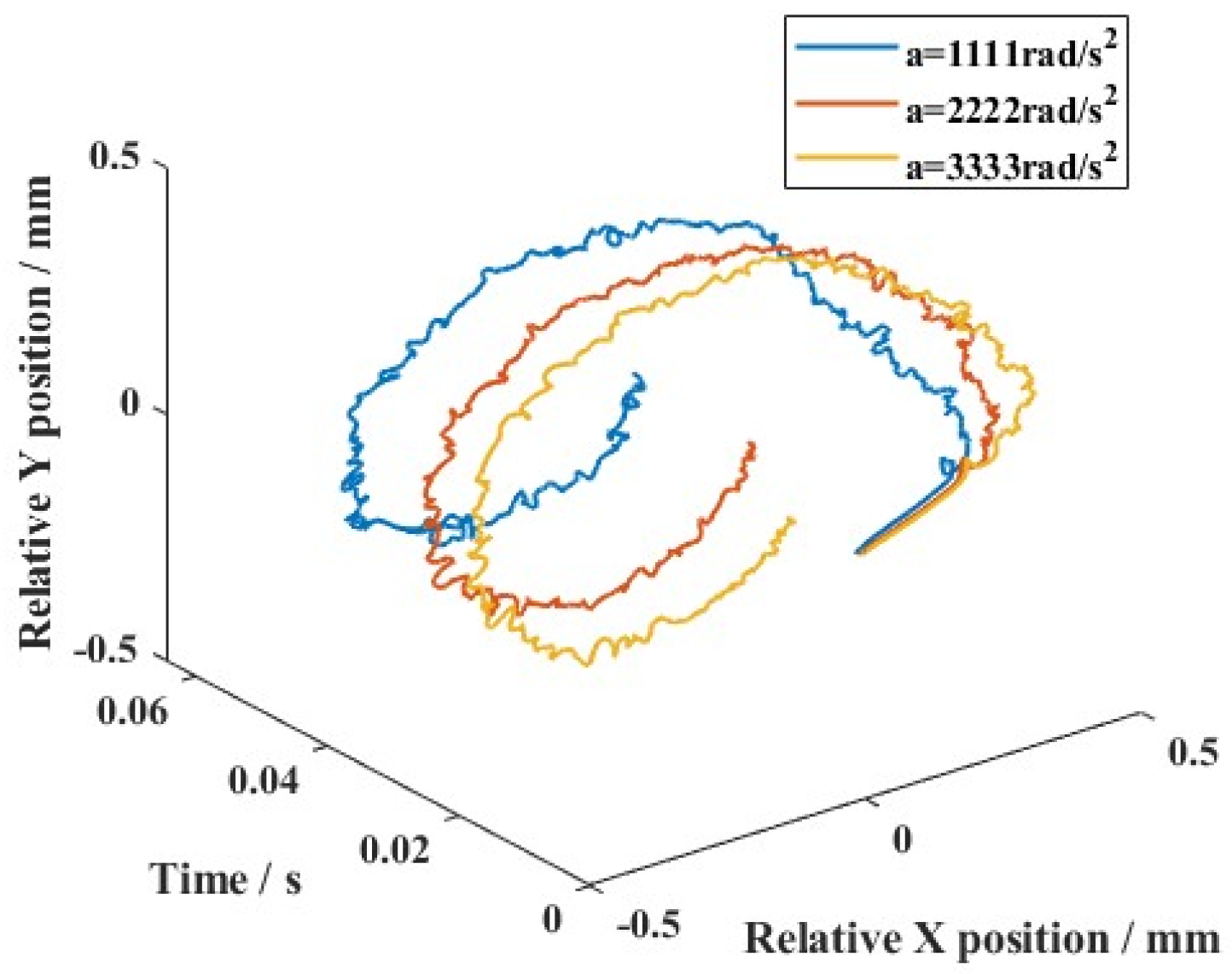
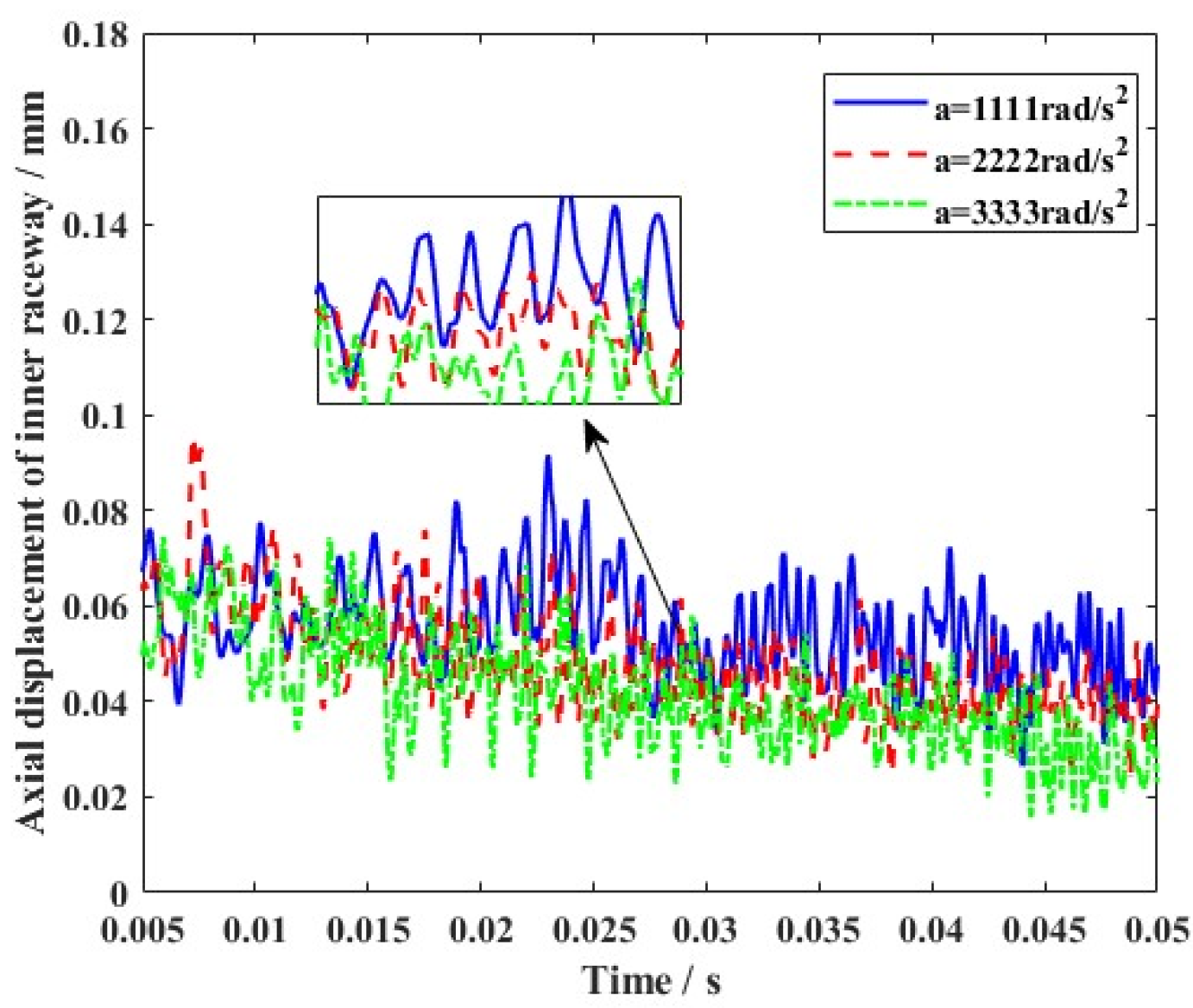
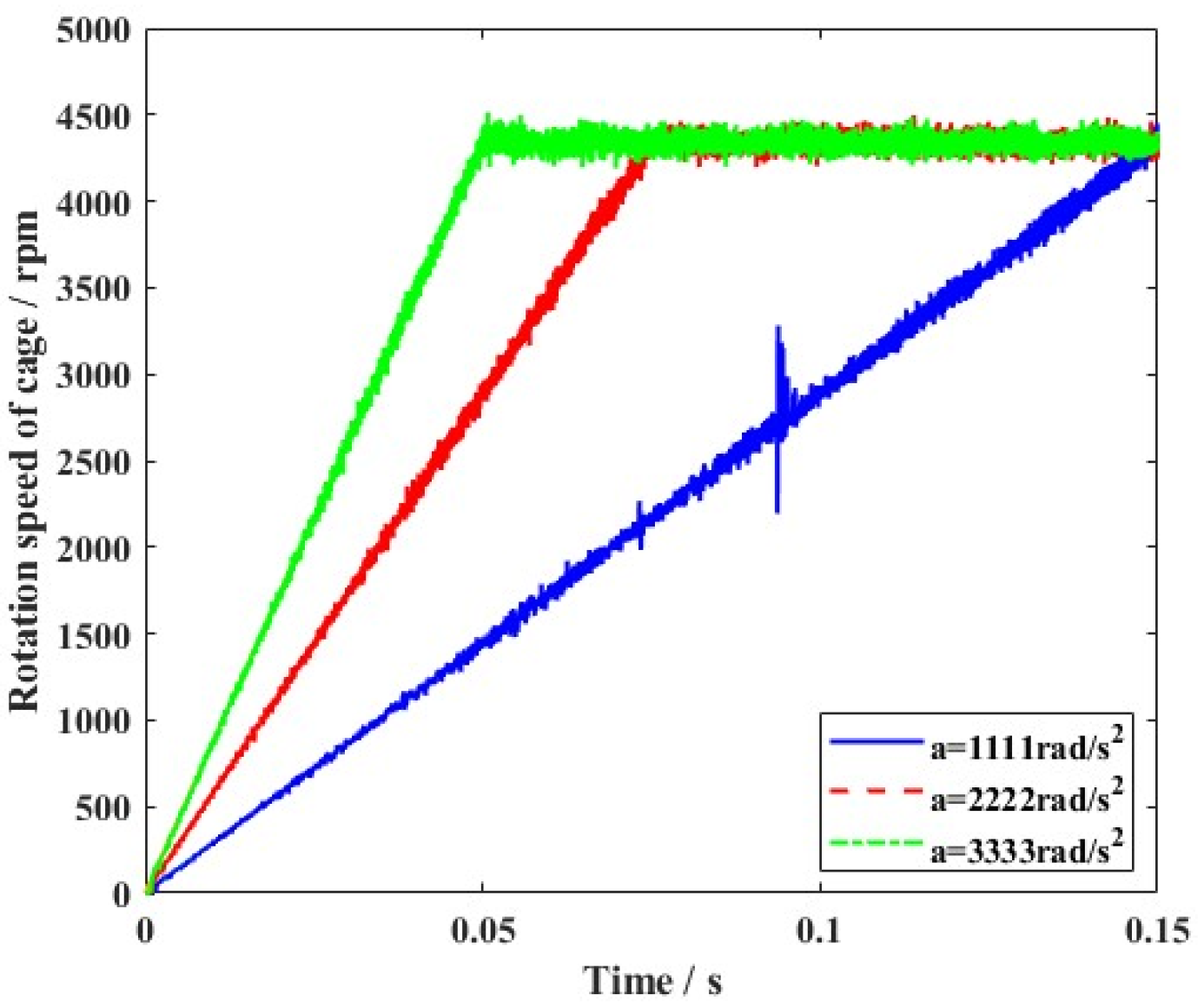
4.2. Dynamic Characteristics of the Ball Bearing Under Various Motion States
5. Conclusions
- (1)
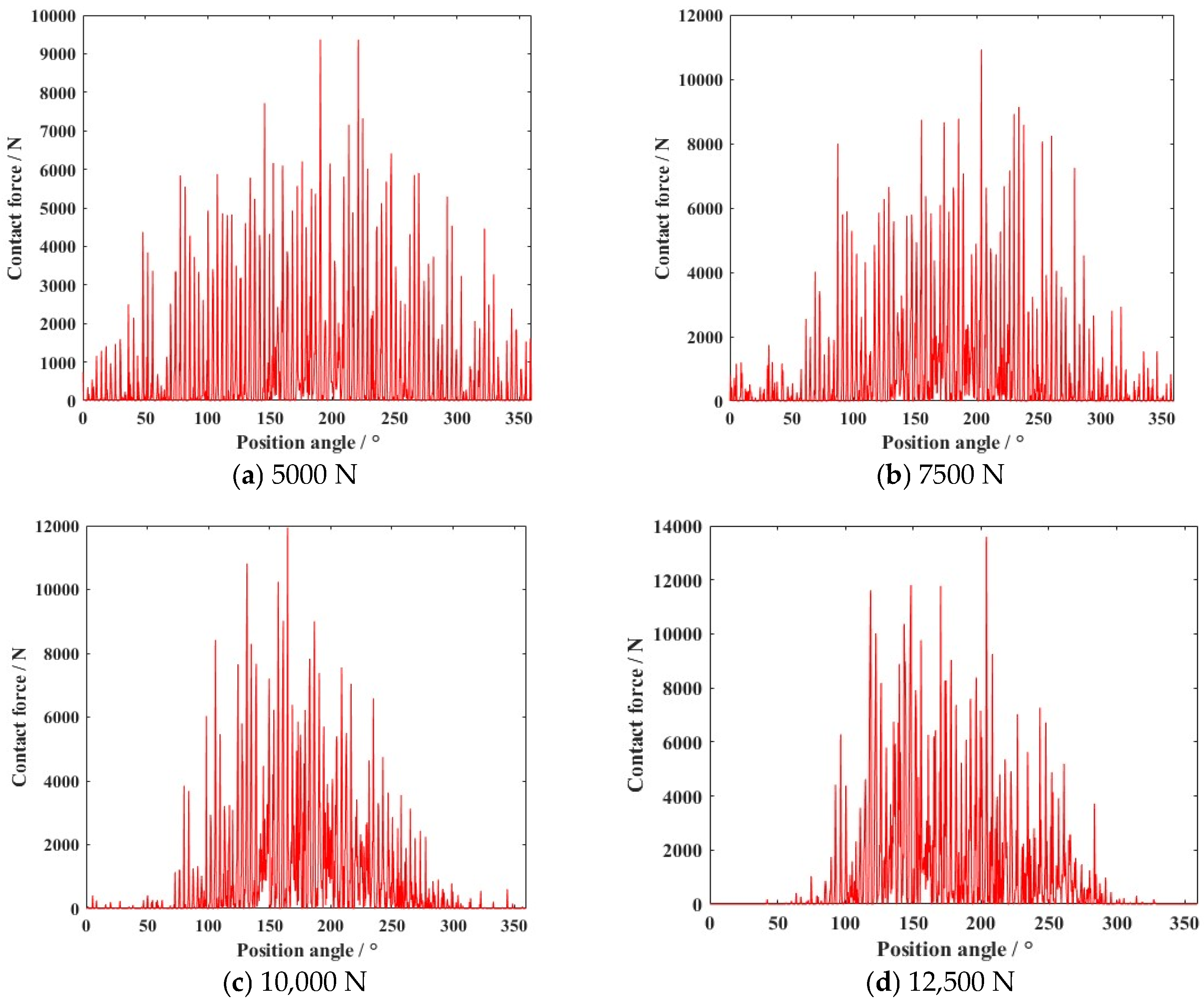
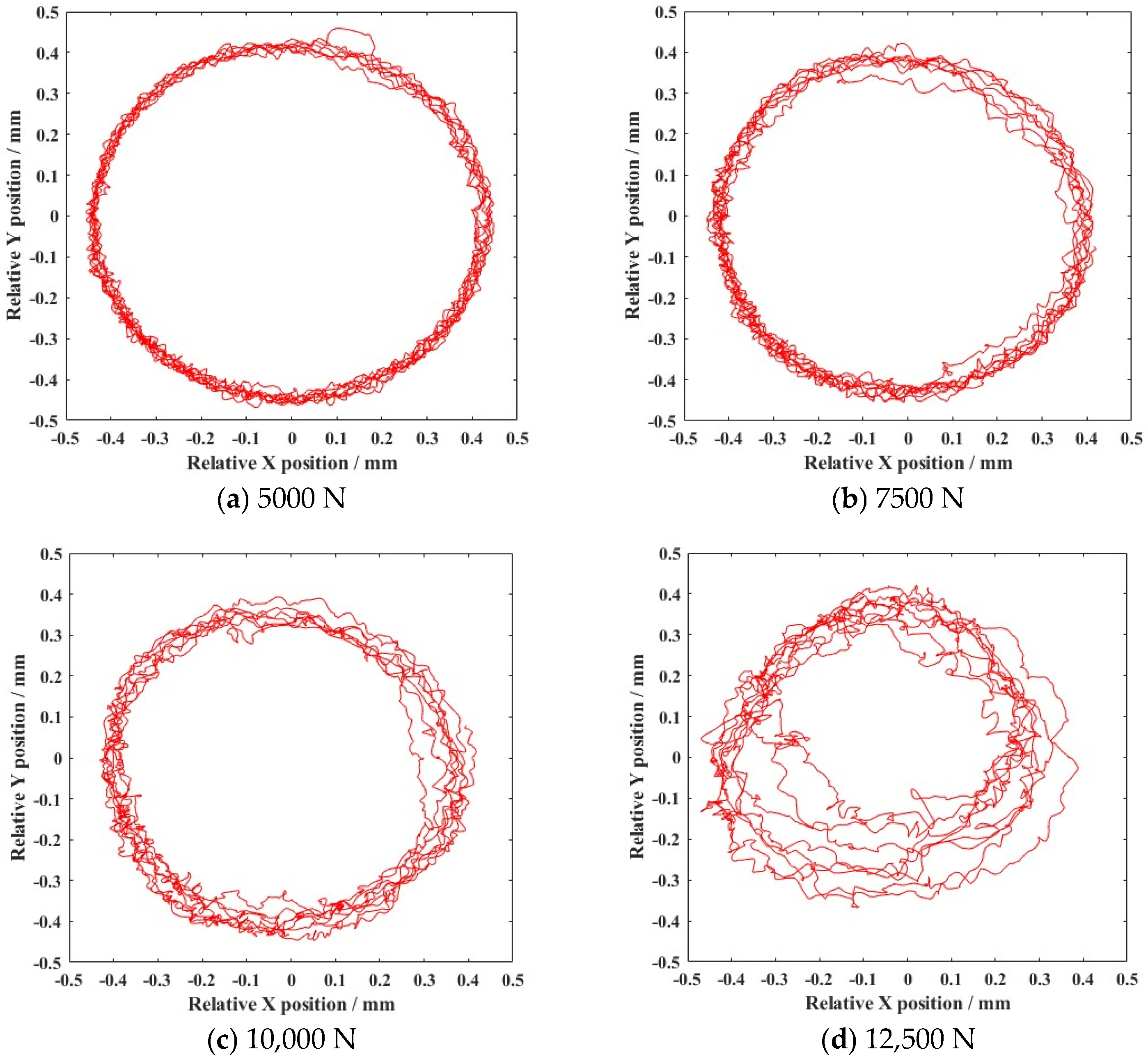
- According to the simulation results, clearance caused high-frequency collisions of the ball bearing elements. In the uniform motion state, the contact force increased with the growth in rotation speed, and the deviation in vortex motion led to worsened stability of the cage.
- (2)
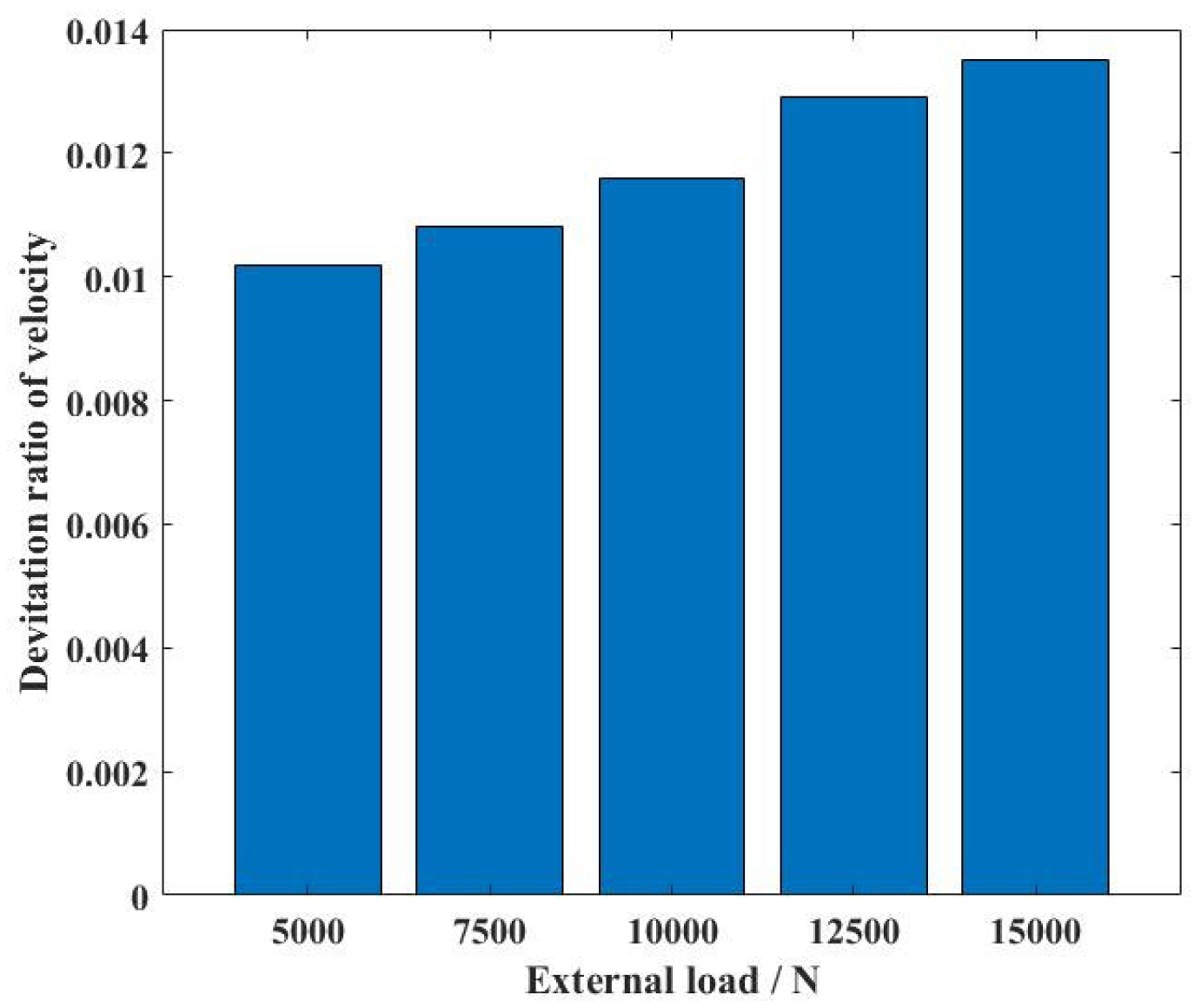
- The variation in external load and clearance size were the main factors contributing to the appearance of nonlinear dynamic responses. With the growth in external load increase (from 5000 N to 12,500 N), the deviation ratio of the cage’s mass center velocity increased to 24.44%. The change of clearance size (from 0.02 mm to 0.14 mm) improved the deviation ratio of cage’s mass center velocity (33.11%).
- (3)
- Furthermore, variable clearance in ball bearing components was produced in various motion states. Although vibration was always observed during motion, the varying gradient was sensitive to the outline of the rotation speed wave. The slow change in operating conditions helped restrain the nonlinear vibration characteristics, which was more suitable for the stability of angular contact ball bearings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, S.; Gu, J.; Cui, Y. Dynamic analysis of a tapered roller bearing. Ind. Lubr. Tribol. 2017, 70, 191–200. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y. Modeling of a deep-groove ball bearing with waviness defects in planar multibody system. Multibody Sys. Dyn. 2015, 33, 229–258. [Google Scholar] [CrossRef]
- Bover, C.; Zamponi, I. An approach for predicting the internal behavior of ball bearings under high moment load. Mech. Mach. Theory 2016, 101, 1–22. [Google Scholar]
- Chen, Y.; Wu, X.; Wang, X. Clearance-induced contact trajectory uncertainty of angular contact ball bearing under coupling operating condition. Meccanica 2023, 58, 43–66. [Google Scholar] [CrossRef]
- Liu, J.; Shao, Y. Dynamic modeling for rigid rotor bearing systems with a localized defect considering additional deformations at the sharp edegs. J. Sound Vib. 2017, 398, 84–102. [Google Scholar] [CrossRef]
- Xi, H.; Wang, H.; Han, W. Contact trajectory of angular contact ball bearings under dynamic operating condition. Tribol. Int. 2016, 104, 247–262. [Google Scholar] [CrossRef]
- Ma, S.; Li, W.; Yan, K.; Li, Y.; Zhu, Y.; Hong, J. A study on the dynamic contact feature of four-contact-point ball bearing. Mech. Syst. Signal Pract. 2022, 174, 109111. [Google Scholar] [CrossRef]
- Chen, X.; Wang, T.; Jiang, S. Study on dynamic behavior of planar multibody system with multiple lubrication clearance joints. Eur. J. Mech. A Solid. 2022, 91, 104404. [Google Scholar] [CrossRef]
- Yao, T.; Xian, L.; Wang, L.; Liu, X. Multibody contact dynamics on mechanisms with deep groove ball bearing joints. J. Mech. Sci. Technol. 2017, 31, 4119–4135. [Google Scholar] [CrossRef]
- Yan, K.; Wang, N.; Zhai, Q.; Zhu, Y.; Zhang, J.; Niu, Q. Theoretical and experimental investigation on the thermal characteristics of double-row tapered roller bearings of high speed locomotive. Int. J. Heat Mass Transf. 2015, 84, 1119–1130. [Google Scholar] [CrossRef]
- Han, Q.; Li, X.; Chu, F. Skidding behavior of cylindrical roller bearings under time-variable load conditions. Int. J. Mech. Sci. 2018, 135, 203–214. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Liu, Y.; Liu, H. Dynamic characteristics of ball bearing with flexible cage lintel and wear. Eng. Fail. Anal. 2020, 117, 104956. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H. A coupled model of angular-contact ball bearing-elastic rotor system and its dynamic characteristics under asymmetric support. J. Vib. Eng. Technol. 2021, 9, 1175–1192. [Google Scholar] [CrossRef]
- Zhang, D.; Wu, D.; Han, Q.; Wang, H. Dynamic force transmissibility of flywheel rotor systems supported by angular contact ball bearings considering clearance fit. Eur. J. Mech. A Solids 2022, 92, 104457. [Google Scholar] [CrossRef]
- Liu, P.; Wang, L.Q.; Ma, F.; Zheng, D.; Wu, J.; Li, Z. Influence of assembly clearance on vibration characteristics of angular contact ball bearings in the thermal environment. Tribol. Int. 2023, 181, 108317. [Google Scholar] [CrossRef]
- Prashant, H.J.; Santosh, P.B. Mathematical modeling, simulation and analysis of non-linear vibrations of a ball bearing due to radial clearance and number of balls. Mater. Today Proc. 2023, 72, 927–936. [Google Scholar]
- Gao, S.; Wang, L.; Zhang, Y. Modeling and dynamic characteristics analysis of high speed angular contact ball bearing with variable clearance. Tribol. Int. 2023, 182, 108330. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, S.; Wang, H.; Lin, Y.; Song, M.; Zhang, H. Nonlinear dynamics of coupling rub-impact of double translational joints with subsidence considering the flexibility of piston rod. Nonlinear Dyn. 2020, 100, 1203–1229. [Google Scholar] [CrossRef]
- Shishvan, S.S.; Zarnagh, M.H.D.; Deshpande, V.S. Energy dissipation and effective properties of a nominally elastic composite material. Eur. J. Mech. A Solids 2022, 92, 104452. [Google Scholar] [CrossRef]
- Saeed, E.; Esmaeil, S.; Mohsen, M. Application of the method of multiple scales for nonlinear vibration analysis of mechanical systems with dry and lubricated clearance joints. J. Theor. Appl. Vib. Acoust. 2017, 3, 41–60. [Google Scholar]
- Zheng, E.; Wang, T.; Guo, J. Dynamic modeling and error analysis of planar flexible multilink mechanism with clearance and spindle-bearing structure. Mech. Mach. Theory 2019, 131, 234–260. [Google Scholar] [CrossRef]
- Mohamed, G.; Yildirim, H. A new contact force model for low coefficient of restitution impact. J. Appl. Mech. 2012, 79, 064506. [Google Scholar]
- Wang, X.; Liu, G.; Ma, S. Dynamic analysis of planar mechanical systems with clearance joints using a new nonlinear contact force model. J. Mech. Sci. Technol. 2016, 30, 1537–1545. [Google Scholar] [CrossRef]
- Qi, Z.; Wang, G.; Zhang, Z. Contact analysis of deep groove ball bearings in multibody systems. Multibody Syst. Dyn. 2015, 33, 115–141. [Google Scholar] [CrossRef]
- Hu, S.; Guo, X. A dissipative contact force model for impact analysis in multibody dynamics. Mulibody Syst. Dyn. 2015, 35, 131–151. [Google Scholar] [CrossRef]
- Tian, Q.; Lou, J.; Mikkola, A. A new elastohydrodynamic lubricated spherical joint model for rigi-flexible multibody dynamics. Mech. Mach. Theory 2017, 107, 210–228. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Bai, Z.; Sun, Y. A study on dynamics of planar multibody mechanical systems with multiple revolute clearance joints. Eur. J. Mech. A Solids 2016, 60, 95–111. [Google Scholar] [CrossRef]
- Bai, Z.; Jiang, X.; Li, J.; Zhao, J.; Zhao, Y. Dynamic analysis of mechanical system considering radial and axial clearances in 3D revolute clearance joints. J. Vib. Control 2020, 27, 1893–1909. [Google Scholar] [CrossRef]
- Gao, S.; Chatterton, S.; Naldi, L.; Pennacchi, P. Ball bearing skidding and over-skidding in large-scale angular contact ball bearings: Nonlinear dynamic model with thermal effects and experimental results. Mech. Syst. Signal Process. 2021, 147, 107120. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Wang, C.; Huang, W. Planar rigid-flexible coupling spacecraft modeling and control considering solar array deployment and joint clearance. Acta Astronaut. 2018, 142, 138–151. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Li, M.; Liu, Y.; Huang, Y. Dynamics analysis and wear prediction of rigid-flexible coupling deployable solar array system with clearance joints considering solid lubrication. Mech. Syst. Signal Process. 2022, 162, 108059. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, B.; Yan, K.; Hong, J. A novel model for high-speed angular contact ball bearing by considering variable contact angles. J. Mech. Sci. Technol. 2020, 34, 809–816. [Google Scholar] [CrossRef]
- Bai, Z.; Chen, J.; Sun, Y. Effects of contact force model on dynamics characteristics of mechanical system with revolute clearance joints. IJST Trans. Mech. Eng. 2014, 38, 375–388. [Google Scholar]
- Tu, W.; He, H.; Luo, Y. Dynamic skidding behavior of rolling elements under bearing steady working conditions. J. Vib. Shock 2019, 38, 94–99. [Google Scholar]
- Liu, J.; Shao, Y. An improved analytical model for a lubricated roller bearing including a localized defect with different edge shapes. J. Vib. Control 2018, 24, 3894–3907. [Google Scholar] [CrossRef]
- Yu, C.; Zhu, Y.; Shi, F. Accurate prediction method of initial value of high-speed ball bearing model and gyroscopic torque. J. Sound Vib. 2020, 481, 115419. [Google Scholar] [CrossRef]



| Description | Value | Description | Value |
|---|---|---|---|
| Inner diameter (mm) | 50 | Elasticity modulus (ball and raceway (GPa) | 207 |
| Outer diameter (mm) | 80 | Poisson’s ration of the ball and raceway | 0.29 |
| Pitch diameter (mm) | 64.94 | Density of the ball and raceway (kg/m3) | 7800 |
| Rolling element diameter (mm) | 8.73 | Elasticity modulus (cage) (GPa) | 28.3 |
| Mass of the inner ring (kg) | 0.088 | Poisson’s ration of the cage | 0.4 |
| Mass of the outer ring (kg) | 0.113 | Density of the cage (kg/m3) | 1150 |
| Mass of the cage (kg) | 0.027 | Contact angle (°) | 15 |
| Mass of the ball (kg) | 0.003 | External load in axial direction (N) | 1500 |
| Number of balls | 18 | Rotation speed (rpm) | 8000 |
| Groove curvature of inner (mm) | 4.58 | Groove curvature of outer (mm) | 4.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Peng, X.; Chen, Y. An Approach for Predicting the Vibro-Impact Behavior of Angular Contact Ball Bearing Considering Variable Clearance. Lubricants 2025, 13, 216. https://doi.org/10.3390/lubricants13050216
Zhou Y, Peng X, Chen Y. An Approach for Predicting the Vibro-Impact Behavior of Angular Contact Ball Bearing Considering Variable Clearance. Lubricants. 2025; 13(5):216. https://doi.org/10.3390/lubricants13050216
Chicago/Turabian StyleZhou, Yuqi, Xu Peng, and Yu Chen. 2025. "An Approach for Predicting the Vibro-Impact Behavior of Angular Contact Ball Bearing Considering Variable Clearance" Lubricants 13, no. 5: 216. https://doi.org/10.3390/lubricants13050216
APA StyleZhou, Y., Peng, X., & Chen, Y. (2025). An Approach for Predicting the Vibro-Impact Behavior of Angular Contact Ball Bearing Considering Variable Clearance. Lubricants, 13(5), 216. https://doi.org/10.3390/lubricants13050216




