Abstract
This paper presents a number of thrust-collar-specific effects to consider when simulating the elastohydrodynamic lubrication state. Plate bending can lead to edge loading and can be considered via an FEM model of the solids. When bending is of no concern, the effect of the close outside edge needs to be corrected in half-space deformation theory. Track heating requires a unique version of the Carslaw/Jaeger flash temperature solution for curved trajectories. Especially, the adapted treatment of stiffness effects leads to vastly different results in, e.g., lubrication gap height.
1. Introduction
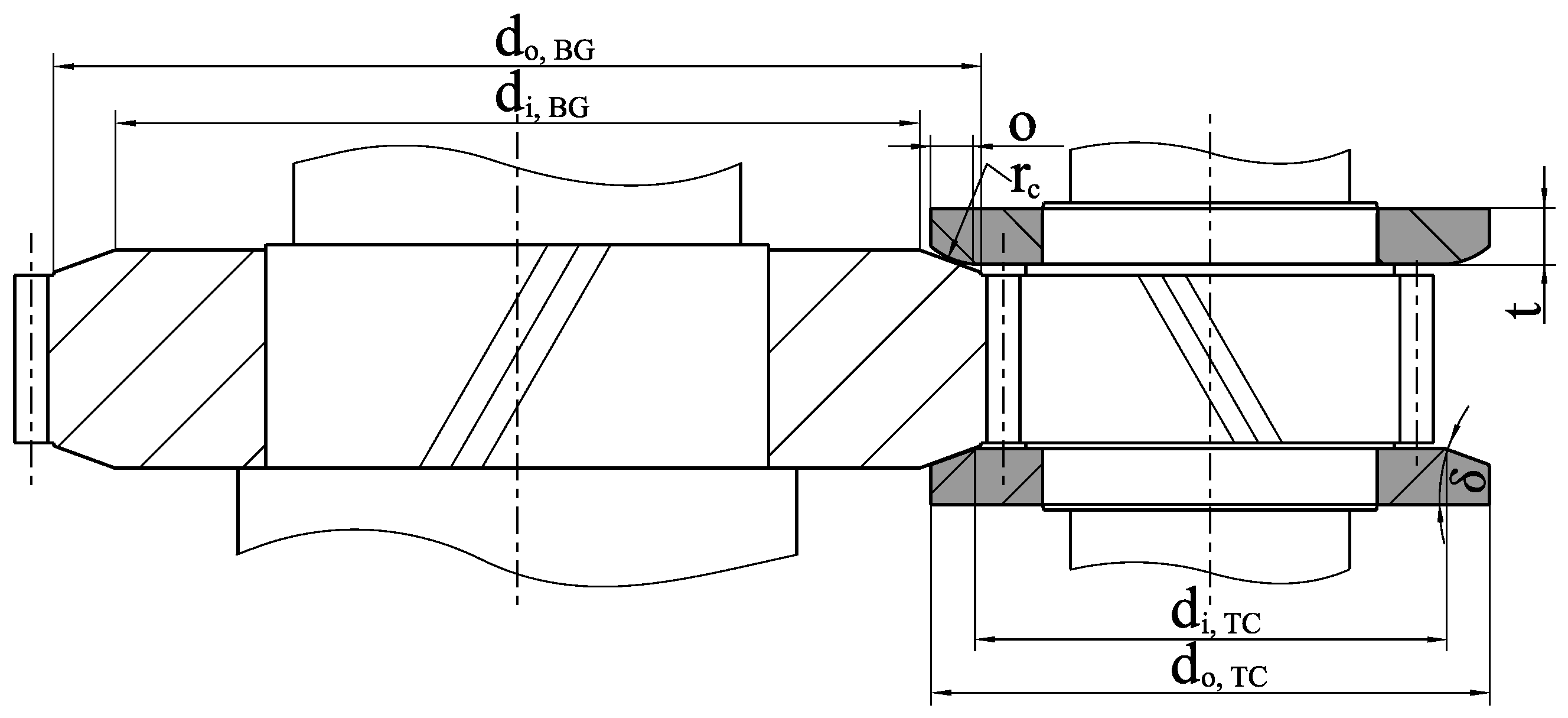
Thrust collars are a standard component of integrally geared compressors, which transfer thrust from the compressor wheel to the bull gear. This leads to greater overall efficiency, as no hydrodynamic axial bearing is needed on the high speed side, which would have a greater power loss than the slow speed side axial bearing and the thrust collar combined. Thrust collar bearings consist of disks mounted next to the pinion acting on a track ground on the side face of the bull gear (Figure 1). The tracks are conical, which leads to a convergent gap with a very large reduced radius, usually in the order of meters. Apart from their main application in compressors, they are employed to deal with the issues caused by the tilting moment generated by the axial force of helical gears, e.g., in very large single-stage gear ratios or when the gear is mounted on the outside ring of a bearing in a planetary gearbox.
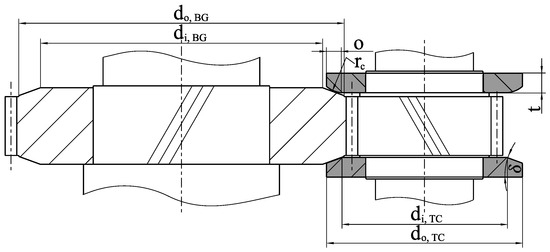
Figure 1.
Thrust collar acting on a helical gear with cone angle , overlap o and plate thickness t. The upper thrust collar is crowned with radius , and the lower is straight.
Previous thrust collar simulation programs [1,2,3,4,5,6,7] do not differ fundamentally from elastohydrodynamics (or rigid-hydrodynamics) simulation codes one would use for other machine elements like gears or roller bearings except for their unique geometry generation algorithm. Some employ rigid tracks [6] or make isothermal assumptions [1,5,7]. Refs. [4,6] do not consider flash track heating in their thermal calculations.
An overarching research goal is to increase specific thrust collar load, as this can lead to more efficient thrust collars with less overlap o (cf. Figure 1) and therefore less slip closer to the gear pitch circle as well as enabling previously inaccessible applications outside of compressors. To this end, arising failures need to be better understood. In industrial practice [8,9] as well as test rig operation [10], failures often occur only on part of the track due to angular errors from tolerances and plate bending. In order to correctly simulate their lubrication state and to compare these failures to the general knowledge in tribology, novel calculation methods incorporating these effects are required.
Straight (unprofiled) thrust collars exhibit a phenomenon called “edge thinning” [3], in which the minimum lubrication gap occurs on the edges of the tracks. Computations using FEM models developed to simulate plate bending (as described in this paper) showed the need for corrections to the half-space assumption, which is usually used in scenarios where no computationally expensive plate bending FE models are needed.
When trying to analyze failures of specimens run in the mixed-lubrication regime, anisothermal calculations seem appropriate. Preceding complex experimental measurements of local temperatures, it is reasonable to gauge the importance of heating using simulation tools that have been validated on other machine elements. Previously, thermal simulation methods employed simplifications concerning track heating along a clearly inaccurate straight path instead of the correct curved one, although estimates were made to justify these assumptions [3].
This paper accordingly discusses implementations of these three previously neglected effects. The general approach to elastohydrodynamics (EHD) simulation is not discussed, as the treatment of the thrust-collar-specific issues could be incorporated into arbitrary EHD codes (the authors’ code is based on the methods described in [11]).
For completeness, this report starts with a geometry generation algorithm, which is simpler than previously described ones.
2. Geometry Generation
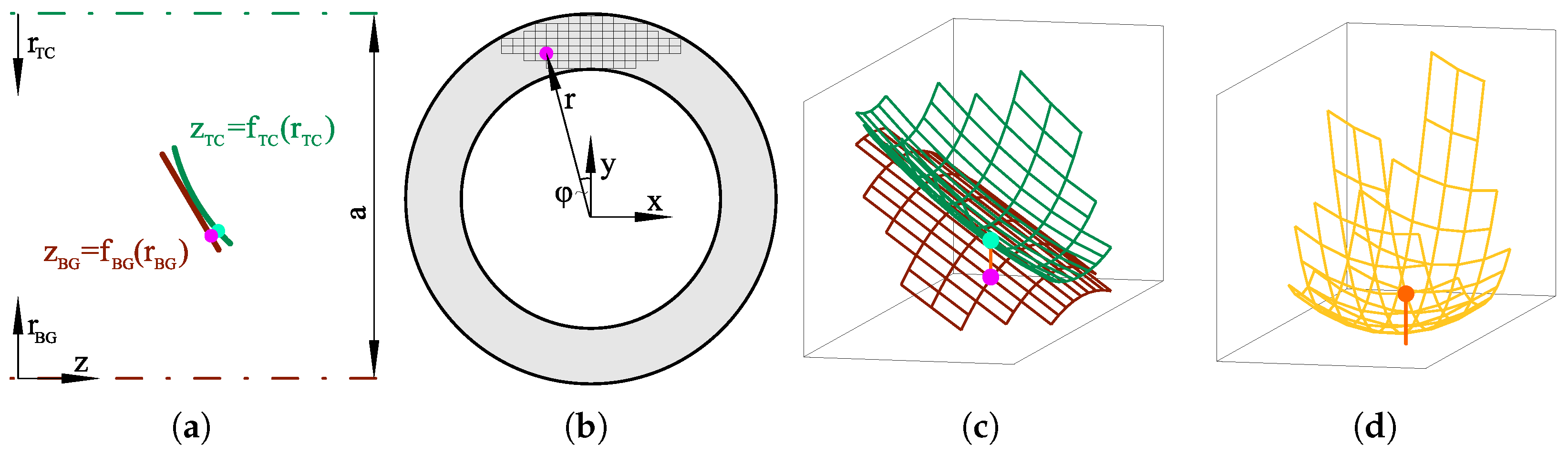
The steps for generating the lubrication gap geometry formed by the thrust collar (TC) and bull gear (BG) track as an essential simulation input are visualized in Figure 2. The profiles are defined on a 2D section plane (the same as used in Figure 1) as functions z of the radius r (Figure 2a). For a “straight” profile, i.e., a cone in 3D, it is a triangle:
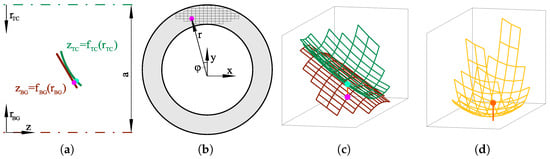
Figure 2.
Steps for generating the lubrication gap geometry [12]. (a) 2D geometry functions. (b) Calculation of the profile height in a Cartesian coordinate system. (c) 3D height profiles of TC&BG. (d) Combined gap height.
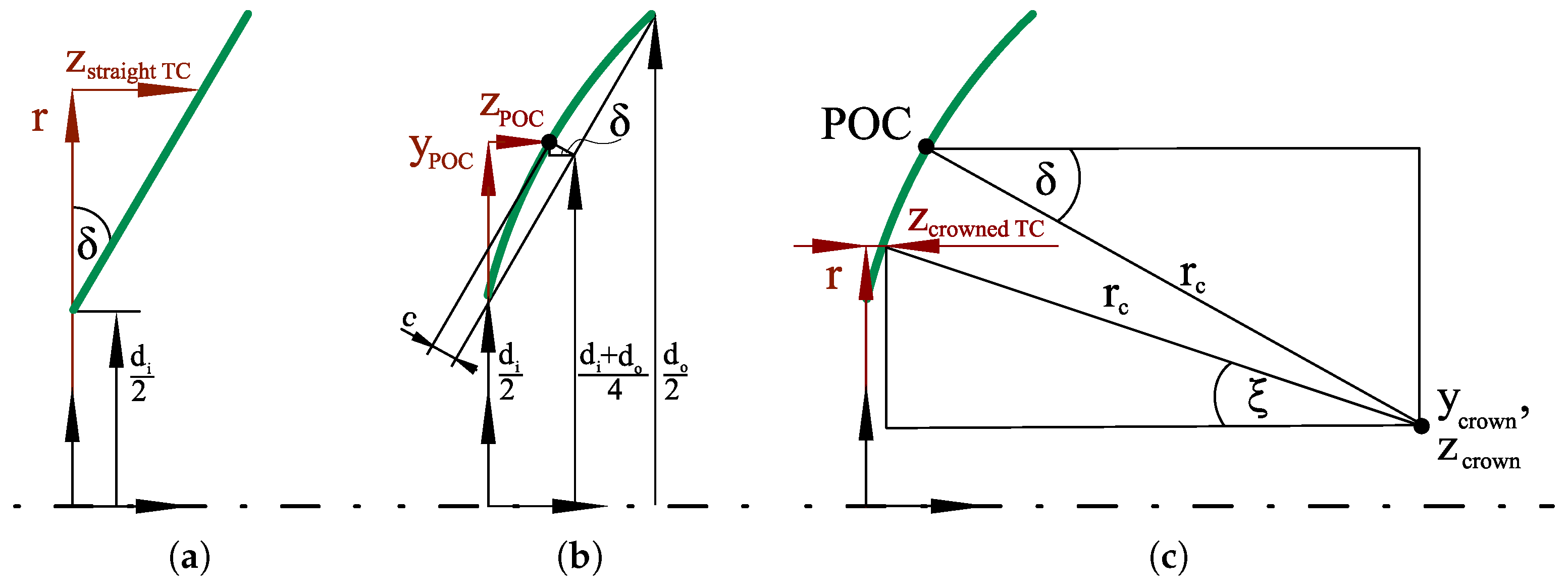
For crowned profiles, the point of contact (POC) needs to be found first:
Sketches used for obtaining these formulas via trigonometric analysis are provided in Figure 3 as an expansion of Figure 2a. These functions with polar coordinate input are evaluated at each position of the mesh spanning the area overlapped by both tracks after coordinate transformation from Cartesian coordinates (Figure 2b). In this way, gap height distributions of the thrust collar and bull gear track are obtained as shown in Figure 2c. The height input to the Reynolds equation is calculated by subtracting these two profiles to obtain the combined gap height (Figure 2d).
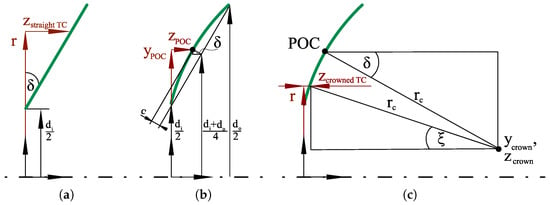
Figure 3.
Geometric analysis for track profile calculation. (a) Equation (1). (b) Equations (2) and (3). (c) Equations (4)–(7).
The track speeds u in direction x and v in direction y as well as the speed differences can be calculated at the radial coordinates by the following equations:
3. Plate Stiffness from FEM
The simplest and fastest way to obtain track deformation under pressure is the use of a Boussinesq half-space approximation. This assumes that the tracks are not bounded on any side (see the following section) and infinitely deep. This is a reasonable approximation when the pressure build-up is situated relatively far from the edges and when the bodies are thick compared to the interior stress field caused by the surface pressure, as is the case for contacts with smaller radii like roller bearings. When thrust collars are mounted via interference fits, which is standard practice in compressors, they are very thick to prevent gaping of the interface under the eccentric circulating force, which would lead to fretting corrosion [13]; the issue with plate thickness is not relevant in these cases. When thrust collars are welded to the shaft, which is standard practice in vehicular gearboxes (e.g., [14]), they can be built considerably thinner, which can lead to issues with the infinite depth assumption. Furthermore, thrust collars bend under load—more so with thinner designs. Most thrust collars do not satisfy the assumptions of the Kirchhoff plate theory [13]. For a full analysis of these effects, which would be neglected by the Boussinesq half-space theory, the finite element method (FEM) is an obvious tool.
A first implementation of plate stiffness into a solver for thrust collars was published in [15]. In this version, the FE stiffness matrix was obtained from an automatically meshed thrust collar geometry; thus, the meshes of the solid and fluid simulation did not match. Quantities were interpolated between these two meshes via radial basis functions.
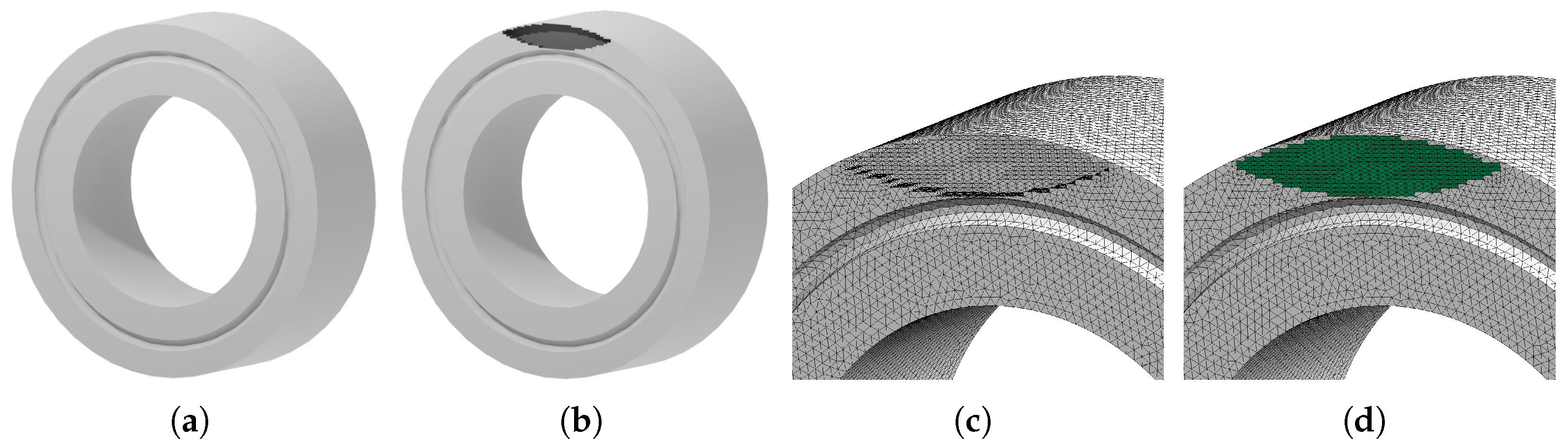
In order to simulate highly loaded thrust collars, a different solution method to the Reynolds equation from the one employed at the time of the mentioned publication was needed for stability when simulating parallel gaps. The newly implemented solution method based on [11] requires the solid stiffness at specific fluid mesh points for its relaxation technique. As point loads can not reasonably be interpolated between meshes, the solid and fluid simulation meshes need to match. In order to be able to simulate more complex geometries than hollow cylinders, such as the annular groove used as a grinding run-out shown in Figure 5a, a combination of an automatic mesh generator and manually programmed routines seems optimal.
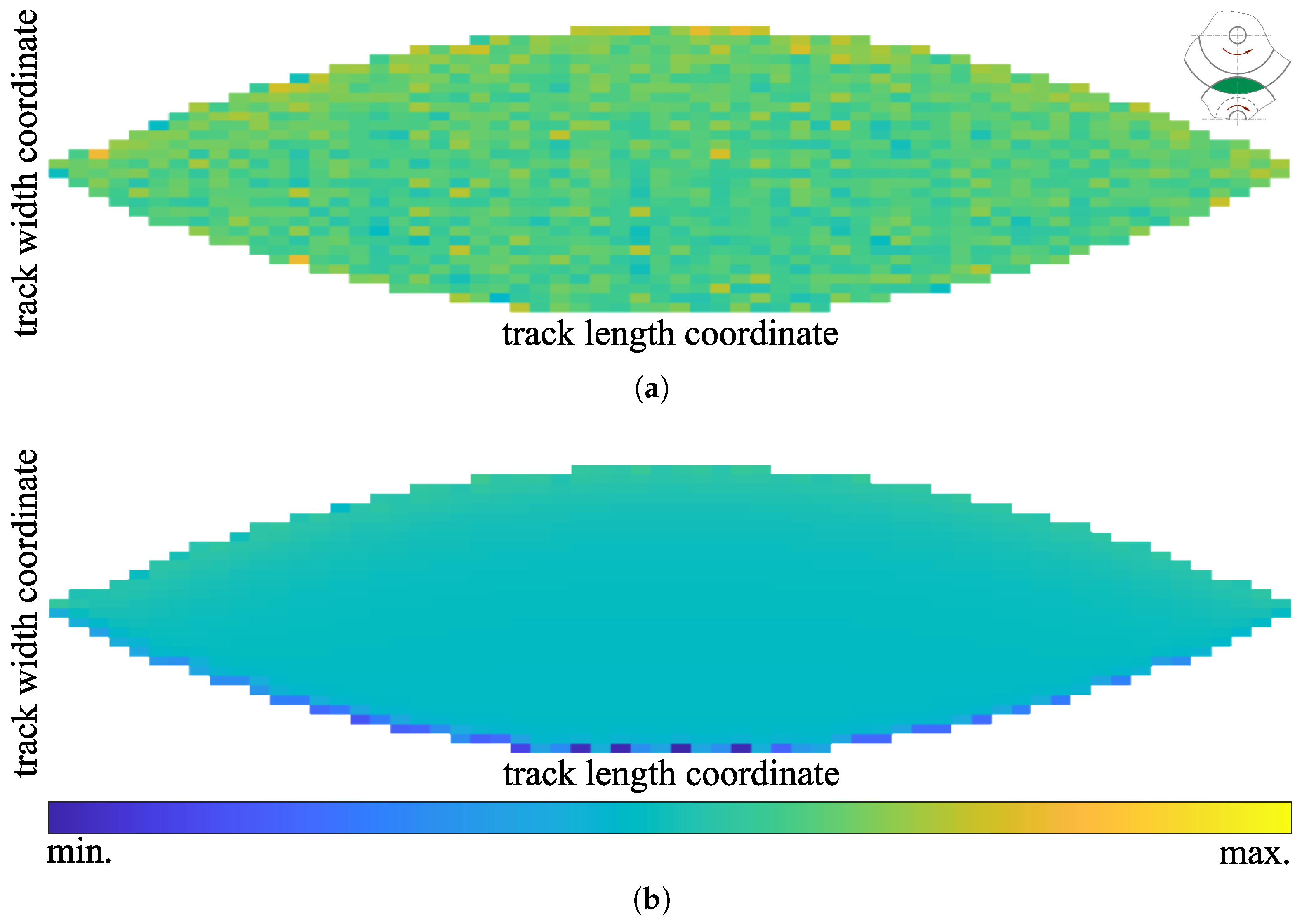
An initial attempt was made using the simple technique of embedding nodes, as this is readily available in most meshers and does not require special provisions on the users’ side. When embedding nodes, nodes from the fluid mesh are prescribed to the automatic mesh generator for incorporation into its solid mesh. As a quick plausibility check of the obtained mesh, the continuity of the distribution of the maximum depressions resulting from individual nodal loadings can be examined. Neighboring nodes should sink in similarly. The result of this sequence of individual solutions for single point loads is plotted in Figure 4a in a concatenated form where the square colorization shows the maximum depression at each successively probed node. The results from the mesh using embedded nodes are significantly non-monotonous despite not violating common mesh quality metrics (scaled Jacobian); albeit visual inspection shows a considerably distorted tetrahedral mesh.
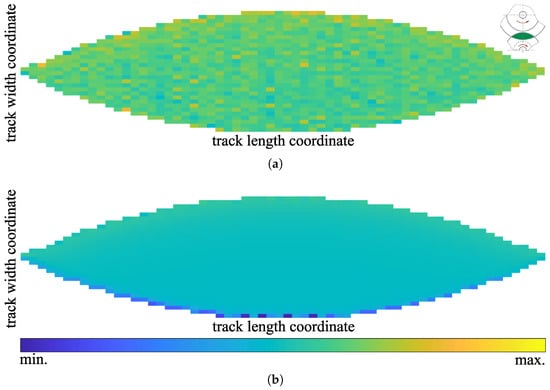
Figure 4.
Compliance of nodes when applying a point load to them. (a) Embedded nodes in automatically generated tetrahedral mesh (min./max.-discrepancy of 44%). (b) Manual mesh in cut out of automatically generated tetrahedral mesh.
Figure 4b shows the expected, physically sound result (from the ultimately implemented method), where there is no oscillation between neighboring points and a small increase towards the outside edge, which lies at the top of this plot. The oscillation on the bottom of Figure 4b is caused by bad quality elements due to the annular groove as shown in Figure 5a.

Figure 5.
Steps for meshing thrust collars with provided fluid mesh [12]. (a) CAD base geometry. (b) Cut out contact region. (c) Automatically meshed base geometry. (d) Manually meshed contact region.
The meshing steps of a refined method are visualized in Figure 5. First, a base geometry is created as a computer-aided design (CAD) model (Figure 5a). The prescribed fluid mesh is then cut out from the contact region (Figure 5b). This resulting geometry is meshed by an automatic mesh generator—this work uses GMSH [16]. For automeshing, numbers of divisions are prescribed at the edges of the cut out contact region to generate a compatible mesh transition without hanging nodes. Finally, the elements for the cut out region are added via a manually programmed routine (Figure 5d). A Cholesky decomposition of the stiffness matrix of this mesh is calculated, as the FEM equation system is now solved repeatedly for various right hand sides. By consecutively setting the entries of , each node of the contact region is loaded with a unit load of 1 and the corresponding displacement of the nodes in the contact region is saved in a matrix , which can be used the same way as when using the Boussinesq half-space theory (see, e.g., [17]) for calculating depression w at position due to pressure p at position :
All illustrating calculations in this paper are performed on an example gearbox derived from a gear test rig. The details are given in Table 1. The reduced radius in this instance is :

Table 1.
Data of example thrust collar.
Figure 6 provides a cross-section view of the gap at its minimum height orthogonal to the direction of lubricant entrainment for a Boussinesq half-space solution (without edge correction; see following section), for equally thick thrust collar and bull gear and for a combination of a thick bull gear and a relatively thin thrust collar .
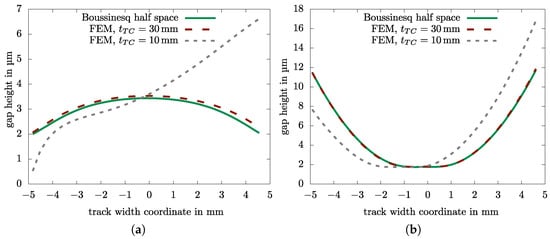
Figure 6.
Calculation results for example configuration from Table 1 for different plate bending scenarios. (a) Straight track. (b) Crowned track.
The results are very close for the thick geometry and the Boussinesq solution. In this specific example, minor plate bending evens out differences from uncorrected edge effects (following section). For the thin thrust collar, edge loading sets in for the straight track (Figure 6a). The crowned track is able to compensate; the contact point moves radially (Figure 6b). There remains some margin before the thin crowned collar would experience edge loading as well; this margin is needed in order to compensate for further angular errors from manufacturing tolerances, etc., which are not input into the geometry generator in this instance.
4. Edge Effect on Half-Space
As the precomputation of from FEM takes a long time and requires a rather large amount of memory not present in most personal computers when using fast direct solvers, a half-space method is preferred for rough dimensioning of thick thrust collars. Plate bending can be approximated by a tilting angle chosen from engineering experience in this case. The tilting angle from bending needs to be added to other sources of misalignment, also required for FEM-based calculations, such as manufacturing tolerances and possibly shaft bending and movement in bearing clearances.
In this case, the effect of the close edge remains to be corrected for. The larger and more extensive depression due to a unit load close to the edge is compared exemplarily to a unit load in the center in Figure 7.
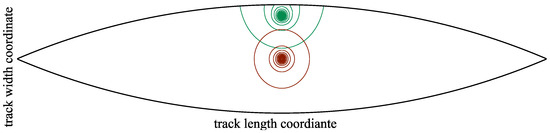
Figure 7.
Gap deformation (lines of equal height) due to a unit load close to the edge (green) and in the center (red). FEM results. The back sides are supported, i.e., there is no plate bending.
Reusner [18] proposed an approximate correction of the edge effect to model an elastic “quarter-space” instead of a “half-space” by mirroring the pressure distribution along the edge to the outside, technically nonexistent region when using half-space theory. This correctly compensates the shear stresses to the same state as in the case of a free surface but doubles the normal stresses in the mirror plane. Exploratory FEM calculations, discussed in depth below, were not satisfactory using this simple Reusner correction for conditions relevant to thrust collars (Figure 9).
Hetényi introduced an iterative—and therefore computationally expensive—method for correcting this issue [19,20]. On this basis, Guilbault [21] developed a simplified method which corrects the mirrored pressure in the Reusner method by a factor :
For the standard case of for steel, equals 1.39. Calculations by [21] for general contacts have an error of 9.55% instead of 21.9% without this correction factor.
In contrast to the quarter-space, a thrust collar does not have a planar but a curved edge. The “mirroring method” thus becomes a “radial projection method”. For a radial projection of a point inside the contact area, its position in a polar coordinate system about the thrust collar or bull gear rotation axis is
The position of the projected point is found by extending the position vector by twice the distance to the edge of the TC/BG:
The deformation w of the lubrication gap at position due to pressure p at position can be calculated by (cf. Equation (16))
C is a distance weighting factor according to the Boussinesq half-space theory, e.g., described in [17].
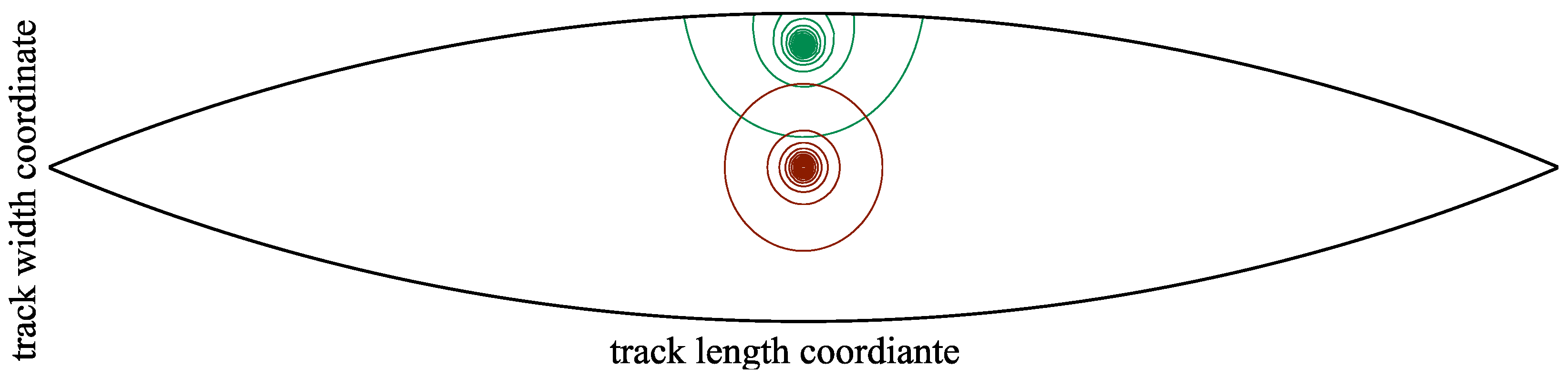
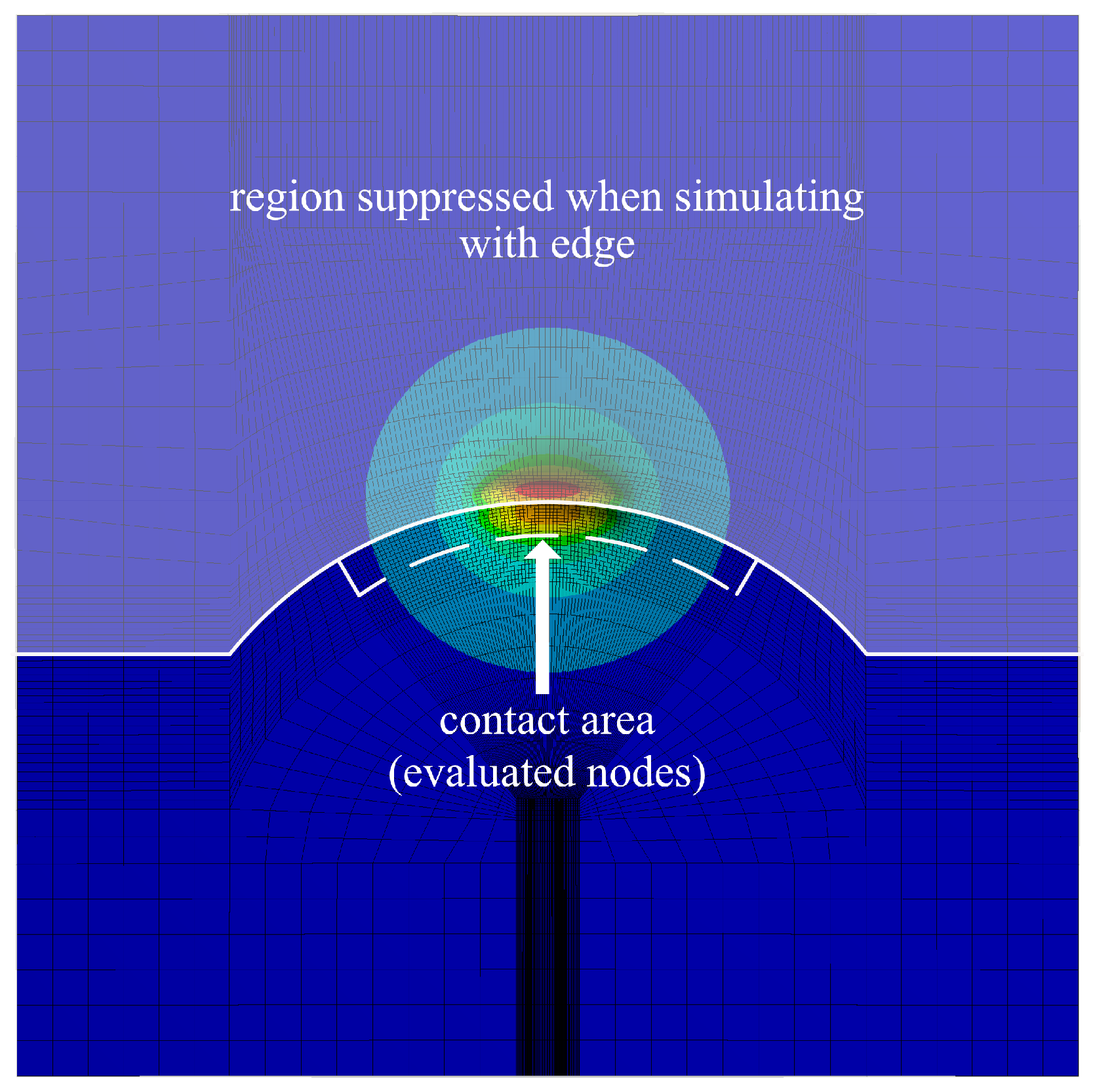
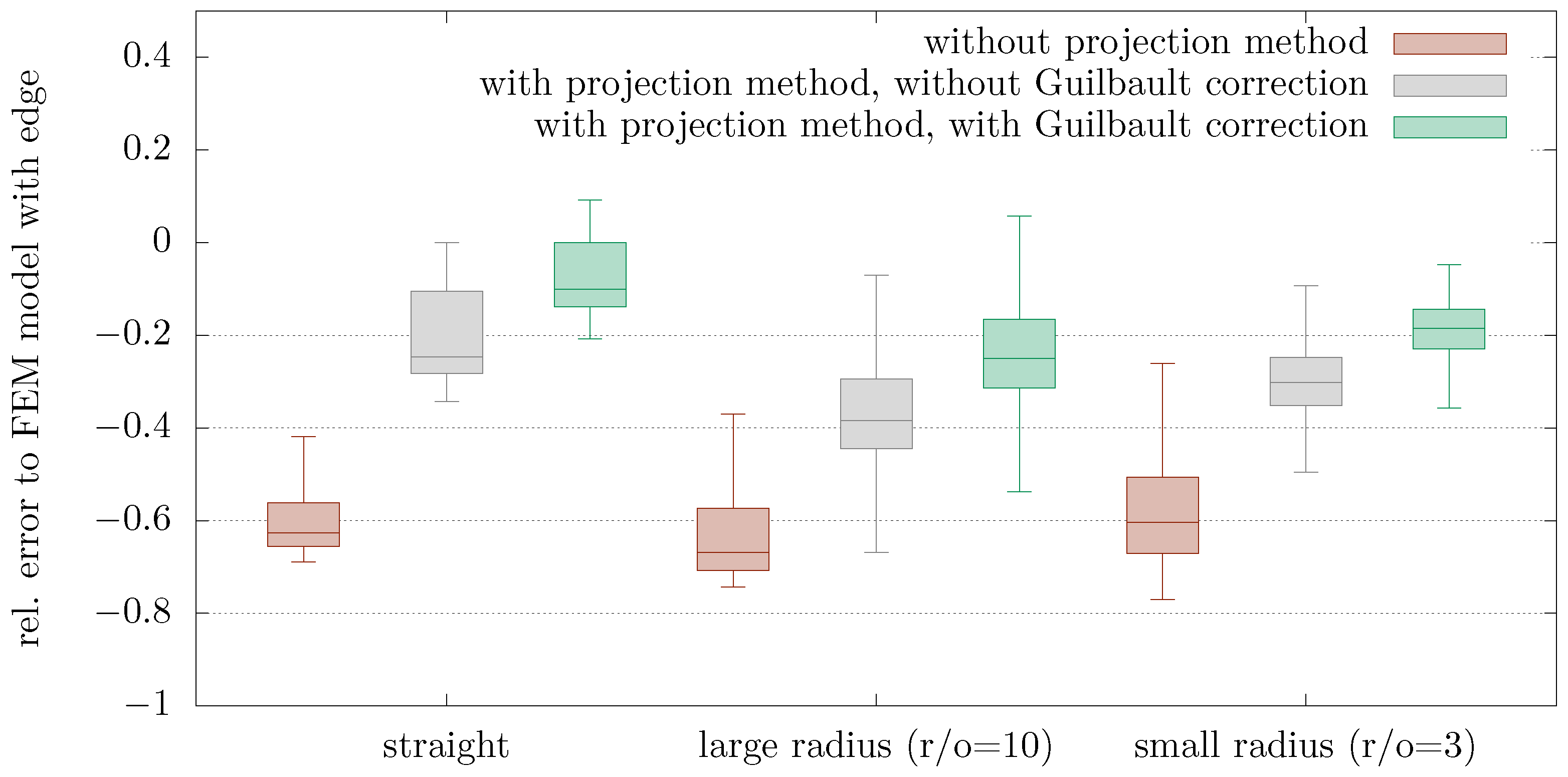
The suitability of this correction method is checked for variously curved edges by comparing it to the results obtained from an FEM model. In one version of this model, a half-space is approximated by a large cuboid, and the pressures are either not projected or projected with or without correction; in another, part of it is suppressed to create an edge close to the pressurized region. An exemplary result can be found in Figure 8; the region that is suppressed when simulating with an edge is displayed as semiopaque. A variety of Hertzian pressure distributions relevant to thrust collars with ratios of pressure ellipse width to contact area width of and ratios of pressure ellipse width to length of are investigated. Figure 9 compares the distribution of the relative error of all mesh nodes of the contact area (dashed line in Figure 8) and all geometrical ratios combined. This summary is chosen as the error is distributed quite uniformly inside the contact area.
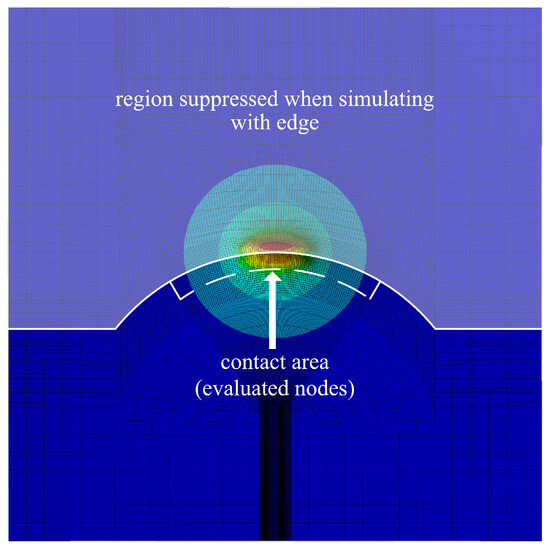
Figure 8.
FEM deformation result with mirrored and corrected pressure. The upper, semiopaque part is suppressed when simulating with an edge.
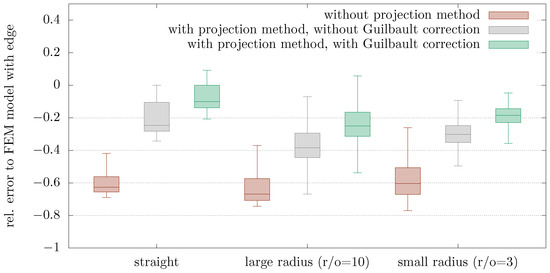
Figure 9.
Comparison of error distribution at all nodes of the contact area when using different half-space correction methods.
The projection method can apparently be used for curved edges, and the correction methods work. However, the error is larger than it is for straight edges.
We choose not to correct the remaining error by using the more expensive Hetényi method, as the FEM method is available for more precise calculations and additionally does not rely on approximations for plate bending.
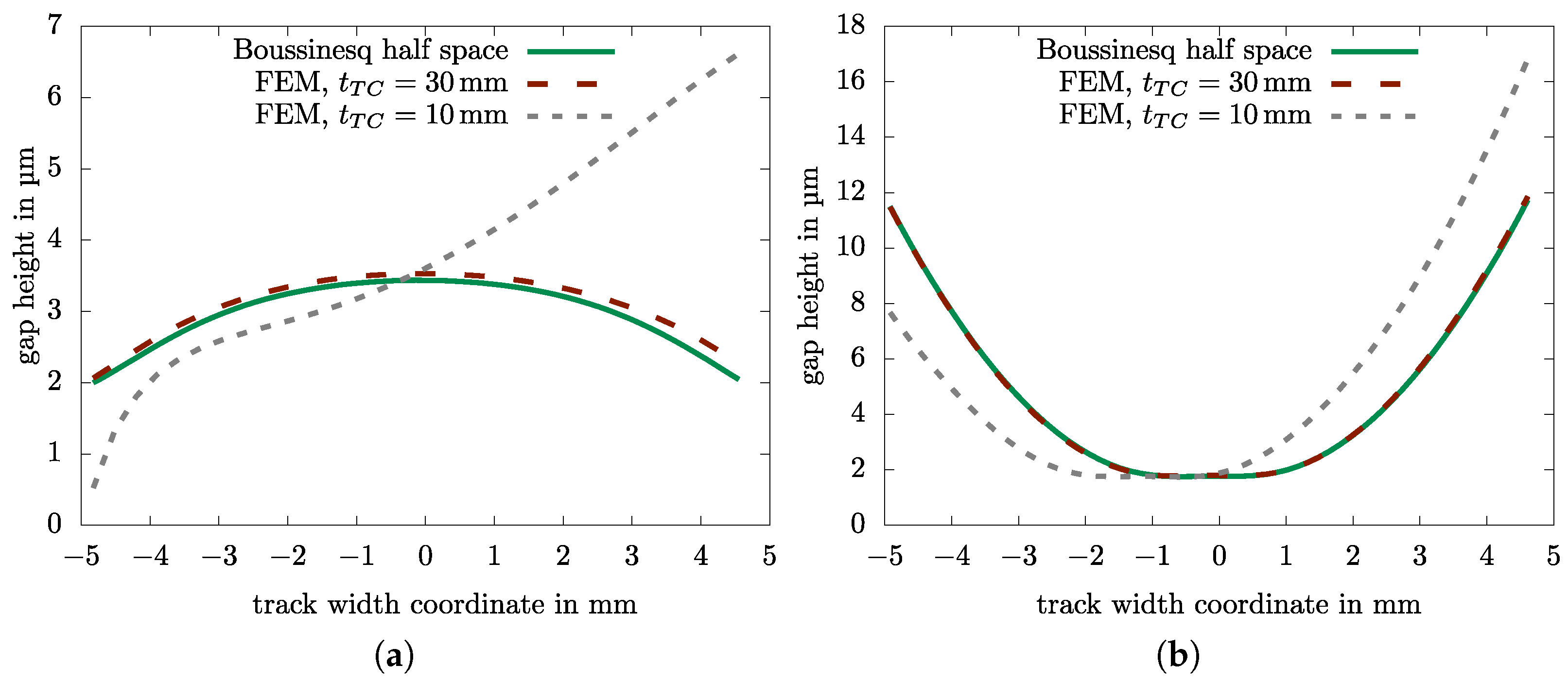
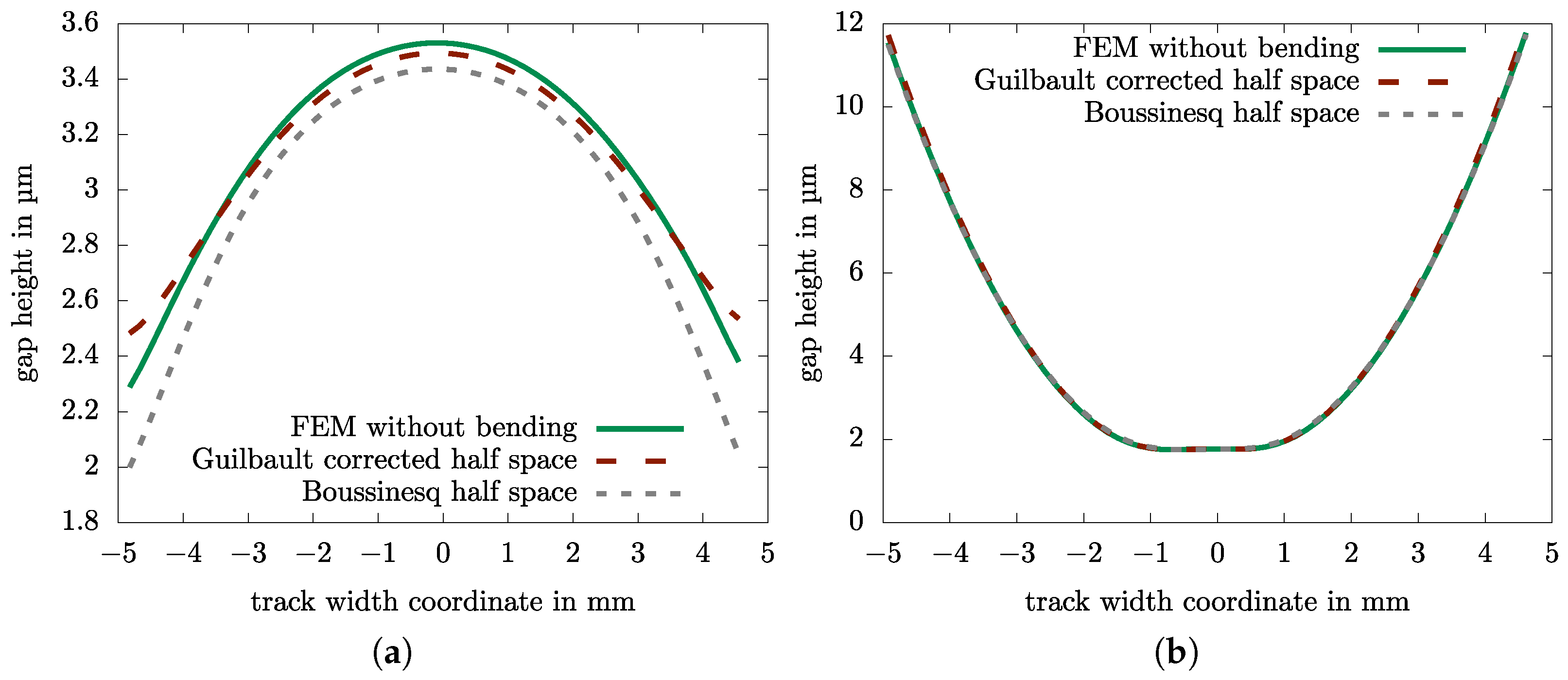
Figure 10 provides a cross-section view of the gap at its minimum height orthogonal to the direction of lubricant entrainment for an uncorrected Boussinesq half-space solution, for a Guilbault-corrected half-space solution and for an FEM based solution (model described in Figure 5) with the back sides supported in order to suppress bending deformation for the example thrust collar from Table 1.
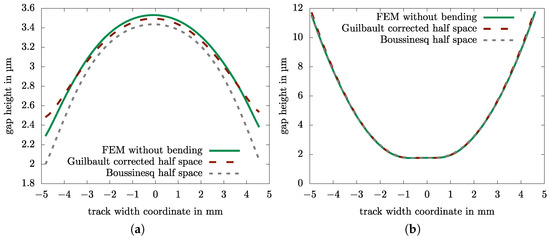
Figure 10.
Calculation results for example configuration from Table 1 for different treatments of the edge effect. (a) Straight track. (b) Crowned track.
When the load zone lies far away from the edges, as is the case for this crowning radius needed to compensate for thin plate bending, the edge effect is irrelevant (Figure 10b). For the straight track (Figure 10a), as well as for crowned tracks simulated with large angular errors, differences can be found. The Guilbault-corrected half-space solution is closer to the FEM solution than the uncorrected Boussinesq half-space, yet there is no exact match.
5. Track Heating on a Circular Arc
Whereas a Cartesian grid (Figure 2b) is preferred for a finite volume discretization for the solution of the Reynolds equation, points on the tracks of thrust collar and bull gear do not follow an axis of this grid but move through it on circular arcs. The calculation of track heating thus is more complicated than, e.g., in gears.
Track heating due to a heat flow from the sheared lubricant can be calculated using the Carslaw/Jaeger solution for a moving point heat source on an infinite heat sink [22]. The temperature rise at point due to a heat flow q at point from time to is given by:
An analytical solution of the space integral over a grid element is known for horizontal movement along the x-axis [23]; time integration has to be performed numerically using the substitution as a treatment of the singularity at :
R is the heat kernel [23]:
This can readily be modified for a movement along a circular arc:
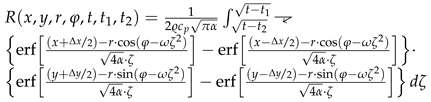
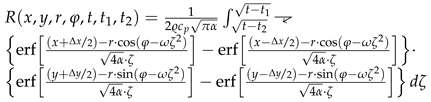
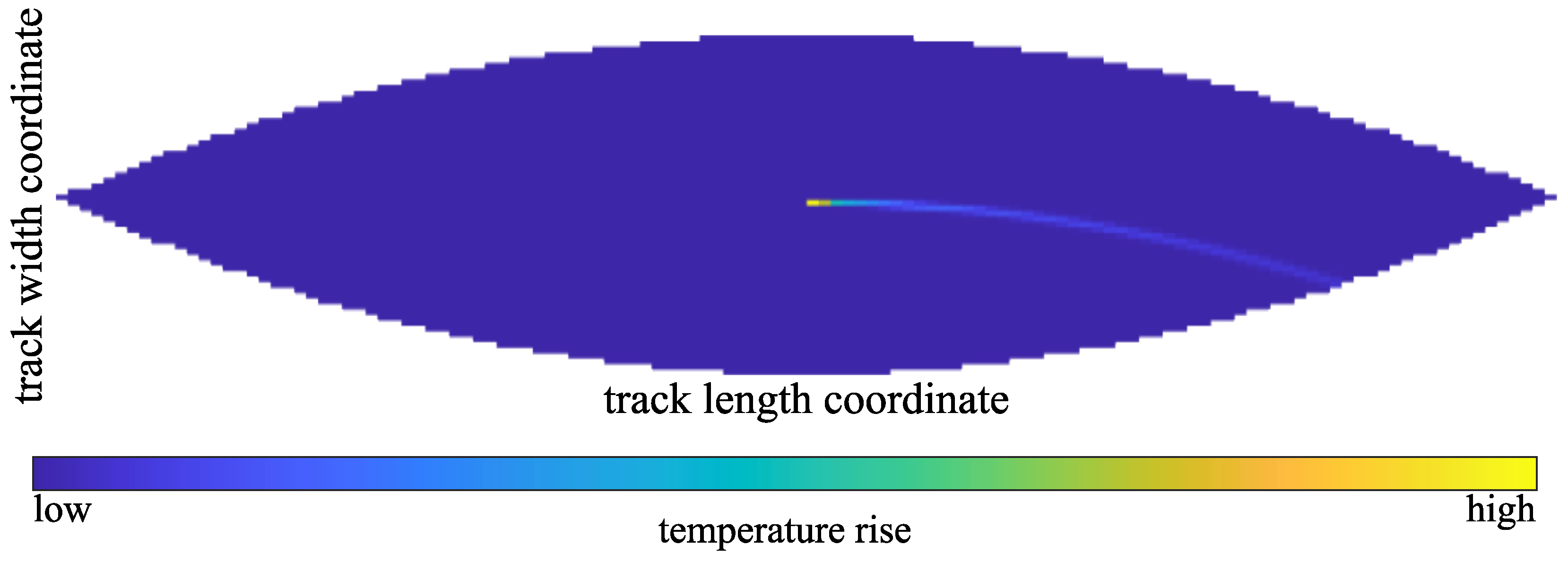
Attention should be paid to the surface instead of the heat source moving through the reference system, as is the case in the classical Carslaw/Jaeger solution, when choosing the integration direction. Figure 11 shows the track heating due to a point heat source at the center. The heated center point is the hottest; the temperature trace goes through the nodes which have already passed under the heat source.
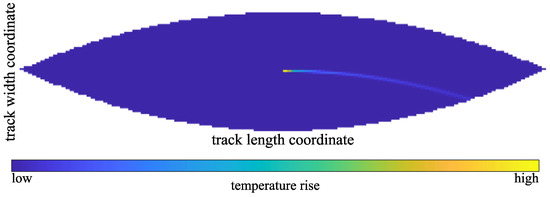
Figure 11.
Track heating due to a point heat source at the center of the reference system (movement from right to left, axis of rotation below).
For a movement along a Cartesian axis, all path integrals are the same, therefore only one integration has to be performed explicitly, and the heat kernels for the remaining nodes can be obtained by shifting the solution. For a movement along a circular arc, a numerical integration has to be performed for each node individually, which is much more time consuming. As the influence of far away nodes is negligible, the path integration can be started at the current time and truncated if the contribution of the past remote point is substantially less than at the current time.
The Carslaw/Jaeger half-space heating solution inherently has the same issues regarding edge effects as the previously discussed Boussinesq deformation solution. However, it can be concluded from Figure 11, that thermal edge effects are much more insignificant than deformation effects, as the thermal trail primarily extends along the 1D trajectory trailing the point source and is hardly orthogonal to it.
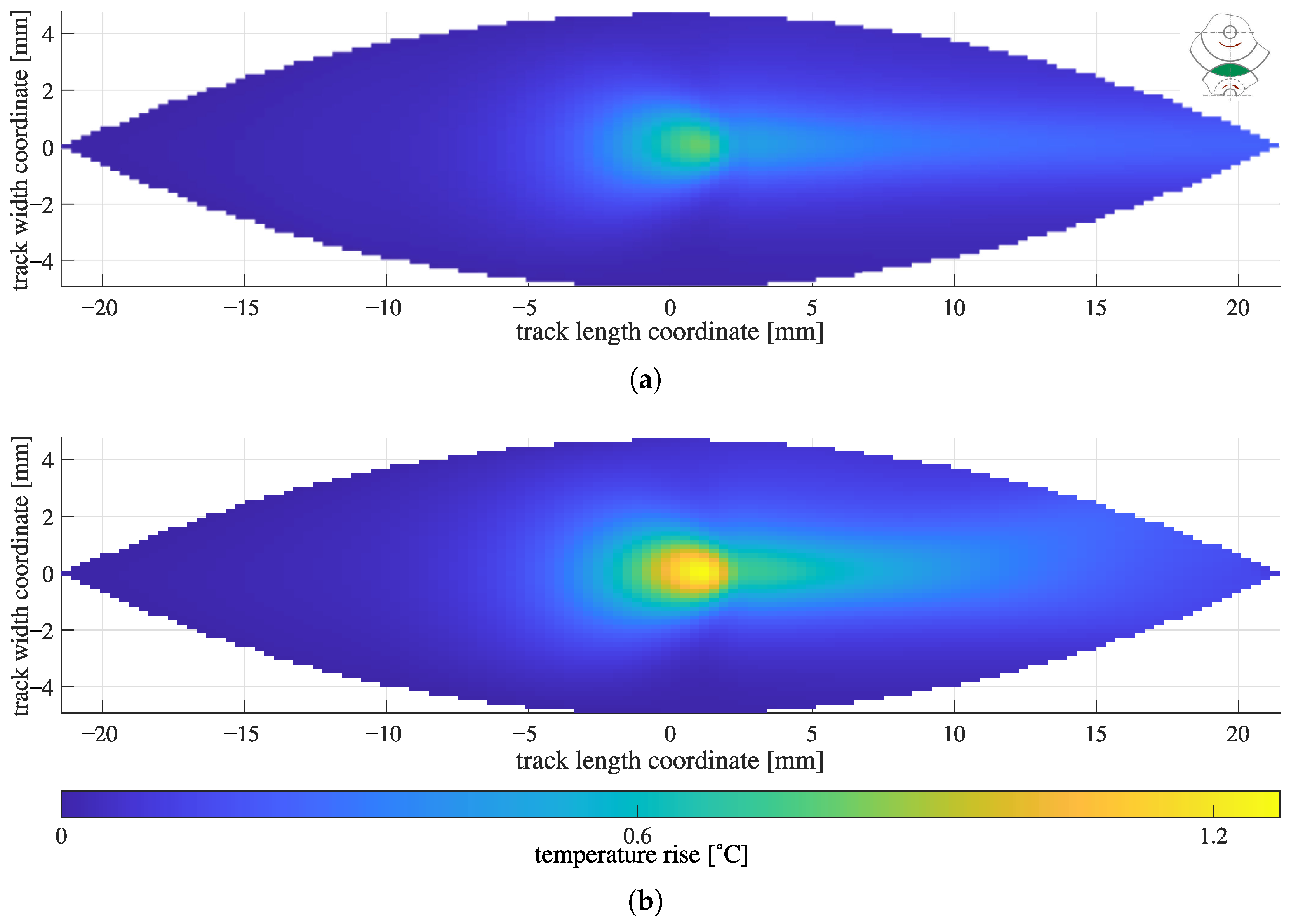
Figure 12a shows the thrust collar track heating of the example thrust collar from Table 1 for a straight trajectory following the horizontal axis. Figure 12a shows the thrust collar track heating for a (correct) curved trajectory.
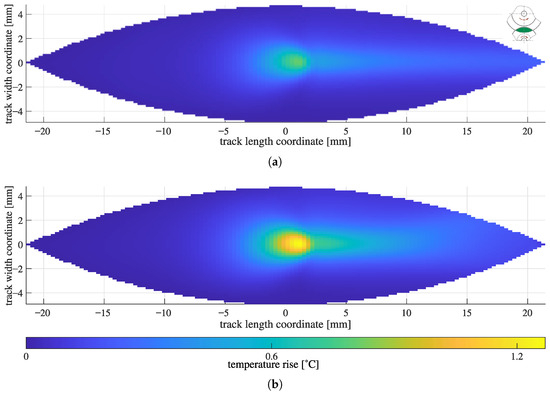
Figure 12.
Mean film temperature rise for example configuration from Table 1 for different track heating treatments. (a) straight trajectory. (b) curved trajectory.
Due to the very high efficiency of thrust collars, in this example with a power loss of a mere 14 , thermal effects could be disregarded. For comparing the mechanisms of the two track heating implementations, this case is advantageous, as only the temperature distribution changes significantly but not the gap height or power loss, which would retroact on temperature. In cases where temperature is relevant, i.e., at very high speeds or in the mixed lubrication regime, one can only see outright differences but not their inherent causes.
Two faint branches can be distinguished in the outlet of the curved trajectory variant (Figure 12b) compared to a temperature rise just in the middle of the track in the straight trajectory variant (Figure 12b). As this is in the outlet, the effect on temperature (and gap height) in the loaded zone is minor. The peak temperature is noticeably higher for the curved trajectory variant. This is caused by the greater arc length going through the heated zone in the case of the curved variant. Off the middle, the arc length going through the heated zone is longer for one track (e.g., the thrust collar) and shorter for the other (e.g., the bull gear) when going to a specific point. This reciprocity is not even though and in sum leads to greater temperatures. This can be proven by calculating the temperature rise in a single off-center point of the two tracks passing under the same temperature distribution for curved and straight heating calculations.
6. Boundary Conditions
A further thrust-collar-specific issue is the need to correctly implement boundary conditions not only for the pressure equaling zero at the edges of the contact area (Dirichlet boundary condition) but also for its derivative to be zero (Neumann condition) as pressure distributions can reach the edges of the contact area leading to “geometry-induced starved lubrication”. This is not an issue for, e.g., ball bearings, where commonly only the Dirichlet condition is implemented and the derivative condition is accomplished non-explicitly by discretizing an area that is larger than the geometrically unconstrained pressurized region.
7. Conclusions
The improved modeling of thrust collar stiffness leads to vastly different results compared to those which would be obtained by simulation programs not adapted to thrust collars. When edge loading is possible, the results are so disparate that no general error estimate can be given. In order to match simulation and experimental results, the consideration of these effects seems indispensable. Equally, curved trajectories lead to vastly different temperature results compared to straight trajectories, although there are many practical applications where isothermal simulation is sufficient.
The precomputations needed for the FEM-based method are computationally expensive. Theoretically, they could be parallelized without limit by solving the FEM equation system for unit loading of each node at the same time; in practice, this is heavily limited by the available computing capacity. An intermediate method based on correction methods to plate theory, possibly combined with the Hetényi edge correction method, seems worthwhile to pursue.
Author Contributions
Conceptualization, C.H.; Software, C.H.; Formal analysis, C.H.; Writing—original draft, C.H.; Supervision, A.L.; Project administration, A.L.; Funding acquisition, A.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project Number 514068987, with the title “Dimensioning of highly loaded thrust collars”. The authors thank the DFG for financial support. We acknowledge support by the Open Access Publishing Fund of Technische Universiät Clausthal.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Abbreviations | |
| BG | Bull gear |
| CAD | Computer-aided design |
| EHD | Elastohydrodynamics |
| FEM | Finite element method |
| POC | Point of contact |
| TC | Thrust collar |
| Latin Symbols | |
| C | Boussinesq distance weighting factor |
| matrix of deformation factors | |
| E | Young’s modulus |
| c | chord height |
| heat capacity | |
| inner diameter of track | |
| mean track diameter | |
| outer diameter of track | |
| nodal force vector | |
| FEM stiffness matrix | |
| o | overlap/width of contact area |
| p | pressure |
| mirrored pressure | |
| q | heat flow |
| r | radius |
| R | heat kernel |
| crown radius | |
| t | time |
| t | plate thickness |
| u | speed in direction of x |
| nodal displacement vector | |
| speed difference in direction of x | |
| v | speed in direction of y |
| speed difference in direction of y | |
| w | deformation in direction of z |
| x | coordinate |
| y | coordinate |
| distance of the contact coordinate system from the rotation axis | |
| z | profile function/coordinate |
| Greek Symbols | |
| thermal diffusivity | |
| cone angle | |
| temperature rise | |
| grid spacing | |
| substitution variable | |
| temperature | |
| Poisson’s ratio | |
| angle | |
| density | |
| polar coordinate | |
| Guilbault correction factor | |
| angular frequency | |
| Mathematical operators | |
| atan2 | four quadrant version of arcus tangent |
| erf | Gauss error function |
References
- Langer, H. Hydrodynamische Axialkraftübertragung bei Wellen schnellaufender Getriebe. Konstruktion 1982, 34, 473–478. [Google Scholar]
- Simon, V. Thermal elastohydrodynamic lubrication of rider rings. J. Tribol. 1984, 106, 492–498. [Google Scholar] [CrossRef]
- Barragan de Ling, F.d.M. Lubrication of Thrust Cones. Ph.D. Thesis, University of Wales, Cardiff, Wales, 1993. [Google Scholar]
- Гoршенин, К.И. (Gorshenin, K.I.). Кoнтактнo-гидрoдинамический расчет характеристик смазoчнoгo слoя упoрных гребней кoсoзубых передач мультипликатoрoв мнoгoвальных центрoбежных кoмпрессoрoв (Contact-Hydrodynamic Calculation of the Characteristics of the Lubrication of Thrust Collars of Helically Geared Transmissions of Integrally Geared Compressors). Ph.D. Thesis, Kazan State Technological University, Kazan, Russia, 1999. [Google Scholar]
- Thoden, D. Genaue Schmierfilmberechnung als Hilfsmittel zur Druckkamm-Auslegung. Mitteilungen aus dem Inst. für Maschinenwesen der Tech. Univ. Clausthal 2011, 36, 63–68. [Google Scholar]
- Cable, T. Analysis of Oil Lubricated Thrust Collars for Application in Integrally Geared Compressors. Master’s Thesis, Texas A&M University, College Station, TX, USA, 2015. [Google Scholar]
- Heß, M. Einsatz von Druckkämmen zur Effizienzsteigerung von schrägverzahnten Getrieben. Ph.D. Thesis, TU Clausthal, Clausthal-Zellerfeld, Germany, 2018. [Google Scholar]
- Hopkins, P. Recent RN Gearing Experiences. J. Nav. Eng. 2005, 42, 504–520. [Google Scholar]
- Qiao, J.; Liang, D.; Chen, Y.; Zhang, D.; Zhou, S.; Jiang, C. 齿轮箱异响故障诊断与排除方法的研究 (Study on Fault Diagnosis and Troubleshooting Method of Gearbox Noise). 机械管理开发 Mech. Manag. Dev. 2020, 205, 118–120. [Google Scholar] [CrossRef]
- Heß, M. Untersuchung an Laufflächen von Druckkammlagern im Mischreibungsgebiet. Mitteilungen aus dem Inst. für Maschinenwesen der Tech. Univ. Clausthal 2016, 41, 47–60. [Google Scholar]
- Venner, C.H.; Lubrecht, A.A. Multilevel Methods in Lubrication, 1st ed.; Tribology Series; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 2000. [Google Scholar]
- Heinrich, C.; Lohrengel, A. Simulation von hoch belasteten Druckkammlagerungen. Mitteilungen aus dem Inst. für Maschinenwesen der Tech. Univ. Clausthal 2024, 48, 23–34. [Google Scholar]
- Dietz, P.; Mupende, I. Druckkamm–ein altes Maschinenelement mit neuem Anwendungspotential. Konstruktion 2006, 58, 69–75. [Google Scholar]
- Panowitz, D.; Somschor, B. Getriebeanordnung eines Schienenfahrzeugs. German Patent No. DE102012205368A1, 10 October 2013. [Google Scholar]
- Heinrich, C. Druckkammsimulation unter Berücksichtigung der Platten- und Wellensteifigkeit. In Proceedings of the 17. Gemeinsames Kolloquium Konstruktionstechnik, KT2019, Aachen, Germany, 1–2 October 2019; pp. 126–137. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Reusner, H. Druckflächenbelastung und Oberflächenverschiebung im Wälzkontakt von Rotationskörpern. Ph.D. Thesis, Universität Karlsruhe, Karlsruhe, Germany, 1977. [Google Scholar]
- Hetényi, M. A Method of Solution for the Elastic Quarter-Plane. J. Appl. Mech. 1960, 27, 289–296. [Google Scholar] [CrossRef]
- Hetényi, M. A General Solution for the Elastic Quarter Space. J. Appl. Mech. 1970, 37, 70–76. [Google Scholar] [CrossRef]
- Guilbault, R. A fast correction for traction-free surface of elastic quarter-space. In Proceedings of the Tribology and Design 2010, Algarve, Portugal, 19–21 April 2010; pp. 37–48. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon: Oxford, UK, 1959. [Google Scholar]
- Bartel, D. Simulation von Tribosystemen: Grundlagen und Anwendungen, 1st ed.; Vieweg+Teubner: Wiesbaden, Germany, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).