A Numerical Investigation of Non-Ideal Gas Effects on the Saturation Pressure of Water Under High Pressure and Temperature
Abstract
1. Introduction
2. Assumptions and Methods
2.1. Fugacity in Gas Phase
2.2. Fugacity of the Liquid Phase
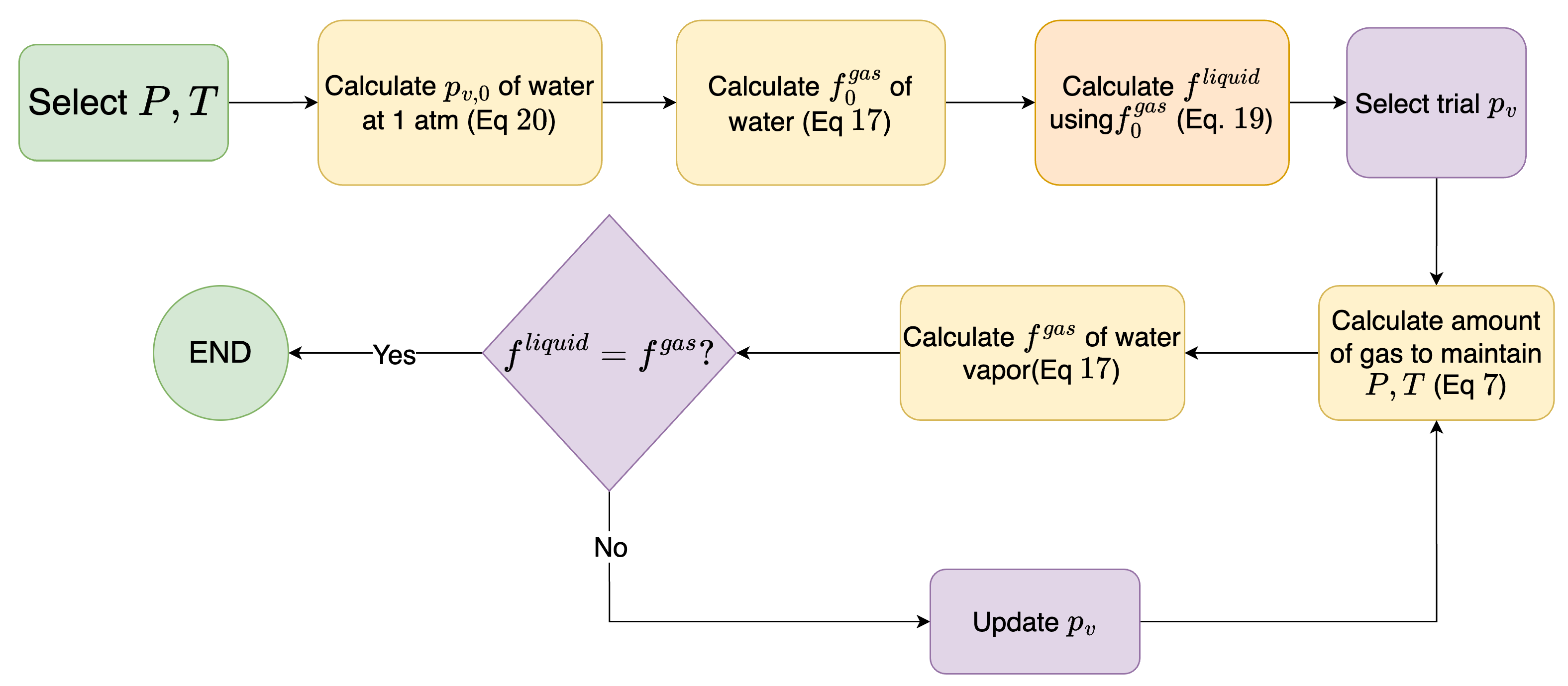
2.3. Calculating Saturation Pressure
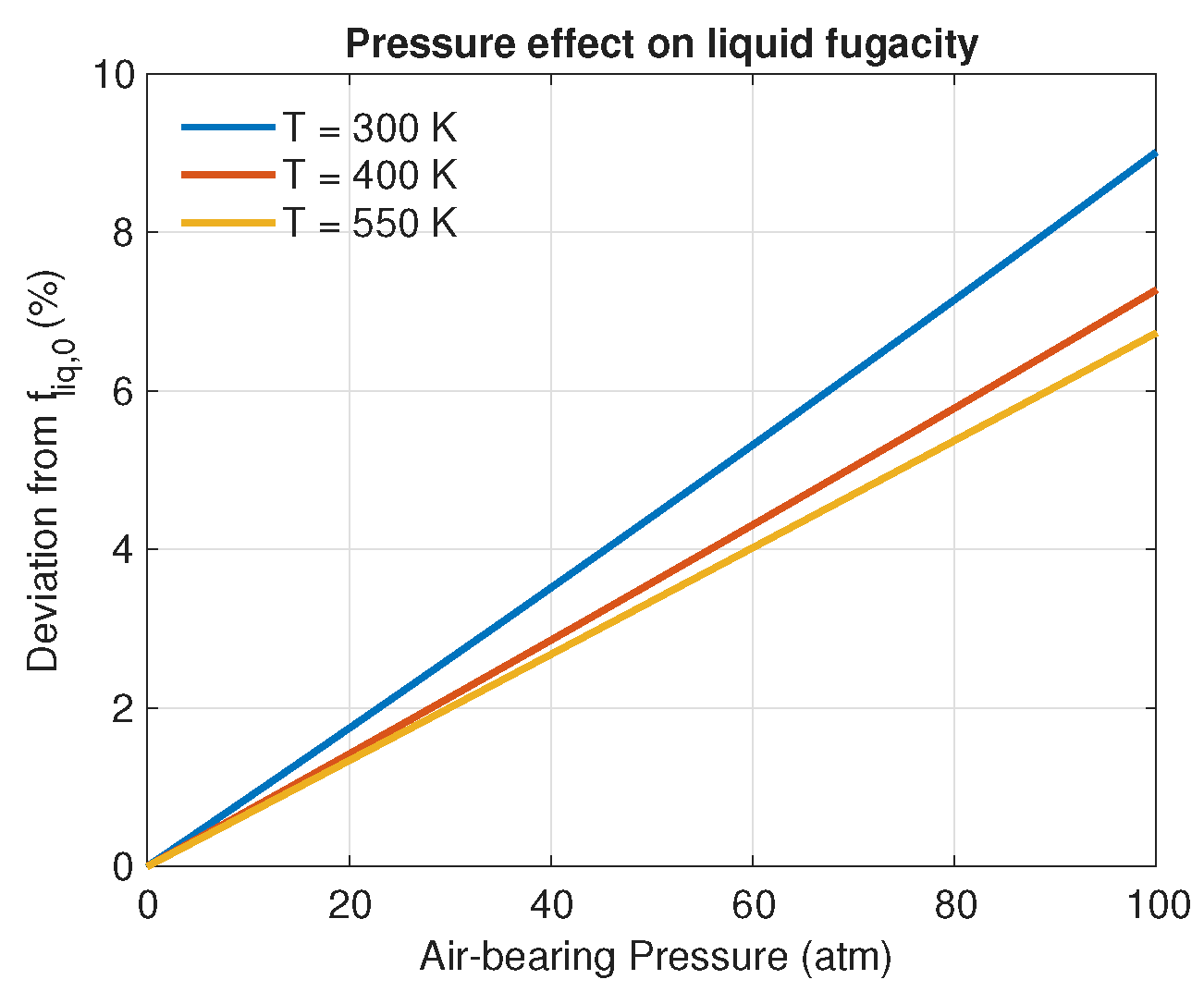
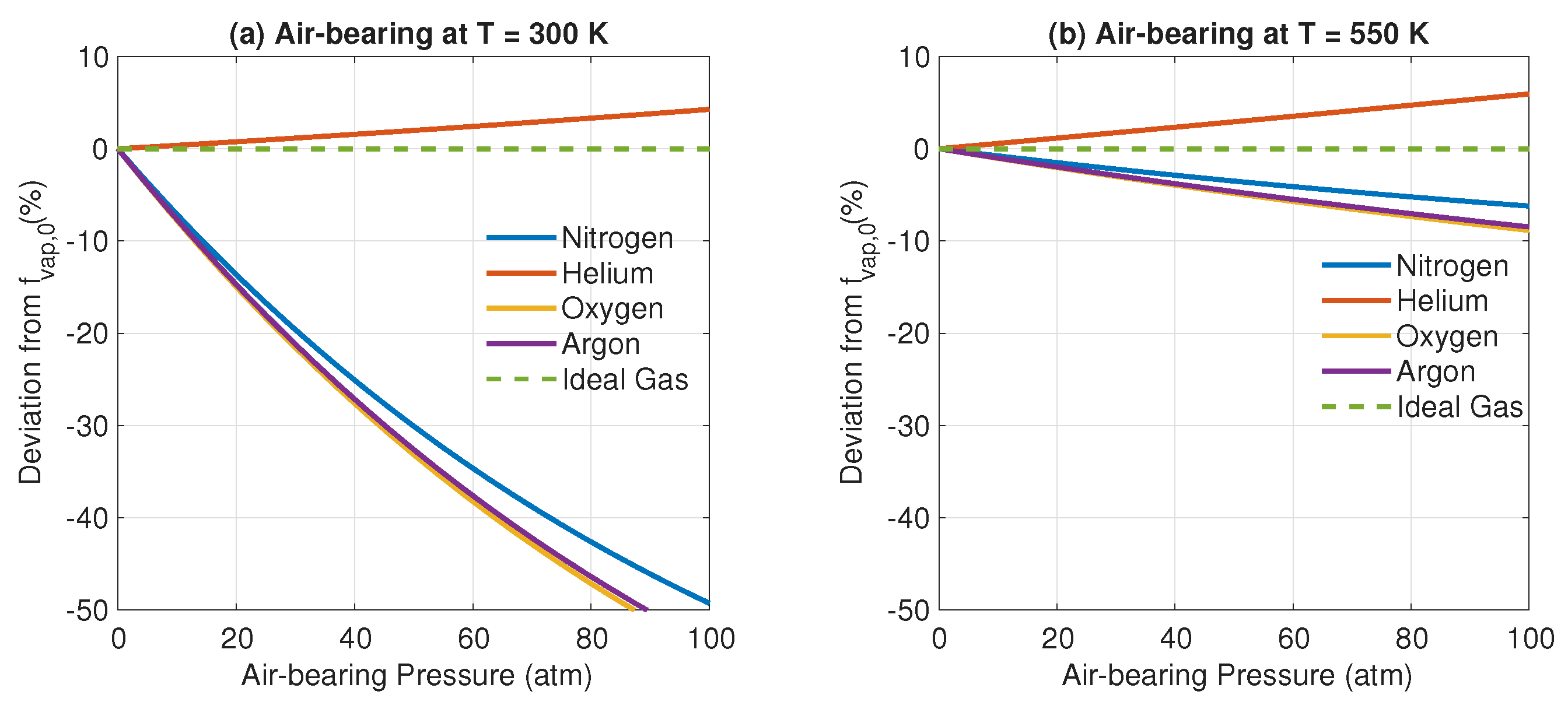
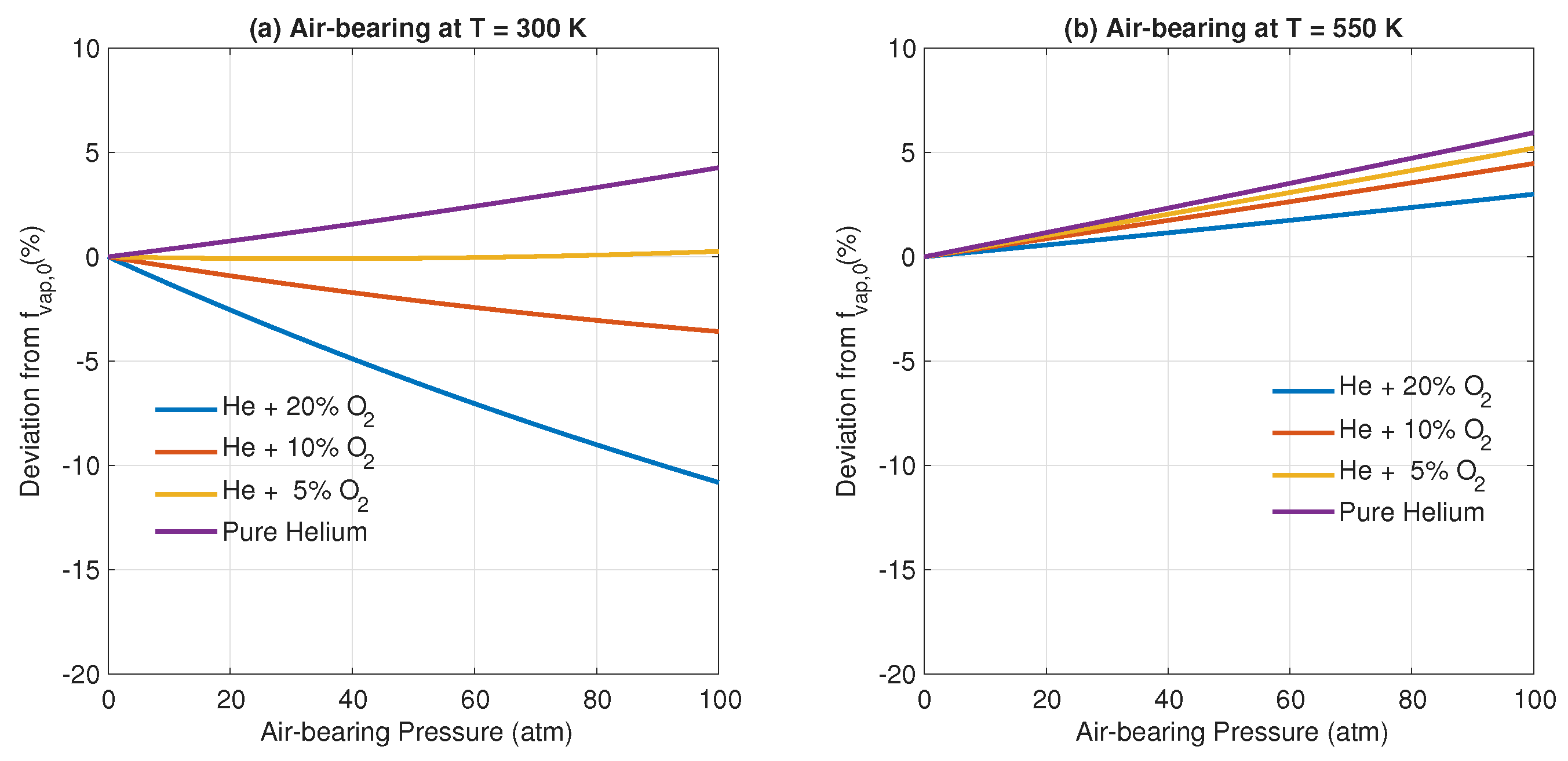
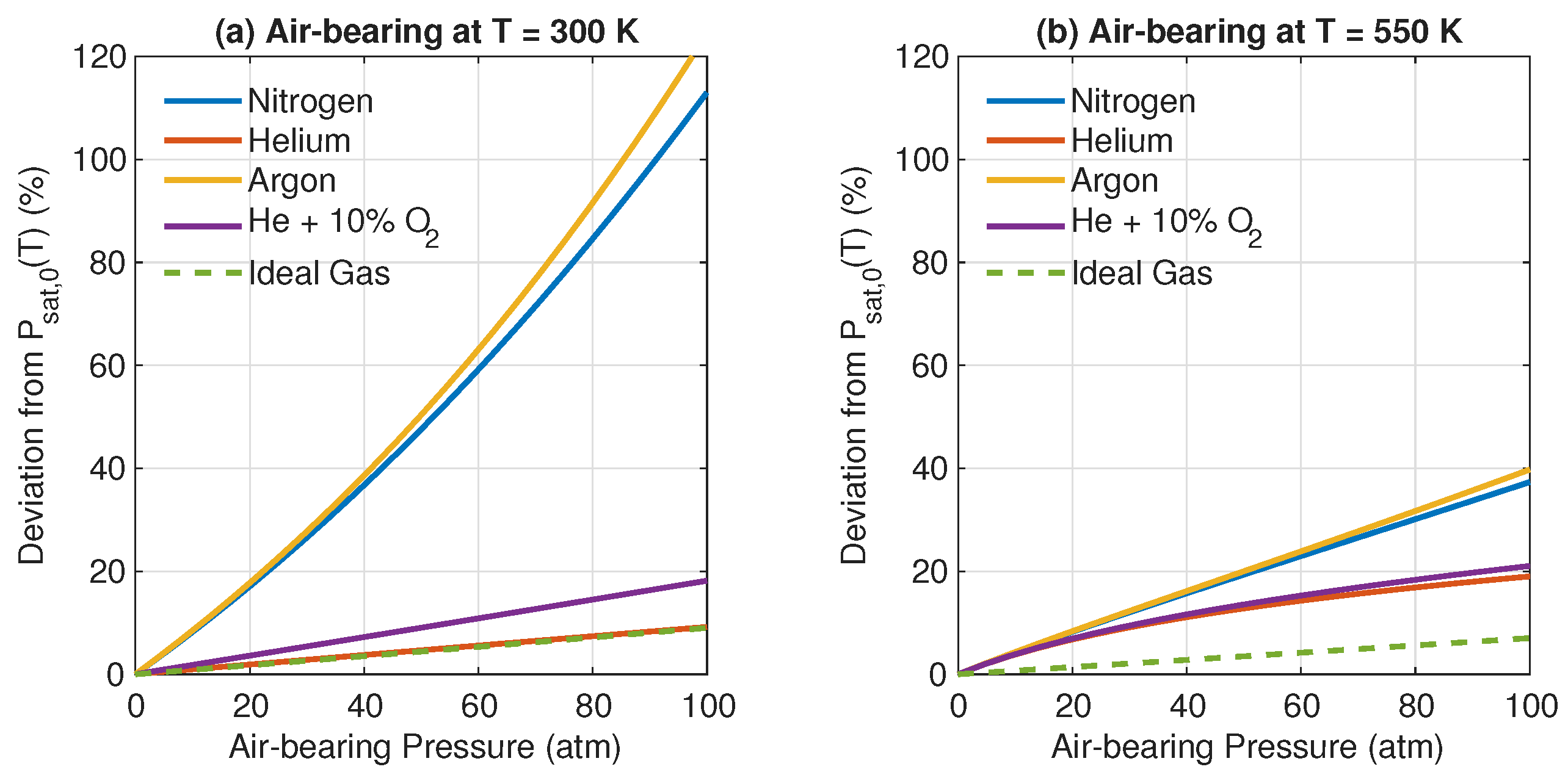
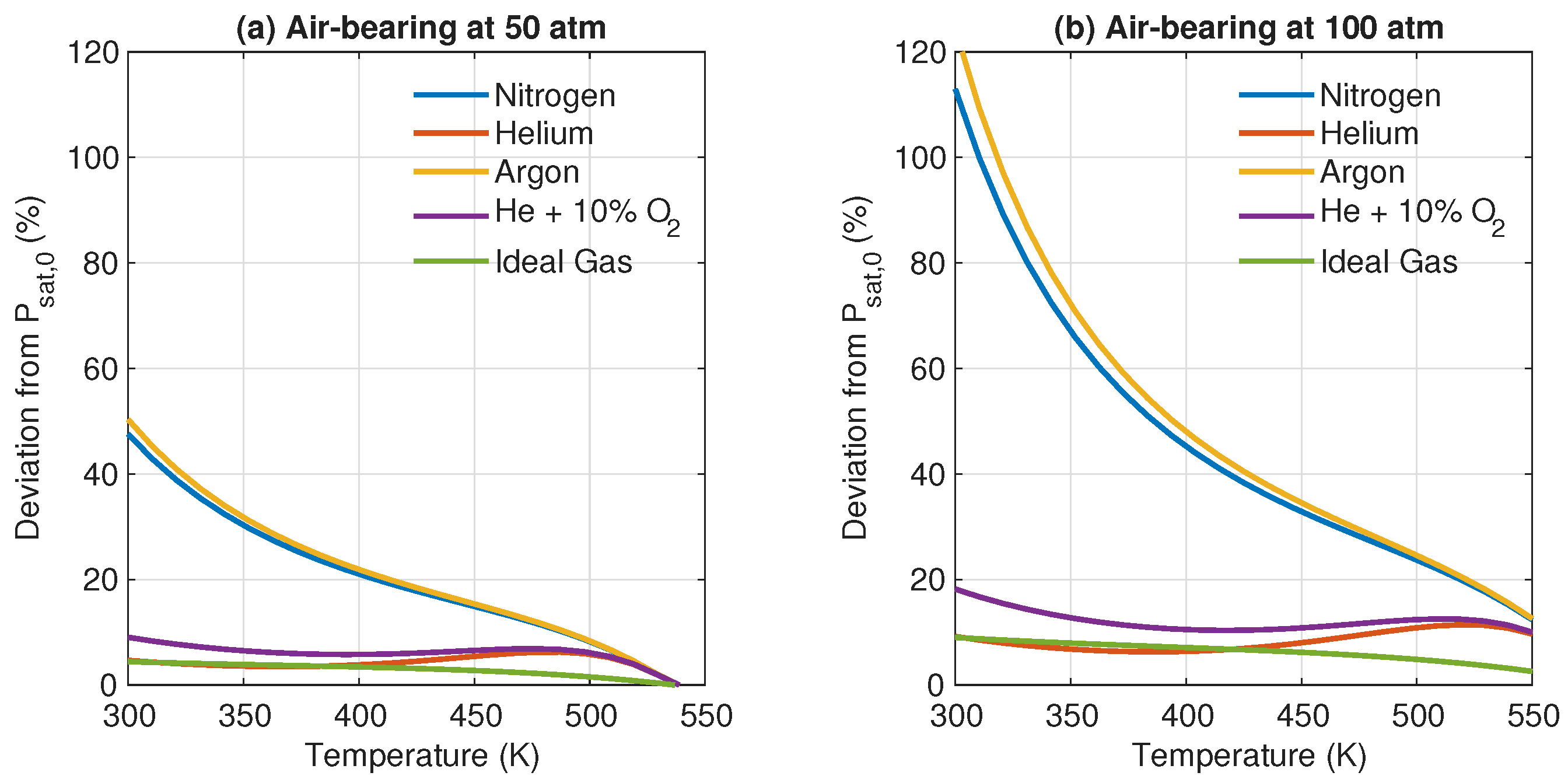
3. Results and Discussion
4. Conclusions and Scope for Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kryder, M.; Gage, E.; McDaniel, T.; Challener, W.; Rottmayer, R.; Ju, G.; Hsia, Y.T.; Erden, M. Heat Assisted Magnetic Recording. Proc. IEEE 2008, 96, 1810–1835. [Google Scholar] [CrossRef]
- Cheng, Q.; Wang, H.; Sakhalkar, S.V.; Bogy, D.B. Measurement of angstrom-level laser induced protrusion using touchdown in heat-assisted magnetic recording. Appl. Phys. Lett. 2020, 117, 153105. [Google Scholar] [CrossRef]
- Tom, R.M.; Smith, R.; Ruiz, O.; Dai, Q.; Bogy, D.B. Optical forces in heat-assisted magnetic recording head-disk interface. Sci. Rep. 2023, 13, 8451. [Google Scholar] [CrossRef] [PubMed]
- Kiely, J.D.; Jones, P.M.; Yang, Y.; Brand, J.L.; Anaya-Dufresne, M.; Fletcher, P.C.; Zavaliche, F.; Toivola, Y.; Duda, J.C.; Johnson, M.T. Write-Induced Head Contamination in Heat-Assisted Magnetic Recording. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Cheng, Q.; Tom, R.M.; Bogy, D.B. Two strategies to mitigate thermally-induced material buildup in heat-assisted magnetic recording. Tribol. Lett. 2023, 71, 50. [Google Scholar] [CrossRef]
- Kiely, J.D.; Jones, P.M.; Hoehn, J. Materials challenges for the heat-assisted magnetic recording head–disk interface. MRS Bull. 2018, 43, 119–124. [Google Scholar] [CrossRef]
- Lancaster, J. A review of the influence of environmental humidity and water on friction, lubrication and wear. Tribol. Int. 1990, 23, 371–389. [Google Scholar] [CrossRef]
- Kim, S.H.; Dai, Q.; Marchon, B.; Flechsig, K. Humidity effects on lubricant transfer in the head-disk interface of a hard disk drive. J. Appl. Phys. 2009, 105, 07B70. [Google Scholar] [CrossRef]
- Tani, H.; Kurafuji, H.; Tagawa, N.; Kawada, S.; Lu, R.; Koganezawa, S. Effect of Humidity on Head Smear Generation in Head-Assisted Magnetic Recording. IEEE Trans. Magn. 2023, 59, 1–5. [Google Scholar] [CrossRef]
- Karis, T.E. Water Adsorption on Thin Film Media. J. Colloid Interface Sci. 2000, 225, 196–203. [Google Scholar] [CrossRef]
- Lei, R.Z.; Gellman, A.J. Humidity Effects on PFPE Lubricant Bonding to a-CHx Overcoats. Langmuir 2000, 16, 6628–6635. [Google Scholar] [CrossRef]
- Tyndall, G.W.; Waltman, R.J.; Pacansky, J. Effect of adsorbed water on perfluoropolyether-lubricated magnetic recording disks. J. Appl. Phys. 2001, 90, 6287–6296. [Google Scholar] [CrossRef]
- Dubin, R.R.; Winn, K.D.; Davis, L.P.; Cutler, R.A. Degradation of Co-based thin-film recording materials in selected corrosive environments. J. Appl. Phys. 1982, 53, 2579–2581. [Google Scholar] [CrossRef]
- Cheng, Q.; Sakhalkar, S.; Ghafari, A.; Ma, Y.; Bogy, D. Dependence of nanoscale heat transfer across a closing gap on the substrate material and ambient humidity. Appl. Phys. Lett. 2020, 116, 213102. [Google Scholar] [CrossRef]
- Trinh, T.D.; Schade, C.; Johnson, M.; Talke, F.E. Investigation of Bias Voltage and Relative Humidity on Wear and Pit Formation at the Head–Disk Interface. IEEE Trans. Magn. 2020, 56, 1–7. [Google Scholar] [CrossRef]
- Cheng, Q.; Ma, Y.; Bogy, D. Effect of humidity on the nanoscale heat transfer at the head-media interface. In Proceedings of the Information Storage and Processing Systems. American Society of Mechanical Engineers, San Diego, CA, USA, 27–28 June 2019; Volume 59124, p. V001T03A004. [Google Scholar] [CrossRef]
- Shukla, N.; Gellman, A.J.; Ma, X.; Gui, J. Effect of Humidity on Lubricated Carbon Overcoats. Tribol. Lett. 2002, 12, 105–109. [Google Scholar] [CrossRef]
- Sakhalkar, S.V.; Bogy, D.B. Effect of rheology and slip on lubricant deformation and disk-to-head transfer during heat-assisted magnetic recording (HAMR). Tribol. Lett. 2018, 66, 1–19. [Google Scholar] [CrossRef]
- Carey, V.P. Liquid-Vapor Phase-Change Phenomena: An Introduction to the Thermophysics of Vaporization and Condensation Processes in Heat Transfer Equipment; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Jung, Y.; Yeo, C. Mechano-Chemical Properties and Tribological Performance of Thin Perfluoropolyether (PFPE) Lubricant Film under Environmental Contaminants. Lubricants 2023, 11, 306. [Google Scholar] [CrossRef]
- Zou, A.; Poudel, S.; Gupta, M.; Maroo, S.C. Disjoining pressure of water in nanochannels. Nano Lett. 2021, 21, 7769–7774. [Google Scholar] [CrossRef]
- Peng, T.; Peng, K.; Li, Q. Methodology for disjoining pressure of free water nanofilms. J. Phys. Chem. C 2015, 119, 14273–14280. [Google Scholar] [CrossRef]
- Kretzschmar, H.J.; Wagner, W. International Steam Tables; Springer: Berlin, Germany, 2019. [Google Scholar]
- Sechrist, F. Effect of Carbon Dioxide on Evaporation of Water. Nature 1963, 199, 899–900. [Google Scholar] [CrossRef]
- Mansfield, W.W. Influence of Gases on the Rate of Evaporation of Water. Nature 1965, 205, 278. [Google Scholar] [CrossRef]
- Factorovich, M.H.; Molinero, V.; Scherlis, D.A. Vapor pressure of water nanodroplets. J. Am. Chem. Soc. 2014, 136, 4508–4514. [Google Scholar] [CrossRef] [PubMed]
- Huang, J. A Simple Accurate Formula for Calculating Saturation Vapor Pressure of Water and Ice. J. Appl. Meteorol. Climatol. 2018, 57, 1265–1272. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, J.; Chu, H.W.; Zhang, G.; Fan, X. A Review on Water Vapor Pressure Model for Moisture Permeable Materials Subjected to Rapid Heating. Appl. Mech. Rev. 2018, 70, 020803. [Google Scholar] [CrossRef]
- Lewis, G.N. The Law of Physico-Chemical Change. Proc. Am. Acad. Arts Sci. 1901, 37, 49. [Google Scholar] [CrossRef]
- Chueh, P.L.; Prausnitz, J.M. Vapor-Liquid Equilibria at High Pressures. Vapor-Phase Fugacity Coefficients in Nonpolar and Quantum-Gas Mixtures. Ind. Eng. Chem. Fundam. 1967, 6, 492–498. [Google Scholar] [CrossRef]
- Chueh, P.L.; Prausnitz, J. Calculation of high pressure vapor=liquid equilibria. Ind. Eng. Chem. 1968, 60, 34–52. [Google Scholar] [CrossRef]
- Klauda, J.B.; Sandler, S.I. A Fugacity Model for Gas Hydrate Phase Equilibria. Ind. Eng. Chem. Res. 2000, 39, 3377–3386. [Google Scholar] [CrossRef]
- Mathias, P.M.; Naheiri, T.; Oh, E.M. A density correction for the Peng—Robinson equation of state. Fluid Phase Equilibria 1989, 47, 77–87. [Google Scholar] [CrossRef]
- Lee, B.I.; Kesler, M.G. A generalized thermodynamic correlation based on three-parameter corresponding states. AIChE J. 1975, 21, 510–527. [Google Scholar] [CrossRef]
- Kingdon, K.H. Enhancement of the evaporation of water by foreign molecules adsorbed on the surface. J. Phys. Chem. 1963, 67, 2732–2737. [Google Scholar] [CrossRef]

| Gas | (K) | (bar) | (bar/mol2) | (L/mol) | (with Water) | |
|---|---|---|---|---|---|---|
| Helium | 10.47 | 6.758 | 0 | 0.0155 | 0.01117 | 0.4953 |
| Hydrogen | 33 | 13 | −0.220 | 0.1423 | 0.01830 | 1.4530 |
| Water | 647 | 220.5 | 0.344 | 14.28 | 0.02115 | - |
| Nitrogen | 126 | 34 | 0.04 | 1.550 | 0.02671 | 4.9062 |
| Oxygen | 154.4 | 50.5 | 0.022 | 1.735 | 0.02204 | 5.2463 |
| Argon | 151 | 48.7 | 0 | 1.7013 | 0.02235 | 5.1795 |
| Ideal gas | N/A | N/A | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tom, R.M.; Rajauria, S.; Dai, Q.; Cheng, Q. A Numerical Investigation of Non-Ideal Gas Effects on the Saturation Pressure of Water Under High Pressure and Temperature. Lubricants 2025, 13, 197. https://doi.org/10.3390/lubricants13050197
Tom RM, Rajauria S, Dai Q, Cheng Q. A Numerical Investigation of Non-Ideal Gas Effects on the Saturation Pressure of Water Under High Pressure and Temperature. Lubricants. 2025; 13(5):197. https://doi.org/10.3390/lubricants13050197
Chicago/Turabian StyleTom, Roshan Mathew, Sukumar Rajauria, Qing Dai, and Qilong Cheng. 2025. "A Numerical Investigation of Non-Ideal Gas Effects on the Saturation Pressure of Water Under High Pressure and Temperature" Lubricants 13, no. 5: 197. https://doi.org/10.3390/lubricants13050197
APA StyleTom, R. M., Rajauria, S., Dai, Q., & Cheng, Q. (2025). A Numerical Investigation of Non-Ideal Gas Effects on the Saturation Pressure of Water Under High Pressure and Temperature. Lubricants, 13(5), 197. https://doi.org/10.3390/lubricants13050197





