Prediction of Friction Torque in Paired Tapered Roller Bearings of Disc Cutter Under Tri-Axial Rock-Breaking Loads and Preload
Abstract
:1. Introduction
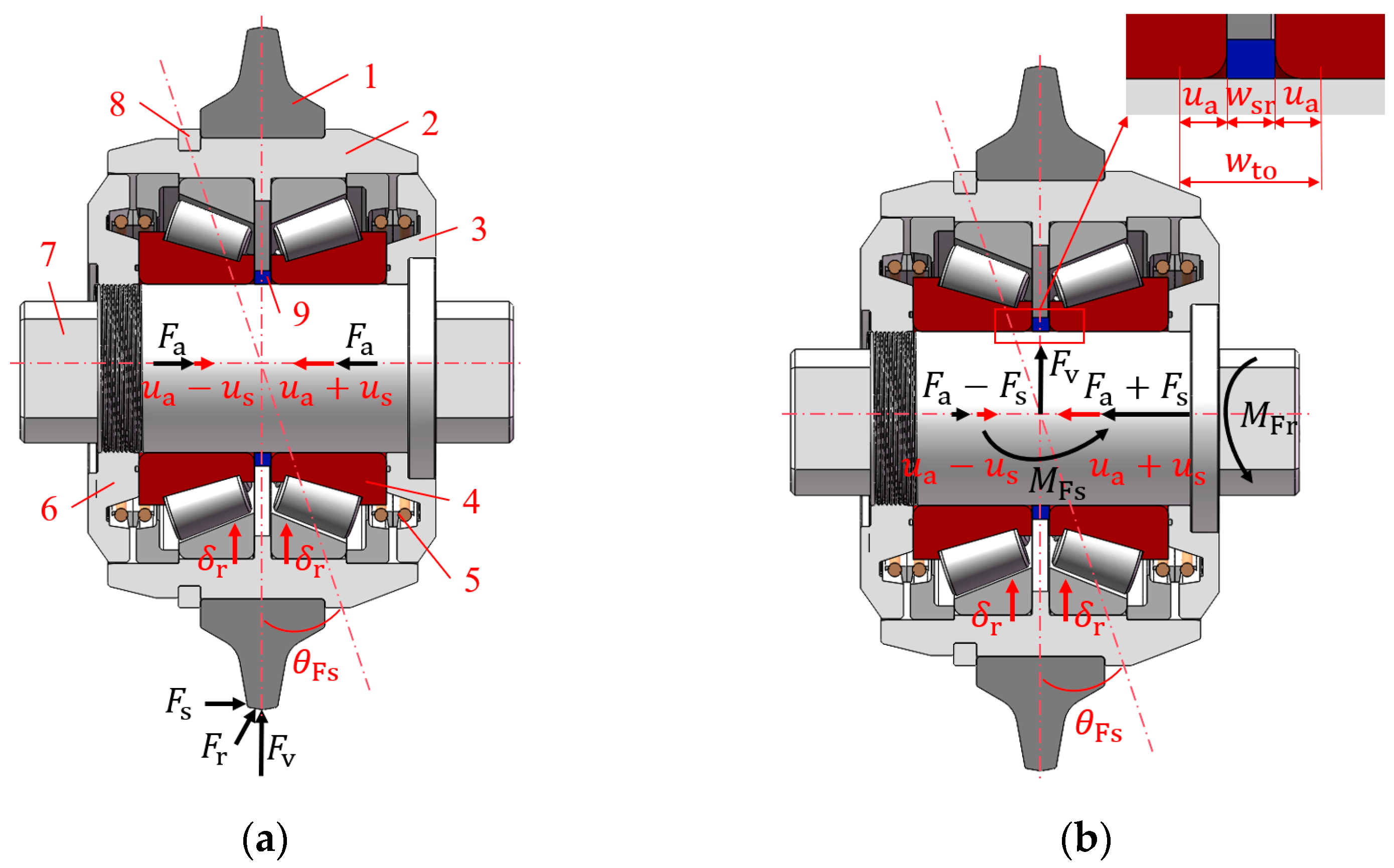
2. Construction of the Friction Torque Model for Paired Tapered Roller Bearings in the Disc Cutter
2.1. Relationship Between Disc Cutter Forces and Bearing Load Distribution
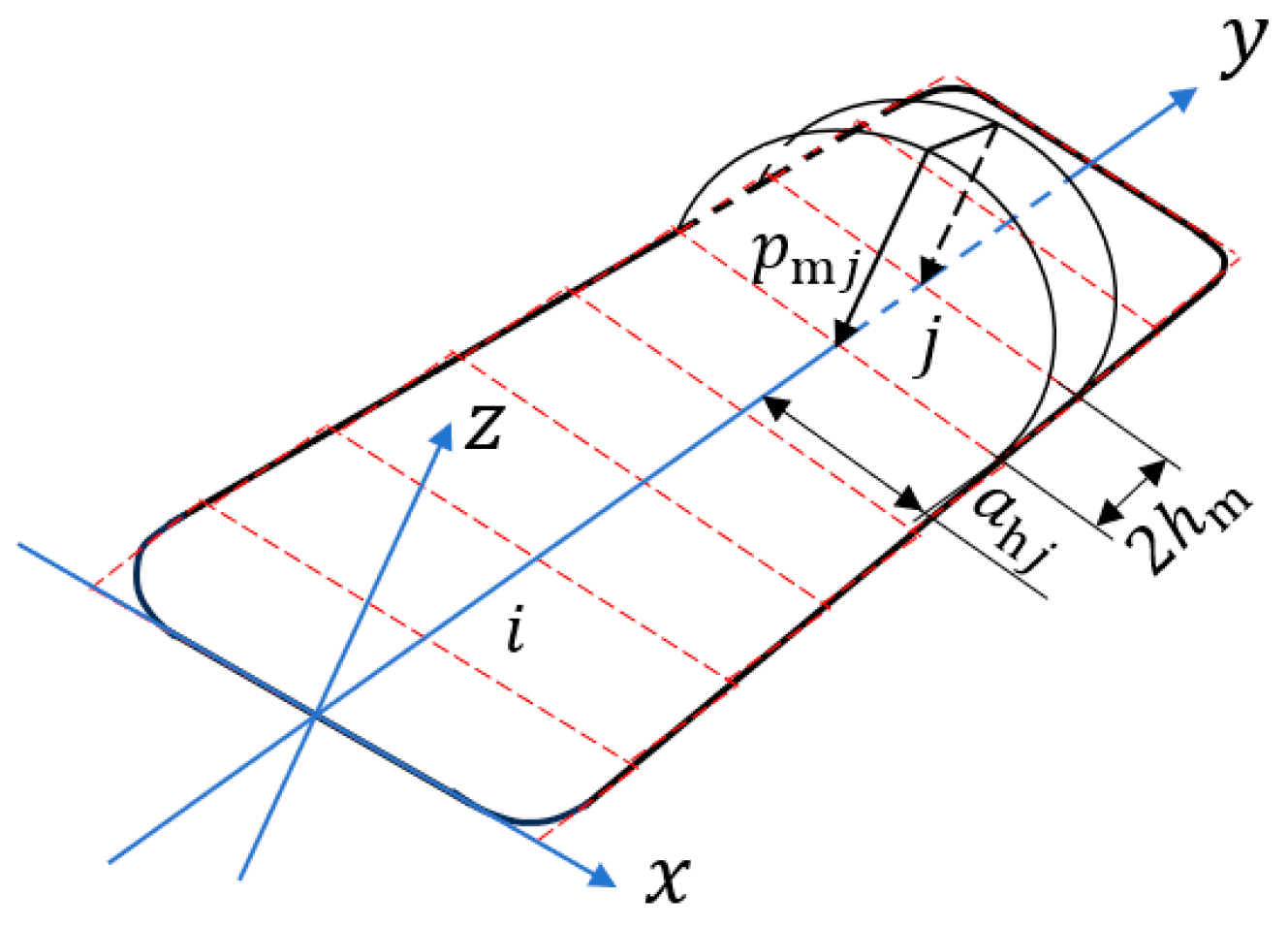
2.1.1. Solution for the Deformation Displacement of the Rollers
2.1.2. Roller Load Calculation
2.1.3. Relationship Between External Forces and Bearing Load
2.2. Construction of the Bearing Friction Torque Model
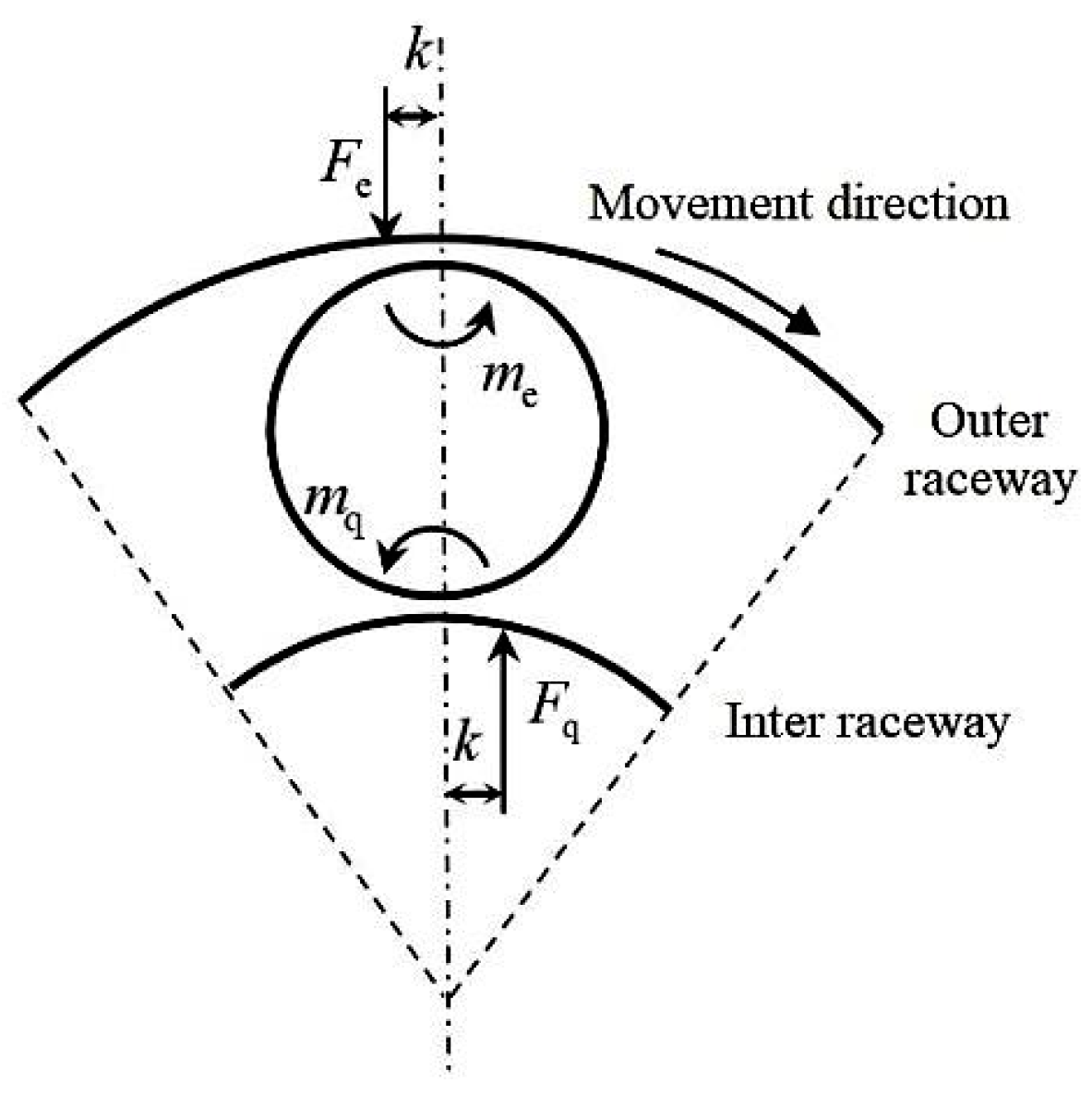
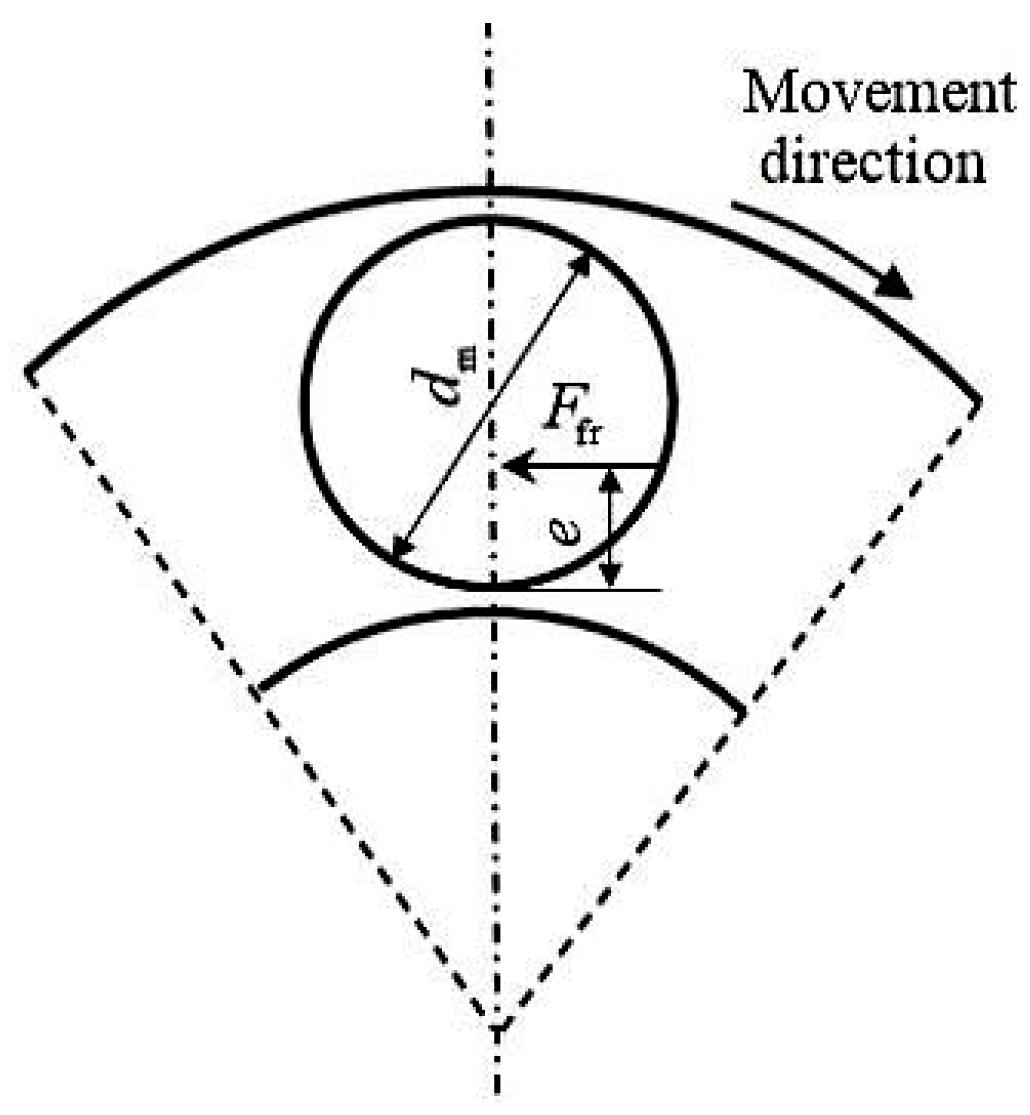
2.2.1. Relationship Between Bearing Load and Rolling Friction Torque
2.2.2. Relationship Between Bearing Load and Sliding Friction Torque
3. Simulation Analysis of the Relationship Between Bearing Preload and Preload Displacement
3.1. Establishment of the Bearing Finite Element Model
3.1.1. Material Properties and Mesh Division
3.1.2. Setting Analysis Step and Interaction Parameters
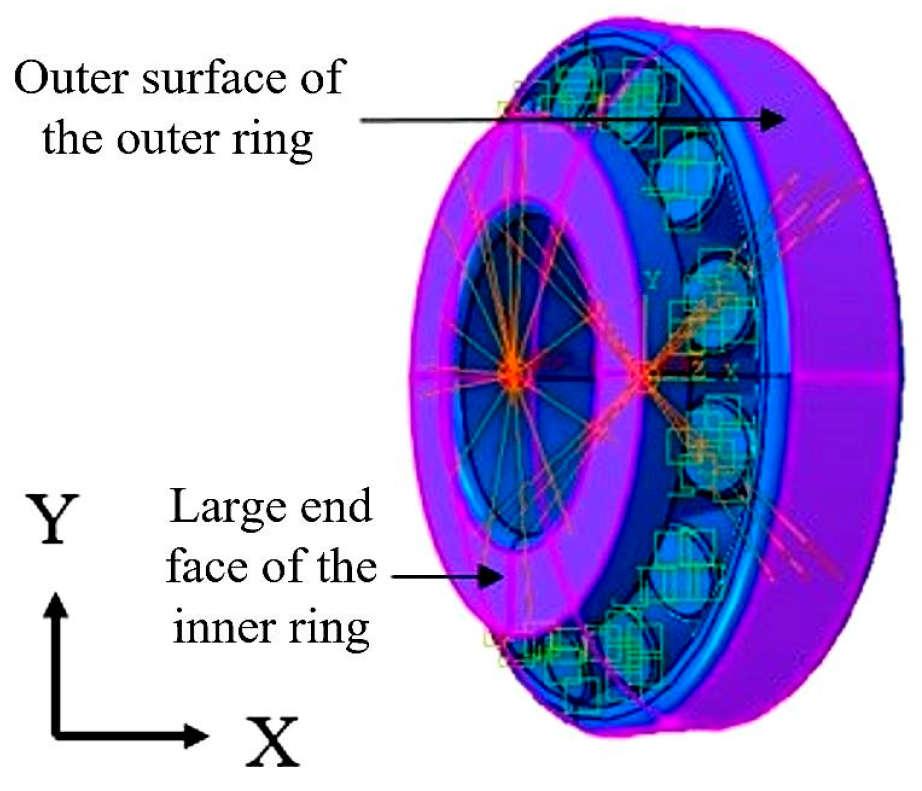
3.1.3. Setting of Boundary Conditions
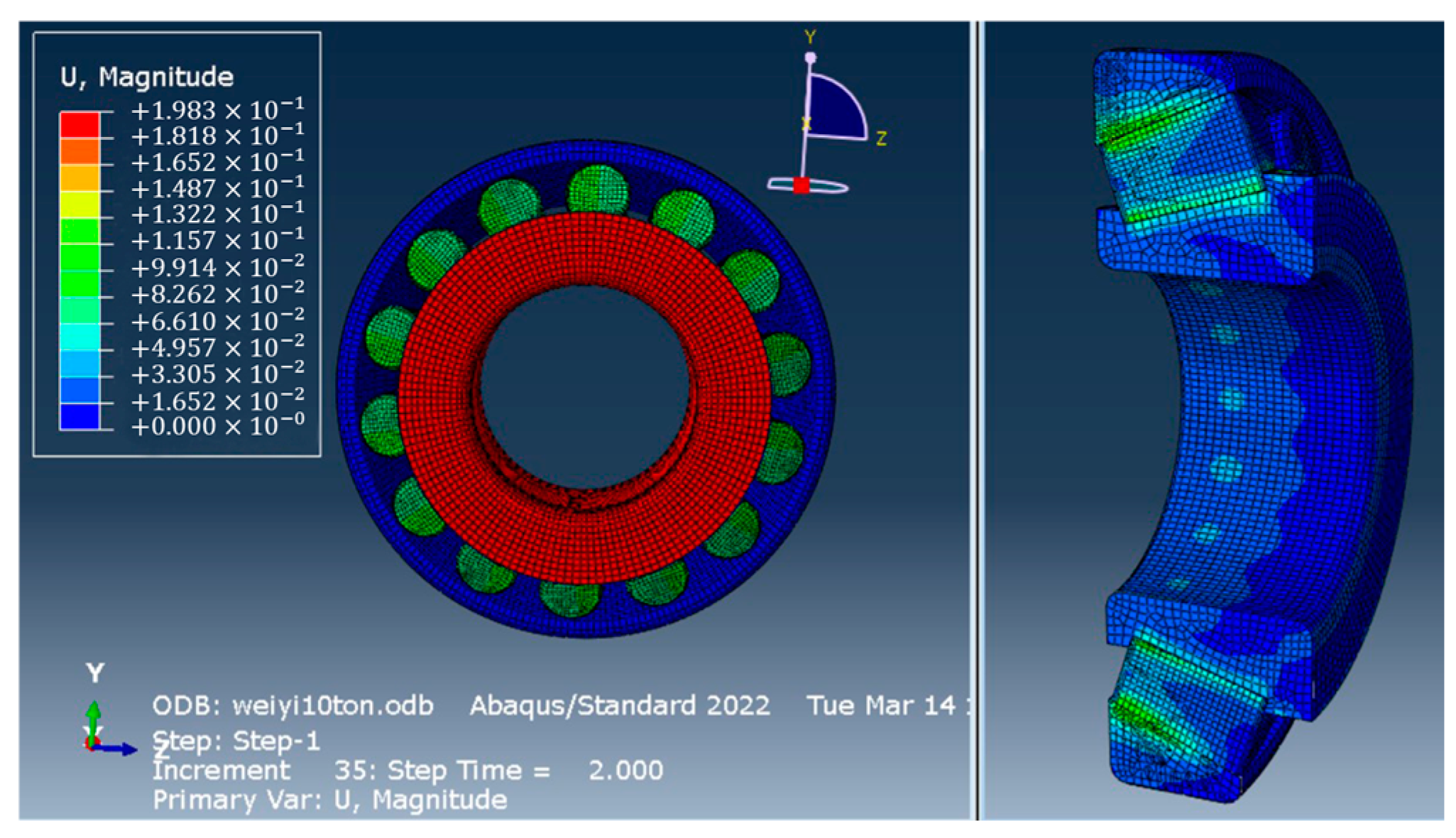
3.2. Results of Finite Element Analysis
3.2.1. Analysis of Bearing Preload
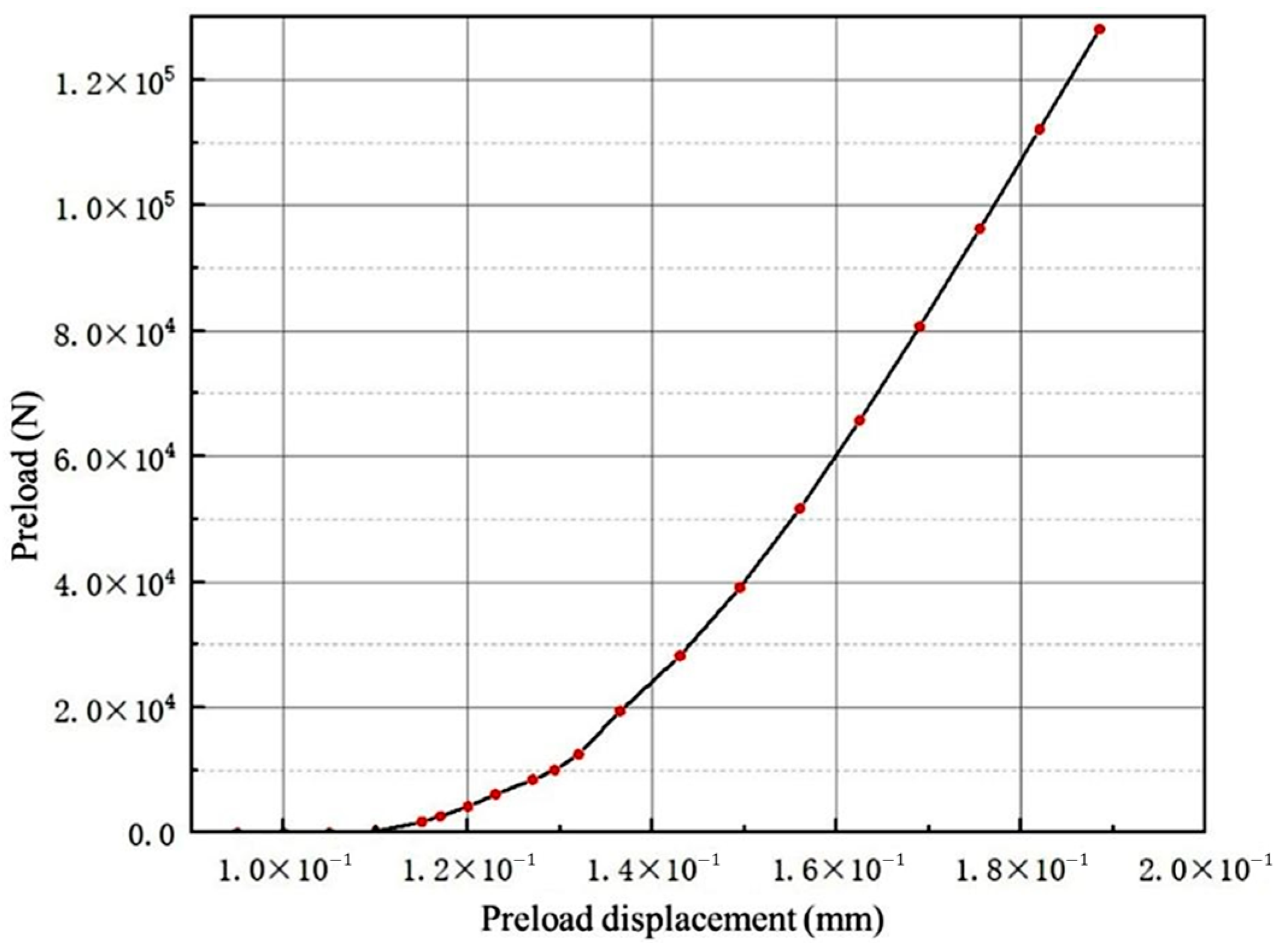
3.2.2. Relationship Between Preload and Preload Displacement
4. Experiments of Disc Cutter Preload Displacement and Friction Torque
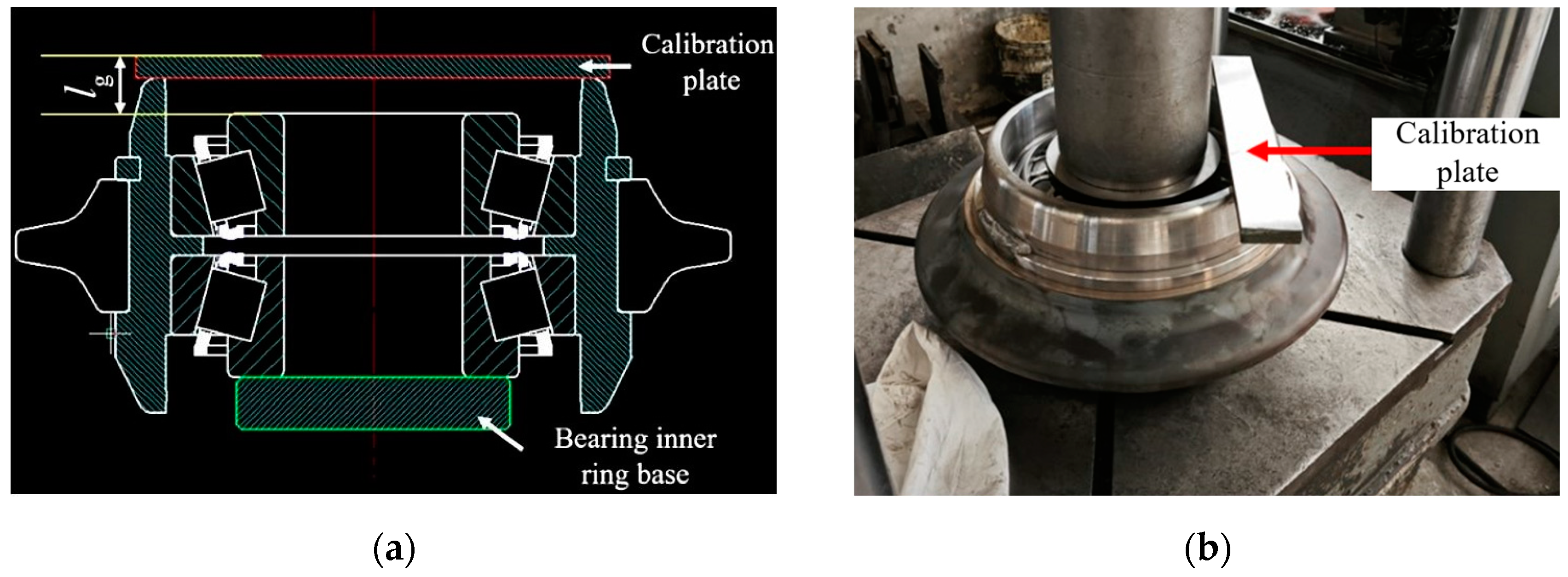
4.1. Experiment of Disc Cutter Preload Displacement
- Experimental setup
- Preload displacement measurement
- Analysis of preload displacement experimental results
- Error analysis
4.2. Experiment of Disc Cutter Bearing Friction Torque
- Experimental setup
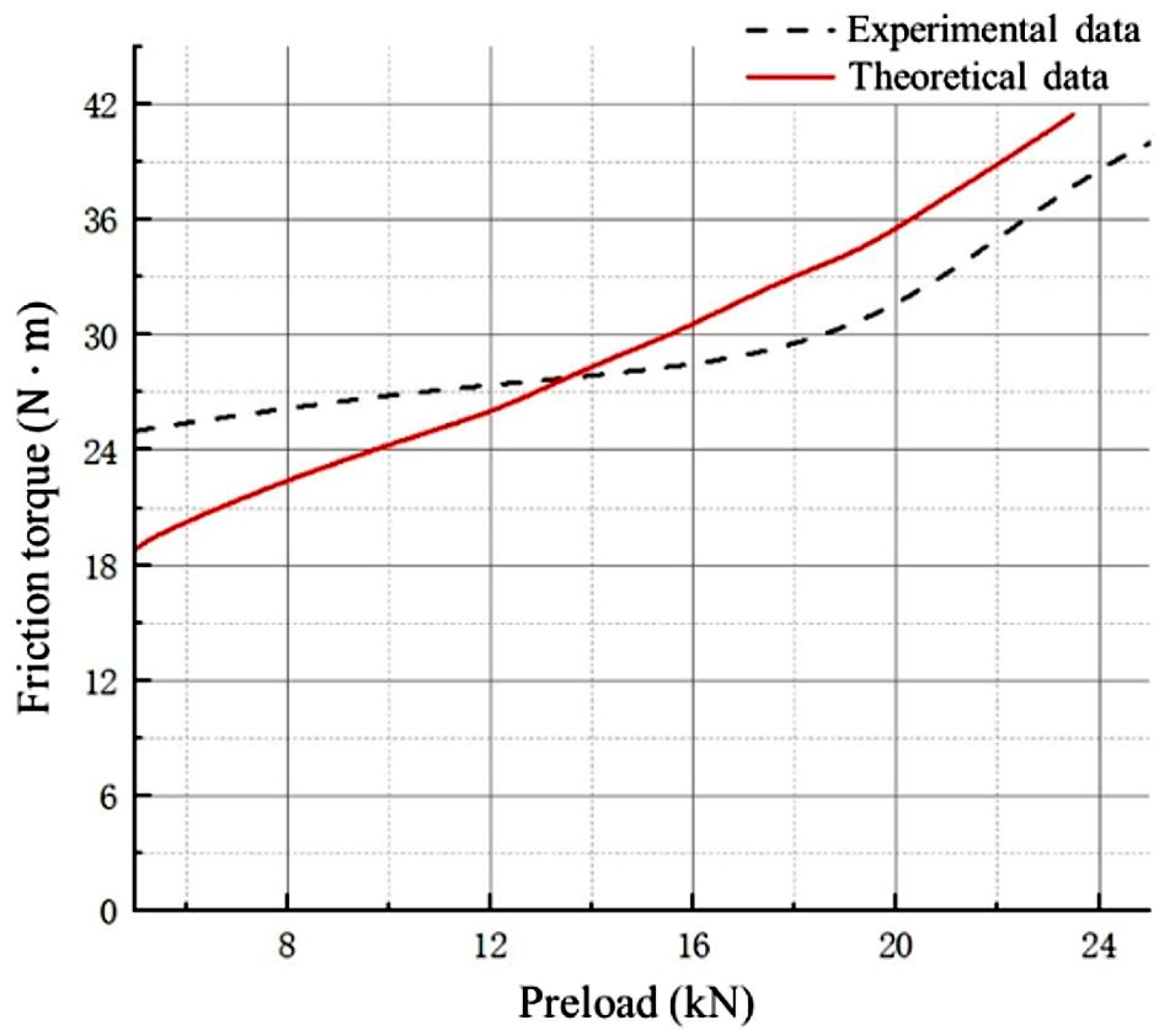
- Analysis of friction torque experimental results
- Error analysis
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, J.; Liu, H.; Feng, L.; Wu, D.; Tang, H.; Xia, Y. Wear performance of modified H-13 and H418E steels for TBM disc cutter ring. Eng. Fail. Anal. 2024, 156, 107783. [Google Scholar] [CrossRef]
- Shen, X.; Chen, X.; Fu, Y.; Cao, C.; Yuan, D.; Li, X.; Xiao, Y. Prediction and analysis of slurry shield TBM disc cutter wear and its application in cutter change time. Wear 2022, 498, 204314. [Google Scholar] [CrossRef]
- Hu, G.; Zhao, H.; Fu, J.; Xue, J.; Xia, Y. Impact fracture failure analysis and mechanism study of a TBM disc cutter ring. Eng. Fail. Anal. 2024, 163, 108508. [Google Scholar] [CrossRef]
- Yang, H.; Liu, B.; Wang, Y.; Li, C. Prediction model for normal and flat wear of disc cutters during TBM tunneling process. Int. J. Geomech. 2021, 21, 6021002. [Google Scholar]
- Hu, G.; Yu, L.; Zhang, Z.; Yang, C.; Fu, J.; Xue, J.; Zhao, H.; Xia, Y.; Yu, L.; Chang, L. Research on fatigue failure analysis and fracture mechanisms of a cutter ring in tunnel boring machine. Eng. Fail. Anal. 2025, 169, 109232. [Google Scholar] [CrossRef]
- Sun, R.; Mo, J.; Zhang, M.; Su, Y.; Zhou, Z. Cutting performance and contact behavior of partial-wear TBM disc cutters: A laboratory scale investigation. Eng. Fail. Anal. 2022, 137, 106253. [Google Scholar] [CrossRef]
- Ge, Y.; Liu, Y.; Lin, P.; Xu, Z. Effects of rock properties on the wear of TBM disc cutter: A case study of the Yellow River diversion project, China. Int. J. Geomech. 2022, 22, 4022011. [Google Scholar]
- Pan, Y.; Liu, Q.; Peng, X.; Kong, X.; Liu, J.; Zhang, X. Full-Scale Rotary Cutting Test to Study the Influence of Disc Cutter Installment Radius on Rock Cutting Forces. Rock. Mech. Rock. Eng. 2018, 51, 2223–2236. [Google Scholar] [CrossRef]
- Huang, Y.; Hao, R.; Li, J.; Wang, H.; Guo, J. Failure Analysis on the Chordal Eccentric Wear of Disk Cutter in Shield Machine. J. Fail. Anal. Prev. 2024, 24, 817–827. [Google Scholar] [CrossRef]
- Cheng, Y.F. Mechanism Analysis and Maintenance of Cutter Head Damage Phenomenon in TBM Construction. Plant Maint. Eng. 2022, 4, 112–113. [Google Scholar] [CrossRef]
- Tang, H. Improvement of Shield Cutters Used in Guangzhou Mass Transit Rail Line. Rock Drill. Mach. Pneum. Tools 2023, 49, 31–36. [Google Scholar] [CrossRef]
- Li, F.; Li, S.X.; Liu, Q.Q. Wear and wear reduction measures of shield cutters. J. Mach. Des. 2021, 38, 126–130. [Google Scholar] [CrossRef]
- Sun, J.; Wang, K.; Wei, J.; Shang, Y.; Sun, C.; Ma, F. A mechanics model of constant cross-section type disc cutter based on dense core forming mechanism. Tunn. Undergr. Space Technol. 2023, 140, 105301. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Liu, J.; Lin, L.; Zheng, X. Research on Spatial Kinematics and Cutting Load Characteristics of TBM Disc Cutters. Geotech. Geol. Eng. 2023, 41, 337–352. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, K.; Dong, W.; Zhang, B. Study of Rock-Cutting Process by Disc Cutters in Mixed Ground based on Three-dimensional Particle Flow Model. Rock. Mech. Rock. Eng. 2020, 53, 3485–3506. [Google Scholar] [CrossRef]
- Labra, C.; Rojek, J.; Onate, E. Discrete/Finite Element Modelling of Rock Cutting with a TBM Disc Cutter. Rock. Mech. Rock. Eng. 2017, 50, 621–638. [Google Scholar] [CrossRef]
- Entacher, M.; Lorenz, S.; Galler, R. Tunnel boring machine performance prediction with scaled rock cutting tests. Int. J. Rock. Mech. Min. Sci. 2014, 70, 450–459. [Google Scholar] [CrossRef]
- Thyagarajan, M.V.; Rostami, J. Study of cutting forces acting on a disc cutter and impact of variable penetration measured by full scale linear cutting tests. Int. J. Rock. Mech. Min. Sci. 2024, 175, 105675. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Y.; Gong, G.; Yang, H. Experimental Study on Partial Wear of TBM Disc Cutter. In Proceedings of the 2024 Prognostics and System Health Management Conference (PHM), Stockholm, Sweden, 28–31 May 2024; pp. 260–265. [Google Scholar]
- Hammami, M.; Martins, R.; Fernandes, C.; Seabra, J.; Abbes, M.S.; Haddar, M. Friction torque in rolling bearings lubricated with axle gear oils. Tribol. Int. 2018, 119, 419–435. [Google Scholar] [CrossRef]
- Houpert, L. Ball bearing and tapered roller bearing torque: Analytical, numerical and experimental results. Tribol. Trans. 2002, 45, 345–353. [Google Scholar] [CrossRef]
- Cai, G.; Hou, Y.; Wang, X.; Sun, S.; Zhang, Y.; Wang, N. A measurement method for friction torque between rollers and raceways of tapered roller bearings under radial heavy load conditions. Tribol. Int. 2024, 200, 110071. [Google Scholar] [CrossRef]
- Wu, C.; Yang, K.; Ni, J.; Lu, S.; Yao, L.; Li, X. Investigations for vibration and friction torque behaviors of thrust ball bearing with self-driven textured guiding surface. Friction 2023, 11, 894–910. [Google Scholar] [CrossRef]
- Liu, J.; Yan, Z.; Shao, Y. An investigation for the friction torque of a needle roller bearing with the roundness error. Mech. Mach. Theory 2018, 121, 259–272. [Google Scholar] [CrossRef]
- Heras, I.; Aguirrebeitia, J.; Abasolo, M.; Coria, I.; Escanciano, I. Load distribution and friction torque in four-point contact slewing bearings considering manufacturing errors and ring flexibility. Mech. Mach. Theory 2019, 137, 23–36. [Google Scholar] [CrossRef]
- Escanciano, I.; Heras, I.; Macareno, L.M.; Aguirrebeitia, J. An engineering approach to assess friction torque in generally loaded four-point contact slewing bearings. Mech. Mach. Theory 2024, 192, 105542. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, X.; Wang, J.; Liu, X. An Investigation for the Friction Torque of a Tapered Roller Bearing Considering the Geometric Homogeneity of Rollers. Lubricants 2022, 10, 154. [Google Scholar] [CrossRef]
- Zhang, C.; Gu, L.; Mao, Y.; Wang, L. Modeling the frictional torque of a dry-lubricated tapered roller bearing considering the roller skewing. Friction 2019, 7, 551–563. [Google Scholar] [CrossRef]
- Wingertszahn, P.; Koch, O.; Maccioni, L.; Concli, F.; Sauer, B. Predicting Friction of Tapered Roller Bearings with Detailed Multi-Body Simulation Models. Lubricants 2023, 11, 369. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, J.; Ren, L.; Chen, J. Influence of axial clearance on load distribution in double supported tapered roller bearings of wind turbine main shaft. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 10536–10552. [Google Scholar] [CrossRef]
- Sun, B.; Guo, W.; Zhu, D.H.; Song, L.W.; Liu, J.Q.; Sun, H.Y. The Improvement of TBM Cutter’s force Formula Based on CSM Model. Mach. Des. Res. 2015, 31, 121–124. [Google Scholar] [CrossRef]
- Ning, B.; Xia, Y.; Lin, L.; Zhang, X.; He, Y.; Liu, Y. Experimental study on the adaptability of cutters with different blade widths under hard rock and extremely hard rock conditions. Acta Geotech. 2020, 15, 3283–3294. [Google Scholar] [CrossRef]
- Xu, C.; Chen, Q.; Li, B.X.; Yuan, W. Relationship between axial loading and tightening torque of tapered roller bearing. Machinery 2012, 39, 24–26. [Google Scholar]
- Huo, J.Z.; Sun, X.L.; Li, G.Q.; Li, T. The structural design and dynamic characteristics of a new type of disc cutter under sliding support. J. Harbin Eng. Univ. 2015, 36, 1509–1514. [Google Scholar]
- Li, Y.; Gao, Y. Internal load distribution of single-row tapered roller bearings doubly supporting main shaft of wind turbine. Adv. Mech. Eng. 2022, 14, 1669512079. [Google Scholar] [CrossRef]
- Stirling, J. Internal Load Modelling of Tapered-Roller Main Bearings in Wind Turbines. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2023. [Google Scholar]
- Wei, Q.L. On the Rolling Friction Law of Coulombian Bodies. J. Wuhan. Univ. Sci. Technol. 1985, 2, 108–110. [Google Scholar]
- Wrzochal, M.; Adamczak, S.; Domagalski, R.; Piotrowicz, G.; Wnuk, S. A New Device Proposed for the Industrial Measurement of Rolling Bearing Friction Torque. Strojniski Vestn.-J. Mech. Eng. 2022, 68, 610–622. [Google Scholar] [CrossRef]










| Poisson’s Ratio | |||
|---|---|---|---|
| 7.8 × 10−9 | 208,000 | 0.3 | 518 |
| Quality Parameter | Warpage | Aspect Ratio | Minimum Angle | Maximum Angle | Jacobian Value |
|---|---|---|---|---|---|
| Value | 12° | 4.16 | 48.4° | 120° | 0.72 |
| Function Type | SSE | R-sq | Adj R-sq | RMSE | Coeff |
|---|---|---|---|---|---|
| Second-order exponential | 0.9931 | 0.9901 | 446.04 | 4 | |
| Fourth-order Fourier | 1.0000 | 0.9998 | 68.84 | 10 | |
| Fifth-order polynomial | 0.9995 | 0.9991 | 136.40 | 6 | |
| Sixth-order polynomial | 0.9999 | 0.9997 | 79.41 | 7 |
| Coefficient | |||||||
|---|---|---|---|---|---|---|---|
| Value |
| Serial Number | 1 | 2 | 3 | 4 | 5 | 6 |
| Preload Force (kN) | 5 | 10 | 15 | 20 | 25 | 30 |
| Preload Displacement (mm) | 0.09 | 0.08 | 0.10 | 0.11 | 0.14 | 0.11 |
| Serial Number | 7 | 8 | 9 | 10 | 11 | 12 |
| Preload Force (kN) | 35 | 40 | 45 | 50 | 55 | 60 |
| Preload Displacement (mm) | 0.12 | 0.14 | 0.15 | 0.16 | 0.16 | 0.18 |
| Preload Force (kN) | 5 | 10 | 15 | 20 | 25 |
| ) | 25 | 27 | 28 | 30 | 42 |
| Parameter Symbol | Parameter Name | Reference Value | Unit |
|---|---|---|---|
| Contact angle | 12 | ° | |
| 9.5 | |||
| 7 | |||
| Equivalent diameter of the tapered roller | 43 | mm | |
| Raceway diameter | 169.672 | mm | |
| Roller length | 48 | mm | |
| Disc cutter blade width | 22 | mm | |
| Disc cutter outer diameter | 482.6 | mm | |
| Tip pressure distribution coefficient | −0.2~0.2 | / | |
| Penetration depth | 5 | mm | |
| Cutter edge angle | 22 | ° | |
| Elastic modulus of bearing material | 208 | GPa | |
| Poisson’s ratio of bearing material | 0.3 | / | |
| Friction coefficient between shaft and inner ring | 0.03 | / | |
| Friction coefficient between roller and inner ring | 0.03 | / | |
| Contact area between shaft and inner ring | 6,321,161.6 | mm2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Yang, C.; Li, H.; Zhao, H.; Zhang, Z. Prediction of Friction Torque in Paired Tapered Roller Bearings of Disc Cutter Under Tri-Axial Rock-Breaking Loads and Preload. Lubricants 2025, 13, 160. https://doi.org/10.3390/lubricants13040160
Hu G, Yang C, Li H, Zhao H, Zhang Z. Prediction of Friction Torque in Paired Tapered Roller Bearings of Disc Cutter Under Tri-Axial Rock-Breaking Loads and Preload. Lubricants. 2025; 13(4):160. https://doi.org/10.3390/lubricants13040160
Chicago/Turabian StyleHu, Gang, Chaoyu Yang, Huanqiang Li, Haiming Zhao, and Zhihao Zhang. 2025. "Prediction of Friction Torque in Paired Tapered Roller Bearings of Disc Cutter Under Tri-Axial Rock-Breaking Loads and Preload" Lubricants 13, no. 4: 160. https://doi.org/10.3390/lubricants13040160
APA StyleHu, G., Yang, C., Li, H., Zhao, H., & Zhang, Z. (2025). Prediction of Friction Torque in Paired Tapered Roller Bearings of Disc Cutter Under Tri-Axial Rock-Breaking Loads and Preload. Lubricants, 13(4), 160. https://doi.org/10.3390/lubricants13040160







