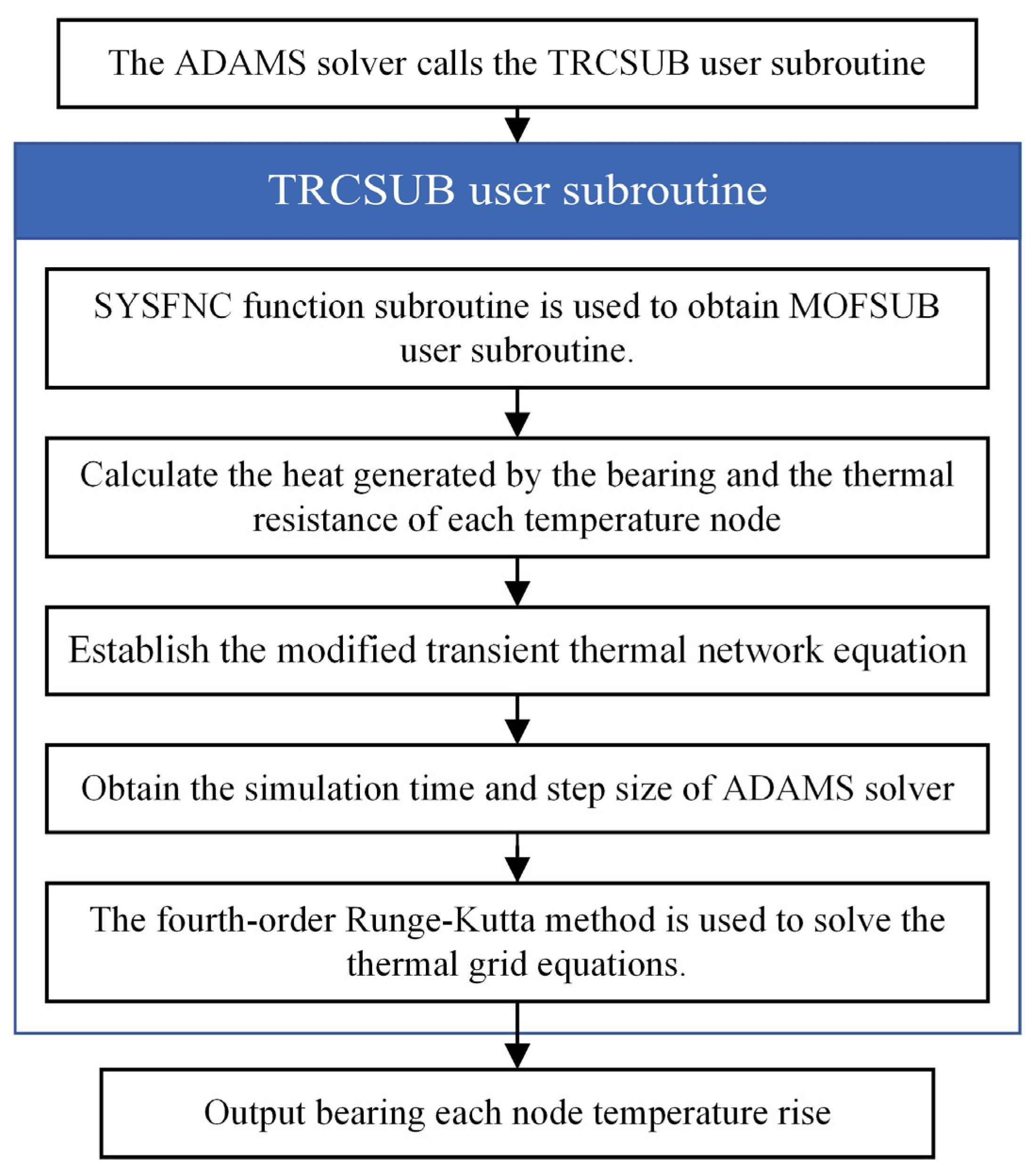
Thermal–Mechanical Coupling Model of a Double-Piece Inner Ring Ball Bearing Based on ADAMS Secondary Development
Abstract
1. Introduction
2. Thermal–Mechanical Coupling Transient Temperature Field Model of Double-Piece Inner Ring Ball Bearing
2.1. Dynamic Model of Bearing Considering Thermal–Mechanical Coupling Effect
2.2. Calculation of Heat Generation in Bearings
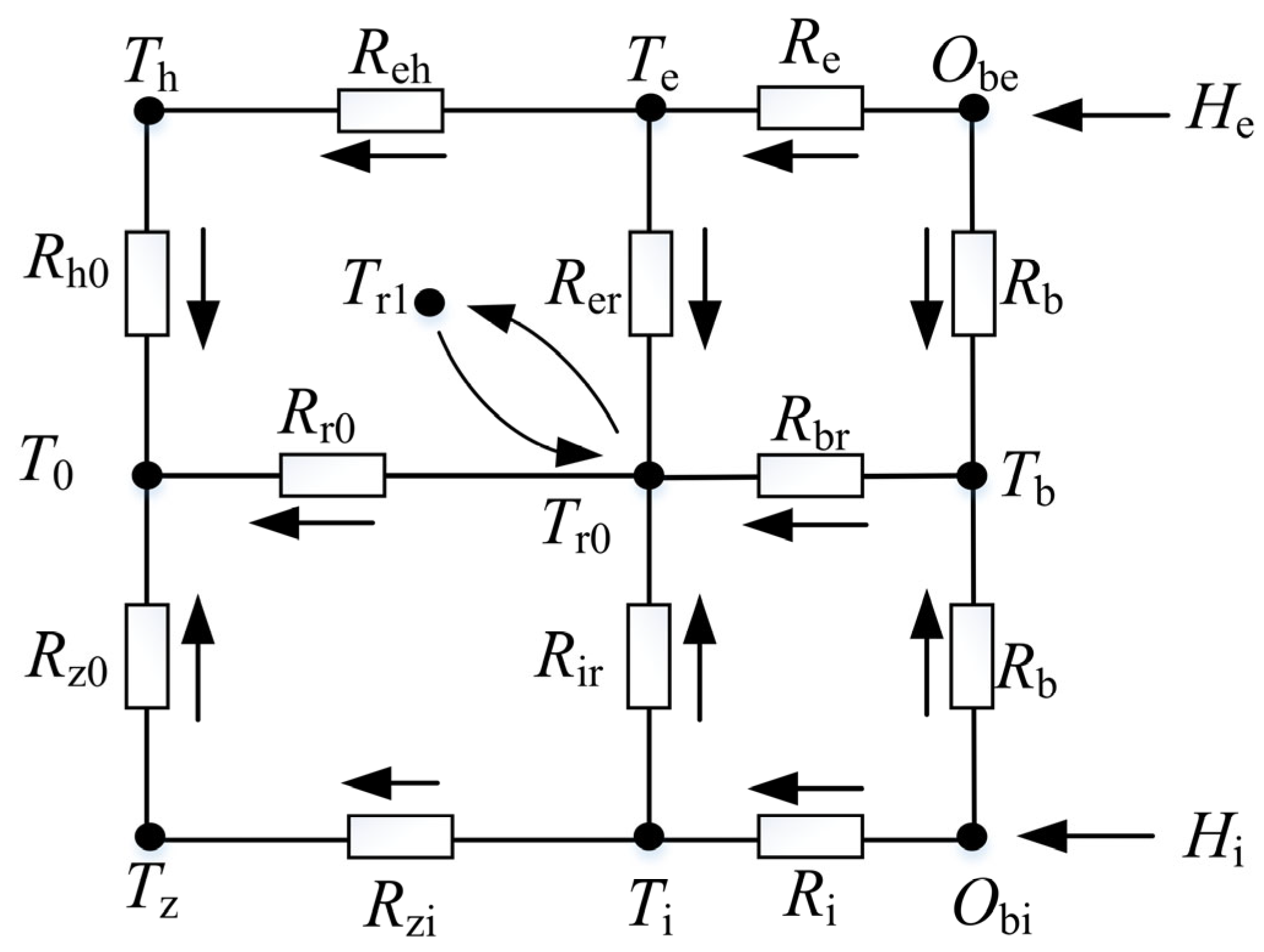
2.3. Modified Transient Thermal Network Equation of Double-Piece Inner Ring Ball Bearing
2.3.1. Heat Transfer Resistance Calculation of Bearing
- (1)
- Thermal resistance of bearing
- (2)
- Convective heat transfer resistance between bearing and lubricant
- (3)
- Thermal resistance of lubricant outside bearing cavity
2.3.2. Transient Thermal Network Equation Considering Lubricant Circulating Flow
2.3.3. Transient Thermal Network Equation Based on Lubricant Penetration Rate
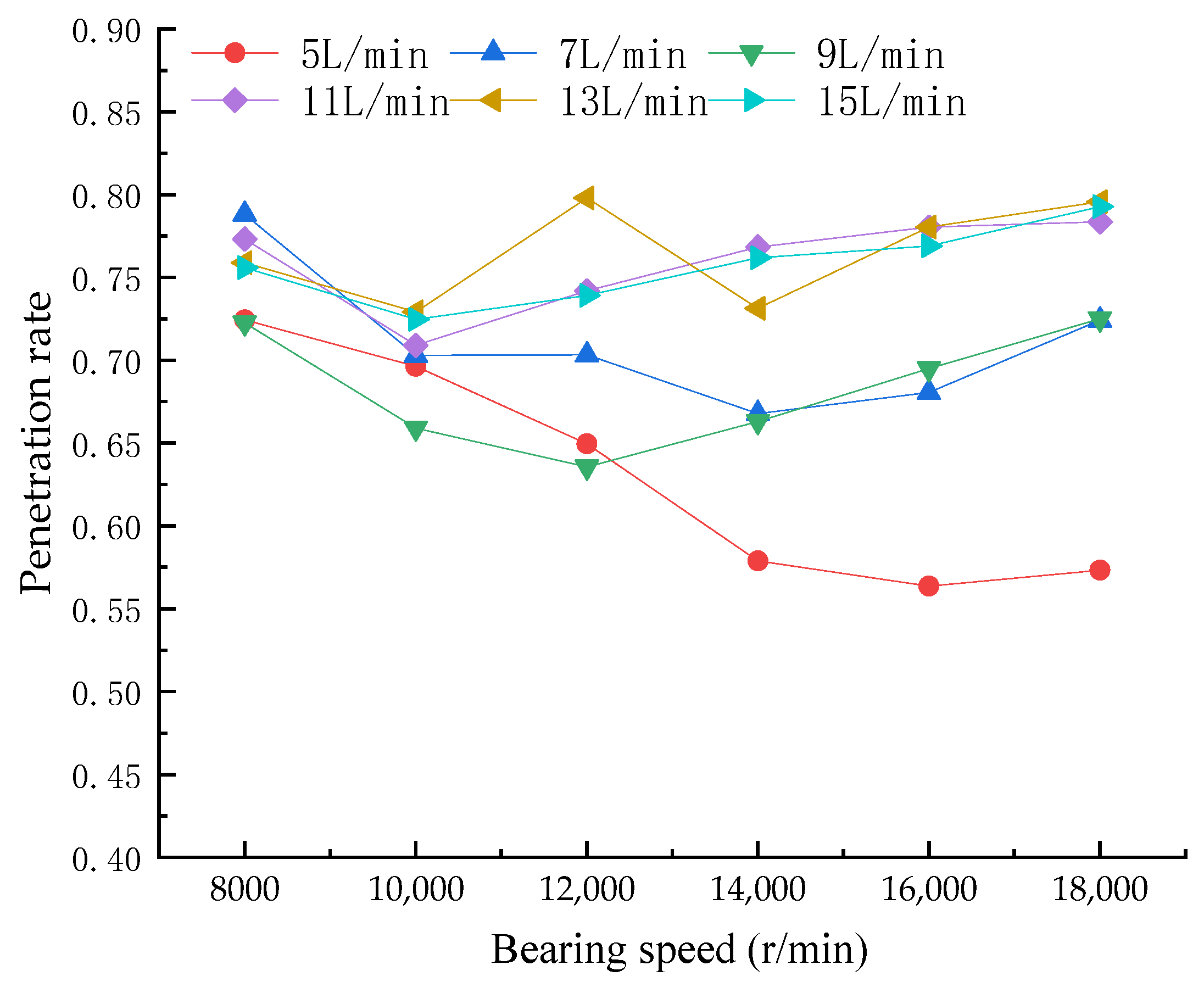
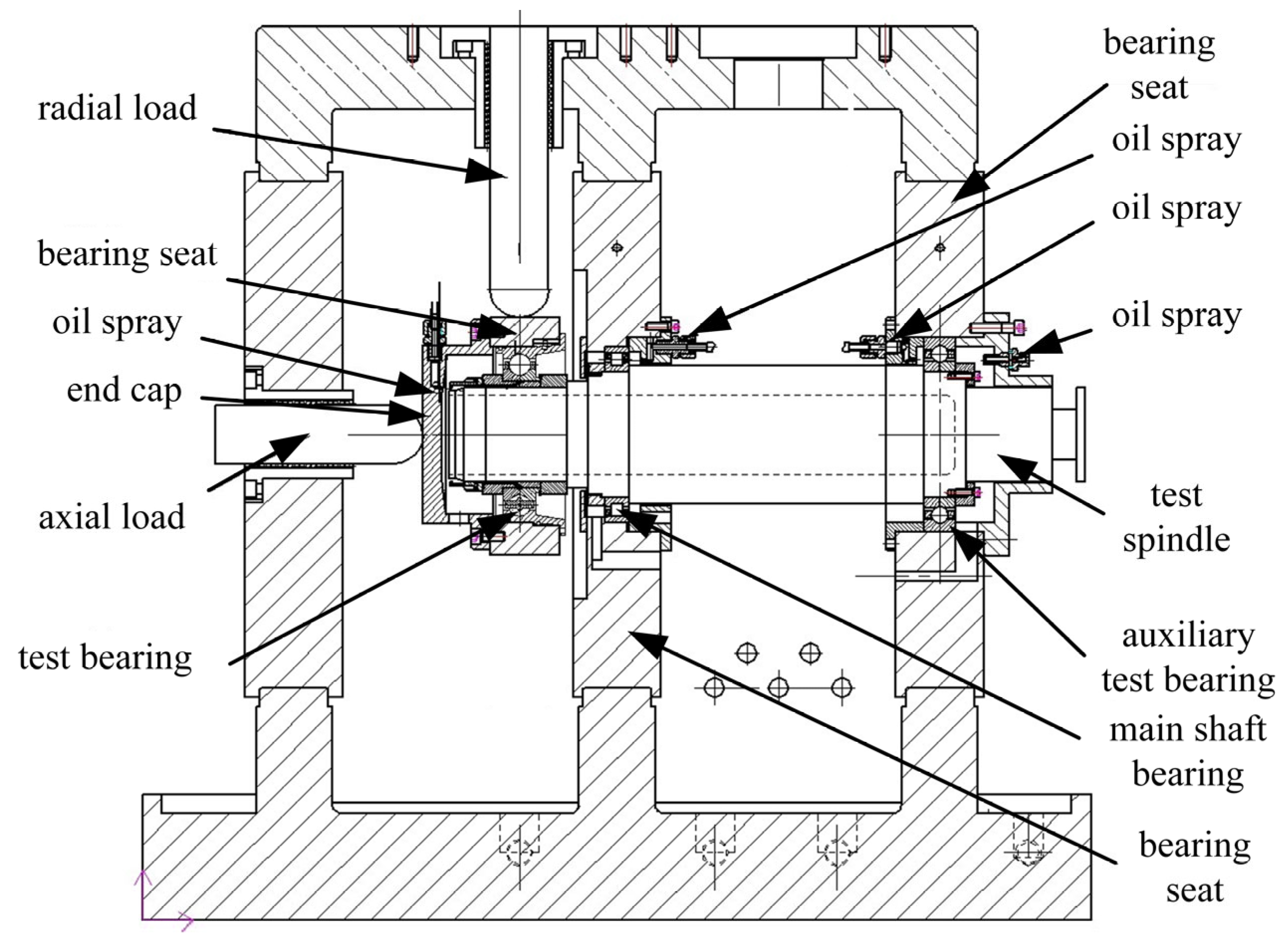
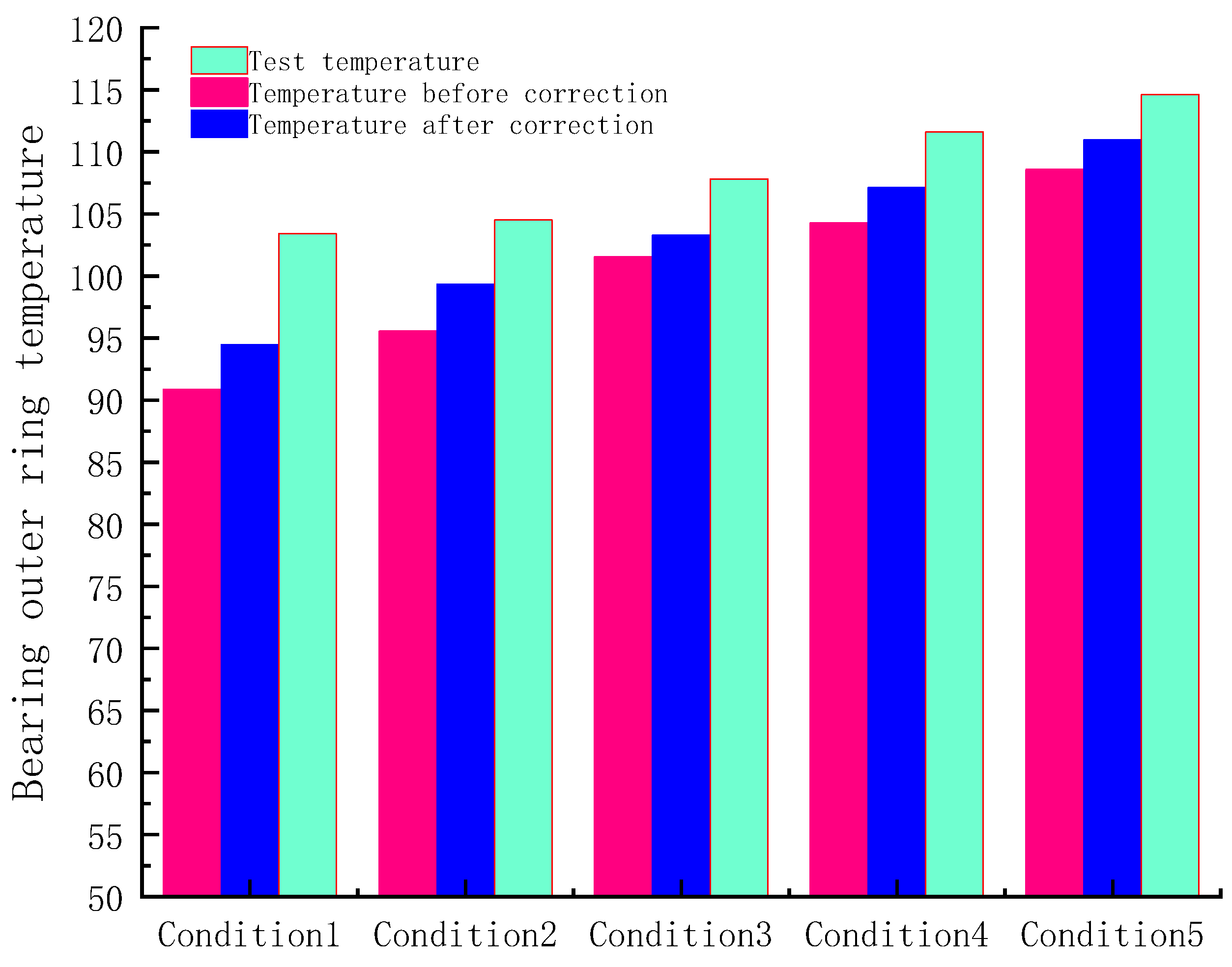
3. Model Validation
4. Discussion
5. Conclusions
- (1)
- Theoretical advancement
- a.
- This model considers the heat exchange of the lubricant circulating outside the bearing chamber and can simulate the temperature change during lubricant circulation. The oil inlet temperature is affected by the overall bearing temperature, which solves the problem of ignoring the change in oil inlet temperature in the traditional temperature-field model.
- b.
- In this model, the lubricant temperature node in the oil tank is added to the traditional thermal network method, and the lubricant penetration rate is defined as the correction coefficient to modify the thermal network equation; thus, the modified transient thermal network equation of the double-piece inner ring ball bearing is established.
- (2)
- Methodological paradigm shift
- (3)
- Practical application
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | oil tank surface area | m2 |
| a0 | bearing contact angle | ° |
| B | ring width | m |
| c | specific heat capacity | J/(kg·°C) |
| cr | lubricant specific heat capacity | J/(kg·°C) |
| cmax | maximum damping coefficient | N/(m/s) |
| D | ring outer diameter | m |
| Dp | pipeline outer diameter | m |
| Dw | ball diameter | m |
| d | ring inner diameter | m |
| dm | bearing pitch circle diameter | m |
| dp | pipe inner diameter | m |
| E | comprehensive elastic modulus of ball surface and raceway | Pa |
| e | Euler constant | Dimensionless |
| e1 | collision force index | Dimensionless |
| ep | ellipticity | Dimensionless |
| F | tangential friction force | N |
| G | dimensionless material parameter | Dimensionless |
| H | overall bearing heat generation | W |
| Hi | inner heat generated | W |
| He | outer heat generated | W |
| hmin | oil film thickness | m |
| K | comprehensive contact stiffness | N/m |
| Kl | Hertz contact stiffness | N/m |
| Kw | oil film stiffness | N/m |
| ka | lubricating oil convective heat transfer coefficient | W/(m2·K) |
| kpr | convective heat transfer coefficient between lubricant and pipeline inner wall | W/(m2·K) |
| kp0 | convective heat transfer coefficient between pipeline outer wall and air | W/(m2·K) |
| ktr | convective heat transfer coefficient between lubricant and oil tank inner wall | W/(m2·K) |
| kt0 | oil tank outer wall and air convection heat transfer coefficient | W/(m2·K) |
| Lp | pipe length | m |
| m | lubricant oil supply | L/min |
| M | bearing friction torque | N∙m |
| n | bearing speed | r/min |
| Pr | fluid Prandtl number | Dimensionless |
| Q | normal contact force | N |
| Qa | load on the convex peak of the contact area | N |
| R | circular bearing part thermal resistance | K/W |
| Rb | ball heat transfer resistance | K/W |
| Rbr | heat transfer resistance between ball and lubricant | K/W |
| Rd | lubricant convective heat transfer resistance | K/W |
| Re | heat transfer thermal resistance between outer ring and ball | K/W |
| Reh | heat transfer thermal resistance between outer ring and bearing seat | K/W |
| Rer | heat transfer thermal resistance between outer ring and lubricant | K/W |
| Rg | equivalent radius of curvature in the long axis direction of the contact area | m |
| Rh0 | heat transfer thermal resistance between the bearing seat and the air | K/W |
| Ri | heat transfer thermal resistance between the bearing inner ring and the ball | K/W |
| Rir | heat transfer thermal resistance between the bearing inner ring and the lubricants | K/W |
| Rr0 | total thermal resistance of the lubricant cooling in the oil tank and the pipeline | K/W |
| Rp | oil pipeline total thermal resistance | K/W |
| Rt | tank total thermal resistance | K/W |
| Rr0 | total thermal resistance of lubricant heat dissipation outside the bearing. | K/W |
| Rz0 | heat transfer thermal resistance between the spindle and the air | K/W |
| Rzi | heat transfer thermal resistance between the bearing inner ring and the spindle | K/W |
| S | convective heat transfer area | m2 |
| T0 | ambient temperature | °C |
| Th | bearing seat temperature | °C |
| Te | outer ring temperature | °C |
| Tb | ball temperature | °C |
| Ti | bearing inner ring temperature | °C |
| Tz | spindle temperature | °C |
| Tr0 | oil inlet temperature | °C |
| Tr1 | oil outlet temperature | °C |
| U | dimensionless velocity parameter | Dimensionless |
| V | volume | m3 |
| Vr0 | volume of lubricant in the tank | m3 |
| Vr1 | total volume of the lubricant entering the bearing cavity | m3 |
| Vri | lubricant volume in the fluid domain of the inner ring | m3 |
| Vre | lubricant volume in the fluid domain of the outer ring | m3 |
| x | mutual penetration depth of two objects | m |
| ΔI | variation in the actual distance of the surface of the two collision parts caused by the thermal effect | m |
| ΔT | temperature variation | °C |
| δ | lubricant penetration rate | Dimensionless |
| η | lubricant dynamic viscosity | Pa∙s |
| λ | thermal conductivity | W/(m·K) |
| λr | lubricant thermal conductivity | W/(m·K) |
| λp | pipe thermal conductivity | W/(m·K) |
| μ | lubricant film drag coefficient | Dimensionless |
| μa | contact area peak friction coefficient | Dimensionless |
| ν | lubricant kinematic viscosity | m2/s |
| ρ | density | Kg/m3 |
| ρr | lubricant density | Kg/m3 |
| σi | inner ring thermal expansion coefficient | °C−1 |
| σe | outer ring thermal expansion coefficient | °C−1 |
| σb | ball thermal expansion coefficient | °C−1 |
| τ | film thickness ratio | Dimensionless |
| φ | heat flow into the node | W |
| φTr | heat absorbed by the lubricant | W |
References
- Palmgren, A. Ball and Roller Bearing Engineering; SKF Industries Inc.: Philadelphia, PA, USA, 1959. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis; CRC Press, Taylor Francis Group: New York, NY, USA, 2006. [Google Scholar]
- Kim, K.S.; Lee, D.W.; Lee, S.M.; Lee, S.J.; Hwang, J.H. A numerical approach to determine the frictional torque and temperature of an angular contact ball bearing in a spindle system. Int. J. Precis. Eng. Manuf. 2015, 16, 135–142. [Google Scholar]
- Wu, W.; Hu, C.; Hu, J.; Yuan, S. Jet cooling for rolling bearings: Flow visualization and temperature distribution. Appl. Therm. Eng. 2016, 105, 217–224. [Google Scholar]
- Wu, W.; Hu, J.; Yuan, S.; Hu, C. Numerical and experimental investigation of the stratified air-oil flow inside ball bearings. Int. J. Heat Mass Transf. 2016, 103, 619–626. [Google Scholar]
- Li, Y.; Yang, Z.; Chen, F.; Zhao, J. Effect of air inlet flow rate on flow uniformity under oil-air lubrication. Ind. Lubr. Tribol. 2018, 70, 282–289. [Google Scholar]
- Gao, W.; Nelias, D.; Li, K.; Liu, Z.; Lyu, Y. A multiphase computational study of oil distribution inside roller bearings with under-race lubrication. Tribol. Int. 2019, 140, 105862. [Google Scholar]
- Li, M.; Wang, Y.; Chen, W.; Zhu, R. Temperature rise characteristics for angular-contact ball bearings with oil-air lubrication based on fluid-solid conjugate heat transfer. Adv. Mech. Eng. 2021, 13, 1687814021990927. [Google Scholar]
- Bao, H.; Hou, X.; Tang, X.; Lu, F. Analysis of temperature field and convection heat transfer of oil-air two-phase flow for ball bearing with under-race lubrication. Ind. Lubr. Tribol. 2021, 73, 817–821. [Google Scholar]
- Dong, Y.; Ma, Y.; Qiu, M.; Chen, F.; He, K. Analysis and experimental research of transient temperature rise characteristics of high-speed cylindrical roller bearing. Sci. Rep. 2024, 14, 711. [Google Scholar]
- Xu, K.; Hu, H.; Guo, N.; Ma, X.; Li, X. Research on Temperature Rise Characteristics Prediction of Main Shaft Dual-Rotor Rolling Bearings in Aircraft Engines. Lubricants 2024, 12, 210. [Google Scholar] [CrossRef]
- Winer, W.O.; Bair, S.; Gecim, B. Thermal resistance of a tapered roller bearing. ASLE Trans. 1986, 29, 539–547. [Google Scholar]
- Bossmanns, B.; Tu, J.F. A thermal model for high speed motorized spindles. Int. J. Mach. Tools Manuf. 1999, 39, 1345–1366. [Google Scholar]
- Cole, K.D.; Tarawneh, C.M.; Fuentes, A.A.; Wilson, B.M.; Navarro, L. Thermal models of railroad wheels and bearings. Int. J. Heat Mass Transf. 2010, 53, 1636–1645. [Google Scholar]
- Neurouth, A.; Changenet, C.; Ville, F.; Arnaudon, A. Thermal modeling of a grease lubricated thrust ball bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 1266–1275. [Google Scholar]
- Yan, K.; Hong, J.; Zhang, J.; Mi, W.; Wu, W. Thermal-deformation coupling in thermal network for transient analysis of spindle-bearing system. Int. J. Therm. Sci. 2016, 104, 1–12. [Google Scholar]
- Zheng, D.; Chen, W. Thermal performances on angular contact ball bearing of high-speed spindle considering structural constraints under oil-air lubrication. Tribol. Int. 2017, 109, 593–601. [Google Scholar]
- Zheng, D.X.; Chen, W.F. Effect of structure and assembly constraints on temperature of high-speed angular contact ball bearings with thermal network method. Mech. Syst. Signal Process. 2020, 145, 106929. [Google Scholar]
- Brossier, P.; Niel, D.; Changenet, C.; Ville, F.; Belmonte, J. Experimental and numerical investigations on rolling element bearing thermal behaviour. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 842–853. [Google Scholar]
- Lei, J.; Su, B.; Zhang, S.; Yang, H.; Cui, Y. Dynamics-based thermal analysis of high-speed angular contact ball bearings with under-race lubrication. Machines 2023, 11, 691. [Google Scholar] [CrossRef]
- Tao, X.; Yuli, C.; Tao, C.; Shoujing, Z.; Qing, Z. A Thermal Preload Analysis Method of Angular Ball Bearing Considering Temperature Rise. Int. J. Precis. Eng. Manuf. 2024, 25, 2625–2637. [Google Scholar]
- Liu, Y.; Chen, Z.; Zhai, W.; Lei, Y. Investigation on skidding behavior of a lubricated rolling bearing with fluid–solid-heat coupling effect. Mech. Syst. Signal Process. 2024, 206, 110922. [Google Scholar]
- Yang, X.Q. Contact Mechanics Theory and Rolling Bearing Design Analysis; Huazhong University of Science & Technology Press: Wuhan, China, 2018. [Google Scholar]
- Deng, S.E.; Jia, Q.; Xue, J. Rolling Bearing Design Principle; China Standard Press: Beijing, China, 2014; p. 132. [Google Scholar]
- Tan, D.; Chen, Z. On a general formula of fourth order Runge-Kutta method. J. Math. Sci. Math. Educ. 2012, 7, 1–10. [Google Scholar]
- Latif, M. Jiji. In Heat Convection, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
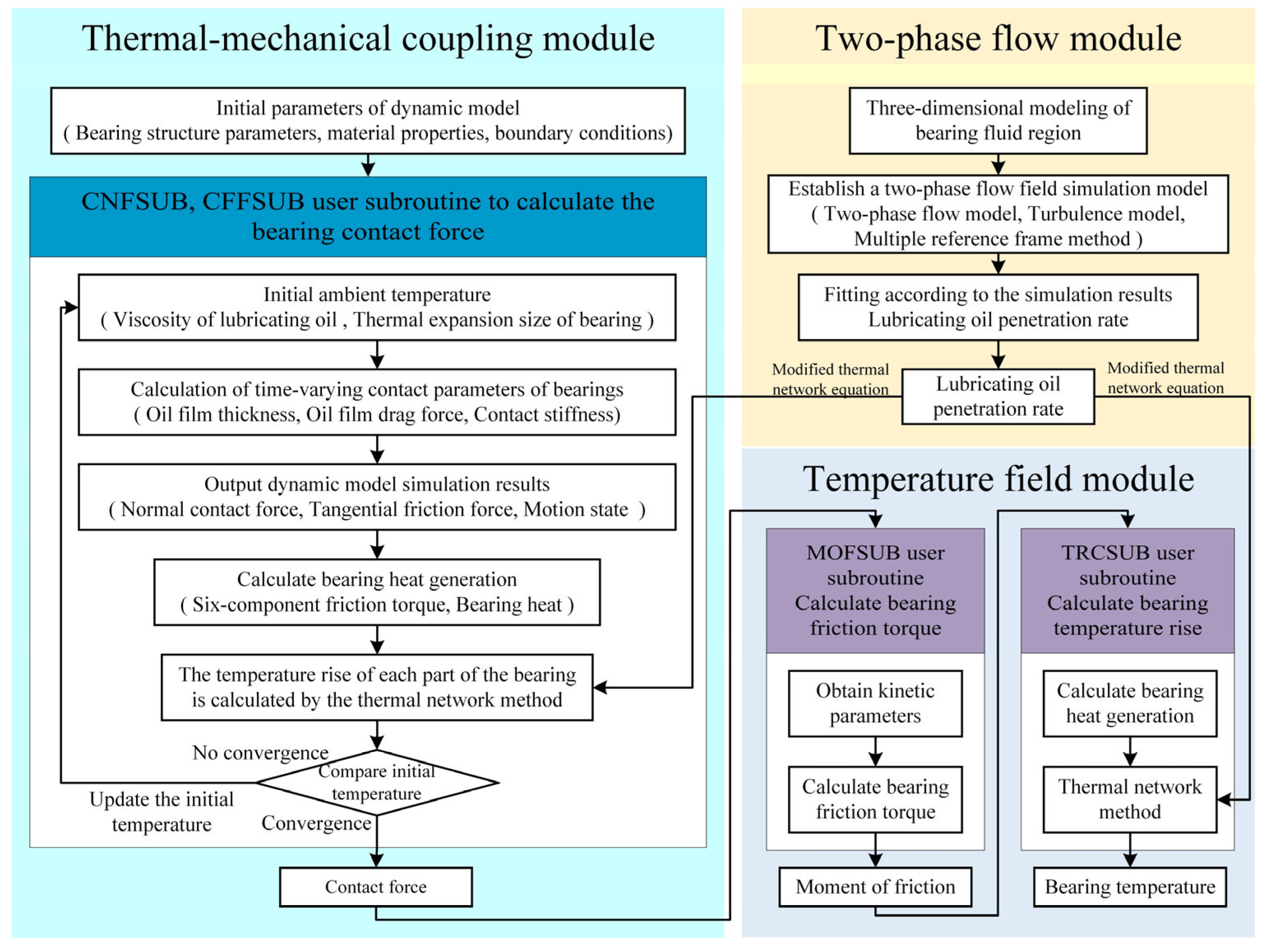

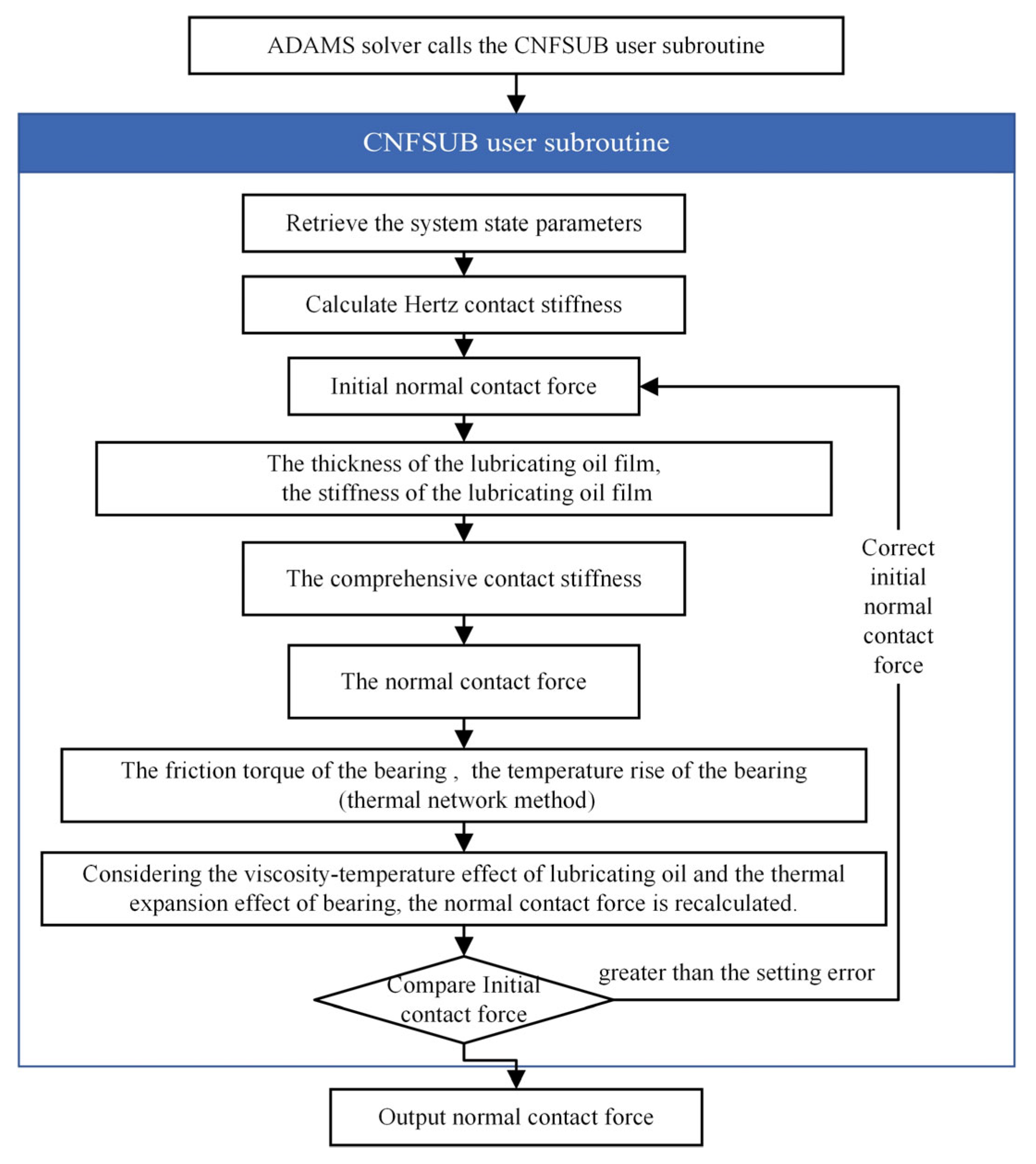
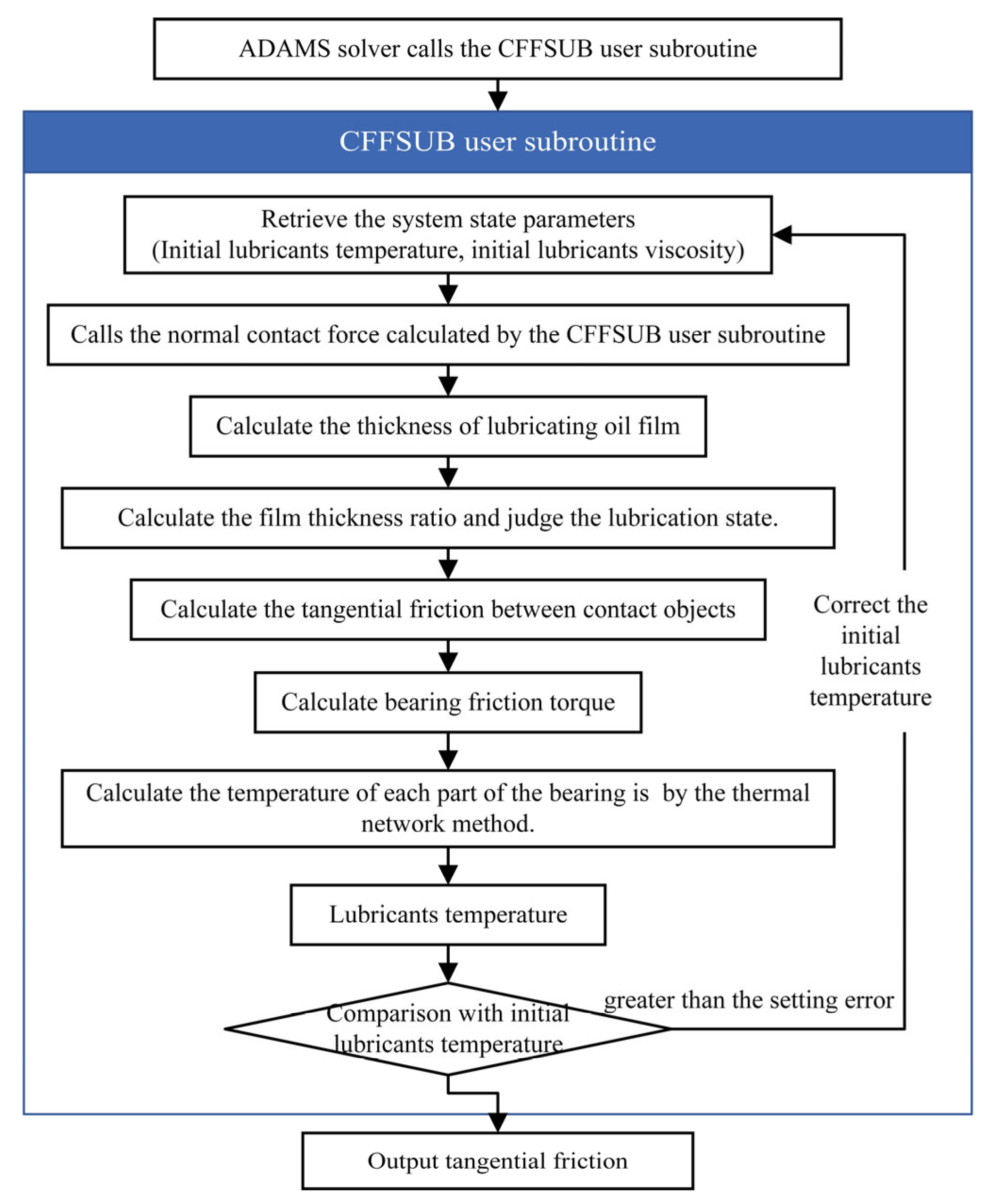
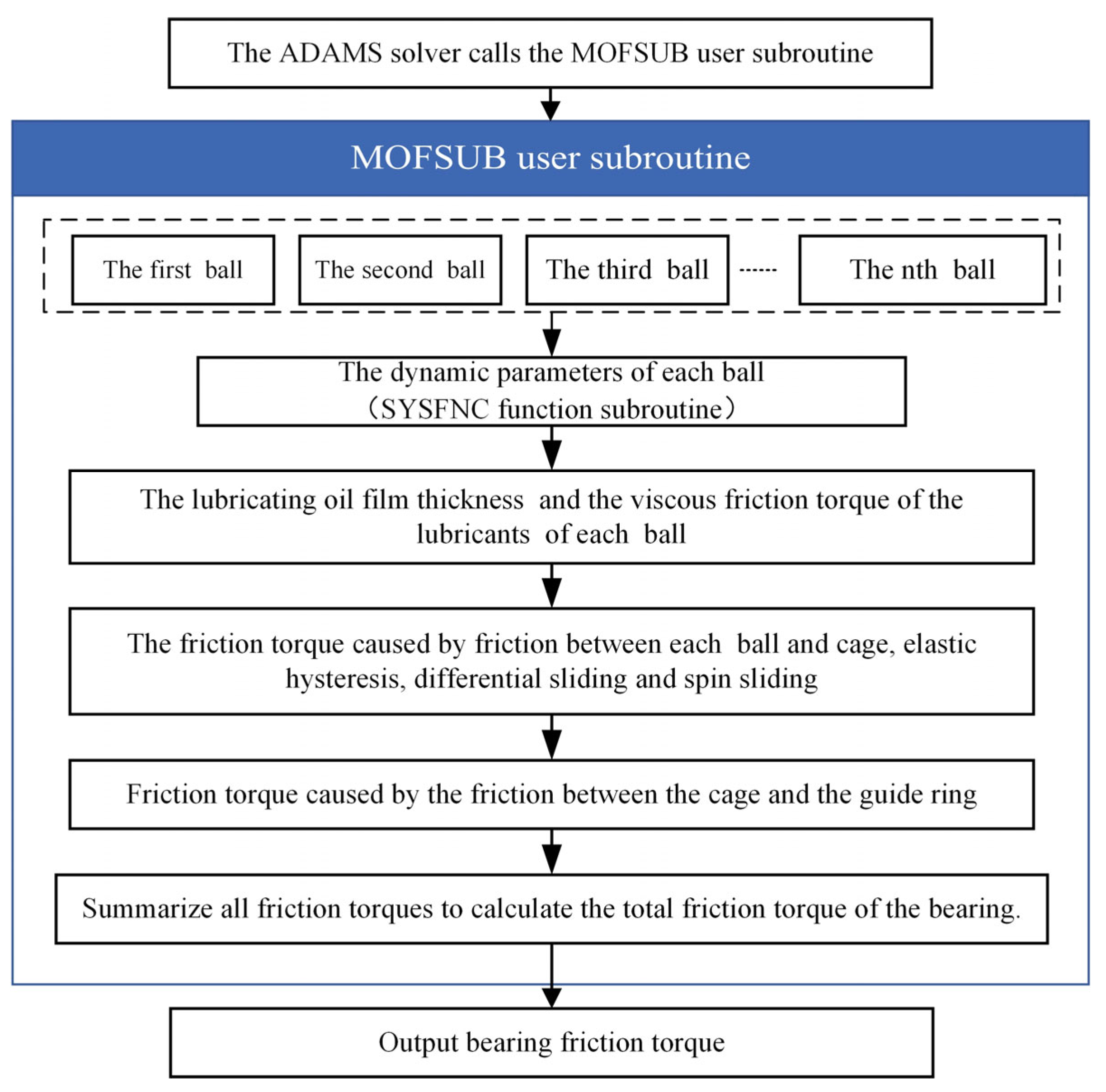


| Thermal Resistance | Value (K/W) | Thermal Resistance | Value (K/W) |
|---|---|---|---|
| Rh0 | 0.3677 | Rb | 0.174 |
| Rz0 | 1.055 | Rbr | 0.386 |
| Reh | 0.0834 | Rer | 0.294 |
| Rzi | 0.1203 | Rir | 0.21 |
| Re | 0.008 | Rr0 | 0.114 |
| Ri | 0.012 |
| Parameter Name | Value |
|---|---|
| Number of balls | 17 |
| Bearing width (mm) | 35 |
| Ball diameter (mm) | 23.225 |
| Bearing bore diameter (mm) | 105 |
| Bearing outside diameter (mm) | 185 |
| Pitch diameter (mm) | 141.4 |
| Initial contact angle (°) | 30 |
| Radius of curvature of inner ring (mm) | 12.075 |
| Radius of curvature of outer circle (mm) | 11.823 |
| Elastic modulus of ball, inner and outer ring (GPa) | 210 |
| Ball, inner and outer ring Poisson’s ratio | 0.3 |
| Bearing Components | Materials |
|---|---|
| Inner ring | 8Cr4Mo4V |
| Outer ring | 8Cr4Mo4V |
| Ball | 8Cr4Mo4V |
| Cage | 40CrNiMo |
| Working Condition | Axial Load (N) | Radial Load (N) |
|---|---|---|
| Condition 1 | 3123 | 2611 |
| Condition 2 | 3399 | 2611 |
| Condition 3 | 3821 | 2598 |
| Condition 4 | 4105 | 2596 |
| Condition 5 | 4657 | 2607 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Y.; Meng, F.; Yu, Y.; Cai, H. Thermal–Mechanical Coupling Model of a Double-Piece Inner Ring Ball Bearing Based on ADAMS Secondary Development. Lubricants 2025, 13, 154. https://doi.org/10.3390/lubricants13040154
Xue Y, Meng F, Yu Y, Cai H. Thermal–Mechanical Coupling Model of a Double-Piece Inner Ring Ball Bearing Based on ADAMS Secondary Development. Lubricants. 2025; 13(4):154. https://doi.org/10.3390/lubricants13040154
Chicago/Turabian StyleXue, Yujun, Fanjing Meng, Yongjian Yu, and Haichao Cai. 2025. "Thermal–Mechanical Coupling Model of a Double-Piece Inner Ring Ball Bearing Based on ADAMS Secondary Development" Lubricants 13, no. 4: 154. https://doi.org/10.3390/lubricants13040154
APA StyleXue, Y., Meng, F., Yu, Y., & Cai, H. (2025). Thermal–Mechanical Coupling Model of a Double-Piece Inner Ring Ball Bearing Based on ADAMS Secondary Development. Lubricants, 13(4), 154. https://doi.org/10.3390/lubricants13040154





