Turbulence Effects on the Dynamic Characteristics of Non-Circular Journal Bearings Under Large Sommerfeld Number Conditions
Abstract
1. Introduction
2. Theoretical Model
2.1. Bearing Configuration
2.2. Governing Equation
2.3. Linear Perturbation Method
2.4. Nonlinear Trajectory Method
2.5. Numerical Algorithms
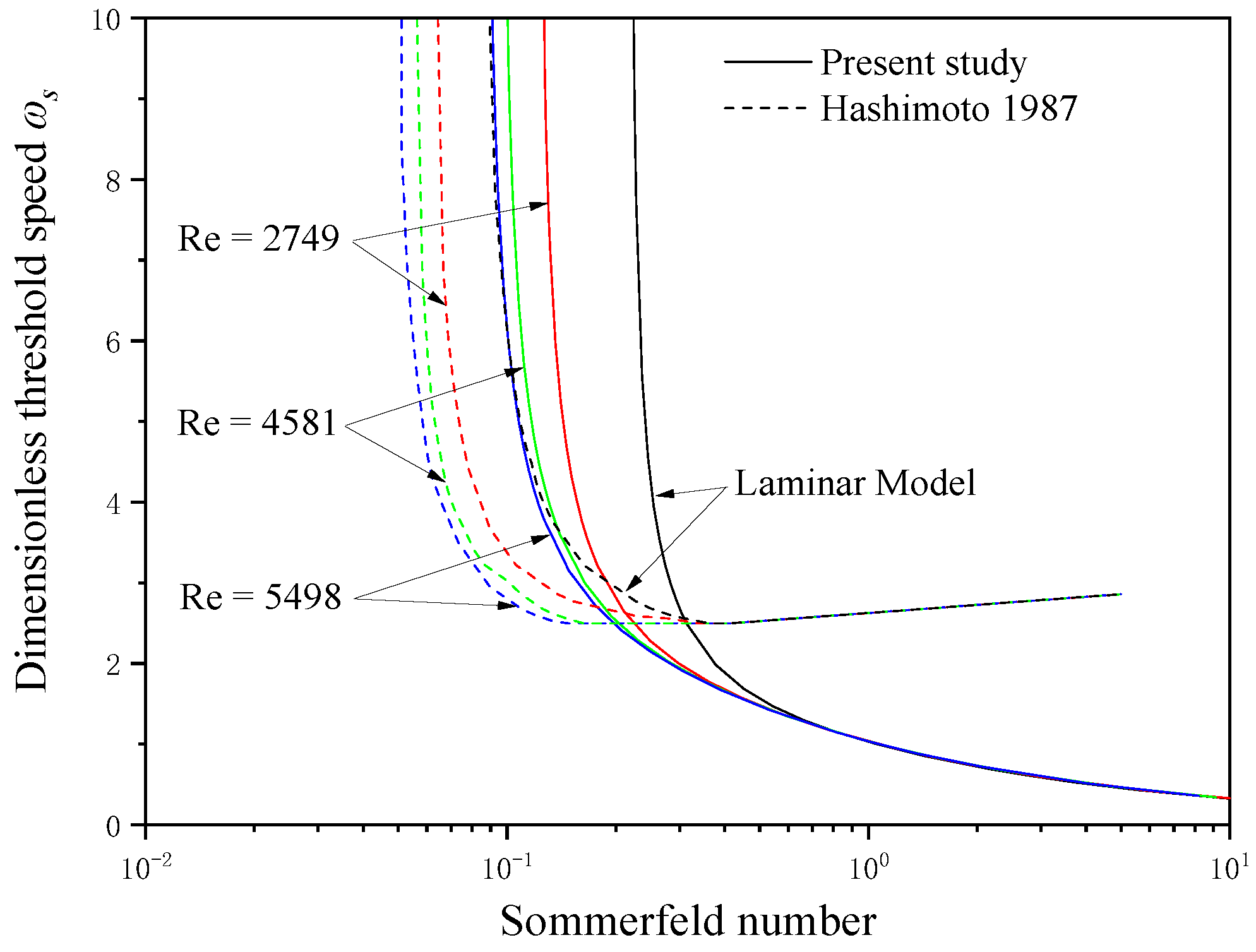
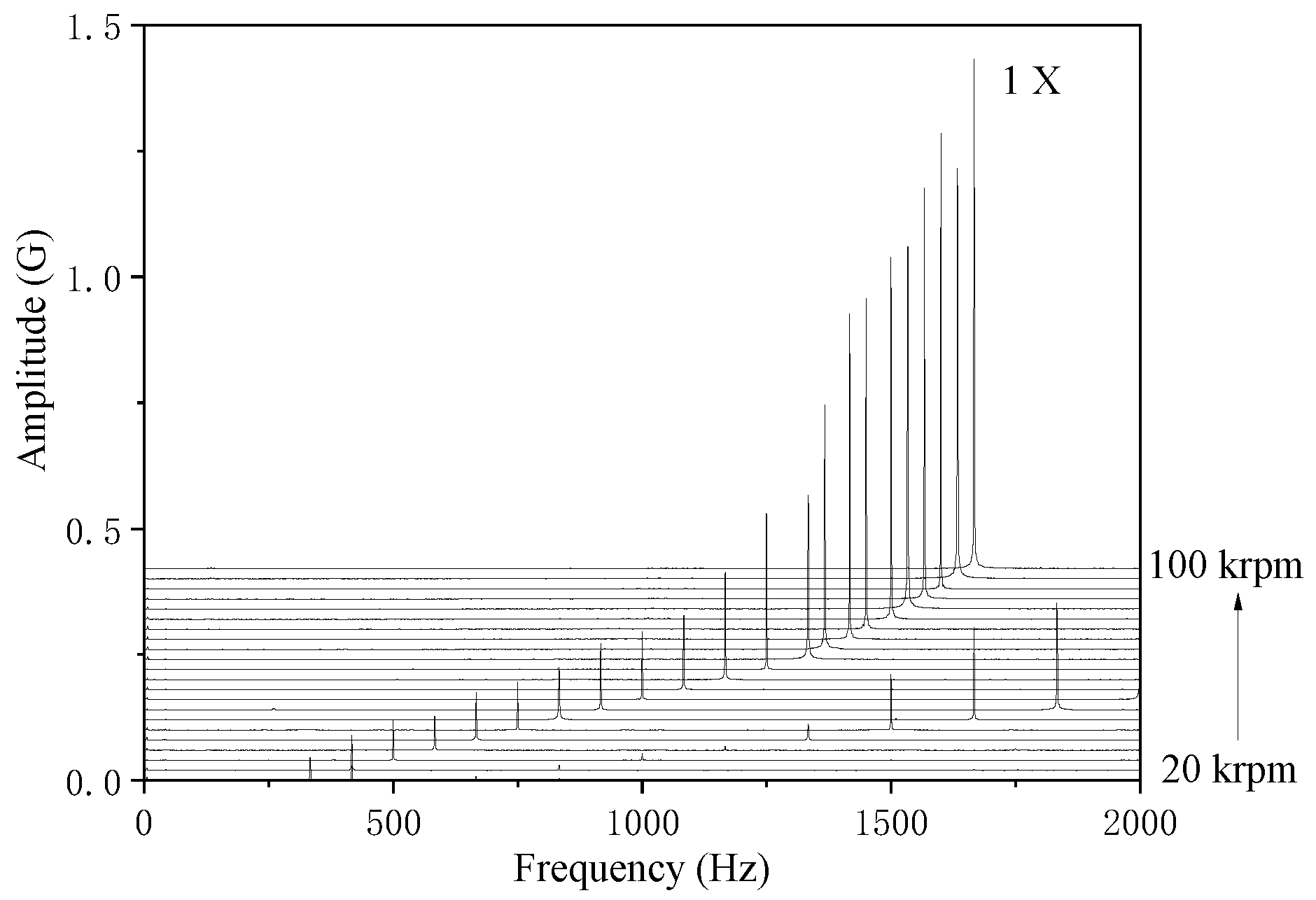
3. Verification
4. Results and Discussion
4.1. TLB
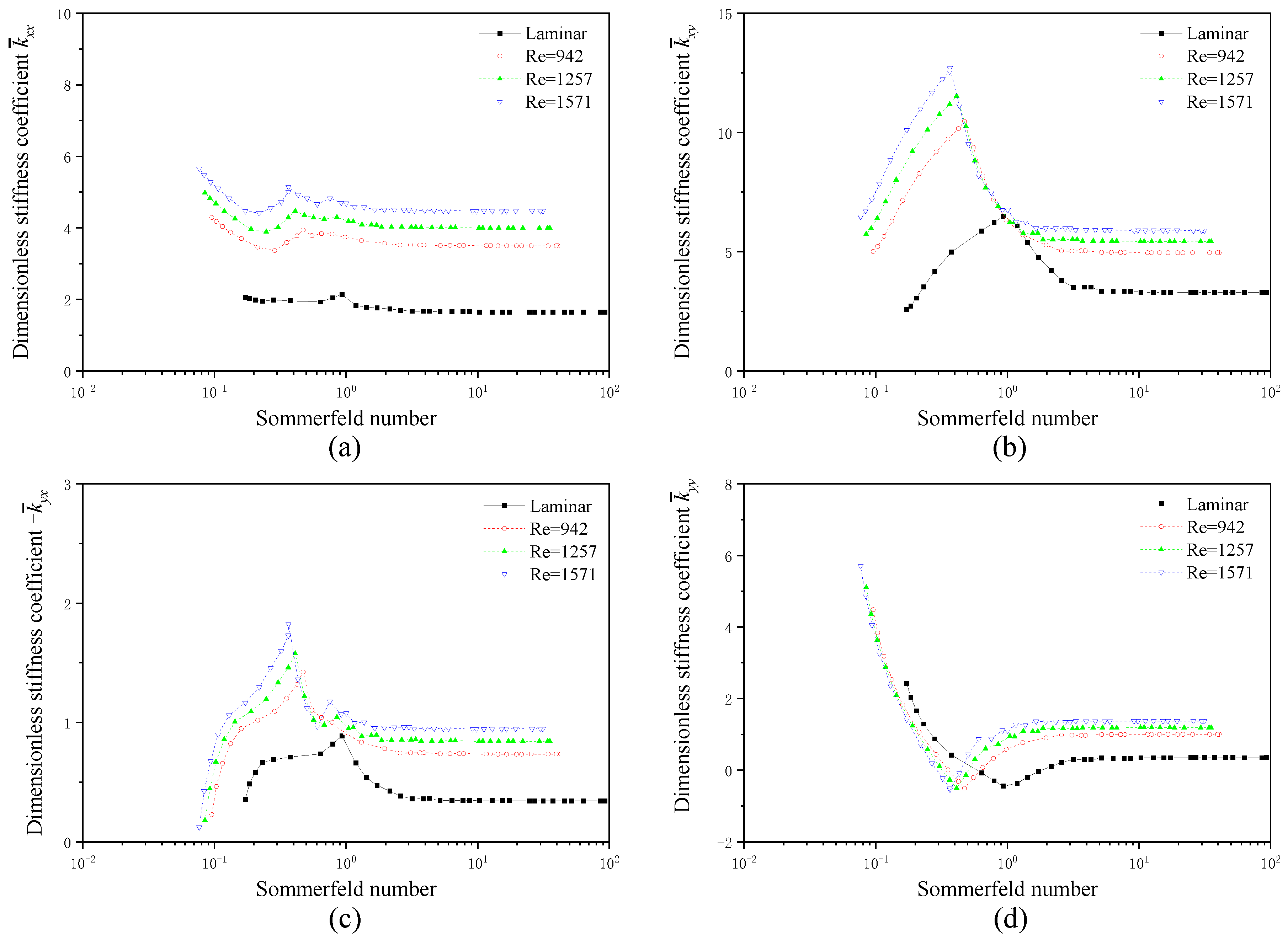
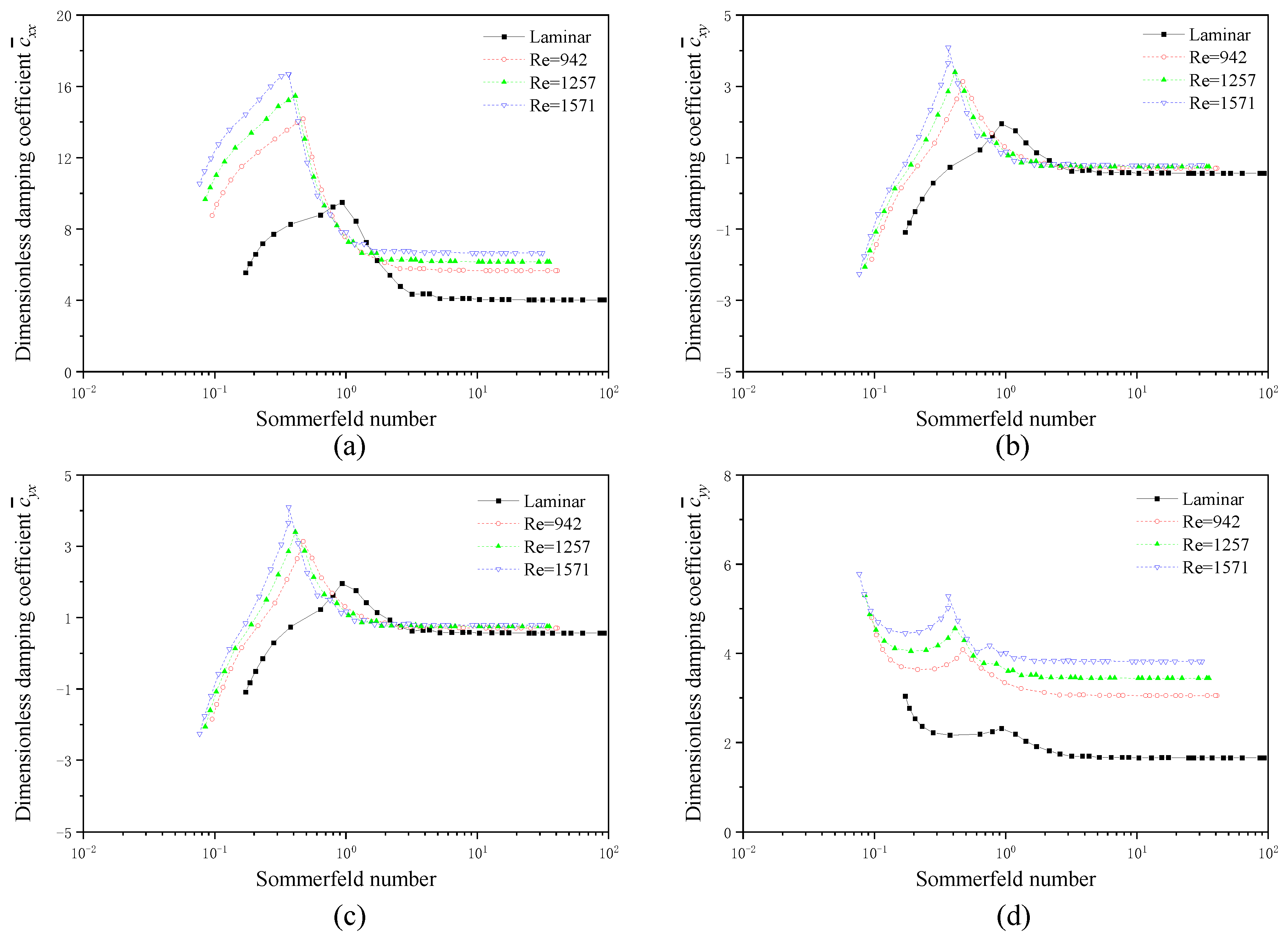
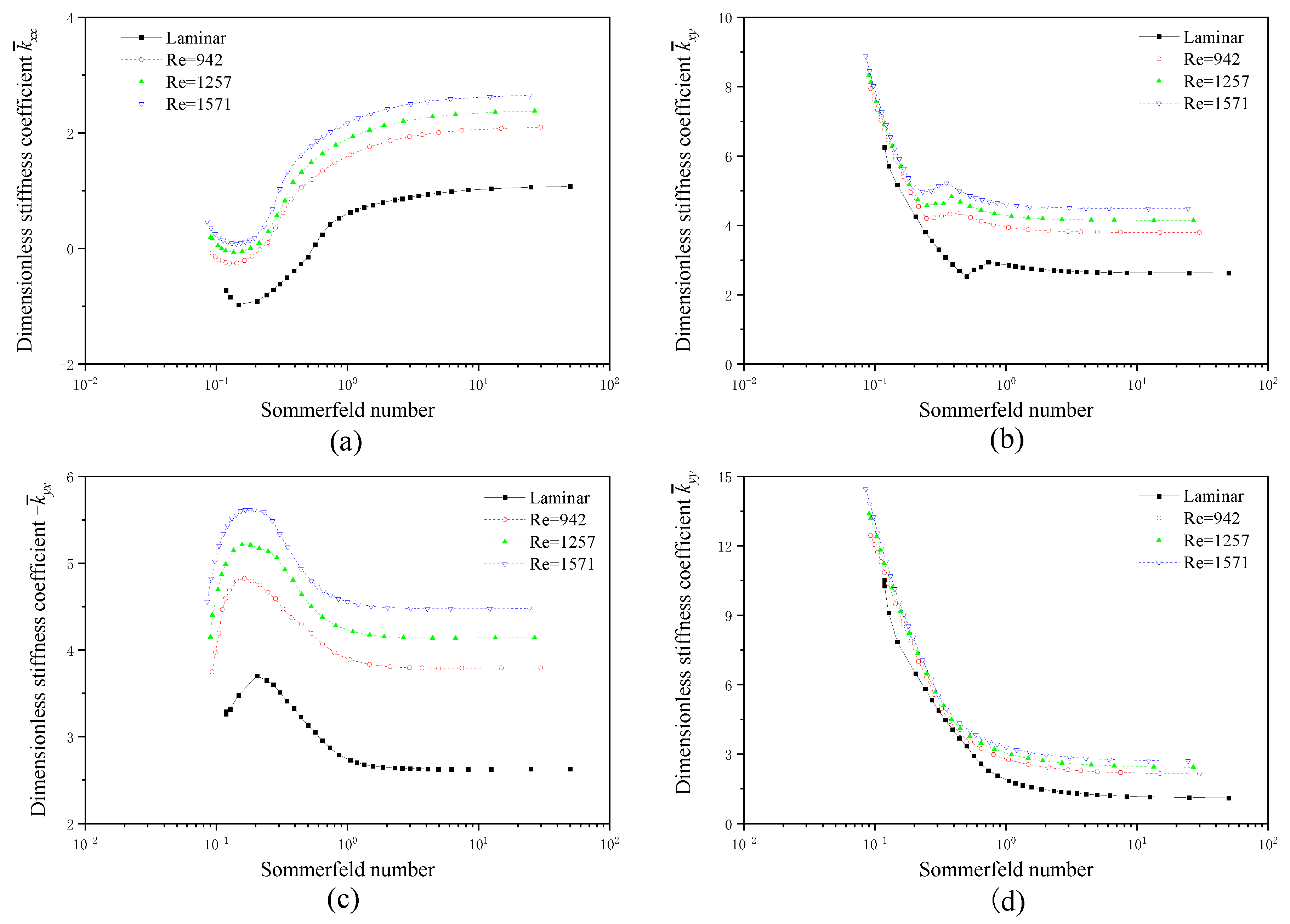
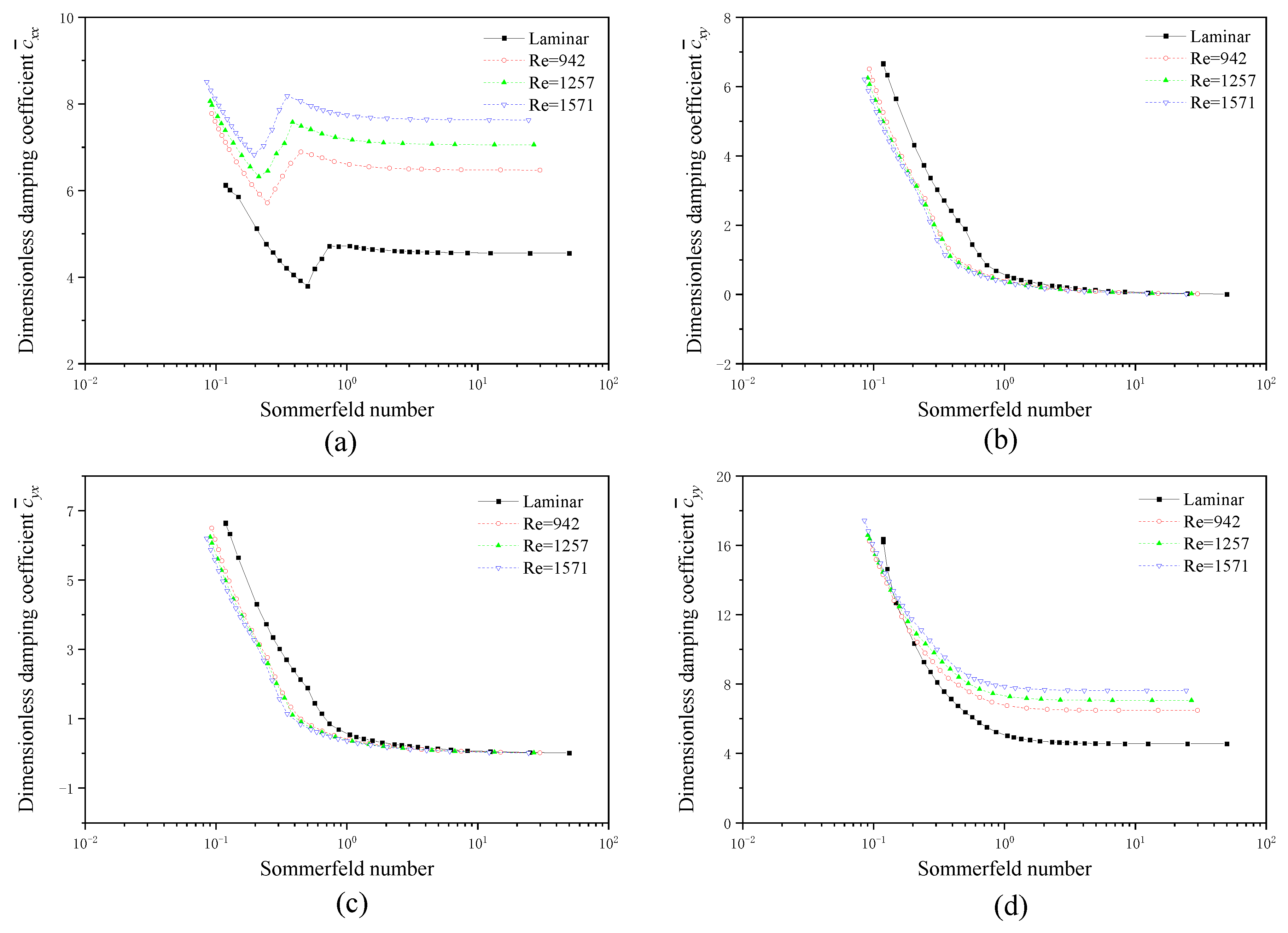
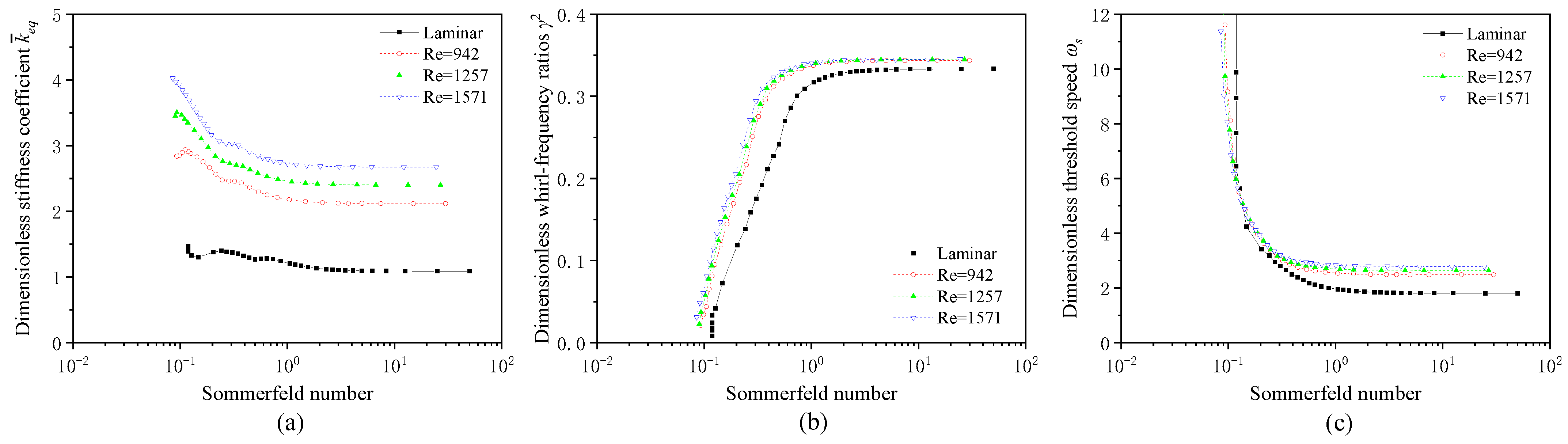
4.1.1. Dynamic Coefficients and Threshold Speed
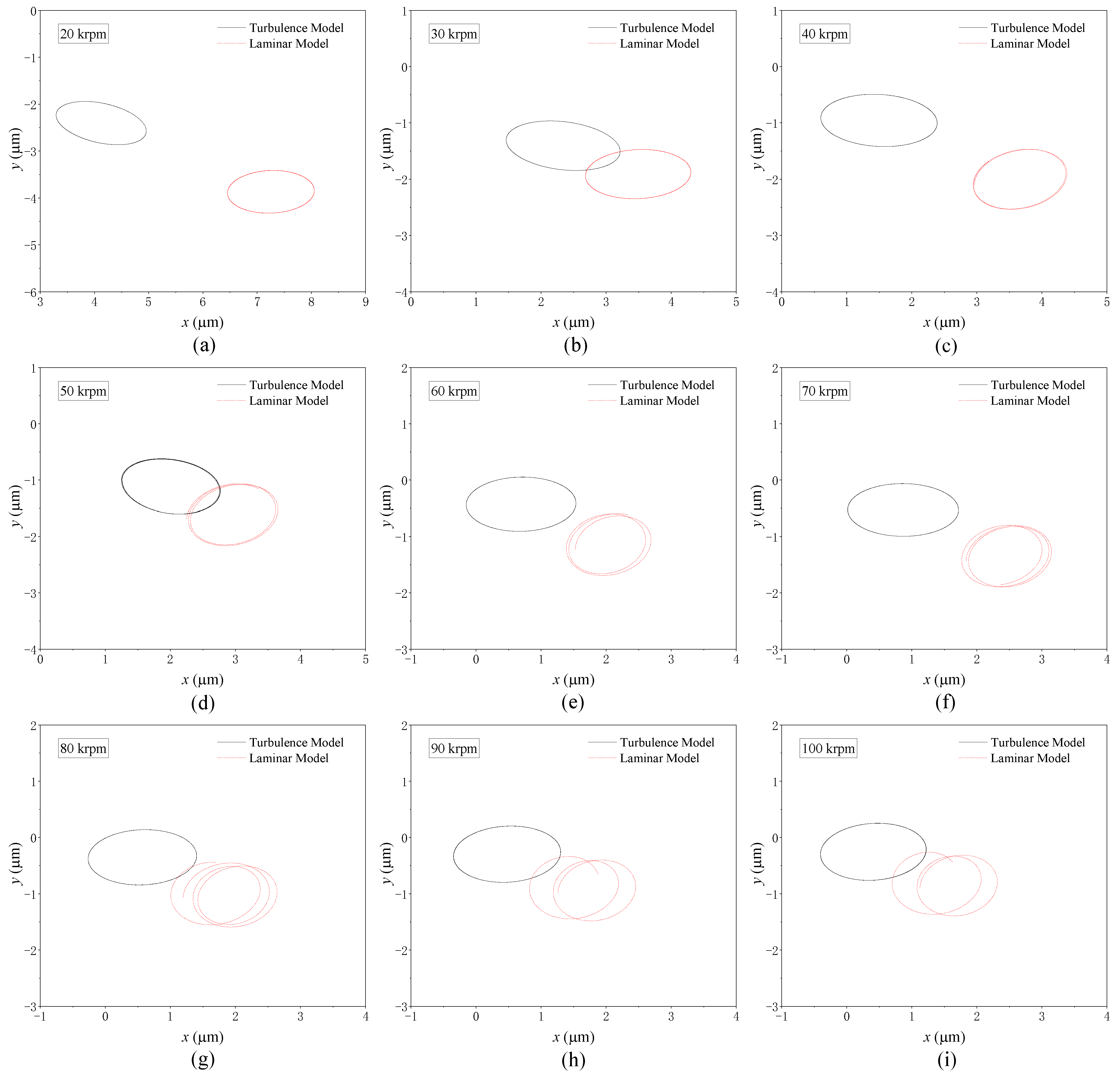
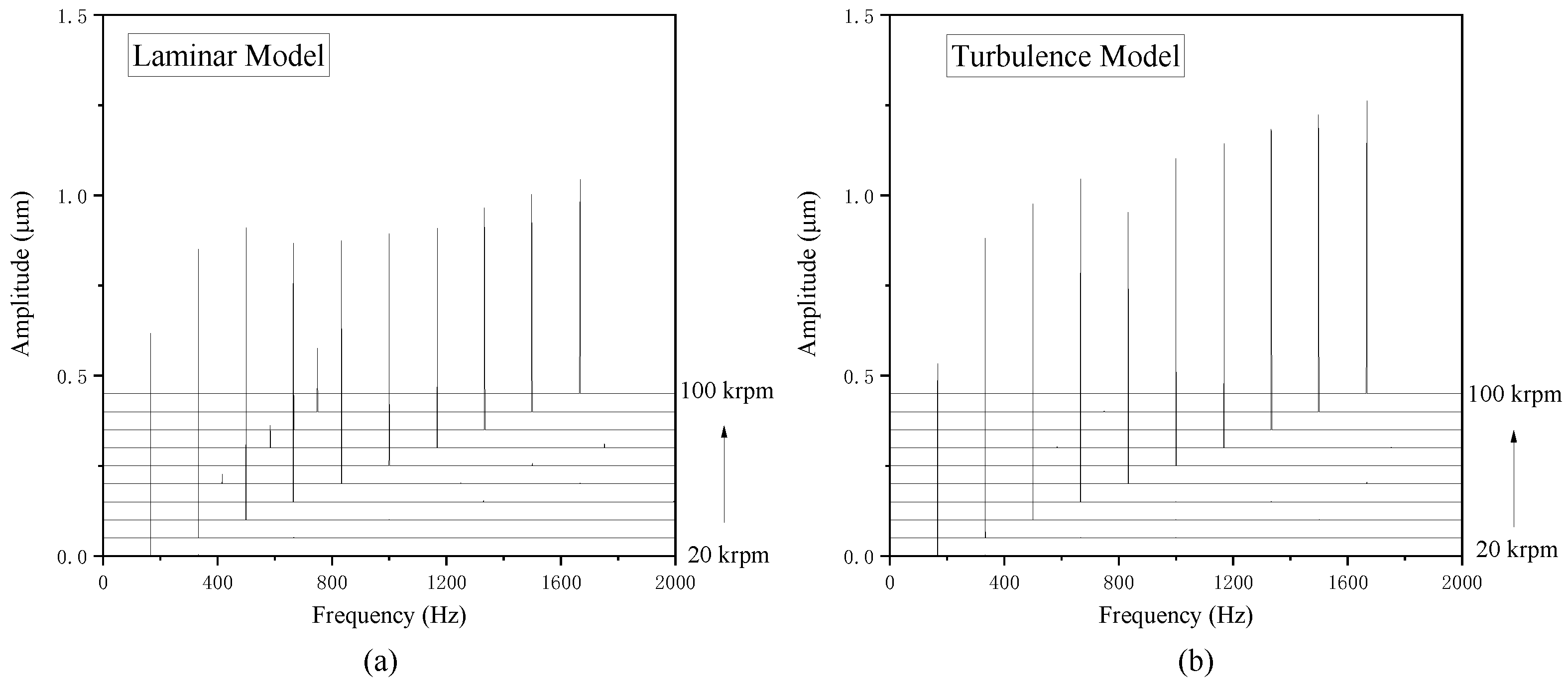
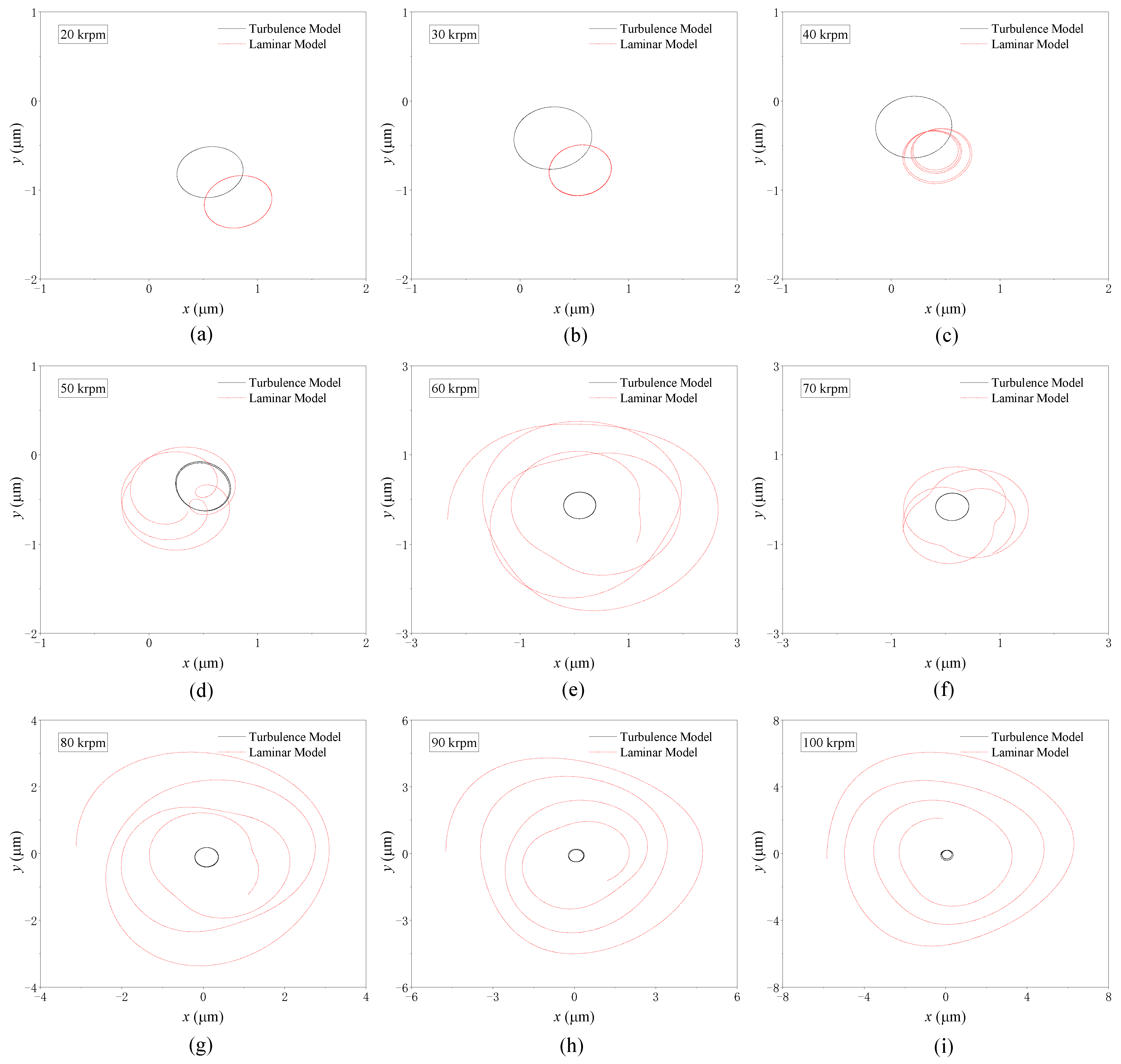
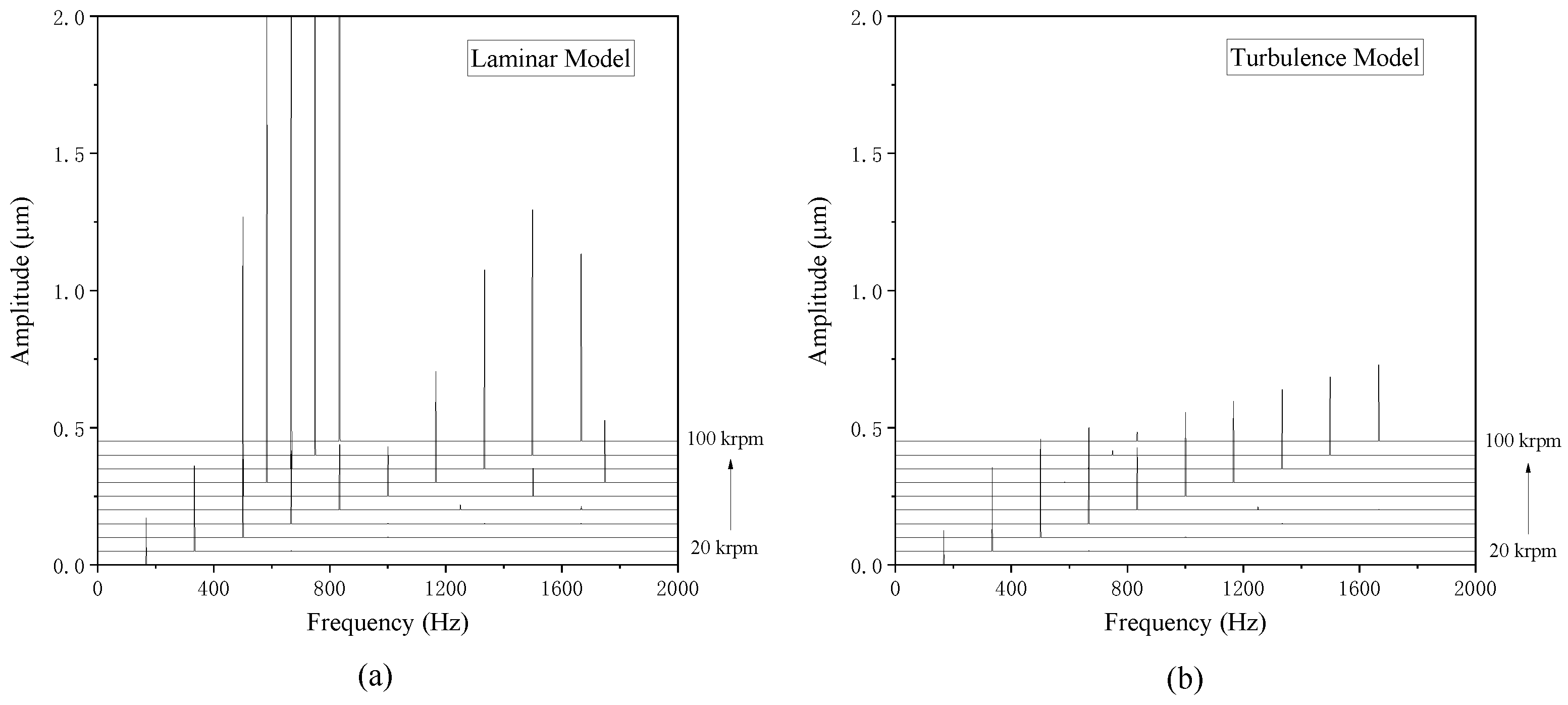
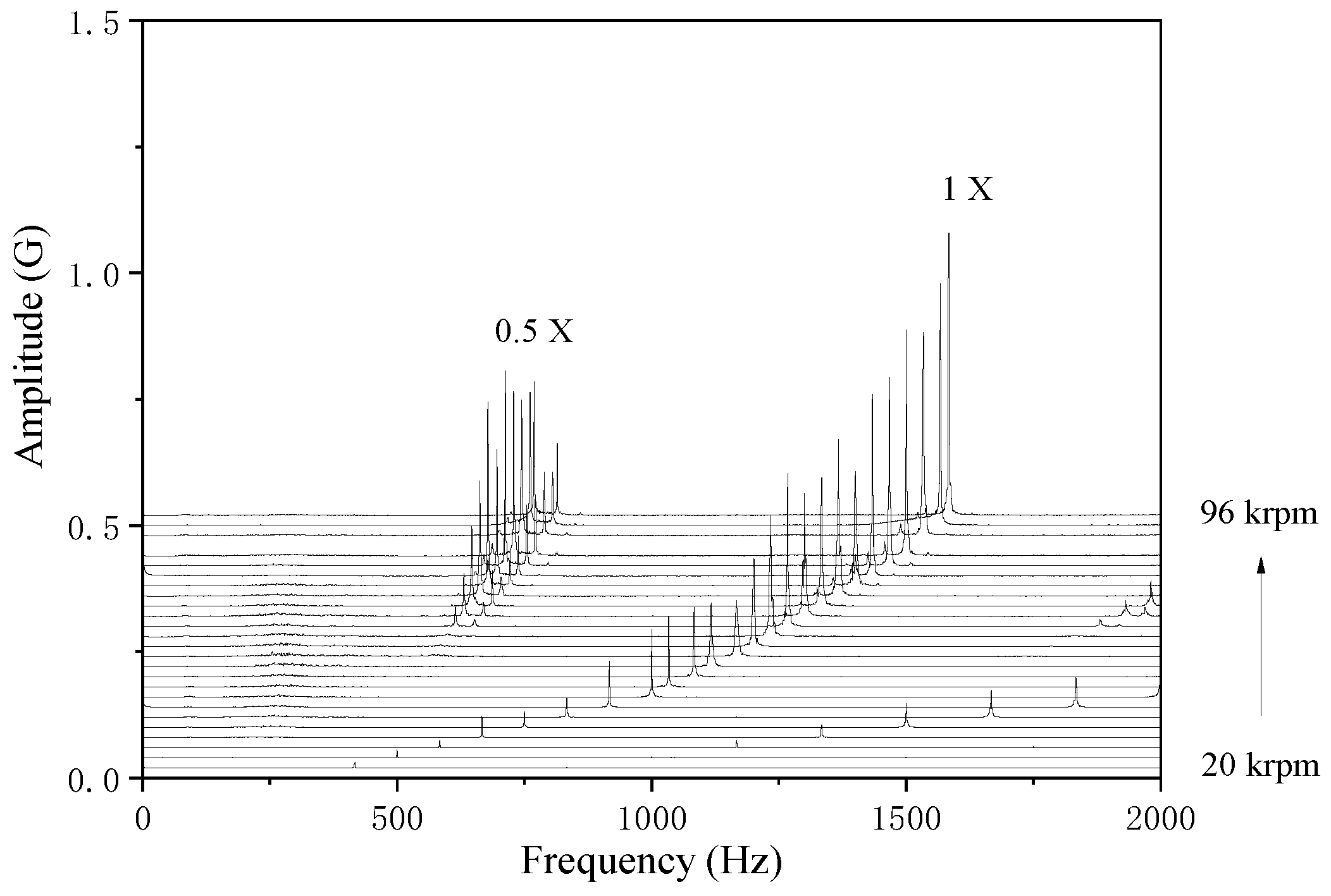
4.1.2. Nonlinear Trajectory
4.2. TSRB
4.2.1. Dynamic Coefficients and Threshold Speed
4.2.2. Nonlinear Trajectory
5. Conclusions
- (1)
- As the Sommerfeld number increases, the equivalent stiffnesses of the two bearings exhibit a general decreasing trend. The whirl ratios demonstrate an increasing tendency, and the threshold speeds decrease. However, when the Sommerfeld number exceeds 2, its influence diminishes;
- (2)
- The influence of turbulence on the dynamic characteristics of two non-circular bearings is closely related to the Sommerfeld number. Under small Sommerfeld number conditions, turbulence has a negative effect on the bearing stability performance; however, under large Sommerfeld number conditions, turbulence is beneficial for improving the bearing dynamic characteristic;
- (3)
- The effect of turbulence on the two different bearings is the same. However, the analysis of the threshold speed and the nonlinear trajectory both show that TLB has better stability performance than TRSB. Geometry design is an important aspect in the development of high-speed fluid film journal bearings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fedorynenko, D.; Kirigaya, R.; Nakao, Y. Dynamic Characteristics of Spindle with Water-Lubricated Hydrostatic Bearings for Ultra-Precision Machine Tools. Precis. Eng. 2020, 63, 187–196. [Google Scholar] [CrossRef]
- Yu, X.; Gao, W.; Feng, Y.; Shi, G.; Li, S.; Chen, M.; Zhang, R.; Wang, J.; Jia, W.; Jiao, J.; et al. Research Progress of Hydrostatic Bearing and Hydrostatic-Hydrodynamic Hybrid Bearing in High-End Computer Numerical Control Machine Equipment. Int. J. Precis. Eng. Manuf. 2023, 24, 1053–1081. [Google Scholar] [CrossRef]
- Massoudi, S.; Schiffmann, J. Robust Design of Herringbone Grooved Journal Bearings Using Multi-Objective Optimization with Artificial Neural Networks. J. Turbomach. 2023, 145, 111010. [Google Scholar] [CrossRef]
- Liu, W.; Gjika, K.; Schiffmann, J. Design and Experimental Investigation of a Herringbone Grooved Gas Bearing Supported Turbocharger. Mech. Syst. Signal Process. 2023, 186, 109828. [Google Scholar] [CrossRef]
- Yang, T.; Xiang, G.; Cai, J.; Wang, L.; Lin, X.; Wang, J.; Zhou, G. Five-DOF Nonlinear Tribo-Dynamic Analysis for Coupled Bearings during Start-Up. Int. J. Mech. Sci. 2024, 269, 109068. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Z. Analysis of Properties of Thrust Bearing in Ship Propulsion System. J. Marine. Sci. Appl. 2010, 9, 220–222. [Google Scholar] [CrossRef]
- Zha, J.; Cheng, K.; Xue, F.; Wu, D.; Liu, X. Hydrostatic Guideways for Precision Machines: The State-of-the-Art and Future Perspectives. Tribol. Int. 2024, 200, 110060. [Google Scholar] [CrossRef]
- Ren, T.; Feng, M. Theoretical and Experimental Study on the Stability of Water Lubricated High Speed Journal Bearing with Lobe Pockets. Tribol. Int. 2023, 187, 10866. [Google Scholar] [CrossRef]
- Xie, J.; Peng, C.; Zhang, W.; Zhao, C.; Feng, Q. Experimental and Simulated Investigation of Lubrication Characteristics of a Water-Lubricated Bearing in a Single-Screw Compressor. Appl. Sci. 2021, 11, 992. [Google Scholar] [CrossRef]
- Ten, B.; Yang, Q.; Wang, C.; Zhao, Y.; Li, L. Analysis of Static Characteristics of Journal Gas Bearing Used in Refrigeration Compressor. Lubr. Eng. 2021, 46, 34–40. (In Chinese) [Google Scholar]
- Wang, C.; Zhong, H.; Lei, B.; Wu, J. Two-Phase Lubrication Characteristics of Journal Bearing in Refrigerant-Oil System under High-Pressure Environment Considering Gaseous Cavitation. Int. J. Refrig. 2024, 158, 253–263. [Google Scholar]
- Song, L.; Yuan, G.; Zhang, H.; Ding, Y.; Cheng, K. The Stability of Spiral-Grooved Air Journal Bearings in Ultrahigh Speeds. Materials 2022, 15, 1759. [Google Scholar] [CrossRef] [PubMed]
- Bättig, P.K.; Wagner, P.H.; Schiffmann, J.A. Experimental Investigation of Enhanced Grooves for Herringbone Grooved Journal Bearings. J. Tribol. 2022, 144, 091801. [Google Scholar]
- Lin, L.; Qiao, Y.; Li, H.; Zhou, C. Comparative Study on Static and Dynamic Characteristics of Pumping-out and Pumping-in Herringbone Grooved Journal Bearings. Adv. Mech. Eng. 2023, 15, 1–16. [Google Scholar]
- Soni, S. Turbulence Effect on Dynamic Performance of Non-Circular Floating Ring Bearing. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 290–302. [Google Scholar]
- Wang, L.; Xu, H. Experimental Study on the Dynamic Performance of a New High-Speed Spindle Supported by Water-Lubricated Hybrid Bearings. Shock Vib. 2016, 2016, 8297834. [Google Scholar]
- Ren, G. A New Method to Calculate Water Film Stiffness and Damping for Water Lubricated Bearing with Multiple Axial Grooves. Chin. J. Mech. Eng. 2020, 33, 72. [Google Scholar]
- He, W.; Feng, M.; Ren, T. A Numerical Algorithm for Gas Foil Bearing Simulation with Considering Three-Dimensional Structure. Mech. Syst. Signal Process. 2024, 212, 111315. [Google Scholar]
- Jiang, Y.; Xu, B.; Zhu, Q.; Huang, Z.; Gao, D. Parameter Effects on the Static Characteristics of the Multi-Foil Aerodynamic Journal Bearing with Bump-Backing Foils. Lubricants 2024, 12, 246. [Google Scholar] [CrossRef]
- Silva, H.A.P.; Nicoletti, R. Rotor Vibration Control Using Tilting-Pad Journal Bearing with Active Pads—Numerical and Experimental Results. J. Sound Vib. 2023, 546, 117441. [Google Scholar]
- Han, D.; Bi, C.; Chen, C.; Yang, J. Dynamic Coefficients of Tilting Pad Bearing by Perturbing the Turbulence Model. Appl. Sci. 2022, 12, 6348. [Google Scholar] [CrossRef]
- Pierart, F.G.; Santos, I.F. Adjustable Hybrid Gas Bearing—Influence of Piezoelectrically Adjusted Injection on Damping Factors and Natural Frequencies of a Flexible Rotor Operating under Critical Speeds. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 1209–1220. [Google Scholar]
- Zhang, L.; Xu, H. Effect of Radial Clearance on the Dynamic Behavior of Adjustable Journal Bearings in Turbulent and Laminar Flow Regimes. AIP Adv. 2023, 13, 025362. [Google Scholar]
- Du, Y.; Lan, J.; Quan, H.; Sun, C.; Liu, X.; Yang, X. Effect of Different Turbulent Lubrication Models on the Lubrication Characteristics of Water-Lubricated Rubber Bearings at a High Reynolds Number. Phys. Fluids 2021, 33, 065118. [Google Scholar]
- Yang, M.; Lu, H.; Zhang, X.; Zhang, Y.Q.; Li, Z.J.; Zhang, W. Mixed Lubrication Performances of Misaligned Stern Bearing Considering Turbulence and Elastic Deformation. ILT 2023, 75, 645–653. [Google Scholar]
- Hashimoto, H.; Wada, S.; Ito, J. An Application of Short Bearing Theory to Dynamic Characteristic Problems of Turbulent Journal Bearings. J. Tribol. 1987, 109, 307–314. [Google Scholar]
- Hashimoto, H.; Wada, S. Dynamic Behavior of Unbalanced Rigid Shaft Supported on Turbulent Journal Bearings—Theory and Experiment. J. Tribol. 1990, 112, 404–408. [Google Scholar]
- Feng, H.; Jiang, S.; Ji, A. Investigations of the Static and Dynamic Characteristics of Water-Lubricated Hydrodynamic Journal Bearing Considering Turbulent, Thermohydrodynamic and Misaligned Effects. Tribol. Int. 2019, 130, 245–260. [Google Scholar]
- Koondilogpiboon, N.; Inoue, T. Investigation of Turbulence Effects on the Nonlinear Vibration of a Rigid Rotor Supported by Finite Length 2-Lobe and Circular Bearings. J. Comput. Nonlinear Dyn. 2019, 14, 121003. [Google Scholar]
- Liu, W.; Bättig, P.; Wagner, P.H.; Schiffmann, J. Nonlinear Study on a Rigid Rotor Supported by Herringbone Grooved Gas Bearings: Theory and Validation. Mech. Syst. Signal Process. 2021, 146, 106983. [Google Scholar]
- Hu, B.; Yang, X.; Hou, A.; Wang, R.; Wu, Z.; Ni, Q.; Li, Z. Nonlinear Dynamic Responses of Rigid Rotor Supported by Thick Top Foil Bearings. Lubricants 2023, 11, 453. [Google Scholar] [CrossRef]
- Ng, C.-W.; Pan, C.H.T. A Linearized Turbulent Lubrication Theory. J. Basic Eng. 1965, 87, 675–682. [Google Scholar]
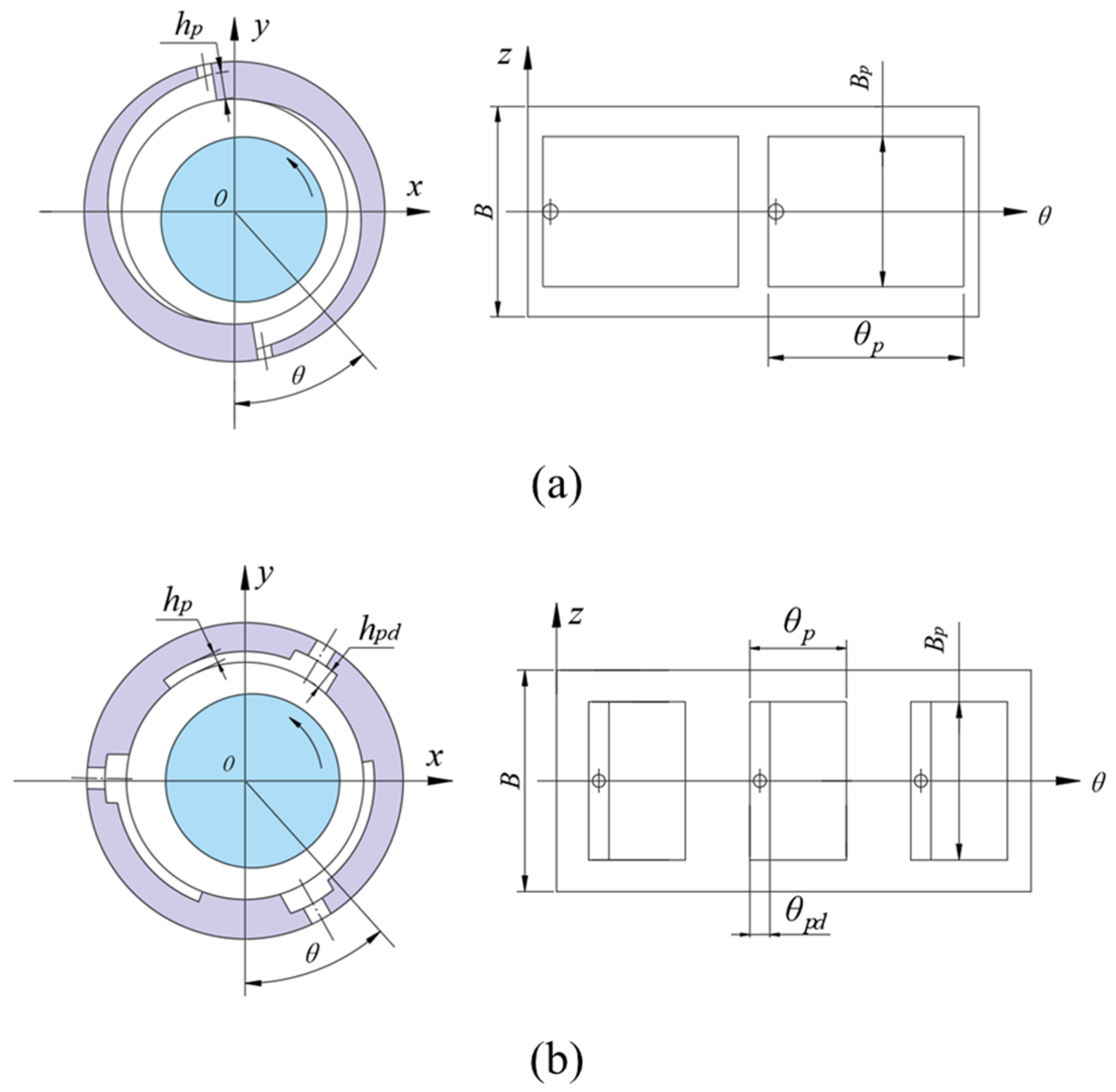



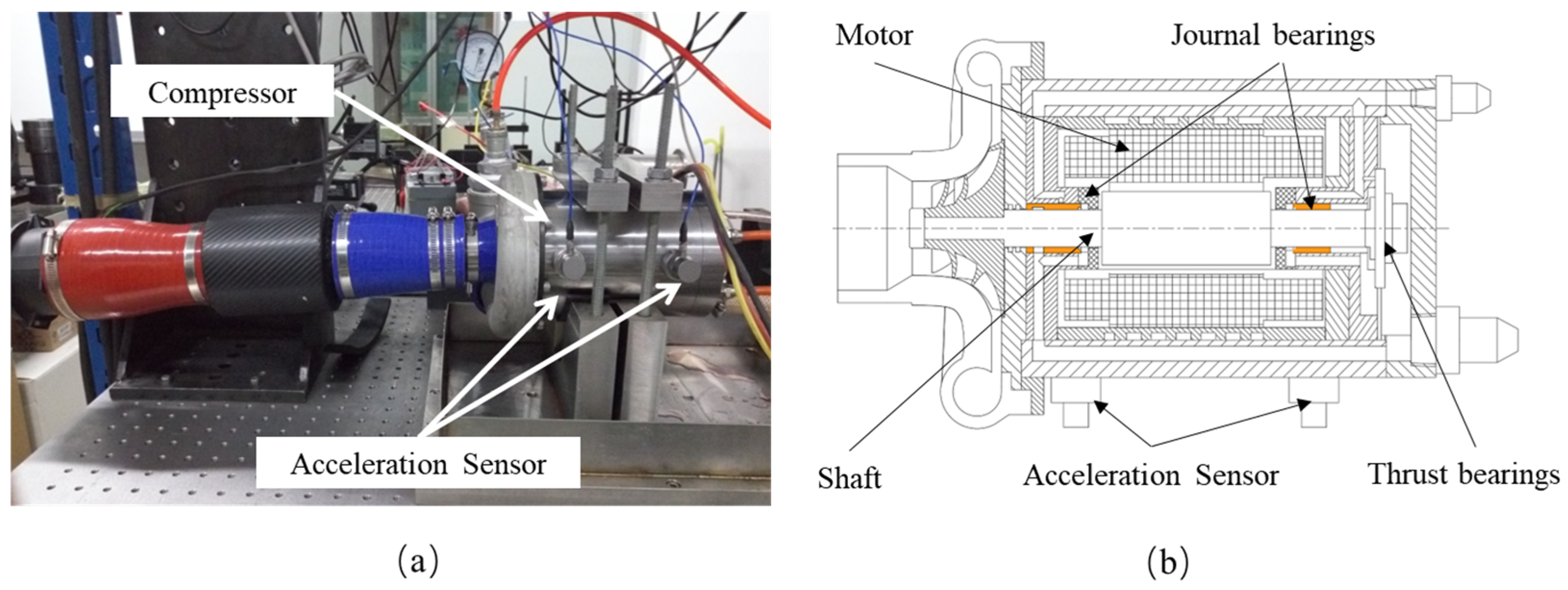
| Item | TLB | TSRB |
|---|---|---|
| Bearing radius R/mm | 7.5 | |
| Bearing length B/mm | 14 | |
| Radius clearance h0/mm | 0.02 | |
| Lobe/recess depth hp/mm | 0.08 | 0.025 |
| Deep recess depth hpd/mm | - | 0.08 |
| Lobe/recess axial width Bp/mm | 10 | |
| Lobe/recess circumferential width θp/° | 162 | 80 |
| Deep recess circumferential width θpd/° | - | 15 |
| Diameter of supply orifice d0/mm | 1.0 | |
| Water supply pressure Ps/bar | 1.7 | |
| Water viscosity μ/Pa·s | 1.0 × 10−3 | |
| Water density ρ/kg·m−3 | 1000 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, T.; Feng, M. Turbulence Effects on the Dynamic Characteristics of Non-Circular Journal Bearings Under Large Sommerfeld Number Conditions. Lubricants 2025, 13, 139. https://doi.org/10.3390/lubricants13040139
Ren T, Feng M. Turbulence Effects on the Dynamic Characteristics of Non-Circular Journal Bearings Under Large Sommerfeld Number Conditions. Lubricants. 2025; 13(4):139. https://doi.org/10.3390/lubricants13040139
Chicago/Turabian StyleRen, Tianming, and Ming Feng. 2025. "Turbulence Effects on the Dynamic Characteristics of Non-Circular Journal Bearings Under Large Sommerfeld Number Conditions" Lubricants 13, no. 4: 139. https://doi.org/10.3390/lubricants13040139
APA StyleRen, T., & Feng, M. (2025). Turbulence Effects on the Dynamic Characteristics of Non-Circular Journal Bearings Under Large Sommerfeld Number Conditions. Lubricants, 13(4), 139. https://doi.org/10.3390/lubricants13040139





