Friction Prediction in Asphalt Pavements: The Role of Separated Macro- and Micro-Texture Parameters Under Dry and Wet Conditions
Abstract
1. Introduction
- To separate the asphalt pavement surface into macro-texture and micro-texture components;
- To compute surface texture characteristic parameters specified in the ISO standards using three-dimensional point cloud data;
- To analyze the relationship between macro-texture and the dry friction coefficient, as well as between micro-texture and the wet friction coefficient;
- To establish regression relationships between characteristic parameters and both dry and wet friction coefficients based on the analysis results.
2. Materials and Methods
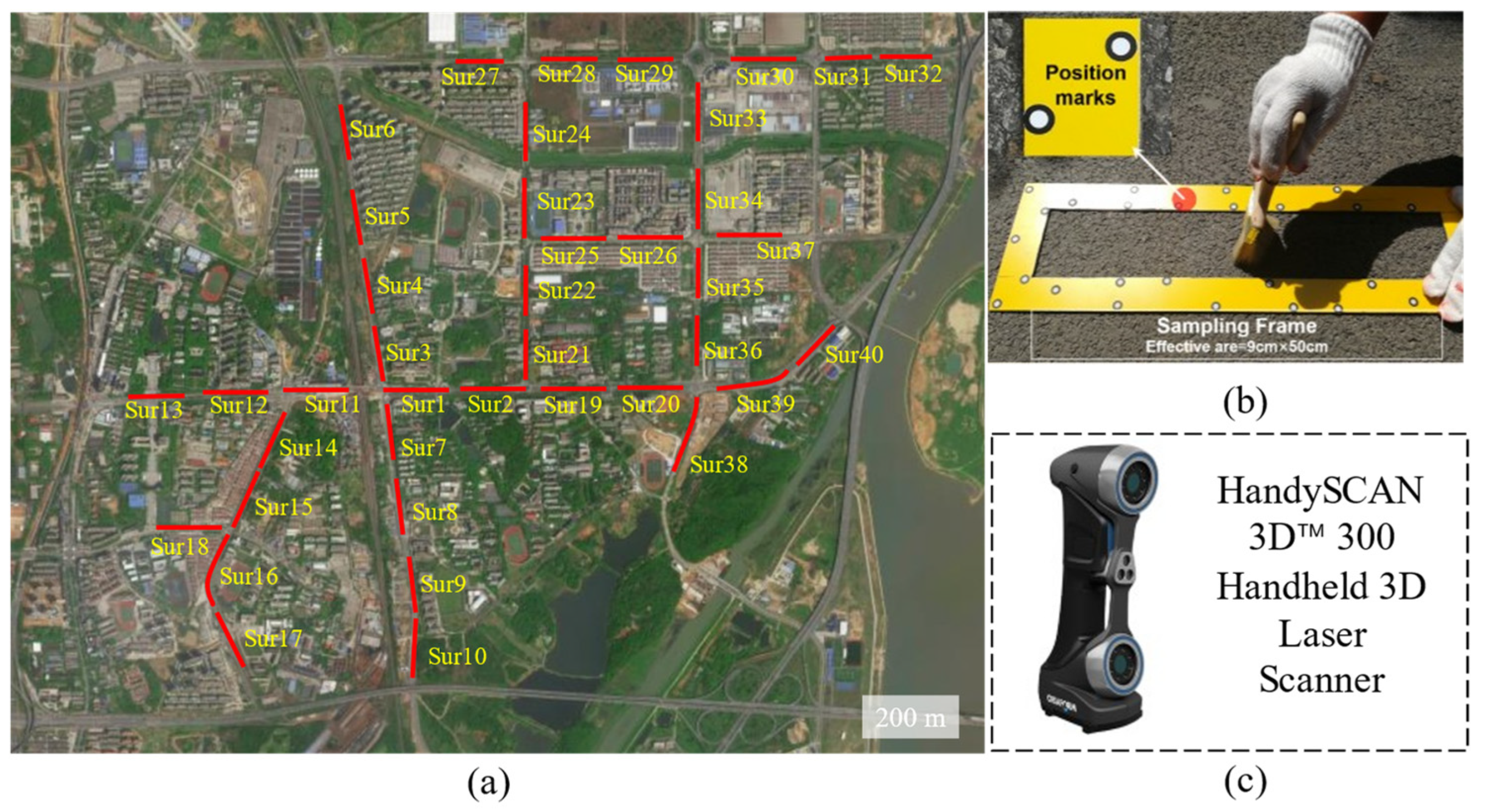
2.1. Pavement Texture Data Collection and Characterization
2.1.1. Collection and Preprocessing Methods
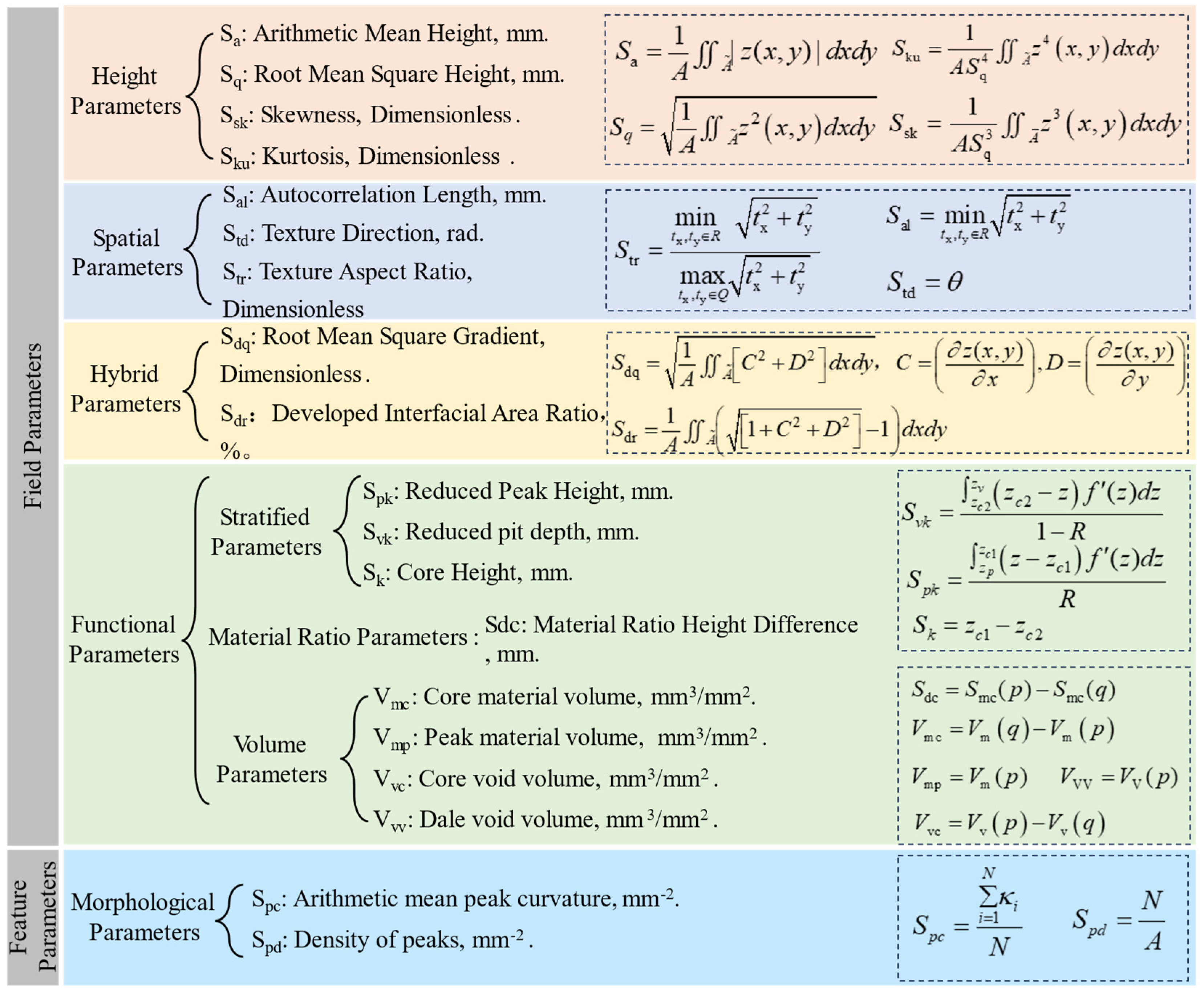
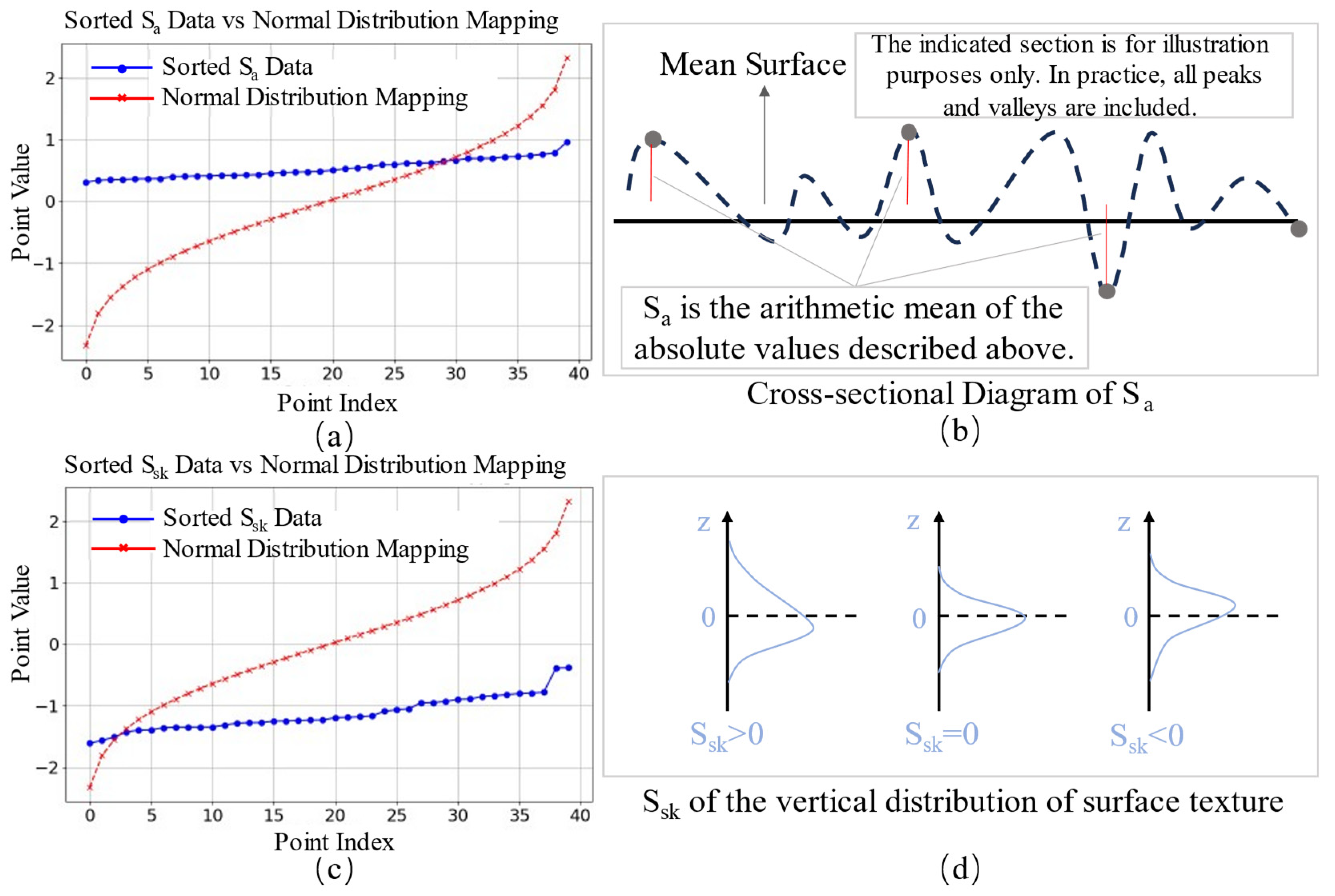
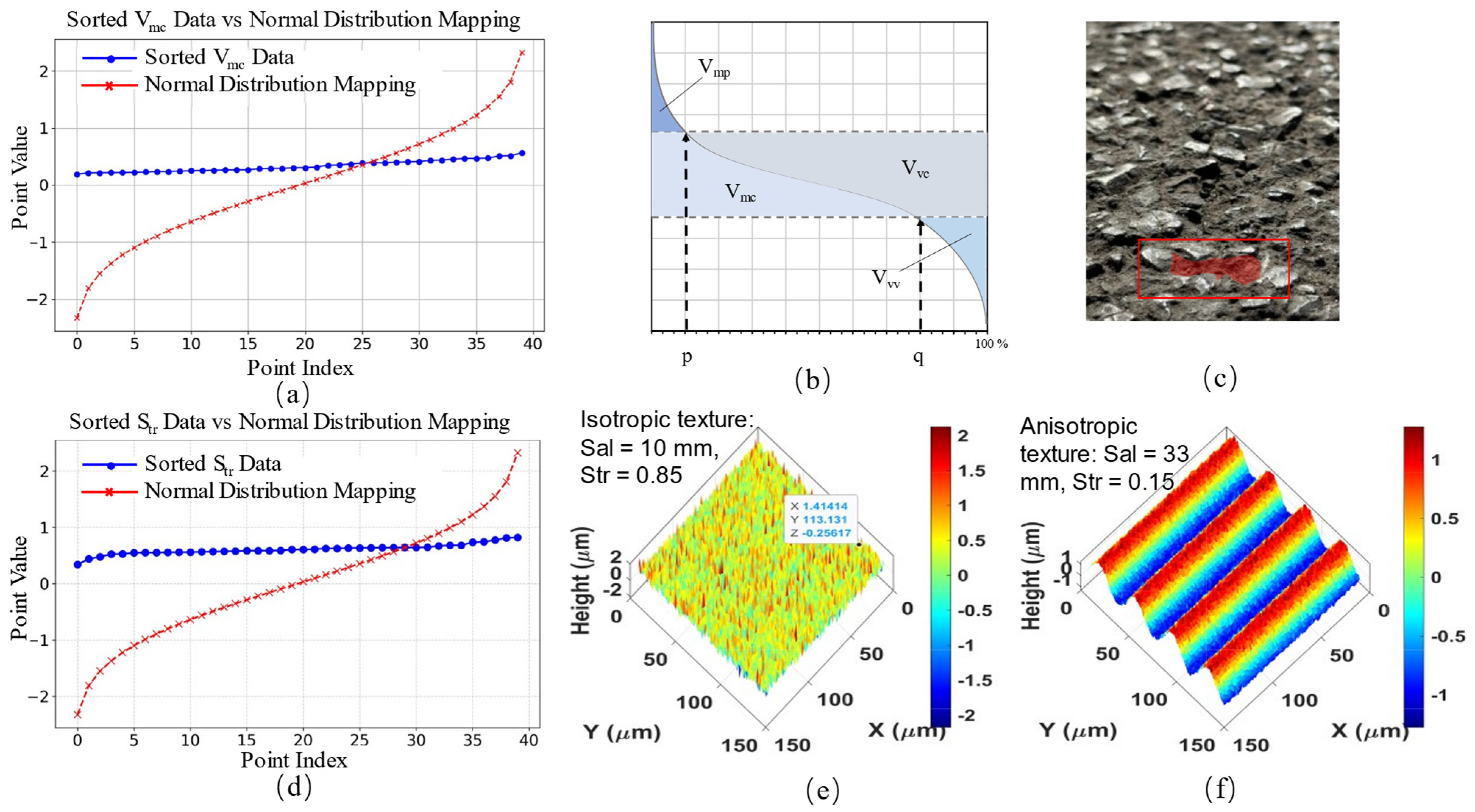
2.1.2. Characterization of Texture Features
2.2. Pavement Friction Coefficient Data Collection and Results
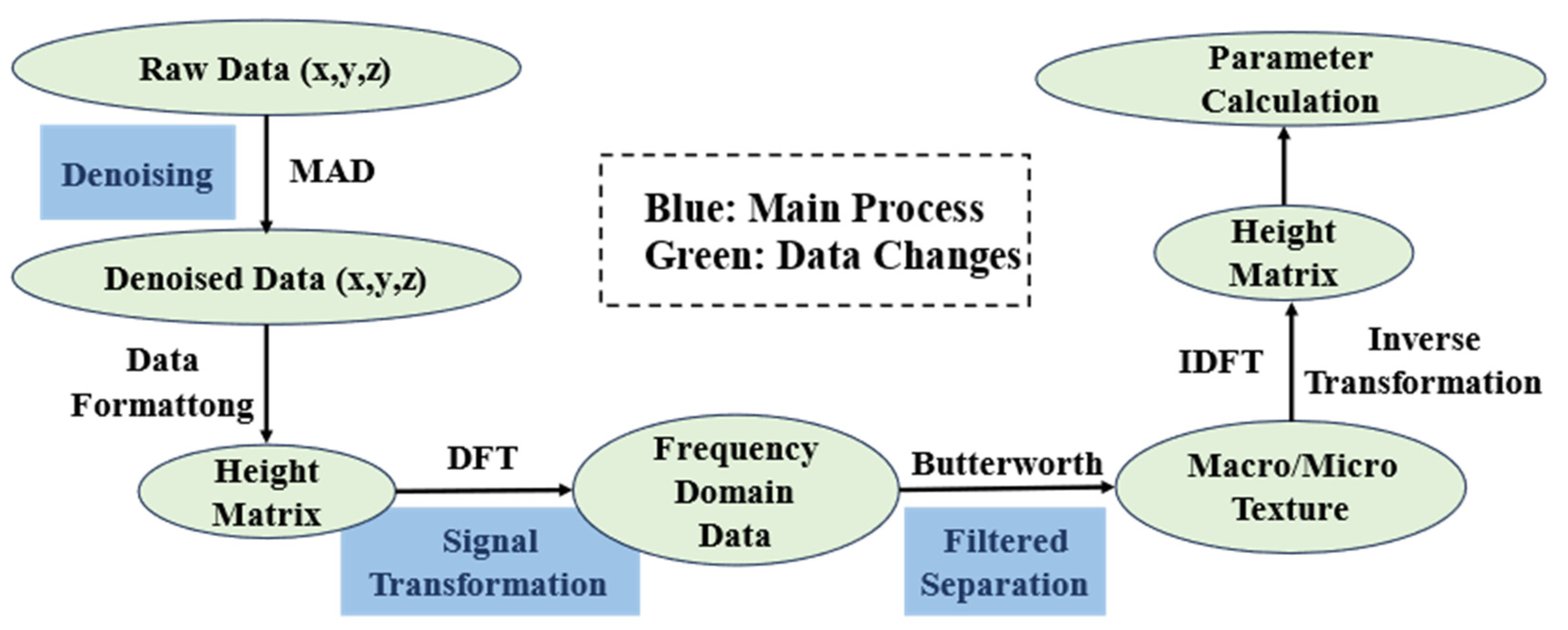
2.3. Separation of Pavement Macro/Micro Texture
3. Results and Discussion
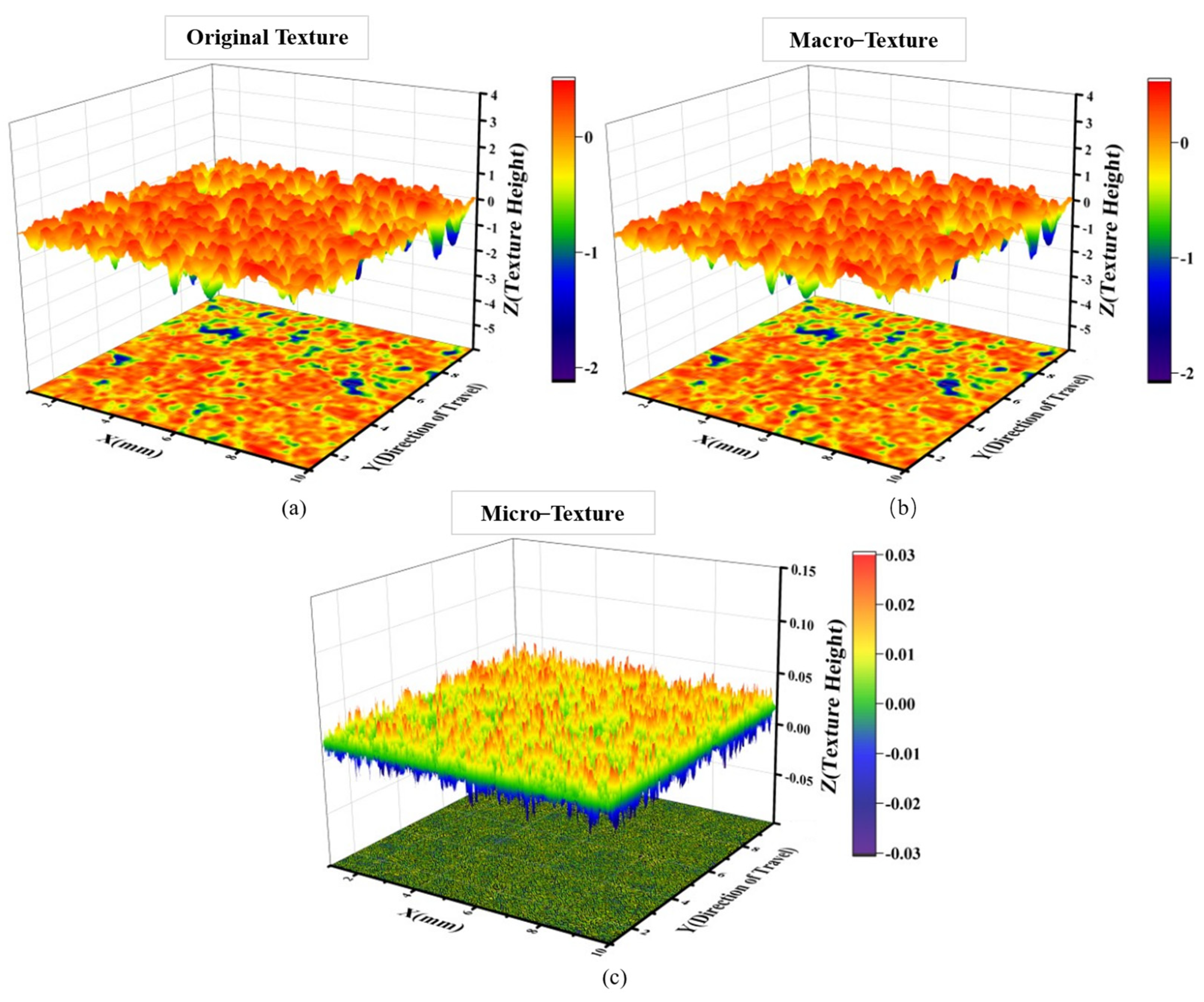
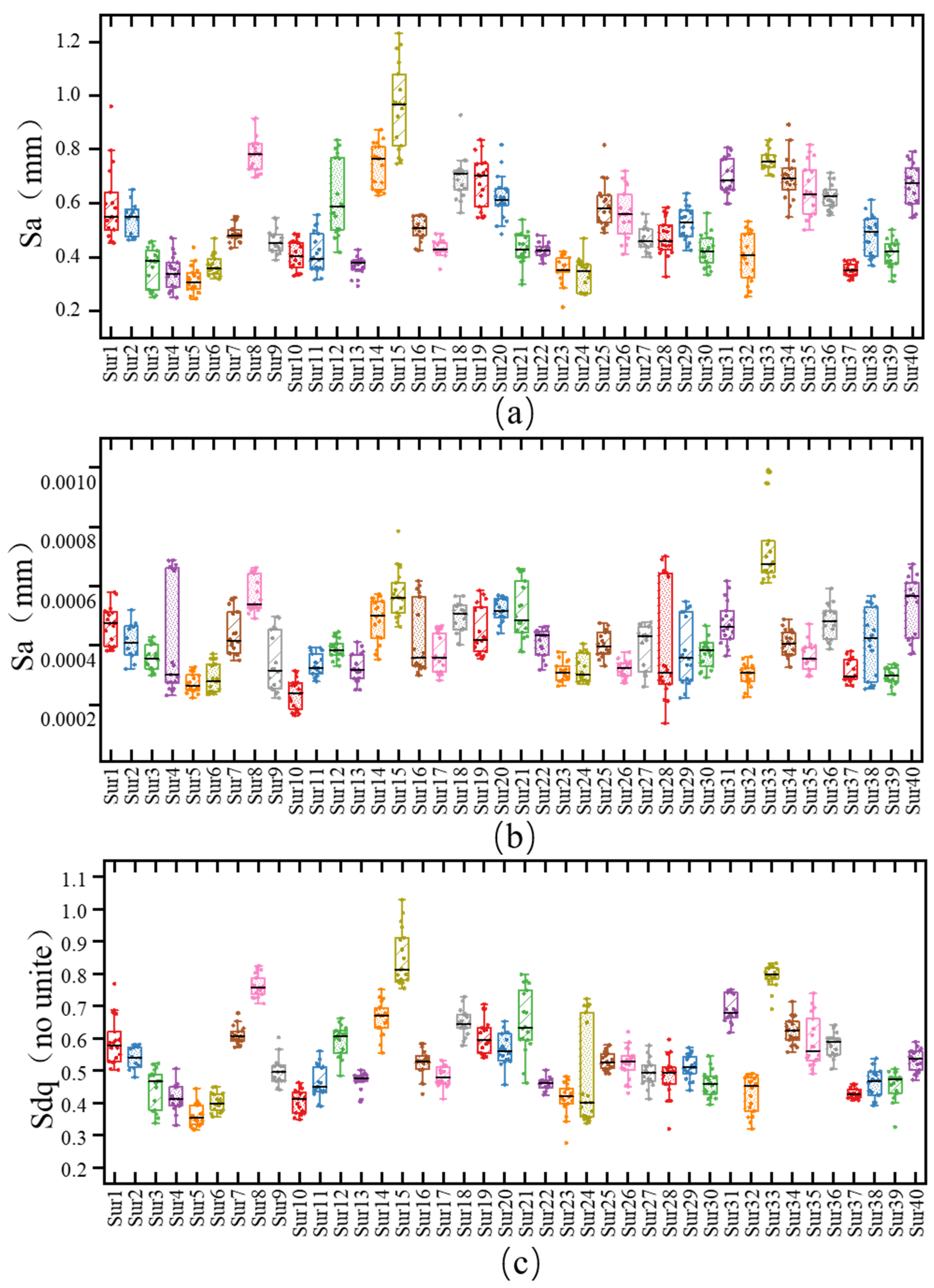
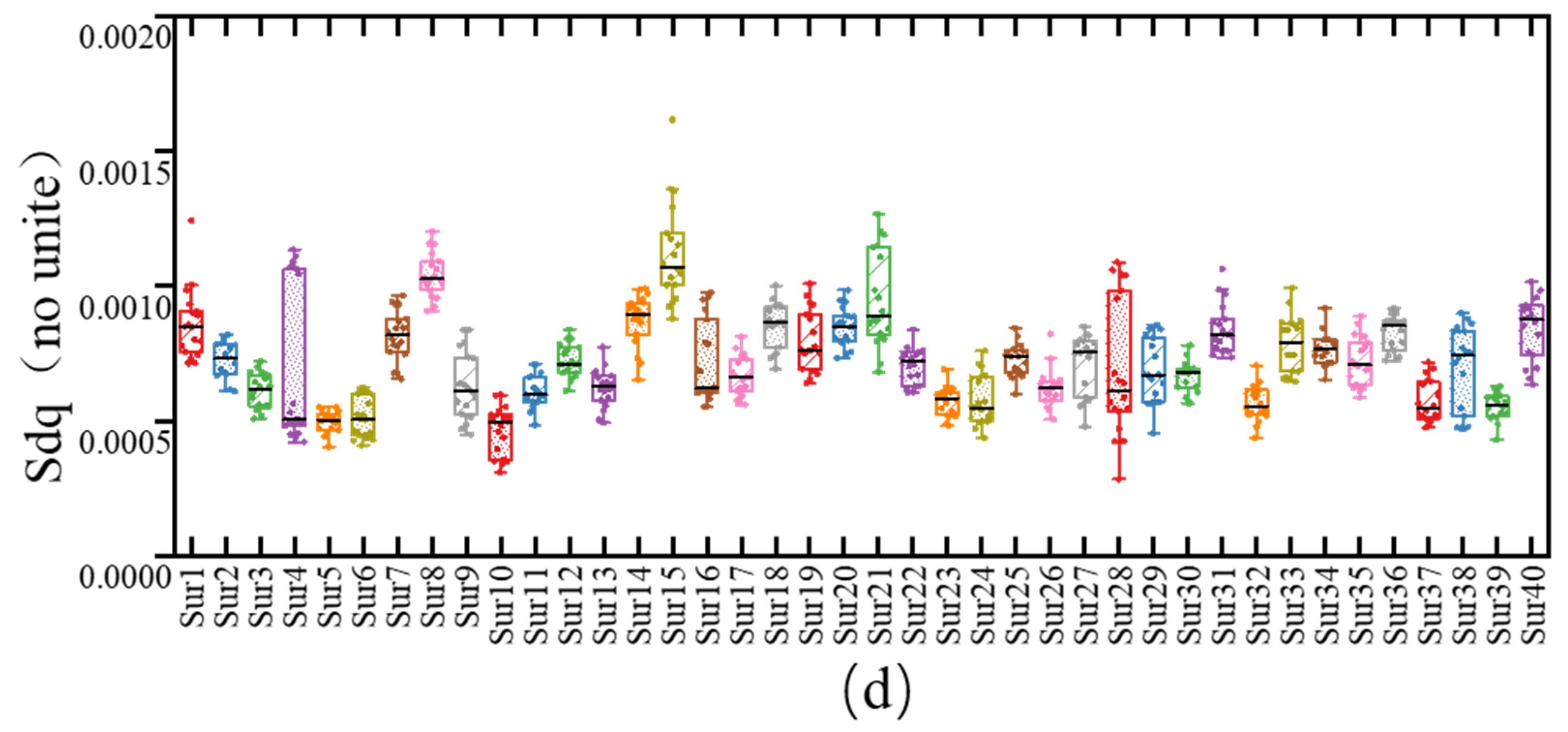
3.1. Pavement Texture Characterization and Separation Outcomes
3.2. Impact of Macro-Texture on Dry and Wet Friction Coefficients
3.3. The Influence of Micro-Texture on Dry and Wet Friction Coefficients
4. Conclusions
- Data Collection Issues and Rectification. Gaps in the collected data were identified. This phenomenon primarily arises from the irregular distribution of pavement texture, which creates blind spots that cannot be captured during the scanning process. Additionally, poor operational quality during repeated data collection can adversely affect data accuracy. To address this, specialized software was employed to convert the 3D point cloud data into a surface model, supplement the missing points, and subsequently reconvert it into point data.
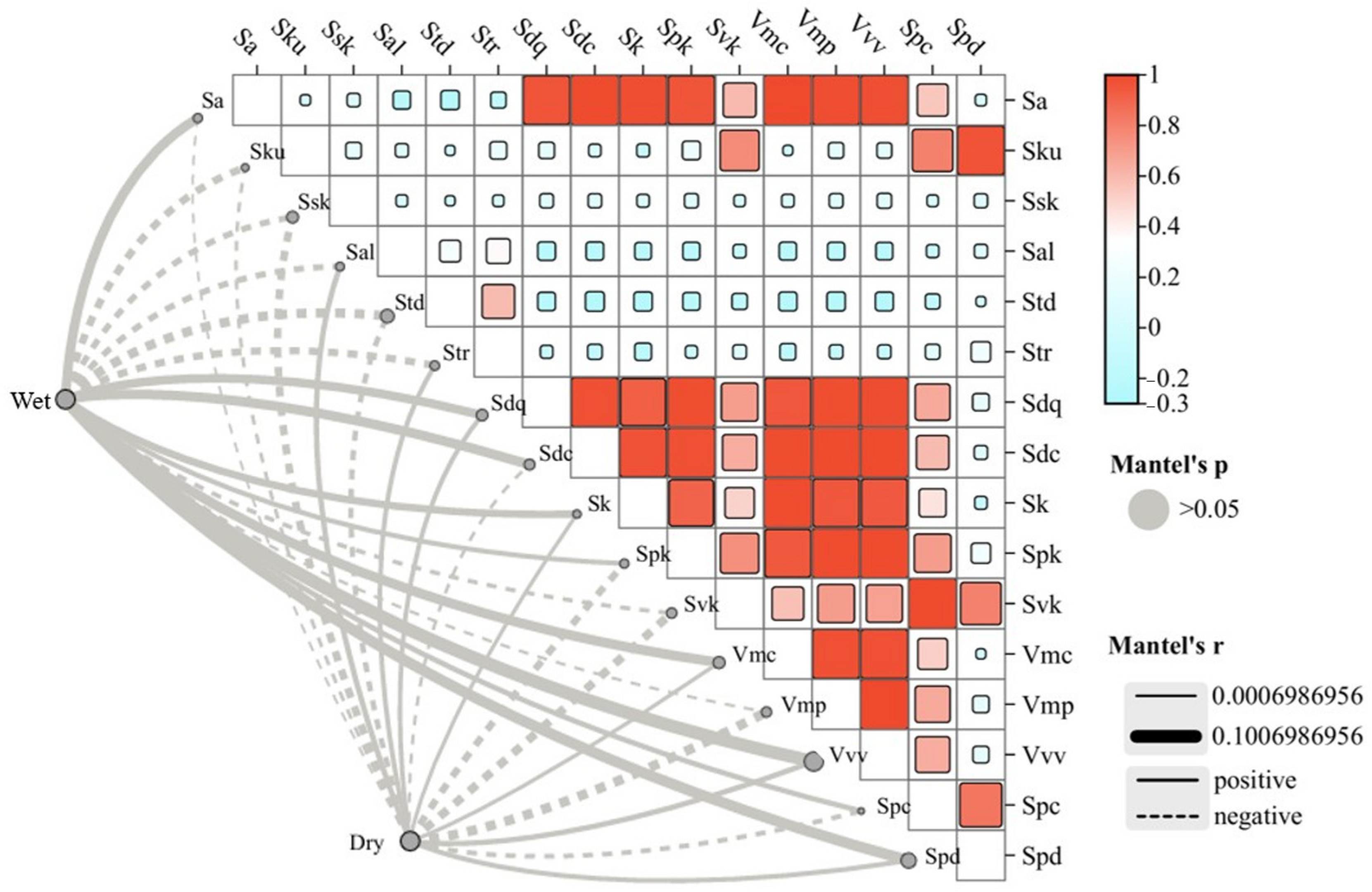
- Separation and Characterization of Macro- and Micro-Textures. The actual pavement texture was successfully separated into macro- and micro-textures, and 16 characteristic parameters were calculated for each. By applying a combination of Fourier transform and Butterworth high-pass and band-pass filters, the separation process was completed and visualized in three dimensions. The presented images allow for a clear observation of overall texture changes and parameter comparisons between the two texture types. These characteristic parameters were further utilized to estimate pavement surface texture conditions and interpret the role of each parameter in influencing skid resistance.
- Correlation and Regression Analysis of Texture Parameters. The relationships between macro- and micro-textures and their characteristic parameters were analyzed, and regression equations linking these parameters to dry and wet friction coefficients were developed. The results for macro-texture indicate significant correlations between Sa, Str, Vmc, Ssk, and FDry, with Ssk showing a negative correlation, while Sa, Str, and Vmc exhibit positive correlations. All four parameters were found to be highly significant. For micro-texture, Sa, Sdc, Vvv, and Spd all demonstrate significant positive correlations with FWet. The regression equations derived can be used to calculate dry and wet friction coefficients based on the characteristic parameters of the three-dimensional texture.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, W.; Li, J.; Luo, W.; Yang, J.; Zhu, X.; Yan, J. A new method for solving parameter mutation analysis in periodic structure bandgap calculation. Eur. J. Mech.-A/Solids 2025, 111, 105572. [Google Scholar]
- Yao, Y.; Yang, J.; Gao, J.; Zheng, M.; Song, L.; Xu, J.; Sun, C. RAP chunks produced in cold milling operation of asphalt pavement: Evaluation, mechanism, and engineering investigation in China. J. Traffic Transp. Eng. (Engl. Ed.) 2024, 11, 972–1000. [Google Scholar]
- Liu, Z.; Feng, T.; Zhu, X.; Gao, J.; Hu, K.; Guo, M.; Gu, F.; Li, F. Bird’s-eye view of recycled solid wastes in road engineering. J. Road Eng. 2024, 4, 93–150. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, J.; Gao, J.; Xu, J.; Zhang, Y.; Yu, S.; Muhammad, N.S. Blending behavior of reclaimed asphalt and virgin asphalt in recycled asphalt mixtures: A comprehensive analysis on material composition and mixing process. Constr. Build. Mater. 2025, 465, 140229. [Google Scholar]
- Vélez Rodríguez, K.X.; Katicha, S.W.; Flintsch, G.W. Enhanced Methodology for the Identification of Locations with High Risk of Wet Crashes. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 29–37. [Google Scholar]
- Bitelli, G.; Simone, A.; Girardi, F.; Lantieri, C. Laser Scanning on Road Pavements: A New Approach for Characterizing Surface Texture. Sensors 2012, 12, 9110–9128. [Google Scholar] [CrossRef]
- Acai, J.; Amadi-Echendu, J. Pavement Infrastructure Sustainability Assessment: A Systematic Review. In Proceedings of the 2018 Portland International Conference on Management of Engineering and Technology Inc. (PICMET), Honolulu, HI, USA, 19–23 August 2018. [Google Scholar]
- Davies, R.B.; Cenek, P.D.; Henderson, R.J. The effect of skid resistance and texture on crash risk. In Proceedings of the Surface Friction Roads and Runways, Christchurch, New Zealand, 1–4 May 2005. [Google Scholar]
- Ghaffarpour Jahromi, S. Investigation of damage and deterioration hazard in asphalt mixtures due to moisture. Proc. Inst. Civ. Eng.-Transp. 2018, 171, 98–105. [Google Scholar]
- Du, Y.; Weng, Z.; Liu, C.; Wu, D. Dynamic Pavement Distress Image Stitching Based on Fine-Grained Feature Matching. J. Adv. Transp. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Amarasiri, S.; Muhunthan, B. Evaluating the effectiveness of pavement preventive-maintenance treatments in mitigating longitudinal cracks in wet-freeze climatic zones. J. Transp. Eng. Part B Pavements 2020, 146, 4020014. [Google Scholar]
- Du, Y.; Weng, Z.; Li, F.; Ablat, G.; Wu, D.; Liu, C. A novel approach for pavement texture characterisation using 2D-wavelet decomposition. Int. J. Pavement Eng. 2022, 23, 1851–1866. [Google Scholar]
- Yu, M.; Xiao, B.; You, Z.; Wu, G.; Li, X.; Ding, Y. Dynamic friction coefficient between tire and compacted asphalt mixtures using tire-pavement dynamic friction analyzer. Constr. Build. Mater. 2020, 258, 119492. [Google Scholar]
- Jiao, Y.; Liu, X.; Liu, K. Wettability of laser textured surface: A parametric study based on numerical simulation and experimentation. Ind. Lubr. Tribol. 2018, 70, 977–983. [Google Scholar]
- Zou, Y.; Yang, G.; Cao, M. Neural network-based prediction of sideway force coefficient for asphalt pavement using high-resolution 3D texture data. Int. J. Pavement Eng. 2022, 23, 3157–3166. [Google Scholar]
- Deng, Q.; Zhan, Y.; Liu, C.; Qiu, Y.; Zhang, A. Multiscale power spectrum analysis of 3D surface texture for prediction of asphalt pavement friction. Constr. Build. Mater. 2021, 293, 123506. [Google Scholar]
- Hu, L.; Yun, D.; Liu, Z.; Du, S.; Zhang, Z.; Bao, Y. Effect of three-dimensional macrotexture characteristics on dynamic frictional coefficient of asphalt pavement surface. Constr. Build. Mater. 2016, 126, 720–729. [Google Scholar]
- Li, Q.J.; Yang, G.; Wang, K.C.P.; Zhan, Y.J.; Wang, C. Novel Macro- and Microtexture Indicators for Pavement Friction by Using High-Resolution Three-Dimensional Surface Data. Transp. Res. Rec. J. Transp. Res. Board 2017, 2641, 164–176. [Google Scholar]
- Li, Q.J.; Zhan, Y.; Yang, G.; Wang, K.C.P. Pavement skid resistance as a function of pavement surface and aggregate texture properties. Int. J. Pavement Eng. 2020, 21, 1159–1169. [Google Scholar]
- Ayenu-Prah, A.Y.; Attoh-Okine, N.O. Comparative study of Hilbert-Huang transform, Fourier transform and wavelet transform in pavement profile analysis. Veh. Syst. Dyn. 2009, 47, 437–456. [Google Scholar]
- Zelelew, H.M.; Papagiannakis, A.T.; de León Izeppi, E.D. Pavement macro-texture analysis using wavelets. Int. J. Pavement Eng. 2013, 14, 725–735. [Google Scholar]
- Katicha, S.W.; Mogrovejo, D.E.; Flintsch, G.W.; de León Izeppi, E.D. Adaptive Spike Removal Method for High-Speed Pavement Macrotexture Measurements by Controlling the False Discovery Rate. Transp. Res. Rec. J. Transp. Res. Board 2015, 2525, 100–110. [Google Scholar]
- Katicha, S.W.; Mogrovejo, D.E.; Flintsch, G.W.; de León Izeppi, E.; Carrasco, D.M. Latest Development in the Processing of Pavement Macrotexture Measurements of High Speed Laser Devices. In Proceedings of the 9th International Conference on Managing, Alexandria, VA, USA, 18–21 May 2015. [Google Scholar]
- ISO 25178-2 2021; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- Zuñiga Garcia, N. Predicting Friction with Improved Texture Characterization. Ph.D. Dissertation, The University of Texas at Austin, Austin, TX, USA, 2017. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics: A Step-by-Step Approach; Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Yu, B.; Kong, L.; Sun, Y.; Yao, B.; Gao, Z. A bi-level programming for bus lane network design. Transp. Res. Part C Emerg. Technol. 2015, 55, 310–327. [Google Scholar] [CrossRef]
- Ding, S.; Wang, K.C.; Yang, E.; Zhan, Y. Influence of effective texture depth on pavement friction based on 3D texture area. Constr. Build. Mater. 2021, 287, 123002. [Google Scholar]




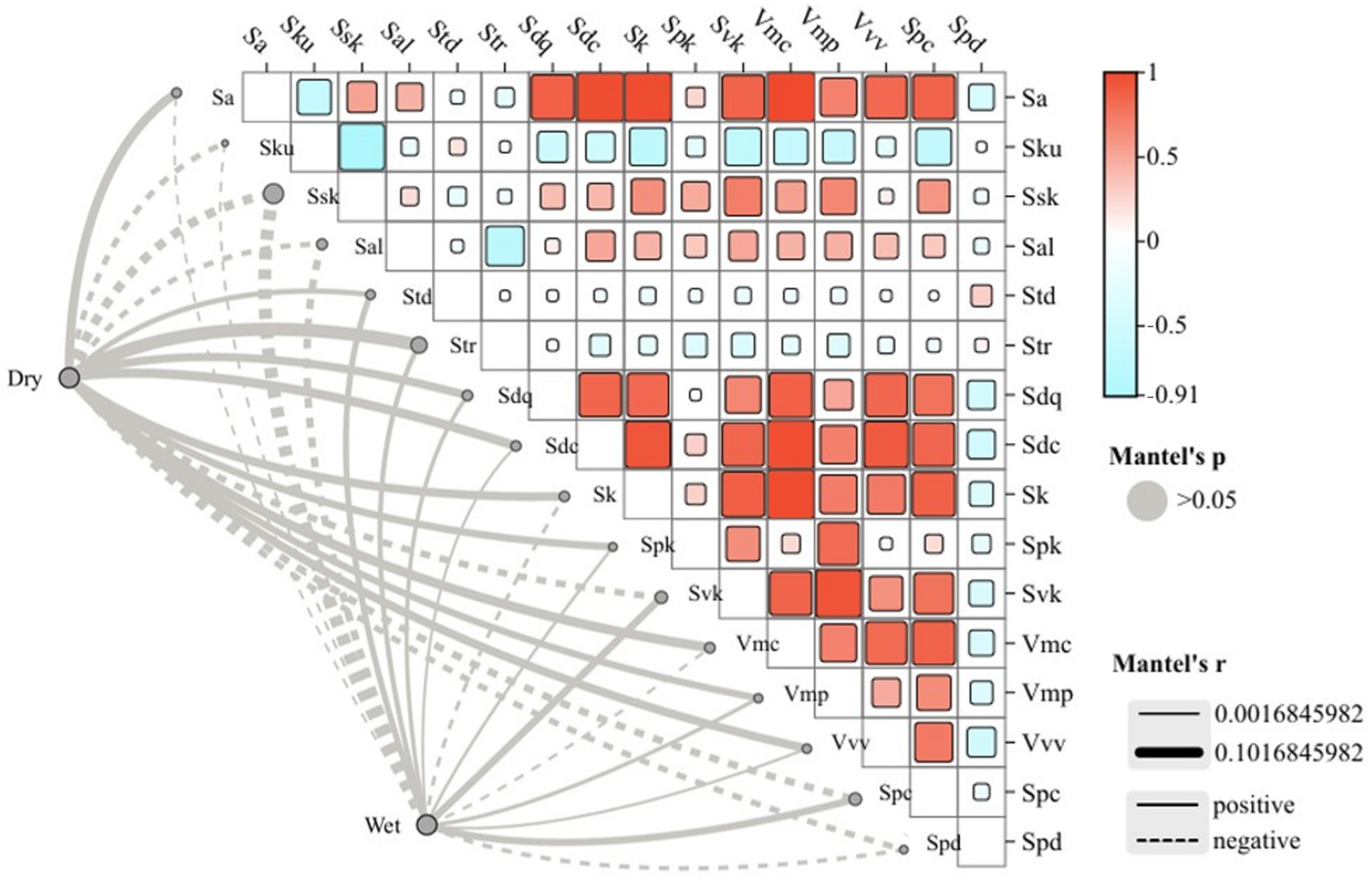


| Parameters | Mantel’r | Mantel’p | Performance on 3D Surfaces | Impact on Skid Resistance |
|---|---|---|---|---|
| Sa | 0.065 | 0.214 | Average variation amplitude of height | Higher Sa can improve skid resistance |
| Ssk | 0.065 | 0.071 | Negative skewness (more peaks) or positive skewness (more valleys) | Negative skewness enhances skid resistance, while positive skewness reduces it |
| Str | 0.101 | 0.077 | Isotropic or anisotropic texture | High Str provides more stable skid resistance |
| Vmc | 0.068 | 0.192 | Larger volume increases the contact area | Higher Vmc values can enhance skid resistance |
| Model Overview | |||||||
| Model | R | R2 | Adjusted R2 | Standard Error of the Estimate | Durbin Watson | ||
| 1 | 0.845 | 0.714 | 0.699 | 0.050 | 1.792 | ||
| Predicted Value (Constant), Vmc, Sa; Dependent Variable: FDry | |||||||
| Analysis of Variance (ANOVA) | |||||||
| Sum of Squares | DOF | Mean Square | F | Sig. | |||
| Regression | 0.238 | 2 | 0.119 | 46.215 | 0.000 b | ||
| Residual | 0.095 | 37 | 0.003 | ||||
| Total | 0.334 | 39 | |||||
| Coefficient | |||||||
| Unstandardized | Standardized | t | Sig. | ||||
| B | Standard Error | Trial Version | |||||
| (Constant) | 0.142 | 0.039 | 3.672 | 0.001 | |||
| Vmc | 1.513 | 0.159 | 1.199 | 9.521 | 0.000 | ||
| Sa | −0.639 | 0.082 | −0.976 | −7.752 | 0.000 | ||
| Regression Model | |||||||
| Parameters | Mantel’r | Mantel’p | Performance on 3D Surfaces | Impact on Skid Resistance |
|---|---|---|---|---|
| Sa | 0.091 | 0.103 | Average variation amplitude of height | Higher Sa can improve skid resistance |
| Sdc | 0.092 | 0.110 | Surface peak support ratio | Higher Sdc provides stronger support, enhancing friction |
| Vvv | 0.093 | 0.095 | Volume of surface recess areas | Higher Vvv improves drainage performamce, enhancing skid resistance in wet condition |
| Spd | 0.107 | 0.134 | Number of surface peaks per unit area | Higher Spd provides friction and improves skid resistance |
| Model Overview | |||||||
| Model | R | R2 | Adjusted R2 | Standard Error of the Estimate | Durbin Watson | ||
| 1 | 0.808 | 0.653 | 0.653 | 0.061 | 1.720 | ||
| Predicted Value (Constant), Vvv, Spd; Dependent Variable: FWet | |||||||
| Analysis of Variance (ANOVA) | |||||||
| Sum of Squares | DOF | Mean Square | F | Sig. | |||
| Regression | 0.260 | 2 | 0.130 | 34.811 | 0.000 b | ||
| Residual | 0.138 | 37 | 0.004 | ||||
| Total | 0.398 | 39 | |||||
| Coefficient | |||||||
| Unstandardized | Standardized | t | Sig. | ||||
| B | Standard Error | Trial Version | |||||
| (Constant) | 0.250 | 0.038 | 6.545 | 0.000 | |||
| Spd | −0.038 | 0.014 | −0.269 | −0.269 | 0.009 | ||
| Vvv | 5600.242 | 706.969 | 0.767 | 7.921 | 0.000 | ||
| Regression Model | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Fan, J.; Gao, C.; Song, L. Friction Prediction in Asphalt Pavements: The Role of Separated Macro- and Micro-Texture Parameters Under Dry and Wet Conditions. Lubricants 2025, 13, 138. https://doi.org/10.3390/lubricants13040138
Gao J, Fan J, Gao C, Song L. Friction Prediction in Asphalt Pavements: The Role of Separated Macro- and Micro-Texture Parameters Under Dry and Wet Conditions. Lubricants. 2025; 13(4):138. https://doi.org/10.3390/lubricants13040138
Chicago/Turabian StyleGao, Jie, Jingjing Fan, Chong Gao, and Liang Song. 2025. "Friction Prediction in Asphalt Pavements: The Role of Separated Macro- and Micro-Texture Parameters Under Dry and Wet Conditions" Lubricants 13, no. 4: 138. https://doi.org/10.3390/lubricants13040138
APA StyleGao, J., Fan, J., Gao, C., & Song, L. (2025). Friction Prediction in Asphalt Pavements: The Role of Separated Macro- and Micro-Texture Parameters Under Dry and Wet Conditions. Lubricants, 13(4), 138. https://doi.org/10.3390/lubricants13040138




