RUL Prediction of Rolling Bearings Based on Fruit Fly Optimization Algorithm Optimized CNN-LSTM Neural Network
Abstract
1. Introduction
2. Methods
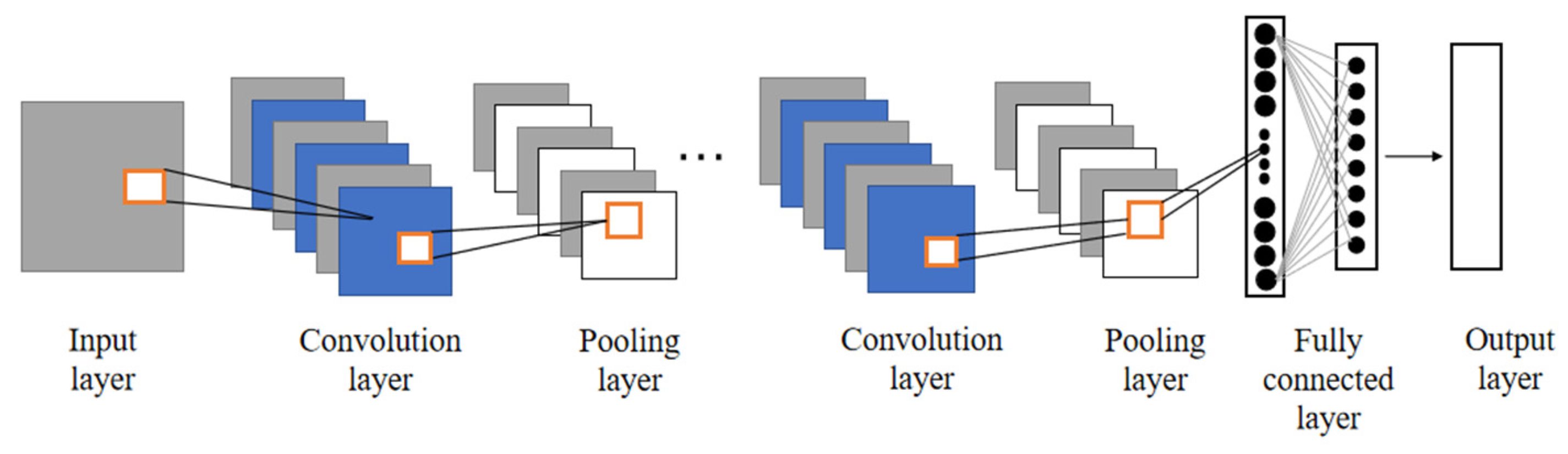
2.1. Convolutional Neural Network
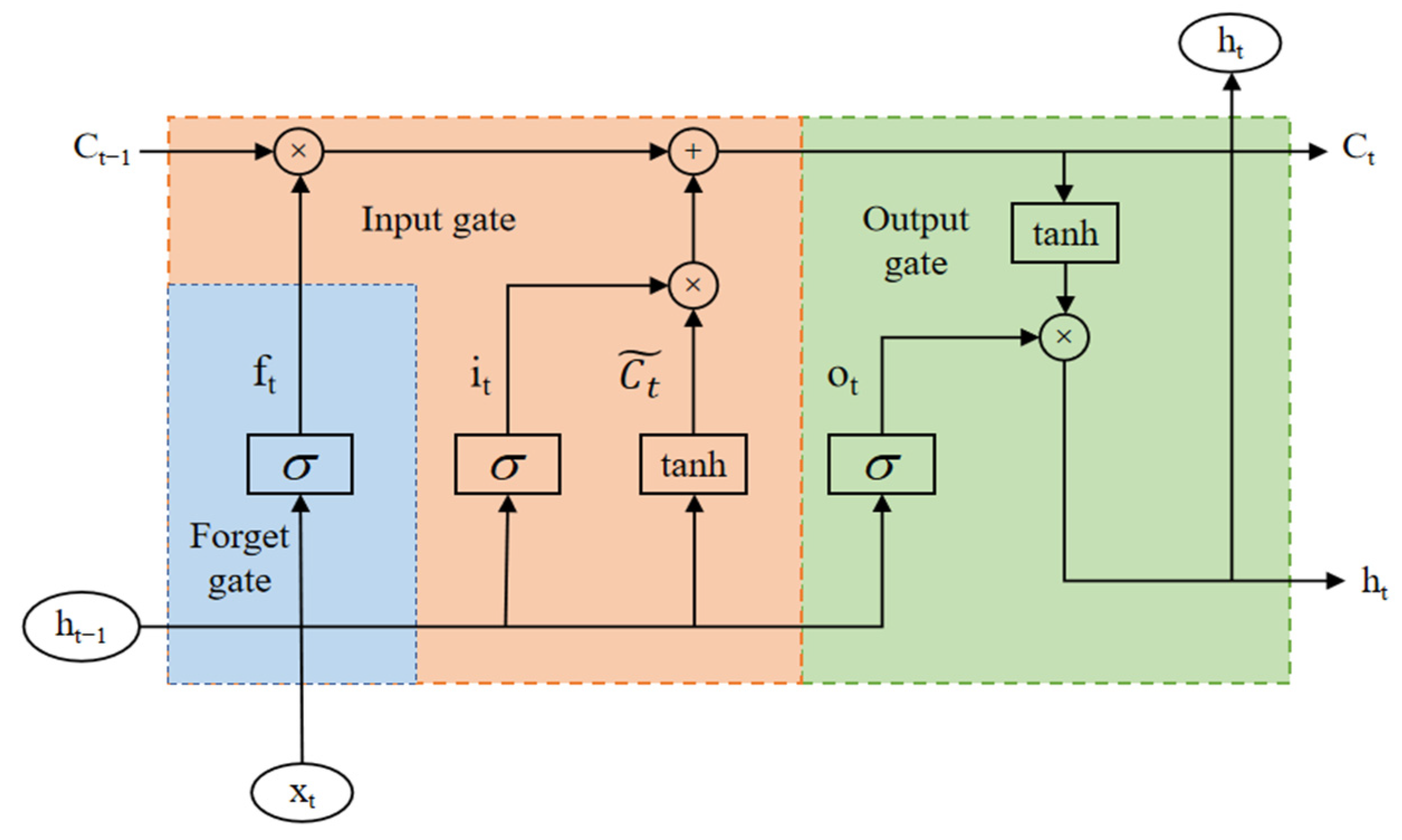
2.2. Long Short-Term Memory
2.3. Fruit Fly Optimization Algorithm
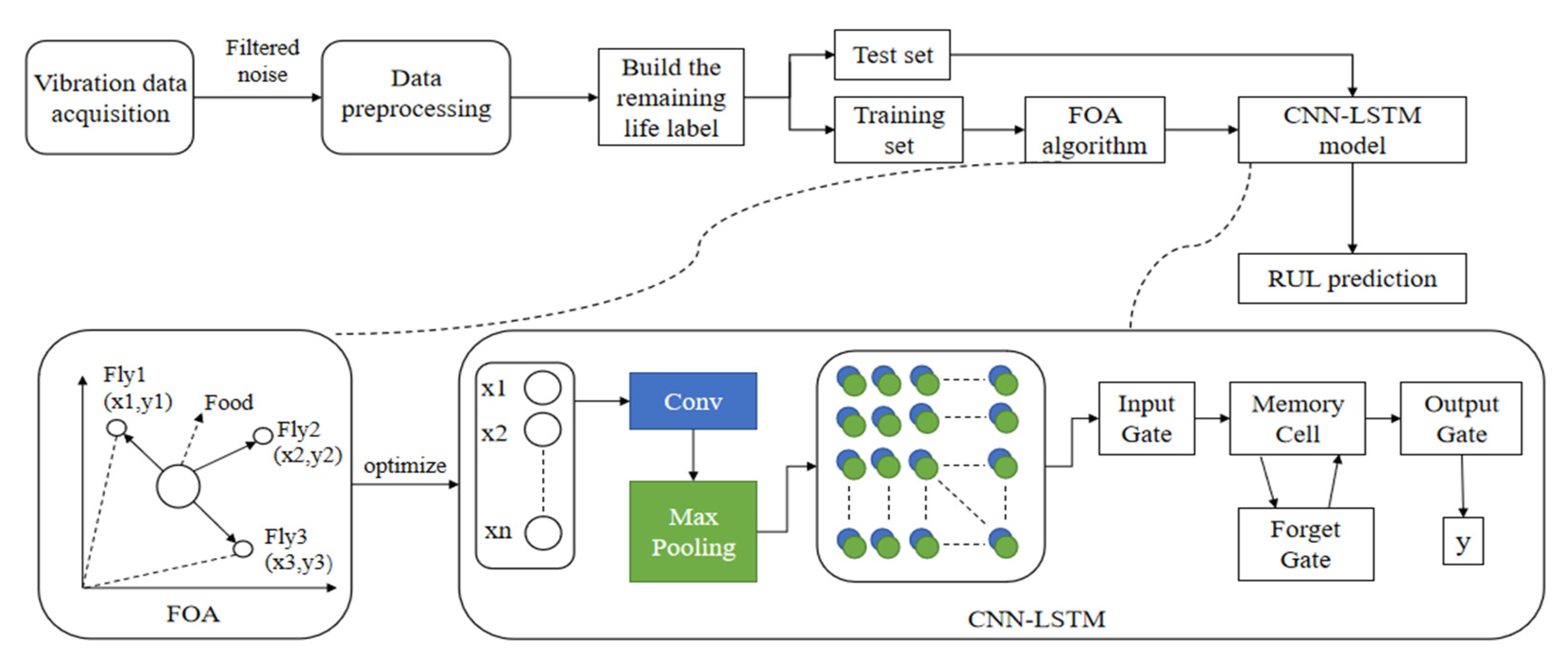
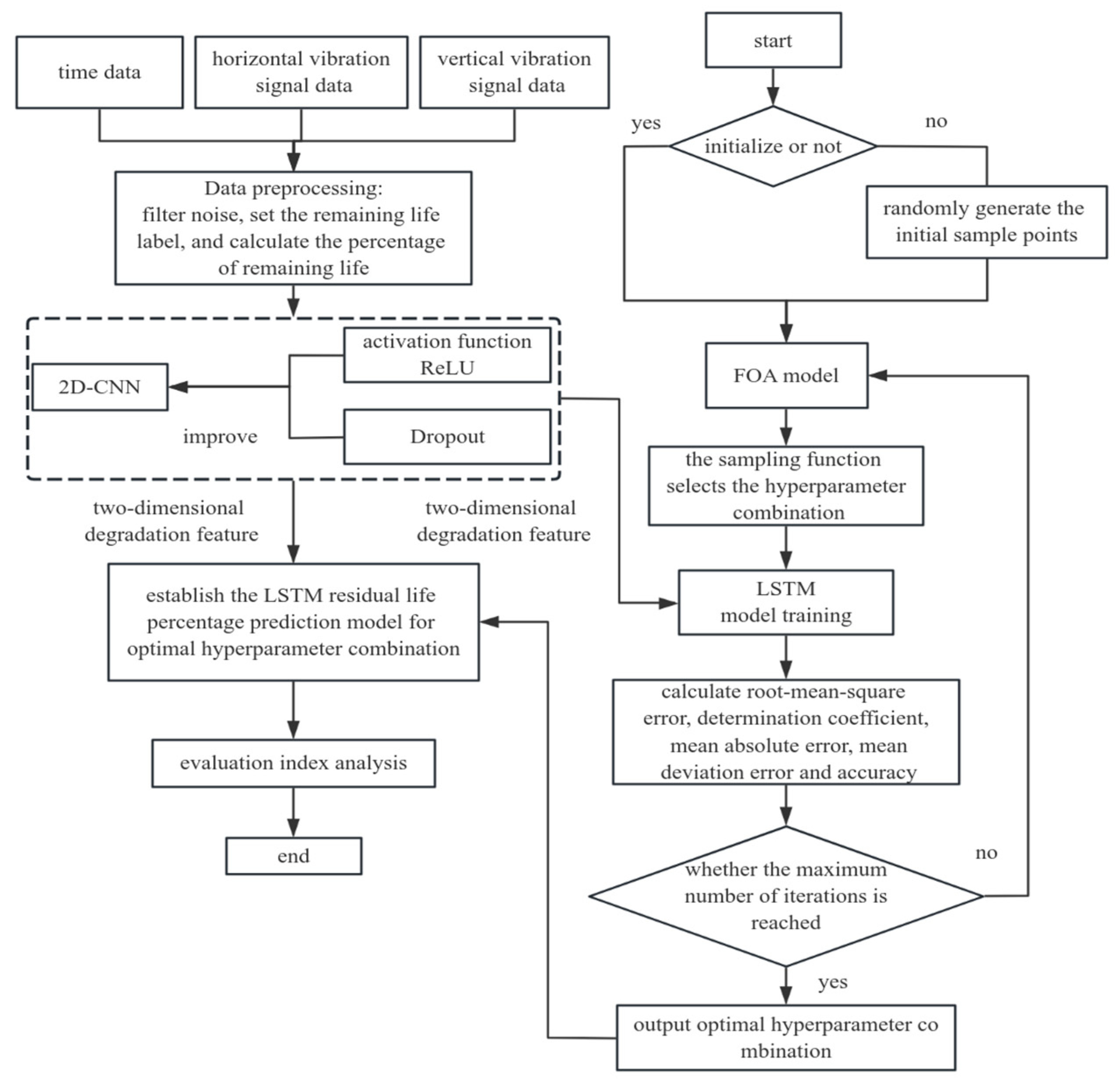
3. Proposed Methodology
4. Test Verification
4.1. Data Description
4.1.1. Data Pre-Processing
4.1.2. Remaining Life Label Setting
4.2. Evaluation Metrics
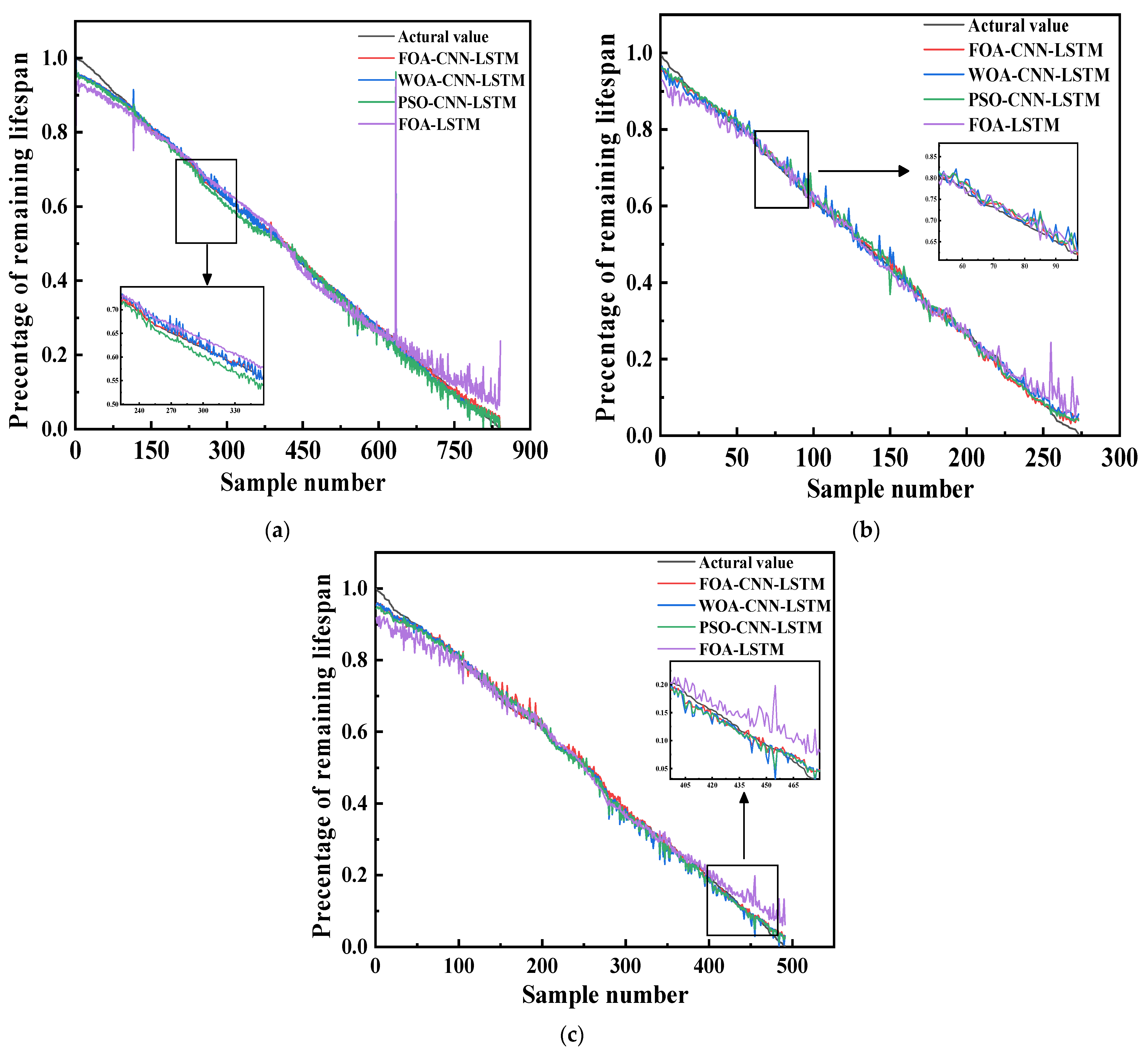
4.3. Test Results
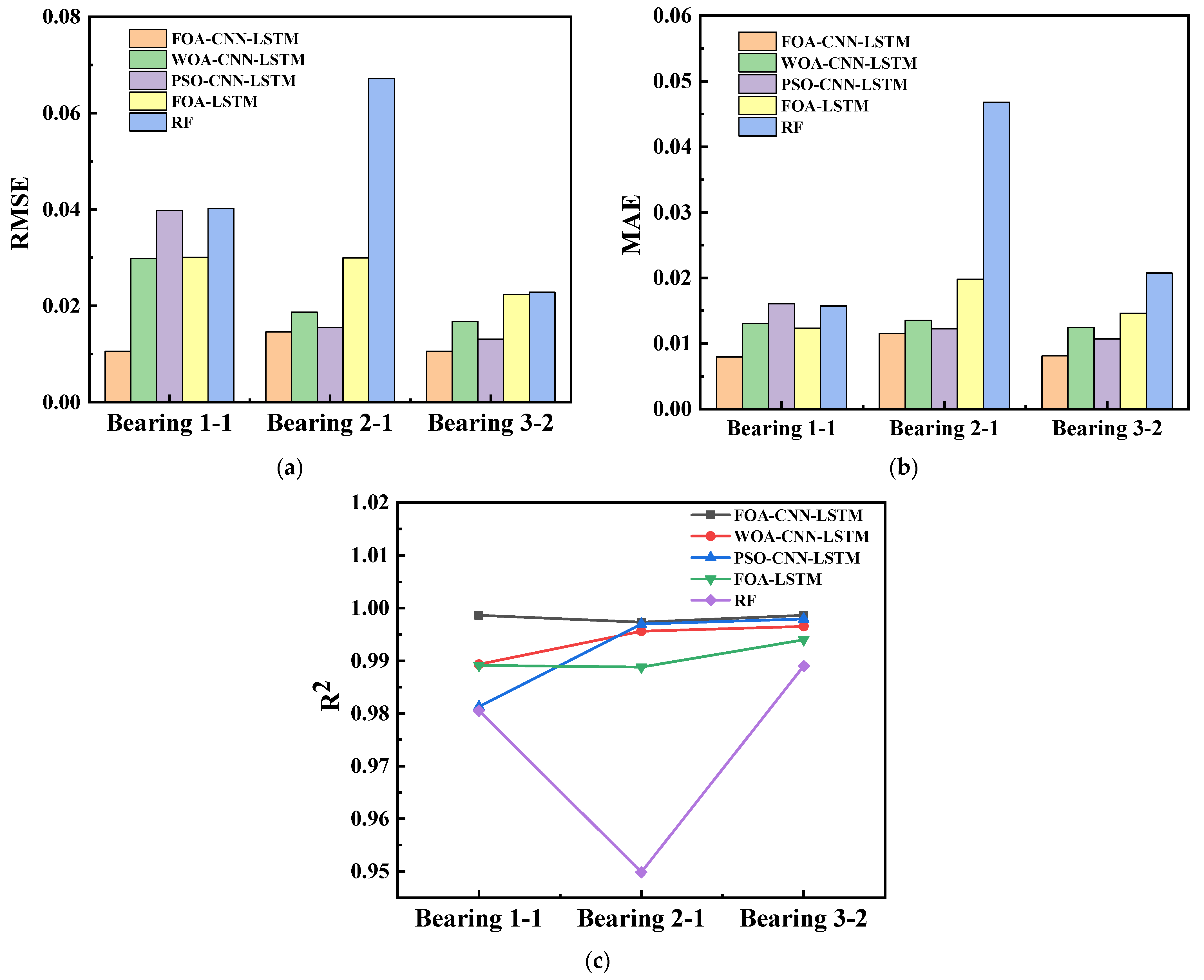
4.4. Contrast Experiments and Comparative Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RUL | Remaining Useful Life |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory Network |
| FOA | Fruit Fly Optimization Algorithm |
| WOA | Whale Optimization Algorithm |
| PSO | Particle Swarm Optimization |
| RF | Random Forest |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| R2 | Coefficient of determination |
| Eri | The percentage of real residual life |
References
- Babu, T.N.; Saraya, J.; Singh, K.; Prabha, D.R. Rolling element bearing fault diagnosis using discrete mayer wavelet and fault classification using machine learning algorithms. J. Vib. Eng. Technol. 2025, 13, 87. [Google Scholar] [CrossRef]
- Mao, W.T.; Liu, Y.M.; Ding, L.; Safian, A.; Liang, X.H. A new structured domain adversarial neural network for transfer fault diagnosis of rolling bearings under different working conditions. IEEE Trans. Instrum. Meas. 2021, 70, 3509013. [Google Scholar] [CrossRef]
- Ma, S.J.; Zhang, X.H.; Yan, K.; Zhu, Y.S.; Hong, J. A study on bearing dynamic features under the condition of multiball-cage collision. Lubricants 2022, 10, 9. [Google Scholar] [CrossRef]
- Cheng, H.; Kong, X.G.; Chen, G.; Wang, Q.B.; Wang, R.B. Transferable convolutional neural network based remaining useful life prediction of bearing under multiple failure behaviors. Measurement 2021, 168, 108286. [Google Scholar] [CrossRef]
- Xu, J.; Duan, S.Y.; Chen, W.W.; Wang, D.F.; Fan, Y.Q. SACGNet: A remaining useful life prediction of bearing with self-attention augmented convolution GRU network. Lubricants 2022, 10, 21. [Google Scholar] [CrossRef]
- Ansean, D.; Dubarry, M.; Devie, A.; Liaw, B.Y.; Garcia, V.M.; Viera, J.C.; Gonzalez, M. Fast charging technique for high power LiFePO4 batteries: A mechanistic analysis of aging. J. Power Sources 2016, 321, 201–209. [Google Scholar] [CrossRef]
- Londhe, N.D.; Arakere, N.K.; Haftka, R.T. Reevaluation of rolling element bearing load-Life equation based on fatigue endurance data. Tribol. Trans. 2015, 58, 815–828. [Google Scholar] [CrossRef]
- Londhe, N.D.; Arakere, N.K.; Subhash, G. Extended hertz theory of contact mechanics for case-hardened steels with implications for bearing fatigue life. J. Tribol. 2018, 140, 021401. [Google Scholar] [CrossRef]
- Mao, W.T.; He, J.L.; Zuo, M.J. Predicting remaining useful life of rolling bearings based on deep feature representation and transfer learning. IEEE Trans. Instrum. Meas. 2020, 69, 1594–1608. [Google Scholar] [CrossRef]
- Xie, G.; Peng, X.; Li, X.; Hei, X.H.; Hu, S.L. Remaining useful life prediction of lithium-ion battery based on an improved particle filter algorithm. Can. J. Chem. Eng. 2020, 98, 1365–1376. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Ni, Y.L.; Li, N.; Lu, S.; Zhang, S.D.; Feng, Z.B.; Wang, J.G. A method based on improved ant lion optimization and support vector regression for remaining useful life estimation of lithium-ion batteries. Energy Sci. Eng. 2019, 7, 2797–2813. [Google Scholar] [CrossRef]
- Ma, G.J.; Zhang, Y.; Cheng, C.; Zhou, B.T.; Hu, P.C.; Yuan, Y. Remaining useful life prediction of lithium-ion batteries based on false nearest neighbors and a hybrid neural network. Appl. Energy 2019, 253, 113626. [Google Scholar] [CrossRef]
- Ma, P.; Li, G.F.; Zhang, H.L.; Wang, C.; Li, X.K. Prediction of remaining useful life of rolling bearings based on multiscale efficient channel attention CNN and bidirectional GRU. IEEE Trans. Instrum. Meas. 2024, 73, 2508413. [Google Scholar] [CrossRef]
- Han, G.D.; Cao, Y.P.; Xu, Z.Q.; Wang, W.Y. Research on the SMIV-1DCNN remaining useful life prediction method for marine gas turbine. J. Eng. Therm. Energy Power 2022, 37, 25–32. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction. Reliab. Eng. Syst. Saf. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Wang, X.; Mao, D.X.; Li, X.D. Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 2021, 173, 108518. [Google Scholar] [CrossRef]
- Liu, Y.; Dan, B.B.; Yi, C.C.; Li, S.H.; Yan, X.G.; Xiao, H. Similarity indicator and CG-CGAN prediction model for remaining useful life of rolling bearings. Meas. Sci. Technol. 2024, 35, 086107. [Google Scholar] [CrossRef]
- Yan, X.; Jin, X.P.; Jiang, D.; Xiang, L. Remaining useful life prediction of rolling bearings based on CNN-GRU-MSA with multi-channel feature fusion. Nondestruct. Test. Eval. 2024, 1–26. [Google Scholar] [CrossRef]
- Deng, L.F.; Li, W.; Yan, X.H. An intelligent hybrid deep learning model for rolling bearing remaining useful life prediction. Nondestruct. Test. Eval. 2024, 1–28. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Guo, J.Y.; Wang, J.; Yang, Y.L.; Dai, L.; Huang, C.G.; Wan, J.L. A deep learning based health indicator construction and fault prognosis with uncertainty quantification for rolling bearings. Meas. Sci. Technol. 2023, 34, 105105. [Google Scholar] [CrossRef]
- He, J.L.; Wu, C.C.; Luo, W.; Qian, C.H.; Liu, S.Y. Remaining useful life prediction and uncertainty quantification for bearings based on cascaded multiscale convolutional neural network. IEEE Trans. Instrum. Meas. 2024, 73, 3506713. [Google Scholar] [CrossRef]
- Yang, B.Y.; Liu, R.N.; Zio, E. Remaining useful life prediction based on a double-convolutional neural network architecture. IEEE Trans. Ind. Electron. 2019, 66, 9521–9530. [Google Scholar] [CrossRef]
- Wu, C.B.; You, A.G.; Ge, M.F.; Liu, J.; Zhang, J.C.; Chen, Q. A novel multi-scale gated convolutional neural network based on informer for predicting the remaining useful life of rotating machinery. Meas. Sci. Technol. 2024, 35, 126138. [Google Scholar] [CrossRef]
- Liu, Z.H.; Meng, X.D.; Wei, H.L.; Chen, L.; Lu, B.L.; Wang, Z.H.; Chen, L. A regularized LSTM method for predicting remaining useful life of rolling bearings. Int. J. Autom. Comput. 2021, 18, 581–593. [Google Scholar] [CrossRef]
- Li, L.Y.; Wang, H.R.; Zhu, G.F. Remaining useful life prediction of turbofan engine based on improved 1D-CNN and LSTM. J. Eng. Therm. Energy Power 2023, 38, 194–202. [Google Scholar] [CrossRef]
- Marei, M.; Li, W.D. Cutting tool prognostics enabled by hybrid CNN-LSTM with transfer learning. Int. J. Adv. Manuf. Technol. 2022, 118, 817–836. [Google Scholar] [CrossRef]
- Lei, N.; Tang, Y.F.; Li, A.; Jiang, P.C. Research on the remaining life prediction method of rolling bearings based on optimized TPA-LSTM. Machines 2024, 12, 224. [Google Scholar] [CrossRef]
- Song, F.; Wang, Z.H.; Liu, X.Q.; Ren, G.A.; Liu, T. Remaining life prediction of rolling bearings with secondary feature selection and BSBiLSTM. Meas. Sci. Technol. 2024, 35, 076127. [Google Scholar] [CrossRef]
- Yao, X.J.; Zhu, J.J.; Jiang, Q.S.; Yao, Q.; Shen, Y.H.; Zhu, Q.X. RUL prediction method for rolling bearing using convolutional denoising autoencoder and bidirectional LSTM. Meas. Sci. Technol. 2024, 35, 035111. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, J.W.; Li, C.; He, Z.Q.; Wang, Z.M. A rul prediction method of rolling bearings based on degradation detection and deep BiLSTM. Electron. Res. Arch. 2024, 32, 3145–3161. [Google Scholar] [CrossRef]
- Zhang, X.G.; Yang, J.Z.; Yang, X.M. Residual life prediction of rolling bearings based on a CEEMDAN algorithm fused with CNN-attention-based bidirectional LSTM modeling. Processes 2024, 12, 8. [Google Scholar] [CrossRef]
- Yang, L.; Jiang, Y.B.; Zeng, K.; Peng, T. Rolling bearing remaining useful life prediction based on CNN-VAE-MBiLSTM. Sensors 2024, 24, 2992. [Google Scholar] [CrossRef]
- Wei, L.P.; Peng, X.Y.; Cao, Y.P. Enhanced fault diagnosis of rolling bearings using an improved inception-lstm network. Nondestruct. Test. Eval. 2024, 1–20. [Google Scholar] [CrossRef]
- Sun, W.Q.; Wang, Y.; You, X.Y.; Zhang, D.; Zhang, J.Y.; Zhao, X.H. Optimization of variational mode decomposition-convolutional neural network-bidirectional long short term memory rolling bearing fault diagnosis model based on improved dung beetle optimizer algorithm. Lubricants 2024, 12, 239. [Google Scholar] [CrossRef]
- Yang, J.Z.; Zhang, X.G.; Liu, S.; Yang, X.M.; Li, S.F. Rolling bearing residual useful life prediction model based on the particle swarm optimization-optimized fusion of convolutional neural network and bidirectional long-short-term memory-multihead self-attention. Electronics 2024, 13, 2120. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.C.; Feng, K. Data-Driven Prognostic Scheme for Bearings Based on a Novel Health Indicator and Gated Recurrent Unit Network. IEEE Trans. Industr. Inform. 2023, 19, 1301–1311. [Google Scholar] [CrossRef]
- Huang, K.; Jia, G.Z.; Jiao, Z.Y.; Luo, T.Y.; Wang, Q.; Cai, Y.J. MSTAN: Multi-scale spatiotemporal attention network with adaptive relationship mining for remaining useful life prediction in complex systems. Meas. Sci. Technol. 2024, 35, 125019. [Google Scholar] [CrossRef]
- Cui, L.L.; Xiao, Y.C.; Liu, D.D.; Han, H.G. Digital twin-driven graph domain adaptation neural network for remaining useful life prediction of rolling bearing. Reliab. Eng. Syst. Saf. 2024, 245, 109991. [Google Scholar] [CrossRef]
- Bienefeld, C.; Kirchner, E.; Vogt, A.; Kacmar, M. On the importance of temporal information for remaining useful life prediction of rolling bearings using a random forest regressor. Lubricants 2022, 10, 67. [Google Scholar] [CrossRef]
- Lu, X.C.; Yao, X.J.; Jiang, Q.S.; Shen, Y.H.; Xu, F.Y.; Zhu, Q.X. Remaining useful life prediction model of cross-domain rolling bearing via dynamic hybrid domain adaptation and attention contrastive learning. Comput. Ind. 2024, 164, 104172. [Google Scholar] [CrossRef]
- Li, C.; Chen, H.X.; Han, Y.; Zuo, S.J.; Zhao, L.G. A survey of convolution neural networks in deep learning algorithm. J. Electron. Test. 2018, 23, 61–62. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.S.; Hu, C.H.; Zhang, J.X. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Wang, H.Y.; Song, W.Q.; Zio, E.; Kudreyko, A.; Zhang, Y.J. Remaining useful life prediction for lithium-ion batteries using fractional brownian motion and fruit-fly optimization algorithm. Measurement 2020, 161, 2069–2080. [Google Scholar] [CrossRef]
- Ren, L.; Sun, Y.Q.; Wang, H.; Zhang, L. Prediction of bearing remaining useful life with deep convolution neural network. IEEE Access 2018, 6, 13041–13049. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, PHM’12, Denver, CO, USA, 18–21 June 2012; pp. 1–8. [Google Scholar]

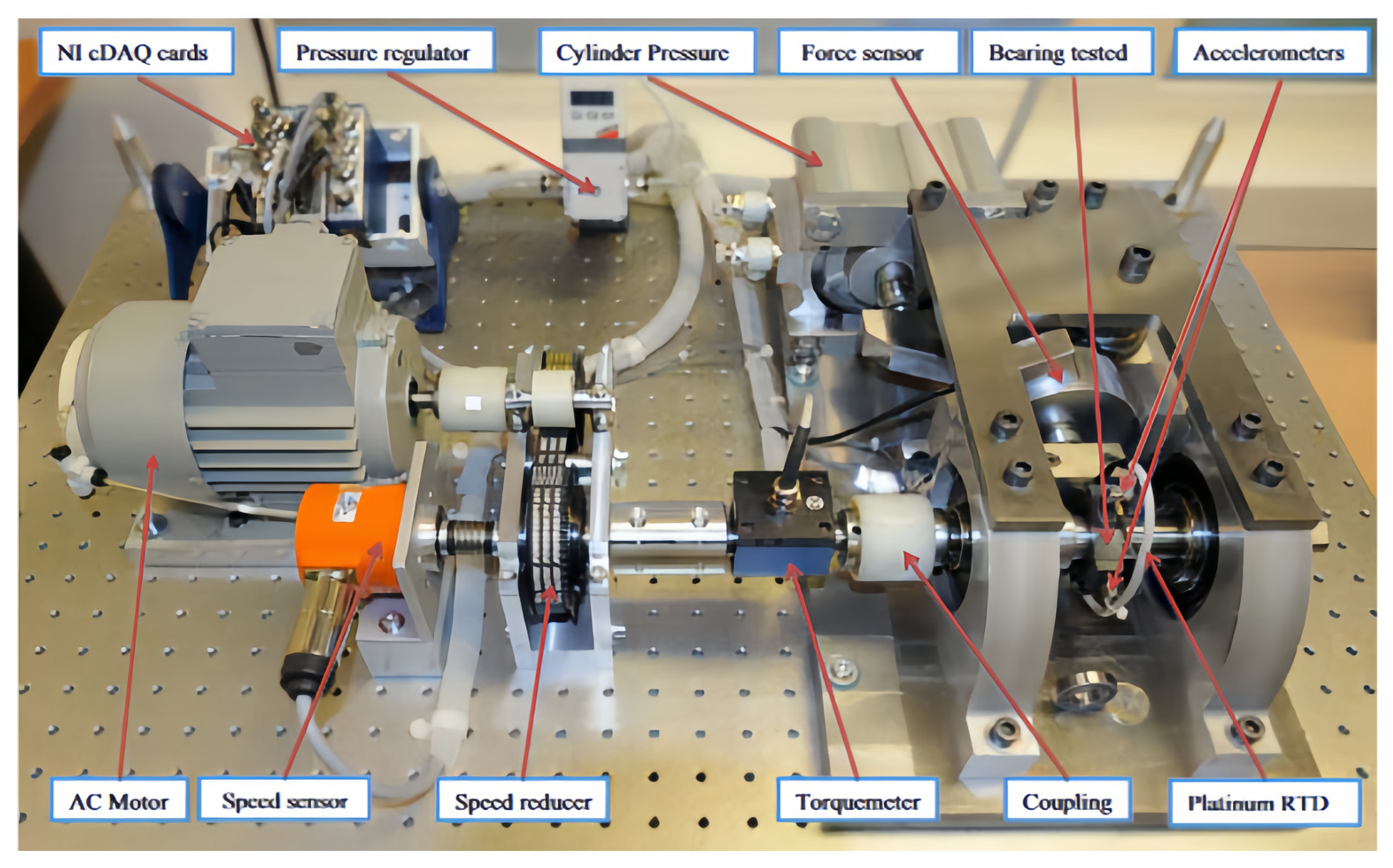
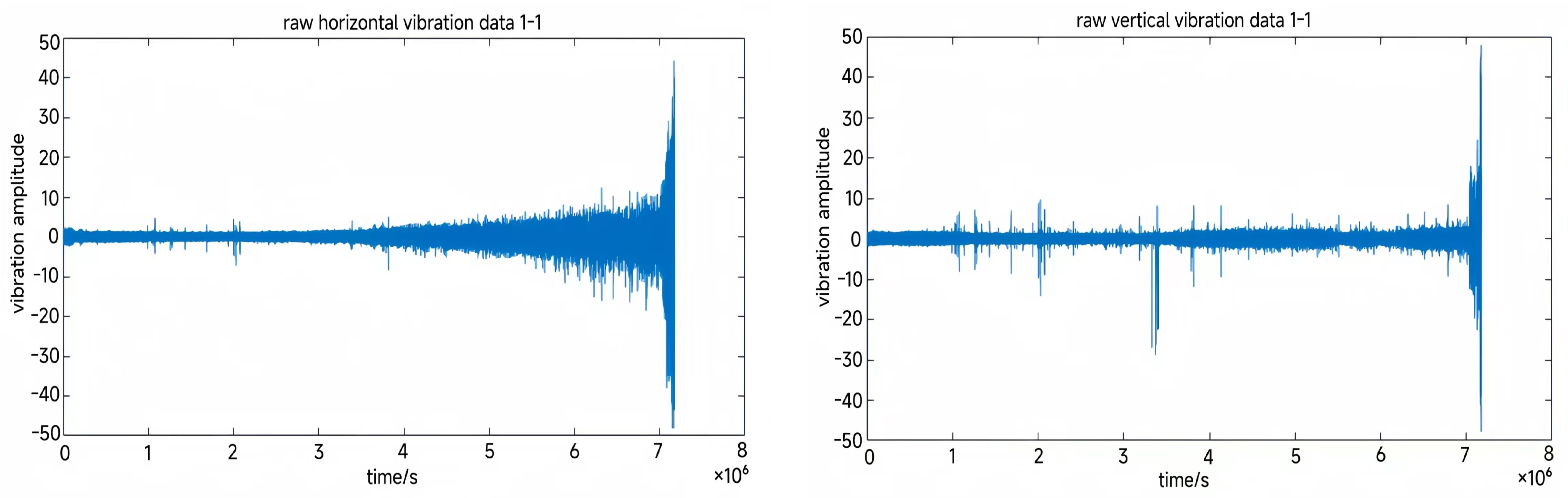
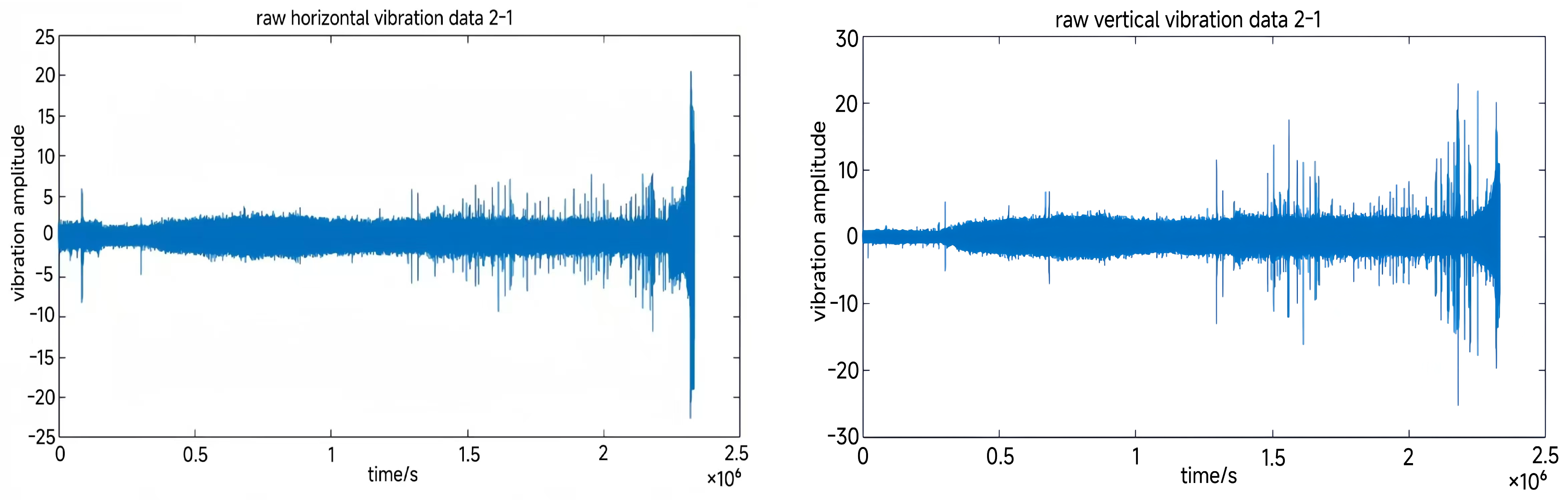





| Operating Condition | Rolling Bearing Number | Load/N | Rotation Speed/(r·min−1) |
|---|---|---|---|
| Operating condition 1 | 1-1, 1-2, 1-3 1-4, 1-5, 1-6, 1-7 | 4000 | 1800 |
| Operating condition 2 | 2-1, 2-2, 2-3 2-4, 2-5, 2-6, 2-7 | 4200 | 1650 |
| Operating condition 3 | 3-1, 3-2, 3-3 | 5000 | 1500 |
| Methods | Accuracy | R2 | ||||
|---|---|---|---|---|---|---|
| 1-1 | 2-1 | 3-2 | 1-1 | 2-1 | 3-2 | |
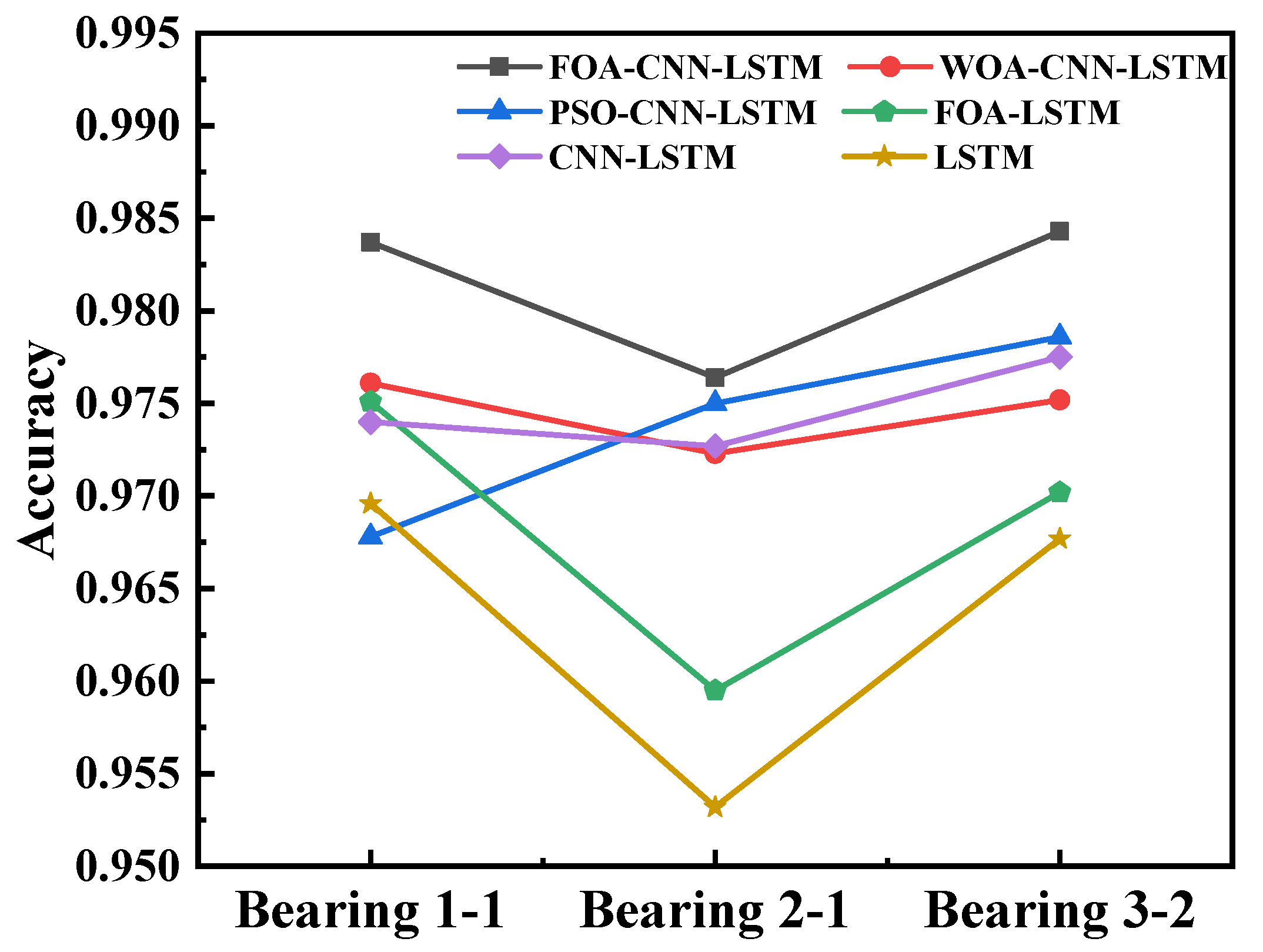
| FOA-CNN-LSTM | 98.24% | 97.63% | 98.39% | 0.99228 | 0.99717 | 0.99876 |
| WOA-CNN-LSTM | 97.61% | 97.28% | 97.56% | 0.99372 | 0.99533 | 0.99701 |
| PSO-CNN-LSTM | 97.24% | 97.57% | 98.00% | 0.9965 | 0.99724 | 0.99817 |
| FOA-LSTM | 97.62% | 95.87% | 97.21% | 0.99338 | 0.98961 | 0.99522 |
| CNN-LSTM | 97.61% | 97.42% | 97.70% | 0.99401 | 0.99665 | 0.99734 |
| LSTM | 97.41% | 95.34% | 96.21% | 0.99012 | 0.98789 | 0.99325 |
| RF | 96.84% | 94.54% | 96.88% | 0.99109 | 0.98024 | 0.98901 |
| Methods | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| 1-1 | 2-1 | 3-2 | 1-1 | 2-1 | 3-2 | |
| FOA-CNN-LSTM | 0.025305 | 0.015486 | 0.010159 | 0.0088953 | 0.01196 | 0.007936 |
| WOA-CNN-LSTM | 0.022858 | 0.019884 | 0.015851 | 0.012085 | 0.013709 | 0.012148 |
| PSO-CNN-LSTM | 0.017006 | 0.015268 | 0.012326 | 0.013817 | 0.012232 | 0.009977 |
| FOA-LSTM | 0.023476 | 0.029645 | 0.019948 | 0.011934 | 0.020793 | 0.01404 |
| CNN-LSTM | 0.022137 | 0.016842 | 0.014987 | 0.011876 | 0.012994 | 0.011439 |
| LSTM | 0.028483 | 0.032003 | 0.024021 | 0.01296 | 0.023501 | 0.018265 |
| RF | 0.027249 | 0.039869 | 0.020742 | 0.023338 | 0.027362 | 0.015766 |
| Methods | Accuracy | R2 | ||||
|---|---|---|---|---|---|---|
| 1-1 | 2-1 | 3-2 | 1-1 | 2-1 | 3-2 | |
| FOA-CNN-LSTM | 98.37% | 97.64% | 98.43% | 0.99866 | 0.99734 | 0.99865 |
| WOA-CNN-LSTM | 97.32% | 97.23% | 97.52% | 0.98933 | 0.99564 | 0.99655 |
| PSO-CNN-LSTM | 96.78% | 97.50% | 97.86% | 0.98131 | 0.99699 | 0.99796 |
| FOA-LSTM | 97.51% | 95.95% | 97.02% | 0.98915 | 0.98881 | 0.99401 |
| CNN-LSTM | 97.40% | 97.27% | 97.75% | 0.99108 | 0.99623 | 0.99737 |
| LSTM | 96.96% | 95.32% | 96.77% | 0.98847 | 0.98823 | 0.99284 |
| RF | 95.37% | 90.56% | 95.73% | 0.98055 | 0.94986 | 0.98901 |
| Methods | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| 1-1 | 2-1 | 3-2 | 1-1 | 2-1 | 3-2 | |
| FOA-CNN-LSTM | 0.010599 | 0.014596 | 0.010652 | 0.0079401 | 0.011534 | 0.0080978 |
| WOA-CNN-LSTM | 0.029818 | 0.018707 | 0.016778 | 0.01306 | 0.013562 | 0.012486 |
| PSO-CNN-LSTM | 0.039788 | 0.015543 | 0.01307 | 0.016042 | 0.012219 | 0.010699 |
| FOA-LSTM | 0.030077 | 0.029971 | 0.022387 | 0.012354 | 0.019813 | 0.01463 |
| CNN-LSTM | 0.029187 | 0.0174 | 0.014599 | 0.013235 | 0.013373 | 0.011311 |
| LSTM | 0.031582 | 0.030729 | 0.024021 | 0.014993 | 0.022898 | 0.017483 |
| RF | 0.040264 | 0.067222 | 0.022823 | 0.023338 | 0.046827 | 0.020742 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Zhou, H.; Jin, M.; Jin, Z.; Wang, Q.; Mu, Y.; Hong, Z. RUL Prediction of Rolling Bearings Based on Fruit Fly Optimization Algorithm Optimized CNN-LSTM Neural Network. Lubricants 2025, 13, 81. https://doi.org/10.3390/lubricants13020081
Shen J, Zhou H, Jin M, Jin Z, Wang Q, Mu Y, Hong Z. RUL Prediction of Rolling Bearings Based on Fruit Fly Optimization Algorithm Optimized CNN-LSTM Neural Network. Lubricants. 2025; 13(2):81. https://doi.org/10.3390/lubricants13020081
Chicago/Turabian StyleShen, Jiaping, Haiting Zhou, Muda Jin, Zhongping Jin, Qiang Wang, Yanchun Mu, and Zhiming Hong. 2025. "RUL Prediction of Rolling Bearings Based on Fruit Fly Optimization Algorithm Optimized CNN-LSTM Neural Network" Lubricants 13, no. 2: 81. https://doi.org/10.3390/lubricants13020081
APA StyleShen, J., Zhou, H., Jin, M., Jin, Z., Wang, Q., Mu, Y., & Hong, Z. (2025). RUL Prediction of Rolling Bearings Based on Fruit Fly Optimization Algorithm Optimized CNN-LSTM Neural Network. Lubricants, 13(2), 81. https://doi.org/10.3390/lubricants13020081





