Intelligent Analysis and Optimization of Lubrication Status Factor Based on Dynamically Loaded Roll Gap in Cold Strip Rolling
Abstract
1. Introduction
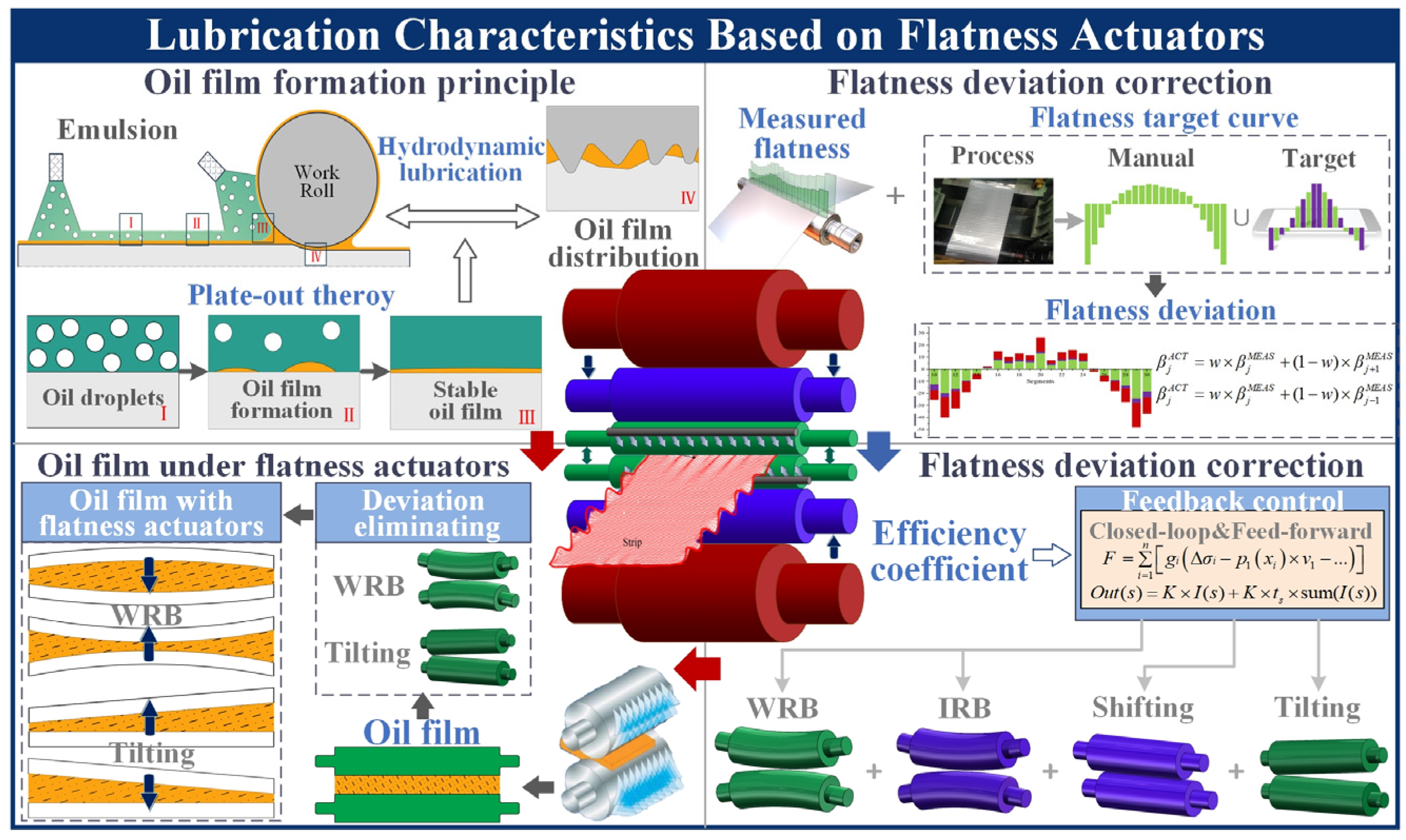
- Based on the high-order flatness target, the online flatness deviation correction model for the intermediate roll bending, work roll bending, and tilting roll has been established by considering the influence of the rolling process parameters and the different flatness actuators and has been applied to the rolling production;
- Based on the Reynolds equation and the oil film thickness characteristics in the inlet zone, a model for characterizing the instantaneous oil film thickness at any position in the work zone according to the profile of the loaded roll gap has been derived;
- Based on the symbolic regression, the relationship between the LSC and the instantaneous oil film thickness, work roll bending, and tilting roll in the rolling force model of the final stand is established, and the influence of each variable on the LSC is revealed;
- The research method in the paper can ensure that the setting value of the rolling force in the final stand is closer to the actual rolling state and can improve the accuracy of the strip gauge.
2. Calculation Model
2.1. Flatness Actuators Setting Model
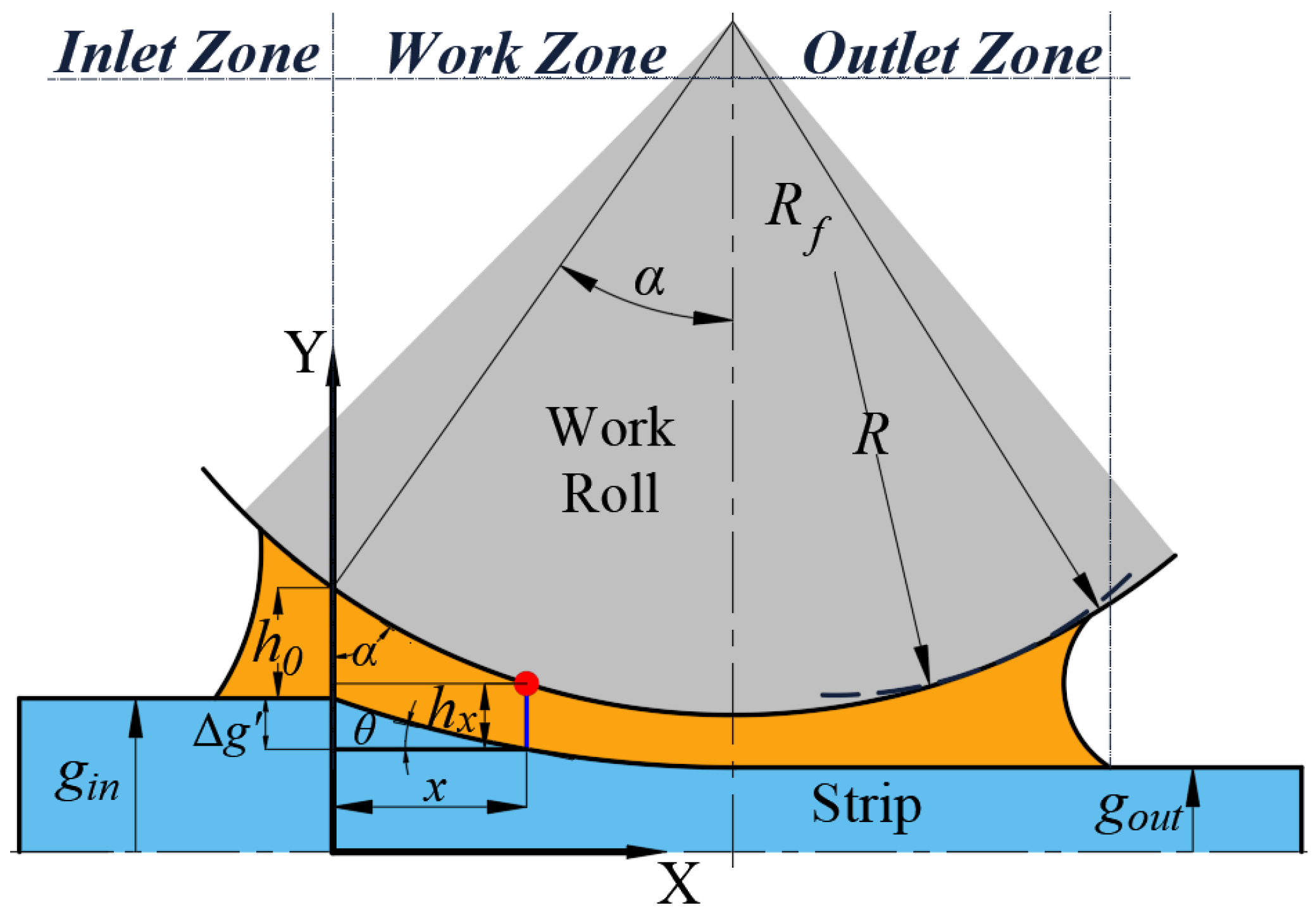
2.2. Instantaneous Oil Film Thickness in Work Zone
2.3. Lubrication Status Factor
3. AI-Based Optimization Methods Modeling
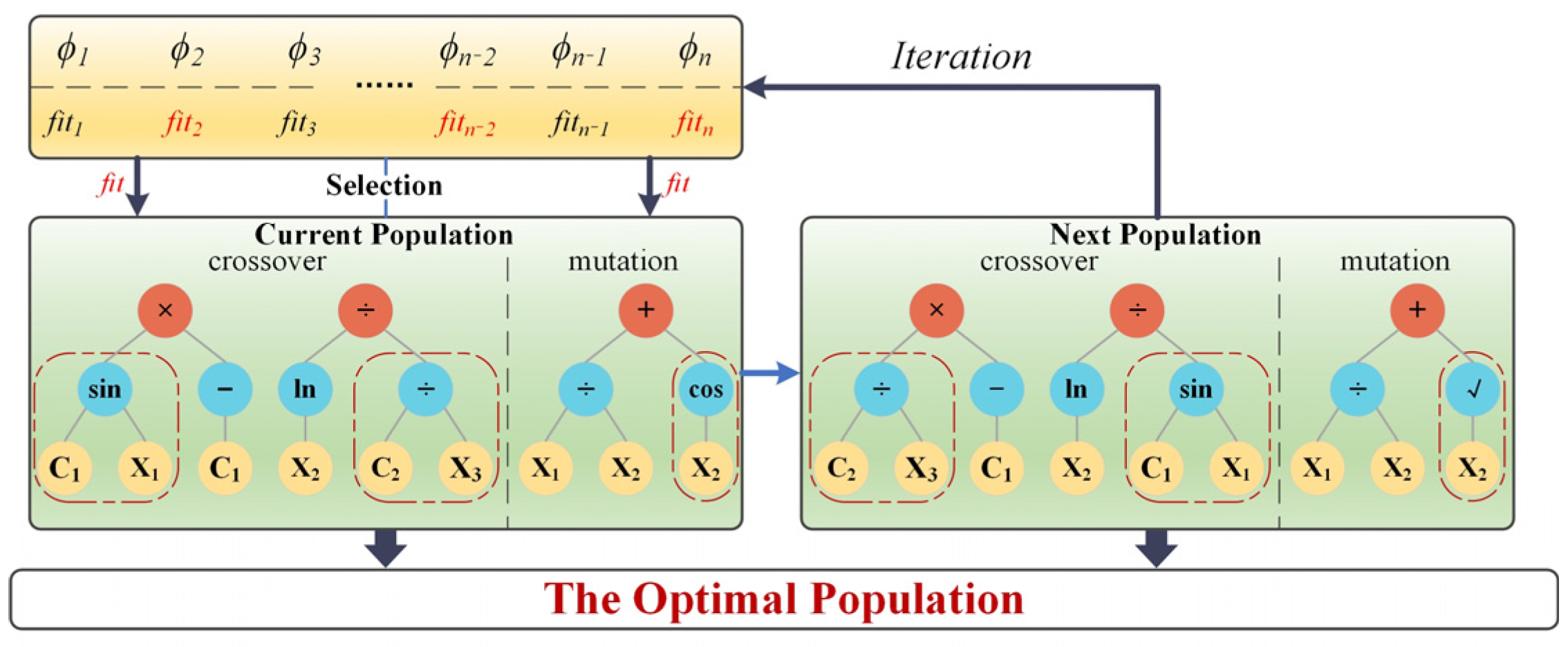
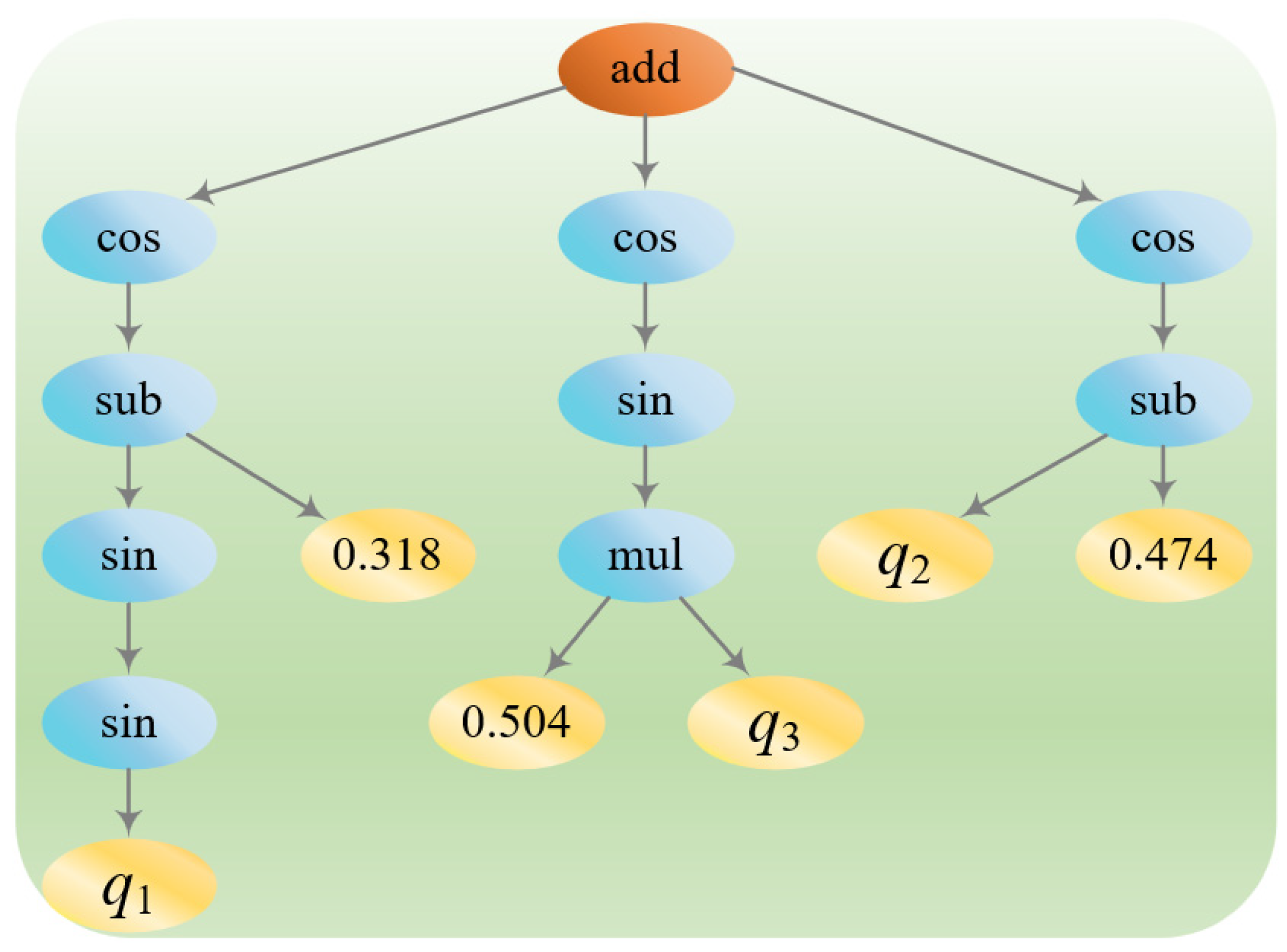
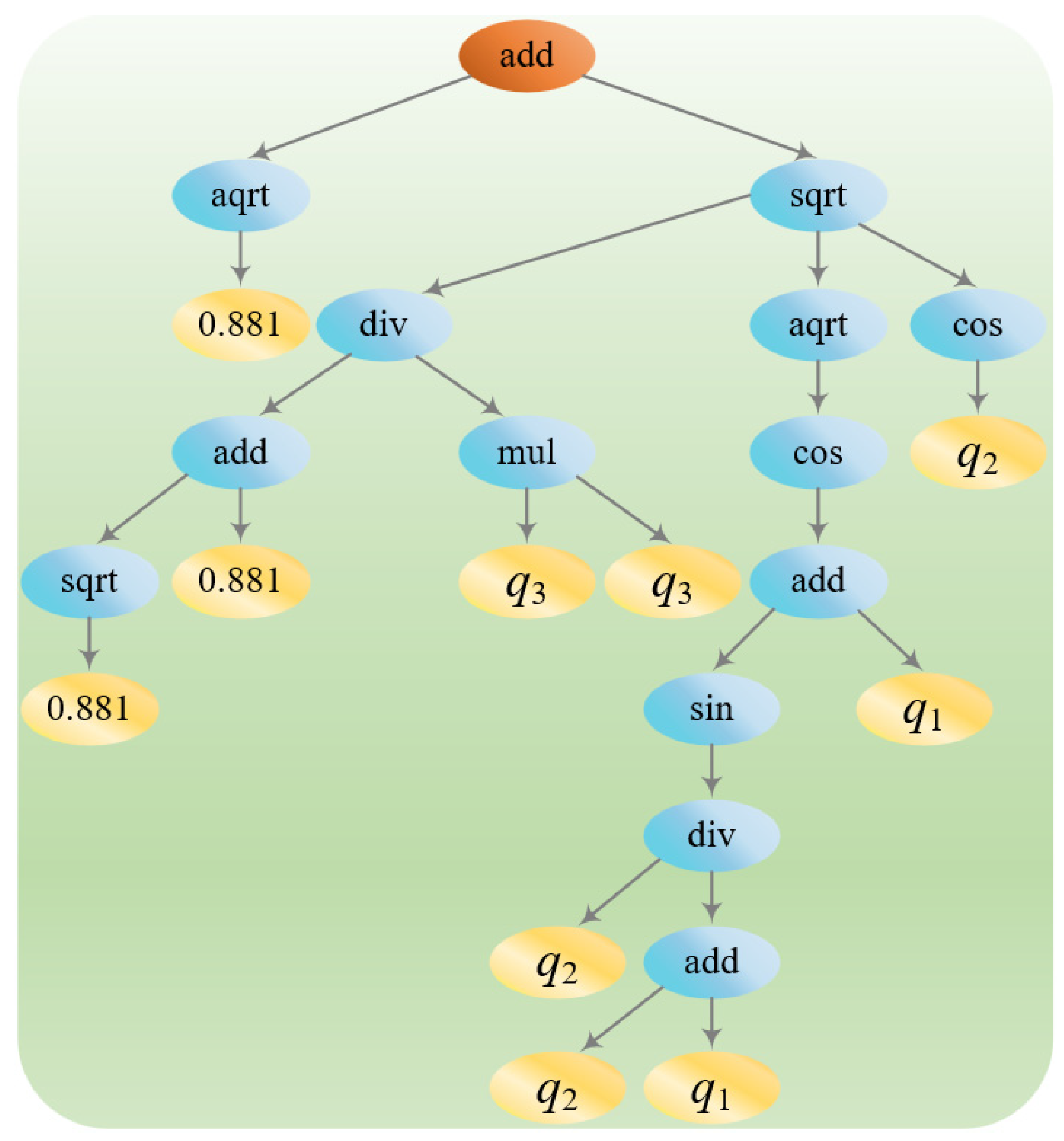
3.1. Symbolic Regression
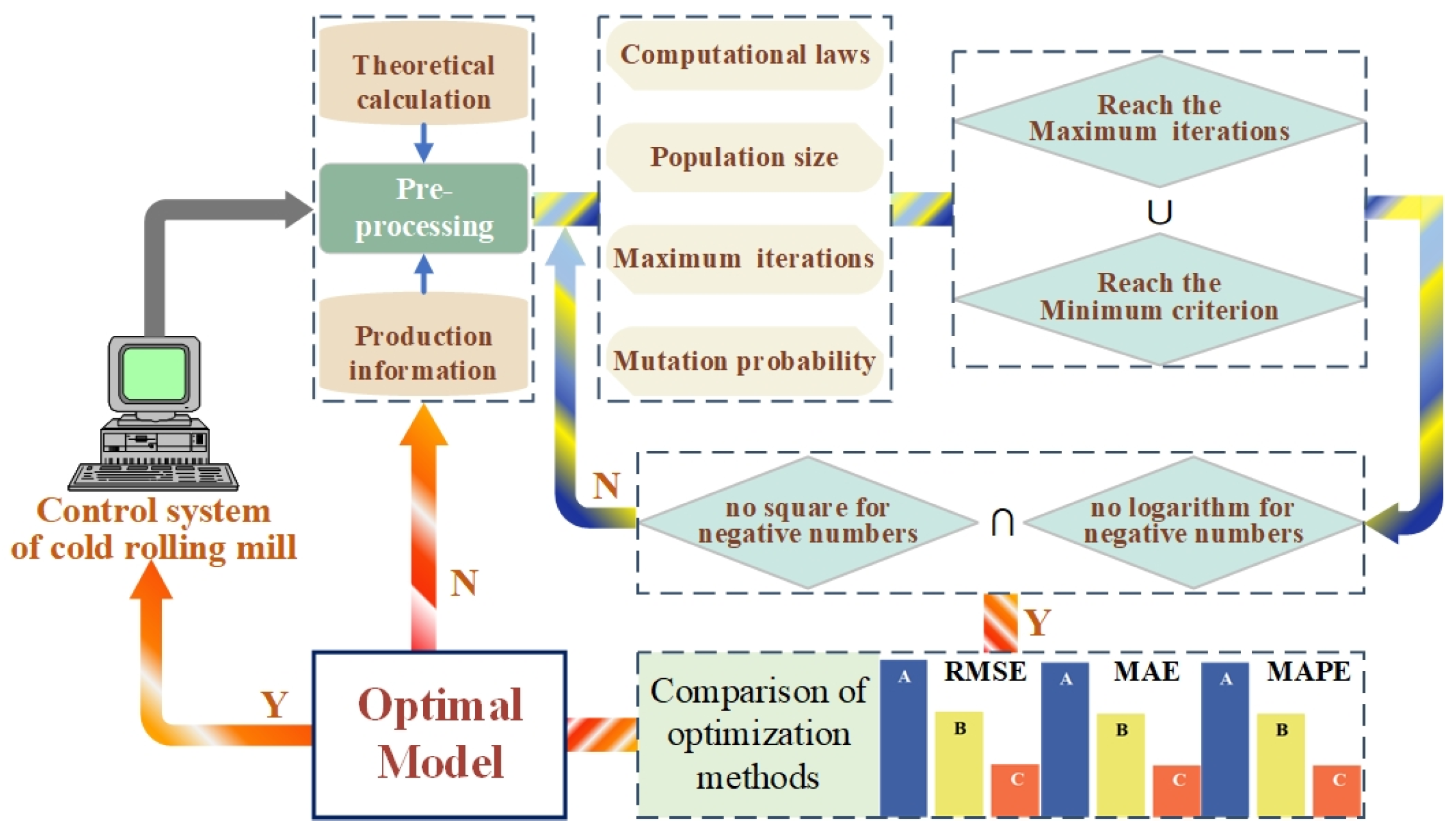
3.2. Analysis Structure
3.3. Target Variables and Pre-Processing
3.4. Evaluation Strategy
- Extract or compute the training data for selected variables and implement preprocessing for the training data;
- Establish the symbolic regression analysis architecture based on the genetic algorithm, determine initial values for the number of populations, the maximum number of iterations, and the variation probability in the architecture, and formulate the initial law of calculation;
- The analysis results are obtained when the number of iterations reaches the maximum value or the fitness reaches the required value;
- Adjust the maximum number of iterations and the optimal fitness threshold based on the results of Step 3 and adjust the law of calculation by analyzing the function structure of the results;
- Check the function’s structure to ensure no structure for logarithms and squares for negative numbers;
- Repeat Step 3 to Step 5 until the optimum analysis result is obtained;
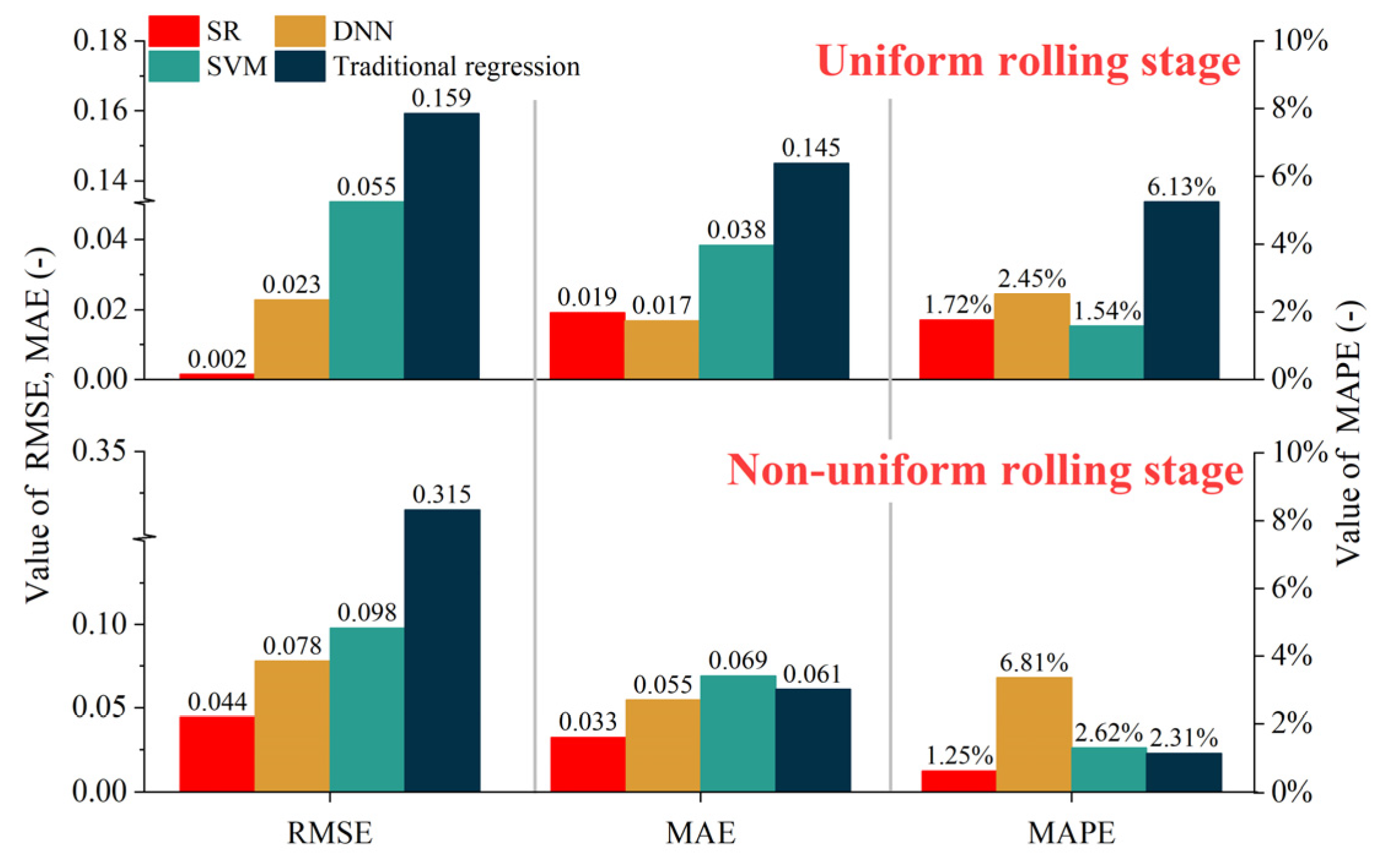
- Select several optimization methods in the same and different categories as symbolic regression and show the applicability of the selected analysis results by RMSE, MAE, and MAPE;
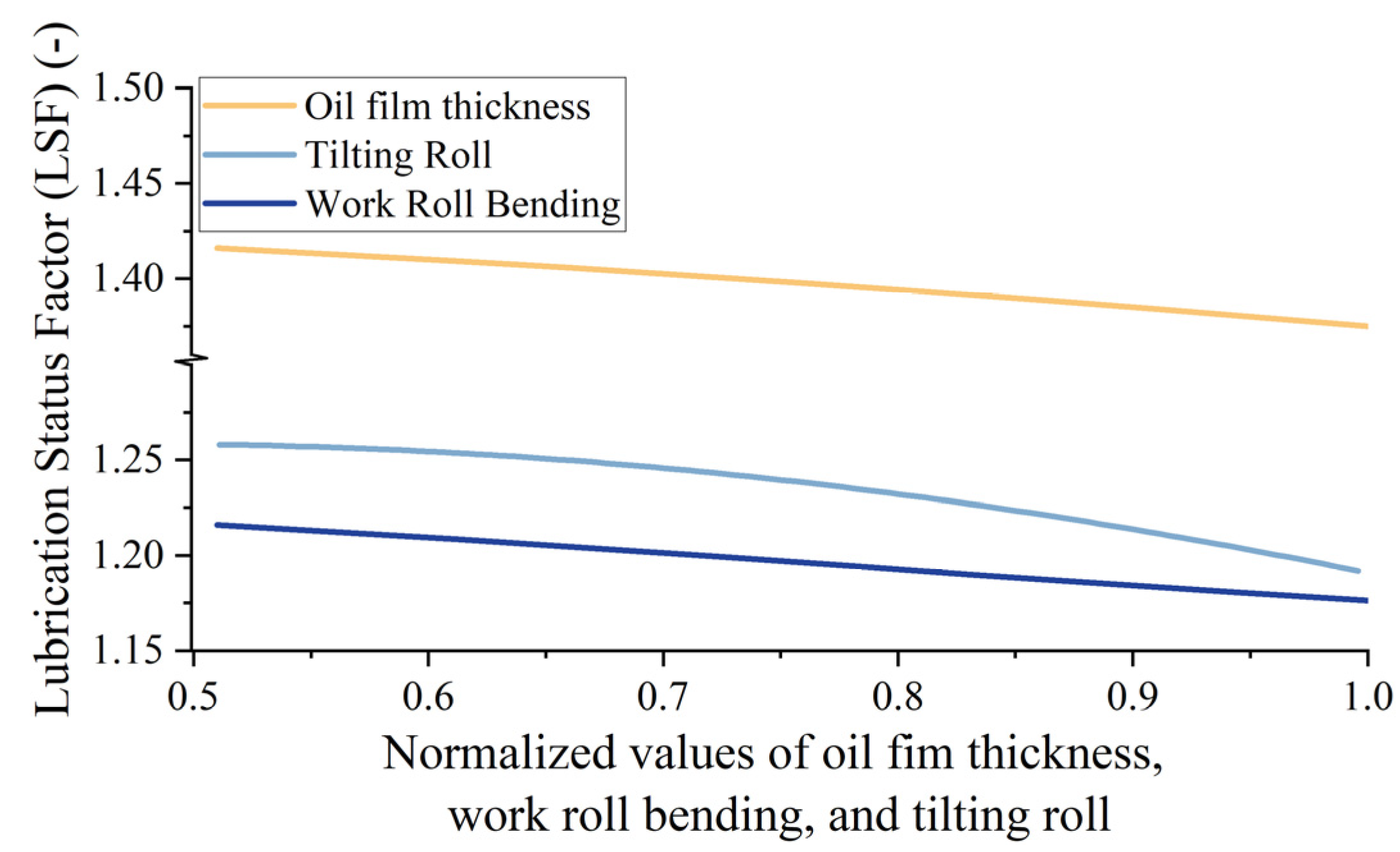
- The influence of the variables in the optimization results on the analytical objectives is analyzed by single-factor analysis.
4. Analysis and Applications
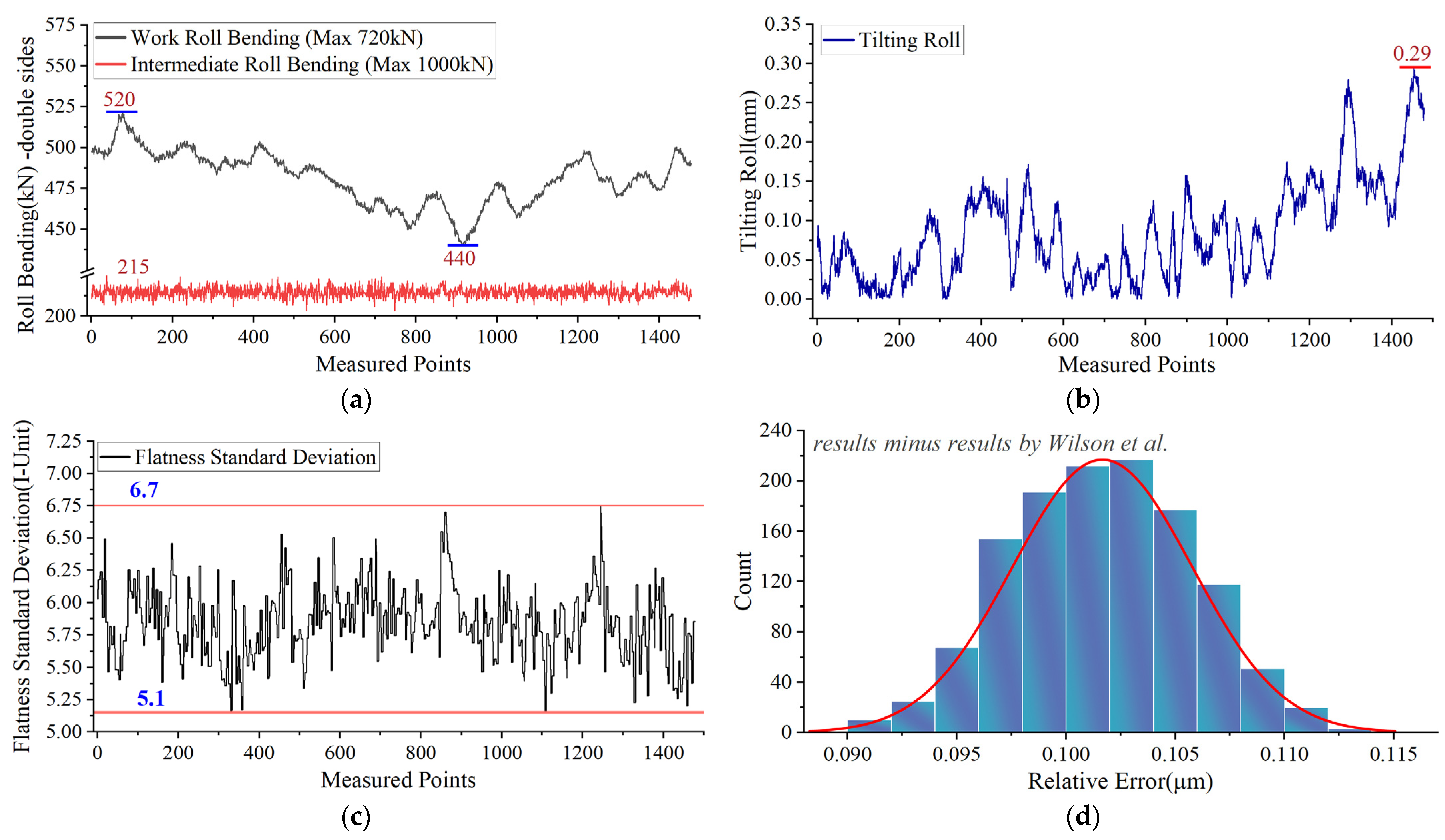
4.1. Results and Analysis
- Computational rules. Computational laws define the operators and algorithms available in symbolic regression and are determined by the nature of the data and the context of the problem, directly affecting the search space of symbolic regression. A restricted computational law can prevent the model from capturing the complex patterns of the data, and a broad computational law can lead to excessive computational overhead and overfitting;
- Population size. The population size indicates the number of candidate solutions used for selection, crossover, and mutation in each generation, and the choice is based on a combination of computational cost and search capability. A too-small population tends to cause the optimization model to fall into a local optimum solution, and a too-large population leads to slower convergence of the optimization model;
- Maximum number of iterations. The maximum number of iterations is the maximum number of optimizations that can be performed and is chosen based on the complexity of the data and computational resources. Too few iterations can leave the search unfinished and miss the best solution, and too many iterations can lead to over-computation and waste of resources;
- Crossover. Crossover is the generation of new individuals by combining the expression structures of two-parent individuals. In symbolic regression, crossover usually generates new expressions by swapping certain subtrees of the parents. Crossover patterns can affect the algorithm’s ability to jump in the search space, and poor choices may result in expressions of the child individuals being too similar, leading to a loss of diversity and thus affecting the optimization process;
- Mutation. Mutation is the process of increasing the diversity of the search space by randomly modifying some part of the mathematical expression represented by the mutation probability. The mutation probability controls the likelihood that each individual will make a mutation. Mutation probability is generally low to prevent too frequent random changes from destroying existing good genes; too low a mutation probability tends to make the model converge prematurely, and too high a mutation probability can lead to too random a search process and loss of convergence;
- Training set ratio. The training set ratio refers to the proportion of data selected from the overall data set for model training, generally 70% to 80% of the total data set. Too small a training set ratio will cause the optimization model to be under fitted and unable to learn the full picture of the data, while too large a training set ratio will cause the model to overfit the training data and reduce its prediction ability for new data;
- Test set ratio. The proportion of the test set refers to the appropriate proportion of data from the total data set used to test the model effect; the test set does not participate in the training of the model and is only used to evaluate the performance of the model, generally 20% to 30% of the total data set. Too small a test set will lead to unreliable evaluation results and fail to accurately reflect the generalization ability of the model, while too large a test set will lead to insufficient training data and affect the learning effect of the model.
- Selection and processing of analyzed data: Since the calculation in Section 2 has included key basic rolling information such as thickness, width, and instantaneous viscosity of the lubricant and is centered on the research theme of this paper, the analyzed variables are only selected as oil film thickness, work roll bending, and tilting roll, to avoid the coupling between the variables and the occurrence of the overfitting phenomenon. Based on the on-site investigation, a few outliers were also eliminated to ensure the consistency of the data characteristics;
- Parameter setting of the analytical model: select the universal and representative algorithms. Meanwhile, the initial value of the model parameters is set to the value that can be obtained with higher accuracy and less overfitting according to the research experience of scholars [45], and some parameters are adjusted appropriately to improve the accuracy of the analysis based on the unique data characteristics in this paper;
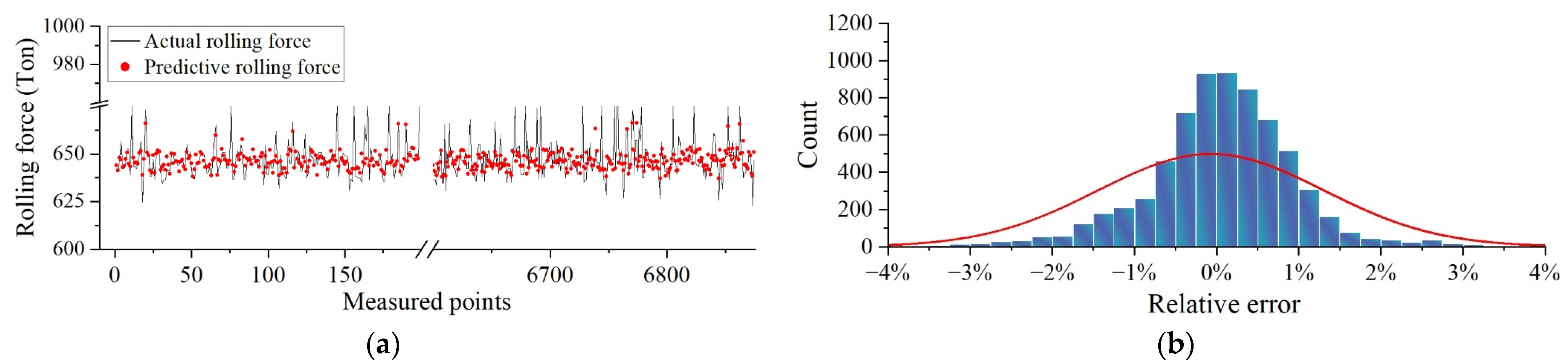
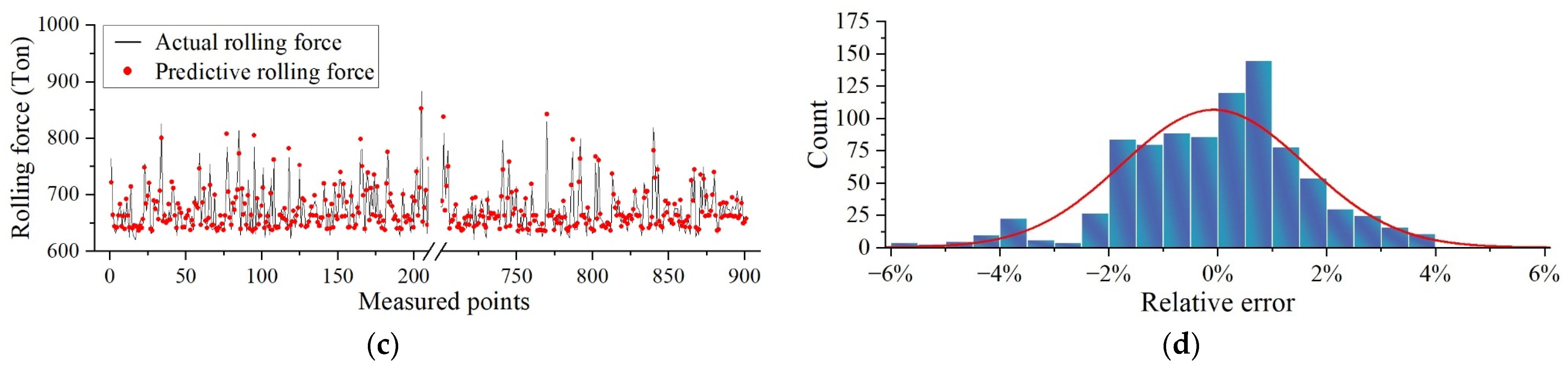
- Validation of analysis results: data other than the training and validation sets are added to validate the accuracy of the results and the prediction trends and to check whether the model has an overfitting trend.
4.2. Experimental Validation
5. Conclusions
- Based on the research results of the high-order flatness target characteristics and considering the mutual influence between each flatness actuator, the flatness deviation correction model of work roll bending, intermediate roll bending, and tilting roll based on the width of the strip, after rolling thickness, rolling force, and intermediate roll transverse shifting is established, and served as the basic data for the AI-based optimization analysis of lubrication status factor;
- Based on the hydrodynamic lubrication and the geometrical characteristics of the loaded roll gap, the geometrical characterization equation of the oil film thickness at any position within the work zone is derived from Reynolds’ equation and also served as the basic data for AI-based optimization analysis of lubrication status factor;
- The pre-treatment method of analyzed data is determined by summarizing and interpreting symbolic regression’s form, principle, and composition. The explicit characterization equations between the lubrication status factor and the oil film thickness, the work roll bending, and the tilting roll are constructed according to the characteristics of the strip rolling process in the uniform rolling stage and the non-uniform rolling stage, respectively;
- The error frequency distribution characteristics discuss the accuracy and superiority of the research results, prediction trend analysis, RMSE, MAE, and MAPE. The influence of the work roll bending and tilting roll in the flatness actuators on the lubrication characteristics in the cold strip rolling is verified by combining the theoretical and experimental analyses. The reasons for the above-influencing characteristics are explained based on the hydrodynamic lubrication.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| width of strip | mm | |
| target strip gauge | mm | |
| initial strip gauge | mm | |
| reduction | mm | |
| instantaneous reduction | mm | |
| Elastic modulus of work roll | MPa | |
| Poisson ratio of work roll | - | |
| bite angle | rad | |
| the angle based on | rad | |
| change rate of | rad/s | |
| reduction rate | - | |
| Yield stress of strip | MPa | |
| rolling force | kN | |
| the rolling force of the final stand | kN | |
| oil film pressure | MPa | |
| intermediate roll transverse shifting of the final stand | mm | |
| oil film thickness in the work zone | μm | |
| oil film thickness in the inlet zone | μm | |
| change rate of | μm | |
| coefficient of pressure-viscosity | - | |
| initial emulsion viscosity | mm2/s | |
| instantaneous lubricant viscosity | mm2/s | |
| contact arc length | mm | |
| flattening radius of the work roll | mm | |
| radius of work roll | mm | |
| coefficient of friction between strip and work roll | - | |
| coefficient of lubrication factor | - | |
| coefficient of deformation resistance | - | |
| back tension stress | MPa | |
| forward tension stress | MPa | |
| correction of flatness deviation for work roll bending | kN | |
| correction of flatness deviation for intermediate roll bending | kN | |
| correction of flatness deviation for tilting roll | mm |
References
- Ojeda-Lopez, A.; Botana-Galvin, M.; Gonzalez-Rovira, L.; Botana, F.J. Numerical Simulation as a Tool for the Study, Development, and Optimization of Rolling Processes: A Review. Metals 2024, 14, 737. [Google Scholar] [CrossRef]
- Cao, L.; Li, X.; Wang, Q.; Zhang, D. Vibration analysis and numerical simulation of rolling interface during cold rolling with unsteady lubrication. Tribol. Int. 2021, 153, 106604. [Google Scholar] [CrossRef]
- Valigi, M.C.; Malvezzi, M.; Logozzo, S. A Numerical Procedure Based on Orowan’s Theory for Predicting the Behavior of the Cold Rolling Mill Process in Full Film Lubrication. Lubricants 2020, 8, 2. [Google Scholar] [CrossRef]
- Bukvic, M.; Gajevic, S.; Skulic, A.; Savic, S.; Asonja, A.; Stojanovic, B. Tribological Application of Nanocomposite Additives in Industrial Oils. Lubricants 2024, 12, 6. [Google Scholar] [CrossRef]
- Shimura, M.; Kasai, D.; Otsuka, T.; Yamashita, N.; Hirayama, T. Measurement of Oil Film Thickness Distribution in Roll Bite during Cold Rolling Using Quantum Dots. Tetsu-to-Hagane 2023, 109, 865–879. [Google Scholar] [CrossRef]
- Ma, L.; Ma, L.; Lian, J.; Wang, C.; Ma, X.; Zhao, J. Tribological Behavior and Cold-Rolling Lubrication Performance of Water-Based Nanolubricants with Varying Concentrations of Nano-TiO2 Additives. Lubricants 2024, 12, 361. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.S.; Jin, X.; Xiang, Y.G.; Li, X.G. Multi-objective optimization of rolling schedule for tandem cold strip rolling based on NSGA-II. J. Manuf. Processes 2020, 60, 257–267. [Google Scholar] [CrossRef]
- Sun, W.; Li, J.; Kong, N.; Zhang, J. Flatness defect control during cold rolling of SUS430 stainless steel. Mater. Test. 2024, 66, 896–912. [Google Scholar] [CrossRef]
- Tao, L.; Wang, Q.; Wu, H. Establishment and Numerical Analysis of Rolling Force Model Based on Dynamic Roll Gap. Appl. Sci. 2023, 13, 7394. [Google Scholar] [CrossRef]
- Tieu, A.; Liu, Y.J. Friction variation in the cold-rolling process. Tribol. Int. 2004, 37, 177–183. [Google Scholar] [CrossRef]
- Smmura, M.; Kasai, D.; Otsuka, T. Mechanisms of Slip Generation in Cold Rolling of AHSS. Tetsu-to-Hagane 2023, 109, 377–386. [Google Scholar] [CrossRef]
- Lv, C.; Jiao, Z.J.; Liu, X.H.; Wang, G.D. Hill explicit expression of rolling force taking into consideration elastic deformation of rolled stock. Res. Iron Steel 2000, 3, 32–33+46. [Google Scholar]
- Mercuri, A.; Fanelli, P.; Giorgetti, F.; Rubino, G.; Stefanini, C. Experimental and numerical analysis of roll bending process of thick metal sheets. In Proceedings of the 49th Italian Association for Stress Analysis Conference (AIAS), Genova, Italy, 2–5 September 2020. [Google Scholar]
- Jacobs, L.J.M.; Van Dam, K.N.H.; Wentink, D.J.; De Rooij, M.B.; Van der Lugt, J.; Schipper, D.J.; Hoefnagels, J.P.M. Effect of asymmetric material entrance on lubrication in cold rolling. Tribol. Int. 2022, 175, 107810. [Google Scholar] [CrossRef]
- Le, H.R.; Sutcliffe, M.P.F. A multi-scale model for friction in cold rolling of aluminium alloy. Tribol. Lett. 2006, 22, 95–104. [Google Scholar] [CrossRef]
- Domhof, A.T.M.; Waanders, D.; Hol, J.; Sigvant, M. Friction and lubrication modelling in sheet metal forming: Influence of local tool roughness on product quality. In Proceedings of the 42nd Conference of the International Deep Drawing Research Group (IDDRG), Luleå, Sweden, 19–22 June 2023. [Google Scholar]
- Trzepiecinski, T.; Najm, S.M. Application of Artificial Neural Networks to the Analysis of Friction Behaviour in a Drawbead Profile in Sheet Metal Forming. Materials 2022, 15, 9022. [Google Scholar] [CrossRef] [PubMed]
- Rowe, G.W. Computing the Coefficient of Friction in the Roll Bite from Mill Data. Blast Furn. Steel Plant 1967, 55, 499–508. [Google Scholar]
- Bland, D.R.; Ford, H. The Calculation of Roll Force and Torque in Cold Strip Rolling with Tensions. Proc. Inst. Mech. Eng. 1948, 159, 144–163. [Google Scholar] [CrossRef]
- Zhao, J.W.; Li, J.D.; Qie, H.T.; Wang, X.C.; Shao, J.; Yang, Q. Predicting flatness of strip tandem cold rolling using a general regression neural network optimized by differential evolution algorithm. Int. J. Adv. Manuf. Technol. 2023, 126, 3219–3233. [Google Scholar] [CrossRef]
- Lee, S.H.; Song, G.H.; Lee, S.J.; Kim, B.M. Study on the improved accuracy of strip profile using numerical formula model in continuous cold rolling with 6-high mill. J. Mech. Sci. Technol. 2011, 25, 2101–2109. [Google Scholar] [CrossRef]
- Li, J.D.; Wang, X.C.; Zhao, J.W.; Yang, Q.; Qie, H.T. Predicting mechanical properties lower upper bound for cold-rolling strip by machine learning-based artificial intelligence. ISA Trans. 2024, 147, 328–336. [Google Scholar] [CrossRef]
- Bu, H.N.; Zhou, H.G.; Yan, Z.W.; Zhang, D.H. Multi-objective optimization of bending force preset in cold rolling. Eng. Comput. 2019, 36, 2048–2065. [Google Scholar] [CrossRef]
- Wang, P.F.; Deng, J.K.; Li, X.; Hua, C.C.; Su, L.H.; Deng, G.Y. A novel strategy based on machine learning of selective cooling control of work roll for improvement of cold rolled strip flatness. J. Intell. Manuf. 2024, 35, 3559–3576. [Google Scholar] [CrossRef]
- Jin, S.R.; Li, X.; Wang, P.F.; Li, X.H.; Zhang, D.H. Research and application of the flatness target curve discrete dynamic programming based on two-dimensional decision making. Expert Syst. Appl. 2024, 256, 124947. [Google Scholar] [CrossRef]
- Fu, K.; Zang, Y.; Gao, Z.Y. Partial Film Lubrication Characteristics of Inlet Zone in Cold Strip Rolling. J. Tribol.-Trans. ASME 2014, 136, 041502. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Pawelski, H. An analytical model for dependence of force and forward slip on speed in cold rolling. Steel Res. Int. 2003, 74, 293–299. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Zhang, Z.; Chen, H.Q.; Guo, S.; Zhao, J.W. Characteristics of unsteady lubrication film in metal-forming process with dynamic roll gap. J. Cent. South Univ. 2014, 21, 3787–3792. [Google Scholar] [CrossRef]
- Heidari, A.; Forouzan, M.R.; Niroomand, M.R. Development and evaluation of friction models for chatter simulation in cold strip rolling. Int. J. Adv. Manuf. Technol. 2018, 96, 2055–2075. [Google Scholar] [CrossRef]
- Li, J.D.; Wang, X.C.; Yang, Q.; Guo, Z.; Song, L.B.; Mao, X. Rolling force prediction in cold rolling process based on combined method of T-S fuzzy neural network and analytical model. Int. J. Adv. Manuf. Technol. 2022, 121, 4087–4098. [Google Scholar] [CrossRef]
- Li, L.; Matsumoto, R.; Utsunomiya, H. Experimental Study of Roll Flattening in Cold Rolling Process. ISIJ Int. 2018, 58, 714–720. [Google Scholar] [CrossRef]
- Wang, H.; Guo, W.; Li, Y.L.; Chen, F.; Wen, J.; Yu, M.; Wang, F.Q. Research on Level 2 Rolling Model of Tin Plate Double Cold Reduction Process. In Proceedings of the Materials Processing Fundamentals Symposium Held at the TMS Annual Meeting and Exhibition, San Antonio, TX, USA, 10–14 March 2019; Springer: Cham, Switzerland, 2019; pp. 131–139. [Google Scholar]
- Makke, N.; Chawla, S. Interpretable scientific discovery with symbolic regression: A review. Artif. Intell. Rev. 2024, 57, 2. [Google Scholar] [CrossRef]
- Engle, M.R.; Sahinidis, N.V. Deterministic symbolic regression with derivative information: General methodology and application to equations of state. AlChE J. 2022, 68, e17457. [Google Scholar] [CrossRef]
- Zhang, H.Z.; Zhou, A.; Qian, H.; Zhang, H. PS-Tree: A piecewise symbolic regression tree. Swarm Evol. Comput. 2022, 71, 101061. [Google Scholar] [CrossRef]
- Song, C.N.; Cao, J.G.; Sun, L.; Tan, X.Y.; Xia, W.H.; Sun, S.T. A multi-stand work roll bending and shifting approach for profile contour and flatness control of electrical steel in multi-width schedule-free rolling using NSGA-II algorithm. J. Manuf. Processes 2024, 120, 895–910. [Google Scholar] [CrossRef]
- Wang, P.F.; Zhang, D.H.; Li, X.; Zhang, W.X. Research and Application of Dynamic Substitution Control of Actuators in Flatness Control of Cold Rolling Mill. Steel Res. Int. 2011, 82, 379–387. [Google Scholar] [CrossRef]
- Fujita, N.; Kimura, Y. Influence of Plate-out Oil Film on Lubrication Characteristics in Cold Rolling. ISIJ Int. 2012, 52, 850–857. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Mendo, L. Estimation of a Probability with Guaranteed Normalized Mean Absolute Error. IEEE Commun. Lett. 2009, 13, 817–819. [Google Scholar] [CrossRef]
- Elkatatny, S.; Al-AbdulJabbar, A.; Abdelgawad, K. A New Model for Predicting Rate of Penetration Using an Artificial Neural Network. Sensors 2020, 20, 2058. [Google Scholar] [CrossRef] [PubMed]
- Bu, H.N.; Yan, Z.W.; Zhang, D.H. A novel approach to improve the computing accuracy of rolling force and forward slip. Ironmak Steelmak 2019, 46, 269–276. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Chang, D.F. Low speed mixed lubrication of bulk metal forming processes. J. Tribol.-Trans. ASME 1996, 118, 83–89. [Google Scholar] [CrossRef]
- Trzepiecinski, T.; Lemu, H.G. Improving Prediction of Springback in Sheet Metal Forming Using Multilayer Perceptron-Based Genetic Algorithm. Materials 2020, 13, 3129. [Google Scholar] [CrossRef]
- Lee, R.T.; Yang, K.T.; Chiou, Y.C. Mixture Lubrication with Emulsions in Cold Rolling. Tribol. Trans. 2016, 59, 748–757. [Google Scholar] [CrossRef]
- Li, X.J.; Cui, Y.Y.; He, Z.L.; Bai, Z.H. Model and influence factors of oil film thickness in the deformation zone of double cold reduction mill. Ironmak Steelmak 2020, 47, 757–763. [Google Scholar] [CrossRef]

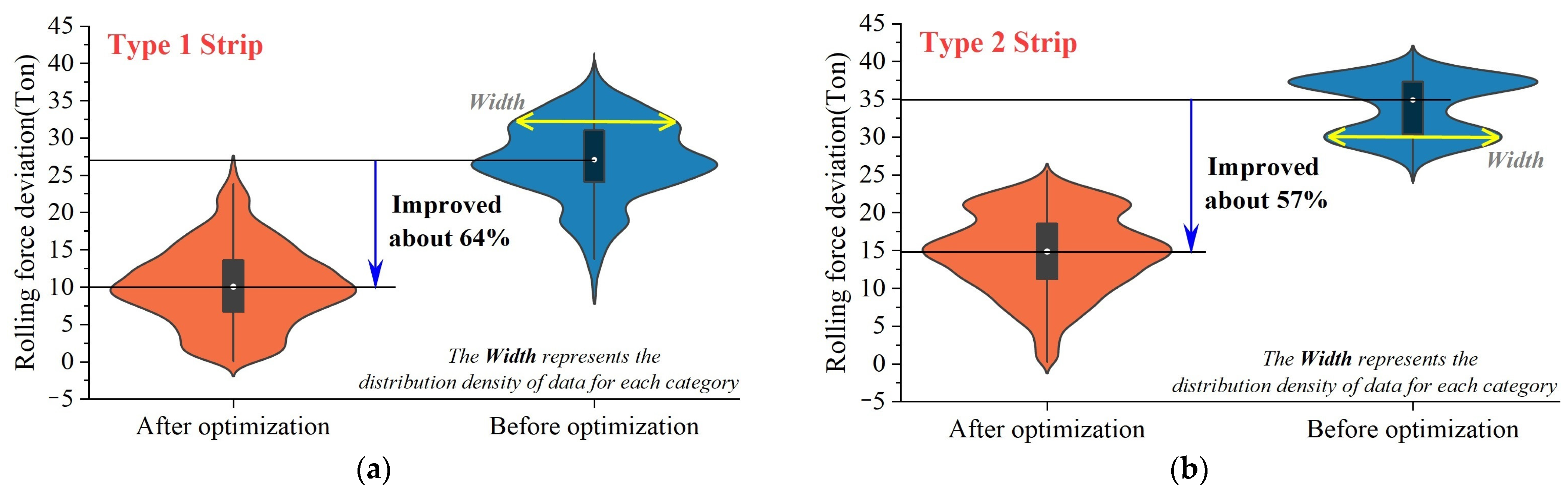
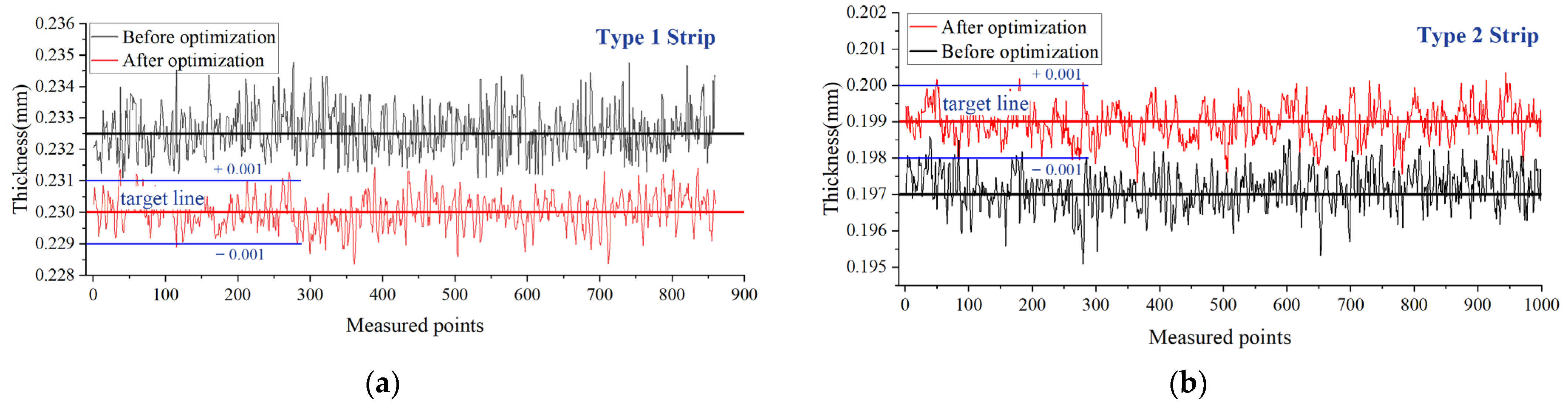
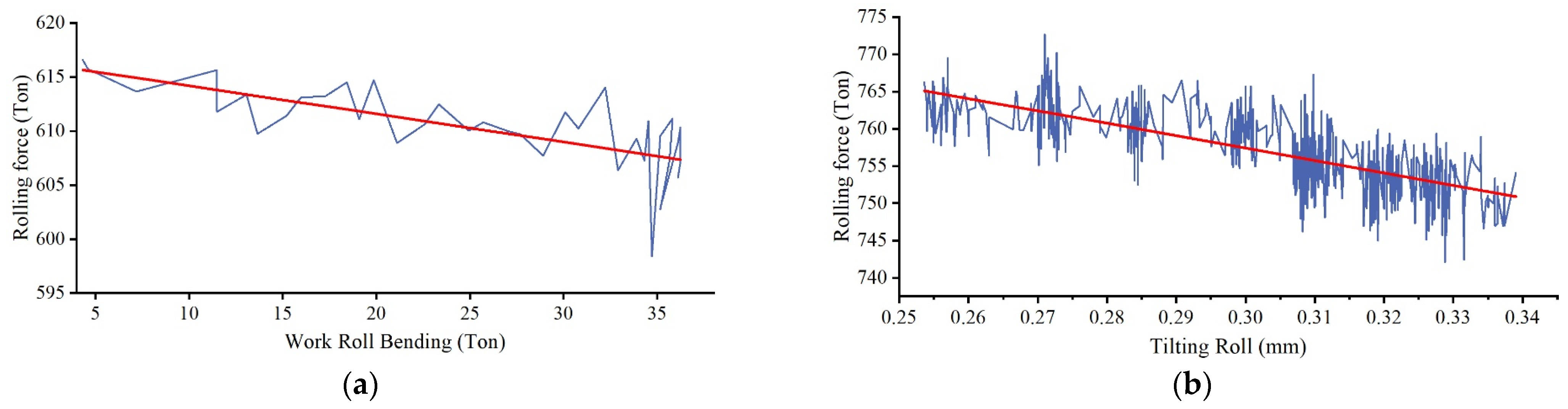
| Items | Parameters |
|---|---|
| Max rolling force (kN) | dynamic pressure: 18,000 static pressure: 20,000 |
| Max rolling velocity (m/min) | 1400 |
| Dimension of the work roll (mm) | φ395/φ435 × 1450 |
| Dimension of the intermediate roll (mm) | φ440/φ490 × 1400 |
| Dimension of the support roll (mm) | φ1150/φ1250 × 1350 |
| Gauge of raw material/finished product (mm) | 2.0~3.0/0.18~0.55 |
| Width of raw material/finished product (mm) | 800~1130/800~1130 |
| Minimum opening of work roll/mm | 30 |
| Work roll positive/negative bending force (kN) | individual roll on one side: 360/180 |
| Intermediate roll positive bending force (kN) | individual roll on one side: 500 |
| Maximum transverse shifting of intermediate roller (mm) | 275 |
| Tilting roll range (mm) | −1.5~1.5 |
| Items | Parameters |
|---|---|
| Computational laws | +, −, ×, ÷, sin, cos, √, ln(), x2, x3 |
| Population size | 11,000 |
| Maximum number of iterations | 50 |
| Crossover pattern | Subtree swapping crossover |
| Mutation probability | 20% |
| Proportion of training set | 0.8 |
| Proportion of test set | 0.2 |
| DNNs | |
|---|---|
| Optimizer | adam |
| Batch size | 10 |
| Epochs | 100 |
| Network architecture | input layer (64 neurons) |
| hidden layer (32 neurons) | |
| output layer (1 neuron) | |
| Activation function | ReLU |
| Loss function | mean squared error |
| SVM | |
| Kernel | RBF |
| Epsilon | 0.1 |
| Range of penalty coefficient | [0.1, 10] |
| Step size of penalty coefficient | 0.1 |
| Range of gamma | scale |
| Step size of gamma | 0.1 |
| Work Roll Bending Experiment | |||||||
|---|---|---|---|---|---|---|---|
| Accumulated change in work roll bending (Ton) | initial value | WRB 1 | WRB 2 | WRB 3 | WRB 4 | WRB 5 | WRB 6 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | |
| maintenance period (s) | 2 (each step) | ||||||
| Tilting roll experiment | |||||||
| Accumulated change in (mm) | initial value | TR 1 | TR 2 | TR 3 | TR 4 | TR 5 | TR 6 |
| 0.255 | 0.27 | 0.285 | 0.3 | 0.315 | 0.33 | 0.345 | |
| maintenance period (s) | 2 (each step) | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, S.; Li, X.; Wang, P.; Luan, F.; Chen, F.; Zhang, D.; Zhang, H. Intelligent Analysis and Optimization of Lubrication Status Factor Based on Dynamically Loaded Roll Gap in Cold Strip Rolling. Lubricants 2025, 13, 54. https://doi.org/10.3390/lubricants13020054
Jin S, Li X, Wang P, Luan F, Chen F, Zhang D, Zhang H. Intelligent Analysis and Optimization of Lubrication Status Factor Based on Dynamically Loaded Roll Gap in Cold Strip Rolling. Lubricants. 2025; 13(2):54. https://doi.org/10.3390/lubricants13020054
Chicago/Turabian StyleJin, Shuren, Xu Li, Pengfei Wang, Feng Luan, Fangsheng Chen, Dianhua Zhang, and Haidong Zhang. 2025. "Intelligent Analysis and Optimization of Lubrication Status Factor Based on Dynamically Loaded Roll Gap in Cold Strip Rolling" Lubricants 13, no. 2: 54. https://doi.org/10.3390/lubricants13020054
APA StyleJin, S., Li, X., Wang, P., Luan, F., Chen, F., Zhang, D., & Zhang, H. (2025). Intelligent Analysis and Optimization of Lubrication Status Factor Based on Dynamically Loaded Roll Gap in Cold Strip Rolling. Lubricants, 13(2), 54. https://doi.org/10.3390/lubricants13020054





