A Review of Friction and Lubricant in Metal Forming
Abstract
1. Introduction
1.1. Significance of Friction in Metal Forming
1.2. Main Factors Affecting Friction
1.3. Reality and Issues of Friction
1.4. MFS and Friction Identification
1.5. Background and Purpose of the Paper
1.6. Review Methodology and List of Contents
2. Metal Forming Focusing on Tribology
2.1. Tribological Issues in Metal Forming
2.2. Various Factors Affecting Friction
- Pressure: Among the main factors affecting friction, the one with the most significant impact on friction is pressure. In an extreme case, without pressure there is no friction. Due to the complexity of mechanics in metal forming, however, pressure has become the most controversial topic. When friction stress is given (i.e., traction prescribed), the displacement or velocity in that direction should remain unknown. Despite this, there is a tendency to equate the friction factor of 1 with sticking (velocity boundary) [69]. This misunderstanding provides fertile ground for many controversial theoretical developments related to friction in metal forming.
- Relative velocity: It has at least a right to determine the direction of friction stress. When the right vanishes, the friction stress becomes unknown and has nothing to do with the frictional law. Svoboda and Jopek [43] experimentally showed the significant dependence of the friction coefficient on the strain rate (which is almost proportional to the relative velocity) at elevated temperatures. They showed that the friction coefficient decreases when the relative velocity is incredible.
- Lubricant: Kahhal et al. [47] determined the friction coefficient for each graphite, mica, and glass powder lubricant during the hot metal forming of an alloy steel. The results showed that the predicted friction coefficient for dry samples was 0.62, whereas the friction coefficients obtained using graphite, mica, and glass powder were 0.46, 0.29, and 0.18, respectively. Özakın and Erdil [49] conducted a study to replace synthetic-based lubricants for cold metal forming with vegetable lubricants. They reported that the performance of the new lubricant did not meet that of the existing synthetic lubricants in terms of the roughness transfer ratio. However, such attempts and advancements will continue in response to the modern demand for green manufacturing with a healthy shopfloor [158,159].
- Temperature, strain rate: Mirahmadi et al. [39] investigated the effect of the temperature and strain rate of the Ti6Al4V alloy on the friction factor using the isothermal compression test at elevated temperatures. It was found that they significantly affect the friction factor in a specific temperature range. Sheng et al. [27] experimentally showed the significant effect of temperature and test load on the friction coefficient. They revealed that the oxide layers favor obtaining a low friction coefficient under all the experimental conditions. The average friction coefficient decreased with the increasing load at 300 °C in a ball-on-disk tribometer, whereas it increased with the increase in applied load at 500 °C.
- Surface expansion, surface flow pattern including sliding velocity: Noh et al. [44] revealed through ring compression tests of perfectly plastic materials and FEM that the factors determining low and high friction include surface expansion and other surface flow patterns, such as sliding velocity and so on.
- Coating: Patil et al. [48] utilized the tin coating layer as a solid lubricant in cold steel tube drawing. They argued that an optimal thickness of the coating layer exists from the perspective of friction, specifically in drawing load. Using the Reynolds equation, Patri and Cheng [54,55] researched friction in thin or thick film lubrication regimes.
- Surface roughness: Zhang et al. [58] conducted a numerical analysis on the effect of surface roughness on friction under 2D planar conditions, while Mahrenholtz et al. [59] did so in a 3D space. Sigvant et al. [42] studied the effect of tool roughness and strain rate on the material flow in SMF, focusing on the CAE application.
- Various factors: Zhang et al. [58] studied the microscopic friction model to reveal the effect of roughness, pressure, adhesive friction coefficient, and relative velocity on the friction stress at the unlubricated material–die interface. They also studied the local friction model relying on the dimensionless lubrication number employed for calculating the varying friction coefficient with dynamic lubricant viscosity, relative velocity, contact pressure, and surface roughness. In the microscopic friction model, the friction coefficient increased with the velocity, while in the local friction model, the friction coefficient decreased with the velocity.
2.3. Lubrication Regime and LRC
3. Friction Modeling and Solving
3.1. Identification of Friction Laws
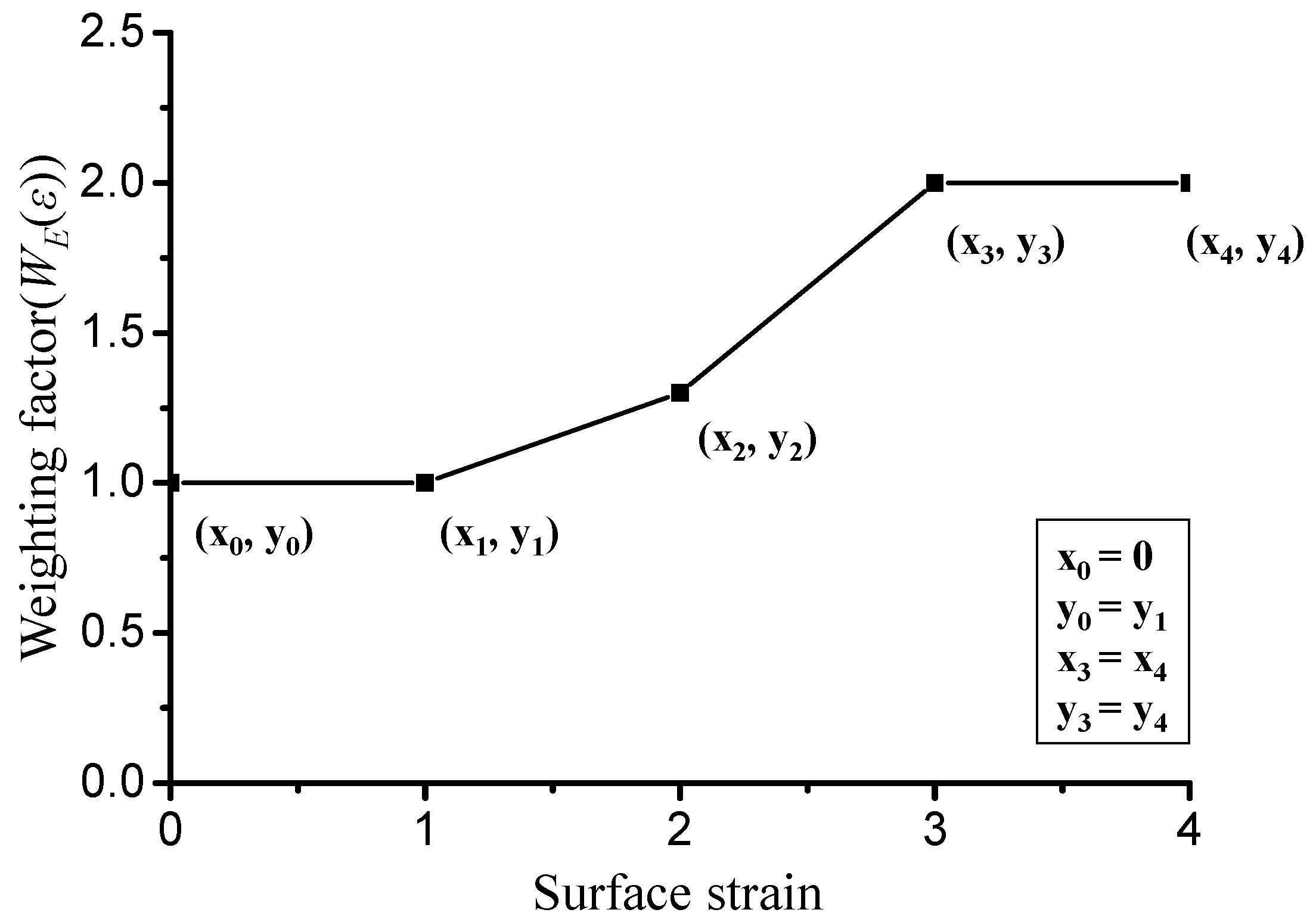
3.2. Modified Friction Laws for the Varying Friction Condition During Metal Forming
3.3. Issues Regarding the CFL and Sticking Phenomenon
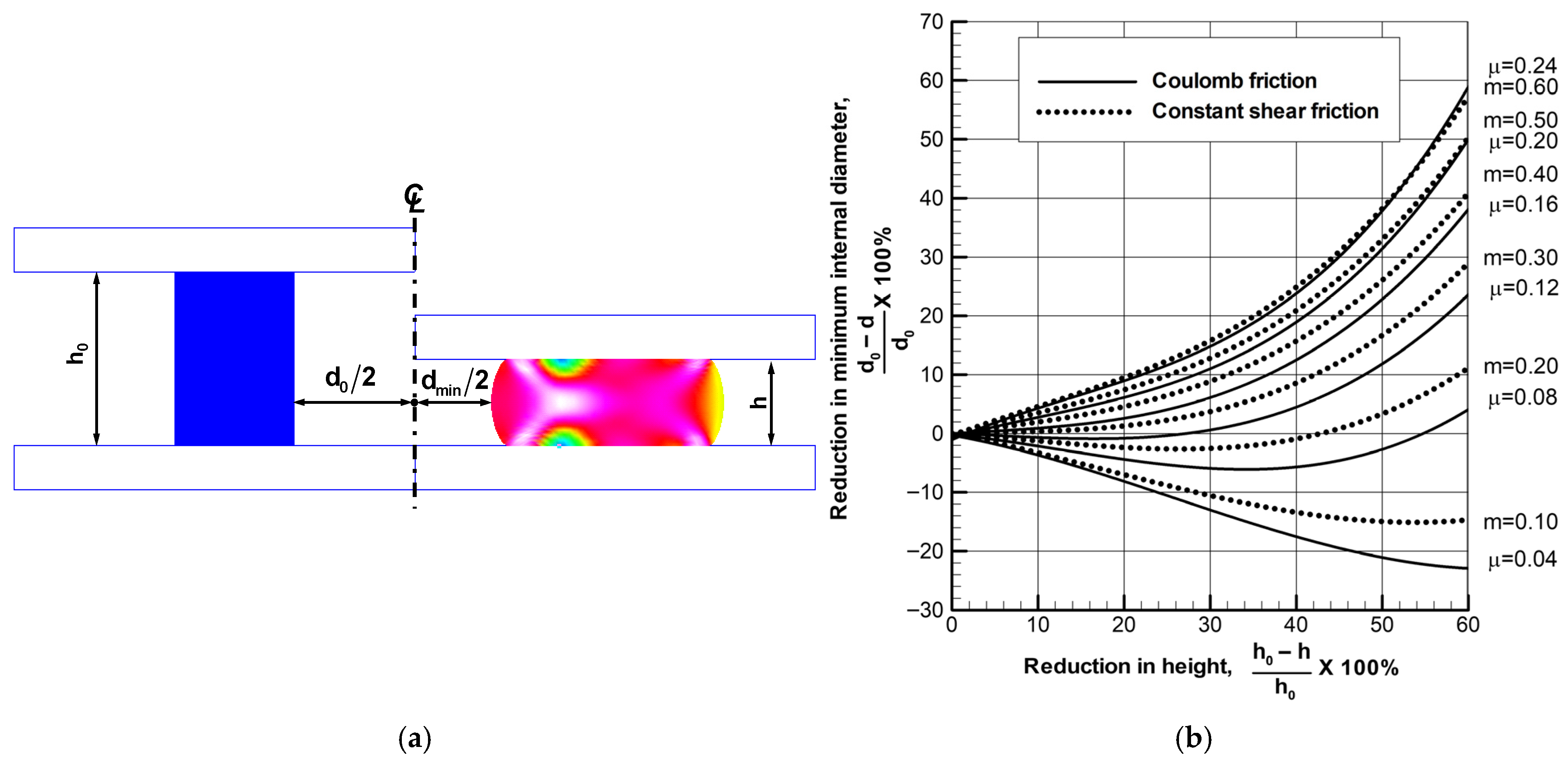
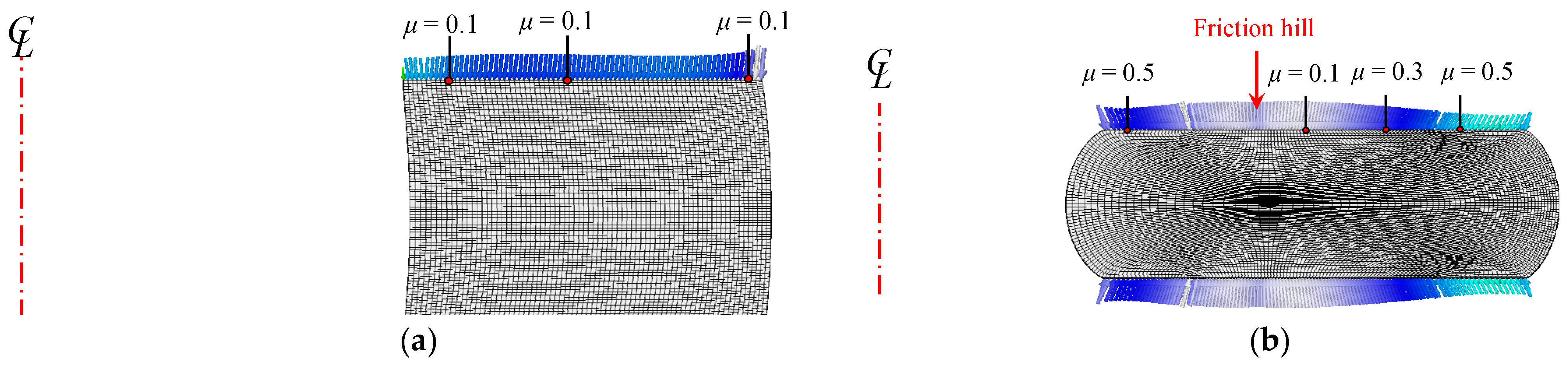
3.4. Ring Compression Test
3.5. Similarity and Difference Between CFL and CSFL
3.6. Critique of Traditional Friction Laws with a Constant Friction Coefficient or Factor
- -
- Flow stress: ;
- -
- Punch’s speed: 1 mm/s.
- -
- Friction conditions:
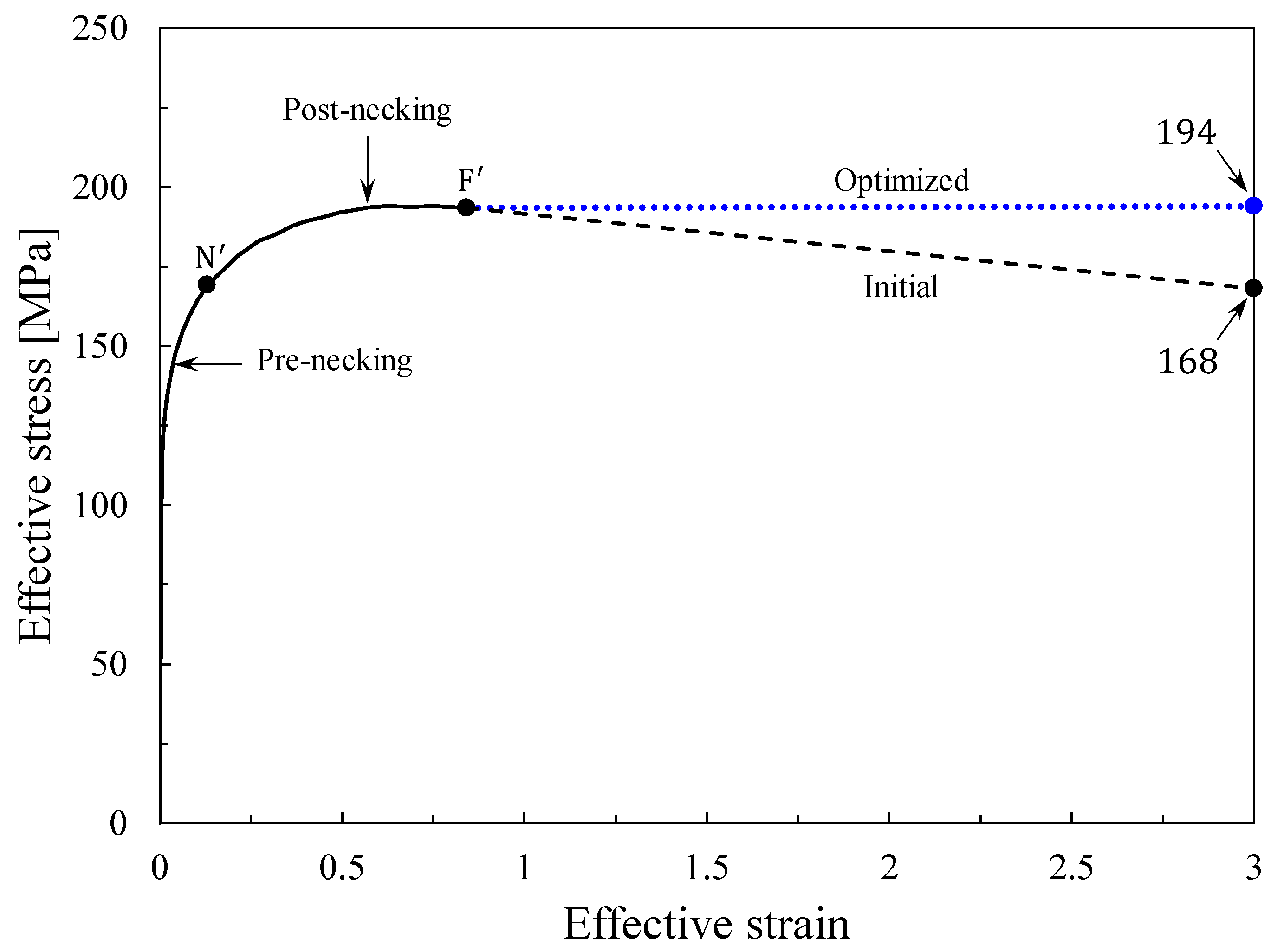
3.7. HFL and State Variabilization of the Friction Coefficient and Factor
3.8. Typical Examples of LRC
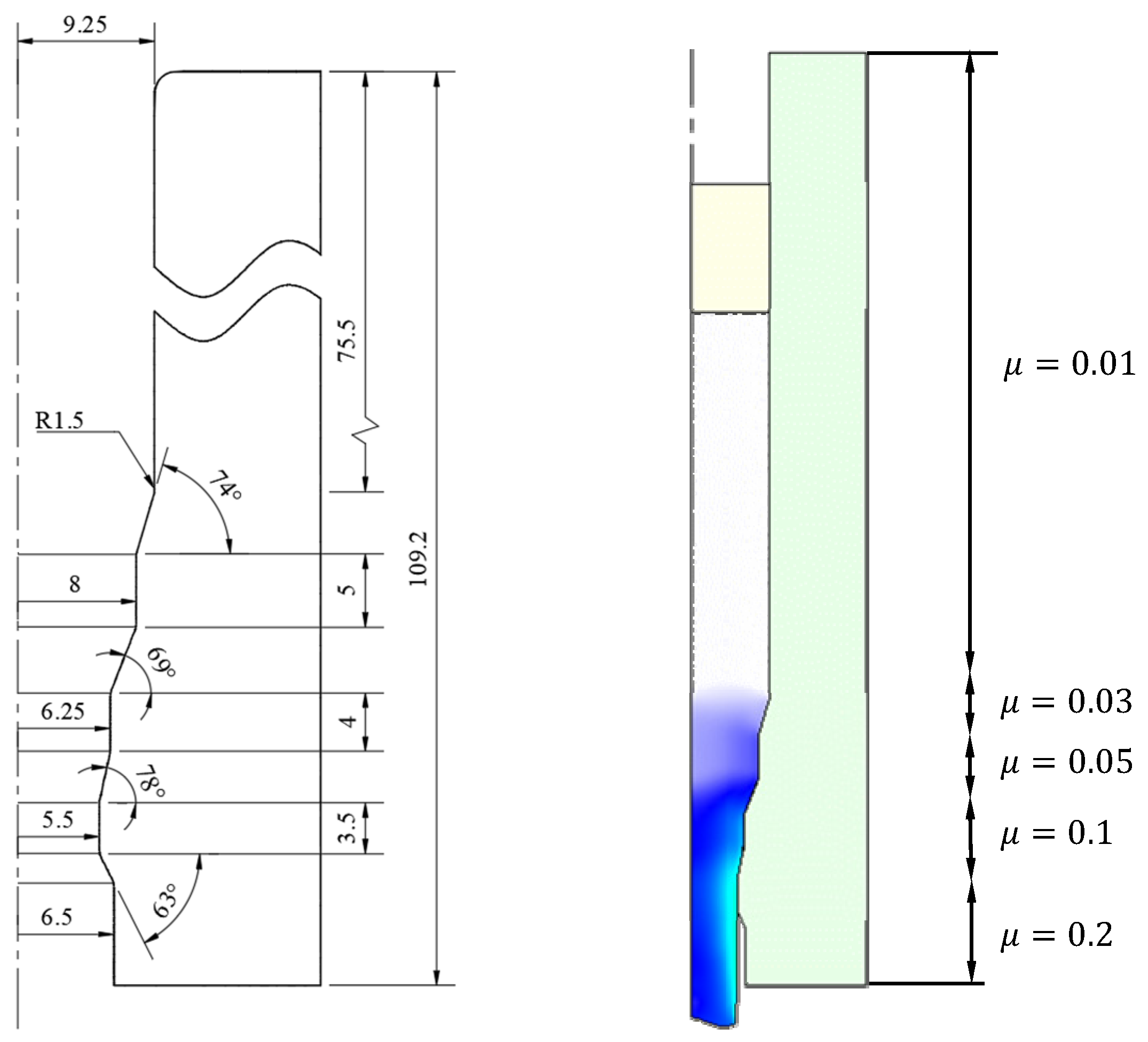
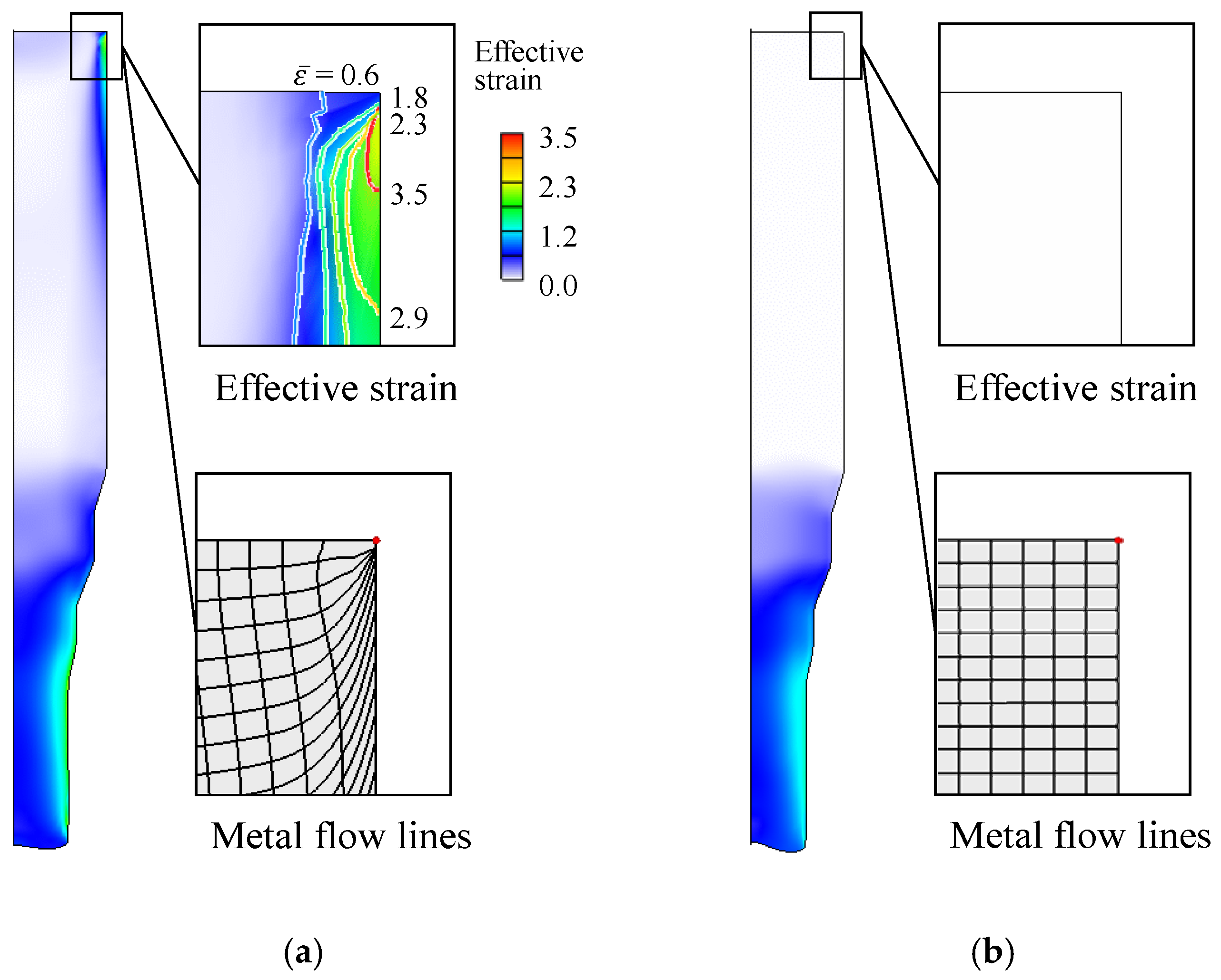
3.8.1. Cold Forward and Backward Extrusion of an A6061 Alloy
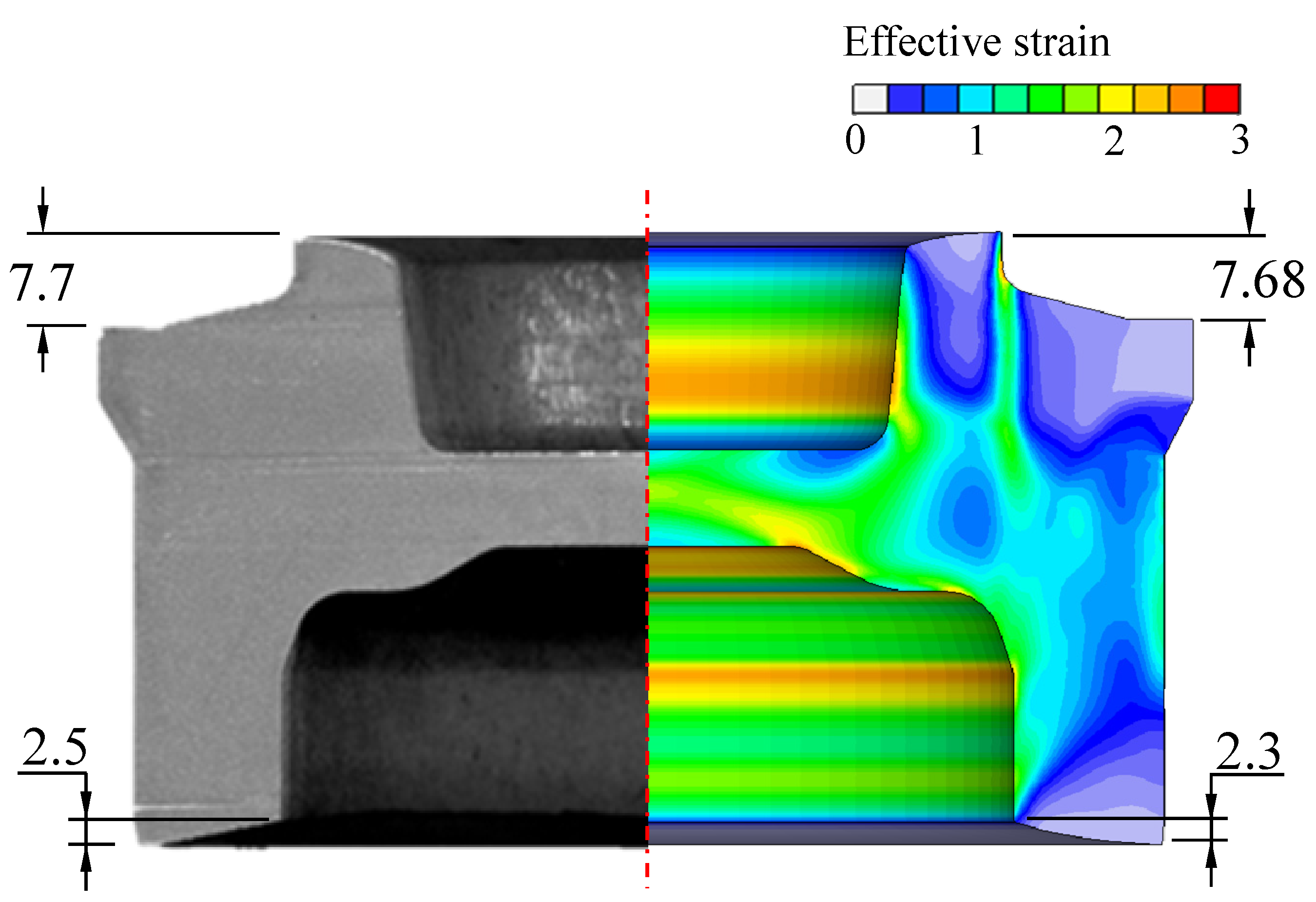
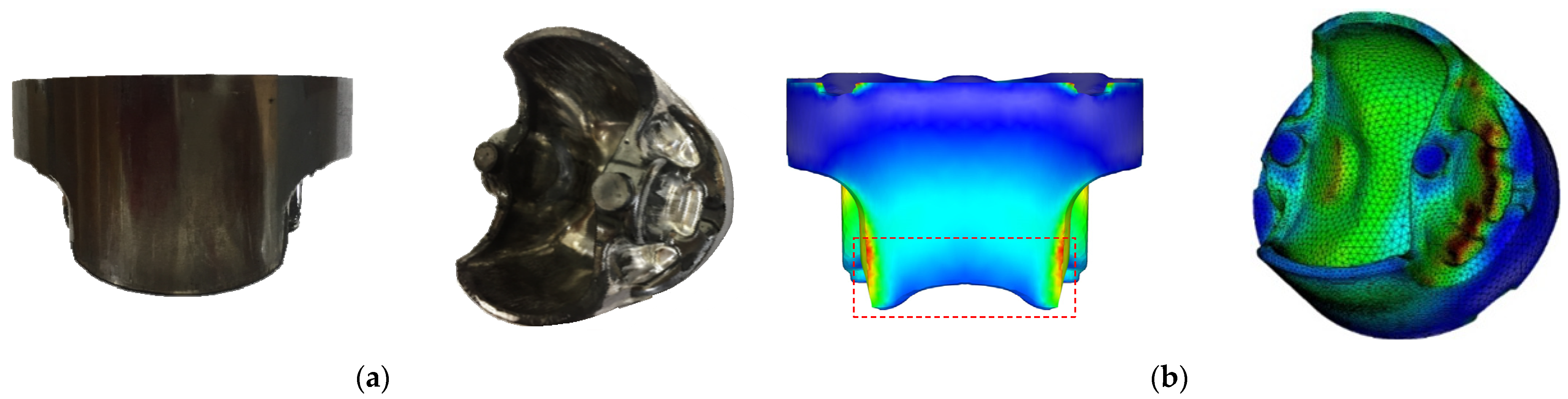
3.8.2. Hot Forging of an A4032 Alloy Piston
4. Lubricants
5. Friction Test and Acquisition of Tribological Parameters
- Complementary or non-standard ring compression test: Since a pressure higher than the flow stress is applied in ring compression testing, there are limitations in evaluating the friction state of exceptional processes (e.g., forward extrusion with low extrusion ratio) where experiments are conducted at a pressure lower than this. Petersen et al. [9] used a new complementary ring-test geometry to reduce the increase in ring compression load due to barreling. In this model, normal stresses over some areas of the material–die interface are lower than the material’s flow stress. They used inverse analysis technology to identify the friction condition shown in Figure 2, focusing on the GFL. Sanodiya and Choudhary [96] identified friction from the compression tests of non-standard (or differently shaped) specimens that can replace standard ring compression test specimens. It was confirmed that the results obtained from the non-standard specimens were similar to those obtained from the existing specimens.
- Warm and hot upsetting sliding test: Soranansri et al. [106] used the warm and hot upsetting sliding test to identify the friction coefficient and friction factor during aluminum forming processes at elevated temperatures. The experiment was conducted for the A6082-T6 alloy using the AISI H13 tool steel under dry contact conditions at 400 °C. It was experimentally found that the friction coefficient was 0.57, and the friction factor ranged between 0.76 and 0.90, depending on the flow behavior.
- Upsetting or cylinder compression: In cylinder compression tests, the deformation shape, namely the barrel shape, is sensitive to friction. Utilizing this point, numerous studies have been conducted to evaluate friction. However, the compressive load does not sensitively change to friction. Friction increases the material’s resistance to deformation, which leads to an increase in the compressive load. However, friction reduces the rate of increase in the area of the interfacial surface directly related to the compressive load. Therefore, the sensitivity of friction to the compressive load decreases [15,105]. Ebrahimi and Najafizadeh [101] presented the method for calculating the friction factor using cold and hot cylinder compression tests. They used only the measured barreling of the compressed cylinder with the upper-bound solutions to calculate the friction factor since the barreling is dependent on the friction and the initial height-to-diameter ratio.
- Theoretical (numerical or analytical) methods: Sun et al. [239] presented a novel method to calculate the interfacial friction stress in friction stir welding without determining the friction factor first. The interfacial stress was described by a function of temperature and calculated by a three-dimensional computational fluid dynamics (CFD) model. Based on slip line analysis, Challen and Oxley [132] used two-dimensional rigid cylindrical asperities to identify the CFL during material removal occurring in moving contact between abrasive or polishing grits and softer workpieces. Their approach contributed to the works of Ma et al. [136] and Hol et al. [153] for their multi-scale friction models. Ma et al. [136] presented a multi-asperity macro-scale friction model for the aluminum extrusion process by adapting a wedge-shaped single asperity model to determine the friction force at each sheet material–die contact patch from which the overall friction coefficient was calculated.
- Various extrusion tests: Nakamura et al. [107] established a friction testing method with a combined forward rod–backward can extrusion, obtained the theoretical FCCs, and evaluated a friction coefficient and friction factor along the container wall and the conical die surface in the forward rod extrusion without information about the forming forces and the flow stress of the material. Hsu and Huang [108] investigated the friction distribution in a combined forward and backward extrusion process. They developed an inverse analysis technique to determine the friction coefficient of the lubricated material–die interface where grease or different lubricants were applied. Buschhausen et al. [109] proposed a friction test, based on a double backward extrusion process, to obtain a friction factor from the most significant difference in extruded cup heights. The FCCs were constructed.
- Contact area test: Wang et al. [16] conducted the contact test. They proposed a friction coefficient model based on real contact area change, which accurately predicted friction changes with normal pressure and material properties compared to the classical CFL.
- Double cup and spike forging tests: Kim et al. [120] created FCCs to determine the friction factor through finite element analysis in double cup and spike forging tests. They emphasized that different tribo-testing methods yielded different friction factors under the lubricating condition of dry-in-place coating (by the water-based lubricants) with forming oil. Xu and Rao [117] conducted FE simulations of the spike forging processes to reveal the effects of different geometric parameters, processing variables, and interfacial conditions on the instantaneous spike height under cold and hot forming conditions. Hu et al. [118] developed an optimized spike forging test method using FEM and optimization techniques. Hu et al. [119] studied the effect of tooling surface on the friction during cold forging of an aluminum alloy using a ring-with-boss compression test and an optimum spike forging test. They emphasized the friction anisotropy, which hindered the friction factor from being determined directly with flat ground platens.
- Ball or pin-on-disk friction test: Sheng et al. [27] used the ball-on-disk tribometer to reveal the effect of temperature and test load on the friction coefficient. Wang et al. [121] studied the load-dependence of tribological behaviors of the sodium carbonate coating on stainless steel using the ball-on-disk friction test at elevated temperatures. Wang et al. [122] studied an experimental method of pin-on-disk testing for developing a pressure-dependent variable friction model for DP780 AHSS sheet sliding against the DC53 cold-work tool, aiming at more accurately predicting the springback. The developed model was successfully applied to the forming and springback of U-shaped bending under tension, focusing on the accurate springback prediction. Grüebler and Hora [38] conducted the pin-on-disk test of the stainless steel sheet to reveal the effect of temperature and velocity dependence on friction. They identified the friction coefficient using the combined FEM and experiment method. Friction tests using different temperatures showed a change in the friction regime.
- Sheet strip stretch or rotation test: Karadogan and Hatipoglu [125] easily and roughly calculated the stress and the friction coefficient at the material–die interface from the strain information measured by an optical strain measurement system, assuming the flow behavior of the sheet material through a sheet strip stretch test. Karupannasamy et al. [126] conducted the rotational friction test to measure friction under loading/reloading for SMF processes.
- Deep drawing test: Hu and Vollertsen [127] presented the friction test method for deep drawing applications to study the size effects. The friction coefficient function was derived from the results of strip drawing investigations to describe the friction behavior in the whole deep drawing process.
- Erichsen test: Giuliano [128] employed the Erichsen test to identify the friction coefficient of the CFL by coupling experimental and numerical results.
- Simulative twist compression test: Yang et al. [115] employed the simulative twist compression test to obtain the friction conditions for a rotary draw bending process where friction influences wrinkling, wall thickness variation, and cross-section deformation. Ma et al. [116] identified the significant influential factors affecting rules and mechanisms on the friction coefficient using the high-temperature twist compression test combined with the design of experiments. They also presented a pressure- and temperature-related dynamic friction model, which is better than the CFL at predicting the defect in metal forming.
- Ball ironing test: Sae-eaw and Aue-u-lan [129] proposed a ball ironing test as a simulative tribo-test to evaluate the lubricants of the thick sheet ironing process, focusing on a large surface expansion, large pressure, and high relative velocity. Finite element modeling and statistical analysis were employed to determine the maximum load and the specimen’s final height. According to the results, the maximum load is very sensitive to the friction, which is used as an indicator to evaluate and approximate the friction coefficient with FCCs.
- Strip tensile or drawing test: To evaluate friction under conditions, Duncan et al. [123] developed the tensile strip test that simulates the stretching of a sheet over the punch corner radius in forming a shallow stamping in a typical draw die. Hao et al. [124] developed two physical models or friction simulators based on stretching a strip around a pin to characterize SMF friction. They determined the effects of strain, stretching speed, lubrication, pin radius, and wrap angle on the friction coefficient. Trzepieciński and Fejkiel [240] studied the effect of sheet deformation on the change in the surface roughness and friction coefficient and the correlation between the surface roughness and frictional conditions of the tested sheets in the strip drawing test. According to their friction and wear behavior, Kondratiuk and Kuhn [241] evaluated the hot dip aluminum–silicon and electroplated zinc alloy coatings for hot forming applications. The friction coefficient was revealed in hot strip drawing experiments. Additionally, wear characteristics were evaluated in hot forming tests.
- Inverse analysis technique: Szeliga et al. [10] applied the inverse analysis to identify friction and rheological models in metal forming.
- Flat die friction test—sheet metal friction test: Lee et al. [131] studied the effect of surface roughness and lubricants using a sheet metal friction tester, i.e., a flat die friction tester. They formulated the friction coefficient as a function of surface roughness. Han and Kim [40] studied the effect of contact pressure on friction, focusing on the SMF of high-strength materials. They conducted the flat-type friction test with a high-strength bare steel sheet under various contact pressures, revealing that the effect of contact pressure on the friction behavior of the steel sheet is significant, especially on HSS stamping with a wide range of contact pressures.
- Scuffing test: Schipper and De Gee [130] studied the relationship between a lubrication mode diagram for concentrated contacts and the ‘IRG transition’ diagram. The scuffing test was conducted using a two-disk apparatus, revealing that three distinct lubrication regimes could be observed, including elastohydrodynamic lubrication, mixed lubrication, and boundary lubrication.
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Joun, M.S. Workshop of metal forming CAE technology 1996 (MFCAE 1996). In Proceedings of the First International Conference on Formal Methods in Computer-Aided Design (FMCAD ‘96), Palo Alto, CA, USA, 6–8 November 1996. [Google Scholar]
- Srikanth, A.; Zabaras, N. Shape optimization and preform design in metal forming processes. Comput. Methods. Appl. Mech. Eng. 2000, 109, 1859–1901. [Google Scholar] [CrossRef]
- António, C.C.; Castro, C.F.; Sousa, L.C. Optimization of metal forming processes. Comput. Struct. 2004, 82, 1425–1433. [Google Scholar] [CrossRef]
- Bonte, M.H.A.; van den Boogaard, A.H.; Huétink, J. An optimization strategy for industrial metal forming processes. Struct. Multidisc. Optim. 2008, 35, 571–586. [Google Scholar] [CrossRef]
- Ozturk, M.; Kocaoglan, S.; Sonmez, F.O. Concurrent design and process optimization of forging. Comput. Struct. 2016, 167, 24–36. [Google Scholar] [CrossRef]
- Kim, M.C.; Chung, S.H.; Joun, M.S. Optimal process design in hot forging in terms of grain flow quality. Int. J. Automot. Technol. 2019, 20, 45–56. [Google Scholar] [CrossRef]
- Razali, M.K.; Kim, S.W.; Irani, M.; Kim, M.C.; Joun, M.S. Practical quantification of the effects of flow stress, friction, microstructural properties, and the tribological environment on macro-and micro-structure formation during hot forging. Tribol. Int. 2021, 164, 107226. [Google Scholar] [CrossRef]
- Wagener, H.W.; Wolf, J. Coefficient of friction in cold extrusion. J. Mater. Process. Technol. 1994, 44, 283–291. [Google Scholar] [CrossRef]
- Petersen, S.B.; Martins, P.A.F.; Bay, N. An alternative ring-test geometry for the evaluation of friction under low normal pressure. J. Mater. Process. Technol. 1998, 79, 14–24. [Google Scholar] [CrossRef]
- Szeliga, D.; Gawad, J.; Pietrzyk, M. Inverse analysis for identification of rheological and friction models in metal forming. Comput. Methods. Appl. Mech. Eng. 2006, 195, 6778–6798. [Google Scholar] [CrossRef]
- Gavrus, A.; Pham, D.T.; Francillette, H. Identification of friction parameters from the inverse analysis of a direct extrusion test. AIP Conf. Proc. 2011, 1315, 1455–1460. [Google Scholar] [CrossRef]
- Gavrus, A.; Francillette, H.; Pham, D.T. An optimal forward extrusion device proposed for numerical and experimental analysis of materials tribological properties corresponding to bulk forming processes. Tribol. Int. 2012, 47, 105–121. [Google Scholar] [CrossRef]
- Ghassemali, E.; Tan, M.-J.; Jarfors, A.E.W.; Lim, S.C.V. Progressive microforming process: Towards the mass production of micro-parts using sheet metal. Int. J. Adv. Manuf. Technol. 2013, 66, 611–621. [Google Scholar] [CrossRef]
- Li, W.Q.; Ma, Q.X. Evaluation of rheological behavior and interfacial friction under the adhesive condition by upsetting method. Int. J. Adv. Manuf. Technol. 2015, 79, 255–263. [Google Scholar] [CrossRef]
- Gomez, D.; Ledesma, E.; Hino, R.; Aguilera, E.; Ruiz, I. Friction assessment in hot forging operations using large-scale ring compression test. In Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, Virtual, 1–5 November 2021; Advanced Manufacturing. Volume 2A. [Google Scholar] [CrossRef]
- Wang, H.; Chen, G.; Zhu, Q.; Zhang, P.; Wang, C. Frictional behavior of pure titanium thin sheet in stamping process: Experiments and modeling. Tribol. Int. 2024, 191, 109131. [Google Scholar] [CrossRef]
- Hamid, N.A.; Kim, K.M.; Hwang, T.M.; Choi, J.M.; Joun, M.S. Tribological shifting phenomena during automatic multistage cold forging of an automotive Al6082-T6 steering yoke. J. Manuf. Proc. 2024, 114, 178–195. [Google Scholar] [CrossRef]
- Lee, H.M.; Kwak, H.M.; Choi, J.M.; Kim, H.J.; Chung, W.J.; Joun, M.S. Novel finite element analysis model for three-roller fillet rolling focusing on its strength of accuracy and practicability. J. Mater. Res. Technol. 2025, 37, 3788–3800. [Google Scholar] [CrossRef]
- Wilson, W.R.D. Friction and lubrication in bulk metal-forming processes. J. Appl. Met. 1978, 1, 7–19. [Google Scholar] [CrossRef]
- Han, X.; Hua, L. Friction behaviors in cold rotary forging of 20CrMnTi alloy. Tribol. Int. 2012, 55, 29–39. [Google Scholar] [CrossRef]
- Alexandrov, S.; Jeng, Y.R.; Kuo, C.Y.; Chen, C.Y. Towards the theoretical/experimental description of the evolution of material properties at frictional interfaces in metal forming processes. Tribol. Int. 2022, 171, 107518. [Google Scholar] [CrossRef]
- Zhong, W.; Liu, Y.; Hu, Y.; Li, S.; Lai, M. Research on the mechanism of flash line defect in coining. Int. J. Adv. Manuf. Technol. 2012, 63, 939–953. [Google Scholar] [CrossRef]
- Stott, F.H.; Jordan, M.P. The effects of load and substrate hardness on the development and maintenance of wear-protective layers during sliding at elevated temperatures. Wear 2001, 250, 391–400. [Google Scholar] [CrossRef]
- Cheng, X.; Jiang, Z.; Kosasih, B.; Wu, H.; Luo, S.; Jiang, L. Influence of Cr-rich oxide scale on sliding wear mechanism of ferritic stainless steel at high temperature. Tribol. Lett. 2016, 63, 28. [Google Scholar] [CrossRef]
- Torres, H.; Varga, M.; Adam, K.; Ripoll, M.R. The role of load on wear mechanisms in high temperature sliding contacts. Wear 2016, 364–365, 73–83. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Liu, H.; Wang, J.; Yan, F. Interrelated effects of temperature and load on fretting behavior of SAF 2507 super duplex stainless steel. Tribol. Int. 2019, 136, 140–147. [Google Scholar] [CrossRef]
- Sheng, S.; Zhou, H.; Wang, X.; Qiao, Y.; Yuan, H.; Chen, J.; Yang, L.; Wang, D.; Liu, Z.; Zou, J.; et al. Friction and wear behaviors of Fe-19Cr-15Mn-0.66 N steel at high temperature. Coatings 2021, 11, 1285. [Google Scholar] [CrossRef]
- Zhang, D.W.; Yang, H. Numerical study of the friction effects on the metal flow under local loading way. Int. J. Adv. Manuf. Technol. 2013, 68, 1339–1350. [Google Scholar] [CrossRef]
- Kato, K. Wear in relation to friction—A review. Wear 2000, 241, 151–157. [Google Scholar] [CrossRef]
- Holmberg, K.; Ronkainen, H.; Laukkanen, A.; Wallin, K. Friction and wear of coated surfaces—Scales, modelling and simulation of tribomechanisms. Surf. Coat. Technol. 2007, 202, 1034–1049. [Google Scholar] [CrossRef]
- Luo, S.Y.; Wang, Q.; Zhang, P.; Li, J.; Liu, Q.L. Effect of friction conditions on phase transformation characteristics in hot forging process of Ti-6Al-4V turbine blade. J. Mater. Res. Technol. 2020, 9, 2107–2115. [Google Scholar] [CrossRef]
- Orowan, E. The calculation of roll pressure in hot and cold flat rolling. Proc. Inst. Mech. Eng. 1943, 150, 140–167. [Google Scholar] [CrossRef]
- Hwang, S.M.; Joun, M.S.; Park, J.S. A penalty rigid-plastic finite element method for the determination of stress distributions at the tool-workpiece interface in metal forming. Trans. Namri. Sme. 1990, 18, 13–19. [Google Scholar]
- Tabor, D. The mechanism of rolling friction II. The elastic range. Proc. R. Soc. Lond. Ser. A 1955, 229, 198–220. [Google Scholar] [CrossRef]
- Suh, N.P.; Sin, H.C. The genesis of friction. Wear 1981, 69, 91–114. [Google Scholar] [CrossRef]
- Felder, E.; Samper, V. Experimental study and theoretical interpretation of the frictional mechanisms in steel sheet forming. Wear 1994, 178, 85–94. [Google Scholar] [CrossRef]
- Azushima, A.; Kudo, H. Direct observation of contact behaviour to interpret the pressure dependence of the coefficient of friction in sheet metal forming. CIRP Ann. 1995, 44, 209–212. [Google Scholar] [CrossRef]
- Grüebler, R.; Hora, P. Temperature dependent friction modeling for sheet metal forming. Int. J. Mater. Form. 2009, 2, 251–254. [Google Scholar] [CrossRef]
- Mirahmadi, S.J.; Hamedi, M.; Cheraghzadeh, M. Investigating friction factor in forging of Ti-6Al-4V through isothermal ring compression test. Tribol. Trans. 2015, 58, 778–785. [Google Scholar] [CrossRef]
- Han, S.S.; Kim, D.J. Contact pressure effect on frictional characteristics of steel sheet for autobody. AIP Conf. Proc. 2011, 1383, 780–783. [Google Scholar] [CrossRef]
- Luo, S.Y.; Zhu, D.H.; Qian, D.S.; Hua, L.; Yan, S.J.; Zhang, J.J. Effects of friction model on forging process of Ti-6Al-4V turbine blade considering the influence of sliding velocity. Int. J. Adv. Manuf. Technol. 2016, 82, 1993–2002. [Google Scholar] [CrossRef]
- Sigvant, M.; Pilthammar, J.; Hol, J.; Wiebenga, J.H.; Chezan, T.; Carleer, B.; van den Boogaard, T. Friction in sheet metal forming: Influence of surface roughness and strain rate on sheet metal forming simulation results. Procedia. Manuf. 2019, 29, 512–519. [Google Scholar] [CrossRef]
- Svoboda, P.; Jopek, M. The effect of strain rate on the friction coefficient. Manuf. Technol. 2024, 24, 289–293. [Google Scholar] [CrossRef]
- Noh, J.H.; Kim, M.T.; Hwang, B.B. Stress profiles at contact interface in ring compression test. J. Mech. Sci. Technol. 2010, 24, 1611–1616. [Google Scholar] [CrossRef]
- Leu, D.K. A simple dry friction model for metal forming process. J. Mater. Process. Technol. 2009, 209, 2361–2368. [Google Scholar] [CrossRef]
- Daouben, E.; Dubois, A.; Dubar, M.; Dubar, L.; Deltombe, R.; Dinh, N.G.T.; Lazzarotto, L. Effects of lubricant and lubrication parameters on friction during hot steel forging. Int. J. Mater. Form. 2008, 1, 1223–1226. [Google Scholar] [CrossRef]
- Kahhal, P.; Yeganehfar, M.; Kashfi, M. An experimental and numerical evaluation of steel A105 friction coefficient using different lubricants at high temperature. Tribol. Trans. 2021, 65, 25–31. [Google Scholar] [CrossRef]
- Patil, M.; Singh, V.; Regalla, S.P.; Gupta, A.K.; Bera, T.C.; Bade, S.; Srinivas, K. Producing high quality cold-drawn steel tubes using an optimal thickness of tin as a tribo-layer. Int. J. Adv. Manuf. Technol. 2022, 121, 4663–4675. [Google Scholar] [CrossRef]
- Özakın, B.; Erdil, İ. Investigation of the performance of vegetable lubricants in cold pressing. In Proceedings of the 3rd International Conference on Innovative Academic Studies (ICIAS), Konya, Turkey, 26–28 September 2023; pp. 26–28. [Google Scholar] [CrossRef]
- Hardell, J.; Prakash, B. Tribological performance of surface engineered tool steel at elevated temperatures. Int. J. Refract. Met. Hard Mater. 2010, 28, 106–114. [Google Scholar] [CrossRef]
- Schutze, M. Protective Oxide Scale; Wiley: Sheffield, UK, 1991. [Google Scholar]
- Lepesant, P.; Boher, C.; Berthier, Y.; Rézai-Aria, F. A phenomenological model of the third body particles circulation in a high temperature contact. Wear 2013, 298–299, 66–79. [Google Scholar] [CrossRef]
- Dohda, K.; Boher, C.; Rezai-Aria, F.; Mahayotsanun, N. Tribology in metal forming at elevated temperatures. Friction 2015, 3, 1–27. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Tribol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Bay, N. Friction stress and normal stress in bulk metal-forming processes. J. Mech. Work. Technol. 1987, 14, 203–223. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Ser. A 1996, 295, 300–319. [Google Scholar] [CrossRef]
- Zhang, S.; Hodgson, P.D.; Cardew-Hall, M.J.; Kalyanasundaram, S. A finite element simulation of micro-mechanical frictional behavior in metal forming. J. Mater. Process. Technol. 2003, 134, 81–91. [Google Scholar] [CrossRef]
- Mahrenholtz, O.; Bontcheva, N.; Iankov, R. Influence of surface roughness on friction during metal forming processes. J. Mater. Process. Technol. 2005, 159, 9–16. [Google Scholar] [CrossRef]
- Karupannasamy, D.K.; de Rooij, M.B.; Schipper, D.J. Multi-scale friction modelling for rough contacts under sliding conditions. Wear 2013, 308, 222–231. [Google Scholar] [CrossRef]
- Chen, C.C.; Kobayashi, S. Rigid plastic finite element analysis of ring compression. Appl. Numer. Methods Form. Process. 1978, 28, 163–174. [Google Scholar]
- van de Vrande, B.L.; van Campen, D.H.; de Kraker, A. An approximate analysis of dry-friction-induced stick-slip vibrations by a smoothing procedure. Nonlinear. Dyn. 1999, 19, 159–171. [Google Scholar] [CrossRef]
- Lee, K.J.; Moon, C.M.; Lee, M.G. A review on friction and lubrication in automotive metal forming: Experiment and modeling. Int. J. Automt. Technol. 2021, 22, 1743–1761. [Google Scholar] [CrossRef]
- Tabor, D. Junction growth in metallic friction: The role of combined stresses and surface contamination. Proc. R. Soc. Ser. A 1959, 251, 378–393. [Google Scholar] [CrossRef]
- Behrens, A.; Schafstall, H. 2D and 3D simulation of complex multistage forging processes by use of adaptive friction coefficient. J. Mater. Process. Technol. 1998, 80–81, 298–303. [Google Scholar] [CrossRef]
- Balasundar, I.; Raghu, T. Effect of friction model in numerical analysis of equal channel angular pressing process. Mater. Des. 2010, 31, 449–457. [Google Scholar] [CrossRef]
- Hatzenbichler, T.; Harrer, O.; Wallner, S.; Planitzer, F.; Kuss, M.; Pschera, R.; Buchmayr, B. Deviation of the results obtained from different commercial finite element solvers due to friction formulation. Tribol. Int. 2012, 49, 75–79. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Bouguecha, A.; Hadifi, T.; Mielke, J. Advanced friction modeling for bulk metal forming processes. Prod. Eng. 2011, 5, 621–627. [Google Scholar] [CrossRef]
- Murillo-Marrodan, A.; Garcia, E.; Cortes, F. A study of friction model performance in a skew rolling process numerical simulation. Int. J. Simul. Model. 2018, 17, 569–582. [Google Scholar] [CrossRef] [PubMed]
- Joun, M.S.; Moon, H.G.; Choi, I.S.; Lee, M.C.; Jun, B.Y. Effects of friction laws on metal forming processes. Tribol. Int. 2009, 42, 311–319. [Google Scholar] [CrossRef]
- Abd Ghawi, A.A.; Razali, M.K.; Salleh, N.A.M.; Joun, M.S. Coupled elastoplastic FEM analysis of frictional boss forming. Next Res. 2025, 2, 100416. [Google Scholar] [CrossRef]
- De Coulomb, C.A. Théorie des Machines Simples: En Ayant égard au Frottement de Leurs Parties et à la Roideur des Cordages; Bachelier: Paris, France, 1821. [Google Scholar]
- Von Karman, T. On the theory of rolling. Z. Angew. Math. Mech. 1925, 5, 130–141. [Google Scholar]
- Kačmarčik, I.; Movrin, D.; Ivanišević, A. One contribution to the friction investigation in bulk metal forming. J. Technol. Plast. 2011, 36, 35–48. [Google Scholar] [CrossRef]
- Siebel, E. Resistance and deformation and the flow material during rolling. Stahl. Eisen. 1930, 50, 1769–1775. [Google Scholar]
- Joun, M.S.; Heo, Y.; Kim, N.H.; Kim, N.Y. On lubrication regime changes during forward extrusion, forging, and drawing. Lubricants 2024, 12, 352. [Google Scholar] [CrossRef]
- Wanheim, T.; Bay, N. A model for friction in metal forming processes. CIRP Ann. 1978, 27, 189–194. [Google Scholar]
- Joun, M.S. Iterative and non-iterative schemes for Coulomb frictional law in metal forming simulation and their numerical characteristics. Commun. Numer. Methods Eng. 1999, 15, 515–525. [Google Scholar] [CrossRef]
- Hwang, S.M.; Joun, M.S. Analysis of hot-strip rolling by a penalty rigid-viscoplastic finite element method. Int. J. Mech. Sci. 1992, 34, 971–984. [Google Scholar] [CrossRef]
- Zhang, Q.; Felder, E.; Bruschi, S. Evaluation of friction condition in cold forging by using T-shape compression test. J. Mater. Process. Technol. 2009, 209, 5720–5729. [Google Scholar] [CrossRef]
- Kchaou, M. New framework for studying High Temperature Tribology (HTT) using a coupling between experimental design and machine learning. Tribologia 2024, 41, 4–12. [Google Scholar] [CrossRef]
- Chenot, J.L.; Bernacki, M.; Bouchard, P.O.; Fourment, L.; Hachem, E.; Perchat, E. Recent and future developments in finite element metal forming simulation. In Proceedings of the 11th International Conference on Technology of Plasticity, Nagoya, Japan, 19–24 October 2014; pp. 265–293. [Google Scholar]
- Bambach, M. Fast simulation of incremental sheet metal forming by adaptive remeshing and subcycling. Int. J. Mater. Form. 2016, 9, 353–360. [Google Scholar] [CrossRef]
- Joun, M.S.; Lee, M.C.; Eom, J.G. Intelligent metal-forming simulation. Int. Manuf. Sci. Eng. Conf. 2011, 44304, 161–168. [Google Scholar] [CrossRef]
- Joun, M.S. Recent advances in metal forming simulation technology for automobile parts by AFDEX. IOP Conf. Ser. Mater. Sci. Eng. 2020, 834, 12016. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Sani, S.A.; Ebrahimi, G.R.; Vafaeenezhad, H.; Kiani-Rashid, A.R. Modeling of hot deformation behavior and prediction of flow stress in a magnesium alloy using constitutive equation and artificial neural network (ANN) mode. J. Magnes. Alloy. 2018, 6, 134–144. [Google Scholar] [CrossRef]
- Joun, M.S.; Razali, M.K.; Yoo, J.D.; Kim, M.C.; Choi, J.M. Novel extended C-m models of flow stress for accurate mechanical and metallurgical calculations and comparison with traditional flow models. J. Magnes. Alloy. 2022, 10, 2516–2533. [Google Scholar] [CrossRef]
- Engel, U. Tribology in microforming. Wear 2006, 260, 265–273. [Google Scholar] [CrossRef]
- Trzepiecinski, T.; Lemu, H.G. Recent developments and trends in the friction testing for conventional sheet metal forming and incremental sheet forming. Metals 2020, 10, 47. [Google Scholar] [CrossRef]
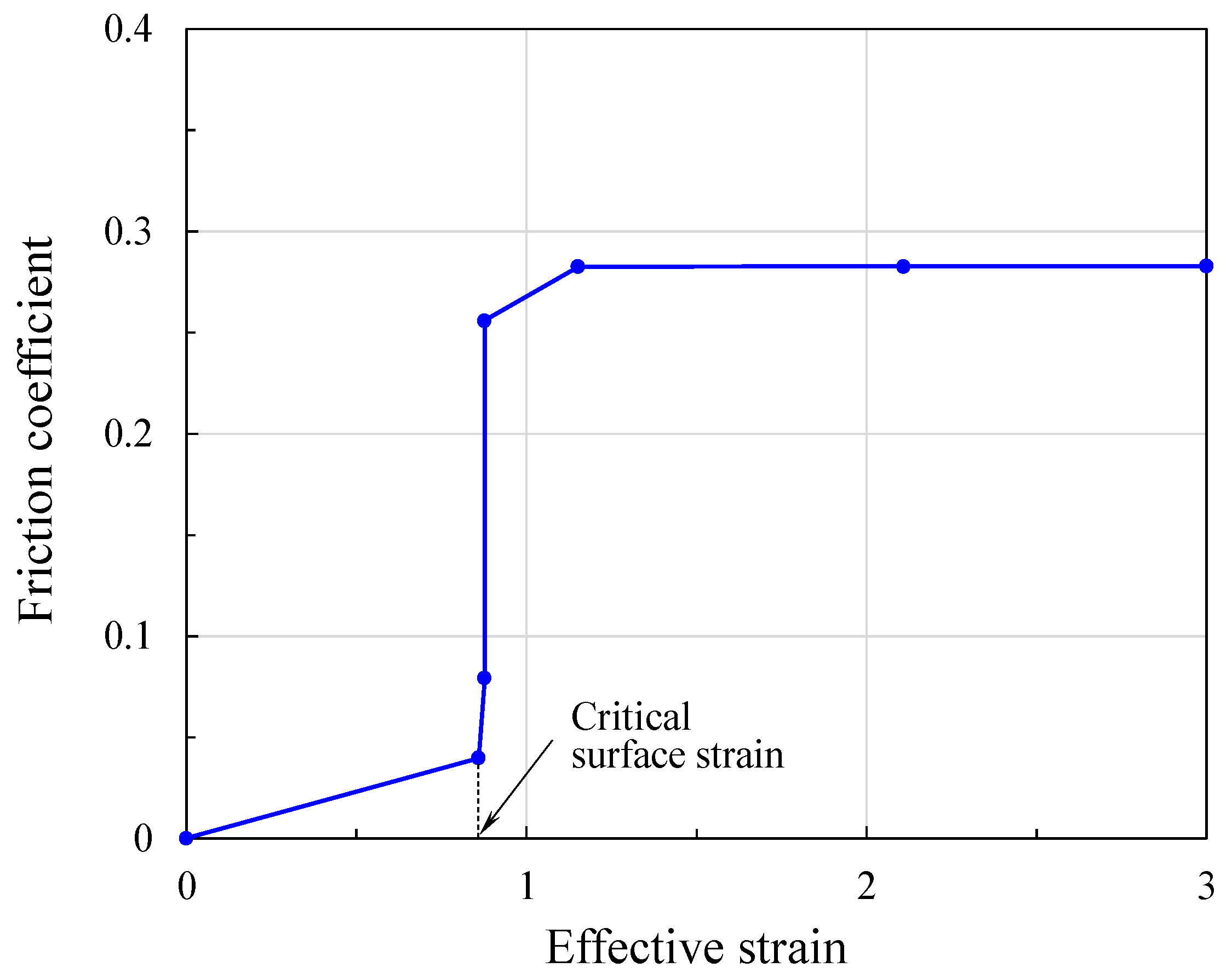
- Lee, S.W.; Lee, J.M.; Joun, M.S. On critical surface strain during hot forging of lubricated aluminum alloy. Tribol. Int. 2020, 141, 105855. [Google Scholar] [CrossRef]
- Isogawa, S.; Ito, S. Recent evaluation method for forging lubricants. Denki-Seiko 2007, 78, 249–258. [Google Scholar] [CrossRef][Green Version]
- DePierre, V.; Gurney, F. A method for determination of constant and varying friction factors during ring compression tests. J. Lubr. Technol. 1974, 96, 482–487. [Google Scholar] [CrossRef]
- Rao, K.P.; Xu, W.L. Neural evaluation of friction and flow stress adaptive to ring geometry. JSME Int. J. Ser. A Mech. Mater. Eng. 1995, 38, 506–514. [Google Scholar] [CrossRef]
- Gzyl, M.; Rosochowski, A.; Olejnik, L.; Sikora, K.; Qarni, M.J. Determination of friction factor by ring compression testing and FE analysis. Comput. Method. Mater. Sci. 2015, 15, 156–161. [Google Scholar] [CrossRef]
- Sanodiya, S.; Choudhary, K. Non conventional specimens FEA and exergy analysis effects of geometrical parameters in ring compression test. Mater. Today 2017, 4, 2580–2591. [Google Scholar] [CrossRef]
- Zhang, D.W.; Cui, M.C.; Cao, M.; Ben, N.Y.; Zhao, S.D. Determination of friction conditions in cold-rolling process of shaft part by using incremental ring compression test. Int. J. Adv. Manuf. Technol. 2017, 91, 3823–3831. [Google Scholar] [CrossRef]
- Mittelman, B.; Priel, E.; Navi, N.U. A finite element study of thermo-mechanical fields and their relation to friction conditions in Al1050 ring compression tests. J. Manuf. Mater. Proc. 2018, 2, 83. [Google Scholar] [CrossRef]
- Hill, S.; P. Turner, R. Thermo-mechanical forging of 708M40 steel ring samples: Experiments and modelling. Int. J. Adv. Manuf. Technol. 2021, 116, 2577–2590. [Google Scholar] [CrossRef]
- Dudkiewicz, Ł.; Hawryluk, M.; Ziemba, J.; Miżejewski, A.; Polak, S.; Marzec, J.; Szymańska, T. Determination of the friction coefficient in the ring test for selected lubricants dedicated to the hot forging process of precision steel products. Lubricants 2023, 11, 399. [Google Scholar] [CrossRef]
- Ebrahimi, R.; Najafizadeh, A. A new method for evaluation of friction in bulk metal forming. J. Mater. Process. Technol. 2004, 152, 136–143. [Google Scholar] [CrossRef]
- Lin, Z.C.; Chen, C.K. Inverse calculation of the friction coefficient for upsetting a cylindrical mild steel by the experimental load. J. Mater. Process. Technol. 2006, 178, 297–306. [Google Scholar] [CrossRef]
- Azushima, A.; Yoneyama, S.; Utsunomiya, H. Friction coefficient at interface of lubricated upsetting process. Wear 2012, 286–287, 3–7. [Google Scholar] [CrossRef]
- Chen, X.; Wen, T.; Liu, K.; Hong, Y. Test of friction parameters in bulk metal forming based on forward extrusion processes. J. Shanghai Jiaotong Univ. Sci. 2020, 25, 333–339. [Google Scholar] [CrossRef]
- Joun, M.S.; Ji, S.M.; Yoo, J.D.; Chung, S.H.; Moon, H.K.; Kim, E.J.; Yoon, D.J.; Choi, J.M.; Babu, A. Characterization of AZ31B, AZ61A and AZ80A magnesium alloys with an emphasis on temperature compensation for their application to a hot forging. J. Manuf. Proc. 2022, 84, 764–785. [Google Scholar] [CrossRef]
- Soranansri, P.; Dubois, A.; Moreau, P.; Funazuka, T.; Dohda, K.; Dubar, L. Identification of Coulomb and constant shear frictions in hot aluminum forming by using warm and hot upsetting sliding test. Int. J. Mater. Form. 2024, 17, 55. [Google Scholar] [CrossRef]
- Nakamura, T.; Bay, N.; Zhang, Z.L. FEM simulation of a friction testing method based on combined forward rod–backward can extrusion. J. Tribol. 1997, 119, 501–506. [Google Scholar] [CrossRef]
- Hus, T.C.; Huang, C.C. The friction modeling of different tribological interfaces in extrusion process. J. Mater. Process. Technol. 2003, 140, 49–53. [Google Scholar] [CrossRef]
- Buschhausen, A.; Weinmann, K.; Lee, J.Y.; Altan, T. Evaluation of lubrication and friction in cold forging using a double backward-extrusion process. J. Mater. Process. Technol. 1992, 33, 95–108. [Google Scholar] [CrossRef]
- Gariety, M.; Ngaile, G.; Altan, T. Evaluation of new cold forging lubricants without zinc phosphate precoat. Int. J. Mach. Tool. Manuf. 2007, 47, 673–681. [Google Scholar] [CrossRef]
- Sofuoglu, H.; Gedikli, H. Determination of friction coefficient encountered in large deformation processes. Tribol. Int. 2002, 35, 27–34. [Google Scholar] [CrossRef]
- Ito, S.; Yoshida, H.; Isogawa, S.; Doi, Y.; Dohda, K. Proposal of tribosimulator for forging by taper cup test. J. Jpn. Soc. Technol. Plast. 2007, 48, 303–307. [Google Scholar] [CrossRef]
- Takahashi, I.; Hayakawa, K.; Kubota, Y.; Ishibashi, I.; Nakamura, T. Effect of production rate on lubrication performance of environmentally-friendly lubricant in combined forward-can and backward-can cold extrusion test of aluminum alloy. Mater. Trans. 2020, 61, 289–294. [Google Scholar] [CrossRef]
- Bay, N.; Wibom, O.; Nielsen, J.A. A new friction and lubrication test for cold forging. CIRP. Ann. 1995, 44, 217–221. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Zhan, M. Friction role in bending behaviors of thin-walled tube in rotary-draw-bending under small bending radii. J. Mater. Process. Technol. 2010, 210, 2273–2284. [Google Scholar] [CrossRef]
- Ma, J.; Li, H.; Wang, D.; Fu, M.W.; Tao, Z.J. Tribological behaviors in titanium sheet and tube forming at elevated temperatures: Evaluation and modeling. Int. J. Adv. Manuf. Technol. 2018, 97, 657–674. [Google Scholar] [CrossRef]
- Xu, W.L.; Rao, K.P. Analysis of the deformation characteristics of spike-forging process through FE simulations and experiments. J. Mater. Process. Technol. 1997, 70, 122–128. [Google Scholar] [CrossRef]
- Hu, C.; Ou, H.; Zhao, Z. Investigation of tribological condition in cold forging using an optimized design of spike forging test. Adv. Mech. Eng. 2015, 7, 1687814015587212. [Google Scholar] [CrossRef]
- Hu, C.; Ding, T.; Ou, H.; Zhao, Z. Effect of tooling surface on friction conditions in cold forging of an aluminum alloy. Tribol. Int. 2019, 131, 353–362. [Google Scholar] [CrossRef]
- Kim, J.H.; Ko, B.H.; Kim, J.H.; Lee, K.H.; Moon, Y.H.; Ko, D.C. Evaluation of friction using double cup and spike forging test for dry-in-place coating and forming oils. Tribol. Int. 2020, 150, 106361. [Google Scholar] [CrossRef]
- Wang, L.; Tieu, A.K.; Wang, J.; Sang, P.T.; Xia, C.; Zhu, H.; Deng, G. High load capability, sticking scale inhabitation and promising lubrication of sodium carbonate coating for steel/steel contact at elevated temperatures. Tribol. Int. 2021, 153, 106594. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Y.; Wang, Z.; Hua, M.; Wei, X. A study on variable friction model in sheet metal forming with advanced high strength steels. Tribol. Int. 2016, 93, 17–28. [Google Scholar] [CrossRef]
- Duncan, J.L.; Shabel, B.S.; Filho, J.G. A Tensile Strip Test for Evaluating Friction in Sheet Metal Forming; SAE Technical Paper, 780391; SAE International: Pittsburgh, PA, USA, 1978. [Google Scholar] [CrossRef]
- Hao, S.; Klamecki, B.E.; Ramalingam, S. Friction measurement apparatus for sheet metal forming. Wear 1999, 224, 1–7. [Google Scholar] [CrossRef]
- Karadogan, C.; Hatipoglu, H.A. Direct evaluation of friction coefficient from sheet strip stretch test on a cylinder surface. Adv. Mater. Res. 2014, 966–967, 242–248. [Google Scholar] [CrossRef]
- Karupannasamy, D.K.; Hol, J.; de Rooij, M.B.; Meinders, T.; Schipper, D.J. A friction model for loading and reloading effects in deep drawing processes. Wear 2014, 318, 27–39. [Google Scholar] [CrossRef]
- Hu, Z.; Vollertsen, F. A new friction test method. J. Technol. Plast. 2004, 29, 1–10. [Google Scholar]
- Giuliano, G. Evaluation of the friction coefficient by the erichsen test. Appl. Mech. Mater. 2013, 365–366, 1190–1193. [Google Scholar] [CrossRef]
- Sae-eaw, N.; Aue-u-lan, Y. Evaluation of lubricant performance for thick sheet ironing process by ball ironing test. In Proceedings of the Forming the Future: Proceedings of the 13th ICTP, Online, 25–30 July 2021. [Google Scholar] [CrossRef]
- Schipper, D.J.; De Gee, A.W.J. Lubrication modes and the IRG transition diagram. Lubr. Sci. 1995, 8, 27–35. [Google Scholar] [CrossRef]
- Lee, B.H.; Keum, Y.T.; Wagoner, R.H. Modeling of the friction caused by lubrication and surface roughness in sheet metal forming. J. Mater. Process. Technol. 2002, 130–131, 60–63. [Google Scholar] [CrossRef]
- Challen, J.M.; Oxley, P.L.B. Slip-line fields for explaining the mechanics of polishing and related processes. Int. J. Mech. Sci. 1984, 26, 403–418. [Google Scholar] [CrossRef]
- Sutcliffe, M.P.F. Surface asperity deformation in metal forming processes. Int. J. Mech. Sci. 1988, 30, 847–868. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Sheu, S. Real area of contact and boundary friction in metal forming. Int. J. Mech. Sci. 1988, 30, 457–489. [Google Scholar] [CrossRef]
- Westeneng, J.D. Modelling of Contact and Friction in Deep Drawing Processes; University of Twente: Enschede, The Netherlands, 2001. [Google Scholar]
- Ma, X.; de Rooij, M.; Schipper, D. A load dependent friction model for fully plastic contact conditions. Wear 2010, 269, 790–796. [Google Scholar] [CrossRef]
- Mishra, T.; de Rooij, M.; Shisode, M.; Hazrati, J.; Schipper, D.J. An analytical model to study the effect of asperity geometry on forces in ploughing by an elliptical asperity. Tribol. Int. 2019, 137, 405–419. [Google Scholar] [CrossRef]
- Shisode, M.P.; Hazrati, J.; Mishra, T.; de Rooij, M.B.; van den Boogaard, A.H. Semi-analytical contact model to determine the flattening behavior of coated sheets under normal load. Tribol. Int. 2020, 146, 106182. [Google Scholar] [CrossRef]
- Shisode, M.; Hazrati, J.; Mishra, T.; de Rooij, M.; ten Horn, C.; van Beeck, J.; van den Boogaard, T. Modeling boundary friction of coated sheets in sheet metal forming. Tribol. Int. 2021, 153, 106554. [Google Scholar] [CrossRef]
- Jain, V.K.; Foster, B.J. Investigation of friction behaviour during non-isothermal deformation-processing. ASME Pap. PED 1991, 54, 187–201. [Google Scholar]
- Tan, X. Comparisons of friction models in bulk metal forming. Tribol. Int. 2002, 35, 385–393. [Google Scholar] [CrossRef]
- Joun, M.S. Forging Simulation; Jinsaem Media: Ansan, South Korea, 2013. [Google Scholar]
- Zhang, D.W.; Yang, H. Analytical and numerical analyses of local loading forming process of T-shape component by using Coulomb, shear and hybrid friction laws. Tribol. Int. 2015, 92, 259–271. [Google Scholar] [CrossRef]
- Bašić, H. Friction models comparison in finite volume method simulation of bulk metal forming technologies. J. Technol. Plast. 2008, 33, 113–123. Available online: https://ijiemjournal.uns.ac.rs/index.php/atm/article/view/jtp.2008.33.1-2.10 (accessed on 20 September 2025).
- Beynon, J.H. Tribology of hot metal forming. Tribol. Int. 1998, 31, 73–77. [Google Scholar] [CrossRef]
- Nielsen, C.V.; Bay, N. Review of friction modeling in metal forming processes. J. Mater. Process. Technol. 2018, 255, 234–241. [Google Scholar] [CrossRef]
- Seshacharyulu, K.; Bandhavi, C.; Naik, B.B.; Rao, S.S.; Singh, S.K. Understanding friction in sheet metal forming–A review. Mater. Today Proc. 2018, 5, 18238–18244. [Google Scholar] [CrossRef]
- Ahmad, N.A.; Samion, S.; Rahim, E.A.; Jamir, M.R.M. Environmentally approach for enhancing tribological characteristics in metal forming: A review. J. Tribol. 2020, 26, 37–59. [Google Scholar]
- Yang, X.; Liu, H.; Zhang, L.; Hu, Y.; Politis, D.J.; Gharbi, M.M.; Wang, L. Interactive mechanism and friction modelling of transient tribological phenomena in metal forming processes: A review. Friction 2024, 12, 375–395. [Google Scholar] [CrossRef]
- Aiman, Y.; Syahrullail, S.; Kameil, A.H. Tribological in metal forming progress and the use of bio lubricant as metal forming lubricant: A review. J. Teknol. 2024, 86, 95–114. [Google Scholar] [CrossRef]
- Bay, N.; Üstünyagiz, E.; Sulaiman, M.H.; Moghadam, M.; Nielsen, C.V. Review on development and testing of new tribology systems for sheet metal forming. In Proceedings of the 14th ICTP: Current Trends in the Technology of Plasticity, Online, 29 August 2023. [Google Scholar] [CrossRef]
- Challen, J.M.; Oxley, P.L.B. An explanation of the different regimes of friction and wear using asperity deformation models. Wear 1979, 53, 229–243. [Google Scholar] [CrossRef]
- Hol, J.; Meinders, V.T.; de Rooij, M.B.; van den Boogaard, A.H. Multi-scale friction modeling for sheet metal forming: The boundary lubrication regime. Tribol. Int. 2015, 81, 112–128. [Google Scholar] [CrossRef]
- Heo, Y.; Kim, N.Y.; Nam, J.W.; Chung, I.G.; Joun, M.S. Friction heat ball in round-to-half circle drawing and its effect on the material’s skin shearing. Tribol. Int. 2024, 197, 109755. [Google Scholar] [CrossRef]
- Fontalvo, G.A.; Humer, R.; Mitterer, C.; Sammt, K.; Schemmel, I. Microstructural aspects determining the adhesive wear of tool steels. Wear 2006, 260, 1028–1034. [Google Scholar] [CrossRef]
- Raj, R.; Chiu, L.N.; Marla, D.; Huang, A. Understanding the dynamics of in-situ micro-rolling in directed energy deposition using thermo-mechanical finite-element analyses. Finite Elem. Anal. Des. 2024, 238, 104194. [Google Scholar] [CrossRef]
- Navarrete, Á.; Izquierdo, J.M.; López, M.; Celentano, D.; Walczak, M.; García-Hererra, C.; Pinto, H.C. Simulation-assisted approach for determining wear-limited tool life in the coining process. Int. J. Adv. Manuf. Technol. 2020, 111, 2243–2257. [Google Scholar] [CrossRef]
- Awasthi, A.; Saxena, K.K.; Arun, V. Sustainable and smart metal forming, manufacturing process. Mater. Today Proc. 2021, 44, 2069–2079. [Google Scholar] [CrossRef]
- Geng, M.; Cai, L.; Kim, J.C.; Choi, H.S.; Hong, S.T. Recent development of dry metal forming. Int. J. Precis. Eng. Manuf. 2023, 24, 309–324. [Google Scholar] [CrossRef]
- Wilson, W.R.D. Strategy for friction modelling in computer simulations of metalforming. In Proceedings of the 16th North American Manufacturing Research Conference (NAMRC, XVI, SME), Urbana, IL, USA, 24–27 May 1988; pp. 48–54. [Google Scholar]
- Wilson, W.R.D.; Hsu, T.-C.; Huang, X.B. A realistic friction model for computer simulation of sheet metal forming processes. J. Eng. Ind. 1995, 117, 202–209. [Google Scholar] [CrossRef]
- Carleer, B.D.; Haar, R.T.; Huétink, H.; Schipper, D.J. Sheet metal forming simulations with a friction model based on local contract conditions. In Proceedings of the 3rd International Conference NUMISHEET ’96, Columbus, OH, USA, 29 September–3 October 1996; pp. 40–46. [Google Scholar]
- Westeneng, J.D.; Schipper, D.J.; ter Haar, R. Influence of deformation and roughness on friction in sheet metal forming process. In AUSTRIB ’98, Tribology at Work: Proceedings of the 5th International Tribology, Brisbane, Australia, 6–9 December 1998; Institution of Engineers: Barton, Australia, 1998; pp. 531–536. [Google Scholar]
- Johnson, K.L.; Greenwood, J.A.; Poon, S.Y. A simple theory of asperity contact in elastohydro-dynamic lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Schmid, S.R.; Jacobson, B.O. Fundamentals of Fluid Film Lubrication, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar] [CrossRef]
- Karupannasamy, D.K.; Hol, J.; de Rooij, M.B.; Meinders, T.; Schipper, D.J. Modelling mixed lubrication for deep drawing processes. Wear 2012, 294–295, 296–304. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, B.; Li, J.; Cui, M.; Zhao, S. Variation of the friction conditions in cold ring compression tests of medium carbon steel. Friction 2020, 8, 311–322. [Google Scholar] [CrossRef]
- Zhang, D.; Yang, G.; Zhao, S. Frictional behavior during cold ring compression process of aluminum alloy 5052. Chin. J. Aeronaut. 2021, 34, 47–64. [Google Scholar] [CrossRef]
- Hossen, M.S.; Westrum, J.; Shultz, M.; Tan, H.; Kim, D. Variable friction model development and implementation to the pulling force prediction of the split-sleeve cold expansion process for aluminum 2024-T3. J. Tribol. 2025, 147, 084501. [Google Scholar] [CrossRef]
- Darendeliler, H.; Akkök, M.; Yücesoy, C.A. Effect of variable friction coefficient on sheet metal drawing. Tribol. Int. 2002, 35, 97–104. [Google Scholar] [CrossRef]
- Zhang, D.W.; Ou, H. Relationship between friction parameters in a Coulomb–Tresca friction model for bulk metal forming. Tribol. Int. 2016, 95, 13–18. [Google Scholar] [CrossRef]
- Assidi, M.; Fourment, L.; Guerdoux, S.; Nelson, T. Friction model for friction stir welding process simulation: Calibrations from welding experiments. Int. J. Mach. Tool. Manuf. 2010, 50, 143–155. [Google Scholar] [CrossRef]
- Bernhardt, R. Ein Beitrag zur experimentellen und numerischen Analyse lokaler Kontaktspannungen und Kontakttemperaturen in der Wirkfuge von Gesenkgravuren unter besonderer Beachtung des Randreibungsproblems. Freib. Forschungshefte-Reihe B-Metall. Werkst. 1998, 286. Available online: https://katalog.ub.rwth-aachen.de/discovery/fulldisplay?vid=49HBZ_UBA:VU1&docid=alma991001622999706448&context=L (accessed on 20 September 2025).
- Doege, E.; Bederna, C. Analysis of boundary stress and temperatures in hot massive forming. Prod. Eng. Res. Devel. 1996, 3, 89–92. [Google Scholar]
- Hol, J.; Cid Alfaro, M.V.; de Rooij, M.B.; Meinders, T. Advanced friction modeling for sheet metal forming. Wear 2012, 286–287, 66–78. [Google Scholar] [CrossRef]
- Tzou, G.Y.; Huang, M.N. Analytical modified model of the cold bond rolling of unbounded double-layers sheet considering hybrid friction. J. Mater. Process. Technol. 2003, 140, 622–627. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Cazeault, P. Measurement of frictional conditions in lubricated strip drawing. In Proceedings of the Fourth NAMRC, Columbus, OH, USA, 17–19 May 1976; pp. 165–171. [Google Scholar]
- Lee, S.W.; Jo, J.W.; Joun, M.S.; Lee, J.M. Effect of friction conditions on material flow in FE analysis of Al piston forging process. Int. J. Precis. Eng. Manuf. 2019, 20, 1643–1652. [Google Scholar] [CrossRef]
- Tekkaya, A.E. A guide for validation of FE-simulations in bulk metal forming. Arabian J. Sci. Eng. 2005, 30, 113–136. [Google Scholar]
- Kunogi, M. A new method of cold extrusion. J. Sci. Res. Inst. 1956, 50, 215–246. [Google Scholar] [CrossRef]
- Kudo, H. Some analytical and experimental studies of axisymmetric cold forging and extrusion. Int. J. Mech. Sci. 1960, 2, 102–127. [Google Scholar] [CrossRef]
- Male, A.T.; Cockcroft, M.G. A method for the determination of the friction coefficient of metals under conditions of bulk plastic deformation. J. Inst. Met. 1964, 93, 38–46. [Google Scholar]
- Hawkyard, J.B.; Johnson, W. An analysis of the changes in geometry of a short hollow cylinder during axial compression. Int. J. Mech. Sci. 1967, 9, 163–182. [Google Scholar] [CrossRef]
- Burgdorf, M. Über die Ermittlung des Reibwertes für Verfahren der Massivumformung Durch den Ringstauchversuch. Ind. Anzeiger. 1967, 89, 799–804. [Google Scholar]
- Sofuoglu, H.; Rasty, J. On the measurement of friction coefficient utilizing the ring compression test. Tribol. Int. 1999, 32, 327–335. [Google Scholar] [CrossRef]
- Avitzur, B. Metal Forming Process and Analysis; McGraw Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Nagpal, V.; Lahoti, G.D.; Altan, T. A numerical method for simultaneous prediction of metal flow and temperatures in upset forging of rings. J. Eng. Ind. 1978, 100, 413–420. [Google Scholar] [CrossRef]
- Petersen, S.B.; Martins, P.A.F.; Bay, N. Friction in bulk metal forming—A general friction model vs. the law of constant friction. J. Mater. Process. Technol. 1997, 66, 186–194. [Google Scholar] [CrossRef]
- Zhu, Y.; Zeng, W.; Ma, X.; Tai, Q.; Li, Z.; Li, X. Determination of the friction factor of Ti– 6Al–4V titanium alloy in hot forging by means of ring-compression test using FEM. Tribol. Int. 2011, 44, 2074–2080. [Google Scholar] [CrossRef]
- Cristino, V.A.M.; Rosa, P.A.R.; Martins, P.A.F. Surface roughness and material strength of tribo-pairs in ring compression tests. Tribol. Int. 2011, 44, 134–143. [Google Scholar] [CrossRef]
- Rao, K.P.; Prasad, Y.; Xie, C.L. Further evaluation of boric acid vis-à-vis other lubricants for cold forming applications. Tribol. Int. 2011, 44, 1118–1126. [Google Scholar] [CrossRef]
- Noh, J.H.; Min, K.H.; Hwang, B.B. Deformation characteristics at contact interface in ring compression. Tribol. Int. 2011, 44, 947–955. [Google Scholar] [CrossRef]
- Zhang, D.W.; Yang, H.; Li, H.W.; Fan, X.G. Friction factor evaluation by FEM and experiment for TA15 titanium alloy in isothermal forming process. Int. J. Adv. Manuf. Technol. 2012, 60, 527–536. [Google Scholar] [CrossRef]
- Joun, M.S.; Chung, W.J.; Hong, S.M. Macroscopic Modeling of Metal Forming Processes by FEM; Jinsaem Media: Ansan, Republic of Korea, 2019. [Google Scholar]
- Rajesh, E.; SivaPrakash, M. Analysis of friction factor by employing the ring compression test under different lubricants. Int. J. Sci. Eng. Res. 2013, 4, 1163–1171. [Google Scholar]
- Ghassemali, E.; Song, X.; Zarinejad, M.; Atsushi, D.; Tan, M.J. Bulk metal forming processes in manufacturing. In Handbook of Manufacturing Engineering and Technology; Springer: London, UK, 2013; pp. 1–50. [Google Scholar]
- Kuzman, K.; Pfeifer, E.; Bay, N.; Hunding, J. Control of material flow in a combined backward can—Forward rod extrusion. J. Mater. Process. Technol. 1996, 60, 141–147. [Google Scholar] [CrossRef]
- Huang, M.N.; Tzou, G.Y. Study on compression forming of a rotating disk considering hybrid friction. J. Mater. Process. Technol. 2002, 125–126, 421–426. [Google Scholar] [CrossRef]
- Heo, Y.; Joun, M.S. Dependence of contact states of friction. In Proceedings of the Korean Society of Technology of Plasticity (KSTP), Jeju, Republic of Korea, 17 October 2024; p. 140. [Google Scholar]
- Joun, M.S.; Eom, J.G.; Lee, M.C. A new method for acquiring true stress-strain curves over a large range of strains using a tensile test and finite element method. Mech. Mater. 2008, 40, 586–593. [Google Scholar] [CrossRef]
- Kim, N.Y.; Kim, N.H.; Razali, M.K.; Lee, H.M.; Joun, M.S. Analytical and numerical evaluation of the relationship between elongation calibration function and cyber standard tensile tests for ductile materials. Mater. Des. 2025, 253, 113851. [Google Scholar] [CrossRef]
- Hersey, M.D. The laws of lubrication of horizontal journal bearings. J. Wash. Acad. Sci. 1914, 4, 542–552. Available online: https://www.jstor.org/stable/24520857 (accessed on 20 September 2025).
- Bowden, F.P.; Tabor, D. The lubrication by thin metallic films and the action of bearing metals. J. Appl. Phys. 1943, 14, 141–151. [Google Scholar] [CrossRef]
- Green, A.P. Friction between unlubricated metals: A theoretical analysis of the junction model. Math. Phys. Sci. Eng. 1955, 228, 191–204. [Google Scholar] [CrossRef]
- Montgomery, R.S. Chemical effects on wear in the lubrication of aluminum. Wear 1965, 8, 289–302. [Google Scholar] [CrossRef]
- Nayak, P.R. Random process model of rough surfaces. J. Lubr. Technol. 1971, 93, 398–407. [Google Scholar] [CrossRef]
- Wilson, W.R.D. The temporary breakdown of hydrodynamic lubrication during the initiation of extrusion. Int. J. Mech. Sci. 1971, 13, 17–28. [Google Scholar] [CrossRef]
- Booker, J.F.; Huebner, K.H. Application of finite element methods to lubrication: An engineering approach. J. Lubr. Technol. 1972, 94, 313–323. [Google Scholar] [CrossRef]
- Challen, J.M.; Oxley, P.L.B. A slip line field analysis of the transition from local asperity contact to full contact in metallic sliding friction. Wear 1984, 100, 171–193. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Wang, J.J. Hydrodynamic lubrication in simple stretch forming processes. J. Tribol. 1984, 106, 70–77. [Google Scholar] [CrossRef]
- Black, A.J.; Kopalinsky, E.M.; Oxley, P.L.B. An investigation of the different regimes of deformation which can occur when a hard wedge slides over a soft surface: The influence of wedge angle, lubrication and prior plastic working of the surface. Wear 1988, 123, 97–114. [Google Scholar] [CrossRef]
- Wilson, W.R.D. Friction models for metal forming in the boundary lubrication regime. J. Eng. Mater. Technol. 1991, 113, 60–68. [Google Scholar] [CrossRef]
- Bay, N.; Eriksen, M.; Tan, X.; Wibom, O. A friction model for cold forging of aluminum, steel and stainless steel provided with conversion coating and solid film lubricant. CIRP Ann. 2011, 60, 303–306. [Google Scholar] [CrossRef]
- Godfrey, D. The lubrication mechanism of tricresyl phosphate on steel. ASLE Trans. 1965, 8, 1–11. [Google Scholar] [CrossRef]
- Kim, S.M.; Sit, C.Y.; Komvopoulos, K.; Yamaguchi, E.S.; Ryason, P.R. Boundary lubrication of steel surfaces with borate, phosphorus, and sulfur containing lubricants at relatively low and elevated temperatures. Tribol. Trans. 2000, 43, 569–578. [Google Scholar] [CrossRef]
- Johnson, D.W.; Morrow, S.; Forster, N.H.; Saba, C.S. Vapor-phase lubrication: Reaction of phosphate ester vapors with iron and steel. Chem. Mater. 2002, 14, 3767–3775. [Google Scholar] [CrossRef]
- Farias, M.C.M.; Santos, C.A.L.; Panossian, Z.; Sinatora, A. Friction behavior of lubricated zinc phosphate coatings. Wear 2009, 266, 873–877. [Google Scholar] [CrossRef]
- Bay, N. New tribo-system for cold forging of steel, stainless steel and aluminum alloys. In Proceedings of the 46th ICFG Plenary Meeting, Paris, France, 15 September 2013; pp. 171–178. [Google Scholar]
- Dubois, A.; Dubar, M.; Dubar, L. Warm and hot upsetting sliding test: Tribology of metal processes at high temperature. Procedia Eng. 2014, 81, 1964–1969. [Google Scholar] [CrossRef]
- Wang, Z.G.; Komiyama, S.; Yoshikawa, Y.; Suzuki, T.; Osakada, K. Evaluation of lubricants without zinc phosphate precoat in multi-stage cold forging. CIRP Ann. 2015, 64, 285–288. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H. Influence of manganese phosphating on wear resistance of steel piston material under boundary lubrication condition. Surf. Coat. Technol. 2016, 304, 530–536. [Google Scholar] [CrossRef]
- Lorenz, R.; Hagenah, H.; Merklein, M. Experimental evaluation of cold forging lubricants using double-cup-extrusion-tests. Mater. Sci. Forum. 2018, 918, 65–70. [Google Scholar] [CrossRef]
- Fleming, C. An investigation into the behaviour of selected boundary regime lubricants when cold forging steel under rolling-sliding conditions. Tribol. Int. 2021, 157, 106771. [Google Scholar] [CrossRef]
- Bay, N.; Olsson, D.D.; Andreasen, J.L. Lubricant test methods for sheet metal forming. Tribol. Int. 2008, 41, 844–853. [Google Scholar] [CrossRef]
- Byon, S.M.; Lee, S.J.; Lee, D.W.; Lee, Y.H.; Lee, Y. Effect of coating material and lubricant on forming force and surface defects in wire drawing process. TNMS China 2011, 21, 104–110. [Google Scholar] [CrossRef]
- Bay, N. The state of the art in cold forging lubrication. J. Mater. Process. Technol. 1994, 46, 19–40. [Google Scholar] [CrossRef]
- Manisekar, K.; Narayanasamy, R. Barreling in square billets of aluminum during cold upset forging under dissimilar friction. Trans. Indian Inst. Met. 2004, 57, 141–147. Available online: https://d1wqtxts1xzle7.cloudfront.net/79316149/TP-1882-libre.pdf (accessed on 21 September 2025).
- Malayappan, S.; Narayanasamy, R. An experimental analysis of upset forging of aluminum cylindrical billets considering the dissimilar frictional conditions at flat die surfaces. Int. J. Adv. Manuf. Technol. 2004, 23, 636–643. [Google Scholar] [CrossRef]
- Petrov, P. Generalized approach to the choice of lubricant for hot isothermal forging of aluminum alloys. Comput. Methods Mater. Sci. 2007, 7, 106–111. Available online: https://www.cmms.agh.edu.pl/public_repo/2007_1_0128.pdf (accessed on 22 September 2025).
- Baskaran, K.; Narayanasamy, R. Some aspects of barreling in elliptical shaped billets of aluminum during cold upset forging with lubricant. Mater. Des. 2008, 29, 638–661. [Google Scholar] [CrossRef]
- Narayanasamy, R.; Baskaran, K.; Arunachalam, S.; Krishna, D.M. An experimental investigation on barreling of aluminum alloy billets during extrusion forging using different lubricants. Mater. Des. 2008, 29, 2076–2088. [Google Scholar] [CrossRef]
- Sagisaka, Y.; Nakamura, T.; Hayakawa, K.; Ishibashi, I. Evaluation of environmentally friendly lubricant for aluminum cold forging using friction test based on spline extrusion. J. Manuf. Process. 2013, 15, 96–101. [Google Scholar] [CrossRef]
- Feyzullahoğlu, E.; Ertürk, A.T.; Güven, E.A. Influence of forging and heat treatment on wear properties of Al–Si and Al–Pb bearing alloys in oil lubricated conditions. Trans. Nonferrous Met. Soc. China 2013, 23, 3575–3583. [Google Scholar] [CrossRef]
- Medea, F.; Ghiotti, A.; Bruschi, S. Temperature effects on organic lubricants in cold forging of AA1050 alloy. Procedia. Manuf. 2016, 5, 308–318. [Google Scholar] [CrossRef]
- Priyadarshini, A.; Kiran, C.P.; Suresh, K. Effect of friction on barreling during cold upset forging of aluminum 6082 alloy solid cylinders. Mater. Sci. Eng. 2018, 330, 012072. [Google Scholar] [CrossRef]
- Yang, X.; Liu, X.; Liu, H.; Politis, D.J.; Leyvraz, D.; Wang, L. Experimental and modelling study of friction evolution and lubricant breakdown behaviour under varying contact conditions in warm aluminum forming processes. Tribol. Int. 2021, 158, 106934. [Google Scholar] [CrossRef]
- Schell, L.; Emele, M.; Holzbeck, A.; Groche, P. Investigation of different lubricant classes for aluminum warm and hot forming based on a strip drawing test. Tribol. Int. 2022, 168, 107449. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Arsenault, R.J.; Beeler, J.R.; Esterling, D.M. Friction modeling in forging. In Computer Simulation in Material Science; American Society for Metals: Detroit, MI, USA, 1988; pp. 237–267. [Google Scholar]
- Sun, Z.; Wu, C.S.; Kumar, S. Determination of heat generation by correlating the interfacial friction stress with temperature in friction stir welding. J. Manuf. Proc. 2018, 31, 801–811. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Fejkiel, R. On the influence of deformation of deep drawing quality steel sheet on surface topography and friction. Tribol. Int. 2017, 115, 78–88. [Google Scholar] [CrossRef]
- Kondratiuk, J.; Kuhn, P. Tribological investigation on friction and wear behaviour of coatings for hot sheet metal forming. Wear 2011, 270, 839–849. [Google Scholar] [CrossRef]





| Topics | Keywords | Section |
|---|---|---|
| Tribological issues in metal forming | Tribological issues, friction, lubrication | Section 2.1 |
| Various factors affecting friction | Pressure, relative velocity, lubricant, temperature, strain rate, surface expansion | Section 2.2 |
| Lubrication regime and LRC | Thick film, thin film, mixed, boundary lubrication, LRC | Section 2.3 |
| Identification of friction laws | Nominal friction stress, friction law, Coulomb, constant shear, general, hybrid, smoothing function | Section 3.1 |
| Modified friction laws for the varying friction condition during metal forming | Generalized friction coefficient parameter, critical surface strain, LRC, state variable effect | Section 3.2 |
| Issues regarding the CFL and sticking phenomenon | Penalty scheme, sticking, CFL | Section 3.3 |
| Ring compression test | Ring compression, friction calibration, sticking, friction hill | Section 3.4 |
| Similarity and difference between CFL and CSFL | CFL, CoCSFL | Section 3.5 |
| Critique of traditional friction laws with a constant friction coefficient or factor | Constant friction coefficient, constant friction factor, LRC, forward extrusion, | Section 3.6 |
| HFL and state variabilization of the friction coefficient and factor | Hybrid friction law (HFL), friction coefficient | Section 3.7 |
| Typical examples of LRC | Critical surface strain, cold forward and backward extrusion, hot forging, low strain hardening | Section 3.8 |
| Lubricants | Lubricant | Section 4 |
| Friction test and acquisition of tribological parameters | Friction test, tribometer | Section 5 |
| Friction Law | Formulation | Features | Reference |
|---|---|---|---|
| CFL | Equation (1) | Constant friction coefficient Large normal stress issue | [73] |
| CSFL | Equation (2) | Constant friction factor Low normal stress issue | [75] |
| GFL | Equation (3) | Improved CSFL, contact area ratio | [77] |
| HFL | Equation (4) | Combined CFL and CSFL | [12,143,171] |
| Neumaier friction law | Equation (8) | Modified CSFL | [141] |
| Norton friction law | Equation (9) | Viscous friction model | [172] |
| IFUM friction law | Equation (10) | Mixed friction law of CFL and CSFL | [68] |
| Bernhardt friction law | Equation (11) | Avoid the normal stress issue in the CFL | [173] |
| Coulomb–Amonton friction law | Equation (12) | Avoid the normal stress issue in the CFL | [174] |
| Hol et al.’s FL | None | Not a closed-form function model considering the surface texture change | [175] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joun, M.S.; Park, M.C.; Heo, Y.; Kim, D.H. A Review of Friction and Lubricant in Metal Forming. Lubricants 2025, 13, 512. https://doi.org/10.3390/lubricants13120512
Joun MS, Park MC, Heo Y, Kim DH. A Review of Friction and Lubricant in Metal Forming. Lubricants. 2025; 13(12):512. https://doi.org/10.3390/lubricants13120512
Chicago/Turabian StyleJoun, Man Soo, Min Cheol Park, Yun Heo, and Dong Hwan Kim. 2025. "A Review of Friction and Lubricant in Metal Forming" Lubricants 13, no. 12: 512. https://doi.org/10.3390/lubricants13120512
APA StyleJoun, M. S., Park, M. C., Heo, Y., & Kim, D. H. (2025). A Review of Friction and Lubricant in Metal Forming. Lubricants, 13(12), 512. https://doi.org/10.3390/lubricants13120512





