Primary Prediction of Oil Film Cavitation Between Rotating Friction Pairs with Various Types of Surface Textures
Abstract
1. Introduction
- (1)
- Comparatively investigating the influence of three typical micro-texture shapes—hexahedral, cylindrical, and hemispherical—at different area ratios on the evolution process of oil film cavitation.
- (2)
- Elucidating the underlying physical mechanisms connecting key texture parameters (geometry, area ratio, and depth) with the inception location, development pattern, and final intensity of cavitation.
- (3)
- Proposing an optimized design strategy for textures aimed at suppressing cavitation while ensuring a sufficient hydrodynamic pressure effect, based on the analysis of the flow and pressure fields.
- (4)
- Validating the effectiveness of the simulation results through high-speed photography and torque measurement experiments and revealing the actual impact of texturing on torque transmission characteristics.
2. Materials and Methods
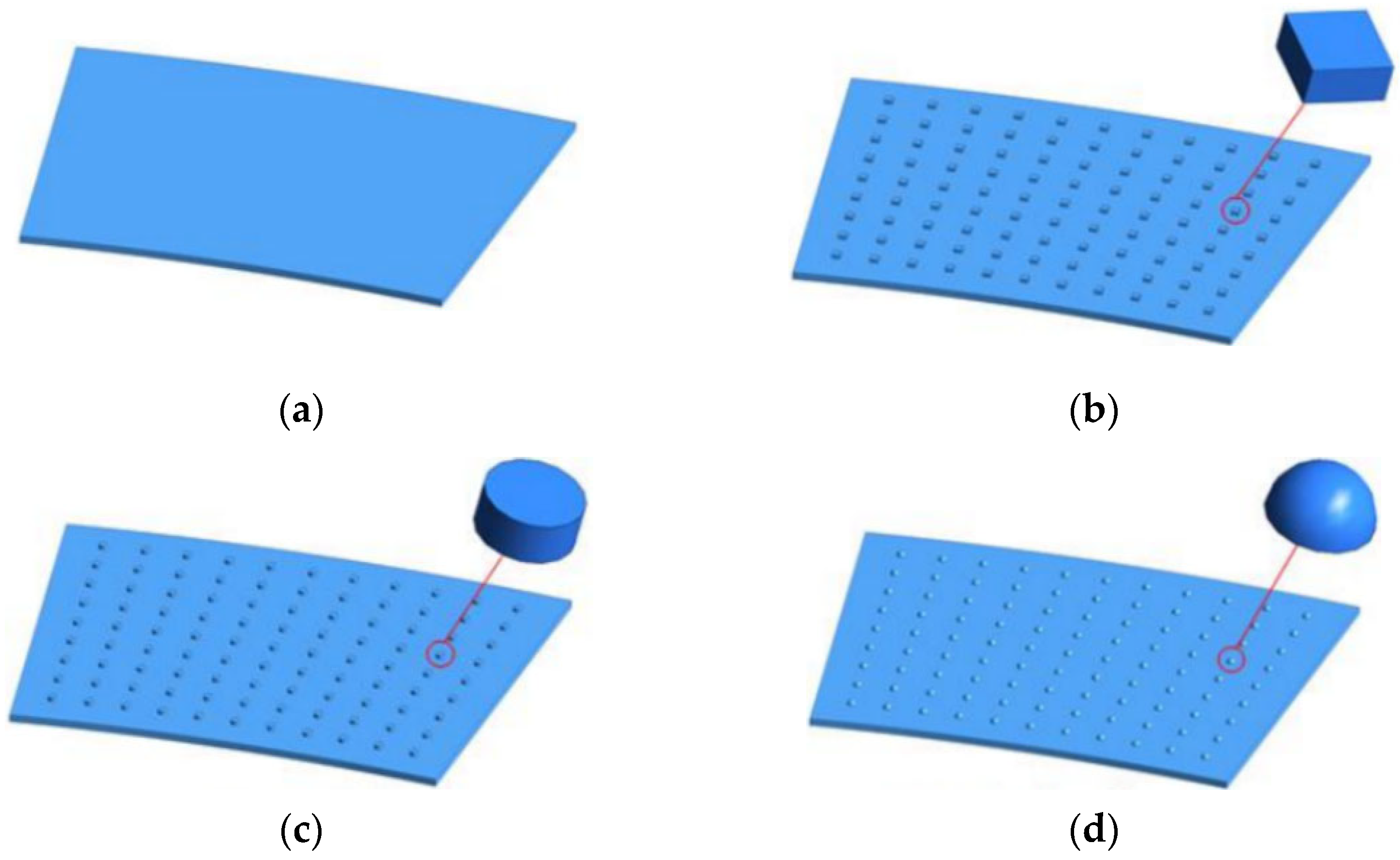
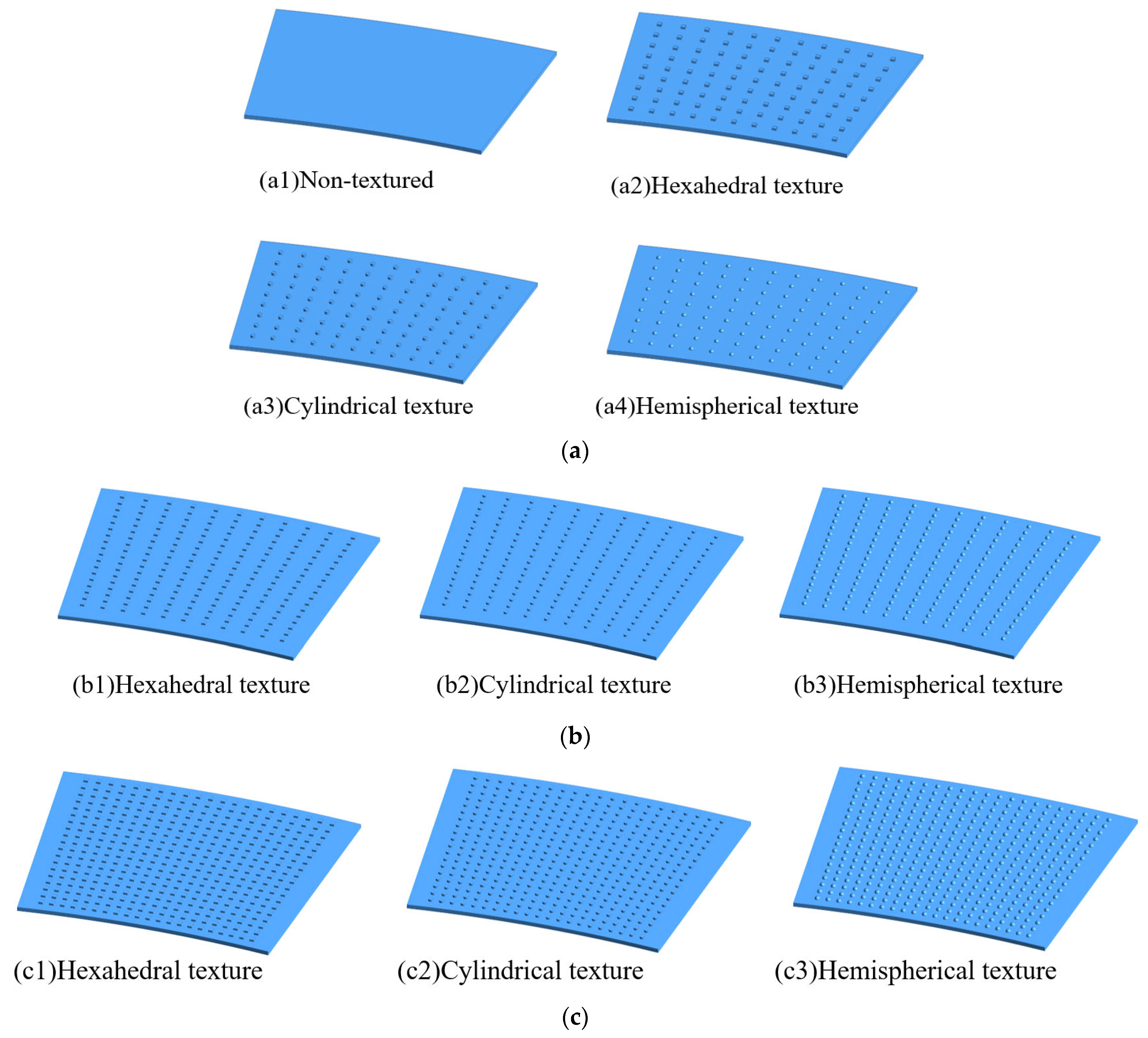
2.1. Surface Texture Design
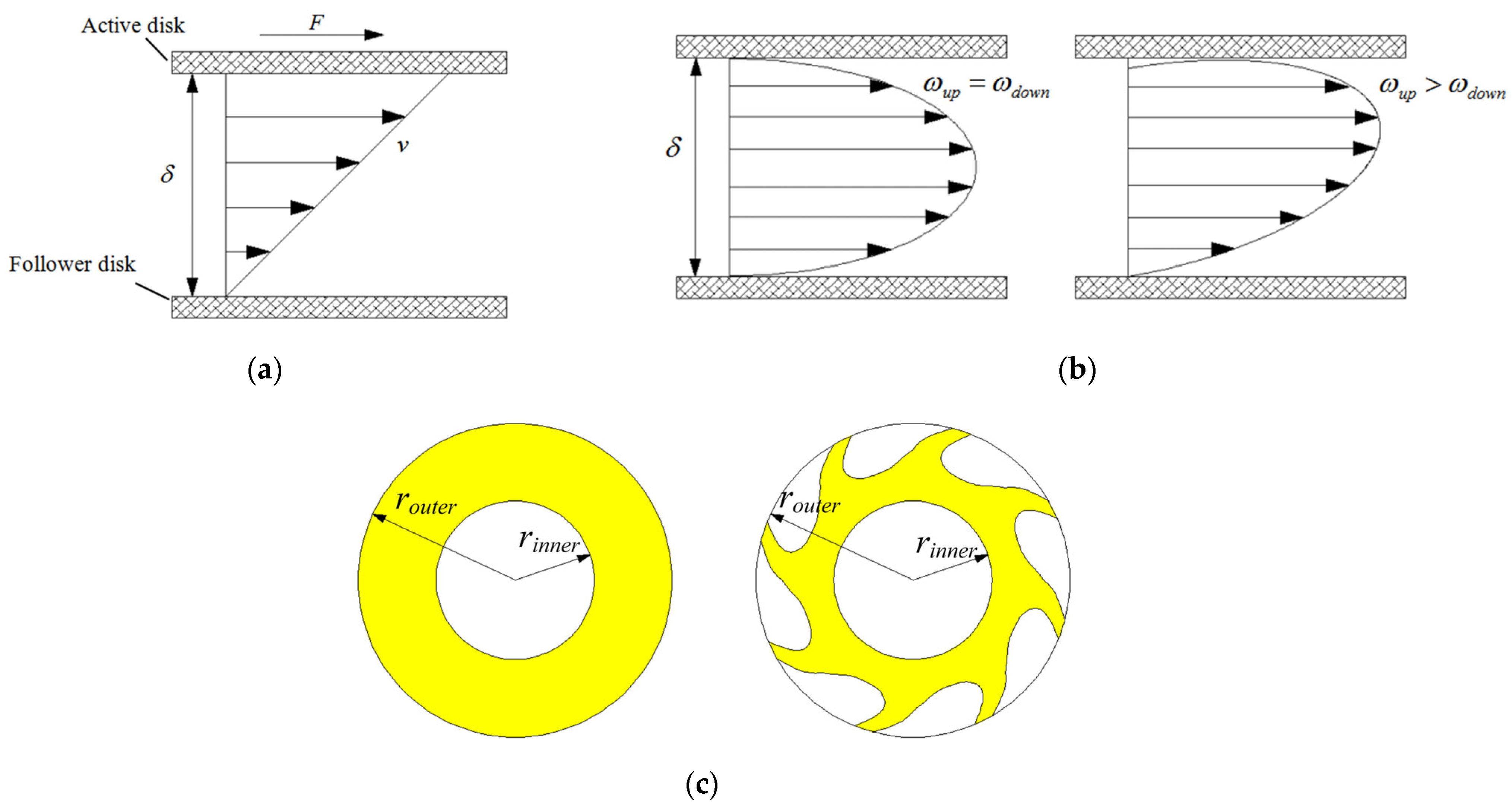
2.2. Operating Mechanism of Hydrodynamic Lubrication in Rotational Friction Interfaces
2.3. The Primary Mechanism and Critical Conditions of Cavitation
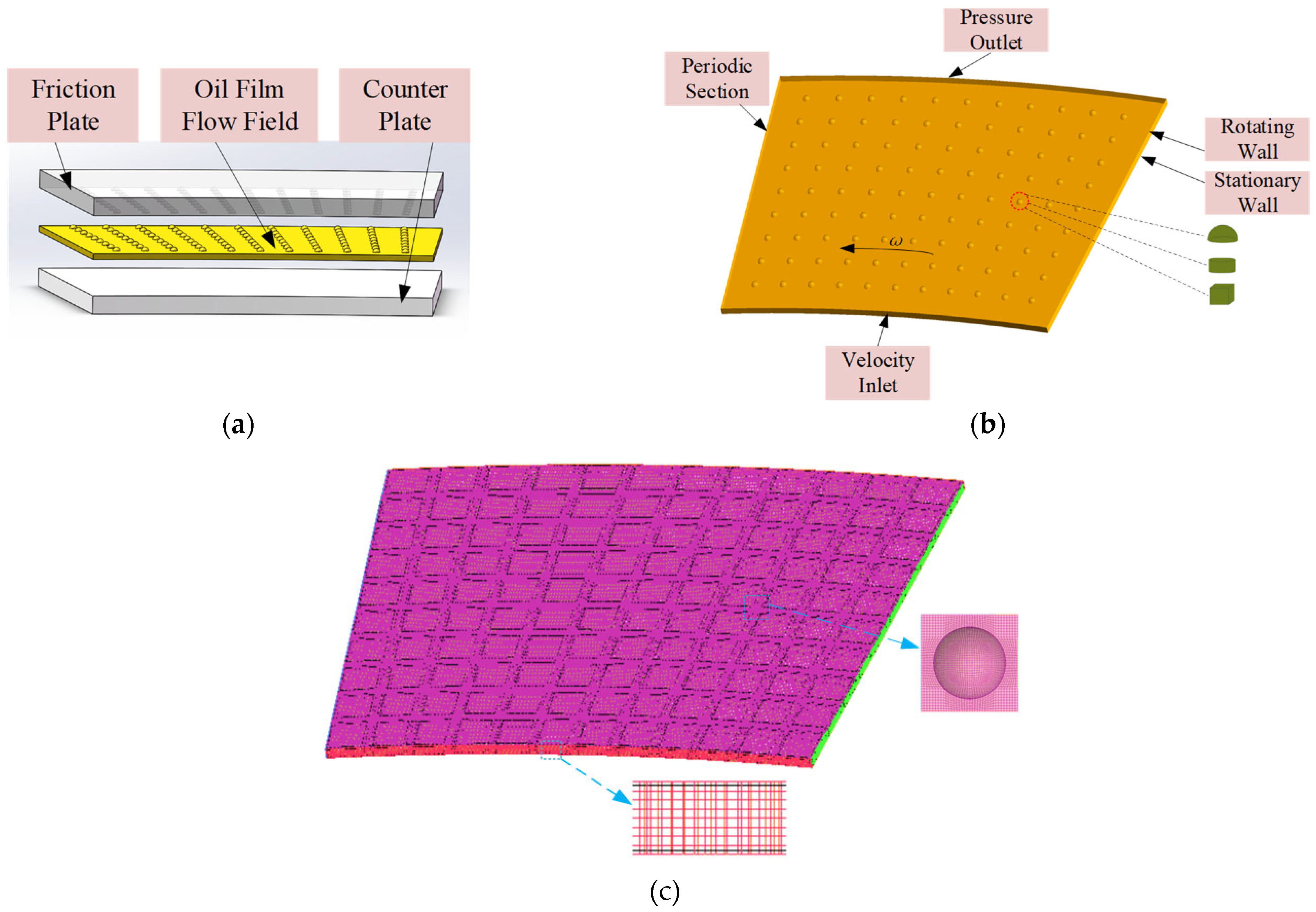
2.4. Simulation Test Method
2.4.1. Finite Element Modeling of Oil Film
2.4.2. Simulation and Experimental Study of Oil Films with Different Types of Surface Textures
2.5. Experimental Validation
3. Results and Discussion
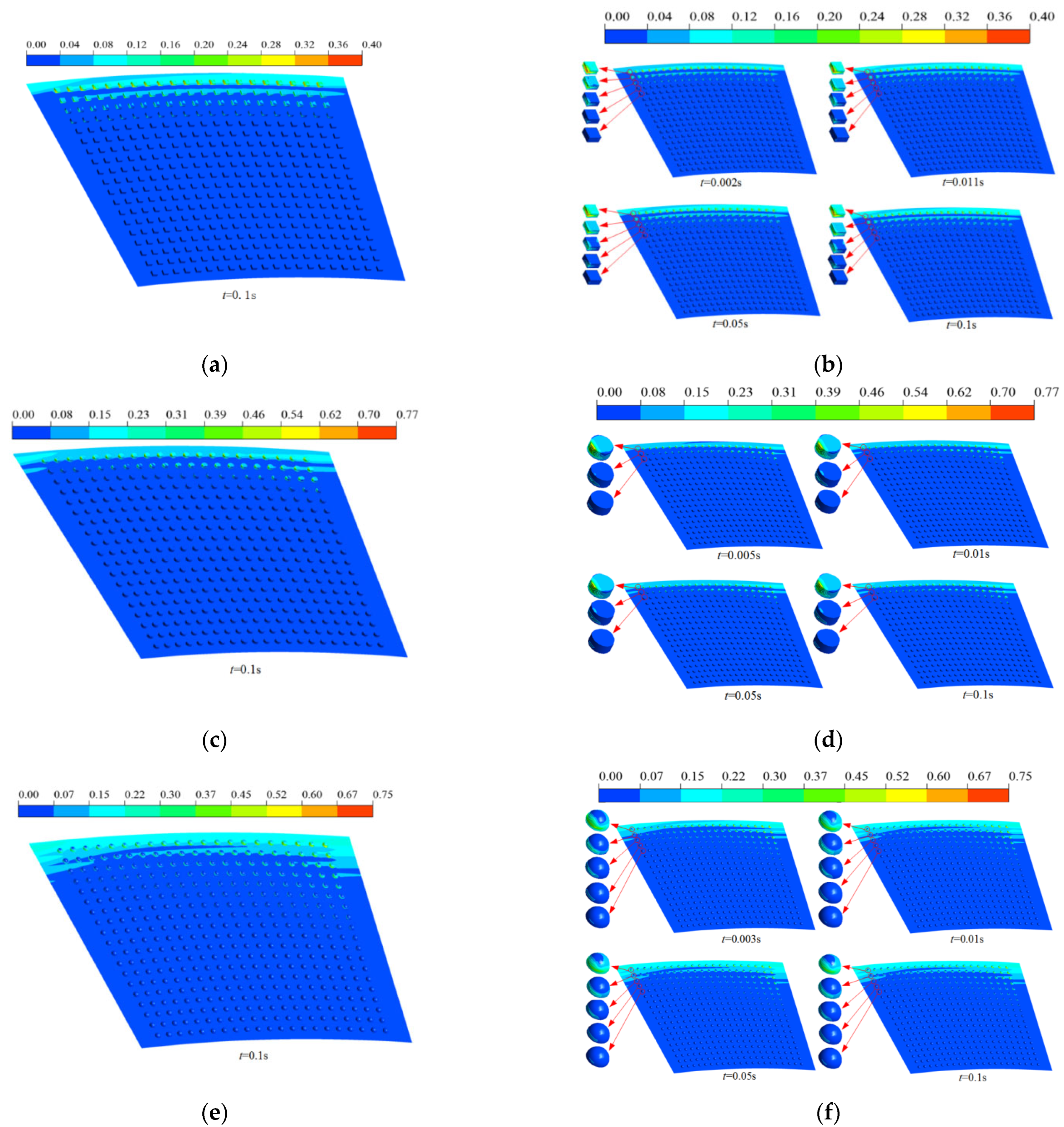
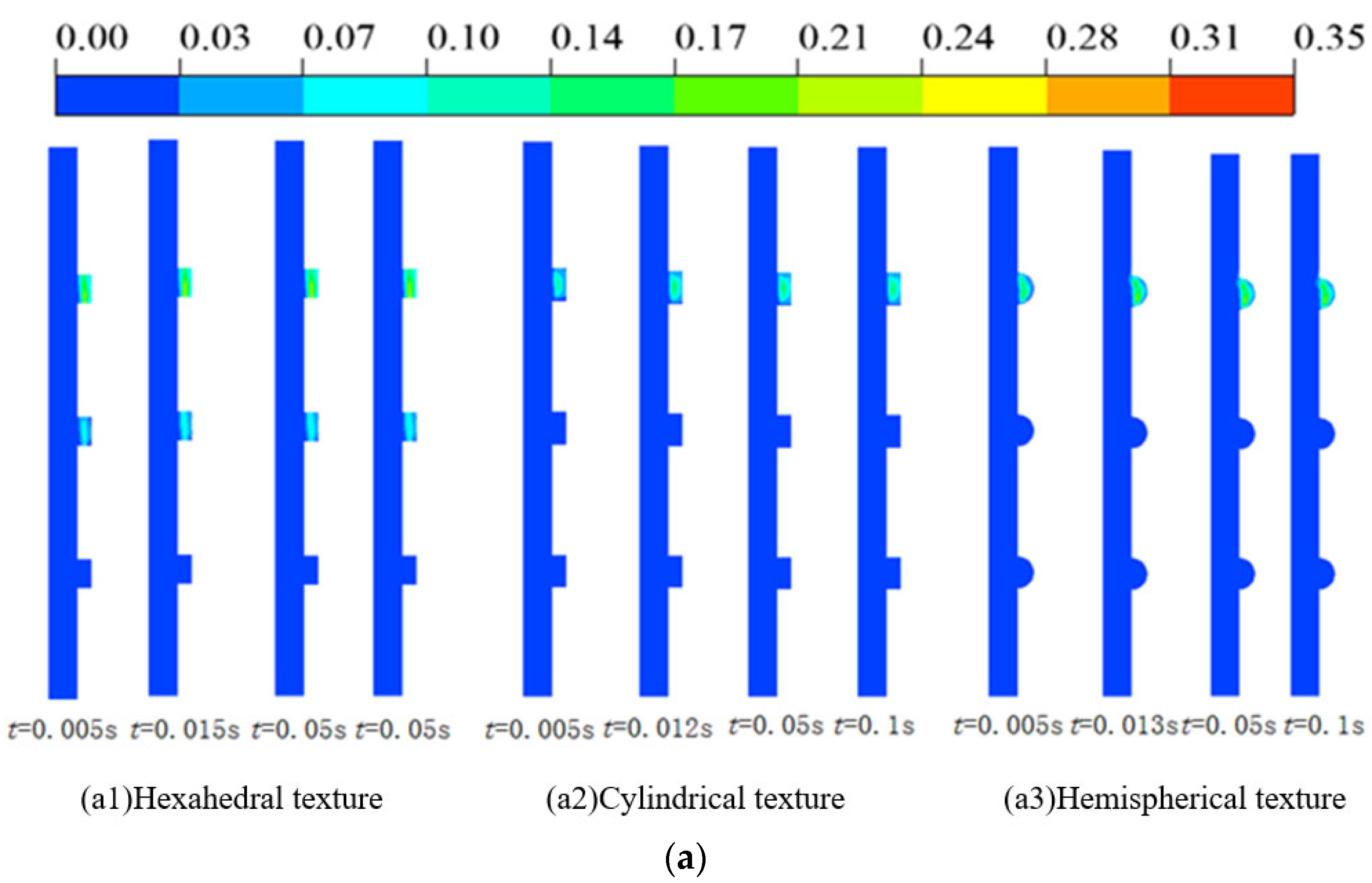
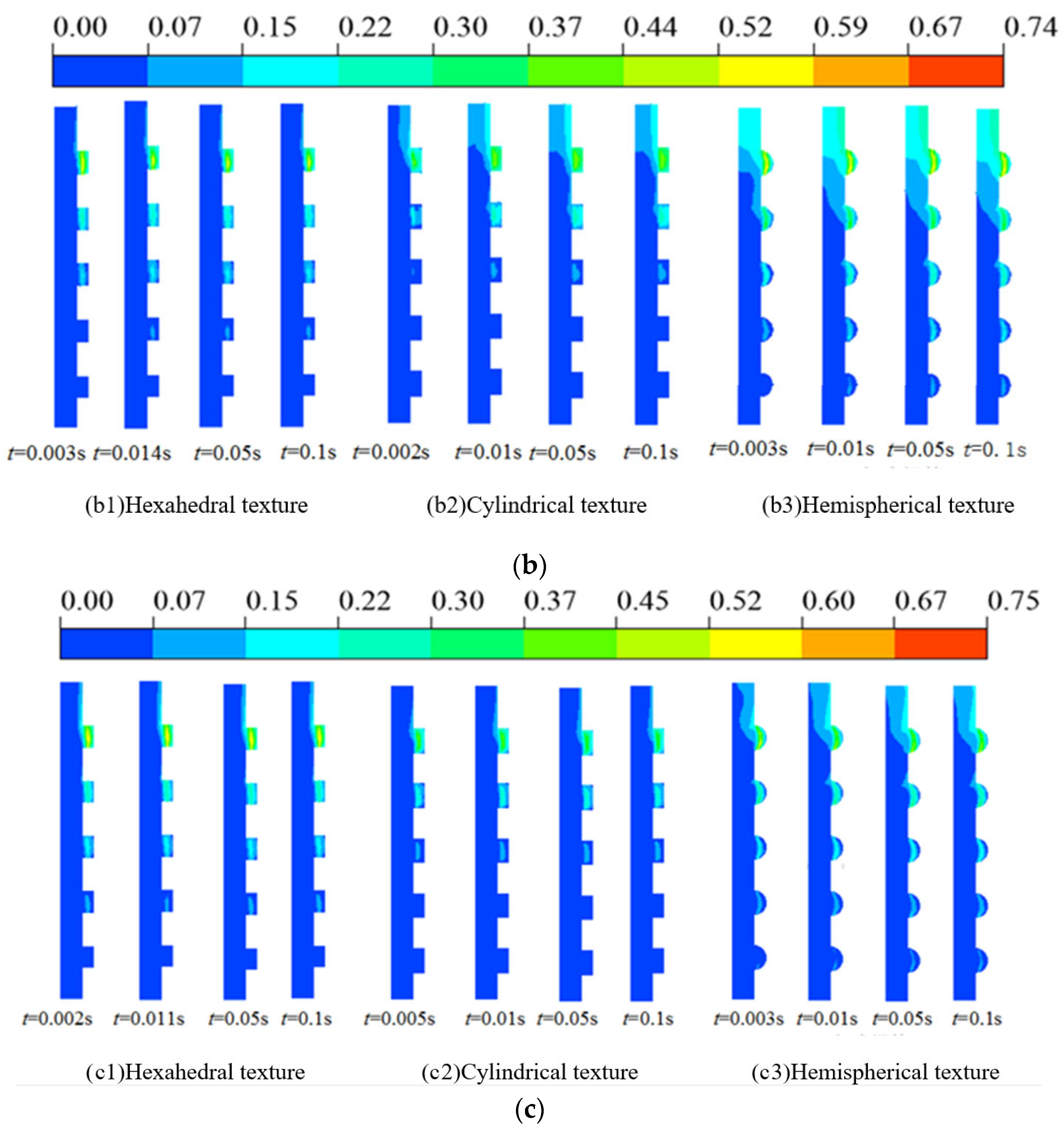
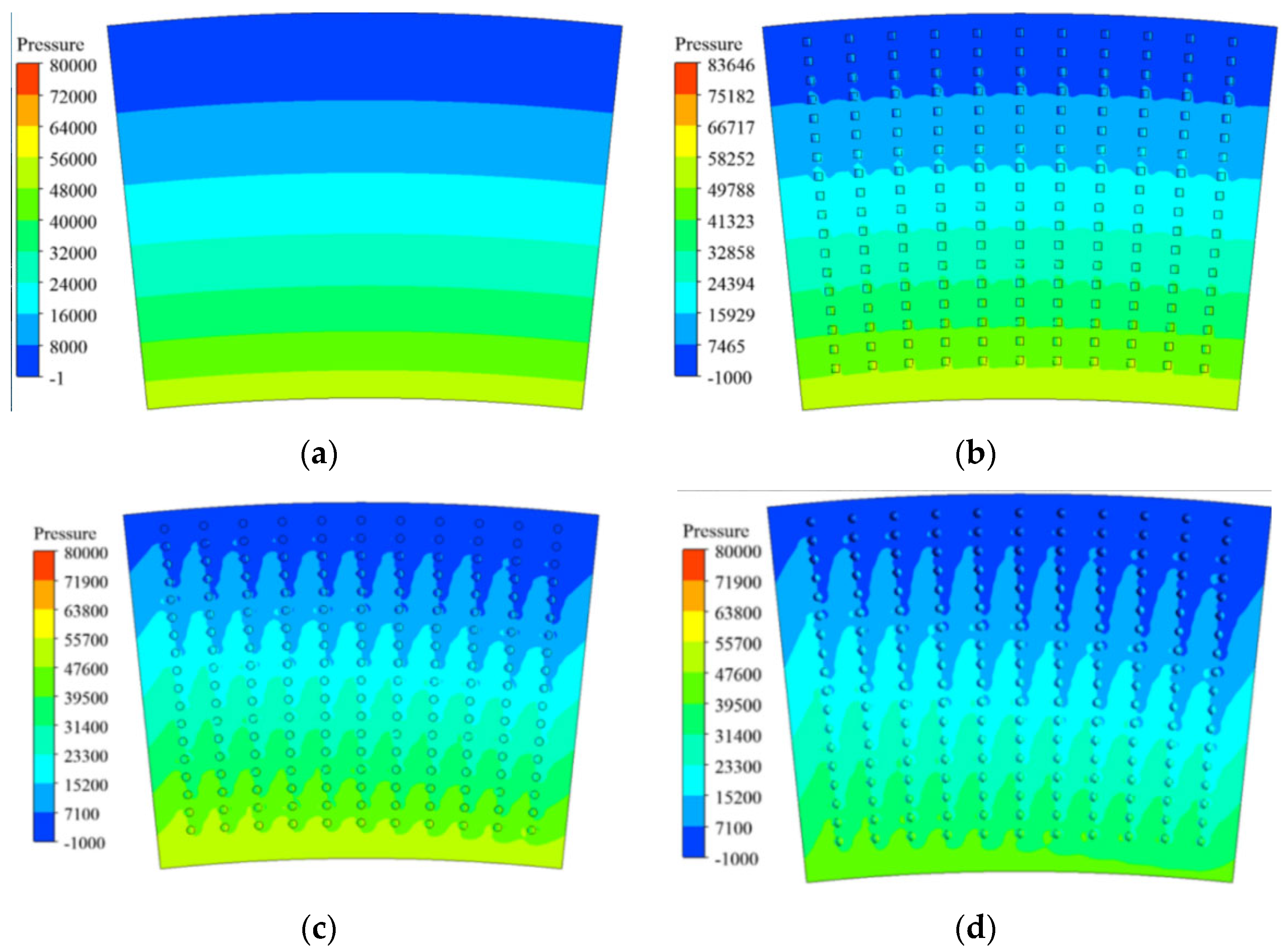
3.1. Simulation Results of Different Surface Textures
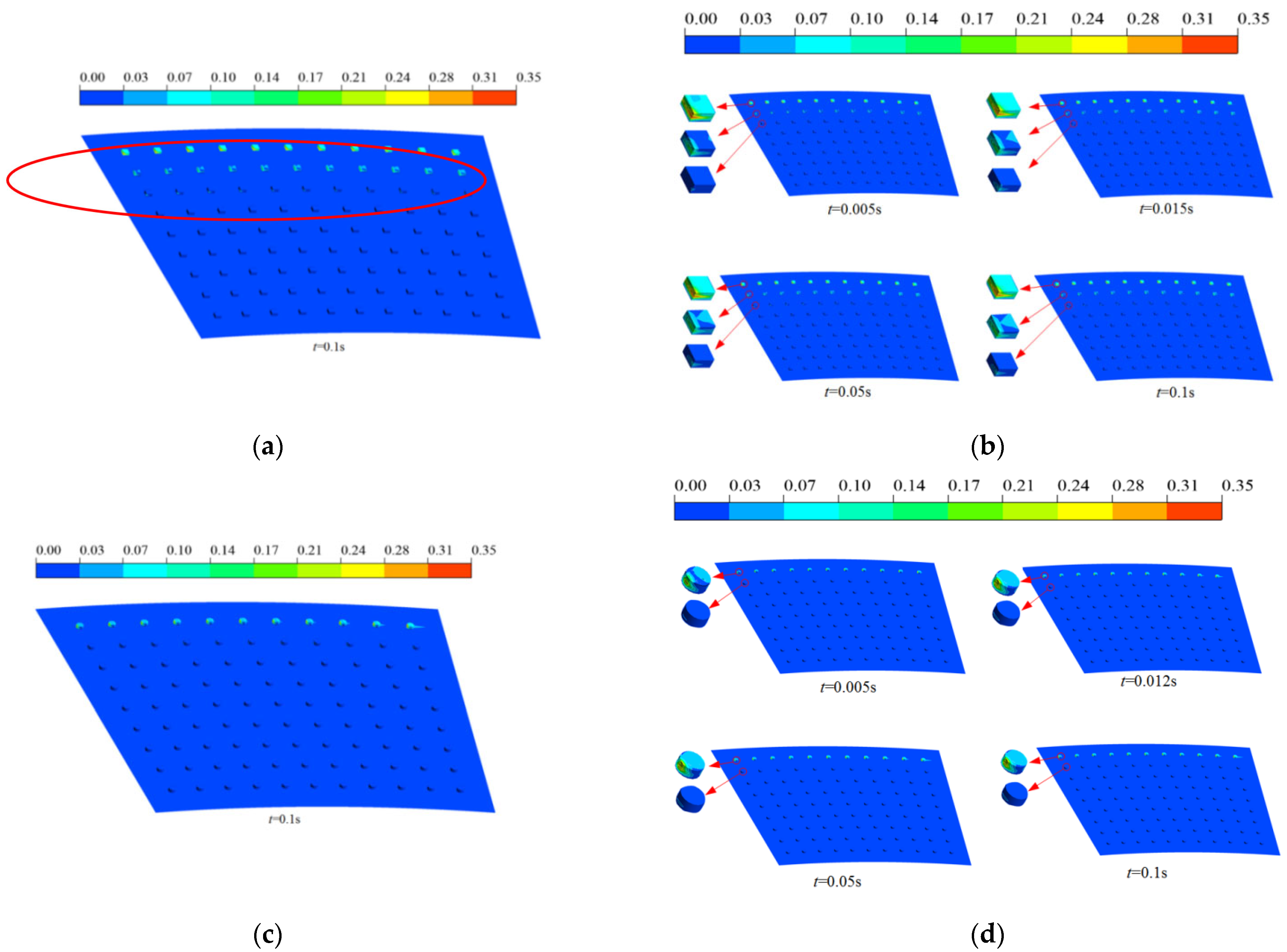
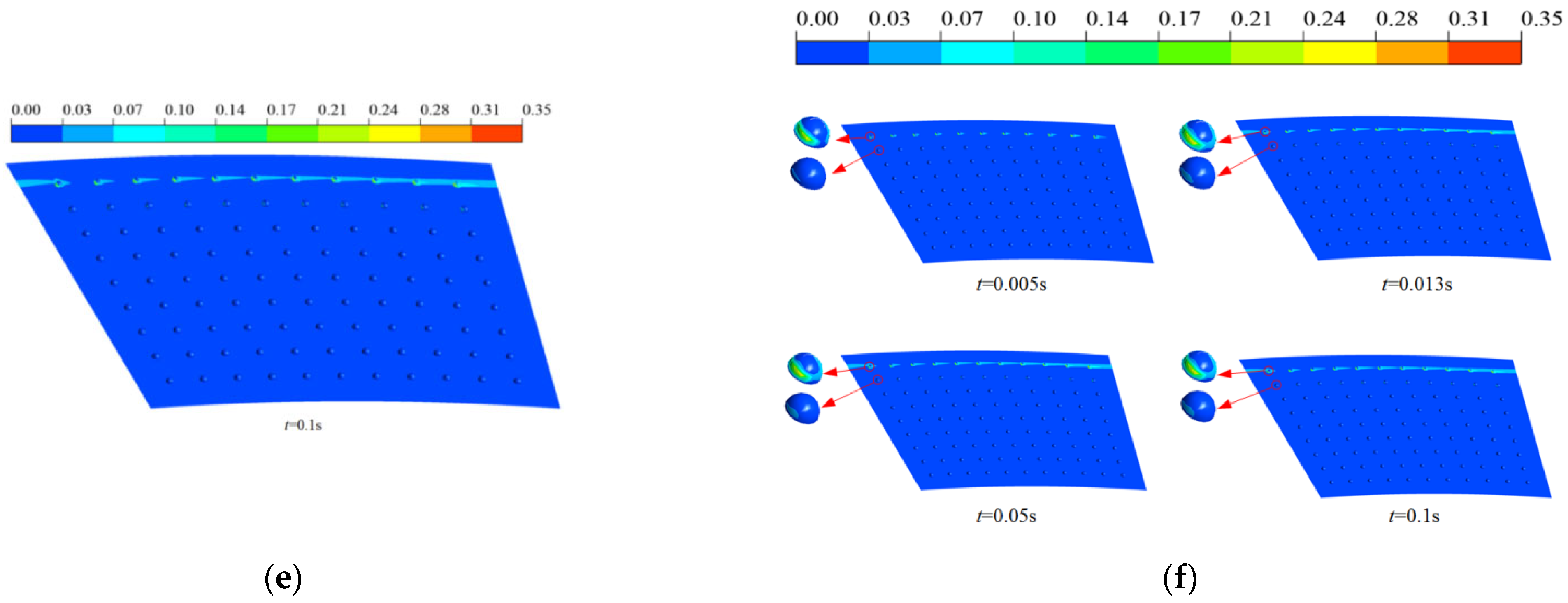
3.1.1. Evolution Process of Cavitation Morphology
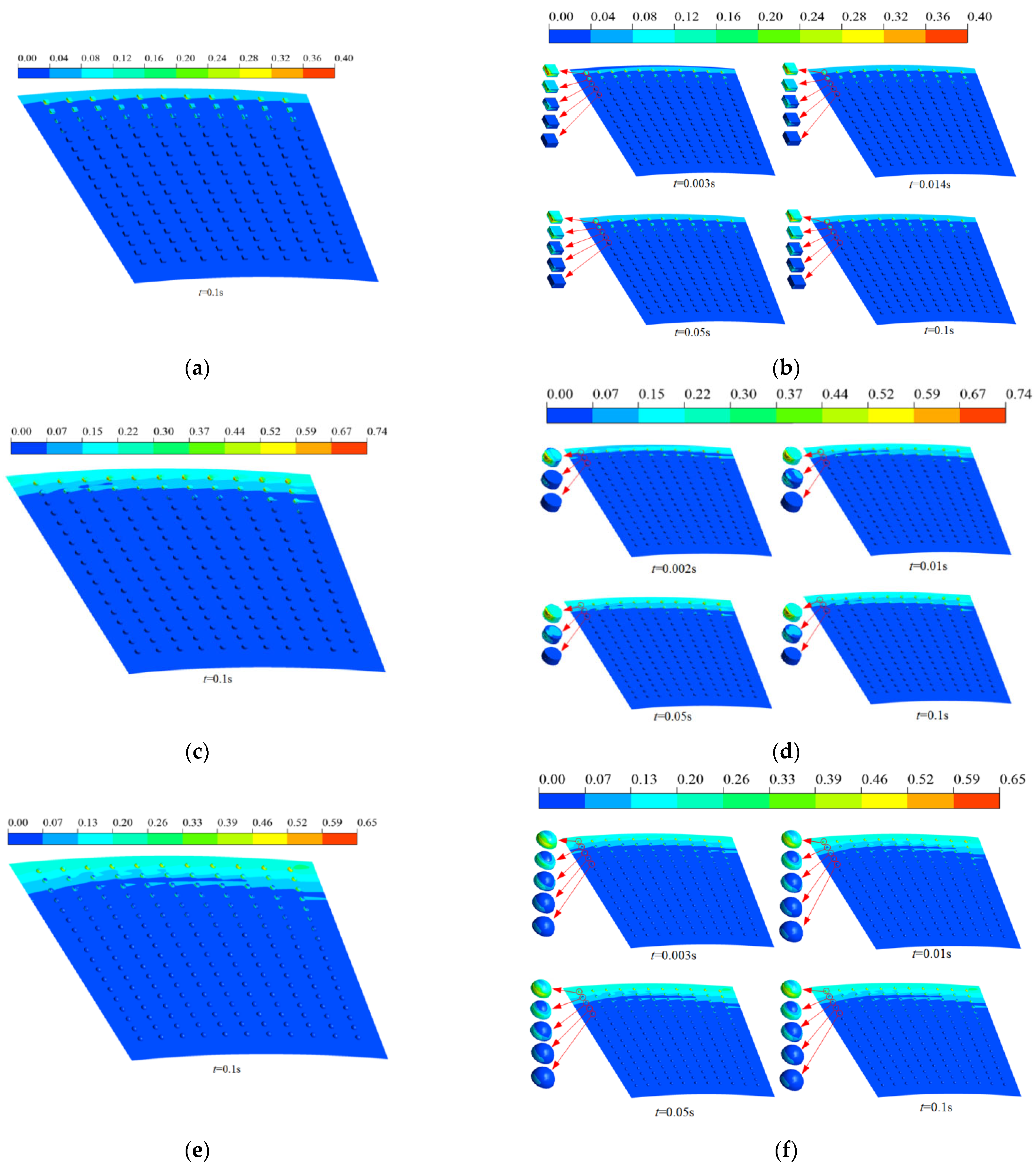
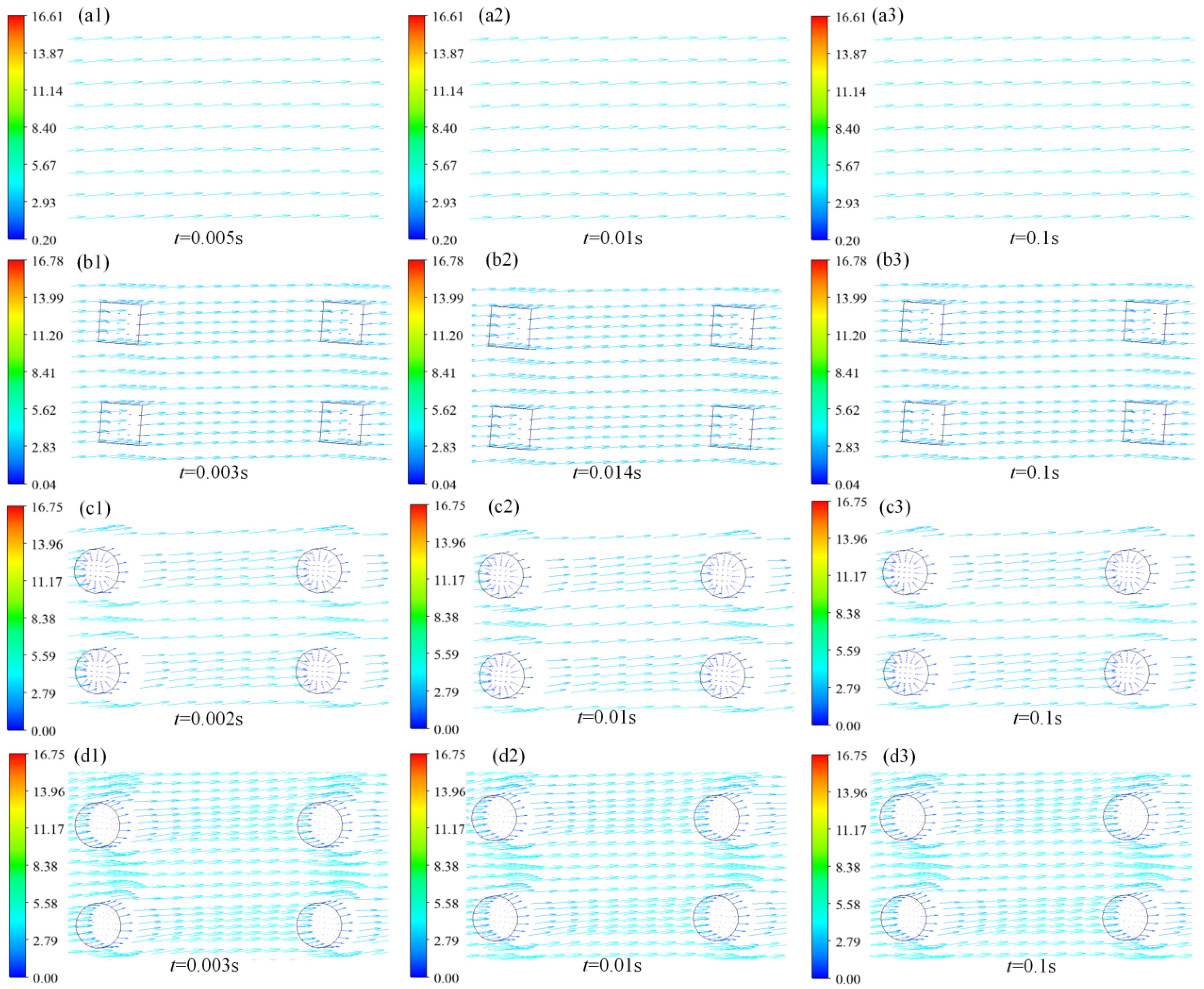
3.1.2. Oil Flow Velocity Field Analysis
3.1.3. Gas Velocity Field Analysis
3.1.4. Streamline Diagrams of Oil Flow and Cavitation Gas
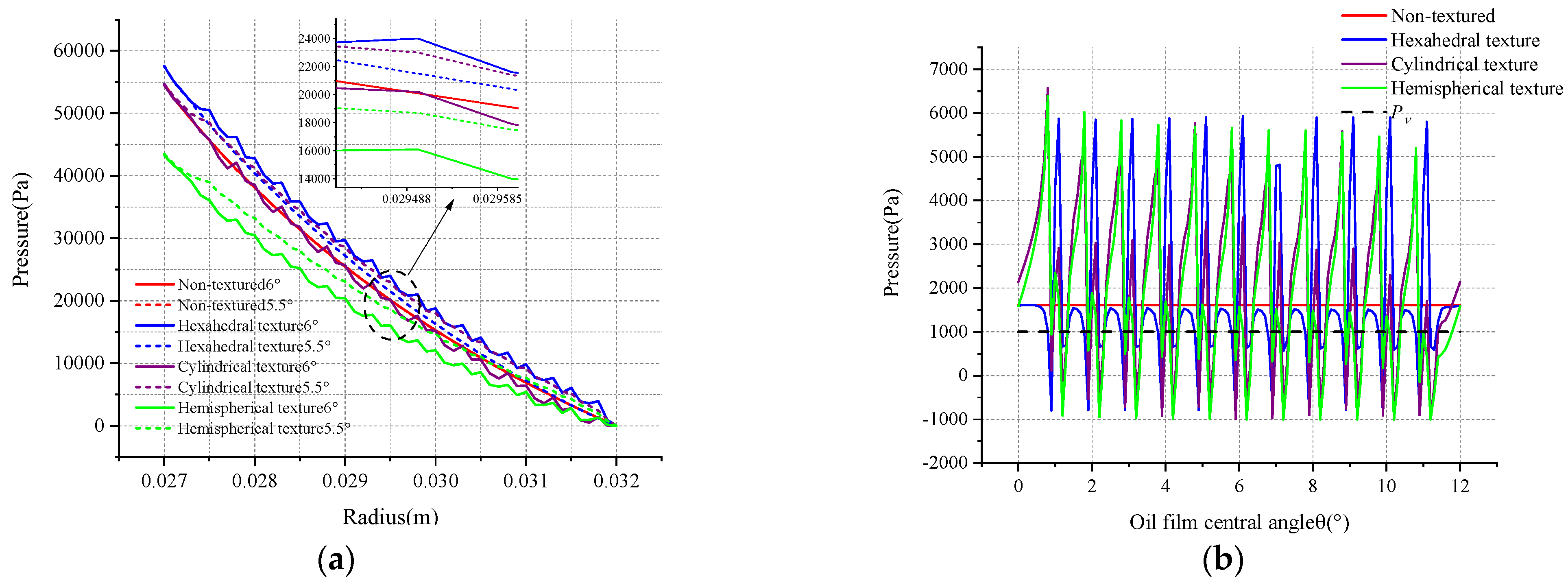
3.1.5. Cavitation Pressure Field Analysis
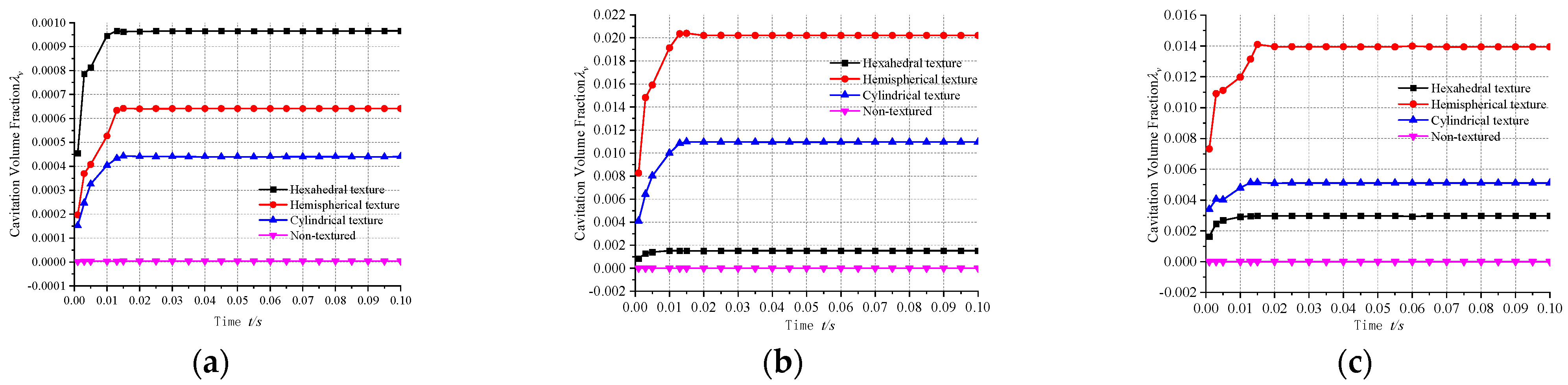
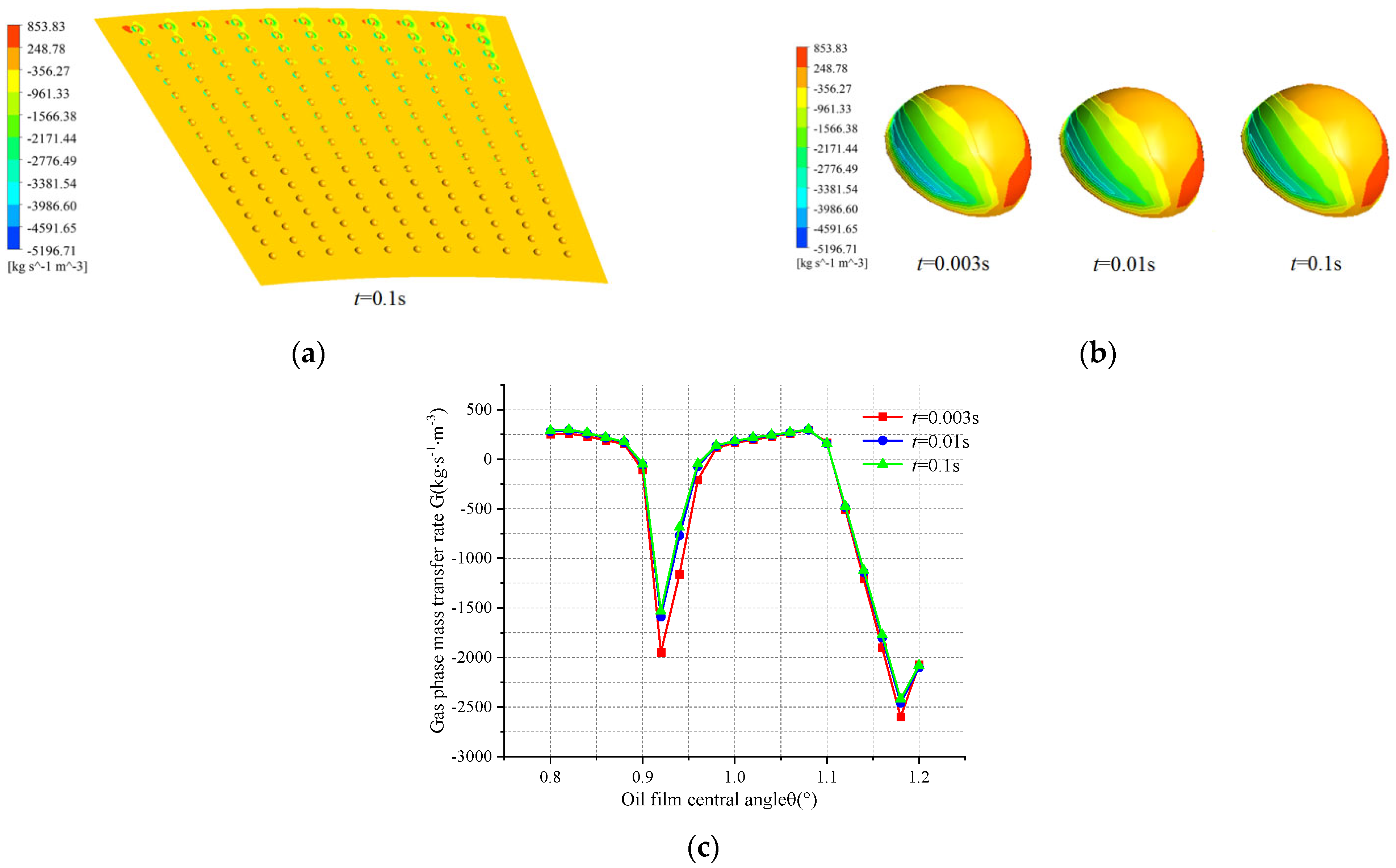
3.1.6. Cavitation Mass Transfer Rate Analysis
3.2. Experimental Results of Friction Pairs
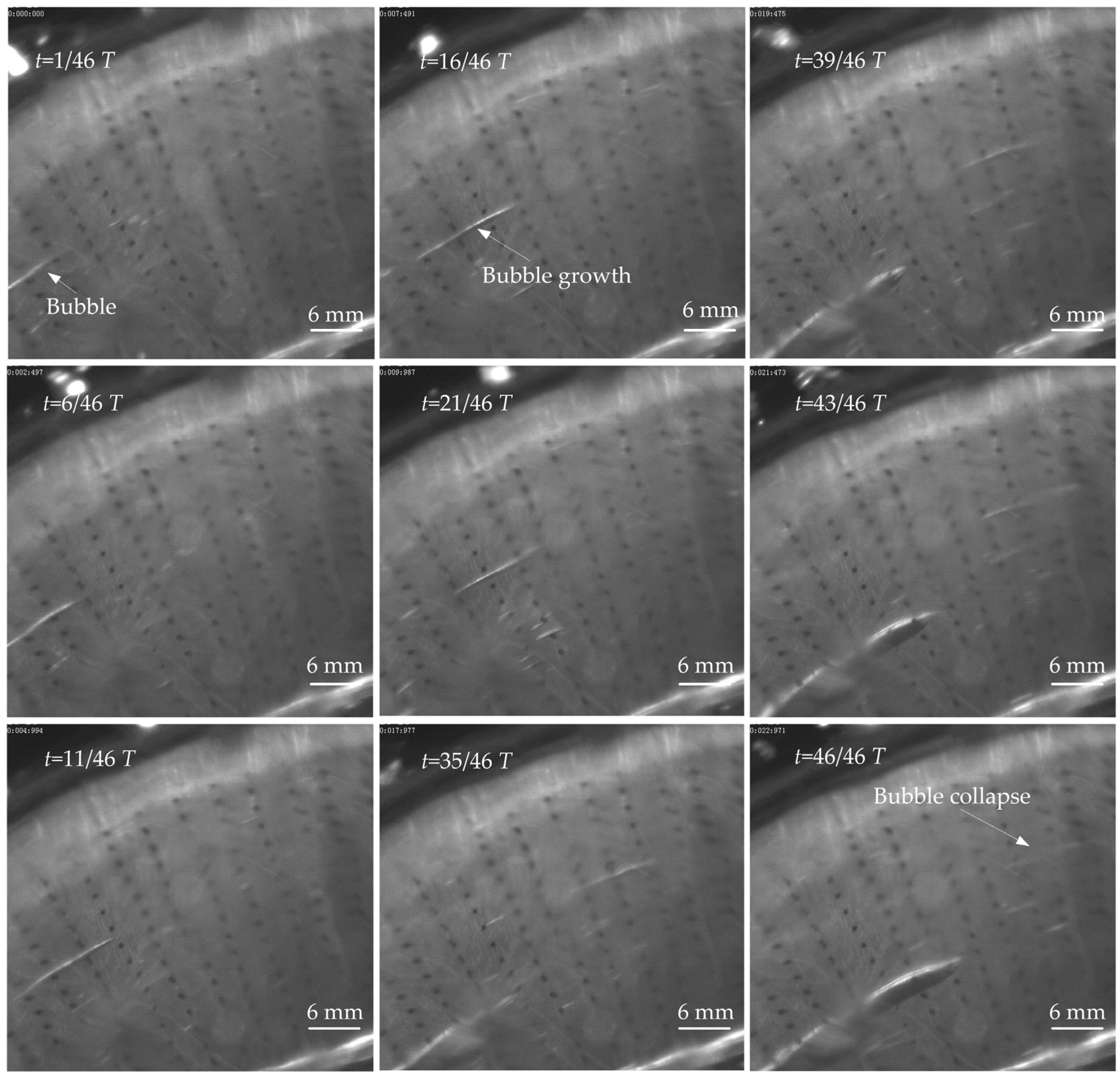
3.2.1. Effect of Surface Texturing on Cavitation
3.2.2. Analysis of Oil Film Shear Cavitation Process
3.2.3. Comparison Between Simulation and Experiment
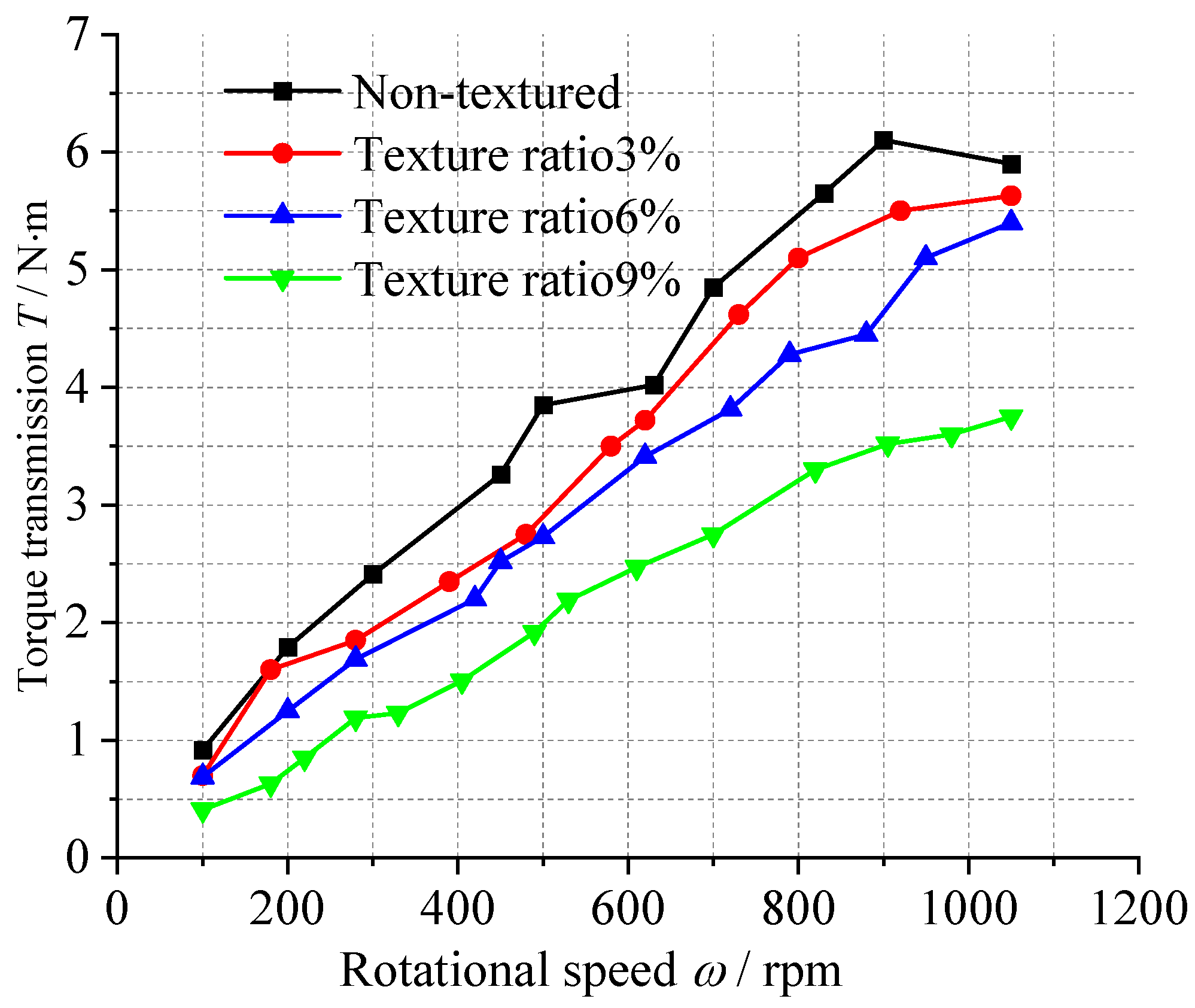
3.2.4. Torque Transmission Tests Under Different Texture Ratios
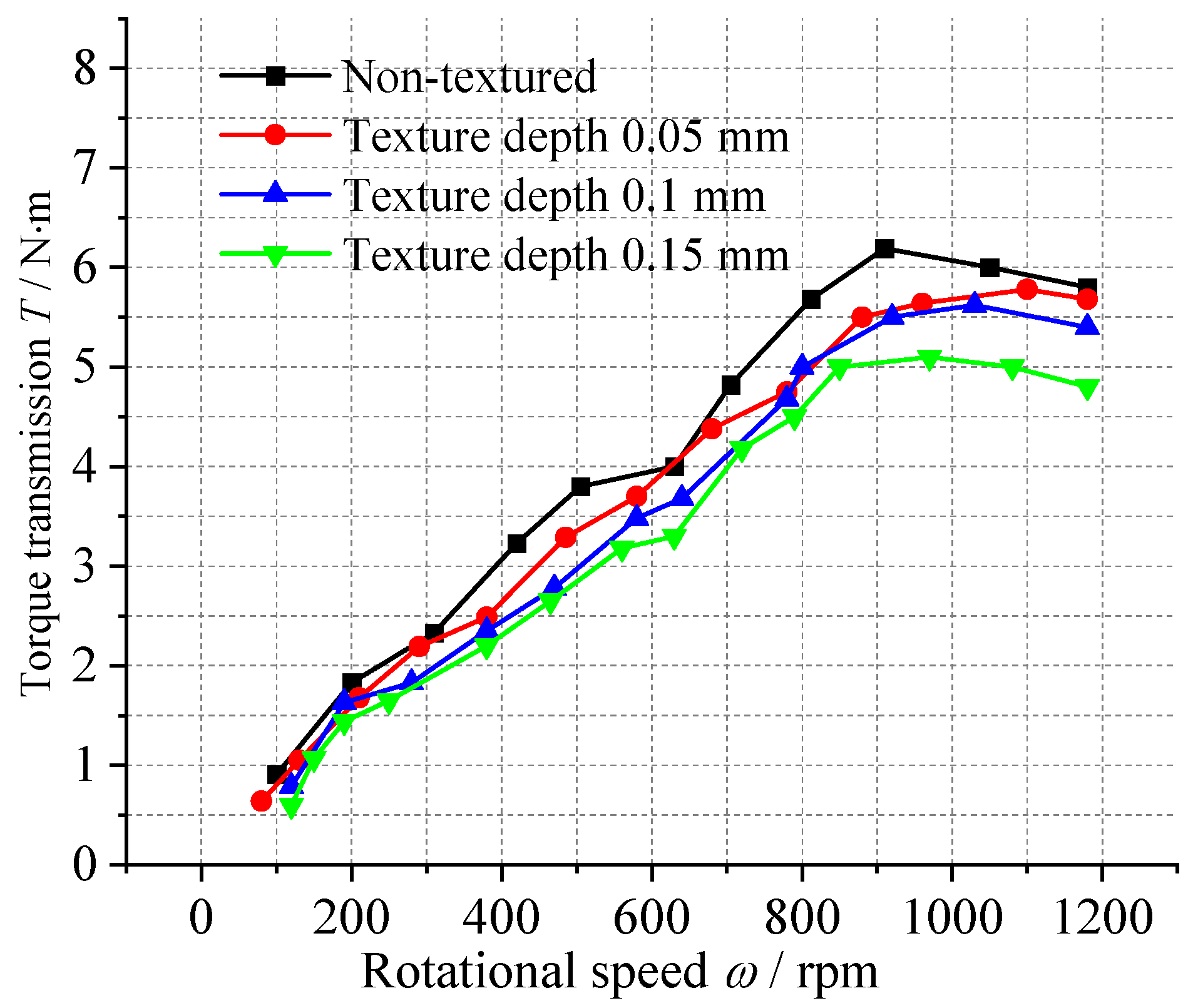
3.2.5. Torque Transmission Tests Under Different Texture Depths
4. Conclusions
- (1)
- Texture morphology is the dominant factor in determining cavitation intensity. Under an identical texture ratio of 6.41%, different morphologies exhibited significant differences in cavitation performance: the hemispherical texture resulted in the highest cavitation volume fraction (0.020215), while the hexahedral texture yielded the lowest (0.0015197)—a difference of more than an order of magnitude. Hexahedral textures demonstrated the most effective flow field stability and cavitation suppression capabilities.
- (2)
- An optimal design range exists for texture parameters. The effect of the texture ratio on cavitation is nonlinear, with cavitation intensity peaking at a ratio of approximately 6.41%. As the texture ratio increases to 12.917%, cavitation is mitigated due to the homogenization of flow field disturbances. Furthermore, increasing texture depth effectively reduces fluid shear stress within the dimples, thereby significantly suppressing cavitation development.
- (3)
- Among the operational parameters, rotational speed has the most significant impact on cavitation. At a high speed of 6000 rpm, the cavitation volume fraction increases substantially. Conversely, increasing the inlet pressure effectively suppresses cavitation by enhancing radial flow. A greater oil film thickness exacerbates cavitation, while variations in oil temperature primarily affect the time required for cavitation to stabilize.
- (4)
- The study proposes a design criterion based on a multi-objective balance. To achieve an optimal equilibrium between hydrodynamic pressure effects and cavitation suppression, employing a high texture ratio (exceeding 45%) with either hexahedral or cylindrical textures is recommended. This approach can reduce the pressure drop in the low-pressure zone by more than 30%, providing a crucial theoretical basis and engineering guidance for the development of high-reliability wet clutch surface textures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bao, H.; Xu, T.; Jin, G.; Huang, W. Analysis of Dynamic Engaged Characteristics of Wet Clutch in Variable Speed Transmission of a Helicopter. Processes 2020, 8, 1474. [Google Scholar] [CrossRef]
- Zhao, J.; Xiao, M.H.; Bartos, P.; Bohata, A. Dynamic engagement characteristics of wet clutch based on hydro-mechanical continuously variable transmission. J. Cent. South Univ. 2021, 28, 1377–1389. [Google Scholar] [CrossRef]
- Brotchie, A.; Grieser, F.; Ashokkumar, M. Characterization of acoustic cavitation bubbles in different sound fields. J. Phys. Chem. B 2010, 114, 11010–11016. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Jia, X.; Liu, J.; Wang, G.; Zhao, S.; Ji, L.; Yoon, J.Y.; Chen, S. Investigation on the characteristics of an advanced rotational hydrodynamic cavitation reactor for water treatment-ScienceDirect. Sep. Purif. Technol. 2020, 251, 117252. [Google Scholar] [CrossRef]
- Yusvika, M.; Prabowo, A.R.; Baek, S.J.; Tjahjana, D.D.D.P. Achievements in Observation and Prediction of Cavitation: Effect and Damage on the Ship Propellers. Procedia Struct. Integr. 2020, 27, 109–116. [Google Scholar] [CrossRef]
- Abreu, M.; Sundberg, J.; Elfsberg, J.; Jonsson, S. Morphology and mechanisms of cavitation damage on lamellar gray iron surfaces. Wear 2020, 456–457, 203324. [Google Scholar] [CrossRef]
- Mizuki, K.; Ryo, T.; Shinya, S. A Study on In-situ Observation of the Micro Flow of Lubricant on the Textured Surface. Procedia Eng. 2013, 68, 12–18. [Google Scholar] [CrossRef]
- Ibatan, T.; Uddin, M.S.; Chowdhury, M.A.K. Recent development on surface texturing in enhancing tribological performance of bearing sliders. Surf. Coat. Technol. 2015, 272, 102–120. [Google Scholar] [CrossRef]
- Mo, F.; Shen, C.; Zhou, J.; Khonsari, M.M. Statistical Analysis of Surface Texture Performance with Provisions with Uncertainty in Texture Dimensions. IEEE Access 2017, 5, 5388–5398. [Google Scholar] [CrossRef]
- Wos, S.; Koszela, W.; Pawlus, P.; Drabik, J.; Rogos, E. Effects of surface texturing and kind of lubricant on the coefficient of friction at ambient and elevated temperatures. Tribol. Int. 2018, 117, 174–179. [Google Scholar] [CrossRef]
- Liu, W.; Ni, H.; Wang, P.; Chen, H. Investigation on the Tribological Performance of Micro-dimples Textured Surface Combined with Longitudinal or Transverse Vibration under Hydrodynamic Lubrication. Int. J. Mech. Sci. 2020, 174, 105474. [Google Scholar] [CrossRef]
- Cui, J.; Tang, H. A review on flow instability in hydro-viscous drive. Phys. Fluids 2024, 36, 041301. [Google Scholar] [CrossRef]
- Sun, J.; Chen, L.; Zhang, B.; Huang, H.; Qian, P. Cavitation Morphology Study between Hemispherical Textured Rotating Friction Pairs. Lubricants 2022, 10, 249. [Google Scholar] [CrossRef]
- Meng, Y.; Xu, J.; Ma, L.; Jin, Z.; Prakash, B.; Ma, T.; Wang, W. A review of advances in tribology in 2020–2021. Friction 2022, 10, 1443–1595. [Google Scholar] [CrossRef] [PubMed Central]
- Sun, J.; Chen, L.; Huang, H.; Zhang, B.; Qian, P. Comprehensive Investigations on Fluid Flow and Cavitation Characteristics in Rotating Disk System. Appl. Sci. 2022, 12, 12303. [Google Scholar] [CrossRef]
- Pan, S.; Peng, X. Cavitation Mechanisms; National Defense Industry Press: Arlington, VA, USA, 2013. [Google Scholar]
- Jia, C. Numerical Analysis of Flow Field Around a Body of Revolution; Northwestern Polytechnical University: Xi’an, China, 2002. [Google Scholar]
- Cao, Z. Research on Wear State Assessment and Life Prediction of Compound Planetary Gearbox Based on Multi-Source Information Fusion; Xi’an Technological University: Xi’an, China, 2024. [Google Scholar] [CrossRef]


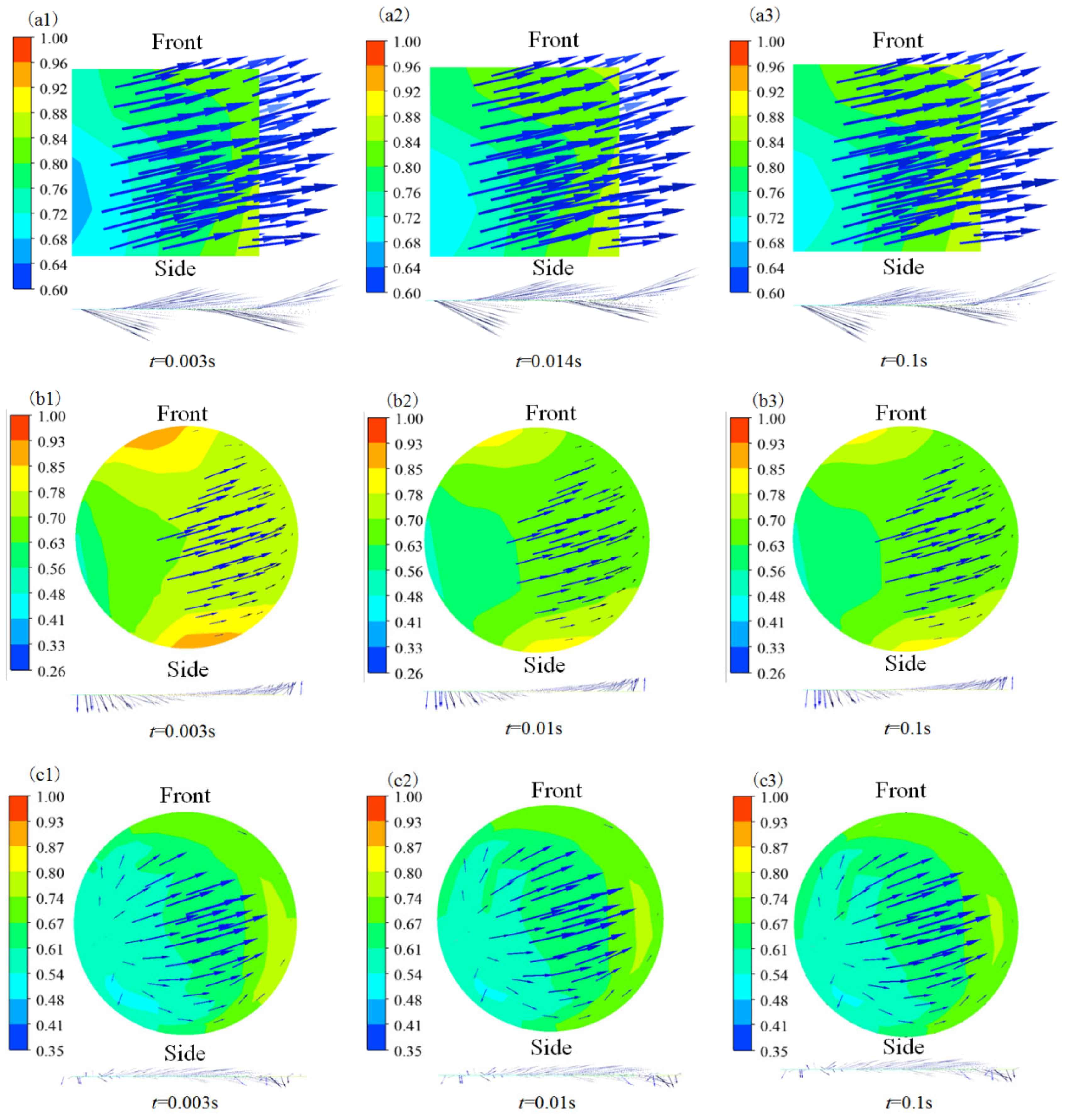
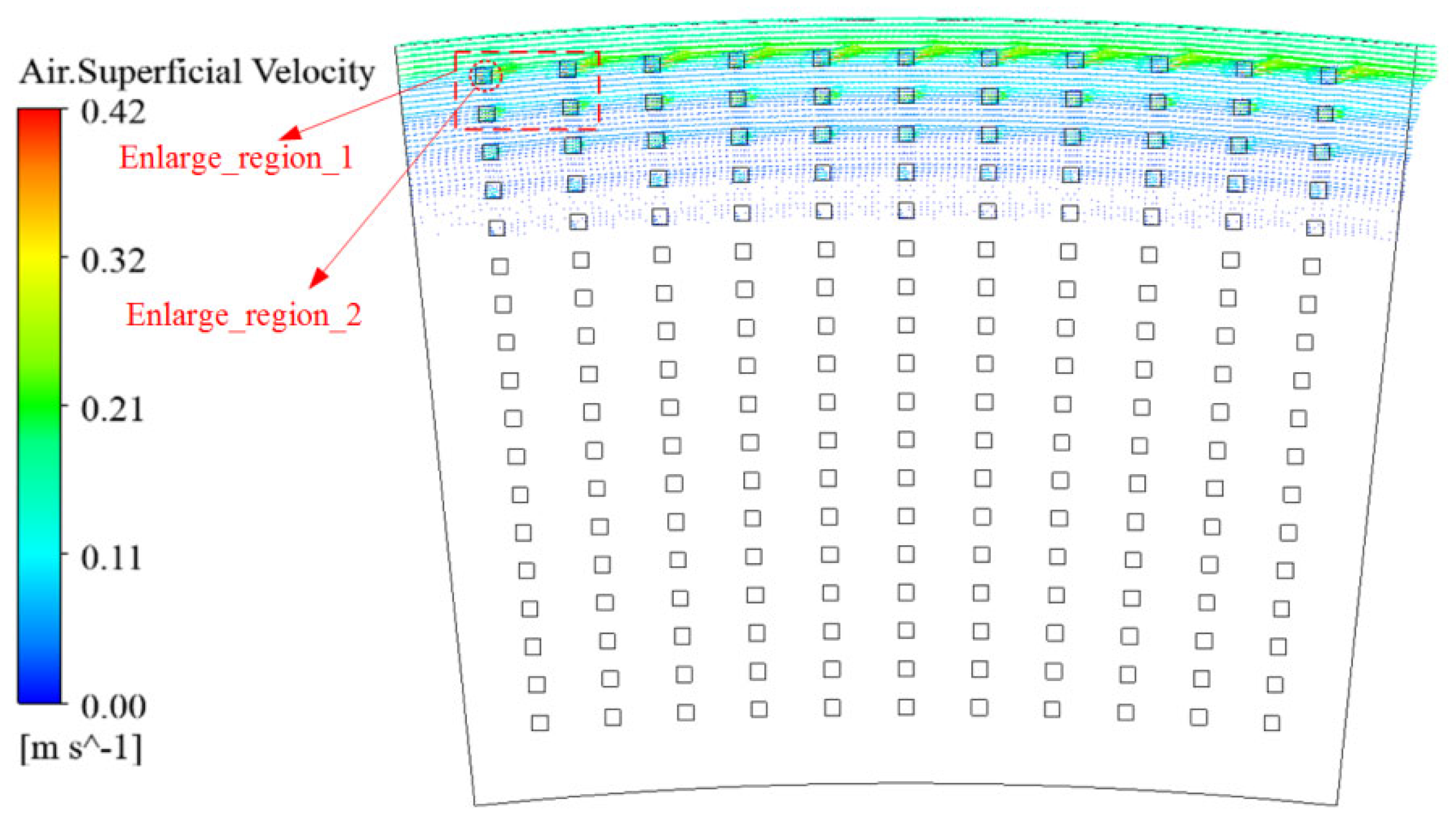
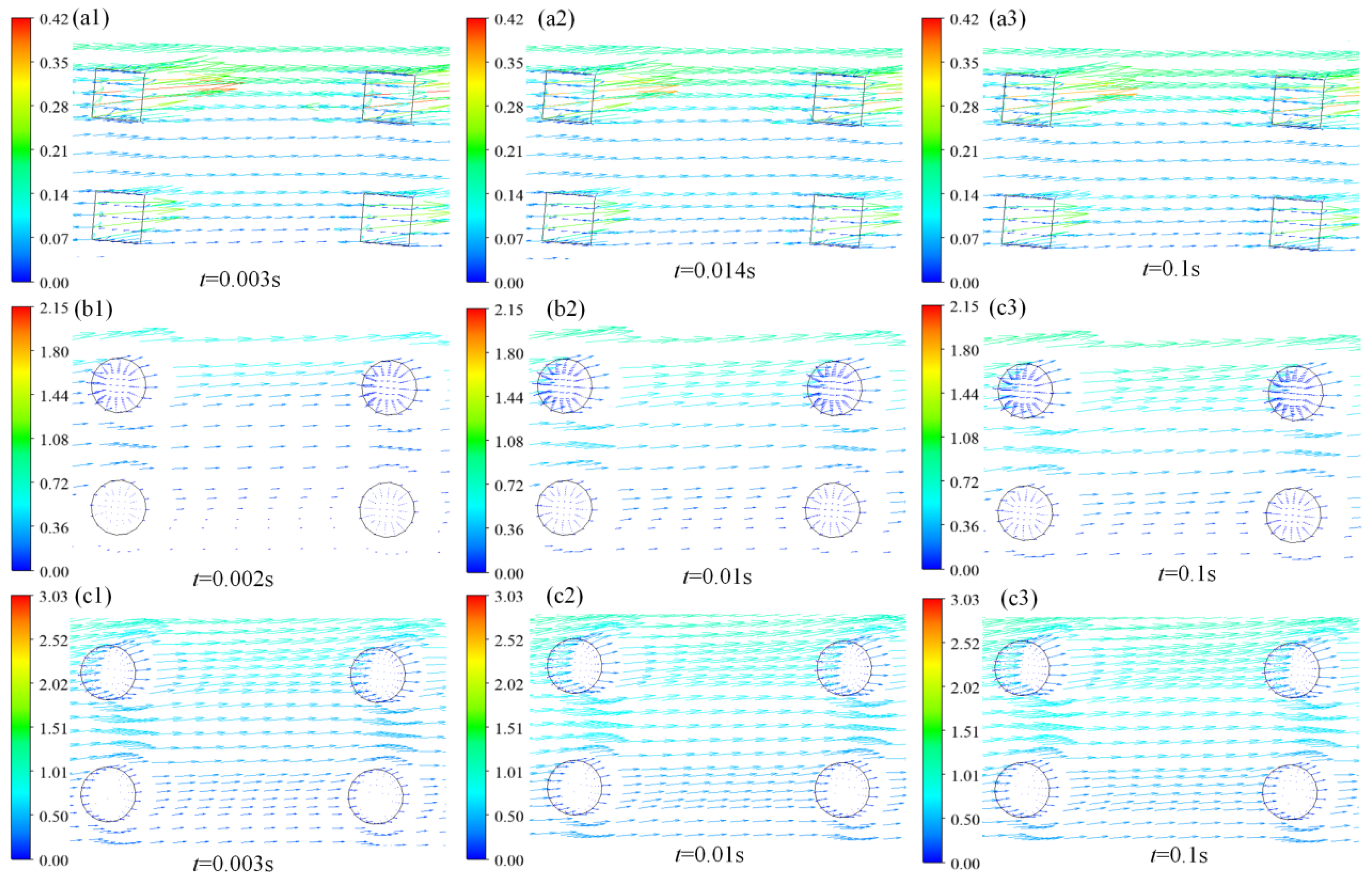
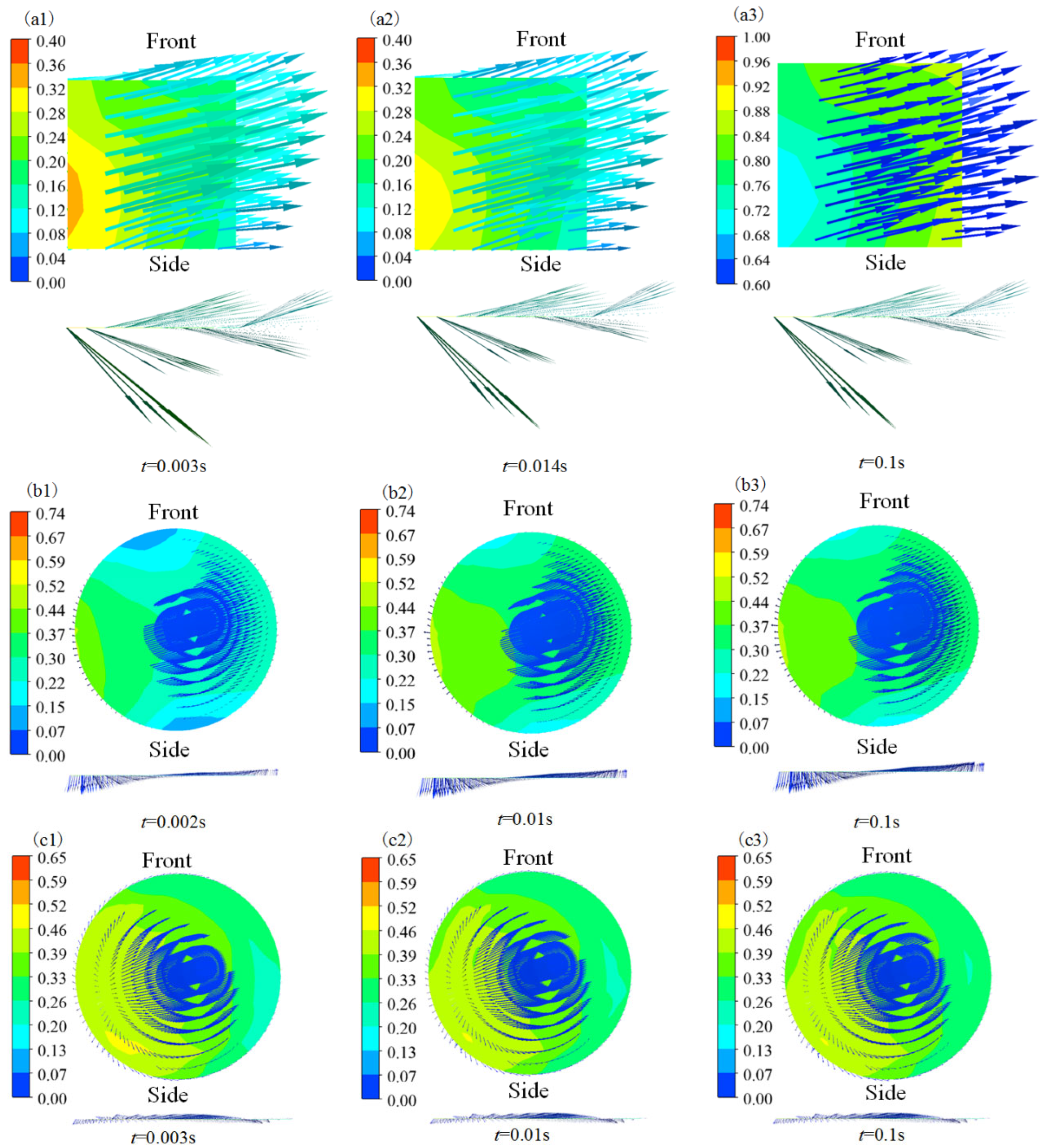






| Parameter Name | Liquid Oil | Vapor |
|---|---|---|
| Density ρ (kg/m3) | 865 | 0.023 |
| Specific Heat c (J/kg·K−1) | 2093.5 | 1911.6 |
| Thermal Conductivity w (m·K) | 0.12 | 0.0185 |
| Dynamic Viscosity μ (Pa·s) | Interpolation function | 9.86 × 10−6 |
| Saturation Vapor Pressure Pv (Pa) | 1000 | 1000 |
| Texture Type | Simulated Mean Torque (N m) | Experimental Mean Torque (N m) | Relative Error (%) |
|---|---|---|---|
| Untextured | 12.5 | 13.5 | 7.4% |
| Hexahedral | 10.8 | 11.8 | 8.5% |
| Hemispherical | 11.2 | 12.4 | 9.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, H.; Che, H.; Shi, F.; Wang, S. Primary Prediction of Oil Film Cavitation Between Rotating Friction Pairs with Various Types of Surface Textures. Lubricants 2025, 13, 513. https://doi.org/10.3390/lubricants13120513
Qiu H, Che H, Shi F, Wang S. Primary Prediction of Oil Film Cavitation Between Rotating Friction Pairs with Various Types of Surface Textures. Lubricants. 2025; 13(12):513. https://doi.org/10.3390/lubricants13120513
Chicago/Turabian StyleQiu, Huipeng, Hailong Che, Fuxi Shi, and Sanmin Wang. 2025. "Primary Prediction of Oil Film Cavitation Between Rotating Friction Pairs with Various Types of Surface Textures" Lubricants 13, no. 12: 513. https://doi.org/10.3390/lubricants13120513
APA StyleQiu, H., Che, H., Shi, F., & Wang, S. (2025). Primary Prediction of Oil Film Cavitation Between Rotating Friction Pairs with Various Types of Surface Textures. Lubricants, 13(12), 513. https://doi.org/10.3390/lubricants13120513




