Tool Wear Condition Monitoring Based on Improved Symmetrized Dot Pattern Enhanced Resnet18 Under Small Samples
Abstract
1. Introduction
- (1)
- Heavy reliance on data. The above-mentioned models require a large amount of annotated data for training, but acquiring wear data in the entire life cycle of a cutting tool in real industrial scenes can be very costly and time-consuming.
- (2)
- Limited feature extraction capability. Under the condition of a small sample size, signal features (such as frequency domain components of cutting force) are difficult to fully express the nonlinear evolution law of wear. Traditional feature extraction methods suffer from insufficient automatic feature learning due to paucity of data.
- (1)
- An SDP-ResNet18 method is proposed to improve the classification accuracy of tool condition monitoring under small samples.
- (2)
- A parameter optimization algorithm for SDP based on minimizing the cross-correlation coefficient is proposed to avoid the subjective influence on SDP performance.
2. Related Theories
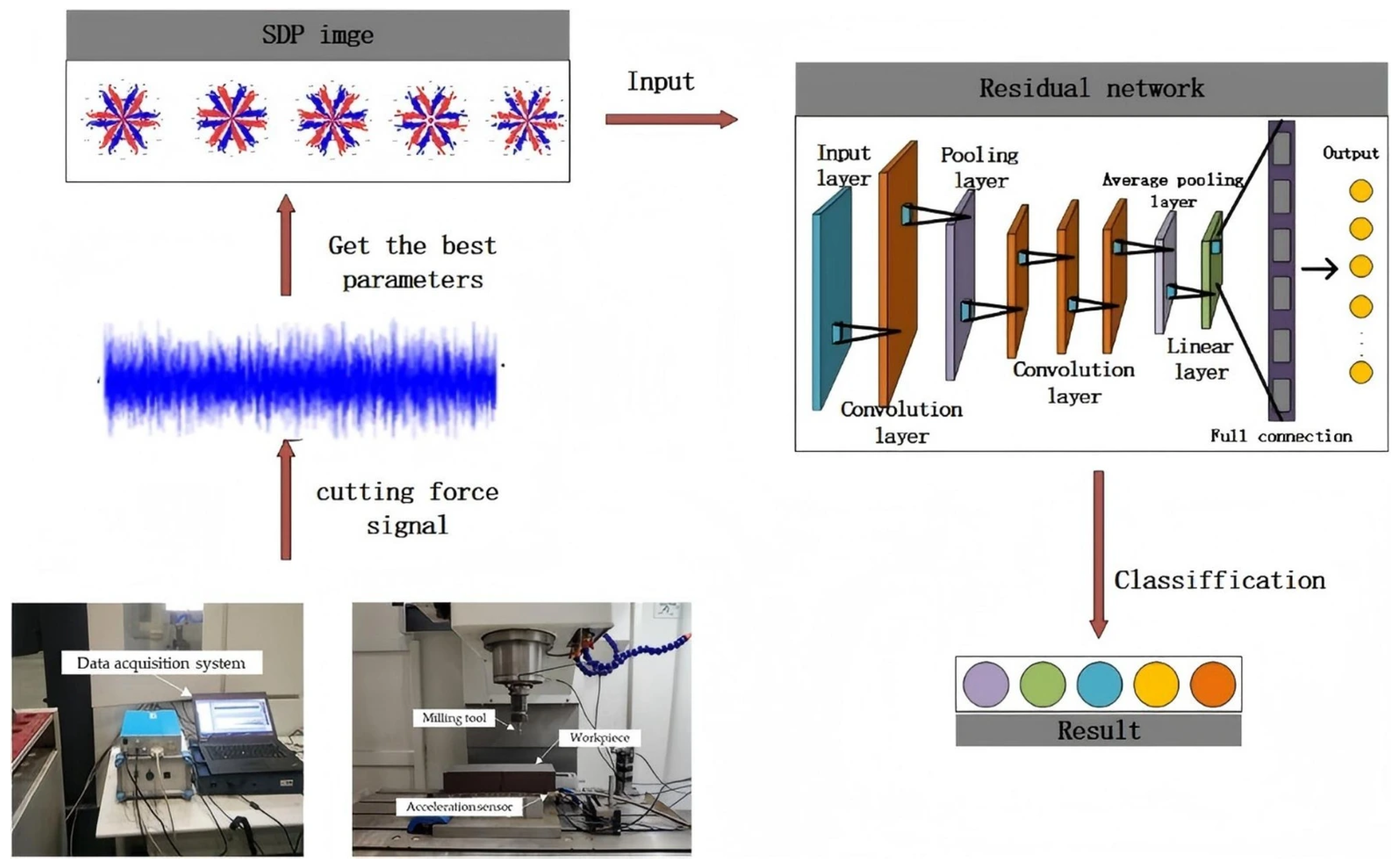
2.1. Methodological Framework
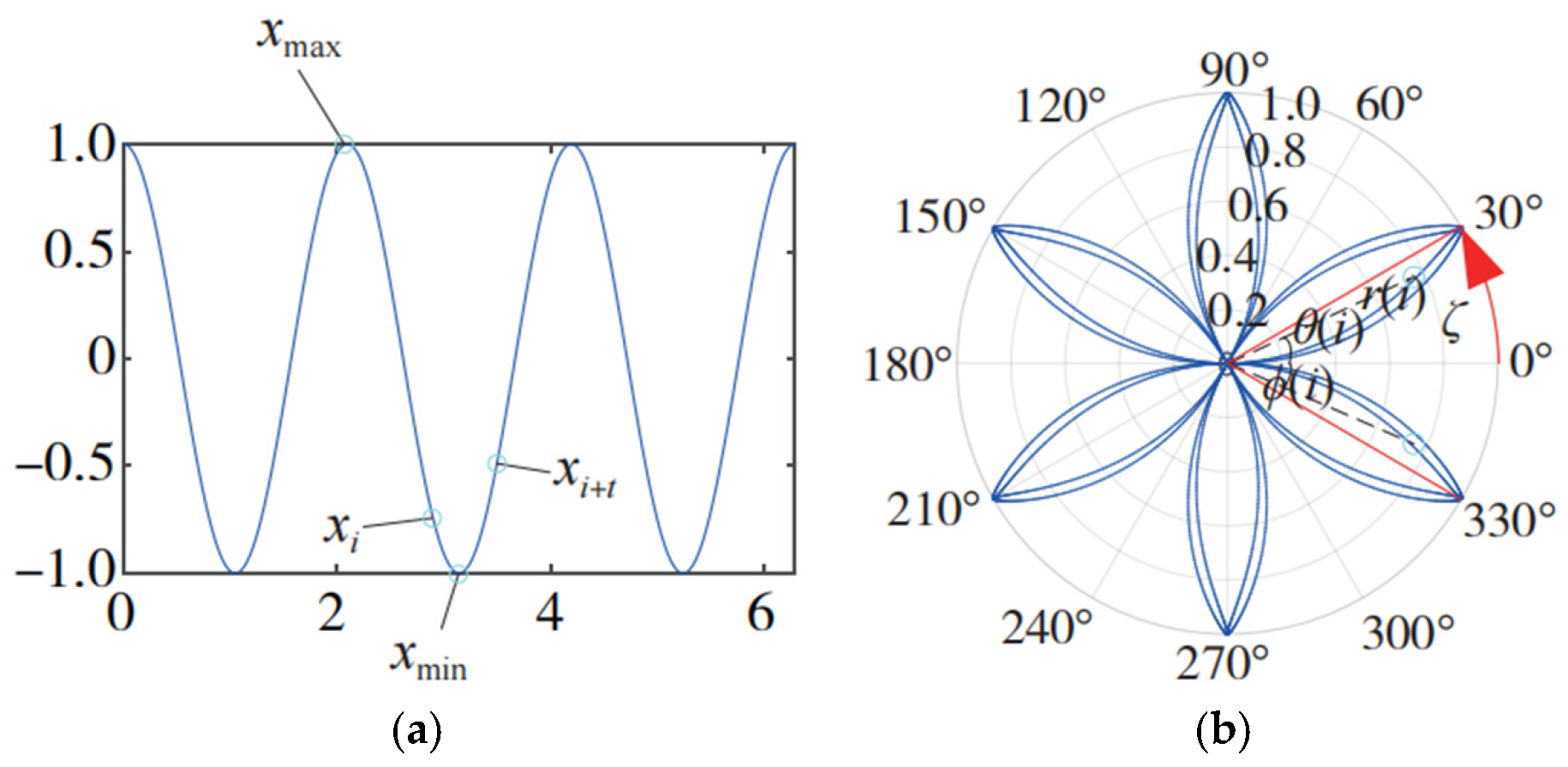
2.2. Symmetric Dot Pattern (SDP)
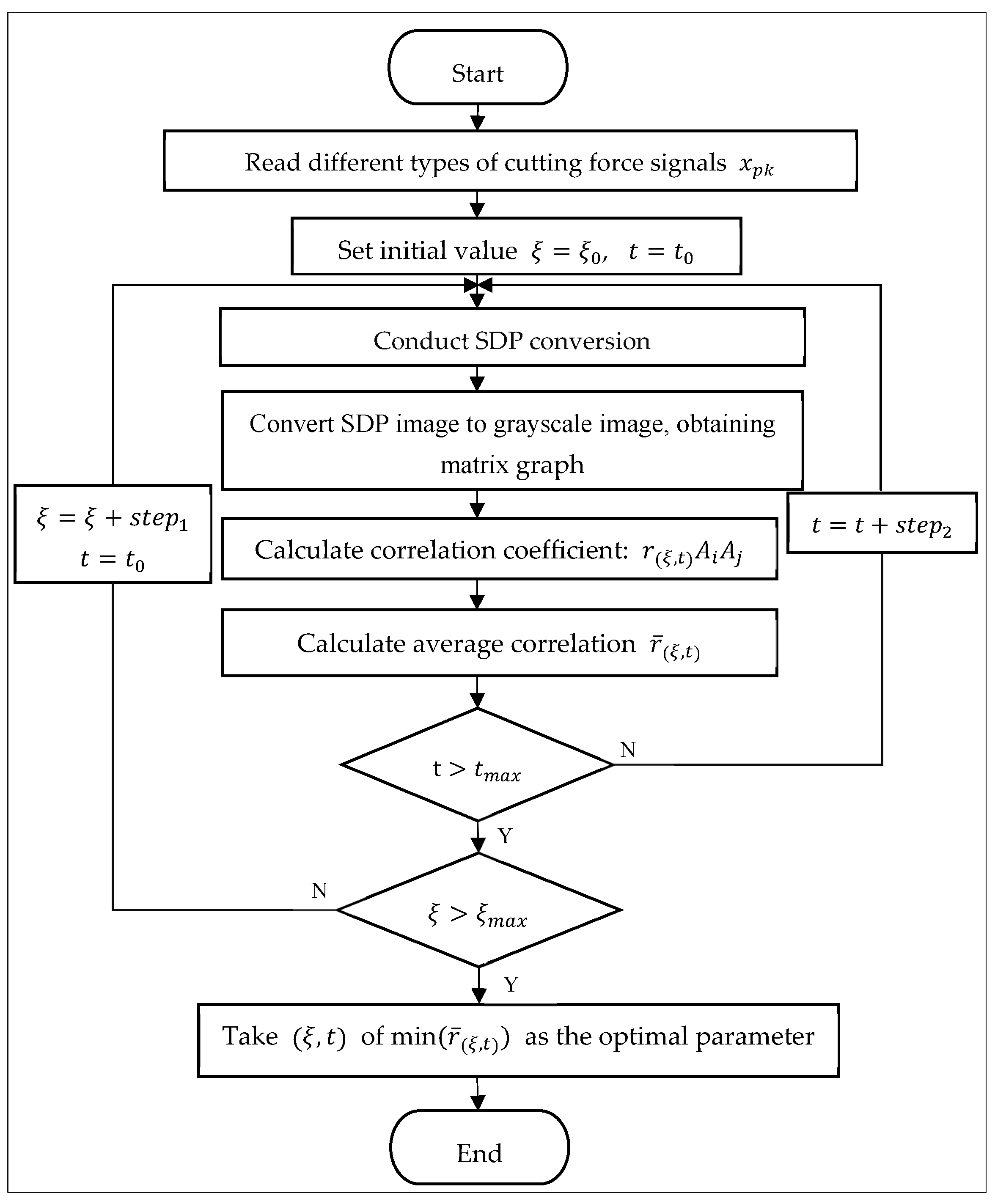
2.3. SDP Parameters Optimization Algorithm
- (1)
- Data selection: Select cutting force sample signals {xpk, p = 1, 2, …, P, k = 1, 2, …, K}, p and k represent tool conditions and the sample number of each condition, P and K are the number of tool conditions and the sample size of each condition, respectively;
- (2)
- Setting parameter range and step size: Set the ranges of ξ and t to ξ0 < ξ < ξmax, t0 < t < tmax, and their respective step sizes are step1 and step2;
- (3)
- SDP conversion and grayscale image generation: Perform SDP conversion on the cutting force signal xpk based on the parameter set (ξ, t), and convert it into a grayscale image;
- (4)
- Calculation of cross-correlation coefficient: Select two samples Api and Aqj (p, q = 1, 2, …, P, i, j = 1, 2, …, K, p ≠ q) from different categories, and calculate the cross-correlation coefficient r(ξ,t)ApiAqj using Equation (3);
- (5)
- Determination of optimal parameter: Calculate the average value of the correlation coefficient in the way shown in Equation (4). The values of t and ξ corresponding to the minimum value of the average value are the optimal parameter values.
2.4. ResNet18 Model
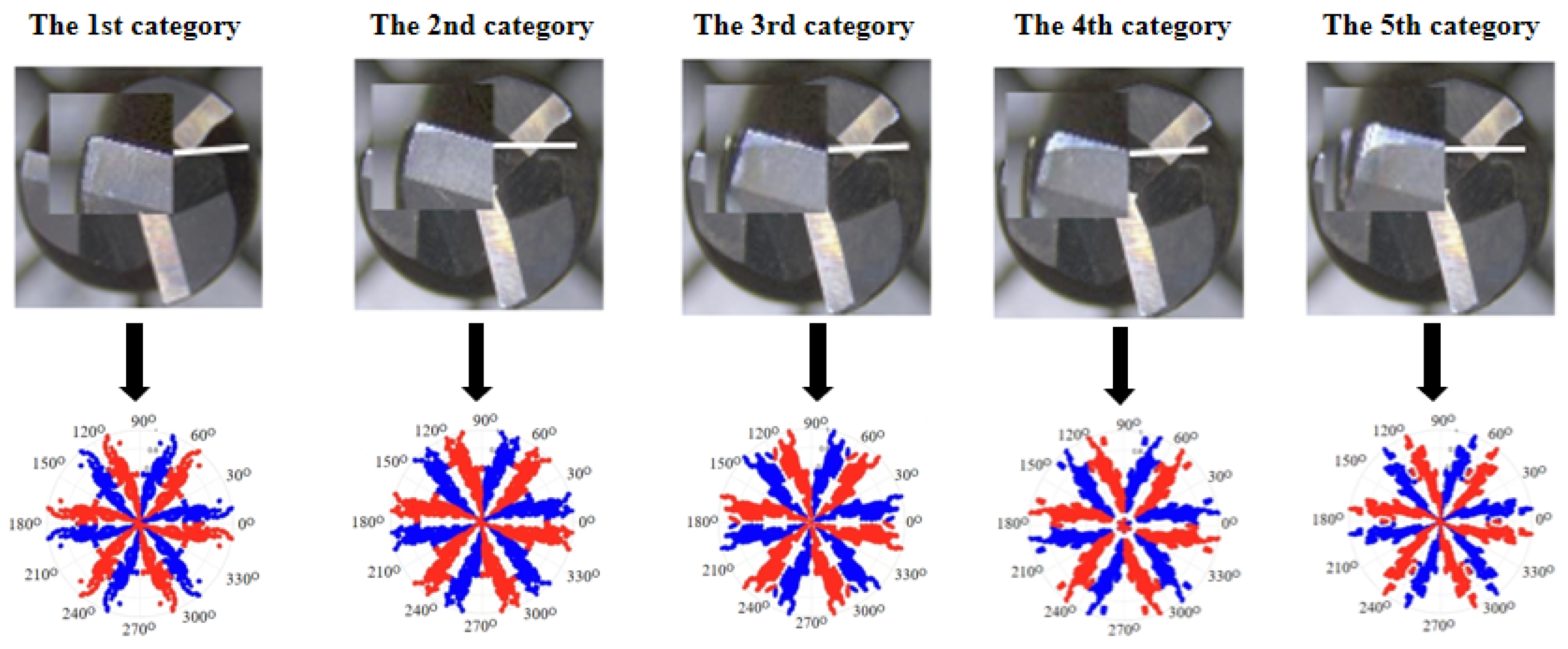
3. Experiment and Observation
4. Results and Discussion
4.1. Optimization of SDP Parameters
4.2. Comparison of Model Results
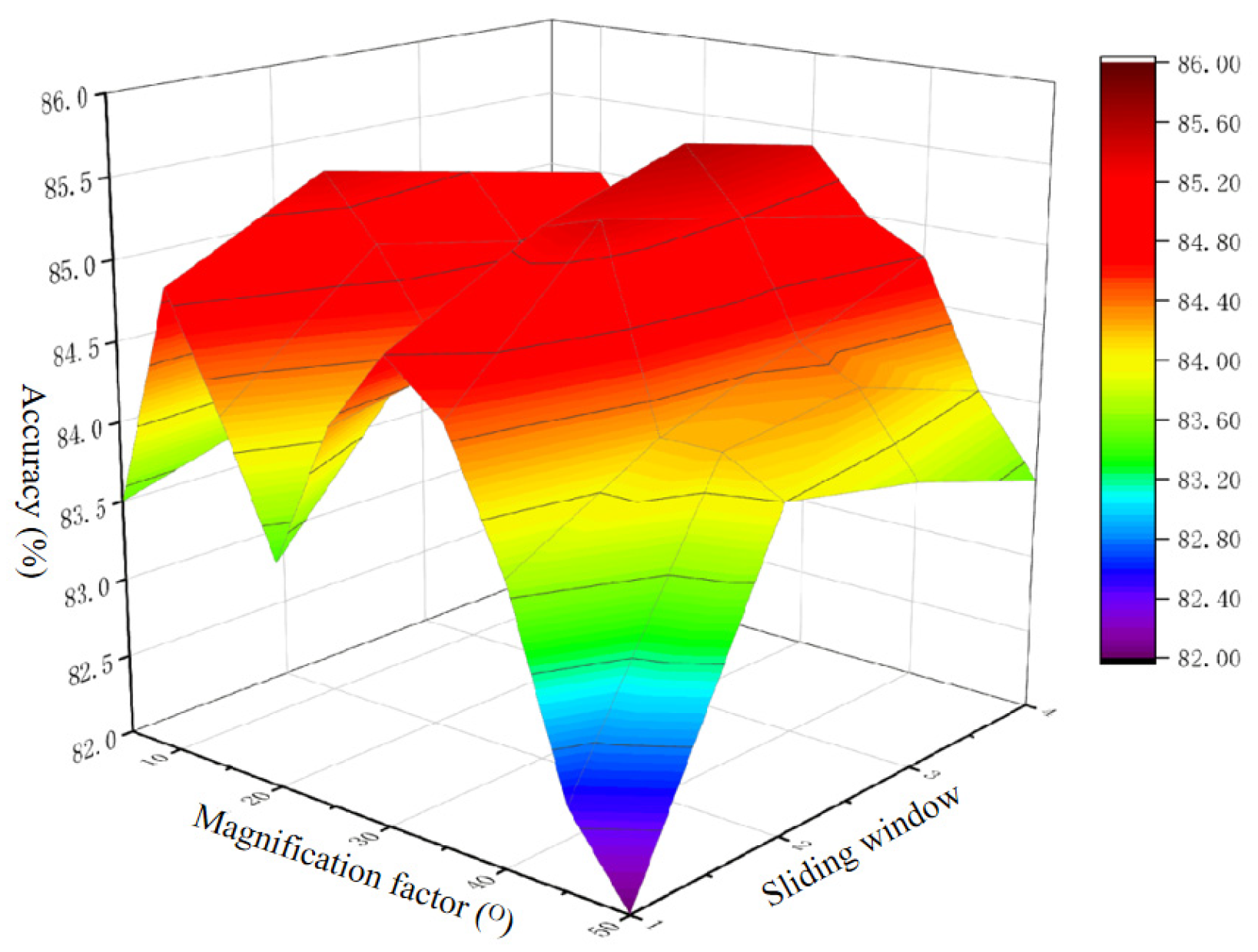
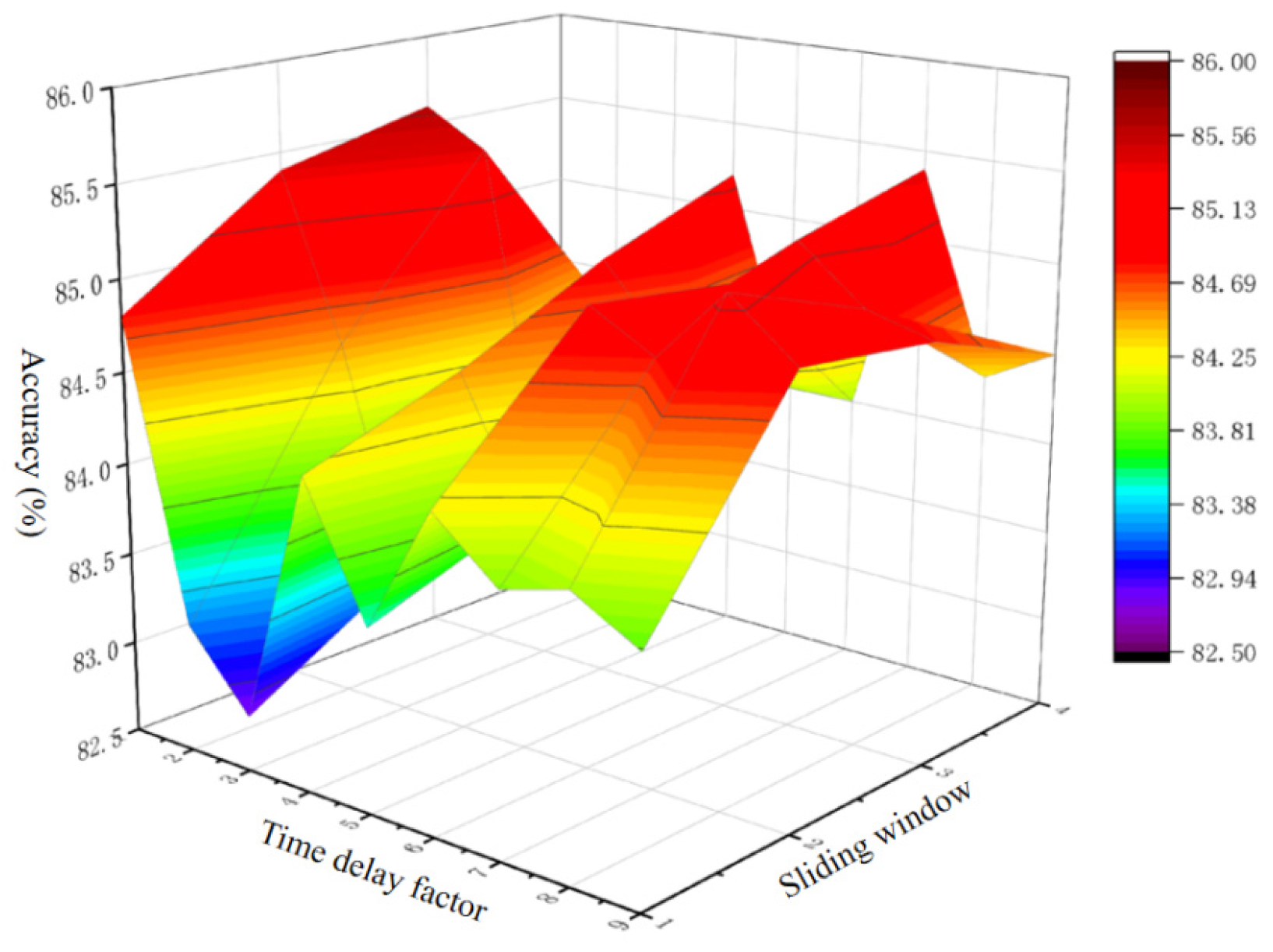
4.3. Sensitivity Analysis
5. Conclusions
- (1)
- The proposed SDP enhanced ResNet 18 method for TCM achieves an improvement of the classification accuracy of over 10% compared to methods based on STFT and GAF.
- (2)
- The model parameters have a significant impact on the SDP results, and the algorithm proposed to optimize the SDP parameters by minimizing the cross-correlation coefficient can obtain effective model parameters, avoiding the subjective influence on SDP performance.
- (3)
- In the case of small samples, the TCM classification results based on the Resnet18 model are about 3% higher than those based on the VGG16 model.
- (1)
- Optimize the SDP algorithm to obtain better feature imaging samples, such as parameter optimization based on evolutionary theory, and obtain richer feature information combining other feature extraction technologies.
- (2)
- Only 14 tools were conducted in the TCM experiments; leading the repetitive errors are difficult to estimate. Thus, more tool tests will be conducted in the future to eliminate random measurement errors.
- (3)
- There is a strong correlation between cutting temperature and tool condition. Combining the non-contact advantage of temperature measurement, studying temperature-based TCM methods has great value for industrial applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mohanraj, T.; Kirubakaran, E.; Madheswaran, D.; Naren, M.; Dharshan, S.; Ibrahim, M. Review of advances in tool condition monitoring techniques in the milling process. Meas. Sci. Technol. 2024, 35, 092002. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, W. Review of tool condition monitoring methods in milling processes. Int. J. Adv. Manuf. Technol. 2018, 96, 2509–2523. [Google Scholar] [CrossRef]
- Kulkarni, N.; Valente, N.; Sabato, A. Time-Inferred Autoencoder: A noise adaptive condition monitoring tool. Mech. Syst. Signal Process. 2023, 204, 110789. [Google Scholar] [CrossRef]
- Jing, C.; He, X.; Xu, G.; Li, L.; Yao, Y. Finite Element Modeling Assisted Deep Subdomain Adaptation Method for Tool Condition Monitoring. Processes 2025, 13, 545. [Google Scholar] [CrossRef]
- Hei, Z.; Sun, B.; Wang, G.; Lou, Y.; Zhou, Y. Multi-feature spatial distribution alignment enhanced domain adaptive method for tool condition monitoring. Eksploat. I Niezawodn. Maint. Reliab. 2023, 25, 171750. [Google Scholar] [CrossRef]
- Zhi, G.; He, D.; Sun, W.; Zhou, Y.; Pan, X.; Gao, C. An edge-labeling graph neural network method for tool wear condition monitoring using wear image with small samples. Meas. Sci. Technol. 2021, 32, 064006. [Google Scholar] [CrossRef]
- Mishra, D.; Pattipati, K.; Bollas, G. Gaussian mixture model for tool condition monitoring. J. Manuf. Process. 2024, 131, 1001–1013. [Google Scholar] [CrossRef]
- Fu, Y.; Zhong, M.; Huang, J.; Jiang, Y.; Sun, W.; Lou, Y.; Wang, G.; Zhou, Y. Denoising diffusion probabilistic model enhanced tool condition monitoring method under imbalanced conditions. Meas. Sci. Technol. 2024, 36, 015018. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Wang, G.; Kumar, A.; Sun, W.; Xiang, J. Semi-Supervised Multiscale Permutation Entropy-Enhanced Contrastive Learning for Fault Diagnosis of Rotating Machinery. IEEE Trans. Instrum. Meas. 2023, 72, 3525610. [Google Scholar] [CrossRef]
- Zhao, P.; Lin, B.; Zhou, J.; Lv, B.; Li, J.; Zhang, J.; Wang, L.; Sui, T. Review of grinding temperature theory and measurement for the needs of the times: Promoting the development of advanced manufacturing. J. Mater. Process. Technol. 2025, 337, 118744. [Google Scholar] [CrossRef]
- Chen, X.; Kong, X.; Yang, M.; Qiang, F.; Zhang, Y.; Cui, X.; Liu, M.; Li, B.; Ma, X.; Li, C. Heat transfer in cutting and grinding processes: Mechanisms, models, and applications. Front. Mech. Eng. 2025, 20, 22. [Google Scholar] [CrossRef]
- Kumar, A. Research overview and prospect in condition monitoring of compressors. Expert Syst. Appl. 2025, 277, 127284. [Google Scholar] [CrossRef]
- Gao, C.; Nuawi, M.; Wang, J. Tool condition monitoring using I-kaz enhanced kernel extreme learning machine. Eng. Res. Express 2024, 6, 045569. [Google Scholar] [CrossRef]
- Yin, H.; Wang, Y.; Sun, W.; Wang, L. Fault diagnosis of hydraulic system based on D-S evidence theory and SVM. Int. J. Hydromechatron. 2024, 7, 1–15. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, M.; Deng, W.; Zhang, Z.; Jiang, X.; Liu, G. Research on electro-mechanical actuator fault diagnosis based on ensemble learning method. Int. J. Hydromechatron. 2024, 7, 113–131. [Google Scholar] [CrossRef]
- Zhu, Q.; Sun, B.; Zhou, Y.; Sun, W.; Xiang, J. Sample augmentation for intelligent milling tool wear condition monitoring using numerical simulation and generative adversarial network. IEEE Trans. Instrum. Meas. 2021, 70, 3516610. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, B.; Sun, W.; Lei, Z. Tool wear condition monitoring based on a two-layer angle kernel extreme learning machine using sound sensor for milling process. J. Intell. Manuf. 2022, 33, 247–258. [Google Scholar] [CrossRef]
- He, X.; Zhong, M.; He, C.; Wu, J.; Yang, H.; Zhao, Z.; Yang, W.; Jing, C.; Li, Y.; Gao, C. A Novel Tool Wear Identification Method Based on a Semi-Supervised LSTM. Lubricants 2025, 13, 72. [Google Scholar] [CrossRef]
- Hei, Z.; Yang, H.; Sun, W.; Zhong, M.; Wang, G.; Kumar, A.; Xiang, J.; Zhou, Y. Multiscale conditional adversarial networks based domain-adaptive method for rotating machinery fault diagnosis under variable working conditions. ISA Trans. 2024, 154, 352–370. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Yuan, R.; Lv, Y.; Li, L.; Song, H. A Novel Multivariate Cutting Force-Based Tool Wear Monitoring Method Using One-Dimensional Convolutional Neural Network. Sensors 2022, 22, 8343. [Google Scholar] [CrossRef]
- Cheng, Y.; Xue, J.; Lu, M.; Zhou, S.; Gai, X.; Guan, R. MS-DenseNet-GRU tool wear prediction method based on attention mechanism. Struct. Health Monit. 2025, 24, 517–533. [Google Scholar] [CrossRef]
- Dai, L.; Liu, T.; Liu, Z.; Jackson, L.; Goodall, P.; Shen, C.; Mao, L. An Improved Deep Learning Model for Online Tool Condition Monitoring Using Output Power Signals. Shock. Vib. 2020, 2020, 8843314. [Google Scholar] [CrossRef]
- Li, S.; Li, M.; Gao, Y. Deep Learning Tool Wear State Identification Method Based on Cutting Force Signal. Sensors 2025, 25, 662. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Li, S. Bearing fault diagnosis based on optimal convolution neural network. Measurement 2022, 190, 110702. [Google Scholar] [CrossRef]
- Liang, G.; Song, X.; Liao, Z.; Jia, B. Optimal Time Frequency Fusion Symmetrized Dot Pattern Bearing Fault Feature Enhancement and Diagnosis. Sensors 2024, 24, 4186. [Google Scholar] [CrossRef]
- Wang, H.; Xu, J.; Gao, Y. New intelligent bearing fault diagnosis method using SDP representation and SE-CNN. IEEE Trans. Instrum. Meas. 2020, 69, 2377–2389. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhi, G.; Chen, W.; Qian, Q.; He, D.; Dun, B.; Sun, W. A new tool wear condition monitoring method based on deep learning under small samples. Measurement 2022, 189, 110622. [Google Scholar] [CrossRef]
- Zheng, Y.; Niu, L.; Xiong, X.; Qi, H.; Xie, H. Fault diagnosis of CNN bearing cage based on EMD-SDP feature fusion. J. Mech. Electr. Eng. 2021, 38, 81–87. [Google Scholar] [CrossRef]
- Wang, J.; Abdullah, S.; Arifin, A.; Singh, S.; Gao, C. A Semi-supervised Fault Diagnosis Method for Rolling Bearing Using TimeFrequency Transform Enhanced Contrastive Learning. Eksploat. I Niezawodn. Maint. Reliab. 2026, 28, 207015. [Google Scholar] [CrossRef]
- Wang, H.; Sun, W.; Sun, W.; Ren, Y.; Zhou, Y.; Qian, Q.; Kumar, A. A novel tool condition monitoring based on Gramian angular field and comparative learning. Int. J. Hydromechatron. 2023, 6, 93–107. [Google Scholar] [CrossRef]
- Fatima, T.; Soliman, H. Application of VGG16 Transfer Learning for Breast Cancer Detection. Information 2025, 16, 227. [Google Scholar] [CrossRef]



| A (MPa) | B (MPa) | C | n | m | Troom (°C) | Tmelt (°C) | |
|---|---|---|---|---|---|---|---|
| Value | 553.1 | 600.8 | 0.0134 | 0.23 | 1 | 20 | 1460 |
| S/N | Spindle Speed (rpm) | Cutting Depth (mm) | Feed Rate (mm/min) | S/N | Spindle Speed (rpm) | Cutting Depth (mm) | Feed Rate (mm/min) |
|---|---|---|---|---|---|---|---|
| 1 | 2300 | 0.4 | 400 | 8 | 2500 | 0.5 | 400 |
| 2 | 2300 | 0.5 | 450 | 9 | 2500 | 0.6 | 450 |
| 3 | 2300 | 0.6 | 500 | 10 | 2300 | 0.4 | 500 |
| 4 | 2400 | 0.4 | 450 | 11 | 2300 | 0.6 | 400 |
| 5 | 2400 | 0.5 | 500 | 12 | 2500 | 0.6 | 500 |
| 6 | 2400 | 0.6 | 400 | 13 | 2500 | 0.6 | 400 |
| 7 | 2500 | 0.4 | 500 | 14 | 2500 | 0.4 | 400 |
| Tool Category | Tool Wear Condition | |
|---|---|---|
| 1 | [0, 0.1) | Initial wear |
| 2 | [0.1, 0.3) | Slight wear |
| 3 | [0.3, 0.5) | Stable wear |
| 4 | [0.5, 0.8) | Sharp wear |
| 5 | [0.8, +∞) | Failure |
| Component | ResNet18 | VGG16 |
|---|---|---|
| Total Layers | 18 layers | 16 layers |
| Convolutional Layers | 17 layers with 3 × 3 kernel | 13 (all 3 × 3 kernels) |
| Fully connected layers | 1 layer with 1 × 1 kernel | 3 layers (FC6, FC7, FC8) |
| Activation Function | ReLU (after each batch norm) | ReLU (after every conv/FC) |
| Pooling | Average pooling before FC layer | 5 MaxPool layers (2 × 2, stride 2) |
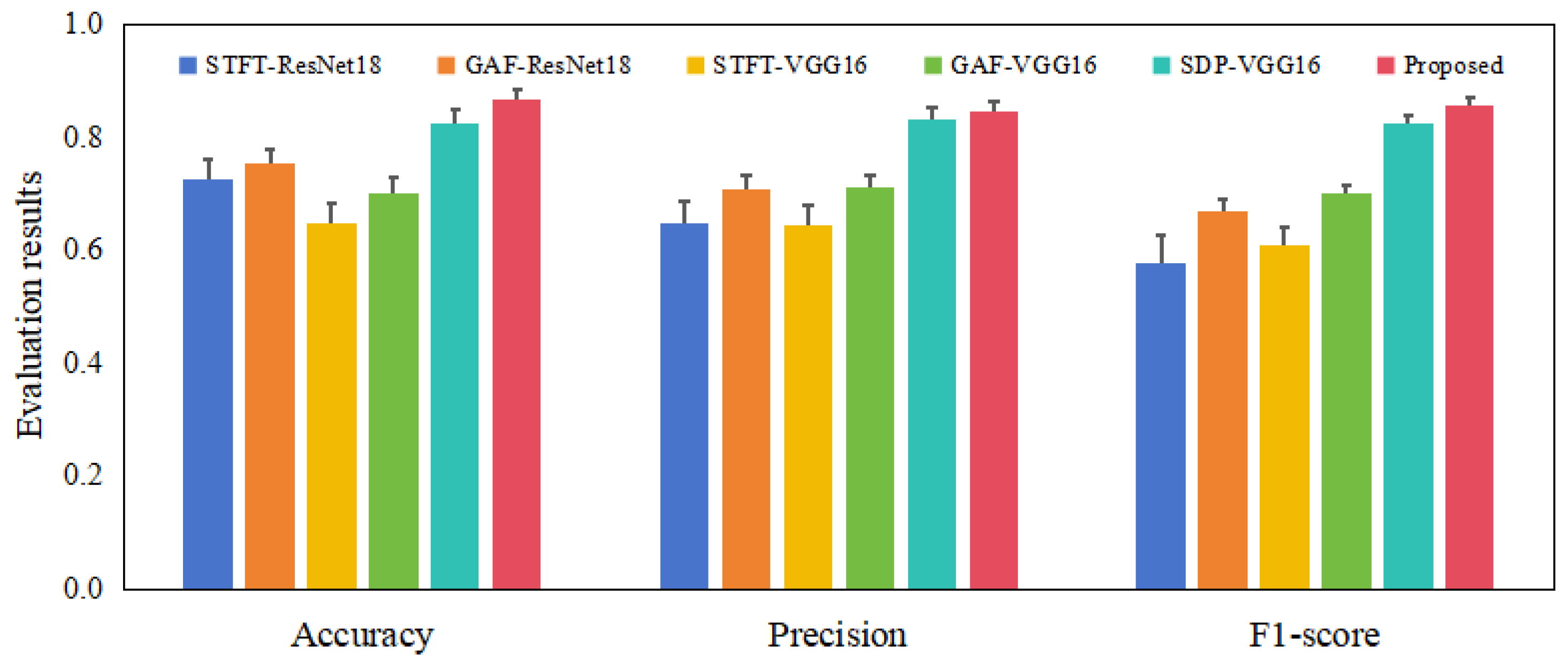
| STFT-ResNet18 | GAF-ResNet18 | STFT-VGG16 | GAF-VGG16 | SDP-VGG16 | Proposed | |
|---|---|---|---|---|---|---|
| Accuracy | 0.725 ± 0.0363 | 0.753 ± 0.0235 | 0.646 ± 0.0378 | 0.701 ± 0.0285 | 0.823 ± 0.0240 | 0.856 ± 0.0181 |
| Precision | 0.646 ± 0.0384 | 0.707 ± 0.0259 | 0.645 ± 0.0337 | 0.711 ± 0.0193 | 0.832 ± 0.0191 | 0.857 ± 0.0156 |
| F1-score | 0.578 ± 0.0496 | 0.669 ± 0.0226 | 0.608 ± 0.0312 | 0.699 ± 0.0152 | 0.817 ± 0.0145 | 0.841 ± 0.0143 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Wang, G.; Fu, Y.; Zhang, H.; Gao, C. Tool Wear Condition Monitoring Based on Improved Symmetrized Dot Pattern Enhanced Resnet18 Under Small Samples. Lubricants 2025, 13, 503. https://doi.org/10.3390/lubricants13110503
Chen X, Wang G, Fu Y, Zhang H, Gao C. Tool Wear Condition Monitoring Based on Improved Symmetrized Dot Pattern Enhanced Resnet18 Under Small Samples. Lubricants. 2025; 13(11):503. https://doi.org/10.3390/lubricants13110503
Chicago/Turabian StyleChen, Xiaoqin, Gonghai Wang, Yuandie Fu, Huan Zhang, and Chen Gao. 2025. "Tool Wear Condition Monitoring Based on Improved Symmetrized Dot Pattern Enhanced Resnet18 Under Small Samples" Lubricants 13, no. 11: 503. https://doi.org/10.3390/lubricants13110503
APA StyleChen, X., Wang, G., Fu, Y., Zhang, H., & Gao, C. (2025). Tool Wear Condition Monitoring Based on Improved Symmetrized Dot Pattern Enhanced Resnet18 Under Small Samples. Lubricants, 13(11), 503. https://doi.org/10.3390/lubricants13110503





