Research on Interfacial Instability Control During CO2 Displacement of Non-Newtonian Fluids
Abstract
1. Introduction
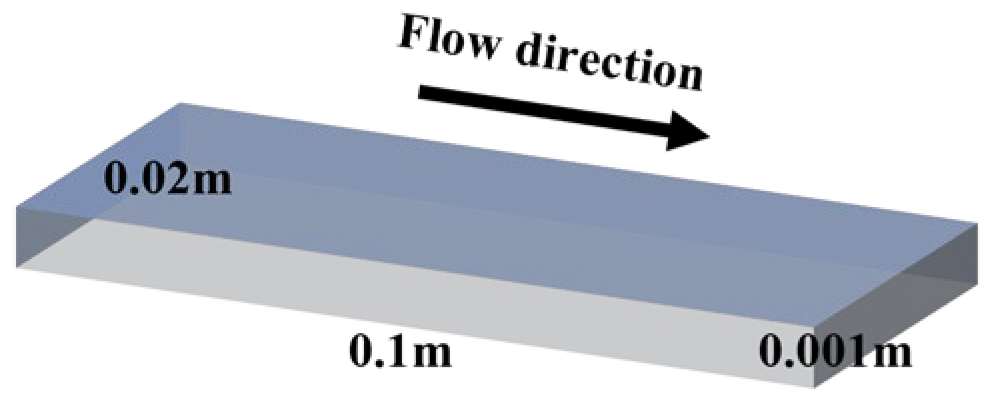
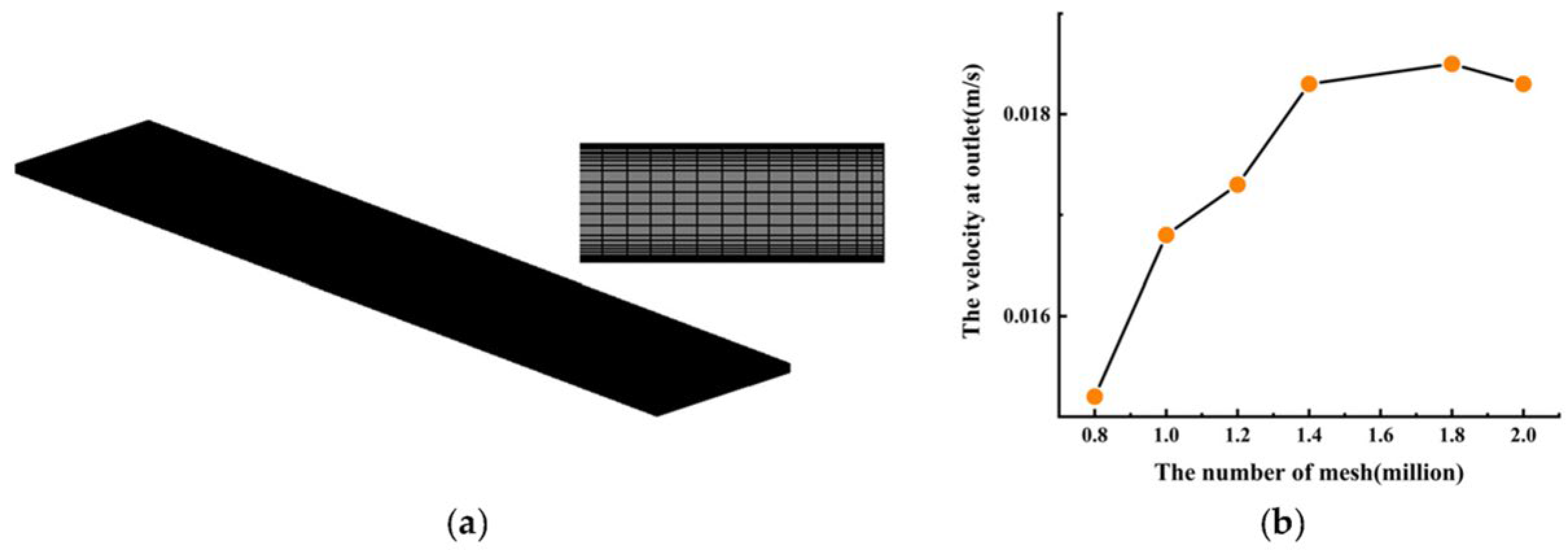
2. Numerical Method
3. The Effects of Wall Temperature on Viscous Fingering During Displacement Processes
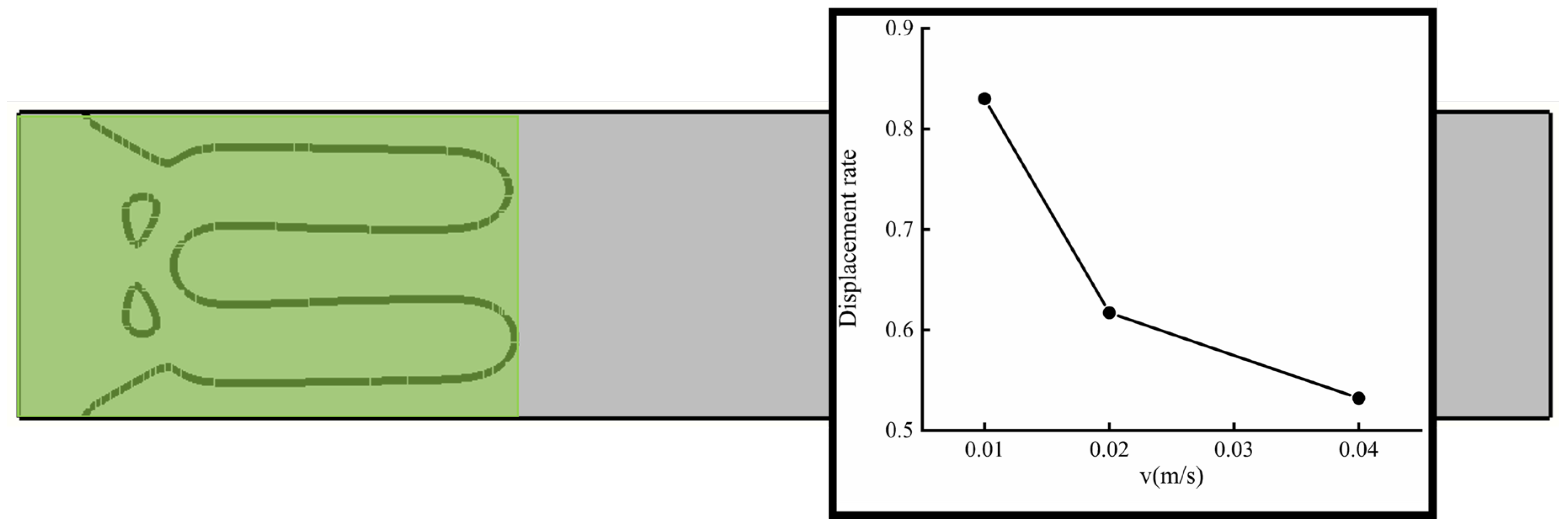
4. Effects of CO2 Displacement Velocity on Viscous Fingering Instabilities
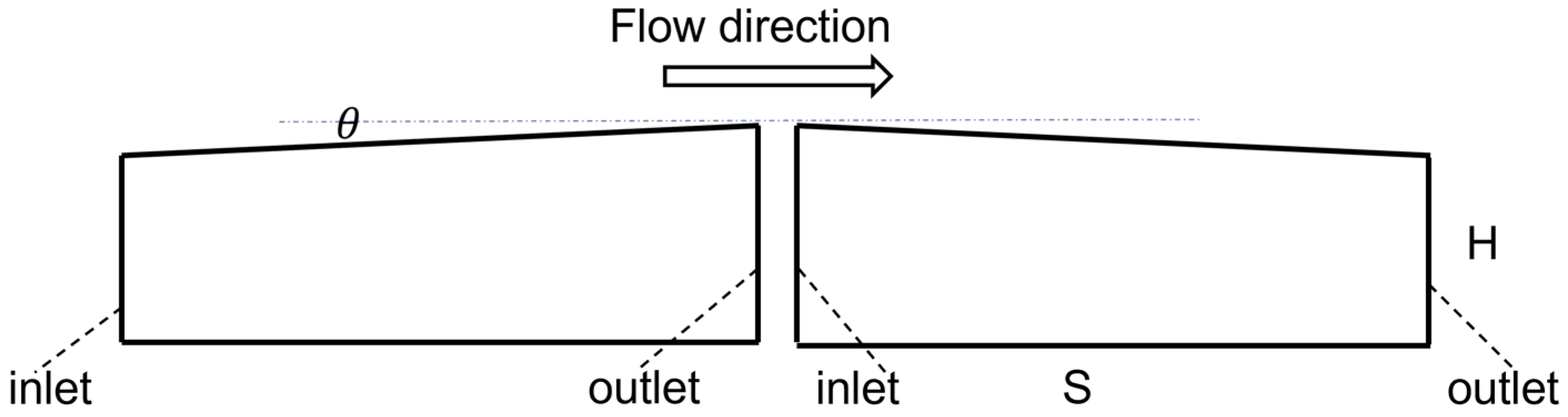
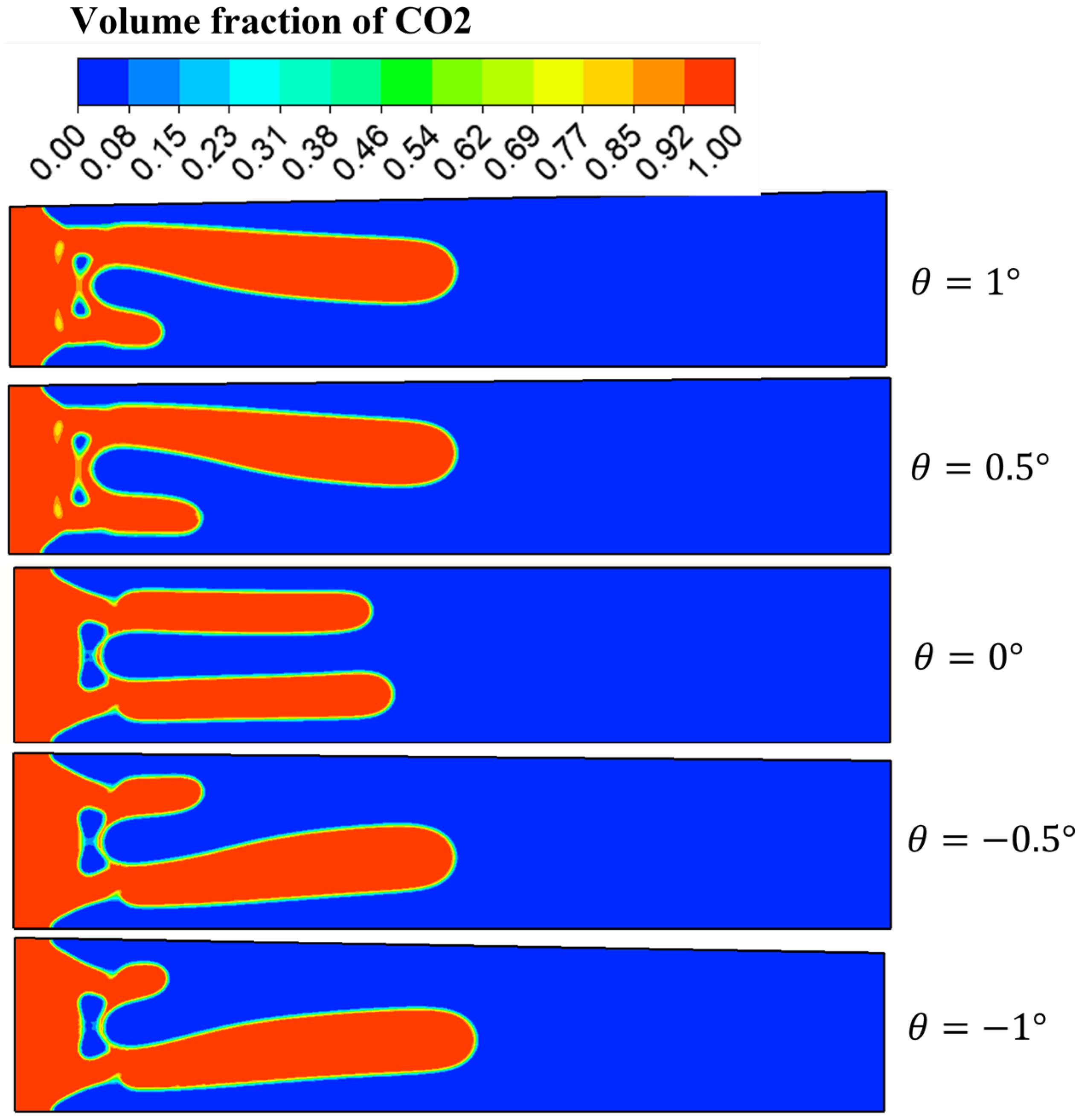
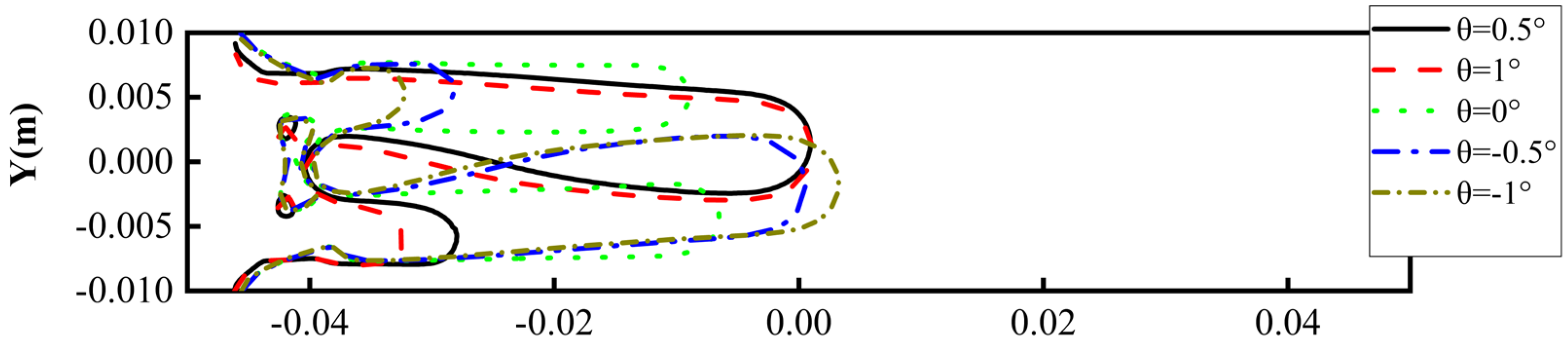
5. Effects of Depth Gradient on Viscous Fingering Instabilities in Modified HSC
6. Conclusions
- (1)
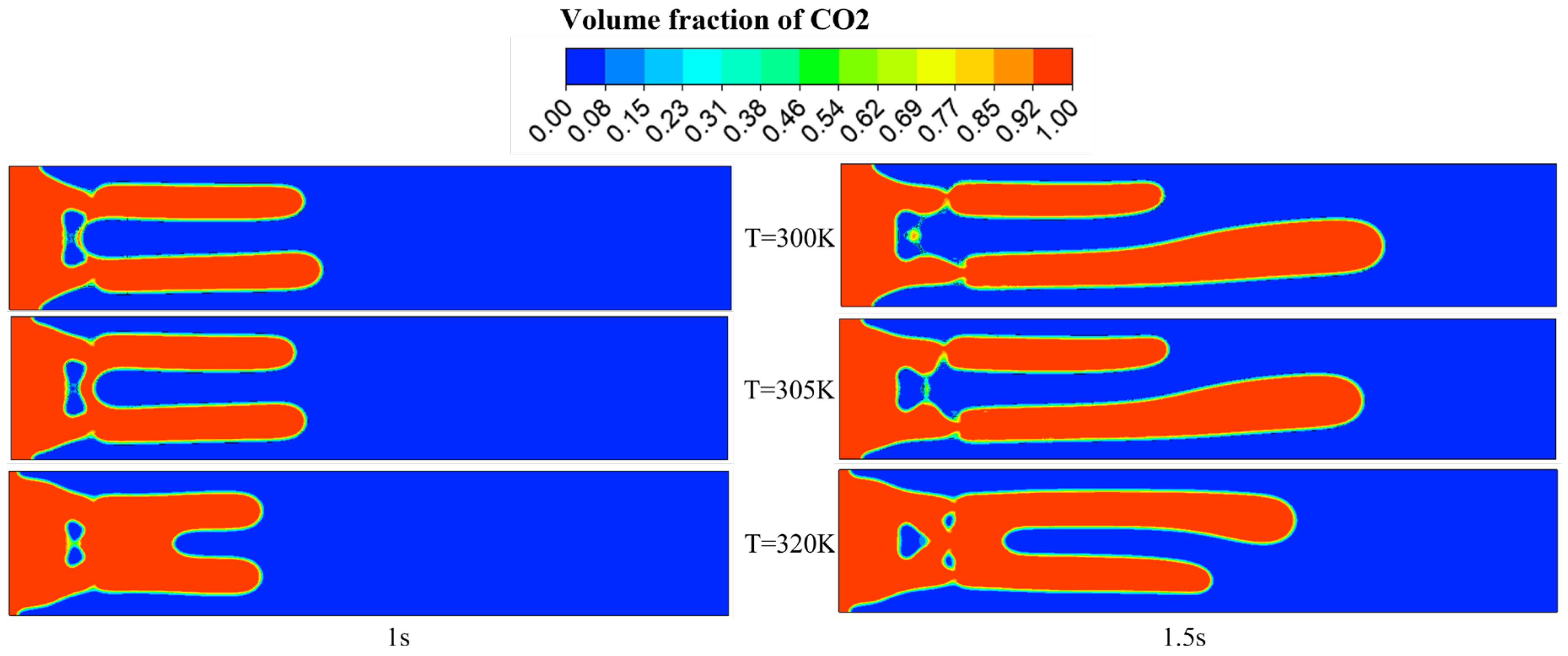
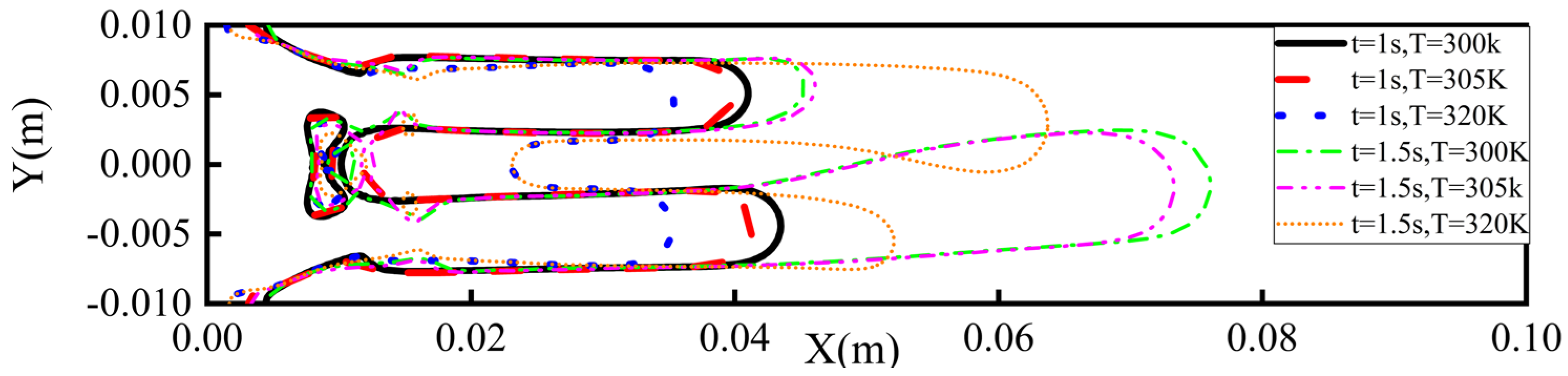
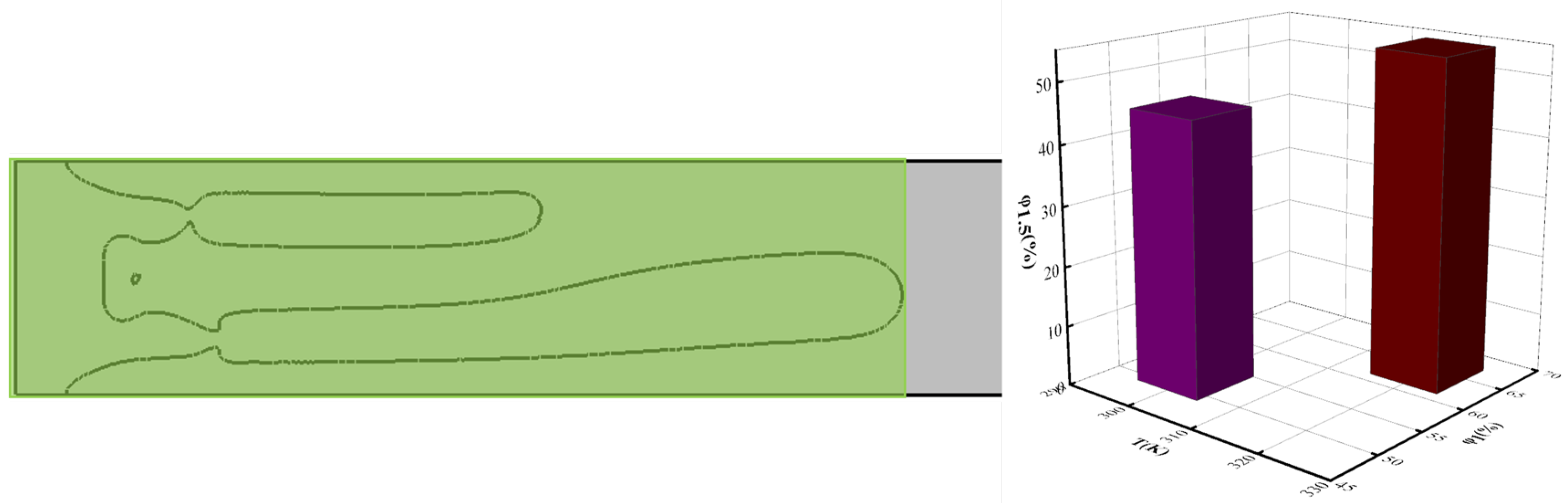
- Through comparative analysis of displacement behaviors at 300 K, 305 K, and 320 K, it is consistently observed that symmetrically bifurcated fingering structures develop across all temperature conditions, accompanied by cavitation nucleation phenomena localized at the fingering roots. However, with increasing temperature, the fingering propagation distance decreases, the root thickness of the fingering structures increases, and the intermediate cavitation zone progressively contracts. Furthermore, the sweep efficiency exhibits a positive correlation with increasing temperature, indicating a reduction in residual non-Newtonian fluid within the displaced zones and a consequent enhancement in displacement efficiency. Due to the increase in temperature, the kinetic energy of molecular thermal motion is enhanced, breaking the existing weak interactions, resulting in a macroscopic decrease in viscosity, which helps CO2 to be better absorbed in the reservoir. In addition, an increase in temperature will accelerate the diffusion of molecules at the interface, making it easier for displacement phase molecules to diffuse into the displaced phase, expanding the displacement range and improving displacement efficiency. This holds profound strategic significance for enhancing hydrocarbon recovery in both oil and gas reservoirs. The thermally expanded sweep coverage enables efficient mobilization and displacement of previously inaccessible fluid phases trapped in complex pore networks, thereby unlocking substantial volumes of challenging reserves.
- (2)
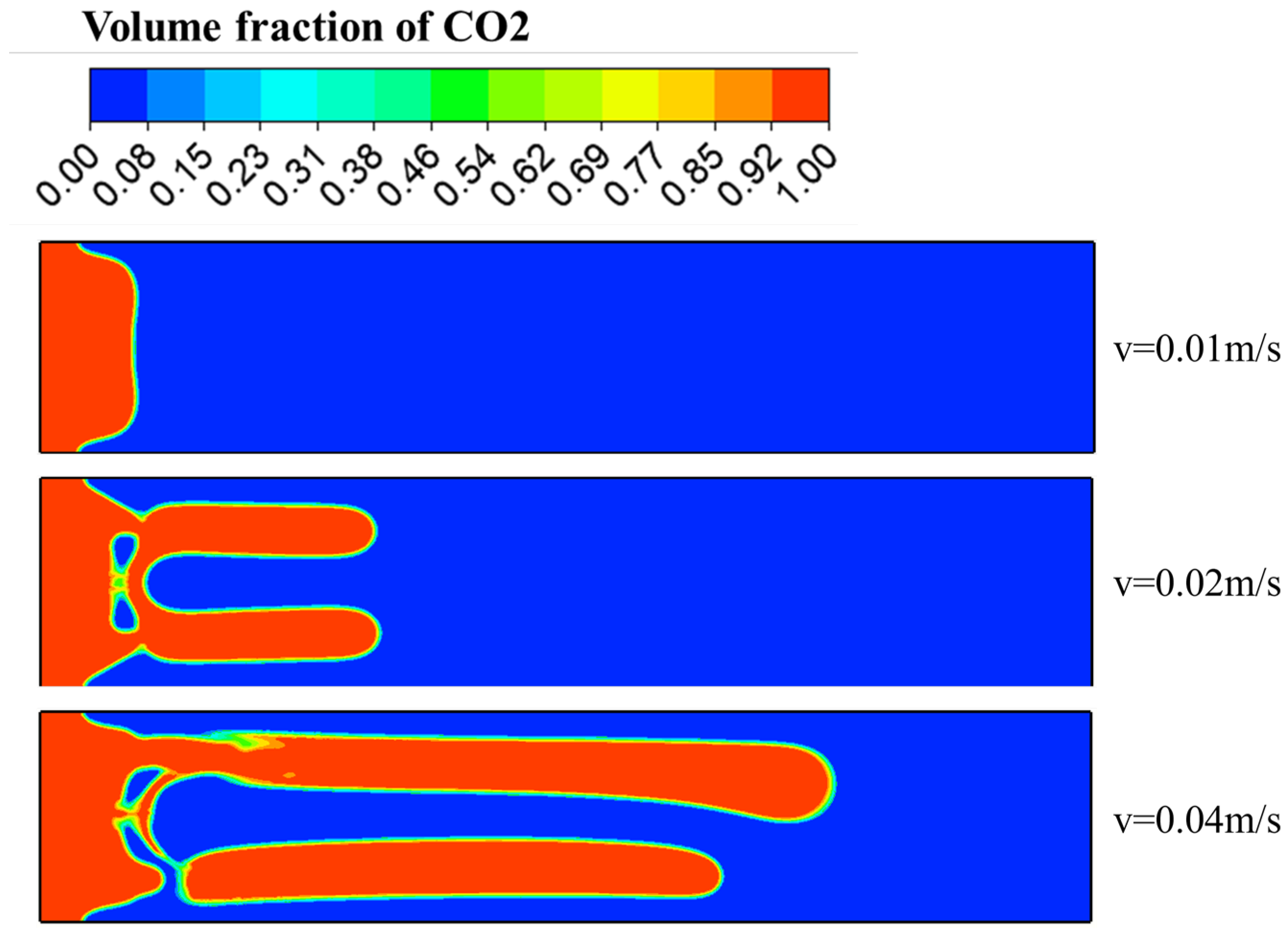
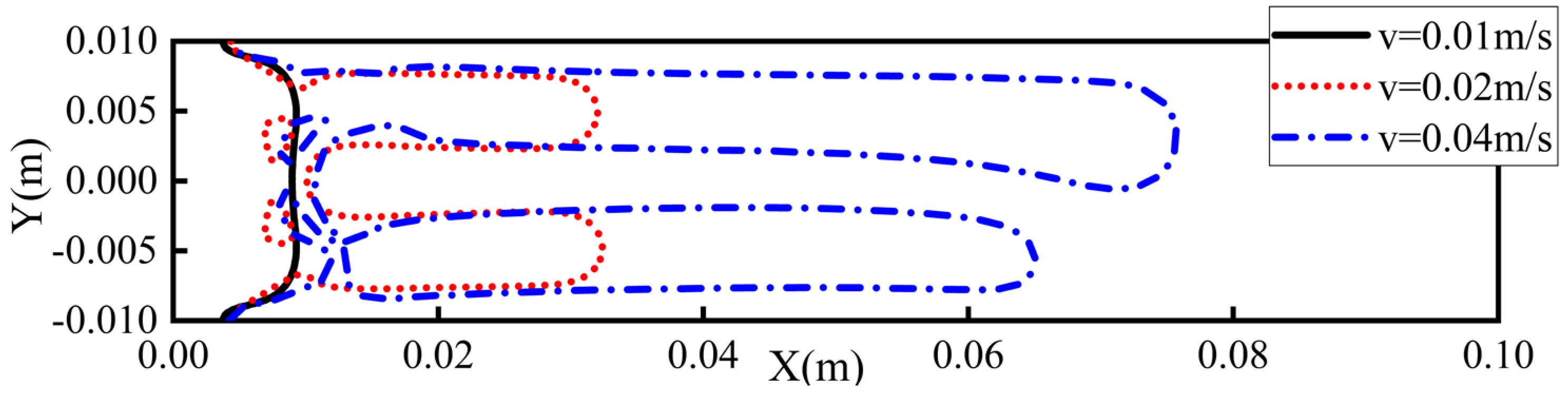
- To investigate the influence of velocity on fingering, three representative velocities of 0.01 m/s, 0.02 m/s, and 0.04 m/s were selected. At the velocity of 0.01 m/s, the displacement interface is relatively smooth, showing a relatively stable advancing pattern of the displacement front. When the velocity increases, the displacement interface becomes more disordered, and the distribution of the air volume fraction becomes more scattered. This phenomenon arises from a fundamental shift in hydrodynamic dominance: at lower velocities, viscous forces govern flow behavior, while increasing velocity progressively amplifies inertial effects. The dynamic interplay between these competing forces dictates the evolution of interfacial morphology, sweep coverage, and displacement efficiency. Moreover, under low-velocity conditions, while sweep efficiency reaches its peak value, the sluggish advancement of the displacement front results in diminished volumetric displacement rates per unit time, leading to suboptimal displacement efficiency on a temporal basis. When the velocity increases, the sweep coverage expands; however, due to excessive viscous fingering, this results in a non-uniform displacement process, lower sweep efficiency, and a higher residual volume of non-Newtonian fluid. Therefore, in various engineering applications, both sweep efficiency and displacement efficiency should be comprehensively considered to determine (or achieve) an appropriate overall recovery efficiency.
- (3)
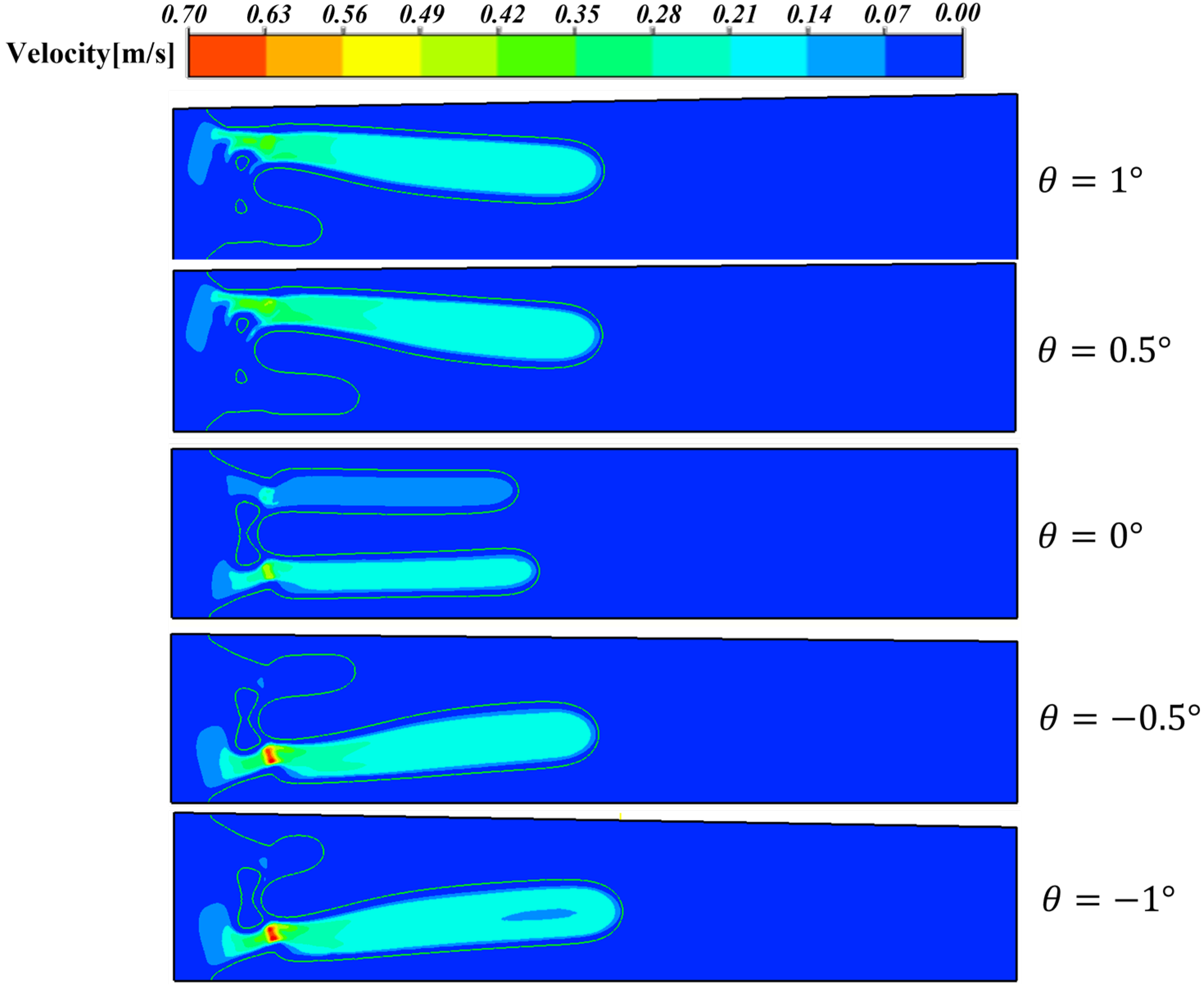
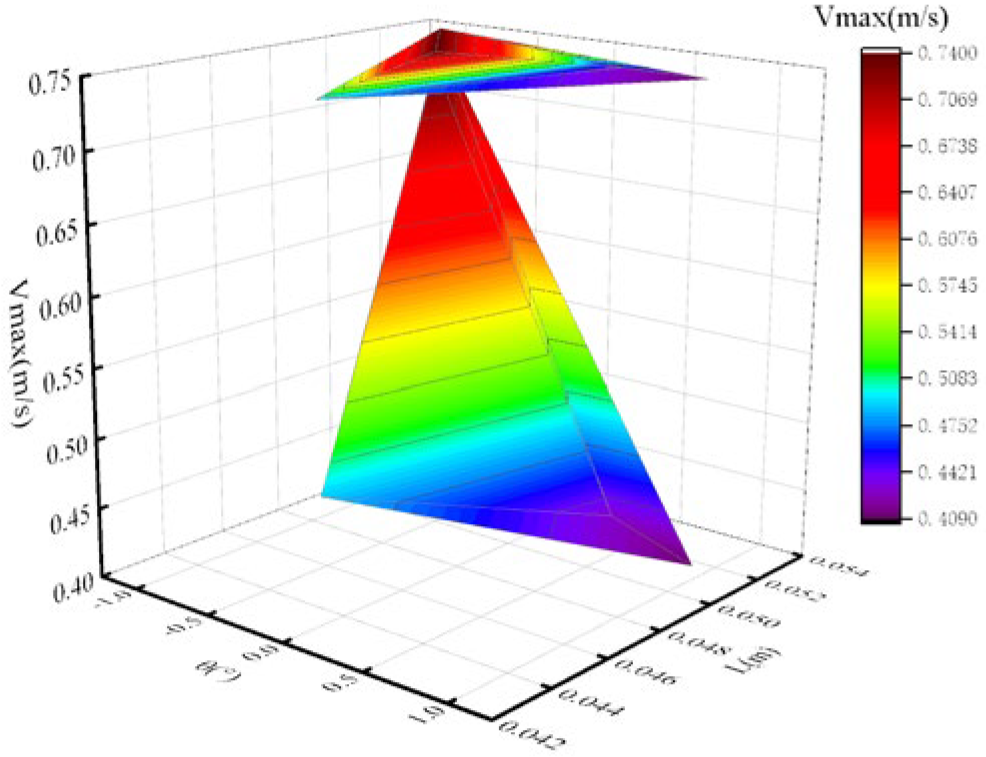
- In the variant study of the classical HSC model, four depth gradients, −0.5°, −1°, +0.5° and +1°, were introduced. It was found that both the direction and magnitude of the depth gradient significantly influence the morphology and extension length of viscous fingering. Both positive and negative depth gradients promote the development of fingering on one side. In the absence of a gradient, the two fingers develop relatively uniformly. This phenomenon fundamentally stems from flow field redistribution induced by depth variations along the flow conduit. The presence of a depth gradient establishes preferential flow pathways in specific spatial orientations, thereby amplifying fingering instabilities through localized flow intensification. Furthermore, as the depth gradient changes from negative to positive, that is from −1° to +1°, the maximum velocity within the fingers gradually decreases. This occurs because the increasing gradient magnitude transforms the flow channel from a narrowing configuration to a widening one, thereby causing a reduction in velocity. Therefore, depth gradients fundamentally modulate the morphology and propagation of viscous fingering by dynamically altering the geometric confinement of flow conduits, thereby strategically reconfiguring the spatial distribution of velocity fields. In engineering applications, deliberate modulation of depth gradients within flow conduits enables strategic control over displacement dynamics, facilitating targeted suppression or triggering of interfacial instabilities as required by operational objectives.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Homsy, M.G. Viscous Fingering in Porous Media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Bensimon, D.; Kadanoff, L.P.; Liang, S.; Shraiman, B.I.; Tang, C. Viscous flows in two dimensions. Rev. Mod. Phys. 1986, 58, 977. [Google Scholar] [CrossRef]
- Ganesh, A.; Douarche, C.; Auradou, H. Active Saffman-Taylor Viscous Fingering. Phys. Rev. Lett. 2025, 134, 128301. [Google Scholar] [CrossRef] [PubMed]
- Fahad, M.; Hussain, F.; Rahman, S.S.; Cinar, Y. Experimental investigation of upscaling relative permeability for two phase flow in fractured porous media. J. Pet. Sci. Eng. 2017, 149, 367–382. [Google Scholar] [CrossRef]
- Arab, D.; Kantzas, A.; Bryant, S.L. Water flooding of oil reservoirs: Effect of oil viscosity and injection velocity on the interplay between capillary and viscous forces. J. Pet. Sci. Eng. 2020, 186, 106691. [Google Scholar] [CrossRef]
- Lyu, S.; Hwang, W. Selective superhydrophilic/phobic coating using capillary pressure for positive-displacement nanoliter dispensing. Surf. Coat. Technol. 2015, 277, 258–261. [Google Scholar] [CrossRef]
- Ji, S.; Li, H.; Wang, G.; Lu, T.; Ma, W.; Wang, J.; Zhu, H.; Xu, H. Rheological behaviors of a novel exopolysaccharide produced by Sphingomonas WG and the potential application in enhanced oil recovery. Int. J. Biol. Macromol. 2020, 162, 1816–1824. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Liu, Z.; Trivedi, J.; Tang, Y.; Sui, M. Visualized investigation of the immiscible displacement: Influencing factors, improved method, and EOR effect. Fuel 2023, 331, 125841. [Google Scholar] [CrossRef]
- Chen, Z.; Schmid, R.; Wang, X.; Fu, M.; Han, Z.; Fan, Q.; Scheer, E.; Huang, M.; Nielaba, P.; Cölfen, H. Growth strategy for solution-phase growth of two-dimensional nanomaterials via a unified model. Nat. Synth. 2023, 2, 670–677. [Google Scholar] [CrossRef]
- Abu Jarad, N.; IWeitz, J.; Didar, T. Advancements in Surface Modification Strategies of Blood-contacting Biomaterials to Improve Biocompatibility and Tissue Integration. ChemRxiv 2023. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, B.; Hu, Y.; Yang, D.; Ma, D.; Huang, S. Extraordinary sensitive mechanochromic hydrogels for visually detecting ultrasmall pressure. Cell Rep. Phys. Sci. 2023, 4, 101387. [Google Scholar] [CrossRef]
- Kargozarfard, Z.; Riazi, M.; Ayatollahi, S. Viscous fingering and its effect on areal sweep efficiency during waterflooding: An experimental study. Pet. Sci. 2019, 16, 105–116. [Google Scholar] [CrossRef]
- Gorell, B.S.; Homsy, M.G. A Theory of the Optimal Policy of Oil Recovery by Secondary Displacement Processes. SIAM J. Appl. Math. 2006, 43, 79–98. [Google Scholar] [CrossRef]
- Orr, F.M.; Taber, J.J. Use of Carbon Dioxide in Enhanced Oil Recovery. Science 1984, 224, 563–569. [Google Scholar] [CrossRef]
- Regaieg, M.; McDougall, S.; Bondino, I.; Hamon, G. Finger Thickening during Extra-Heavy Oil Waterflooding: Simulation and Interpretation Using Pore-Scale Modelling. PLoS ONE 2017, 12, e0169727. [Google Scholar] [CrossRef]
- Raut, S.; Raihan, M.K.; Song, Y.; Xuan, X. Fluid shear thinning effects on particle focusing in a spiral microchannel. Phys. Fluids 2024, 36, 112036. [Google Scholar] [CrossRef]
- Yadali Jamaloei, B.; Babolmorad, R.; Kharrat, R. Visualization and analysis of viscous fingering in alcohol-assisted surfactant waterflooding of heavy oil in a two-dimensional sandstone micromodel. Fuel 2016, 184, 169–179. [Google Scholar] [CrossRef]
- Chuoke, R.L.; Van Der Meurs, P.; Van Der Poel, C. The instability of slow, immiscible, viscous liquid-liquid displacement in permeable media. Trans. AIME 1959, 216, 188–194. [Google Scholar] [CrossRef]
- Hamid, A.A.S.; Muggeridge, H.A. Analytical solution of polymer slug injection with viscous fingering. Comput. Geosci. 2018, 22, 711–723. [Google Scholar] [CrossRef]
- Beteta, A.; Sorbie, K.S.; Skauge, A. Immiscible Viscous Fingering: The Simulation of Tertiary Polymer Displacements of Viscous Oils in 2D Slab Floods. Polymers 2022, 14, 4159. [Google Scholar] [CrossRef] [PubMed]
- Salmo, I.C.; Sorbie, K.S.; Skauge, A.; Alzaabi, M.A. Immiscible Viscous Fingering: Modelling Unstable Water–Oil Displacement Experiments in Porous Media. Transp. Porous Media 2022, 145, 291–322. [Google Scholar] [CrossRef]
- Sajjad, H.R.; Dani, O.; Ying, L.; Lai, C.Y.; Lu, N.B.; Datta, S.S.; Stone, H.A.; Shokri, N. Suppressing viscous fingering in structured porous media. Proc. Natl. Acad. Sci. USA 2018, 115, 4833–4838. [Google Scholar] [CrossRef]
- Zhao, B.; Mohanty, K.K. Effect of wettability on immiscible viscous fingering in porous media. J. Pet. Sci. Eng. 2019, 174, 738–746. [Google Scholar] [CrossRef]
- Esmaeilpour, M.; Gholami Korzani, M. Analyzing Impacts of Interfacial Instabilities on the Sweeping Power of Newtonian Fluids to Immiscibly Displace Power-Law Materials. Processes 2021, 9, 742. [Google Scholar] [CrossRef]
- Redapangu, R.P.; Vanka, S.; Sahu, C.K. Multiphase lattice Boltzmann simulations of buoyancy-induced flow of two immiscible fluids with different viscosities. Eur. J. Mech./B Fluids 2012, 34, 105–114. [Google Scholar] [CrossRef]
- Bakharev, F.; Campoli, L.; Enin, A.; Matveenko, S.; Petrova, Y.; Tikhomirov, S.; Yakovlev, A. Numerical Investigation of Viscous Fingering Phenomenon for Raw Field Data. Transp. Porous Media 2020, 132, 443–464. [Google Scholar] [CrossRef]
- Yang, X.; Tang, Y.; Li, M.; Li, C.; Wang, M.; Li, X.; Zhao, J. Effect of shear-thinning of non-Newtonian fluid on the crossover from capillary fingering to viscous fingering in porous media. Phys. Lett. A 2022, 449, 128364. [Google Scholar] [CrossRef]
- Ahmadikhamsi, S.; Golfier, F.; Oltean, C.; Lefèvre, E.; Bahrani, S.A. Impact of surfactant addition on non-Newtonian fluid behavior during viscous fingering in Hele-Shaw cell. Phys. Fluids 2020, 32, 012103. [Google Scholar] [CrossRef]
- Shokri, H.; Kayhani, H.M.; Norouzi, M. On the miscible thermo-viscous fingering instability of non-Newtonian fluids in heterogeneous porous media. Rheol. Acta 2019, 58, 755–769. [Google Scholar] [CrossRef]
- Logvinov, A.O. Radial Viscous Fingering in Case of Poorly Miscible Fluids. Transp. Porous Media 2018, 124, 495–508. [Google Scholar] [CrossRef]
- Mafi, M.; Qin, Z.; Wu, Y.; Lyu, S.-K.; Ma, C. Research on the Interfacial Instability of Non-Newtonian Fluid Displacement Using Flow Geometry. Coatings 2023, 13, 1848. [Google Scholar] [CrossRef]
- Singh, A.; Pandey, K.M.; Singh, Y. CFD analysis of viscous fingering in Hele-Shaw cell for air-glycerin system. Mater. Today Proc. 2021, 45, 6381–6385. [Google Scholar] [CrossRef]
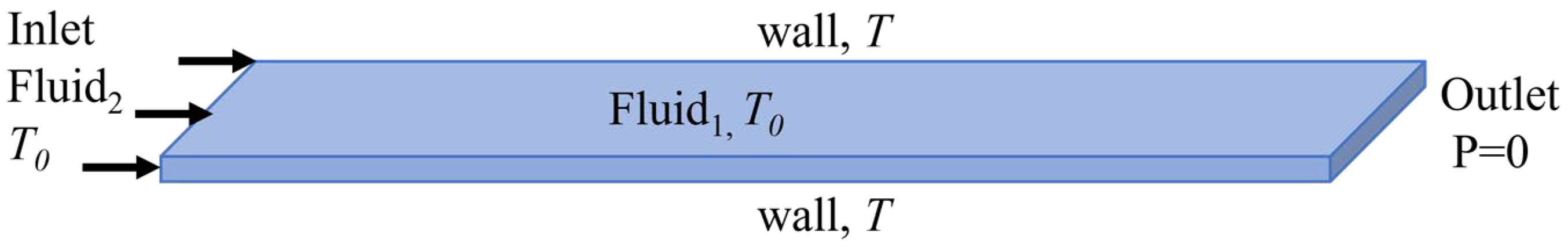
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.-T.; Lyu, S.-K.; Qin, Z.; Zhang, J.; Qiao, H. Research on Interfacial Instability Control During CO2 Displacement of Non-Newtonian Fluids. Lubricants 2025, 13, 478. https://doi.org/10.3390/lubricants13110478
Wu Y-T, Lyu S-K, Qin Z, Zhang J, Qiao H. Research on Interfacial Instability Control During CO2 Displacement of Non-Newtonian Fluids. Lubricants. 2025; 13(11):478. https://doi.org/10.3390/lubricants13110478
Chicago/Turabian StyleWu, Yu-Ting, Sung-Ki Lyu, Zhen Qin, Jie Zhang, and Hua Qiao. 2025. "Research on Interfacial Instability Control During CO2 Displacement of Non-Newtonian Fluids" Lubricants 13, no. 11: 478. https://doi.org/10.3390/lubricants13110478
APA StyleWu, Y.-T., Lyu, S.-K., Qin, Z., Zhang, J., & Qiao, H. (2025). Research on Interfacial Instability Control During CO2 Displacement of Non-Newtonian Fluids. Lubricants, 13(11), 478. https://doi.org/10.3390/lubricants13110478




