Research on the Lubrication and Friction Characteristics of New Water-Lubricated Bearings Made of PEEK Material in Salt-Sand Water Environments
Abstract
1. Introduction
2. Model Establishment
2.1. Mathematical Model
2.1.1. Control Equations of the Fluid Domain
2.1.2. Control Equations of the Solid Domain
2.1.3. Thermal-Fluid-Structure Coupling Equation
2.1.4. Friction Coefficient
2.2. Physical Model
2.2.1. Bearing Structure and Parameters
2.2.2. Boundary Conditions and Mesh Generation
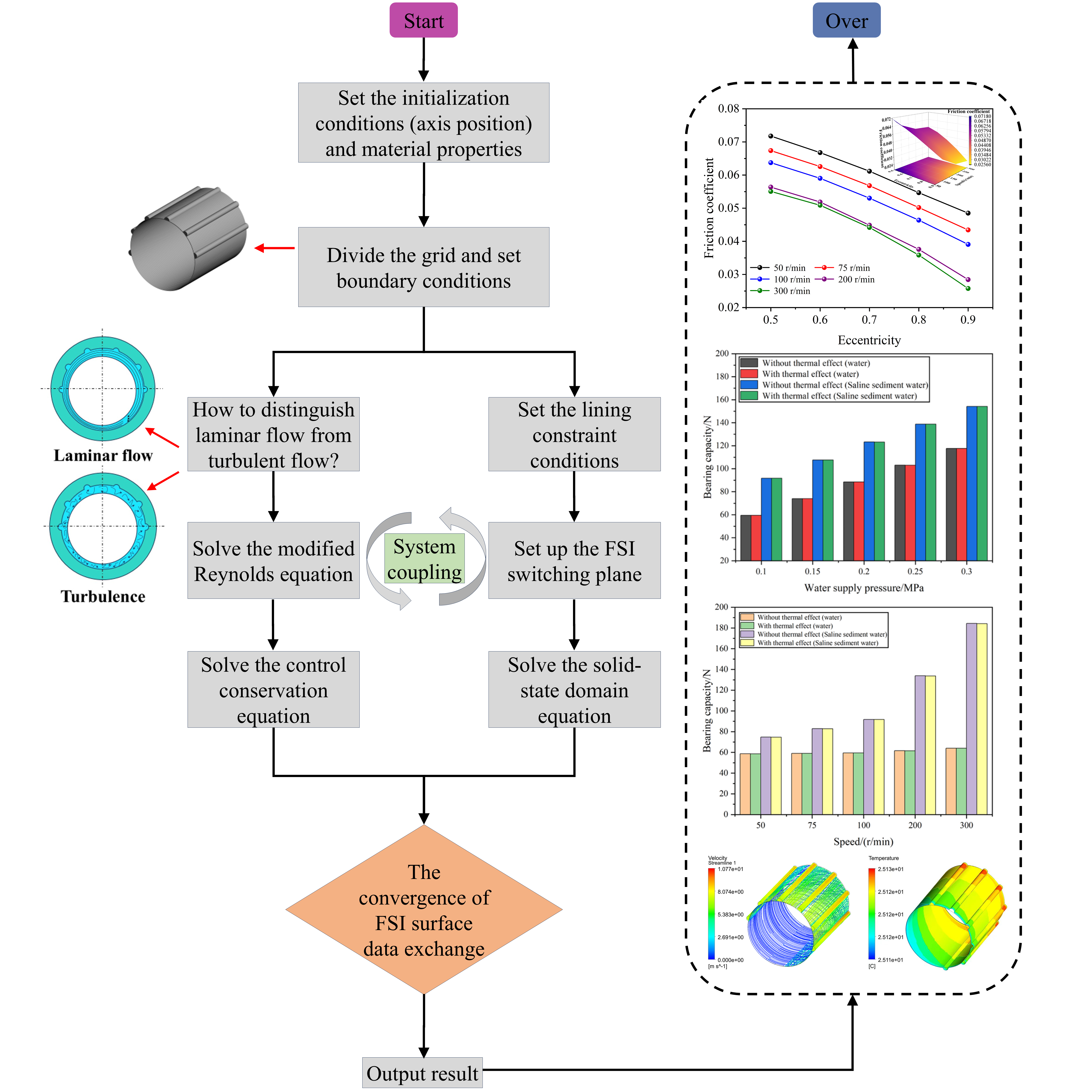
2.3. Solution Process
3. Simulation Analysis
3.1. Lubrication Characteristics of Bearings Considering Thermal Effects at Different Rotational Speeds
3.2. Bearing Lubrication Characteristics After Considering Thermal Effects Under Different Water Supply Pressures
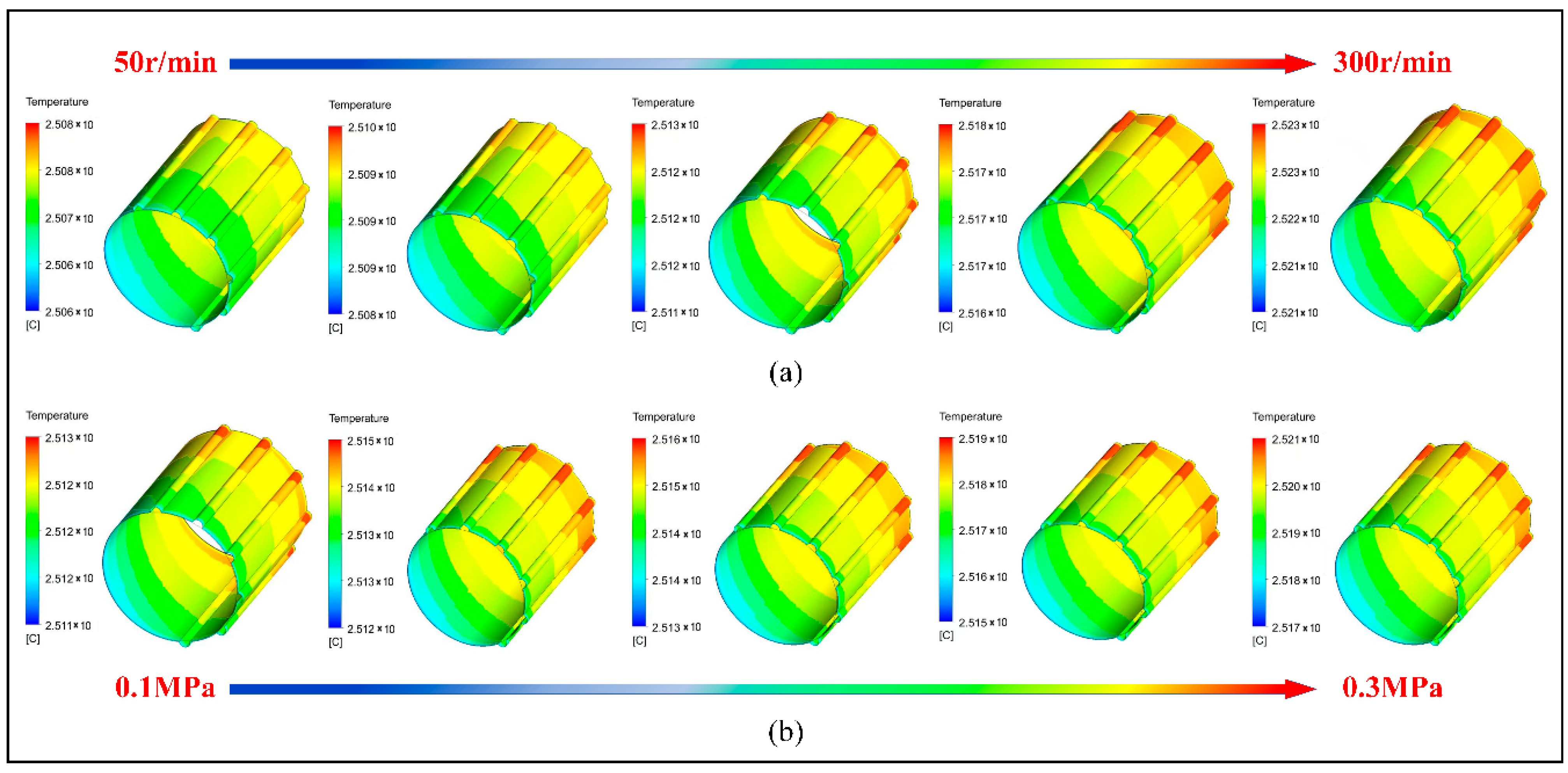
3.3. Distribution of Water Film Temperature Under Different Rotational Speeds and Different Water Supply Pressures
3.4. Bearing Lubrication Characteristics Under the Coupling of Eccentricity and Rotational Speed
3.5. Bearing Lubrication Characteristics Under the Coupling of Roughness and Rotational Speed
3.6. Distribution of the Flow Velocity of the Water Film Flow Field Under Different Rotational Speeds and Different Eccentricities
4. Experimental Test
4.1. Test Environment and Test Bench
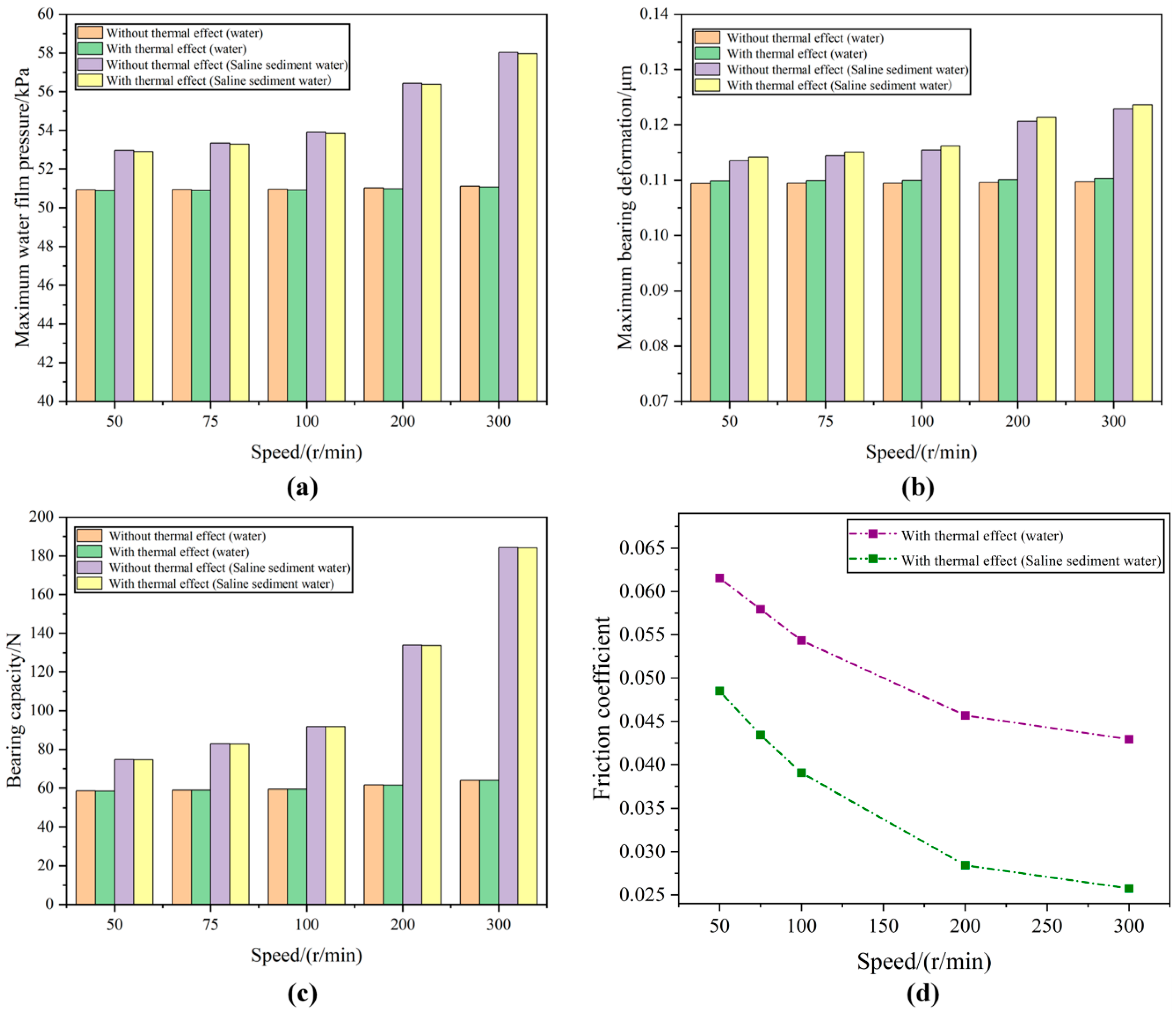
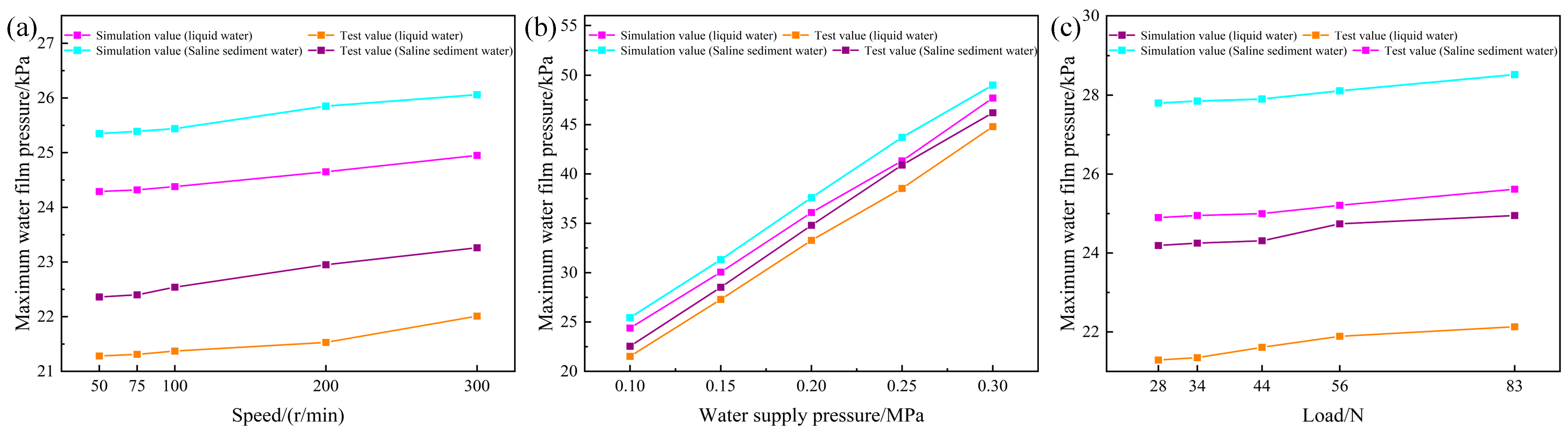
4.2. Water Film Pressure Tests of Bearings Under Different Working Conditions
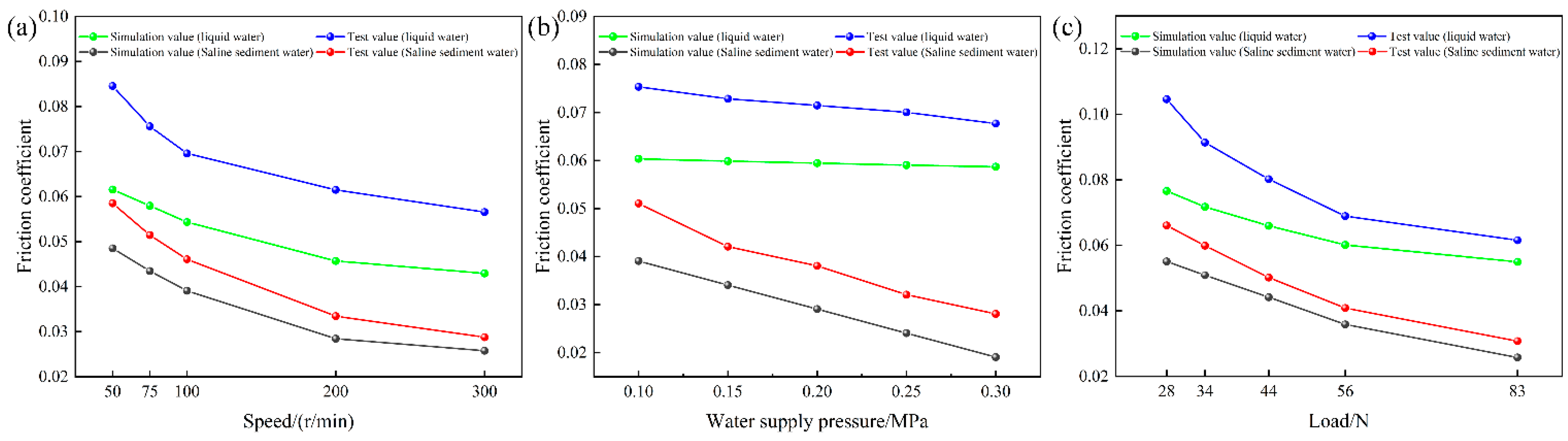
4.3. Tests on the Friction Coefficient of Bearings Under Different Working Conditions
5. Conclusions
- (1)
- In a saline sand water environment, the maximum water film pressure, bush deformation, and bearing capacity of the bearing all increase with increasing rotational speed and water supply pressure. As the eccentricity increases, the bearing wedge gap increases, the friction coefficient decreases, and the hydrodynamic effect becomes significant. An increase in the surface roughness of the bush leads to a slight decrease in the water film pressure and bush deformation and an increase in the friction coefficient. However, the presence of salt and sand particles can fill the gaps between asperities, weakening the negative impact of roughness on lubrication performance. Meanwhile, the high viscosity of saline sand water and the filling effect of the particles enhance the hydrodynamic effect of the fluid, making the lubrication performance of the bearing superior to that in liquid water.
- (2)
- After considering the thermal effect, the mechanical and thermal loads act together on the bush. The maximum bush deformation increases by 0.47% and 0.6% in liquid water and saline sand water, respectively, while the water film pressure and bearing capacity both slightly decrease by 0.11%. This indicates that the thermal effect reduces the lubrication effect of the fluid. The water film temperature increases slightly with increasing rotational speed and water supply pressure, and due to axial flow water supply and temperature boundaries, the highest temperatures accumulate in the grooves at the water film outlet.
- (3)
- The local upper half-groove structure can still exhibit good lubrication characteristics even in the presence of salt and sand particles. It not only improves the bearing capacity but also facilitates the discharge of water film temperature and salt and sand particles through the grooves. The PEEK water-lubricated bearing also demonstrates insensitivity to temperature, low friction, and good mechanical properties, with a minimum friction coefficient of up to 0.019.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, X.; Liang, X.; Liu, Z. Research progress of marine water lubricated stern bearing. Ship Build. China 2017, 58, 221–232. [Google Scholar]
- Zhou, X.; Kuang, F.; Huang, J. Water-lubricated stern bearing rubber layer construction and material parameters: Effects on frictional vibration based on computer vision. Tribol. Trans. 2021, 64, 65–81. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, W.; Liang, X. Review of the evolution and prevention of friction, wear, and noise for water-lubricated bearings used in ships. Friction 2024, 12, 1–38. [Google Scholar] [CrossRef]
- Jiang, S.; Wong, J.; Puhan, D. Tribological evaluation of thermoplastic polyurethane-based bearing materials under water lubrication: Effect of load, sliding speed, and temperature. Friction 2024, 12, 1801–1815. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, C.; Nardin, P. Effects of sliding velocity and applied load on the tribological mechanism of amorphous poly-ether–ether–ketone (PEEK). Tribol. Int. 2008, 41, 79–86. [Google Scholar] [CrossRef]
- Shukla, D.; Negi, Y.S.; Uppadhyaya, J.S. Synthesis and modification of poly (ether ether ketone) and their properties: A review. Polym. Rev. 2012, 52, 189–228. [Google Scholar] [CrossRef]
- Panayotov, I.V.; Orti, V.; Cuisinier, F. Polyetheretherketone (PEEK) for medical applications. J. Mater. Sci. Mater. Med. 2016, 27, 118. [Google Scholar] [CrossRef]
- Han, Y.; Yin, L.; Xiang, G. An experimental study on the tribological performance of water-lubricated journal bearings with three different materials. Ind. Lubr. Tribol. 2020, 72, 1159–1165. [Google Scholar] [CrossRef]
- Ma, H.Q.; Wang, Y.Q.; Liu, X.F. Research Progress on Friction and Wear of Water Lubricated Bearing Modified PEEK Materials. Bearing 2023, 11, 1–12. [Google Scholar]
- Xie, Z.L.; Jiao, J.; Yang, M. Investigation on the Fluid-structure-acoustic Multi-field Interaction Characteristics of the Water-lubricated Sandwich Liner Bearing. J. Mech. Eng. 2024, 60, 340–349. [Google Scholar]
- Litwin, W.; Wasilczuk, M.; Wodtke, M. The influence of polymer bearing material and lubricating grooves layout on wear of journal bearings lubricated with contaminated water. Tribol. Int. 2023, 179, 108159. [Google Scholar] [CrossRef]
- Liu, Q.; Ouyang, W.; Li, R. Experimental exploration on the nonlinear dynamic behavior of marine propeller shaft-bearing system. Ocean Eng. 2024, 310, 118595. [Google Scholar] [CrossRef]
- Lv, F.; Jiao, C.; Jia, Q. Influence of structural and operating parameters on lubrication performance of water-lubricated polymer bearing with journal misalignment. Lubricants 2022, 10, 336. [Google Scholar] [CrossRef]
- Wodtke, M.; Litwin, W. Water-lubricated stern tube bearing−experimental and theoretical investigations of thermal effects. Tribol. Int. 2021, 153, 106608. [Google Scholar] [CrossRef]
- Ouyang, W.; Zhang, Z.; Nie, Y.; Liu, B.; Vanierschot, M. Parametric modeling and collaborative optimization of a rim-driven thruster considering propeller-duct interactions. Ocean Eng. 2025, 337, 121746. [Google Scholar] [CrossRef]
- Xie, Z.L.; Zhang, H.; Yang, M. Research on the Influence of Bidirectional Misalignment on the Lubrication Characteristics of Water-Lubricated Grooved Bearings. Tribology 2024, 11, 1–17. [Google Scholar]
- Chen, Y.H.; Wang, N.; Wang, M.W. Study on Effect Mechanism of Bi-directional Journal Tilt on Characteristics of Water-Lubricated Stern Bearings. Mech. Sci. Technol. Aerosp. Eng. 2025, 44, 994–1002. [Google Scholar]
- Liu, Q.; Ouyang, W.; Cheng, Q. Influences of bidirectional shaft inclination on lubrication and dynamic characteristics of the water-lubricated stern bearing. Mech. Syst. Signal Process. 2022, 169, 108623. [Google Scholar] [CrossRef]
- Ouyang, W.; Liu, Q.; Jin, Y.; Dong, X. Semi-active control for transverse vibration of ship propulsion shafting with magnetorheological squeeze film damper. Mech. Syst. Signal Process. 2025, 233, 112763. [Google Scholar] [CrossRef]
- Chen, P.; Wang, T.; Ma, W. Characteristic analysis of water lubricated plain journal bearing under transient load. J. Phys. Conf. Ser. 2022, 2160, 012073. [Google Scholar] [CrossRef]
- Wu, J.; He, T.; Zhang, F. Influence of Bearing Bush Elastic Deformation on Bearing Performance of Water-Lubricated Bearings. China Offshore Platf. 2022, 37, 33–37. [Google Scholar]
- Yang, H.; Yan, K.H.; Huang, D. Analysis on journal bearing’s lubrication characteristics with thermo-fluid-solid coupling taken into account. J. Mach. Des. 2022, 39, 10–16. [Google Scholar]
- Wu, Z.; Yuan, C.; Guo, Z. Effect of the groove parameters on the lubricating performance of the water-lubricated bearing under low speed. Wear 2023, 522, 204708. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, X.X.; Xiang, Y.K. Experimental Study on the Friction and Vibration Performance of Water-Lubricated Bearings with Different Groove Structures. Lubr. Eng. 2025, 50, 118–125. [Google Scholar]
- Yang, C.; Zhou, X.; Huang, J. Effects of sediment size and type on the tribological properties of NBR in water. Wear 2021, 477, 203800. [Google Scholar] [CrossRef]
- Hu, D.; Guo, Z.W.; Yuan, C.Q. Influence of Sand Particles on Water Lubrication of UHMWPE Material. Ship Eng. 2019, 41, 98–104. [Google Scholar]
- Leng, Z.; Lv, F.; Zhang, J. Study of dynamic coefficients of water film in marine sterntube bearing considering roughness and deformation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 2257–2271. [Google Scholar] [CrossRef]
- Charamis, D.; Nikolakopoulos, P.G. Investigation of cavitated flow in water-lubricated bearings considering surface roughness, thermal, and elastic effects. Lubricants 2024, 12, 107. [Google Scholar] [CrossRef]
- Yang, H.; Ouyang, W.; Jin, Y. Study on the Elastohydrodynamic Lubrication of Marine Water Lubricated Polymer Bearings Considering Roughness. Lubr. Eng. 2023, 48, 45–50. [Google Scholar]
- Wang, L.L.; Duan, J.D.; Li, L.C. Performance of Water-lubricated Composite Micro-texture Thrust Bearing Considering Roughness. Surf. Technol. 2023, 52, 256–265, 409. [Google Scholar]
- Li, Q.; Liu, X.L.; Zhang, Z. Mixed Lubrication Performances of Water-Lubricated Bearing Materials Under Low Speed Conditions. Bearing 2024, 32, 84–91. [Google Scholar]
- Cao, Y.Z.; Liang, P.; Guo, F. Effects of Surface Roughness on Transient Performance of Water Lubricated Bearings During Start-Up under Different Working Conditions. J. Propuls. Technol. 2022, 43, 457–469. [Google Scholar]
- Xie, Z.L.; Jiao, J.; Yang, K. Theoretical and experimental study on the fluid-structure-acoustic coupling dynamics of a new water lubricated bearing. Tribol. Int. 2023, 177, 107982. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. Trans. ASME J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between RoughSliding Surfaces. Trans. ASME J. Lubr. Technol. 1979, 101, 220–230. [Google Scholar] [CrossRef]
- Jing, H.B.; Wang, N.; Li, D.H. Analysis on Lubrication Characteristics of a Novel Strain Sensor-Embedded Water-Lubricated Bearing. Lubr. Eng. 2024, 12, 1–10. [Google Scholar]
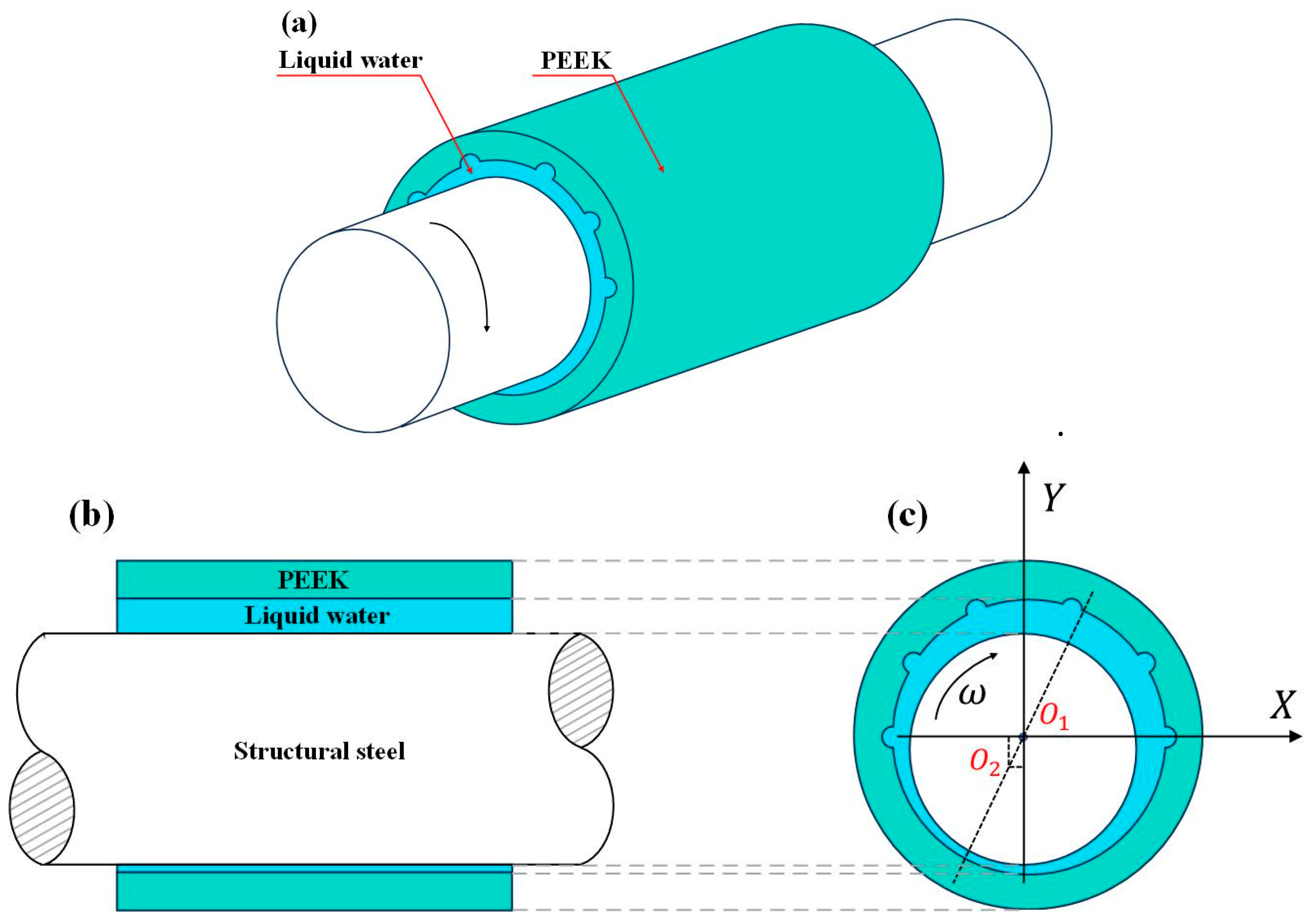
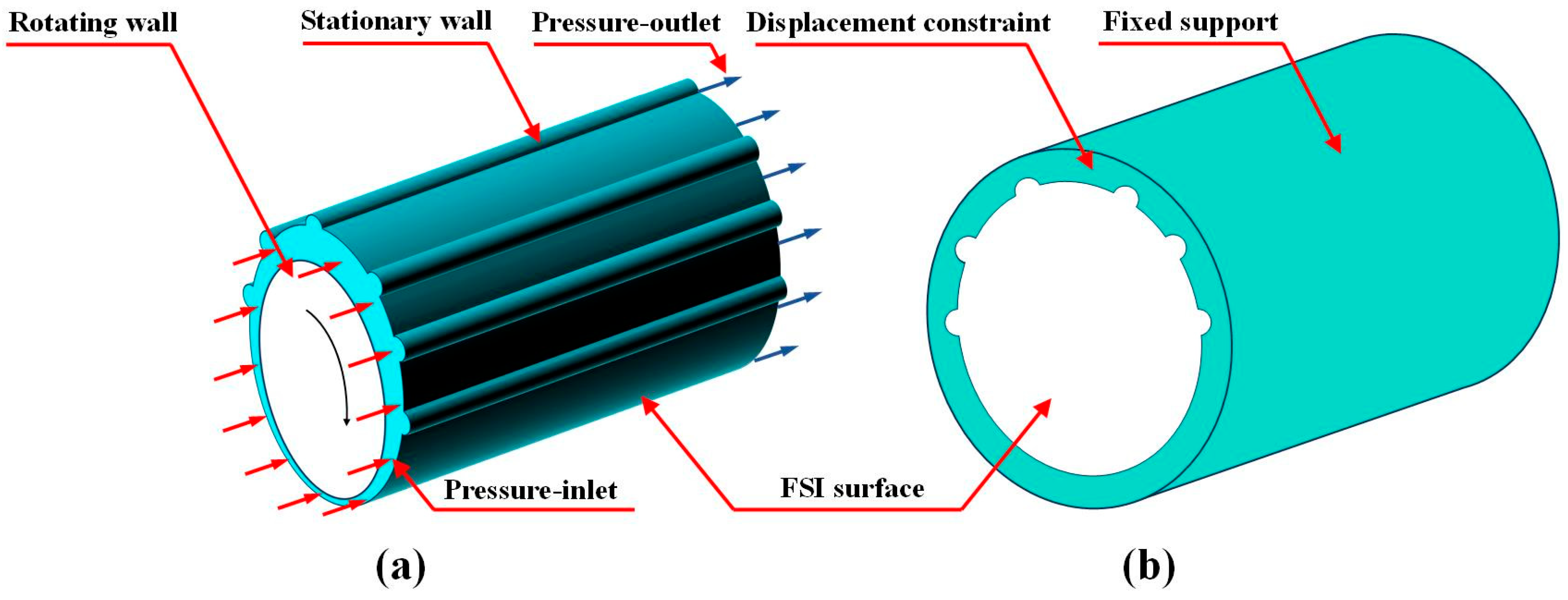

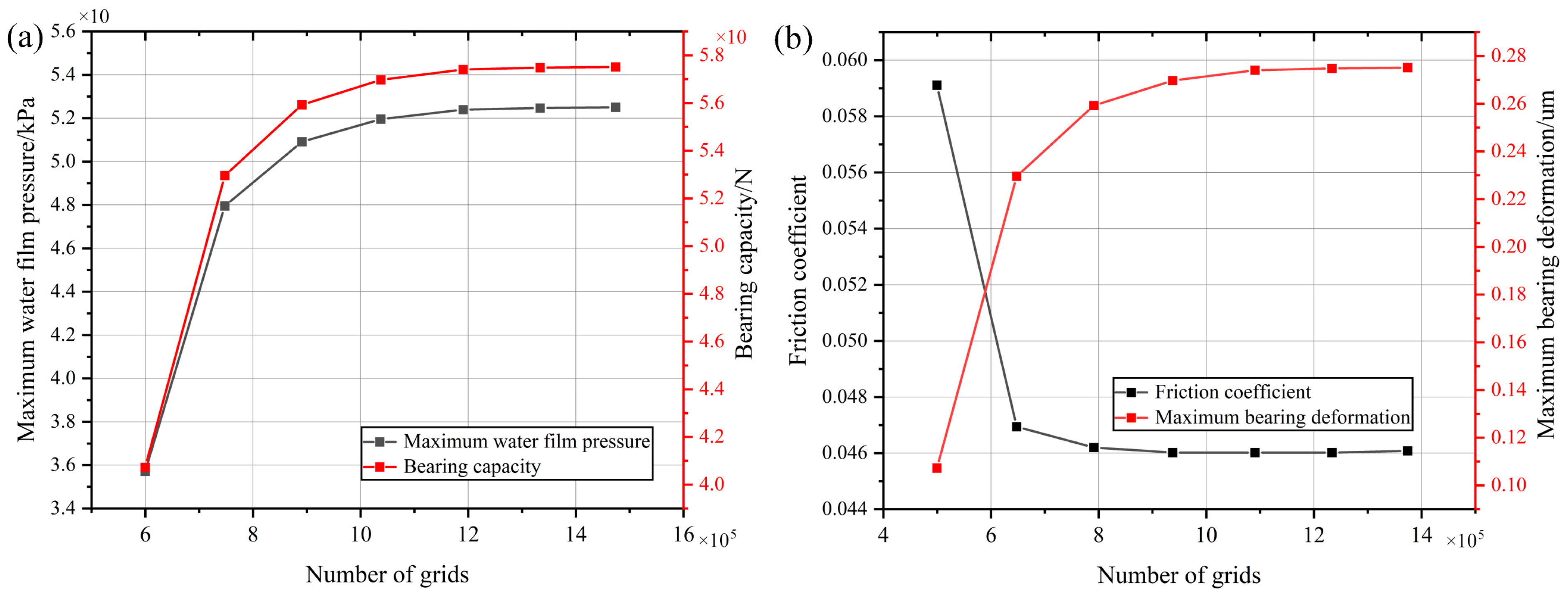



| Structural Parameters | Parameter Value | Material Parameters | Parameter Value |
|---|---|---|---|
| Bearing length, L/mm | 120 | Density, ρ/(kg · m−3) | 1300 |
| Bearing outer diameter, D1/mm | 130 | Poisson’s ratio, β/k−1 | 0.4 |
| Bearing inner diameter, D2/mm | 100 | Elastic modulus, /GPa | 3.5 |
| Journal radius, R/mm | 99.2 | Thermal conductivity, k/(W · m−1 · K−1) | 0.29 |
| Radius of the groove, h/mm | 4 | Coefficient of thermal expansion, β/K−1 | 5.5 × 10−5 |
| Number of grooves, N | 6 | Specific heat, C/(J · kg−1 · K−1) | 2200 |
| Lubricating Medium | Density, kg/m−3 | Viscosity, kg/m−s | Particle Size, μm |
|---|---|---|---|
| Liquid water | 998.2 | 0.001003 | - |
| Sea salt | 1026.8 | 0.001085 | 0.1 |
| Saline sand water | 1650 | 0.5 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, H.; Wang, N.; Qi, J.; Zhang, Z.; Zhang, M.; Wang, J.; Liu, A.; Cheng, Y.; Wang, P. Research on the Lubrication and Friction Characteristics of New Water-Lubricated Bearings Made of PEEK Material in Salt-Sand Water Environments. Lubricants 2025, 13, 470. https://doi.org/10.3390/lubricants13110470
Jing H, Wang N, Qi J, Zhang Z, Zhang M, Wang J, Liu A, Cheng Y, Wang P. Research on the Lubrication and Friction Characteristics of New Water-Lubricated Bearings Made of PEEK Material in Salt-Sand Water Environments. Lubricants. 2025; 13(11):470. https://doi.org/10.3390/lubricants13110470
Chicago/Turabian StyleJing, Huabing, Nan Wang, Jiayun Qi, Zhenfeng Zhang, Mingjin Zhang, Jia Wang, An Liu, Yu Cheng, and Peng Wang. 2025. "Research on the Lubrication and Friction Characteristics of New Water-Lubricated Bearings Made of PEEK Material in Salt-Sand Water Environments" Lubricants 13, no. 11: 470. https://doi.org/10.3390/lubricants13110470
APA StyleJing, H., Wang, N., Qi, J., Zhang, Z., Zhang, M., Wang, J., Liu, A., Cheng, Y., & Wang, P. (2025). Research on the Lubrication and Friction Characteristics of New Water-Lubricated Bearings Made of PEEK Material in Salt-Sand Water Environments. Lubricants, 13(11), 470. https://doi.org/10.3390/lubricants13110470





