Fluid–Structure Interaction Mechanisms of Layered Thickness Effects on Lubrication Performance and Energy Dissipation in Water-Lubricated Bearings
Abstract
1. Introduction
2. Theoretical Analysis of Water-Lubricated Bearings with a Layered Structure
2.1. Governing Equations of the Fluid Domain
2.2. Solid Domain Control Equation
3. Theoretical Physical Model of Water-Lubricated Bearings with a Laminated Structure
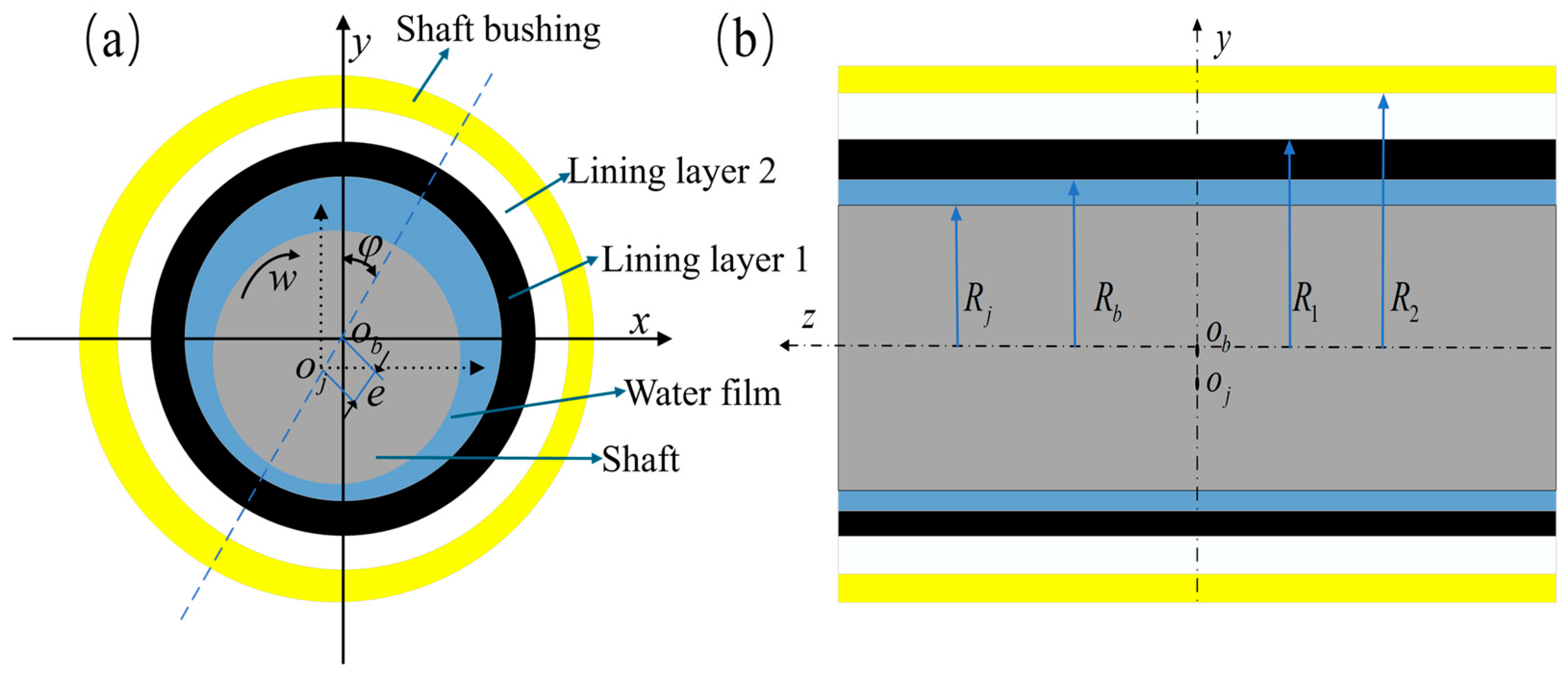
3.1. Bearing Structure
| Parameter | Water Film | Lining 1 | Lining 2 |
|---|---|---|---|
| Inner diameter/mm | 151.2 | 152 | 162 |
| Outer diameter/mm | 152 | 162 | 172 |
| Radial clearance/mm | 0.4 | --- | --- |
| Eccentricity | 0.5~0.9 | --- | --- |
| Thickness/mm | --- | 3, 5, 7, 9, 11, 13 | 3, 5, 7, 9, 11, 13 |
| Materials | Liquid water | Rubber-plastic blend composite materials | UHMWPE |
| Length/mm | 320 | 320 | 320 |
| Parameter | Rubber-Plastic Blend Composite Materials | UHMWPE |
|---|---|---|
| Density/(kg/m3) | 1500 | 1700 |
| Elastic modulus/Mpa | 7.84 | 1000 |
| Poisson’s ratio | 0.47 | 0.4 |
3.2. Boundary Conditions and Meshing
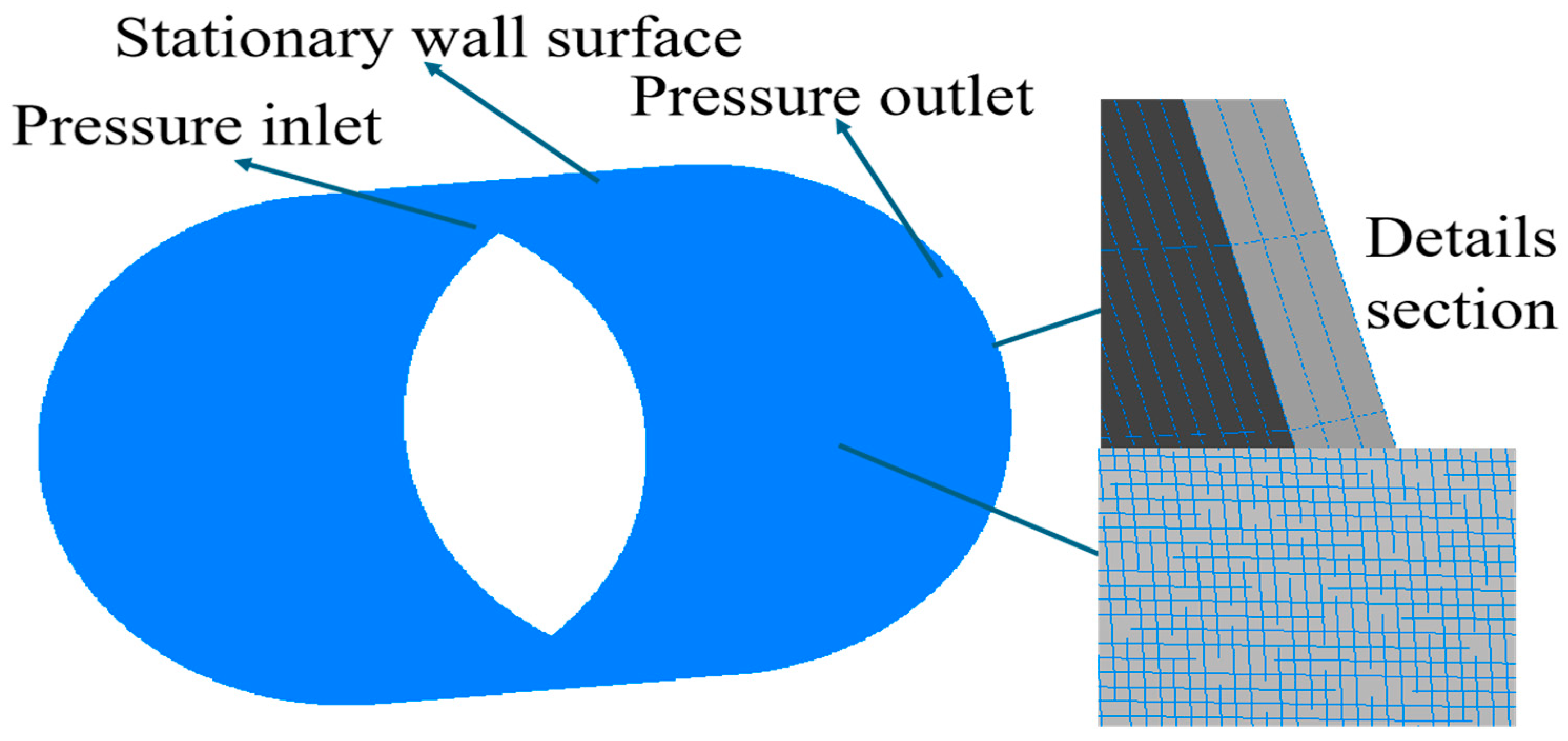
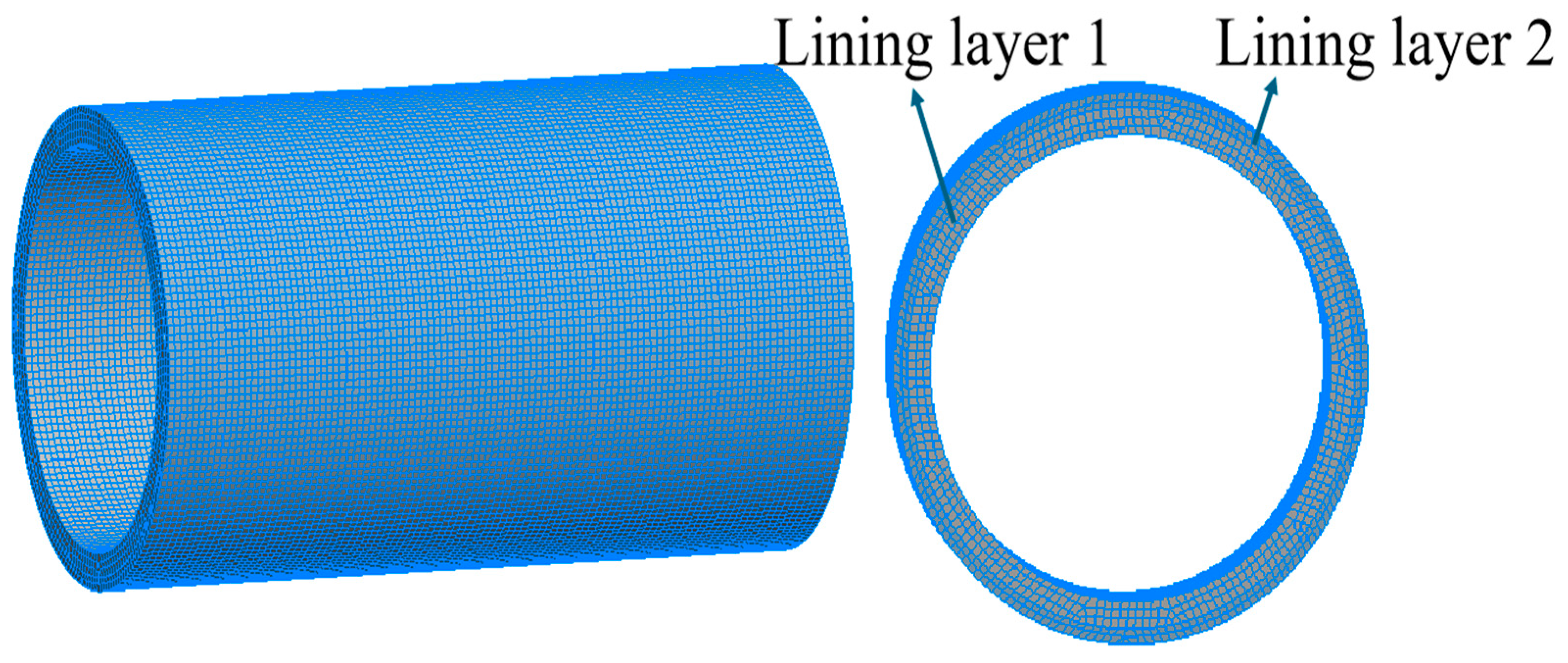
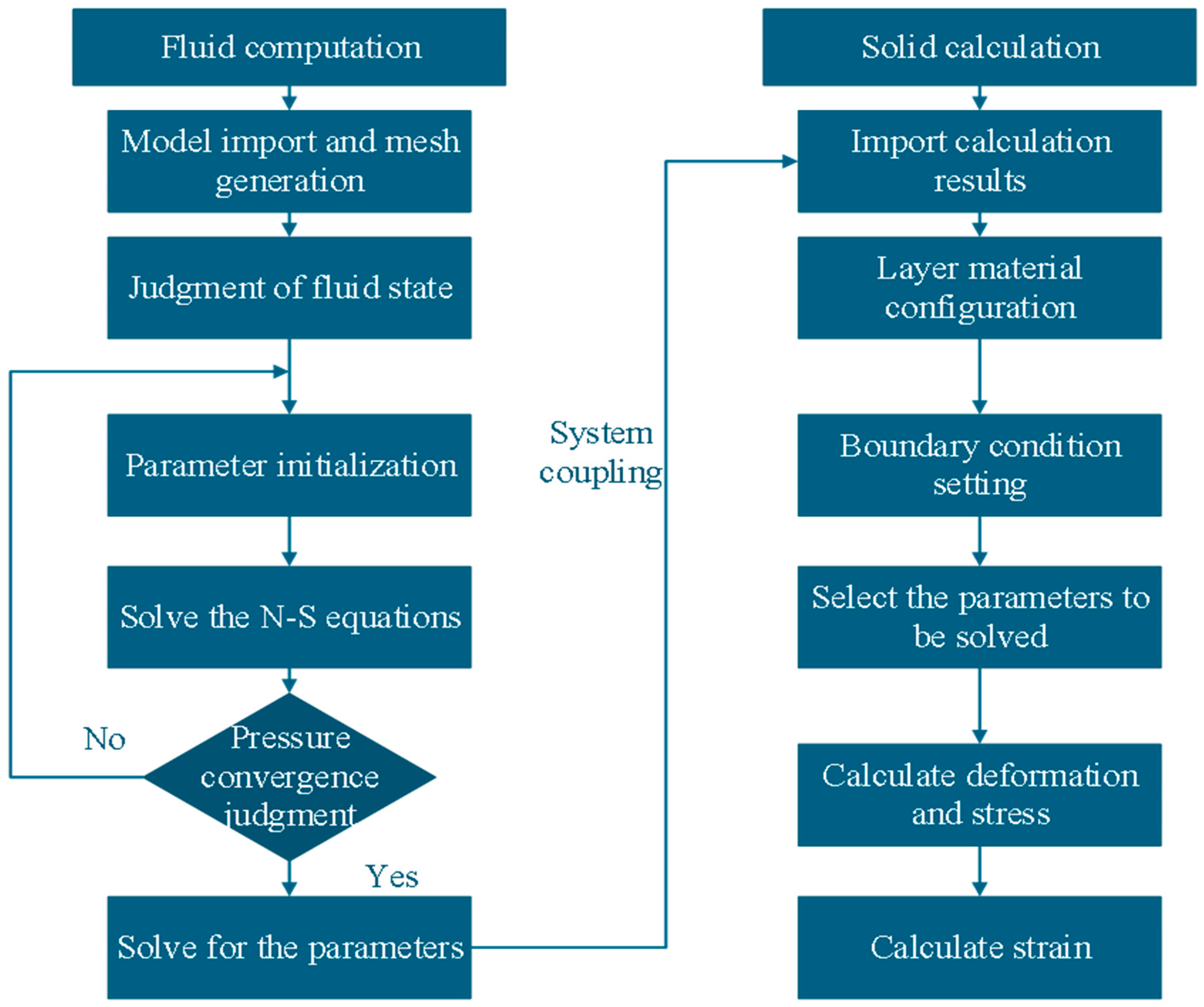
3.3. Solution Computation Flowchart
4. Results and Discussion
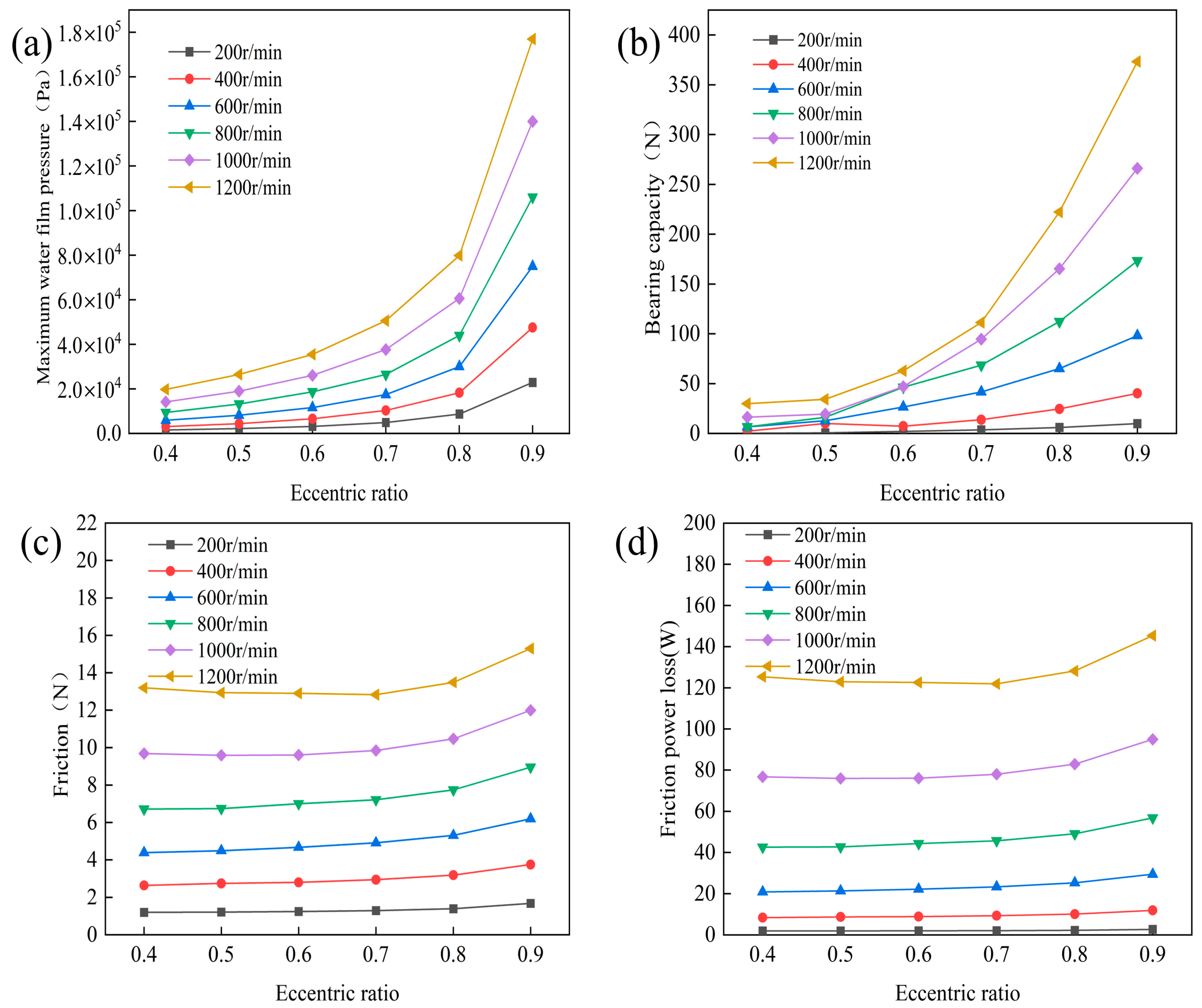
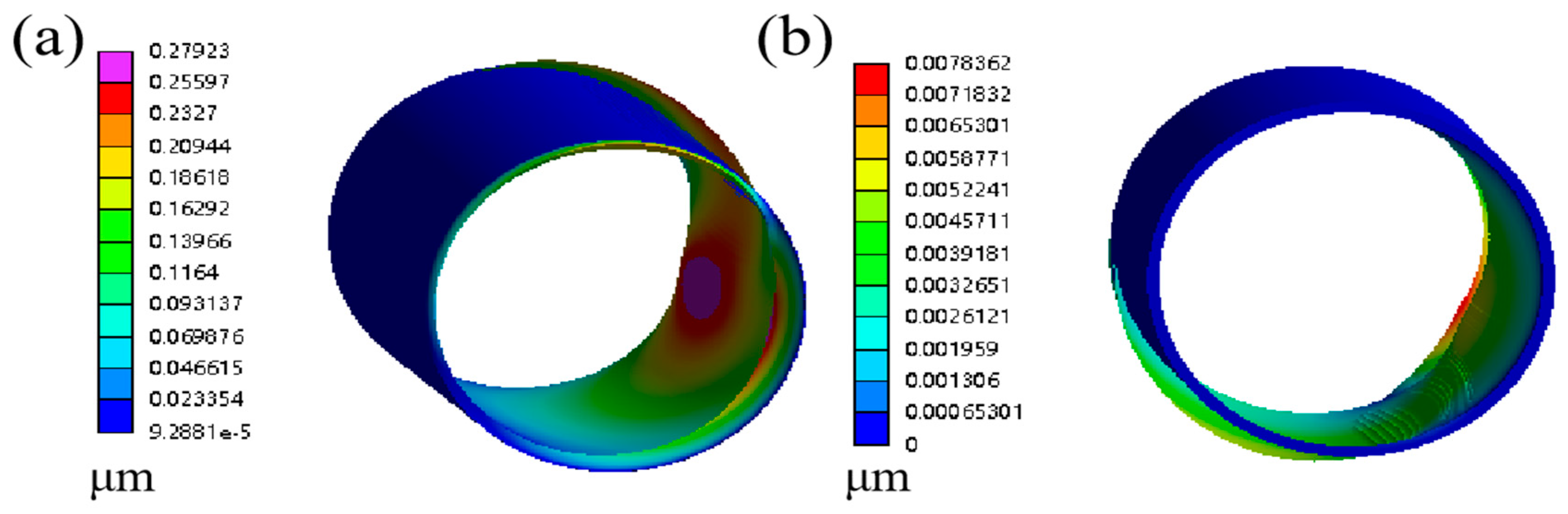
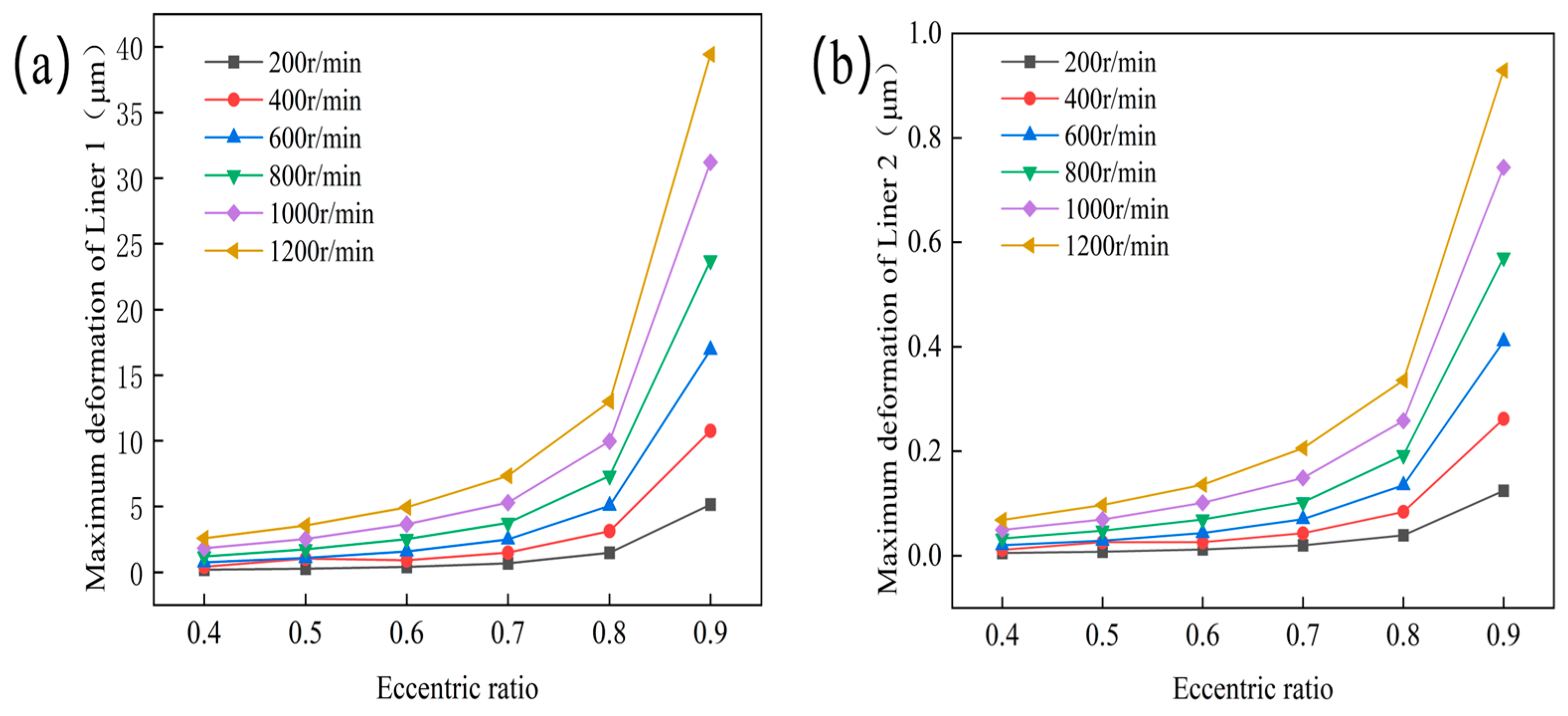
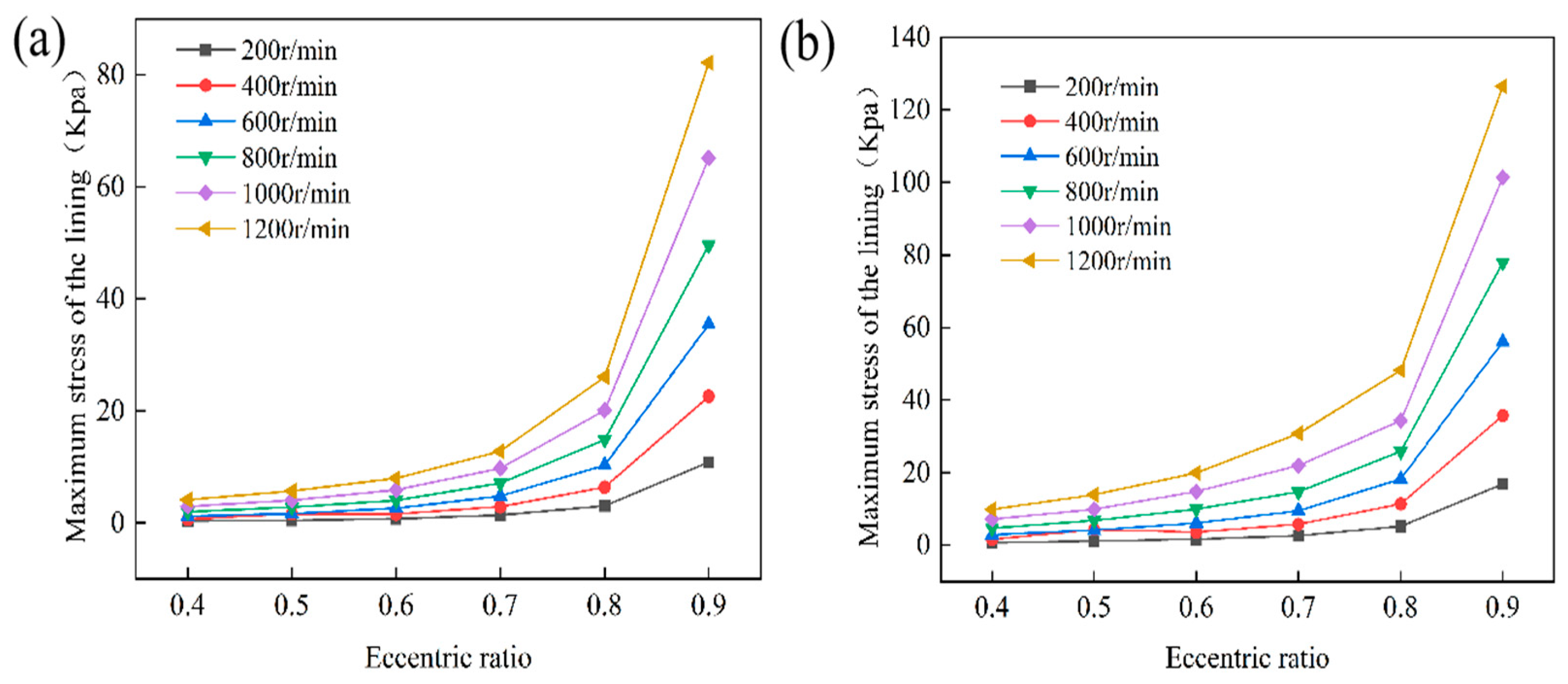
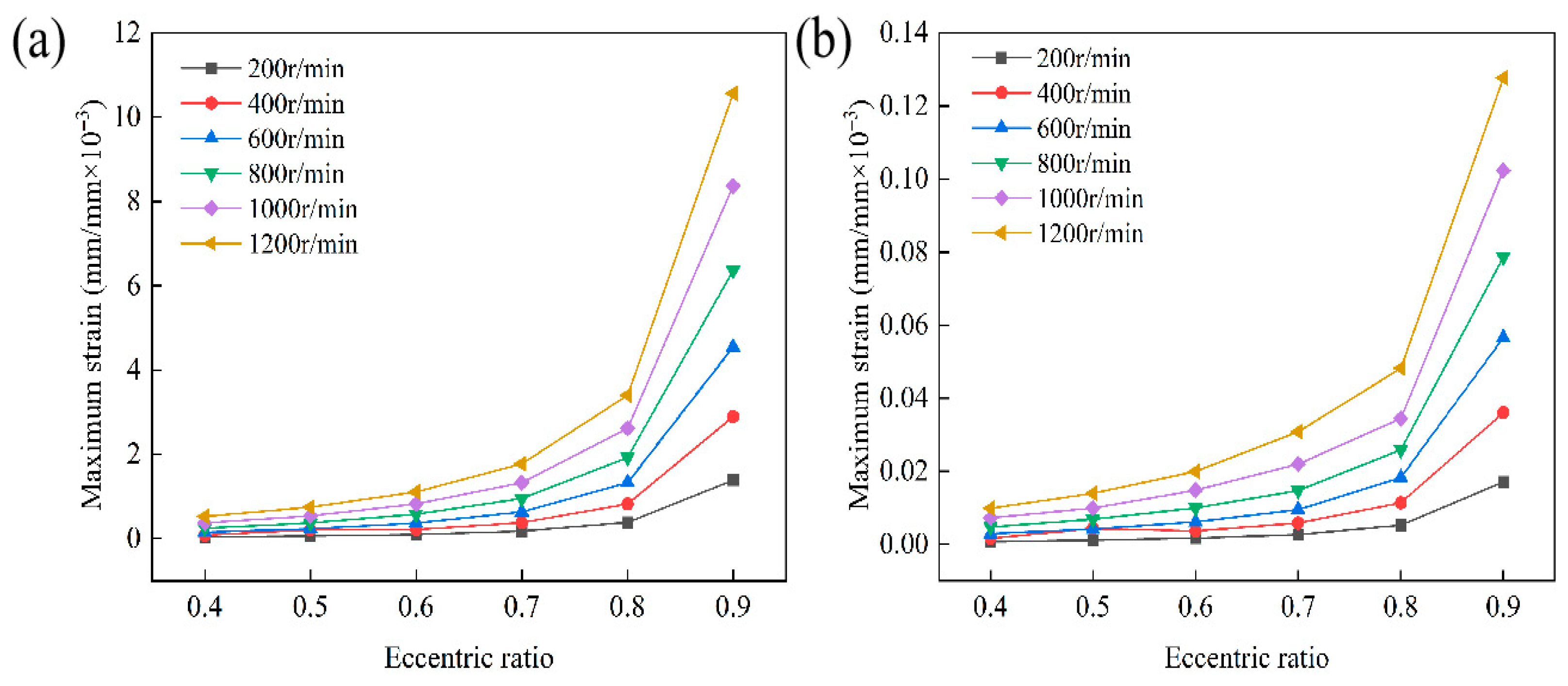
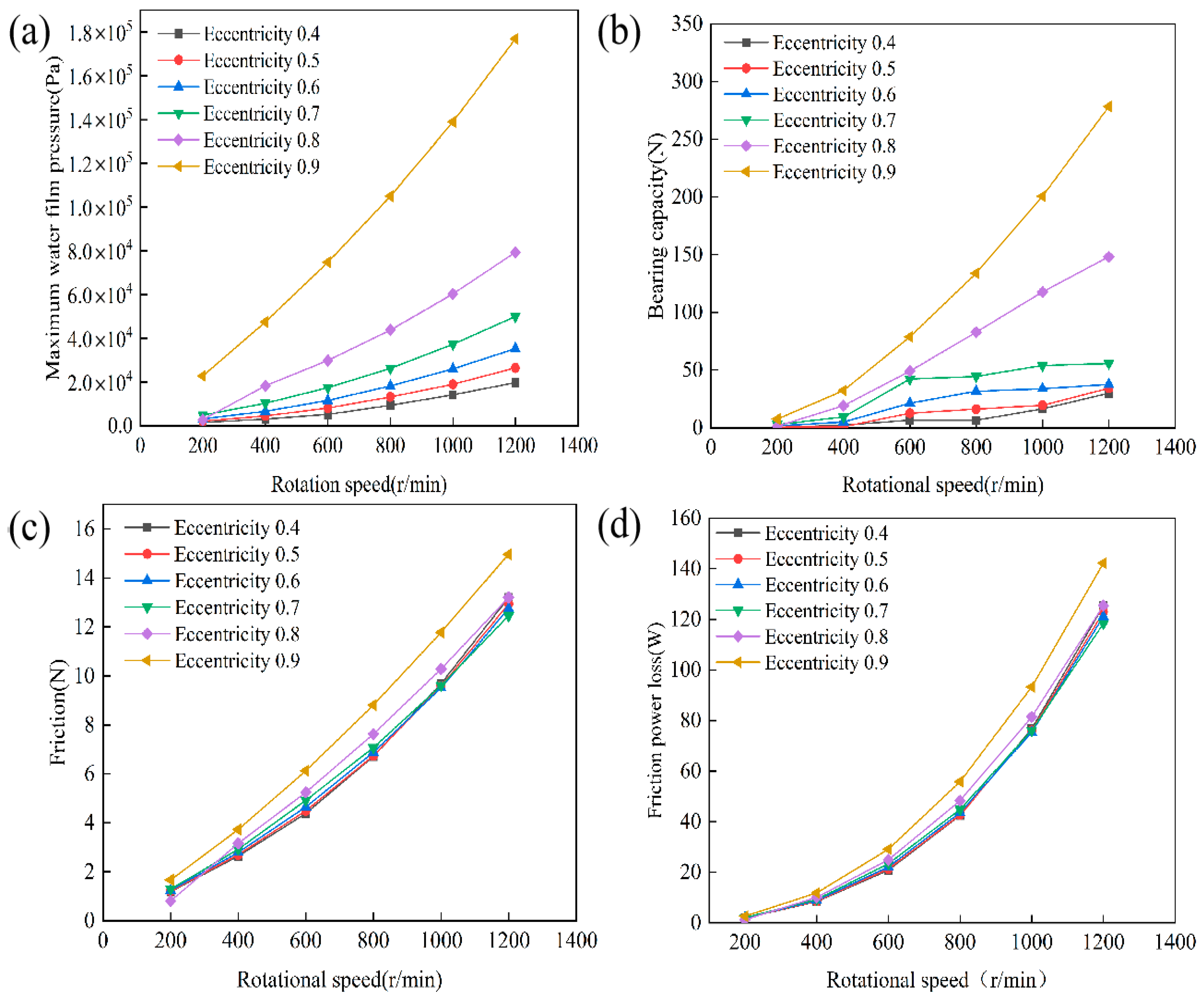
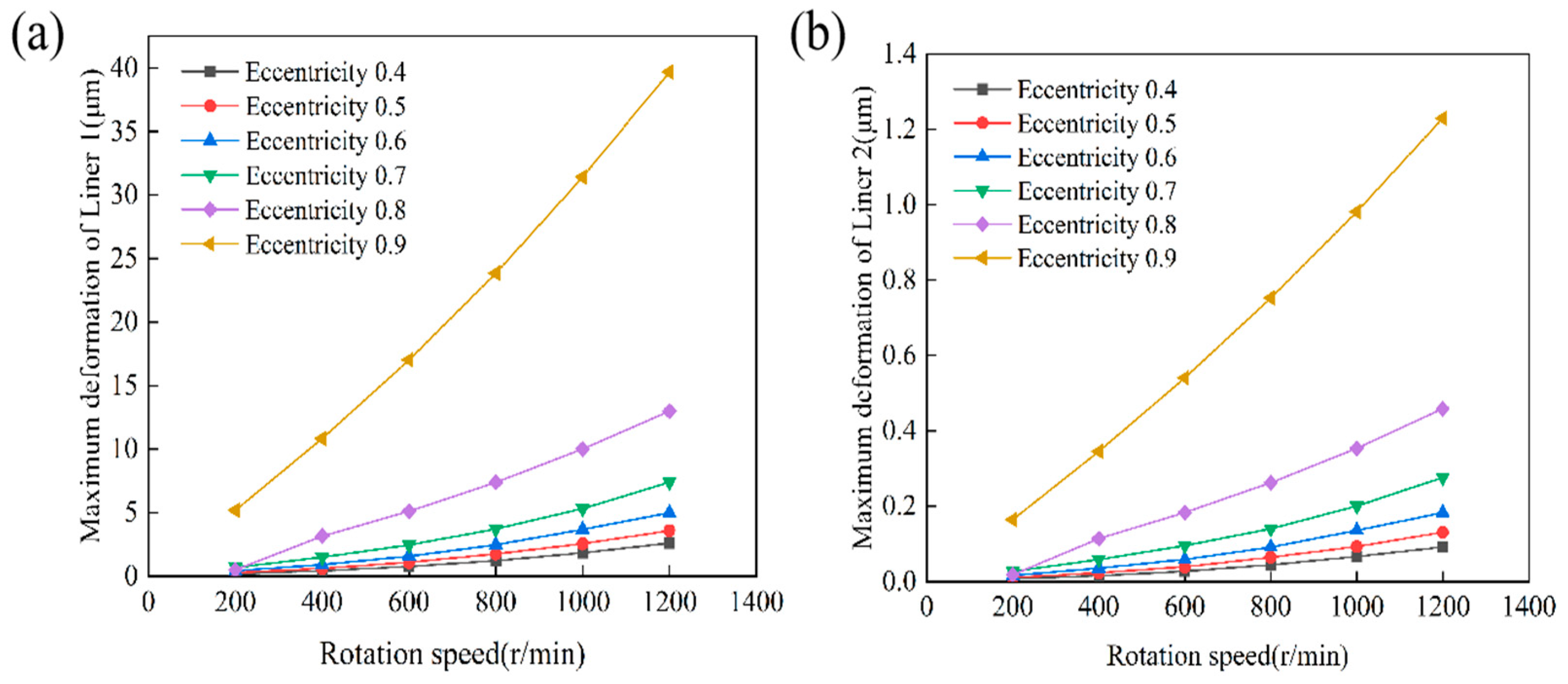
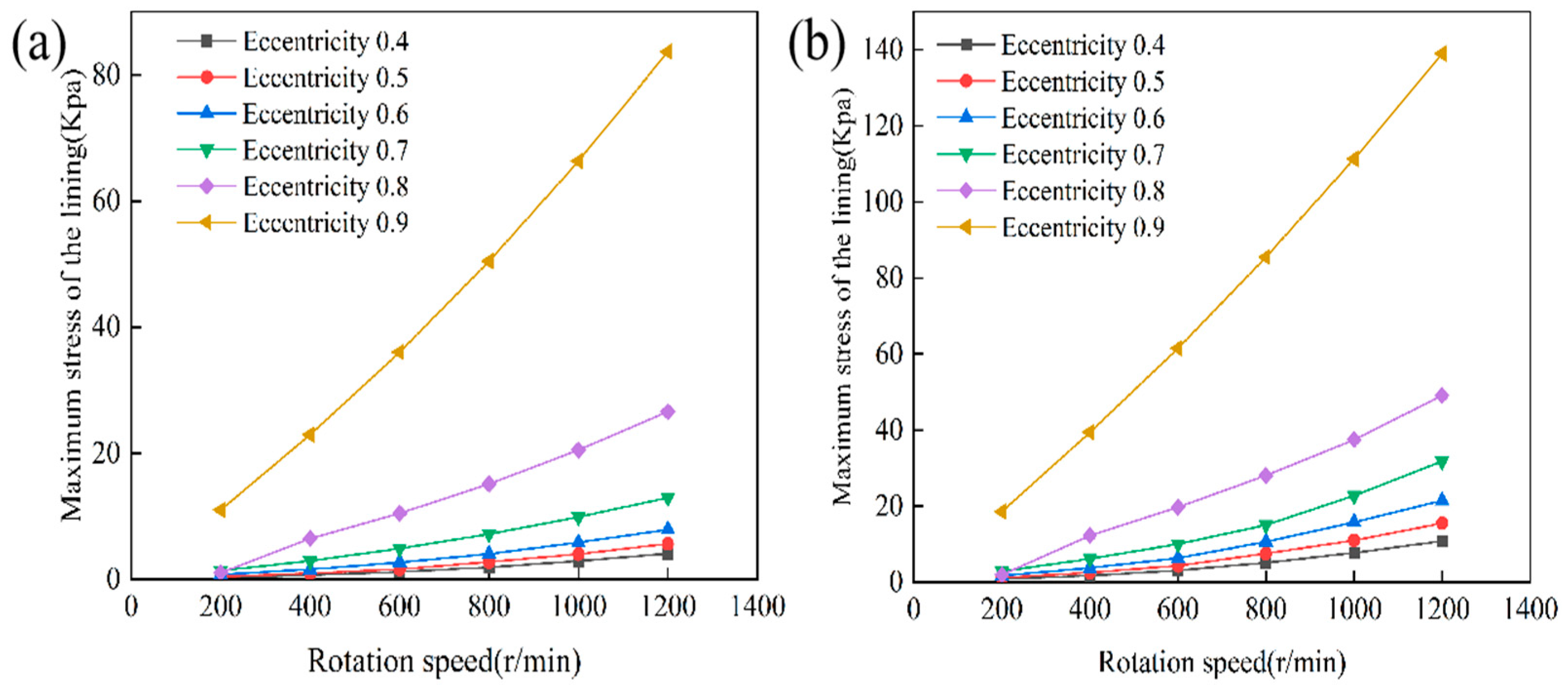
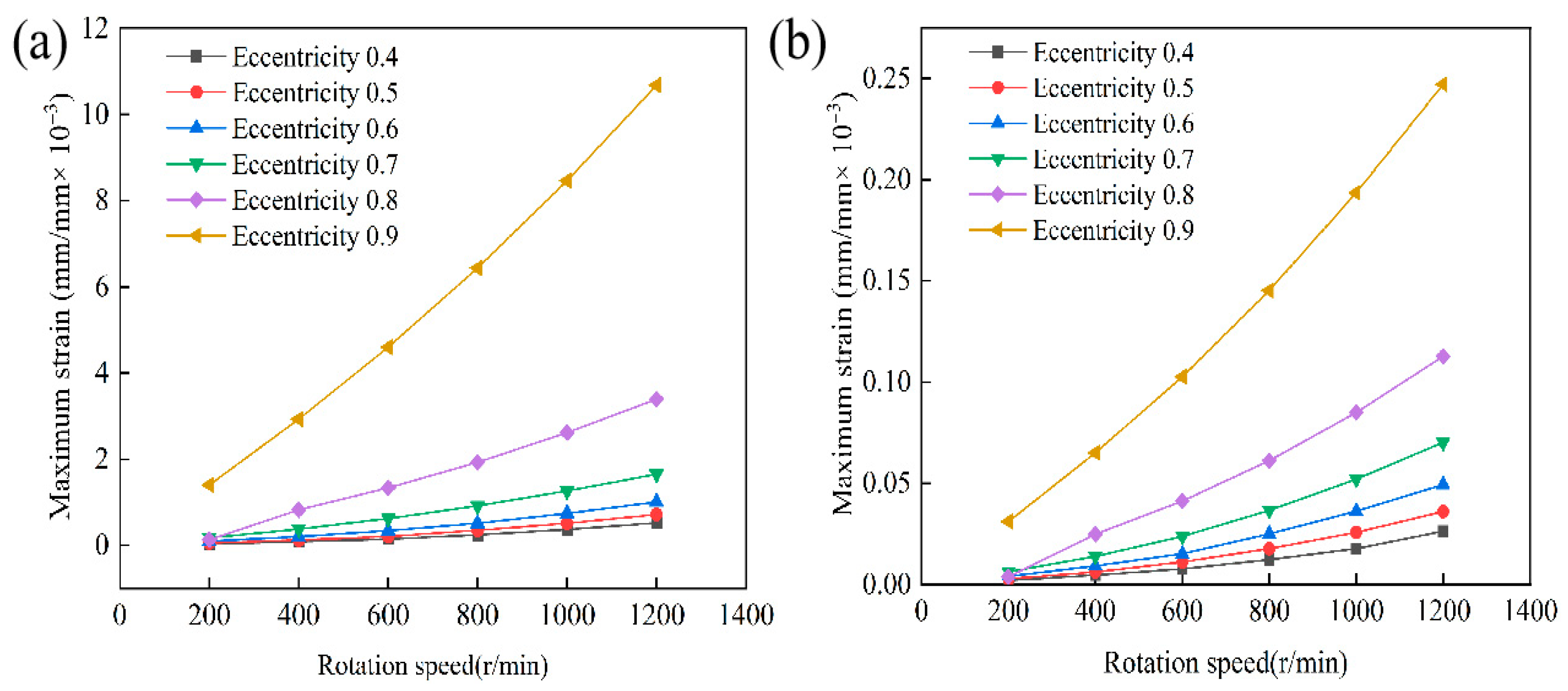
4.1. Analysis of the Influence of Eccentricity on the Lubrication Performance
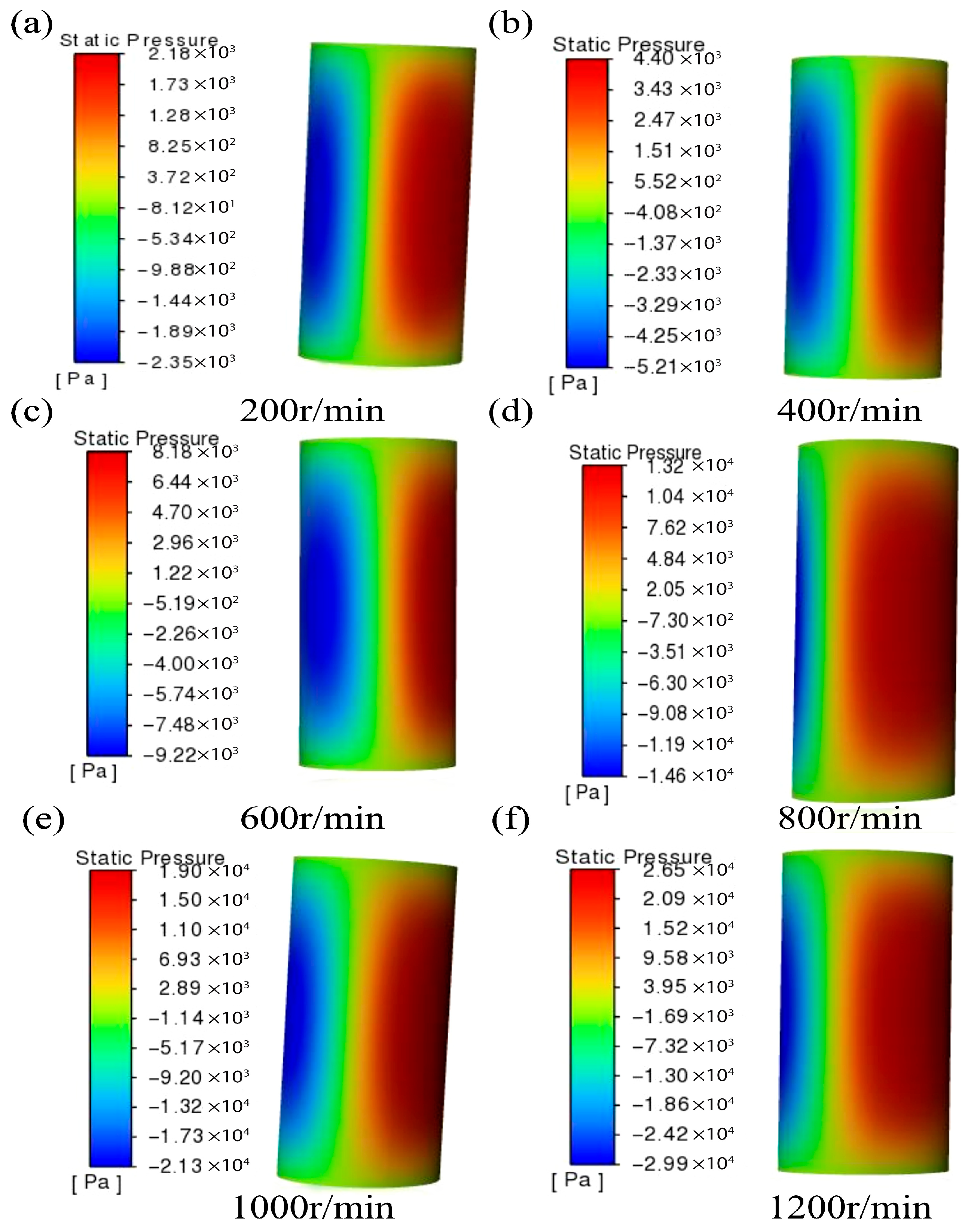
4.2. Analysis of the Influence of Rotational Speed on the Lubrication Performance
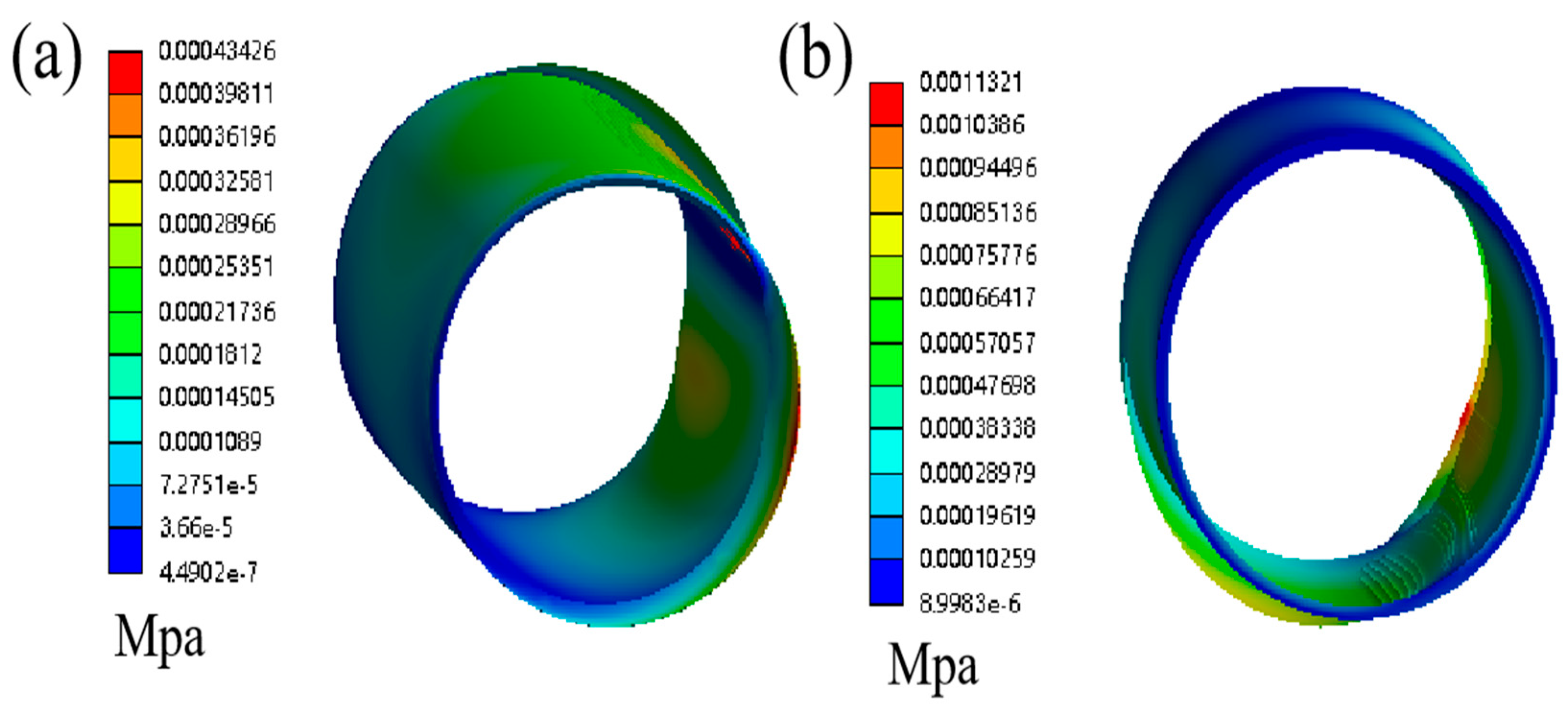
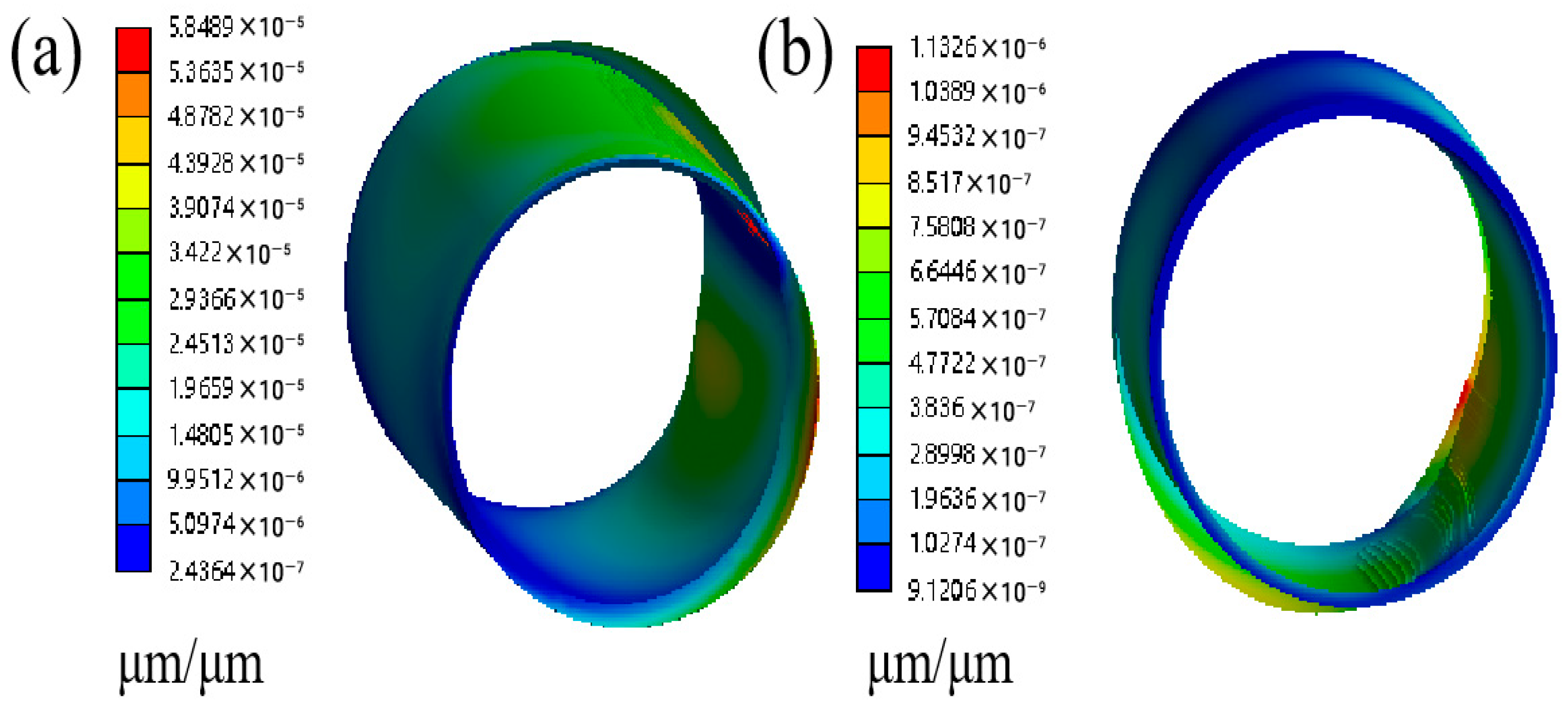
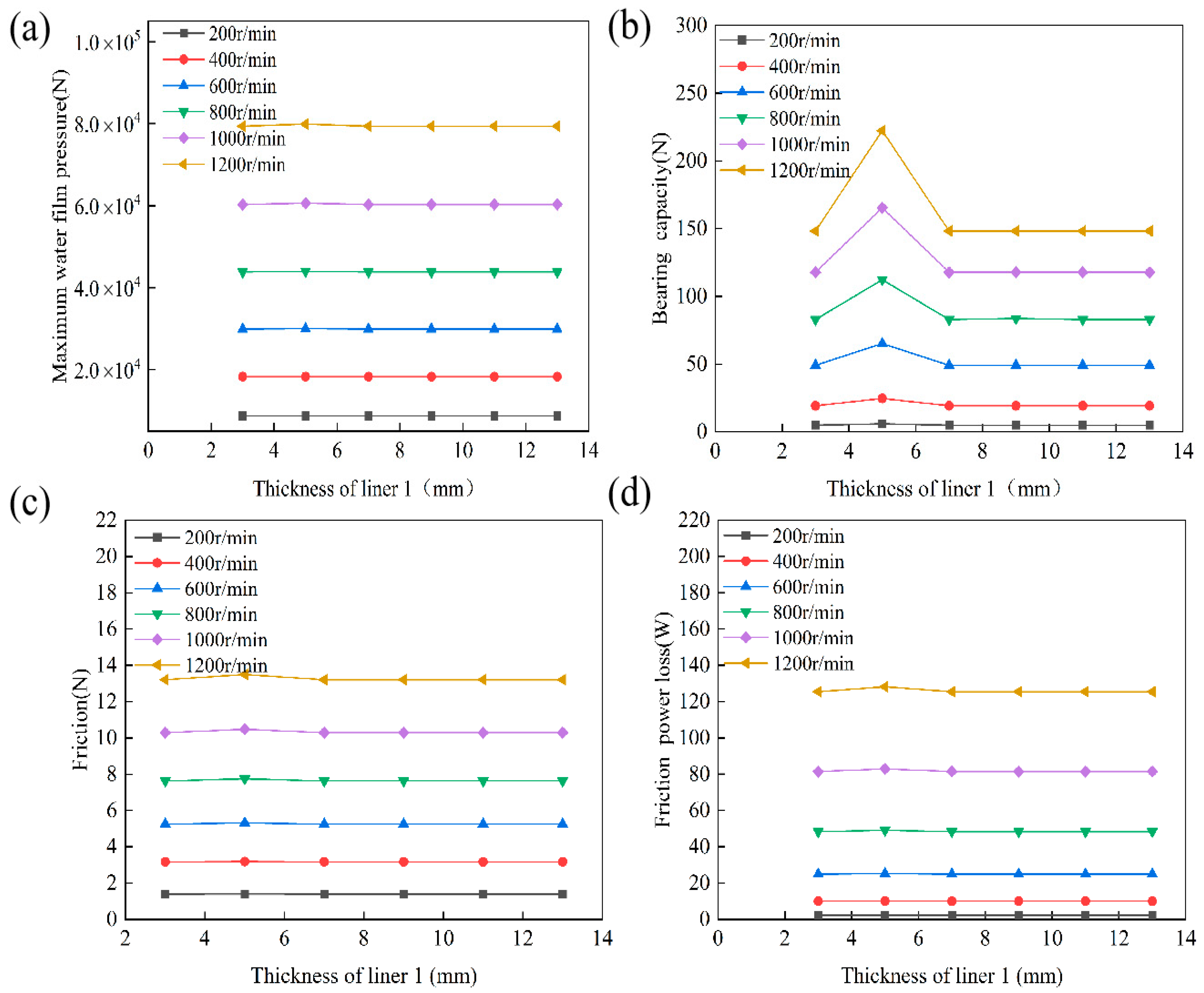
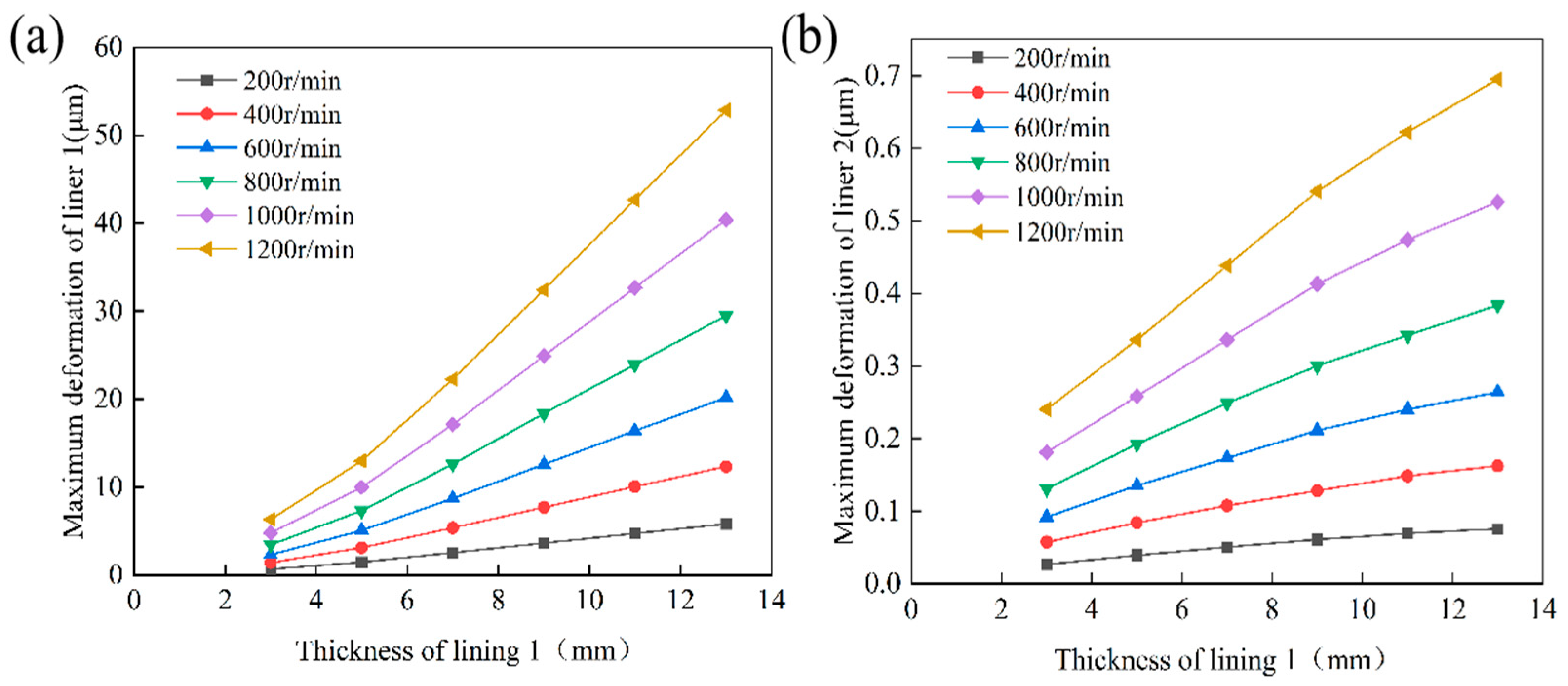
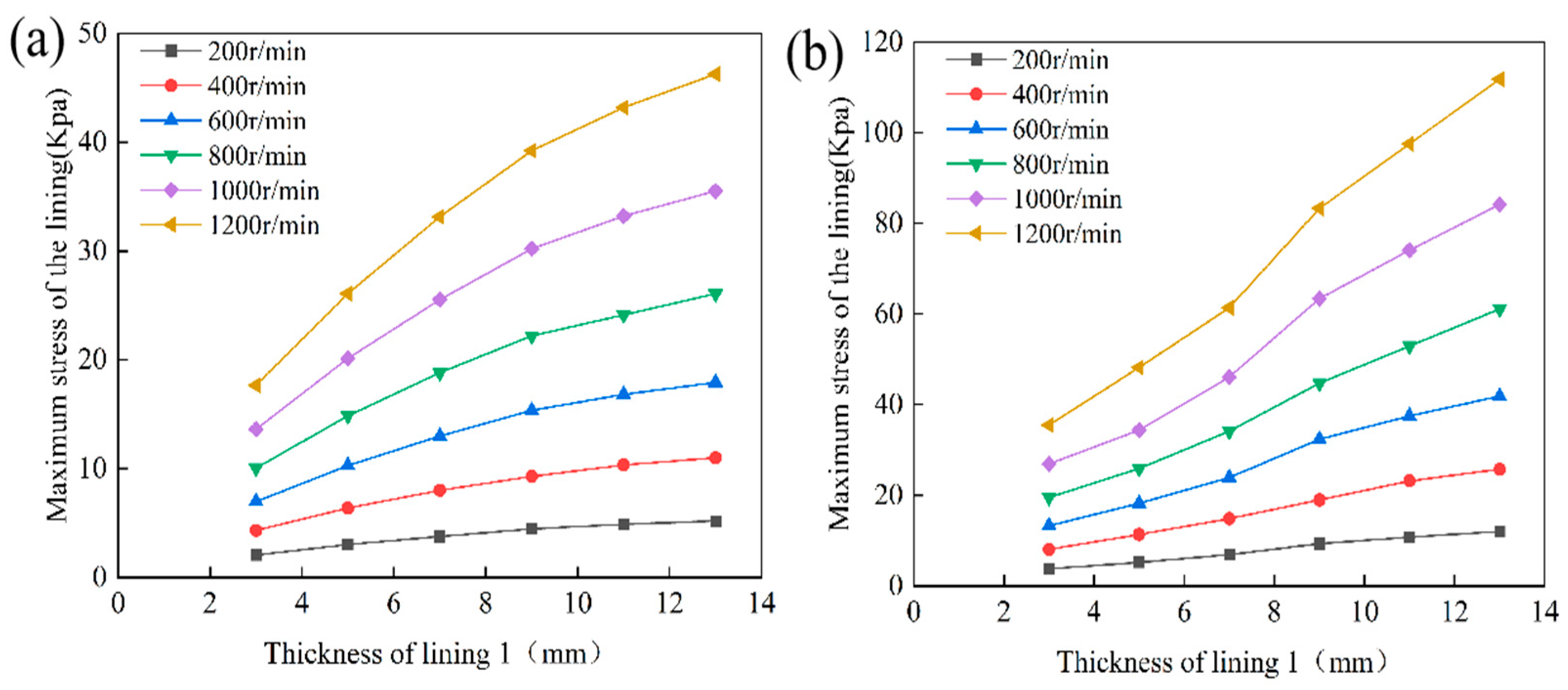
4.3. Analysis of the Effect of Layer Thickness on Lubrication Performance
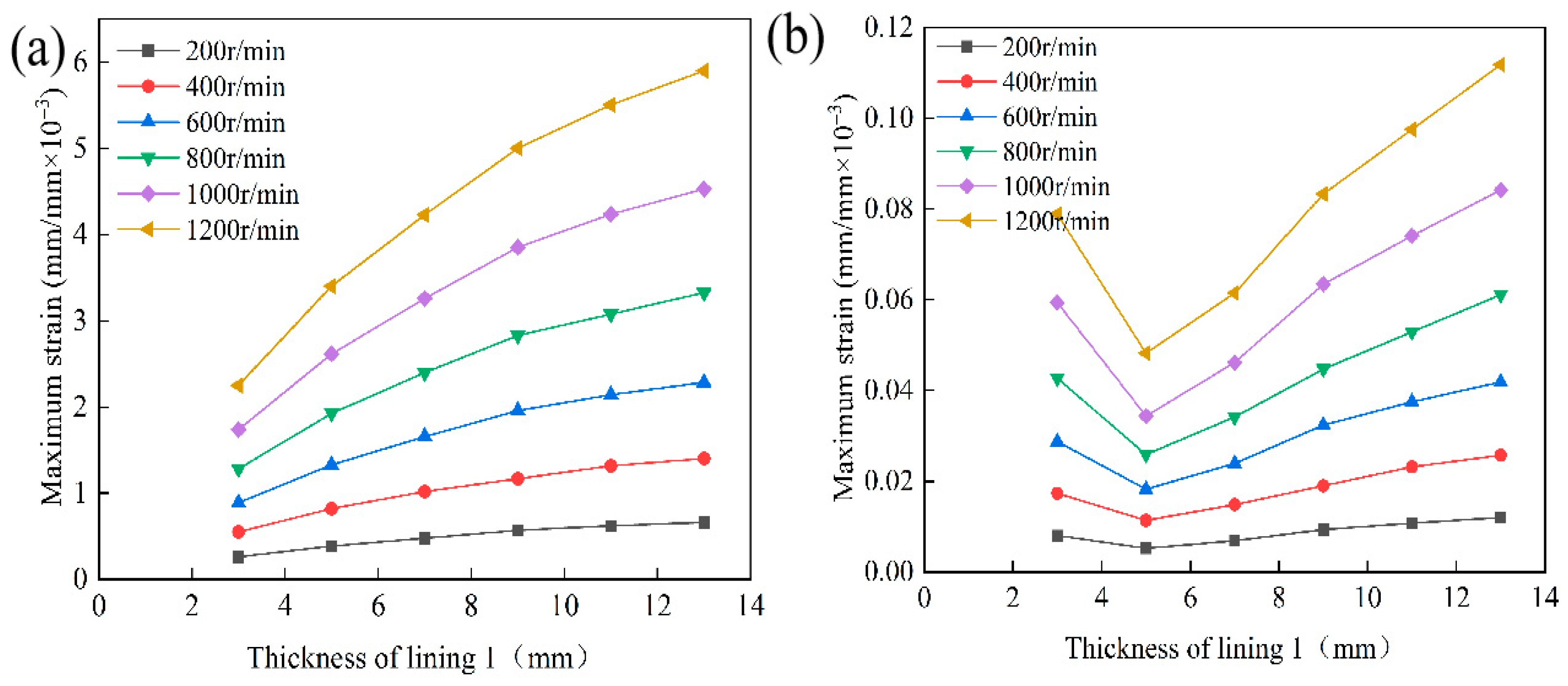
4.3.1. Analysis of the Effect of Layer 1 Thickness on Lubrication Performance
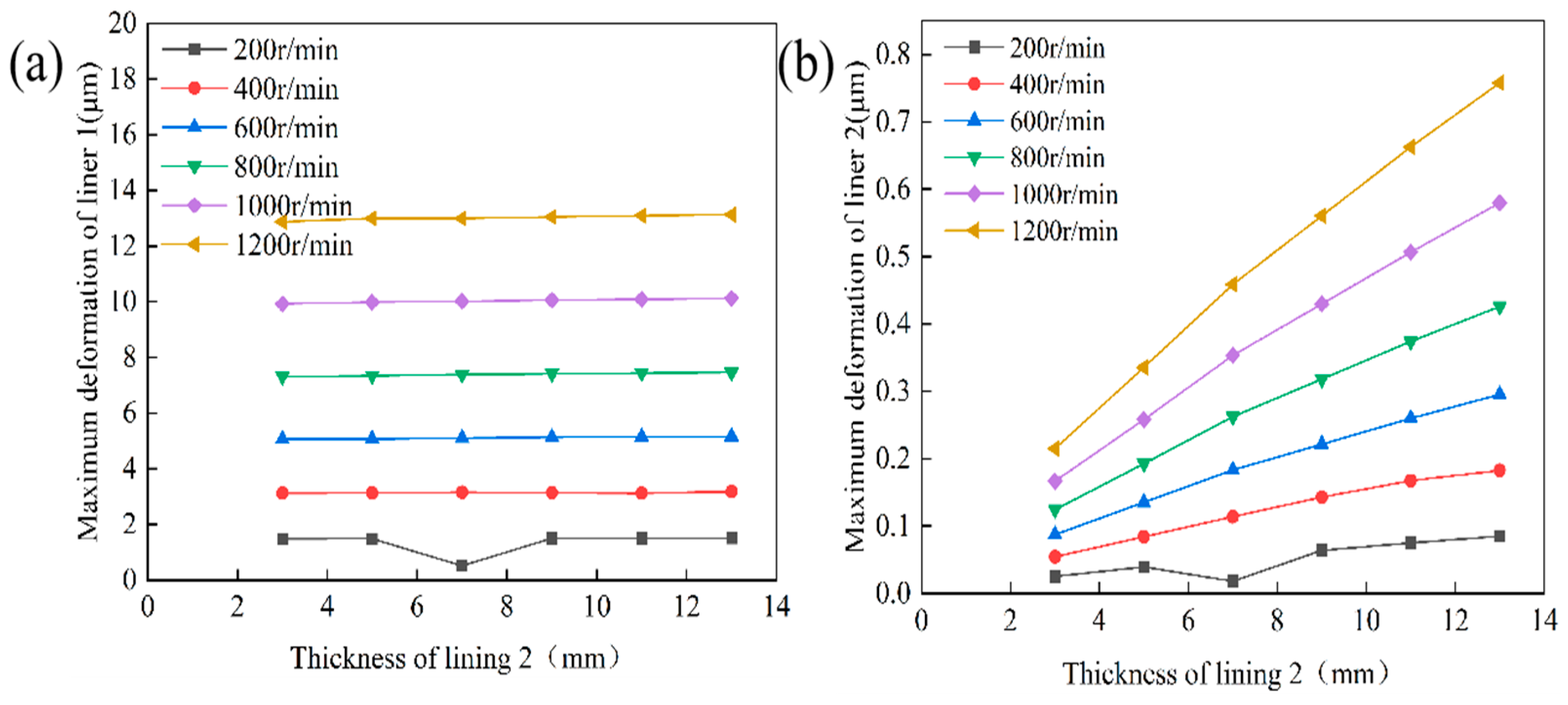
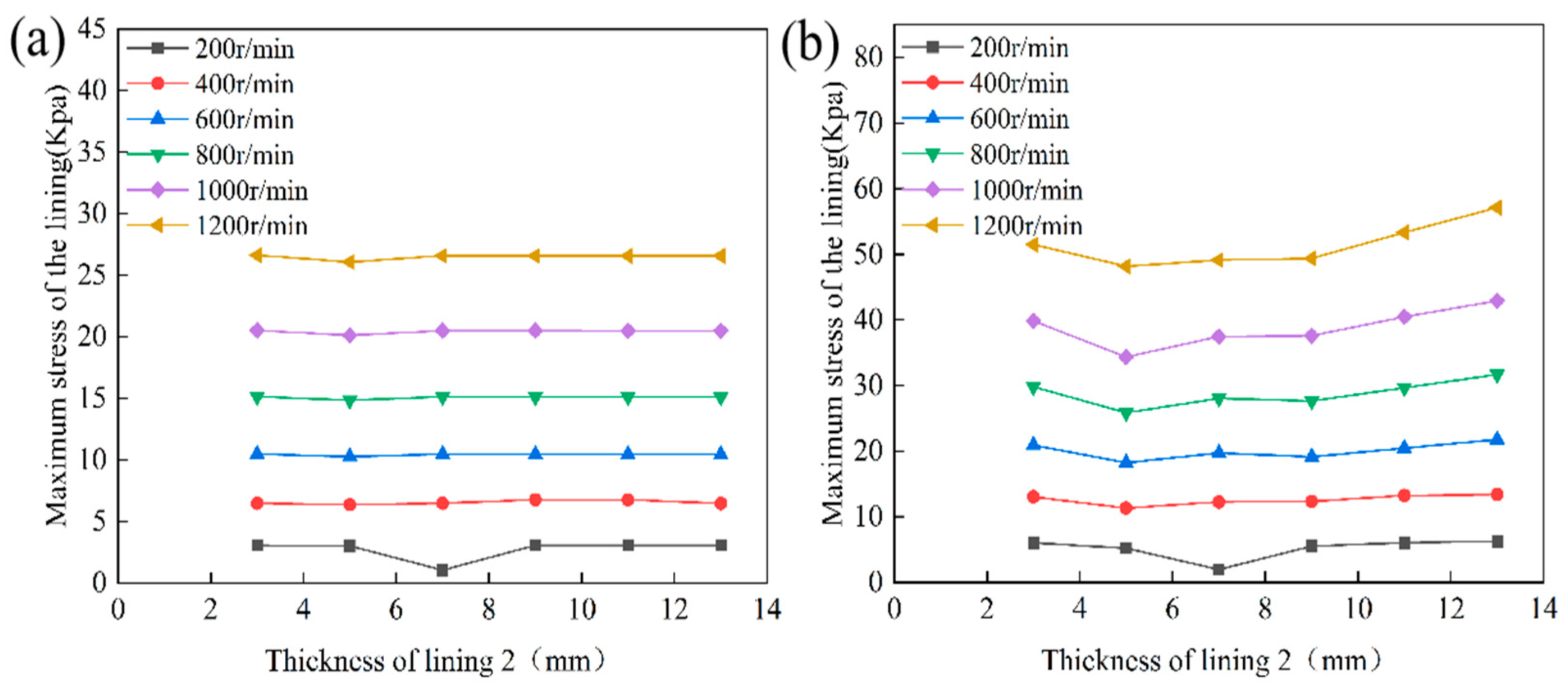
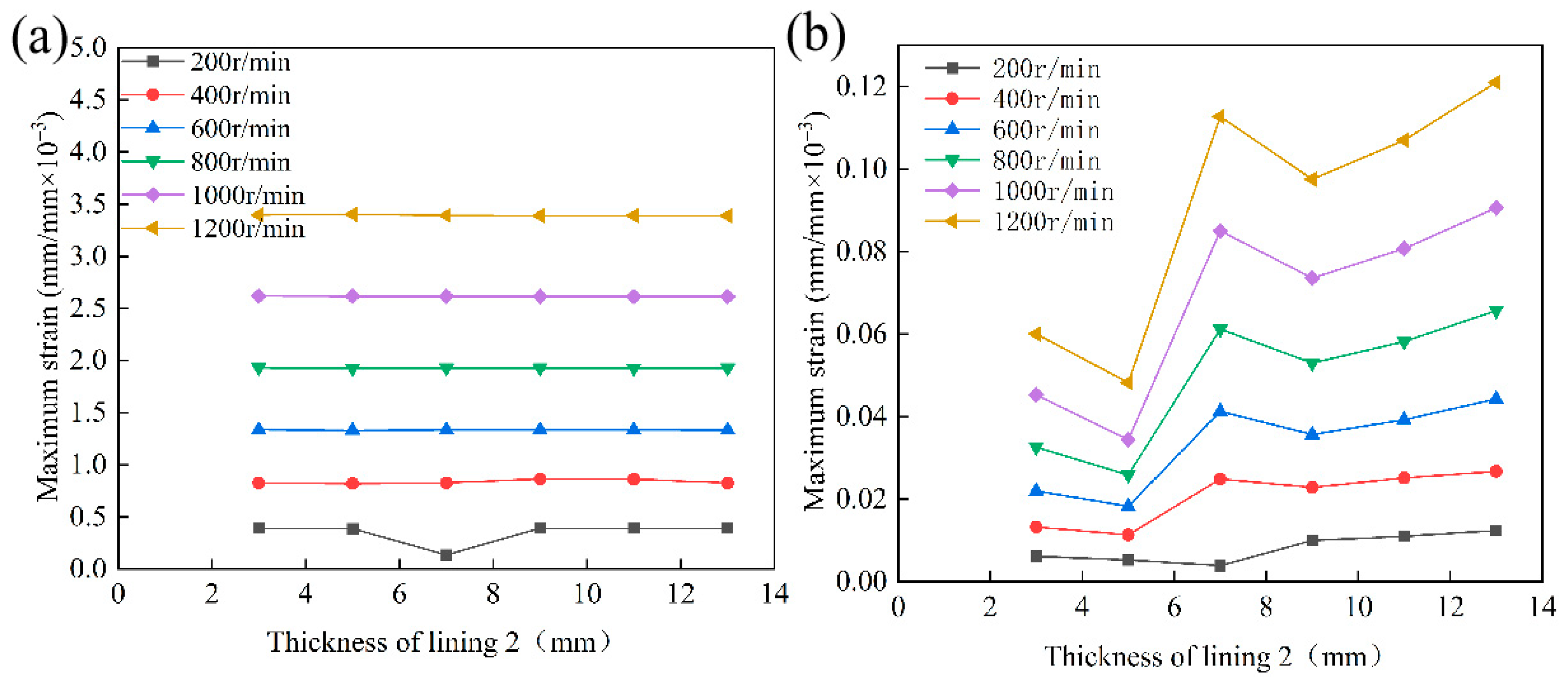
4.3.2. Analysis of the Effect of Layer 2 Thickness on Lubrication Performance
4.4. Experimental Validation of Laminated Water-Lubricated Bearing Specimens
4.4.1. Experimental Materials and Equipment
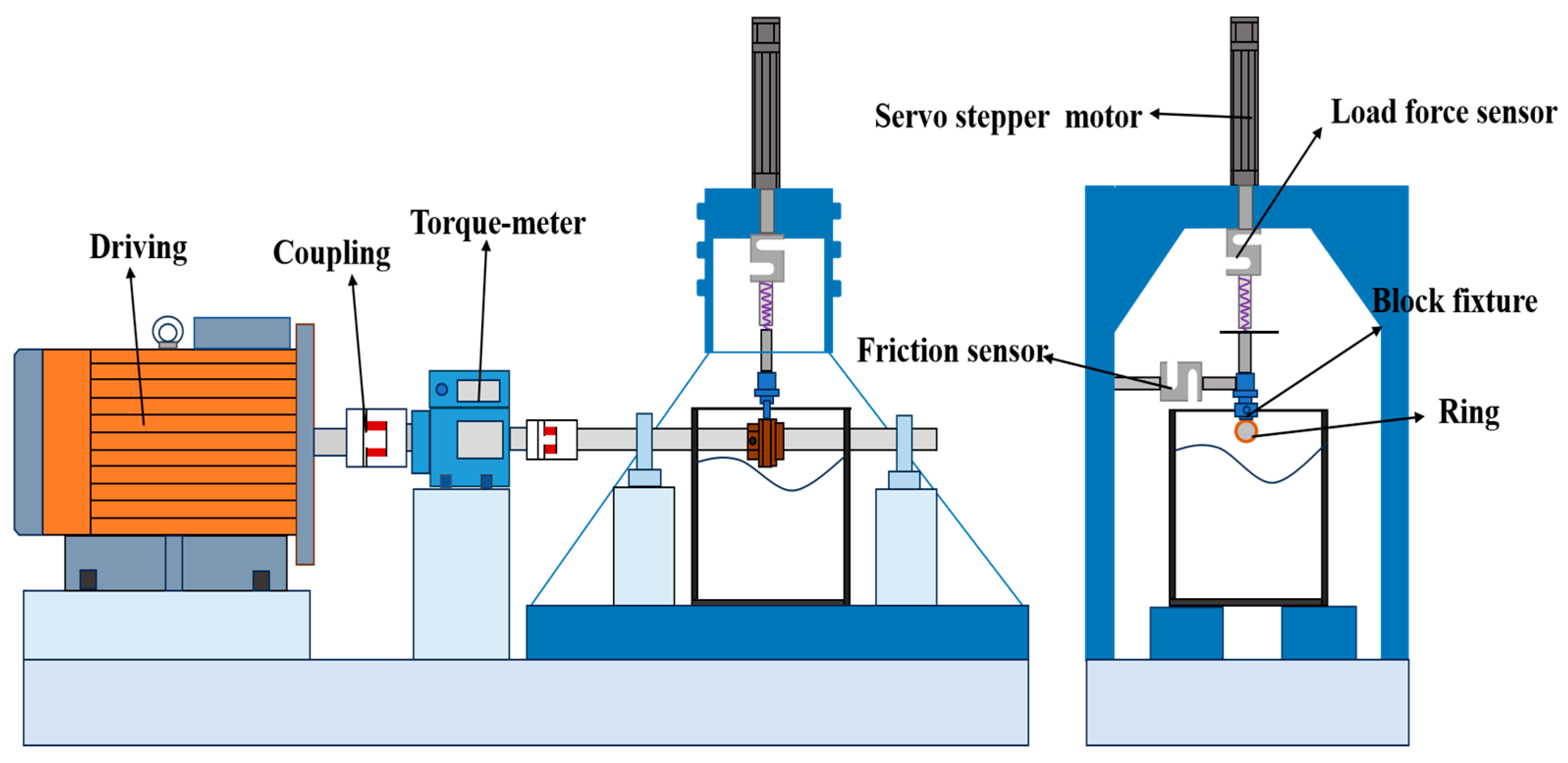
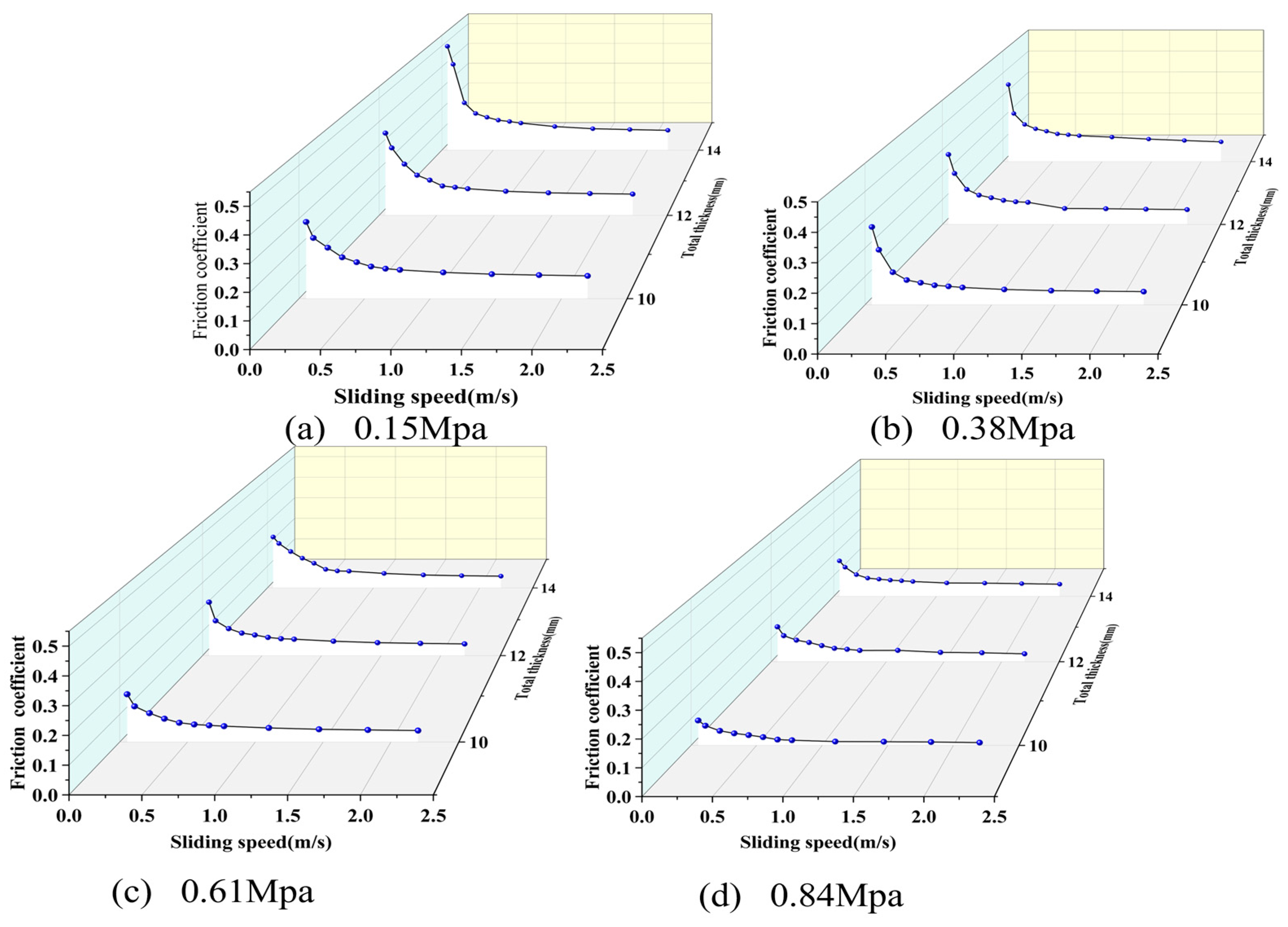
4.4.2. Analysis of Test Results
4.5. Analysis of Energy Dissipation Mechanism in Layered Structure Hydro-Lubricated Bearings
5. Conclusions
- (1)
- Eccentricity and rotational speed are the primary factors influencing lubrication performance and structural response. Increasing eccentricity reduces the minimum film thickness but enhances the hydrodynamic effect. This results in a higher maximum water film pressure and enhances load-carrying capacity. Higher rotational speed further strengthens the hydrodynamic effect. However, it also increases frictional power loss and the amplitude of structural response. The combined effects of eccentricity and speed make the system highly sensitive under high-eccentricity and high-speed conditions. These factors have a decisive influence on operational stability and energy efficiency.
- (2)
- The thickness of the lining layers directly affects both load-carrying capacity and structural safety. The rubber composite layer performs optimally at a thickness of 5 mm. If it is too thick, deformation and stress concentration increase. If it is too thin, buffering capacity and energy dissipation decrease. The UHMWPE layer maintains low stress and strain at a thickness of 5–7 mm. When it exceeds this range, stress levels increase and the risk of local failure rises. Proper thickness matching improves load-carrying capacity and structural reliability.
- (3)
- The appropriate matching of liner layer thicknesses strongly affects load transfer and energy dissipation in the fluid film–liner 1–liner 2 system. Optimizing thickness uniformity improves pressure distribution and limits local stress. The viscoelastic hysteresis of the rubber layer and dual damping further boost energy dissipation. This results in improved load capacity and energy efficiency, particularly under high eccentricity and high speed conditions. The findings offer theoretical guidance and a framework for engineering laminated water-lubricated bearings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UHMWPE | Ultra-high-molecular-weight polyethylene |
| CNC | Computer numerical control |
| MoS2 | Molybdenum disulfide |
| CF | Carbon fibers |
| ZGB | Zwart–Gerber–Belamri |
| FSI | Fluid–structure interaction |
References
- Ohdar, S.K.; Behera, S.K. A comprehensive review on advancements in water-lubricated bearings: Surface texture, tribological performance, and thermal effects. Proc. Inst. Mech. Eng. Part J-Eng. Tribol. 2025, 239, 955–984. [Google Scholar] [CrossRef]
- Ouyang, W.; Zhang, Z.; Nie, Y.; Liu, B.; Vanierschot, M. Parametric modeling and collaborative optimization of a rim-driven thruster considering propeller-duct interactions. Ocean Eng. 2025, 337, 121746. [Google Scholar] [CrossRef]
- Pan, F.; Ouyang, W.; Ning, C.; Dong, X. Wide-Area Film Thickness Measurement Method of Water-Lubricated Polymer Bearing Based on Ultrasonic Reflection Coefficient Phase. Measurement 2025, 242, 116121. [Google Scholar] [CrossRef]
- Żochowski, T.; Litwin, W. Innovative 3D Measuring Technique for Identifying Geometrical Imperfections and Wear in Small Marine Stern Tube Liners. Pol. Marit. Res. 2025, 32, 129–136. [Google Scholar] [CrossRef]
- Gong, H.; Yu, C.; Zhang, L.; Xie, G.; Guo, D.; Luo, J. Intelligent Lubricating Materials: A Review. Compos. Part B Eng. 2020, 202, 108450. [Google Scholar] [CrossRef]
- Zhang, Z.; Ouyang, W.; Liang, X.; Yan, X.; Yuan, C.; Zhou, X.; Guo, Z.; Dong, C.; Liu, Z.; Jin, Y.; et al. Review of the Evolution and Prevention of Friction, Wear, and Noise for Water-Lubricated Bearings Used in Ships. Friction 2024, 12, 1–38. [Google Scholar] [CrossRef]
- Xue, E.; Guo, Z.; Zhao, H.; Yuan, C. A Review of the Design and Feasibility of Intelligent Water-Lubrication Bearings. J. Mar. Sci. Appl. 2022, 21, 23–45. [Google Scholar] [CrossRef]
- Meng, Y.; Xu, J.; Jin, Z.; Prakash, B.; Hu, Y. A Review of Recent Advances in Tribology. Friction 2020, 8, 221–300. [Google Scholar] [CrossRef]
- Song, S.; Zhu, Z.; Du, S.; Li, Y.; Liu, C. Research on Polymer Wear under Water Conditions: A Review. Lubricants 2024, 12, 312. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, Z.; Yuan, C.; Bai, X.; Wang, C. Effect of Self-Healing Microcapsules on the Tribological Properties of UHMWPE Composites. J. Tsinghua Univ. Sci. Technol. 2025, 65, 312–324. [Google Scholar] [CrossRef]
- Smith, E.H. On the Design and Lubrication of Water-Lubricated, Rubber, Cutlass Bearings Operating in the Soft EHL Regime. Lubricants 2020, 8, 75. [Google Scholar] [CrossRef]
- Mallya, R.; Shenoy, S.B.; Pai, R. Static Characteristics of Misaligned Multiple Axial Groove Water-Lubricated Bearing in the Turbulent Regime. Proc. Inst. Mech. Eng. Part J-Eng. Tribol. 2016, 231, 385–398. [Google Scholar] [CrossRef]
- Kraker, A.D.; van Ostayen, R.A.J.; Rixen, D.J. Calculation of Stribeck Curves for (Water) Lubricated Journal Bearings. Tribol. Int. 2007, 40, 459–469. [Google Scholar] [CrossRef]
- Litwin, W. Water-Lubricated Bearings of Ship Propeller Shafts—Problems, Experimental Tests and Theoretical Investigations. Pol. Marit. Res. 2009, 16, 41–49. [Google Scholar] [CrossRef]
- Du, Y.; Li, M. Effects on Lubrication Characteristics of Water-Lubricated Rubber Bearings with Journal Tilting and Surface Roughness. Proc. Inst. Mech. Eng. Part J-Eng. Tribol. 2020, 234, 161–171. [Google Scholar] [CrossRef]
- Yang, S.; Li, M. Elastohydrodynamic Lubrication Characteristics of Water-Lubricated Rubber Bearings with Mixed Groove Structures. Bearing 2018, 2, 38–42. (In Chinese) [Google Scholar] [CrossRef]
- Li, W.; Wang, J.; Ding, X.; Cheng, M. Influence of Rubber Layer Thickness on Lubrication Performance of Water-Lubricated Bearings. Lubr. Seal. 2014, 39, 64–67. (In Chinese) [Google Scholar] [CrossRef]
- He, J.; Li, X.; Zhang, Z. Recent progress in tribological modification of polymer matrix composites. Tribology 2012, 32, 199–208. (In Chinese) [Google Scholar]
- Ma, S.; Scaraggi, M.; Wang, D.; Wang, X.; Liang, Y.; Liu, W.; Dini, D.; Zhou, F. Nanoporous Substrate-Infiltrated Hydrogels: A Bioinspired Regenerable Surface for High Load Bearing and Tunable Friction. Adv. Funct. Mater. 2015, 25, 7366–7374. [Google Scholar] [CrossRef]
- Liu, G.; Feng, Y.; Zhao, N.; Chen, Z.; Shi, J.; Zhou, F. Polymer-Based Lubricating Materials for Functional Hydration Lubrication. Chem. Eng. J. 2021, 429, 132324. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, X.; Zhu, H.; Huang, Q.; Wang, L.; Xing, S.; Gryllias, K. Optimization Study on the Lubrication Performance of Ship Stern Bearings Based on Curved Boring. Ocean Eng. 2025, 332, 121431. [Google Scholar] [CrossRef]
- Wang, C.; Bai, X.; Dong, C.; Guo, Z.; Yuan, C. Friction Properties of Polyacrylamide Hydrogel Particle/HDPE Composite under Water Lubrication. Polymer 2019, 180, 121703. [Google Scholar] [CrossRef]
- Qu, C.; Zhang, N.; Wang, C.; Wang, T.; Wang, Q.; Li, S.; Chen, S. MoS2/CF Synergistic Reinforcement on Tribological Properties of NBR/PU/EP Interpenetrating Polymer Networks. Tribol. Int. 2022, 167, 107384. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, X.; Huang, Q.; Xing, S.; Zhou, Z.; Liu, X. Effect of Sediment Particle Size on the Friction and Wear Performance of NBR/Copper Rings under Contaminated Water Lubrication Conditions. Wear 2025, 571, 205832. [Google Scholar] [CrossRef]
- Liang, X.; Yan, X.; Ouyang, W.; Liu, Z. Experimental Research on Tribological and Vibration Performance of Water-Lubricated Hydrodynamic Thrust Bearings Used in Marine Shaft-less Rim Driven Thrusters. Wear 2019, 426–427, 778–791. [Google Scholar] [CrossRef]
- Xie, Z.; Tian, Y.; Liu, S.; Ma, W.; Gao, W.; Du, P.; Zhao, B. Fluid-Structure Interaction Analysis of a Novel Water-Lubricated Bearing with Particle-Dynamic Effect: Theory and Experiment. Tribol. Int. 2025, 204, 110474. [Google Scholar] [CrossRef]
- Du, Y.; Li, M. Lubrication Characteristics Analysis of Several Water-Lubricated Bearings with Different Lining Materials. Lubr. Eng. 2018, 43, 52–56+62. (In Chinese) [Google Scholar] [CrossRef]
- Lv, F.; Zhang, X.; Ji, C.; Rao, Z. Theoretical and Experimental Investigation on Local Turbulence Effect on Mixed-Lubrication Journal Bearing During Speeding Up. Phys. Fluids 2022, 34, 113104. [Google Scholar] [CrossRef]
- Qin, H.; Yang, C.; Zhu, H.; Li, X.; Li, Z.; Xu, X. Experimental Analysis on Friction-Induced Vibration of Water-Lubricated Bearings in a Submarine Propulsion System. Ocean Eng. 2020, 203, 107239. [Google Scholar] [CrossRef]
- Liu, Q.; Ouyang, W.; Li, R.; Jin, Y.; He, T. Experimental Research on Lubrication and Vibration Characteristics of Water-Lubricated Stern Bearing for Underwater Vehicles under Extreme Working Conditions. Wear 2023, 523, 204778. [Google Scholar] [CrossRef]
- Zhou, X.; Kuang, F.; Huang, J.; Liu, X.; Gryllias, K. Water-Lubricated Stern Bearing Rubber Layer Construction and Material Parameters: Effects on Frictional Vibration Based on Computer Vision. Tribol. Trans. 2021, 64, 65–81. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Zhu, W.; Tian, W.; Hao, L. Theoretical and Experimental Investigation on the Influences of Misalignment on the Lubrication Performances and Lubrication Regimes Transition of Water-Lubricated Bearing. Mech. Syst. Signal Process. 2020, 149, 107211. [Google Scholar] [CrossRef]
- Li, S.; Dong, C.; Yuan, C.; Bai, X. Dual nanoparticles effect on the frictional and vibrational dissipation behaviors of polymer-based water-lubricated bearing materials. J. Appl. Polym. Sci. 2024, 141, e56190. [Google Scholar] [CrossRef]
- Tao, R.; Wang, Z. Comparative Numerical Studies for the Flow Energy Dissipation Features in a Pump-Turbine in Pump Mode and Turbine Mode. J. Energy Storage 2021, 41, 102835. [Google Scholar] [CrossRef]
- Liu, X.; Deng, Y.; Zhou, X.; Huang, J.; Guo, X.; Li, B. Study on Friction and Wear Properties of Water-Lubricated Bearing Material in Different Watersheds. Wear 2025, 570, 205999. [Google Scholar] [CrossRef]
- Zhao, Z.; Rui, Z. Theoretical and Experimental Analysis of a Water-Lubricated Rubber Journal Bearing with a Large Aspect Ratio. Ind. Lubr. Tribol. 2020, 72, 797–803. [Google Scholar] [CrossRef]
- Chen, S.; Cai, J.; Xiang, G.; Zhang, J.; Liu, Z.; Fillon, M. Tribo-Dynamic-Wear Coupling Analysis for Water-Lubricated Bearings with Journal Surface Imperfection under Repeated Start-Stop Cycles. Tribol. Int. 2024, 200, 110093. [Google Scholar] [CrossRef]
- Zhou, G.; Mi, X.; Wang, J.; Hu, R. Experimental Comparison between the Stribeck Curves of Water-Lubricated Rubber Bearing with Straight and Spiral Grooves. Ind. Lubr. Tribol. 2018, 70, 1326–1330. [Google Scholar] [CrossRef]
- Moldovan, S.I.; Braun, M.J.; Balasoiu, A.M. A Three-Dimensional Parametric Study and Numerical/Experimental Flow Visualization of a Six-Pocket Hydrostatic Journal Bearing. Tribol. Trans. 2013, 56, 1–26. [Google Scholar] [CrossRef]
- Chang, X.; Liu, J.; Yan, X.; Sun, F.; Zhu, H.; Wang, C. Experimental Study on the Effects of Controllable Parameters on the Healthy Operation of SF-2A Material Water-Lubricated Stern Bearing in Multi-Point Ultra-Long Shaft Systems of Ships. J. Mar. Sci. Eng. 2025, 13, 14. [Google Scholar] [CrossRef]
- MIL-DTL-17901C SH; Bearing Components, Bonded Synthetic Rubber, Water Lubricated. US Navy Military Standard: Washington, DC, USA, 2005.
- CB/T 769–2008; Marine Integral Rubber Bearings. State Science, Technology and Industry Commission: Beijing, China, 2008.



| Parameter | Lining 1 | Lining 2 | Water Film |
|---|---|---|---|
| Number of nodes | 3,704,186 | 3,959,326 | 472,416 |
| Number of units | 806,673 | 862,848 | 235,616 |
| Unit mass | 0.9813 | 0.98135 | 0.71451 |
| Aspect ratio | 1.0882 | 1.0904 | 2.3224 |
| Skewness | 9.2024 × 10−2 | 8.9033 × 10−2 | 3.3784 × 10−3 |
| Jacobi ratio (MAPDL) | 1.0732 | 1.0749 | 1.0053 |
| Jacobi ratio (angular node) | 0.94704 | 0.94683 | 0.99474 |
| Jacobi ratio (Gauss point) | 0.95862 | 0.9584 | 0.99696 |
| Orthogonal quality | 0.98097 | 0.98171 | 0.93264 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhou, X.; Zhu, H.; Huang, Q.; Zhou, Z.; Xing, S.; Liu, X. Fluid–Structure Interaction Mechanisms of Layered Thickness Effects on Lubrication Performance and Energy Dissipation in Water-Lubricated Bearings. Lubricants 2025, 13, 445. https://doi.org/10.3390/lubricants13100445
Wang L, Zhou X, Zhu H, Huang Q, Zhou Z, Xing S, Liu X. Fluid–Structure Interaction Mechanisms of Layered Thickness Effects on Lubrication Performance and Energy Dissipation in Water-Lubricated Bearings. Lubricants. 2025; 13(10):445. https://doi.org/10.3390/lubricants13100445
Chicago/Turabian StyleWang, Lun, Xincong Zhou, Hanhua Zhu, Qipeng Huang, Zhenjiang Zhou, Shaopeng Xing, and Xueshen Liu. 2025. "Fluid–Structure Interaction Mechanisms of Layered Thickness Effects on Lubrication Performance and Energy Dissipation in Water-Lubricated Bearings" Lubricants 13, no. 10: 445. https://doi.org/10.3390/lubricants13100445
APA StyleWang, L., Zhou, X., Zhu, H., Huang, Q., Zhou, Z., Xing, S., & Liu, X. (2025). Fluid–Structure Interaction Mechanisms of Layered Thickness Effects on Lubrication Performance and Energy Dissipation in Water-Lubricated Bearings. Lubricants, 13(10), 445. https://doi.org/10.3390/lubricants13100445





