Experimental Investigation and Modelling of High-Speed Turn-Milling of H13 Tool Steel: Surface Roughness and Tool Wear
Abstract
1. Introduction
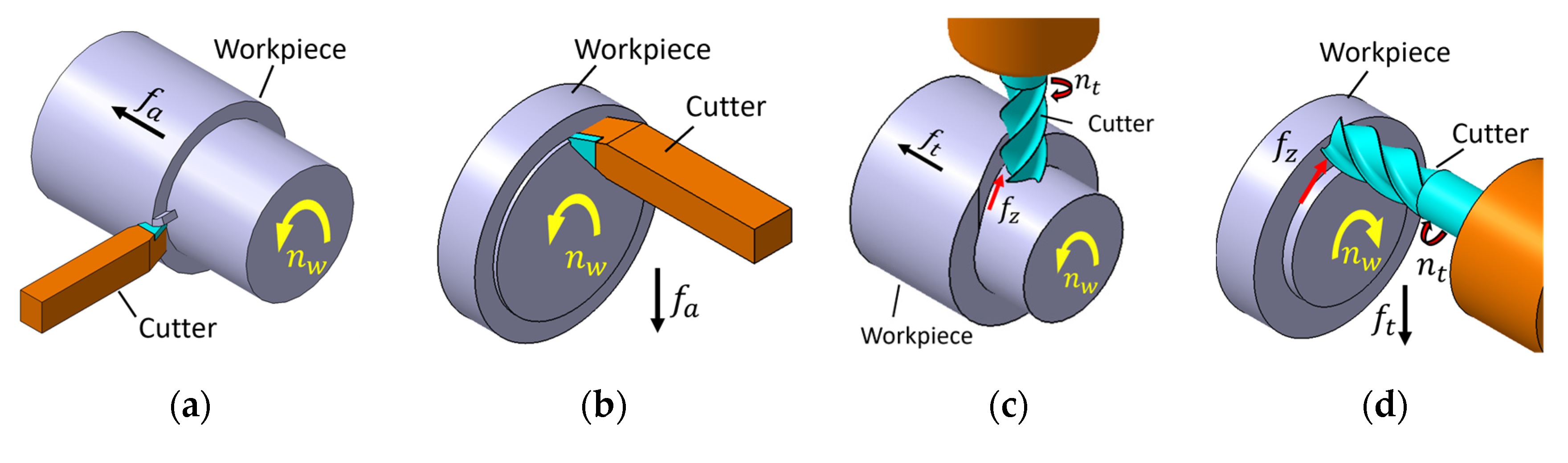
2. Experimental Setup and Methodology
2.1. Workpiece Material and Cutting Tool

| Mechanical Property | Value |
|---|---|
| Yield Strength (MPa) | 1648 |
| Poisson’s ratio | 0.3 |
| Hardness | Rockwell C54 |
| Coefficient of Thermal Expansion (/°C) at 93 °C | 10.4 × 10−6 |
| Density (kg/m3) | 7800 |
| Elongation (%) | 9 |
| C | Mn | Si | Cr | Mo | V | Ni | Fe |
|---|---|---|---|---|---|---|---|
| 0.38 | 0.35 | 1.00 | 5.25 | 1.35 | 1.05 | 0.15 | Remainder |
2.2. Machine Setup and Measurement System
2.3. Design of Experiments (DOE)
3. Results and Discussion
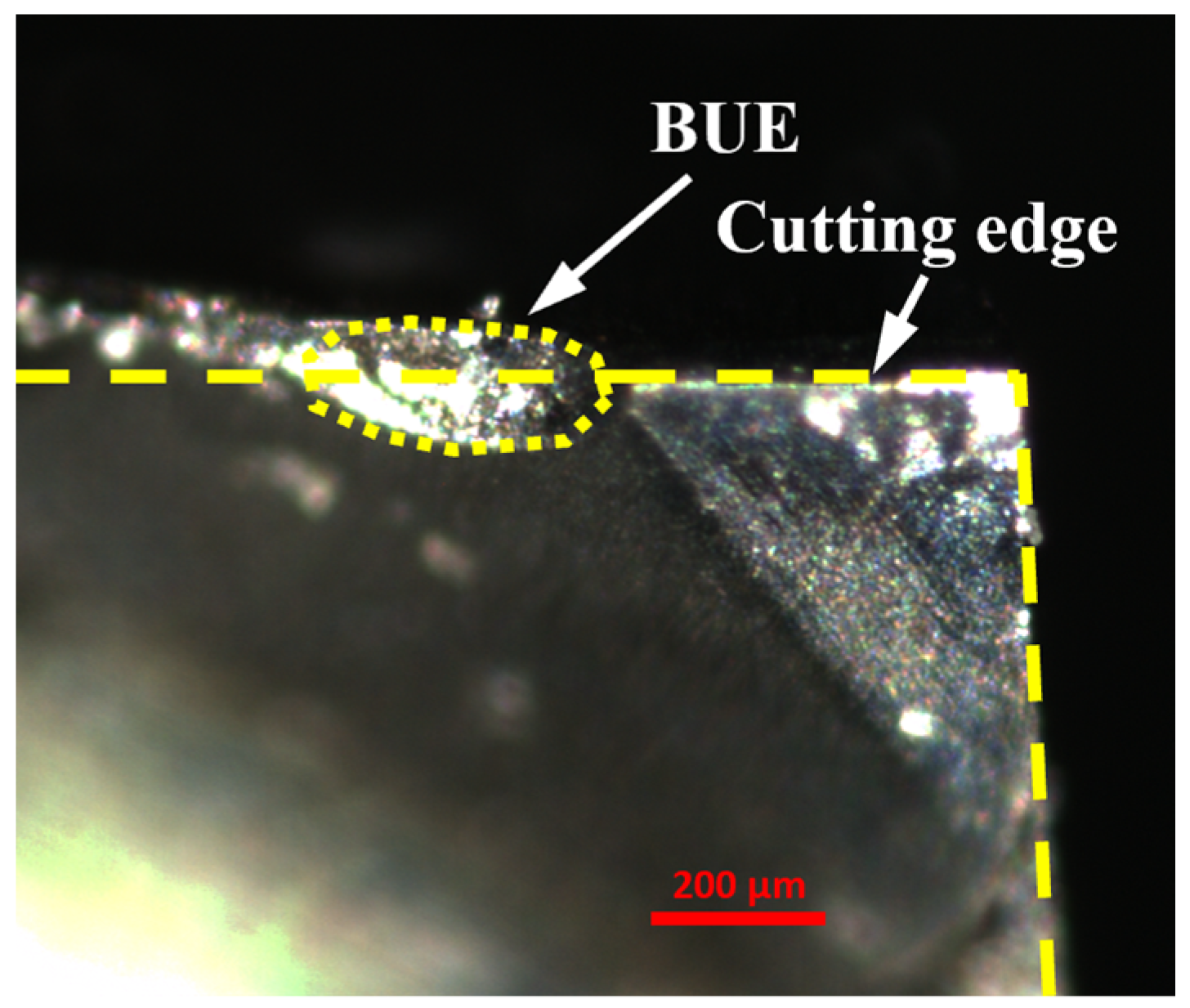
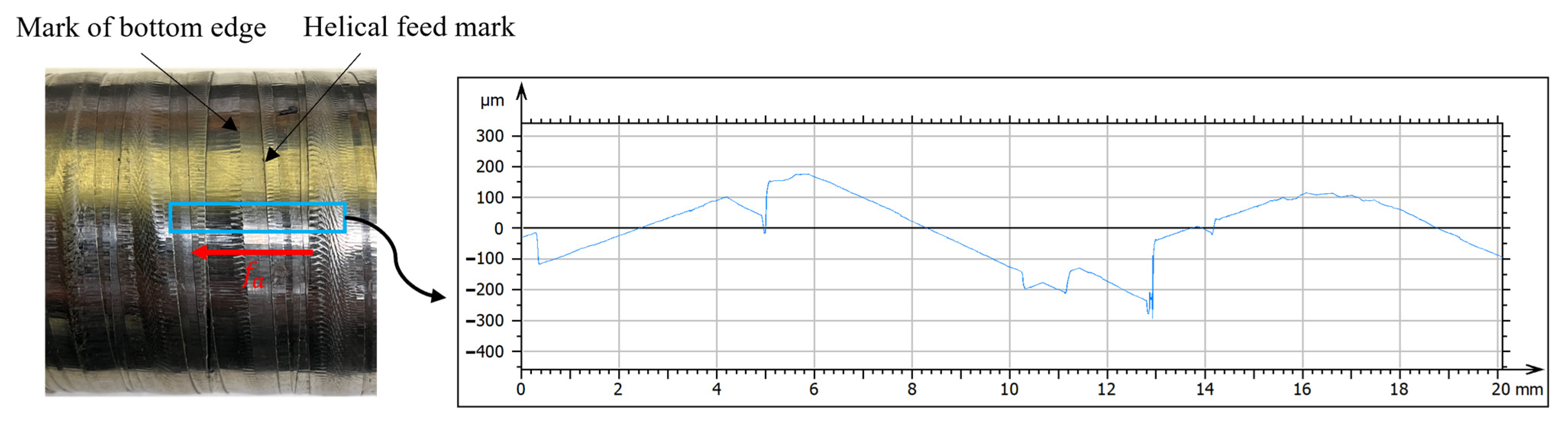
3.1. Chip Formation and Surface Quality
3.2. Surface Roughness

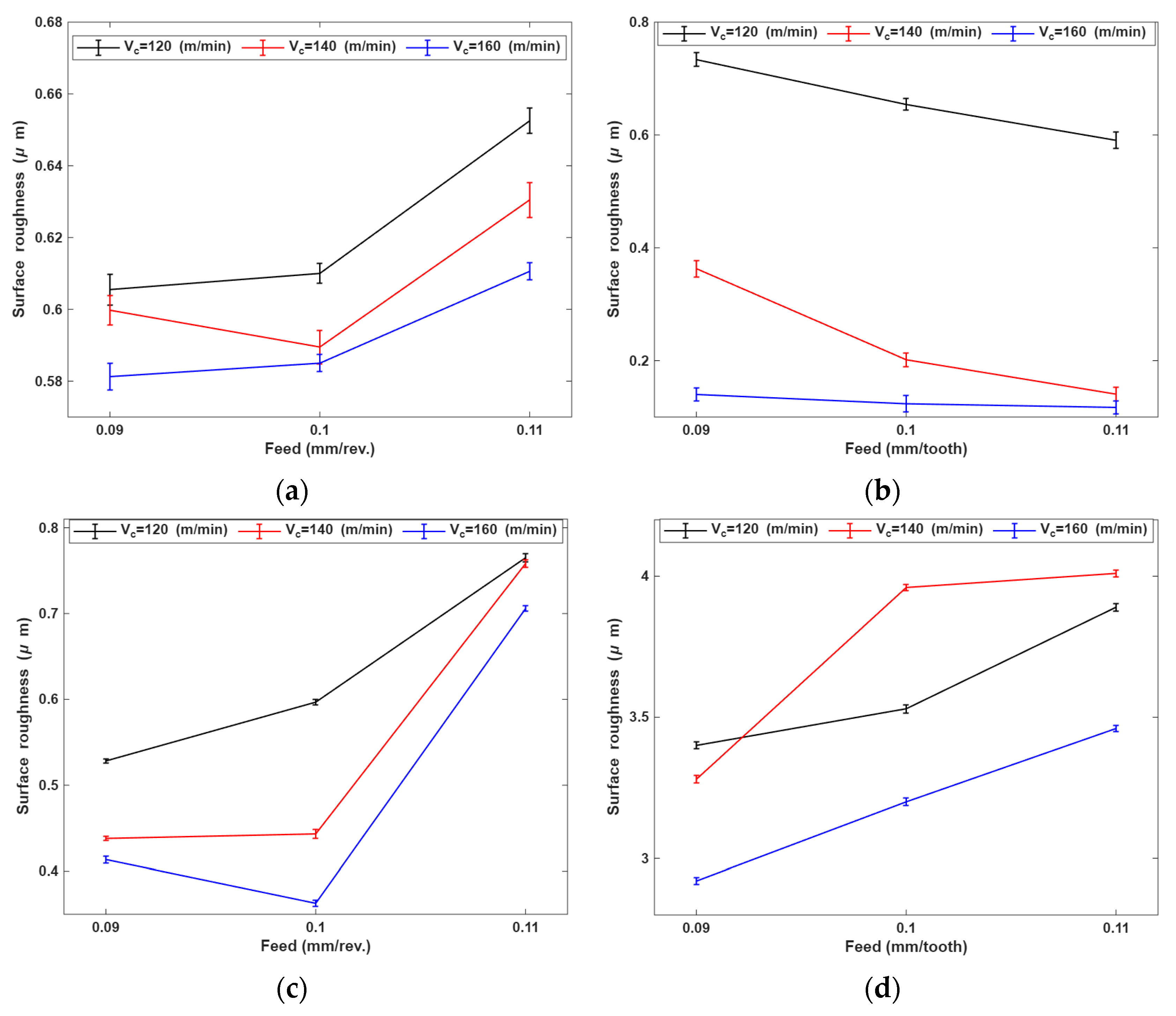
| Turning | Turn-Milling | |||
|---|---|---|---|---|
| Theoretical Ra Equation (2) (µm) | Measurement (µm) | Theoretical Ra Equation (3) (µm) | Measurement (µm) | |
| = 0.09 (mm/rev.) = 0.09 (mm/tooth) | 0.316 | [0.413–0.605] | 0.179 | [0.14–3.23] |
| = 0.1 (mm/rev.) = 0.1 (mm/tooth) | 0.391 | [0.363–0.610] | 0.206 | [0.123–3.869] |
| = 0.11 (mm/rev.) = 0.11 (mm/tooth) | 0.473 | [0.611–0.765] | 0.252 | [0.117–3.891] |
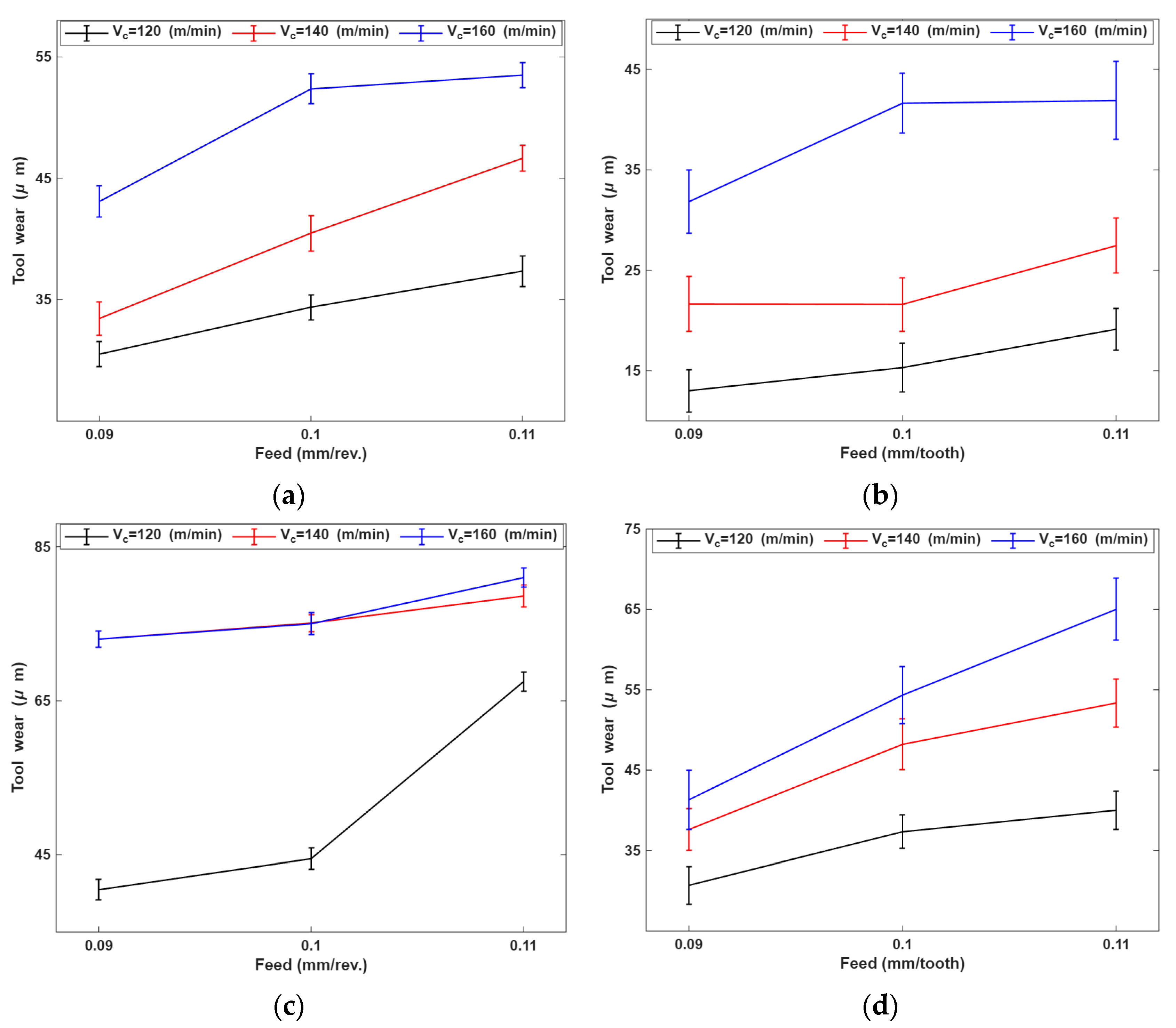
3.3. Tool Wear
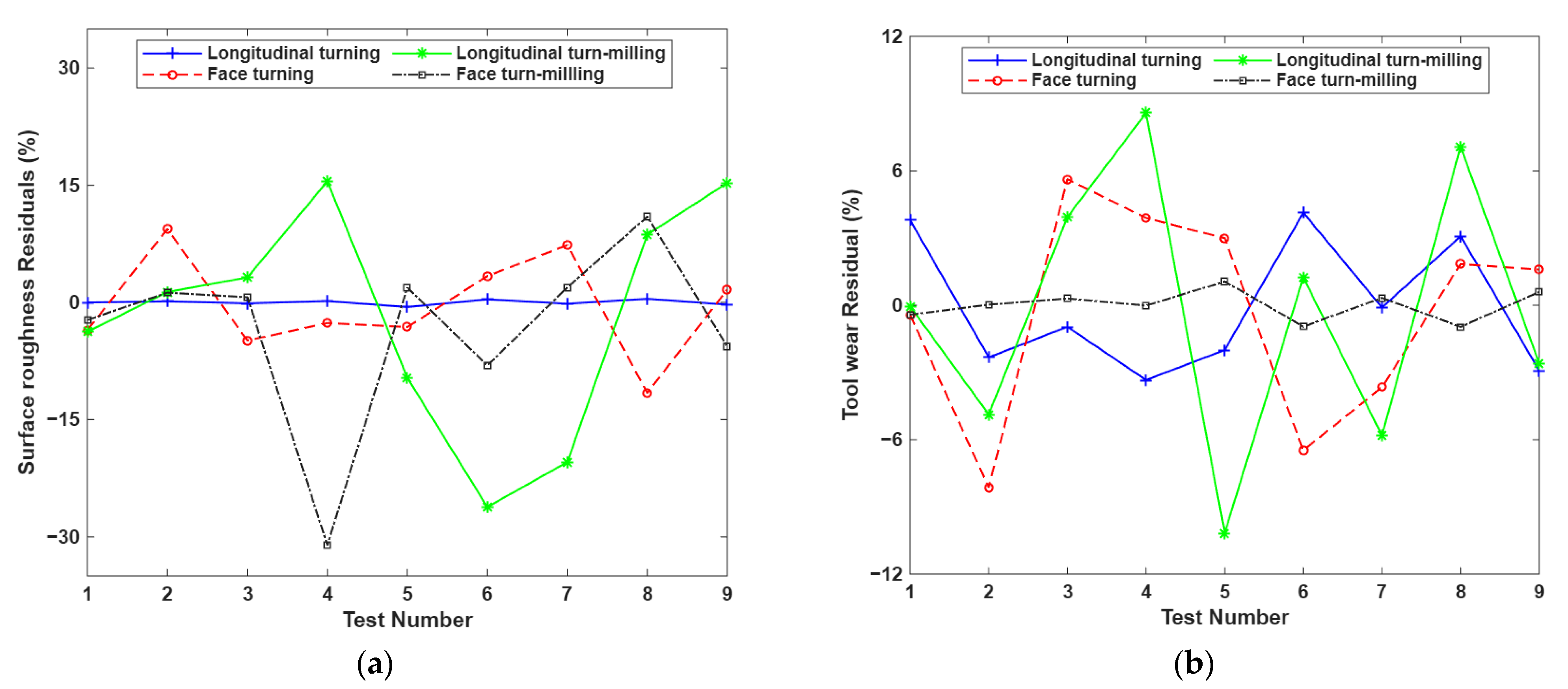
3.4. RSM Modeling
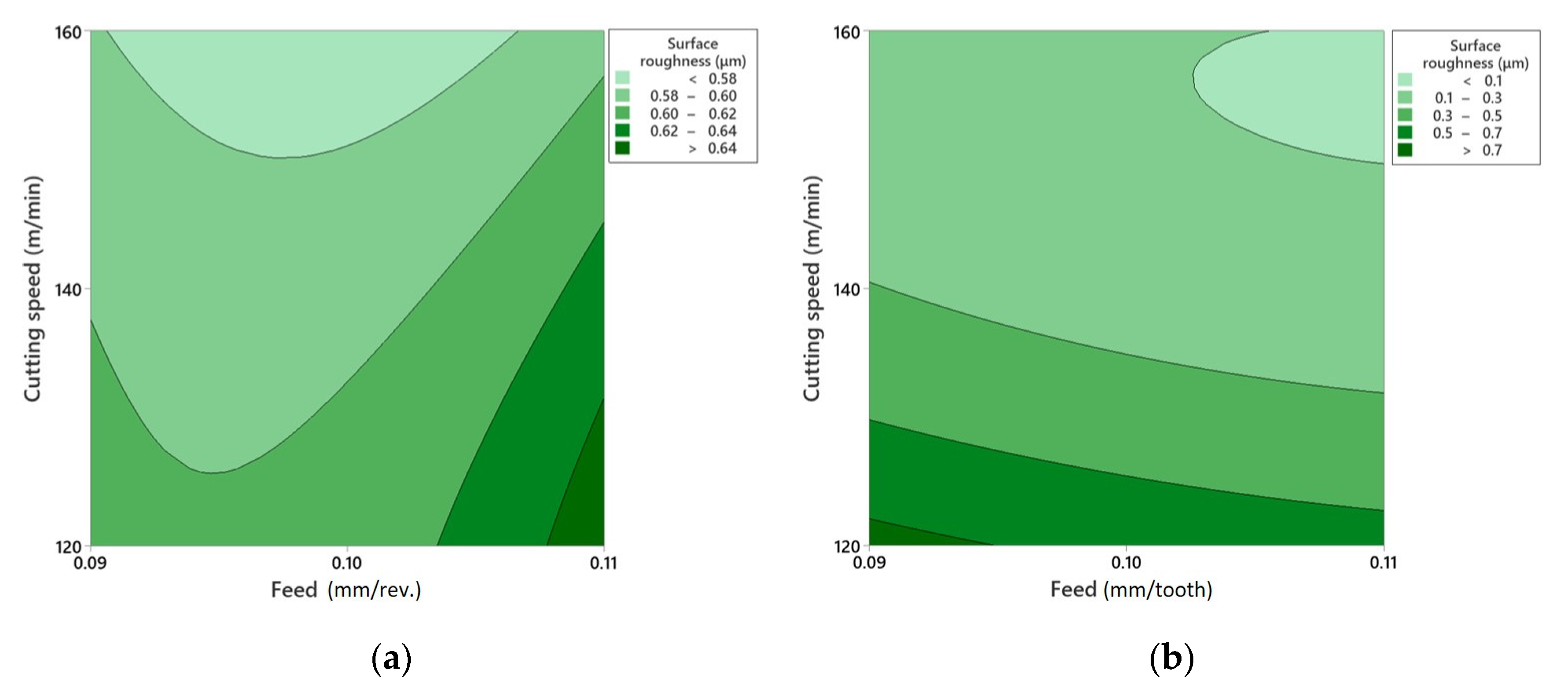
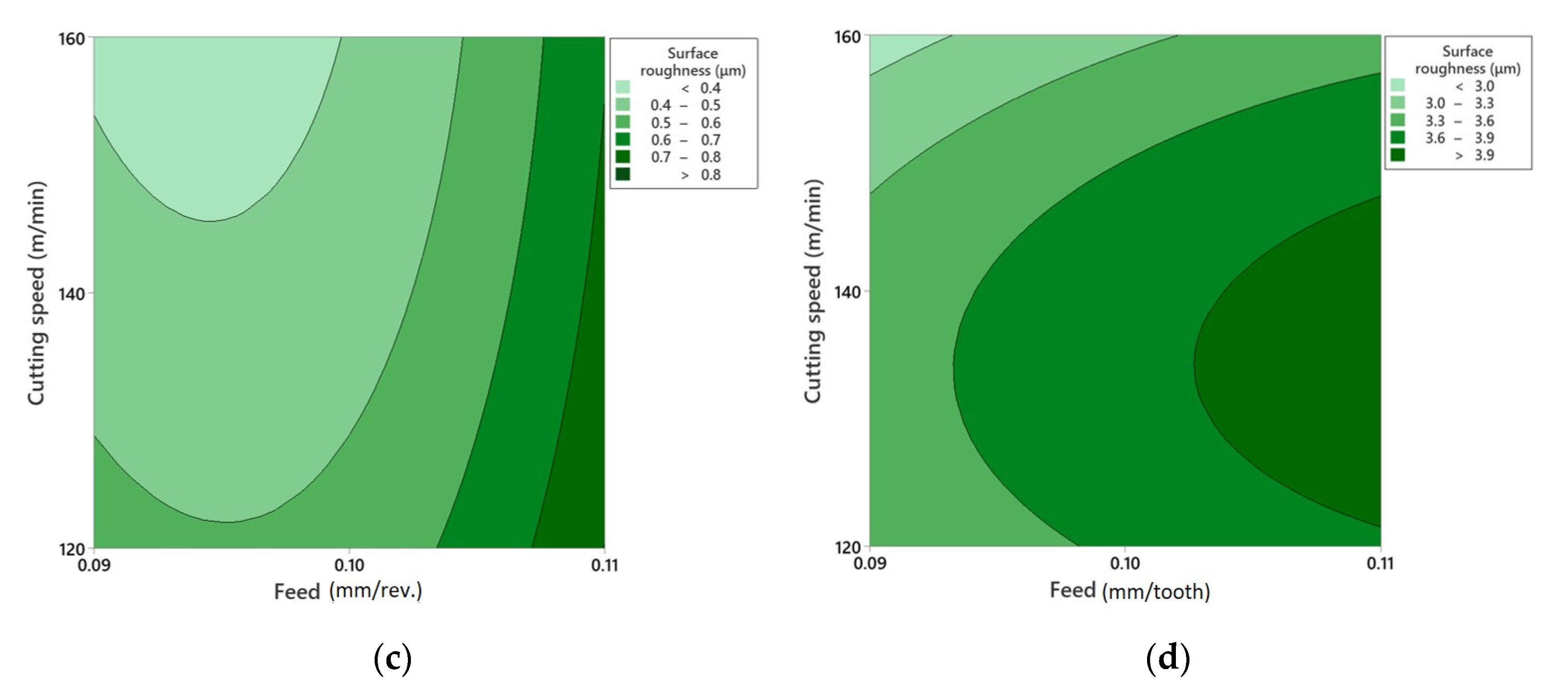
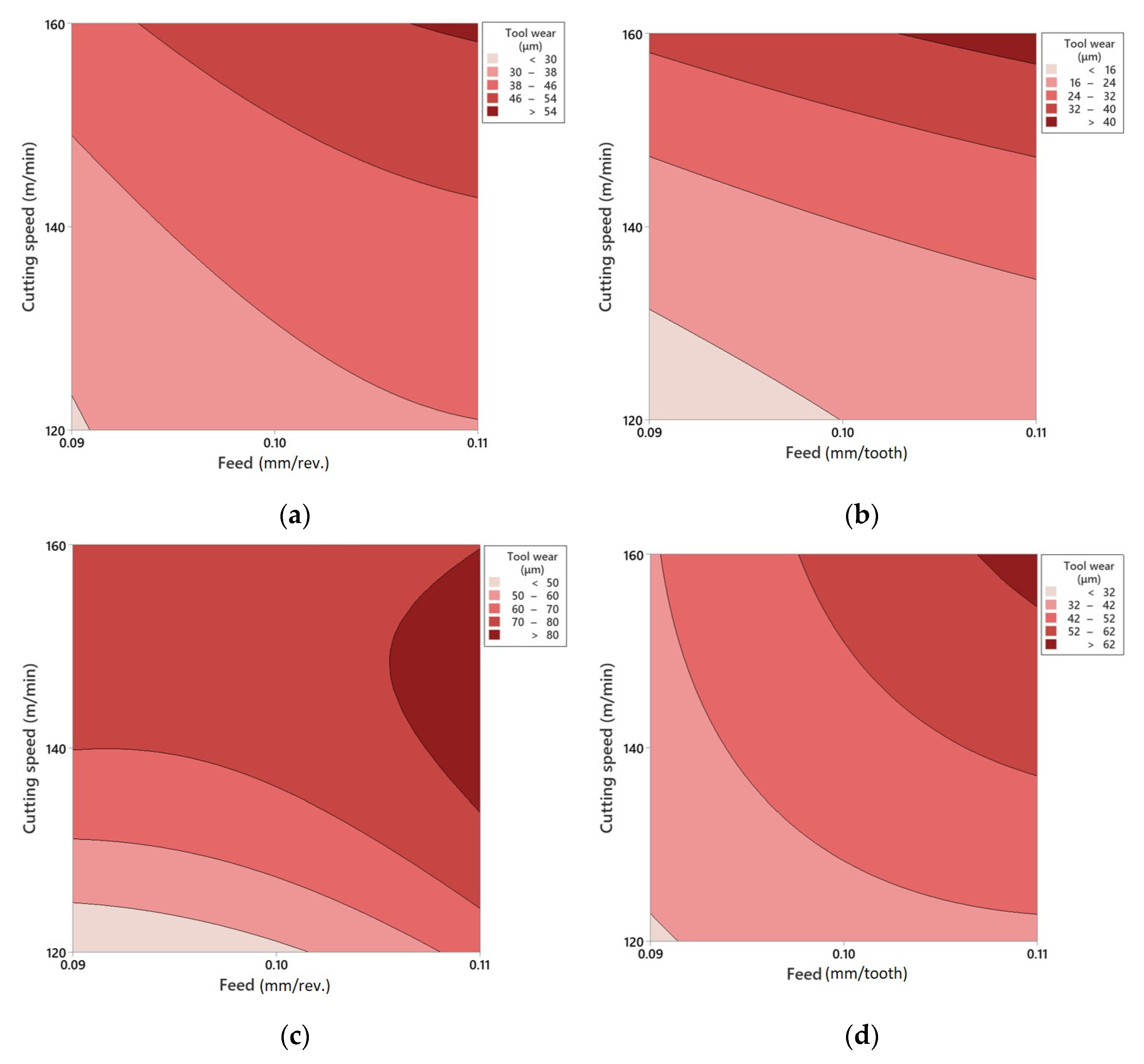
| Operation | Output | Feed | Cutting Speed | Cutting Speed × Feed |
|---|---|---|---|---|
| Longitudinal turning | Surface roughness | ▲ | ▲ | |
| Tool wear | ▲ | ▲ | ||
| Longitudinal turn-milling | Surface roughness | ▲ | ▲ | |
| Tool wear | ▲ | ▲ | ||
| Face turning | Surface roughness | ▲ | ▲ | |
| Tool wear | ▲ | ▲ | ||
| Face turn-milling | Surface roughness | ▲ | ▲ | |
| Tool wear | ▲ | ▲ | ▲ |
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed ANOVA Results of RSM Models
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 0.004064 | 0.000813 | 26.87 | 0.011 |
| Linear | 2 | 0.003298 | 0.001649 | 54.52 | 0.004 |
| 1 | 0.001386 | 0.001386 | 45.82 | 0.007 | |
| 1 | 0.001912 | 0.001912 | 63.23 | 0.004 | |
| Square | 2 | 0.000688 | 0.000344 | 11.37 | 0.040 |
| 1 | 0.000002 | 0.000002 | 0.05 | 0.833 | |
| 1 | 0.000686 | 0.000686 | 22.68 | 0.018 | |
| 2-Way Interaction | 1 | 0.000078 | 0.000078 | 2.58 | 0.206 |
| 1 | 0.000078 | 0.000078 | 2.58 | 0.206 | |
| Error | 3 | 0.000091 | 0.000030 | ||
| Total | 8 | 0.004155 |
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 531.812 | 106.362 | 24.97 | 0.012 |
| Linear | 2 | 517.603 | 258.801 | 60.76 | 0.004 |
| 1 | 363.170 | 363.170 | 85.26 | 0.003 | |
| 1 | 154.432 | 154.432 | 36.26 | 0.009 | |
| Square | 2 | 11.023 | 5.511 | 1.29 | 0.393 |
| 1 | 5.578 | 5.578 | 1.31 | 0.336 | |
| 1 | 5.445 | 5.445 | 1.28 | 0.340 | |
| 2-Way Interaction | 1 | 3.186 | 3.186 | 0.75 | 0.451 |
| 1 | 3.186 | 3.186 | 0.75 | 0.451 | |
| Error | 3 | 12.779 | 4.260 | ||
| Total | 8 | 544.590 |
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 0.504959 | 0.100992 | 41.27 | 0.006 |
| Linear | 2 | 0.450490 | 0.225245 | 92.06 | 0.002 |
| 1 | 0.425334 | 0.425334 | 173.83 | 0.001 | |
| 1 | 0.025155 | 0.025155 | 10.28 | 0.049 | |
| Square | 2 | 0.050870 | 0.025435 | 10.40 | 0.045 |
| 1 | 0.049981 | 0.049981 | 20.43 | 0.020 | |
| 1 | 0.000889 | 0.000889 | 0.36 | 0.589 | |
| 2-Way Interaction | 1 | 0.003600 | 0.003600 | 1.47 | 0.312 |
| 1 | 0.003600 | 0.003600 | 1.47 | 0.312 | |
| Error | 3 | 0.007340 | 0.002447 | ||
| Total | 8 | 0.512300 |
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 879.683 | 175.937 | 23.17 | 0.013 |
| Linear | 2 | 850.006 | 425.003 | 55.96 | 0.004 |
| 1 | 769.156 | 769.156 | 101.27 | 0.002 | |
| 1 | 80.850 | 80.850 | 10.65 | 0.047 | |
| Square | 2 | 25.776 | 12.888 | 1.70 | 0.321 |
| 1 | 25.522 | 25.522 | 3.36 | 0.164 | |
| 1 | 0.255 | 0.255 | 0.03 | 0.866 | |
| 2-Way Interaction | 1 | 3.901 | 3.901 | 0.51 | 0.525 |
| 1 | 3.901 | 3.901 | 0.51 | 0.525 | |
| Error | 3 | 22.784 | 7.595 | ||
| Total | 8 | 902.468 |
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 0.185043 | 0.037009 | 12.79 | 0.031 |
| Linear | 2 | 0.147947 | 0.073974 | 25.57 | 0.013 |
| 1 | 0.027744 | 0.027744 | 9.59 | 0.053 | |
| 1 | 0.120204 | 0.120204 | 41.54 | 0.008 | |
| Square | 2 | 0.036326 | 0.018163 | 6.28 | 0.085 |
| 1 | 0.000481 | 0.000481 | 0.17 | 0.711 | |
| 1 | 0.035845 | 0.035845 | 12.39 | 0.039 | |
| 2-Way Interaction | 1 | 0.000770 | 0.000770 | 0.27 | 0.642 |
| 1 | 0.000770 | 0.000770 | 0.27 | 0.642 | |
| Error | 3 | 0.008680 | 0.002893 | ||
| Total | 8 | 0.193723 |
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 1660.63 | 332.13 | 12.89 | 0.031 |
| Linear | 2 | 1250.10 | 625.05 | 24.26 | 0.014 |
| 1 | 975.38 | 975.38 | 37.86 | 0.009 | |
| 1 | 274.73 | 274.73 | 10.66 | 0.047 | |
| Square | 2 | 320.28 | 160.14 | 6.22 | 0.086 |
| 1 | 287.20 | 287.20 | 11.15 | 0.044 | |
| 1 | 33.08 | 33.08 | 1.28 | 0.340 | |
| 2-Way Interaction | 1 | 90.25 | 90.25 | 3.50 | 0.158 |
| 1 | 90.25 | 90.25 | 3.50 | 0.158 | |
| Error | 3 | 77.29 | 25.76 | ||
| Total | 8 | 1737.92 |
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 1.02796 | 0.205592 | 7.65 | 0.062 |
| Linear | 2 | 0.77253 | 0.386267 | 14.37 | 0.029 |
| 1 | 0.25627 | 0.256267 | 9.53 | 0.054 | |
| 1 | 0.51627 | 0.516267 | 19.21 | 0.022 | |
| Square | 2 | 0.25480 | 0.127400 | 4.74 | 0.118 |
| 1 | 0.24500 | 0.245000 | 9.11 | 0.057 | |
| 1 | 0.00980 | 0.009800 | 0.36 | 0.589 | |
| 2-Way Interaction | 1 | 0.00062 | 0.000625 | 0.02 | 0.888 |
| 1 | 0.00062 | 0.000625 | 0.02 | 0.888 | |
| Error | 3 | 0.08064 | 0.026881 | ||
| Total | 8 | 1.10860 |
| Parameter | Degree of Freedom | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5 | 921.984 | 184.397 | 559.62 | 0.000 |
| Linear | 2 | 857.308 | 428.654 | 1300.91 | 0.000 |
| 1 | 461.214 | 461.214 | 1399.72 | 0.000 | |
| 1 | 396.094 | 396.094 | 1202.09 | 0.000 | |
| Square | 2 | 12.836 | 6.418 | 19.48 | 0.019 |
| 1 | 5.179 | 5.179 | 15.72 | 0.029 | |
| 1 | 7.657 | 7.657 | 23.24 | 0.017 | |
| 2-Way Interaction | 1 | 51.840 | 51.840 | 157.33 | 0.001 |
| 1 | 51.840 | 51.840 | 157.33 | 0.001 | |
| Error | 3 | 0.989 | 0.330 | ||
| Total | 8 | 922.973 |
References
- M’Saoubi, R.; Axinte, D.; Soo, S.L.; Nobel, C.; Attia, H.; Kappmeyer, G.; Engin, S.; Sim, W.-M. High performance cutting of advanced aerospace alloys and composite materials (Keynote Paper). CIRP Ann. 2015, 64, 557–580. [Google Scholar] [CrossRef]
- Yan, H.; Hua, J.; Shivpuri, R. Flow stress of AISI H13 die steel in hard machining. Mater. Des. 2007, 28, 272–277. [Google Scholar] [CrossRef]
- Coldwell, H.; Woods, R.; Paul, M.; Koshy, P.; Dewes, R.; Aspinwall, D. Rapid machining of hardened AISI H13 and D2 moulds, dies and press tools. J. Mater. Process. Technol. 2003, 135, 301–311. [Google Scholar] [CrossRef]
- Bakar, H.A.; Ghani, J.; Haron, C.C.; Ghazali, M.; Kasim, M.; Al-Zubaidi, S.; Jouini, N. Wear mechanisms of solid carbide cutting tools in dry and cryogenic machining of AISI H13 steel with varying cutting-edge radius. Wear 2023, 523, 204758. [Google Scholar] [CrossRef]
- Ng, E.-G.; Aspinwall, D.K. The effect of workpiece hardness and cutting speed on the machinability of AISI H13 hot work die steel when using PCBN tooling. J. Manuf. Sci. Eng. 2002, 124, 588–594. [Google Scholar] [CrossRef]
- Özel, T.; Hsu, T.-K.; Zeren, E. Effects of cutting edge geometry, workpiece hardness, feed rate and cutting speed on surface roughness and forces in finish turning of hardened AISI H13 steel. Int. J. Adv. Manuf. Technol. 2005, 25, 262–269. [Google Scholar] [CrossRef]
- Cicek, A.; Ekici, E.; Kıvak, T.; Kara, F.; Uçak, N. Performance of multilayer coated and cryo-treated uncoated tools in machining of AISI H13 tool steel—Part 2: HSS end mills. J. Mater. Eng. Perform. 2021, 30, 3446–3457. [Google Scholar] [CrossRef]
- Cicek, A.; Kıvak, T.; Ekici, E.; Kara, F.; Ucak, N. Performance of multilayer coated and cryo-treated uncoated tools in machining of AISI H13 tool steel—Part 1: Tungsten carbide end mills. J. Mater. Eng. Perform. 2021, 30, 3436–3445. [Google Scholar] [CrossRef]
- Venkata Ajay Kumar, G.; A, R.; Shilpa, M. Modelling and optimization based on RSM in dry turning parameters of AISI H13 steel using novel hybrid design texture tool. Cogent Eng. 2024, 11, 2375427. [Google Scholar] [CrossRef]
- Outeiro, J. Surface integrity predictions and optimisation of machining conditions in the turning of AISI H13 tool steel. Int. J. Mach. Mach. Mater. 7 2014, 15, 122–134. [Google Scholar] [CrossRef]
- Suresh, R.; Basavarajappa, S. Effect of process parameters on tool wear and surface roughness during turning of hardened steel with coated ceramic tool. Procedia Mater. Sci. 2014, 5, 1450–1459. [Google Scholar] [CrossRef]
- Suresh, R.; Joshi, A.G.; Manjaiah, M. Experimental investigation on tool wear in AISI H13 die steel turning using RSM and ANN methods. Arab. J. Sci. Eng. 2021, 46, 2311–2325. [Google Scholar] [CrossRef]
- Umer, U. High speed turning of H-13 tool steel using ceramics and PCBN. J. Mater. Eng. Perform. 2012, 21, 1857–1861. [Google Scholar] [CrossRef]
- Tuli, N.T.; Amin, A.N.; Kaisar, R.; Dhrubo, F.I.; Bin Rashid, A. Optimisation of machining parameters in high-speed end milling of hardened AISI H13 die steel by integrating RSM and GA. Adv. Mater. Process. Technol. 2024, 11, 1564–1582. [Google Scholar] [CrossRef]
- Vikram, K.A.; Prasad, R.; Lakshmi, V.; Praveen, A. Overview of turn-milling machining processes–A review. In Proceedings of the 2nd International Conference & Exposition on Mechanical, Material, and Manufacturing Technology (ICE3MT 2022), Hyderabad, India, 28–29 October 2022; p. 020011. [Google Scholar]
- Schulz, H.; Kneisel, T. Turn-milling of hardened steel-an alternative to turning. CIRP Ann. 1994, 43, 93–96. [Google Scholar] [CrossRef]
- Choudhury, S.; Bajpai, J. Investigation in orthogonal turn-milling towards better surface finish. J. Mater. Process. Technol. 2005, 170, 487–493. [Google Scholar] [CrossRef]
- Savas, V.; Ozay, C. Analysis of the surface roughness of tangential turn-milling for machining with end milling cutter. J. Mater. Process. Technol. 2007, 186, 279–283. [Google Scholar] [CrossRef]
- Schulz, H.; Spur, G. High speed turn-milling—A new precision manufacturing technology for the machining of rotationally symmetrical workpieces. CIRP Ann. 1990, 39, 107–109. [Google Scholar] [CrossRef]
- Sasahara, H.; Kato, A.; Nakajima, H.; Yamamoto, H.; Muraki, T.; Tsutsumi, M. High-speed rotary cutting of difficult-to-cut materials on multitasking lathe. Int. J. Mach. Tools Manuf. 2008, 48, 841–850. [Google Scholar] [CrossRef]
- Karaguzel, U.; Olgun, U.; Uysal, E.; Budak, E.; Bakkal, M. Increasing tool life in machining of difficult-to-cut materials using nonconventional turning processes. Int. J. Adv. Manuf. Technol. 2015, 77, 1993–2004. [Google Scholar] [CrossRef]
- Berenji, K.R.; Kara, M.E.; Budak, E. Investigating high productivity conditions for turn-milling in comparison to conventional turning. Procedia CIRP 2018, 77, 259–262. [Google Scholar] [CrossRef]
- Özel, T.; Karpat, Y. Predictive modeling of surface roughness and tool wear in hard turning using regression and neural networks. Int. J. Mach. Tools Manuf. 2005, 45, 467–479. [Google Scholar] [CrossRef]
- Thai, N.; Shi, B.; Ghorbani, H.; Attia, H. Experimental investigation and simulation of laser surface heating and its effects on residual stresses and microstructure for AISI 52100 and H13. Procedia CIRP 2025, 133, 501–506. [Google Scholar] [CrossRef]
- Otalora-Ortega, H.; Osoro, P.A.; Arriola, P.J.A. Analytical modeling of the uncut chip geometry to predict cutting forces in orthogonal centric turn-milling operations. Int. J. Mach. Tools Manuf. 2019, 144, 103428. [Google Scholar] [CrossRef]
- Barry, J.; Byrne, G. The mechanisms of chip formation in machining hardened steels. J. Manuf. Sci. Eng. 2002, 124, 528–535. [Google Scholar] [CrossRef]
- Dogra, M.; Sharma, V.S.; Sachdeva, A.; Suri, N.M.; Dureja, J.S. Tool wear, chip formation and workpiece surface issues in CBN hard turning: A review. Int. J. Precis. Eng. Manuf. 2010, 11, 341–358. [Google Scholar] [CrossRef]
- Karagüzel, U.; Uysal, E.; Budak, E.; Bakkal, M. Analytical modeling of turn-milling process geometry, kinematics and mechanics. Int. J. Mach. Tools Manuf. 2015, 91, 24–33. [Google Scholar] [CrossRef]
- Santhakumar, J. Parametric optimization of trochoidal step on surface roughness and dish angle in end milling of AISID3 steel using precise measurements. Materials 2019, 12, 1335. [Google Scholar] [CrossRef]
- Wang, X.; Feng, C. Development of empirical models for surface roughness prediction in finish turning. Int. J. Adv. Manuf. Technol. 2002, 20, 348–356. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 3685:1993, Tool-Life Testing with Single-Point Turning Tools. Available online: https://www.iso.org/standard/9151.html (accessed on 1 October 2025).
- International Organization for Standardization. ISO 8688-2:1989, Tool Life testing in Milling Part 2: End Milling. Available online: https://www.iso.org/standard/16092.html (accessed on 1 October 2025).
- Ramesh, S.; Karunamoorthy, L.; Palanikumar, K. Measurement and analysis of surface roughness in turning of aerospace titanium alloy (gr5). Measurement 2012, 45, 1266–1276. [Google Scholar] [CrossRef]
- Neşeli, S.; Yaldız, S.; Türkeş, E. Optimization of tool geometry parameters for turning operations based on the response surface methodology. Measurement 2011, 44, 580–587. [Google Scholar] [CrossRef]
- Singh, D.; Rao, P.V. A surface roughness prediction model for hard turning process. Int. J. Adv. Manuf. Technol. 2007, 32, 1115–1124. [Google Scholar] [CrossRef]
- Astakhov, V.P. The assessment of cutting tool wear. Int. J. Mach. Tools Manuf. 2004, 44, 637–647. [Google Scholar] [CrossRef]
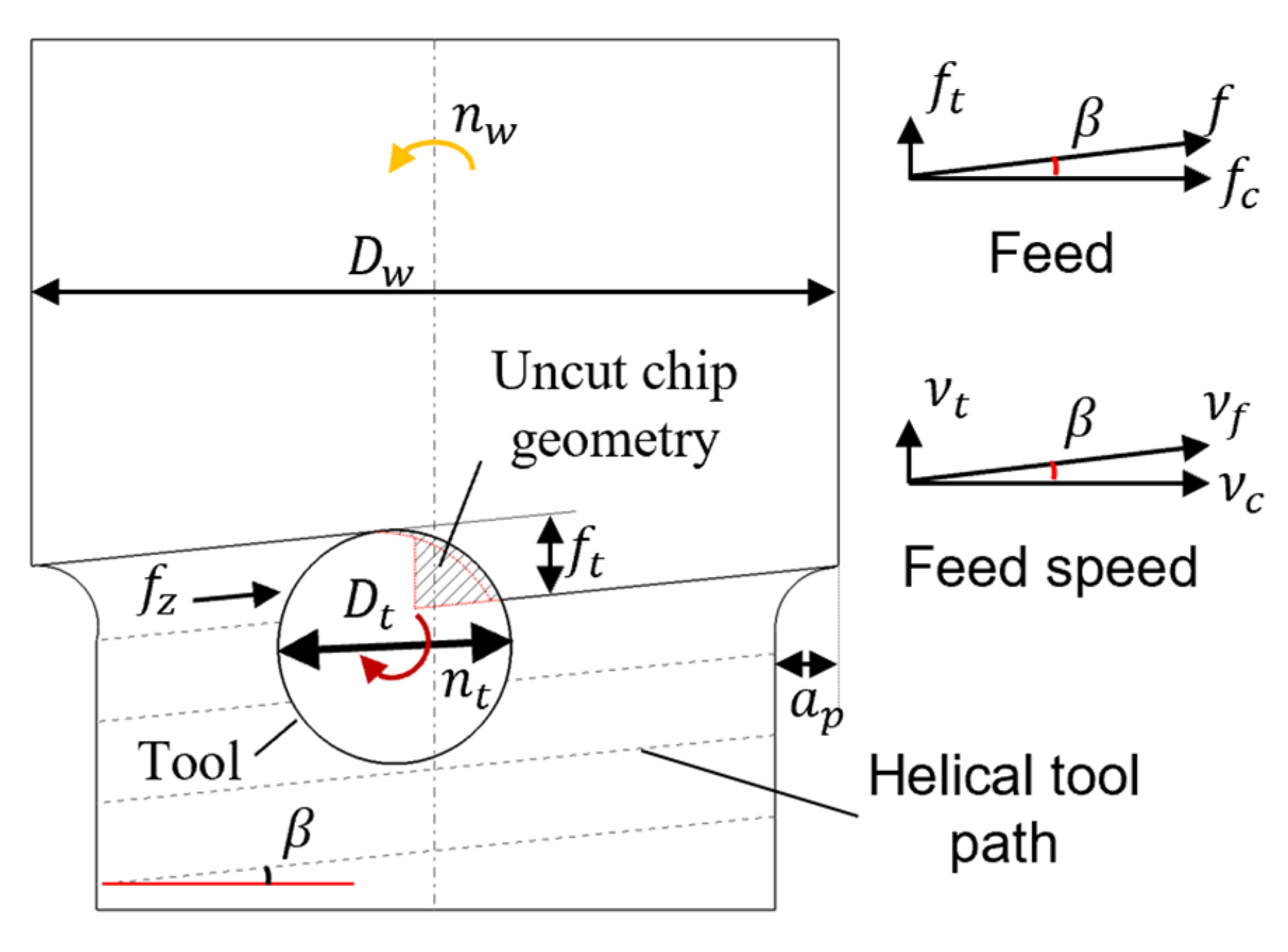




| Cutting Parameters | Units | Symbol | Level 1 | Level 2 | Level 3 |
|---|---|---|---|---|---|
| Cutting speed | m/min | 120 | 140 | 160 | |
| Feed (turning) | mm/workpiece rev | 0.09 | 0.1 | 0.11 | |
| Feed (turn-milling) | mm/tooth | 0.09 | 0.1 | 0.11 |
| Operation | Exp. No. | (rpm) | (rpm) | (m/min) | (Turn-Milling) (mm/rev.) | (mm/Tooth) | MRR (mm3/min) | Surface Roughness Ra (µm) | Tool Wear (µm) |
|---|---|---|---|---|---|---|---|---|---|
| Longitudinal turning | 1 | - | 765 | 120 | 0.09 | - | 5404 | 0.605 | 30.52 |
| 2 | - | 765 | 120 | 0.1 | - | 6005 | 0.610 | 34.39 | |
| 3 | - | 765 | 120 | 0.11 | - | 6605 | 0.652 | 37.36 | |
| 4 | - | 890 | 140 | 0.09 | - | 6288 | 0.599 | 33.46 | |
| 5 | - | 890 | 140 | 0.1 | - | 6986 | 0.589 | 40.49 | |
| 6 | - | 890 | 140 | 0.11 | - | 7686 | 0.631 | 46.65 | |
| 7 | - | 1015 | 160 | 0.09 | - | 7170 | 0.581 | 43.09 | |
| 8 | - | 1015 | 160 | 0.1 | - | 7967 | 0.585 | 52.36 | |
| 9 | - | 1015 | 160 | 0.11 | - | 8764 | 0.611 | 53.50 | |
| Longitudinal turn-milling | 1 | 3000 | 7 | 120 | 10 | 0.09 | 5604 | 0.733 | 13.01 |
| 2 | 3000 | 7.5 | 120 | 10 | 0.1 | 6005 | 0.654 | 15.30 | |
| 3 | 3000 | 8.3 | 120 | 10 | 0.11 | 6645 | 0.591 | 19.12 | |
| 4 | 3500 | 8 | 140 | 10 | 0.09 | 6405 | 0.363 | 21.62 | |
| 5 | 3500 | 9 | 140 | 10 | 0.1 | 7206 | 0.201 | 21.60 | |
| 6 | 3500 | 9.7 | 140 | 10 | 0.11 | 7766 | 0.140 | 27.45 | |
| 7 | 4000 | 9 | 160 | 10 | 0.09 | 7206 | 0.14 | 31.82 | |
| 8 | 4000 | 10 | 160 | 10 | 0.1 | 8007 | 0.123 | 41.63 | |
| 9 | 4000 | 11 | 160 | 10 | 0.11 | 8807 | 0.117 | 41.90 | |
| Face turning | 1 | - | 765 | 120 | 0.09 | - | 5404 | 0.528 | 40.50 |
| 2 | - | 765 | 120 | 0.1 | - | 6005 | 0.597 | 44.50 | |
| 3 | - | 765 | 120 | 0.11 | - | 6605 | 0.765 | 67.50 | |
| 4 | - | 890 | 140 | 0.09 | - | 6288 | 0.438 | 73.00 | |
| 5 | - | 890 | 140 | 0.1 | - | 6986 | 0.443 | 75.10 | |
| 6 | - | 890 | 140 | 0.11 | - | 7686 | 0.758 | 78.63 | |
| 7 | - | 1015 | 160 | 0.09 | - | 7170 | 0.413 | 73.10 | |
| 8 | - | 1015 | 160 | 0.1 | - | 7967 | 0.363 | 75.05 | |
| 9 | - | 1015 | 160 | 0.11 | - | 8764 | 0.706 | 81.02 | |
| Face turn-milling | 1 | 3000 | 7 | 120 | 10 | 0.09 | 5495 | 3.230 | 30.72 |
| 2 | 3000 | 7.5 | 120 | 10 | 0.1 | 5887 | 3.700 | 37.32 | |
| 3 | 3000 | 8.3 | 120 | 10 | 0.11 | 6437 | 3.891 | 40.00 | |
| 4 | 3500 | 8 | 140 | 10 | 0.09 | 6280 | 2.622 | 37.60 | |
| 5 | 3500 | 9 | 140 | 10 | 0.1 | 7065 | 3.869 | 48.20 | |
| 6 | 3500 | 9.7 | 140 | 10 | 0.11 | 7536 | 3.720 | 53.35 | |
| 7 | 4000 | 9 | 160 | 10 | 0.09 | 7065 | 2.921 | 41.31 | |
| 8 | 4000 | 10 | 160 | 10 | 0.1 | 7850 | 3.643 | 54.33 | |
| 9 | 4000 | 11 | 160 | 10 | 0.11 | 8635 | 3.290 | 65.03 |
| Operation | Output | RSM Model |
|---|---|---|
| Longitudinal turning | ) | ; R2 = 97.82%, R2 (adj) = 94.18%, R2 (pred) = 79.15% |
| ) | ; R2 = 97.65%, R2 (adj) = 93.74%, R2 (pred) = 72.68% | |
| Longitudinal turn-milling | ) | ; R2 = 98.89%, R2 (adj) = 96.18%, R2 (pred) = 83.32% |
| ) | ; R2 = 97.48%, R2 (adj) = 93.27%, R2 (pred) = 74.94% | |
| Face turning | ) | ; R2 = 95.52%, R2 (adj) = 88.05%, R2 (pred) = 46.46% |
| ) | ; R2 = 95.55%, R2 (adj) = 88.14%, R2 (pred) = 48.88% | |
| Face turn-milling | ) | ; R2 = 92.73%, R2 (adj) = 80.60%, R2 (pred) = 37.05% |
| ) | ; R2 = 99.89%, R2 (adj) = 99.71%, R2 (pred) = 99% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghorbani, H.; Shi, B.; Attia, H. Experimental Investigation and Modelling of High-Speed Turn-Milling of H13 Tool Steel: Surface Roughness and Tool Wear. Lubricants 2025, 13, 444. https://doi.org/10.3390/lubricants13100444
Ghorbani H, Shi B, Attia H. Experimental Investigation and Modelling of High-Speed Turn-Milling of H13 Tool Steel: Surface Roughness and Tool Wear. Lubricants. 2025; 13(10):444. https://doi.org/10.3390/lubricants13100444
Chicago/Turabian StyleGhorbani, Hamid, Bin Shi, and Helmi Attia. 2025. "Experimental Investigation and Modelling of High-Speed Turn-Milling of H13 Tool Steel: Surface Roughness and Tool Wear" Lubricants 13, no. 10: 444. https://doi.org/10.3390/lubricants13100444
APA StyleGhorbani, H., Shi, B., & Attia, H. (2025). Experimental Investigation and Modelling of High-Speed Turn-Milling of H13 Tool Steel: Surface Roughness and Tool Wear. Lubricants, 13(10), 444. https://doi.org/10.3390/lubricants13100444






