An Analysis on Negative Effects of Shaft Deflection on Angular Misalignment of Rollers Inside Tapered Roller Bearing

Abstract

Shaft deflection degrades roller alignment and intensifies stress concentration/edge effects at roller-ends and raceway edges, ultimately compromising service performance of tapered roller bearings (TRBs). Therefore, a dynamic model was developed for a TRB subjected to a deflected shaft in which Johnson’s load–deformation relationship was applied to reflect non-uniform cross-sectional structures of the tapered rollers and raceways, viscous damping was integrated into the roller/cage interaction, and friction actions at the raceways and flange areas were treated separately. Then, moment load and angular misalignment of the tapered roller were analyzed under various shaft deflection and operating conditions. Results indicate that tilt angle remains orders of magnitude smaller than skew angle. Shaft deflection amplifies both skew and tilt, and the influence level is proportional to the bearing size. Centrifugal effect primarily affects skew motion, whereas gyroscopic effect mainly influences tilt motion. Axial forces exert greater influence on roller skew than tilt. The flange typically constrains roller skew, whereas both raceways may induce bidirectional tilt/skew motion.

1. Introduction

In some machines, such as high-speed trains, automobiles, and rolling mills, the tapered roller bearing is widely used as a swivel and support component, as it can withstand combined radial and axial forces. However, due to installation error, mass mounted on the shaft, and load from gear systems, etc., the bearing shaft would be more or less deflected [1,2]. For certain slender shaft and bearing systems, the shaft may also experience deflection during rotation due to its inherent elastic modal behavior [3,4,5]. The deflected shaft, in turn, occasions the TRB, both rollers and rings, in a misaligned state. In addition, even for aligned TRB, the roller is always in a misaligned state due to normal and tangential interactions with the cage and rings [6,7,8,9]. Here, it refers to the angular misalignment caused by the roller tilt and skew [6]. Eventually, the misaligned state will aggravate the stress edge/concentration effect at the roller/raceway pair, and weaken load-carrying capacity and service life of the TRB [9,10]. Given this situation, the angular misalignment of rolling elements inside the TRB subjected to the aligned or deflected shaft needs to be addressed, as it will lay the foundation for the roller profile design and the bearing service life analysis [9,11].

For prediction of the roller’s motions, the dynamic approach is one of the effective theoretical solutions. Gupta [6] established a basic framework for modeling TRB dynamics. The analysis in this paper mainly refers to Gupta’s work. Deng et al. [8] evaluated effects of operating conditions, cage pocket clearance, and flange frictional behavior on the roller’s tilt and skew. In this work, lubrication states at the bearing contacts were involved. Sakaguchi et al. [12] simulated the skew motion with commercially available software, and friction forces at the TRB contacts were determined by considering both the oil film and asperity contact factors. Wang et al. [13] established a dynamic model of cylindrical roller bearings assessing load distribution and roller misalignment under combined loads.

The static, quasi-static, and quasi-dynamic approaches are also employed for analyzing the roller’s behavior. With consideration of bearing structure and kinematics, Creju et al. [7] developed a quasi-dynamic model for the TRB operating under combined loads and flooded lubrication conditions. Assuming that the TRB is oil-rich lubricated, Nelias et al. [14] developed a quasi-static model to determine the roller’s skew angle, but the roller/cage interplay was not considered. John et al. [15] employed static analysis to the tilt and contact of the cylindrical roller under shaft deflection caused by applied force. In addition, Li et al. [16] developed a 5-DOF static model of single-row TRBs for doubly supporting the wind turbine, which considered the axial preload, cone defection, and roller crown. In John et al.’s [15] and Li et al.’s [16] works, the roller skew was not included. Similarly, other studies on stiffness and fatigue of TRBs also ignored the roller skew issue [17,18,19].

Some roller analyses are performed on commercial software [20,21,22]. Based on ANSYS/LS-DYNA, Xia et al. [20] analyzed dynamic vibration characteristics of the TRB, and the friction coefficient was fixed at 0.1 (static) and 0.05 (dynamic) for the bearing contacts. With the assumptions that all frictions are ignored and pure rolling without slipping of the TRB, Yang et al. [21] studied the mechanical behavior of double-row TRB under moment loads with static method. With the similar assumptions in [21], Razpotnik et al. [22] presented a bottom-up approach to characterizing the dynamics of the TRB.

Zhou et al. [23] developed a fluid–solid coupling lubrication model using the full-system finite element method for an aero-–engine main bearing, and the effects of the roller tilt and skew were investigated. Similarly, Liu et al. [24] analyzed this problem using a fully numerical method, and all indicate that the roller’s angular misalignment significantly affects lubrication.

Some studies experimentally investigated roller misalignment [25,26,27,28,29,30]. Yang et al. [25,26] and Falodi et al. [27] used the same test method and different sensors to measure the roller’s skew angle in single-row and double-row TRBs, respectively. This provides a reference for the theoretical analysis in this paper. To validate the defined friction model at the flange/roller-end contact, Majdoub et al. [28,29] experimentally evaluated roller skew and compared the results with those from the kinematic equilibrium model. The defined friction model is based on the film thickness ratio, and does not explicitly include the sliding–rolling characteristic at the flange. Shafiee et al. [30] designed a novel test rig employing high-speed camera technology to observe roller slide, tilt, and skew behaviors in real-time for double-row spherical roller bearings.

This paper aims to clarify the tapered roller’s alignment state inside the oil-lubricated TRB when the shaft is deflected. So, differential equations of the TRB dynamics, which contain actual structures of the bearing parts, as well as fluid actions at the bearing contacts, were presented to describe angular vibration of the tapered roller. Then, by equating the shaft deflection as a constant angular constraint of the TRB, effects of the deflected shaft on the roller tilt and skew were numerically analyzed. Meanwhile, the roller’s angular misalignment under different operating conditions was studied.

2. Theoretical Formulation

The TRB is a type of roller bearing with strong structural nonlinearity. As depicted in Figure 1a,b, the inertial frame o_i-x_iy_iz_i is arranged at the cone’s mass center, and the cone body-fixed frame o_b-x_by_bz_b coincides with the o_i-x_iy_iz_i frame in the original state. The cone is shaft-mounted with a tight fit, so shaft deflection can be regarded as the cone’s axis o_b-x_b unparalleled to the inertial axis o_i-x_i. Body-fixed frames o_r-x_ry_rz_r (roller) and o_p-x_py_pz_p (cage) are similarly fixed at their respective mass centers. Thus, translations and rotations of the TRB parts are described in the inertial frame and body-fixed frames, respectively. Bearing internal interactions are solved with reference to Gupta’s method [6]. Assuming the cup is macroscopically stationary, the cone rotates about the o_b-x_b axis at a constant speed ω_i. The roller’s angular misalignment refers to the tilt and skew motions [6].

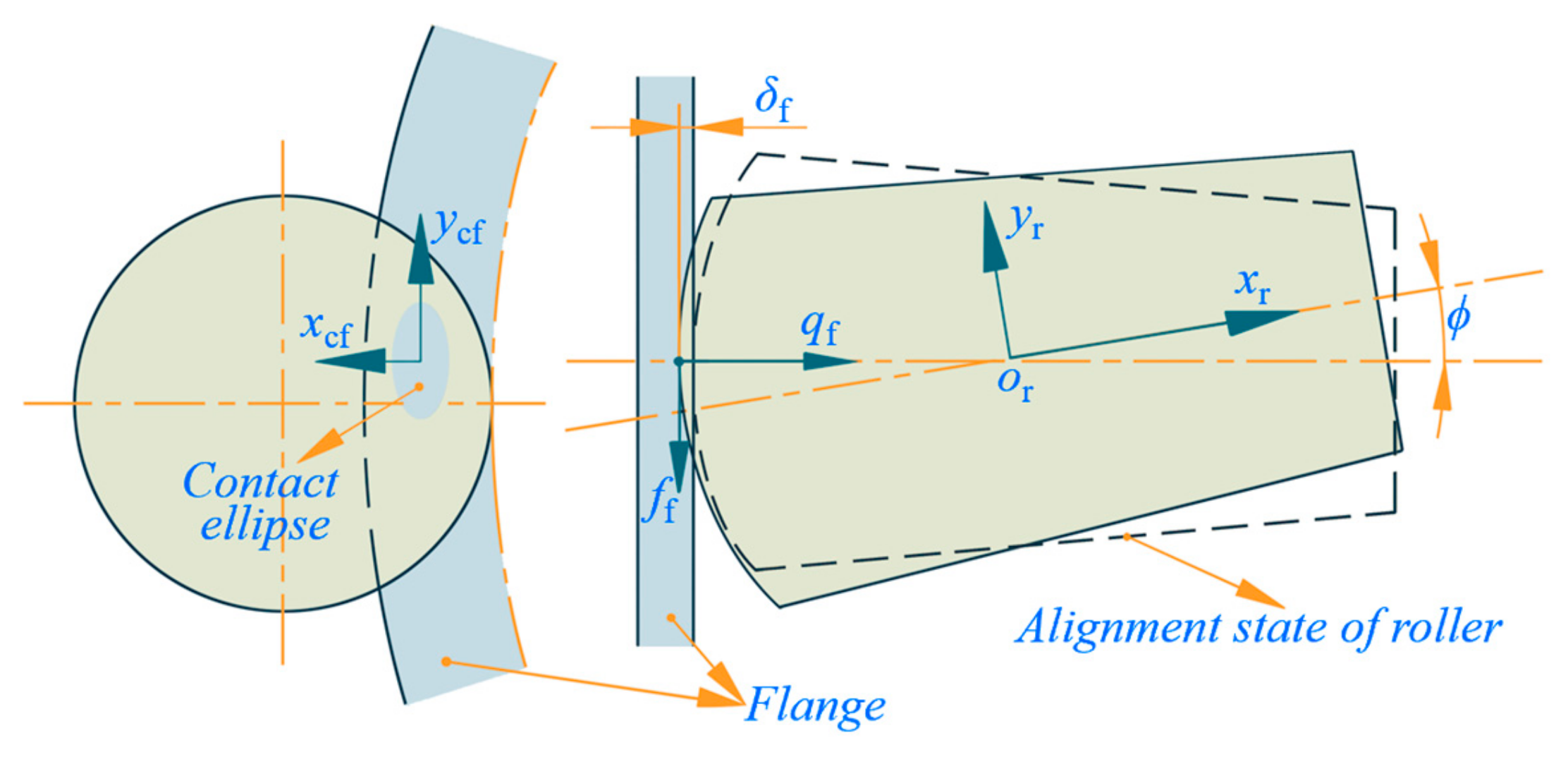
2.1. Roller/Raceway Interaction

As illustrated in Figure 1c, the roller/raceway interaction is dealt through the slicing method [6,10], wherein the roller is discretized into *s* slices. Unlike cylindrical roller bearings, TRB rollers and raceways exhibit non-uniform cross-sections. To characterize this geometry, Johnson’s load–deformation relationship [31] is applied. Accordingly, the normal force of the *k*-th slice with the cone and cup is

$$q_{\mathrm{i},\mathrm{o}}=\pm {\displaystyle \frac{\pi l_{\mathrm{e}}{\delta }_{\mathrm{i},\mathrm{o}}{\overline{E}}_{\mathrm{rb}}}{s}}{\left(2\ln {\displaystyle \frac{4{\overline{R}}_{\mathrm{i},\mathrm{o}}}{\sqrt{2{\overline{R}}_{\mathrm{i},\mathrm{o}}{\delta }_{\mathrm{i},\mathrm{o}}}}}-1\right)}^{-1}$$

(1)

$${\displaystyle \frac{1}{{\overline{E}}_{\mathrm{rb}}}}={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1-{\upsilon }_{\mathrm{r}}^2}{E_{\mathrm{r}}}}+{\displaystyle \frac{1-{\upsilon }_{\mathrm{b}}^2}{E_{\mathrm{b}}}}\right)$$

(2)

$${\overline{R}}_{\mathrm{i},\mathrm{o}}=k_{\mathrm{e}}{\displaystyle \frac{R_{\mathrm{r}}{R}_{\mathrm{i},\mathrm{o}}}{R_{\mathrm{r}}\pm R_{\mathrm{i},\mathrm{o}}}}$$

(3)

$$k_{\mathrm{e}}={\displaystyle \frac{1+2{\sin }^2{\alpha }_{\mathrm{h}}+4{\sin }^4{\alpha }_{\mathrm{h}}\sec \left(2{\alpha }_{\mathrm{h}}\right)}{\cos {\alpha }_{\mathrm{h}}+\sin {\alpha }_{\mathrm{h}}\tan \left(2{\alpha }_{\mathrm{h}}\right)}}$$

(4)

where δ_i,o represent contact deformations; R_r,i,o are radii of the roller and raceways at the *k*-th slice; and k_e is projection coefficient of R_r,i,o in the o_ci-y_ciz_ci/o_co-y_coz_co plane.

Deformations δ_i,o are derived from roller/ring positions [6]. For the inner raceway, the contact point e in the o_b-x_by_bz_b frame is

$$r_{\mathrm{i}}=T_{\mathrm{i}}^{\mathrm{ib}}\left[v+T_{\mathrm{i}}^{\mathrm{ir}\prime }\left[x_{\mathrm{r}},-R_{\mathrm{r}}\sin \vartheta ,R_{\mathrm{r}}\cos \vartheta \right]-u\right]$$

(5)

where $T_{\mathrm{i}}^{\mathrm{ib}}\left[0,\xi ,\zeta \right]$ denotes the conversion matrix from the o_i-x_iy_iz_i frame to the o_b-x_by_bz_b frame, ξ and ζ are shaft/cone deflection angles; $T_{\mathrm{i}}^{\mathrm{ir}}\left[\beta ,\theta ,\varphi \right]$ is conversion from the o_i-x_iy_iz_i frame to the o_r-x_ry_rz_r frame, β, θ and ϕ denote rotation, tilt, and skew angles of the *j*-th roller, respectively; and ϑ is computed under the constraint that r_i3 is maximized [6]. For calculations δ_i and δ_o, u denotes the displacement of the cone and cup in the o_i-x_iy_iz_i frame, respectively.

Then, the deformation δ_i at the *k*-th slice in the contact frame o_ci-x_ciy_ciz_ci is

$${\delta }_{\mathrm{i}}=\left[R_{\mathrm{i}}\left(r_{\mathrm{i}1}\right)-\sqrt{r_{\mathrm{i}2}^2+r_{\mathrm{i}3}^2}\right]\cos {\alpha }_{\mathrm{h}}$$

(6)

If the interference δ_i > 0, it means that the contact takes place. The derivation of δ_o is similar to that of δ_i. Then, the friction force at the *k*-th slice is

$$f_{\mathrm{i},\mathrm{o}}={\mu }_{\mathrm{bi},\mathrm{bo}}{q}_{\mathrm{i},\mathrm{o}}$$

(7)

The friction coefficient μ_b is governed by the lubrication state at the slice/raceway pair. Three states may occur: boundary (BL), mixed (ML), and full-film lubrication (FL). Under the BL state, μ_b is adapted from Kragelskii’s model [32]. For the FL state, μ_b is calculated with the experimental regression formula in Wang’s study [33]. Consequently, μ_b is defined as follows [12,32,33]:

$${\mu }_{\mathrm{b}}=\left\{\begin{array}{l}\left(-0.1+22.28\left|s_{\mathrm{r}}\right|\right)\exp \left(-181.46\left|s_{\mathrm{r}}\right|\right)+0.1 \mathrm{if} \lambda <{\lambda }_{\mathrm{bd}}\\ {\displaystyle \frac{{\mu }_{\mathrm{bd}}-{\mu }_{\mathrm{hd}}}{{\left({\lambda }_{\mathrm{bd}}-{\lambda }_{\mathrm{hd}}\right)}^6}}{\left(\lambda -{\lambda }_{\mathrm{hd}}\right)}^6+{\mu }_{\mathrm{hd}} \mathrm{if} {\lambda }_{\mathrm{bd}}\le \lambda <{\lambda }_{\mathrm{hd}}\\ \left(A+B\left|s_{\mathrm{r}}\right|\right)\exp \left(-C\left|s_{\mathrm{r}}\right|\right)+D \mathrm{if} {\lambda }_{\mathrm{hd}}\le \lambda \end{array}\right.$$

(8)

where s_r is the slide-to-roll ratio at the *k*-th slice; A, B, C, and D are functions of oil parameters, normal load, and velocity of the two contact bodies [33]; λ is film thickness ratio, λ = h_m/σ, with λ_bd = 0.01 and λ_hd = 1.50.

The central film thickness h_m at the *k*-th slice is [34]

$$h_{\mathrm{mi},\mathrm{mo}}=2.922{\displaystyle \frac{l_{\mathrm{e}}^{0.166}{\alpha }^{1.162}{\overline{R}}_{\mathrm{i},\mathrm{o}}^{1.474}{q}_{\mathrm{i},\mathrm{o}}^{0.166}{u}_{\mathrm{ei},\mathrm{eo}}^{0.692}}{{\overline{E}}_{\mathrm{rb}}^{0.056}{s}^{0.166}}}$$

(9)

where u_ei,eo are oil entrainment speeds at the inner/outer contacts.

Then, in the contact frame o_c-x_cy_cz_c, the interaction force at the *k*-th slice is

$$Q_{\mathrm{i},\mathrm{o}}^{jk}={\left[0,f_{\mathrm{i},\mathrm{o}}^{jk},q_{\mathrm{i},\mathrm{o}}^{jk}\right]}^T$$

(10)

where the directions of $f_{\mathrm{i},\mathrm{o}}^{\mathrm{jk}}$ depend on the relative speed between the roller surface and the raceway surface.

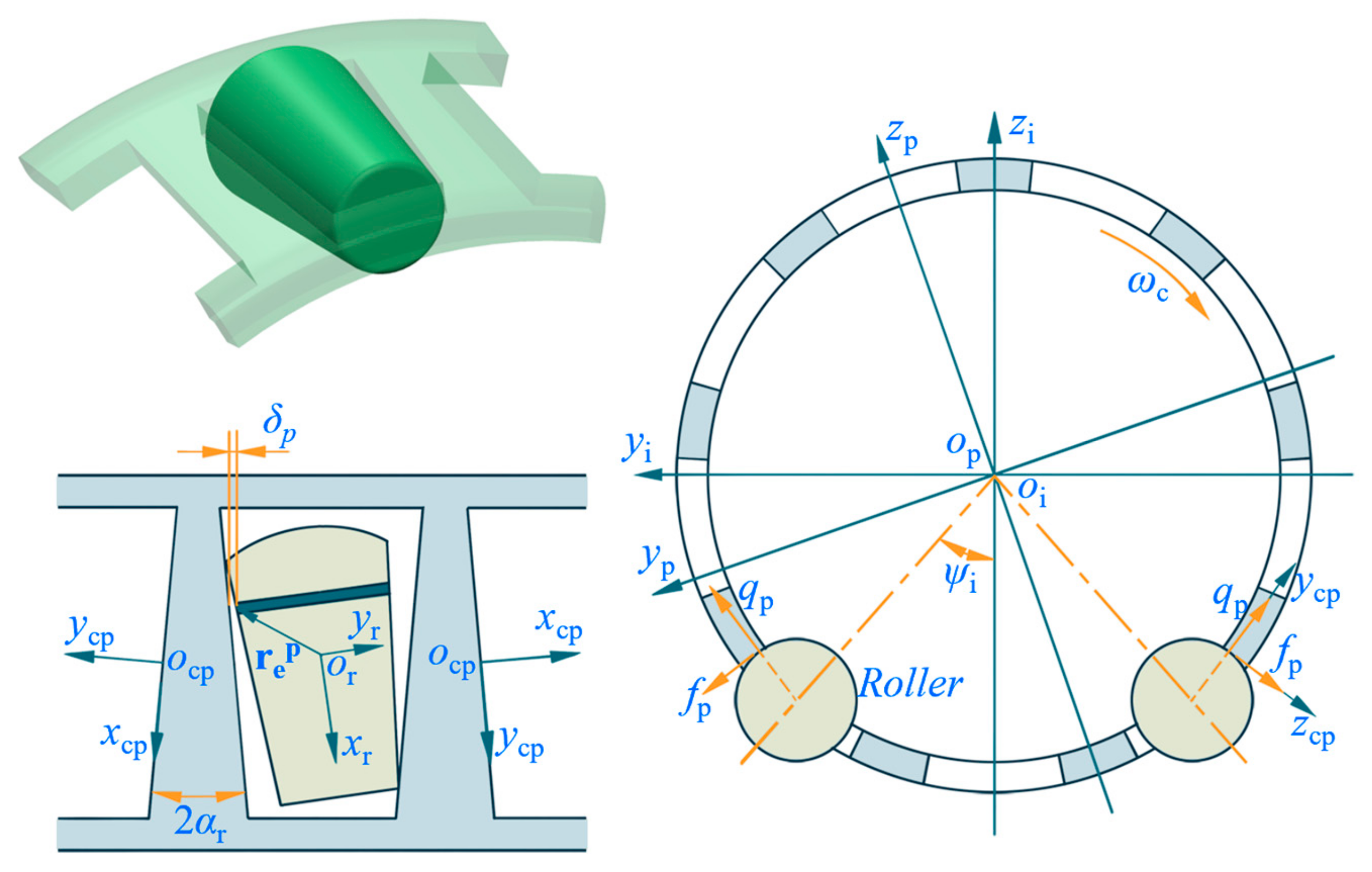
2.2. Flange/Roller-End Interaction

As shown in Figure 2, the conical flange and spherical roller-end forms a typical elliptical contact, so the normal force at this contact is [31]

$$q_{\mathrm{f}}={\displaystyle \frac{c_{\mathrm{v}}{\overline{E}}_{\mathrm{rb}}}{3}}{\left({\displaystyle \frac{2{\delta }_{\mathrm{f}}}{{\delta }_0{c}_{\mathrm{v}}}}\right)}^{3/2}$$

(11)

where δ_f is contact deformation [6]; c_v is the sum of principal curvatures; and δ₀ is a geometry-dependent constant.

For the derivation of δ_f, the spherical center of the roller-end in the o_b-x_by_bz_b frame is

$$r_{\mathrm{sb}}=T_{\mathrm{i}}^{\mathrm{ib}}\left[v+{T^{\prime }}_{\mathrm{ir}}{\left[x_{\mathrm{rs}},0,0\right]}^T-u\right]$$

(12)

where $x_{\mathrm{rs}}^j$ locates the spherical center on the o_r-x_r axis.

Then, the flange frame o_f-x_fy_fz_f is arranged at the point o_f (see Figure 1c), and its axes are parallel to the o_cf-x_cfy_cfz_cf frame. The spherical center in the o_f-x_fy_fz_f frame is

$$r_{\mathrm{sf}}=T_{\mathrm{f}}^{\mathrm{af}}\left(T_{\mathrm{f}}^{\mathrm{ba}}{r}_{\mathrm{sb}}-r_{\mathrm{fa}}\right)$$

(13)

where $T_{\mathrm{f}}^{\mathrm{ba}}\left[\psi ,0,0\right]$ is a conversion from the cone frame to the azimuth frame, with ψ = tan⁻¹ (r_sb2/r_sb3); r_fa stands for position of o_f in the azimuth frame; and $T_{\mathrm{f}}^{\mathrm{af}}\left[0,{\alpha }_{\mathrm{f}},0\right]$ is a conversion between the azimuth and flange frames.

Then, the deformation δ_f of the *j*-th roller with respect to the flange is

$${\delta }_{\mathrm{f}}=R_{\mathrm{s}}-r_{\mathrm{fs}1}$$

(14)

Tangential friction at the flange also depends on the lubrication state, and the friction coefficient μ_f under ML and BL states is the same as that at the roller/raceway pair. Since the slide-to-roll ratio in Wang’s experiments reached only 0.20 [33], to address flange/roller-end traction at a higher ratio (s_r is about 0.25~0.50), the viscous shear force is addressed, as it significantly exceeds the rolling resistance force [12]. The traction force f_f is

$$f_{\mathrm{f}}={\displaystyle {\int }_{-a}^{+a}{\displaystyle {\int }_{-b}^{+b}\tau \left(x,y\right)\mathrm{d}x\mathrm{d}y}}$$

(15)

$$\tau \left(x,y\right)=\eta \left(x,y\right){\displaystyle \frac{u_{\mathrm{flange}}-u_{\mathrm{end}}}{h_{\mathrm{c}}}}$$

(16)

$$\eta \left(x,y\right)={\eta }_0\exp \left\{\left(\ln {\eta }_0+9.67\right)\left[-1+{\left(1+5.1\times {10}^{-9}{p}_{\mathrm{f}}\left(x,y\right)\right)}^{z_0}\right]\right\}$$

(17)

where u_flange and u_end are surface velocities of two contact bodies; p_f is film pressure, p_f = p_h(1 − x²/a² − y²/b²)^1/2; z₀ is pressure–viscosity index, typically 0 ≤ z₀ ≤ 0.8 [35], in this paper z₀ = 0.4.

The central film thickness h_c at the flange/roller-end contact is [36]

$$h_{\mathrm{c}}=4.310{\displaystyle \frac{{\alpha }^{1.170}{\overline{R}}_{\mathrm{f}}^{0.466}{u}_{\mathrm{ef}}^{0.680}}{{\overline{E}}_{\mathrm{rb}}^{0.117}{q}_{\mathrm{f}}^{0.073}}}\left(1-e^{-1.280{\chi }_j}\right)$$

(18)

where u_ef and ${\overline{R}}_{\mathrm{f}}$ are oil entrainment speed and effective radius in the o_cf-y_cf direction.

Accordingly, in the contact frame o_cf-x_cfy_cfz_cf, the interaction force at the flange/roller-end contact is

$$Q_{\mathrm{f}}^j={\left[f_{\mathrm{fx}}^j,f_{\mathrm{fy}}^j,q_{\mathrm{f}}^j\right]}^T$$

(19)

where the directions of f_fx and f_fy are determined by the relative surface speeds between the roller-end and the flange in the o_cf-x_cf and o_cf-y_cf directions.

2.3. Roller/Cage Interaction

Due to differences in displacement and velocity, the master–slave relationship of the cage and roller evolves dynamically. In Figure 3, the contact frame o_cp-x_cpy_cpz_cp is located at the pocket wall that is in contact with the roller. Define Δ_p as the critical film thickness for contact state transition, and Δ_p is the composite roughness of contact surfaces. When pocket clearance δ_p at the *k*-th roller slice is greater than Δ_p, i.e., δ_p ≥ Δ_p, the slice/pocket is deemed in the hydrodynamic contact. The normal force q_p generated by the film pressure and the traction force f_p produced by the film shearing are [37]

$$q_{\mathrm{p}}=q_{\mathrm{pe}}=2.44{\displaystyle \frac{l_{\mathrm{e}}{\eta }_0\left|u_{\mathrm{r}}+u_{\mathrm{p}}\right|R_{\mathrm{r}}}{{\delta }_{\mathrm{p}}s}}$$

(20)

$$f_{\mathrm{p}}=4.58{\displaystyle \frac{l_{\mathrm{e}}{\eta }_0\left|u_{\mathrm{r}}+u_{\mathrm{p}}\right|R_{\mathrm{r}}^{1/2}}{{\delta }_{\mathrm{p}}s}}$$

(21)

where u_r and u_p are surface speeds of the pocket and roller in the o_cp-x_cpy_cpz_cp frame, respectively.

When δ_p < Δ_p, the *k*-th roller slice and the cage pocket are in Hertzian contact. The interaction forces are

$$q_{\mathrm{p}}=q_{\mathrm{pe}}+\left({\delta }_{\mathrm{p}}-{\Delta }_{\mathrm{p}}\right)k_{\mathrm{ph}}+{\dot{\delta }}_{\mathrm{p}}{c}_{\mathrm{ph}}$$

(22)

$$f_{\mathrm{p}}={\mu }_{\mathrm{p}}{q}_{\mathrm{p}}$$

(23)

where k_ph is Hertzian linearized contact stiffness [38]; c_ph is viscous damping from Herbert’s model [39]; and μ_p is the boundary friction coefficient [32]. The k_ph and c_ph are as follows:

$$k_{\mathrm{ph}}={\displaystyle \frac{\pi l_{\mathrm{e}}}{2s}}{\left({\displaystyle \frac{1-{\upsilon }_{\mathrm{r}}^2}{E_{\mathrm{r}}}}+{\displaystyle \frac{1-{\upsilon }_{\mathrm{p}}^2}{E_{\mathrm{p}}}}\right)}^{-1}$$

(24)

$$c_{\mathrm{ph}}={\displaystyle \frac{2\sqrt{m^{\ast }{k}_{\mathrm{ph}}}\ln \kappa }{\sqrt{{\left(2\ln \kappa \right)}^2+\pi }}}, m^{\ast }={\left({\displaystyle \frac{1}{m_{\mathrm{r}}}}+{\displaystyle \frac{1}{m_{\mathrm{p}}}}\right)}^{-1},\kappa =1-0.026{\dot{\delta }}_{\mathrm{p}}^{1/3}$$

(25)

Then, in the contact frame o_cp-x_cpy_cpz_cp, the interaction force of the *k*-th roller slice with the pocket is

$$Q_{\mathrm{p}}^{jk}={\left[0,f_{\mathrm{p}}^{jk},q_{\mathrm{p}}^{jk}\right]}^T$$

(26)

2.4. Cage/Guiding-Ring Interaction

The cage/guiding-ring interaction (centering and guiding surfaces) follows the same treatment as the roller/cage assembly. When clearance δ_g < Δ_g, Hertzian contact dominates and can be modeled using Equations (22) and (23). For the case of δ_g ≥ Δ_g, hydrodynamic action can be approximated as a short journal bearing. The resulting hydrodynamic force q_g and traction force f_g are [37]

$$q_{\mathrm{g}}={\displaystyle \frac{{\eta }_0{u}_{\mathrm{eg}}{b}_{\mathrm{c}}^3\epsilon }{c^2\left(1-{\epsilon }^2\right)}}\sqrt{{\displaystyle \frac{16{\epsilon }^2+{\pi }^2\left(1-{\epsilon }^2\right)}{16{\left(1-{\epsilon }^2\right)}^2}}}$$

(27)

$$f_{\mathrm{g}}={\displaystyle \frac{2\pi {\eta }_0{u}_{\mathrm{eg}}{R}_{\mathrm{c}}{b}_{\mathrm{c}}}{c}}{\displaystyle \frac{1}{{\left(1-{\epsilon }^2\right)}^{1/2}}}$$

(28)

Then, the interaction force at the cage/ring interface is

$$Q_{\mathrm{g}}={\left[0,f_{\mathrm{g}},q_{\mathrm{g}}\right]}^T$$

(29)

2.5. Differential Equations of TRB Dynamics

The motion of the tapered roller contains six degrees of freedom, and its translational motion is described in the cylindrical frame o_i-x_ir_iθ_i. Considering centrifugal and gyroscopic effects, the differential equations for the *j*-th roller are

$$\begin{array}{c}{\left[m_{\mathrm{r}}{\ddot{x}}_{\mathrm{r}}^j,m_{\mathrm{r}}{r}_{\mathrm{r}}^j{\ddot{\theta }}_{\mathrm{r}}^j+2m_{\mathrm{r}}{r}_{\mathrm{r}}^j{\dot{\theta }}_{\mathrm{r}}^j,m_{\mathrm{r}}{\ddot{r}}_{\mathrm{r}}^j-m_{\mathrm{r}}{\dot{\theta }}_{\mathrm{r}}^{j2}\right]}^T\\ ={\displaystyle \sum _{k=1}^s{T}_{\mathrm{i}}^{\mathrm{ci}}{Q}_{\mathrm{i}}^{jk}}+{\displaystyle \sum _{k=1}^s{T}_{\mathrm{o}}^{\mathrm{ci}}{Q}_{\mathrm{o}}^{jk}}+{\displaystyle \sum _{k=1}^s{T}_{\mathrm{p}}^{\mathrm{ci}}{Q}_{\mathrm{p}}^{jk}}+T_{\mathrm{f}}^{\mathrm{ci}}{Q}_{\mathrm{f}}^{jk}\end{array}$$

(30)

$$\begin{array}{c}{\displaystyle \frac{\mathrm{d}{H}_r^j}{\mathrm{d}t}}+{\dot{\omega }}_{\mathrm{r}}^j\times H_{\mathrm{r}}^j={\displaystyle \sum _{k=1}^s{r}_{\mathrm{i}}^{jk}\times T_{\mathrm{i}}^{\mathrm{cr}}{Q}_{\mathrm{i}}^{jk}}+{\displaystyle \sum _{k=1}^s{r}_{\mathrm{o}}^{jk}\times T_{\mathrm{o}}^{\mathrm{cr}}{Q}_{\mathrm{o}}^{jk}}\\ +{\displaystyle \sum _{k=1}^s{r}_{\mathrm{p}}^{jk}\times T_{\mathrm{p}}^{\mathrm{cr}}{Q}_{\mathrm{p}}^{jk}}+r_{\mathrm{f}}^j\times T_{\mathrm{f}}^{\mathrm{cr}}{Q}_{\mathrm{f}}^j+{\left[0,M_{\mathrm{gr}}^j,0\right]}^T\end{array}$$

(31)

where [x_r, r_r, θ_r]^T is roller displacement; H_r is roller angular momentum; ω_r is roller angular velocity; $T_{\mathrm{i},\mathrm{o},\mathrm{p},\mathrm{f}}^{\mathrm{ci}}$ are conversion matrices from contact frames o_c-x_cy_cz_c at the rings, cup, and flange to the o_i-x_ir_iθ_i frame; $T_{\mathrm{i},\mathrm{o},\mathrm{p},\mathrm{f}}^{\mathrm{cr}}$ are conversions from the frames o_c-x_cy_cz_c to the roller frame o_r-x_ry_rz_r; and $r_{\mathrm{i},\mathrm{o},\mathrm{p},\mathrm{f}}$ are locations of contact points e in o_r-x_ry_rz_r.

Neglecting overturning in the radial plane o_i-y_iz_i, the cage consists of four degrees of freedom. The differential equations for the cage are

$${\left[m_{\mathrm{p}}{\ddot{x}}_{\mathrm{p}},m_{\mathrm{p}}{\ddot{y}}_{\mathrm{p}},m_{\mathrm{p}}{\ddot{z}}_{\mathrm{p}}\right]}^T={\displaystyle \sum _{j=1}^n{\displaystyle \sum _{k=1}^s{T}_{\mathrm{p}}^{\mathrm{ci}}{Q}_{\mathrm{p}}^{jk}}}+T_{\mathrm{g}}^{\mathrm{ci}}{Q}_{\mathrm{g}}$$

(32)

$${\displaystyle \frac{\mathrm{d}{H}_{\mathrm{p}}}{\mathrm{d}t}}+{\dot{\omega }}_p\times H_{\mathrm{p}}={\displaystyle \sum _{j=1}^n{\displaystyle \sum _{k=1}^s{r}_{\mathrm{ep}}^{jk}\times T_{\mathrm{p}}^{\mathrm{cp}}{Q}_{\mathrm{p}}^{jk}}}+r_{\mathrm{eg}}\times T_{\mathrm{g}}^{\mathrm{cp}}{Q}_{\mathrm{g}}$$

(33)

where [x_p, y_p, z_p]^T is the cage displacement; H_p is cage angular momentum; ω_p is angular velocity; $T_{\mathrm{p},\mathrm{g}}^{\mathrm{ci}}$ are conversion matrices from contact frames o_c-x_cy_cz_c at the cage pocket and the guiding ring to o_i-x_iy_iz_i; $T_{\mathrm{p},\mathrm{g}}^{\mathrm{cp}}$ are conversion matrices from the frames o_c-x_cy_cz_c to the cage frame o_p-x_py_pz_p; and r_ep,eg denote locations of contact points e in o_p-x_py_pz_p.

The cone’s differential equations are similar to those of the cage, and it consists of three translational freedoms in the o_i-x_iy_iz_i frame. Additionally, the shaft deflection is equivalent to a constant angular displacement constraint to the cone.

3. Numerical Method

The parameters of the tapered roller bearing and oil lubricant used for the present study are detailed in

Table 1. Parameters of the TRB and the oil lubricant.

Parameters	Value
Bearing bore diameter [mm]	130.00
Bearing outside diameter [mm]	230.00
Bearing width [mm]	70.00
Number of rollers	17
Roller length [mm]	42.06
Roller average diameter [mm]	21.37
Roller half-cone angle [deg]	5.00
Radius of roller spherical end [mm]	153.95
Pitch diameter of roller set [mm]	177.91
Outer contact angle [deg]	15.00
Inner contact angle [deg]	5.00
Flange contact angle [deg]	83.00
Young’s modulus of roller and rings [GPa]	201.00
Poisson’s ratio of roller and rings	0.28
Young’s modulus of cage [GPa]	8.30
Poisson’s ratio of cage	0.30
Lubricant brand	4109
Dynamic viscosity [Pa∙s]	0.0330
Pressure–viscosity coefficient [Pa−1]	1.28 × 10−8

. The bearing operates at an ambient temperature of 25 °C. Differential equations (30~33) of the TRB dynamics were numerically solved with the Gill equation and the Miline–Hamming predictor–corrector method. For the TRB initial state, supposing tapered rollers are evenly distributed and symmetrically distributed about the o_i-z_i axis, the cage is also in alignment state.

4. Results and Discussions

The behavior of the tapered roller can be regarded as a function of factors such as the structure, load-carrying, and lubrication of the TRB. Tilt and skew phenomena of the roller in the case of aligned shaft or cone have been emphasized in quantities of literatures, and effects of operating conditions and structural parameters on it have been revealed [6,7,8,10,11,12,13,14,25,26,27,28,29,30]. Nevertheless, when the TRB is subjected to deflected shaft or cone, the roller’s behavior would be more complicated, as well as effects of operating conditions.

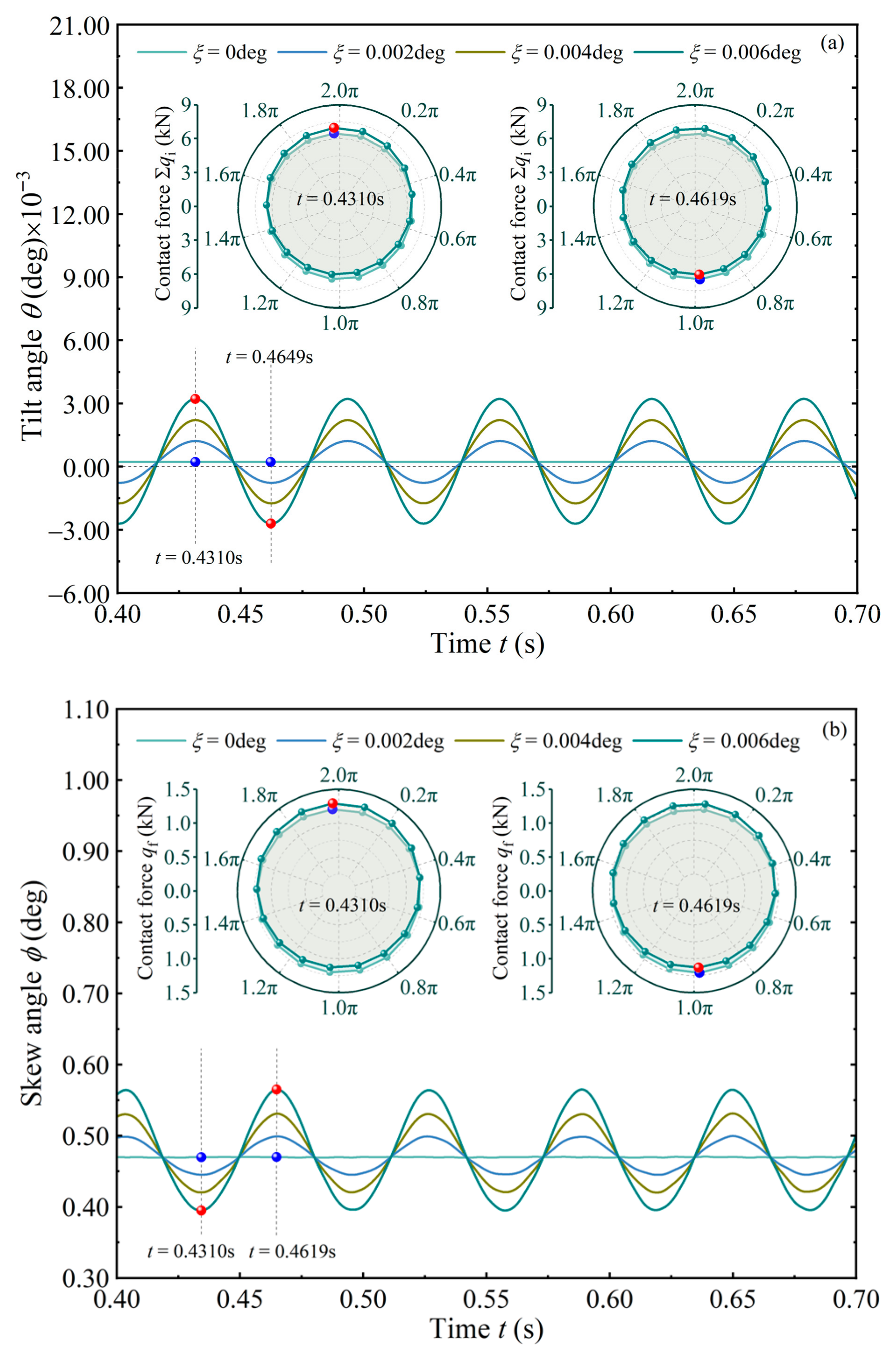
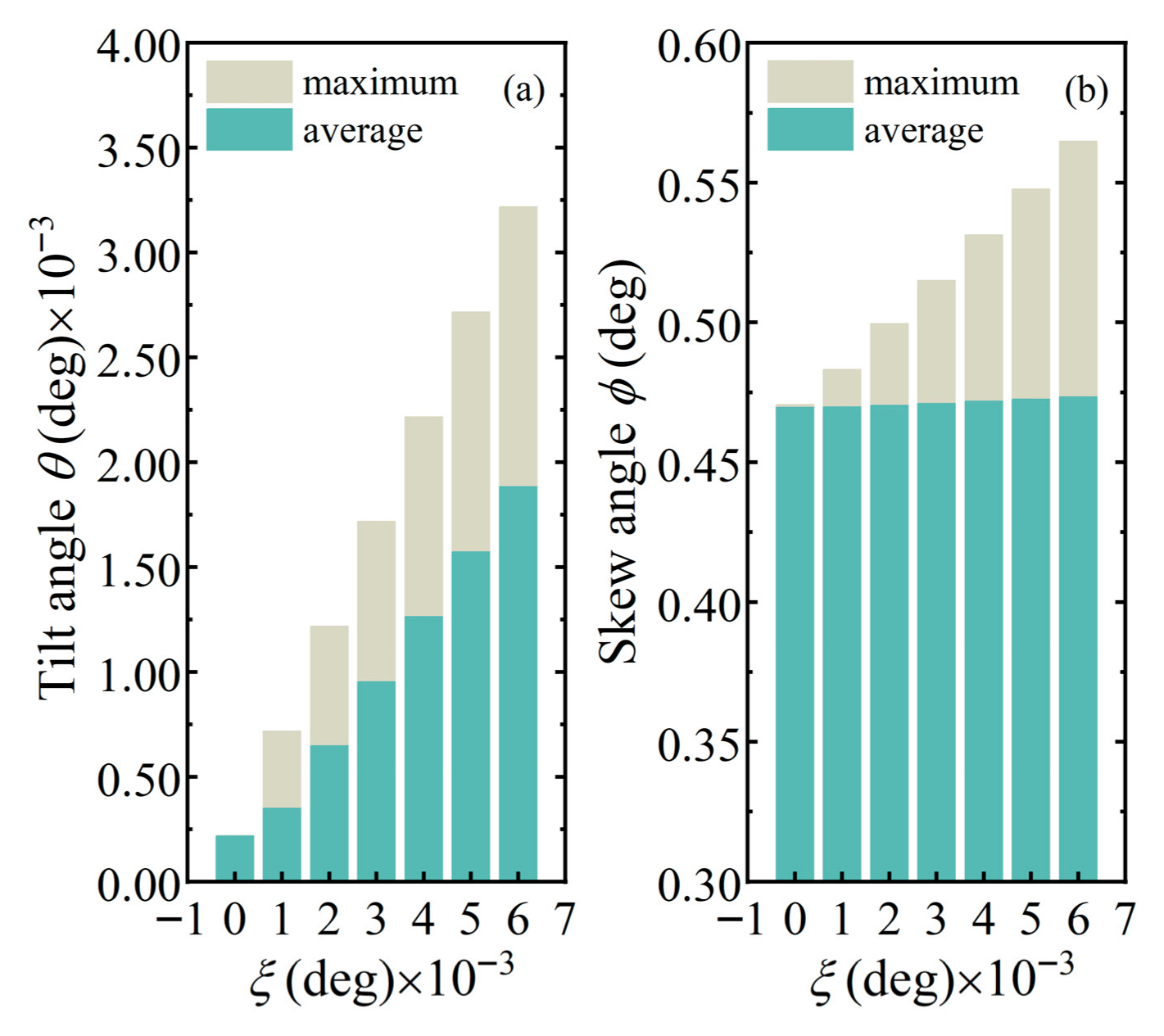
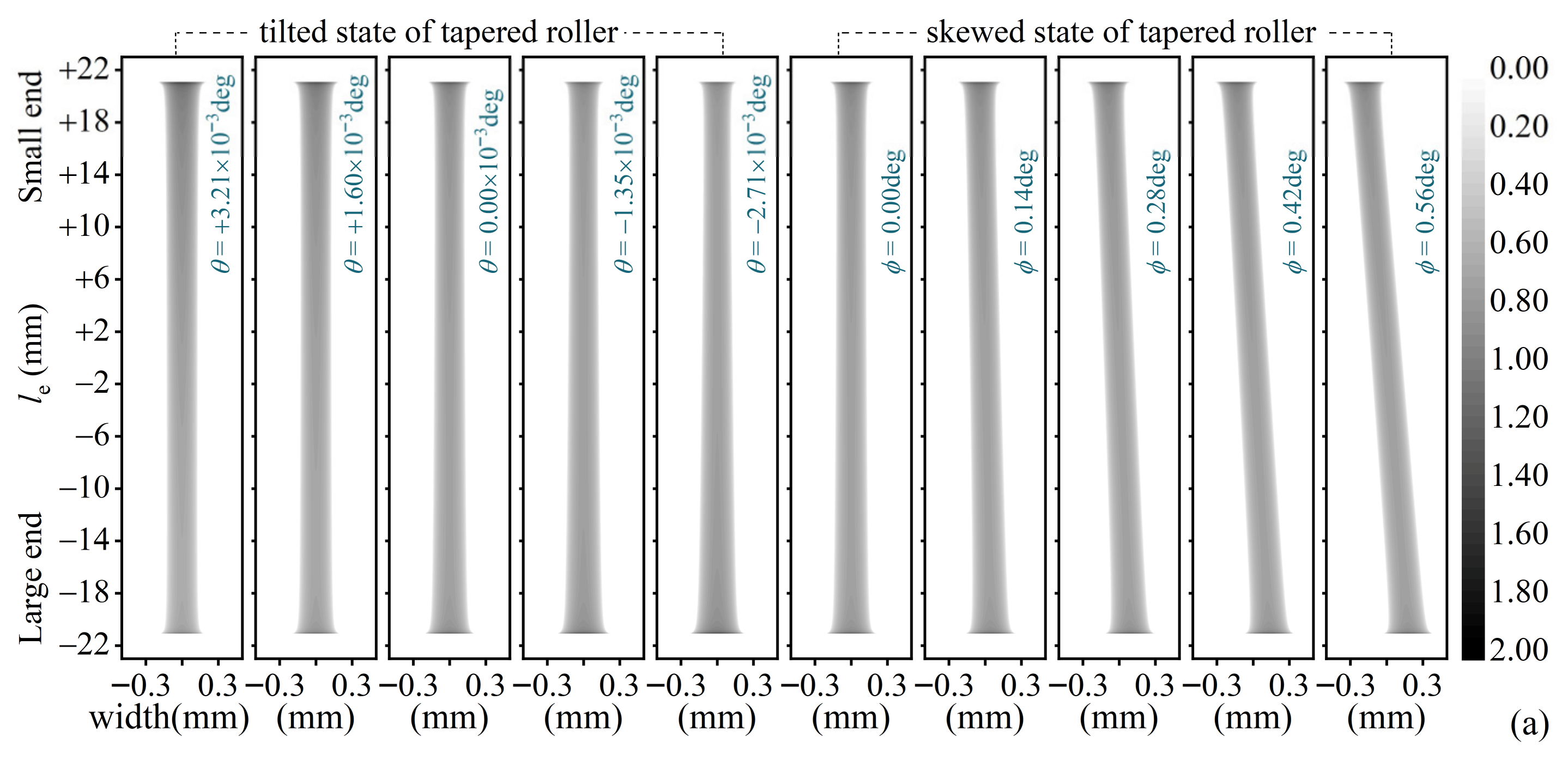
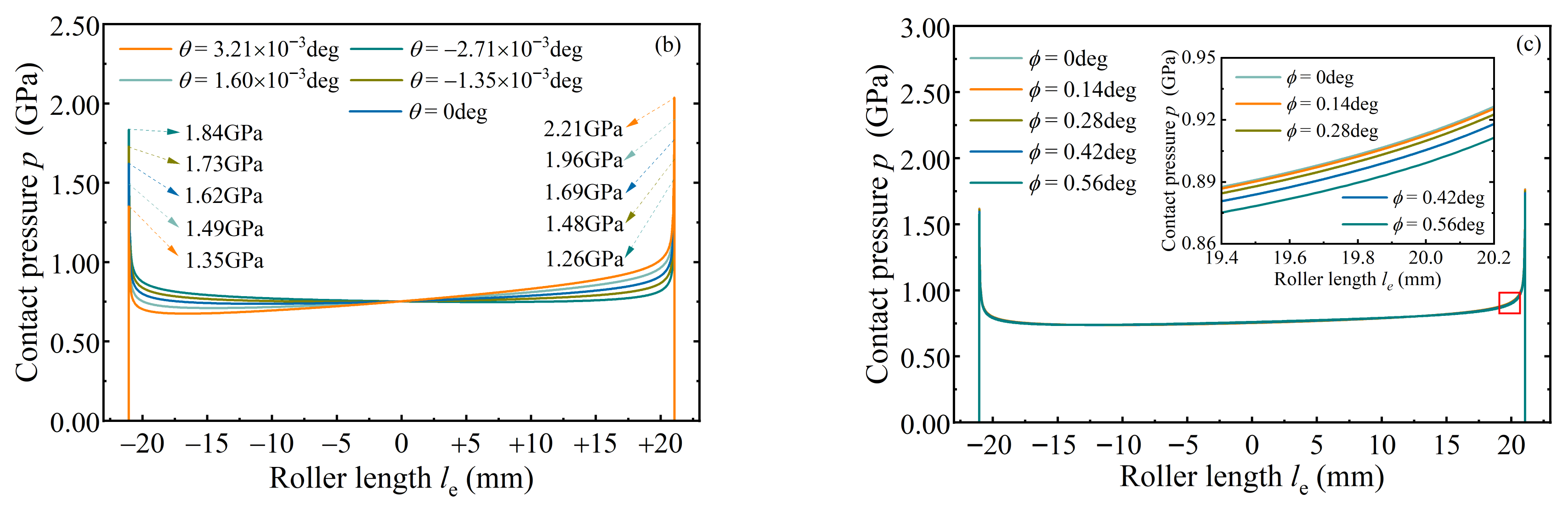
4.1. Effects of Shaft Deflection on Roller Behavior

Generally, shaft deflection is undesirable for the bearings that do not have a spherical capacity, but the problem may be unavoidable for certain machines. Therefore, it is necessary to clarify negative effects of the deflected shaft on the roller’s behavior, which is conducive to improve service reliability and safety of the TRB. Figure 4 shows roller angular motions when axial force F_a = 30 kN and bearing speed ω_i = 3500 rpm. To avoid the complexity of the issue, the deflection angle is specified directly here. The true deflection angle can be determined by establishing a shaft/bearing elastodynamic model [3].

In Figure 4, if the shaft is in an aligned state (ξ = 0), the roller is already tilted at a negative state (θ < 0) and skewed at a positive state (ϕ > 0). This is associated with the uneven pressure distribution when it is in contact with the raceway and the flange [9]. Moreover, the angular vibrations are consistent with results in [8,14]. Once the shaft is deflected (ξ ≠ 0, deflected direction is based on the right-hand rule), the tapered roller presents a periodic vibration, and the period is about one revolution time of the roller. In addition, tilt and skew vibrations resemble two sine waves with opposite phases. Amplitude of the tilt angle θ is far greater than that when ξ = 0, and it is positively correlated with the deflected angle ξ. Roller skew magnitude is affected in a similar way. No matter how severe the shaft is deflected, the roller is always in a negative skewed state. Polar diagrams in Figure 4 depict distribution of contact forces (Σq_i and q_f) at the inner raceway and the flange when t = 0.4310 s and t = 0.4619 s. The shaft deflection causes uneven force distribution inside the TRB. The force distribution at the two times is basically similar, revealing that roller misalignment can be approximately predicted by the quasi-dynamic method [6,7].

Figure 5 illustrates contributions of the cup and cone to roller misalignment. When shaft deflection is absent (Figure 5a,b), moments acting on the roller are relatively stable, with tilt moment typically 2~3 orders of magnitude greater than skew moment. It is evident that the sum of moments acting on the roller at any moment does not equal zero, indicating that the forces exerted by the flange and raceways form a triangular set [9]. Based on moment magnitudes, the outer raceway exerts dominant influence on the roller tilt, followed by the inner raceway and flange; meanwhile, the flange has the greatest impact on the roller skew, followed by the outer and inner raceways. If the shaft is deflected (Figure 5c,d), moments exhibit a significant periodic fluctuation with increased amplitudes. The variation of N_ft is relatively gentle and always drives the roller toward negative skew. However, the flange’s contribution to the roller tilt is relatively weak compared to both raceways. The directions of N_it and N_ot are almost opposite (with curve intersection near 0). In Section 2.2, the flange/roller-end is approximated as an elliptical contact. It can be inferred that the shaft deflection may have a different effect on ball bearings than on roller bearings. Regarding skew moment, two raceways induce the roller skewed in both positive and negative directions, but contribute primarily to positive skew most of the time. This is different from the ξ = 0 case. As evident in Figure 5b,d, the flange predominantly hinders the roller skew to some extent.

Figure 6 presents statistics of the roller’s angular displacement. As the shaft deflects from 0 deg to 0.006 deg, the average tilt angle θ_avg is about 2.20 × 10⁻⁴, 3.51 × 10⁻⁴, 6.48 × 10⁻⁴, 9.55 × 10⁻⁴, 1.26 × 10⁻³, 1.57 × 10⁻³, and 1.88 × 10⁻³ deg, and the maximum tilt angle θ_max is about 2.21 × 10⁻⁴, 7.17 × 10⁻⁴, 1.22 × 10⁻³, 1.72 × 10⁻³, 2.22 × 10⁻³, 2.72 × 10⁻³, and 3.22 × 10⁻³ deg. It shows that θ_max has exceeded the shaft deflection angle ξ. In [40], the TRB’s bore diameter is 30 mm and ξ can reach 5 mrad (about 0.29 deg). In this analysis, they are 130 mm and 0.006 deg. It can be speculated that if the TRB had a large bore diameter, the allowable angle of shaft deflection should be smaller. In the case of ξ = 0, the average ϕ_avg and maximum ϕ_max of the skew angle are about 0.47 deg. Both are comparable to existing works [8,25,26,27], in which the skew angle ϕ is in the ranges of 0.20~0.40 deg [8], 0.15~0.60 deg [25,26], and 0.07~0.42 deg [27]. In addition, the effect of misaligned shaft on ϕ_avg is mild, while on ϕ_max, it is apparent. If angular misalignment of the shaft or cone is relatively large, such as it is in [14], it can reach 0.50 deg, and the skew is also very prominent.

If the tapered roller is in an angular misalignment, the contact with raceways will deviate from expected state. Taking the inner raceway contact as object, referring to maximum load (Σq_i)_max and angular displacements in Figure 5, the dry contact under tilt and skew states was calculated with the conjugate gradient method (CGM). Among these, the tilt and skew angles serve as displacement constraints for the roller, a treatment analogous to that employed by John et al. [15]. Axis legends in Figure 7 for each cloud plot are the same. In Figure 7a of pressure contours, with the roller tilted from negative to positive, the maximum contact width changes from small end to large end of the roller. The contact area Ω_p > 0 skews as the roller skews. In Figure 7b,c, the tilt effect on pressure profile along roller length is remarkable, and it exacerbates the stress edge effect at the roller-end. Because the roller profile crowning is ignored, the edge effect exists in the alignment state (θ = 0). Compared with the tilt, the skew has a slight influence on the pressure profile, which is due to the relatively large radius ratio (it is about 7.37) of the inner raceway to roller. So, although the tilt is slight, its impact on the roller/raceway pair is more profound. Under lubricated conditions, the roller’s angular displacement also induces a change in lubricant entrainment speed, thereby affecting film-forming state inside the bearing [23,24]. Meanwhile, the skew motion is a potential cause of heat generation in roller bearings [27].

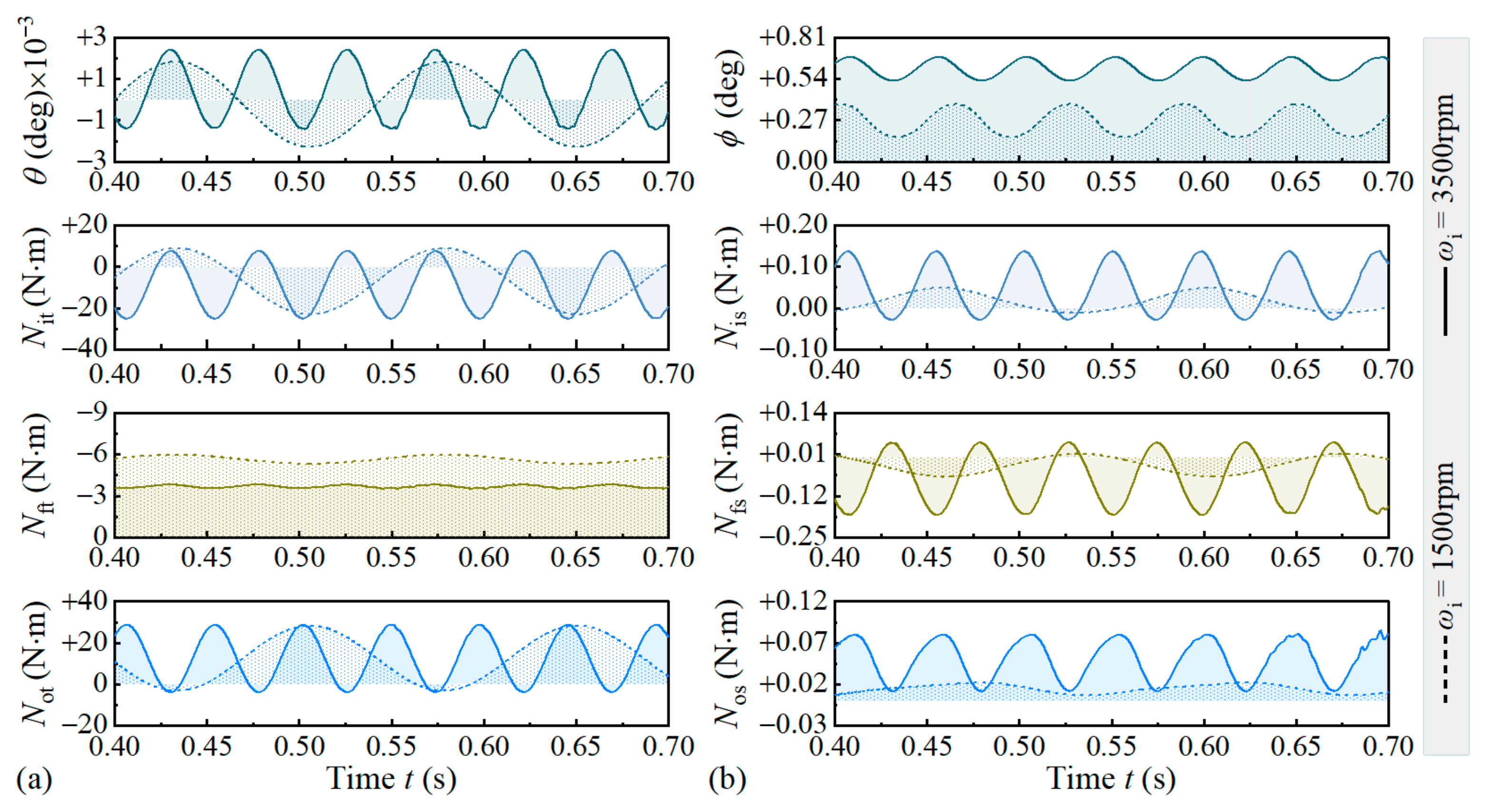
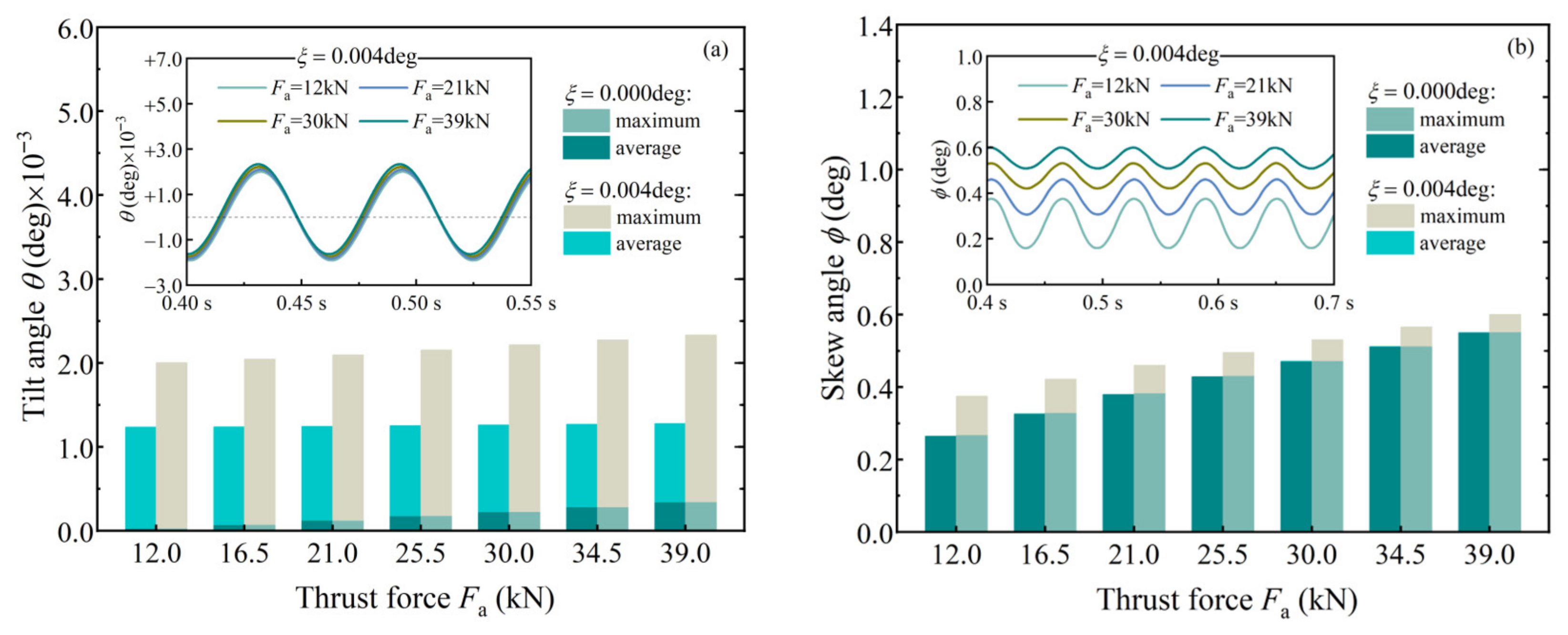
4.2. Effects of Operating Parameters on Roller Behavior Under Shaft Deflection

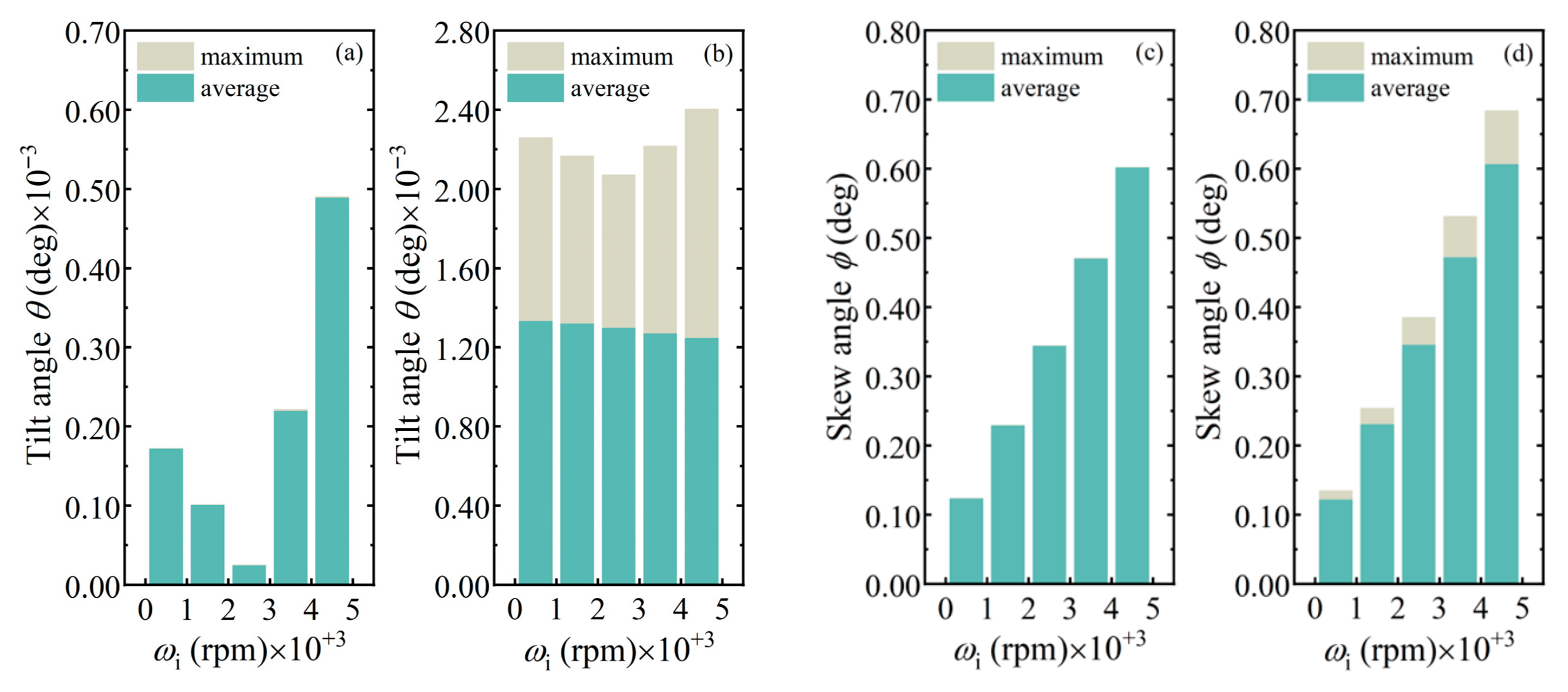
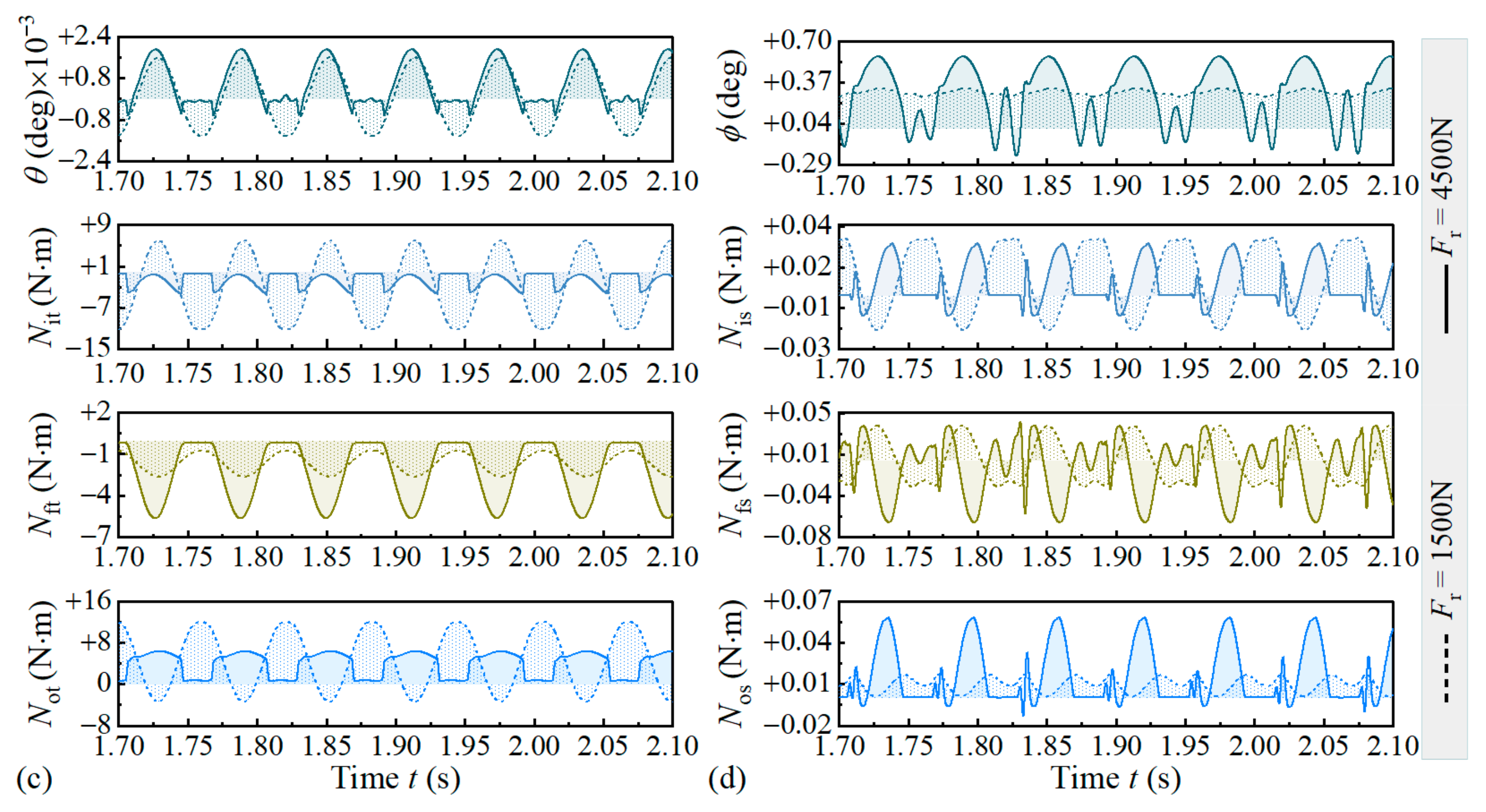
4.2.1. At Different Bearing Speeds

Generally, the TRB is implemented in a certain speed range within the limiting speed. According to the characterization of tangential friction forces, bearing speed ω_i is the main factor that induces the roller angular misalignment. The tilt and skew angles can be regarded as roller attitude angles. Figure 8 reveals the attitude angles as a function of operating time at different bearing speeds.

In Figure 8a, as bearing speed ω_i rises, the tilt vibration frequency is augmented. This means that in the same time, the number of times the roller is in a severely tilted state is increased. Meanwhile, the accelerated ω_i accentuates the roller’s gyroscopic motion, resulting in a decrease in the negative tilt amplitude and an increase in the positive tilt amplitude. In Figure 8b, bearing speed ω_i has a significant influence on the roller skew. Similarly, frequency and amplitude of the skew vibration are raised in general.

Figure 9 demonstrates that as bearing speed ω_i rises, moment fluctuations and angular vibrations always maintain identical cycles. In Figure 9a, the inner raceway keeps the roller tilted in the negative direction, while N_ot and N_ft let the roller tilt in both directions. Furthermore, fluctuation of N_it remains slight across all speeds. It is well known that centrifugal force affects the roller/raceway interaction, but its influence on tilt moment is not significant. In Figure 9b, as bearing speed ω_i rises, the skew moment exerted on the roller generally increases. Here, N_is consistently aligns with the skew direction, while the flange moment N_fs prevents the roller from positive skew most of the time. Centrifugal force causes the inner raceway to be ‘relaxed’, resulting in a reduction in contact force. This reduction, however, increases slide-to-roll ratio s_r, and ultimately elevates frictional force/moment. In Figure 5 and Figure 9, it can be found that although the flange/roller-end is in sliding–rolling contact, it appears to have a corrective effect on the roller misalignment, and, in particular, on the roller skew.

Figure 10a,b displays variations of maximum θ_max and average θ_avg with bearing speed ω_i. For ξ = 0, the two are very close, both first decreasing and then increasing as ω_i rises. In fact, as a result of the gyroscopic effect, the roller tilt transitions from negative at ω_i = 500 rpm to positive at ω_i = 4500 rpm. For ξ = 0.004 deg, θ_max follows the same variation trend, but θ_avg shows a decreasing trend. θ_max is one order of magnitude higher than when ξ = 0, indicating that the shaft deflection leaves the roller in a serious misalignment state. In Figure 10c,d, increasing trends of the roller skew with bearing speed ω_i are basically the same, and skew amplitude is not much different under the ξ = 0 and ξ ≠ 0 cases. As ω_i varies from 500 rpm to 4500 rpm, ϕ_max is about 0.12, 0.23, 0.34, 0.47, and 0.60 deg subjected to aligned shaft, and it is about 0.13, 0.25, 0.39, 0.53, and 0.68 deg subjected to misaligned shaft.

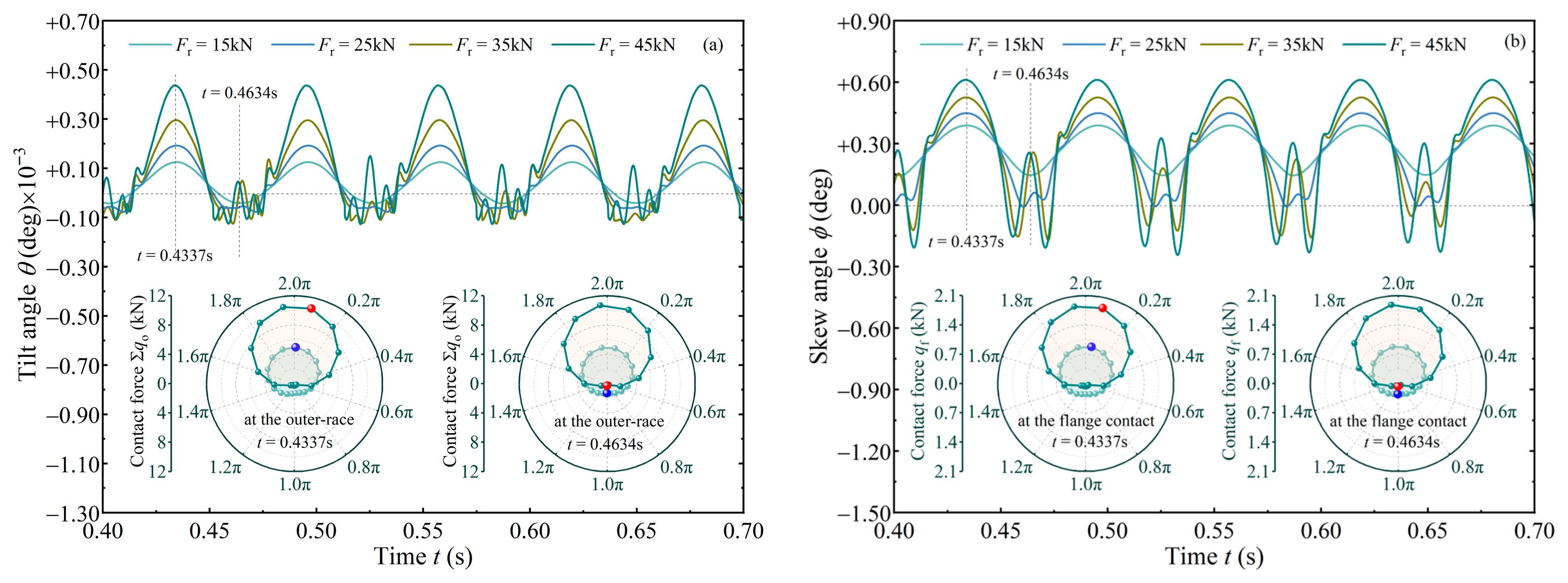
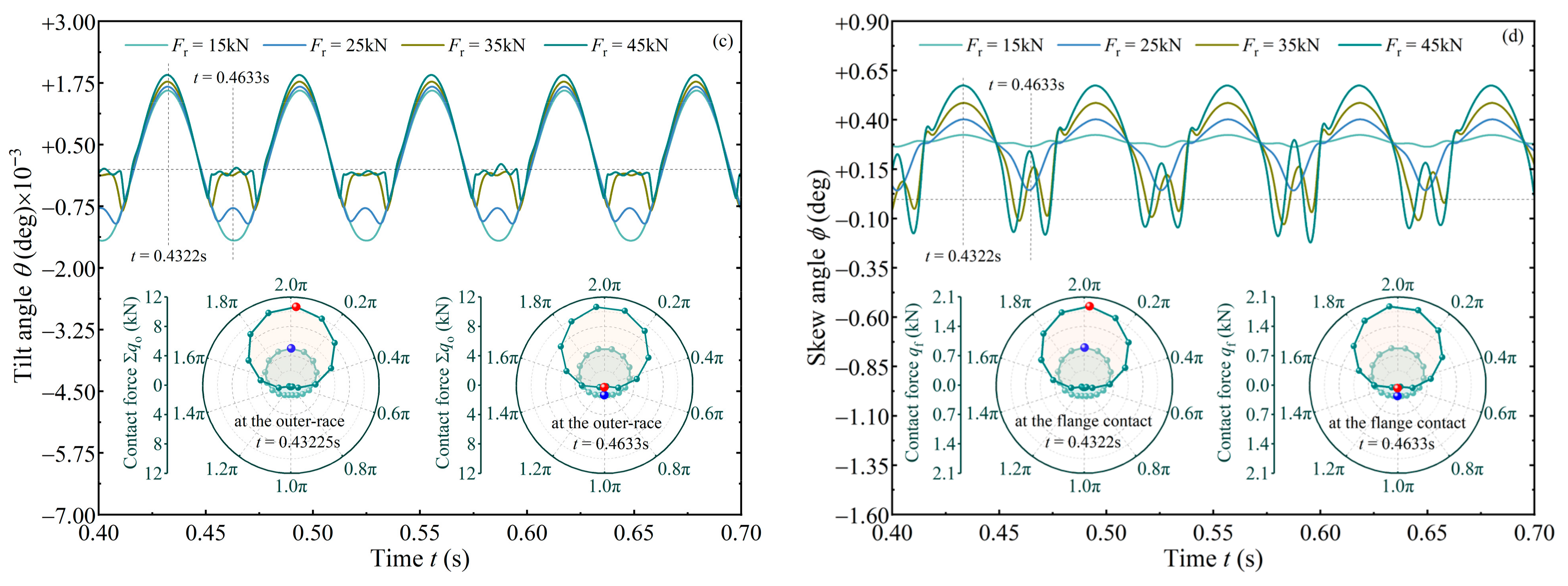
4.2.2. Under Different Force Loading Conditions

The angular misalignment of tapered roller was analyzed in two loading conditions. Namely, the TRB is loaded by a pure axial force F_a, and is loaded by a radial force F_r (in the o_i-z_i axis direction) but preloaded by a constant axial displacement δ_a.

Since axial force F_a will contribute to skew and tilt moments, its increase would inevitably deteriorate the roller’s alignment state. Figure 11 exhibits the deterioration when the TRB carries pure axial force F_a and the shaft is deflected at 0 deg and 0.004 deg. Whether the shaft is deflected or not, tilt fluctuation under different axial forces F_a is consistent. Tilt amplitude increases gradually by a small amount. For the skew motion, the effect of F_a is remarkable, and the amplitude increase is large. For ξ = 0, with F_a varying from 12 kN to 39 kN, θ_max is raised from 2.10 × 10⁻⁵ deg to 3.37 × 10⁻⁴ deg and ϕ_max is raised from 0.27 deg to 0.55 deg. For ξ = 0.004 deg, θ_max and ϕ_max are in the ranges of 2.00 × 10⁻³~2.33 × 10⁻³ deg and 0.38~0.60 deg, respectively. The average ϕ_avg when ξ = 0.004 deg is quite close to ϕ_avg or ϕ_max when ξ = 0. Under the shaft-deflected case, the change of roller skew with axial force F_a is similar to that in [8,14].

Figure 12 displays moments under different axial forces (ξ = 0.004 deg). In Figure 12a, although F_a minimally affects the roller tilt, its perturbation on the tilt moment is pronounced. The moment amplitude increases variably across positions, and N_ot shifts toward a positive value. Differing sensitivities of the tilt moment and tilt angle to F_a may relate to the structural characteristics of TRBs. In Figure 12b, driven by the axial force F_a, the fluctuation amplitude of the skew moment increases, and N_os similarly shifts toward positive values. Additionally, the disturbance to the flange moment N_fs is relatively obvious.

The effects of different radial forces on the roller misalignment were seldom concerned in existing works [12,13,14,25,26,27,28,29,30]. Figure 13 reveals the roller’s angular vibrations under different radial forces and a displacement preload δ_a. The tilt and skew are quite different from those without radial force F_r (Figure 11). Even if the shaft is aligned (ξ = 0), as exhibited in Figure 13a,b, the roller also shows a periodic angular fluctuation due to F_r. Polar diagrams in Figure 13a,b depict contact forces (Σq_o and q_f) at the outer raceway and the flange. As F_r increases, the TRB is transformed into a major and a minor load-carrying zone. This means that some rollers bear more load, while others are ‘relaxed’. When F_r = 15 kN, all rollers are in the load-carrying state, and angular fluctuations are relatively gentle. For the heavy loading condition (F_r = 45 kN), the roller fluctuates sharply in the minor or ‘relaxed’ zone. Due to the gyroscopic effect, the roller in the ‘relaxed’ zone tends to be positively tilted. In the major zone, tilt and skew amplitudes increase as radial force F_r increases.

When the shaft is deflected (Figure 13c,d), effects of radial force F_r resemble that when the shaft is aligned. The roller misalignment also amplifies as F_r increases. Additionally, shaft deflection shows no significant impact on force distribution inside the TRB. This situation should be limited to the F_r ≠ 0 and δ_a ≠ 0 case. Since shaft deflection reduces bearing clearance in the minor zone, the intensity of the roller’s angular motion decreases locally. In the major zone, the disturbance of F_r on tilt amplitude diminishes, though its impact on skew amplitude remains pronounced. The observed skew amplitude remains generally consistent with Nelias’s work [14]. In summary, the roller’s angular misalignment presents a complicated state under varying TRB operating conditions, and shaft deflection unequivocally exacerbates this effect.

Figure 14a,b illustrates loads exerted on the tapered roller at different radial forces when ξ = 0, and they exhibit the same periodicity as the roller’s angular vibrations. For F_r = 1500 N, rollers are all loaded, so tilt and skew moments fluctuate sinusoidally. For F_r = 4500 N, the minor and major load-carrying zones are evident. In the minor zone, the roller is mainly subjected to centrifugal and gyroscopic effects, yielding a smaller moment load. However, the enlarged bearing clearance induces a significant vibration. In the major zone, variations of tilt and skew moments with time or position match the F_r = 1500 N case, but amplitudes are undoubtedly increased. As the roller just runs into the main zone, a slight instability occurs in the skew moment, causing perturbation to roller skew.

Figure 14c,d illustrates the ξ = 0.003 deg case, and moments acting on the roller are significantly more complex. For F_r = 1500 N, the tilt moment of the rings exerting on the roller is higher than that when ξ = 0. The skew moment loses sinusoidal characteristics, and multiple peaks appear within the minor load-carrying zone. Additionally, skew moment from the outer raceway and flange increases, while little change occurs at the inner raceway. For Fr = 4500 N, the minor and major zones re-emerge with modified boundaries, and tilt and skew moments decrease universally compared to that when ξ = 0. Case comparison shows that at F_r = 1500 N, the deflected shaft reverses overall time trends of N_ot, N_it, N_os, N_is, and N_fs, and at F_r = 4500 N, it only affects the overall time trend of N_it. This is actually a reflection of structural nonlinearity of TRBs.

5. Conclusions

Differential equations for the TRB dynamics subjected to a deflected shaft were presented, in which the shaft deflection is equivalent to an angular displacement constraint of the TRB. Tilt and skew vibrations of the tapered roller were numerically studied, as well as negative effects of deflected shaft and operating parameters on roller alignment state.

(1)

The amplitude of the tilt moment borne by the roller is 2~3 orders of magnitude higher than the skew moment, but the tilt angle is several orders of magnitude lower than the skew angle. Compared with skew motion, tilt motion is more likely to aggravate the stress edge effect at the roller-end.

(2)

The deflected shaft increases tilt and skew amplitudes of the tapered roller. Tilt amplitude may exceed the deflected angle.

(3)

In aligned and misaligned states of the shaft, both bearing speed and axial force significantly affect roller skew, while slightly affecting tilt motion. These factors similarly influence the moments exerted on the roller by the cone and cup.

(4)

Within the load conditions analyzed, flange drives the roller to tilt toward the negative direction and prevents roller skew most of the time, whereas both raceways may drive the roller to tilt/skew toward either the positive or negative direction.

(5)

When a major and a minor load-carrying zone distinctly exists inside the TRB, the roller will exhibit a pronounced angular vibration when it is in the minor zone or just orbited to the major zone.