Grease Film Behavior in Ball Bearings
Abstract
1. Introduction
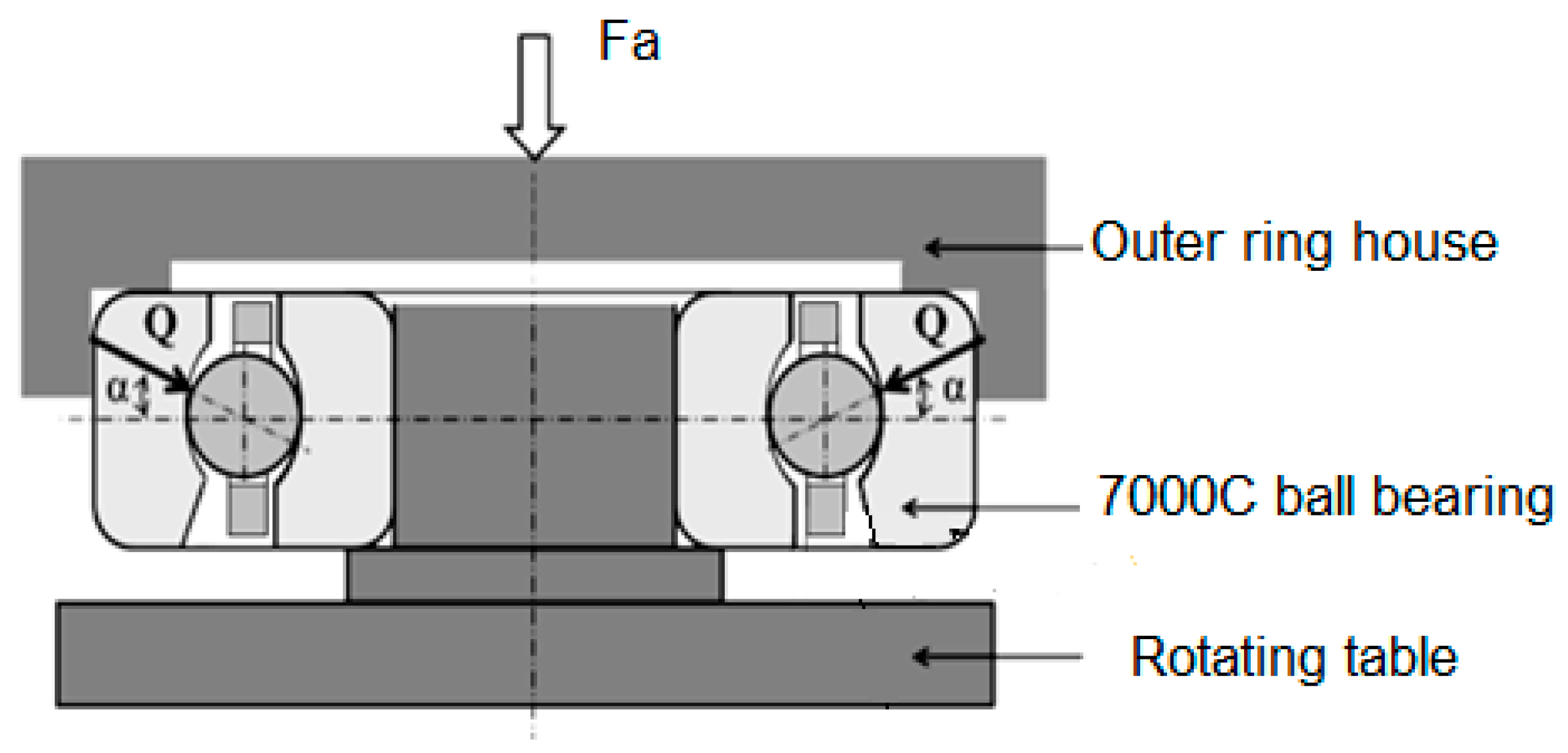
2. Experimental Equipment and Procedure
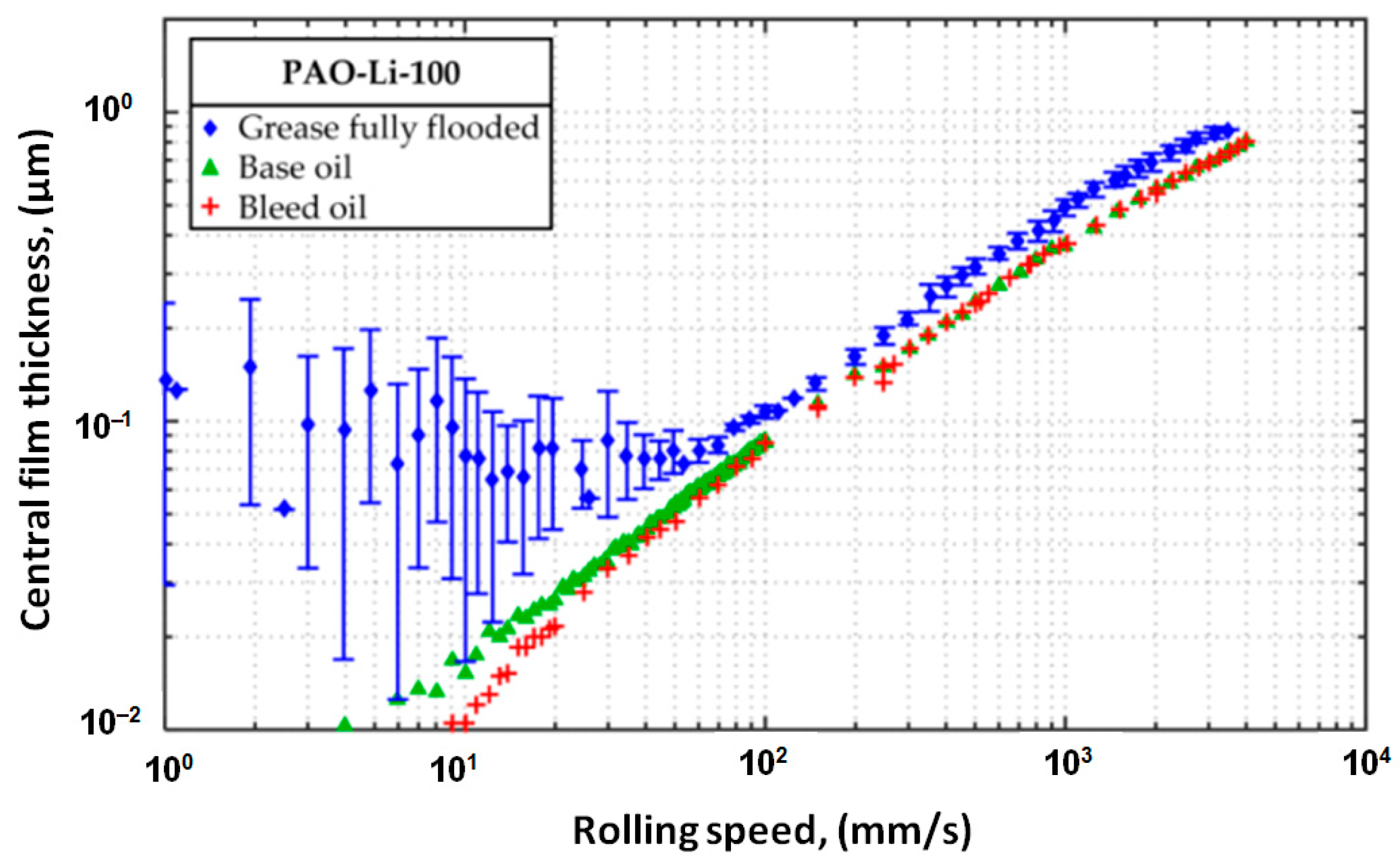
3. Experimental Results to Demonstrate the “V-Shape Pattern”
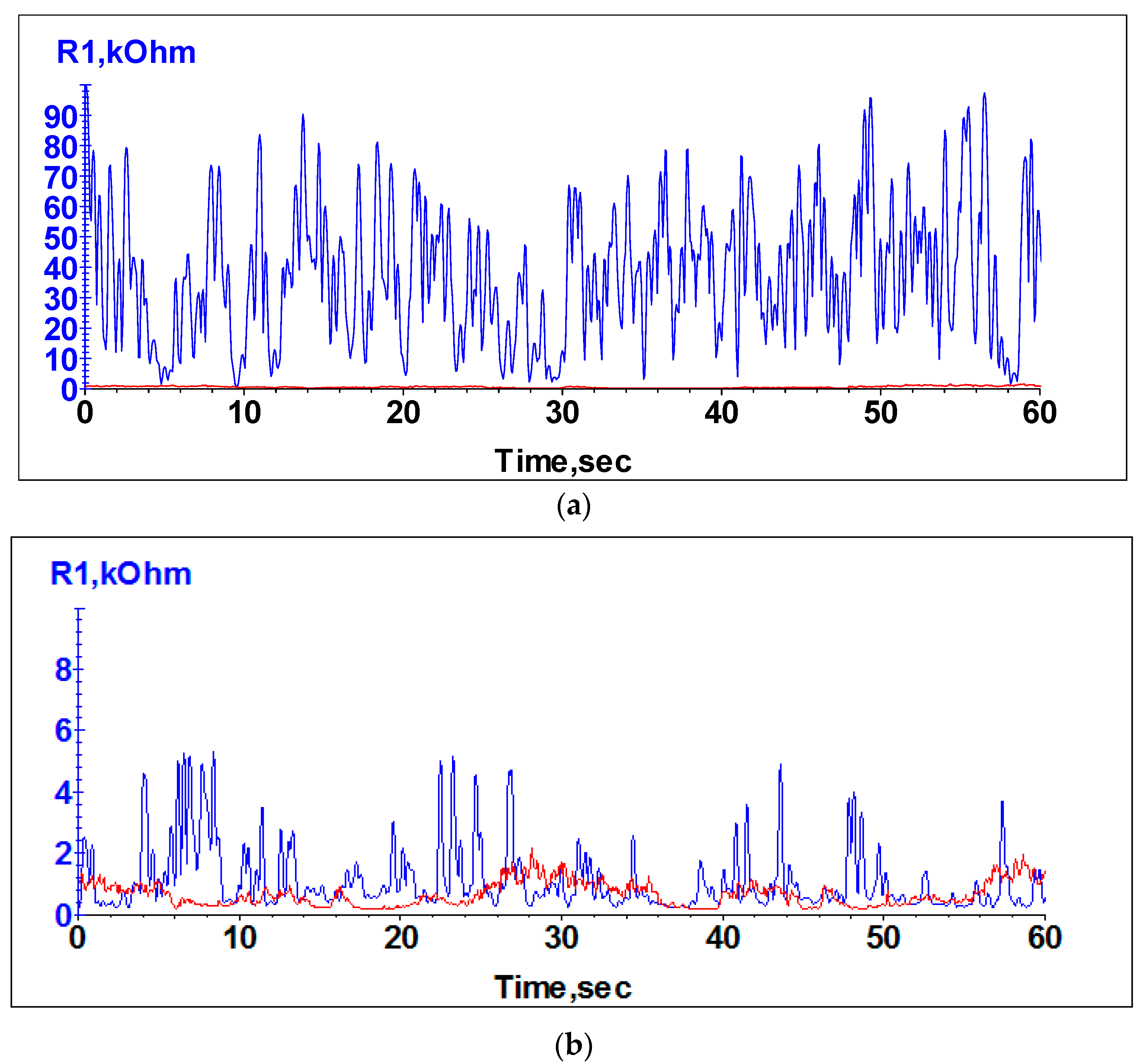
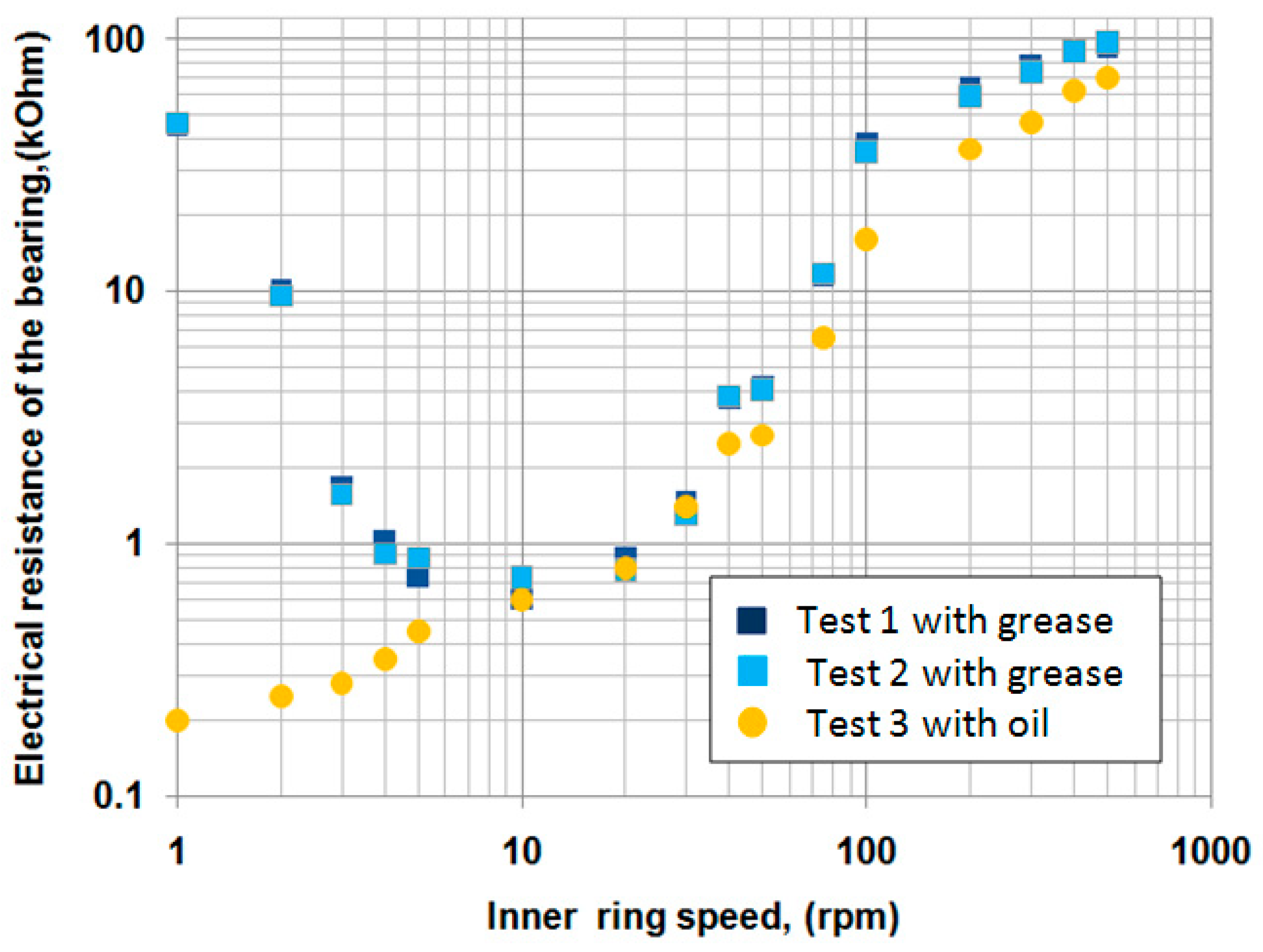
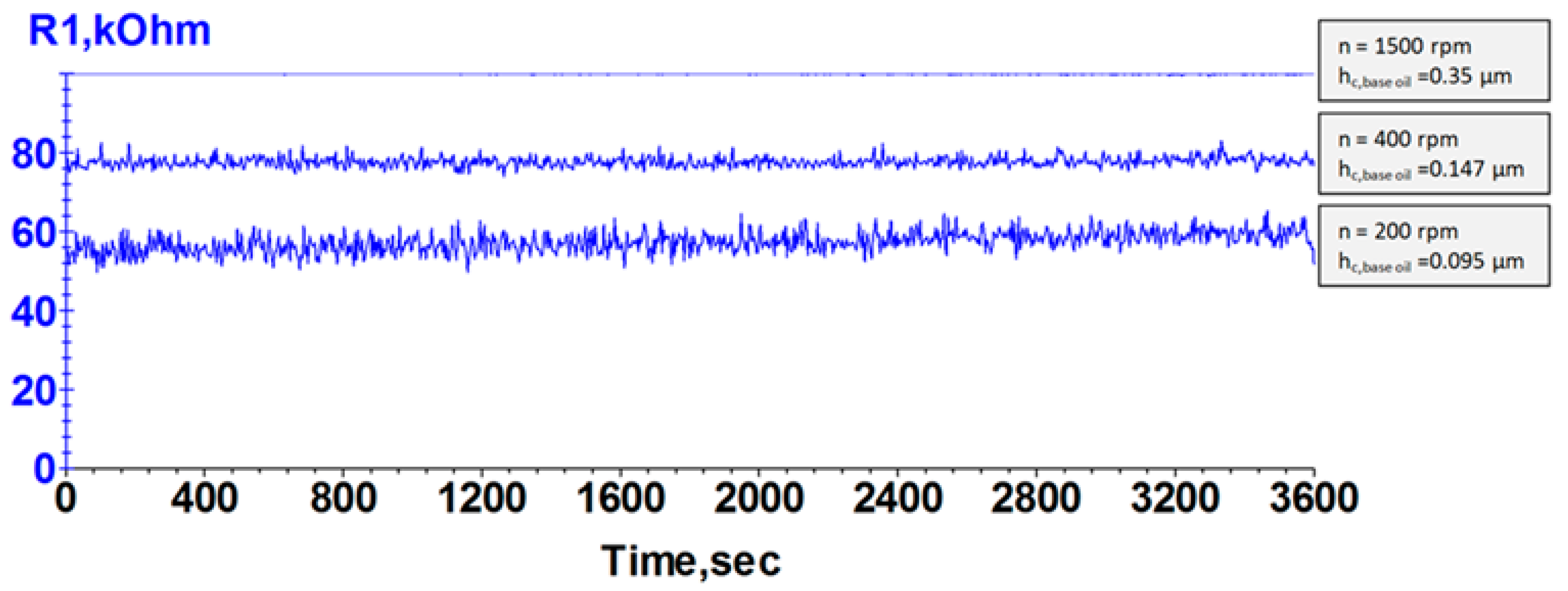
3.1. Determination of the Variation of Electrical Resistance with Rotational Speed
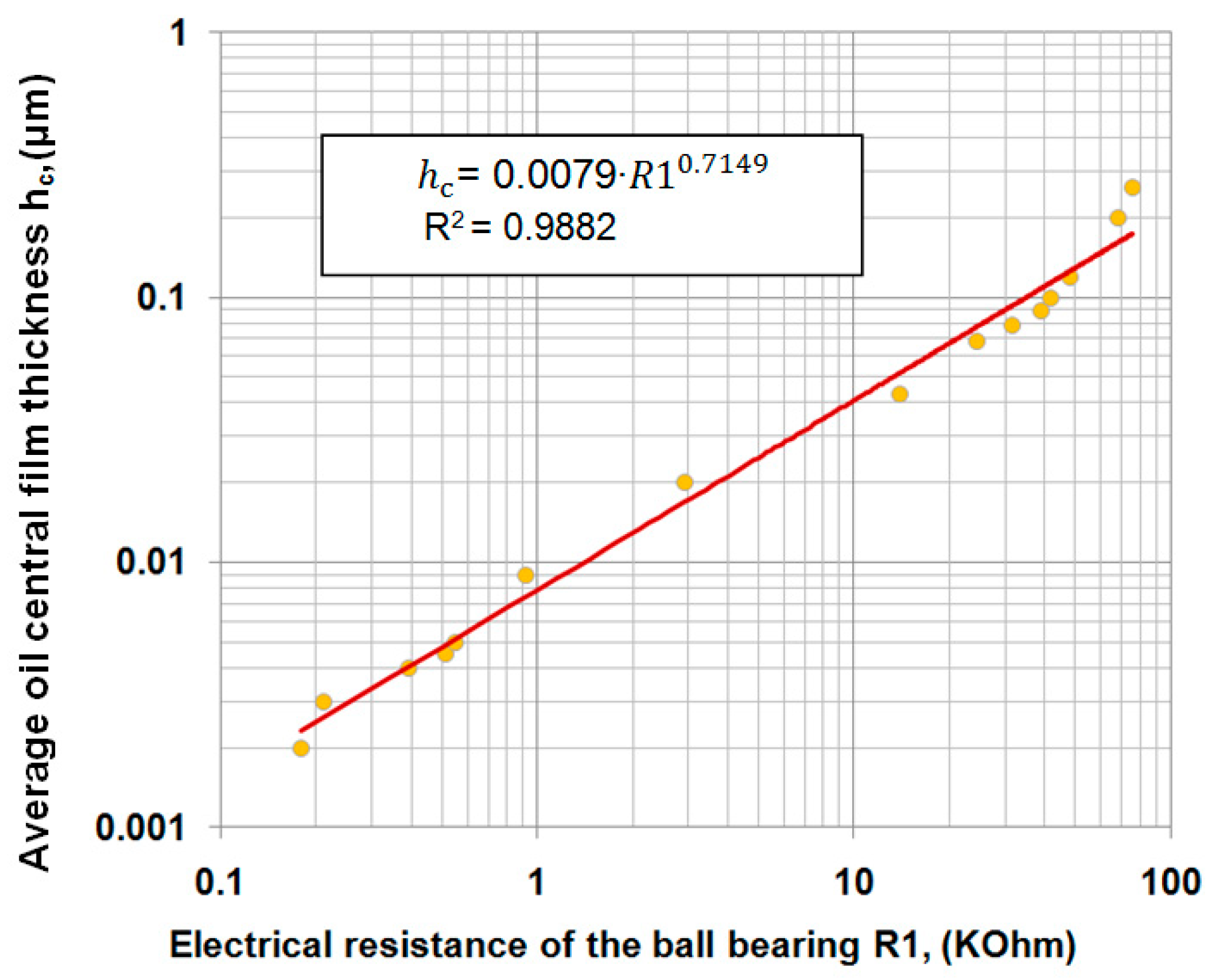
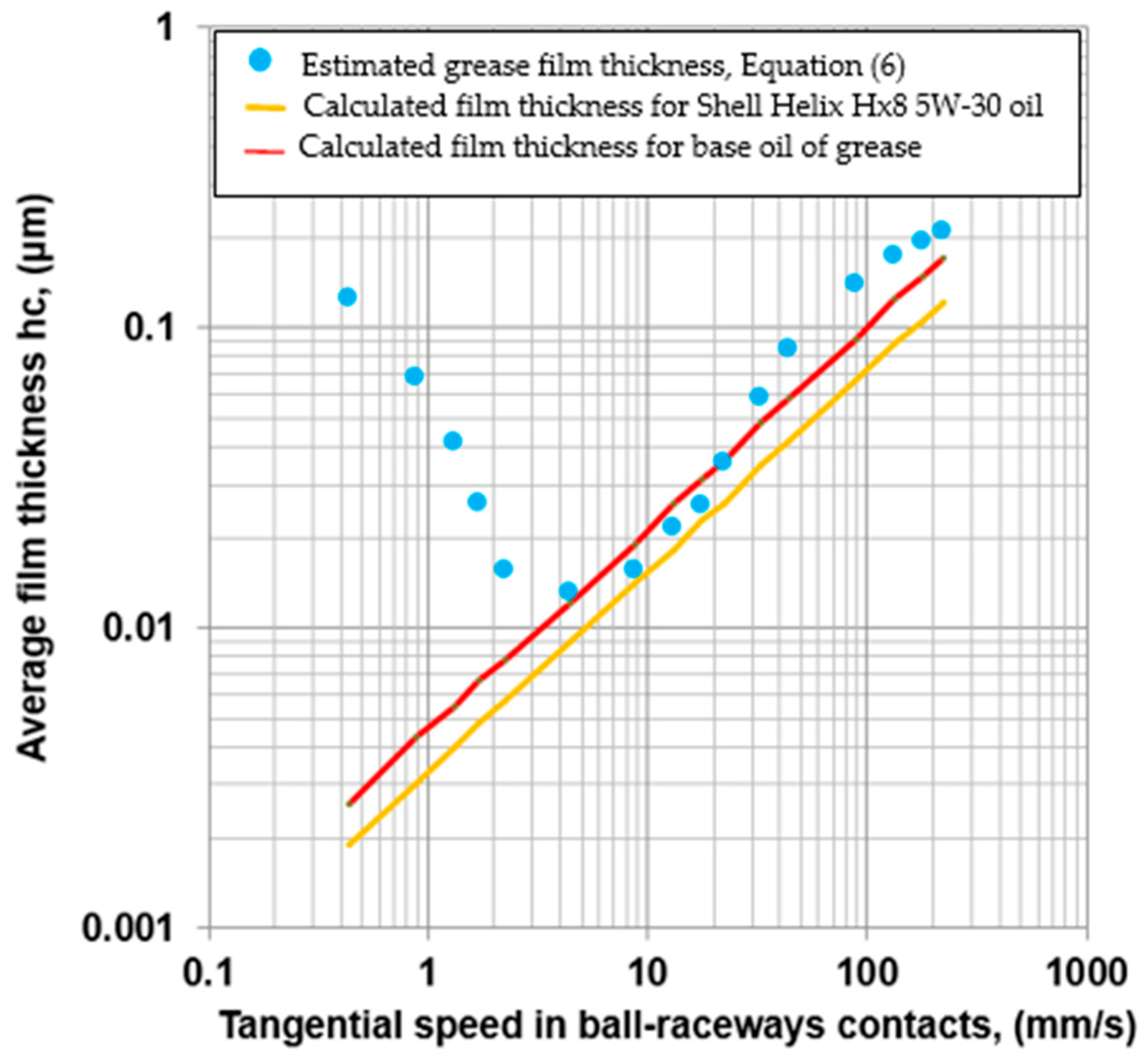
3.2. Correlation Between Calculated Oil Film Thickness and Measured Electrical Resistance
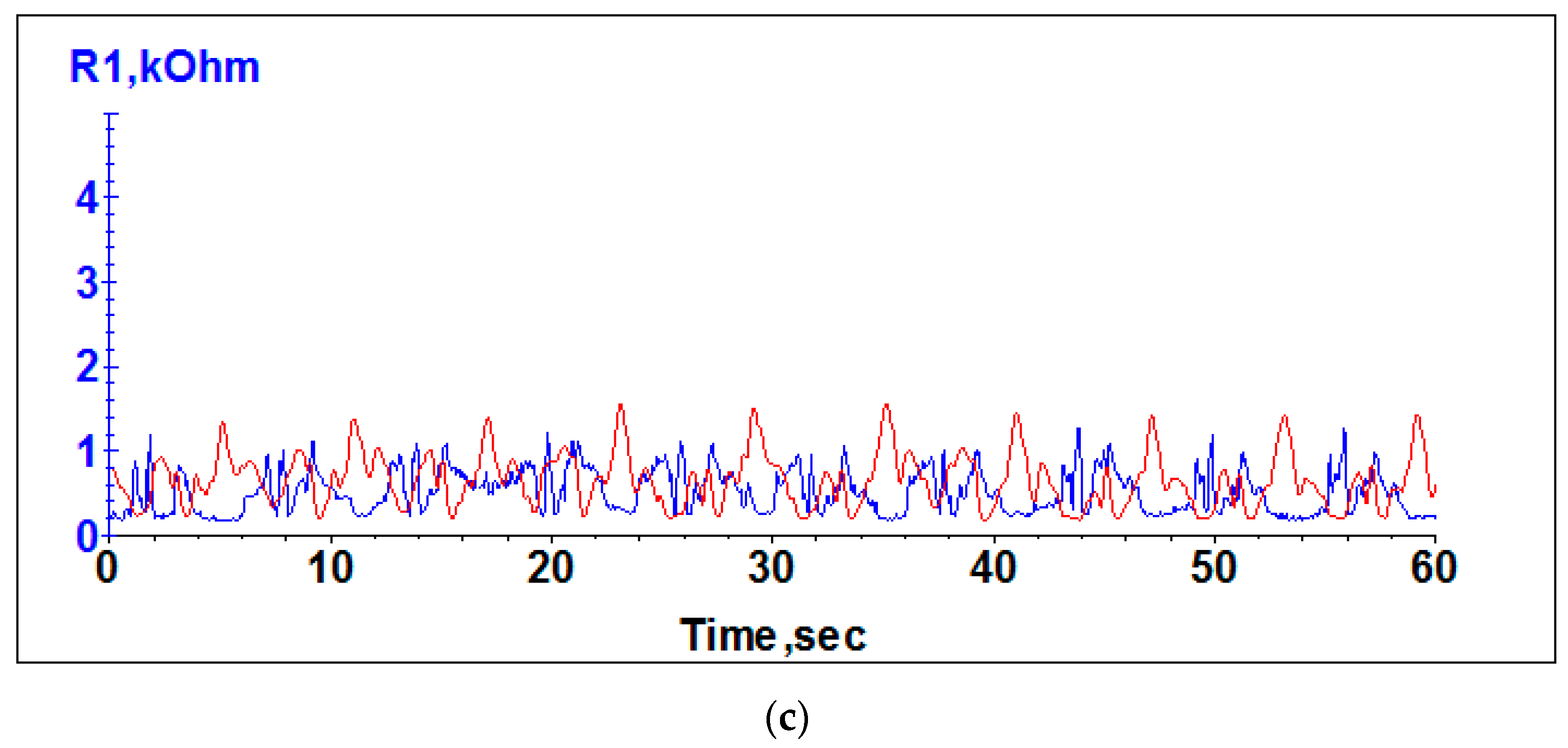
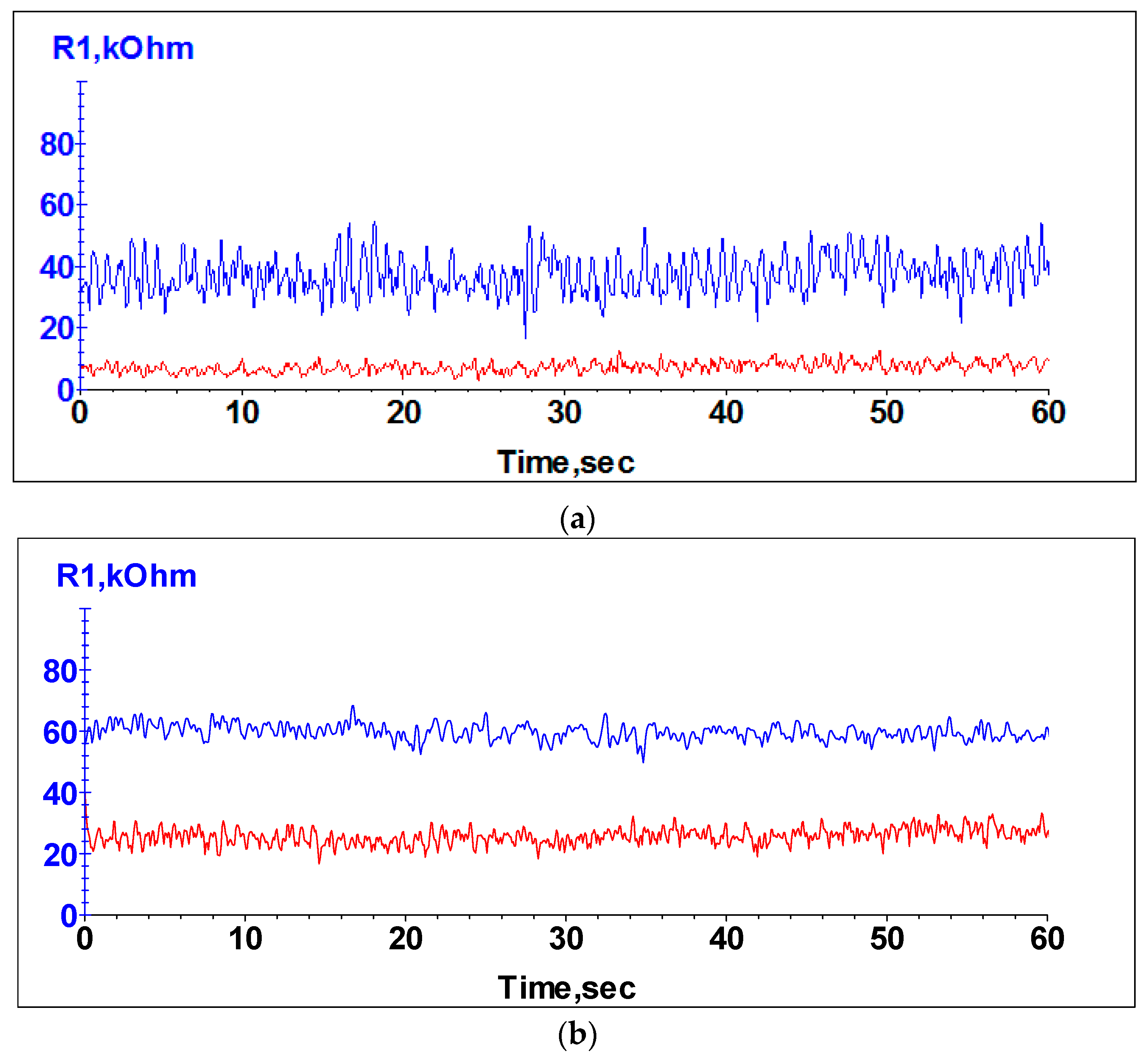
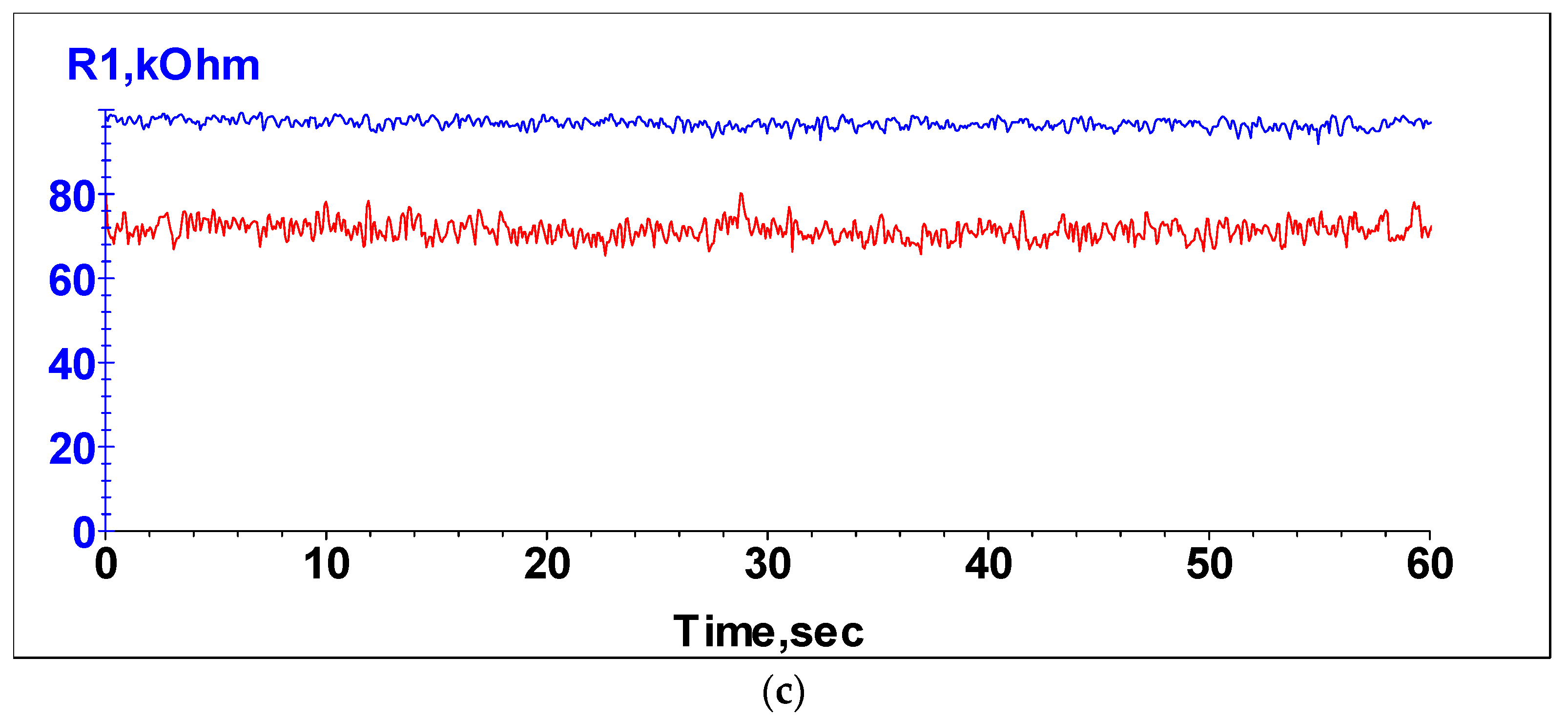
4. Determination of the Grease Film Stability
5. Conclusions
- The behavior of the average grease-lubricated film thickness in an angular contact ball bearing is consistent with the results obtained by interferometry for a single ball–glass disc grease-lubricated contacts reported in the literature.
- At low rotational speeds of the ball bearing, the so-called “V-shape pattern” behavior of the grease film thickness was obtained with a maximum value at 1 rpm and minimum value around 10 rpm.
- At rotational speeds between 100 and 500 rpm, the average grease film thickness increase was similar to the average base oil film thickness and exceed the average base oil film thickness with (15–25)%. The “V-shape pattern” and the results obtained by the authors are in good agreement with those reported by Fischer et al. [1], both in terms of film thickness and the tangential speeds.
- The stability of the grease film thickness at eight different rotational speeds between 200 rpm and 1500 rpm was demonstrated by the constant electrical resistance for a period of 60 min for each rotational speed.
- For rotational speeds between 200 rpm and 1500 rpm, the average lubricant parameters Λ calculated with the grease base oil varied between 1.35 and 5.22, indicating both mixed and fully flooded lubrication conditions.
- The time between two successive balls for the rotational speed between 200 and 1500 rpm was determined, and it was concluded that the time for bleed oil to refill the track left by the balls is less than the time between two successive ball passes, explaining the absence of the starvation phenomenon.
- Using scanning electron microscopy (SEM), the fresh and stressed grease microstructure was investigated, revealing minor fragmentations of the soap filaments after 8 h of operating at various rotational speeds.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| db | ball diameter [m] |
| dm | average diameter of ball bearing [m] |
| ki,o | ellipticity parameter [dimensionless] |
| fi,o | inner and outer race conformity [dimensionless] |
| hc | average central film thickness [µm] |
| n | rotational speed of the inner race [min−1] |
| v | average entrainment speed in ball-race contacts [ms−1] |
| E* | equivalent Young’s modulus of the two elements in contact [Pa] |
| Fa | axial load acting of the ball bearing [N] |
| Q | normal load in ball-race contact [N] |
| Rx,i,o | reduced radii of curvature in the rolling direction [m] |
| Ry,i,o | reduced radii of curvature in the transverse direction [m] |
| Z | number of the balls [dimensionless] |
| α | contact angle of the ball bearing [degrees] |
| αp | piezo-viscous parameter of lubricant [Pa−1] |
| γ | angular contact ball bearing parameter [dimensionless] |
| ηo | dynamic viscosity of base oil for grease [Pa·s] |
| Λ | lubricant parameter [dimensionless] |
Appendix A. Determination of the Oils Characteristics at Operating Temperature
Appendix A.1. Determination of the Oil Viscosity at a Given Temperature
Appendix A.2. Determination of the Piezo-Viscosity Coefficients for Oils
Appendix B. Determination of the Film Thickness in the Balls-Races Contacts
Appendix B.1. Average Central Film Thickness for Shell Helix Hx8 5W-30
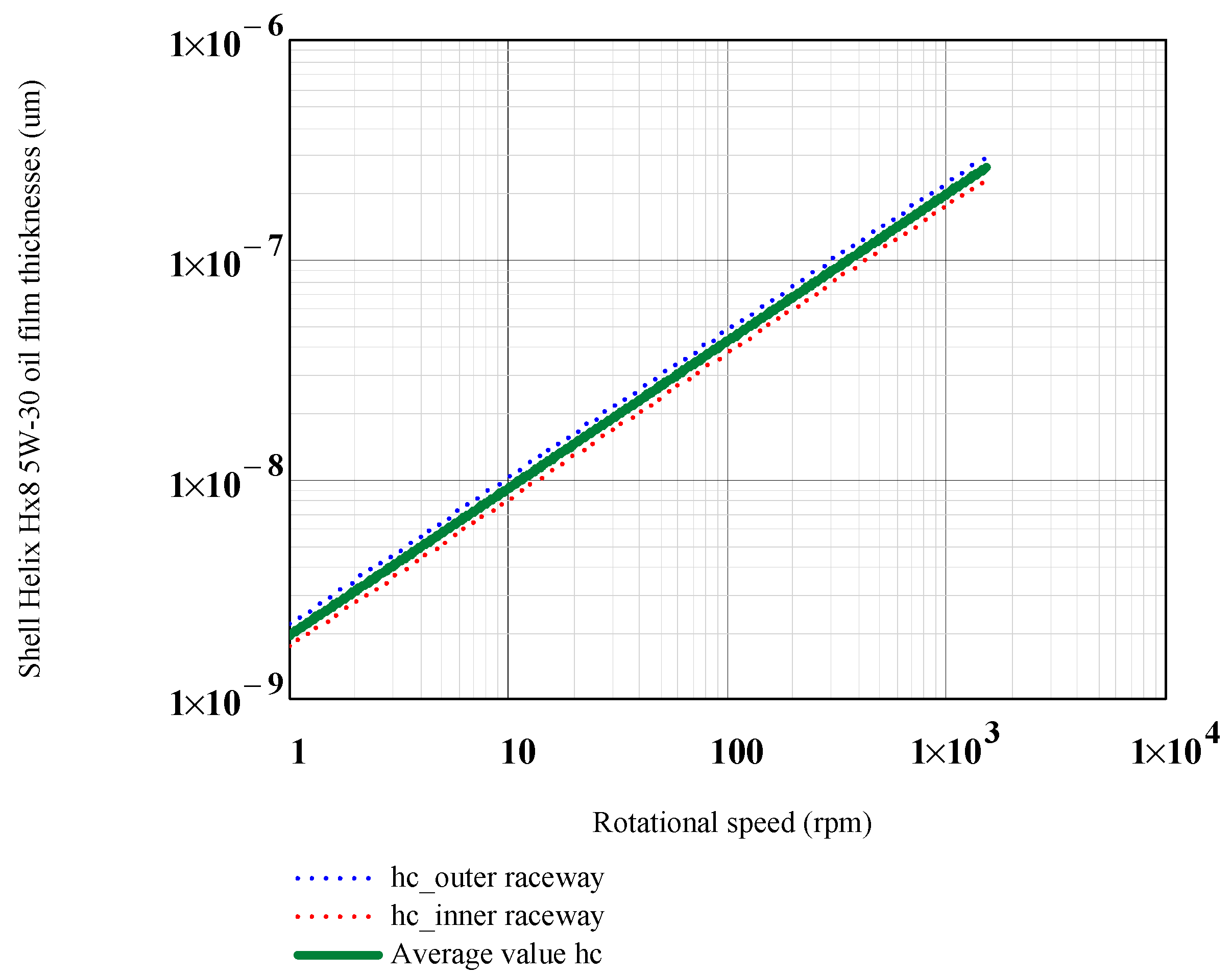
Appendix B.2. Average Central Film Thickness for Base Oil of the Grease Shell Gadus S2 V100 2

References
- Fischer, D.; Jacobs, G.; Stratmann, A.; Burghardt, G. Effect of base oil type in grease composition on the lubricating film formation in EHD contacts. Lubricants 2018, 6, 32. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Ball Bearing Lubrication, The Elastohydrodynamics of Elliptical Contacts; John Willey & Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Cann, P.M.; Spikes, H.A. Film Thickness Measurements of Lubricating Greases Under Normally Starved Conditions. NLGI Spokesm. 1992, 56, 21–27. [Google Scholar]
- Cen, H.; Lugt, P.M.; Morales-Espejel, G. Film Thickness of Mechanically Worked Lubricating Grease at Very Low Speeds. Tribol. Trans. 2014, 57, 1066–1071. [Google Scholar] [CrossRef]
- Cen, H.; Lugt, P.M.; Morales-Espejel, G. On the Film Thickness of Grease-Lubricated Contacts at Low Speeds. Tribol. Trans. 2014, 57, 668–678. [Google Scholar] [CrossRef]
- Zhang, S. Calculation of the Lubricating Film Thickness in Grease-Lubricated Rolling Contacts. Ph.D. Disertation, Institute for Machine Elements and Systems Engineering (MSE) at RWTH Aachen University, Aachen, Germany, 2024. Available online: https://publications.rwth-aachen.de/record/992739/files/992739.pdf (accessed on 3 April 2025).
- Cen, H.; Bai, D.; Chao, Y.; Li, Y.; Li, R. EHL film thickness in rolling element bearings evaluated by electrical capacitance method: A review. In Tribology-Materials, Surfaces and Interfaces; Taylor and Francis Ltd.: Oxfordshire, UK, 2021; Volume 15, pp. 55–77. [Google Scholar]
- Zhang, Q.; Mugele, F.; van den Ende, D.; Lugt, P.M. A model configuration for studying stationary grease bleed in rolling bearings. Tribol. Trans. 2021, 64, 1127–1137. [Google Scholar] [CrossRef]
- Shetty, P.; Meijer, R.J.; Osara, J.A.; Lugt, P.M. Measuring film thickness in starved grease-lubricated ball bearings: An improved electrical capacitance method. Tribol. Trans. 2022, 65, 869–879. [Google Scholar] [CrossRef]
- Nagata, Y. EHD Phenomena in Grease Lubrication Contacts. Ph.D. Thesis, University of Sussex, Brighton, UK, 2011. Available online: https://sussex.figshare.com/articles/thesis/EHD_phenomena_in_grease_lubricated_contacts/23315012?file=41103371 (accessed on 28 March 2025).
- Cann, P.M. Grease film thickness and friction in EHL contacts. In Proceedings of the Scientific Achievements, Industrial Applications, Future Challenges, the 2nd World Tribology Congress, Vienna, Austria, 3–7 September 2001; Franek, F., Ed.; Österreichische Tribologische Gesellschaft: Wien, Austria, 2001; pp. 159–164, ISBN 3-901657-07-X. [Google Scholar]
- Maruyama, T.; Maeda, M.; Nakano, K. Lubrication Condition Monitoring of Practical Ball Bearings by Electrical Impedance Method. Tribol. Online 2019, 14, 327–338. [Google Scholar] [CrossRef]
- Cojocaru, D.; Ianuş, G.; Cârlescu, V. Film thickness în miniature ball bearing grease lubricated. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1262, 012005. [Google Scholar] [CrossRef]
- Harris, T.A. Rolling Bearing Analysis, 4th ed.; John Willey & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Lugt, P.M. A review on grease lubrication in rolling bearings. Tribol. Trans. 2009, 52, 470–480. [Google Scholar] [CrossRef]
- Khonsary, M.N.; Booser, E.R. Applied Tribology. Bearing Design and Lubrication, 3rd ed.; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]






| Properties | Units | Values |
|---|---|---|
| Kinematic viscosity at 40 °C | mm2/s | 61.7 |
| Kinematic viscosity at 100 °C | mm2/s | 11 |
| Density at 15 °C | kg/m3 | 850 |
| Piezo-viscous parameter of base oil at 25 °C | Pa−1 | 2.5 × 10−8 |
| Viscosity index | 172 |
| Properties | Units | Values |
|---|---|---|
| NLGI Consistency | 2 | |
| Soap Type: Lithium Hydroxystearate | ||
| Base Oil Type: Mineral | ||
| Base oil kinematic viscosity @40 °C | mm2/s | 100 |
| Base oil kinematic viscosity @100 °C | mm2/s | 11 |
| Dropping point | °C | 180 |
| Dimensions | Values | Units |
|---|---|---|
| D—external diameter | 26 | mm |
| d—internal diameter | 10 | mm |
| dm—pitch diameter dm = (D+d)/2 | 18 | mm |
| db—ball diameter | 4.762 | mm |
| α—contact angle | 15 | degrees |
| Z—number of balls | 8 | - |
| fi, fo—inner and outer races conformities | fi = fo = 0.525 | - |
| Rq,r—root mean square roughness of races | 0.06 | µm |
| Rq,b—root mean square roughness of balls | 0.03 | µm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cojocaru, D.; Ianuș, G.; Cârlescu, V.; Chiriac, B.; Olaru, D. Grease Film Behavior in Ball Bearings. Lubricants 2025, 13, 429. https://doi.org/10.3390/lubricants13100429
Cojocaru D, Ianuș G, Cârlescu V, Chiriac B, Olaru D. Grease Film Behavior in Ball Bearings. Lubricants. 2025; 13(10):429. https://doi.org/10.3390/lubricants13100429
Chicago/Turabian StyleCojocaru, Denis, Gelu Ianuș, Vlad Cârlescu, Bogdan Chiriac, and Dumitru Olaru. 2025. "Grease Film Behavior in Ball Bearings" Lubricants 13, no. 10: 429. https://doi.org/10.3390/lubricants13100429
APA StyleCojocaru, D., Ianuș, G., Cârlescu, V., Chiriac, B., & Olaru, D. (2025). Grease Film Behavior in Ball Bearings. Lubricants, 13(10), 429. https://doi.org/10.3390/lubricants13100429





