Numerical Study on Characteristics of Lead-Bismuth Lubricated Hydrodynamic Bearing Considering Non-Condensable Gas
Abstract
1. Introduction
2. Method and Model
2.1. Numerical Model and Setup
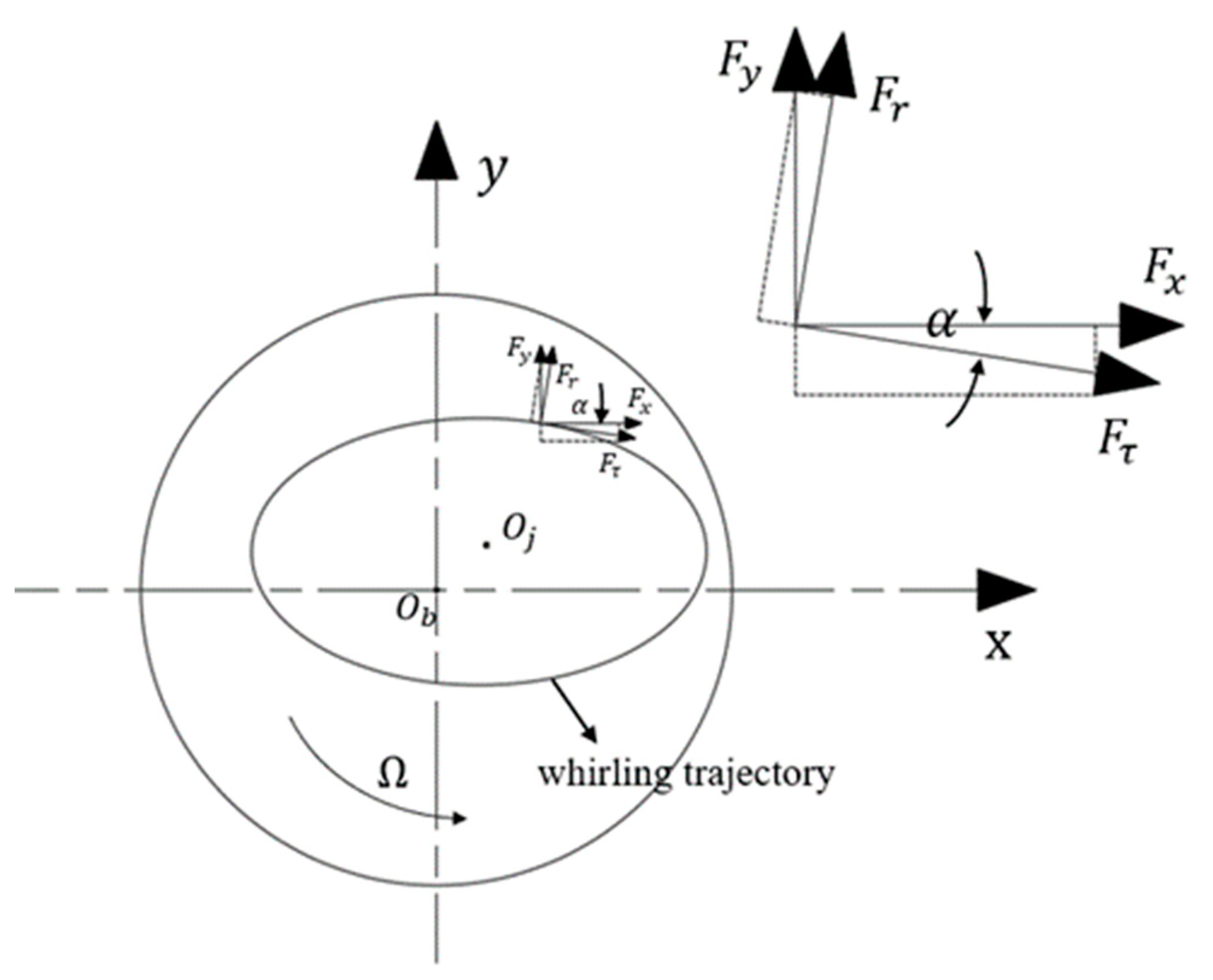
2.2. Calculate Model and Boundary Conditions
2.3. Fluid Structure Interaction Simulation
2.4. Validation
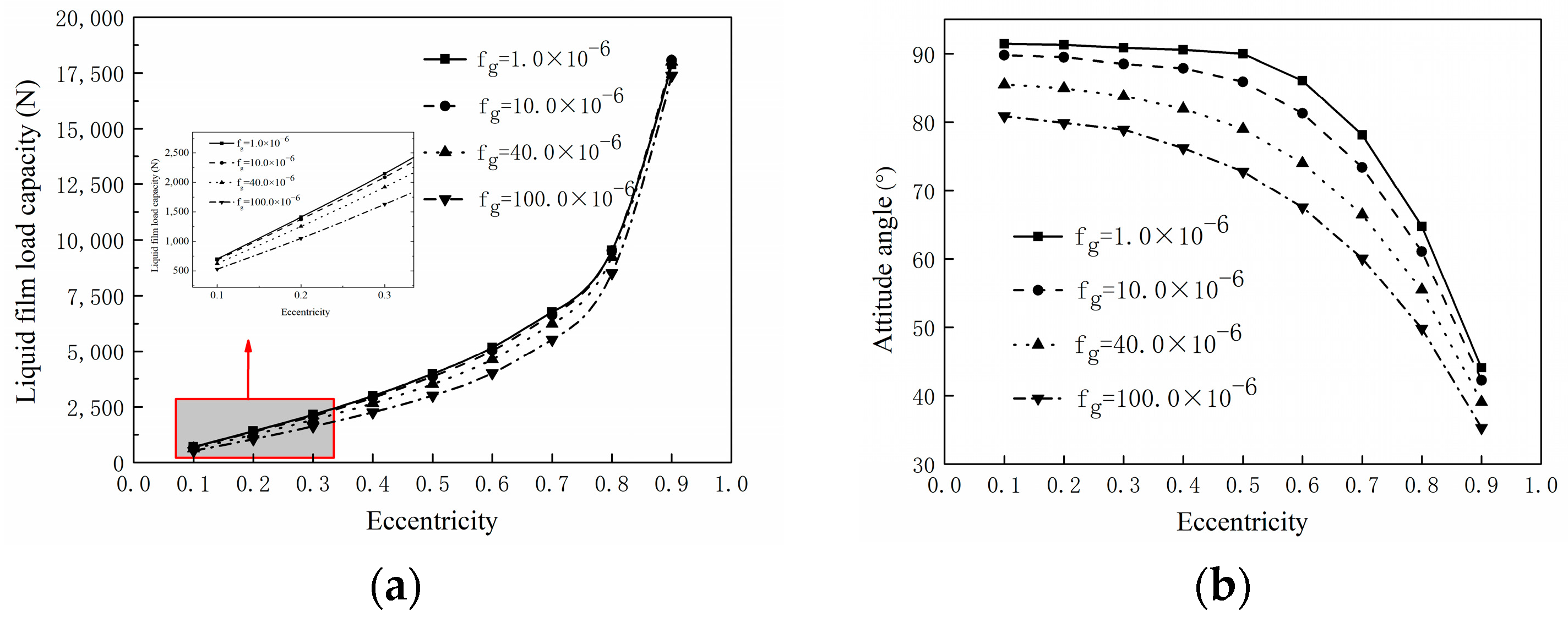
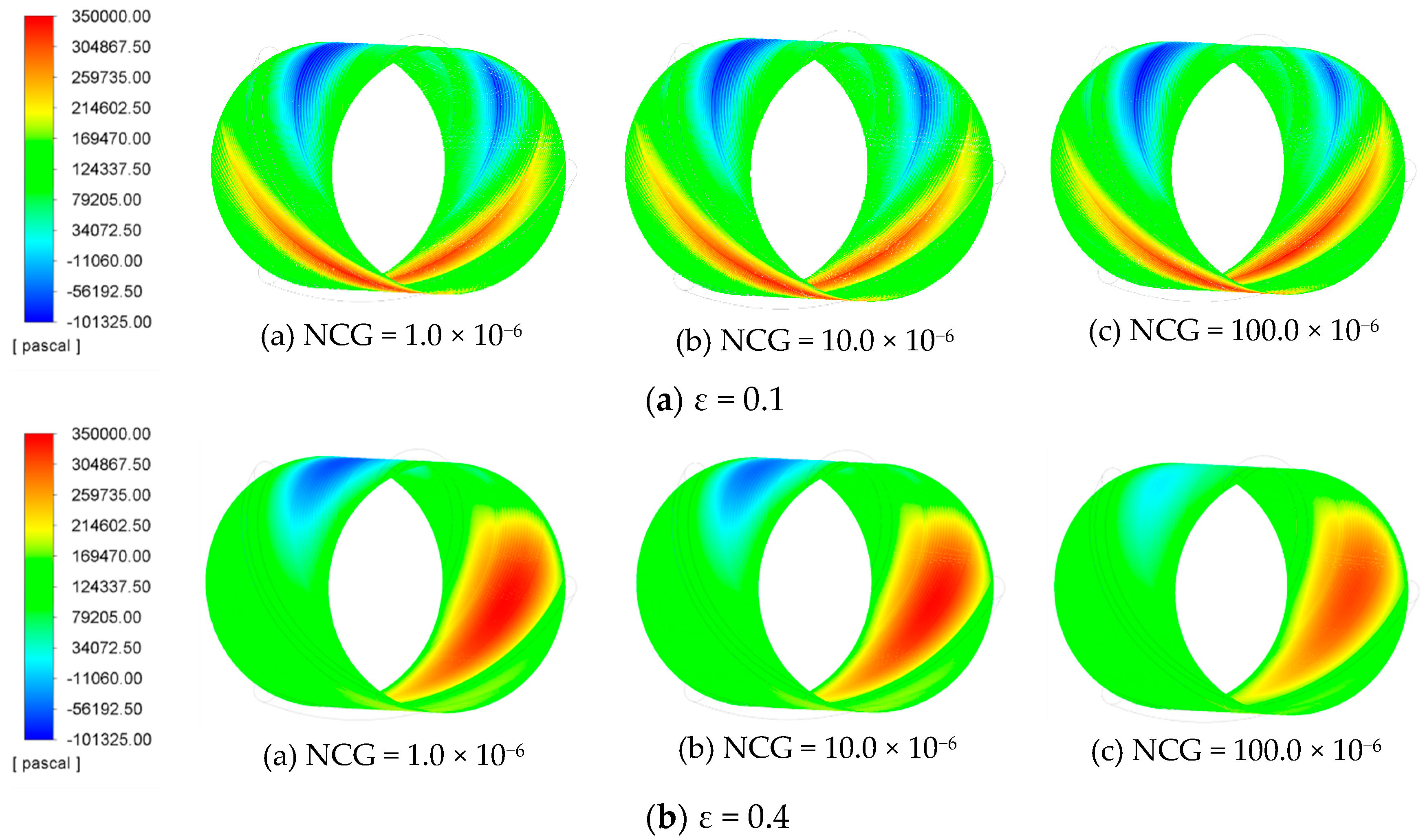
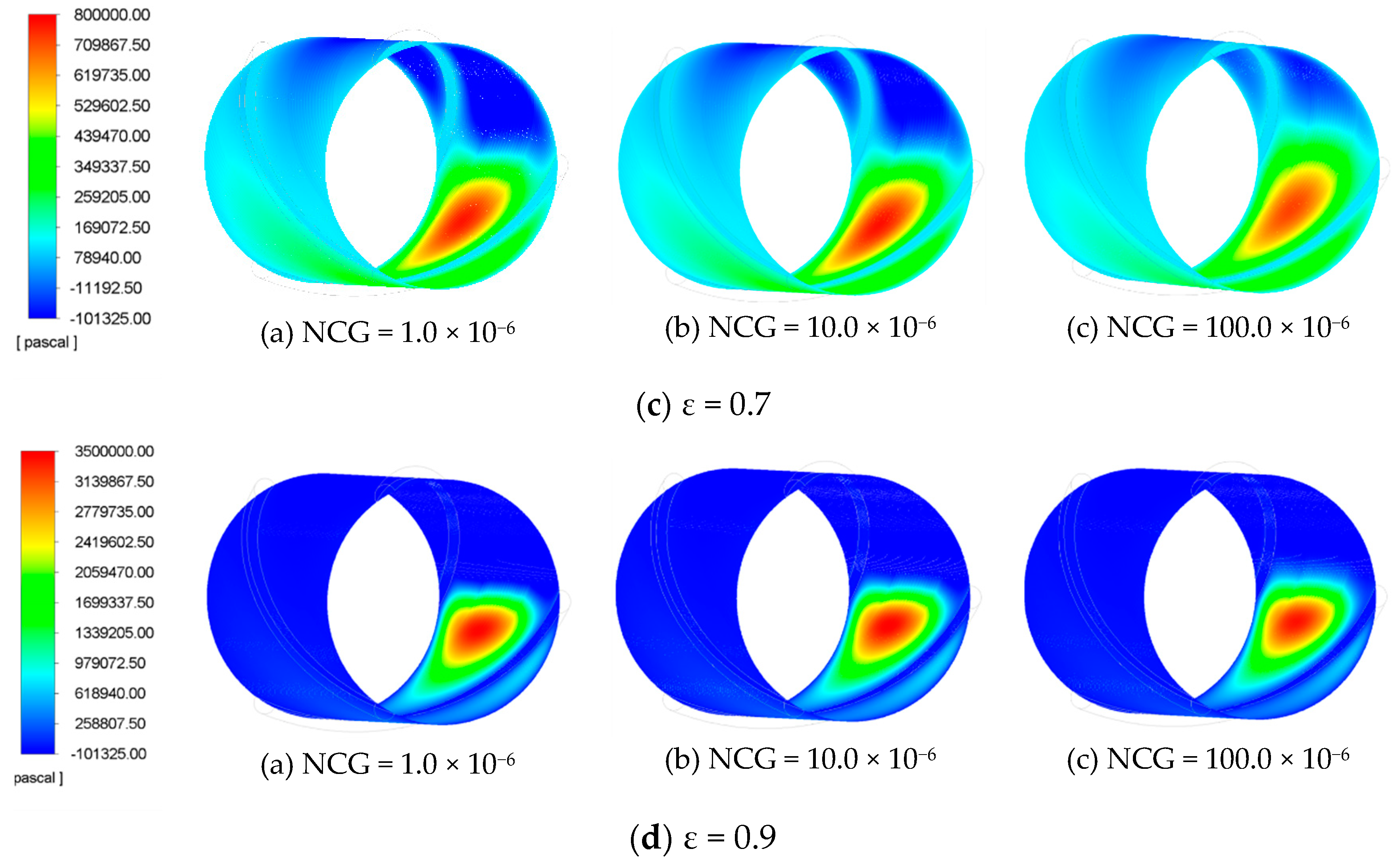
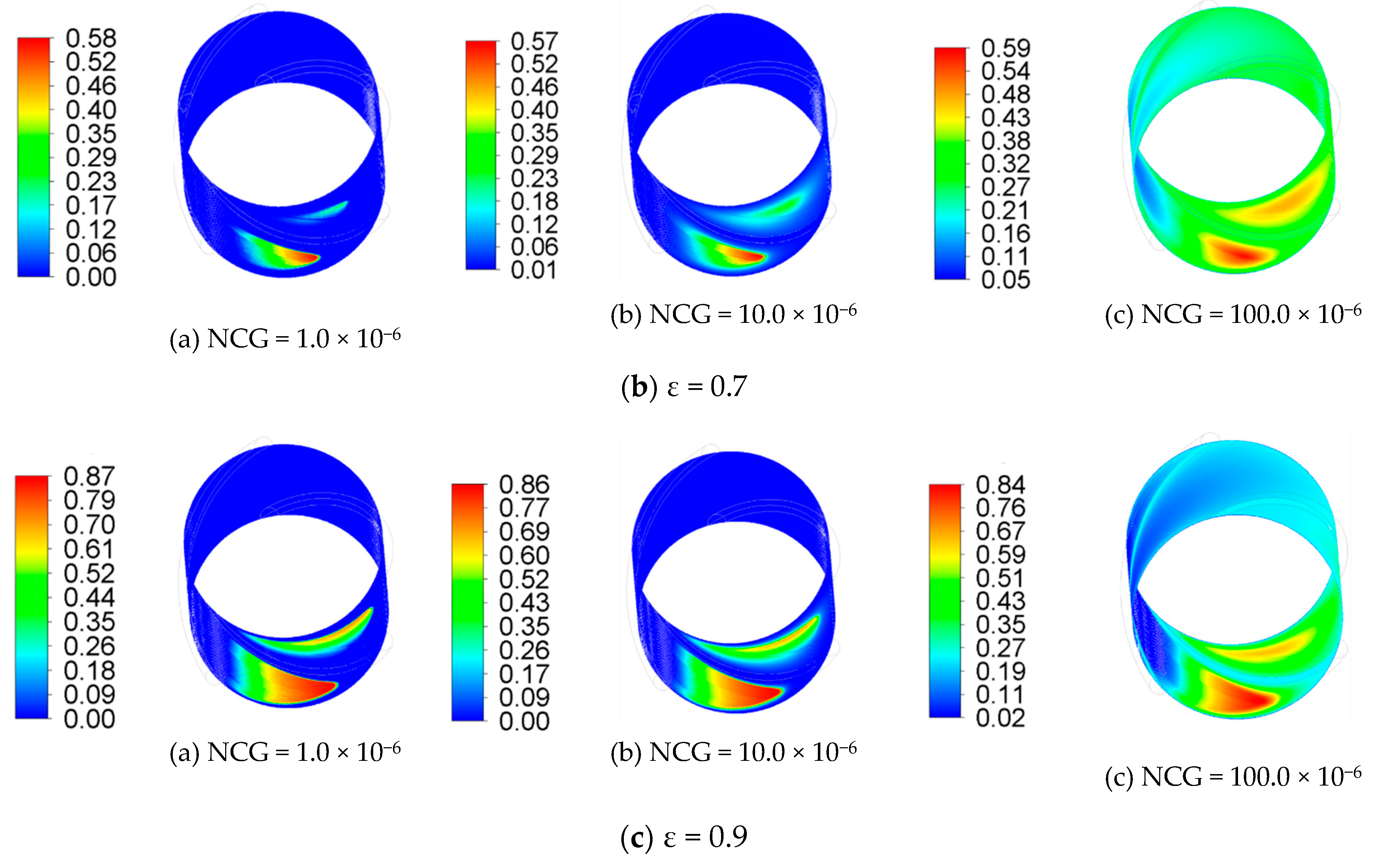
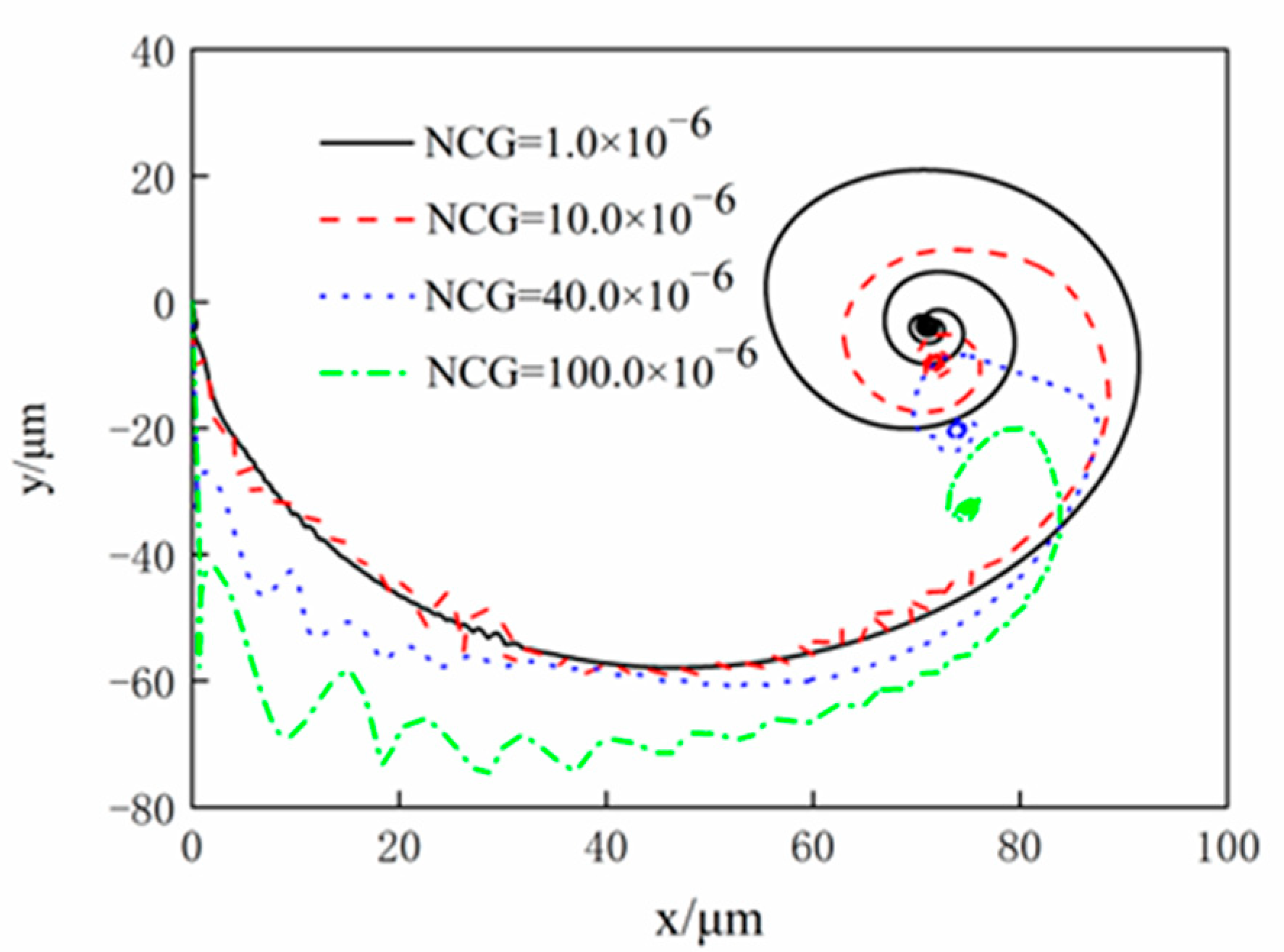
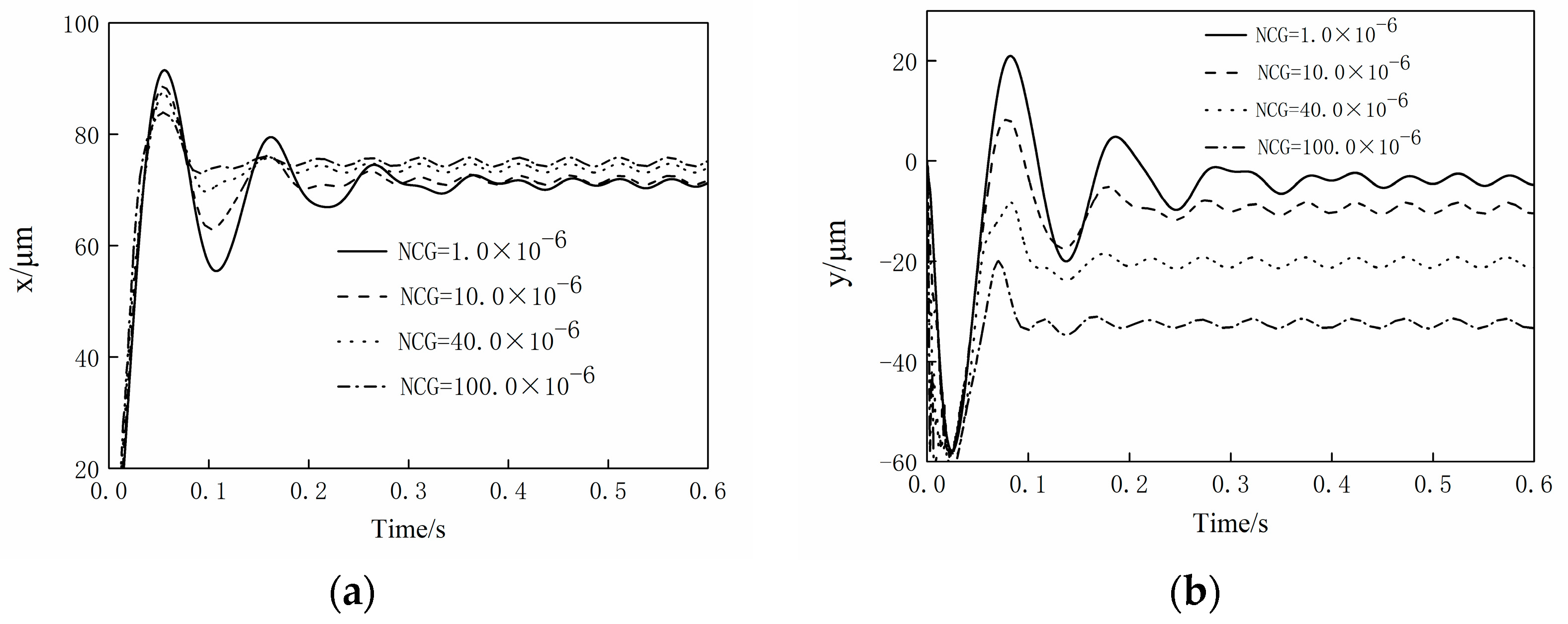
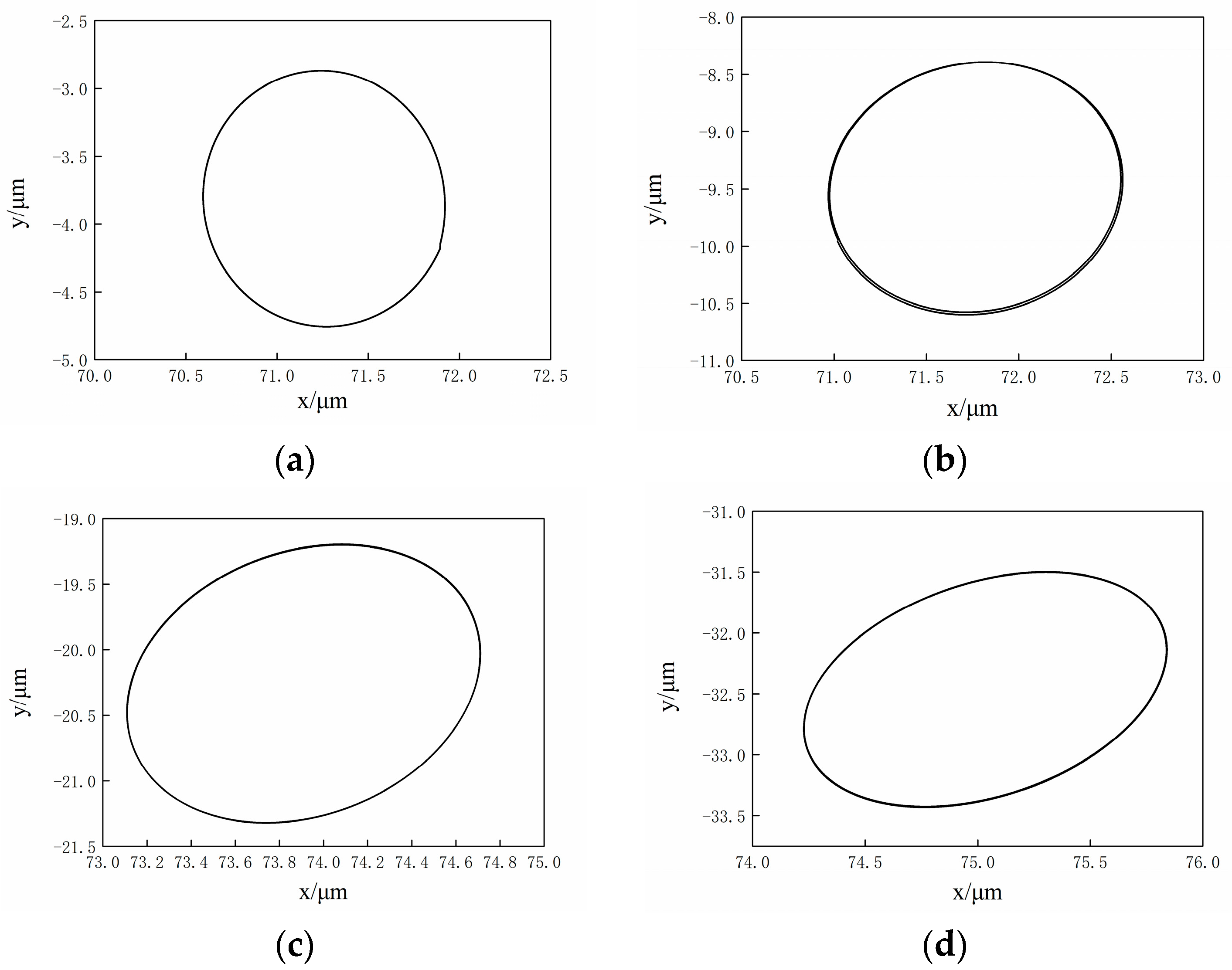
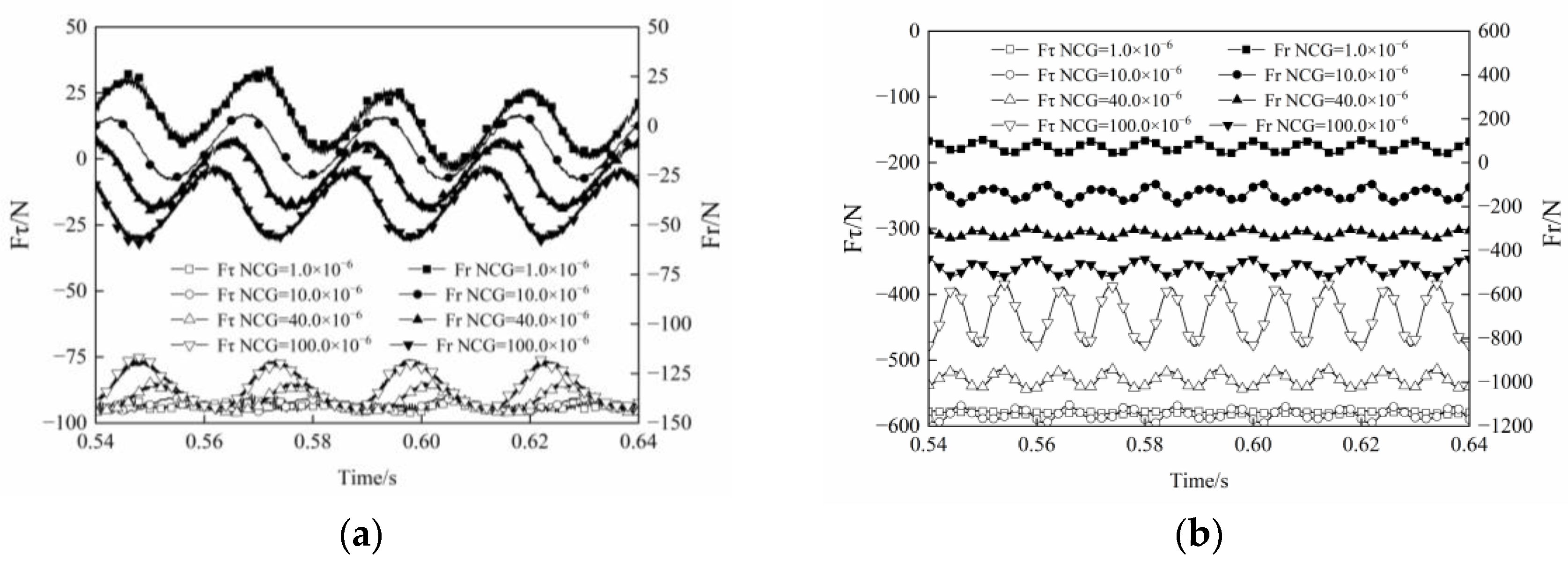
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- OECD; Nuclear Energy Agency. Handbook on Lead-Bismuth Eutectic Alloy and Lead Properties: Materials Compatibility, Thermal-hydraulics and Technologies; Nuclear Energy Agency: Paris, France, 2007. [Google Scholar]
- Wu, Y.; Bai, Y.; Song, Y.; Huang, Q.; Zhao, Z.; Hu, L. Development strategy and conceptual design of China lead-based research reactor. Ann. Nucl. Energy 2016, 87, 511–516. [Google Scholar] [CrossRef]
- Wallenius, J.; Qvist, S.; Mickus, I.; Bortot, S.; Szakalos, P.; Ejenstam, J. Design of Sealer, a very small lead-cooled reactor for commercial power production in off-grid applications. Nucl. Eng. Des. 2018, 338, 23–33. [Google Scholar] [CrossRef]
- Engelen, J.; Abderrahim, H.A.; Baeten, P.; De Bruyn, D.; Leysen, P. MYRRHA: Preliminary front-end engineering design. Int. J. Hydrog. Energy 2015, 40, 15137–15147. [Google Scholar] [CrossRef]
- Stachowiak, G.; Batchelor, A. Engineering Tribology; Butterworth Heinemann: Oxford, UK, 2013. [Google Scholar]
- Xie, Z.; Rao, Z.; Liu, H. Effect of surface topography and structural parameters on the lubrication performance of a water-lubricated bearing: Theoretical and experimental study. Coatings 2019, 9, 23. [Google Scholar] [CrossRef]
- Bokova, T.; Bokov, P.; Marov, A.; Volkov, N. Research on slipper bearings of pumps of reactor systems with lead-bismuth coolant at relatively low temperatures. IOP Conf. Ser. Mater. Sci. Eng. 2020, 996, 012007. [Google Scholar] [CrossRef]
- Constantinescu, V. On the Influence of Inertia Forces in Turbulent and Laminar Self-Acting Films. J. Lubr. Technol. 1970, 92, 473–481. [Google Scholar] [CrossRef]
- Ng, C.; Pan, C. A Linearized Turbulent Lubrication Theory. J. Basic Eng. 1965, 87, 675–688. [Google Scholar] [CrossRef]
- Elrod, H.; Ng, C. A Theory for Turbulent Fluid Films and Its Application to Bearings. J. Lubr. Technol. 1967, 89, 346–362. [Google Scholar] [CrossRef]
- Hirs, G. A Bulk-Flow Theory for Turbulence in Lubricant Films. J. Lubr. Technol. 1973, 95, 137–146. [Google Scholar] [CrossRef]
- Dousti, S.; Allaire, P.; Dimond, T.; Cao, J. An extended reynold equation applicable to high reduced reynolds number operation of journal bearings. Tribol. Int. 2016, 102, 182–197. [Google Scholar] [CrossRef]
- Armentrout, R.; He, M.; Haykin, T.; Reed, A. Analysis of turbulence and convective inertia in a water-lubricated tilting-pad journal bearing using conventional and cfd approaches. Tribol. Trans. 2016, 60, 1129–1147. [Google Scholar] [CrossRef]
- Guo, Z.; Hirano, T.; Kirk, R. Application of cfd analysis for rotating machinery—Part I: Hydrodynamic, hydrostatic bearings and squeeze film damper. J. Eng. Gas Turbines Power 2005, 127, 445–451. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, R.; Sugita, N.; Mao, J.; Shinshi, T. Identification of bearing dynamic parameters and unbalanced forces in a flexible rotor system supported by oil-film bearings and active magnetic devices. Actuators 2021, 10, 216. [Google Scholar] [CrossRef]
- Sun, W.; Yan, Z.; Tan, T.; Zhao, D.; Luo, X. Nonlinear characterization of the rotor-bearing system with the oil-film and unbalance forces considering the effect of the oil-film temperature. Nonlinear Dyn. 2018, 92, 1119–1145. [Google Scholar] [CrossRef]
- Takenaka, K.; Hayashi, T.; Miyagawa, K. Application of CFD analysis for static and dynamic characteristics of hydrodynamic journal bearing. In Proceedings of the International Symposium on Transport Phenomena and Dynamics of Rotating Machinery (ISROMAC 2017), Maui, HI, USA, 16–21 December 2017. [Google Scholar]
- Li, Q.; Liu, S.; Pan, X. A new method for studying the 3d transient flow of misaligned journal bearings in flexible rotor-bearing systems. J. Zhejiang Univ. Sci. A 2012, 13, 293–310. [Google Scholar] [CrossRef]
- Li, Q.; Yu, G.; Liu, S.; Zheng, S. Application of computational fluid dynamics and fluid structure interaction techniques for calculating the 3d transient flow of journal bearings coupled with rotor systems. Chin. J. Mech. Eng. 2012, 25, 926–932. [Google Scholar] [CrossRef]
- Kostornov, A.; Zozulya, V.; Sin’kov, V.; Shevchuk, M.S. Bearing materials based on fibers and liquid-metal lubricants. Sov. Powder Metall. Met. Ceram. 1973, 12, 534–537. [Google Scholar] [CrossRef]
- Xu, M.; Chen, W. Research Progress and Prospect of Liquid Metals Used as Lubricants. J. Mech. Eng. 2020, 56, 137–146. [Google Scholar]
- Zhang, J.; Yao, Y.; Sheng, L.; Liu, J. Self-fueled biomimetic liquid metal mollusk. Adv. Mater. 2015, 27, 2648–2655. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Zhu, W.; Liu, H.; Shi, J.; Wang, Y.; Tian, W. Dynamic characteristics analysis of the hydro-hybrid liquid sodium lubricated bearing-rotor coupled system in the two-circuit main loop liquid sodium pump system. Ann. Nucl. Energy 2020, 136, 107059. [Google Scholar] [CrossRef]
- Huang, B.; Yun, Y.; Pu, K.; Zhao, B.; Wu, K. Lubrication performance analysis of Lead-Bismuth Internal-Feedback bearings in the nuclear main pump system. Ann. Nucl. Energy 2023, 192, 109936. [Google Scholar] [CrossRef]
- Bokov, P.; Baranova, V.; Kustov, M.; Antonenkov, M.; Besnosov, A. Peculiarities of hydrodynamics of lead and lead-bismuth coolant flows of reactor loops. In Proceedings of the 18th International Conference on Nuclear Engineering, Xi’an, China, 17–21 May 2010. [Google Scholar] [CrossRef]
- Singhal, A.; Athavale, M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing Corporation: Washington, DC, USA, 1980. [Google Scholar]
- Li, Q.; Zhang, S.; Xu, W. Analysis of nonlinear oil film force of journal bearings based on 3D transient flow field calculation. J. Vib. Shock. 2018, 37, 141–147. [Google Scholar]






| Parameter | Symbol | Value |
|---|---|---|
| Radius of stationary wall | 65.12 mm | |
| Radius of rotating wall | 65 mm | |
| Groove radius | 6 mm | |
| Bearing length | L | 195 mm |
| Rotating speed | N | 1200 r/min |
| Viscosity of LBE | μ | 0.001761 Pa·s |
| Density of LBE | ρ | 10,298 kg·m−3 |
| Saturated vapor pressure | 1 × 10−7 Pa | |
| Pressure inlet | 0.1 MPa (relative pressure) | |
| Pressure outlet | 0.1 MPa (relative pressure) |
| Numerical Method | Stiffness Coefficients (106 N/m) | Damping Coefficients (104 N·s/m) | ||||||
|---|---|---|---|---|---|---|---|---|
| Kxx | Kyx | Kxy | Kyy | Cxx | Cyx | Cxy | Cyy | |
| VT-FAST [14] | 40 | 87.2 | −19.4 | 59.1 | 5.75 | 5.41 | 4.93 | 16.7 |
| DyRoBeS-BePerf [14] | 38 | 84.8 | −15.2 | 65.2 | 4.86 | 4.29 | 4.29 | 16.1 |
| VT-EXPRESS [14] | 33.9 | 85.3 | −13.1 | 65 | 4.38 | 4.5 | 3.87 | 15.9 |
| CFX-TASCflow [14] | 41.2 | 88 | −21.9 | 56 | 6.92 | 5.9 | 6.66 | 18.2 |
| FLUENT with mixture model | 41.2 | 86.6 | −19.7 | 62.3 | 7.98 | 4.31 | 4.42 | 12.7 |
| N/r·min−1 | NCG Content | |||
|---|---|---|---|---|
| 1.0 × 10−6 | 10.0 × 10−6 | 40.0 × 10−6 | 100.0 × 10−6 | |
| 1200 | −4.65 × 10−4 | −5.55 × 10−4 | −5.27 × 10−4 | −6.99 × 10−4 |
| 3000 | −6.93 × 10−3 | −5.39 × 10−3 | −8.18 × 10−3 | −8.73 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, K.; Zhang, Y.; Ma, X.; Cheng, Z. Numerical Study on Characteristics of Lead-Bismuth Lubricated Hydrodynamic Bearing Considering Non-Condensable Gas. Lubricants 2024, 12, 326. https://doi.org/10.3390/lubricants12090326
Lyu K, Zhang Y, Ma X, Cheng Z. Numerical Study on Characteristics of Lead-Bismuth Lubricated Hydrodynamic Bearing Considering Non-Condensable Gas. Lubricants. 2024; 12(9):326. https://doi.org/10.3390/lubricants12090326
Chicago/Turabian StyleLyu, Kefeng, Yuanyuan Zhang, Xudan Ma, and Zude Cheng. 2024. "Numerical Study on Characteristics of Lead-Bismuth Lubricated Hydrodynamic Bearing Considering Non-Condensable Gas" Lubricants 12, no. 9: 326. https://doi.org/10.3390/lubricants12090326
APA StyleLyu, K., Zhang, Y., Ma, X., & Cheng, Z. (2024). Numerical Study on Characteristics of Lead-Bismuth Lubricated Hydrodynamic Bearing Considering Non-Condensable Gas. Lubricants, 12(9), 326. https://doi.org/10.3390/lubricants12090326





