1. Introduction
Nowadays, the Brayton cycle system with S-CO
2 (supercritical CO
2) as the working medium offers the benefits of high efficiency, high energy density, and small equipment size. For this reason, it has attracted the wide attention of the scientific community [
1,
2,
3]. For such a closed-cycle system, the shaft-end seal’s sealing effect significantly affects the efficiency of its turbomachinery [
4]. Compared to other types of seals, the dry gas seal has the best comprehensive sealing performance under harsh S-CO
2 turbomachinery operating conditions and is, therefore, recommended [
5]. Current research on the S-CO
2 dry gas seal focuses on several aspects of the steady-state seal performance, including the real gas effect, centrifugal inertia force effect, thermal–fluid–solid coupling deformation, choked flow, and turbulence effect [
6,
7,
8,
9,
10,
11,
12,
13,
14]. However, the balanced gas film is always disturbed during seal operation due to the existence of manufacturing defects, axial eccentricity, assembly misalignment, and rotor runout [
15]. The dynamic characteristics of the gas film not only directly affect the tracking response of the stationary ring to the rotating ring, but also have become the source of instability of the dry gas seal dynamics system [
16]. The S-CO
2 dry gas seals operate at high pressure, temperature, and rotational speed conditions. Therefore, to enable the S-CO
2 dry gas seal to operate stably without contact and damage, the dynamic characteristics of its gas film need to be studied.
The dynamic characteristics of the gas film, as an essential part of the dry gas seal dynamics, have been extensively studied in the literature. Three main theoretical calculation methods have been used to analyse the dynamic characteristics of dry gas sealing systems, namely, the step jump [
17,
18], the perturbation method [
19,
20], and direct numerical simulation [
15,
21]. The perturbation method has been widely used because of its comparative advantages, such as fast calculation speed and reliable prediction of dynamic performance change trends. Once the dynamic stiffness and damping coefficients are obtained using the perturbation method, it is possible to assess the dry gas seal’s dynamic characteristics and determine whether the seal system will be destabilised by self-excited vibrations [
22]. Furthermore, the dynamic stiffness and damping coefficients can be used to formulate the differential equations of motion and then analytically calculate the dynamic behaviour of the seal ring. Zirkelback et al. [
23] solved the zero-order and first-order equations characterising the static and dynamic performance of a spiral groove dry gas seal using the finite element and perturbation methods. The authors derived the axial stiffness and damping coefficients, which depend on the perturbation frequency. Subsequently, Faria [
24] found that the frequency dependence of the gas film dynamic coefficient became more significant at high excitation frequencies. In another interesting work, Liu et al. [
16] numerically solved the stiffness and damping coefficients of the end-face gas film seal using frequency perturbation and finite element methods. The authors pointed out that the cross effect between the axial and angular perturbations was small. Similarly, Ruan [
20] reported that the dynamic coefficients of the gas film have frequency dependence, and the axial and angular modes are decoupled from each other. The above-mentioned findings provide theoretical support for simplifying the three-degrees-of-freedom perturbation motion of the dry gas seal into two mutually independent perturbation motions. In this regard, Ding and Han et al. [
25,
26] studied the spiral-groove dry gas seal’s axial and angular vortex motion by applying the PH linearisation method. The seal structure parameters for seal system destabilisation under certain conditions were obtained. Yuan et al. [
27] analysed the rotor dynamic performance of the designed DGS using the frequency-dependent rotor dynamic coefficients stiffness damping model and mesh deformation technique, which showed that the tilt of the seal rings brings undesired influences on both the static and rotor dynamic performance of S-CO
2 DGS. Xu et al. [
28] investigated the variation rule of the angular vibration stability threshold of the spiral-groove dry gas seal with operating condition parameters and structural parameters and pointed out that the vibration stability in the angular direction is independent of the spring stiffness.
With the development of dry gas seals, more extensive research on the dynamic properties of the gas film based on the perturbation method has been conducted. Zhang et al. [
29] obtained the gas film stiffness and damping coefficients of a dynamic–static hybrid gas seal and presented a critical instability criterion for axial self-oscillation. By studying the impact of the real gas on the gas film dynamic characteristics of the T-groove dry gas seal, Song et al. [
30] pointed out that the effect of the real gas on the gas film stiffness and gas film damping is related to its deviation from the ideal gas. Chen et al. [
31] revealed the influence mechanism of the dynamic stiffness and damping coefficient of the dry gas seal with the hyperelliptic curved groove on the dynamic tracking performance. Later, by performing kinetic theory and experiments, Chen et al. [
32] investigated the dynamic characteristics of a spiral-groove dry gas seal at high speed. The experimental results showed that the existence of a larger amplitude of the film thickness perturbation led to a higher degree of nonlinearity in the dynamic stiffness and damping of the gas film. Li and Li et al. [
33,
34] indicated that the larger viscosity of the oil and gas two-phase fluid enables the two-phase dynamic pressure seal to have a larger stiffness coefficient, damping coefficient, and better dynamic tracking characteristics. Teng et al. [
35] investigated the two-degrees-of-freedom angular free vibration system of a dry gas seal and pointed out that the angular main damping and main stiffness were not simply the larger the better, but there were preferred values in the interval greater than the stability threshold. Recently, Park et al. [
36] showed that turbulence effects increase the stiffness and damping coefficients and slip effects decrease the stiffness and damping coefficients. The above-mentioned works provide an essential impetus for analysing the dynamic properties of the gas film. However, they are mainly based on the laminar flow assumption and do not consider centrifugal inertia force effects. In addition, the impact of physical parameters’ (density, viscosity, specific heat capacity, etc.) perturbations on the dynamic properties of gas films have also not been taken into account.
For the S-CO
2 dry gas seal, the centrifugal inertia force and turbulence effects within the gas film are accentuated due to its operation at high rotational speeds and the properties of supercritical carbon dioxide with high density and low viscosity [
12]. In addition, the CO
2 on the high-pressure side of the seal inlet is in a supercritical state with high energy density. There are also large nonlinear variations in the fluid transport properties (viscosity, thermal conductivity, specific heat capacity, etc.) and thermodynamic behaviours during the flow along the seal surface to the low-pressure side. Therefore, the influence of multiple complex effects, such as the centrifugal inertia force effect, turbulence effect, real gas effect, viscosity, density, specific heat capacity, etc., should be taken into account when calculating the dynamic characteristics of gas film for the S-CO
2 dry gas seal. Bi et al. [
37] developed an extension of the frequency perturbation method to perturb the density, viscosity, Reynolds number, and turbulence coefficients for dynamic coefficient calculations for S-CO
2 lubricated bearings. The frequency-dependent stiffness and damping coefficients were then obtained by numerically calculating the compressible turbulent Reynolds equation containing the kinetic variables. Later, Jiang et al. [
38] investigated the dynamic properties of the S-CO
2 dry gas seal using the frequency perturbation approach developed by Bi et al. The authors noted that turbulence and real gas effects had a considerable impact on the dynamic properties of the dry gas seal. The work of Bi and Jiang has greatly promoted the study of the gas film dynamic properties in the field of bearings and seals with S-CO
2 as the medium. However, their research was carried out in an isothermal field, i.e., the temperature perturbation was not considered. According to the literature, the flow within the S-CO
2 dry gas seal is closer to adiabatic flow [
39]. Moreover, there is a large temperature gradient in the temperature distribution within the flow field. Hence, when the gas film thickness is perturbed by the frequency perturbation method, apart from the pressure change of the gas film, the temperature of the gas film will also change. Because the density, viscosity, specific heat capacity, etc., are also functions of pressure and temperature, they will be perturbed by both pressure and temperature. The perturbation of these physical parameters will further cause the perturbation of turbulence and inertia coefficients. Consequently, taking temperature into account when studying the dynamic characteristics of the gas film can be more accurate and comprehensive.
To accurately obtain the gas film’s dynamic coefficient of the S-CO2 dry gas seal, the frequency perturbation method was employed in this work to perturb the associated variables. More specifically, the film thickness, pressure, temperature, physical parameters, Reynolds number, turbulence coefficient, and inertia coefficient were perturbed in the non-constant Reynolds and energy equations; then, a complete variable perturbation model (CVPM) applicable to the adiabatic flow process was established. The finite difference method was also used to solve the CVPM. The dynamic stiffness and damping coefficients of the gas film were calculated and analysed under a variety of conditions, operating parameters, and frequency ratios. These findings provide additional support for future dynamic analyses of S-CO2 dry gas sealing.
2. Method of Analysis
2.1. Gas Film Dynamic Characteristic Coefficient
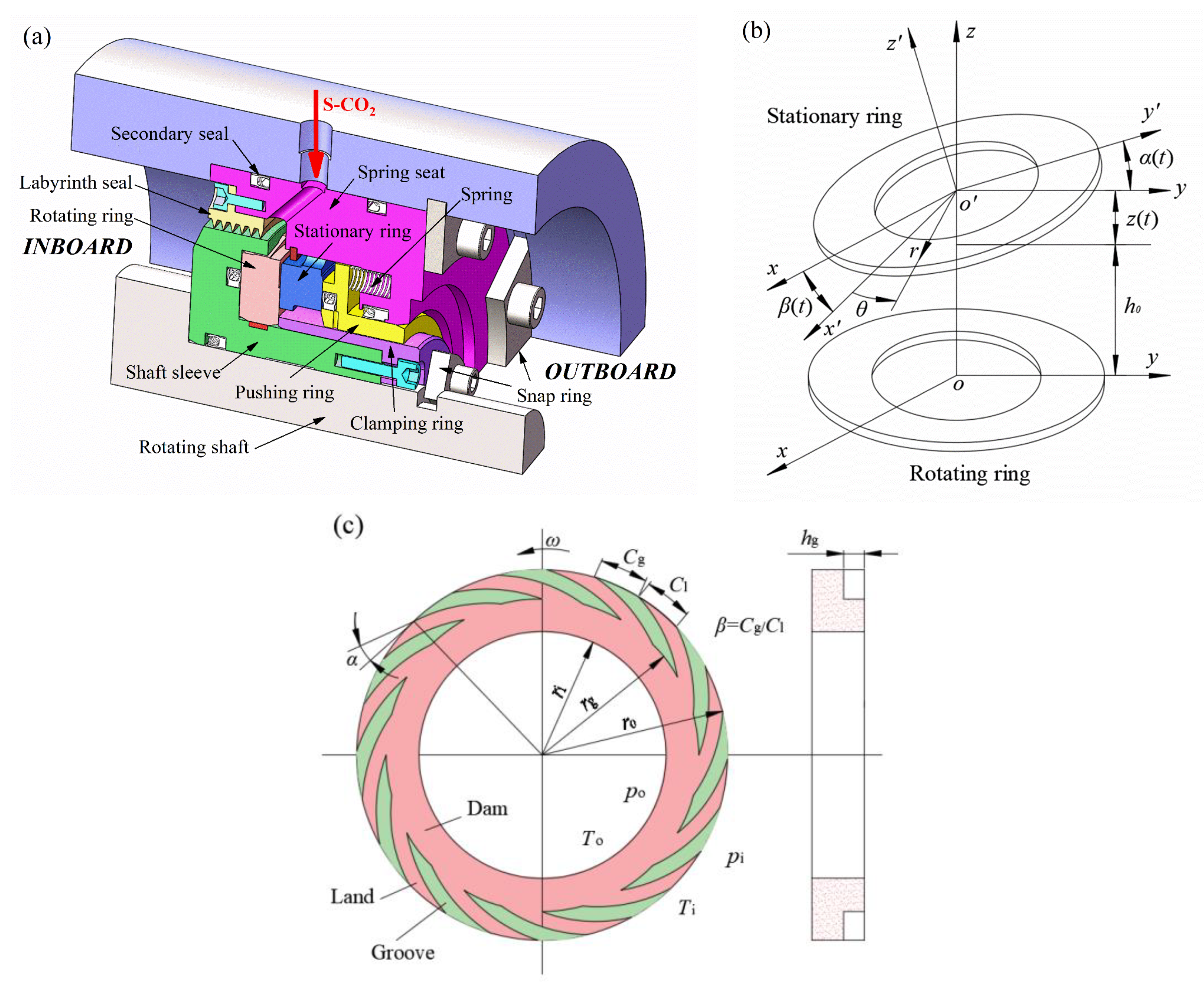
Figure 1a depicts a schematic diagram of the S-CO
2 dry gas seal. The rotating ring is mounted on the shaft sleeve and then forms a rotating assembly with the shaft under the action of the clamping ring and snap ring. The stationary ring, push ring, spring, and spring seat form the static assembly. The hydrostatic pressure and spring force hold the rotating and stationary rings together when the shaft is motionless. A hydrodynamic pressure is created by the spiral groove on the rotating ring’s end face as it revolves with the shaft, separating the rotating and stationary rings. Meanwhile, a very thin gas film exists between the sealing surfaces. In the dynamic analysis of the dry gas seal, the role of the gas film is often equated to that of a spring and a damper. Thus, the stiffness coefficient and damping coefficient of the gas film can be used to characterise and analyse the ability of the gas film to resist external disturbances. The key to the dynamic analysis of a dry gas seal is to determine these dynamic properties’ coefficients. The stationary ring is mounted on a push ring supported by a flexible spring, which can track the motion of the rotating ring both in the axial direction and in the two angular directions of the orthogonal axis. Hence, the dynamic coefficients of the gas film have three degrees of freedom. These coefficients were calculated here based on the equilibrium state when the sealing surfaces were completely aligned. Miller et al. [
40] pointed out that the equilibrium state offers a standard reference condition irrespective of the rotating or stationary ring misalignment. However, a well-designed seal will maintain a small movement at this equilibrium state even if there is misalignment. Thus, the error introduced in the gas film characteristic coefficients will be small. According to the sealing structure in
Figure 1a, a three-degrees-of-freedom gas film’s dynamic analysis model was established, as shown in
Figure 1b.
Figure 1c shows the geometry of the rotating ring. A number of logarithmic spiral grooves with a groove depth of
hg are arranged between the groove root diameter,
rg, and the outer diameter,
ro. The groove width ratio,
β, is the ratio between the arc length,
Cg, of the groove area and the arc length,
Cl, of the land area at the outer diameter side.
The forces and moments of the gas film on the stationary ring are
Fz,
Mx, and
My, respectively:
where
p is the pressure, and
r and
θ denote the radius and angle of the seal end face at any point, respectively.
The small perturbation technique was used to perturb the displacement and velocity at the equilibrium position shown in
Figure 1b. The perturbed displacement and velocity are
z and
, and the perturbed angle and angular velocity are
α,
β,
, and
, respectively.
z denotes the movement along the axial direction and
α and
β refer to the angular oscillation around the
x and
y axes. The perturbation displacement (or angle) and velocity (or angular velocity) affect the gas film pressure through the film thickness, further causing a change in the force and moment acting on the stationary ring. Thus, a Taylor expansion of
Fz,
Mx, and
My induced by the perturbation displacement (or angle) and velocity (or angular velocity), retaining the linear terms, yielded the following relationship:
where,
Fz0,
Mx0, and
My0 denote the quantities in the equilibrium position. According to the above-mentioned equation, the nine stiffness coefficients and nine damping coefficients can be defined as follows:
where
m is taken as
z,
α, and
β, respectively, and
n is taken as
,
, and
. The first subscripts of the stiffness coefficient,
k, and the damping coefficient,
c, indicate the direction of the force or moment. The second subscripts signify the direction of the perturbation displacement or velocity.
In this work, the small perturbation quantity was given by the harmonic motion at a frequency
s. Then, the perturbation displacement and velocity in the three coordinate directions can be expressed as follows:
where
is the perturbation displacement amplitude. Moreover,
and
represent the perturbation angle amplitude,
s is the perturbation frequency, and
refers to the frequency ratio.
The dynamic film thickness,
h, will be composed of two parts: the equilibrium film thickness,
h0, and the perturbed film thickness,
. Combining with
Figure 1, the dynamic gas film thickness can be expressed according to the displacement perturbation in three coordinate directions, as follows:
For the S-CO2 dry gas seals, pressure and temperature are coupled with each other. The impact of the perturbation displacement on the film thickness will cause a change in the gas film pressure and temperature.
In addition, the perturbation dynamic pressure and temperature need to be expressed as complex variables because the perturbation dynamic film thickness contains an imaginary part. Based on the above-mentioned analysis, the dynamic pressure and temperature can be expressed as the sum of equilibrium and perturbation quantities, and the specific expressions are defined as follows:
where
p0 and
T0 are the steady-state pressure and temperature, respectively,
pz and
Tz are the axial perturbation dynamic pressure and temperature, respectively,
pα and
pβ state the angular perturbation dynamic pressures, respectively, and
Tα and
Tβ are the angular perturbation dynamic temperatures, respectively.
As can be seen from Equations (1)–(3) and (5), the real part,
pkr, and the imaginary part,
pki, of the perturbation dynamic pressure will correspond to the gas film’s stiffness and damping, respectively. Thus, the gas film stiffness and damping can be expressed as follows:
Generally, the above dynamic coefficients need to be converted into a dimensionless form for convenient analysis. Via nondimensionalisation, the following dimensionless forms of dynamic stiffness coefficients and damping coefficients of the gas film were obtained:
where
pa is the ambient pressure,
hg stands for the depth of the spiral groove,
ω denotes the angular velocity of the rotating ring, and
ri represents the inner diameter of the seal ring.
From Equation (8), it can be observed that pkr and pki need to be obtained from the gas film’s perturbation control equation to determine and analyse the stiffness and damping coefficients. In the following, the film thickness, pressure, temperature, density, viscosity, constant pressure specific heat, Reynolds number, turbulence coefficient, and inertia coefficient will be perturbed by the frequency perturbation method based on the non-constant Reynolds and energy equations. Then, the pressure and temperature perturbation equations will be established.
2.2. Flow Field Governing Equation in Gas Film
The deformation of the seal end face was ignored, the fluid was assumed to be a Newtonian fluid, and the pressure gradient in the direction of the film thickness was neglected. In the turbulent flow regime, the compressible unsteady Reynolds equation considering the impact of the centrifugal inertial forces is as follows [
32,
33]:
where
η is the viscosity,
ρ is the density, and
ω is the rotational speed.
Gθ,
Gr, and
λ represent the circumferential turbulence coefficient, the radial turbulence coefficient, and the inertia coefficient, respectively, which are related to the local Reynolds number,
Rh =
ρωrh/
η. In this work, the Ng-Pan model [
41] was used. When
Rh ≤ 1000, the flow is laminar:
,
, and
. When
Rh >1000, the flow is turbulent:
,
,
,
,
, and
.
The pressure and temperature fields of the gas film of the S-CO
2 dry gas seal can be coupled together. Therefore, the energy equation also needs to be solved when solving the pressure field. Yan et al. [
39] showed that the flow process within the S-CO
2 dry gas seal is close to adiabatic flow. In this regard, the simplified energy equation for a compressible fluid under adiabatic conditions from the literature [
39] was used in this work, which contains the impact of turbulence and centrifugal inertia force, and can be expressed as follows:
where
T is temperature,
cp is the specific heat capacity at constant pressure, and
ur and
uθ denote the radial and circumferential mean velocities, respectively.
2.3. Multivariable Perturbation Involving Pressure and Temperature
When the pressure and temperature are perturbed, the corresponding physical parameters of CO
2 will be also perturbed. In the previous works by Bi [
37] and Jiang [
38], the pressure perturbation was only considered, and the temperature perturbation on the physical parameters was neglected. In this work, both pressure and temperature perturbations were taken into account. The CO
2 physical parameter,
ϕ (density, viscosity, specific heat at constant pressure, etc.) is a binary function, with the pressure,
p, and temperature,
T, as independent variables. Thus, by performing a Taylor series expansion for the dynamic physical parameter
ϕ at
, with perturbation pressure,
, and perturbation temperature,
, and retaining the zero-order and first-order terms, the following relationship can be obtained:
where
is the value of the physical parameter
at
,
denotes the partial derivative of the physical parameter
ϕ to the pressure,
p, at the point
, and
states the partial derivative of the physical parameter
ϕ to the temperature,
T, at the point
.
According to Equation (12), the density, viscosity, and specific heat of constant pressure of CO
2 can be expressed as the sum of the equilibrium and perturbation quantities, respectively, using the following expressions:
where
, and
.
where
and
.
where
and
.
The turbulence coefficient, inertia coefficient, and Reynolds number in the Reynolds equation and energy equation are related to the physical parameters and the film thickness. Therefore, they need to be expressed one-by-one for establishing the perturbation control equations.
Substituting Equations (4), (13), and (14) into the Reynolds number,
Rh =
ρωrh/
η, and neglecting small quantities of order two or more, the following relationship can be derived:
where
is the Reynolds number at the equilibrium position.
Both the turbulence coefficient and the inertia coefficient contain
. Therefore, Equation (16) was expanded to the
β power to facilitate the analytical calculation, and the small quantities above the second order were neglected, yielding the following relationship:
Substituting Equation (17) into Equations (10b)–(10d), the following relationship can be obtained by operation:
where
,
, and
are the circumferential turbulence coefficient, radial turbulence coefficient, and inertia coefficient at the equilibrium position, respectively.
2.4. Complete Variable Perturbation Model (CVPM)
The film thickness, pressure, physical parameters, turbulence coefficients, and inertia coefficients containing perturbation quantities can be substituted into the Reynolds equation shown in Equation (10a). The latter can be linearly expanded by the perturbation method, and then, retaining and separating the steady-state term and the first-order term, the steady-state and perturbed Reynolds equation of the following form can be obtained.
Steady-state Reynolds equation:
Perturbed Reynolds equation:
The constants
ξ1,
ξ2,
ξ3,
t1, and
t2 in Equation (20) are as follows:
As can be seen from Equation (20), the equation is not convenient for solving the perturbed dynamic pressure. Therefore, to determine the real part,
pkr, and imaginary part,
pki, of the dynamic pressure in each perturbation direction, Equation (20) needs to be separated. By taking the partial derivatives of Equation (20) with respect to
zε,
αε, and
βε, respectively, and separating the real and imaginary parts, the real equation of
pkr and the imaginary equation of
pki, as shown in
Appendix A, can be obtained. The perturbed Reynolds equation in the separated form in
Appendix A is a generalised form in three-degrees-of-freedom directions (one axial and two angulars). Thus, by taking
z,
α, and
β for the subscript
k, the perturbative pressure equations on the corresponding degrees of freedom can be obtained. In this way, a convenient solution for the perturbed dynamic pressure is provided.
The film thickness, pressure, temperature, physical parameters, turbulence coefficients, and inertia coefficients containing perturbation quantities can be substituted with the same method into the energy equation. Then, the steady-state and perturbation energy equations in the following forms can be obtained by retaining and separating the zero-order and first-order terms.
Steady-state energy equation:
Perturbed energy equation:
with the following constants:
To determine the real part,
Tkr, and imaginary part,
Tki, of the perturbed dynamic temperature, the partial derivatives of Equation (22) were derived with respect to
zε,
αε, and
βε, respectively. Then, the real and imaginary parts were separated to obtain the real equation of
Tkr and the imaginary equation of
Tki, as shown in
Appendix B. Taking the subscript
k for the equations in the separated form shown in
Appendix B as
z,
α, and
β, respectively, the perturbed energy equation on the corresponding degrees of freedom can be obtained.
The physical parameters, Reynolds number, turbulence coefficient, and inertia coefficient within the gas film are fundamentally affected by the pressure and temperature of the flow field, which in turn act on the flow field. Hence, there is a strong nonlinear relationship between them. A more comprehensive and accurate representation of this nonlinear relationship can be achieved by perturbing the temperature on the foundation of the pressure perturbation. To this end, all variables in the governing equation were perturbed when establishing the proposed model. Therefore, this model can be called CVPM. The CVPM consists of the steady-state Reynolds equation, the steady-state energy equation, the perturbed Reynolds equation, and the perturbed energy equation. Generally, the CVPM further extends and improves the existing frequency perturbation method. Suppose the turbulence coefficients in the present model are set by laminar flow under isothermal conditions, and thus, the viscosity perturbation and inertia effects are not considered. In that case, the CVPM can be reduced to the classical perturbation model [
14,
18].
2.5. Boundary Conditions and Numerical Methods
At the inlet of the gas film on the seal end face, the pressure and temperature satisfy the Dirichlet boundary conditions:
The outlet of the seal end face uses the choked flow boundary condition [
9,
10,
34]. The Mach number,
M, at the outlet determines whether the flow is choked. The Mach number is
M =
V0/
c, where
c denotes the sound speed, and
refers to the total velocity. For the outlet Mach number
Moutlet ≤ 1, the outlet pressure was set to
po = 0.101 MPa. For the outlet Mach number
Moutlet > 1, the outlet pressure was changed until the outlet Mach number was equal to 1, as follows:
The seal ring’s circumferential direction has the periodic pressure and temperature boundary conditions shown below:
The subscripts in Equations (23a), (23b), (24b), (25a), and (25b) are taken as z, α, and β, respectively.
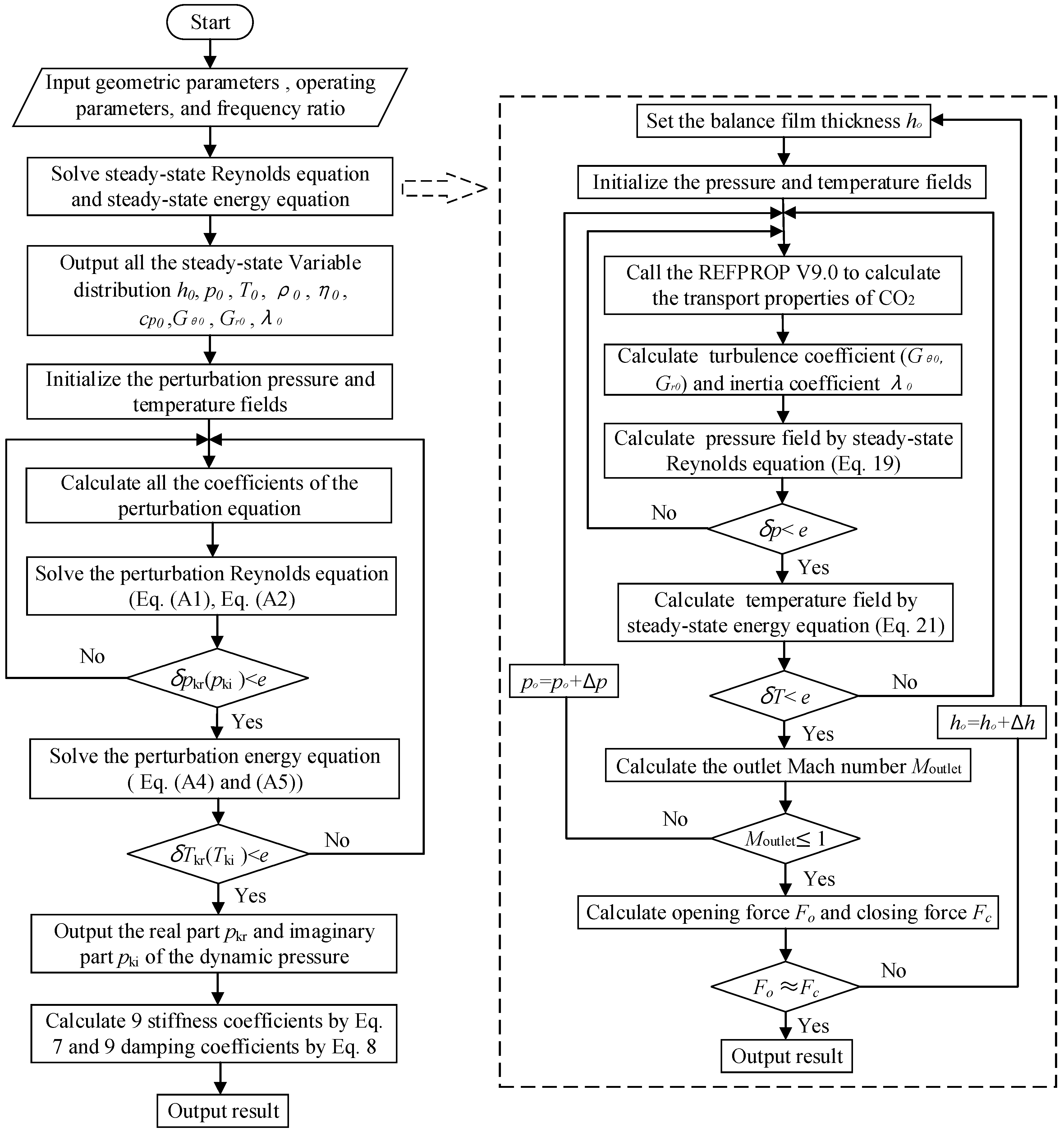
In the process of solving, to accurately access the CO
2 physical property parameters and thermodynamic parameters, REFPROP [
42], namely, a physical property calculation software released by NIST, was directly called in this work. The CVPM was discretised using a five-grid difference scheme, and a coupled solution was used to obtain the steady-state pressure and temperature distributions of the gas film inside the seal end face, as well as the perturbation pressure and temperature distributions. Then, the stiffness and damping coefficient of the gas film could be calculated. The solution process is depicted in
Figure 2. The solution steps enclosed by dotted lines in
Figure 2 belong to the steady-state flow field calculation part. The latter stems from the fact that the pressure and the temperature fields were coupled together. Therefore, repeated coupling iterations of the pressure and temperature fields were required until the pressure field, the temperature field, and the exit boundary conditions satisfied their respective convergence conditions. As a result, a converged steady-state gas film flow field could be obtained. If the calculation was based on a constant film thickness, the step of the force balance judgment was not carried out.
Based on the steady-state solution and combining the equations in
Appendix A and
Appendix B, the real part,
pkr, and imaginary part,
pki, of the dynamic pressure could be obtained by the numerical solutions. However, it is easy to note from the perturbative Reynolds equation in
Appendix A and the perturbative energy equation in
Appendix B that the perturbative dynamic pressure and temperature were not only coupled together. Nevertheless, their respective real and imaginary parts were also coupled together. Fortunately, each perturbation direction is independent, so it was only necessary to solve the equations for each perturbation direction. The difficulty of solving the perturbation Reynolds equation and the perturbation energy equation was further reduced because the separated form of the perturbation Reynolds equation and the perturbation energy equation were linear equations and did not contain the time term. However, four equations still needed to be solved simultaneously, coupled in each direction, i.e., pressure–real part equation, pressure–imaginary part equation, temperature–real part equation, and temperature–imaginary part equation. The real part,
pkr, and the imaginary part,
pki, of the perturbed dynamic pressure could be calculated after solving the perturbed equations in three perturbation directions (a total of twelve perturbed equations). Finally, the gas film’s nine stiffness and nine damping coefficients could be obtained.
3. Results and Discussion
The perturbed equations established in this work were first validated. Next, the calculation and analysis of the gas film dynamic characteristic coefficients under different calculation conditions were carried out. Two validation cases were used to validate the model, and the geometrical structure parameters and operating conditions are listed in
Table 1 and
Table 2, respectively. In addition, the data in column 4 shown in
Table 1 and
Table 2 were used to calculate the dynamic coefficients of the gas film in the adiabatic state, unless otherwise specified in the text.
3.1. Validation of CVPM
In the field of dry gas seals, the current calculation of gas film dynamic characteristic coefficients was carried out under isothermal conditions. Therefore, no consistent examples can be used to validate the CVPM considering temperature changes. However, if the temperature perturbation is not considered, the CVPM will be degenerated to an isothermal model so that it can be verified by two steps.
First, the gas film dynamic coefficients were verified under isothermal conditions using the parameters from Ruan’s work [
20], i.e., without considering the temperature perturbation, which is referred to as validation case I. It should be noted that Ruan calculated the gas film characteristic coefficients under the assumption of isothermal and isoviscosity. However, it was not specified which medium was used in this work, and only the viscosity was presented. In dry gas seals, nitrogen is usually used as the sealing gas. Moreover, the viscosity of nitrogen varies from 1.789 × 10
−5 and 1.791 × 10
−5 Pa·s when the pressure is between 0.101 and 0.303 MPa and the temperature is 300 K, which is very close to the viscosity of 1.79 × 10
−5 Pa·s presented by Ruan. Hence, the isothermal and isoviscous conditions in Ruan’s work were approximately equivalent to nitrogen under pressure between 0.101 and 0.303 MPa and temperature at 300 K. Theoretically, the more grids used in the calculation, the more accurate the results are. However, in order to save computational costs, the model in this paper adopted 11,532 nodes in the calculation. This is because the stiffness obtained at such a grid number was nearly close to Ruan’s data. In the case of no special instructions, 11,532 nodes were used in all the calculations below.
The dynamic stiffness and damping of the gas film were obtained by the perturbation solution, which in turn depended on the steady-state solution. Therefore, if there existed one isothermal flow process and one adiabatic flow process with the same operating conditions and sealing structure parameters, the steady-state solutions were relatively close. Therefore, the dynamic coefficients of these two processes were also relatively close. In Case 4 in [
39], the pressure distributions under adiabatic and isothermal flow were very close. Additionally, the leakage rates were also relatively close, which infers that the dynamic coefficient of the gas film under these two flows should be relatively close. Consequently, the CVPM could be validated using the test conditions corresponding to Case 4 in [
39], which is called validation case II. The seal geometry and operating parameters for the above two validation examples are presented in
Table 1 and
Table 2.
From the distribution of gas film stiffness coefficients in
Figure 3a, it can be observed that there was a good agreement between the current model and Ruan’s data [
20]. However, there were some deviations between them, but the maximum relative error did not exceed 6.5%. Under the same calculation conditions, the turbulence coefficients in the current model were consistent with those at laminar flow. Therefore, the main reason for the deviation is that the current calculations consider the viscosity perturbation with pressure and the centrifugal inertia effect. Since the real part pressure,
pkr, and the imaginary part pressure,
pki, are coupled solutions, the validity of the stiffness coefficient can also reflect the validity of the damping coefficient calculation. Therefore, the correctness of the CVPM and the solution procedure under isothermal conditions was proven by validation case I.
After the calculations, the leakage rate of verification case II under isothermal and adiabatic conditions was 2.17 g/s and 1.83 g/s, respectively, which is close to the experimental value of 1.64 g/s in [
39]. This result reflects that the calculation procedure and method of the steady-state solution were correct. The gas film’s stiffness coefficient distribution for verification case II is displayed in
Figure 3b. As expected, the stiffness coefficients for isothermal and adiabatic flows were relatively close and had a consistent trend, but they still differed from each other, with a maximum relative error of no more than 33%. This difference can be attributed to two aspects: on the one hand, the steady-state solutions of the temperature field under the two flows were inconsistent; on the other hand, there was no temperature perturbation in the isothermal flow. The above two examples confirmed the feasibility and correctness of the CVPM and the calculation method in this work.
3.2. Dynamic Coefficients
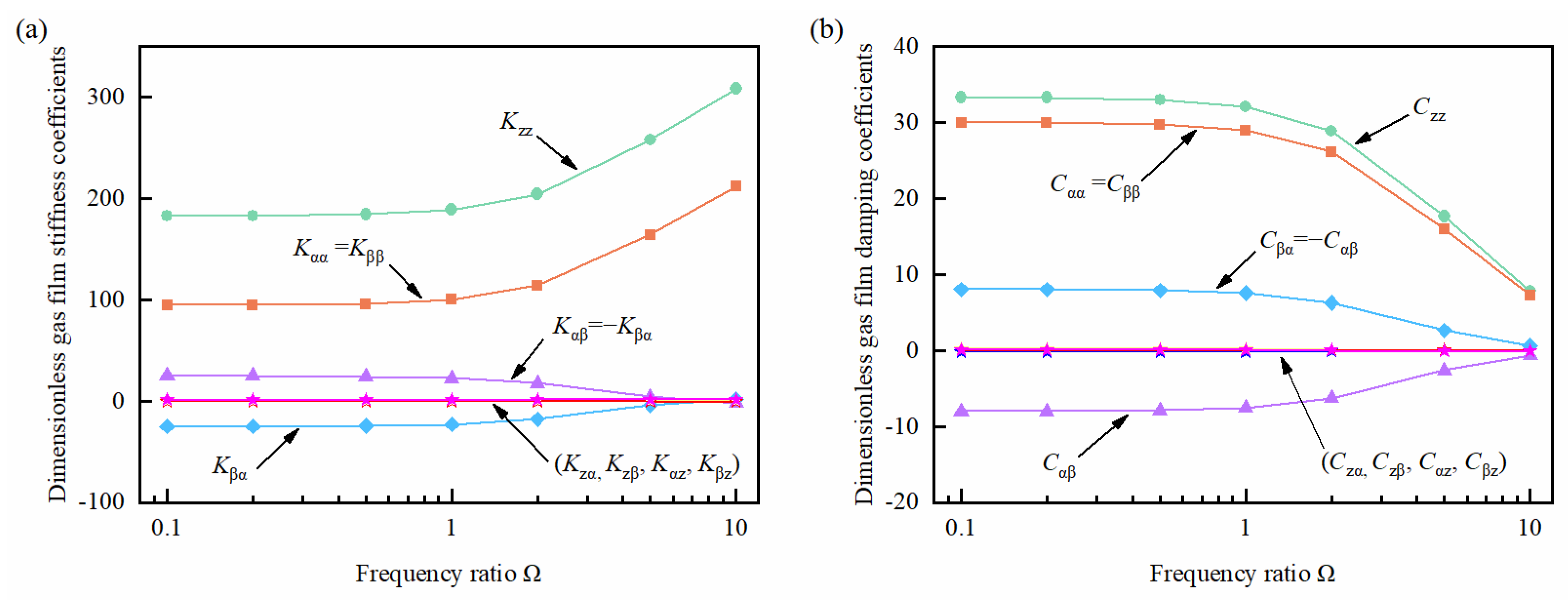
To understand the distribution features of the gas film’s dynamic coefficient of the S-CO
2 dry gas seal, the stiffness coefficients and damping coefficients with frequency ratios ranging from 0.1 to 10 were calculated using the CVPM, as shown in
Figure 4.
From
Figure 4, it can be observed that the gas film dynamic coefficients had the following characteristics. First, the cross-stiffness and -damping between the angular and axial (or axial and angular) directions were approximately zero. This outcome implies that the cross effect between the axial and angular perturbations was small, and the three-degrees-of-freedom perturbed motion could be reduced to two mutually independent perturbed motions, which is consistent with the results of Liu [
16] and Ruan [
20]. Second, the angular cross-stiffness and -damping have symmetry about the zero-coordinate axis, and they are equal in magnitude and opposite in sign. Thus, to facilitate the analysis of the gas film dynamic coefficient, it is only necessary to describe the angular cross-stiffness and -damping in one direction. Finally, these dynamic coefficients had frequency dependence. The stiffness and damping coefficients were insensitive to the frequency dependence for the frequency ratio between 0.1 and 1. When the frequency ratio was greater than 1, the main stiffness coefficients increased nonlinearly with the frequency, while the angular cross-stiffness coefficients were smaller and decreased nonlinearly with the frequency. In contrast, the main damping and angular cross-damping coefficients decreased nonlinearly by increasing the frequency.
3.3. Effect of Different Perturbed Factors
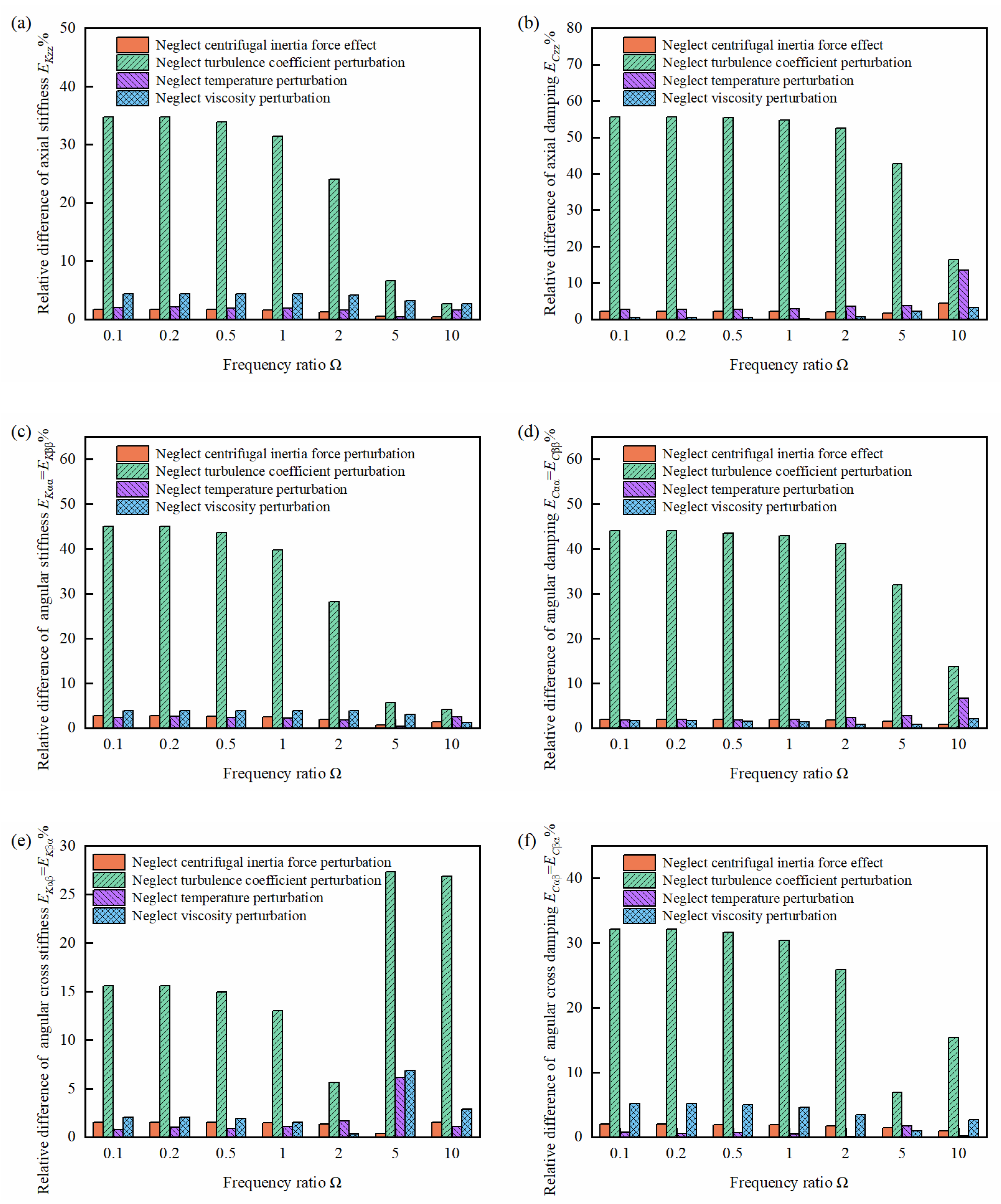
To gain insight into the perturbation intensity of the temperature, viscosity, turbulence coefficient, and centrifugal inertia force in the perturbed Reynolds equation and the perturbed energy equation, a relative difference analysis of the dynamic coefficient of the gas film was performed by neglecting the terms corresponding to these factors in Equations (A1), (A2), (A4), and (A5). The relative difference is defined as: , where is the stiffness (or damping) ignoring a factor, and denotes the stiffness (or damping) of the CVPM. It should also be mentioned that the stiffness and damping coefficients for neglecting different perturbed factors were calculated employing the same steady-state solution, i.e., the steady-state solution of the CVPM. The purpose of using the same steady-state solution was that the perturbed strength of each factor in the perturbed equation can be accurately compared at the same baseline. The term containing the density to the pressure partial derivative in the CVPM was equivalent to the pressure perturbed term in the classical perturbation model. Therefore, the density perturbation was not discussed in this work.
Figure 5 illustrates the distribution of the gas film dynamic coefficient for neglecting different perturbed factors, respectively. It can be concluded that the deviation of the stiffness and damping coefficients from the calculated values of the CVPM was relatively small when the perturbations of viscosity and centrifugal inertia force were neglected. Under these two conditions, the maximum relative difference with the CVPM did not exceed 7% for either the stiffness coefficient or the damping coefficient. When neglecting the temperature perturbation, the maximum relative difference in the stiffness coefficient and the damping coefficient with respect to the CVPM did not exceed more than 14%. The maximum relative difference in the stiffness coefficient was 46% and the maximum relative difference in the damping coefficient was 56% when the turbulence coefficient perturbation was neglected. Overall, the turbulence coefficient perturbation had the most significant impact on the dynamic coefficient of the gas film compared to temperature, viscosity, and centrifugal inertia force.
From Equations (A1) and (A2), it can be observed that the partial derivatives of viscosity, namely, ηp and ηT, and the partial derivatives of density, namely, ρp and ρT, appeared simultaneously in the equations. The viscosity of CO2 was much smaller than the density, and the viscosity variation with pressure and temperature was much less drastic than the variation in the density with pressure and temperature. As a result, the dynamic characteristic coefficient of the gas film did not change much when the viscosity was neglected. For S-CO2 dry gas seals operating at high operating parameters, the centrifugal inertia force effect was accentuated at high inlet pressures and high rotational speeds. Thus, neglecting the centrifugal inertia force perturbation inevitably had an impact on the dynamic coefficient of the gas film. The temperature perturbation indirectly affected the perturbed pressure by density and viscosity, while large temperature variations existed within the S-CO2 dry gas seal gas film. As a result, the dynamic coefficient of the gas film neglecting temperature will deviate from the CVPM. Moreover, it is easy to notice from Equations (A1) and (A2) that the terms containing temperature perturbations were on the right side of the equation, while the perturbed pressure to be determined was on the left side of the equation. Neglecting the temperature perturbation indicated that the terms containing the perturbed temperature on the right-hand side of the equation were zero. Hence, the gas film characteristic coefficients for neglecting the temperature perturbation will deviate from the values under the CVPM. In the turbulent flow state, the values of β1, β2, and β3 were taken as 0.9, 0.96, and 0.367, respectively. Neglecting the turbulence coefficient perturbation implied that β1, β2, and β3 in Equations (A1), (A2), (A4), and (A5) were zero. Thus, the terms containing β1, β2, and β3 in the perturbed equation will be amplified, resulting in considerable changes in the dynamic coefficient.
It can also be seen from
Figure 5 that the relative difference in stiffness coefficients (or damping coefficients) when neglecting viscosity, centrifugal inertia force, and turbulence coefficient perturbations basically decreased with the increasing frequency ratios for frequency ratios 0.1 ≤ Ω ≤ 2. Similarly, in this frequency range, the relative difference in the cross-stiffness coefficient (or cross-damping coefficient) increased with the increase in the frequency ratio, except that the difference in the principal stiffness coefficient (or cross-damping coefficient) decreased with the increase in the frequency ratio when the temperature perturbation was ignored. When the frequency ratio was 2 < Ω ≤ 10, the relative difference in the stiffness coefficient (or damping coefficient) when different factors were ignored had both an increasing trend and a decreasing trend with the increase in the frequency ratio. The reason why the above change trend exists was caused by the following two factors. First, as the frequency ratio increased, the term containing the perturbation frequency on the right-hand side of Equation (20) (or Equation (21a)) enlarged, which led to a reduction in the difference between the equation ignoring various perturbation factors and the CVPM. Second, relative differences were used in conducting the discrepancy analysis, implying that even small differences will result in large relative differences if the two values being analysed are small. However, despite that the principal stiffness coefficient (axial stiffness and angular stiffness) increased with the increase in the frequency ratio, the cross-stiffness coefficient and damping coefficient both decreased with the increase in the frequency ratio, which can be seen from
Figure 4. Therefore, there was a large discrepancy in the relative difference in cross-stiffness coefficients (or damping coefficients) in the high-frequency range.
For a kinetic system consisting of a rotating ring, gas film, stationary ring, and spring, the stiffness and damping of the gas film play a crucial role in its stability. Therefore, in addition to turbulence coefficient perturbations, even very small changes in dynamic coefficients due to temperature, viscosity, and centrifugal inertia force perturbations need to be carefully considered when performing seal stability analysis.
3.4. Influence of the Flow Process
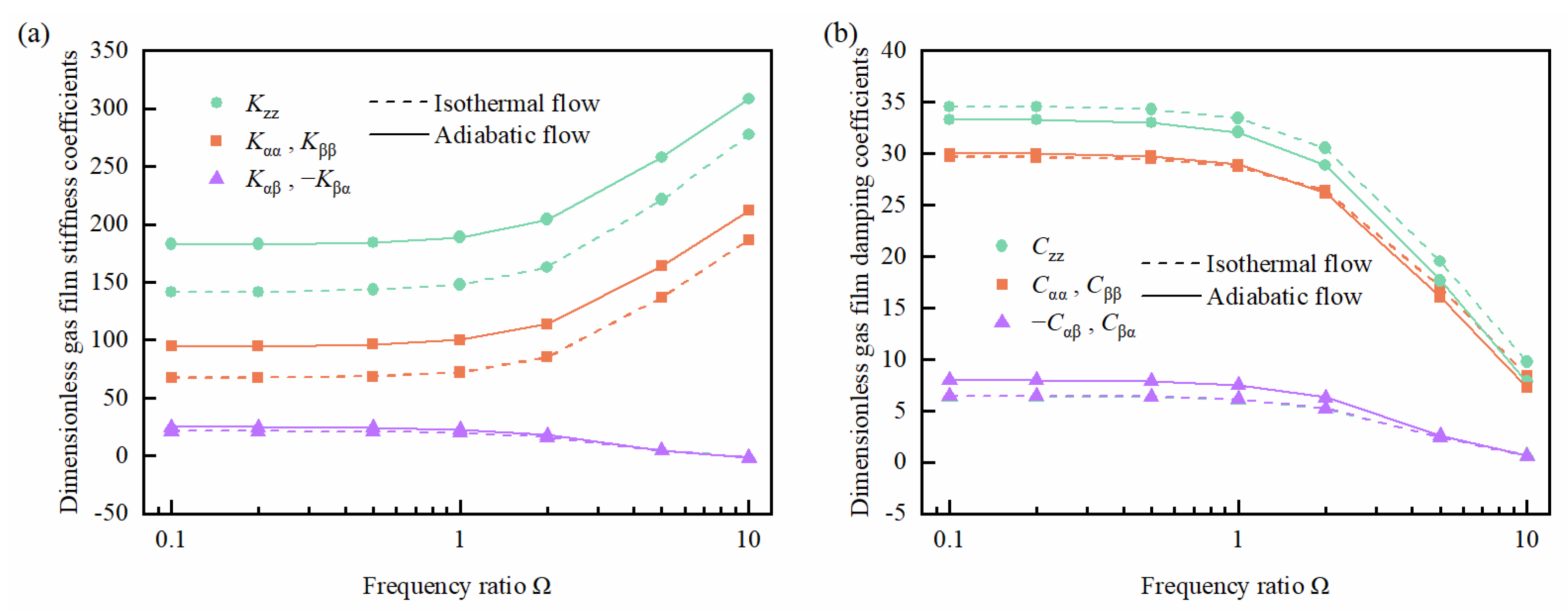
The flow process of S-CO2 along the sealing surface to the low-pressure side was close to adiabatic flow. Hence, the gas film’s dynamic coefficient obtained under isothermal conditions inevitably deviated from the actual situation. To reveal the influence of the flow process, the dynamic coefficients under isothermal and adiabatic flow were calculated and analysed in this section.
The stiffness and damping coefficients under isothermal and adiabatic flow are shown in
Figure 6. As can be observed, the stiffness coefficients (or damping coefficients) under isothermal and adiabatic flow had the same variation trend with the frequency ratio. However, the main stiffness coefficient under adiabatic flow was remarkably larger than that under isothermal flow. The angular cross-stiffness coefficients were nearly equal under both flow conditions. The axial damping coefficient under adiabatic flow was less than that under isothermal flow. When the frequency ratio was less than 1, the angular damping coefficient under adiabatic flow was greater than the value under isothermal flow; on the contrary, when the frequency ratio was greater than 1, the angular damping coefficient under adiabatic flow was less than that under isothermal flow. The angular cross-damping coefficient exhibited values greater than those under isothermal flow. The difference in the flow processes led to a discrepancy in the pressure and temperature distribution of the gas film, which further induced a discrepancy in the density, viscosity, specific heat, and sound speed within the gas film. Therefore, the gas film dynamic coefficients showed differences between the two flow processes. It should also be noted that when the frequency ratio was greater than 1, the difference between the stiffness coefficients (or angular cross-damping coefficients) for both flow conditions decreased as the frequency increased, except for the axial damping coefficient and the angular damping coefficient. Therefore, it can be concluded that the dynamic coefficients of the gas film were affected not only by the flow process but also by the disturbance frequency ratio.
3.5. Influence of Inlet Pressure and Inlet Temperature
The critical pressure and critical temperature of CO
2 were
Pc = 7.38 MPa and
Tc = 304.13 K, respectively, while the S-CO
2 dry gas seal will encounter inlet conditions both near and far from the critical point in actual operation. Hence, to gain insights into the impact of inlet conditions on the gas film dynamic coefficient, the inlet pressures of 8 MPa and 20 MPa and inlet temperatures of 375 K and 450 K were selected for our analysis. To facilitate the calculation and analysis, the gas film dynamic coefficients were calculated at a constant film thickness in this section. The balance film thickness of
h0 = 3 μm was taken, and the rest of the seal geometry parameters were taken from the fourth column of
Table 1.
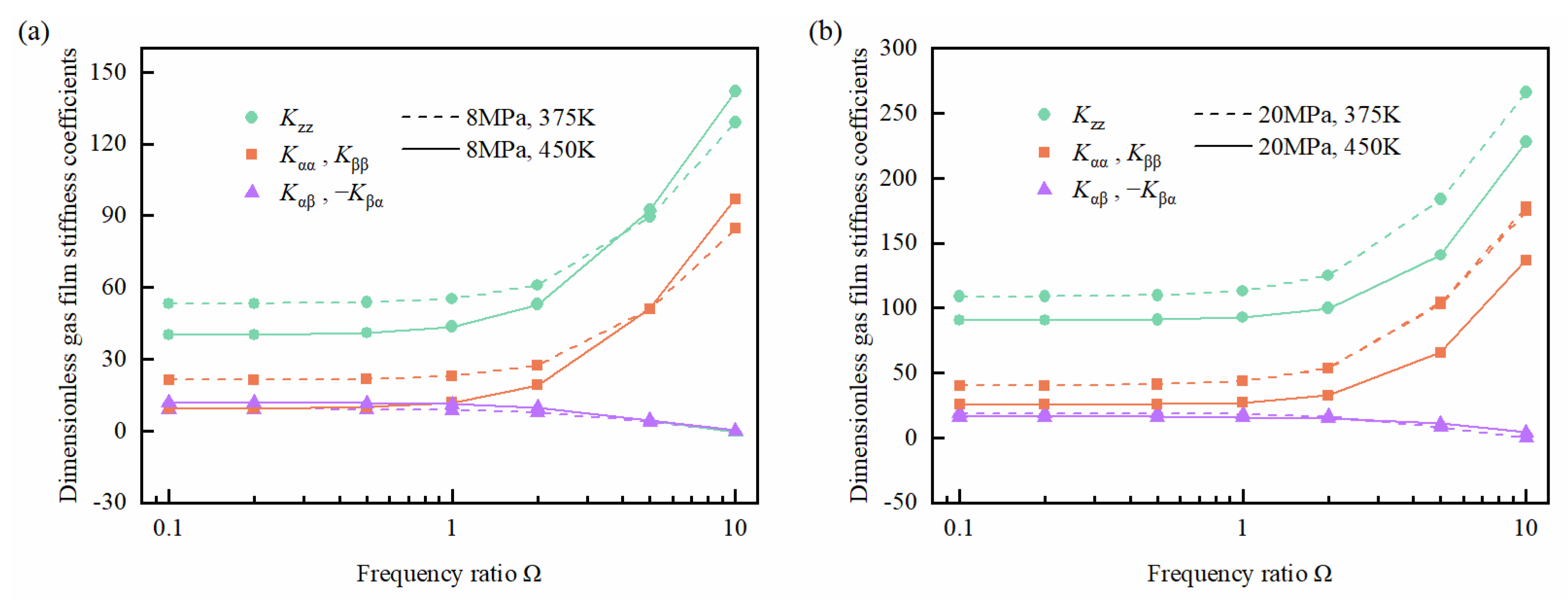
3.5.1. Stiffness Coefficient
Figure 7 depicts the gas film stiffness coefficients at different inlet pressure and temperature conditions. Regardless of the inlet pressure and temperature, the gas film stiffness coefficient showed a consistent trend. The stiffness coefficient was nearly frequency-independent for frequency ratios between 0.1 and 1. For frequency ratios greater than 1, the axial stiffness and angular stiffness coefficients sharply increased with the frequency in a nonlinear manner. In contrast, the angular cross-stiffness coefficients decreased nonlinearly with the frequency. When the inlet pressure was
pi = 8 MPa, the main stiffness coefficient between frequency ratios 0.1 and 5 decreased with the increase in the inlet temperature. Conversely, for frequency ratios larger than 5, the main stiffness coefficient increased as the inlet temperature rose. That is, the closer to the critical point of CO
2 in a certain frequency range, the greater the main stiffness coefficient. When the inlet pressure was
pi = 20 MPa, the main stiffness coefficient significantly decreased as the inlet temperature increased. Regardless of the variation in the inlet pressure, the impact of the inlet temperature on angular cross-stiffness was very small and could be approximately neglected. From the above analysis, it can be seen that the variation in the main stiffness coefficient was closely related to the inlet pressure and inlet temperature. The existence of a higher inlet temperature led to a lower density of carbon dioxide flowing into the seal gap. However, the lower density of carbon dioxide facilitated its compression. Thereby, the gas film stiffness coefficients decreased at high temperatures. This phenomenon indicated that increasing the inlet temperature would weaken the ability of the gas film to resist external perturbations. On the contrary, the stiffness coefficient remarkably increased with the increasing inlet pressure when keeping the inlet temperature constant, which was again attributable to the density. A higher pressure induced a higher density of carbon dioxide. The reduced compressibility of carbon dioxide caused an increase in the stiffness coefficient. Increasing the inlet pressure was also beneficial from the point of view of improving the stability of the gas film.
The main stiffness coefficient at high temperatures was greater than that at low temperatures when the frequency ratio was greater than 5, as seen in
Figure 7a. However, it is not present in
Figure 7b. This indicates that the change rate of the main stiffness coefficient under a high-frequency ratio was also affected by other factors. For the inlet pressure
pi = 8 MPa, the average value of the partial derivatives,
, of density with respect to temperature was −0.53 and −0.25 at 375 K and 450 K, respectively. Separating the last term on the right-hand side of Equation (A1), the value of the coefficient containing
in front of
will be greater at 450 K than at 375 K. At relatively low perturbation frequencies, an increase in
did not cause a significant change in the solution
of Equation (A1). At this time, the change in the stiffness coefficient was still determined by the density of carbon dioxide flowing into the seal gap. However, under the action of a high-frequency ratio, the value of
at 450 K will be significantly greater than that at 375 K, which will lead to an increase in the change rate of the main stiffness coefficient. Therefore, at a high-frequency ratio, the main stiffness coefficient at 450 K will be larger than the value at 375 K. Under the inlet pressure
pi = 20 MPa, the average values of the partial derivative,
, of density with respect to temperature at 375 K and 450 K were −3.38 and −0.95, respectively. It is not difficult to see that
under
pi = 20 MPa was significantly smaller than that under
pi = 8 MPa at any inlet temperature. Therefore, at
pi = 20 MPa, although
increased at 450 K, the value of
was much smaller than that at
pi = 8 MPa. Moreover, at low-frequency ratios, the main stiffness coefficients at
pi = 20 MPa were significantly higher than the values at
pi = 8 MPa. Based on the above two points, the change rate of the main stiffness coefficient at
pi = 20 MPa did not significantly alter with the increase in the frequency ratio. Therefore, the main stiffness coefficient at 450 K in
Figure 7b was smaller than the value at 375 K.
3.5.2. Damping Coefficient
Figure 8 displays the gas film damping coefficients at different inlet pressure and temperature conditions. The gas film damping coefficient showed the same trend regardless of the inlet pressure and temperature variation. The damping coefficient was nearly constant between the frequency ratios of 0.1 and 1. When the frequency ratio was greater than 1, the damping coefficient decreased nonlinearly by increasing the frequency, where the main damping coefficient changed most obviously. At a certain pressure, the damping coefficients at low and high inlet pressures showed a different variation regularity by increasing the temperature. At low inlet pressure conditions, the damping coefficient increased by increasing the temperature. In contrast, the damping coefficient decreased by increasing the temperature at high inlet pressures. That is, the closer to the critical point of CO
2 in a certain frequency range, the smaller the damping coefficient. Damping is a dissipative mechanism in a dynamical system. Therefore, it can be speculated that the variation in gas film damping was related to the CO
2 viscosity. The existence of a greater viscosity led to a higher damping of the gas film. At the inlet pressure
pi = 8 MPa, the average viscosity values of the gas film at inlet temperatures of 375 K and 450 K were 19.2 μPa·s and 22.0 μPa·s, respectively. The average viscosity values of the gas film at inlet temperatures of 375 K and 450 K for inlet pressure of
pi = 20 MPa were 28.8 μPa·s and 25.5 μPa·s, respectively. The variation in the viscosity data corroborated the speculation regarding the increase in the gas film damping with the viscosity. The damping coefficients significantly increased with the increasing inlet pressure when maintaining a constant inlet temperature. It is not difficult to find that this variation principle was also related to the increasing viscosity of CO
2. On top of that, it is worth also noting that a higher viscosity induced a faster decreasing trend of the gas film damping coefficient at high frequencies.
The main damping coefficient at high temperatures was larger than that at low temperatures when the frequency ratio was greater than 5, as shown in
Figure 8b. However, the phenomenon does not appear in
Figure 8a. Likewise, it was indicated that the change rate of the main damping coefficient at high-frequency ratios was also affected by other factors. When the inlet pressure
pi = 20 MPa, the mean values of the partial derivative,
, of density with respect to temperature at 375 K and 450 K were −3.38 and −0.95, respectively. Similarly, separating the last term on the right-hand side of Equation (A2), the value of the coefficient containing
before
will be smaller at 375 K than at 450 K. At relatively low perturbation frequencies, a decrease in
did not cause a significant change in the solution
of Equation (A2). At this point, the change in damping coefficient was still determined by the viscosity of carbon dioxide. However, under the effect of high-frequency ratios, the value of
at 375 K will be significantly smaller than that at 450 K, which will cause an increase in the change rate of the main damping coefficient. Hence, the main damping coefficient at 375 K at high-frequency ratios will be smaller than the value at 450 K. From
Section 3.5.1, it can be seen that the values at
pi = 8 MPa were significantly larger than those at
pi = 20 MPa, regardless of the inlet temperature. Thus, at
pi = 8 MPa, although
decreased at 375 K, the value of
was much larger than the case at
pi = 20 MPa. Based on the above analysis, the change rate of the main damping coefficient in
Figure 8a did not change significantly with the decrease in
as the frequency ratio increased.
4. Conclusions
In this work, the gas film dynamic characteristics of the S-CO2 dry gas seal were systematically investigated by taking into account multiple complex effects. Particularly, the film thickness, pressure, temperature, physical parameters, Reynolds number, turbulence coefficient, and inertia coefficient were completely perturbed by using the frequency perturbation method. Then, a model (CVPM) applicable to the adiabatic flow process was established. The dynamic coefficients of the gas film under different conditions and frequency ratios were calculated and analysed.
The cross-stiffness and -damping values between the angular and axial (or axial and angular) directions were extracted as approximately zero. The three-degrees-of-freedom perturbed motion could be reduced to two independent perturbed motions. When the frequency ratio was between 0.1 and 1, the stiffness and damping coefficients were insensitive to the frequency dependence. In striking contrast, when the frequency ratio was greater than 1, the dynamic coefficient of the gas film exhibited a strong frequency dependence.
The turbulence coefficient perturbation had the most remarkable influence on the gas film dynamic coefficient compared to the temperature, viscosity, and centrifugal inertia force perturbations. The stiffness coefficients (or damping coefficients) under isothermal and adiabatic flow presented the same variation trend with the frequency ratio. The main stiffness coefficients under adiabatic flow were significantly larger than the value under isothermal flow. However, the angular cross-stiffness coefficients were nearly equal under both flow conditions. The axial damping coefficient under adiabatic flow was less than the value under isothermal flow, while the angular cross-damping coefficient was greater than the value under isothermal flow.
The variation in the inlet pressure and inlet temperature had no noticeable impact on the trend of the gas film dynamic characteristic coefficient with frequency but affected the magnitude of its value. At lower inlet pressures, the variation in the main stiffness coefficient was proven to be related to the inlet temperature and the magnitude of the frequency ratio. At higher inlet pressures, the variation in the main stiffness coefficient was related to the inlet temperature. The stiffness coefficient remarkably increased with the increasing inlet pressure when keeping the inlet temperature constant. The damping coefficient of the gas film was demonstrated to be related to the viscosity of carbon dioxide, which increased with the increase in the viscosity.
A positive impetus to the current kinetic analysis of S-CO2 dry gas seals was provided in this work. Future work can be based on the current model, combined with the stationary ring equations of motion, to identify whether the sealing system will be destabilised due to self-excited vibration, as well as to analyse the behaviour of the stationary ring dynamic response under forced vibration.