Abstract
Owing to the requirements for high performance and long life, the friction and wear problems of rolling piston type rotary compressors have drawn much attention. Various theoretical models have been developed and improved to reveal the inner state of the compressor and obtain the optimization schemes. However, there remain some disadvantages and research gaps in the corresponding modeling and mixed lubrication analyses, and a comprehensive summary is lacking. To have a better understanding of the research status, this paper reviews the theoretical model development and mixed lubrication analyses of the compressor in the past decades. The determination of compression pressure, the modeling process of moving components, and the key findings are presented in detail. On this basis, some important influencing factors and the problems remaining to be solved are also discussed. This paper provides multifaceted guidance for manufacturers and researchers to conduct further theoretical analysis and optimal design.
1. Introduction
Developed in the 1960s, rolling piston type rotary compressors are the key components in household air conditioners to realize refrigerant pressurization [1,2,3]. They are mounted between the evaporator and the condenser (see Figure 1), and the compression process is achieved with a piston and cylinder arrangement [4,5]. The special working principle of it results in the unique inner structures, which are much different from those of the scroll compressor [6,7], the reciprocating compressor [8,9], and the sliding vane compressor [10,11]. Owing to the advantages in structure, size, and weight, they are taking an increasing share compared to other types of compressors [2,12]. Correspondingly, the volumetric efficiency, consumption power, noise, and vibration of the compressor have been the concern of researchers for a long time [13,14,15,16,17]. In the rolling piston type rotary compressor, the energy losses mainly consist of the friction loss, the motor loss, the compression loss, and the lubricant pumping loss, and the mass flow losses are mainly composed of the leakage loss, the suction gas heating loss, and the clearance volume loss [5]. Among them, the friction loss and the leakage loss play the most significant roles. With the wide applications of household air conditioners, the friction loss within the compressor counts a lot in energy conservation and environmental protection. In the current stage, the annual global production volume of the rotary compressor is around 200 million units, and China is responsible for approximately 90% of that prouction [3]. Meanwhile, higher working frequency and lower viscosity are adopted for high-performance compressors [1]. Severe operation conditions will result in surface wear, thus influencing the reliability and service life of the compressor. Under these circumstances, the friction and wear of rotary compressors have become more and more important, and many tribologists have paid much attention in the latest decades [18,19,20,21,22,23].
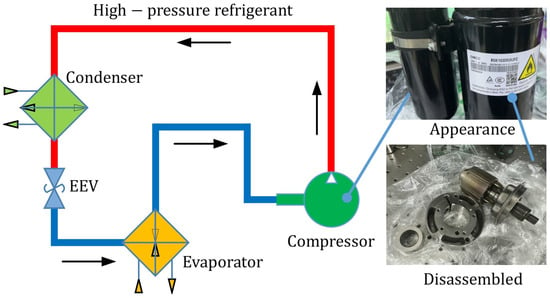
Figure 1.
Refrigerating system and rotary compressor in household air conditioners.
On the one hand, the friction and wear of rotary compressors largely result from the complex motions of the components. A rotary compressor contains many specially designed components (see Figure 2), such as a rolling piston, sliding vane, crankshaft, cylinder, main bearing, and sub-bearing [1,24]. Driven by an AC motor, the former three components undergo complex motions during operation, thus leading to the time-varying interacting forces between the components [20,25]. In the working process of the compressor, the complex motions of the moving components will change the lubrication performance of the interacting surfaces, which can enter into a mixed lubrication regime when the load-carrying capacity of the oil film is not enough. As shown in Figure 3, owing to the angular displacement of the vane, the severe wear of the vane slot on the suction side occurs in the region close to the cylinder wall. On the other hand, different types of friction pairs within a compressor with coupling effects increase the complexity of the tribological process. For a typical rotary compressor, there are mainly seven friction pairs (see Figure 4), which can be affected by each other owing to multi-body coupling [2,26,27]. During operation, these different types of friction pairs show different operation performances, and the mutual influence between them is a nonnegligible factor.
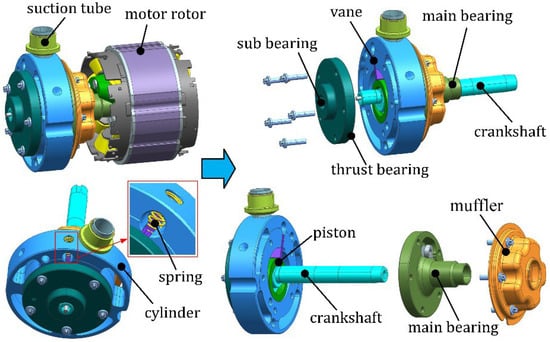
Figure 2.
Structure characteristics of rotary compressor (Reproduced with permission from [1], Copyright 2024, Elsevier).
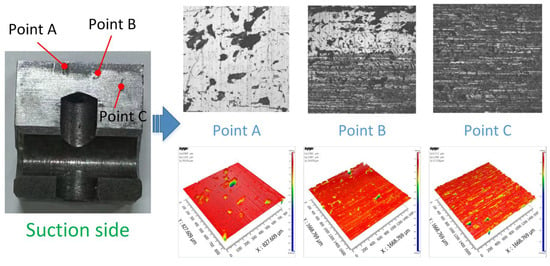
Figure 3.
Surface wear of vane slot on suction side in engineering applications.
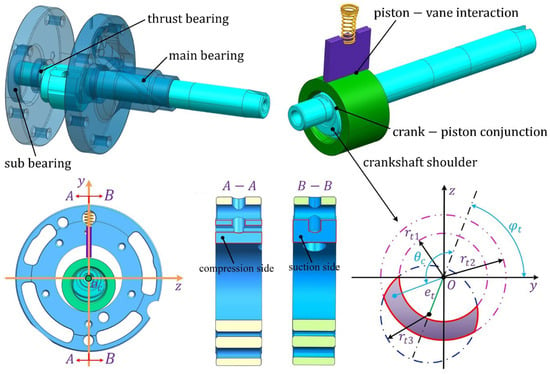
Figure 4.
Different types of friction pairs in a rotary compressor (Reproduced with permission from [1,2], Copyright 2023/2024, Elsevier).
In addition, the special working environment of the rotary compressor influences the lubrication characteristics between interacting surfaces. To provide a high-pressure refrigerant, all the friction pairs of the compressor must be in the hermetic space [28,29], which will influence the formation of oil film pressure and cavitation [19]. Exposed to the lubricant oil and the refrigerant vapor [12], the clearance between the mating surfaces may be filled with the mixture instead of the pure oil [30]. The solubility of the refrigerant may greatly influence the tribological performance of the conjunction by changing the rheological properties [31]. However, accurate modeling of the mixture is very difficult, as the solubility of the refrigerant is affected by many factors. For simplification, a constant solubility can be applied, and its influence can be further revealed. In the past, ozone-harming chlorofluorocarbon refrigerants and replacement refrigerants such as R410a and R134a were widely applied [3,32,33]. With the increasing requirements for environmental protection, some new refrigerants such as R32 and R290 are being produced and spread [3,12,34,35].
To understand the working state of the rotary compressor and conduct optimal design, theoretical analysis is often the preference. Though experimental studies have been conducted to some extent, further measurements become extremely difficult considering the high-pressure hermetic space and the compact size [12,36,37,38,39]. By comparison, theoretical analysis is more convenient and can reveal multiphysics characteristics within the compressor. With the development of mixed lubrication theory and tribodynamic modeling, the tribological analysis of the rotary compressor has been conducted for many years and is gradually being improved. Based on simulations, the optimal designs of various structure parameters have been determined and applied [2,18,26]. However, there still remain some disadvantages and research gaps, and a comprehensive summary is lacking. To provide comprehensive guidance for manufacturers and researchers, this paper reviews the theoretical model development and mixed lubrication analysis of rolling piston type rotary compressors. The model development and analysis of the compression pressure, rolling piston, sliding vane, and crankshaft are presented first in detail. Then, the theoretical research status regarding a whole compressor in different stages is further summarized. As the supplement, several influencing factors are discussed, along with the potential problems remaining to be solved.
2. Model Development and Analyses
In engineering applications, the mating surfaces are under a hydrodynamic lubrication regime when the oil film between them is large enough; otherwise, the mixed lubrication regime will occur, resulting in surface wear. In the latest decades, the mixed lubrication theory was developed both in the governing equation [40,41,42] and the asperity contact [43,44,45]. Simplified from the Navier–Stokes equations, the Reynolds equation with the Reynolds cavitation model [46,47] or the Jakobsson–Floberg–Olsson (JFO) cavitation model [48,49] is widely applied to obtain the film characteristics. The mass-conserving JFO cavitation model is more accurate than the Reynolds cavitation model, and its predicted results with are closer to the experimental data [50]. As the JFO cavitation model is more difficult to implement, the Reynolds cavitation model after being verified is often the preference in mixed lubrication analysis [2,19]. In terms of roughness effects, the deterministic method considering roughness distribution in detail is more accurate, especially in scuffing failure analysis [51]. However, considering the time-consuming problem of this method, the average flow model [40,41] and the homogenized model [52,53] were the preferences in mixed lubrication analysis. Correspondingly, the theoretical model and mixed lubrication analysis of the rotary compressor have also been developed and improved. In the early stage, the theoretical analysis of a part of the moving components or a part of the friction pairs was the preference considering the solution efficiency [54,55]. Later on, simulations of the whole compressor considering multibody coupling were presented [20]. Further studies began to consider the effects of elastic deformation [4], thermal performance [56], groove distribution [1,2] and other important influencing factors.
2.1. Determination of Compression Pressure
During operation, the outer surface of the rolling piston is surrounded by the refrigerant, and the refrigerant also applies forces on part of the sliding vane [57]. Therefore, the compression pressure in the cylinder has been studied to obtain the boundary conditions for dynamic analysis and lubrication analysis (see Figure 5).
Owing to the advantage in calculation efficiency, the function expressions of the compression pressure have been proposed and widely applied. Based on the geometrical relationships, Pandeya et al. [5] obtained the volume angle and pressure angle expressions. Considering the limitation of the discharge pressure, Okada et al. [58] presented a piecewise function. In their derivation, the compression pressure remains constant when reaching the discharge pressure. To describe the process after the discharge valve opens, Yanagisawa et al. [59] improved the expression, in which the compression pressure after the discharge angle decreases linearly with the crank angle. To further consider the angle of the discharge valve, the pressure angle relationship was further modified with a three-segment function, which is still widely applied in the current stage [2,54,60]. The three-segment function is expressed as follows [25]:
where and are the compression pressure and the suction pressure, respectively, denotes the discharge pressure, represents the correction coefficient, represents the suction chamber volume, represents the compression chamber volume, is the crank angle, is the starting angle of the refrigerant discharge, and is the angle of the discharge valve.
Apart from the chamber volume, the compression pressure is also influenced by the supercharging effect [61], the thermodynamics [32] and the valve dynamics [62]. Based on a nonlinear gas dynamic model, Liu et al. [63] studied the supercharging phenomenon in a variable-speed compressor and found that it can increase the capacity of the compressor. To consider the relationship between pressure, temperature, and mass, the thermodynamics model was developed, along with the geometry model and the valve flow model [32]. To describe the internal flow more accurately, three-dimensional (3D) computational fluid dynamics (CFD) analysis was also carried out to obtain the pressure–volume diagram [64,65,66,67]. In the period between the opening and closing of the discharge valve, the variation in the compression pressure is dramatically affected by the valve dynamics. For this reason, some researchers have established improved methods to obtain the compression pressure by analyzing the valve motion. By regarding the valve as a beam with varying width, Ooi et al. [68] analyzed the valve dynamics and obtained the chamber pressure considering the valve deflection. To consider the valve motion and the refrigerant flow together, fluid–structure interaction models were further established with commercial software [69,70,71]. However, as these methods and models were much more complex, they were rarely applied in the lubrication analysis and dynamic analysis of moving components.
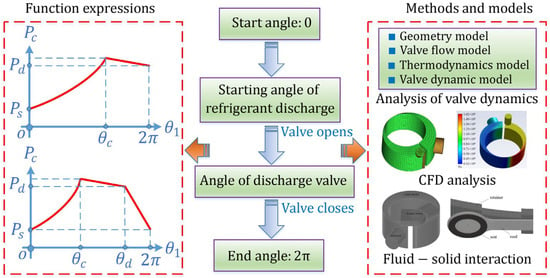
Figure 5.
Determination of compression pressure (Reproduced with permission from [66], Creative Commons CC BY license; reproduced with permission from [71], Copyright 2017, Elsevier).
2.2. Sliding Vane and Rolling Piston
In view of the vane–piston interaction, the sliding vane and the rolling piston were considered together in theoretical modeling and analysis. To achieve decoupling, the translational movements in three directions and the angular displacements in two directions of the crankshaft are ignored, which only rotates along the rotor axis. The vane–slot conjunction and the vane–piston interaction are the main friction pairs for the sliding vane, while those for the rolling piston are the crank–piston conjunction and the vane–piston interaction. For performance improvement, the mixed lubrication performance of these friction pairs has been investigated for a long time.
With the chamber pressure acting as the boundary pressure, kinematic and mixed lubrication analysis of the sliding vane and the rolling piston have been conducted comprehensively (see Table 1 and Figure 6). In 1978, Pandeya et al. [5] analyzed the rotation speed of the rolling piston and proposed convenient formulas to calculate the vane tip–piston friction force and the piston–cylinder head friction torque. By solving the equation of motion of the rolling piston and the equilibrium equations of the sliding vane together, Okada et al. [58] discussed the kinematic behaviors of the rolling piston. It was found that the rotation direction of the rolling piston is the same as that of the crank, which varies with time periodically. However, the direction of the vane–piston friction was proved to be a variable, thus influencing the rotation speed of the piston. Yanagisawa et al. [59] also analyzed the rotating motion of the rolling piston, and the conclusions verified with the experimental results were drawn. However, the rotation direction of the rolling piston was found to be positive and negative alternately for the cases studied. Further investigation on the rolling piston was conducted by Ito and Xu [72,73] and it was found that the piston–vane sliding velocity can be reduced with a decrease in the piston weight. In Refs. [58,59,72], the piston–crank interaction was determined by solving the traditional Reynolds equation, while the piston–vane conjunction and the vane–slot conjunction were described with the Coulomb friction law. Instead of using the Coulomb friction law, Yoshimura et al. [27] began to apply the mixed elastohydrodynamic lubrication (EHL) theory to analyze piston–vane friction. The one-dimensional average flow model was used to obtain the oil film pressure, and the asperity contact was described with the Greenwood and Tripp contact model. It was found that the mating surfaces are supported by the oil film and the metallic contact, between which the friction coefficient changes from 0.04 to 0.08. Based on the mixed EHL analysis, Tanaka et al. [74] found that the oil viscosity significantly influences the asperity contact friction loss and the viscous friction loss. Later on, Cho et al. [31,75] further revealed the partial EHL characteristics between the sliding vane and the rolling piston with the same theory. After their comparison, the solubility of the refrigerant was proved to dramatically affect the piston–vane friction. A mixed lubrication analysis of the vane–slot conjunction was first implemented by Ito et al. [54], in which the second-order motion of the vane was considered. By coupling the equations of motion of the vane, the average Reynolds equation, and the contact model, a proposed model was applied for optimal design of the vane. It was found that the period of mixed lubrication and the friction loss decreases with the increasing vane slot length. Using the same models, Yang et al. [76] analyzed the friction power and wear of the vane–slot conjunction, which were in good agreement with their durability experiment. In the subsequent work of Ito et al. [77], the influence of the cylinder deformation was considered by using the finite element method. The results showed that the cylinder deformation contributes to the smooth reciprocating motion of the sliding vane. Based on the kinematics of the compressor, Yanagisawa et al. [78] analyzed the friction losses in the vane–slot conjunction, the piston–vane interaction, and the rolling piston bearing. It was found that the cylinder with a short length/diameter configuration is beneficial to reduce the total loss. To improve the model accuracy, Ito et al. [25] further proposed an improved numerical model by conducting mixed lubrication analysis of the piston–crank conjunction and the vane–slot conjunction together. The simulation results indicated that the piston–vane friction force has the most important influence on piston rotation compared to other friction forces. It was also found that the working frequency and the chamber pressure difference greatly change the piston rotation speed and the piston–vane sliding velocity.

Table 1.
Theoretical research on rolling piston and vane.
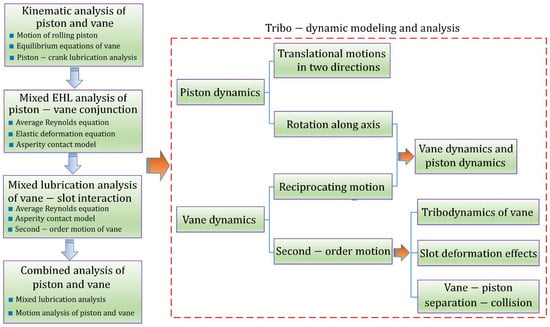
Figure 6.
Theoretical modeling and analysis of rolling piston and sliding vane in the last decades.
Considering the increasing impacts of dynamic processes, tribodynamic models coupling dynamic behaviors and mixed lubrication have become the preferences in the current stage (see Table 1 and Figure 6). Considering the one-dimensional vane dynamics and the one-dimensional piston dynamics together, Padhy [79] proposed a mathematical model to analyze the tribo-dynamic performance of the compressor, which was verified by their experiments [82]. Coupling the momentum equations and the Reynolds equation, a two-degree-of-freedom tribodynamic model of the rolling piston was first built by Minami et al. [80]. By comparison, the results showed that the lubrication performance with R410a refrigerant is better than that with R22. Considering second-order motion, Geng et al. [81] first established a two-degree-of-freedom tribodynamic model of the sliding vane. Based on their dynamic solution, it was found that second-order motion characteristics worsen the lubrication status of the vane–slot conjunction on the suction side. Later on, the mathematical model was modified to analyze the separation–collision process between the vane tip and the rolling piston [36]. The simulation results indicated that the separation–collision behaviors are closely related to the spring stiffness and the rotation velocity of the shaft. In engineering applications, both the vane slot and the sliding vane are processed with the groove structures, such as the spring groove, the vertical groove, and the dovetail groove. To consider groove effects, Li et al. [18] proposed an improved tribodynamic model for the sliding vane, in which the cylinder deformation caused by the chamber pressures is also calculated. In their work, the fluid pressure within the groove was assumed to be equal to the discharge pressure, and the pressure distribution at the boundaries was also defined. As the interacting area between the vane and the slot changed with the crank angle, the pressure boundary conditions were updated before the pressure iteration. It was found that the cylinder deformation has a significant influence on the second-order motion of the vane and the mixed lubrication performance of the vane–slot conjunction (see Figure 7). After their comparison, the optimal vertical groove was proved to reduce the friction loss and wear between the sliding vane and the vane slot. In Geng and Li’s work, it was assumed that the direction of the sliding speed between the vane tip and the rolling piston remained unchanged, and the normal interacting force of the vane–piston conjunction was obtained based on the force equilibrium.
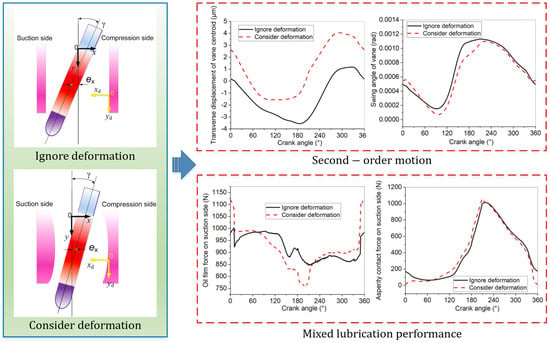
Figure 7.
Effects of vane slot deformation on the tribodynamic performance of vane (Reproduced with permission from [18], Copyright 2021, Elsevier).
2.3. Crankshaft
During operation, the main bearing, the sub-bearing, the thrust bearing, and the inner surface of the piston interact with the crankshaft [83], and the friction and wear of the corresponding friction pairs have also been studied for a long time. Under the action of an electric current, magnetic forces between the rotor assembly and the stator assembly will occur [84]. To conduct dynamic balance, the upper and lower balancers are mounted on the proper positions of the rotor [19,85]. To make the refrigeration capacity variable, frequency conversion technology has been widely applied [86,87], resulting in the acceleration and deceleration processes of the crankshaft. In addition, with the rotary compressor developing towards high power density, twin-cylinder and three-cylinder schemes began to be applied [88,89,90], which further worsened the operation conditions of the crankshaft.
In the last decades, dynamic analysis of the crankshaft–journal bearing system has been conducted by some researchers, especially at the early stage (see Table 2). To achieve decoupling, the gas forces and unbalance forces caused by the rolling piston need to be determined in advance. To estimate the reliability and conduct the optimal design of the bearing, Hattori et al. [55] established a dynamic model for the rotor in a twin rotary compressor. In their model, the bearing reaction forces were obtained using the short bearing theory, and the unbalanced forces and the gas forces were all considered. It was found that the whirling locus and elastic deformation of the rotor are smaller than those of the single rotary compressor with the same discharging capacity. By developing a finite element model of rotor–crankshaft assembly, Dufour et al. [91] discovered that modification of the bearing clearance partially improves the rotor dynamics of the variable-speed compressor. Based on dynamic simulations, Seve et al. [85] further analyzed the balancing of this type of compressor. By comparing different schemes, they proposed improved balancing, which satisfies the requirements for the vibration level and industrial implementation. Considering the electromagnetic force acting on the motor rotor, Zhang et al. [84] established a two-degree-of-freedom tribodynamic model for vibration analysis of the rotor. It was found that the amplitude of the triplet frequency is higher than that of the double frequency owing to the coupling effects of the bearing force and the electromagnetic force.

Table 2.
Theoretical research on crankshaft.
With the detailed lubrication simulations, great efforts have been devoted to the tribological performance analysis of the bearings associated with the crankshaft (see Table 2). With the Reynolds equation and the load equation, Fu et al. [92] analyzed the lubrication characteristics of the main bearing and the sub-bearing. It was found that the wear-out may occur at the bottom of the sub-bearing when the oil viscosity is low. Considering the roughness effects, Yu et al. [93] further conducted numerical analysis and optimization of the main bearing and the sub-bearing. After mixed lubrication analysis, the results showed that the optimized width–diameter ratio can increase the load carrying capacity of the oil film and reduce the friction power of the sub-bearing by more than 80%. By coupling the average Reynolds equation, the contact equation, and the elastic deformation, Hirayama et al. [94] proposed an analytical method for the journal bearings. The simulation results indicated that the optimally smoothed surface roughness improves the ability of the lubrication film formation. With the finite element model and the Reynolds equation, Xie et al. [95] also analyzed the lubrication performance of the bearings. It was found that the bottom of the sub-bearing housing under low speed and the top of the main bearing housing under high speed were in relatively severe working conditions. Based on mixed EHL analysis, Kitsunai et al. [96] found that an annular depression on the shaft surface reduces the losses and increases the volume efficiency. Zhang et al. [88] analyzed the dynamic behaviors of the crankshaft for both single-cylinder and twin-cylinder compressors and discussed the configuration of balancers. The simulation results revealed that proper dynamic balance can improve the wear performance of journal bearings. To realize crankshaft optimization, Meier et al. [97] conducted sensitivity analysis of the surface roughness, bearing lengths, and clearances of the friction power losses. By coupling the crankshaft deformation and the mixed lubrication model, Wang et al. [4] developed a numerical model to evaluate the lubricating condition of the compressor under tested conditions. In the tribodynamic models mentioned above, only the journal bearings were considered, and the effects of the thrust bearing were ignored. To further improve the simulation accuracy, Liu et al. [19] constructed a complete coupled journal–thrust bearing model. Their simulation results showed that high ambient pressure contributes a lot to the dynamic performance of the crankshaft and the wear of the thrust bearing (see Figure 8). With three different stochastic optimization algorithms and a similar tribodynamic model, Lyu et al. [26] further conducted texture optimization for the thrust bearing. The simulation results indicated that the optimized textures greatly reduce the contact forces and wear of the thrust bearing under a high working frequency.
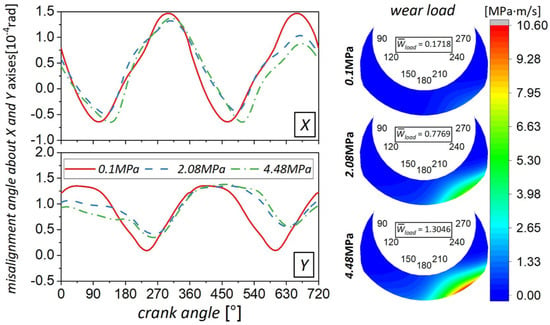
Figure 8.
Influence of ambient pressure on dynamic performance of crankshaft and wear of thrust bearing (Reproduced with permission from [19], Copyright 2021, Elsevier).
2.4. Whole Compressor
In the references mentioned above, only a part of the moving components was considered in theoretical models and analysis. With the rotary compressor developing towards high working frequency, multibody coupling effects become more and more important, and a tribodynamic model for the whole compressor is required. The theoretical research status on the whole compressor is presented in Table 3. In the early stage, the vibration and mechanical loss of the whole compressor were analyzed. In 1984, Jorgensen et al. [98] developed a mechanical loss model of the rotary compressor, which was verified by their experiments. Based on the dynamic model of the moving parts, Jun et al. [99] studied the mechanical loss of the two-cylinder type rotary compressor. Using a multibody dynamic analysis method, Han et al. [100] studied the vibration characteristics of the compressor. It was found that the mass of the balancer dramatically affects the acceleration. Venugopal et al. [101] also investigated the vibration performance of the rotary compressor by analyzing the dynamic behaviors of the moving components, the constraint forces, and the sliding speed. The results showed that the speed variation of the crankshaft is one of the major factors to cause compressor vibration. By analyzing the hydrodynamic lubrication and dynamics of the rolling piston and the crankshaft, as well as the kinematics of the sliding vane, Mi et al. [20] first established a tribodynamic model for the whole compressor. However, the surface roughness effects and the dynamic performance of the vane were ignored, as well as the dynamic of the crankshaft in the axial direction. Later on, with the aid of the dynamic analysis in Ref. [20], they carried out a thermohydrodynamic lubrication analysis of the piston–crank conjunction, the main bearing, and the sub-bearing [56]. By solving the Reynolds equation and the energy equation, the temperature characteristics of the oil film were presented. To improve the model accuracy of the whole compressor, Wen et al. [2] calculated bearing deformation with the compliance matrix method and established an eight-degree-of-freedom tribodynamic model with the average Reynolds equation, the asperity contact equation, and dynamic differential equations. Based on the solution, the impacts of the oil supply structures on the main bearing, the sub-bearing, and the crank were revealed (see Figure 9). To study the dynamic behaviors of the vane, they further developed an eleven-degree-of-freedom tribodynamic model [1]. With this model, the effects of the vane width, the conical structure, and the suction pressure were revealed (see Figure 10). It was found that the proper conical structure on the vane slot of the suction side can greatly reduce the maximum wear load of the vane slot.

Table 3.
Theoretical research on the whole compressor.
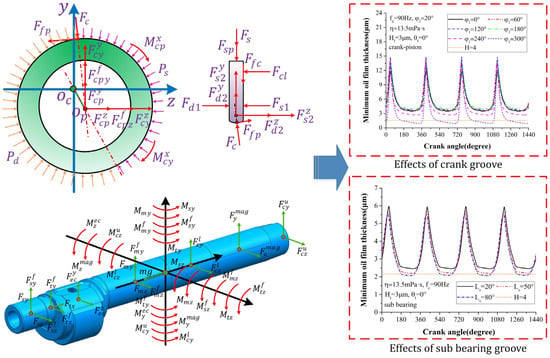
Figure 9.
Tribodynamic modeling of whole compressor and optimization analysis of different oil supply structures (Reproduced with permission from [2], Copyright 2023, Elsevier).
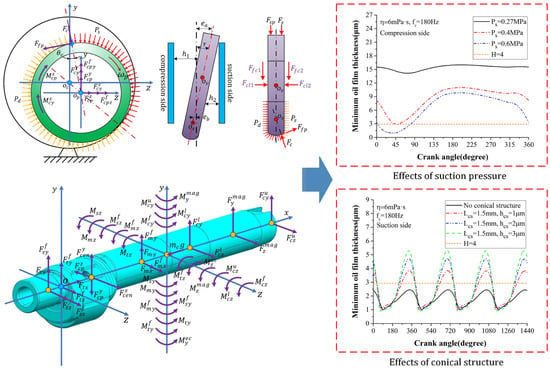
Figure 10.
Eleven-degree-of-freedom tribodynamic model of whole compressor and performance analysis of sliding vane (Reproduced with permission from [1], Copyright 2024, Elsevier).
3. Influencing Factors and Problems
During the working process to realize refrigerant compression, the tribological performance of the rotary compressor is influenced by many factors. Some influencing factors have been analyzed comprehensively by many researchers, and other influencing factors remain to be discussed.
Though the lubricant oil is provided for the friction pairs with the aid of an oil pick up at the end of the crankshaft [102,103], starved lubrication will also occur, especially for the vane–slot conjunction. Under a starved lubrication regime, the friction and wear between the mating surfaces are much different from that under a fully flooded lubrication regime, thus influencing the service performance of the compressor. However, in the previous studies, it was generally assumed that all the friction pairs were under a fully flooded lubrication regime. To reveal the inner state of the compressor comprehensively, the effects of starved lubrication need to be studied. However, the oil flow and oil distribution within the compressor are extremely complex [102,103,104], and the starved lubrication analysis is full of challenges. In the field of tribology, there are several methods dealing with the starved lubrication problem. By applying the volume of fluid (VOF) model in the CFD method, the distributions of refrigerant vapor and lubricant oil at the inlet can be defined, thus describing the severity of lubricant starvation. In the previous investigations, this model has been frequently applied to obtain the oil distribution and oil flow in the mechanical components [105,106]. The mass-conserving JFO model can also be used to describe the lubricant starvation with the cavity fraction. The JFO model for the journal bearing in the mixed lubrication analysis can be expressed as follows [40,107,108]:
where denotes the cavity fraction; , , , and are the flow factors [40,41,107]; and are the position parameters; is the oil film pressure; is the journal radius; represents the time; and are the density and viscosity of the lubricant, respectively; is the oil film thickness, is the composite roughness, and represents the rotation speed. In addition, the inlet boundary condition can also be described with the oil supply flow rate, which has been widely applied in the starved lubrication analysis of friction pairs [109,110]. The corresponding expressions in this method are as follows [109]:
where represents the inlet position, and denote the lubricant flow rate and the oil supply flow rate, is the sliding speed, is the supplied lubricant film thickness, and is the oil film thickness at the inlet.
Owing to the complex interacting forces, the elastic deformation of the compressor components is an important influencing factor. In general, there are two methods to calculate the elastic deformation, namely the finite element method [4] and the compliance matrix method [19]. Compared to the former, the compliance matrix method has advantages in calculation efficiency, in which the finite element analysis only needs to be conducted to obtain the compliance matrix in advance. With the compliance matrix, the elastic deformation is determined as follows [111,112]:
where denotes the compliance matrix value; denotes the grid area; is the elastic deformation; and , , and are the oil film pressure, the contact pressure, and the boundary pressure, respectively. To date, these two methods have been frequently applied to consider the effects of elastic deformation [2,19,88,94]. For stationary components such as the main bearing and the sub-bearing, both methods have enough accuracy [2,94]. However, for a moving component such as the crankshaft, the finite element method is more suitable by considering it as the flexible body [4,19]. In Liu’s work [19], to obtain the elastic deformation of the crankshaft, the compliance matrix method was still applied with the two-dimensional bearing elements of Combi214 providing the motion constraints. However, the constant bearing stiffnesses were used, which in the fact changed obviously with the eccentricity. In the past, the impacts of the elastic deformation on one moving component were generally conducted. As the tribodynamic model of the whole compressor has been established in recent years, coupling analysis of elastic deformation and multibody movements for the whole compressor can be further carried out.
In addition, the thermal characteristics of the rotary compressor have also been given much attention considering their significant effects. The thermal analysis of the rolling piston type rotary compressor can be divided into three aspects: one is for the friction pairs [56,113], another is for the temperature distribution of the components [29], and the third is for the vapor compression [83,114]. In the last decades, thermohydrodynamic lubrication analysis of the journal bearings in the rotary compressor has been presented by Mi et al. [56,113]. However, mixed thermohydrodynamic lubrication analysis of the compressor has rarely been conducted. In addition, temperature distribution simulations of the compressor can be used to provide the boundary conditions for different friction pairs. The coupling analysis of temperature distribution and mixed lubrication remains to be finished in the future.
During variable-speed processes, such as start-ups and stops, the operation performance of the compressor can be greatly affected. For this reason, the starting and stopping characteristics of the compressor have been studied in the last decades. In the early stage, the starting torque of the rotary compressor was given much attention, which was estimated theoretically and experimentally [115,116]. Based on the experiment results, Ishii et al. [117] analyzed the cylinder pressure, the mechanical vibration, and the crankshaft behaviors after the motor was shut down. Later on, some studies have been carried out to reveal the starting performance of the compressor. Lin et al. [118] experimentally investigated the start-up process of the rotary compressor under a low ambient temperature heating condition, while Wu et al. [119] focused on the cold start-up under cooling conditions. To analyze the temperature distribution during start-up, Guo et al. [120] established a transient mathematical model and discussed the heat exchange characteristics between the solid and the fluid. To reveal the start-up performance of the rotary compressor, Zhao et al. [121] proposed a heat and mass transfer model and studied transient characteristics such as the heat exchange rate and the phase change rate. However, in the references mentioned above, the experimental investigations mainly focused on the pressure, the temperature, the heat exchange rate, and the liquid level of the oil sump, and the tribodynamic modeling and the tribological analysis were rarely seen. During the variable-speed process, the operation condition of the mating surface becomes severe, and the surface wear easily occurs. Variation in the tribological performance of the rotary compressor during the start-ups and the stops is an extremely important topic, which needs to be discussed comprehensively in the future.
4. Conclusions
Owing to the requirements for high performance and long life, the tribological problems of rolling piston type rotary compressors have drawn much attention. The stability and service life of the compressor will be affected when the friction pairs suffer a mixed lubrication regime. In the latest decades, various theoretical models have been developed and improved to reveal the inner state of the compressor and obtain the optimization schemes. However, some disadvantages and research gaps still exist, and a comprehensive summary is lacking. To provide the research status and identify future trends, the theoretical model development and mixed lubrication analyses of the rotary compressor are summarized in this paper. The conclusions can be drawn as follows:
- (1)
- To provide the pressure boundary conditions, the three-segment function of the compression pressure is widely adopted in current models. To consider the effects of supercharging, thermodynamics, and valve dynamics, more comprehensive analyses of the compression process have been conducted. However, the corresponding methods and models are much more complex, limiting their applications in mixed lubrication analysis.
- (2)
- Considering the disadvantages of the theoretical models of a part of the moving components or a part of the friction pairs, tribodynamic modeling of the whole compressor has been implemented in recent years. To conduct the modeling study of the vane–piston system and the crankshaft separately, decoupling of the moving components needs to be achieved, resulting in the extra assumptions. To improve decoupling model accuracy, second-order motion, elastic deformation, and groove distribution have been considered in the previous studies. With the increasing effects of multibody coupling, the modeling and analysis of the whole compressor is the preference.
- (3)
- Based on mixed lubrication analyses, various optimal designs of the compressor have been achieved. Optimized textures can greatly reduce the contact forces and wear of the thrust bearing under a high working frequency. An optimal vertical groove can reduce the friction loss and wear of the vane–slot conjunction. Proper conical structure on the vane slot of the suction side can greatly reduce the maximum wear load of the vane slot. In addition, optimally smoothed surface roughness can improve the ability of the lubrication film formation of journal bearings.
- (4)
- To reveal the service performance of the rotary compressor comprehensively, some important influencing factors need to be further analyzed in the future. Starved lubrication analysis of the compressor is full of challenges and has not been carried out so far. The coupling analysis of elastic deformation and multibody movements for the whole compressor needs to be addressed more. The thermal performance analysis of friction pairs under mixed lubrication regime is also very limited. During variable-speed processes, the lubrication and wear characteristics of the rotary compressor have not been investigated theoretically, which is also an important topic for the future study.
Author Contributions
C.W.: Methodology, Formal analysis, Investigation, Writing—Original Draft; P.B.: Methodology, Formal analysis, Resources; H.Z.: Methodology, Writing—Review and Editing; S.Z.: Methodology, Writing—Review and Editing; X.M.: Methodology, Conceptualization; Y.M.: Methodology, Conceptualization; Y.T.: Conceptualization, Resources, Methodology, Data Curation, Writing—Review and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 52305199) and the Science Foundation of China University of Petroleum, Beijing (No. 2462024YJRC022).
Acknowledgments
The authors are deeply grateful to the Midea Group for providing the technical support.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| correction coefficient | |
| compliance matrix value | |
| oil film thickness | |
| supplied lubricant film thickness | |
| oil film thickness at the inlet | |
| oil film pressure | |
| boundary pressure | |
| contact pressure | |
| compression pressure | |
| discharge pressure | |
| suction pressure | |
| oil supply flow rate | |
| lubricant flow rate | |
| journal radius | |
| time | |
| sliding speed | |
| compression chamber volume | |
| suction chamber volume | |
| position parameters | |
| inlet position | |
| cavity fraction | |
| elastic deformation | |
| grid area | |
| viscosity of lubricant | |
| starting angle of refrigerant discharge | |
| angle of discharge valve | |
| crank angle | |
| specific heat ratio of refrigerant gas | |
| density of the lubricant | |
| composite roughness | |
| contact factor | |
| shear flow factor | |
| pressure flow factors | |
| rotation speed |
References
- Wen, C.; Liu, Z.; Wen, X.; Gao, K.; Guan, J.; Bai, P.; Meng, Y.; Tian, Y. Dynamic modeling and characteristics analysis of sliding vane in a high-speed rotary compressor considering groove distribution and multi-body coupling. Tribol. Int. 2024, 194, 109505. [Google Scholar] [CrossRef]
- Wen, C.; Liu, Z.; Bai, P.; Guan, J.; Gao, K.; Wen, X.; Tian, Y. Modeling and performance analysis of rotary compressor considering multi-body coupling and bearing deformation. Tribol. Int. 2023, 189, 108981. [Google Scholar] [CrossRef]
- Aw, K.T.; Ooi, K.T. A Review on Sliding Vane and Rolling Piston Compressors. Machines 2021, 9, 125. [Google Scholar] [CrossRef]
- Wang, C.; Wu, J.; Du, Y.; Lei, B. Lubricating condition evaluation of the rotary compressor under high ambient temperature. Int. J. Refrig. 2020, 118, 220–229. [Google Scholar] [CrossRef]
- Pandeya, P.N.; Soedel, W. Rolling Piston Type Rotary Compressors with Special Attention to Friction and Leakage. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 19–21 July 1978. [Google Scholar]
- Wang, C.; Zhang, S.; Lei, B.; Cheng, J.; Wu, J. Analysis on influence factors of back pressure in an asymmetrical algebraic scroll compressor. Int. J. Refrig. 2022, 138, 97–107. [Google Scholar] [CrossRef]
- Cheng, S.; Feng, Y.; Wang, K.; Meng, X. Tribo-dynamics modeling and analysis of key friction pairs in scroll compressor with floating fixed scroll design. Eng. Appl. Comput. Fluid Mech. 2022, 16, 2270–2285. [Google Scholar] [CrossRef]
- Pont, A.; López, J.; Rigola, J.; Pérez-Segarra, C.D. Numerical dynamic analysis of reciprocating compressor mechanism. Parametric studies for optimization purposes. Tribol. Int. 2017, 105, 1–14. [Google Scholar] [CrossRef]
- Cho, J.R.; Moon, S.J. A numerical analysis of the interaction between the piston oil film and the component deformation in a reciprocating compressor. Tribol. Int. 2005, 38, 459–468. [Google Scholar] [CrossRef]
- Bianchi, G.; Cipollone, R. Theoretical modeling and experimental investigations for the improvement of the mechanical efficiency in sliding vane rotary compressors. Appl. Energy 2015, 142, 95–107. [Google Scholar] [CrossRef]
- Gu, H.; Ye, F.; Chen, Y.; Wu, J.; Li, W.; Sundén, B. Performance investigation and design optimization of novel rotating-cylinder sliding vane rotary compressors. Int. J. Refrig. 2022, 142, 137–147. [Google Scholar] [CrossRef]
- Meng, X.; Qi, Y.; Sheng, L.; Li, Q.; Su, L. Investigations on efficiency improvement of rolling piston type rotary compressor with a new-designed cylinder. Appl. Therm. Eng. 2023, 222, 119920. [Google Scholar] [CrossRef]
- Shiga, T.; Ishijima, K.; Sakainc, M.; Chu, I. Analysis of The Rolling-Piston Type Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 19–21 July 1978. [Google Scholar]
- Tanaka, H.; Ishijima, K. Noise and Efficiency of Rolling Piston Type Refrigeration Compressor for Household Refrigerator and Freazer. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 1 January 1980. [Google Scholar]
- Imaichi, K.; Fukushima, M.; Muramatsu, S.; Ishii, N. Vibration Analysis of Rotary Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 1 January 1982. [Google Scholar]
- Huang, Z.; Jiang, W.; Zhang, H.; Liu, C.; Jin, H.; Zhou, Y.; He, J. An effective experimental method for identifying radiated noise of different angular ranges for the rolling-piston compressor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 2409–2417. [Google Scholar] [CrossRef]
- Wu, J.H.; Shi, H.Y.; Zhang, S.; Li, J.C.; Lei, B.W.; Du, Y.J. Experimental and numerical analysis of the performance of the R290 rotary compressor used in a split-room air conditioner at high ambient temperature. Sci. Technol. Built Environ. 2020, 27, 226–239. [Google Scholar] [CrossRef]
- Li, R.; Jing, L.; Meng, X.; Liu, Z.; Zhang, R. Numerical analysis of vane–slot friction pair in a rolling piston compressor considering deformation and groove design. Tribol. Int. 2021, 162, 107124. [Google Scholar] [CrossRef]
- Liu, R.; Jing, L.; Meng, X.; Lyu, B. Mixed elastohydrodynamic analysis of a coupled journal-thrust bearing system in a rotary compressor under high ambient pressure. Tribol. Int. 2021, 159, 106943. [Google Scholar] [CrossRef]
- Mi, J.; Meng, Y. Numerical Analyses of Hydrodynamic Lubrication and Dynamics of the Rolling Piston and Crankshaft in a Rotary Compressor. Tribol. Trans. 2014, 57, 1136–1147. [Google Scholar] [CrossRef]
- Padhy, S.K.; Scheldorf, G.O. Wear and Tribodynamics of a Rolling Piston Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 19–22 July 1994. [Google Scholar]
- Wu, J. Dynamic Analysis of Roller and Vane of Inverter Controlled Rotary Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 25–28 July 2000. [Google Scholar]
- Lee, Y.-Z.; Oh, S.-D. Friction and wear of the rotary compressor vane–roller surfaces for several sliding conditions. Wear 2003, 255, 1168–1173. [Google Scholar] [CrossRef]
- Wu, J.; Shi, H.; Li, J. Analysis on the reliability of R290 rotary compressor in the high ambient temperature. Int. J. Refrig. 2020, 110, 132–141. [Google Scholar] [CrossRef]
- Ito, Y.; Hattori, H.; Miura, K. Lubricating characteristics and motion characteristics of a rolling piston for rotary compressors in air conditioners. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 984–996. [Google Scholar] [CrossRef]
- Lyu, B.; Jing, L.; Meng, X.; Liu, R. Texture Optimization and Verification for the Thrust Bearing Used in Rotary Compressors Based on a Transient Tribo-Dynamics Model. J. Tribol. 2022, 144, 1–19. [Google Scholar] [CrossRef]
- Yoshimura, T.; Ono, K.; Inagaki, K.; Kotsuka, H.; Korenaga, A. Analysis of Lubricating Cliaracteristics of Rotary Compressors for Domestic Refrigerators. Trans. ASME 1999, 121, 510–516. [Google Scholar] [CrossRef]
- Wu, J.; Chen, A. A new structure and theoretical analysis on leakage and performance of an oil-free R290 rolling piston compressor. Int. J. Refrig. 2015, 49, 110–118. [Google Scholar] [CrossRef]
- Wu, J.; Hu, J.; Chen, A.; Mei, P.; Zhou, X.; Chen, Z. Numerical analysis of temperature distribution of motor-refrigerant in a R32 rotary compressor. Appl. Therm. Eng. 2016, 95, 365–373. [Google Scholar] [CrossRef]
- Gasche, J.L.; Ferreira, R.T.S.; Prata, A.T. Two-Phase Flow of Oil-Refrigerant Mixture Through the Radial Clearance in Rolling Piston Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 25–28 July 2000. [Google Scholar]
- Cho, I.-S.; Oh, S.-H.; Jung, J.-Y. Lubrication Characteristics Between the Vane and the Rolling Piston in a Rotary Compressor Used for Refrigeration and Air-Conditioning Systems. KSME Int. J. 2001, 15, 562–568. [Google Scholar] [CrossRef]
- Ooi, K.T.; Wong, T.N.; Kwek, E.C. A Real Gas Simulation of a Refrigeration Compressor and its Performance Comparison for CFCs and Non-CFCs. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 14–17 July 1992. [Google Scholar]
- Hwang, S.; Kim, K.; Lee, S.; Kim, J.; Park, S. Development of the high efficiency rolling piston type rotary compressor for alternative refrigerant R410a. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 14–17 July 1998. [Google Scholar]
- Fang, X.; Lin, J.; Ma, X. Simulation study on compression characteristics of low GWP refrigerants in the cylinder of rotary compressors. Appl. Therm. Eng. 2021, 193, 117056. [Google Scholar] [CrossRef]
- Cai, D.; He, G.; Yokoyama, T.; Tian, Q.; Yang, X.; Pan, J. Simulation and comparison of leakage characteristics of R290 in rolling piston type rotary compressor. Int. J. Refrig. 2015, 53, 42–54. [Google Scholar] [CrossRef]
- Geng, K.; Yan, C.; Wei, W.; Shi, D.; Zheng, X.; Lei, Y. Numerical and experimental investigation of vane–piston separation–collision in variable-speed compressors. Int. J. Refrig. 2022, 139, 148–157. [Google Scholar] [CrossRef]
- Cho, I.-S.; Baek, I.-H.; Oh, S.-H.; Jung, J.-Y. Friction characteristics between vane and rolling piston in a rotary compressor used for refrigeration and air-conditioning systems. KSTLE Int. J. 2008, 9, 17–21. [Google Scholar]
- Jeon, H.-G.; Oh, S.-D.; Lee, Y.-Z. Friction and wear of the lubricated vane and roller materials in a carbon dioxide refrigerant. Wear 2009, 267, 1252–1256. [Google Scholar] [CrossRef]
- Ahn, H.J.; Han, D.C.; Hwang, I.S. A built-in bearing sensor to measure the shaft motion of a small rotary compressor for air conditioning. Tribol. Int. 2003, 36, 561–572. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, M.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. J. Lubr. Technol. 1979, 101, 220–229. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Xie, Y.; Zhang, D. Mixed lubrication problems in the presence of textures: An efficient solution to the cavitation problem with consideration of roughness effects. Tribol. Int. 2016, 103, 516–528. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Tripp, J.H. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–634. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A finite element based elastic-plastic model for the contact of rough surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Wen, C.; Meng, X.; Xie, Y.; Liu, R.; Kong, X.; Li, R.; Liu, Z.; Fang, C. Online measurement of piston-assembly friction with wireless IMEP method under fired conditions and comparison with numerical analysis. Measurement 2021, 174, 109009. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Xie, Y.; Kong, X. Performance of Surface Texturing During Start-Up Under Starved and Mixed Lubrication. J. Tribol. 2017, 139, 011702. [Google Scholar] [CrossRef]
- Jakobsson, B.; Floberg, L. The finite journal bearing considering vaporization. Trans. Chalmers Univ. Technol. 1957, 190, 1–116. [Google Scholar]
- Olsson, K. Cavitation in dynamically loaded bearings. Trans. Chalmers Univ. Technol. 1965, 308, 1–60. [Google Scholar]
- Zhang, J.; Meng, Y. Direct Observation of Cavitation Phenomenon and Hydrodynamic Lubrication Analysis of Textured Surfaces. Tribol. Lett. 2012, 46, 147–158. [Google Scholar] [CrossRef]
- Lyu, B.; Meng, X.; Zhang, R.; Wen, C. A deterministic contact evolution and scuffing failure analysis considering lubrication deterioration due to temperature rise under heavy loads. Eng. Fail. Anal. 2021, 123, 105276. [Google Scholar] [CrossRef]
- Almqvist, A. Homogenization of the Reynolds equation governing hydrodynamic flow in a rotating device. J. Tribol. 2011, 133, 021705. [Google Scholar] [CrossRef]
- Almqvist, A.; Fabricius, J.; Spencer, A.; Wall, P. Similarities and differences between the flow factor method by Patir and Cheng and homogenization. J. Tribol. 2011, 133, 031702. [Google Scholar] [CrossRef]
- Ito, Y.; Hattori, H.; Miura, K.; Hirayama, T. Mixed Lubrication Analysis of Vane Sliding Surface in Rotary Compressor Mechanisms. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 17–20 July 2006. [Google Scholar]
- Hattori, H.; Kawashima, N. Dynamic Analysis of a Rotor-Journal Bearing System for Twin Rotary Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 17–20 July 1990. [Google Scholar]
- Mi, J.; Meng, Y. THD Analysis of Rolling Piston and Journal Bearings in Rotary Compressors. Tribol. Trans. 2016, 59, 195–207. [Google Scholar] [CrossRef]
- Liu, Y.; Kosco, J. Vane Dynamics Analysis of a Tilted Vane Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 14–17 July 1998. [Google Scholar]
- Okada, K.; Kuyama, K. Motion of Rolling Piston in Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 1 January 1982; pp. 178–184. [Google Scholar]
- Yanagisawa, T.; Shimizu, T.; Chu, I.; Ishijima, K. Motion Analysis of Rolling Piston in Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 1 January 1982. [Google Scholar]
- Tanaka, S.; Kyogoku, K.; Nakahara, T. Lubrication Characteristics of Refrigerating/Air Conditioning Rotary Compressor: Mixed Lubrication Analysis on Vane Tip. Jpn. J. Tribol. 1996, 41, 253–268. [Google Scholar]
- Liu, Z.; Soedel, W. Performance Study of a Variable Speed Compressor with Special Attention to Supercharging Effect. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 19–22 July 1994. [Google Scholar]
- Deng, W.-J.; Zhang, Y.-l.; Zhu, Z.-P.; Yue, X.-J.; Ba, D.-C.; Che, S.-G. Fluid–solid coupling numerical simulation for the performance prediction and valve dynamic analysis of a rotary compressor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 6928–6938. [Google Scholar] [CrossRef]
- Liu, Z.; Soedel, W. Using a Gas Dynamic Model to Predict the Supercharging Phenomenon in a Variable Speed Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 19–22 July 1994. [Google Scholar]
- Geng, W.; Liu, C.; Wang, Y. The Performance Optimization of Rolling Piston Compressors Based on CFD Simulation. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 12–15 July 2004. [Google Scholar]
- Liu, C.H.; Geng, W. Research on Suction Performance of Two-Cylinder Rolling Piston Type Rotary Compressors Based on CFD Simulation. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 12–15 July 2004. [Google Scholar]
- Guo, N.; Lin, J.; Wu, J. Simulation on two-phase refrigerant compression in the cylinder of rotary compressors using CFD method. Sci. Rep. 2024, 14, 6075. [Google Scholar] [CrossRef] [PubMed]
- Brancher, R.D.; Deschamps, C.J. Modeling of Rolling-Piston Compressors with Special Attention to the Suction and Discharge Processes. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 14–17 July 2014. [Google Scholar]
- Ooi, K.T.; Wong, T.N. A computer simulation of a rotary compressor for household refrigerators. Appl. Therm. Eng. 1996, 17, 65–78. [Google Scholar] [CrossRef]
- Chae, H.M.; Kim, C.N. A numerical study with FSI mode on the characteristics of pressure fluctuation and discharge valve motion in rotary compressors with single and dual muffler. Int. J. Precis. Eng. Manuf. 2010, 11, 589–596. [Google Scholar] [CrossRef]
- Tan, Q.; Pan, S.-l.; Feng, Q.-k.; Yu, X.-l.; Wang, Z.-l. Fluid–structure interaction model of dynamic behavior of the discharge valve in a rotary compressor. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2014, 229, 280–289. [Google Scholar] [CrossRef]
- Yu, X.; Tan, Q.; Ren, Y.; Jia, X.; Jin, L. Numerical Study of the Reed Valve Impact in the Rotary Compressor by FSI Model. Energy Procedia 2017, 105, 4890–4897. [Google Scholar] [CrossRef]
- Ito, Y.; Hattori, H.; Miura, K. Numerical Analysis for Rotating Motion of a Rolling Piston in Rotary Compressors—Effective Factors for Characteristics of Rotating Motion of a Rolling Piston. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 12–15 July 2010. [Google Scholar]
- Xu, J.; Yu, B.; Yang, O.X.; Ding, S.P.; Zhao, H.H. Research on motion and friction of rolling piston in rotary compressor. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1180, 012047. [Google Scholar] [CrossRef]
- Tanaka, S.; Nakahara, T.; Kyogoku, K. Mixed Lubrication Analysis of Vane Tip in Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 25–28 July 2000. [Google Scholar]
- Cho, I.-S.; Jung, J.-Y. The influence of vane on the lubrication characteristics between the vane and rolling piston of a rotary compressor. J. Mech. Sci. Technol. 2006, 20, 2242–2249. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, H.; Jiang, B.; Zhu, B. Numerical Analysis of Friction power and Wear of Vane in Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 9–12 July 2018. [Google Scholar]
- Ito, Y.; Hattori, H.; Miura, K. Mixed Lubrication Analysis of Vane Sliding Surface in Rotary Compressor Mechanisms- Influences of Elastic Deformation at Surface End of Vane Slot. Tribol. Online 2009, 4, 96–102. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Shimizu, T. Friction losses in rolling piston type rotary compressors. Int. J. Refrig. 1985, 8, 159–165. [Google Scholar] [CrossRef]
- Padhy, S.K. On the Dynamics of a Rotary Compressor: Part 1-Mathematical Modeling. Adv. Des. Autom. 1993, 65, 207–217. [Google Scholar]
- Minami, K.; Hattori, H.; Hayano, M. Lubrication Analysis of Rotary Compressors for HFC Refrigerants. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 14–17 July 1998. [Google Scholar]
- Geng, K.; Geng, A.; Wang, X.; Zheng, X.; Wei, W.; Zhao, T.; Lei, Y.; He, Y. Frictional characteristics of the vane–chute pair in a rolling piston compressor based on the second-order motion. Tribol. Int. 2019, 133, 111–125. [Google Scholar] [CrossRef]
- Padhy, S.K. On the dynamics of a rotary compressor: Part 2- Experimental validation and sensitivity analysis. Adv. Des. Autom. 1993, 65, 219–227. [Google Scholar]
- Lin, J.; Guo, N.; Hong, L.; Wu, J.; Jiang, J.; Zhao, T. Simulation of single and two-phase refrigerant compression in rotary compressors. Appl. Therm. Eng. 2022, 211, 118465. [Google Scholar] [CrossRef]
- Zhang, A.; Sun, H. Dynamics Analysis of a Rolling Rotor Compressor Considering the Electromagnetic Force. J. Comput. Electron. Inf. Manag. 2023, 10, 91–94. [Google Scholar] [CrossRef]
- Seve, F.; Berlioz, A.; Dufour, R.; Dufour, R.; Peyaud, F. Balancing of a Variable Speed Rotary Compressor: Experimental and Numerical Investigations. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 25–28 July 2000. [Google Scholar]
- Wang, Z.; Yu, X.; Liu, F.; Feng, Q.; Tan, Q. Dynamic analyses for the rotor-journal bearing system of a variable speed rotary compressor. Int. J. Refrig. 2013, 36, 1938–1950. [Google Scholar] [CrossRef]
- Park, Y.C. Transient analysis of a variable speed rotary compressor. Energy Convers. Manag. 2010, 51, 277–287. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, J.; Xie, F.; Chen, A.; Li, Y. Dynamic behaviors of the crankshafts in single-cylinder and twin-cylinder rotary compressors. Int. J. Refrig. 2014, 47, 36–45. [Google Scholar] [CrossRef]
- Hirayama, T.; Ito, Y.; Shida, S.; Kawabe, I.; Hirano, K. Development of large capacity rotary compressor with three cylinders. First report: Prototype designs and their efficiencies. Int. J. Refrig. 2021, 130, 278–287. [Google Scholar] [CrossRef]
- Hirayama, T.; Shida, S.; Hirano, K.; Ito, Y.; Monasry, J.F. Development of large capacity rotary compressor with three cylinders. Second report: Vibration and sound. Int. J. Refrig. 2021, 130, 261–270. [Google Scholar] [CrossRef]
- Dufour, R.; Charreyron, M.; Gerard, M. Dynamics Prediction of Refrigerant Rotary Compressor Crankshaft. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 14–17 July 1998. [Google Scholar]
- Fu, Y.; Zhou, X.; Guo, H.; Mei, P. Lubrication Analysis of Journal Bearings in R410A Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 11–14 July 2016. [Google Scholar]
- Yu, B.; Yang, O.; Xu, J.; Wei, H.; Zhao, H. Numerical Analysis and Optimization for Hydrodynamic Lubrication in Journal Bearings of Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 24–28 May 2021. [Google Scholar]
- Hirayama, T.; Miura, K.; Hattori, H.; Ito, Y. Numerical Analysis for Mixed Lubrication in Journal Bearings of Rotary Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 17–20 July 2006. [Google Scholar]
- Xie, F.; Zhang, H.; Wu, J.; Ma, W.; Liu, C. Dynamic Analysis of a Rotor-Journal Bearing System of Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 17–20 July 2006. [Google Scholar]
- Kitsunai, Y.; Matsui, M.; Oyagi, S. High Efficiency Development of a Rotary Compressor by Clarification of its Shaft Dynamic Motion. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 12–15 July 2010. [Google Scholar]
- Meier, A.M.; Tada, M.P.; Espindola, G. Compressor Friction Losses due to Oil Viscosity and Asperity Contact Surfaces: A numerical study on crankshaft bearings lengths, clearances and roughness parameters. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 9–12 July 2018. [Google Scholar]
- Jorgensen, S.H.; Nissen, H.S. Mechanical Loss Model of Rolling Piston Rotary Compressor with Special Importance Attached to Journal Bearing. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 11–13 July 1984. [Google Scholar]
- Yang, J. Mechanical Loss Analysis Of Inverter Controlled Two Cylinders Type Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 16–19 July 2002. [Google Scholar]
- Han, H.-S.; Hwang, S.-W. Vibration Analysis of a Rotary Compressor. Int. J. Precis. Eng. Manuf. 2004, 5, 43–53. [Google Scholar]
- Pinninti, R.R. Rotary Behavior of Crank Shaft and Piston of the Compressor Housing. Int. J. Adv. Eng. Res. Technol. 2014, 2, 359–367. [Google Scholar]
- Kima, H.J.; Lancey, T.W. Numerical study on the lubrication oil distribution in a refrigeration rotary compressor. Int. J. Refrig. 2003, 26, 800–808. [Google Scholar] [CrossRef]
- Padhy, S.K. Lubrication analysis of a rolling piston rotary compressor Part 1: Mathematical modelling. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1994, 208, 83–94. [Google Scholar] [CrossRef]
- Padhy, S.K. Lubrication analysis of a rolling piston rotary compressor Part 2: Experimental validation and results. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1994, 208, 95–104. [Google Scholar] [CrossRef]
- Chen, H.; Liang, H.; Wang, W.; Zhang, S. Investigation on the oil transfer behaviors and the air-oil interfacial flow patterns in a ball bearing under different capillary conditions. Friction 2022, 11, 228–245. [Google Scholar] [CrossRef]
- Yan, B.; Dong, L.; Yan, K.; Chen, F.; Zhu, Y.; Wang, D. Effects of oil-air lubrication methods on the internal fluid flow and heat dissipation of high-speed ball bearings. Mech. Syst. Signal Process. 2021, 151, 107409. [Google Scholar] [CrossRef]
- Wu, C.; Zheng, L. An Average Reynolds Equation Lubrication with a Contact Factor. Trans. ASME 1989, 111, 188–191. [Google Scholar] [CrossRef]
- Liu, R.; Meng, X.; Cui, Y. Influence of numerous start-ups and stops on tribological performance evolution of engine main bearings. Int. J. Engine Res. 2018, 21, 1362–1380. [Google Scholar] [CrossRef]
- Liu, Z.; Meng, X.; Wen, C.; Yu, S.; Zhou, Z. On the oil-gas-solid mixed bearing between compression ring and cylinder liner under starved lubrication and high boundary pressures. Tribol. Int. 2019, 140, 105869. [Google Scholar] [CrossRef]
- Gu, C.; Meng, X.; Xie, Y.; Yang, Y. Effects of surface texturing on ring/liner friction under starved lubrication. Tribol. Int. 2016, 94, 591–605. [Google Scholar] [CrossRef]
- Woodward, W.S.; Paul, B. Contact Stresses for Closely Conforming Bodies—Application to Cylinders and Spheres; U.S. Department of Transportation: Washington, DC, USA, 1976.
- Xiang, G.; Han, Y.; Wang, J.; Wang, J.; Ni, X. Coupling transient mixed lubrication and wear for journal bearing modeling. Tribol. Int. 2019, 138, 1–15. [Google Scholar] [CrossRef]
- Meng, Y.; Mi, J. Numerical analyses of THD lubrication and dynamics of rolling piston and bearings in a rotary compressor. In Positive Displacement Machines; Elsevier: Amsterdam, The Netherlands, 2019; pp. 225–261. [Google Scholar]
- Lin, J.; Lian, Y.; Wu, J. Numerical investigation on vapor-liquid two-phase compression in the cylinder of rotary compressors. Appl. Therm. Eng. 2020, 170, 115022. [Google Scholar] [CrossRef]
- Nagatomo, S.; Kato, S. Estimation of the Starting Torque of Refrigerant Rotary Compressors. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 1 January 1980. [Google Scholar]
- Yanagisawa, T.; Shimizu, T.; Horioka, T. A Study on Starting Characteristics of a Rolling Piston Type Rotary Compressor. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 4–7 August 1986. [Google Scholar]
- Ishii, N.; Imaichi, K.; Muramatsu, S.; Fukushima, M.; Matsunaga, H. The Study of Rolling Piston, Rotary Compressor Dynamic Behavior When Stopping to Reduce Noise and Vibration Level. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 11–13 July 1984. [Google Scholar]
- Lin, J.; Wu, J.; Zhang, Z.; Chen, Z.; Xie, J.; Lu, J. Experimental investigation of startup characteristics of R290 rotary compressor under low ambient temperature heating condition. Int. J. Refrig. 2017, 77, 128–135. [Google Scholar] [CrossRef]
- Wu, J.; Lin, J.; Zhang, Z.; Chen, Z.; Xie, J.; Lu, J. Experimental investigation on cold startup characteristics of a rotary compressor in the R290 air-conditioning system under cooling condition. Int. J. Refrig. 2016, 65, 209–217. [Google Scholar] [CrossRef]
- Guo, N.; Lin, J.; Wu, J.; Zhao, Y. Transient thermal analysis of the rotary compressor during startup process. Int. J. Refrig. 2024, 157, 34–42. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, Y.; Lin, J.; Guo, N.; Wu, J. Start-up characteristics of a R290 rotary compressor for an air source heat pump under low ambient temperature condition. Int. J. Refrig. 2024, 159, 385–394. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).