Abstract
Despite the ubiquity and prevalence of rheological consistency across a wide range of industries, there is no clear consensus on its meaning or on one particular technique for quantifying it. Instead, there exist various definitions of “consistency” that are each specific to a given context, and each industry has its own procedure for measuring it. This paper organizes the many subjects and terminologies associated with consistency, providing a comprehensive guide of fundamental mechanics, fundamental properties, modeling techniques, and standardized tests that describe consistency. This includes outlining the rheological models that describe the behavior of viscoelastic and non-Newtonian materials as well as the identification of numerous parameters that can be individually evaluated to comprehensively understand and quantify consistency. Such an understanding of consistency and its underlying mechanical properties encourages the refinement of current consistency test methods and development of new ones.
Keywords:
consistency; rheology; non-Newtonian; viscoelastic; semi-fluid; structured liquid; soft solid 1. Introduction
Consistency is a quantification of the structural integrity of a material that exhibits both fluid- and solid-like behavior. Such materials include non-Newtonian fluids, viscoelastic materials, dispersions, structured liquids, soft solids, semi-fluids, semi-solids, and more. Some of these terms are organized in Figure 1. Such a chart should only be used for a basic understanding of the subject, as many materials do not neatly fit within the organizational structure given due to the overlapping scopes of many of the terms contained within. Because of this ambiguity, the present authors adopt the term “rheological material” to include all materials for which the term “consistency” applies in a mechanical sense. These materials are used in a vast range of fields, such as food/dairy, pharmaceutical, cosmetic, lubricating grease, cement/concrete, grout/mortar, bitumen, paints/coatings, paper pulp, printing ink, toothpaste, blood tests, drilling mud, sewage, and soil analysis [1,2,3,4,5,6,7].
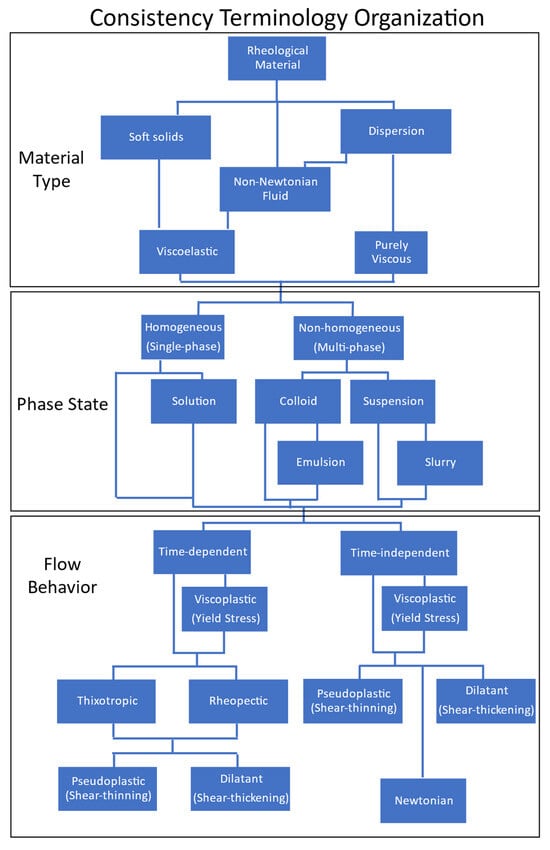
Figure 1.
Organization of terms associated with consistency.
Across these areas, there are various definitions and vastly different methods for testing material consistency. A review of the existing literature shows that there is no unifying definition and method for the quantification of consistency. Rather, there are individual definitions that apply to a specific situation. Numerous explicit and implicit definitions of consistency and the context for which they apply are given in Table 1.
Most of these definitions are quite similar and could be combined to form a definition for consistency, such as “the ability of a material to resist movement when subjected to stress”. This is quite similar to shear viscosity, which is generally regarded as the most important material function in an industrial context [8]. What differentiates consistency from viscosity is that it applies to a wider range of materials and contexts where a simple viscosity cannot be calculated. According to ASTM F1080 [9], a device called the Bostwick consistometer (later discussed in Section 4) is used because viscosity measurements cannot predict consistency “due to surface tension and density effects”. There are clearly properties other than viscosity that determine consistency.
Overall, McGuigan [10] broadly defines consistency as “a subjective term descriptive of the flow properties of a liquid usually measured in an empirical manner and in arbitrary units.” To add to this, the notes for ASTM D907 indicate that “consistency is not a fundamental property” but is instead “composed of viscosity, plasticity, and other phenomena” [11]. Thus, one could say that consistency is not a permanent feature of a rheological material; instead, it is a representation of how the material behaves at a particular point in time under a particular set of conditions. As the underlying fundamental properties that make up consistency change with time, so too does consistency.

Table 1.
Definitions of consistency across various industries
Table 1.
Definitions of consistency across various industries
| Context | Definition of Consistency |
|---|---|
| Cementitious mixtures | “Relative mobility or ability to flow” [12] |
| Soil | “Relative ease with which a soil can be deformed” [13] |
| Lubricating grease | Degree of resistance to movement by force [14,15] |
| Relative stiffness or hardness [16,17] | |
| Cohesiveness [18] | |
| Self-flowing castable refractories | “Degree of mobility under its own weight” [19] |
| Liquid adhesives | “Material’s ability to resist deformation” [11] |
| Food | Degree of mobility down a ramp due to gravity [9] |
| Force or deformation needed to cause yielding [20] | |
| Average size of food particles [21] | |
| Subjective texture [22] |
Many different industries arbitrarily define consistency as the result of a particular test. For lubricating grease, consistency is defined by the cone penetration test [23]. For concrete, consistency is measured by the slump test [24]. Other tests are sometimes used in these cases, but they have not seen widespread acceptance. However, in all contexts, consistency may be determined by some combination of more fundamental properties such as apparent viscosity, viscoelasticity, adhesiveness, density, thixotropy, yield stress, crossover stress, surface tension, elastic modulus, particle size, particle agglomeration, and tackiness. A more thorough discussion of these properties is provided later.
A quantification of consistency may be needed for safety purposes in foods and medications or even in concrete to ensure correct structural properties. There may also be quality control purposes for quantifying consistency in products such as lotions, foods, and cosmetics to give a certain brand a competitive subjective advantage. Further, there may be efficiency improvements that can be made by optimizing the consistency of a product to match a specific application, such as lubricating grease or drilling mud. In such industries, a batch of product with the wrong consistency may need to be discarded, generally with significant financial impact. Thus, an understanding of the mechanics of consistency during manufacturing [25] and appropriate test methods to ensure proper consistency are critical.
In this paper, the fundamental mechanics of consistency are described in Section 2, covering the microscopic and macroscopic interactions that lead to consistency. Section 3 covers concepts in the field of rheology that are useful in understanding and modelling consistency. Section 4 covers the main empirical tests currently used across a wide range of industries with a focus on applications. Section 5 then covers rheological tests useful in measuring the fundamental parameters that give rise to consistency. These parameters are summarized in Section 6. Then, conclusions and recommendations for future work are given in Section 7.
2. Mechanics of Consistency
2.1. Categorizing Rheological Materials
Rheological materials can be categorized according to their phase state, as shown in the second section of Figure 1. They may be homogeneous (single-phase) systems or non-homogeneous (multi-phase systems/dispersions). The main homogeneous materials of concern in rheology are solutions, mainly polymer solutions. The main colloid relevant in rheology is emulsions, though sols, aerosols, and foams are also important in various contexts. The other type of structured fluid is suspensions, of which the most common type for study in rheology is slurries [26]. The term “structured fluid” or “complex fluid” [27,28] may include solutions, colloids, and suspensions.
Solutions are a type of simple fluid where the particle size is on the order of nanometers, corresponding to atoms, ions, and/or molecules. These homogeneous mixtures have one phase and cannot be filtered by traditional means. Most rheological materials of interest have multiple phases, however.
The simplest type of multi-phase material is a colloid: a nearly homogeneous mixture that also cannot be filtered by traditional means, though they may be separated by techniques such as ultrafiltration, nanofiltration, and the use of dialysis membranes [29,30]. At least one dimension of the size of a colloid particle is on the order of 0.01–10 microns [31], roughly corresponding to large molecules or aggregates and existing on the mesoscopic scale. Often, the attraction between two contacting colloidal particles is sufficient for them to permanently stick together, forming a colloidal aggregate [27]. The nonhomogeneous nature of colloids means that a theoretical description of their behavior is usually given using statistical mechanics [32]. This concept also applies to other types of rheological materials.
Suspensions are the other type of multi-phase rheological material, which are mixtures where the dispersed phase can be separated by filtering. The dispersed particles are generally much larger than the particle sizes of a solution, often meaning over 100 microns [33]. Suspensions must be constantly agitated, or else particles will settle out of the suspension. An important type of suspension is a slurry, where dense solids are suspended in a liquid. Examples of slurries include cement slurries, coal slurries, and drilling mud [26].
A large portion of rheological materials fall into the categories of solutions, colloids, or suspensions. The underlying phenomena that cause a material to fit into one of these categories include interactions on various length and time scales. Understanding these interactions gives key insight into the nature of a material and allows for the modification of chemical structure or processing to yield changes to physical properties.
2.2. Intermolecular Interactions
Every interaction among the constitutive particles within a material is generally analyzed by comparing the strength of the interaction to the thermal energy [34,35]. The thermal energy is given by T, where is the Boltzmann constant and T is temperature in Kelvin. For a liquid, the interaction energy of a molecule is on the order of its thermal energy. If the thermal energy is orders of magnitude lower than the interaction energy, the interaction energy dominates, and the material is solid under such conditions. Conversely, if the thermal energy is orders of magnitude larger than the interaction energy, the material evaporates [28]. Because thermal motion serves to disorganize and randomize structures, any interaction that causes structures to form must be significantly stronger than the thermal motion.
The length scale of a typical fluid is the length of a molecule, and its time scale is on the order of the time between successive collisions between it and its neighbors. Rheological materials, however, can have complicated molecular structures and interactions among the molecules, meaning the characteristic length and time scales can be orders of magnitude larger than for simple fluids [28,36]. Because these lengths can be so long, the distance between the surfaces of particles is much less than the separation distance of their centers. Thus, the colloidal domain is dominated by surface forces rather than body forces [37,38].
Intermolecular forces are generally grouped into opposites—attractive vs. repulsive, short-ranged vs. long-ranged, strong vs. weak, isotropic vs. directional—but due to their complex nature, this cannot be easily performed with a high degree of accuracy, as there will always be exceptions [39]. Perhaps the best way of categorizing forces is by their physical or chemical origin, though even this approach is not perfect because of the large length scales of many relevant materials. Furthermore, these large-length scales can mean that such forces act in unintuitive manners. Nevertheless, some of the most pertinent intermolecular interactions that are found within rheological materials are summarized in Table 2. Among these, van der Waals forces and electrostatic forces are generally quite significant for colloidal structures [31]. In fact, one of the most important theories in colloid science—DLVO theory [40]—describes the aggregation and stability of dispersions based on a balance between van der Waals forces and electrostatic forces.

Table 2.
Summary of some relevant intermolecular forces.
To summarize, a complicated balance of attractive and repulsive interactions gives rise to rheological materials. Because of the vast range of rheological materials, few generalizations about the most relevant forces can be made. For more information on intermolecular and surface forces, see Israelachvili [39].
2.3. Mesoscopic Interactions
The simplest method of examining an intermolecular force is by considering only two particles interacting with each other. As more particles are added to the analysis, it begins to become more realistic but also significantly more complex [41]. The relevant structures discussed here may be orders of magnitude larger than simple molecules, meaning the summation of all pair potentials can be much larger than the thermal energy, even at large separation distances [39]. In the context of soap-based greases, a convenient scale to interpret overall behavior is the size of a fiber [42], with each fiber roughly consisting of molecules [43]. Most important structures within rheological materials exist in the colloidal domain, coinciding with the mesoscopic scale of materials [31,44]. This domain typically ranges from nanometers to tens of micrometers.
Intermolecular interactions give rise to properties that exist on a larger scale, such as surface tension/energy, capillary forces, and adhesive forces. Especially for larger particles, capillary forces can be quite significant and serve as a core determinant of a material’s behavior [45]. The intermolecular forces that determine surface energy are the same as those that determine latent heat and boiling point [38]. In the absence of strong polar forces, the surface energy can be estimated simply from van der Waals forces.
Many molecules in rheological materials, especially polymers, form “macromolecules” with structures resembling rods, coils, or strings. Such large structures have the ability to deform at a molecular level [27] and have various degrees of effectiveness in terms of thickening the structure when the same phase volume is added. In order from least to most effective thickening structures, there are spheres, grains, plates, and rods [46]. As these structures are sheared, their shapes may change quite dramatically, affecting flow behavior. For instance, directional flow tends to align and straighten the chains of polymers, while Brownian motion constantly counteracts this, slowly shaping them into coils [46].
Typically, the liquid phase’s viscosity plays the most significant role in determining flow properties of a structured fluid [1], but particle size, shape, concentration, and electrostatic or steric forces also must be considered [32]. As long as there are both significant attractive and repulsive forces [27], the structured fluid’s particles will tend to form a network. This network will generally stabilize the structure if left undisturbed but shearing or even Brownian motion can cause the viscosity and overall consistency of the fluid to change.
The viscosity of a dispersion depends on continuous phase viscosity, density/size/shape of the disperse phase, deformability of disperse phase, and strength of interactions [46]. These can all be modified as desired, and additives can even be added specifically to modify the strength of interaction among molecules, allowing for viscosity to be modified as needed for a given application. More familiar to a practitioner is the fact that viscosity is a function of temperature and pressure. The differences a fluidic material encounters are typically insignificant to affect viscosity, but in many lubrication systems, pressure can be quite high, significantly affecting viscosity [46]. This increase in pressure plays a significant role in the tribological behavior of rolling element bearings.
Unlike typical fluids whose main differences in mechanical response are governed by viscosity [28], structured fluids can show similar viscosities in a given context but have dramatically different overall behaviors because their viscosity is a function of shear rate. Measuring viscosity through tests can provide sufficient information about a given material for a basic analysis, but understanding a material’s microstructure is important in being able to formulate the desired product [34]. For instance, laponite has a disc-like microstructure, and when put in a solution, the discs may associate into vastly different configurations that give the material very different flow properties. This allows for the material to have a gel-like configuration at high particle concentrations, become a pseudoplastic fluid at low particle concentrations, and develop yield stress as the electrolyte content in the solution is increased [47]. Thus, a simple viscosity test could lead to problematic analysis of different laponite dispersions.
Often, materials have mechanisms that store energy like a solid and dissipate energy like a fluid. Energy storage mechanisms include potential energy stored in bond, a polymer section being stretched, or entropic energy stored by an isolated polymer coil being deformed from its spherical rest state [46]. Energy dissipation mechanisms include behavior such as internal friction or anything passing through a fluidic continuous phase. Materials showing energy storage and dissipative mechanisms are called viscoelastic materials and show complicated time-dependent behavior. The study of the flow of these materials and other rheological materials is the core focus of the field of rheology.
3. Rheological Descriptions of Consistency
3.1. Viscoelasticity
Rheology primarily describes the flow of non-Newtonian fluids, where some of the core assumptions of fluid mechanics such as no slip and Newtonian viscosity may not hold in a given situation. Many of these materials are viscoelastic, exhibiting creep and relaxation. Creep is where the material strains while being held at constant stress, while relaxation is a decrease in stress as the material is held at constant strain. Materials where consistency is relevant often show these properties, so understanding this behavior allows for modelling these materials.
Viscoelastic behavior can be modelled in many ways, but the simplest mechanical models are constructed by considering a purely elastic spring and a purely viscous dashpot [48]. The Kelvin–Voigt model uses a spring and dashpot in parallel, meaning their displacements or strains are the same. If disturbed, the material will slowly creep toward a finite point of deformation while the force/stress remains. When the disturbance is removed, the configuration will eventually relax to its initial length, showing reversibility. This resembles the characteristics of an elastic material and is used to model creep reasonably well for most cases. However, this model generally does a poor job of modelling relaxation.
The Maxwell model, on the other hand, uses the spring and dashpot in series, meaning the force or stress across them is the same. If disturbed, the stress/force within the material will change as a function of time, even if the displacement is held constant. When the disturbance is removed, the configuration will not return to its initial length, as the dashpot element will have irreversibly changed. This resembles the characteristics of a viscous material, modelling relaxation reasonably well for most cases.
There are more complicated viscoelastic models available that combine the same elements in various ways, but the most comprehensive model that sees common use is the Burgers model. This model is simply a combination of the Kelvin–Voigt and Maxwell models where they are put in series with each other. This second-order mechanical model has two different elastic moduli and characteristic times, given by Equation (5) in Table 3 [49]. This model more accurately describes creep for many viscoelastic materials.

Table 3.
Common viscoelastic models.
The simplest meaningful case for these models is to consider the creep response to a constant stress in the Kelvin–Voigt and Burgers models and to consider the relaxation from a constant strain in the Maxwell model. The corresponding equations and solutions are given in Table 3 [50].
In Table 3, represents strain, represents stress, t denotes time, a dot signifies a time derivative, η represents the dashpot constant between stress and strain rate corresponding to viscosity, G stands for the spring constant between stress and strain corresponding to shear modulus, represents the magnitude of the constant stress applied, and is the magnitude of constant strain.
Creep is one of the most commonly examined properties of viscoelastic materials due to its prevalence in many situations. Almost all materials will creep even at low values of stress, including solids. However, for solid materials, the test temperature and pressure must be brought sufficiently high to elevate the magnitude of creep into a range where it can be measured, and the test may need a prohibitive amount of time to measure any change [51]. Creep is often quantified using creep compliance, , which is simply the creep over time divided by the stress used to induce creep, shown in Equation (7).
The value of creep compliance corresponding to is the equilibrium creep compliance, , which is the inverse of the shear modulus (given by G in above equations). This is often used in place of G.
The description of viscoelastic behavior is the same for all geometrical modes of deformation, including elongational, shear, and volume changes [50]. However, there may be a significant difference in the apparent viscosity of a material when comparing shear flow to elongational flow. Especially for materials with a fibrous structure, being subjected to shear flow will align the particles in the flow direction, allowing for them to pass by each to minimize the disruption to flow [6]. This same material subjected to extensional flow will again force the particles to align in the flow direction, but they are now being stretched by the flow, maximizing the resistance to flow.
The choice of which model to use depends on whether a given viscoelastic material more closely resembles a viscous material or an elastic material under the given test conditions. At higher test speeds (high frequencies or short time scales) or lower temperatures, the elastic nature of a material becomes increasingly significant. At lower test speeds and higher temperatures, the viscous behavior of a material becomes more significant. The Deborah number is a useful parameter that indicates the relative contributions of viscous and elastic behaviors for a material in a given context. This dimensionless number is the ratio of relaxation time to the test time or observation time. The relaxation time may be given by the ratio found in the viscoelastic models. In cases where multiple models are combined, there are multiple relaxation times and typically the longest is the most characteristic of the material.
A material with a low Deborah number in a given context will have a fluid-like response and will likely be modeled reasonably well by the Maxwell model. Conversely, a material with an intermediate or high Deborah number in a given context will show a solid-like response and could be modeled reasonably well with the Kelvin–Voigt model.
One of the most important ways of measuring viscoelastic material behavior is through oscillatory tests. In these tests, a sinusoidal stress or strain is imposed, and the corresponding strain or stress output is measured over time. For a purely elastic material, stress and strain are in phase with one another. Purely viscous materials, on the other hand, show the output as 90 degrees out of phase with the input. Viscoelastic materials have both a viscous and an elastic response, which can each be quantified by considering the phase shift of the response. If an oscillatory stress with amplitude is imposed as Equation (8), then the response with amplitude and phase shift δ is given by Equation (9).
The response is then analyzed by calculating the storage modulus and the loss modulus. The storage modulus or elastic modulus, given by Equation (10) and often referred to as G′, represents the elastic component of the response. The loss modulus, given by Equation (11) and often referred to as G″, represents the viscous component of the response.
Within the linear viscoelastic region, G′ and G″ are dependent on frequency, but not on stress amplitude. This makes oscillatory testing a good choice for observing the microstructure without altering it. If the amplitude is increased, nonlinearities begin to set in, and the linear theory of viscoelasticity is not sufficient to describe the non-Newtonian behavior [47,50]. When amplitudes become high, the material begins to flow, and behavior is characterized in a different manner [52].
3.2. Non-Newtonian Behavior
The complexity in microscopic construction of rheological materials is understood and characterized by looking at a macroscopic sample and using relatively simple models to describe its behavior. The core way of characterizing such a material is through the relationship between stress and strain. Non-Newtonian fluids are treated as fluids with a viscosity that depends on the state of stress. There are many possible models that describe their behavior as a function of shear rate and/or time. Some examples are given in Table 4. In these equations, τ represents shear stress, denotes shear strain rate, represents yield stress, and other symbols are curve fitting parameters.
These equations are generally sufficient for modelling the flow behavior of materials. There exist more complicated equations that may be used for detailed modelling of a particular material [53], but these have not found extensive use due to their complexity [54]. The Cross model covers a wide range of shear rates yet simplifies to the Newtonian model at low shear rates, the power law at moderate shear rates, and the Sisko model at high shear rates.
For materials whose models are constructed with a power fit, including the power law, Herschel–Bulkley, Casson, Sisko, and Robertson–Stiff, the value of the exponent, n, gives important information about how the material is classified. The case of corresponds to a shear-thinning (pseudoplastic) material where the apparent viscosity decreases as shear rate increases. The case of corresponds to a shear-thickening (dilatant) material where the apparent viscosity increases as shear rate increases. In the case of , if there is a yield stress, the material is considered a Bingham plastic over a reasonable range of shear rates [46]; if not, the material is Newtonian. These effects may be combined, as a material with and a yield stress is a Bingham pseudoplastic, and a material with and a yield stress is considered a Bingham dilatant material.

Table 4.
Common non-Newtonian fluid models.
Table 4.
Common non-Newtonian fluid models.
| Model | Description | Examples | Equation | Equation Number |
|---|---|---|---|---|
| Power law | Power fit | Crude oil, blood | (12) | |
| Herschel–Bulkley | Power fit with yield stress | Grease, bentonite suspensions | (13) | |
| Bingham | Linear fit with yield stress | Toothpaste, concrete | (14) | |
| Casson | Bingham model variant | Jelly, tomato sauce, blood [55] | (15) | |
| Sisko | Newtonian and power law | Grease, cement pastes | (16) | |
| Robertson–Stiff | Power fit with correction factor | Drilling fluids, cement slurries [54] | (17) | |
| Cross | General viscosity model | Many materials without yield stress | (18) |
There are numerous mechanisms that cause pseudoplasticity and dilatancy. These include alignment of rod-like particles in the flow direction, loss of junctions in polymer solutions, rearrangement of microstructure in suspensions/emulsions, and breakdown and/or accumulation of flocs. Because all of these take time to develop, the apparent viscosity for these materials is also a function of time [56].
3.3. Time and Temperature Dependence
It is quite common for the apparent viscosity of rheological materials to decrease as a function of time during shearing, meaning a material shows thixotropy. When shearing stops for these materials, Brownian motion causes the structure to eventually rebuild. However, there are some materials that tend to act in the opposite manner, where shearing builds structures within the material and cessation of the shear allows for Brownian motion to de-structure the material. In such a rare case, the material shows antithixotropy, or rheopexy [56]. For the most part, these materials with time-dependent behavior return to their initial state after resting for a sufficient time; however, in some situations, a material may undergo irreversible structure degradation from shear [6,57,58,59], though this is not considered thixotropy [56].
There are different mechanisms for thixotropy depending on the material [56], as there exist various microstructures such as flocculated particles, fibers, rods, and polymer structures. For materials with flocculated particles, thixotropy is mainly from the spatial distribution of these particles: when they are randomly distributed, they show a viscosity maximum, while they show decreased viscosity when aligned asymmetrically in the flow direction [56]. For materials with a fibrous structure, they become aligned in the direction of flow and break up into smaller pieces when sheared, leading to decreased viscosity [60,61]. Polymer solutions, on the other hand, have entanglement density and molecular associations that determine viscosity over time as they are sheared [46].
Thixotropy is generally analyzed in a different region than viscoelasticity. Although a time-dependent response to stress is a fundamental property of viscoelasticity, it may be negligible on a given time scale; thus, thixotropy and rheopexy may be ignored in some experiments [4]. Viscoelastic effects are mainly studied in the linear region where the microstructure responds without changing on a given time scale. However, in the case of thixotropy, the microstructure does change, and this process takes finite time [46]. Overall, thixotropy is most important when its time scale is significantly longer than the observation process, as the history of the material has the potential to affect measurements. In fact, the procedure of loading a thixotropic material into the measurement device has the potential to change its microstructure, meaning it must be given some time to relax before measuring.
All viscoelastic materials show a hysteresis loop due to their time-dependent response to high stress and subsequent recovery. Because breakdown and recovery do not follow the same path for thixotropy, such materials have an especially pronounced hysteresis loop. Because both nonlinear viscoelasticity and thixotropy form this loop, it is often difficult to tell the difference between the two using this method [62], and as such, it is generally not recommended to use this information to assess thixotropy [56]. Instead, the response to step changes in stress or strain with a controlled prehistory can be a better way of isolating thixotropic effects.
The models given by Table 4 are only applicable at a fixed temperature since apparent viscosity is a strong function of temperature. Compared to Newtonian fluids, there is additional complexity with many non-Newtonian materials, as their constitutive model relating shear stress and shear rate may be different at different temperatures. For example, crude oil is modelled quite well by a power law at low temperatures, but then is nearly Newtonian at higher temperatures [63]. In fact, much like the phase changes from solid to liquid to gas as a function of temperature, there exist different flow regimes for all materials depending on temperature.
Perhaps the best example of these different regimes can be observed with polymers. At low temperatures, these materials behave in a glassy manner, with almost exclusively elastic behavior. At moderate temperatures, there is a leathery transition region where viscous behavior becomes more significant [64]. Then as temperatures increase, polymer materials behave in a rubbery manner and may begin to flow [65]. An interesting characteristic of viscoelastic materials is that this behavior can also be noticed at a constant temperature by altering the test frequency or observation time. At very low frequencies, materials will flow, while at very high frequencies, they will show glassy behavior [46].
Overall, temperature is a very important factor in how materials behave, but even at a moderate temperature, common materials may behave in unintuitive manners. For instance, all fluids become non-Newtonian at extremely high shear rates, and many materials also behave in a non-Newtonian manner at extremely low shear rates [46]. At the extremes, the constitutive models that make up all fluids begin to break down. For many fluids, a significant example of this is yielding.
3.4. Yield Stress
Many materials for which consistency is relevant have a negligible degree of flow at low stresses. However, they begin to flow as a fluid once some critical stress is exceeded, indicating that such a material has a yield stress. Yield stress is characterized by an extremely high apparent viscosity at low values of stress, but upon reaching a critical value of stress, a sudden decrease in apparent viscosity. Such a material exhibits plasticity and engages in viscoplastic flow [50]. Viscoelastic fluids often show a superposition of viscoelastic and viscoplastic behavior, especially if the dispersion medium is itself a viscoelastic fluid. In addition, essentially all materials with a yield stress show thixotropy [66].
The transition between solid-like and liquid-like behavior corresponding to “yielding” generally does not occur suddenly; instead, it happens over a wide range of stresses [67]. In addition, there may be multiple yield stresses, characterized by different mechanisms at different length/time scales. To further complicate the matter, some materials may even have “complex” mechanical behavior with a range of yield stresses under similar conditions [67]. One argument is that the Cross model is sufficient to describe materials with a yield stress [68] and that a true “yield stress” does not exist [8]. Nevertheless, this paper will treat yield stress as a practical simplification of behavior and will cover methods for its calculation in Section 5.
4. Quantifying Consistency: Industry Tests
Though the idea of consistency is broadly similar across various industries, there are different ways of quantifying it depending on the industry. These different methods are expected to provide slightly different results that do not exactly correlate with each other. As McGuigan notes [10], most consistency tests are empirical with results presented in arbitrary units. Such tests include a wide range of deformation tests, flow tests, penetration tests, and other similar tests. Each is generally used within a specific industry because the test is simple to perform, provides a reasonable degree of reproducibility, and has at least some capacity to dictate a material’s suitability to a given application.
Because there are fundamentally different consistency tests across a wide range of industries, they are grouped together here by the core concept of the test. The main concepts include deformation by a material’s own weight, forced deformation with minimal constraints, penetration by a foreign object, flow through a fixed geometry, simple viscosity tests, and other tests that are designed to be simple.
The first consistency test concept that will be covered is where a material’s own weight is used to induce flow. Such methods generally test how much a material’s density overpowers cohesive (and to a lesser extent, adhesive) forces when allowed to flow starting from an unstable formation. Such tests include the Bostwick consistometer test [18], castable refractory consistency test [19], concrete slump test [24], and controlled low-strength material (CLSM) flow consistency test [69].
The Bostwick consistometer test [9] measures the distance a material flows down a ramp over a given amount of time. This is primarily used for food products, but it may also be used to measure paint, cosmetics, or other chemicals. This test is used because of its simplicity and ability to be used with a wide range of materials.
The castable refractory consistency test [19] is applied to materials that are often used to construct heat-resistant structures such as ovens and kilns. An appropriate mix of dry castable and mixing liquid is placed into a cone-shaped mold. The mold is then removed from the partially cured refractory mixture, causing it to deform and flow under its own weight. The change to the diameter of the base of the cone is used as the measurement of consistency and can be used to calculate the “percent self-flow”.
A similar test exists for measuring controlled low strength materials (CLSM), such as soil, aggregates, and cementitious material [69]. The procedure is quite similar, and the end result is a disc whose diameter is measured in various places and is averaged to produce an indication of consistency.
These differ slightly from the concrete slump test [24], which uses a similar procedure, but the final height of a slumped cone of concrete is used rather than the diameter of its base. Nevertheless, this test once again measures the change in geometry of a material when left to deform under its own weight from an unstable initial state.
Similar to these tests is the second concept, where the test sample is forced to deform, but there are minimal restrictions on its motion. This means that the initial formation is not necessarily unstable, but the results are less dependent on density than the preceding tests. Two examples are the flow table test for mortar consistency [70] and the vibratory table test for concrete [71].
The mortar consistency test is similar to the castable refractory test and CLSM test, except the sample is on a table that is dropped repeatedly, leading to repeated impacts. Clearly, this causes more deformation than if the sample were left alone.
In the vibratory table test, a stiff concrete mix is placed in a cone mold on a vibratory table. The mold is removed, and a weight is placed on top of it. The table then vibrates until the sample is flat and the time it takes for this to happen is recorded as the consistency.
The third test concept involves penetration of the test sample by a foreign object such as a cone, rod, or needle. This applies to industries such as grease [23,72], petroleum waxes [73], petrolatum [74], bituminous materials [75], cement paste [76], and/or mortars [77,78,79]. These tests have differences in preparation of the samples, geometry of the penetrating tool, and other details, but the overall idea is similar across all of them. In most cases, the penetrating tool is allowed to fall into the sample and the depth it reaches in some amount of time is used as an indication of the consistency. In other cases, the tool is allowed to penetrate until it reaches a steady state. The deeper the tool penetrates, the less firm the consistency. Mechanics of the grease cone penetration test are discussed in detail in other papers focused on grease consistency [80,81].
The fourth general test concept discussed in this paper is the flow of a material through a fixed geometry. This may be through a cone in the case of grout [82] or a syringe in the case of food [21] and lubricating grease [83]. They use gravity or a plunger to force the sample through the fixed geometry and the rate of flow or flow resistance is measured and used to quantify consistency. This is akin to pumpability, where the results depend on properties such as apparent viscosity, wall effects, plug formation, and yield stress. However, if gravity is used as the driving force, the results depend more strongly on density.
The fifth test concept explored here is the testing of a material’s apparent viscosity. This concept mainly applies to materials such as paint, coatings, and slurries. This may be performed with a commercial viscometer [84,85,86] or in the case of slurries, a special machine that is effectively a large-scale viscometer [87]. In this case, a measurement tool with a specific geometry—typically a cylinder or paddle—rotates within a container of the sample and the resistive torque imposed on it is used to calculate the apparent viscosity. Because most of the materials relevant in this paper are not Newtonian fluids, the apparent viscosity depends on the exact conditions imposed by the test.
The last section of tests are qualitative tests used because of their simplicity. Often these are used for field testing or where results only need to be an approximation. Such tests include the ball-in-hand test of refractories [88] and various food tests, including the spoon tilt test, fork drip test, and fork pressure test [89].
The ball-in-hand test of refractories [88] involves forming a ball of the refractory in the practitioner’s hand and visually inspecting consistency by seeing how much flows between the practitioner’s fingers after tossing the ball in the air and catching it.
The International Dysphagia Diet Standardization Initiative outlines various simple tests that can be easily carried out to examine food consistency, including the fork drip test, spoon tilt test, fork or spoon pressure test, chopstick test, and finger test [21,89]. Understanding food consistency is important for the safety of children or those with disabilities, yet a rigorous quantitative test is impractical and not necessary. Using a 10 mL syringe for drinks and standard eating utensils for food allows for anyone to test food consistency quickly and easily.
Overall, consistency is generally quantified with arbitrary measurements that are meant as a way of comparing different samples. This generally means there is some freedom in determining exactly how consistency should be measured. For example, ASTM D1338 [90] demands a consistency test for evaluating adhesive materials, but states that “any means of measuring the viscosity or consistency of the adhesive can be selected.” Because of the high variance in methods, the units of consistency can be distance, time, force, viscosity, or nothing at all because the test is qualitative. Nevertheless, the list of tests provided in this section (summarized in Table 5) is not exhaustive; instead, it is meant to provide an overview of the range of possible tests for quantifying consistency across the wide range of industries for which the concept is relevant.

Table 5.
Common consistency tests across various industries.
Table 5.
Common consistency tests across various industries.
| Test Type | Relevant Properties | Tests Available | Fields Where Relevant |
|---|---|---|---|
| Deformation under own weight | Density, apparent viscosity, yield stress, thixotropy | Bostwick consistometer [9], slump test [24], refractory consistency [19], CLSM consistency [69] | Food, concrete, soil, cement, mortar |
| Minimally constrained forced deformation | Apparent viscosity, yield stress, thixotropy, density | Concrete vibratory table [71], mortar consistency flow table [70] | Concrete, mortar |
| Penetration test | Apparent viscosity, yield stress, adhesiveness, density | Cone penetration [23,72,74,77,78], needle penetration [73,75], rod penetration [76] | Grease, bitumen, petrolatum, soil, cement, mortar |
| Flow through fixed geometry | Apparent viscosity, yield stress, adhesiveness, density | Grout flow cone [82], food syringe test [21], grease die extrusion [83] | Grout, food, grease |
| Viscosity test | Apparent viscosity | Stormer viscometer [86], API paddle [87] | Paint, coatings, slurries |
| Qualitative tests | Density, adhesiveness, apparent viscosity | Spoon tilt/fork drip food tests [21], ball-in-hand refractory test [88] | Food, refractories |
5. Quantifying Consistency: Rheological Tests
5.1. Rheological Testing Equipment
Because there are so many different industry tests for quantifying consistency, each with their own methods and purpose, it is quite useful to have a universal framework with the capability of performing various meaningful measurements. Though there is a wide variety of instruments that could possibly be used [65], rheometers or viscometers are generally common and can perform a wide variety of measurements of parameters associated with consistency. This may be performed in conjunction with standardized procedures [91,92,93,94] or by altering such methods to better match an application.
The main purpose of using a rheometer is to be able to accurately measure properties of a rheological material while using a small sample. When doing so, it is critical to use an appropriate geometry, as making the wrong selection can yield meaningless results [47]. A variety of measurement geometry is available to select from depending on the application and sample available. These geometries may be divided into two groups by the way flow is initiated. The first group uses a moving surface to initiate flow (drag flow), while the second uses pressure to drive flow (pressure flow). Most tests discussed here use a moving surface to initiate flow, but there are mentions of other equipment that uses flow through pipes, channels, or slits. A general overview of measurement geometry is given in Table 6 [35].

Table 6.
Common measurement geometries [35].
The most common measurement setups include plate–plate and cone–plate geometries, but more complicated setups may use a vane, spindle, rotor, paddle, or bob submerged in a cylindrical cup to measure samples. The parallel plate (plate–plate) setup is quite simple and allows for the measurement gap to be adjusted to better match the sample, but inherently causes a shear gradient throughout the sample. This may be alleviated by the cone–plate configuration, but this can be slightly more difficult to set up properly. If a sample dries out easily or shows sedimentation, then a cylindrical geometry may be preferable to expose a minimal amount of sample to the surrounding air. Another option is to use a saturated atmosphere near the edges or to flood the area with solvent [46].
Another major criterion for selecting measurement geometry is the consistency of the sample. The most fluid-like samples are generally tested using cup geometry to contain the sample. The inner rotating piece may be a cylinder, paddle, vane, or even a custom-made part as desired. When a sample has sufficient structure to resist flowing into a flat structure due to gravitational stress, it may be tested using a cone–plate or parallel plate geometry. Samples that are solid or very nearly solid may be tested using extension or torsion while gripped using special attachments at either end, similar to a typical fatigue tester.
Vane geometries are useful in overcoming wall slip [95]; at sufficiently low rotation rates, they act as though the material is sheared between the outside of the vane blades and the inner surface of the external cylinder with the bulk fluid between vane blades being treated as a solid [96,97]. However, at higher shear rates, secondary flow develops between the vane blades and results cannot be compared to those at lower shear rates. The concept of secondary flow applies to all measurement systems, limiting the maximum shear rates that should be applied to any situation.
Once a measurement geometry is selected, there are other considerations that must be made depending on the sample. If using a parallel plate setup, one must ensure that the measurement gap selected is at least ten times larger than the largest particle size of the sample [94]. If this is not carried out, possible issues arise such as particles jamming and aggregating; in addition, the shear rate and strain may be non-affine [47]. Another consideration is the process of loading the sample into the measurement device. Because many rheological materials are viscoelastic and/or thixotropic, the history of the material is relevant to the measurements made. This certainly includes the process for loading the sample into the machine. To minimize the uncertainties involved with sample loading, there are procedures such as a fixed rest time before measurements and different pre-shearing schedules [56].
Often, the rheological behavior of a material may need to be assessed under different conditions [98]. For instance, paints and coatings generally have three regions of shear rates where their rheological behavior should be known. The low shear rates correspond with the material’s behavior as it is applied to a surface and begins to sag, level, and/or settle. Medium shear rates correspond with the mixing and pumpability of the material. High shear rates correspond to the application method, including spraying, brushing, and rolling. Therefore, depending on the purpose of the rheological test, a certain shear rate region may be targeted, meaning the procedure and geometry for evaluation should be adjusted to best match this region.
5.2. Rheological Test Details
Some of the rheological tests that can be used to test fundamental properties of consistency include creep and recovery, stress ramp, stress growth, stress relaxation, oscillatory amplitude sweep, oscillatory frequency sweep, oscillatory time sweep, and stress relaxation [35].
5.2.1. Oscillatory
One of the most important considerations when performing rheological tests with a viscoelastic material is finding the linear viscoelastic region of a material within which viscoelastic measurements should generally take place. To find this region, an oscillatory measurement is taken at a constant frequency with increasing amplitude until the apparent viscosity or elastic modulus decreases significantly. Subsequent tests should then be performed at amplitude values lower than this unless specifically trying to measure properties outside the linear region. Because the linear region is affected by structure breakdown even from the process to load the sample into the rheometer, for many materials, the sample must be given a chance to relax and rebuild its structure before such measurements.
In an amplitude sweep oscillatory test, one has the option of performing a stress sweep or a strain sweep. Results using the two different methods generally cannot be directly compared with each other unless reduced to the same basis [46,99]. Nevertheless, such a test can be analyzed for numerous different parameters, making it a popular choice for measuring viscoelastic materials. Within the linear region, the values of and are constant and these values, particularly the value of G′, may be used to characterize the structural strength of a material. At a very low frequency, the value of may even be used to roughly estimate the zero-shear viscosity according to Equation (19).
at low oscillatory frequencies.
As the amplitude increases and the linear region is exceeded, there are still useful measurements that can be obtained. One method for calculating the yield stress of a material is to find the stress corresponding to the end of the linear viscoelastic region [80]. This can only be measured by exceeding this region. By continuing to increase the amplitude, materials that have will eventually cross back over each other as the structure begins to break and flow. The stress corresponding to this crossover is called “crossover stress” or “flow stress” (see Figure 2) and has found use as an indication of consistency for lubricating grease [80,81]. The magnitude of this stress is dependent on test frequency.
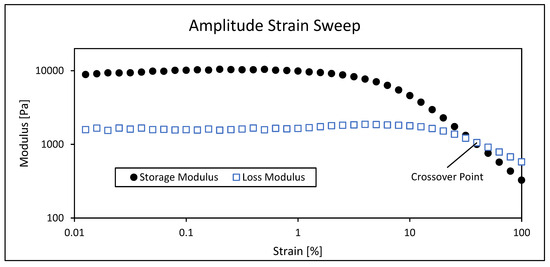
Figure 2.
Results of amplitude strain sweep showing storage and loss moduli vs. strain for a lubricating grease.
Another type of oscillatory test is a time sweep which is useful for monitoring the structure recovery after shearing. This test involves setting a constant frequency and amplitude within the linear region and monitoring the growth of G′ over time.
The last major type of oscillatory test is a frequency sweep. This test describes the time-dependent nature of a material within the linear viscoelastic region and can be used to determine whether a material exhibits gel-like behavior over a certain region [100]. This may also be used to calculate the longest relaxation time, , of a material by finding the frequency, , at which the phase angle reaches 45° [46,48]. This frequency is then converted to a time through Equation (20). This should be performed in the linear region by selecting a strain or stress amplitude sufficiently low. Many rheological materials will not show such a point in a frequency sweep (with reasonable observation times), meaning this equation would not be helpful.
5.2.2. Creep and Relaxation
While oscillatory tests are mainly conducted in the linear viscoelastic region, creep tests easily exceed the deformation needed to show nonlinearities. An example is shown in Figure 3a. In this test, a constant stress is applied and the resulting strain over time is examined. This results in behavior divided into three regions: immediate elastic response, delayed elastic response, and steady state viscous response. After a sufficient amount of time to observe these regions, the imposed stress is stopped, allowing a look at the material’s ability to recover strain. A viscoelastic solid material will recover all the strain, while a viscoelastic fluid material will not recover all the strain and will be irreversibly deformed from this test.
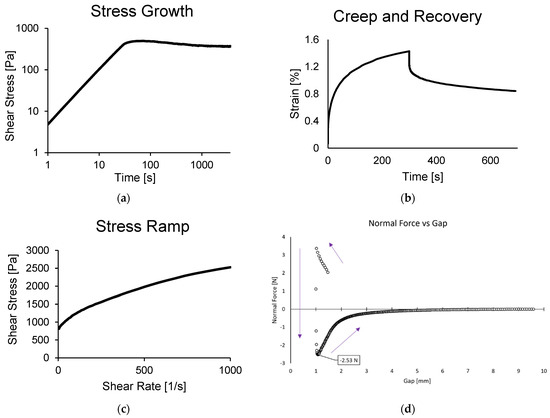
Figure 3.
Typical results of various tests on a lubricating grease: (a) stress growth test at 0.01 1/s; (b) creep at 50 Pa followed by recovery; (c) stress ramp; (d) normal force shown during compression-expansion test at 0.1 mm/s.
The results of a creep test may be interpreted by examining the creep compliance, where the instantaneous strain value is divided by stress (see Equation (7)). The equilibrium creep compliance, corresponding to the approximate initial value of creep compliance, may be calculated by extrapolating the linear creep response toward . This property corresponds to the inverse of the zero-shear viscosity (which may also be found from the frequency sweep oscillatory test). Another method of interpreting creep data is to use a model such as Equation (2) or Equation (6) and solve for the parameters using measured data.
While it is less commonly sought than creep, relaxation is another parameter of interest. Relaxation behavior is measured by applying instantaneous strain and monitoring the stress over time. The results can then be modelled by Equation (4) or a similar model.
5.2.3. Stress Growth/Startup
A start up test, also called a stress growth test, involves setting a constant shear rate and observing the shear stress over time. This is similar to a creep test, but instead of a strain magnitude being held constant, the strain rate is held constant. An example is given in Figure 3b. In this test, one might observe the growth of stress within the material and can view the time-dependence of stress.
The initial behavior shows the elastic response of the material and in some cases of shear-thinning materials, one will observe an overshoot of shear stress followed by a decrease [101,102], such as the result shown in Figure 3a. The exact magnitude of this overshoot was found to be dependent on shear rate and gap, with lower shear rates and smaller gaps leading to more overshoot, indicating this is related to wall slip [101]. Nevertheless, this peak stress value has been identified as a possible way of estimating consistency [81].
5.2.4. Stress Ramp
A stress ramp involves constantly increasing the shear stress over time while monitoring the corresponding strain (see Figure 3c). This is effectively a creep test with a changing shear stress. Such a method may be used to obtain the yield stress and a plot of shear stress vs. shear rate, but thixotropy often plays an important role in these measurements and can be difficult to avoid. In fact, by performing an increasing stress ramp then a decreasing stress ramp, a hysteresis loop is created. This is another type of test that is simple to perform, but often provides misleading results due to the combined effects of nonlinear viscoelasticity, thixotropy, and sample history [46].
Using a stress ramp is a common method for obtaining steady flow curves, where the shear stress is plotted as a function of shear rate over a wide range. However, the existence of a hysteresis loop means that results will be different depending on whether the strain rate is increasing or decreasing as measurements are performed. In addition, using a control strain method of determining flow curves will not lead to the exact same results as control stress [99]. Therefore, it is up to the practitioner to identify the best method for obtaining flow curves that will most resemble the end application.
5.2.5. Extensional Testing
It is possible to test materials that have a high degree of adhesivity and cohesivity through extensional flow. If a material or interface lacks a sufficient degree of either of these, it will either separate or lose contact with the surface. Extensional flow can measure adhesive/cohesive or thread-forming capabilities [103,104,105]. By subjecting a relevant material to compression followed immediately by expansion (see Figure 3d), there is a peak tensile force that may be observed, corresponding to a “pull-off force”, which provides a measure of the sample’s adhesiveness or cohesiveness [106]. A recent study found pull-off force to be correlated with the consistency of grease [81].
The result obtained from a pull-off force test can be considered adhesiveness if the material is pulled from the walls, but cohesiveness (related to extensional viscosity) if the material remains attached to the walls [107]. If the material remains attached to the walls, it can form a thread before eventually splitting into two separate surfaces. The maximum length of this thread before breaking may be considered the “thread length” and can serve as a measurement of the tackiness of a sample [103]. The concept of tackiness is quite important for some materials such as grease and adhesives, though quite poorly defined [6].
5.2.6. Yield Stress
Due to the prevalence of yield stress throughout rheological materials, it is important to consider all the methods for its quantification. There are numerous ways of calculating yield stress apart from rheometers, including viscometer tests, pipe flow tests, penetration tests, and more [108,109,110,111]. However, the simplicity and ease of use of rheometers make them an attractive choice. The main ways of calculating yield stress through rheometry include oscillatory amplitude sweeps and fitting flow curves with a non-Newtonian flow model (see Table 4). Using flow curves is generally a poor idea, however, because yield stress is measured at very low shear rates where wall slip is most prominent. In fact, wall slip may be among the most significant sources of error in rheological testing.
5.3. Testing Errors
Overall errors from rheometry may result from low-torque limit, secondary flow, offset error, instrument inertia, wall slip, gap/particle ratio, wave propagation at high frequency, surface tension forces, interfacial film formation, evaporation, sample uniformity, and sample loading procedure [112]. While some of these are instrument errors, others can be prevented by properly selecting geometry and inspecting the measurement results for abnormalities.
In a viscometer, a material is sheared between a thin gap by the rotation of a spindle or the outer shell. Once shearing begins, the viscosity of a simple, Newtonian fluid may be measured almost instantaneously. However, complex materials have longer time scales and can take a significant amount of time to reach steady state [47]. If insufficient time is given for the material to reach a steady state structure, strange time-dependent behavior will be observed [46].
Time-dependent behavior also results from “wall slip”, where a thin layer of sample near the walls has dramatically different properties from the bulk fluid [113]. For multi-phase systems, there is only “apparent slip” occurring as the phases separate from each other and solid particles are forced away from walls and migrate toward the center [114]. However, true slip may occur for single-phase polymer solutions where there is no phase separation near the walls, leading to a true loss of adhesion between the material and the wall [115]. The result of wall slip is a layer of fluid with apparent viscosity much lower than that of the bulk near the walls, which is the region that interacts with the measuring device. Thus, when slip begins, a lower apparent viscosity is measured. Because this may take time to develop, when testing a material in a startup/stress growth test, there may appear to be a maximum shear stress value at which the material yields; however, much of this behavior is wall slip [101].
The influence of this effect can be minimized by using geometries such as a vane or T-bar [116,117], roughening the measurement surfaces or using structured geometries [113], or by testing using different gap heights and ensuring results are similar in the case of parallel plates [118]. These will generally help for testing non-Newtonian fluids; however, when testing Newtonian fluids with structured geometries, it is possible to observe false viscosity values and false flow behavior [119].
An issue related to wall slip is sample fracturing, where a critical shear strain value may be reached within the sample as shear rate is increased, leading to the sample splitting into two sections with slip occurring between them. This is an example of unintentional flow, much like turbulence and secondary flow. These are issues that arise even in carefully selected geometry if shear rates are not in an appropriate range. Similarly, shear banding, where there are bands of material with different apparent viscosity, may also arise from shear rates that are too high [120]. It is even possible for results to be affected by multiple yielded regions within the material [121]. If one is unable to conduct measurements without such issues, it is possible to perform oscillatory measurements and convert the values to steady shear values using the Cox–Merz rule [122] or an extension of it [123]. However, the accuracy of this approximation depends on the material type [124].
Because the consistency of nonhomogeneous materials is often of interest, there can always be an issue with the sample itself. One must ensure that the sample is representative of the material as a whole, which may be difficult without having additional equipment to mix or otherwise prepare the sample [80]. Even with sufficient preparation, evaporation before or during testing can lead to a sample drying out at its extreme edges where measurements are most critical. There may also be sedimentation and particle migration during measurements.
Many rheometer setups allow for temperature control, which is beneficial since many materials are intended for use at temperatures far from room temperature, but if this is used, there should be an appropriate temperature evolution over time to ensure the sample is at a uniform temperature. This can possibly take a substantial amount of time depending on the desired temperature. One must also consider the potential influence of thermal expansion. In addition, the presence of moisture in the air could condense on the sample at low temperatures and evaporation could affect the sample at high temperatures.
Overall, there are various considerations a practitioner must be aware of when performing rheological experiments in order to obtain results that are meaningful. Further, such considerations must also be made when comparing ones work to another. It is possible that measurements of a similar material made by different operators can be corrected by using relative measurements [125]; however, general standardized procedures should be developed in order to have universal tests for consistency. A general overview of the various tests discussed is provided in Table 7.

Table 7.
Overview of common rheological tests measuring consistency fundamentals.
6. Fundamental Parameters That Determine Consistency
Consistency is a macroscopic property that is made up of numerous fundamental properties, including those outlined in Table 8. In fact, one may think of consistency as a practical simplification of complex behavior that can be measured relatively easily and used to assess a material’s suitability for a given application. The balance of fundamental properties that makes up consistency depends on one’s interpretation of consistency, meaning one must identify the particular parameters that are relevant for a given material in a particular application. Once identified, these parameters may be individually measured and used together to detail exactly how consistency is being defined and how sensitive it is to changes in these properties. Unfortunately, these fundamental parameters are generally not distinct from one another.

Table 8.
Fundamental parameters that determine consistency.
Parameters that may be used include apparent viscosity, adhesion, thixotropy, yield stress, crossover stress, wall depletion, particle shape and size, particle agglomeration tendency, density, tackiness, elastic modulus, creep response, relaxation behavior, surface tension, relaxation time, zero-shear viscosity, and more. Apparent viscosity is generally the most important component of consistency but does not entirely capture the behavior of materials. Most of these parameters may be measured by rheological tests, allowing for almost all the aspects of consistency across a wide range of domains to be measured by a rheometer using different geometries. Many industries, such as cosmetic and pharmaceutical industries, are absent from Section 4, as they mostly use penetration tests and rheological tests to quantify behavior rather than the specific setups of the industry-focused tests discussed.
Pumpability is one way of interpreting consistency but is dependent on apparent viscosity, wall effects, plug formation, yield stress, and thixotropy for many rheological materials, while this is simply a function of viscosity and density for a Newtonian fluid. These properties, particularly thixotropy, govern behavior in materials such as grease and coal suspensions during start/stop pumping. Such a consideration is also relevant in food systems that can lose their suspension properties, causing sedimentation or creaming.
The tests to measure some of these fundamental properties do not necessarily involve rheology. For instance, surface tension and density are relevant parameters in modelling consistency. The magnitude of surface tension, sometimes measured by observing the contact angle of a water droplet [127], means that the materials used to construct test equipment could potentially have a significant effect on the results due to wetting behavior. Awareness of the impact of such variables is needed as methods for quantifying consistency are refined.
7. Conclusions and Future Work
An understanding of consistency and its fundamental underlying parameters has a significant appeal to a wide variety of industries. Though there are numerous ways of defining consistency, every definition refers to the structural integrity of a material in some way. In an industrial context, this structural integrity is measured in a wide variety of manners, each of which is intended on providing a close match to the end application. However, by more closely understanding the end application and the test methods used, the underlying fundamental parameters may be measured individually and used to model the performance of a material more thoughtfully and to design more meaningful consistency tests. Such parameters include apparent viscosity, adhesion, thixotropy, yield stress, crossover stress, wall depletion, particle shape and size, particle agglomeration tendency, density, tackiness, elastic modulus, creep response, relaxation behavior, surface tension, and zero-shear viscosity. Many of these are measured using rheological techniques that can be more thoroughly understood at a fundamental level than specific industry tests. In addition, results of some of these tests have already been found to correlate quite well with some measures of consistency [80,81,128,129,130,131].
A key consideration of consistency is the need to have measurement conditions resemble application conditions since different behaviors may manifest in different regimes. Therefore, steady state measurements may fully characterize a material in one situation, while being completely irrelevant for another situation. Another consideration is that materials that have consistency are generally not homogeneous and have different phases that may separate. Therefore, the specific sample measured may not be indicative of the bulk. For these cases, standardized methods for collecting samples [132,133] should be used to obtain a sample most representative of a larger quantity.
A further understanding of consistency may also be useful in interpreting and designing consistency tests. For instance, results of a cone penetration test have a strong dependence on apparent viscosity and yield stress, but a weak dependence on creep and relaxation due to how short the test generally is. If the test time were extended, these characteristics would become more significant.
Consistency is generally not well defined across all industries and similar concepts arise, such as the idea of workability in concrete. Workability of concrete is suitability for a given context (the ease with which it can be put in its final form for a particular job without segregation), while consistency is considered a material property. The slump test directly measures consistency, indirectly measuring workability. The overall idea of workability is not completely distinct from consistency, meaning they have some overlap. Similar situations of overlapping terminologies exist across many industries where rheological materials are used and are partly responsible for the imprecise definitions of consistency.
Ultimately, consistency is only one macroscopic property of a material and may or may not be relevant when assessing a material’s performance in a certain context. Measuring some of the more fundamental properties that make up consistency may be a better choice, as these may be quantified using generalized methods. As noted before, consistency is simply a characterization of a material at a given point in time under a given set of conditions. Especially for lubricants, these conditions generally change with time, potentially resulting in dramatically different consistency over time. In many cases, understanding and modeling this change is crucial for accurately matching a product to an application.
Author Contributions
Conceptualization, A.G. and M.K.; methodology, A.G.; writing—original draft preparation, A.G.; writing—review and editing, A.G. and M.K.; supervision, M.K. All authors have read and agreed to the published version of the manuscript.
Funding
The authors greatly acknowledge the support of National Lubricating Grease Institute (NLGI) Grant number AM240790 to Louisiana State University.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Franck, A. Understanding Rheology of Structured Fluids; TA Instruments: New Castle, DE, USA, 2004. [Google Scholar]
- Krishnan, J.; Deshpande, A.; Kumar, P.S. Rheology of Complex Fluids; Springer: New York, NY, USA, 2010. [Google Scholar]
- Whorlow, R. Rheological Techniques; Ellis Horwood: New York, NY, USA, 1992. [Google Scholar]
- Chhabra, R. Non-Newtonian Fluids: An Introduction. In Rheology of Complex Fluids; Springer: New York, NY, USA, 2010; pp. 3–34. [Google Scholar]
- Forde, M. ICE Manual of Construction Materials, Volume 1—Fundamentals and Theory; Concrete; Asphalts in Road Construction; Masonry; ICE Publishing: Miami Lakes, FL, USA, 2009. [Google Scholar]
- Lugt, P. Grease Lubrication in Rolling Bearings; Wiley: Culemborg, The Netherlands, 2013. [Google Scholar]
- Vega, C.; Ubbink, J. Molecular gastronomy: A food fad or science supporting innovative cuisine? Trends Food Sci. Technol. 2008, 19, 372–382. [Google Scholar] [CrossRef]
- Barnes, H. The yield stress: A review or ‘παντα ρει’-everything flows? J. Non-Newton. Fluid Mech. 1999, 81, 133–178. [Google Scholar] [CrossRef]
- ASTM F1080-93(2019); Standard Test Method for Determining the Consistency of Viscous Liquids Using a Consistometer. ASTM International: West Conshohocken, PA, USA, 2019.
- McGuigan, J. Viscosity and Consistency; Sward, G., Ed.; ASTM International: West Conshohocken, PA, USA, 1972; pp. 181–212. [Google Scholar]
- ASTM D907-15; Standard Terminology of Adhesives. ASTM International: West Conshohocken, PA, USA, 2015.
- ASTM C125-21a; Standard Terminology Relating to Concrete and Concrete Aggregates. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM D4318-17; Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D4175-20be1; Standard Terminology Relating to Petroleum Products, Liquid Fuels, and Lubricants. ASTM International: West Conshohocken, PA, USA, 2020.
- Wright, J. Grease Basics. Mach. Lubr. 2008. Available online: https://www.machinerylubrication.com/Read/1352/grease-basics (accessed on 25 June 2024).
- Bloch, H.; Bannister, K. Practical Lubrication for Industrial Facilities, 3rd ed.; River Publishers: Aalborg, Denmark, 2017. [Google Scholar]
- Johnson, M. Understanding Grease Construction and Function. Tribol. Lubr. Technol. 2008, 64, 32–38. [Google Scholar]
- Vargo, D. The Adhesiveness of Grease. In Proceedings of the NLGI 81st Annual Meeting, Palm Beach Gardens, FL, USA, 14–17 June 2014. [Google Scholar]
- ASTM C1446-19; Standard Test Method for Measuring Consistency of Self-Flowing Castable Refractories. ASTM International: West Conshohocken, PA, USA, 2019.
- van der Bilt, A.; Abbink, J. The influence of food consistency on chewing rate and muscular work. Arch. Oral. Biol. 2017, 83, 105–110. [Google Scholar] [CrossRef]
- International Dysphagia Diet Standardisation Initiative. Complete IDDSI Framework Detailed Definitions 2.0; IDDSI: New Westminster, BC, Canada, 2019. [Google Scholar]
- Sone, T. Consistency of Foodstuffs; Springer: Dordrecht, The Netherlands, 1972. [Google Scholar]
- ASTM D217-21a; Standard Test Methods for Cone Penetration of Lubricating Grease. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM C143/C143M-20; Standard Test Method for Slump of Hydraulic-Cement Concrete. ASTM International: West Conshohocken, PA, USA, 2020.
- Koottaparambil, L.; Miller, R.; Sanford, A.; Carroll, J.; Khonsari, M. Application of thermodynamics to industrial grease production. Chem. Eng. J. 2024, 489, 151306. [Google Scholar]
- DeBruijn, G.; Whitton, S. Chapter Five—Fluids. In Applied Well Cementing Engineering; Gulf Professional Publishing: Houston, TX, USA, 2021; pp. 163–251. [Google Scholar]
- Witten, T.; Pincus, P. Structured Fluids: Polymers, Colloids, Surfactants; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Witten, T. Structured Fluids. Phys. Today 1990, 43, 21. [Google Scholar] [CrossRef]
- Linkhorst, J.; Beckmann, T.; Go, D. Microfluidic colloid filtration. Sci. Rep. 2016, 6, 22376. [Google Scholar] [CrossRef]
- Al Mamun, M.; Bhattacharjee, S.; Pernitsky, D.; Sadrzadeh, M. Colloidal Fouling of Nanofiltration Membranes: Development of a Standard Operating Procedure. Membranes 2017, 18, 4. [Google Scholar] [CrossRef]
- Hughes, R. An Introduction to Colloids. In Colloid Science: Principles, Methods and Applications; Wiley: Hoboken, NJ, USA, 2010; pp. 1–21. [Google Scholar]
- Ludwig, M. Surface Forces across Colloidal Dispersions. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2021. [Google Scholar]
- Soult, A. Colloids and Suspensions. University of Kentucky, 9 June 2019. [Online]. Available online: https://chem.libretexts.org/@go/page/155673 (accessed on 21 January 2022).
- Mewis, J.; Wagner, N. Colloidal Suspension Rheology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Macosko, C. Rheology—Principles, Measurements and Applications; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Trokhymchuk, A.; Henderson, D. Depletion forces in bulk and in confined domains: From Asakura–Oosawa to recent statistical physics advances. Curr. Opin. Colloid Interface Sci. 2015, 20, 32–38. [Google Scholar] [CrossRef]
- Gerth, M.; Voets, I. Molecular control over colloidal assembly. Chem. Commun. 2017, 53, 4414–4428. [Google Scholar] [CrossRef]
- Briscoe, W. Surface Forces. In Colloid Science: Principles, Methods and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 329–362. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Verwey, E.; Overbeek, J. Theory of Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherlands, 1948. [Google Scholar]
- Kaplan, I.; Rodimova, O. Intermolecular interactions. Sov. Phys. Usp. 1978, 21, 918–943. [Google Scholar] [CrossRef]
- Hodapp, A.; Conrad, A.; Hochstein, B.; Jacob, K.-H.; Willenbacher, N. Effect of Base Oil and Thickener on Texture and Flow of Lubricating Greases: Insights from Bulk Rheometry, Optical Microrheology and Electron Microscopy. Lubricants 2022, 10, 55. [Google Scholar] [CrossRef]
- Meijer, R.; Osara, J.; Lugt, P. On the required energy to break down the thickener structure of lubricating greases. Tribol. Trans. 2024, 67, 123–128. [Google Scholar] [CrossRef]
- Salje, E. Multi-scaling and mesoscopic structures. Philos. Trans. A Math. Phys. Eng. Sci. 2010, 368, 1163–1174. [Google Scholar] [CrossRef]
- Butt, H.; Kappl, M. Normal capillary forces. Adv. Colloid. Interface Sci. 2009, 146, 48–60. [Google Scholar] [CrossRef]
- Barnes, H. A Handbook of Elementary Rheology; University of Wales, Institute of Non-Newtonian Fluid Mechanics: Aberystwyth, UK, 2000. [Google Scholar]
- Hughes, R. Practical Rheology. In Colloid Science: Principles, Methods and Applications; Wiley: Hoboken, NJ, USA, 2010; pp. 245–272. [Google Scholar]
- Franck, A. Viscoelasticity and Dynamic Mechanical Testing; TA Instruments Germany Applications Notes Library Paper AAN004; TA Instruments: Hüllhorst, Germany, 2004. [Google Scholar]
- Prieto-Muñoz, P.; Yin, H.; Testa, R. Mechanics of an Adhesive Anchor System Subjected to a Pullout Load. II: Viscoelastic Analysis. J. Struct. Eng. 2014, 140. [Google Scholar] [CrossRef]
- Malkin, A.; Isayev, A. Rheology Concepts, Methods, and Applications, 3rd ed.; ChemTec Publishing: Toronto, ON, Canada, 2017. [Google Scholar]
- Frost, H.; Ashby, M. Deformation-Mechanism Maps: The Plasticity and Creep of Metals and Ceramics, 1st ed.; Pergamon Press: Oxford, UK, 1982. [Google Scholar]
- Malkin, A.; Ilyin, S.; Kulichikhin, V. Characterization of Material Viscoelasticity at Large Deformations. Appl. Rheol. 2014, 24, 9–18. [Google Scholar]
- Mitsoulis, E. Flows of Viscoplastic Materials: Models and Computations. In Rheology Reviews 2007; British Society of Rheology: London, UK, 2007; pp. 135–178. [Google Scholar]
- Kelessidis, V.; Maglione, R. Modeling rheological behavior of bentonite suspensions as Casson and Robertson–Stiff fluids using Newtonian and true shear rates in Couette viscometry. Powder Technol. 2006, 168, 137–147. [Google Scholar] [CrossRef]
- Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 2014, 5, 205–212. [Google Scholar] [CrossRef]
- Barnes, H. Thixotropy—A review. J. Non-Newton. Fluid Mech. 1997, 70, 1–33. [Google Scholar] [CrossRef]
- Gurt, A.; Khonsari, M. The Use of Entropy in Modeling the Mechanical Degradation of Grease. Lubricants 2019, 7, 82. [Google Scholar] [CrossRef]
- Paszkowski, M. Assessment of the effect of temperature, shear rate and thickener content on the thixotropy of lithium lubricating greases. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 227, 209–219. [Google Scholar] [CrossRef]
- Pan, J.; Cheng, Y.; Yang, J. Structural Degradation of a Lithium Lubricating Grease after Thermal Ageing. J. Chem. Eng. Jpn. 2016, 49, 579–587. [Google Scholar] [CrossRef]
- Rezasoltani, A.; Khonsari, M. On the Correlation Between Mechanical Degradation of Lubricating Grease and Entropy. Tribol. Lett. 2014, 56, 197–204. [Google Scholar] [CrossRef]
- Rezasoltani, A.; Khonsari, M. On Monitoring Physical and Chemical Degradation and Life Estimation Models for Lubricating Greases. Lubricants 2016, 4, 34. [Google Scholar] [CrossRef]
- Greener, J.; Connelly, R. The Response of Viscoelastic Liquids to Complex Strain Histories: The Thixotropic Loop. J. Rheol. 1986, 30, 285–300. [Google Scholar] [CrossRef]
- Keleşoğlu, S.; Pettersen, B.; Sjöblom, J. Flow properties of water-in-North Sea heavy crude oil emulsions. J. Pet. Sci. Eng. 2012, 100, 14–23. [Google Scholar] [CrossRef]
- Koppelmann, V. Uber das dynamische elastische Verhalten hochpolymerer Stoffe. Kolloid Z. 1955, 144, 12–41. [Google Scholar] [CrossRef]
- Lakes, R. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Møller, P.; Mewis, J.; Bonn, D. Yield stress and thixotropy: On the difficulty of measuring yield stresses in practice. Soft Matter 2006, 2, 274–283. [Google Scholar] [CrossRef]
- Thompson, R.; Mendes, P. Rheological material functions at yielding. J. Rheol. 2020, 64, 615–624. [Google Scholar] [CrossRef]
- Barnes, H.; Walters, K. The yield stress myth? Rheol. Acta 1985, 24, 323–326. [Google Scholar] [CrossRef]
- ASTM D6103/D6103M-17e1; Standard Test Method for Flow Consistency of Controlled Low Strength Material (CLSM). ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM C1437-20; Standard Test Method for Flow of Hydraulic Cement Mortar. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM C1170/C1170M-20; Standard Test Method for Determining Consistency and Density of Roller-Compacted Concrete Using a Vibrating Table. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D1403-20b; Standard Test Methods for Cone Penetration of Lubricating Grease Using One-Quarter and One-Half Scale Cone Equipment. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D1321-16a; Standard Test Method for Needle Penetration of Petroleum Waxes. ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM D937-07(2019); Standard Test Method for Cone Penetration of Petrolatum. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM D5/D5M-20; Standard Test Method for Penetration of Bituminous Materials. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM C187-16; Standard Test Method for Amount of Water Required for Normal Consistency of Hydraulic Cement Paste. ASTM International: West Conshohocken, PA, USA, 2016.
- ISO13765-1:2004; Refractory Mortars—Part 1: Determination of Consistency Using the Penetrating Cone Method. International Organization for Standardization: Geneva, Switzerland, 2004.
- ASTM C780-20; Standard Test Method for Preconstruction and Construction Evaluation of Mortars for Plain and Reinforced Unit Masonry. ASTM International: West Conshohocken, PA, USA, 2020.
- Conway, J. A Method for the Determination of Consistency and Consistency Retention (Board Life) of Masonry Mortars. Cem. Concr. Aggreg. CCAGDP 1980, 2, 89–91. [Google Scholar] [CrossRef]
- Gurt, A.; Khonsari, M. Testing Grease Consistency. Lubricants 2021, 9, 14. [Google Scholar] [CrossRef]
- Gurt, A.; Khonsari, M. Comparison of Rheological Methods to Measure Grease Degradation. Lubricants 2023, 11, 468. [Google Scholar] [CrossRef]
- ASTM C939/C939M-16a; Standard Test Method for Flow of Grout for Preplaced-Aggregate Concrete (Flow Cone Method). ASTM International: West Conshohocken, PA, USA, 2016.
- ASTM D7918-17a; Standard Test Method for Measurement of Flow Properties and Evaluation of Wear, Contaminants, and Oxidative Properties of Lubricating Grease by Die Extrusion Method and Preparation. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D1200-10(2018); Standard Test Method for Viscosity by Ford Viscosity Cup. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM D4287-00(2019); Standard Test Method for High-Shear Viscosity Using a Cone/Plate Viscometer. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM D562-10(2018); Standard Test Method for Consistency of Paints Measuring Krebs Unit (KU) Viscosity Using a Stormer-Type Viscometer. ASTM International: West Conshohocken, PA, USA, 2018.
- American Petroleum Institute. Recommended Practice for Testing Well Cements; API RP 10B-2; American Petroleum Institute: Washington, DC, USA, 2013. [Google Scholar]
- ASTM C860-15(2019); Standard Test Method for Determining the Consistency of Refractory Castable Using the Ball-In-Hand Test. ASTM International: West Conshohocken, PA, USA, 2019.
- Park, J.; Kim, I.; Lee, H. Fork test: A new simple and reliable consistency measurement for the dysphagia diet. Geriatr. Nurs. 2016, 37, 292–295. [Google Scholar] [CrossRef]
- ASTM D1338-99(2021); Standard Practice for Working Life of Liquid or Paste Adhesives by Consistency and Bond Strength. ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM D2196-20; Standard Test Methods for Rheological Properties of Non-Newtonian Materials by Rotational Viscometer. ASTM International: West Conshohocken, PA, USA, 2020.
- DIN 53019-1; Viscometry—Measurement of Viscosities and Flow Curves by Means of Rotational Viscometers—Part 1: Principles and Geometry of Measuring System. Deutsches Institut für Normung: Berlin, Germany, 2008.
- DIN 53019-4; Rheometry—Measurement of Rheological Properties Using Rotational Rheometers—Part 4: Oscillatory Rheology. Deutsches Institut für Normung: Berlin, Germany, 2016.
- DIN 51810-2; Testing of lubricants—Testing Rheological Properties of Lubricating Greases—Part 2: Determination of Flow Point Using an Oscillatory Rheometer with a Parallel-Plate Measuring System. Deutsches Institut fur Normung E.V. (DIN): Berlin, Germany, 2017.
- Yan, J.; James, A. The yield surface of viscoelastic and plastic fluids in a vane viscometer. J. Non-Newton. Fluid Mech. 1997, 70, 235–253. [Google Scholar] [CrossRef]
- Barnes, H.; Carnali, J. The vane-in-cup as a novel rheometer geometry for shear thinning and thixotropic materials. J. Rheol. 1990, 34, 841–866. [Google Scholar] [CrossRef]
- Keentok, M. The measurement of the yield stress of liquids. Rheol. Acta 1982, 21, 325–332. [Google Scholar] [CrossRef]
- Franck, A. Paints and Coatings; TA Instruments Applications Notes Library Paper AAN036e; TA Instruments: New Castle, DE, USA.
- Rubio-Hernández, F.; Páez-Flor, N.; Velázquez-Navarro, J. Why monotonous and non-monotonous steady-flow curves can be obtained with the same non-Newtonian fluid? A single explanation. Rheol. Acta 2018, 57, 389–396. [Google Scholar] [CrossRef]
- Ilyin, S.; Gorbacheva, S.; Yadykova, A. Rheology and tribology of nanocellulose-based biodegradable greases: Wear and friction protection mechanisms of cellulose microfibrils. Tribol. Int. 2023, 178, 108080. [Google Scholar] [CrossRef]
- Balan, C.; Franco, J. Influence of the Geometry on the Transient and Steady Flow of Lubricating Greases. Tribol. Trans. 2001, 44, 53–58. [Google Scholar] [CrossRef]
- Delgado, M.; Franco, J.; Valencia, C. Transient shear flow of model lithium lubricating greases. Mech. Time-Depend. Mater. 2009, 13, 63–80. [Google Scholar] [CrossRef]
- Georgiou, E.; Drees, D.; De Bilde, M.; Anderson, M.; Carlstedt, M.; Mollenhauer, O. Quantification of Tackiness of a Grease: The Road to a Method. Lubricants 2021, 9, 32. [Google Scholar] [CrossRef]
- Harmon, M.; Powell, B.; Barlebo-Larsen, I.; Lewis, R. Development of Grease Tackiness Test. Tribol. Trans. 2019, 62, 207–217. [Google Scholar] [CrossRef]
- Achanta, S.; Jungk, M.; Drees, D. Characterisation of cohesion, adhesion, and tackiness of lubricating greases using approach–retraction experiments. Tribol. Int. 2011, 44, 1127–1133. [Google Scholar] [CrossRef]
- Georgiou, E.; Drees, D.; De Bilde, M. Can We Put a Value on the Adhesion and Tackiness of Greases? Tribol. Lett. 2018, 66, 60. [Google Scholar] [CrossRef]
- Verdier, C.; Piau, J. Effect of nonlinear viscoelastic properties on tack. J. Polym. Sci. B Polym. Phys. 2003, 41, 3139–3149. [Google Scholar] [CrossRef]
- Cyriac, F.; Lugt, P.; Bosman, R. On a New Method to Determine the Yield Stress in Lubricating Grease. Tribol. Trans. 2015, 58, 1021–1030. [Google Scholar] [CrossRef]
- Conley, P.; He, C.; Lugt, P. Effective Viscosity Determination for Lubrication Systems Using the Lincoln Ventmeter. Tribol. Trans. 2013, 56, 771–780. [Google Scholar] [CrossRef]
- Bird, R.; Dai, G.; Yarusso, B. The Rheology and Flow of Viscoplastic Materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
- Lundberg, J.; Parida, A.; Söderholm, P. Running Temperature and Mechanical Stability of Grease as Maintenance Parameters of Railway Bearings. Int. J. Autom. Comput. 2010, 7, 160–166. [Google Scholar] [CrossRef]
- Ewoldt, R.; Johnston, M.; Caretta, L. Experimantal Challenges of Shear Rheology: How to Avoid Bad Data. In Complex Fluids in Biological Systems; Springer: New York, NY, USA, 2015; pp. 207–241. [Google Scholar]
- Barnes, H. A review of the slip (wall depletion) of polymer solutions, emulsions and particle suspensions in viscometers: Its cause, character, and cure. J. Non-Newton. Fluid Mech. 1995, 56, 221–251. [Google Scholar] [CrossRef]
- Hubbe, M.; Tayeb, P.; Joyce, M.; Tyagi, P.; Kehoe, M.; Dimic-Misic, K.; Pal, L. Rheology of Nanocellulose-rich Aqueous Suspensions: A Review. BioResources 2017, 12, 9556–9661. [Google Scholar] [CrossRef]
- Rahman, N. Wall Slip in Pipe Rheometry of Multiphase Fluids. Ph.D. Thesis, University of Manchester, Manchester, UK, 2013. [Google Scholar]
- Bennington, C.; Kerekes, R.; Grace, J. The yield stress of fibre suspensions. Can. J. Chem. Eng. 1990, 68, 748–757. [Google Scholar] [CrossRef]
- Teoman, B.; Marron, G.; Potanin, A. Rheological characterization of flow inception of thixotropic yield stress fluids using vane and T-bar geometries. Rheol. Acta 2021, 60, 531–542. [Google Scholar] [CrossRef]
- Walls, H.; Caines, S.; Sanchez, A.; Khan, S. Yield stress and wall slip phenomena in colloidal silica gels. J. Rheol. 2003, 47, 847–868. [Google Scholar] [CrossRef]
- Pawelczyk, S.; Kniepkamp, M.; Jesinghausen, S.; Schmid, H.-J. Absolute Rheological Measurements of Model Suspensions: Influence and Correction of Wall Slip Prevention Measures. Materials 2020, 13, 467. [Google Scholar] [CrossRef]
- Briole, A.; Casanellas, L.; Fardin, M.; Py, C.; Cardoso, O.; Browaeys, J.; Lerouge, S. Shear-banding fluid(s) under time-dependent shear flows. Part I: Spatiotemporal dynamics. J. Rheol. 2021, 65, 1187–1200. [Google Scholar] [CrossRef]
- Hinton, E.; Collis, J.; Sader, J. The motion of a layer of yield-stress material on an oscillating plate. J. Fluid Mech. 2023, 959, A32. [Google Scholar] [CrossRef]
- Cox, W.; Merz, E. Correlation of dynamic and steady flow viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Doraiswamy, D.; Mujumdar, A.; Tsao, I.; Beris, A.; Danforth, S.; Metzner, A. The Cox–Merz rule extended: A rheological model for concentrated suspensions and other materials with a yield stress. J. Rheol. 1991, 35, 647–685. [Google Scholar] [CrossRef]
- Rathner, R.; Roland, W.; Albrecht, H.; Ruemer, F.; Miethlinger, J. Applicability of the Cox-Merz Rule to High-Density Polyethylene Materials with Various Molecular Masses. Polymers 2021, 13, 1218. [Google Scholar] [CrossRef]
- Ferraris, C.; Martys, N. Relating Fresh Concrete Viscosity Measurements from Different Rheometers. J. Res. Natl. Inst. Stand. Technol. 2003, 108, 229–234. [Google Scholar] [CrossRef]
- Shaw, M. On estimating the zero-shear-rate viscosity: Tests with PIB and PDMS. In Proceedings of the Regional Conference Graz 2015—Polymer Processing Society PPS: Conference Papers, Graz, Austria, 21–25 September 2015. [Google Scholar]
- Khonsari, M.; Lijesh, K.; Miller, R.; Shah, R. Evaluating Grease Degradation through Contact Angle Approach. Lubricants 2021, 9, 11. [Google Scholar] [CrossRef]
- Johnson, B. A Better Way to Test Grease Consistency. Mach. Lubr. 2015. [Google Scholar]
- Spiegel, K.; Fricke, J.; Meis, K.; Sonntag, F. Zusammenhang zwischen Penetration und Fließgrenze bei Schmierfetten. Tribol. Und Schmier. 1991, 38, 326–331. [Google Scholar]
- Brunstrum, L.; Sisko, A. Correlation of viscosity with penetration for lubricating greases. NLGI Spokesm. 1962, 25, 311. [Google Scholar]
- Plint, M. Relation between Cone Penetration and Shear Yield Stress of Greases. In Proceedings of the 4th ELGl Annual Meeting, Chester, UK, 21–22 May 1992. [Google Scholar]
- ASTM D5971/D5971M-16; Standard Practice for Sampling Freshly Mixed Controlled Low-Strength Material. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM D7718-11(2019); Standard Practice for Obtaining In-Service Samples of Lubricating Grease. ASTM International: West Conshohocken, PA, USA, 2019.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).