Abstract
This study investigates the potential of a hybrid nanofluid composed of MoS2 and ZnO nanoparticles dispersed in engine oil, aiming to enhance the properties of a lubricant’s chemical reaction with the Soret effect on a stretching sheet under the influence of an applied magnetic field. With the growing demand for efficient lubrication systems in various industrial applications, including automotive engines, the development of novel nanofluid-based lubricants presents a promising avenue for improving engine performance and longevity. However, the synergistic effects of hybrid nanoparticles in engine oil remain relatively unexplored. The present research addresses this gap by examining the thermal conductivity, viscosity, and wear resistance of the hybrid nanofluid, shedding light on its potential as an advanced lubrication solution. Overall, the objectives of studying the hybrid nanolubricant MoS2 + ZnO with engine oil aim to advance the development of more efficient and durable lubrication solutions for automotive engines, contributing to improved reliability, fuel efficiency, and environmental sustainability. In the present study, the heat and mass transformation of a Casson hybrid nanofluid (MoS2 + ZnO) based on engine oil over a stretched wall with chemical reaction and thermo-diffusion effect is analyzed. The governing nonlinear partial differential equations are simplified as ordinary differential equations (ODEs) by utilizing the relevant similarity variables. The MATLAB Bvp4c technique is used to solve the obtained linear ODE equations. The results are presented through graphs and tables for various parameters, namely, M, Q, β, Pr, Ec, Sc, Sr, Kp, Kr, and (hybrid nanolubricant parameters) and various state variables. A comparative survey of all the graphs is presented for the nanofluid (MoS2/engine oil) and the hybrid nanofluid (MoS2 + ZnO/engine oil). The results reveal that the velocity profile diminished against the values of M, Kp, and β, and the temperature profile rises with Ec and Q, whereas Pr decreases. The concentration profile is incremented (decremented) with the value of Sr (Sc and Kr). A comparison of the nanofluid and hybrid nanofluid suggests that the velocity f′ (η) becomes slower with the augmentation of whereas the temperature increases when = 0.6 become slower.
1. Introduction
Researchers are continuously exploring novel combinations of nanoparticles and heat transfer coefficients, how the thermal conductivity of fluids is enhanced by base fluids, and the overall heat transfer performance of nanofluids. Researchers have recently been examining how to optimize nanoparticle concentration, size, shape, and surface properties to achieve superior heat transfer enhancement. Hybrid nanofluids are being investigated for various thermal management applications, including cooling systems in electronics, heat exchangers, solar thermal collectors, and automotive cooling systems. The ability of hybrid nanofluids to improve heat transfer efficiency and thermal stability makes them promising candidates for addressing thermal management challenges in modern engineering systems. Computational modelling and numerical simulation techniques play a crucial role in predicting hybrid nanofluids’ heat and mass transfer characteristics.
Researchers are developing advanced computational models based on techniques such as computational fluid dynamics (CFD), molecular dynamics (MD), and lattice Boltzmann methods to simulate the behaviour of hybrid nanofluids at the nanoscale and macroscopic levels. Despite the promising performance of hybrid nanofluids in laboratory settings, there are practical challenges related to scalability, stability over long-term usage, and cost-effectiveness that need to be addressed for their widespread industrial applications. Researchers are working on developing scalable synthesis methods, improving nanoparticle dispersion techniques, and conducting cost–benefit analyses to facilitate the transition of hybrid nanofluids from the laboratory to real-world applications. Umair Khan et al.’s [1] study was aimed at offering a computational solution to the flow of a wall jet (WJ) incorporating thermal and mass transportation phenomena. Their study focuses on a colloidal suspension consisting of SAE50 and zinc oxide nanoparticles, which are submerged in a Brinkman-extended Darcy model.
The work of Zia Ullah et al. [2] primarily focused on the enhanced rate of chemical processes in the magneto-nanofluid flow and the physical manifestation of viscous dissipation. Zawar Hussain et al. [3] investigated the flow of copper and alumina nanoparticles mixed with a Casson hybrid nanofluid based on sodium alginate across a stretching wall. In this problem, they assumed convective and slip boundary conditions. Najiyah Safwa Khashi’ie et al. [4] investigated the presence of velocity slip and convective conditions; Cu-Al2O3/water nanofluid flowed toward a sheet that was stretching/shrinking. Maintaining an adequate wall mass suction is necessary to maintain the shrinking flow through a permeable sheet. Bilal et al. [5] described how the features of a bidirectional stretched surface restricts the flow of Williamson fluid in the boundary layer in magnetohydrodynamics (MHD). It is assumed that the fluid conductivity varies with temperature. Heat transfer via generative/absorptive processes is also taken into account. Muhammad Ramzan et al. [6] simulated three-dimensional MHD flow over an extending sheet of micropolar and Williamson fluids. Their study examined activation energy and heat radiation influence. Also, Brownian motion, the chemical reaction, and the thermal migration impact were calculated. Numerical investigation was conducted on the continuous three-dimensional mixed convection flow of nanofluids under slip circumstances over a permeable vertical stretching/shrinking sheet in magnetohydrodynamics (MHD) by Anuar Jamaludin et al. [7]. In their study, two types of nanofluids, namely, Cu-water and Ag-water, were examined. Ishtiaq Khan et al. [8] studied the utilization of nanoliquids’ significant potential across various fields including heat exchangers, food processing, biomedicine, cooling electronics, and transportation. Their analysis took account of the impact of velocity slips, zero mass flux, and thermal convection. Interestingly, the zero mass flux situation at the wall negates the hybrid nanoliquid flow’s wall mass transfer rate.
Nanofluids hold considerable importance for researchers owing to their notably high heat transfer rates, making them valuable for industrial applications, as noted by Tanzila Hayat et al. [9]. Recently, a novel class of nanofluids, termed “hybrid nanofluids”, has emerged, aiming to further augment heat transfer rates. A newly developed 3D model is utilized to investigate the effects of heat generation, heat radiation, and chemical reaction on a rotating stretching wall. Awatif Alhowaity et al. [10] examined the energy and mass transfer rates in the movement of a Williamson hybrid nanolubricant in a porous plate that is stretched and contains silver (Ag) and magnesium oxide (MgO) nanoparticles (NPs). By dispersing the magnesium oxide (MgO) and silver (Ag) nanoparticles in the base fluid (engine oil), the hybrid nanofluid is created. Suriya Umadevi et al. [11] studied the novel thermophysical properties of models that have been developed and the experimental thermal conductivity values were compared with their proposed model. Two distinct types of fluids, specifically, hybrid nanofluid (Cu-Al2O3/Water) and nanofluid (Cu/Water), were utilized in the investigation of movement past a stretching sheet.
Ram Prakash Sharma et al.’s [12] study compared the effects of the thermal properties of curved surfaces spiralling in a circle at different distances from a centre using linear and nonlinear stretching sheets. The Soret–Dufour phenomenon is also examined in relation to the injection velocity and heat source/sink. The base fluid for this experiment is water, which contains silver oxide nanoparticles and copper oxide nanoparticles. Revathi et al. [13] studied the flow of a hybrid fluid based on methanol over a curved stretched sheet while taking activation energy and cross-diffusion effects (Soret–Dufour numbers) into account. Motahar Reza et al. [14] conducted a numerical study to examine the effects of the Soret and Dufour phenomena on the creation of entropy in a (AlN-Al2O3) hybrid nanofluid flowing across a stretched plate through a permeable medium saturated with hybrid nanofluid. To explore the impact of thermo-diffusion and diffuse thermal effects on entropy generation in this scenario, a transverse magnetic field was employed. Their study investigated the enhancement of heat transfer rates using a mixture of aluminium nitride (AlN) and alumina (Al2O3) nanoparticles. Asmat Ullah Yahya et al. [15] investigated the demand for improved thermal conductivity to handle boosting the density of heat in miniature and various technical procedures, which prompted an examination of the thermal transport properties of hybrid nanofluids. In this context, MoS2 and ZnO are combined as a highly diluted homogeneous composition within a great quantity of engine oil. This colloidal fluid flows over a stretched sheet through a porous medium, in the presence of heat transformation. Shami Alsallami et al.’s [16] goal was to enhance engine oil’s thermal characteristics by adding a suspension of Williamson hybrid nanofluid. Zinc oxide (ZnO) and molybdenum disulfide (MoS2) were suspended in the hybrid nanofluid. Viscosity dissipation properties and external heat sources were added to increase the system’s heating capability. The problem studied by Sreedevi et al. [17] entailed the analysis of thermal and mass transformation in an inconstant magneto-hydrodynamic movement of a hybrid nanofluid on a stretching sheet. The scenario includes the presence of chemical reactions, suction, slip effects, and thermal radiation.
The work of Mubashar Arshad et al. [18] examined the three-dimensional magneto-hydrodynamic nanofluid flow over two stretching surfaces, taking into account the outcomes of heat radiation and biological reactions in addition to the impact of an inclining magnetized field. In their comparative results, several rotational nanofluids and hybrid nanofluids with a constant angular velocity were investigated. The analysis of a nonlocal fractional model for viscous nanofluid with hybrid nanostructure was presented by Yu-Ming Chu et al. [19]. To develop a hybrid nanolubricant, copper (Cu) and aluminium oxide (Al2O3) nanomaterial were mixed and distributed within a base fluid of water (H2O). Within a microchannel, the magnetohydrodynamic (MHD) free convection motion of the Cu-Al2O3-H2O nanofluid was examined. The movement of an incompressible hybrid nanolubricant over a rotating disk that is endlessly impermeable was examined by Tassaddiq et al. [20]. To improve the examination of the nanoliquid flow’s fine point, the impact of a magnetized field was included. In their work, magnetic ferrite nanoparticles and carbon nanotubes (CNTs) contained in a carrier fluid like water were studied in relation to the classical von Karman flow over a spinning disk. The standard fluid water that suspends two different kinds of hybrid nanoparticles—single-walled CNTs (SWCNTs) and multi-walled CNTs (MWCNTs)—were considered in the study by Shanmugapriya et al. [21]. To further explore the complexities of hybrid nanofluid flow, the effects of thermal radiation, activation energy, and magnetized fields have been included in addition to binary chemical reactions.
The study by Sohail Ahmad et al. [22] revealed that hybrid nanofluids demonstrate superior thermal conductivity, chemical stability, physical toughness, mechanical resistance, and other properties in comparison to individual nanoliquids. Their study aimed to introduce a novel investigation into the magnetohydrodynamic (MHD) flow of hybrid nanoparticles through a permeable medium, considering viscous dissipation, as they pass over a stretching surface. The study of Abdulmajeed Almaneea [23] examined the impact of hybrid nanomaterials on thermo- and mass transformation in both heterogeneous and homogeneous chemical reactions. The Williamson parameter can have a notable effect on momentum transport. The Casson hybrid nanofluid’s Darcy–Forchheimer flow across a curved surface that is constantly expanding was studied by Gohar et al. [24]. The Darcy–Forchheimer effect characterizes the many fluid flows within a porosity area. Hybrid nanofluids are created using carbon nanotubes (CNTs) in cylindrical form and iron oxide. An inquiry to elucidate the flow behaviour of a Ree–Eyring hybrid nanofluid under stretching flow conditions was conducted by Ali et al. [25], who studied SiO2 and GO for their potential use as hybrid nanoparticles in combination with carboxymethyl cellulose (CMC) in water at low concentrations. A concentration range between 0.0 and 0.4% is recommended for use as the base fluid (CMC water). The work of Wei-Feng Xia et al. [26] focused on the three-dimensional micropolar hybrid nanofluid’s nonlinear mixed convective boundary layer flow under numerous slip conditions and in the presence of microorganisms along the narrowing surface. The goal of their study was to learn more about carbon nanotubes (CNTs), which are very popular because of their consistent physicochemical properties, high thermal and electrical conductivities, mechanical and chemical stability, and lightweight design. The objective of the research of Saeed Dinarv et al. [27] was to analyze the Falkner–Skan problem, which is a TiO2-CuO/water hybrid nanofluid flowing in a stable laminar incompressible two-dimensional boundary layer over a stationary or rotating edge or corner.
One-phase hybrid nanofluids are modelled using a novel mass-centric approach in which the masses of the base fluid and the first and second nanoparticles are regarded as essential inputs for establishing the effective thermophysical parameters of the hybrid nanofluid. The extension of a hybrid nanofluid made of Cu, Al2O3, and H2O between two infinite vertical parallel plates is covered in the study of Muhammad Saqib et al. [28], who studied the energy equation in conjunction with the Brinkman-type fluid model to depict the movement between two parallel plates filled with hybrid nanofluids. By using in situ green synthesis, Jun Zhao et al. [29] fabricated Mn3O4 nanoparticles and graphene nanosheets into a sandwich-like nanostructure (Mn3O4@G). A significant reduction in frictional energy consumption can be achieved by incorporating nanoparticles or two-dimensional (2D) nanosheets into lubricants. V. Vicki Wanatasanappan et al. [30] examined the hybrid nanofluid Al2O3-Fe2O3’s viscosity and rheological characteristics and created a new correlation. The primary goals of the research were to establish a correlation for viscosity prediction and assess the impact of the Al2O3-Fe2O3 mixture ratio on the viscosity property. Lee Jongsuk et al. [31] investigated how CNTs’ size phase changes in a base fluid when it is sonicated. They examined in detail how nanofluids containing CNTs in particular size phases behave viscously without the use of surfactants. Seyed Borhan Mousavi et al. [32] examined how temperature and nanoparticle content affect diesel oil viscosity, tribological properties, and physicochemical properties using two different diesel oil-based nanofluids. They also examined the higher kinematic viscosity in ZnO nanofluids at every concentration of nanoparticles compared to MoS2 nanofluids. Given that ZnO nanofluids are more stable and that diesel oil containing nano-MoS2 particles is less volatile, the ZnO nanofluids displayed greater viscosity values at all evaluated temperatures. When it comes to cohesiveness, nano-ZnO particles outperformed MoS2 nanofluids. “When nanoparticles were intruduced into the samples, the kinematic viscosity and viscosity index increased. As nanoparticle concentrations increased, kinematic viscosity also increased. When nanoparticle concentrations were changed, ZnO nanofluids had higher kinematic viscosities than MoS2”.
Overall, research in the field of heat and mass transfer of hybrid nanofluids continues to evolve, driven by the demand for efficient thermal management solutions in various industrial sectors. As advancements in nanomaterial synthesis, characterization techniques, and computational modelling tools progress, hybrid nanofluids are expected to play an increasingly important role in enhancing heat transfer efficiency and sustainability in diverse engineering applications. The present study aims at understanding the heat and mass transformation of Casson hybrid nanofluid (MoS2 + ZnO) based on engine oil over a stretched wall with chemical reaction and thermo-diffusion effects. Here, we use MoS2 + ZnO hybrid nanofluid because this hybrid nanofluid has energy conversion properties.
2. Materials and Methods
Let us consider a mathematical expression for incompressible Casson hybrid nanofluids in two dimensions (2D) flowing across an extended wall. The problem’s design is depicted in Figure 1 with Cartesian coordinates (x, y) and velocity components (u, v) with a fluid flow arrangement. Mass diffusion and heat transport are studied at the interface of an applied magnetic field, changing viscosity, and a porous material. The magnetic field B0 is applied along the x-axis. The regulating formulas of this problem are as follows:
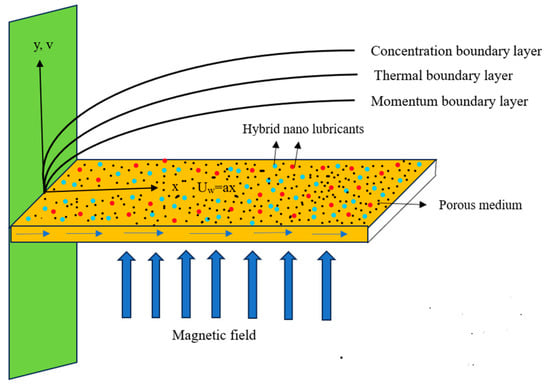
Figure 1.
Schematic diagram of the problem.
The boundary conditions are as follows:
The flow of the hybrid nanofluids is explained here with the help of thermophysical characteristics. , , and are the volume fractions of the hybrid nanofluids. To create the required nanolubricant, ZnO nanoparticles are mixed with 0.01 vol of MoS2/engine oil. We considered that = 0.04 and = 0 for the MoS2/engine oil in this model. For the hybrid nanolubricant, we considered = 0.03 and = 0.01 to yield the MoS2 + ZnO/engine oil in the research.
For clarity, Table 1 presents the valuable thermophysical characteristics of both the nanolubricants and hybrid nanolubricants. The fundamental thermophysical properties of the nanofluids are derived from the literature review mentioned below. Table 2 provides information on the thermophysical properties of the engine oil used as the base fluid.

Table 1.
Engine oil base fluid and nanoparticle thermophysical properties [15].

Table 2.
Nanolubricant and hybrid nanolubricant thermophysical properties [15].
Similarity Variables
In order to solve Equations (1)–(4) subject to the boundary conditions (5), the similarity transformation and stream function are mentioned. They are provided by
The transformed ordinary differential equations are
where M denotes the magnetic parameter, Sc denotes the Schmidt number, Kp denotes the porosity parameter, Sr is the Soret effect parameter, Kr is the chemical reaction parameter, Pr represents the Prandtl number, the Eckert number is Ec, Q denotes the heat source, and β is the Casson fluid parameter.
Also,
The physical quantities of interest are given below:
Utilizing similarity transformation, we get
where Rex is a local Reynolds number, Cfx is the skin friction co-efficient, Nux is the local Nussult number, and Shx is the Sherwood number.
3. Numerical Procedure
This intended hybrid nanofluid flow has a naturally nonlinear boundary value problem, which is represented by Equations (1) to (4). Finding a closed form solution is really difficult, as usual. In order to arrive at an approximate numerical solution for the problem, a numerical method that uses the MATLAB Bvp4c technique is employed. The higher order derivatives in this scheme must be reduced to the first order in the following manner:
4. Results and Discussion
In two cases, numerical solutions are estimated as follows:
- (i)
- MoS2/engine oil (nanolubricant);
- (ii)
- ZnO + MoS2/engine oil (hybrid nanolubricant).
According to Table 3, the above results can be verified if they compare reasonably with previous Pr results in limiting cases. In Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, two results are presented for the single nanolubricant (MoS2/engine oil) and for the hybrid nanolubricant (MoS2/engine oil + ZnO). Figure 2 and Figure 3 depict the effects of the magnetic parameters M and porous parameters Kp on the nondimensional linear speed f′ (η), respectively. Increasing M and Kp dramatically slows down the flow of both the nanolubricant (single nanolubricant) and the hybrid nanolubricant. According to physical principles, a larger value of M indicates a greater Lorentz force opposing the flow. The parameter Kp also corresponds to a medium with a lower porosity and a greater resistance to flow with higher inputs. Figure 4 represents the results of the Casson lubricant parameter on the velocity. A rising Casson fluid parameter value decreases the velocity profile due to its shear-thinning property; hence, the wall thickness decreases. Figure 5 represents the results of the effect of the Prandtl number on the thermal profile. As the value of Pr increases, the temperature profile decreases. Hence, when increasing Pr, the thermal diffusivity of the fluid decreases, which further reduces the thickness of the thermal boundary layer. Furthermore, compared to the single nanofluid, the hybrid nanofluid’s velocity has been observed to be slower. Figure 6 presents the results of effect of the heat source parameter Q on the temperature profile. The temperature profile increases with the increasing value of the heat source parameter Q. Figure 7 represents the outputs of the effect of the Eckert number on the temperature profile. The temperature profile increases with the increasing value of Ec. Thermal dissipation is the process by which mechanical energy is transformed into heat energy, represented by a greater Eckert number. Furthermore, it was noted that the hybrid nanofluids had a higher temperature than the other nanofluids. This is because the hybrid nanofluids have higher thermal conductivities. Figure 8 represents the effects of the Schmidt number on the concentration profile. Increasing the value of the Schmidt number results in a decreased concentration profile.

Table 3.
Comparison of (−θ (0)) with the results of Asmat Ullah et al. [15], Shami A.M. et al. [16], and P. Shreedevi et al. [17], for various values of (Pr), = 0, and = 0; all remaining parameters zero.
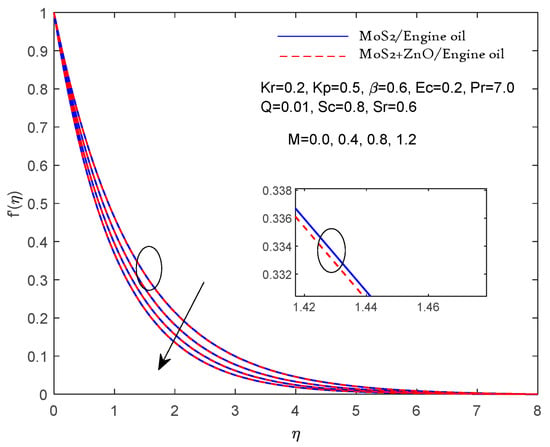
Figure 2.
Velocity f′ (η) fluctuation with M.
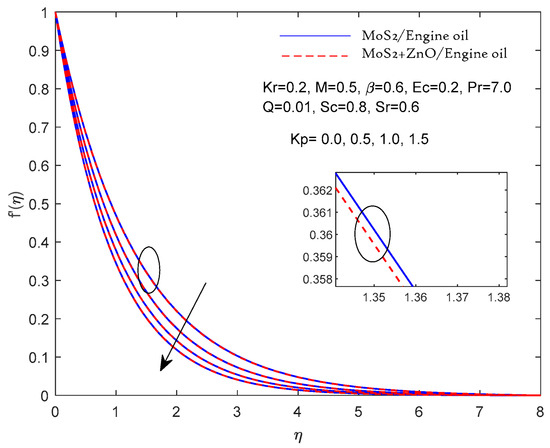
Figure 3.
Velocity f′ (η) fluctuation with Kp.
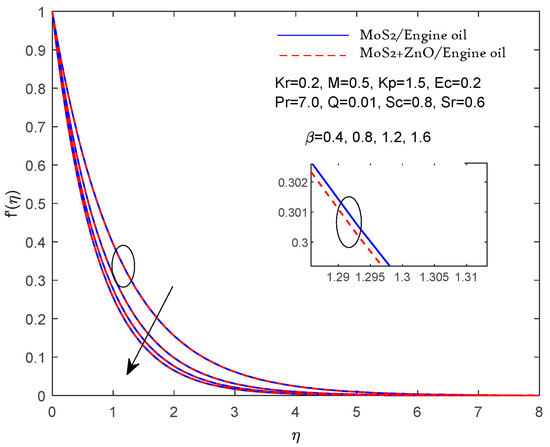
Figure 4.
Velocity f′ (η) fluctuation with β.
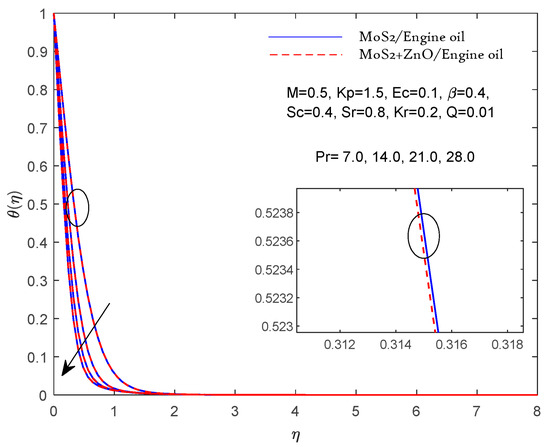
Figure 5.
θ(η) fluctuation with Pr.
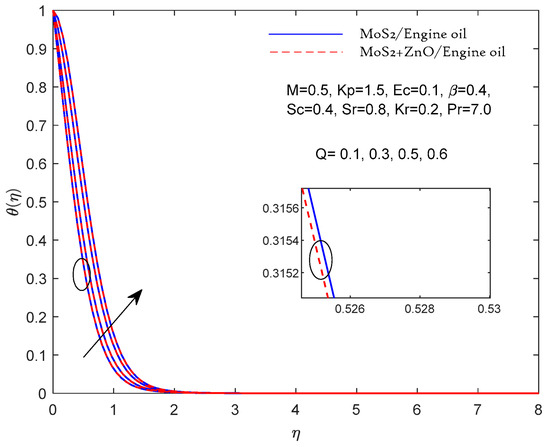
Figure 6.
θ(η) fluctuation with Q.
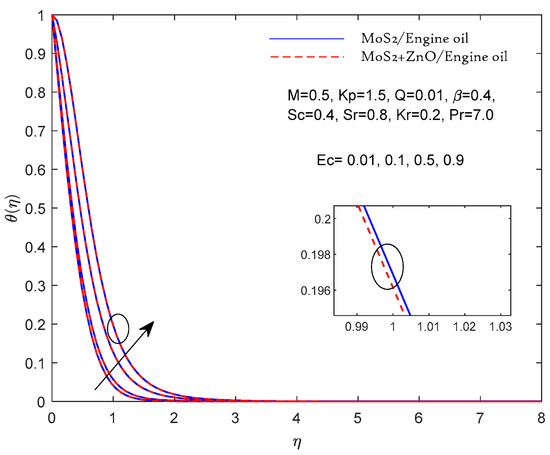
Figure 7.
θ(η) fluctuation with Ec.
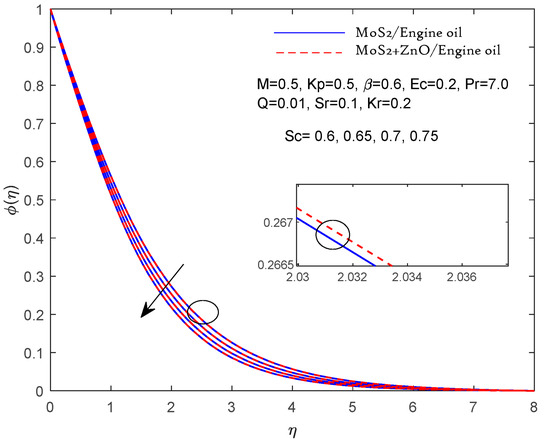
Figure 8.
Fluctuation with Sc.
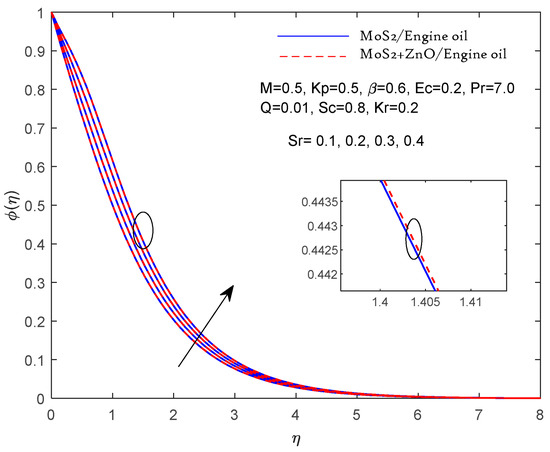
Figure 9.
Fluctuation with Sr.
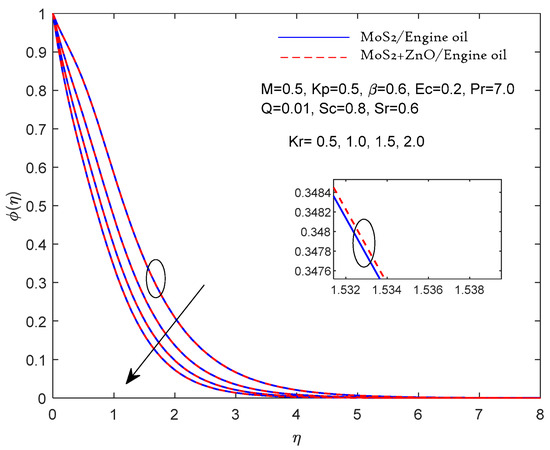
Figure 10.
Fluctuation with Kr.
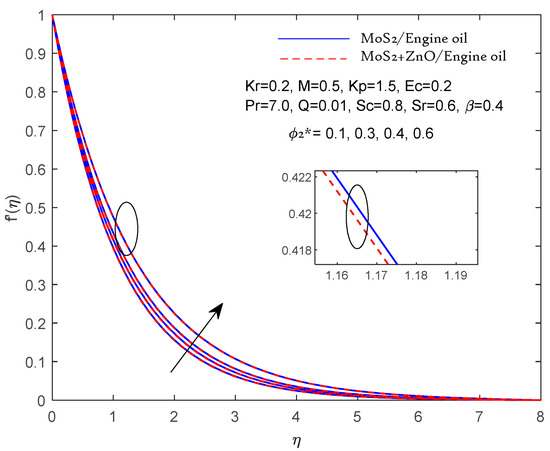
Figure 11.
Velocity f′ (η) fluctuation with
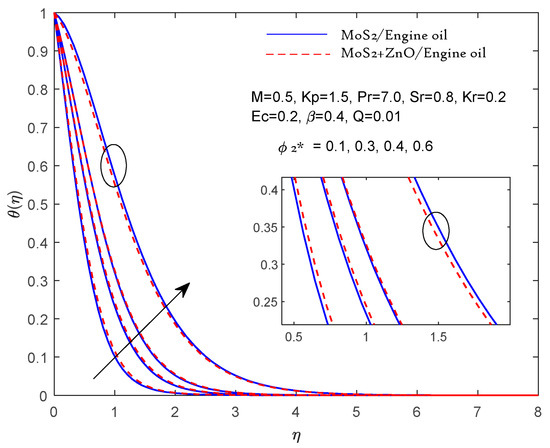
Figure 12.
θ(η) fluctuation with
Figure 9 shows the Soret effect on the concentration profile. An incremented Soret number increases the concentration profile because the temperature gradient is affected by the concentration. A physically higher value of the Soret number corresponds to a higher temperature gradient, which results in a higher convection flow and, hence, the concentration profile rises. Figure 10 shows the effect of the chemical reaction (Kr) on the concentration profile. Increasing the value of Kr decreases the concentration profile due to the consumption character of this chemical reaction; hence, the concentration profile decreases.
Figure 11 and Figure 12 show that as augmentation occurs, the velocity f′ (η) decreases. and the temperature rise until = 0.4 but the temperature increase is slower when > 0.4 due to mass flux and thermal diffusion. The flow is being slowed down because of the viscosity, which increases and has the effect of slowing down the flow. Moreover, Table 4 shows that the skin fraction profile —f″ (0) results for the various given values of M, Kp, and β in the ZnO + MoS2/engine oil (hybrid nanofluid) varies. It is seen that M, Kp, and β rise in absolute values of —f″ (0) because the fluid flow slows down due to the conflicting force of the electromagnetic collaboration and porosity. The accurate value of the Nusselt number −θ′ (0) rises with improved values of Pr. Table 5 provides information about the Prandtl number Pr. Also, it is noted that −θ′(0) decreases reciprocally with the Eckert number Ec and heat source parameter Q. The value of the Sherwood number −(0) increases with Ec, Kr, and Q, as shown in Table 6. It is also observed that −(0) decreases to Pr, Sc, and Sr.

Table 4.
Results for skin friction factor—f′′ (η).

Table 5.
Results for Nusselt number—θ′ (η).

Table 6.
Results for Sherwood number
5. Conclusions
Engine oil serves as the basic liquid in the Casson hybrid nanolubricant, which is theoretically analyzed and contains ZnO + MoS2. We use a Casson fluid model for mass and heat transfer across a stretching sheet to investigate the improved thermal efficiency in a cross-sectional view of hybrid nanolubricants. Comparisons are made between the flow and thermal properties and those of a basic nanolubricant (MoS2/engine oil). Moreover, the flow travels through a porous medium when a heat source, thermal dissipation, and magnetic field are present. The main conclusions are explained as follows:
- The velocity profile is diminished against the values of M, Kp, and β;
- The temperature profile rises in line with increased Ec and Q, and reciprocally goes down in line with Pr;
- The concentration profile is incremented with the value of Sr and decremented with the value of Sc and Kr;
- The velocity f′ (η) becomes slower with the increasing value of , whereas the temperature increase when = 0.6 becomes slower.
Author Contributions
Conceptualization, S.M. and N.B.N.; methodology, S.M.; MATLAB Bvp4c software, S.M. and N.B.N.; validation, S.M. and N.B.N.; formal analysis, S.M. and N.B.N.; writing—original draft preparation, S.M. and N.B.N.; writing—review and editing, N.B.N.; supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Umair, K.; Aurang, Z.; Anuar, I. Impact of Thermal and Activation Energies on Glauert Wall Jet (WJ) Heat and Mass Transfer Flows Induced by ZnO-SAE50 Nano Lubricants with Chemical Reaction: The Case of Brinkman-Extended Darcy Model. Lubricants 2023, 11, 22. [Google Scholar] [CrossRef]
- Zia, U.; Ahmad, H.; Musaad, S.A.; Nifeen, H.A.; Sana, S. Significance of Temperature-Dependent Density on Dissipative and Reactive Flows of Nanofluid along Magnetically Driven Sheet and Applications in Machining and Lubrications. Lubricants 2023, 11, 410. [Google Scholar] [CrossRef]
- Zawar, H.; Fahad, A.; Ayaz, M.; Saeed, I. Significance of Slips and Convective Conditions towards the Non-Newtonian Hybrid Nanofluid Flow over a Bi-Directional Stretching Surface. Int. J. Thermofluids 2023, 2023, 100537. [Google Scholar] [CrossRef]
- Najiyah, S.K.; Norihan, M.A.; Ioan, P.; Roslinda, N.; Ezad, H.H.; Nadihah, W. Three-Dimensional Hybrid Nanofluid Flow and Heat Transfer pasta Permeable Stretching/Shrinking Sheet with Velocity Slip and Convective Condition. Chin. J. Phys. 2020, 66, 157–171. [Google Scholar] [CrossRef]
- Bilal, S.; Khalil, U.R.; Malik, M.Y.; Arif, H.; Mair, K. Effects of temperature dependent conductivity and absorptive/generative heat transfer on MHD three dimensional flow of Williamson fluid due to bidirectional non-linear stretching surface. Results Phys. 2017, 7, 204–212. [Google Scholar] [CrossRef]
- Ramzan, M.; Abdullah, D.; Anwar, S.; Poom, K.; Wiboonsak, W. MHD flow of micropolar and Williamson fluids over a bi-directional stretching sheet. Eur. Phys. J. Plus 2022, 137, 869. [Google Scholar] [CrossRef]
- Anuar, J.; Roslinda, N.; Ioan, P. Three-Dimensional Magnetohydrodynamic Mixed Convection Flow of Nanofluids over a Nonlinearly Permeable Stretching/Shrinking Sheet with Velocity and Thermal Slip. Appl. Sci. 2018, 8, 1128. [Google Scholar] [CrossRef]
- Ishtiaq, K.; Amin, U.R.; Abdullah, D.; Saeed, I.; Aiman, Z. Second-order slip flow of a magnetohydrodynamic hybrid nanofluid past a bi-directional stretching surface with thermal convective and zero mass flux conditions. Adv. Mech. Eng. 2023, 15, 16878132221149894. [Google Scholar] [CrossRef]
- Tanzila, H.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Awatif, A.; Haneen, H.; Muhammad, B.; Aatif, A. Numerical study of Williamson hybrid nanofluid flow with thermal characteristics past over an extending surface. Heat Transf. 2022, 2022, 6641–6655. [Google Scholar] [CrossRef]
- Umadevi, S.S.; Anjalidevi, S.P. Heat Transfer Enhancement of Cu—Al2O3/Water Hybrid Nanofluid Flow over a Stretching Sheet. Niger. Math. Soc. 2017, 36, 419–433. Available online: https://ojs.ictp.it/jnms/index.php/jnms/article/view/147/47 (accessed on 1 March 2024).
- Ram Prakash, S.; Debasish, G.; Kalidas, D. Comparative study on hybrid nanofluid flow of Ag–CuO/H2O over a curved stretching surface with Soret and Dufour effects. Heat Transf. 2022, 51, 6365–6383. [Google Scholar] [CrossRef]
- Revathi, G.; Sajja, V.S.; Babu, M.J.; Raju, C.S.K.; Shehzad, S.A.; Bapanayya, C. Entropy optimization in hybrid radiative nanofluid (CH3OH + SiO2 + Al2O3) flow by a curved stretching sheet with cross-diffusion effects. Appl. Nanosci. 2021, 13, 337–351. [Google Scholar] [CrossRef]
- Motahar, R.; Anindita, B.; Amalendu, R.; Raghunath, P. Soret and Dufour effects on entropy generation for AIN and Al2O3 Hybrid Nanofluid Flow over past a stretching sheet in porous. Indian Soc. Theor. Appl. Mech. 2019, 2019, 9–12. Available online: https://www.researchgate.net/publication/338855239 (accessed on 1 March 2024).
- Asmat, U.Y.; Nadeem, S.; Wen-Hua, H.; Imran, S.; Sohaib, A.; Sajjad, H. Thermal charactristics for the flow of Williamson hybrid nanofluid (MoS2 + ZnO) based with engine oil over a streched sheet. Case Stud. Therm. Eng. 2021, 26, 101196. [Google Scholar] [CrossRef]
- Shami, A.M.A.; Abbas, T.; Al-Zubaidi, A.; Sami, U.K.; Saleem, S. Analytical assessment of heat transfer due to Williamson hybrid nanofluid (MoS2 + ZnO) with engine oil base material due to stretched sheet. Case Stud. Therm. Eng. 2023, 15, 103593. [Google Scholar] [CrossRef]
- Sreedevi, P.; Sudarsana, P.R.; Chamkha, A. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci. 2020, 2, 1222. [Google Scholar] [CrossRef]
- Mubashar, A.; Fahad, M.A.; Ali, H.; Qusain, H.; Abdullah, A.; Sayed, M.E.; Zubair, A.; Laila, A.A.; Ahmed, M.G. Effect of inclined magnetic field on radiative heat and mass transfer in chemically reactive hybrid nanofluid flow due to dual stretching. Sci. Rep. 2023, 13, 7828. [Google Scholar] [CrossRef] [PubMed]
- Yu-Ming, C.; Muhammad, D.I.; Muhammad, I.A.; Ali, A.; Ferial, G. Influence of hybrid nanofluids and heat generation on coupled heat and mass transfer flow of a viscous fluid with novel fractional derivative. J. Therm. Anal. Calorim. 2021, 144, 2057–2077. [Google Scholar] [CrossRef]
- Tassaddiq, A.; Khan, S.; Bilal, M.; Gul, T.; Mukhtar, S.; Shah, Z.; Bonyah, E. Heat and mass transfer together with hybrid nanofluid flow over a rotating disk. AIP Adv. 2020, 10, 055317. [Google Scholar] [CrossRef]
- Shanmugapriya, M.; Sundareswaran, R.; Senthil Kumar, P. Heat and Mass Transfer Enhancement of MHD Hybrid Nanofluid Flow in the Presence of Activation Energy. Int. J. Chem. Eng. 2021, 2021, 9473226. [Google Scholar] [CrossRef]
- Sohail, A.; Kashif, A.; Muhammad, R.; Muhammad, A. Heat and mass transfer attributes of copper–aluminum oxide hybrid nanoparticles flow through a porous medium. Case Stud. Therm. Eng. 2021, 25, 100932. [Google Scholar] [CrossRef]
- Abdulmajeed, A. Numerical study on heat and mass transport enhancement in MHD Williamson fluid via hybrid nanoparticles. Alex. Eng. J. 2022, 16, 8343–8354. [Google Scholar] [CrossRef]
- Gohar; Tahir, S.K.; Ndolane, S.; Abir, M.; Ameni, B. Heat and Mass Transfer of the Darcy-Forchheimer Casson Hybrid Nanofluid Flow due to an Extending Curved Surface. J. Nanomater. 2022, 2022, 3979168. [Google Scholar] [CrossRef]
- Ali, F.; Zaiba, A.; Faizana, M.; Zafara, S.S.; Shalan, A.; Nehad, A.S.; Jae, D.C. Heat and mass exchanger analysis for Ree-Eyring hybrid nanofluid through a stretching sheet utilizing the homotopy perturbation method. Case Stud. Therm. Eng. 2024, 54, 104014. [Google Scholar] [CrossRef]
- Wei-Feng, X.; Shafiq, A.; Naveed, K.M.; Hijaz, A.; Aysha, R.; Jamel, B.; Tuan, N.G. Heat and mass transfer analysis of nonlinear mixed convective hybrid nanofluid flow with multiple slip boundary conditions. Case Stud. Therm. Eng. 2022, 32, 101893. [Google Scholar] [CrossRef]
- Saeed, D.; Mohammadreza, N.R.; Ioan, P. A novel hybridity model for TiO2-CuO/water hybrid nanofluid flow over a static/moving wedge or corner. Sci. Rep. 2019, 9, 16290. [Google Scholar] [CrossRef]
- Saqib, M.; Ilyas, K.; Sharidan, S. Application of fractional differential equations to heat transfer in hybrid nanofluid: Modeling and solution via integral transforms. Adv. Differ. Equ. 2019, 2019, 52. [Google Scholar] [CrossRef]
- Jun, Z.; Yingru, L.; Yongyong, H.; Jianbin, L. In Situ Green Synthesis of the New Sandwichlike Nanostructure of Mn3O4/Graphene as Lubricant Additives. ACS Appl. Mater. Interfaces 2019, 11, 36931–36938. [Google Scholar] [CrossRef] [PubMed]
- Vicki, W.V.; Praveen Kumar, K.; Prabhakar, S.; Husna, N.; Abdullah, M.Z. Viscosity and rheological behavior of Al2O3-Fe2O3/water-EG based hybrid nanofluid: A new correlation based on mixture ratio. J. Mol. Liq. 2023, 375, 121365. [Google Scholar] [CrossRef]
- Jongsuk, L.; Sejin, L.; Chungyeon, C.; Sunghan, K. Experimental study and modeling of the energy density and time-dependent rheological behavior of carbon nanotube nanofluids with sonication. Int. J. Heat Mass Transf. 2022, 192, 122941. [Google Scholar] [CrossRef]
- Seyed, B.M.; Saeed, Z.H.; Patrice, E. Viscosity, tribological and physicochemical features of ZnO and MoS2 diesel oil-based nanofluids: An experimental study. Fuel 2021, 293, 120481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).