Molecular Dynamics Simulation on Polymer Tribology: A Review
Abstract
1. Introduction
2. Three Main MD Research Methods and Their Force Field Used in Polymer Tribology
2.1. All-Atom MD Simulation
2.1.1. COMPASS Force Filed
2.1.2. CVFF Force Field
2.1.3. PCFF Force Field
2.1.4. OPLS-AA Force Field
2.2. Reactive MD Simulation
2.3. Coarse-Grained MD Simulation
3. Typical Polymer Tribological Problems Solved by MD Simulation
3.1. Friction and Wear Mechanisms Revealed by All-Atom MD Simulation
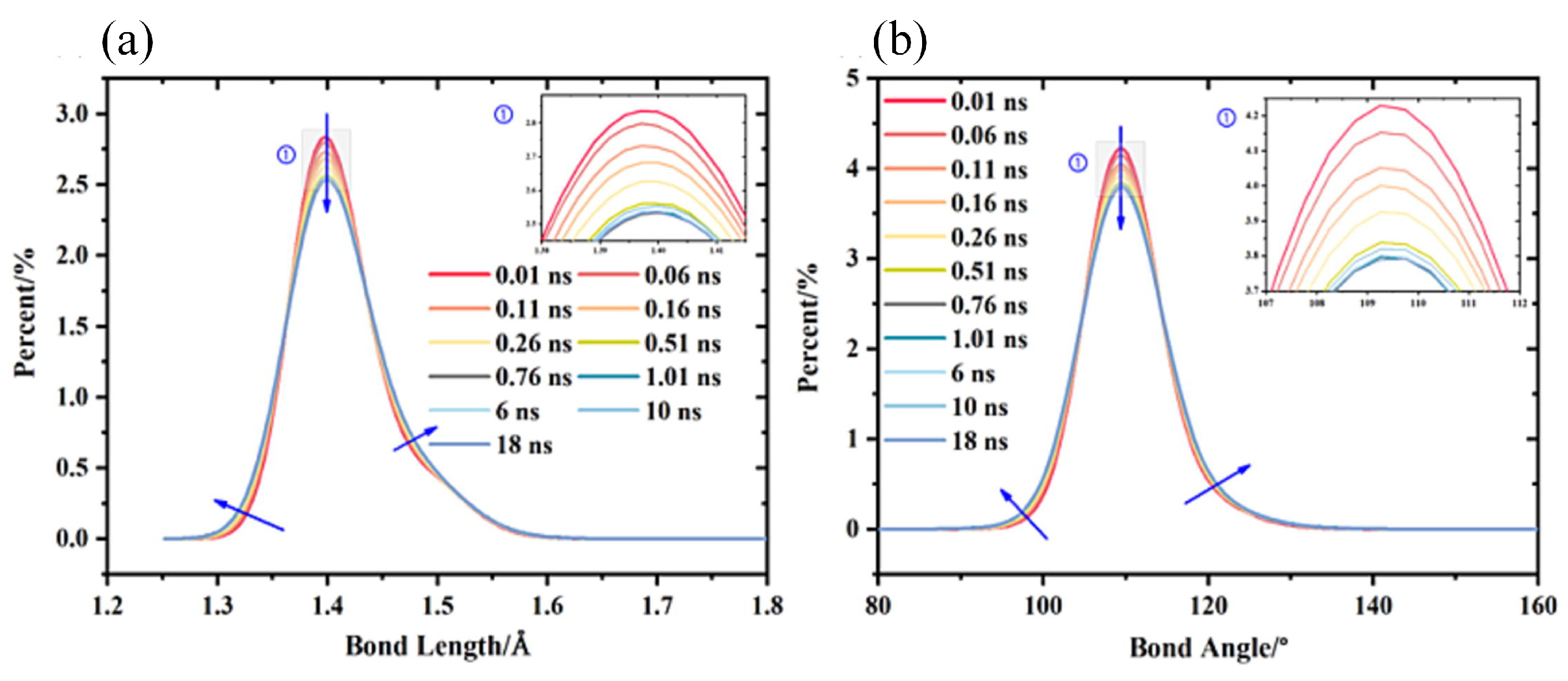
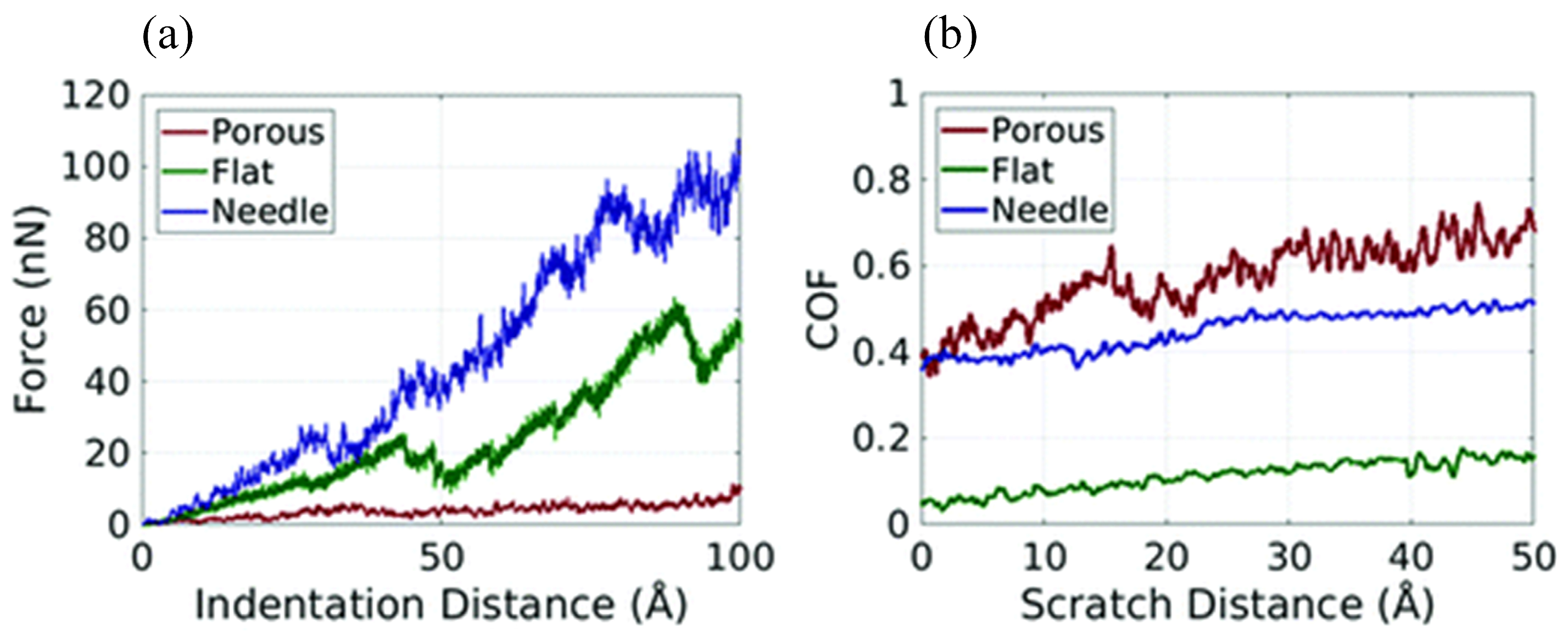
3.1.1. Mechanical Properties
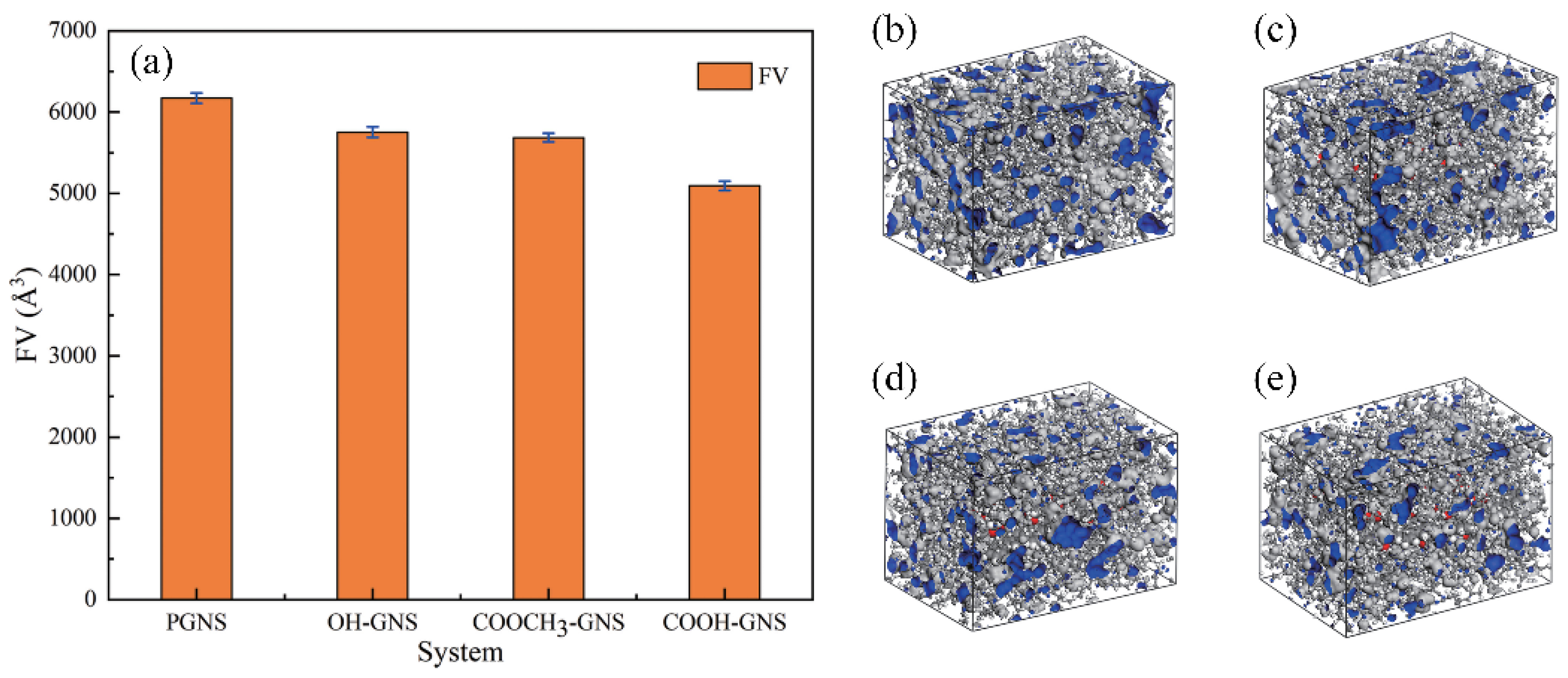
3.1.2. Free Volumes (FVs)
3.1.3. Mean Square Displacement (MSD)
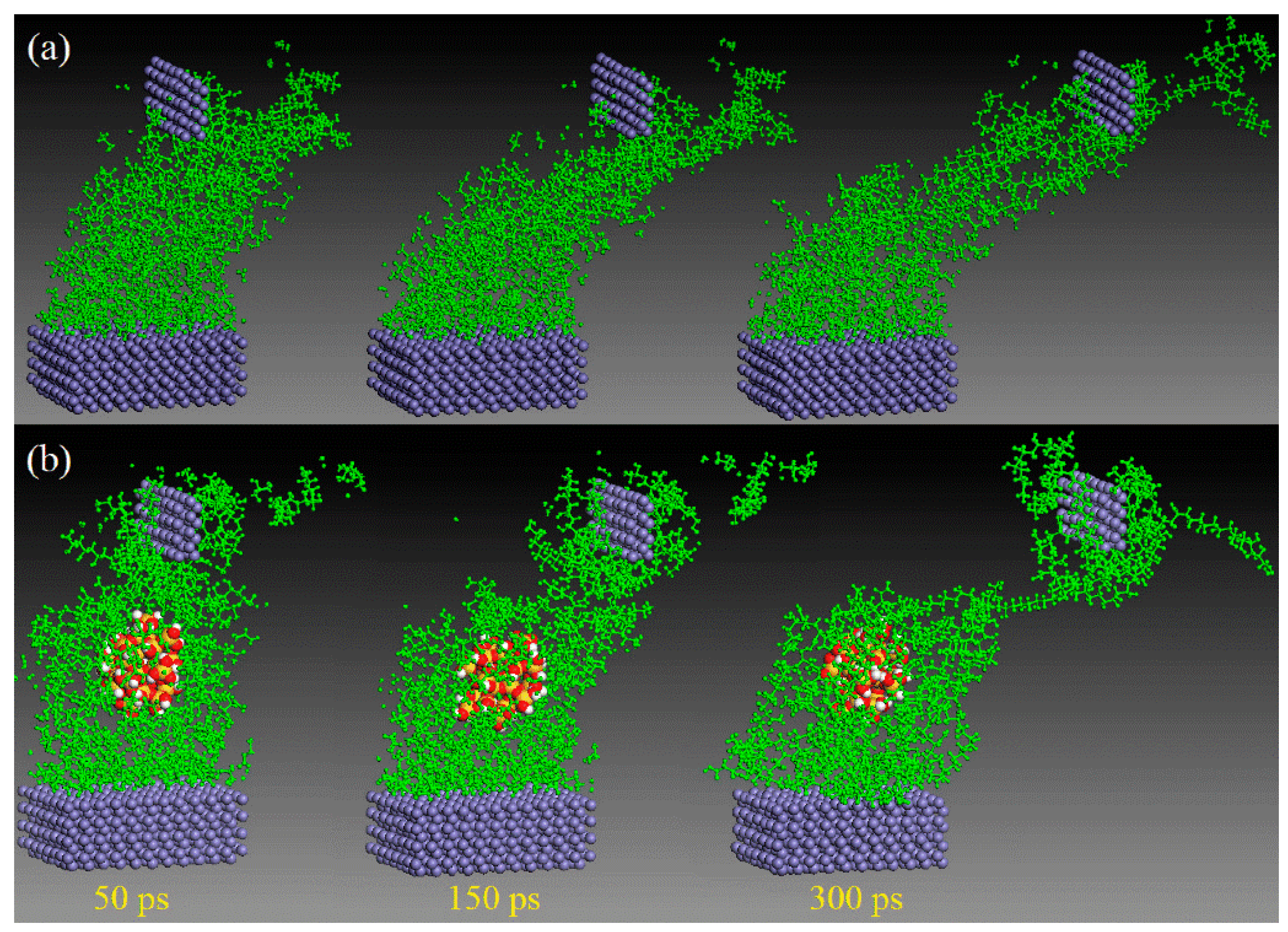
3.1.4. Direct Observation of Frictional Interfaces
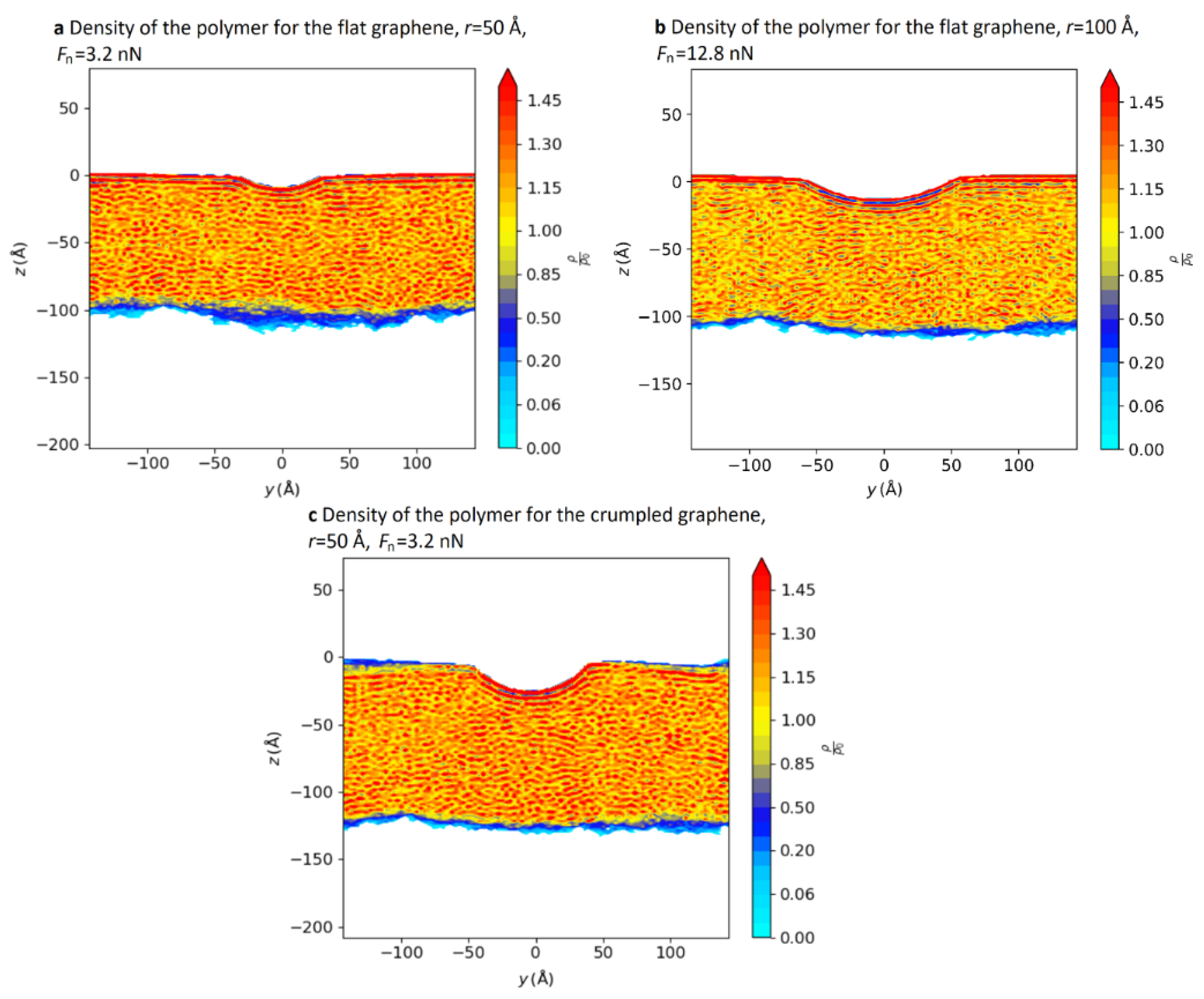
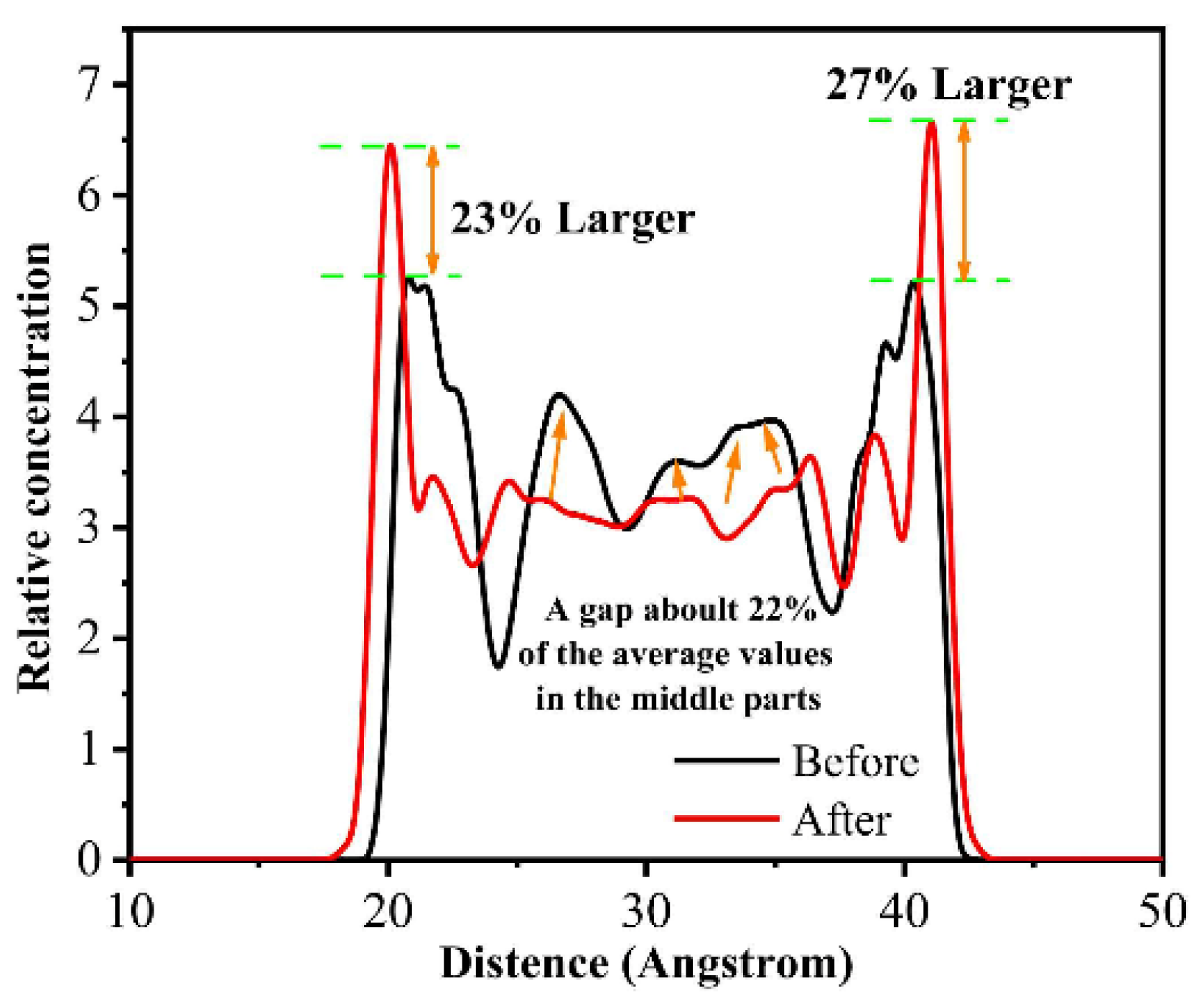
3.1.5. Distribution of Polymer Molecules
3.1.6. Radial Distribution Function (RDF)
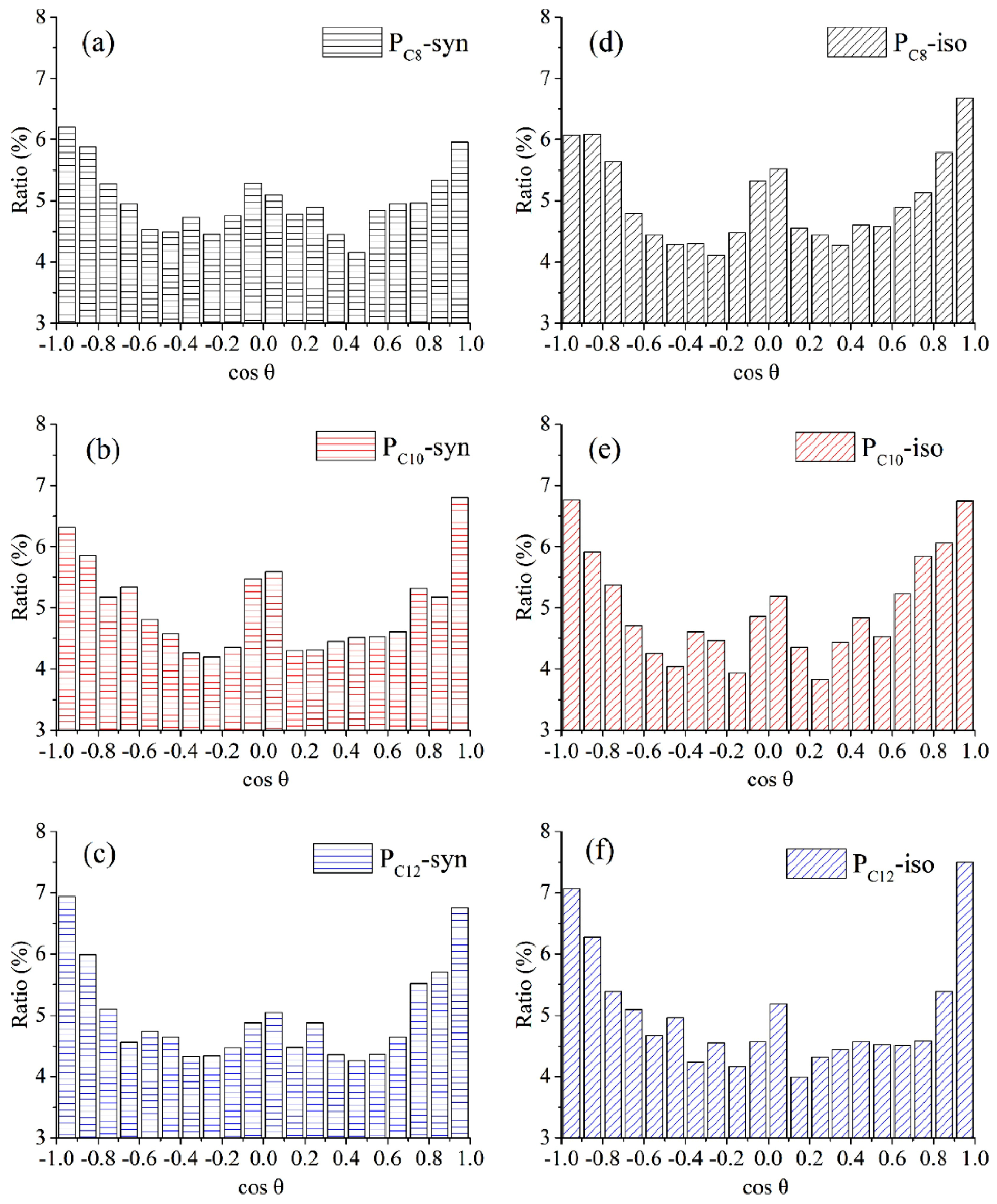
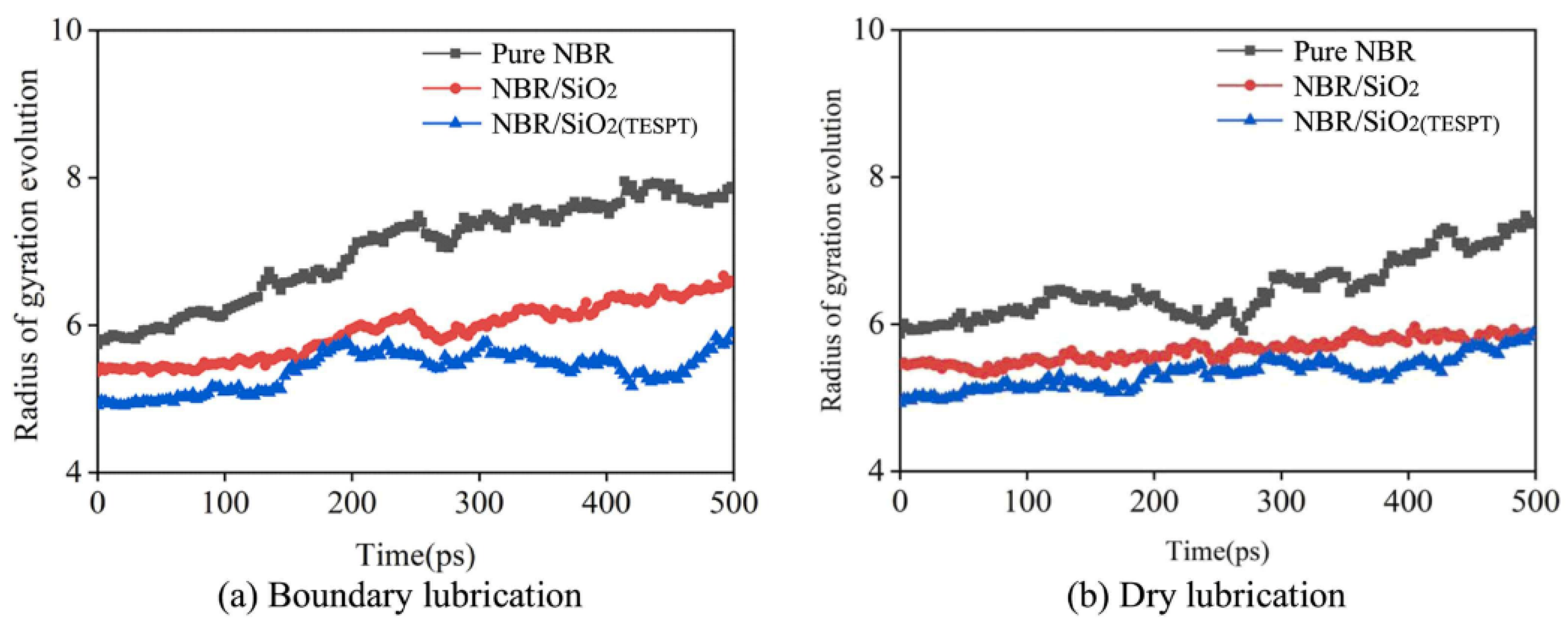
3.1.7. Conformation of Polymers
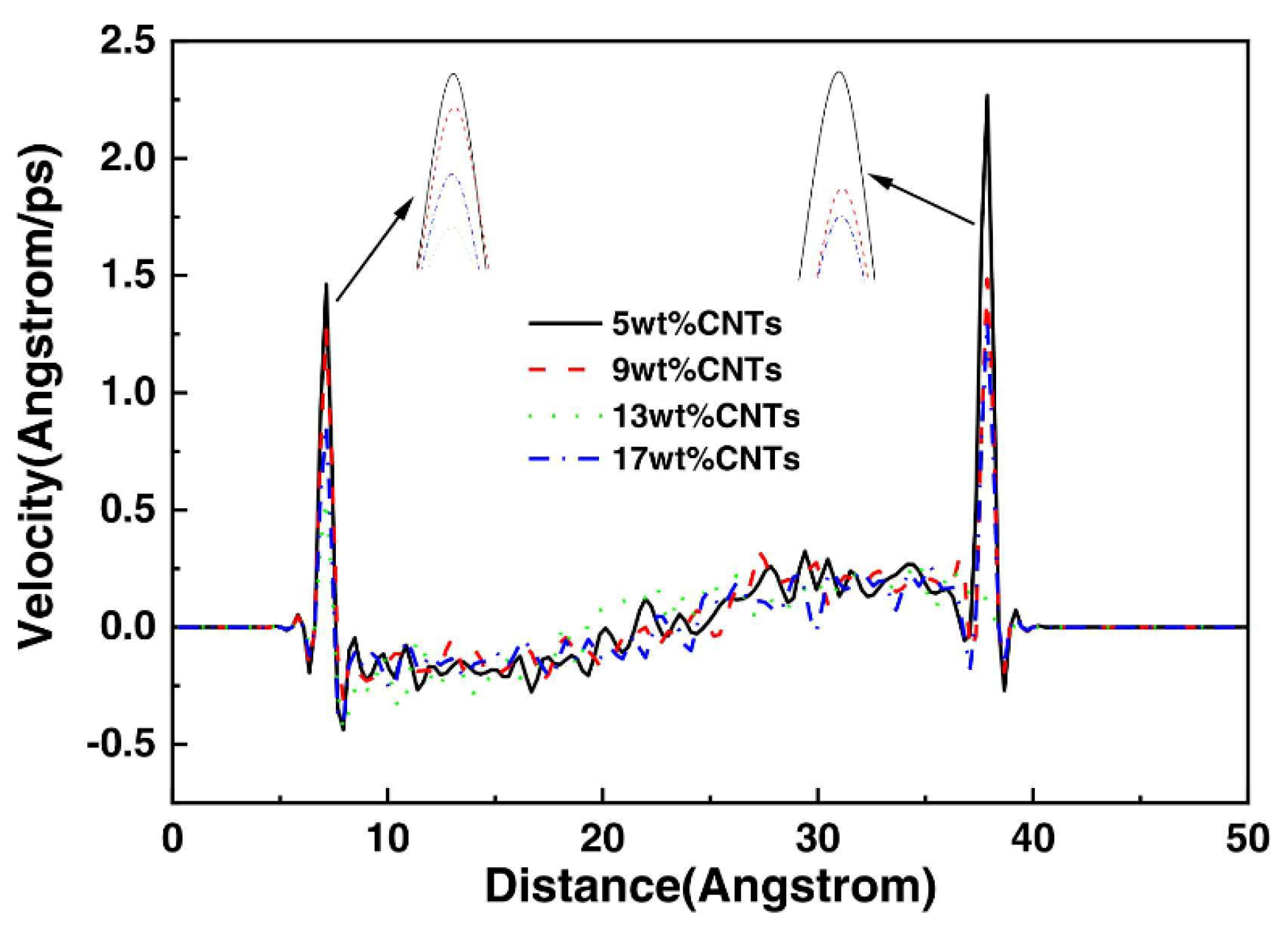
3.1.8. Velocity Distribution
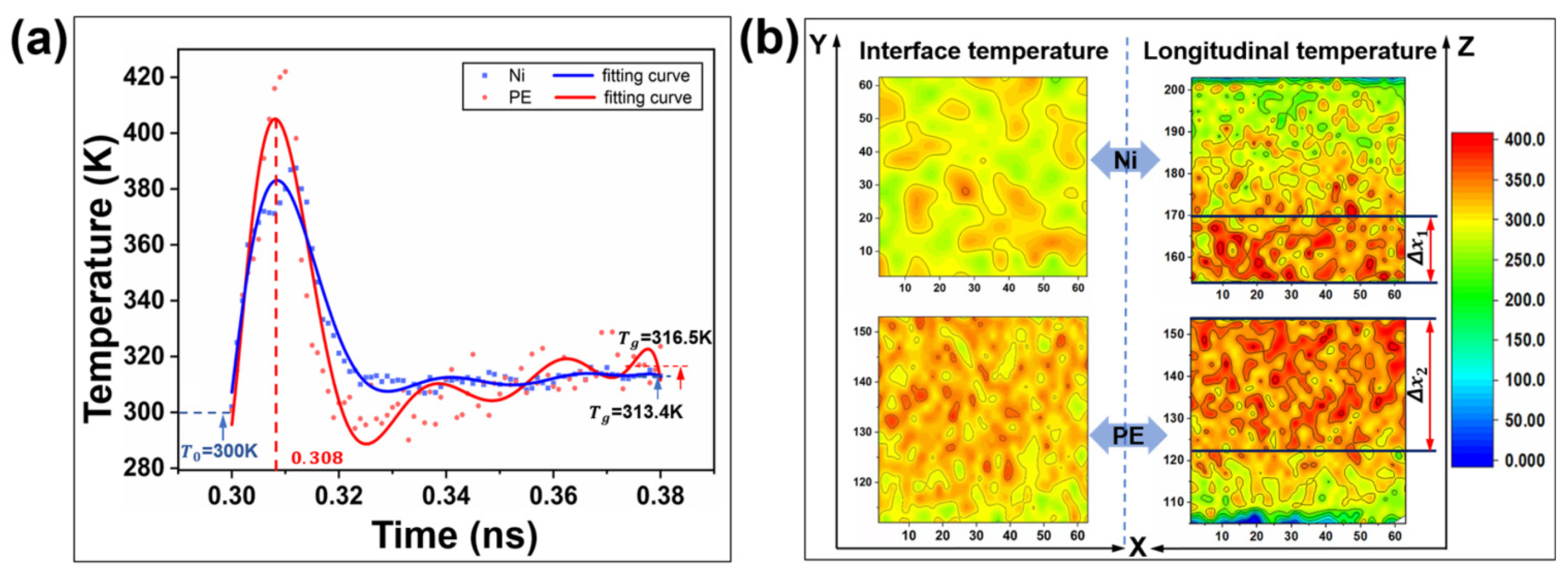
3.1.9. Temperature Variation
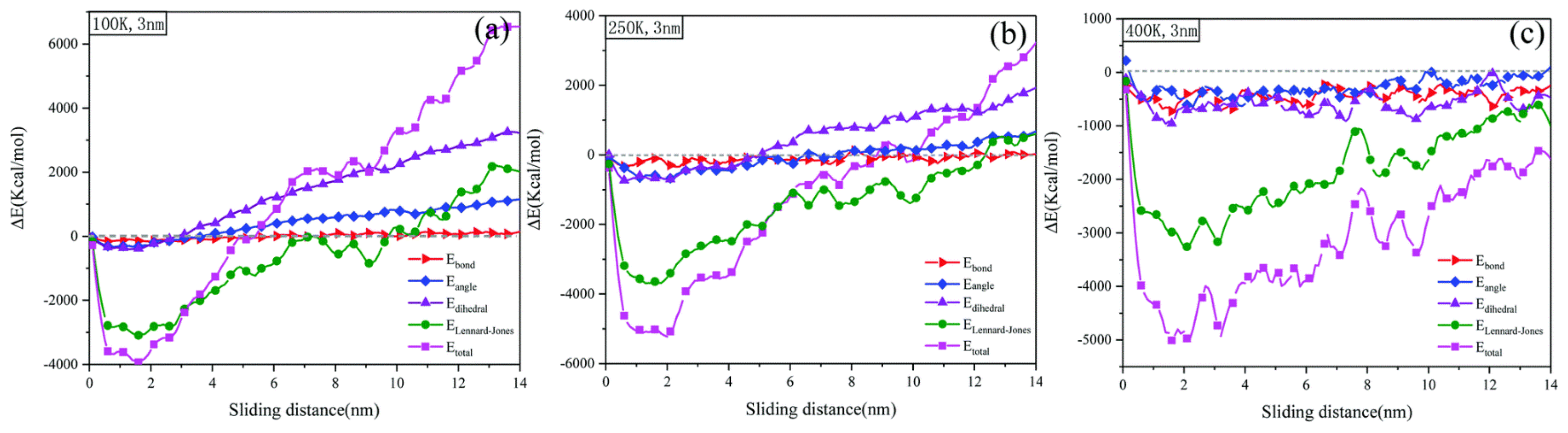
3.1.10. Energy Analysis
3.2. Tribochemical Reactions
3.3. Understanding Friction Process at Larger Spatial and Temporal Scales
4. Current Challenges in MD Simulation for Polymer Tribology
4.1. Broadening the Applicability of Force Fields
4.2. Promoting the Application of Coarse-Grained MD Simulation in Polymer Composites
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Yadav, R.; Singh, M.; Shekhawat, D.; Lee, S.-Y.; Park, S.-J. The role of fillers to enhance the mechanical, thermal, and wear characteristics of polymer composite materials: A review. Compos. Part A Appl. Sci. Manuf. 2023, 175, 107775. [Google Scholar] [CrossRef]
- Kurdi, A.; Chang, L. Recent advances in high performance polymers—Tribological aspects. Lubricants 2018, 7, 2. [Google Scholar] [CrossRef]
- Myshkin, N.; Kovalev, A. Adhesion and surface forces in polymer tribology—A review. Friction 2018, 6, 143–155. [Google Scholar] [CrossRef]
- Chan, J.X.; Wong, J.F.; Petru, M.; Hassan, A.; Nirmal, U.; Othman, N.; Ilyas, R.A. Effect of nanofillers on tribological properties of polymer nanocomposites: A review on recent development. Polymers 2021, 13, 2867. [Google Scholar] [CrossRef]
- Mohammed, L.; Ansari, M.N.M.; Pua, G.; Jawaid, M.; Islam, M.S. A review on natural fiber reinforced polymer composite and its applications. Int. J. Polym. Sci. 2015, 2015, 243947. [Google Scholar] [CrossRef]
- Srivastava, I.; Kotia, A.; Ghosh, S.K.; Ali, M.K.A. Recent advances of molecular dynamics simulations in nanotribology. J. Mol. Liq. 2021, 335, 116154. [Google Scholar] [CrossRef]
- Rossetti, G.; Mandelli, D. How exascale computing can shape drug design: A perspective from multiscale QM/MM molecular dynamics simulations and machine learning-aided enhanced sampling algorithms. Curr. Opin. Struct. Biol. 2024, 86, 102814. [Google Scholar] [CrossRef]
- Bera, I.; Payghan, P.V. Use of molecular dynamics simulations in structure-based drug discovery. Curr. Pharm. Des. 2019, 25, 3339–3349. [Google Scholar] [CrossRef]
- Jónsson, E. Ionic liquids as electrolytes for energy storage applications—A modelling perspective. Energy Storage Mater. 2020, 25, 827–835. [Google Scholar] [CrossRef]
- Formalik, F.; Shi, K.; Joodaki, F.; Wang, X.; Snurr, R.Q. Exploring the structural, dynamic, and functional properties of metal-organic frameworks through molecular modeling. Adv. Funct. Mater. 2023, 2308130. [Google Scholar] [CrossRef]
- Zhou, W.; Wei, M.; Zhang, X.; Xu, F.; Wang, Y. Fast desalination by multilayered covalent organic framework (COF) nanosheets. ACS Appl. Mater. Interfaces 2019, 11, 16847–16854. [Google Scholar] [CrossRef] [PubMed]
- Ewen, J.P.; Heyes, D.M.; Dini, D. Advances in nonequilibrium molecular dynamics simulations of lubricants and additives. Friction 2018, 6, 349–386. [Google Scholar] [CrossRef]
- Talapatra, A.; Datta, D. A review of the mechanical, thermal and tribological properties of graphene reinforced polymer nanocomposites: A molecular dynamics simulations methods. Polym. Bull. 2022, 80, 2299–2328. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-grained protein models and their applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Sun, H. COMPASS: An ab initio force-field optimized for condensed-phase applicationss-overview with details on alkane and benzene compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Model 2016, 22, 47. [Google Scholar] [CrossRef] [PubMed]
- Akkermans, R.L.C.; Spenley, N.A.; Robertson, S.H. COMPASS III: Automated fitting workflows and extension to ionic liquids. Mol. Simul. 2020, 47, 540–551. [Google Scholar] [CrossRef]
- Dauber-Osguthorpe, P.; Roberts, V.A.; Osguthorpe, D.J.; Wolff, J.; Genest, M.; Hagler, A.T. Structure and energetics of ligand binding to proteins: Escherichia coli dihydrofolate reductase-trimethoprim, a drug-receptor system. Proc. Nati. Acad. Sci. USA 1988, 4, 31–47. [Google Scholar]
- Maple, J.R.; Dinur, U.; Hagler, A.T. Derivation of force fields for molecular mechanics and dynamics from ab initio energy surfaces. Proc. Nati. Acad. Sci. USA 1988, 85, 5350–5354. [Google Scholar] [CrossRef]
- Gaedt, K.; Hltje, H.-D. Consistent valence force-field parameterization of bond lengths and angles with quantum chemicalab initio methods applied to some heterocyclic dopamine D3-receptor agonists. J. Comput. Chem. 1998, 19, 935–946. [Google Scholar] [CrossRef]
- Lange, J.; de Souza, F.G.; Nele, M.; Tavares, F.W.; Segtovich, I.S.V.; da Silva, G.C.Q.; Pinto, J.C. Molecular dynamic simulation of oxaliplatin diffusion in poly(lactic acid-co-glycolic acid). Part a: Parameterization and validation of the force-field CVFF. Macromol. Theory Simul. 2016, 25, 45–62. [Google Scholar] [CrossRef]
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An ab Initio CFF93 All-Atom Force Field for Polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- Sun, H. Ab Initio Calculations and Force Field Development for Computer Simulation of Polysilanes. Macromolecules 1995, 28, 701–712. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Doherty, B.; Zhong, X.; Gathiaka, S.; Li, B.; Acevedo, O. Revisiting OPLS force field parameters for ionic liquid simulations. J. Chem. Theory Comput. 2017, 13, 6131–6145. [Google Scholar] [CrossRef] [PubMed]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved peptide and protein torsional energetics with the OPLS-AA force field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef] [PubMed]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M.; et al. The ReaxFF reactive force-field: Development, applications and future directions. npj Comput. Mater. 2016, 2, 15011. [Google Scholar] [CrossRef]
- Russo, M.F.; van Duin, A.C.T. Atomistic-scale simulations of chemical reactions: Bridging from quantum chemistry to engineering. Nucl. Instrum. Methods Phys. Res. 2011, 269, 1549–1554. [Google Scholar] [CrossRef]
- van Duin, A.C.T.; Strachan, A.; Stewman, S.; Zhang, Q.; Xu, X.; Goddard, W.A. ReaxFFSiO reactive force field for silicon and silicon oxide systems. J. Phys. Chem. A 2003, 107, 3803–3811. [Google Scholar] [CrossRef]
- Karimi-Varzaneh, H.A.; van der Vegt, N.F.A.; Müller-Plathe, F.; Carbone, P. How good are coarse-grained polymer models? A comparison for atactic polystyrene. ChemPhysChem 2012, 13, 3428–3439. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Li, W. Recent advances in coarse-grained models for biomolecules and their applications. Int. J. Mol. Sci. 2019, 20, 3774. [Google Scholar] [CrossRef] [PubMed]
- Saunders, M.G.; Voth, G.A. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013, 42, 73–93. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Shi, R.; Zhu, Y.; Qian, H.; Lu, Z. Coarse-grained dynamics simulation in polymer systems: From structures to material properties. Chem. Res. Chin. Univ. 2022, 38, 653–670. [Google Scholar] [CrossRef]
- Souza, P.C.T.; Alessandri, R.; Barnoud, J.; Thallmair, S.; Faustino, I.; Grünewald, F.; Patmanidis, I.; Abdizadeh, H.; Bruininks, B.M.H.; Wassenaar, T.A.; et al. Martini 3: A general purpose force field for coarse-grained molecular dynamics. Nat. Methods 2021, 18, 382–388. [Google Scholar] [CrossRef]
- Weiand, E.; Koenig, P.H.; Rodriguez-Ropero, F.; Roiter, Y.; Angioletti-Uberti, S.; Dini, D.; Ewen, J.P. Boundary lubrication performance of polyelectrolyte-surfactant complexes on biomimetic surfaces. Langmuir 2024, 40, 7933–7946. [Google Scholar] [CrossRef] [PubMed]
- Adroher-Benítez, I.; Morozova, T.I.; Catalini, G.; García, N.A.; Barrat, J.-L.; Luengo, G.S.; Léonforte, F. Effect of polymer architecture on the adsorption and coating stability on heterogeneous biomimetic surfaces. Macromolecules 2023, 56, 10285–10295. [Google Scholar] [CrossRef]
- Coscia, B.J.; Shelley, J.C.; Browning, A.R.; Sanders, J.M.; Chaudret, R.; Rozot, R.; Leonforte, F.; Halls, M.D.; Luengo, G.S. Shearing friction behaviour of synthetic polymers compared to a functionalized polysaccharide on biomimetic surfaces: Models for the prediction of performance of eco-designed formulations. Phys. Chem. Chem. Phys. 2023, 25, 1768–1780. [Google Scholar] [CrossRef]
- Yin, Y.; Song, J.; Zhao, G.; Ding, Q. Improving the high temperature tribology of polyimide by molecular structure design and grafting POSS. Polym. Adv. Technol. 2021, 33, 886–896. [Google Scholar] [CrossRef]
- Liu, C.; Song, J.; Zhao, G.; Yin, Y.; Ding, Q. Improving thermal conductivity and tribological performance of polyimide by filling Cu, CNT, and graphene. Micromachines 2023, 14, 616. [Google Scholar] [CrossRef] [PubMed]
- Qian, C.; Li, Y.; Zhao, J.; Wang, S.; He, E. Thermal-oxidative aging and tribological properties of carbon nanotube/nitrile butadiene rubber composites with varying acrylonitrile content: Molecular dynamics simulations. Polym Eng Sci. 2023, 63, 1516–1527. [Google Scholar] [CrossRef]
- Wu, J.; Teng, F.; Su, B.; Wang, Y. Molecular dynamics study on tribological properties of EUG/NR composites. Comput. Mater. Sci. 2021, 199, 110732. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Qian, C.; Zhao, J.; Wang, S. Molecular dynamics study of the mechanical and tribological properties of graphene oxide-reinforced polyamide 66/nitrile butadiene rubber composites. Appl. Phys. A 2023, 129, 276. [Google Scholar] [CrossRef]
- Cai, P.; Xu, C.; Zheng, F.; Song, J.; Zhao, G. Molecular dynamics study on the mechanical and tribological properties of polyimide reinforced by lanthana. Ind. Lubr. Tribol. 2021, 73, 1319–1324. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, J.; Wang, S.; Wang, Y.; Li, Y. Effects of carbon nanotubes functionalization on mechanical and tribological properties of nitrile rubber nanocomposites: Molecular dynamics simulations. Comput. Mater. Sci. 2021, 196, 110556. [Google Scholar] [CrossRef]
- Yuan, Q.; Li, Y.; Wang, S.; He, E.; Yang, B.; Nie, R. A Molecular Dynamics Simulation Study on Enhancement of Mechanical and Tribological Properties of Nitrile-Butadiene Rubber with Varied Contents of Acrylonitrile. Polymers 2023, 15, 3799. [Google Scholar] [CrossRef]
- Li, S.; Dong, C.; Yuan, C.; Bai, X. Molecular dynamics simulation on performance modulation of graphene-modified polyethylene during friction process. Polym. Adv. Technol. 2022, 33, 3479–3489. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, J.; Wang, S.; Li, Y. A comparative study on enhancement of mechanical and tribological properties of nitrile rubber composites reinforced by different functionalized graphene sheets: Molecular dynamics simulations. Polym. Compos. 2020, 42, 205–219. [Google Scholar] [CrossRef]
- Qian, C.; Li, Y.; Zhao, J.; Wang, S. Effect of single-vacancy- and vacancy-adsorbed-atom-defective CNTs on the mechanical and tribological properties of NBR composites: Molecular dynamics simulations. J. Polym. Res. 2023, 30, 99. [Google Scholar] [CrossRef]
- Wang, M.; Li, Y.; Qian, C.; Zhao, J.; Wang, S. Molecular dynamics simulations of defective carbon nanotubes on the aging and friction properties of nitrile butadiene rubber composites. Polym. Compos. 2022, 44, 1228–1239. [Google Scholar] [CrossRef]
- Yang, Z.; Guo, Z.; Yuan, C.; Bai, X. Tribological behaviors of composites reinforced by different functionalized carbon nanotube using molecular dynamic simulation. Wear 2021, 476, 203669. [Google Scholar] [CrossRef]
- Zuo, Z.; Liang, L.; Bao, Q.; Yan, P.; Jin, X.; Yang, Y. Molecular dynamics calculation on the adhesive interaction between the polytetrafluoroethylene transfer film and iron surface. Front. Chem. 2021, 9, 740447. [Google Scholar] [CrossRef] [PubMed]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Huang, H.; Qu, J.; Ren, R.; He, H.; Huang, F.; Wang, Y. Frictional anisotropy of oriented carbon nanotubes/rubber composites and new insight into its mechanism from the perspective of frictional interface. J. Tribol. 2023, 145, 011704. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Arash, B.; Wang, Q. A study on tribology of nitrile-butadiene rubber composites by incorporation of carbon nanotubes: Molecular dynamics simulations. Carbon 2016, 100, 145–150. [Google Scholar] [CrossRef]
- Teng, F.; Wu, J.; Su, B.; Wang, Y. Enhanced adhesion friction behaviors of nature rubber composites by applications of carbon nanotube: Experiment and molecular insight. Tribol. Int. 2023, 181, 108333. [Google Scholar] [CrossRef]
- Li, C.; Huang, H.; Qu, J.; Cao, J.; Huang, F.; Wang, Y. Mechanism of wear and COF variation of vulcanized rubber under changing loads and sliding velocities: Interpretation at the atomic scale. Tribol. Int. 2022, 170, 107505. [Google Scholar] [CrossRef]
- Yin, B.B.; Huang, J.S.; Ji, W.M.; Liew, K.M. Exploring frictional performance of diamond nanothread reinforced polymer composites from the atomistic simulation and density functional theory. Carbon 2022, 200, 10–20. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, Y.; Rao, Y.; Jiang, A.; Zhang, K.; Lu, T.; Chen, X. Evaluating the effects of nanosilica on mechanical and tribological properties of polyvinyl alcohol/polyacrylamide polymer composites for artificial cartilage from an atomic level. Polymers 2019, 11, 76. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Zhao, G. A molecular dynamics study on water lubrication of PTFE sliding against copper. Tribol. Int. 2019, 136, 234–239. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, X.; Li, Y.; Huang, R.; Xu, J.; Yang, L. Effects of molecular structures of poly α-olefin mixture on nano-scale thin film lubrication. Mater. Today Commun. 2020, 25, 101500. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, J.; Cui, J.; Jiang, B. Molecular dynamics study on enhancement of mechanical and tribological properties of polytetrafluoroethylene composites by incorporating hexagonal boron nitride nanosheets. J. Appl. Polym. Sci. 2023, 140, e53761. [Google Scholar] [CrossRef]
- Zheng, T.; Wang, S.; Zhou, L.; Li, X.; Zhang, H. The disentanglement and shear properties of amorphous polyethylene during friction: Insights from molecular dynamics simulations. Appl. Surf. Sci. 2022, 580, 152301. [Google Scholar] [CrossRef]
- Vacher, R.; de Wijn, A.S. Nanoscale friction and wear of a polymer coated with graphene. Beilstein J. Nanotechnol. 2022, 13, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Sun, B.; Zhang, Y.; Gao, G.; Zhang, P.; Zheng, X. Tribological Properties of Nano-ZrO2 and PEEK Reinforced PTFE Composites Based on Molecular Dynamics. Lubricants 2023, 11, 194. [Google Scholar] [CrossRef]
- Xu, M.; Wang, T.; Wang, Q.; Zhang, X.; Tao, L.; Li, S. Mechanical and tribological properties of polytetrafluoroethylene reinforced by nano-ZrO2: Molecular dynamic simulation. High Perform. Polym. 2022, 34, 397–405. [Google Scholar] [CrossRef]
- Teng, F.; Wu, J.; Su, B.; Wang, Y. Enhanced tribological properties of vulcanized natural rubber composites by applications of carbon nanotube: A molecular dynamics study. Nanomaterials 2021, 11, 2646. [Google Scholar] [CrossRef]
- Chawla, R.; Sharma, S. A molecular dynamics study on Young’s modulus and tribology of carbon nanotube reinforced styrene-butadiene rubber. J. Mol. Model. 2018, 24, 96. [Google Scholar] [CrossRef]
- Qu, F.; Liu, L.; Tao, G.; Zhan, W.; Zhan, S.; Li, Y.; Li, C.; Lv, X.; Shi, Z.; Duan, H. Effect of thermal oxidative ageing on the molecular structure and tribological properties of polytetrafluoroethylene. Tribol. Int. 2023, 188, 108850. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, H.; Li, W.; Chang, X.; Cao, J.; Hua, L. Vulcanization vodeling and mechanism for improved tribological performance of styrene-butadiene rubber at the atomic scale. Tribol. Lett. 2020, 68, 83. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, J.; Hu, Y.-Z.; Ma, T.-B. Tribological rehavior of poly(tetrafluoroethylene) and Its composites reinforced by carbon nanotubes and graphene sheets: Molecular dynamics simulation. Phys. Status Solidi RRL 2021, 16, 2100298. [Google Scholar] [CrossRef]
- Wang, Z.; Su, M.; Duan, X.; Yao, X.; Han, X.; Song, J.; Ma, L. Molecular dynamics simulation of the thermomechanical and tribological properties of graphene-reinforced natural rubber nanocomposites. Polymers 2022, 14, 5056. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, S.; He, E.; Wang, Q. The effect of sliding velocity on the tribological properties of polymer/carbon nanotube composites. Carbon 2016, 106, 106–109. [Google Scholar] [CrossRef]
- Xu, M.; Wang, Q.; Wang, T.; Tao, L.; Li, S. Molecular dynamic simulation study of tribological mechanism of PI composites reinforced by CNTs with different orientations. Polym. Compos. 2022, 43, 1557–1565. [Google Scholar] [CrossRef]
- Sun, W.; Ye, J.; Liu, X.; Liu, K. Atomistic insights into anti-wear mechanisms and protective tribofilm formation in polytetrafluoroethylene composites. J. Tribol. 2022, 144, 091701. [Google Scholar] [CrossRef]
- Song, J.; Lei, H.; Zhao, G. Improved mechanical and tribological properties of polytetrafluoroethylene reinforced by carbon nanotubes: A molecular dynamics study. Comput. Mater. Sci. 2019, 168, 131–136. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, X.; Kuang, F.; Zuo, H.; Huang, J. Mechanical and tribological properties of nitrile rubber reinforced by nano-SiO2: Molecular dynamics simulation. Tribol. Lett. 2021, 69, 54. [Google Scholar] [CrossRef]
- Song, J.; Zhao, G.; Ding, Q.; Yang, Y. Molecular dynamics study on the thermal, mechanical and tribological properties of PBI/PI composites. Mater. Today Commun. 2022, 30, 103077. [Google Scholar] [CrossRef]
- Liu, X.; Huang, J.; Yang, C.; Xing, S.; Wang, P.; Zhou, X. Molecular dynamics simulations probing the effects of interfacial interactions on the tribological properties of nitrile butadiene rubber/nano-SiO2 under water lubrication. Mater. Today Commun. 2022, 32, 104165. [Google Scholar] [CrossRef]
- Liu, D.; Li, H.; Huo, L.; Wang, K.; Sun, K.; Wei, J.; Chen, F. Molecular dynamics simulation of the lubricant conformation changes and energy transfer of the confined thin lubricant film. Chem. Eng. Sci. 2023, 270, 118541. [Google Scholar] [CrossRef]
- He, E.; Wang, S.; Tang, L.; Chen, J. A study on the enhancement of the tribological properties of nitrile-butadiene rubber reinforced by nano-ZnO particles from an atomic view. Mater. Res. Express 2021, 8, 095009. [Google Scholar] [CrossRef]
- von Goeldel, S.; Reichenbach, T.; König, F.; Mayrhofer, L.; Moras, G.; Jacobs, G.; Moseler, M. A combined experimental and atomistic investigation of PTFE double transfer film formation and lubrication in rolling point contacts. Tribol. Lett. 2021, 69, 136. [Google Scholar] [CrossRef]
- Cheng, G.; Chen, B.; Guo, F.; Xiang, C.; Jia, X. Research on the friction and wear mechanism of a polymer interface at low temperature based on molecular dynamics simulation. Tribol. Int. 2023, 183, 108396. [Google Scholar] [CrossRef]
- Li, C.; Liu, Z.; Huo, Y.; Li, F.; Tang, L. Molecular dynamics simulation of mechanical and tribological properties of nitrile butadiene rubber with different length and content carbon nanotubes. Mater. Today Commun. 2023, 36, 106693. [Google Scholar] [CrossRef]
- Xu, M.; Wang, X.; Wang, T.; Wang, Q.; Li, S. Ag nanoparticle decorated graphene for improving tribological properties of fabric/phenolic composites. Tribol. Int. 2022, 176, 107889. [Google Scholar] [CrossRef]
- Qiang, Y.; Wu, W.; Lu, J.; Jiang, B.; Ziegmann, G. Progressive molecular rearrangement and heat generation of amorphous polyethene under sliding friction: Insight from the united-atom molecular dynamics simulations. Langmuir 2020, 36, 11303–11315. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Li, J.; Tang, X.; Yang, W.; Chen, X.; Fan, C.; Wang, K. Molecular dynamics study on the tribological properties of phosphorene/polyethylene composites. Coatings 2019, 9, 342. [Google Scholar] [CrossRef]
- Wu, W.; He, C.; Qiang, Y.; Peng, H.; Zhou, M. Polymer-metal interfacial friction characteristics under ultrasonic plasticizing conditions: A united-atom molecular dynamics study. Int. J. Mol. Sci. 2022, 23, 2829. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, J.; Cui, J.; Jiang, B. Enhanced mechanical and tribological properties of polymer nanocomposites by improving interfacial properties by hexagonal boron nitride nanosheets: Molecular dynamics simulations. J. Appl. Polym. Sci. 2023, 140, e54340. [Google Scholar] [CrossRef]
- Hu, C.; Qi, H.; Song, J.; Zhao, G.; Yu, J.; Zhang, Y.; He, H.; Lai, J. Exploration on the tribological mechanisms of polyimide with different molecular structures in different temperatures. Appl. Surf. Sci. 2021, 560, 150051. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wang, Q.; Xing, M. Molecular dynamics simulations of tribology properties of NBR (Nitrile-Butadiene Rubber) /carbon nanotube composites. Compos. Part B Eng. 2016, 97, 62–67. [Google Scholar] [CrossRef]
- Zhan, S.; Xu, H.; Duan, H.; Pan, L.; Jia, D.; Tu, J.; Liu, L.; Li, J. Molecular dynamics simulation of microscopic friction mechanisms of amorphous polyethylene. Soft Matter 2019, 15, 8827–8839. [Google Scholar] [CrossRef] [PubMed]
- He, E.; Wang, S.; Li, Y.; Wang, Q. Enhanced tribological properties of polymer composites by incorporation of nano-SiO2 particles: A molecular dynamics simulation study. Comput. Mater. Sci. 2017, 134, 93–99. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Wang, Q. Enhancement of tribological properties of polymer composites reinforced by functionalized graphene. Compos. Part B Eng. 2017, 120, 83–91. [Google Scholar] [CrossRef]
- Chen, Y.; Renner, P.; Liang, H. A review of current understanding in tribochemical reactions involving lubricant additives. Friction 2022, 11, 489–512. [Google Scholar] [CrossRef]
- Xu, Q.; Tang, X.; Zhang, J.; Hu, Y.; Ma, T. Unraveling tribochemistry and self-Lubrication mechanism of polytetrafluoroethylene by reactive coarse-grained molecular dynamics simulations. ACS Appl. Mater. Interfaces 2023, 15, 45506–45515. [Google Scholar] [CrossRef] [PubMed]
- Katsukawa, R.; Van Sang, L.; Tomiyama, E.; Washizu, H. High-Pressure Lubrication of Polyethylethylene by Molecular Dynamics Approach. Tribol. Lett. 2022, 70, 101. [Google Scholar] [CrossRef]
- Zheng, T.; Gu, J.; Zhang, Y.; Zhang, H. Evolution of the microstructure of amorphous polyethylene under friction-induced plastic flows: A reactive molecular investigation. J. Chem. Phys. 2023, 159, 104309. [Google Scholar] [CrossRef]
- Onodera, T.; Kawasaki, K.; Nakakawaji, T.; Higuchi, Y.; Ozawa, N.; Kurihara, K.; Kubo, M. Tribocatalytic Reaction of Polytetrafluoroethylene Sliding on an Aluminum Surface. J. Phys. Chem. C 2015, 119, 15954–15962. [Google Scholar] [CrossRef]
- Zheng, F.; Lv, M.; Wang, Q.; Wang, T. Effect of temperature on friction and wear behaviors of polyimide (PI)-based solid-liquid lubricating materials. Polym. Adv. Technol. 2015, 26, 988–993. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Y.; Guo, P.; Cui, L.; Wang, A.; Ke, P. Tribological behavior of Cr/a-C multilayered coating against PEEK under dry sliding condition. Wear 2023, 518–519, 204625. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, J.; Li, X.; van Duin, D.M.; Hu, Y.; van Duin, A.C.T.; Ma, T. How polytetrafluoroethylene lubricates iron: An atomistic view by reactive molecular dynamics. ACS Appl. Mater. Interfaces 2022, 14, 6239–6250. [Google Scholar] [CrossRef] [PubMed]
- Pan, D.; Wang, H.; Sun, L.; Zhu, K.; Hao, X. Effect of temperature on Fe–polytetrafluoroethylene friction coefficient using molecular dynamics simulation. Tribol. Trans. 2022, 65, 705–715. [Google Scholar] [CrossRef]
- Brownell, M.; Nair, A.K. Deformation mechanisms of polytetrafluoroethylene at the nano- and microscales. Phys. Chem. Chem. Phys. 2018, 21, 490–503. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.K.; Kang, C.; Ilg, P.; Crockett, R.; Kroger, M.; Spencer, N.D. Combined experimental and simulation studies of cross-linked polymer brushes under shear. Macromolecules 2018, 51, 10174–10183. [Google Scholar] [CrossRef] [PubMed]
- Erbas, A.; Paturej, J. Friction between ring polymer brushes. Soft Matter 2015, 11, 3139–3148. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Kröger, M.; Spencer, N.D. Effect of Crosslinking on the Microtribological Behavior of Model Polymer Brushes. Tribol. Lett. 2016, 63, 17. [Google Scholar] [CrossRef]
- Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Spencer, N.D.; Kroger, M. Influence of chain stiffness, grafting density and normal load on the tribological and structural behavior of polymer brushes: A nonequilibrium-molecular-dynamics study. Polymers 2016, 8, 254. [Google Scholar] [CrossRef]
- van der Weg, K.J.; Ritsema van Eck, G.C.; de Beer, S. Polymer brush friction in cylindrical geometries. Lubricants 2019, 7, 84. [Google Scholar] [CrossRef]
- Munetoh, S.; Motooka, T.; Moriguchi, K.; Shintani, A. Interatomic potential for Si–O systems using Tersoff parameterization. Comput. Mater. Sci. 2007, 39, 334–339. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, T.; Wang, G.; Guo, Z.; Pan, Y.; Song, J.; Ding, Q.; Zhao, G. Molecular Dynamics Simulation on Polymer Tribology: A Review. Lubricants 2024, 12, 205. https://doi.org/10.3390/lubricants12060205
Yin T, Wang G, Guo Z, Pan Y, Song J, Ding Q, Zhao G. Molecular Dynamics Simulation on Polymer Tribology: A Review. Lubricants. 2024; 12(6):205. https://doi.org/10.3390/lubricants12060205
Chicago/Turabian StyleYin, Tianqiang, Guoqing Wang, Zhiyuan Guo, Yiling Pan, Jingfu Song, Qingjun Ding, and Gai Zhao. 2024. "Molecular Dynamics Simulation on Polymer Tribology: A Review" Lubricants 12, no. 6: 205. https://doi.org/10.3390/lubricants12060205
APA StyleYin, T., Wang, G., Guo, Z., Pan, Y., Song, J., Ding, Q., & Zhao, G. (2024). Molecular Dynamics Simulation on Polymer Tribology: A Review. Lubricants, 12(6), 205. https://doi.org/10.3390/lubricants12060205






