Multi-Objective Optimization of Tribological Characteristics for Aluminum Composite Using Taguchi Grey and TOPSIS Approaches

Abstract

In this study, a multi-objective optimization regarding the tribological characteristics of the hybrid composite with a base material of aluminum alloy A356 as a constituent, reinforced with a 10 wt.% of silicon carbide (SiC), size 39 µm, and 1, 3, and 5 wt.% graphite (Gr), size 35 µm, was performed using the Taguchi method, gray relational analysis (GRA), and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) decision-making methods. Tribological tests were carried out on a “block on disc” type tribometer with lubrication. Load, sliding speed, and graphite mass concentration were analyzed as input parameters. As output parameters, wear rate and coefficient of friction were calculated. An analysis of variance (ANOVA) was conducted to identify all parameters that have a significant influence on the output multi-response. It was found that the normal load has the highest influence of 41.86%, followed by sliding speed at 32.48% and graphite addition at 18.47%, on the tribological characteristics of composites. Multi-objective optimization determined that the minimal wear rate and coefficient of friction are obtained when the load is 40 N, the sliding speed is 1 m/s, and the composite contains 3 wt.% Gr. The optimal combination of parameters achieved by GRA was also confirmed by the TOPSIS method, which indicates that both methods can be used with high reliability to optimize the tribological characteristics. The analysis of worn surfaces using scanning electron microscopy revealed adhesive and delamination wear as dominant mechanisms.

1. Introduction

Aluminum-based composites are used first as a substitute for standard materials like cast iron and gray cast iron. Aluminum-based composites reinforced with micro- and nano-sized particles provide appropriate characteristics for applications in the aerospace, automotive, military, and electronics industries, specifically due to their improved physical and mechanical properties.

Aluminum alloys and composites are also used in the production of highly responsible automotive components such as engine blocks, pistons, cylinders, brake discs, crankshafts, camshafts, and other parts [1,2,3,4,5]. These materials are expected to have good mechanical and tribological characteristics. Hybrid composites are materials that have two or more reinforcements and/or improvers in their composition. SiC, Al₂O₃, B₄C, and TiC are most often used as reinforcements, and Gr and MoS₂ as improvers [6,7,8]. Depending on the size of the reinforcement and/or improver, composites are divided into micro- and nanocomposites. Nanocomposites are composites where the size of the least one reinforcement is at the nano-level [3]. The tribological characteristics of hybrid composites based on A356 reinforced with 10 wt.% SiC and 1, 3, and 5 wt.% graphite obtained by composite casting were analyzed within the scope of the paper.

Tribological tests of hybrid composites determined the wear rate and the coefficient of friction of all analyzed composites according to the defined experimental plan. Given that the results of the experiment are the wear rate and the coefficient of friction, several methods were applied to select the optimal combination of parameters in order to obtain the lowest wear rate and the coefficient of friction. For this purpose, a combination of gray relational analysis (GRA) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) methods was used.

Recently, the application of the Taguchi method, GRA, and Topsis has received increasing attention and has become extremely relevant in various research fields. These methods have proven to be extremely effective tools for process optimization, decision-making, and product quality improvement [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].

The Taguchi method is known to be applied with great success for system optimization when considering a single response output. Due to this limitation, the Taguchi method is combined with GRA, which is intended for multi-response optimization. The TOPSIS method is used in the process of optimizing a process or product in order to obtain the best solutions and, in this case, to check the achieved combination using GRA analysis.

Raghavendra et al. optimized wear parameters and surface roughness on composite coatings using response surface methodology (RSM) based GRA [9]. Analysis of variance (ANOVA) analysis found that normal load has the greatest influence on wear rate and pin temperature, which are 36.88% and 61.26%, respectively. They also determined the optimal variant of the parameters based on the GRG rank. They found that the application of the RSM and GRA methods is very successful in the optimization of wear parameters.

The application of GRA in optimizing wear parameters (wear rate and friction coefficient) has proven to be highly successful in the research conducted by Muthu on LM25/SiC/Cu hybrid metal composites. The ANOVA analysis results help to conclude that sliding velocity affects the multi-performance characteristics of the LM25/SiC/Cu composite the most, with 44.08%, followed by load at 28.14% and sliding distance at 27.53% [10]. Alagarsamy et al. predicted the wear behavior of AA7075-TiO₂ composites under lubrication-free conditions by means of Taguchi-based GRA. They observed the influence of TiO₂ particle content of 0, 5, 10, and 15 wt.%, then load (9.81, 19.62, 29.43, and 39.24 N), sliding speed (0.94, 1.88, 2.82, and 3.76 m/s), and sliding distance (500, 1000, 1500 and 2000 m). On the basis of the applied analyses, we came to the optimal variant of the wear parameters, which is that reinforcement is 15 wt.%, the applied load is 9.81 N, the sliding speed is 3.76 m/s, and the sliding distance is 1000 m. Also, they determined the percentage impact on the multi-performance characteristics, where the TiO₂ particle content parameter of 69.035% and then the load of 26.289% are singled out [11]. Balu Mahandiran et al. considered three parameters, namely sliding speed, load, and sliding distance, on the friction and wear of the Al6061/SiC composite. They used GRA analysis to assess optimal process parameters, while ANOVA analysis identified significant and insignificant parameters. The optimal parameters are a sliding distance of 500 m, a load of 10 N, and a sliding speed of 4 m/s. They determined that the applied load was the most important factor, and the optimized mathematical model, using GRA analysis, showed a high accuracy compared to the experimental data, amounting to 99.94% [12].

Taguchi and GRA techniques were effective in optimizing the parameters of the AA356/Al₂O₃/SiC composite reinforced with from 0 to 8 wt.% in a 2 wt.% step along with a constant 3 wt.% of graphite, leading to five composite samples. A hybrid composite that has an equal presence of both ceramic particles tends to optimize the overall performance criteria of the composite [13].

Konada et al. combined TOPSIS and Artificial Neural Network (ANN) methods to study the specific wear rate and coefficient of friction on bronze fiber-reinforced brake pads. The results obtained by the experiments were additionally confirmed using the ANN technique. The TOPSIS technique is used to predict the best combination of parameters in order to achieve less wear and the desired coefficient of friction of the tested materials. In addition to testing tribological characteristics, they also performed density, heat conductivity, and compressibility tests. Scanning electron microscope (SEM) and Energy Dispersive X-ray Spectroscopy (EDX) analyses were performed to better understand the grain distribution and chemicals present in each sample. The results showed that the inclusion of bronze fibers in the composite gave excellent performance. Also, they established which of the tested materials has the lowest wear rate and the desired coefficient of friction, which is considered the material with the best characteristics, as proven by SEM and EDX analysis [14].

Rathod et al. and others used Taguchi and TOPSIS to find optimum process parameters for turning SS304 using coated carbide tools. The cutting speed, feed rate, and depth of cut were taken into account. This improves tool life while reducing production time and surface roughness. The results showed that the proposed strategy is suitable for solving multi-objective process parameter improvements. A cutting speed of 350 m/min, a feed rate of 0.12 mm/rev, and a depth of cut of 0.40 mm were found to be the best combination of process specifications [15].

Bhaskar et al. applied the TOPSIS method to determine the criteria for the mechanical, tribological, and thermomechanical characteristics of the AA2024-SiC composite (0, 2, 4, and 6 wt.%) in order to obtain a composite of a certain composition [16]. Prathap Singh et al. [17] investigated the aluminum functionally graded metal matrix composite (Al-FGMMC) reinforced with SiC particles. The optimization of the parameters of the drilling operation was carried out with the help of the TOPSIS technique. The TOPSIS method was also used to find the optimal cutting parameters (speed, feed, point angle, and zone distance), which are very important for operational characteristics; the initial study was to investigate the final process of obtaining the AA6082 composite with 3% SiC and 2% aluminum powder [18].

Jamwal et al. investigated copper–SiC–graphite metal matrix hybrid composites produced by the liquid-stir casting process by observing the composite microstructure as well as mechanical and tribological characteristics [19]. The results show that the density of the composite begins to decrease with increasing reinforcement content. The ultimate tensile strength and wear resistance of the copper-based composites improved by including more reinforcements. The TOPSIS methodology was adopted and successfully applied to optimize the physical and mechanical properties of Cu-MMC.

Kannan et al. produced aluminum composites with micro-sized particles (1, 2, wt.%) of Al₂O₃ as reinforcements and nano-sized (5.5, 7 wt.%) Al₂O₃ using stir-squeeze casting. Using the experimental design, they created the L9 matrix for experimental tests. They applied ANOVA analysis to the experimental results in order to determine the influence of the observed parameters, and they found that the most influential is load (62.33%), followed by reinforcement content (19.40%). Using the TOPSIS method, they determined the optimal combination of parameters for obtaining the surface roughness coefficient of friction and wear [20].

In recent years, researchers have increasingly combined different methods in order to achieve optimal solutions and verify the obtained results. This enables more reliable research results through the use and combination of different techniques, which increases the reliability and relevance of the obtained results [21,22,23,24,25]. The application of the GRA and TOPSIS methods was observed when optimizing the turning process parameters of a nickel-based alloy in the research conducted by Mastan Rao et al. By applying these methods, based on the conducted experimental research and analysis of the results, they concluded that there were reductions in surface roughness (SR), tool wear rate (TW), and material removal rate (MRR) by 12.6%, 6.81%, and 44.21%, respectively. At the end of the paper, the comparative results achieved using the TOPSIS method and GRA were presented, indicating the advantages and limitations of each method in achieving the desired optimization because the optimal variants are different using these methods [21]. In the research that dealt with the impact of friction-induced noise arising during steel-on-steel sliding under sesame grease lubrication, conducted by John and Hanief, applying GRA and TOPSIS resulted in the same optimal factor variant. They observed the influence of sliding frequency (10, 20, and 30 Hz) and load (10, 20, and 30 N) on the frictional noise using the L18 Taguchi matrix. ANOVA analysis found that 80.8% is influenced by the test condition, while the load is 13.27% [22].

Alagarsamy et al. optimized the parameters of the electrical discharge machining (EDM) process, which are of great importance in the machining of materials. Experiments were conducted using the L27 Taguchi matrix to analyze various characteristics with the aim of maximizing material removal rate (MRR) and minimizing tool wear rate (TWR) using Taguchi and TOPSIS methodologies [23]. The successful application of optimization methods was recorded in the optimization of parameters during friction stir welding (FSW) processing as well as during friction stir processing (FSP) using ANN, TOPSIS, RSM, and non-dominated sorting genetic algorithm-II (NSGA-II) methods [24,25]. Akbari et al. confirmed the relationship between the parameters, microstructure, and mechanical characteristics of the composite using the ANN method [24]. Akbari et al., using a developed mathematical model that relies on multi-criteria optimization, identified optimal parameter values. They also identified key parameters that have a significant impact on temperature, force, and failure load, which will be of great importance for future research [25]. Based on all the above, it can be established that the application of optimization methods is of great importance for many researchers, regardless of the field of their application. They enable quick access to important information while simultaneously saving resources such as time and money. This approach is of great importance in industry, especially in areas such as the production and processing of new materials, where the speed and efficiency of research are directly reflected in competitiveness and innovation.

In this paper, the influence of parameters, i.e., load, sliding speed, and mass content of graphite, on the tribological characteristics, i.e., wear rate and coefficient of friction, of aluminum composites produced by the compocasting process was studied. The Taguchi method and the TOPSIS approach were used to predict the optimal choice of the considered parameters with the aim of minimizing their tribological characteristics. Moreover, ANOVA was applied to evaluate the significant influence of each parameter on a single response and then a multi-response. The best parameter values were determined by evaluating the combined effects of these factors on the multi-responses. In this paper, the main motivation is to determine the tribological behavior of A356-based composite materials reinforced with Gr particles with different mass contents prepared by the stir casting process and to investigate its dry sliding wear behavior using Taguchi Gray and TOPSIS methods.

2. Experimental Details

2.1. Fabrication of Composite, Chemical Composition, and Microstructure

A356 alloy is an Al-Si alloy that has very good mechanical characteristics, high resistance to wear and corrosion, exceptional ductility, and good weldability and machinability. The chemical composition of A356 alloy is given in

Table 1. Chemical composition of the A356 alloy.

Chemical Composition	Si	Cu	Mg	Mn	Fe	Zn	Ni	Ti	Al
Percentage share (wt.%)	7.20	0.02	0.25	0.01	0.18	0.01	0.02	0.11	Rest

.

Tribological tests were carried out for the hybrid composite with A356 as the base material and included a reinforcement content of 10 wt.% SiC with a particle size of 39 µm and reinforcement of 1, 3, and 5 wt.% Gr with a particle size of 35 µm, which were produced by the composite casting process. The selected types and sizes of reinforcing particles were made on the basis of previous analyses of the literature data, and then certain trial tests were performed; finally, it was decided which composition and which type of reinforcement would be used. A detailed analysis of the above can be found in [26]. A more detailed description of the procedure for obtaining the mentioned materials can be found in the literature [27,28]. Figure 1 shows the microstructures of hybrid composites with 1, 3, and 5 wt.% content of Gr reinforcement.

It can be seen that the base is well-filled with reinforcing particles; that is, the surface of the base without particles is reduced, which indicates a fairly favorable distribution of SiC particles in the base A356 alloy. During mixing, the SiC particles, in addition to the liquid phase, were also distributed in the area of the solid phase of the semi-solidified melt. In addition, silicon nodules are visible around the SiC particles. Soft graphite particles did not retain their average size (35 µm) during the process of obtaining the composite. Specifically, in the preparation process, mixing with SiC particles resulted in their pulverization. The comminution of these particles continued with mixing during the composting process.

2.2. Wear Test

The tests were performed at the University of Kragujevac Faculty of Engineering, in the Center for Tribology, on the TR-95 tribometer. The tribometer with a suitable contact pair is shown in Figure 2. The tribological research was carried out on a tribometer with a geometric characteristic block on disk type, with precisely defined conditions following wear rate (WR) and coefficient of friction (CoF). The material of the contact pair is 90MnCrV8 steel with a hardness of 62–64 HRC and tested composites (A356/10 wt.% SiC/1, 3 and 5 wt.% Gr) for the disc and block, respectively.

For all tests, the same hydraulic oil was used, which, according to the ISO 11158:2023 standard [29], corresponds to type HL, category HM, viscosity grade ISO VG 46. The oil is located in the tank, and lubrication is performed by submerging the disk with its lower part to a depth of 3 mm in the tank with an oil volume of 30 mL.

2.3. Design of Experiments and Experimental Results

The choice of optimal process parameters is very important when studying new materials, specifically when studying the tribological characteristics of aluminum composites. In this research, three parameters were selected, which represented the input parameters, namely load (A), sliding speed (B), and graphite content (C) in the A356 base material.

Table 2. Process parameters and their levels.

Name of Parameters	Unit	Level 1	Level 2	Level 3
A: Normal load	N	40	80	120
B: Siding speed	m/s	0.25	0.5	1
C: Gr addition	wt.%	1	3	5

shows selected parameters on three levels. Based on the Taguchi method, which included the standard orthogonal matrix, it was adopted as the L27 matrix (

Table 3. Experimental and S/N ratio results.

No.	A	B	C	WR, ×10−3 mm3/m	CoF	S/N Ratios for WR, dB	S/N Ratios for CoF, dB
1.	40	0.25	1	0.325	0.104	9.7623	19.6593
2.	40	0.25	3	0.174	0.082	15.1890	21.7237
3.	40	0.25	5	0.204	0.097	13.8074	20.2646
4.	40	0.50	1	0.252	0.098	11.9720	20.1755
5.	40	0.50	3	0.141	0.063	17.0156	24.0132
6.	40	0.50	5	0.168	0.071	15.4938	22.9748
7.	40	1.00	1	0.201	0.086	13.9361	21.3100
8.	40	1.00	3	0.120	0.052	18.4164	25.6799
9.	40	1.00	5	0.151	0.065	16.4205	23.7417
10.	80	0.25	1	0.373	0.120	8.5658	18.4164
11.	80	0.25	3	0.232	0.105	12.6902	19.5762
12.	80	0.25	5	0.286	0.113	10.8727	18.9384
13.	80	0.50	1	0.285	0.104	10.9031	19.6593
14.	80	0.50	3	0.202	0.081	13.8930	21.8303
15.	80	0.50	5	0.236	0.102	12.5418	19.8280
16.	80	1.00	1	0.215	0.091	13.3512	20.8192
17.	80	1.00	3	0.168	0.065	15.4938	23.7417
18.	80	1.00	5	0.195	0.077	14.1993	22.2702
19.	120	0.25	1	0.488	0.130	6.2316	17.7211
20.	120	0.25	3	0.435	0.118	7.2302	18.5624
21.	120	0.25	5	0.472	0.125	6.5212	18.0618
22.	120	0.50	1	0.338	0.115	9.4217	18.7860
23.	120	0.50	3	0.297	0.103	10.5449	19.7433
24.	120	0.50	5	0.385	0.117	8.2908	18.6363
25.	120	1.00	1	0.245	0.097	12.2167	20.2646
26.	120	1.00	3	0.198	0.073	14.0667	22.7335
27.	120	1.00	5	0.307	0.103	10.2572	19.7433

). This implies that it is necessary to conduct 27 experiments in order to determine the optimal levels of each parameter. All experiments were repeated five times, and the mean values of the experimental results are shown in Table 3.

The realization of the planned experiment enables the precise identification of key combinations of parameters that will minimize the analyzed tribological characteristics of aluminum composites.

After the experiment, the results were analyzed in order to optimize the parameters for improving the tribological characteristics of the composite. As mentioned above, three methods are used to realize the results: the Taguchi method, the GRA method, and the TOPSIS method.

In the Taguchi method, the signal-to-noise ratio (S/N) was used to analyze the experimental results. By using the S/N ratio, a summary statistical evaluation is achieved that combines information about mean values and variances into one performance. In this way, the S/N ratio gives an optimal combination of parameter levels, where the variance is minimal while the mean value is close to the target value. The Taguchi method requires the transformation of experimental results into S/N ratios. Generally, three types of quality characteristics are possible to evaluate the S/N ratio: the smaller the better, nominal the better, and larger the better. Depending on the defined and desired output goals, the appropriate quality characteristics are selected [30,31]. Since we require a minimum WR and a minimum CoF for this study, smaller, better characteristics were selected for both outputs in Equation (1).

$$\mathrm{S}/\mathrm{N}=-10log\left(\frac{1}{n}\sum _{i=1}^n{y_i}^2\right),$$

(1)

where$y_i$—i-output value and $n$—number of experiments. Minitab 20 software was used for statistical analysis of the obtained experimental results.

2.4. Analysis of S/N Ratios and ANOVA

This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, and the experimental conclusions that can be drawn.

The interpretation of the S/N ratio results does not depend on the selected quality characteristic. The ideal setting of the parameters is achieved by taking into account a higher S/N ratio, which corresponds to better quality characteristics, that is, a smaller variance of the output characteristic around the target (desired) value [30,31]. The results achieved by analyzing the S/N ratio are shown in

Table 4. Response table for signal-to-noise ratio for WR and CoF.

	WR			CoF
Level	A	B	C	A	B	C
1	14.668	10.097	10.707	22.17	19.21	19.65
2	12.501	12.231	13.838	20.56	20.63	21.96
3	9.420	14.262	12.045	19.36	22.26	20.50
Delta	5.248	4.165	3.131	2.81	3.04	2.31
Rank	1	2	3	2	1	3

, where it can be seen that the first ranked parameter for WR is normal load, while for CoF, the parameter is siding speed. The Gr addition parameter is ranked third for both outputs, which means it has the least impact on WR and CoF. Parameter ranking is determined based on delta values (

Table 5. Analysis of variance for WR and CoF.

	Source	DF	Seq SS	Adj SS	Adj MS	F Value	p Value	% Age Contribution
WR	A	2	125.191	125.191	62.5957	257.00	0.000	45.92	(R-Sq) 99.29%; R-Sq(adj) 97.68%
	B	2	78.088	78.088	39.0442	160.31	0.000	28.64
	C	2	44.425	44.425	22.2126	91.20	0.000	16.29
	A*B	4	4.304	4.304	1.0760	4.42	0.035	1.5
	A*C	4	16.311	16.311	4.0779	16.74	0.001	5.98
	B*C	4	2.367	2.367	0.5919	2.43	0.133	0.87
	Residual Error	8	1.948	1.948	0.2436			0.71
	Total	26	272.636					100.00
CoF	A	2	35.779	35.7789	17.8894	67.24	0.000	31.92	(R-Sq) 98.10%; R-Sq (adj) 93.83%
	B	2	41.718	41.7180	20.8590	78.40	0.000	37.22
	C	2	24.579	24.5786	12.2893	46.19	0.000	21.93
	A*B	4	0.823	0.8228	0.2057	0.77	0.572	0.73
	A*C	4	4.234	4.2335	1.0584	3.98	0.046	3.78
	B*C	4	2.826	2.8263	0.7066	2.66	0.112	2.52
	Residual Error	8	2.129	2.1285	0.2661			1.90
	Total	26	112.087					100.00

DF—degree of freedom; Seq SS—sequential sum of square; Adj SS—adjacent sum of square; Adj MS—adjacent sum of mean square; F value—variance; p value—test statistics.

), while bold values represent the best combination of parameters for WR and CoF. Based on Table 4, it can be established that the optimal combination of parameters to achieve the minimum WR is the following: normal load of 40 N (level 1), siding speed of 1 m/s (level 3), and 3 wt.% Gr (level 2). It is observed that the same combination of parameters achieves the minimum CoF. A more precise analysis regarding the influence of the characteristic parameters (normal load, siding speed, and Gr addition) on wear rate and coefficient of friction was performed using ANOVA. ANOVA analysis was conducted at a 95% confidence level, and the results for WR and CoF are given in Table 5.

When analyzing the percentage of the individual influence of each parameter (Table 5), it can be concluded that the normal load has the largest impact on WR at 45.92%, followed by the sliding distance at 28.64% and Gr content at 16.29%. Observing the individual influences of each parameter on CoF, it is concluded that there is a smaller difference between the first and second parameters compared to the influence on WR; more precisely, the biggest influence has a sliding speed of 37.22%, followed by a normal load of 31.92%. The Gr addition parameter, with 21.93%, has a greater influence on CoF compared to the influence of this parameter on WR. Interactions between parameters whose p-values are above 0.05 are statistically insignificant. Based on the analysis, it is concluded that the interaction of A*B and A*C on WR and the interaction of parameters A*C on CoF should be taken into account when analyzing the tribological characteristics of the composite material.

2.5. Multi-Response Optimization

Solving the complexity of many processes can be effectively achieved using multi-objective optimization, or GRA. It is known that the Taguchi method cannot be directly used to optimize multi-output problems, so it is combined with other optimization methods. In the case of multi-output process optimization, Taguchi’s method is combined with gray relational analysis. GRA analysis, in conjunction with the Taguchi method, represents a newer methodology for multi-objective optimization known as the Taguchi–grey method [32,33,34,35,36]. The advantage of this technique is that multiple responses can be converted into one gray relation grade (GRG). A significant advantage of the GRA technique is the possibility of generating satisfactory results using a relatively small amount of data.

The flow of optimization in GRA analysis consists of the following steps: (1) normalization of experimental results; (2) calculation of deviations from normalized data; (3) calculation of gray relation coefficients, GRC; and (4) calculation of gray relation grade, GRG. The normalization of experimental data ranges from 0 to 1, depending on the expected nature of the output values. There are three types of normalization: “less is better”, “larger is better”, and “nominal is better”. In this research, the characteristic “less is better” was applied for both outputs, where the smallest values of the objective function were expected. Normalization for this characteristic is calculated according to Equation (2), and the results are shown in

Table 6. Results of the GRG analysis.

No.	Normalized, WR	Normalized, CoF	GRC (WR)	GRC (CoF)	GRG	Rang
1.	0.4429	0.3333	0.4730	0.4286	0.4555	21
2.	0.8533	0.6154	0.7731	0.5652	0.6912	6
3.	0.7717	0.4231	0.6866	0.4643	0.5990	11
4.	0.6413	0.4103	0.5823	0.4588	0.5336	16
5.	0.9429	0.8590	0.8976	0.7800	0.8512	2
6.	0.8696	0.7564	0.7931	0.6724	0.7455	5
7.	0.7799	0.5641	0.6943	0.5342	0.6312	10
8.	1.0000	1.0000	1.0000	1.0000	1.0000	1
9.	0.9158	0.8333	0.8558	0.7500	0.8141	3
10.	0.3125	0.1282	0.4211	0.3645	0.3988	23
11.	0.6957	0.3205	0.6216	0.4239	0.5437	15
12.	0.5489	0.2179	0.5257	0.3900	0.4722	19
13.	0.5516	0.3333	0.5272	0.4286	0.4883	17
14.	0.7772	0.6282	0.6917	0.5735	0.6451	9
15.	0.6848	0.3590	0.6133	0.4382	0.5443	13
16.	0.7418	0.5000	0.6595	0.5000	0.5966	12
17.	0.8696	0.8333	0.7931	0.7500	0.7761	4
18.	0.7962	0.6795	0.7104	0.6094	0.6706	8
19.	0.0000	0.0000	0.3333	0.3333	0.3333	27
20.	0.1440	0.1538	0.3687	0.3714	0.3698	25
21.	0.0435	0.0641	0.3433	0.3482	0.3452	26
22.	0.4076	0.1923	0.4577	0.3824	0.4280	22
23.	0.5190	0.3462	0.5097	0.4333	0.4796	18
24.	0.2799	0.1667	0.4098	0.3750	0.3961	24
25.	0.6603	0.4231	0.5955	0.4643	0.5438	14
26.	0.7880	0.7308	0.7023	0.6500	0.6817	7
27.	0.4918	0.3462	0.4960	0.4333	0.4713	20

.

This is example 1 of an equation:

$$x_i\left(k\right)=\frac{max{y}_i\left(k\right)-y_i\left(k\right)}{max{y}_i\left(k\right)-min{y}_i\left(k\right)},$$

(2)

where$k$—number of exits,$i$—number of experiments,$max{y}_i\left(k\right)$—maximal experimental value for k-exit, and $min{y}_i\left(k\right)$—minimal experimental value for k-exit.

To calculate the GRC, it is necessary to first calculate the absolute values of the difference using the normalized values ${\Delta }_{0i}$ according to the equation:

$${\Delta }_{0i}=\Vert x_0\left(k\right)-x_i\left(k\right)\Vert ,$$

(3)

where $x_0\left(k\right)$—reference normalized value $(x_0\left(k\right)=1)$. After obtaining the absolute value of the difference, the gray relational coefficient is calculated according to the equation:

$${\xi }_i\left(k\right)=\frac{{\Delta }_{min}+\phi {\Delta }_{max}}{{\Delta }_{0i}\left(k\right)+\phi {\Delta }_{max}},$$

(4)

where${\Delta }_{min}$ and ${\Delta }_{max}$—the minimal and maximal absolute values of the difference; $\phi$—coefficient of difference, $0\le \phi \le 1$.

In this research, the impact of each output on the process characteristic is calculated using weighting coefficients. Weighting coefficients are obtained based on S/N using Equation (5):

$$w_k=\frac{{\sum }_{j=1}^p{Delta}_{i,j}}{{\sum }_{i=1}^m{\sum }_{j=1}^p{Delta}_{i,j}}.$$

(5)

By calculating the weight coefficients, it is possible to obtain more realistic values of GRG $\left({\gamma }_i\right)$ using Equation (6):

$${\gamma }_i=\sum _{k=1}^n{w_k\xi }_i\left(k\right).$$

(6)

In this way, multi-output problems are converted into single-output problems. The general performance characteristic for the multiple response process depends on the estimated GRG. The higher the value of GRG, the closer it will be to the optimum. Setting the optimal parameter values can be performed using the Taguchi method to maximize GRG.

2.6. Results and Discussion of the GRA Analysis

Determining the value of weighting coefficients on multiple responses (WR and CoF) is crucial for achieving realistic results in GRA analysis. Based on the analysis of the S/N ratio, the weight coefficients for WR and CoF were obtained, which are 0.6059 and 0.3941, respectively. Based on the weighting coefficients and Equation (6), the final equation for GRG was postulated:

$$GRG=0.6059·{GRC}_{WR}+0.3941·{GRC}_{CoF},$$

(7)

where${GRC}_{WR}$—gray relational coefficient of wear rate, and ${GRC}_{CoF}$—gray relational coefficient of the coefficient of friction.

The results of the gray relational analysis are presented in Table 6. In order to facilitate the interpretation of the results, GRG is ranked and shown in the last column of Table 6. ANOVA analysis is used for further optimization.

In order to determine the optimal levels of the parameter, the ANOVA analysis was performed at the 95% confidence level. The results of the ANOVA analysis are presented in

Table 7. Analysis of variance for GRG.

Source	DF	Seq SS	Adj SS	Adj MS	F Value	p Value	% Age Contribution
A	2	67.101	67.1011	33.5506	227.48	0.000	41.86	(R-Sq) 99.26%; R-Sq(adj) 97.61%
B	2	52.062	52.0623	26.0312	176.50	0.000	32.48
C	2	29.542	29.5419	14.7709	100.15	0.000	18.43
A*B	4	1.339	1.3390	0.3348	2.27	0.151	0.84
A*C	4	8.176	8.1763	2.0441	13.86	0.001	5.10
B*C	4	0.904	0.9035	0.2259	1.53	0.281	0.56
Residual Error	8	1.180	1.1799	0.1475			0.74
Total	26	160.304					100.00

DF—degree of freedom; Seq SS—sequential sum of square; Adj SS—adjacent sum of square; Adj MS—adjacent sum of mean square; F value—variance; p value—test statistics.

, while the results of the S/N ratio are presented in

Table 8. Response table for the signal-to-noise ratio for GRG.

Level	A	B	C
1	−3.298	−6.856	−6.354
2	−5.030	−5.169	−3.807
3	−7.153	−3.455	−5.320
Delta	3.855	3.401	2.547
Rank	1	2	3

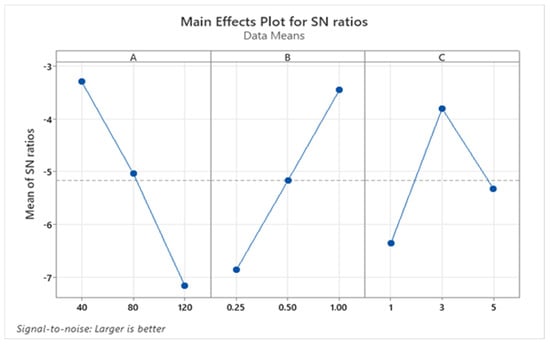
as well as in Figure 3.

Based on the analysis (output multi-response) for GRG, it was found that the normal load is the most influential parameter at 41.86%, followed immediately by siding speed at 32.48%, and finally, Gr addition with an influence of 18.43%. Observing the interactions of the parameters, only the interaction A*C stands out with a share of about 5%. Table 8 provides an analysis of the S/N ratio of GRG, and the bold values represent a combination of parameters for optimizing the tribological characteristics of hybrid composites. The optimal combination of parameters (Table 8 and Figure 3), taking into account both outputs at once, reads as follows: normal load is level 1, i.e., 40 N; siding speed is level 3, i.e., 1 m/s; and level 2 is Gr addition, i.e., 3 wt.%.

The motivation for applying ANOVA analysis is to determine which process parameter strongly influences the tribological characteristics of A356/SiC/Gr. By combining the application of the used methods, i.e., the Taguchi and GRA methods, it is necessary to look at both outputs at once and establish the optimal combination of parameters for achieving the best tribological characteristics of hybrid composites.

Based on Table 8 and Figure 3, it can be concluded that the best combination of parameters is the following: A1B3C2, which means that it is necessary to choose 3 wt.% Gr for the production of hybrid composites in order to achieve minimal wear and coefficient of friction under tribological test conditions of 40 N and 1 m/s. This combination of parameters coincides with the results of the GRA analysis, which are shown as rank 1 in Table 6, and the combination of parameters can be found in Table 3.

3. TOPSIS Method

The method used for ranking according to the criteria is the TOPSIS method. The logic of the method is to first define ideal positive and ideal negative solutions. The optimal alternative is the one that is geometrically closest to the ideal positive solution, that is, the farthest from the ideal negative solution. The ranking of alternatives is based on “relative similarity to the ideal solution”, which avoids the situation that the alternative has the same similarity to the positive ideal and to the negative ideal solution at the same time. The ideal solution is defined using the best rating values of alternatives for each individual criterion; conversely, the negative ideal solution represents the worst rating values of the alternatives. The terms “best” and “worst” are interpreted for each criterion separately, according to whether the criterion is maximized or minimized [36,37].

3.1. Defining Parameter Variations and Criteria

Based on the results received in practice pap, the different variations in parameters are used to achieve the best material performance. Generally, these materials are represented by indexes in the domain {1, …, i, …, I}. The total number of considered variations is denoted as I. The parameter variation index is i, i = 1, …, I. In this paper, 27 different variations with changes in sliding speed, load, and percentage of graphite were considered, i = 1, …, 27. When it comes to sliding speed, the next values were considered: 0.25, 0.5, and 1 m/s. The given load is 40, 80, and 120 N, and the mass fraction of graphite is 1, 3, and 5%. Twenty-seven variations were created from these input data.

According to the experimental results, criteria are obtained based on which a ranking is made. These criteria are represented by a set of indexes, {1, …, k, …, K}. In this paper, two criteria are considered: wear rate (k = 1) and friction coefficient (k = 2).

It should be emphasized that the weights of the criteria are the same.

3.2. The Course of Implementation of the TOPSIS Method

The ranking is performed based on the TOPSIS method, which is shown in the following steps:

Step 1. Define the decision matrix.

$${{[x}_{ik}]}_{IxK}$$

(8)

where $x_{ik}$ is a clear value characteristic for the variation in each parameter. These values are given by standard tests.

Step 2. Construct a normalized decision matrix using a normalization vector.

$${{[r}_{ik}]}_{IxK}$$

(9)

where the following apply:

(a)

The benefit type

$$r_{ik}=\frac{x_{ik}}{\sqrt{\sum _{i=1\dots I}{x_{ik}}^2}}$$

(10)

(b)

The cost type

$$r_{ik}=\frac{\frac{1}{x_{ik}}}{\sqrt{\sum _{i=1\dots I}{\left(\frac{1}{x_{ik}}\right)}^2}}$$

(11)

Step 3. Determine the ideal positive solution (PIS), $r_k^{+},$ and negative ideal solution (NIS), $r_k^{-}$, according to the procedure defined in the conventional TOPSIS method [14,15,16,37]:

$$\begin{gathered} r_k^{+}=\underset{i=1,\dots ,I}{\max }{r}_{ik} \\ {r}_k^{-}=\underset{i=1,\dots ,I}{\min }{r}_{ik} \end{gathered}$$

(12)

Step 4. Determine the distances for each parameter variation, $i=1,\dots ,I{r}_k^{+}$ and $r_k^{-}$:

$$\begin{gathered} {\tilde{d}}_i^{+}={\sum }_{k=1,\dots ,K}{\tilde{\omega }}_k·\left(r_k^{+}-r_{ik}\right) \\ {\tilde{d}}_i^{-}={\sum }_{k=1,\dots ,K}{\tilde{\omega }}_k·\left(r_{ik}-r_k^{-}\right) \end{gathered}$$

(13)

Step 5. Calculate the quasi-values of the closeness coefficient:

$${\tilde{c}}_i=\frac{{\tilde{d}}_i^{-}}{{\tilde{d}}_i^{-}+{\tilde{d}}_i^{+}}$$

(14)

Step 6. Sort clear values, $c_i$, into a non-increasing array. The rank of the considered variations corresponds to the obtained rank, $c_i$. The first place in the ranking is the combination of parameters that has the largest one, $c_i$.

Step 7. The selection of the best combination is made according to the given rank.

3.3. Analysis and Discussion of the Results Using the TOPSIS Method

The experiment that was carried out aimed to find the best possible combination of parameters for hybrid composites with the A356 matrix. The obtained appropriate dependencies, i.e., the combination of ideal load, sliding speed, and percentage of graphite as reinforcement, should create conditions for the wider application of these materials in the industry. Twenty-seven different variations were considered (Table 2), with a change in sliding speed, loading, and percentage of graphite in the mass fraction of the hybrid composite.

The decision matrix is shown in

Table 9. Decision matrix, normalized decision matrix (PIS and NIS), and decision rank.

	Decision Matrix, ${\mathit{x}}_{\mathit{i}\mathit{k}}$		Normalized Decision $\mathbf{Matrix}, {\mathit{r}}_{\mathit{i}\mathit{k}}$		${\mathit{c}}_{\mathit{i}}=1$	$\mathit{R}\mathit{a}\mathit{n}\mathit{k}$
	$\mathit{k}=1$	$\mathit{k}=2$	$\mathit{k}=1$	$\mathit{k}=2$
$i=1$	0.325	0.104	0.128	0.161	0.165	21
$i=2$	0.174	0.082	0.240	0.204	0.504	6
$i=3$	0.204	0.097	0.204	0.172	0.358	12
$i=4$	0.252	0.098	0.165	0.171	0.268	16
$i=5$	0.141	0.063	0.296	0.265	0.763	2
$i=6$	0.168	0.071	0.248	0.236	0.593	5
$i=7$	0.201	0.086	0.207	0.194	0.413	10
$i=8$	0.12	0.052	0.347	0.322	1.000	1
$i=9$	0.151	0.065	0.276	0.257	0.702	3
$i=10$	0.373	0.12	0.112	0.139	0.081	24
$i=11$	0.232	0.105	0.180	0.159	0.275	15
$i=12$	0.286	0.113	0.146	0.148	0.175	20
$i=13$	0.285	0.104	0.146	0.161	0.204	17
$i=14$	0.202	0.081	0.206	0.206	0.437	9
$i=15$	0.236	0.102	0.177	0.164	0.278	14
$i=16$	0.215	0.091	0.194	0.184	0.360	11
$i=17$	0.168	0.065	0.248	0.257	0.640	4
$i=18$	0.195	0.077	0.214	0.217	0.477	8
$i=19$	0.488	0.13	0.085	0.129	0.000	27
$i=20$	0.435	0.118	0.096	0.142	0.052	25
$i=21$	0.472	0.125	0.088	0.134	0.018	26
$i=22$	0.338	0.115	0.123	0.145	0.120	22
$i=23$	0.297	0.103	0.140	0.162	0.195	18
$i=24$	0.385	0.117	0.108	0.143	0.082	23
$i=25$	0.245	0.097	0.170	0.172	0.282	13
$i=26$	0.198	0.073	0.210	0.229	0.496	7
$i=27$	0.307	0.103	0.136	0.162	0.185	19
PIS			0.347	0.322
NIS			0.085	0.129

. Then, the normalized matrix was calculated, as well as PIS and NIS, the values of which were obtained by applying Equations (8)–(12) given in Table 9. After calculating the positive and negative ideal solutions, the similarity coefficient is calculated according to Equation (14). After that, the values are sorted, $c_i$, in descending order. The rank of the considered variations corresponds to the obtained rank, $c_i$. The first place in the ranking is the combination of parameters to which the largest one corresponds, $c_i$ (Table 9).

Based on Table 9, it is concluded that the best combination of parameters is i = 8, where the parameters are as follows: the load is 40 N, the sliding speed is 1 m/s, and the percentage of graphite in the mass fraction of the hybrid composite is 3. The following combination of parameters that can be an alternative is under serial number i = 5, where the load is 40 N, the sliding speed is 0.5 m/s, and the percentage of graphite in the mass fraction of the hybrid composite is 3.

On the other hand, the option that is the worst is i = 19, where the parameters are as follows: the load of 120 N, the sliding speed of 0.25 m/s, and the percentage of graphite in the mass fraction of the hybrid composite of 1. In the penultimate place, i = 21, where the parameters are as follows: the load is 120 N, the sliding speed is 0.25 m/s, and the percentage of graphite in the mass fraction of the hybrid composite is 5.

Using the GRA analysis, the optimal variant of the parameters was established, which was also confirmed by the TOPSIS method. Similar results were obtained by researchers in the study [13], analyzing the composition of composites with ceramic particulates Al₂O₃/SiC (0–8 wt.%, in the step of 2%) using a combination of GRA and TOPSIS methods on mechanical and wear performance composites. Examination of tribological characteristics and surface quality following the influence of sliding load, sliding speed, temperature, and reinforcements with 1, 2, wt.%, and 5.5, 7 wt.% of micro-sized Al₂O₃ and nano-sized Al₂O₃ particles, respectively, in the composite was performed using optimization methods. ANOVA determined that the most influential parameter is load (62.33%), while the content of the reinforcer has an influence of 19.40%. They reported the successful use of the TOPSIS method only with the Taguchi L9 matrix, i.e., by carrying out nine experiments [20]. In comparison with this research, approximately the same influence of the importance of load parameters as the first ranked and reinforcement of about 19% on the tribological characteristics of the composite is observed. The application of multi-objective optimization of dry sliding wear parameters in the AA7068/TiC composite proved to be successful, as they confirmed the results obtained by the GRA analysis in their work [38]. By combining the application of the GRA and TOPSIS methods during multi-objective parameter micro-electric discharge drilling for magnesium alloy, they confirmed with the TOPSIS method the optimal combination of parameters achieved by the GRA method [39]. Another successful application of the Taguchi gray method was reported in the research of wear parameters such as applied load, sliding speed, and sliding distance and their effect on the dry sliding wear performance of AA6063/SiC. Using ANOV, they concluded that sliding distance was found to have the highest significant influence of 61.005%, and then they determined the optimal combination of parameters, which they confirmed by experiment [40]. The optimization of the tribological and mechanical characteristics of the AA356-Al₂O₃/SiC/graphite composite using the Taguchi and AHP-GRA methods was carried out in [13]. In the aforementioned research, it was also determined that Taguchi and GRA techniques give consistent results when optimizing parameters.

4. Morphology of Worn Surfaces

In order to understand the wear mechanisms, the worn surfaces of the A356/10SiC/3Gr composite were analyzed using a scanning electron microscope (SEM). Figure 4 presents SEM microphotographs illustrating the worn surfaces of composite samples for tribological tests conducted at a sliding speed of 1 m/s and a normal load of 40 N.

Figure 4 shows the SEM microscopy with EDS analysis for the composite showing optimal characteristics (A356/10SiC/3Gr). When adding SiC reinforcement, the tribological behavior of the tested composite materials changes. SEM images and EDS analysis show the presence of trace amounts of iron and its oxides. These particles are light-colored in the images, so their position and direction of movement on the wear track can be easily followed (spectrum 3, Figure 4). The EDS analysis of worn traces also shows the presence of graphite (spectrum 1, Figure 4); graphite particles are mostly found in the vicinity of SiC particles (spectrum 2, Figure 4). It is interesting that these particles are grouped mostly on the side of the SiC particles, which is in the direction of movement. The appearance of iron on the contact surface of the composite material occurs due to the transfer of material from the metal counterbody (disc). The main wear mechanisms of these composites are adhesion wear and delamination, which are explained in detail in the paper [41,42].

5. Conclusions

The main goal of the research presented in this paper was to achieve a reduction in wear and coefficient of friction by choosing the most suitable content of Gr in the hybrid composite. This would provide the appropriate tribological characteristics of the material, which affect the longer service life of the products made from the developed composites. For this purpose, a tribological test was carried out on a block-on-disc tribometer in conditions without lubrication. Optimization of multiple response problems was performed using GRA and TOPSIS methods.

In accordance with the adopted research methodology, using the Taguchi method, optimization was first performed for the independent output values of WR and CoF. Then, with the aim of multi-objective optimization, the tribological characteristics of hybrid composites were optimized using the GRA method. By applying ANOVA analysis to GRG results, it was established that the normal load is the most influential parameter at 41.86%, followed by sliding speed at 32.48%, and Gr addition with an influence of 18.43%. Based on the S/N ratio analysis, it was concluded that for the optimal variant of the parameters, it is necessary to choose 3 wt.% Gr for the production of the hybrid A356/10 wt.% SiC composite in order to achieve minimal wear and coefficient of friction under tribological test conditions under a load of 40 N and a sliding speed of 1 m/s.

Then, the TOPSIS method was applied to the experimental results, which determined that the performance of the composite was best achieved by choosing the following combination of parameters: a load of 40 N, a sliding speed of 1 m/s, and a 3% percentage of graphite in the mass fraction of the composite using the TOPSIS method. The combination of parameters, which can be an alternative to the previous one, is as follows: a load of 40 N, a sliding speed of 0.5 m/s, and 3 percent graphite in the mass fraction of the composite.

The TOPSIS method results confirmed the optimal combination of parameters obtained by Taguchi–gray multi-objective optimization. This indicates that both methods can be used with high reliability to analyze and optimize the tribological characteristics of composites. The combination of the methods used enables the precise setting of parameters in order to achieve optimal tribological characteristics of Al-based hybrid composites, which result in materials with adjusted or defined characteristics that are extremely important for the practical application of these materials. According to the SEM microscopy analysis of the worn surfaces of the composite, it was concluded that adhesive wear and delamination are the dominant wear mechanisms for all conditions of tribological tests in conditions with lubrication.