Research on Sudden Unbalance Response of Rigid-Elastic-Oil Coupled Ball Bearings
Abstract
1. Introduction
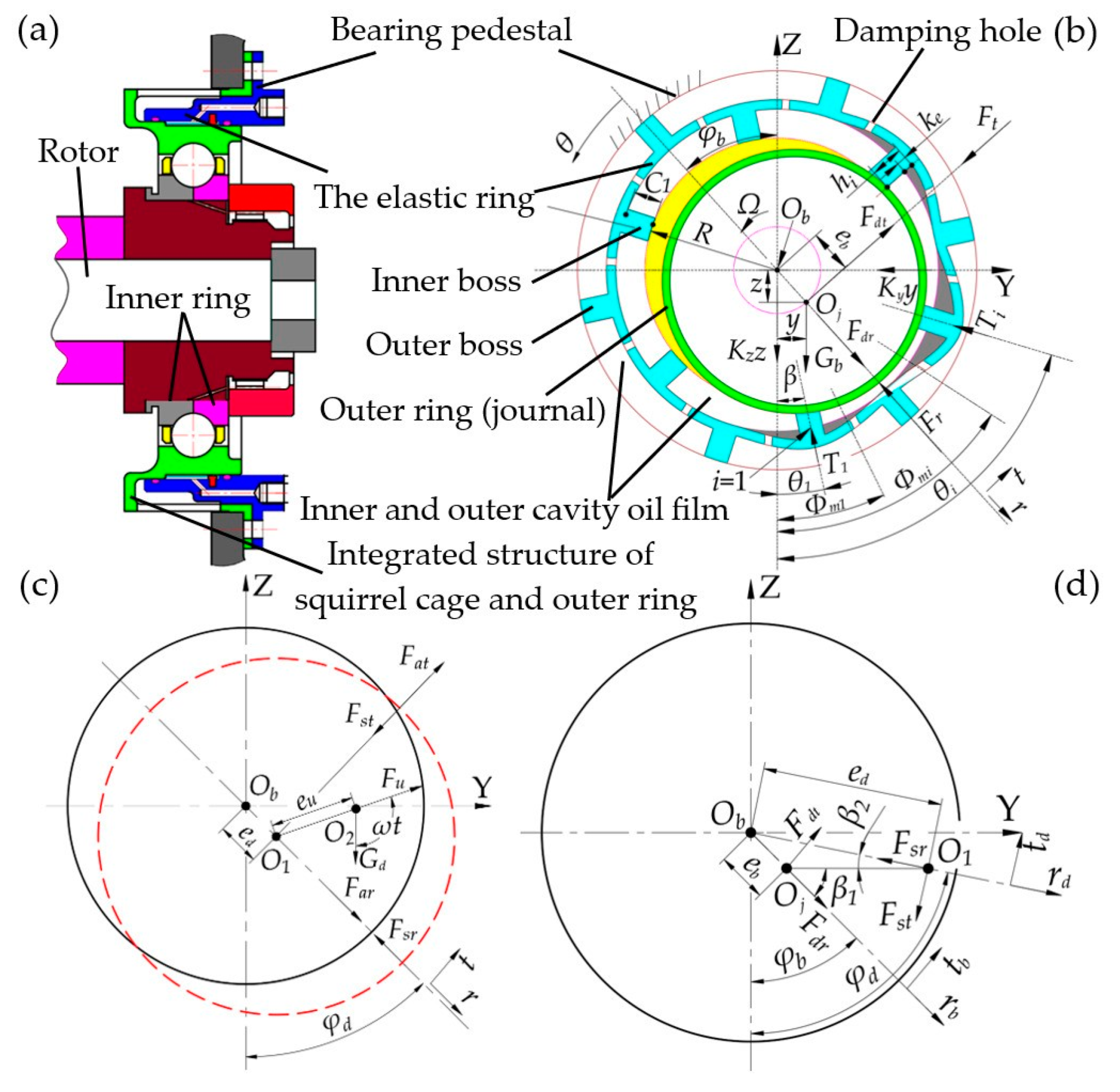
2. Dynamic Model of Ball Bearing with ERSFD
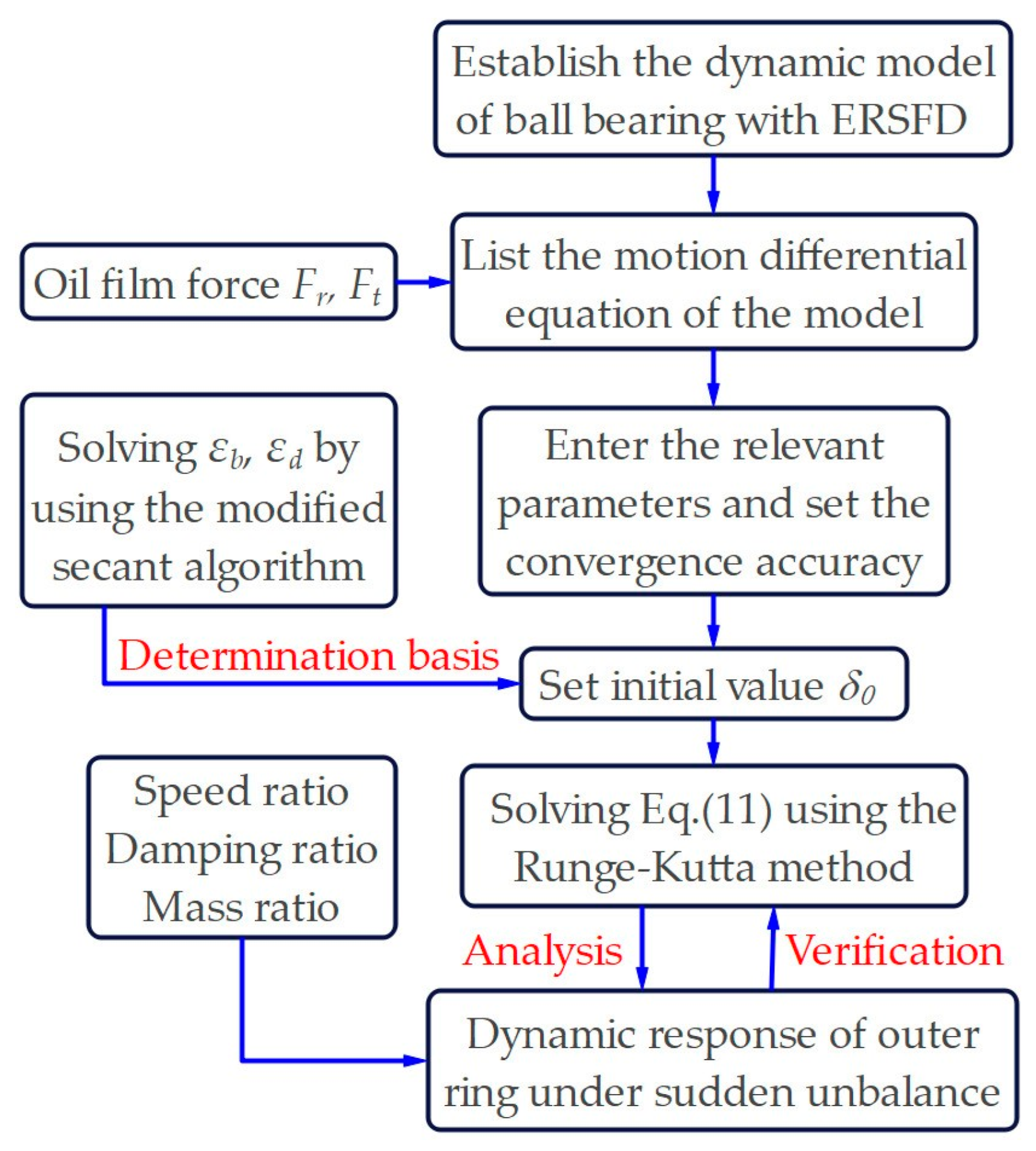
3. Numerical Analysis and Solving Process of the Model
3.1. Solving Process
3.2. Numerical Analysis
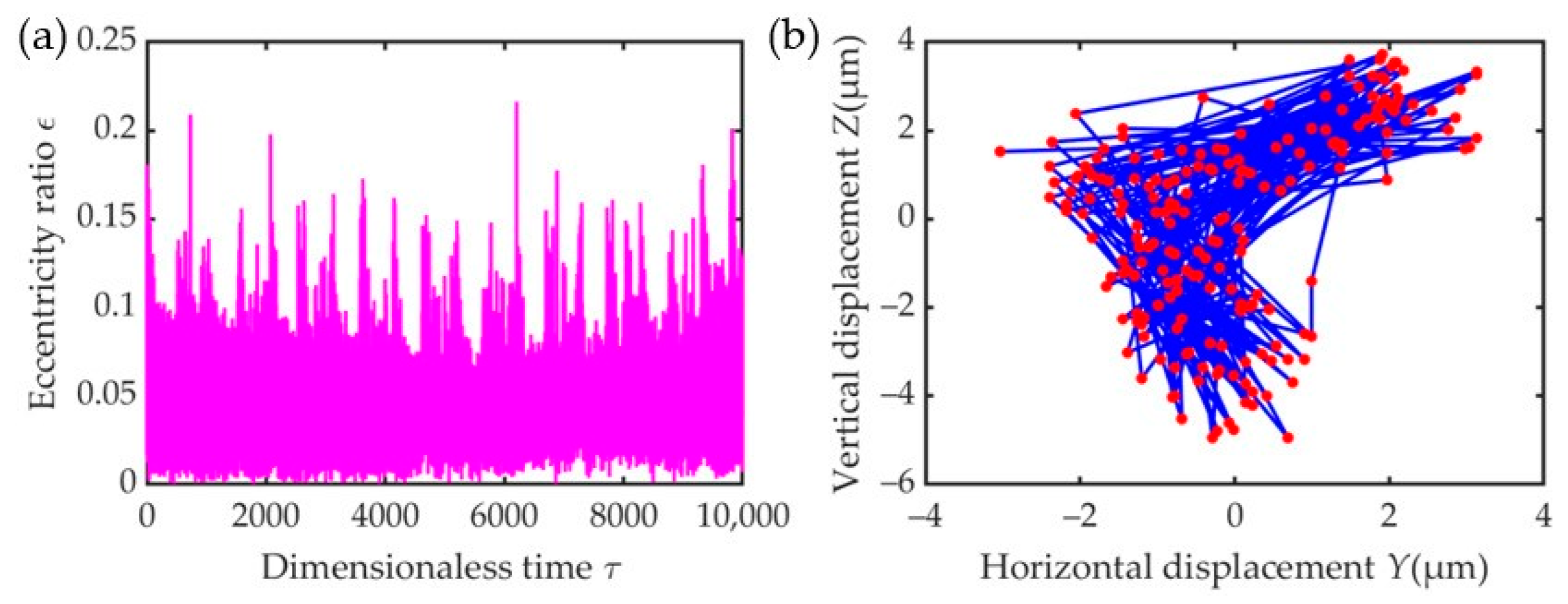
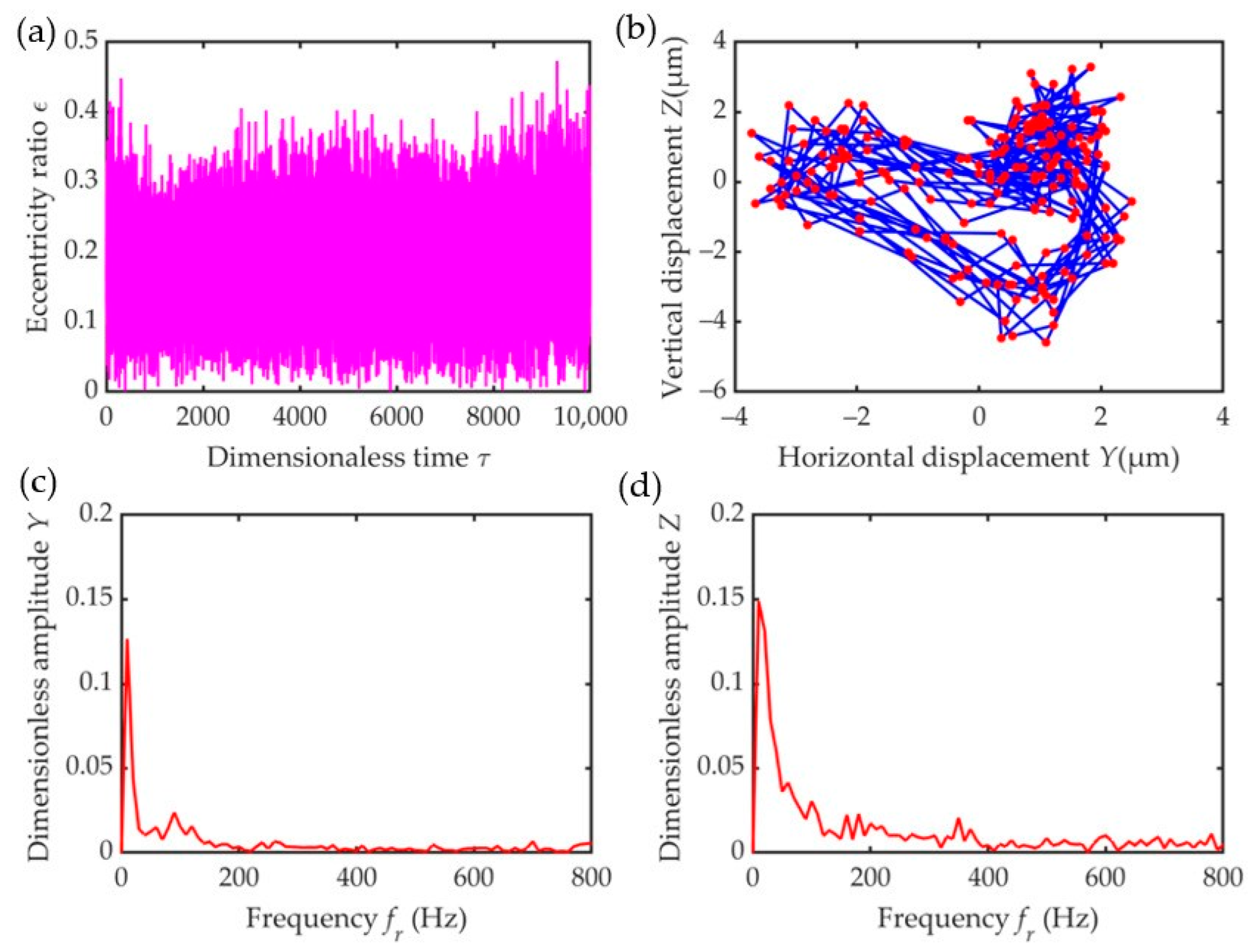
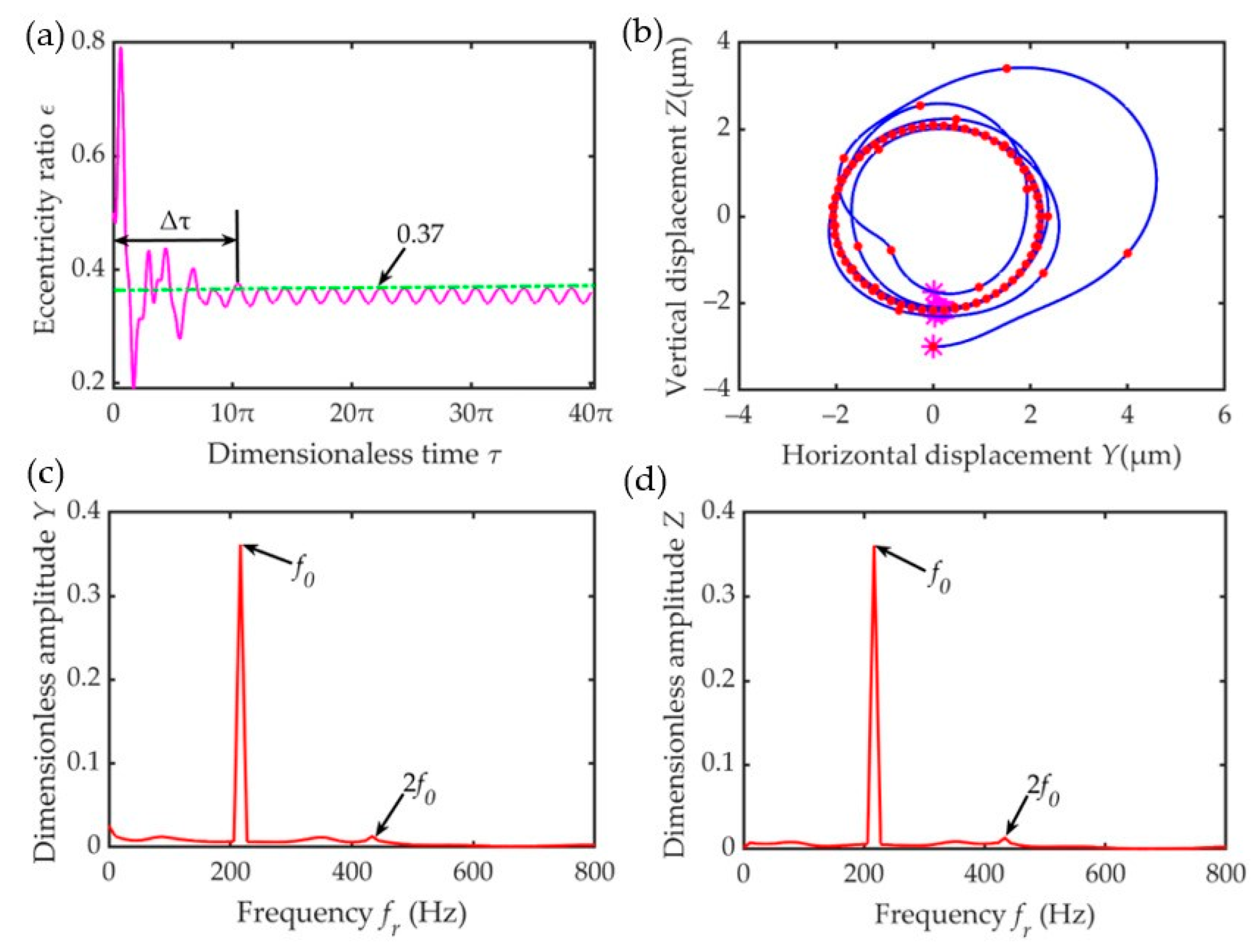
4. Results and Discussion
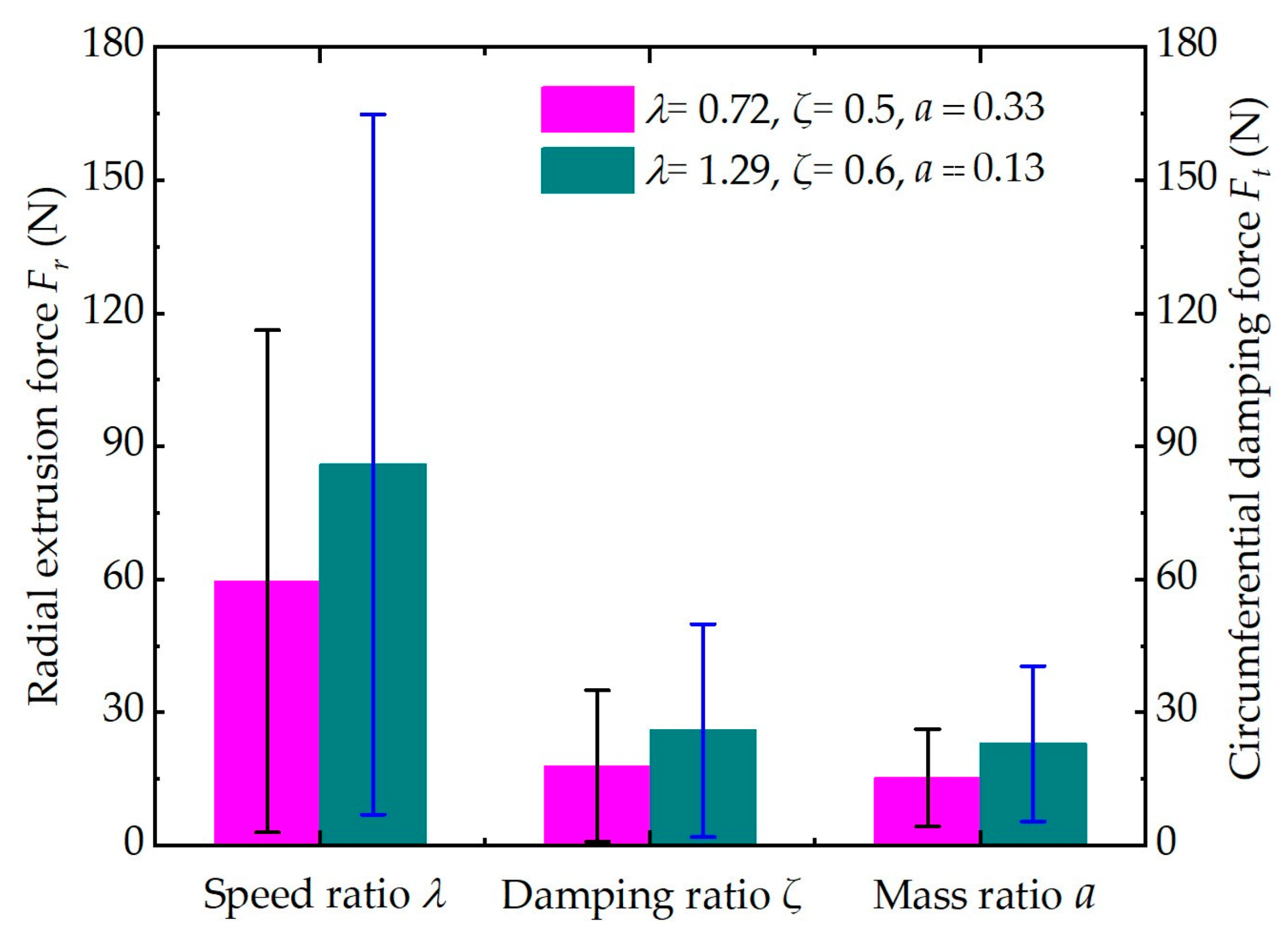
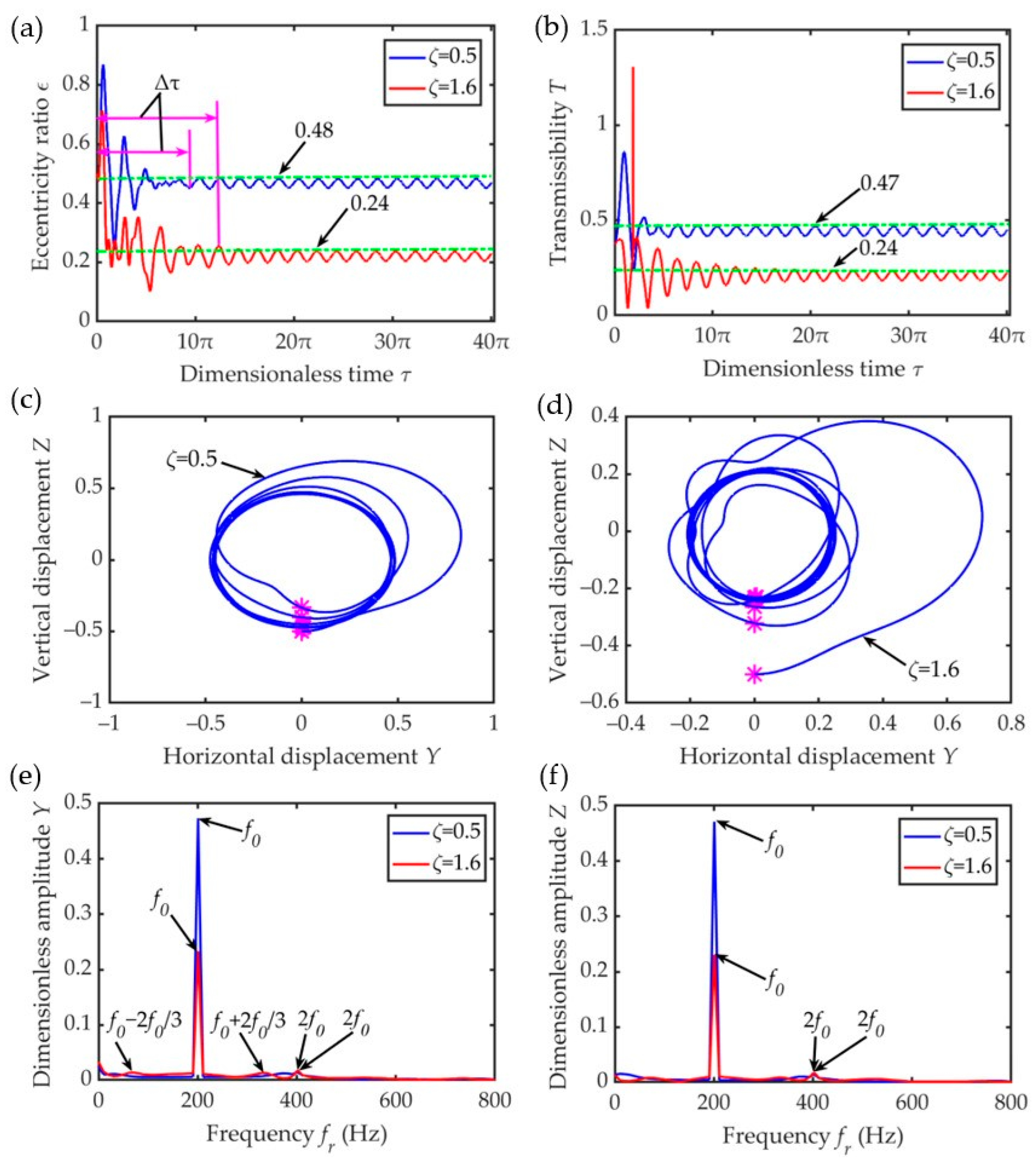
4.1. Influence of Speed Ratio
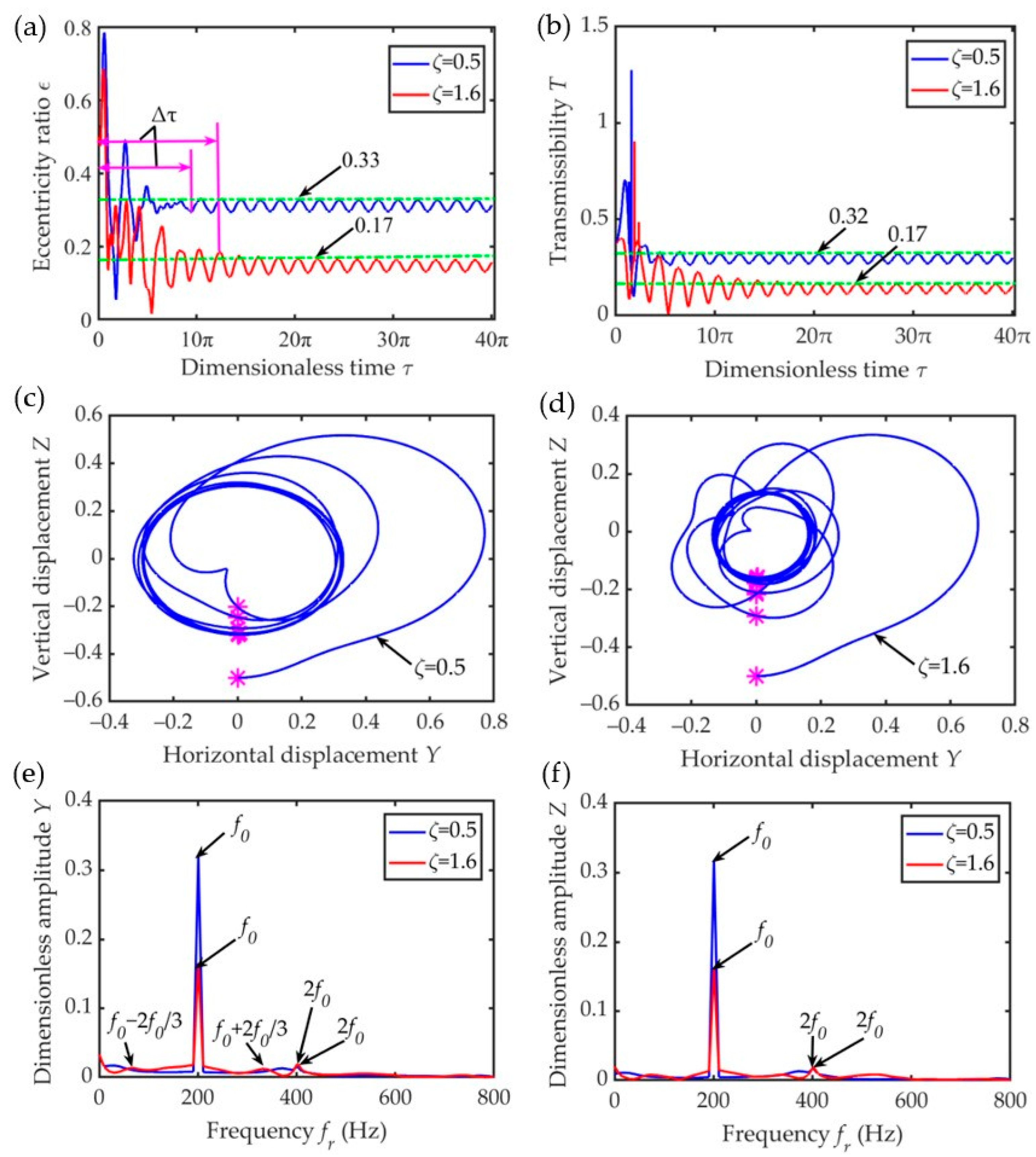
4.2. Influence of Damping Ratio
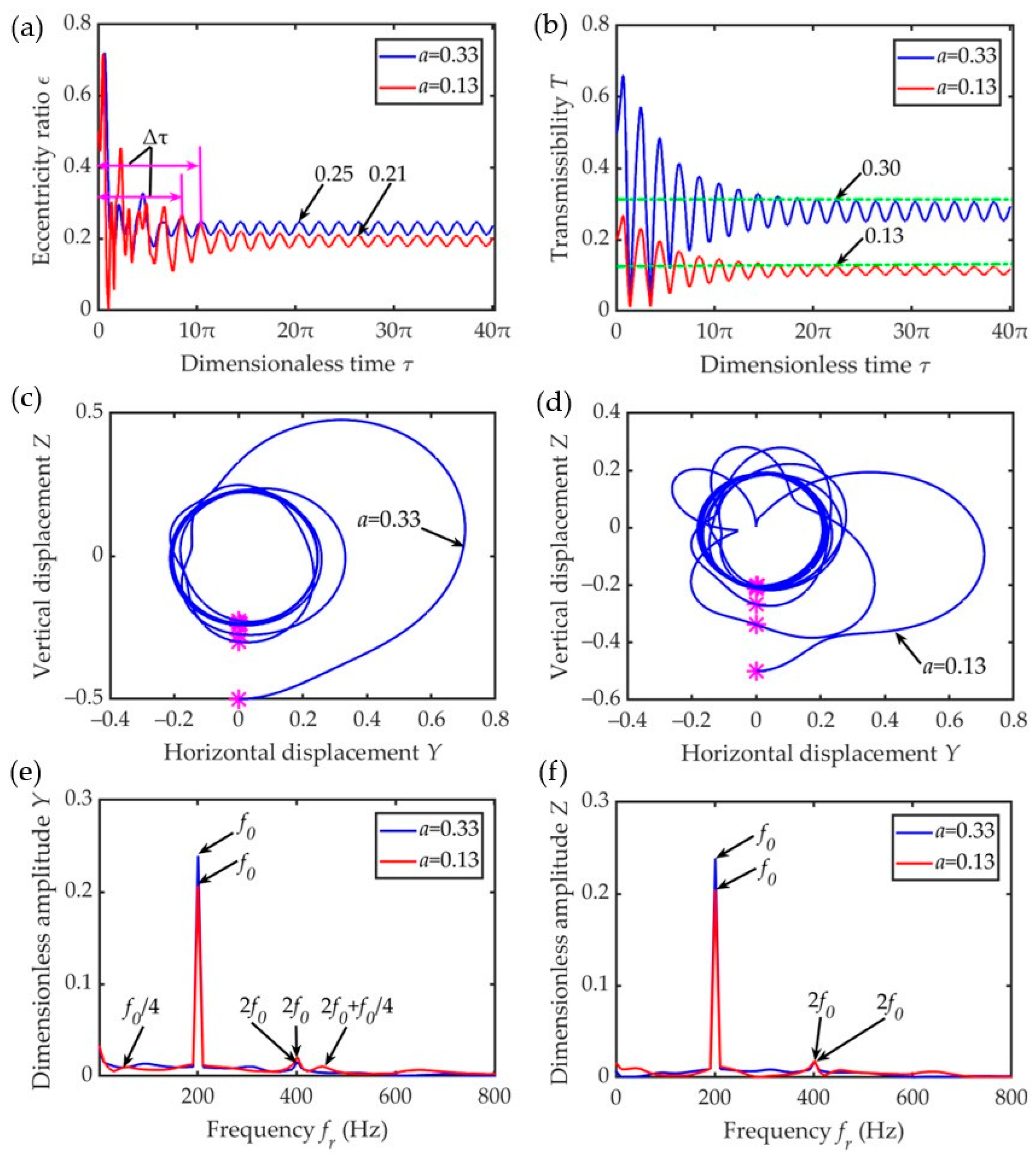
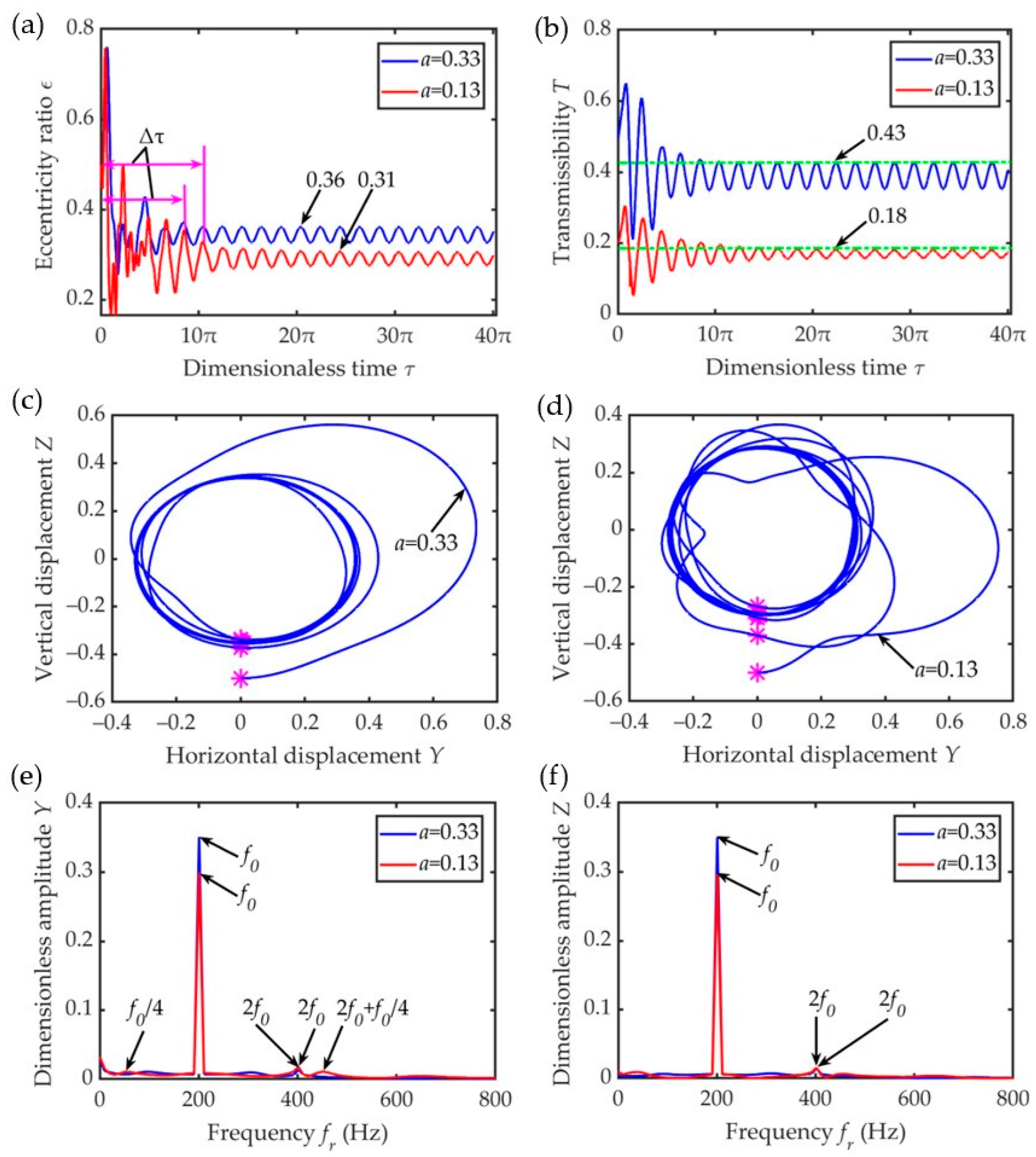
4.3. Influence of Mass Ratio
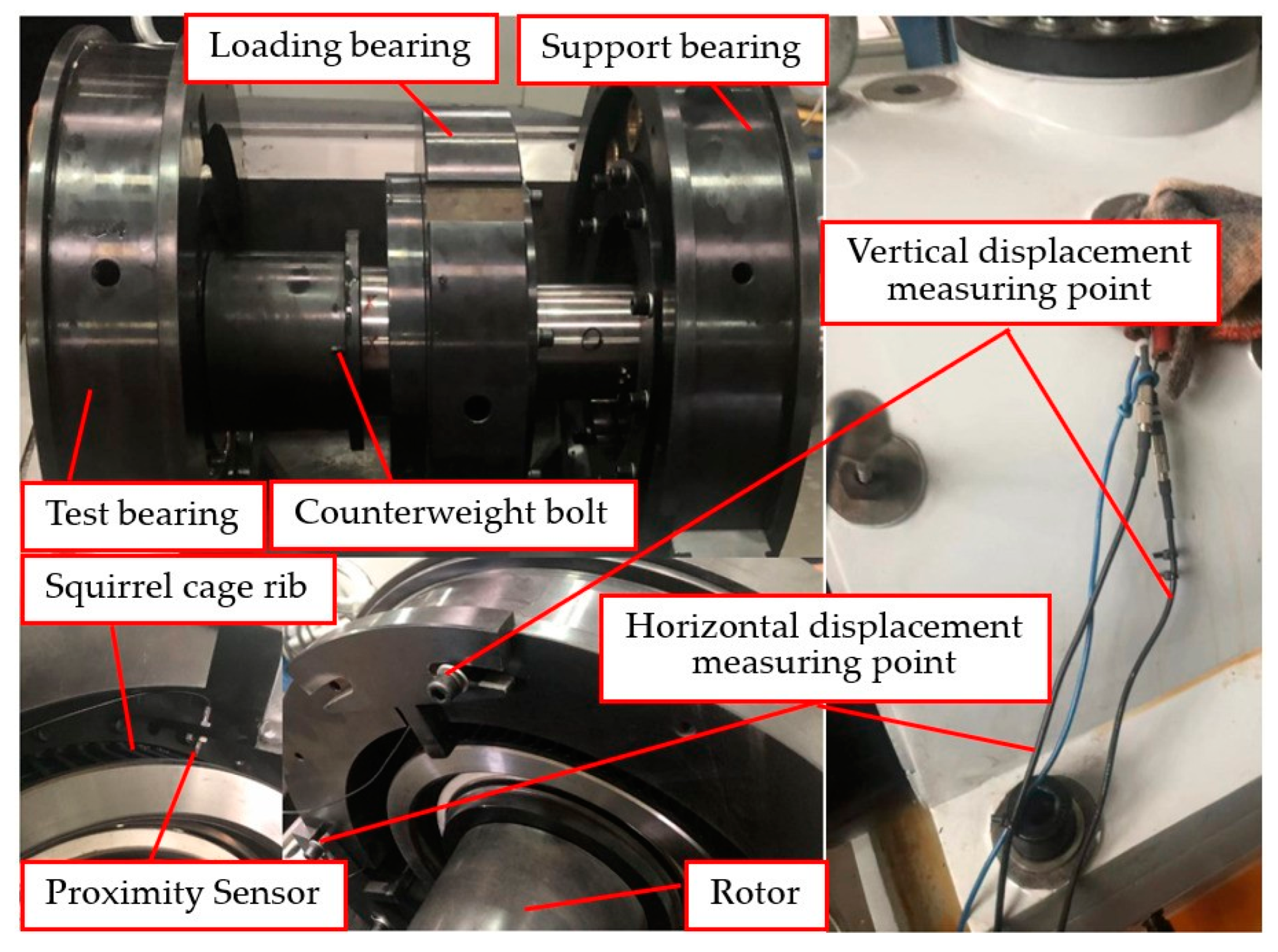
5. Test Verification
6. Conclusions
- (1)
- Under a constant unbalance, the lower the speed ratio, the lower the damping ratio, and the higher the mass ratio, the shorter the transient response time when entering the steady state. At a low-speed ratio, high damping ratio, and low mass ratio, the steady-state amplitude is small, making it more conducive to suppressing the bearing vibration. With an increase in unbalance, the eccentricity, transmissibility, displacement amplitude of the amplitude–frequency response, and the radius of the outer ring center locus increased.
- (2)
- The ERSFD and the ball bearing are coupled to each other. In this case, the sensitivity of the relevant parameters to the oil film force, from high to low, followed the order: speed ratio, damping ratio, and mass ratio.
- (3)
- Due to the existence of various frequency components, such as the fundamental frequency, frequency doubling, and subharmonics, the motion state of the bearing outer ring was found to be more complex in the transient response stage.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| The mass ratio | |
| The installation angle of the first inner boss | |
| The radial clearance of the inner cavity oil film | |
| The angle of the start of positive pressure region measured from the center line | |
| The angle between the ith inner boss and the negative direction of the Z axis | |
| The external damping coefficient | |
| The critical damping coefficient | |
| The eccentricity between the bearing center and the center of the journal | |
| The eccentricity between the bearing center and the center of the disc | |
| The disc eccentricity | |
| The journal eccentricity | |
| The attitude angle of the journal | |
| The radial oil film force | |
| The circumferential oil film force | |
| The radial component of the elastic force acting on the journal | |
| The tangential component of the elastic force acting on the journal | |
| The radial component of the elastic force acting on the disc | |
| The tangential component of the elastic force acting on the disc | |
| The radial component of the external damping force acting on the disc | |
| The tangential component of the external damping force acting on the disc | |
| The unbalanced force concentrated on the disc | |
| The difference between the position angle of the ith boss force and the position angle of the radial deflection point on the elastic ring | |
| The squeeze oil film force | |
| The center spring force | |
| The gravity of the journal | |
| The gravity of the disc | |
| The flexibility coefficient of the elastic ring | |
| The thickness of the oil film in the inner cavity | |
| The elastic ring stiffness | |
| The squirrel cage stiffness in the Y-axis direction | |
| The squirrel cage stiffness in the Z-axis direction | |
| The stiffness of the shaft | |
| The deformation amount of the elastic ring | |
| The stiffness of the squirrel cage | |
| The length of the damper | |
| The speed ratio | |
| The vibration mass concentrated at the journal | |
| The vibration mass at the disc | |
| The dynamic viscosity of the oil | |
| The number of the inner bosses | |
| The bearing center | |
| The center of the journal | |
| The center of the disc | |
| The angular velocity of the journal | |
| The critical angular velocity of the rotor system | |
| The force applied to the inner boss | |
| The radius of the journal | |
| The radial squeeze direction | |
| The direction of circumferential orbital motion | |
| The support reaction at the boss of the elastic ring | |
| Transmissibility | |
| The sudden unbalance | |
| The axial coordinate | |
| , | Represent the offset distance of the journal in the Y-axis and Z-axis, respectively |
| The damping ratio |
References
- Liu, P.; Wang, L.; Ma, F.; Zhang, D.; Wu, J.; Li, Z. Influence of assembly clearance on vibration characteristics of angular contact ball bearings in the thermal environment. Tribol. Int. 2023, 181, 108317. [Google Scholar] [CrossRef]
- Lu, H.; Li, W.; Shen, J.; Chen, T.; Sheng, L. Dynamic Characteristics Analysis of Rotor-Bearing System Considering Bearing Clearance and Hybrid Eccentricity. J. Vib. Eng. Technol. 2024, 12, 2249–2263. [Google Scholar] [CrossRef]
- Zhang, Z.Y. Bifurcations and Hysteresis of Varying Compliance Vibrations of a Ball Bearing-Rotor System; Harbin Institute of Technology: Harbin, China, 2015. [Google Scholar]
- Deng, S.; Fu, J.; Wang, Y.; Yang, H. Analysis on dynamic characteristics of aero-engine rolling bearing/dual-rotor system. J. Aerosp. Power 2013, 28, 195–204. [Google Scholar]
- Deng, S.; He, F.; Yang, H.; Li, Y. Analysis on dynamic characteristics of a dual rotor-rolling bearing coupling system for aero-engine. J. Aerosp. Power 2010, 25, 2386–2395. [Google Scholar]
- Cao, H.; Niu, L.; Xi, S.; Chen, X. Mechanical model development of rolling bearing-rotor systems: A review. Mech. Syst. Signal Process. 2018, 102, 37–58. [Google Scholar] [CrossRef]
- Chen, S.; Shuai, Q.; Chen, X.; Gu, J.; Liu, Z. Influence of rotor unbalance on dynamic coupling characteristics of angular contact ball bearing-rigid rotor system. J. Aerosp. Power 2021, 36, 2126–2138. [Google Scholar]
- Hamzehlouia, S.; Behdinan, K. Squeeze film dampers supporting high-speed rotors: Rotor dynamics. Proc. Imech E Part J J. Eng. Tribol. 2021, 235, 495–508. [Google Scholar] [CrossRef]
- Oliveira, M.; Daniel, G.B. Vibrational signature of journal bearing oil starvation considering thermal effects and rotor unbalance variation. Tribol. Int. 2024, 191, 109132. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, H.; Zhang, L.; Xing, Y.; Guo, Y. Vibration suppression mechanism research of adjustable elliptical journal bearing under synchronous unbalance load. Tribol. Int. 2019, 132, 185–198. [Google Scholar] [CrossRef]
- Li, T.; Ren, X.; Yue, C. Transient response of single-disc rotor system under sudden unbalance load. Mech. Sci. Tech. Aerosp. Eng. 2012, 6, 924–927. [Google Scholar]
- Sun, G.; Palazzolo, A.; Provenza, A.; Lawrence, C.; Carney, K. Long duration blade loss simulations including thermal growths for dual-rotor gas turbine engine. J. Sound Vib. 2008, 316, 147–163. [Google Scholar] [CrossRef]
- Zhao, L.; Liao, M.; Hong, L.; Lei, X.; Li, M.; Wang, S.; Hou, L.; Shao, Z. Analysis of aero-engine vibration response under sudden unbalance. J. Aerosp. Power 2022, 37, 251–262. [Google Scholar]
- Zhao, L.; Liao, M.; Niu, J. Investigation on Steady State Unbalance Response of Rotor with Elastic Ring Squeeze Film Damper. IOP Conf. Ser. Mater. Sci. Eng. 2020, 751, 012043. [Google Scholar] [CrossRef]
- Zhu, C.; Feng, X. Experimental study of nonsynchronous orbits in a flexible rotor-squeeze film damper system. J. Aerosp. Power 1987, 04, 323–327. [Google Scholar]
- Zhu, C.; Feng, X.; Xu, J. The behavior of main resonant bistable operation in nonlinear squeeze film damper-flexible rotor systems. J. Vib. Eng. 1989, 1, 5. [Google Scholar]
- Li, Q.; Zhao, F.; Zhang, S. Experimental investigation on blade loss transient response of rotor with flexible damped support. J. Aerosp. Power 1992, 7, 103–107. [Google Scholar]
- Meng, G.; Xue, Z.; Zhu, C.; Feng, X. Investigation on the non-synchronous responses of flexible rotor-uncentralized squeeze film damper bearings system. J. Aerosp. Power 1987, 02, 121–125. [Google Scholar]
- Dong, H.; Zhang, A.; Shu, H.; Zhang, C. Simultaneous identification method of rotor distributed unbalance and bearing char-acteristic parameters. J. Harbin Inst. Technol. 2022, 54, 128–135. [Google Scholar]
- He, W.; Pan, B.; Bai, J. Transient response analysis of squeezed film damper rotor system under sudden unbalance load. Gas. Turbine. Exp. Res. 2020, 33, 36–40. [Google Scholar]
- Yao, W. Study on Simultaneous Identification of Rotor Unbalance and Bearing Coefficients of a Rotor. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2019. [Google Scholar]
- Ou, X.; Zhang, Y.; Zhang, K.; Wang, Y. Dynamic model of deep groove bearing considering unbalanced force and disturbing force. Mach. Des. Manuf. 2022, 12, 6–10. [Google Scholar]
- Zhu, C.; Robb, D.A.; Ewins, D.J. Analysis of the multiple-solution response of a flexible rotor supported on non-linear squeeze film damper. J. Sound Vib. 2002, 252, 389–408. [Google Scholar] [CrossRef]
- Inayat-Hussain, J.I. Bifurcations in the response of a flexible rotor in squeeze-film dampers with retainer springs. Chaos Solitons Fractals 2009, 39, 519–532. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, Q.; Zheng, T. The stability and bifurcation of a squeeze film damper-sliding bearing-rigid rotor system. Chin. J. Appl. Mech. 1996, 13, 35–40. [Google Scholar]
- Gjika, K.; San Andrés, L.; Larue, G.D. Nonlinear dynamic behavior of turbo charger rotor-bearing systems with hydrodynamic oil film and squeeze film damper in series: Prediction and experiment. J. Comput. Nonlinear Dyn. 2010, 5, 041006. [Google Scholar] [CrossRef]
- Xu, M.; Liao, M. The vibration performance of the Jeffcott rotor system with SFD in maneuver flight. J. Aerosp. Power 2003, 18, 8. [Google Scholar]
- Meng, G. Sudden unbalance responses of flexible rotor supported in squeeze film dampers. Chin. J. Appl. Mech. 1993, 22, 10–16. [Google Scholar]
- Heidari, H.; Ashkooh, M. The influence of asymmetry in centralizing spring of squeeze film damper on stability and bifurca-tion of rigid rotor response. Alex. Eng. J. 2016, 55, 3321–3330. [Google Scholar] [CrossRef][Green Version]
- Chen, H.; Hou, L.; Chen, Y. Bifurcation analysis of a rigid- rotor squeeze film damper system with unsymmetrical stiffness supports. Arch. Appl. Mech. 2017, 87, 1347–1364. [Google Scholar] [CrossRef]
- Chen, X.; Gan, X.; Ren, G. Dynamic modeling and nonlinear analysis of a rotor system supported by squeeze film damper with variable static eccentricity under aircraft turning maneuver. J. Sound Vib. 2017, 485, 11551. [Google Scholar] [CrossRef]
- Zhou, C. Research on the Dynamic Behavior of a Rotor System Supported by Rolling Bearing with Squeeze Film Damper. Master’s Thesis, Shanghai University, Shanghai, China, 2019. [Google Scholar]
- Yang, Z.D. Study on Response Characteristics and Stability of Rotor System under Sudden High Energy Excitation Load. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- Pan, B. Study on Sudden Unbalance Response of Rotor System with Squeeze Film Damper. Master’s Thesis, Civil Aviation University of China, Tianjin, China, 2019. [Google Scholar]
- Jiang, Y.; Bin, G.; Li, C.; Li, J. Study on unbalance phase difference combined vibration response of turboshaft engine combustor rotor considering dynamic characteristics of flexible supports. Mech. Sci. Tech. Aerosp. Eng. 2022, 41, 1524–1529. [Google Scholar]
- Molčan, M.; Ferfecki, P.; Zapoměl, J. The numerical identification of basins of attraction for the vibration response of the rigid rotor with squeeze film dampers. Appl. Sci. 2023, 13, 2864. [Google Scholar] [CrossRef]
- Ri, K.; Ri, Y.; Yun, C.; Kim, K.; Han, P. Analysis of nonlinear vibration and stability of Jeffcott rotor supported on squeeze-film damper by IHB method. AIP Adv. 2022, 12, 025127. [Google Scholar]
- Ye, D. Research of Dynamic Response on High Speed Flexible Rotor Due to Sudden Large Unbalance. Master’s Thesis, Zhejiang University, Hangzhou, China, 2014. [Google Scholar]
- Han, Z.; Ma, Z.; Zhang, W.; Han, B.; Ding, Q. Dynamic analysis of an elastic ring squeeze film damper supported rotor using a semi-analytic method. Eng. Appl. Comp. Fluid Mech. 2020, 14, 1263–1278. [Google Scholar] [CrossRef]
- Zhou, H.; Luo, G.; Ai, Y.; Sun, D. Sudden unbalance response analysis of rotor system supported on floating ring squeeze film damper. J. Aerosp. Power 2014, 29, 7. [Google Scholar]
- Zhou, H.; Luo, G.; Chen, G.; Wang, F. Analysis of the nonlinear dynamic response of a rotor supported on ball bearings with floating-ring squeeze film dampers. Mech. Mach. Theory 2013, 59, 65–77. [Google Scholar] [CrossRef]
- Xia, Y.; Ren, X.; Qin, W.; Deng, W. Analysis of the effect of floating ring squeeze film damper on sudden unbalance response of low pressure rotor. J. Aerosp. Power 2015, 30, 2771–2778. [Google Scholar]
- Zhang, G.; Huang, Y.; Chen, Y.; Wang, Z.; Xu, K.; Feng, L. Experiment on vibration reduction performance of elastic ring squeeze film damper under sudden unbalance. J. Aerosp. Power 2023, 38, 32–40. [Google Scholar]
- Yang, X.; Jiang, B.; Li, Y.; Zhao, Q.; Deng, S.; Zhang, W.; Cui, Y. Dynamic characteristics of elastic ring squeeze film damper coupled high-speed ball bearings. J. Sound Vib. 2022, 537, 117186. [Google Scholar] [CrossRef]
- Li, Y.; Yang, H.; Cui, Y.; Deng, S.; Zhang, W. Nonlinear dynamic properties of rigid-elastic-liquid coupled ball bearings considering external load excitation. Int. J. Struct. Stab. Dy. 2024; in press. [Google Scholar]
- Zhong, X.; Jiang, J.; Bin, G.; Chen, A.; Yang, F. Vibration characteristics of turbocharger rotor system considering internal thread texture parameters of semi-floating ring bearing. Proc. IMechE Part J J. Eng. Tribol. 2023, 237, 1796–1808. [Google Scholar] [CrossRef]
- Deng, S.; Jia, Q.; Xue, J. Rolling Bearing Design Principle, 2nd ed.; Standards Press of China: Beijing, China, 2014. [Google Scholar]
- Liu, J.; Chiu, Y. Analysis of a thin elastic ring under arbitrary loading. J. Eng. Ind. 1974, 96, 870. [Google Scholar] [CrossRef]
- Greenhill, L.M.; Nelson, H.D. Iterative determination of squeeze film damper eccentricity for flexible rotor systems. J. Mech. Des. 1982, 104, 334–338. [Google Scholar] [CrossRef]



| Symbol | Value or Range Variation |
|---|---|
| Equivalent mass of the damper | |
| The vibration mass range at the disc | |
| The stiffness of the shaft | |
| The stiffness [45] of the squirrel cage | |
| The length of the Damper | |
| Inner cavity oil film radius clearance | |
| The radius of the journal | |
| The journal angular velocity range | |
| The critical angular velocity of the rotor system | |
| The damping ratio range | |
| The oil type | |
| Dynamic viscosity of the oil | |
| The stiffness [45] of the elastic ring | |
| The flexibility coefficient [45] of the elastic ring | 0.1 |
| The number of the boss | 20 |
| Run | |||||||
| 0.6 | 15.6 | 1300 | 0.7055 | 0.72, 1.29 | 1 | 0.25 | |
| 0.6 | 15.6 | 1300 | 0.7055 | 0.97 | 0.5, 1.6 | 0.25 | |
| 0.6 | 15.6 | 1300 | 0.7055 | 0.97 | 1 | 0.33, 0.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Cui, Y.; Deng, S. Research on Sudden Unbalance Response of Rigid-Elastic-Oil Coupled Ball Bearings. Lubricants 2024, 12, 161. https://doi.org/10.3390/lubricants12050161
Li Y, Cui Y, Deng S. Research on Sudden Unbalance Response of Rigid-Elastic-Oil Coupled Ball Bearings. Lubricants. 2024; 12(5):161. https://doi.org/10.3390/lubricants12050161
Chicago/Turabian StyleLi, Yan, Yongcun Cui, and Sier Deng. 2024. "Research on Sudden Unbalance Response of Rigid-Elastic-Oil Coupled Ball Bearings" Lubricants 12, no. 5: 161. https://doi.org/10.3390/lubricants12050161
APA StyleLi, Y., Cui, Y., & Deng, S. (2024). Research on Sudden Unbalance Response of Rigid-Elastic-Oil Coupled Ball Bearings. Lubricants, 12(5), 161. https://doi.org/10.3390/lubricants12050161




