Influence of Nanoparticles in Lubricant on Sliding Contact of Atomic Rough Surfaces—A Molecular Dynamics Study
Abstract
1. Introduction
2. Simulation Models and Details
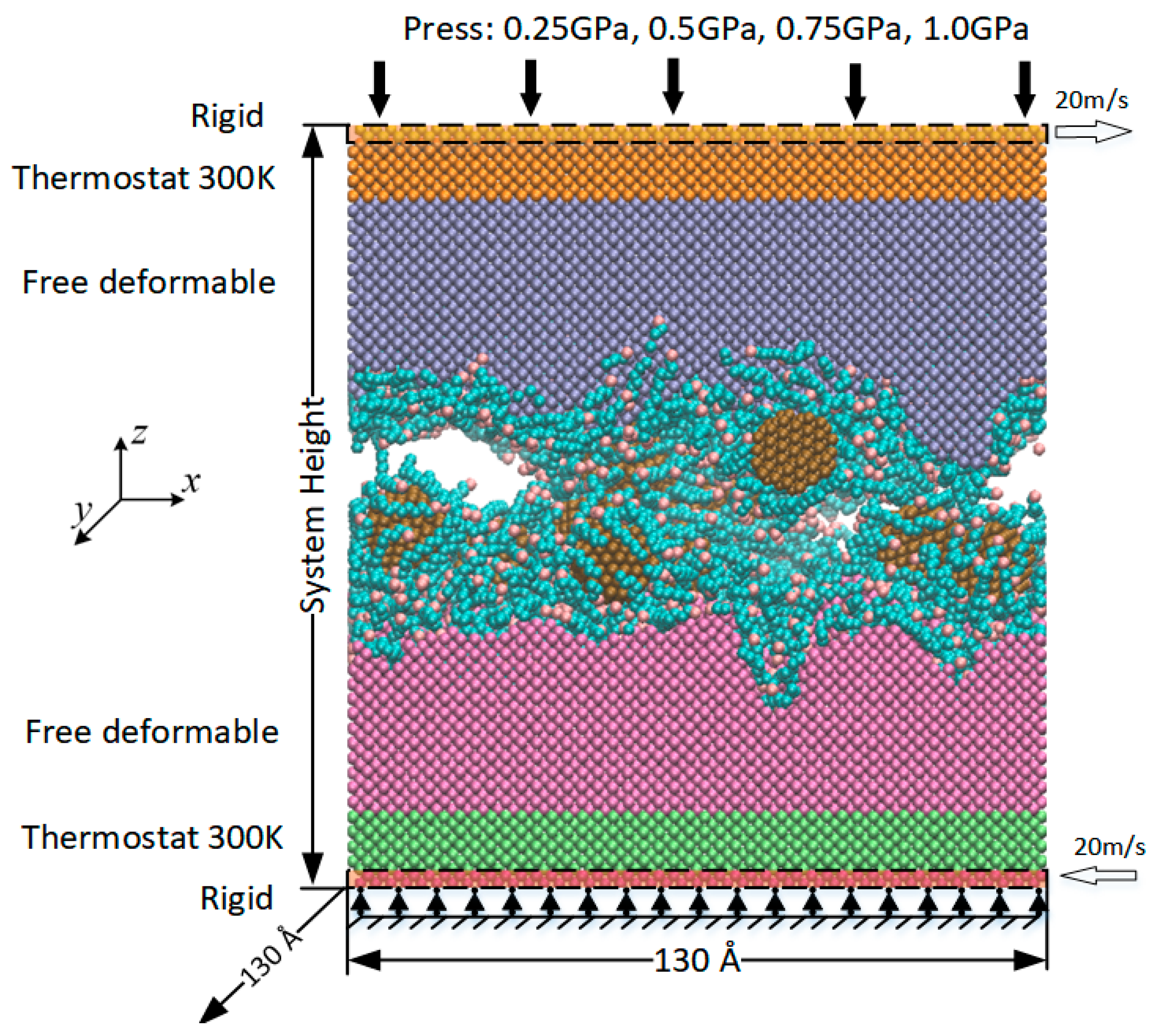
2.1. Simulation Model
2.2. Molecular Dynamics
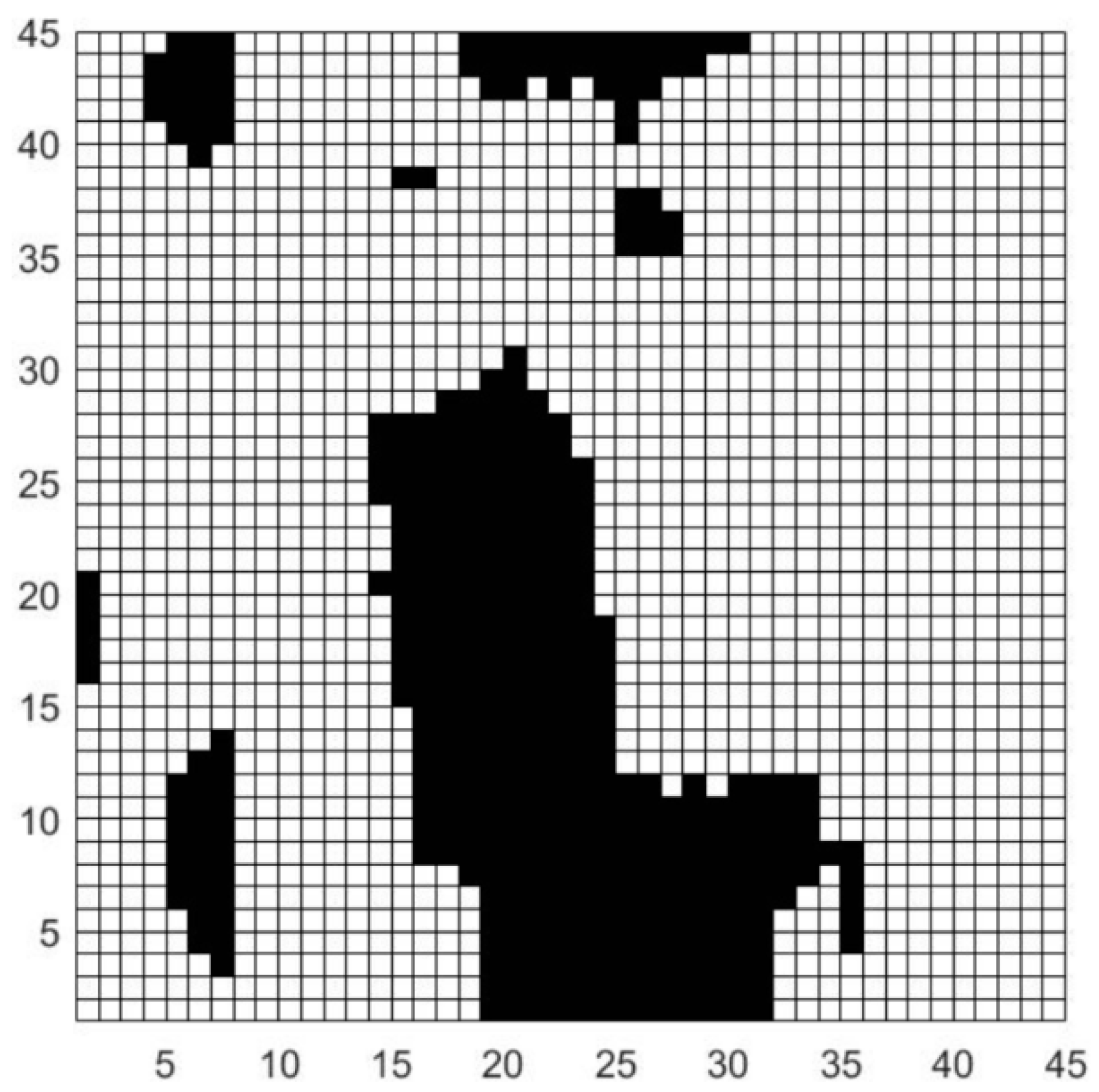
2.3. Atomic Scale Contact Conditions
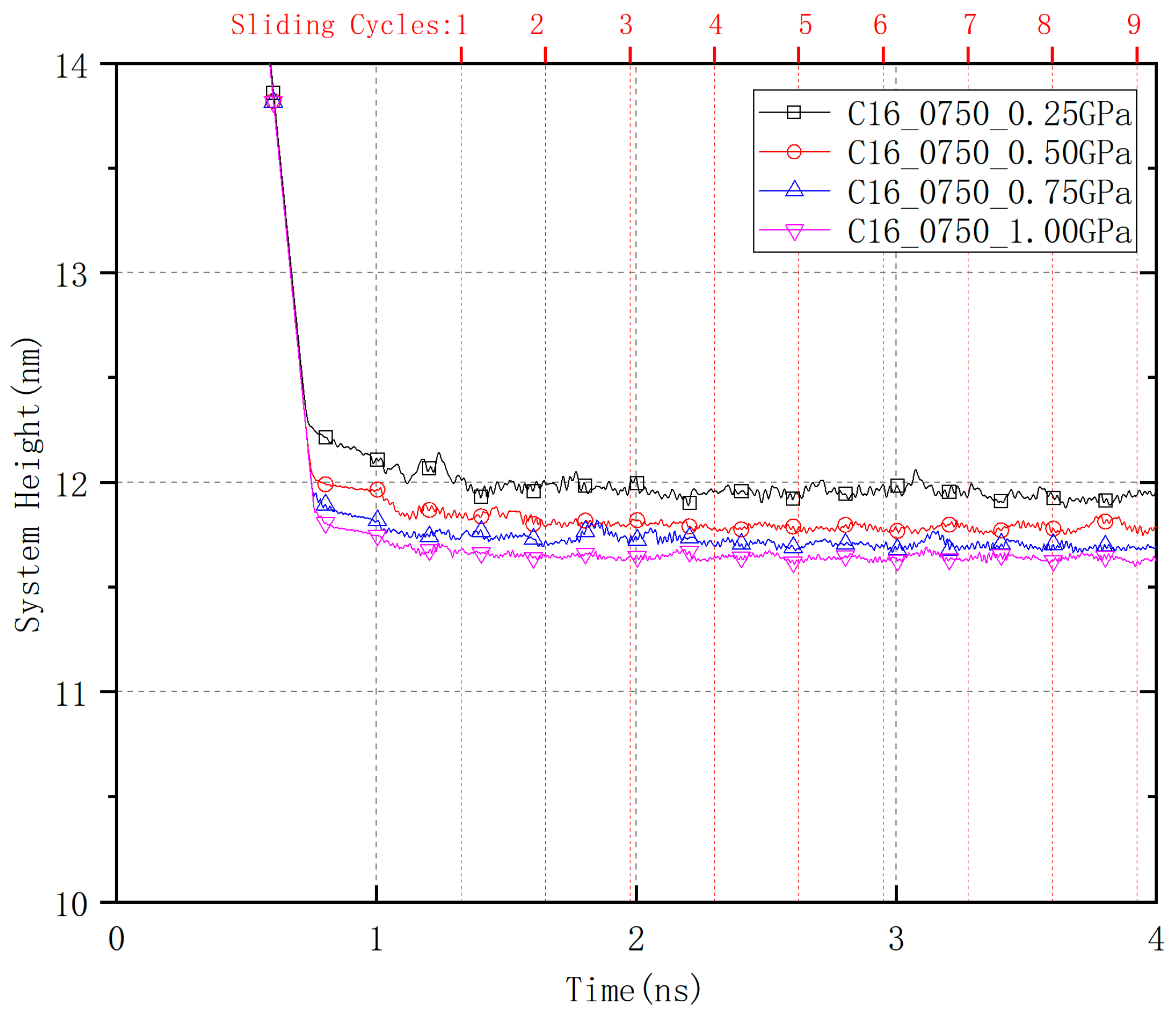
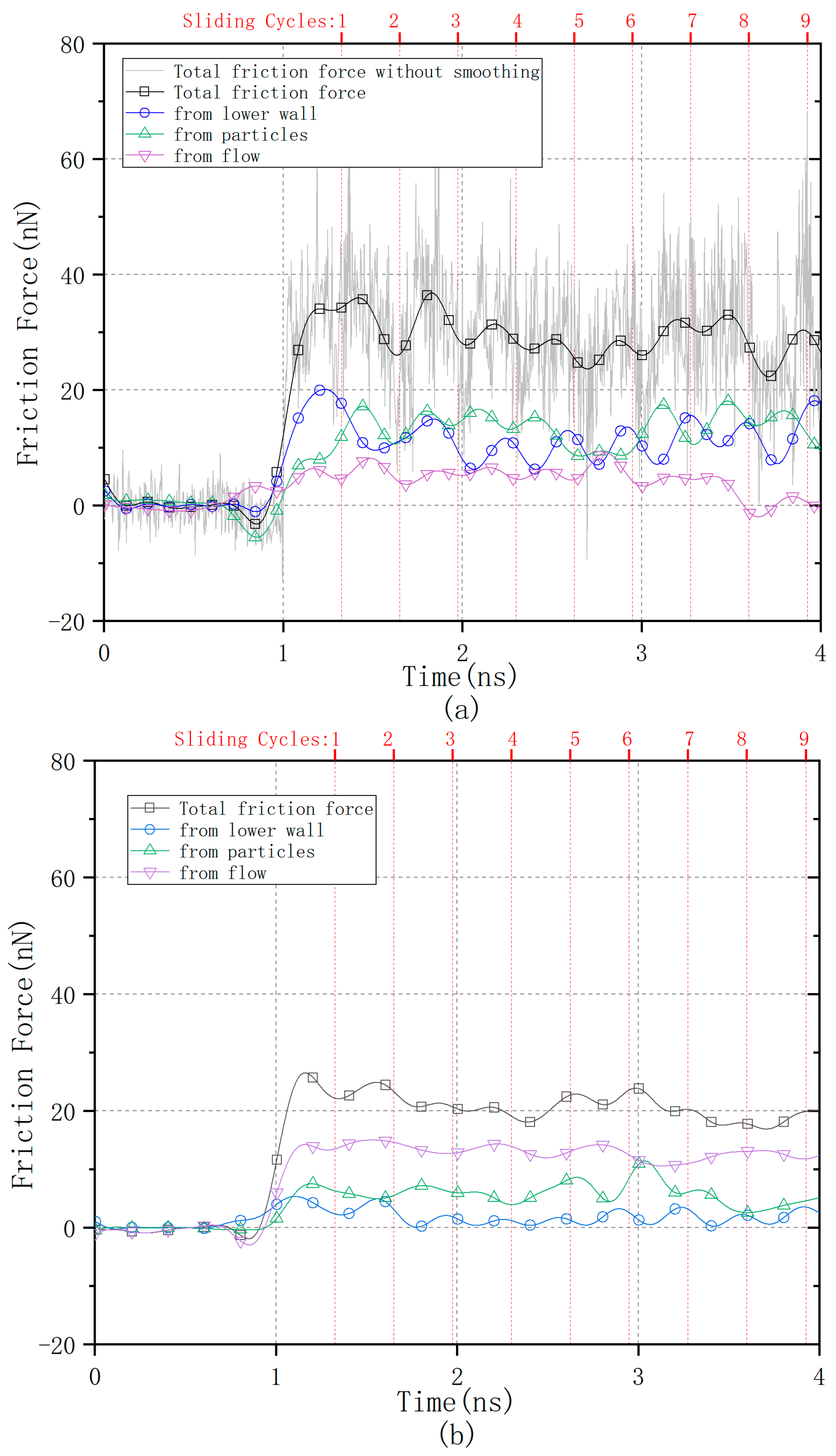
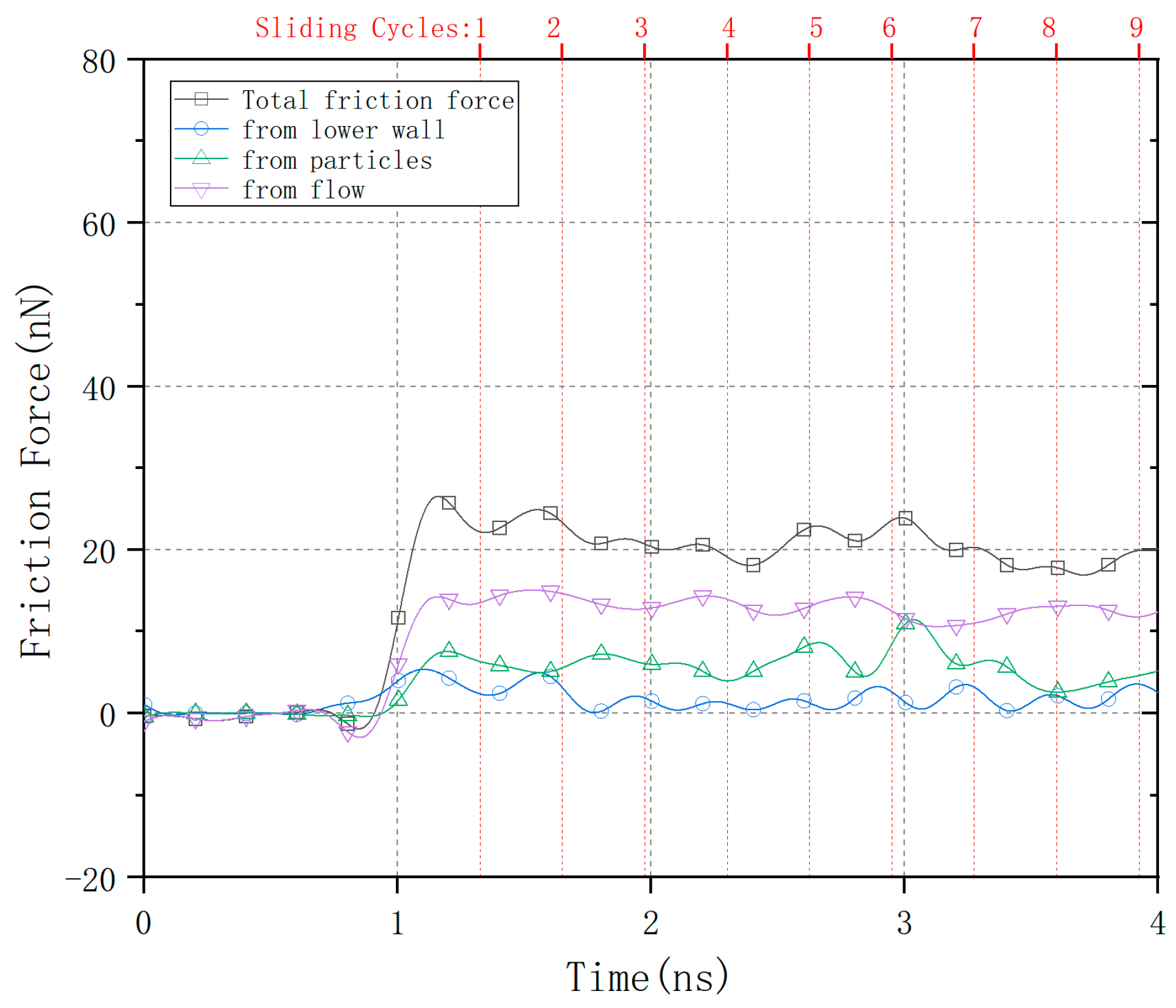
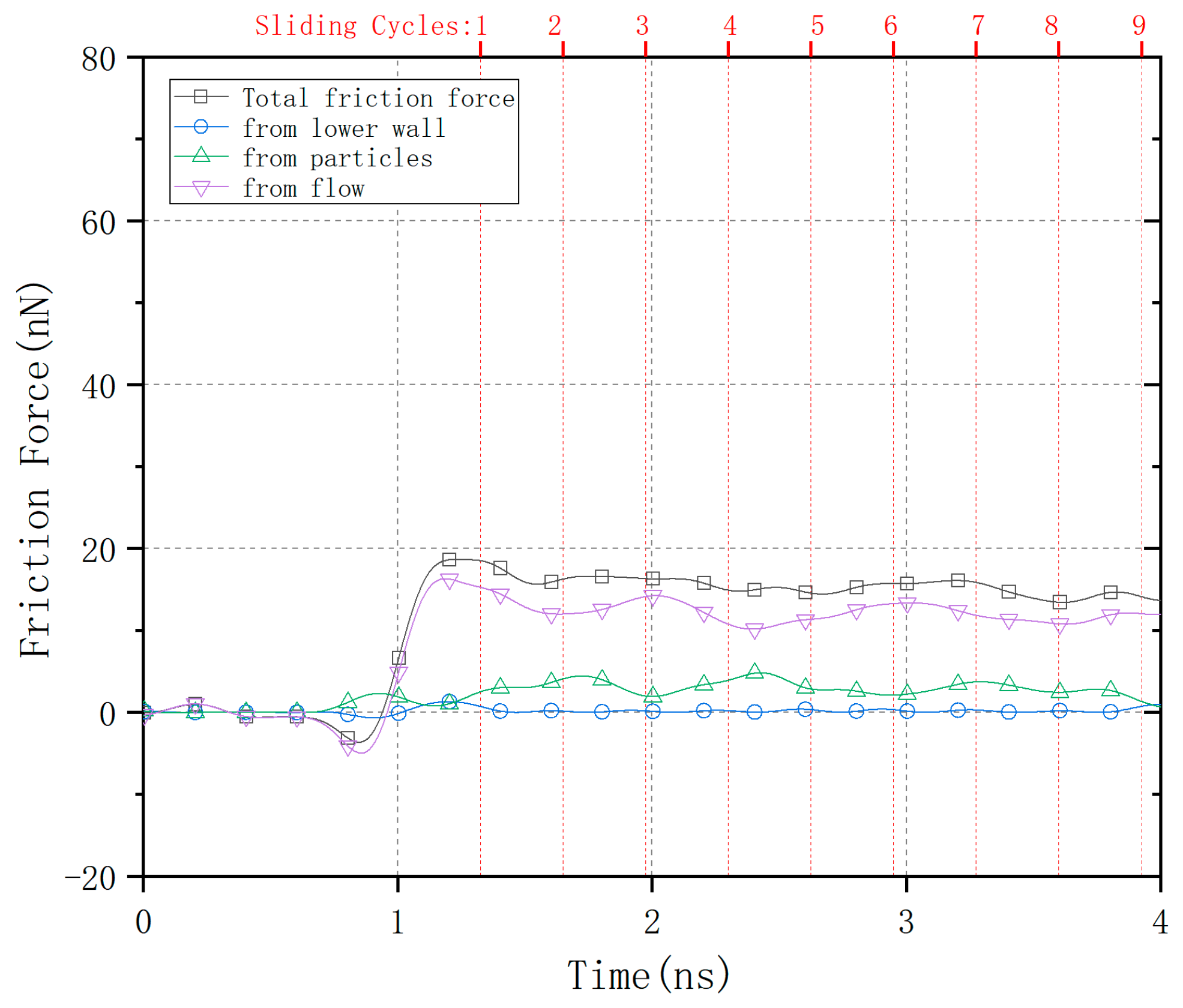
3. Results and Discussion
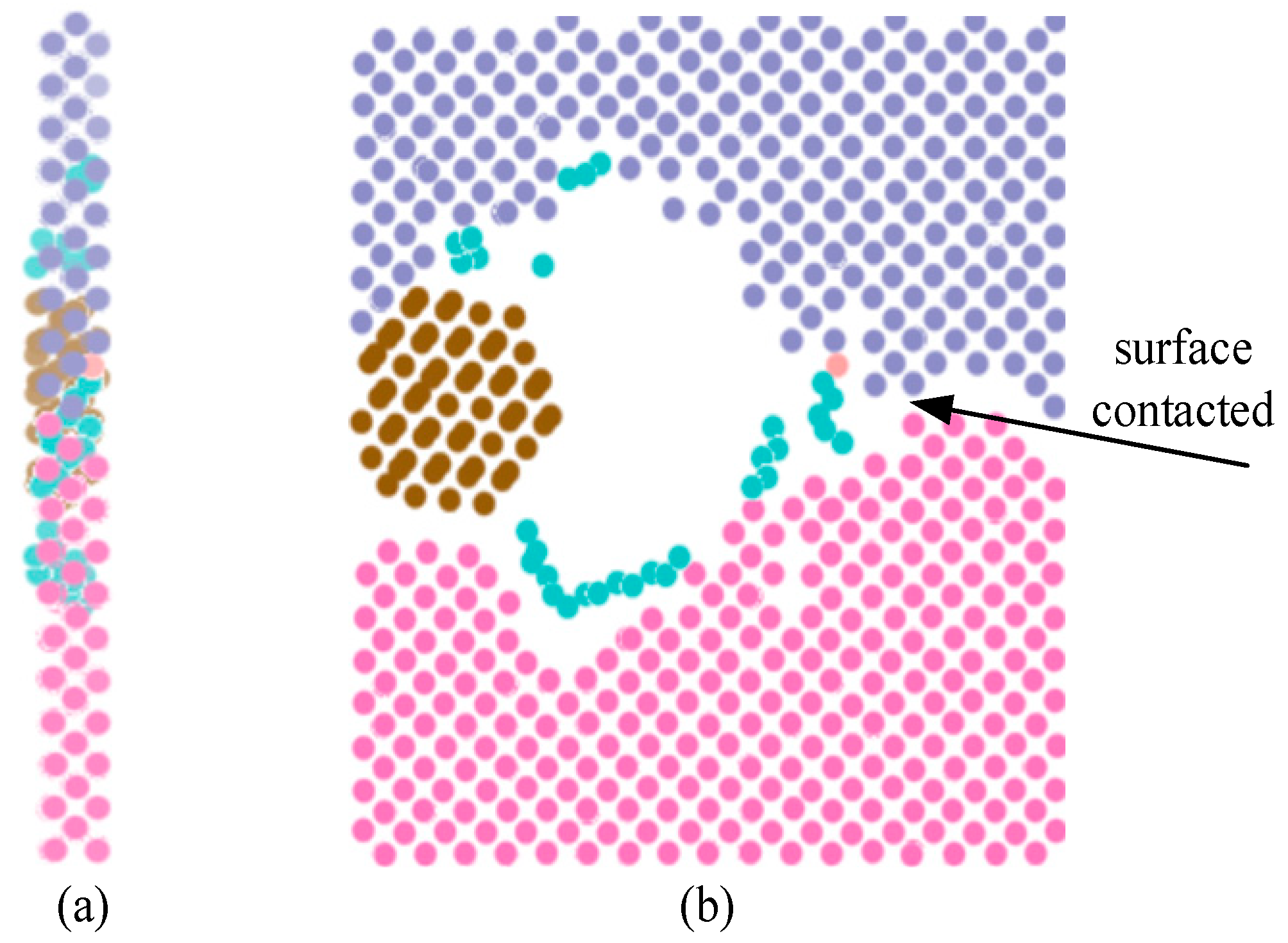
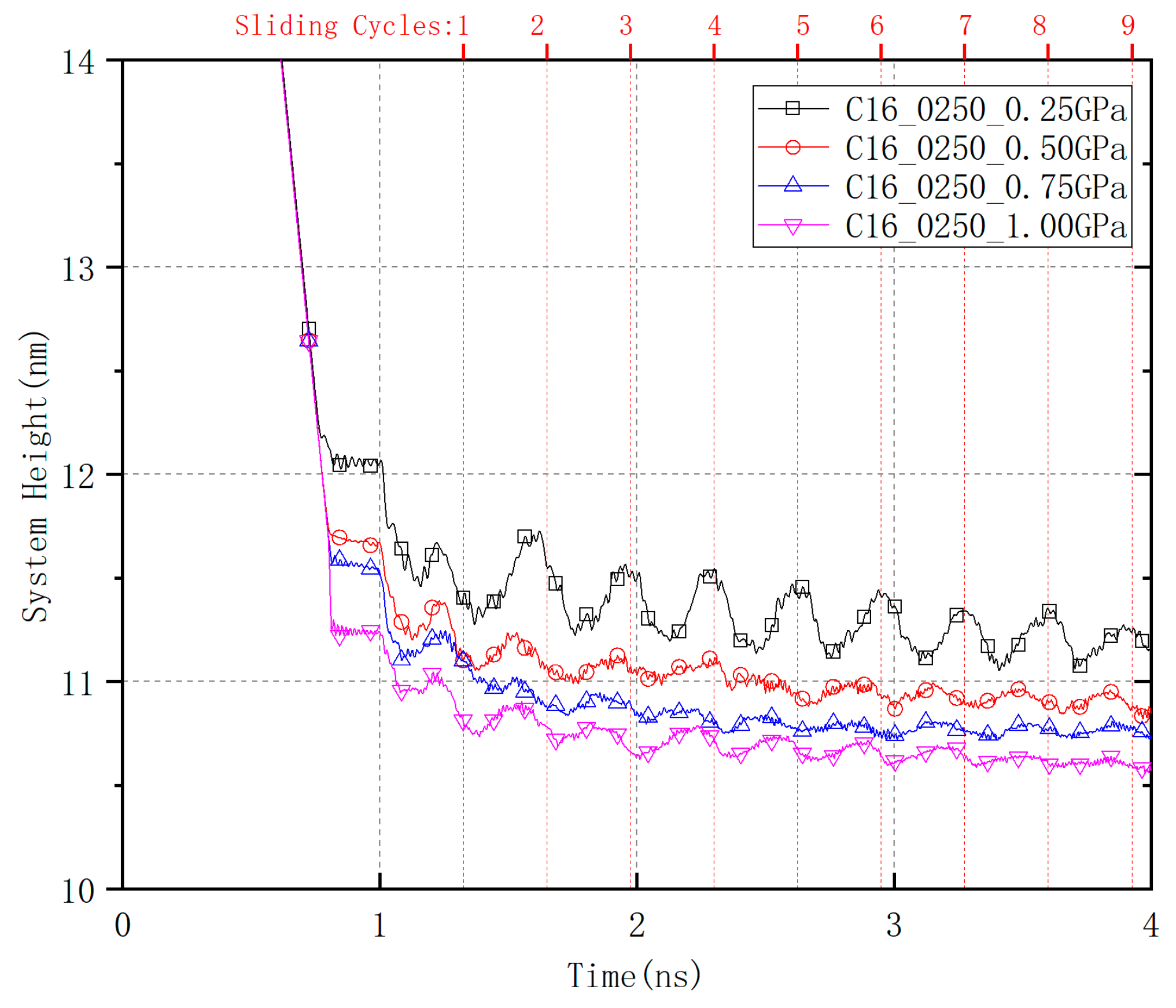
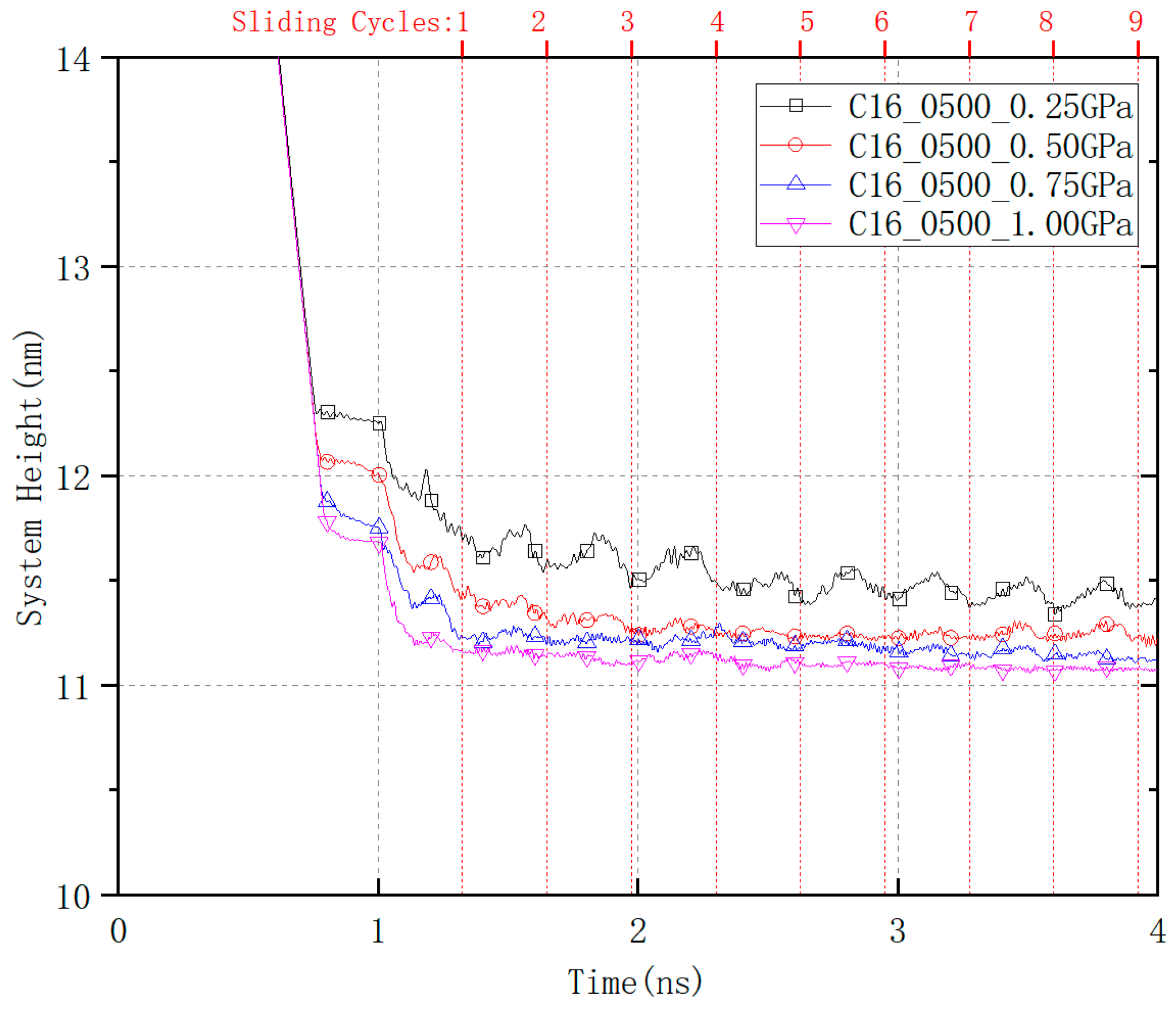
3.1. Relaxation and Compression
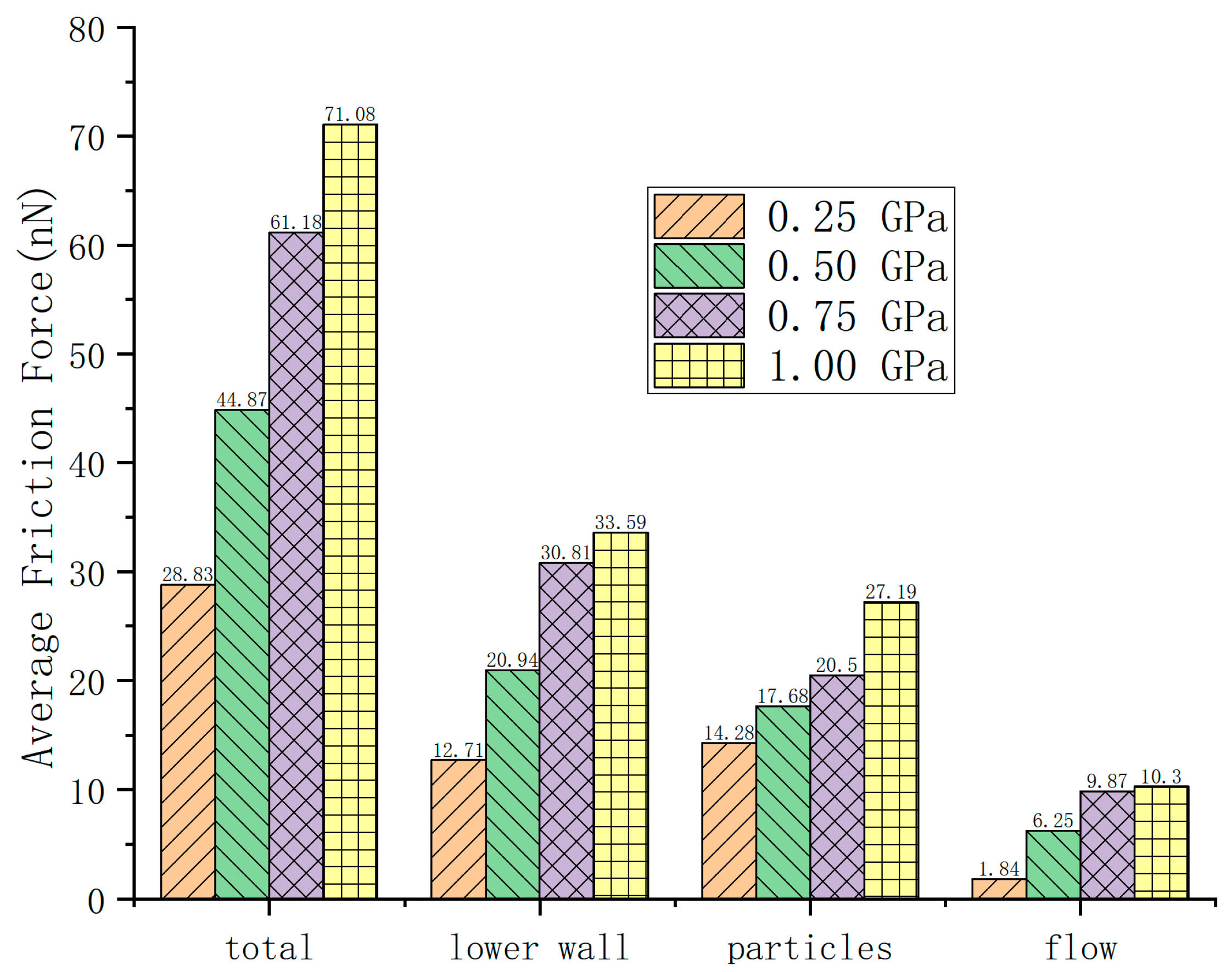
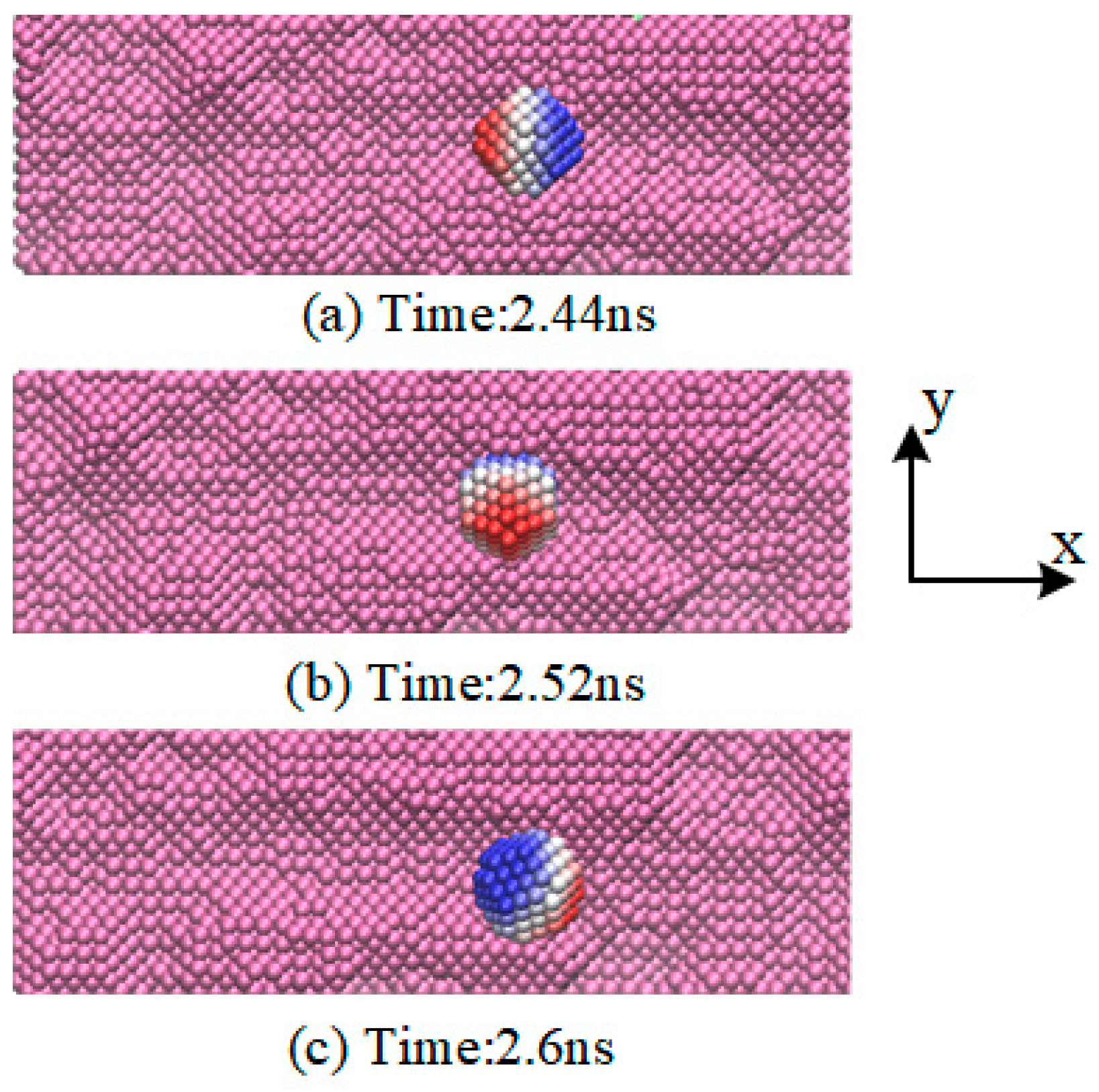
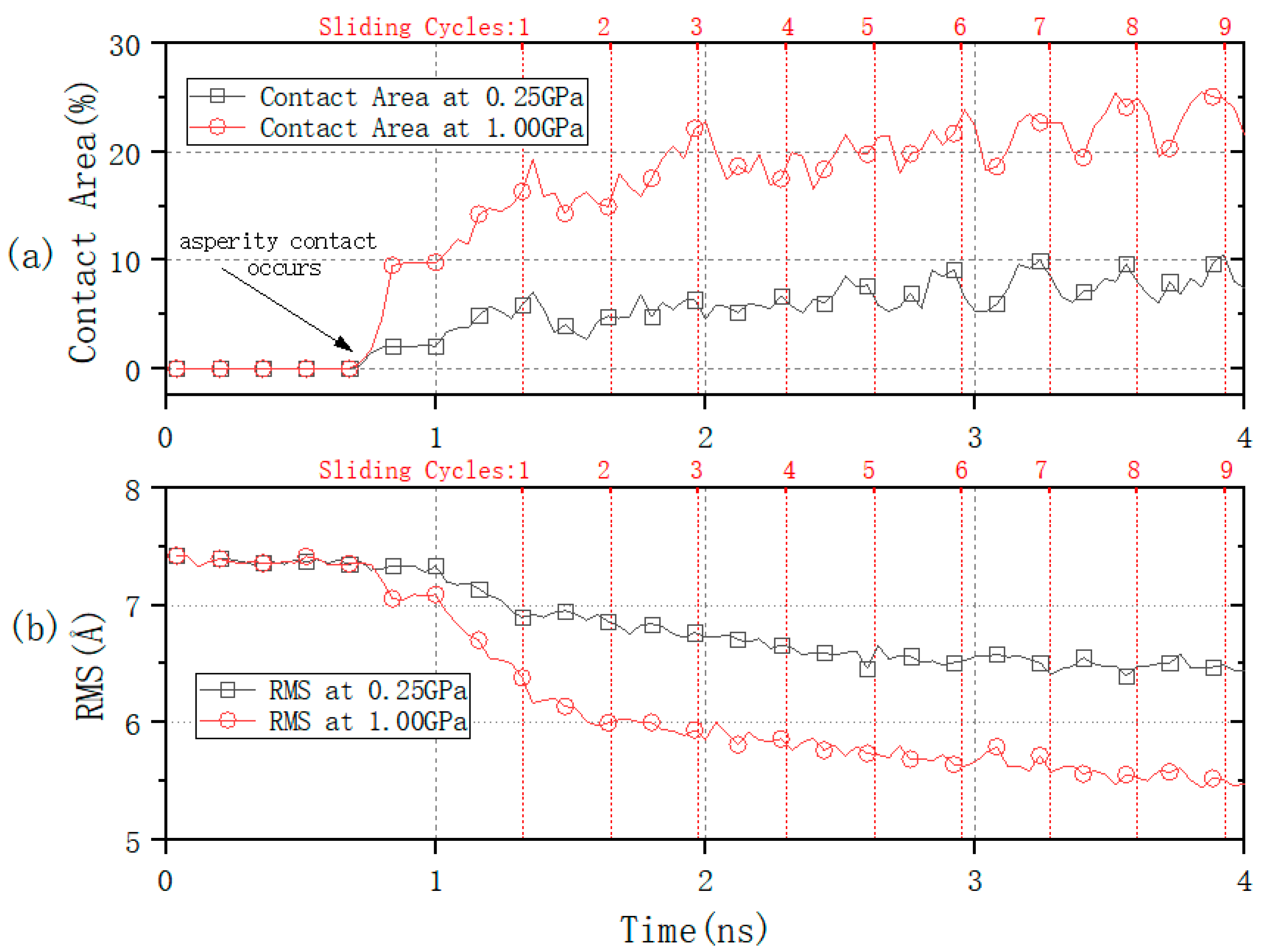
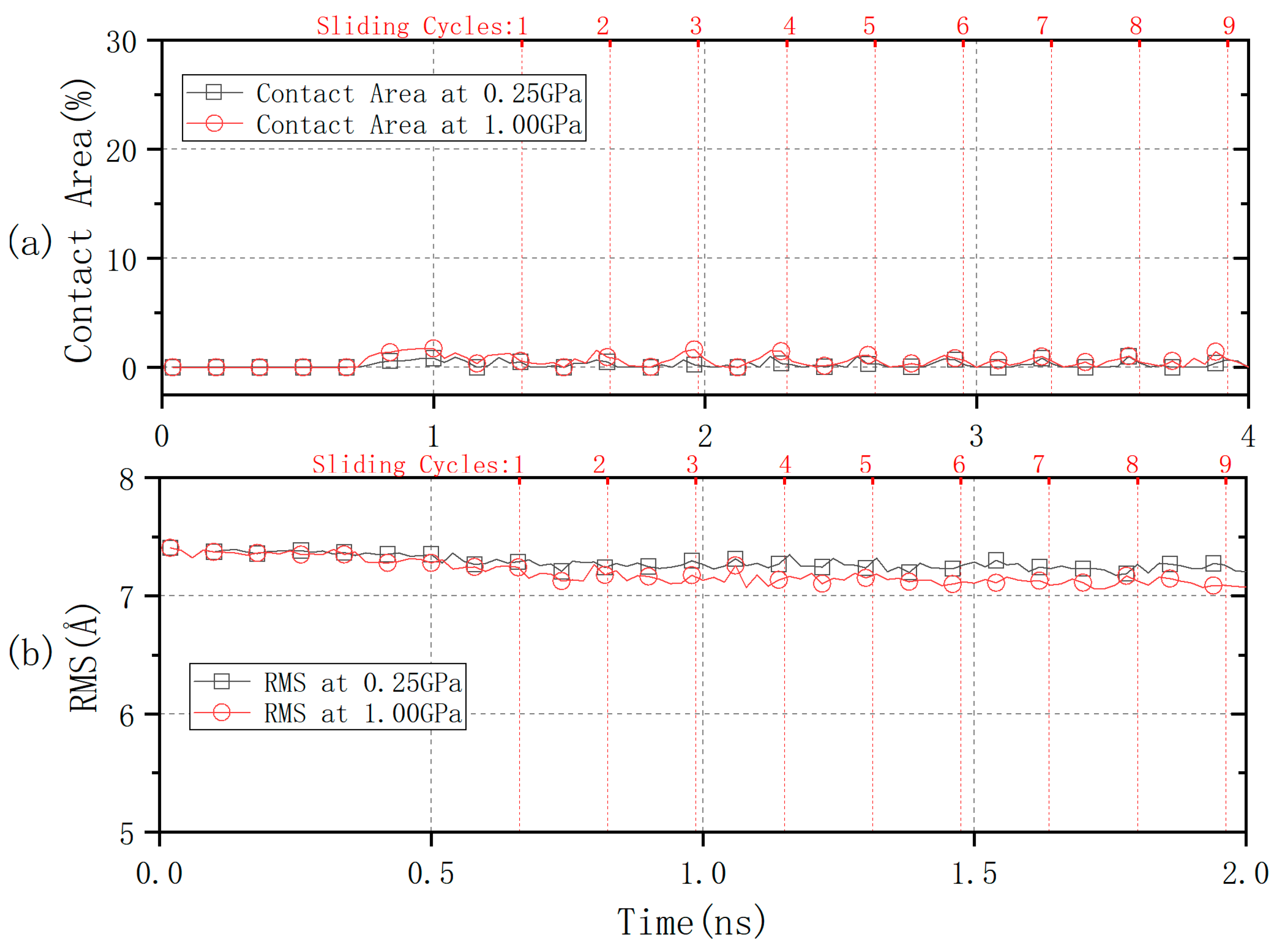
3.2. Sliding Contact Behavior
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, G.; Zhu, H.; Tieu, A.K. Advances in Friction, Lubrication, Wear and Oxidation in Metals Manufacturing. Metals 2023, 13, 505. [Google Scholar] [CrossRef]
- Sun, J.; Mao, X.; Yang, Z.; Zhou, X.; Zhao, X. Effect of gradient microstructure on wear behavior of carbon steel. Mater. Res. Express 2019, 6, 126566. [Google Scholar] [CrossRef]
- Chen, X.; Han, Z. A low-to-high friction transition in gradient nano-grained Cu and Cu-Ag alloys. Friction 2021, 9, 1558–1567. [Google Scholar] [CrossRef]
- Su, L.; Deng, G.; Luzin, V.; Wang, H.; Wang, Z.; Yu, H.; Li, H.; Tieu, A.K. Effect of cryogenic temperature equal channel angular pressing on microstructure, bulk texture and tensile properties of AA1050. Mater. Sci. Eng. A 2020, 780, 139190. [Google Scholar] [CrossRef]
- Zhang, Y.S.; Niu, H.Z.; Zhang, L.C.; Bai, X.F.; Zhang, X.M.; Zhang, P.X. Grain coarsening behavior in a nanocrystalline copper subjected to sliding friction. Mater. Lett. 2014, 123, 261–264. [Google Scholar] [CrossRef]
- Deng, G.; Chong, Y.; Su, L.; Zhan, L.; Wei, P.; Zhao, X.; Zhang, L.; Tian, Y.; Zhu, H.; Tsuji, N. Mechanisms of remarkable wear reduction and evolutions of subsurface microstructure and nano-mechanical properties during sliding of nano-grained Ti6Al4V alloy: A comparative study. Tribol. Int. 2022, 169, 107464. [Google Scholar] [CrossRef]
- Li, G.; Jiang, J.; Ma, H.; Zheng, R.; Gao, S.; Zhao, S.; Ma, C.; Ameyama, K.; Ding, B.; Li, X. Superior strength-ductility synergy in three-dimensional heterogeneous-nanostructured metals. Acta Mater. 2023, 256, 119143. [Google Scholar] [CrossRef]
- Zhou, G.; Ma, H.; Zhang, Z.; Sun, J.; Wang, X.; Zeng, P.; Zheng, R.; Chen, X.; Ameyama, K. Fatigue crack growth behavior in a harmonic structure designed austenitic stainless steel. Mater. Sci. Eng. A 2019, 758, 121–129. [Google Scholar] [CrossRef]
- Zhang, J.; Deng, G.; Li, W.; Su, L.; Liu, X.; Ma, T.; Gao, L. Impacts of chemical short-range orders on nanotribological properties of CrCoNi medium-entropy alloy at room and cryogenic temperatures. Tribol. Int. 2024, 191, 109191. [Google Scholar] [CrossRef]
- Zhang, J.; Li, W.; Qin, R.; Chen, P.; Liu, Y.; Liu, X.; Gao, L. An atomic insight into the stoichiometry effect on the tribological behaviors of CrCoNi medium-entropy alloy. Appl. Surf. Sci. 2022, 593, 153391. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, D.; An, X.; Zhang, Y.; Zhou, Z.; Lu, S.; Munroe, P.; Zhang, S.; Liao, X.; Zhu, T.; et al. Unraveling dual phase transformations in a CrCoNi medium-entropy alloy. Acta Mater. 2021, 215, 117112. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Y.; Zhu, H. A review on the tribological performances of high-entropy alloys. Adv. Eng. Mater. 2022, 24, 2101548. [Google Scholar] [CrossRef]
- Lei, G.; Zhang, Y.; Gao, H.T.; Cui, X.H.; Yu, H.L. Nano-tribological behavior of a CuCoCrFeNi high-entropy alloy at cryogenic temperature: A molecular dynamics study. J. Appl. Phys. 2023, 133, 155901. [Google Scholar] [CrossRef]
- Zhu, Z.X.; Liu, X.B.; Liu, Y.F.; Zhang, S.Y.; Meng, Y.; Zhou, H.B.; Zhang, S.H. Effect of Cu-doping on tribological properties of laser-cladded FeCoCrNiCux high-entropy alloy coatings. Tribol. Int. 2023, 188, 108868. [Google Scholar]
- Sun, Q.; Tan, H.; Zhu, S.; Zhu, Z.; Wang, L.; Cheng, J.; Yang, J. Sing-phase (Hf-Mo-Nb-Ta-Ti)C high-entropy ceramic: A potential high temperature anti-wear material. Tribol. Int. 2021, 157, 106883. [Google Scholar] [CrossRef]
- Shi, P.Y.; Yu, Y.; Xiong, N.N.; Liu, M.Z.; Qiao, Z.H.; Yi, G.W.; Yao, Q.Q.; Zhao, G.P.; Xie, E.Q.; Wang, Q.H. Microstructure and tribological behavior of a novel atmospheric plasma sprayed AlCoCrFeNi high entropy alloy matrix self-lubricating composite coatings. Tribol. Int. 2020, 151, 106470. [Google Scholar] [CrossRef]
- Zhang, A.; Han, J.; Su, B.; Meng, J. A novel CoCrFeNi high entropy alloy matrix self-lubricating composite. J. Alloys Compd. 2017, 725, 700–710. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, J.; Li, J.S.; Kou, H.C.; Liu, W.M. Tribological behavior of AlCoCrFeNi(Ti0.5) high entropy alloys under oil and MACs lubrication. J. Mater. Sci. Technol. 2016, 32, 470. [Google Scholar] [CrossRef]
- Liu, Y.; Tao, C.; Liu, X.; Zhu, Y.; Wang, G.; Meng, Y.; Liang, J.; Xie, J. Research progress on tribological properties of high-entropy alloy coating. Surf. Technol. 2021, 50, 156–169. [Google Scholar]
- Zhang, A.; Han, J.; Su, B.; Meng, J. A promising new high temperature self-lubricating materials: CoCrFeNiS0.5 high entropy alloy. Mater. Sci. Eng. A 2018, 731, 36–43. [Google Scholar] [CrossRef]
- Tran, B.H.; Tieu, A.; Wan, S.; Zhu, H.; Cui, S.; Wang, L. Understanding the tribological impacts of alkali element on lubrication of binary borate melt. RSC Adv. 2018, 8, 28847–28860. [Google Scholar] [CrossRef] [PubMed]
- Ta, T.D.; Tieu, A.K.; Tran, B.H. Molecular dynamics simulations of nanolubricant films of alkali glasses under sliding asperity contacts. ACS Appl. Nano Mater. 2021, 10, 11210–11220. [Google Scholar] [CrossRef]
- Rodrigues, A.C.P.; Yonamine, T.; Albertin, E.; Sinatora, A.; Azevedo, C.R.F. Effect of Cu Particles as an Interfacial Media Addition on the Friction Coefficient and Interface Microstructure during (Steel/Steel) Pin on Disc Tribotest. Wear 2015, 330–331, 70–78. [Google Scholar] [CrossRef]
- Radice, S.; Mischler, S. Effect of Electrochemical and Mechanical Parameters on the Lubrication Behaviour of Al2O3 Nanoparticles in Aqueous Suspensions. Wear 2006, 261, 1032–1041. [Google Scholar] [CrossRef]
- Xie, H.; Jiang, B.; He, J.; Xia, X.; Pan, F. Lubrication Performance of MoS2 and SiO2 Nanoparticles as Lubricant Additives in Magnesium Alloy-Steel Contacts. Tribol. Int. 2016, 93, 63–70. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, W.; Liu, J.; Fu, X.; Chen, G.; Yao, S. The Size Effect of SiO2 Particles on Friction Mechanisms of a Composite Friction Material. Tribol. Lett. 2018, 66, 35. [Google Scholar] [CrossRef]
- Rabaso, P.; Ville, F.; Dassenoy, F.; Diaby, M.; Afanasiev, P.; Cavoret, J.; Vacher, B.; Le Mogne, T. Boundary Lubrication: Influence of the Size and Structure of Inorganic Fullerene-like MoS2 Nanoparticles on Friction and Wear Reduction. Wear 2014, 320, 161–178. [Google Scholar] [CrossRef]
- Cizaire, L.; Vacher, B.; Le Mogne, T.; Martin, J.M.; Rapoport, L.; Margolin, A.; Tenne, R. Mechanisms of Ultra-Low Friction by Hollow Inorganic Fullerene-like MoS2 Nanoparticles. Surf. Coat. Technol. 2002, 160, 282–287. [Google Scholar] [CrossRef]
- Lahouij, I.; Dassenoy, F.; Vacher, B.; Martin, J.M. Real Time TEM Imaging of Compression and Shear of Single Fullerene-Like MoS2 Nanoparticle. Tribol. Lett. 2011, 45, 131–141. [Google Scholar] [CrossRef]
- Hu, C.; Bai, M.; Lv, J.; Kou, Z.; Li, X. Molecular Dynamics Simulation on the Tribology Properties of Two Hard Nanoparticles (Diamond and Silicon Dioxide) Confined by Two Iron Blocks. Tribol. Int. 2015, 90, 297–305. [Google Scholar] [CrossRef]
- Hu, C.; Bai, M.; Lv, J.; Wang, P.; Li, X. Molecular Dynamics Simulation on the Friction Properties of Nanofluids Confined by Idealized Surfaces. Tribol. Int. 2014, 78, 152–159. [Google Scholar] [CrossRef]
- Dai, W.; Kheireddin, B.; Gao, H.; Liang, H. Roles of Nanoparticles in Oil Lubrication. Tribol. Int. 2016, 102, 88–98. [Google Scholar] [CrossRef]
- Moshkovith, A.; Perfiliev, V.; Lapsker, I.; Fleischer, N.; Tenne, R.; Rapoport, L. Friction of Fullerene-like WS2 Nanoparticles: Effect of Agglomeration. Tribol. Lett. 2006, 24, 225–228. [Google Scholar] [CrossRef]
- Tevet, O.; Von-Huth, P.; Popovitz-Biro, R.; Rosentsveig, R.; Wagner, H.D.; Tenne, R. Friction Mechanism of Individual Multilayered Nanoparticles. Proc. Natl. Acad. Sci. USA 2011, 108, 19901–19906. [Google Scholar] [CrossRef]
- Srivastava, I.; Kotia, A.; Ghosh, S.K.; Ali, M.K.A. Recent Advances of Molecular Dynamics Simulations in Nanotribology. J. Mol. Liq. 2021, 335, 116154. [Google Scholar] [CrossRef]
- Dong, S.; Wang, W.; Gao, Y.; Deng, G. Tribological properties of different-sized black phosphorus nanosheets as water-based lubrication additives for steel/titanium alloy wear. Metals 2022, 12, 288. [Google Scholar] [CrossRef]
- Zhang, J.; Su, L.; Wang, Z. Concurrent Multiscale Simulations of Rough Lubricated Contact of Aluminum Single Crystal. Metals 2020, 10, 965. [Google Scholar] [CrossRef]
- Stephan, S.; Lautenschlaeger, M.P.; Alhafez, I.A.; Horsch, M.T.; Urbassek, H.M.; Hasse, H. Molecular Dynamics Simulation Study of Mechanical Effects of Lubrication on a Nanoscale Contact Process. Tribol. Lett. 2018, 66, 126. [Google Scholar] [CrossRef]
- Stephan, S.; Schmitt, S.; Hasse, H. Molecular dynamics simulation of the Stribeck curve: Boundary lubrication, mixed lubrication, and hydrodynamic lubrication on the atomistic level. Friction 2023, 11, 2342–2366. [Google Scholar] [CrossRef]
- Zhang, C. Research on thin film lubrication: State of the art. Tribol. Int. 2005, 38, 443–448. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Harrowell, P.; Tanner, R.I. Low Friction Lubrication between Amorphous Walls: Unraveling the Contributions of Surface Roughness and in-Plane Disorder. J. Chem. Phys. 2006, 125, 034703. [Google Scholar] [CrossRef] [PubMed]
- Jabbarzadeh, A.; Atkinson, J.D.; Tanner, R.I. Effect of the Wall Roughness on Slip and Rheological Properties of Hexadecane in Molecular Dynamics Simulation of Couette Shear Flow between Two Sinusoidal Walls. Phys. Rev. E 2000, 61, 690–699. [Google Scholar] [CrossRef] [PubMed]
- Spijker, P.; Anciaux, G.; Molinari, J.-F. Dry Sliding Contact Between Rough Surfaces at the Atomistic Scale. Tribol. Lett. 2011, 44, 279–285. [Google Scholar] [CrossRef]
- Zheng, X.; Zhu, H.; Tieu, A.K.; Kosasih, B. Roughness and Lubricant Effect on 3D Atomic Asperity Contact. Tribol. Lett. 2013, 53, 215–223. [Google Scholar] [CrossRef]
- Mackowiak, S.; Heyes, D.M.; Dini, D.; Branka, A.C. Non-equilibrium phase behavior and friction of confined molecular films under shear: A non-equilibrium molecular dynamics study. J. Chem. Phys. 2016, 145, 164704. [Google Scholar] [CrossRef]
- Lv, J.; Bai, M.; Cui, W.; Li, X. The Molecular Dynamic Simulation on Impact and Friction Characters of Nanofluids with Many Nanoparticles System. Nanoscale Res. Lett. 2011, 6, 200. [Google Scholar] [CrossRef] [PubMed]
- Ji, C.; Sun, S.; Wang, B.; Lin, B. Molecular Dynamic Simulations of the Roles of Nanoparticles in Sliding Friction Process. Chem. Phys. Lett. 2019, 728, 44–49. [Google Scholar] [CrossRef]
- Zheng, X.; Su, L.; Deng, G.; Zhang, J.; Zhu, H.; Tieu, A.K. Study on lubrication characteristics of C4-Alkane and nanoparticle during boundary friction by molecular dynamics simulation. Metals 2021, 11, 1464. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The Nose–Hoover Thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Albohr, O.; Tartaglino, U.; Volokitin, A.I.; Tosatti, E. On the Nature of Surface Roughness with Application to Contact Mechanics, Sealing, Rubber Friction and Adhesion. J. Phys. Condens. Matter 2004, 17, R1. [Google Scholar] [CrossRef] [PubMed]
- Mendelev, M.I.; Han, S.; Srolovitz, D.J.; Ackland, G.J.; Sun, D.Y.; Asta, M. Development of New Interatomic Potentials Appropriate for Crystalline and Liquid Iron. Phil. Mag. 2003, 83, 3977–3994. [Google Scholar] [CrossRef]
- Savio, D.; Fillot, N.; Vergne, P.; Zaccheddu, M. A Model for Wall Slip Prediction of Confined N-Alkanes: Effect of Wall-Fluid Interaction Versus Fluid Resistance. Tribol. Lett. 2012, 46, 11–22. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Su, L.; Deng, G. Influence of Nanoparticles in Lubricant on Sliding Contact of Atomic Rough Surfaces—A Molecular Dynamics Study. Lubricants 2024, 12, 160. https://doi.org/10.3390/lubricants12050160
Zheng X, Su L, Deng G. Influence of Nanoparticles in Lubricant on Sliding Contact of Atomic Rough Surfaces—A Molecular Dynamics Study. Lubricants. 2024; 12(5):160. https://doi.org/10.3390/lubricants12050160
Chicago/Turabian StyleZheng, Xuan, Lihong Su, and Guanyu Deng. 2024. "Influence of Nanoparticles in Lubricant on Sliding Contact of Atomic Rough Surfaces—A Molecular Dynamics Study" Lubricants 12, no. 5: 160. https://doi.org/10.3390/lubricants12050160
APA StyleZheng, X., Su, L., & Deng, G. (2024). Influence of Nanoparticles in Lubricant on Sliding Contact of Atomic Rough Surfaces—A Molecular Dynamics Study. Lubricants, 12(5), 160. https://doi.org/10.3390/lubricants12050160





