Elastic and Elastoplastic Contact Mechanics of Concentrated Coated Contacts †
Abstract
1. Introduction
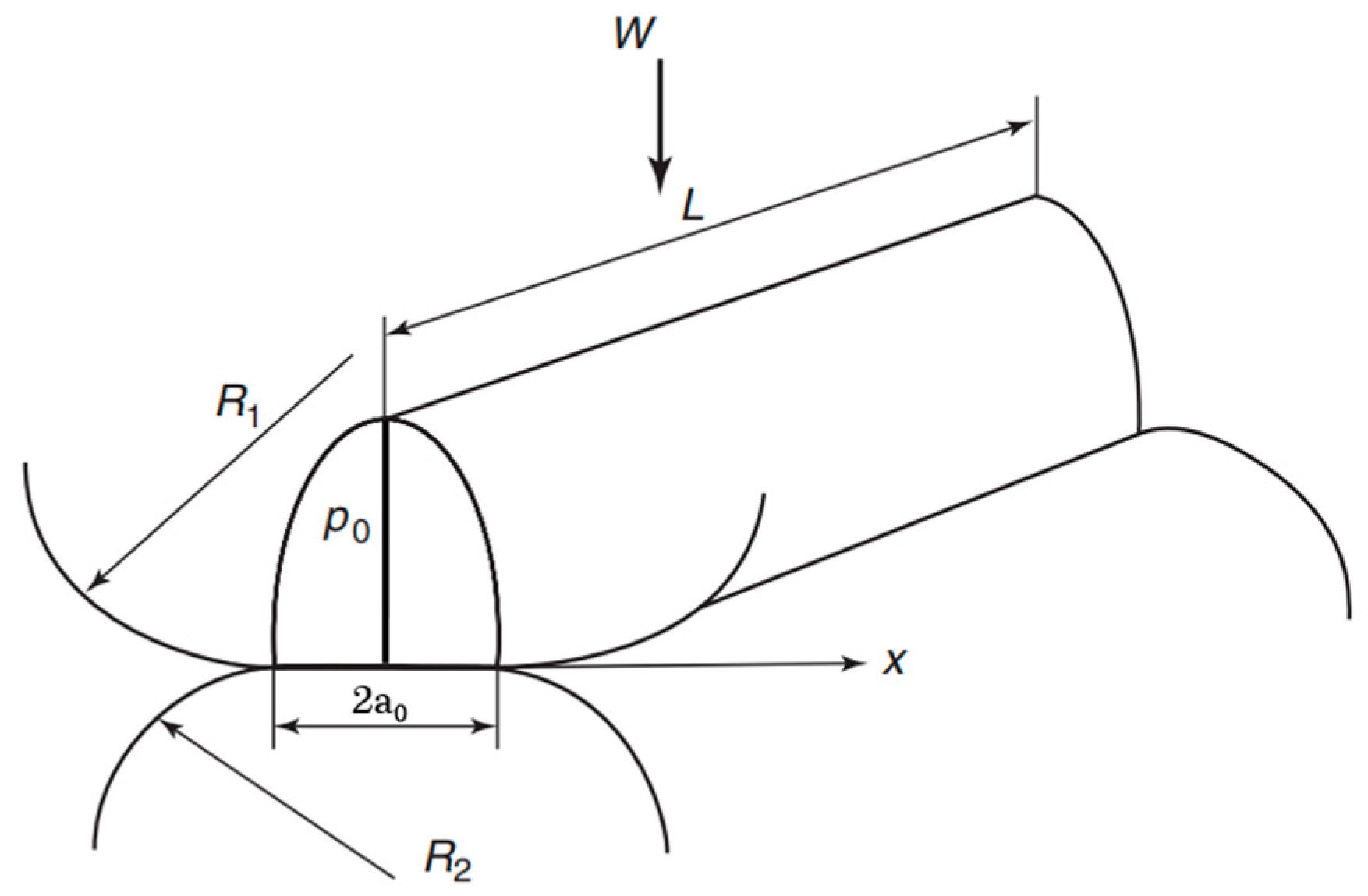
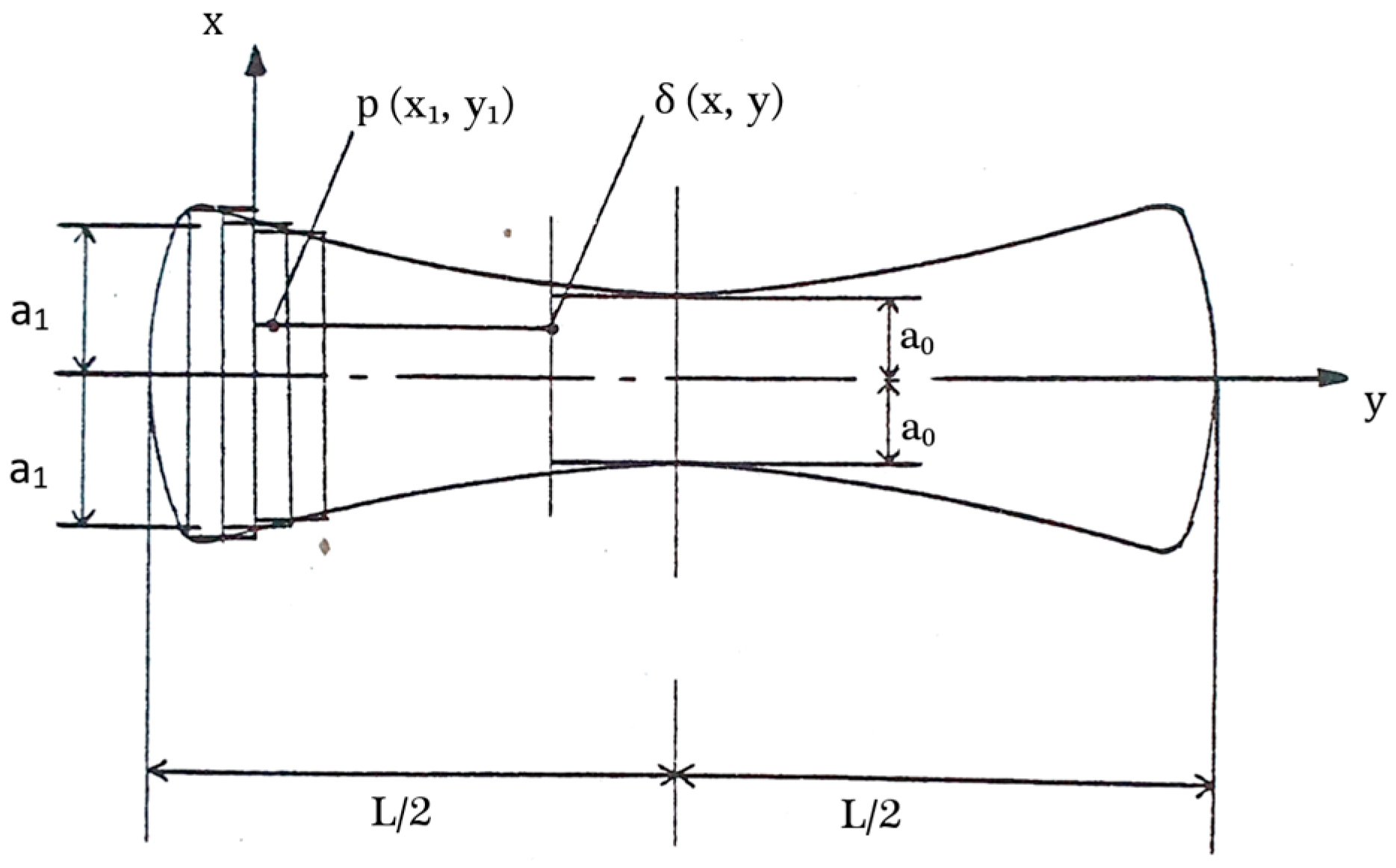
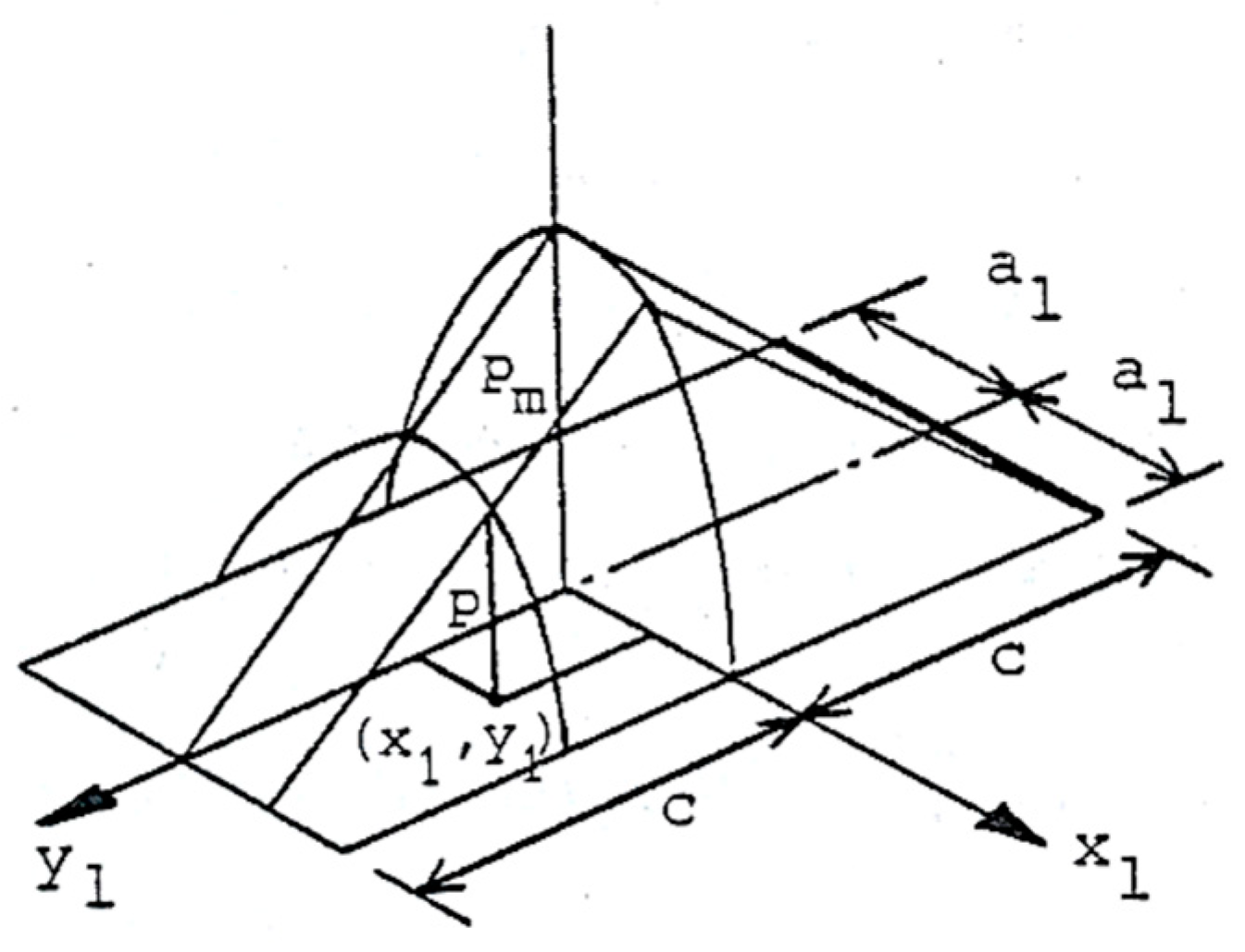
2. Contact Mechanics of Semi-Infinite Finite Line Contacts
3. The Case of Bonded Elastic Layered Solids
4. Contact Mechanics of Elastoplastic Layered Solids
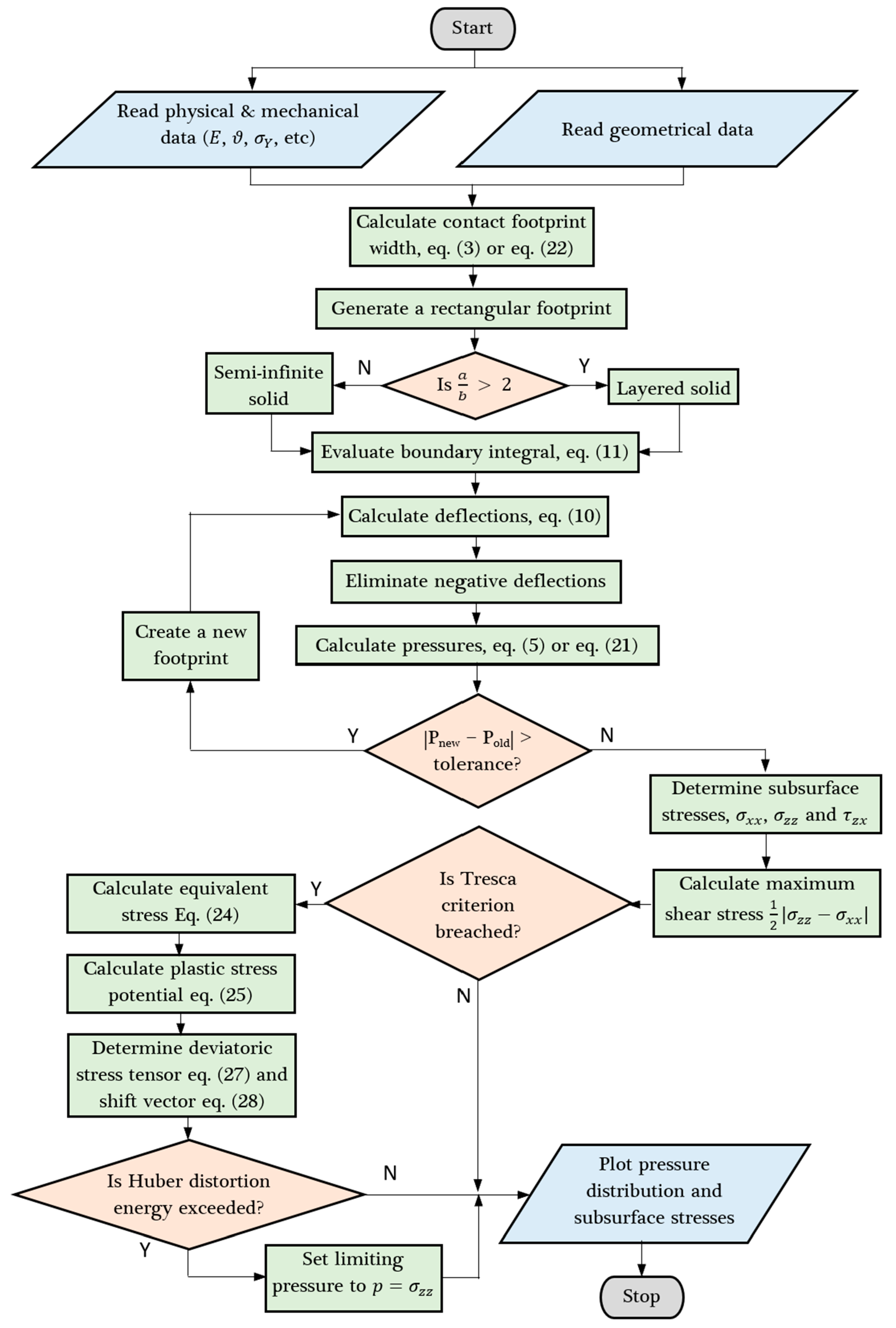
5. Method of Solution
6. Determination of Sub-Surface Stress Field
7. Results and Discussion
8. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Roman Symbols | |
| Semi-half-width at the centre of the contact | |
| Semi-half-width at any contact cross-section | |
| Layer thickness | |
| Half-width of rectangular computational element | |
| Roller diameter | |
| Effective Young’s modulus of elasticity | |
| Modulus of elasticity of contacting bodies | |
| Modulus of elasticity of the layer | |
| Equilibrium modulus of elasticity | |
| Effective elastic modulus of the contact | |
| Bearing reaction | |
| Modulus of rigidity | |
| Length roller (Contact footprint length) | |
| Number of rollers in the bearing | |
| Number of computational elements | |
| Pressure | |
| Central contact pressure | |
| Maximum pressure of any computational element | |
| Effective contact radius | |
| Contact load | |
| Co-ordinates of a point of deflection | |
| Co-ordinates of a point of pressure | |
| Co-ordinate into the depth of elastic solid | |
| Greek Symbols | |
| Yield translation shift | |
| Deflection | |
| Deflection at the centre of the contact | |
| Direct Stress: x, y along the surface, z into the depth of contact | |
| Equivalent stress | |
| Yield stress | |
| Plastic strain | |
| Limit of convergence for pressures | |
| Limit of convergence for elastostatic equilibrium | |
| Localised plastic strain coefficient | |
| Poisson’s ratio | |
| Poisson’s ratio for the layer | |
| Plastic strain potential | |
| Orthogonal reversing shear stress | |
| Maximum shear stress | |
Appendix A
References
- Mohammadpour, M.; Johns-Rahnejat, P.M.; Theodossiades, S.; Rahnejat, H. Effect of tapered roller bearing supports on the dynamic behaviour of hypoid gear pair differentials. Proc. IMechE Part D J. Automob. Eng. 2016, 230, 1090–1104. [Google Scholar] [CrossRef]
- Xu, H.; Kahraman, A. Prediction of friction-related power losses of hypoid gear pairs. Proc. IMechE Part K J. Multi-Body Dyn. 2007, 221, 387–400. [Google Scholar] [CrossRef]
- Sivayogan, G.; Dolatabadi, N.; Johns-Rahnejat, P.; Rahmani, R.; Rahnejat, H. Non-Newtonian Thermo-Elastohydrodynamics and Sub-Surface Stress Field of High-Performance Racing Spur Gears. Lubricants 2022, 10, 146. [Google Scholar] [CrossRef]
- Sivayogan, G.; Rahmani, R.; Rahnejat, H. Transient non-Newtonian elastohydrodynamics of rough meshing hypoid gear teeth subjected to complex contact kinematics. Tribol. Int. 2022, 167, 107398. [Google Scholar] [CrossRef]
- Greco, A.; Sheng, S.; Keller, J.; Erdemir, A. Material wear and fatigue in wind turbine systems. Wear 2013, 302, 1583–1591. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; He, H.; Wei, P. Evaluation of contact fatigue life of a wind turbine gear pair considering residual stress. J. Tribol. 2018, 140, 041102. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings. Measurement 2020, 149, 107002. [Google Scholar] [CrossRef]
- Yucesan, Y.A.; Viana, F.A. A physics-informed neural network for wind turbine main bearing fatigue. Int. J. Progn. Health Manag. 2020, 11, 1–17. [Google Scholar] [CrossRef]
- Johns-Rahnejat, P.M.; Gohar, R. Point contact elastohydrodynamic pressure distribution and sub-surface stress field. In Proceedings of the Tri-Annual Conference on Multi-Body Dynamics: Monitoring and Simulation Techniques, Bradford, UK, 13 March 1997. [Google Scholar]
- Harris, T.A.; Yu, W.K. Lundberg-Palmgren fatigue theory: Considerations of failure stress and stressed volume. J. Tribol. 1999, 121, 85–89. [Google Scholar] [CrossRef]
- Slack, T.; Sadeghi, F. Explicit finite element modeling of subsurface initiated spalling in rolling contacts. Tribol. Int. 2010, 43, 1693–1702. [Google Scholar] [CrossRef]
- Sadeghi, F. Elastohydrodynamic lubrication. In Tribology and Dynamics of Engine and Powertrain; Woodhead Publishing: Cambridge, UK, 2010; pp. 171–226. [Google Scholar]
- Rahnejat, H.; Rahmani, R.; Mohammadpour, M.; Johns-Rahnejat, P.M. Tribology of power train systems. ASM Handb. 2017, 18, 916–934. [Google Scholar]
- Johns-Rahnejat, P.M.; Dolatabadi, N.; Rahnejat, H. Analytical elastostatic contact mechanics of highly-loaded contacts of varying conformity. Lubricants 2020, 8, 89. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Hannah, M. Contact stress and deformation in a thin elastic layer. Q. J. Mech. Appl. Math. 1951, 4, 94–105. [Google Scholar] [CrossRef]
- Barber, J.R. Contact problems for the thin elastic layer. Int. J. Mech. Sci. 1990, 32, 129–132. [Google Scholar] [CrossRef]
- Jaffar, M.J. Asymptotic behaviour of thin elastic layers bonded and unbonded to a rigid foundation. Int. J. Mech. Sci. 1989, 31, 229–235. [Google Scholar] [CrossRef]
- Naghieh, G.R.; Rahnejat, H.; Jin, Z.M. Characteristics of frictionless contact of bonded elastic and viscoelastic layered solids. Wear 1998, 232, 243–249. [Google Scholar] [CrossRef]
- Konvopoulos, K.; Gong, Z.Q. Effect of surface patterning on contact deformation of elastic–plastic layered media. J. Tribol. 2003, 125, 16–24. [Google Scholar]
- Teodorescu, M.; Rahnejat, H.; Gohar, R.; Dowson, D. Harmonic decomposition analysis of contact mechanics of bonded layered elastic solids. Appl. Math. Model. 2009, 33, 467–485. [Google Scholar] [CrossRef]
- Teodorescu, M.; Rahnejat, H. Mathematical modelling of layered contact mechanics of cam–tappet conjunction. Appl. Math. Model. 2007, 31, 2610–2627. [Google Scholar] [CrossRef]
- Chidlow, S.J.; Teodorescu, M. Two-dimensional contact mechanics problems involving inhomogeneously elastic solids split into three distinct layers. Int. J. Eng. Sci. 2013, 70, 102–123. [Google Scholar] [CrossRef]
- Menga, N.; Putignano, C.; Afferrante, L.; Carbone, G. The contact mechanics of coated elastic solids: Effect of coating thickness and stiffness. Tribol. Lett. 2019, 67, 1–10. [Google Scholar] [CrossRef]
- Goltsberg, R.; Etsion, I. Contact area and maximum equivalent stress in elastic spherical contact with thin hard coating. Tribol. Int. 2016, 93, 289–296. [Google Scholar] [CrossRef]
- Xu, K.; Chu, N.R.; Jackson, R.L. An investigation of the elastic cylindrical line contact equations for plane strain and stress considering friction. Proc. IMechE Part J J. Eng. Tribol. 2022, 236, 1889–1897. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E.; Pallot, P. Two-dimensional contact analysis of elastic graded materials. J. Mech. Phys. Solids 2000, 48, 1597–1631. [Google Scholar] [CrossRef]
- Attia, M.A.; El-Shafei, A.G. Modeling and analysis of the nonlinear indentation problems of functionally graded elastic layered solids. Proc. IMechE Part J J. Eng. Tribol. 2019, 233, 1903–1920. [Google Scholar] [CrossRef]
- Çömez, İ. Contact mechanics of the functionally graded monoclinic layer. Eur. J. Mech.-A/Solids 2020, 83, 104018. [Google Scholar] [CrossRef]
- Lyubicheva, A.N.; Mezrin, A.M.; Kuznetsov, V.A.; Torskaya, E.V. Effect of Viscous Intermediate Layer on Uneven Wear of Locally Hardened Steel. Tribol. Lett. 2024, 72, 21. [Google Scholar] [CrossRef]
- Horng, J.H.; Osipenko, N.M.; Stepanov, F.I.; Torskaya, E.V. Theoretical and experimental study of changes in the structure of the intermediate layer during friction between contacting bodies. Materials 2021, 14, 5689. [Google Scholar] [CrossRef]
- Karami, G. Boundary element analysis of elasto-plastic contact problems. Comput. Struct. 1991, 41, 927–935. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C.; Lawn, B.R.; Pajares, A.; Wei, L. Stress analysis of elastic-plastic contact damage in ceramic coatings on metal substrates. J. Am. Ceram. Soc. 1996, 79, 2619–2625. [Google Scholar] [CrossRef]
- Komvopoulos, K. Elastic-Plastic Finite Element Analysis of Indented Layered Media. J. Tribol. 1989, 111, 430–439. [Google Scholar] [CrossRef]
- Chen, Z.; Goltsberg, R.; Etsion, I. A universal model for a frictionless elastic-plastic coated spherical normal contact with moderate to large coating thicknesses. Tribol. Int. 2017, 114, 485–493. [Google Scholar] [CrossRef]
- Song, W.; Li, L.; Ovcharenko, A.; Jia, D.; Etsion, I.; Talke, F.E. Plastic yield inception of an indented coated flat and comparison with a flattened coated sphere. Tribol. Int. 2012, 53, 61–67. [Google Scholar] [CrossRef]
- Brake, M.R. An analytical elastic plastic contact model with strain hardening and frictional effects for normal and oblique impacts. Int. J. Solids Struct. 2015, 62, 104–123. [Google Scholar] [CrossRef]
- Ghaednia, H.; Wang, X.; Saha, S.; Xu, Y.; Sharma, A.; Jackson, R.L. A review of elastic–plastic contact mechanics. Appl. Mech. Rev. 2017, 69, 060804. [Google Scholar] [CrossRef]
- Sharma, A.; Jackson, R.L. A finite element study of an elasto-plastic disk or cylindrical contact against a rigid flat in plane stress with bilinear hardening. Tribol. Lett. 2017, 65, 1–2. [Google Scholar] [CrossRef]
- Gohar, R.; Rahnejat, H. Fundamentals of Tribology, 3rd ed.; World Scientific Publishing: Singapore, 2018. [Google Scholar]
- Ioannides, E.; Harris, T.A. A New Fatigue Life Model for Rolling Bearings. J. Tribol. 1985, 107, 367–378. [Google Scholar] [CrossRef]
- Johns, P.M. The Design of Cylindrical Rollers for Use in Shaft and Bearing Systems. Master’s Thesis, Imperial College of Science and Technology, London, UK, 1978. [Google Scholar]
- Hertz, H. The contact of elastic solids. J. Reine Angew. Math. 1881, 92, 156–171. [Google Scholar]
- Kannel, J.W. Comparison between Predicted and Measured Axial Pressure Distribution between Cylinders. J. Lubr. Technol. 1974, 96, 508–514. [Google Scholar] [CrossRef]
- Heydari, M.; Gohar, R. The Influence of the Axial Profile on Pressure Distribution in Radially Loaded Rollers. J. Mech. Eng. Sci. 1979, 21, 381–388. [Google Scholar] [CrossRef]
- Johns, P.M.; Gohar, R. Roller bearings under radial and eccentric loads. Tribol. Int. 1981, 14, 131–136. [Google Scholar] [CrossRef]
- Johns-Rahnejat, P.M.; Karami, G.; Aini, R.; Rahnejat, H. Fundamentals and advances in elastohydrodynamics: The role of Ramsey Gohar. Lubricants 2021, 9, 120. [Google Scholar] [CrossRef]
- Teodorescu, M.; Votsios, V.; Rahnejat, H. Fundamentals of impact dynamics of semi-infinite and layered solids. In Tribology and Dynamics of Engine and Powertrain; Woodhead Publishing: Cambridge, UK, 2010; pp. 105–132. [Google Scholar]
- Becker, V.; Kamlah, M. A theoretical model for the normal contact force of two elastoplastic ellipsoidal bodies. J. Appl. Mech. 2021, 88, 031006. [Google Scholar] [CrossRef]
- Persson, B.N. Elastoplastic contact between randomly rough surfaces. Phys. Rev. Lett. 2001, 87, 116101. [Google Scholar] [CrossRef] [PubMed]
- Kogut, L.; Etsion, I. Elastic-plastic contact analysis of a sphere and a rigid flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Haupt, P. On the mathematical modelling of material behavior in continuum mechanics. Acta Mech. 1993, 100, 129–154. [Google Scholar] [CrossRef]
- Mielke, A.; Roubíček, T. Rate-independent elastoplasticity at finite strains and its numerical approximation. Math. Models Methods Appl. Sci. 2016, 26, 2203–2236. [Google Scholar] [CrossRef]
- Huber, M.T. Zur Theorie der beruhrung fester elastischer korper. Ann. Phys. 1904, 14, 153–163. [Google Scholar] [CrossRef]
- Lundberg, G.; Palmgren, A. Dynamic capacity of rolling bearings. J. Appl. Mech. 1949, 16, 165–172. [Google Scholar] [CrossRef]
- Tresca, M.H. On further applications of the flow of solids. Proc. IMechE 1878, 29, 301–345. [Google Scholar] [CrossRef]
- Johns-Rahnejat, P.M.; Dolatabadi, N.; Rahnejat, H. Contact mechanics of highly loaded counterformal finite line contacts: Semi-infinite and layered elastic solids. In Proceedings of the Lubrication, Maintenance and Tribotechnology (LUBMAT 2023), Preston, UK, 17–19 July 2023. 10p. [Google Scholar]
- Holmberg, K.; Laukkanen, A.; Ronkainen, H.; Wallin, K.; Varjus, S.; Koskinen, J. Tribological contact analysis of a rigid ball sliding on a hard coated surface: Part I: Modelling stresses and strains. Surf. Coat. Technol. 2006, 200, 3793–3809. [Google Scholar] [CrossRef]
- Nikas, G.K.; Sayles, R.S. Finite-element analysis of layered rolling contacts. Proc. IMechE Part J J. Eng. Tribol. 2008, 222, 865–886. [Google Scholar] [CrossRef]
- Yilmaz, K.B.; Çömez, I.; Güler, M.A.; Yildirim, B.O. Analytical and finite element solution of the sliding frictional contact problem for a homogeneous orthotropic coating-isotropic substrate system. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 2019, 99, e201800117. [Google Scholar] [CrossRef]
- Tang, K.C.; Arnell, R.D. Determination of coating mechanical properties using spherical indenters. Thin Solid Film. 1999, 355, 263–269. [Google Scholar] [CrossRef]
- Komvopoulos, K.; Ye, N. Three-dimensional contact analysis of elastic-plastic layered media with fractal surface topographies. J. Trib. 2001, 123, 632–640. [Google Scholar] [CrossRef]
- Sun, Y.; Bloyce, A.; Bell, T. Finite element analysis of plastic deformation of various TiN coating/substrate systems under normal contact with a rigid sphere. Thin Solid Films 1995, 271, 122–131. [Google Scholar] [CrossRef]
- Li, L.Y.; Wu, C.Y.; Thornton, C. A theoretical model for the contact of elastoplastic bodies. Proc. IMechE Part C J. Mech. Eng. Sci. 2001, 216, 421–431. [Google Scholar] [CrossRef]
- Frohne, J.; Heister, T.; Bangerth, W. Efficient numerical methods for the large-scale, parallel solution of elastoplastic contact problems. Int. J. Numer. Methods Eng. 2016, 105, 416–439. [Google Scholar] [CrossRef]
- Jin, T.; Yin, X.; Zhang, L.; Wang, H.; Yu, B.; Hao, Q. Strain-rate-dependent model for the elastoplastic dynamic contact of sphere and plate. Mater. Res. Express 2020, 7, 066523. [Google Scholar] [CrossRef]
- Qi, K.; Zhou, Q.; Yang, W.; Yang, J. A semi-analytical approach for elastoplastic impact-contact involving coated medium. Int. J. Solids Struct. 2023, 283, 112467. [Google Scholar] [CrossRef]
- Chang, W.R.; Etsion, I.; Bogy, D.B. An elastic-plastic model for the contact of rough surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Persson, B.N. Contact mechanics for randomly rough surfaces. Surf. Sci. Rep. 2006, 61, 201–227. [Google Scholar] [CrossRef]
- Chen, Z.; Etsion, I. Recent development in modeling of coated spherical contact. Materials 2020, 13, 460. [Google Scholar] [CrossRef] [PubMed]



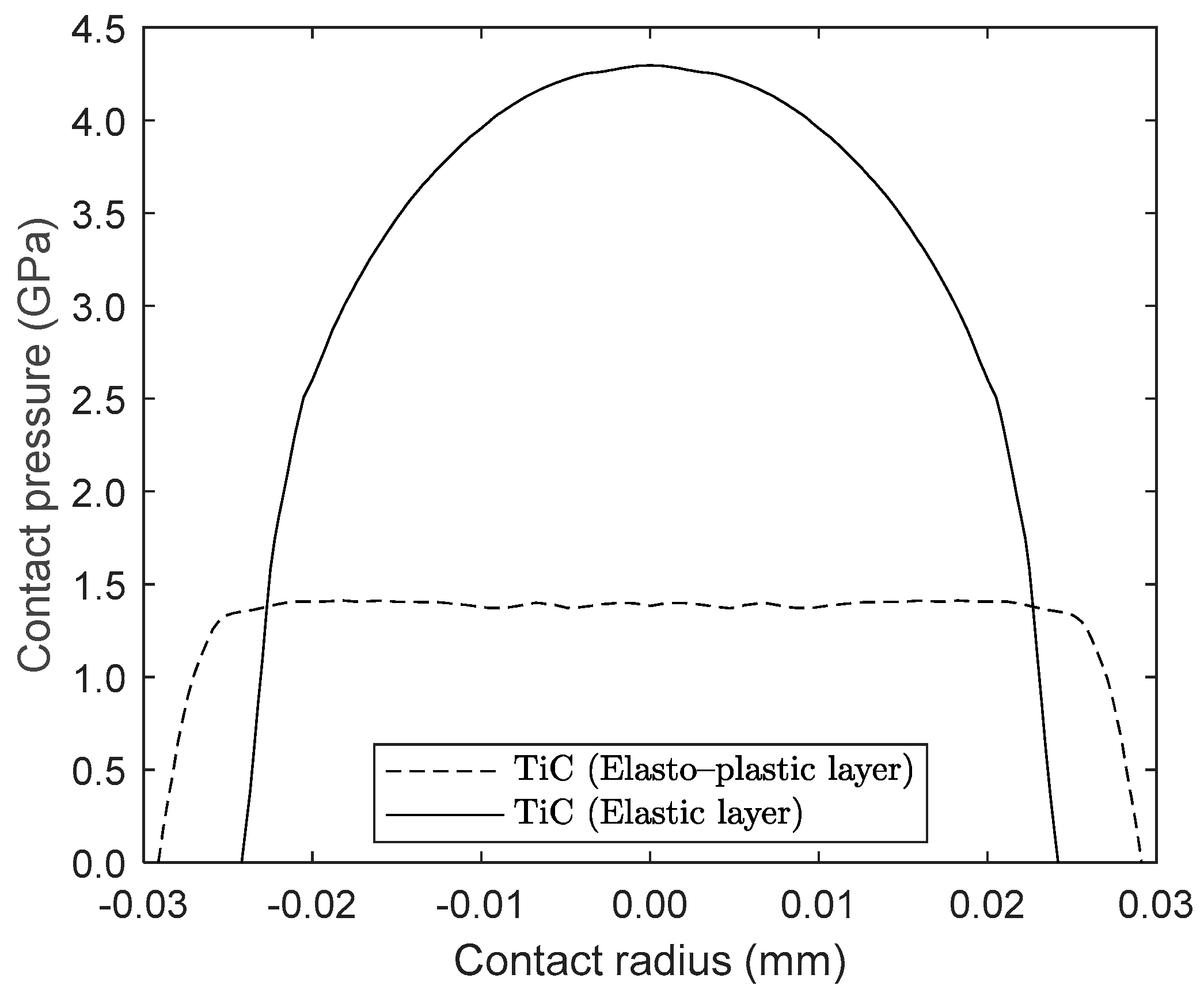
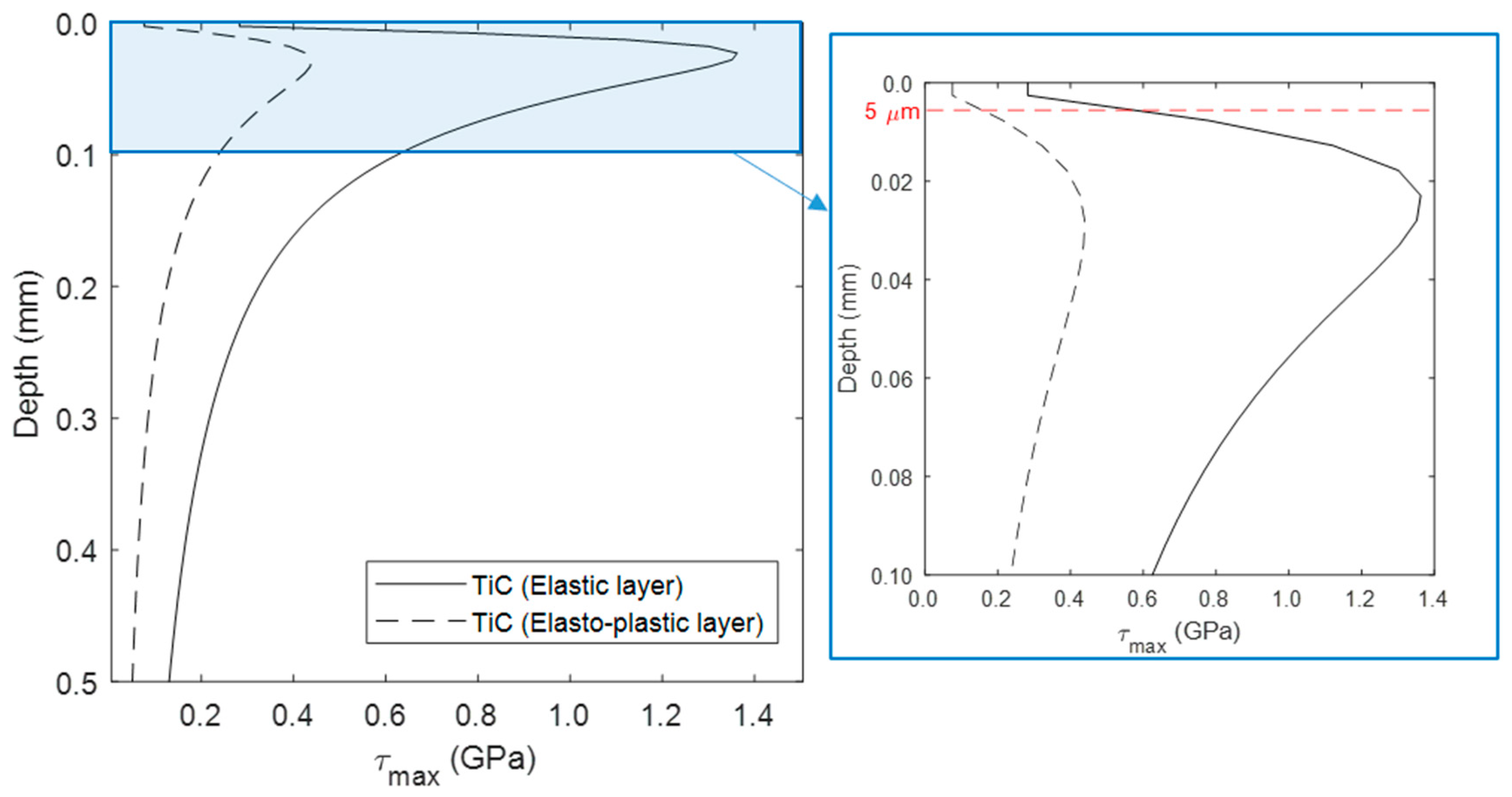
| Material | Modulus of Elasticity, E (GPa) | Poisson’s Ratio | Layer Thickness, b (µm) |
|---|---|---|---|
| Steel | 206 | 0.30 | − |
| Si3N4 | 250 | 0.20 | 6 |
| Al2O3 | 300 | 0.21 | 3 |
| DLC | 220 | 0.21 | 2 |
| TiC | 400 | 0.18 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johns-Rahnejat, P.M.; Dolatabadi, N.; Rahnejat, H. Elastic and Elastoplastic Contact Mechanics of Concentrated Coated Contacts. Lubricants 2024, 12, 162. https://doi.org/10.3390/lubricants12050162
Johns-Rahnejat PM, Dolatabadi N, Rahnejat H. Elastic and Elastoplastic Contact Mechanics of Concentrated Coated Contacts. Lubricants. 2024; 12(5):162. https://doi.org/10.3390/lubricants12050162
Chicago/Turabian StyleJohns-Rahnejat, Patricia M., Nader Dolatabadi, and Homer Rahnejat. 2024. "Elastic and Elastoplastic Contact Mechanics of Concentrated Coated Contacts" Lubricants 12, no. 5: 162. https://doi.org/10.3390/lubricants12050162
APA StyleJohns-Rahnejat, P. M., Dolatabadi, N., & Rahnejat, H. (2024). Elastic and Elastoplastic Contact Mechanics of Concentrated Coated Contacts. Lubricants, 12(5), 162. https://doi.org/10.3390/lubricants12050162







