Minimisation of Friction Resistance of Elastomeric Lip Seals on Rotating Shafts
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Research
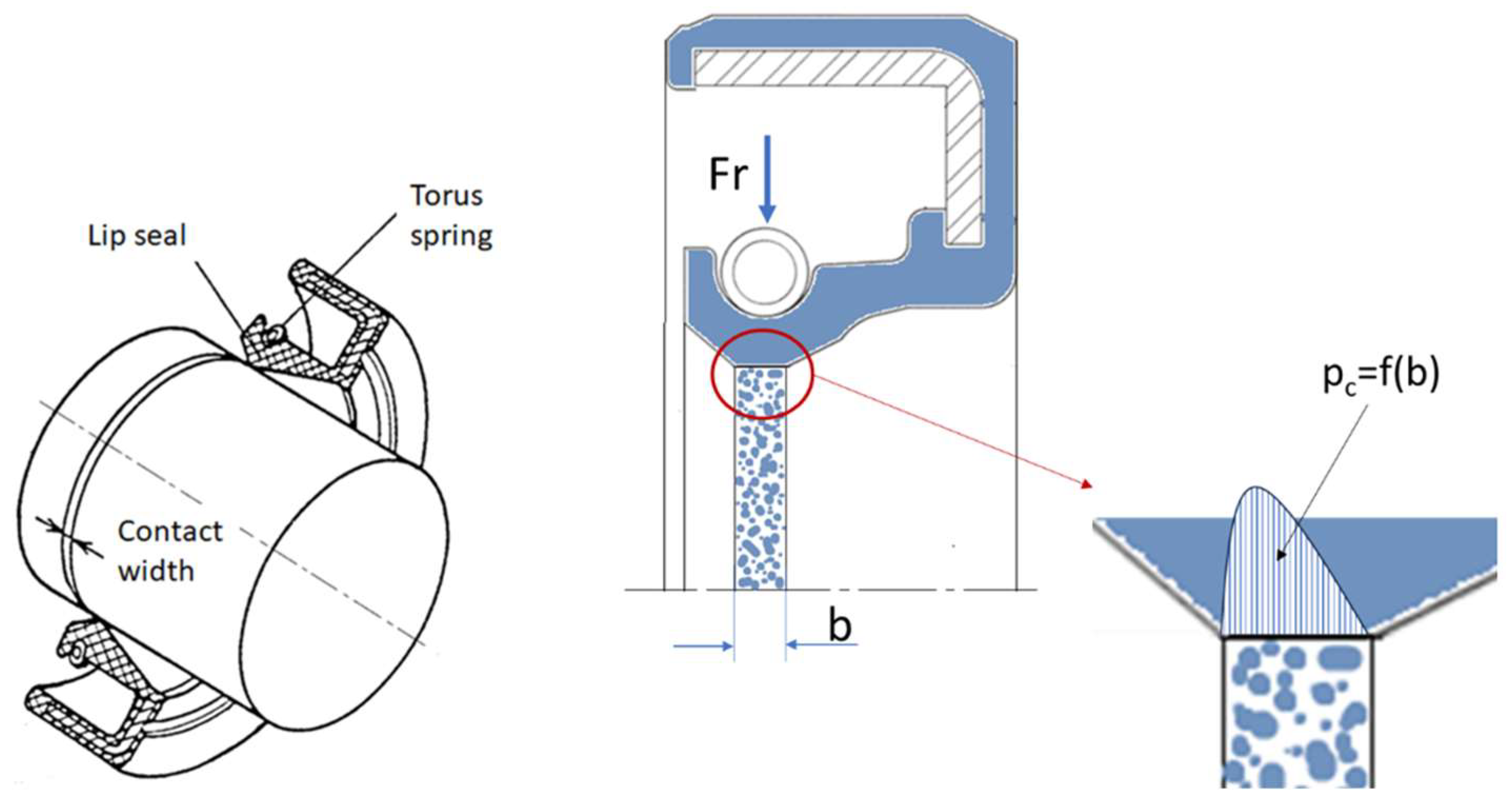
2.1.1. Research Objects
- Ra—a commonly used parameter in surface metrology that quantifies the average surface roughness of a component. It is calculated by measuring the vertical deviations of the roughness profile from the mean line over a specified length and averaging these values.
- Rz—a parameter calculated as the average value of the absolute distances between the highest peaks and the lowest valleys on the surface profile within a specified cutoff length.
- Rt—a parameter calculated by measuring the vertical distance between the highest peak and lowest valley on the surface profile along a specified length.
- Caoutchouc KER N-29 (49.33);
- Zinc oxide (3.95);
- Oleostearine (0.66);
- Antidegradant TMQ (0.99);
- Brown factor (0.99);
- Kaolin KOM (6.58);
- N-550 medium carbon black (9.86);
- Corax N-339 hard carbon black (19.74);
- Dibutyl phthalate (6.58);
- Vulkacit CBS accelerator powder (0.33);
- Vulkacit TMTD-80 accelerator granulate (0.66);
- M-9985-I ground sulphur (0.33).
- Durometer, Shore A: 77;
- Specific gravity: 1.24 g/cm3;
- Tensile: 17 MPa;
- Elongation: 385%;
- Compression at 70 °C and 22 h: 10.5%.
2.1.2. Test Stands and Test Procedures
- Sample diameter—8 mm;
- Sample load—1 MPa;
- Linear speed range—0.31 ÷ 1.79 m/s;
- Experiment time duration—10 s;
- Temperature—25 °C.
- Test time—8 h;
- Shaft rotational speed—3000 rpm;
- Lubrication with 15W40 mineral engine oil.
- The rheological properties of the used oil are as follows:
- Viscosity at 100 °C: 14.5 cSt;
- Viscosity at 40 °C: 109.84 cSt;
- Viscosity index: 135;
- Density at 15 °C: 904 kg/m3;
- Pour point: −27 °C;
- Flash point: 220 °C.
2.2. Numerical Calculations
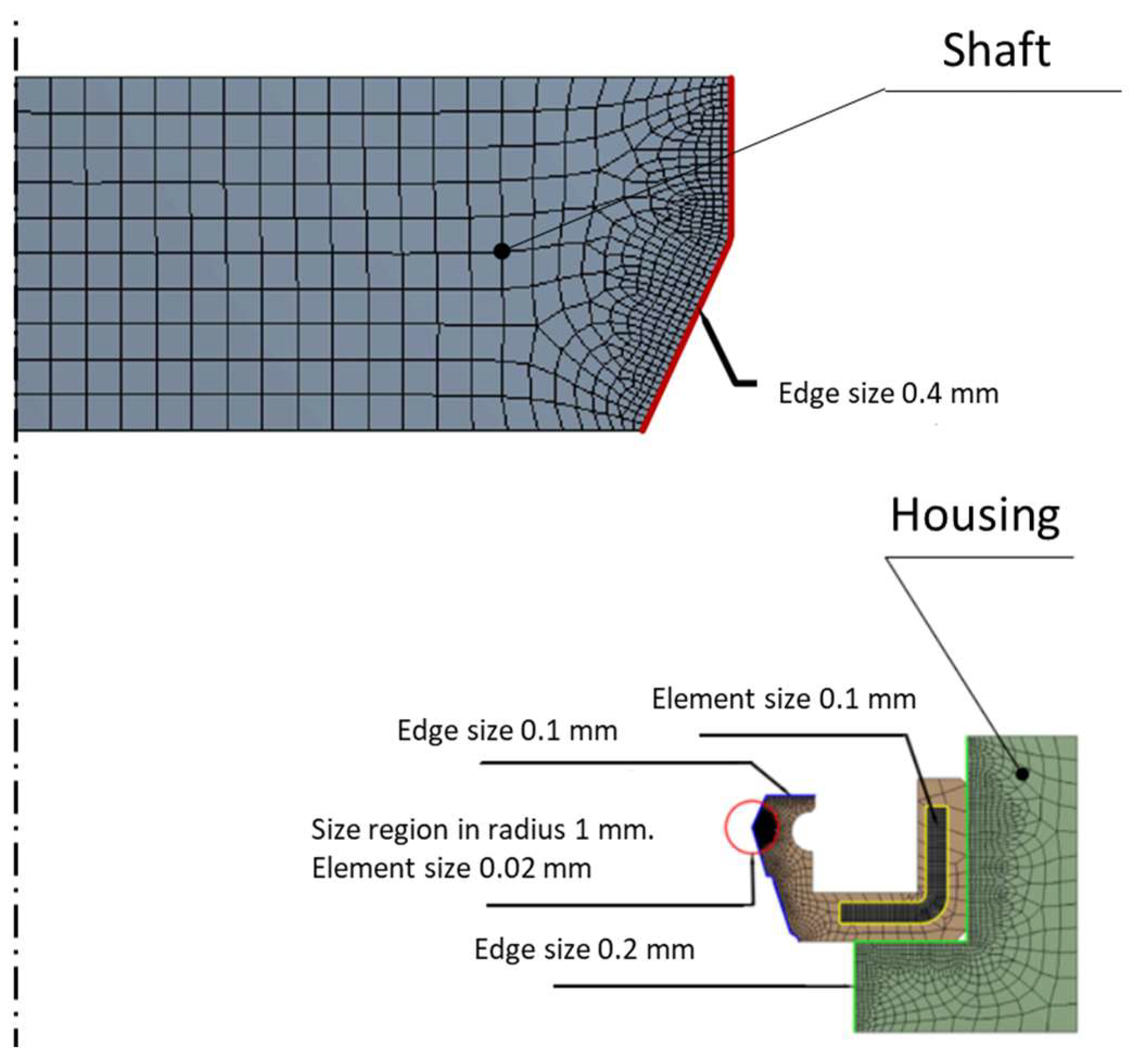
2.2.1. Computational Mesh
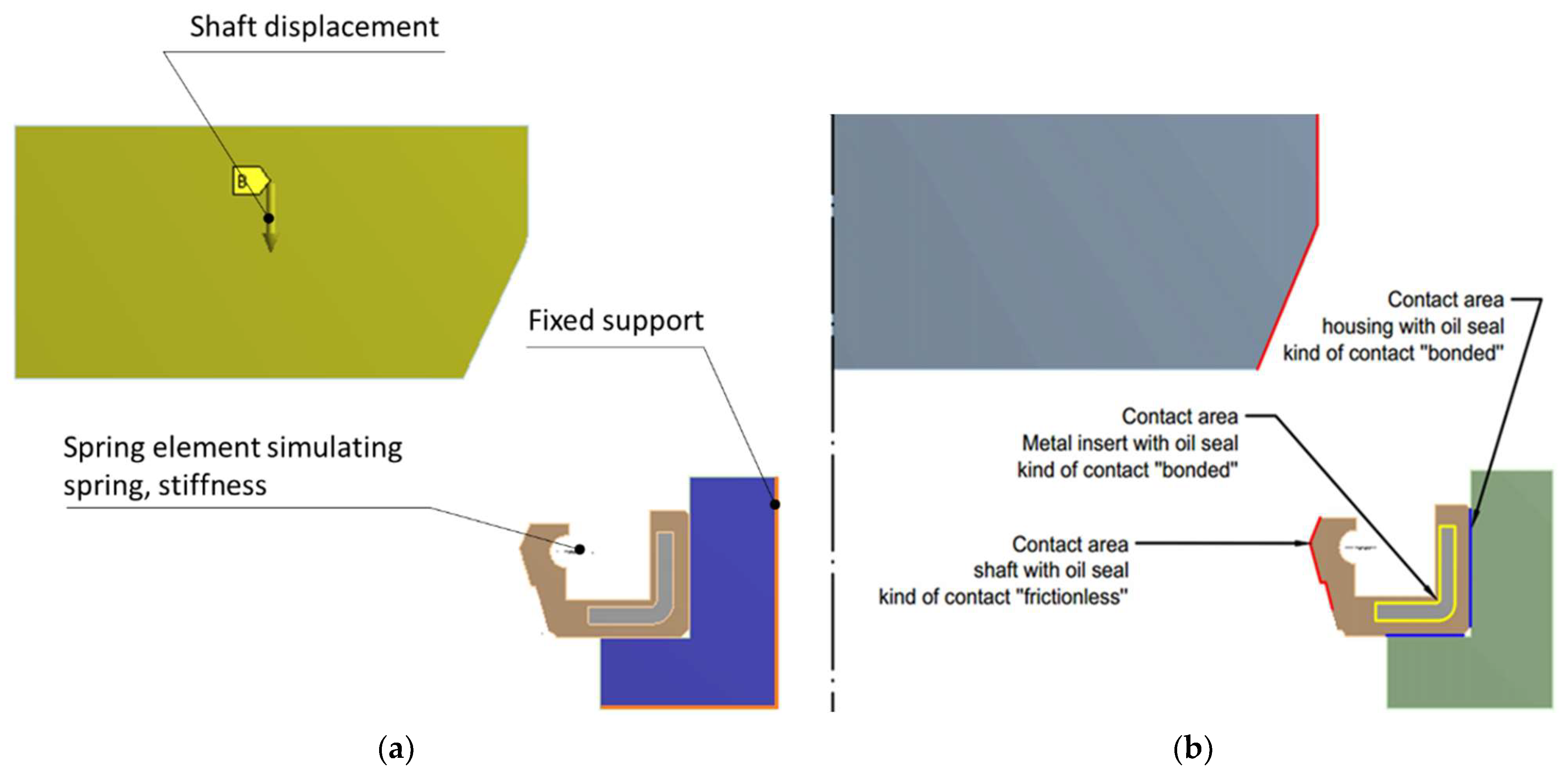
2.2.2. Boundary Conditions
2.2.3. Material Properties
2.3. Analytical Calculations
3. Results
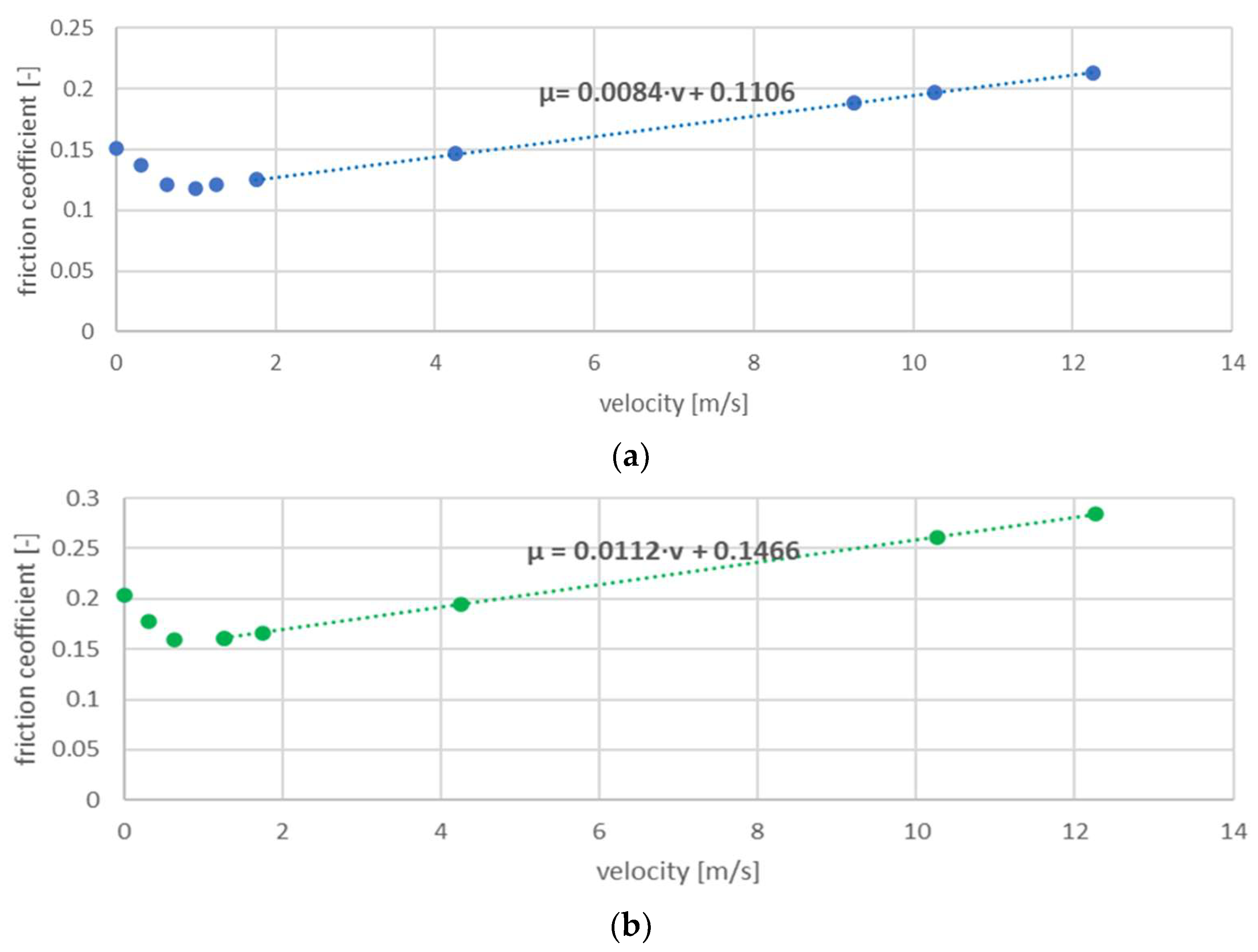
3.1. Experimental Results
- The increase in lip width was 38.3% for the standard sealing ring and 20.8% for the prototype sealing ring.
- The decrease in clamping force was 9.1% for the standard sealing ring and 8.9% for the prototype sealing ring.
- The ring weight loss was 0.46% for the standard sealing ring and 0.4% for the prototype sealing ring.
3.2. Numerical Results
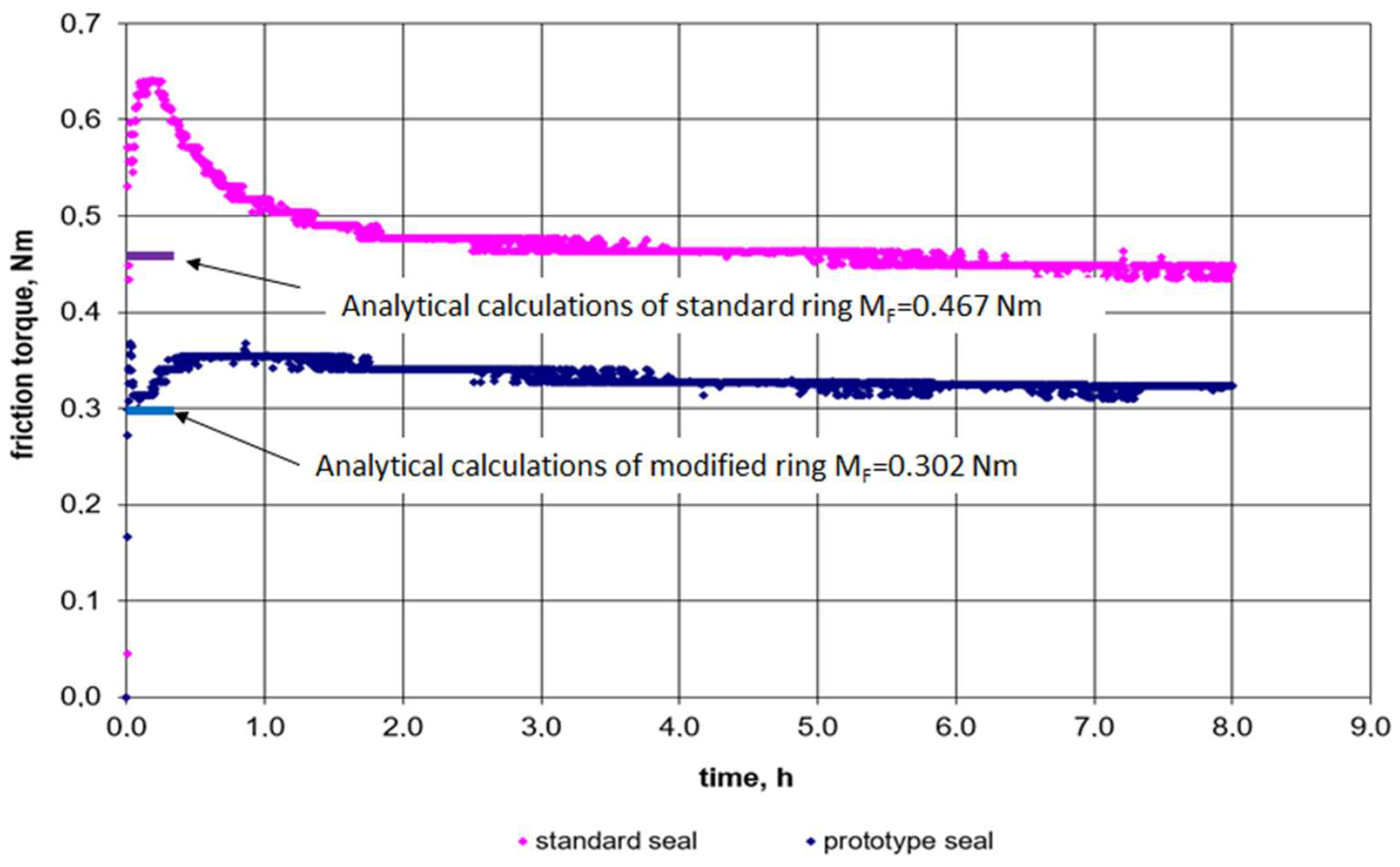
3.3. Analytical Results
4. Discussion
5. Conclusions
- The validity of the thesis that the way to reduce the frictional resistance of the sealing lip-steel shaft pair is to reduce the tangential stiffness of the sealing lip surface layer is demonstrated.
- The data for carrying out the calculations and determining the friction coefficient values were established from the adopted porous body model and the surface model of the substitute surface layer of rubber. The modelling of the rubber surface layer was based on profilograms of rubber samples, the deviation of which from the actual surface was not large.
- The modification used should be considered effective and easy to apply.
- Friction coefficient measurements of rubber samples with a given porosity rubbing against the surface of a metal disc showed satisfactory convergence with the calculated friction coefficient values for the adopted model of interaction of the two surfaces.
- During dry friction of the flat rubber samples, a reduction in the friction coefficient of 5 to 40% was observed compared to the samples with a smooth surface. Also, in the case of lubrication, a reduction in the friction coefficient of up to 50% was observed.
- Modification of the sealing lip surface resulted in a 43% reduction in friction torque in the first hour of sealing operation and a 27% reduction after 8 h of operation.
- Torque deviations between analytical calculations and experimental results are substantiative due to the roughness profile changing under load and movement.
- Modification of the surface layer reduces mass consumption and thermal loading of the lip during the initial period of sealing operation, i.e., when it is the highest.
- No leakage was observed from the sealing rings with the modified sealing lip texture.
- The created numerical model enables the calculation of the friction coefficient of the flat samples and the sealing ring.
- Discrepancies between the model and experiment are due to simplifications to facilitate the calculations, but the differences do not exceed several percent.
- The roughness parameters of the surface layer of the sealing lip in the tested case are the maximum values above which leakage was observed.
- With wear, no reconstruction of the rubber texture was observed due to the specific composition of the rubber. For this reason, the introduced modification is temporary and significantly reduces friction resistance in the initial period of operation, when high thermal loads and run-in occur.
- It seems advisable to carry out research on the influence of fillers in rubber on reproducing the original texture of the surface layer.
- The effectiveness of the proposed modification method when using other materials for lip sealing rings is unknown.
- In the case of other methods of modifying the elastomer surface, such as laser impact, additional technological operations are required.
- The solution proposed in the article guarantees a finished product immediately after removal from the mould.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jaszak, P.; Skrzypacz, J.; Borawski, A.; Grzejda, R. Methodology of leakage prediction in gasketed flange joints at pipeline deformations. Materials 2022, 15, 4354. [Google Scholar] [CrossRef] [PubMed]
- Brown, C.A. Axiomatic design applied to a practical example of the integrity of shaft surfaces for rotating lip seals. Procedia Eng. 2011, 19, 53–59. [Google Scholar] [CrossRef][Green Version]
- Embury, P.; Armour, J. Influence of elastomer compound design on the performance of rotary shaft lip seals. Seal. Technol. 2004, 2004, 7–10. [Google Scholar] [CrossRef]
- Grün, J.; Feldmeth, S.; Bauer, F. Wear on radial lip seals: A numerical study of the influence on the sealing mechanism. Wear 2021, 476, 203674. [Google Scholar] [CrossRef]
- Cankar, M.; Koch, U. New radial shaft seals for turbo applications. MTZ Worldw. 2016, 77, 56–59. [Google Scholar] [CrossRef]
- Rogula, J. Crankshaft Lip Seals with Reduced Friction Resistance; SAE Technical Paper; 2022-01-1098; SAE: Warrendale, PA, USA, 2022. [Google Scholar]
- Gachot, C.; Rosenkranz, A.; Hsu, S.M.; Costa, H.L. A critical assessment of surface texturing for friction and wear improvement. Wear 2017, 372–373, 21–41. [Google Scholar] [CrossRef]
- Salant, R.F. Modelling rotary lip seals. Wear 1997, 207, 92–99. [Google Scholar] [CrossRef]
- Foko Foko, F.; Burkhart, C.; Thielen, S.; Sauer, B. Analysis of the sealing capability of radial shaft sealing rings using a semi-analytical contact model. Tribol. Online 2022, 17, 97–109. [Google Scholar] [CrossRef]
- Keller, D.; Jacobs, G.; Neumann, S. Development of a low-friction radial shaft seal: Using CFD simulations to optimise the microstructured sealing lip. Lubricants 2020, 8, 41. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, J.; Shui, H.; Dong, C. Effect of roughness on sealing performance of oil seals with surface texture. Ind. Lubr. Tribol. 2020, 72, 525–532. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Y. Research on sealing performance of oil seals with micro-dimple texture on lips. Ind. Lubr. Tribol. 2021, 73, 113–119. [Google Scholar] [CrossRef]
- El Gadari, M.; Fatu, A.; Hajjam, M. Shaft roughness effect on elasto-hydrodynamic lubrication of rotary lip seals: Experimentation and numerical simulation. Tribol. Int. 2015, 88, 218–227. [Google Scholar] [CrossRef]
- El Gadari, M.; Fatu, A.; Hajjam, M. Effect of grooved shaft on the rotary lip seal performance in transient condition: Elasto-hydrodynamic simulations. Tribol. Int. 2016, 93, 411–418. [Google Scholar] [CrossRef]
- Warren, K.H.; Stephens, L.S. Effect of shaft microcavity patterns for flow and friction control on radial lip seal performance—A feasibility study. Tribol. Trans. 2009, 52, 731–743. [Google Scholar] [CrossRef]
- Li, W.; Stephens, L.S.; Wenk, J.F. Experimental benchmarking of the numerical model of a radial lip seal with a surface textured shaft. Tribol. Trans. 2013, 56, 75–87. [Google Scholar] [CrossRef]
- Verheyde, B.; Rombouts, M.; Vanhulsel, A.; Havermans, D.; Meneve, J.; Wangenheim, M. Influence of surface treatment of elastomers on their frictional behaviour in sliding contact. Wear 2009, 266, 468–475. [Google Scholar] [CrossRef]
- Sekiguchi, S.; Suzuki, H.; Van Ryper, R.G.; Ritchey, D.J. Development of a new seal material to reduce energy losses in vehicle transmissions. Seal. Technol. 2009, 2009, 8–11. [Google Scholar] [CrossRef]
- Gong, R.; Liu, M.; Zhang, H.; Xu, Y. Experimental investigation on frictional behavior and sealing performance of different composites for seal application. Wear 2015, 342–343, 334–339. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, L.; Tian, M. Effect of expanded graphite (EG) dispersion on the mechanical and tribological properties of nitrile rubber/EG composites. Wear 2012, 276–277, 85–93. [Google Scholar] [CrossRef]
- Degrange, J.-M.; Thomine, M.; Kapsa, P.; Pelletier, J.M.; Chazeau, L.; Vigier, G.; Dudragne, G.; Guerbé, L. Influence of viscoelasticity on the tribological behaviour of carbon black filled nitrile rubber (NBR) for lip seal application. Wear 2005, 259, 684–692. [Google Scholar] [CrossRef]
- Frölich, D.; Magyar, B.; Sauer, B. A comprehensive model of wear, friction and contact temperature in radial shaft seals. Wear 2014, 311, 71–80. [Google Scholar] [CrossRef]
- Foko Foko, F.; Heimes, J.; Magyar, B.; Sauer, B. Friction energy-based wear simulation for radial shaft sealing ring. Lubricants 2020, 8, 15. [Google Scholar] [CrossRef]
- Croft, S. Rotary shaft lip seals—A tale of two standards. Seal. Technol. 2004, 2004, 10–12. [Google Scholar] [CrossRef]
- Gawlinski, M. Local Contact Conditions and Friction Resistance of Elastomeric Lip Sealing Rings; Publishing Office of the Wroclaw University of Science and Technology: Wroclaw, Poland, 2004. (In Polish) [Google Scholar]
- PN-EN ISO 4288; Geometrical Product Specifications (GPS), Surface Texture: Profile Method, Rules and Procedures for the Assessment of Surface Texture. Polish Committee for Standardization: Warsaw, Poland, 2011.
- Gawlinski, M.; Romanik, G. Elastomer Lip Seal of Rotating Shaft, PAT.217180; Polish Patent Office: Warsaw, Poland, 2014. [Google Scholar]
- Jia, X.; Guo, F.; Huang, L.; Wang, L.; Gao, Z.; Wang, Y. Effects of the radial force on the static contact properties and sealing performance of a radial lip seal. Sci. China Technol. Sci. 2014, 57, 1175–1182. [Google Scholar] [CrossRef]
- Dąbrowska, K.Z.; Turek, A.; Grzejda, R.; Kobielarz, M. Mechanical properties of the porcine pericardium extracellular matrix cross-linked with glutaraldehyde and tannic acid. Acta Bioeng. Biomech. 2022, 24, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Jung, S.; Haas, W.; Salant, R.F. Numerical simulation and experimental study of shaft pumping by plunge ground shafts with rotary lip seals. Tribol. Int. 2012, 48, 155–161. [Google Scholar] [CrossRef]
- Tasora, A.; Prati, E.; Marin, T. A method for the characterization of static elastomeric lip seal deformation. Tribol. Int. 2013, 60, 119–126. [Google Scholar] [CrossRef]
- Huang, T.-C.; Lin, C.-Y.; Liao, K.-C. Sealing performance assessments of PTFE rotary lip seals based on the elasto-hydrodynamic analysis with the modified Archard wear model. Tribol. Int. 2022, 176, 107917. [Google Scholar] [CrossRef]
- Jaszak, P. Rationalization of the shape of the rubber diaphragm of shut-off valve. Elastomery 2018, 22, 122–135. [Google Scholar]
- Grzejda, R. Modelling nonlinear preloaded multi-bolted systems on the operational state. Eng. Trans. 2016, 64, 525–531. [Google Scholar]
- Peng, C.; Miao, J.; Bauer, N.; Schmitz, K. Investigation into the inter-lip characteristics of combined seals with double lips in different working conditions. Tribol. Int. 2023, 178, 108036. [Google Scholar] [CrossRef]









| Sample | Ra, µm | Rz, µm | Rt, µm | |||
|---|---|---|---|---|---|---|
| Value | SD 1 | Value | SD 1 | Value | SD 1 | |
| 1B | 3.59 | 0.017 | 22.88 | 0.069 | 34.31 | 0.030 |
| 2B | 2.09 | 0.021 | 13.23 | 0.082 | 17.13 | 0.027 |
| 1C | 8.00 | 0.065 | 42.09 | 0.260 | 65.10 | 0.105 |
| 2C | 4.45 | 0.027 | 25.80 | 0.109 | 31.96 | 0.091 |
| E | 2.92 | 0.021 | 17.43 | 0.085 | 26.10 | 0.064 |
| Ring Version | Ra, µm | Rz, µm | Rt, µm | |||
|---|---|---|---|---|---|---|
| Value | SD 1 | Value | SD 1 | Value | SD 1 | |
| Standard | 0.52 | 0.027 | 2.75 | 0.106 | 4.20 | 0.032 |
| Prototype | 1.97 | 0.026 | 9.02 | 0.104 | 22.89 | 0.034 |
| v, m/s | Dry Conditions | Lubricated Conditions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | ||||||||||||
| 1B | 2B | 1C | 2C | E | SR | 1B | 2B | 1C | 2C | E | SR | |
| 0 | 0.165 | 0.192 | 0.150 | 0.157 | 0.172 | 0.272 | 0.150 | 0.151 | 0.117 | 0.138 | 0.140 | 0.204 |
| 0.31 | 0.598 | 0.638 | 0.557 | 0.561 | 0.604 | 0.671 | 0.110 | 0.137 | 0.089 | 0.104 | 0.119 | 0.178 |
| 0.63 | 0.577 | 0.633 | 0.550 | 0.534 | 0.598 | 0.707 | 0.102 | 0.121 | 0.087 | 0.096 | 0.114 | 0.159 |
| 1.26 | 0.583 | 0.591 | 0.548 | 0.540 | 0.582 | 0.679 | 0.099 | 0.115 | 0.083 | 0.099 | 0.118 | 0.149 |
| 1.79 | 0.592 | 0.618 | 0.536 | 0.518 | 0.609 | 0.717 | 0.114 | 0.130 | 0.084 | 0.097 | 0.123 | 0.173 |
| v, m/s | Dry Conditions | Lubricated Conditions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample | ||||||||||||
| 1B | 2B | 1C | 2C | E | SR | 1B | 2B | 1C | 2C | E | SR | |
| 0 | 0.010 | 0.009 | 0.009 | 0.007 | 0.004 | 0.008 | 0.010 | 0.011 | 0.006 | 0.008 | 0.007 | 0.009 |
| 0.31 | 0.008 | 0.008 | 0.007 | 0.006 | 0.009 | 0.006 | 0.009 | 0.006 | 0.008 | 0.009 | 0.009 | 0.008 |
| 0.63 | 0.007 | 0.010 | 0.009 | 0.004 | 0.008 | 0.007 | 0.008 | 0.005 | 0.007 | 0.006 | 0.004 | 0.009 |
| 1.26 | 0.003 | 0.005 | 0.008 | 0.009 | 0.010 | 0.009 | 0.005 | 0.005 | 0.003 | 0.009 | 0.008 | 0.007 |
| 1.79 | 0.009 | 0.008 | 0.006 | 0.008 | 0.009 | 0.007 | 0.007 | 0.008 | 0.005 | 0.007 | 0.003 | 0.003 |
| Ring Version | Before the Test | After the Test | ||||
|---|---|---|---|---|---|---|
| Wl, mm | Fc, N | Wr, g | Wl, mm | Fc, N | Wr, g | |
| Standard | 0.109 | 36.61 | 56.132 | 0.150 | 33.25 | 55.876 |
| Prototype | 0.089 | 34.65 | 55.848 | 0.107 | 31.55 | 55.624 |
| Ring Version | Before the Test | After the Test | ||||
|---|---|---|---|---|---|---|
| Wl, mm | Fc, N | Wr, g | Wl, mm | Fc, N | Wr, g | |
| Standard | 0.009 | 0.948 | 0.219 | 0.007 | 0.880 | 0.199 |
| Prototype | 0.003 | 0.780 | 0.322 | 0.011 | 0.615 | 0.223 |
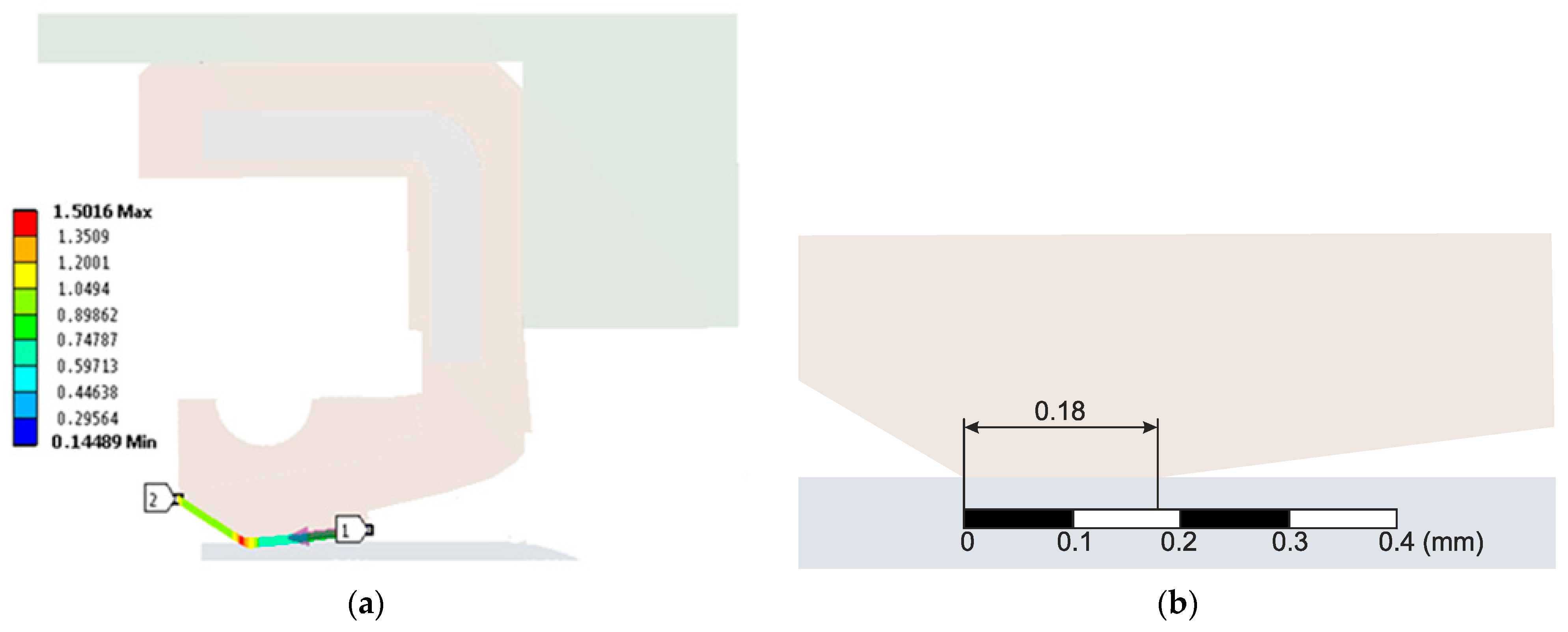
| Ring Version | ε | μ | v, m/s | ds, mm | b, mm | p, MPa | MF, Nm |
|---|---|---|---|---|---|---|---|
| Standard | 0.072 | 0.269 | 11 | 70 | 0.18 | 1.35 | 0.467 |
| Prototype | 0.205 | 0.203 | 11 | 70 | 0.18 | 1.35 | 0.302 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romanik, G.; Jaszak, P.; Grzejda, R.; Zmarzły, P. Minimisation of Friction Resistance of Elastomeric Lip Seals on Rotating Shafts. Lubricants 2024, 12, 103. https://doi.org/10.3390/lubricants12040103
Romanik G, Jaszak P, Grzejda R, Zmarzły P. Minimisation of Friction Resistance of Elastomeric Lip Seals on Rotating Shafts. Lubricants. 2024; 12(4):103. https://doi.org/10.3390/lubricants12040103
Chicago/Turabian StyleRomanik, Grzegorz, Przemysław Jaszak, Rafał Grzejda, and Paweł Zmarzły. 2024. "Minimisation of Friction Resistance of Elastomeric Lip Seals on Rotating Shafts" Lubricants 12, no. 4: 103. https://doi.org/10.3390/lubricants12040103
APA StyleRomanik, G., Jaszak, P., Grzejda, R., & Zmarzły, P. (2024). Minimisation of Friction Resistance of Elastomeric Lip Seals on Rotating Shafts. Lubricants, 12(4), 103. https://doi.org/10.3390/lubricants12040103







