Effect of Surface Roughness on the Friction Moment in a Lubricated Deep Groove Ball Bearing
Abstract
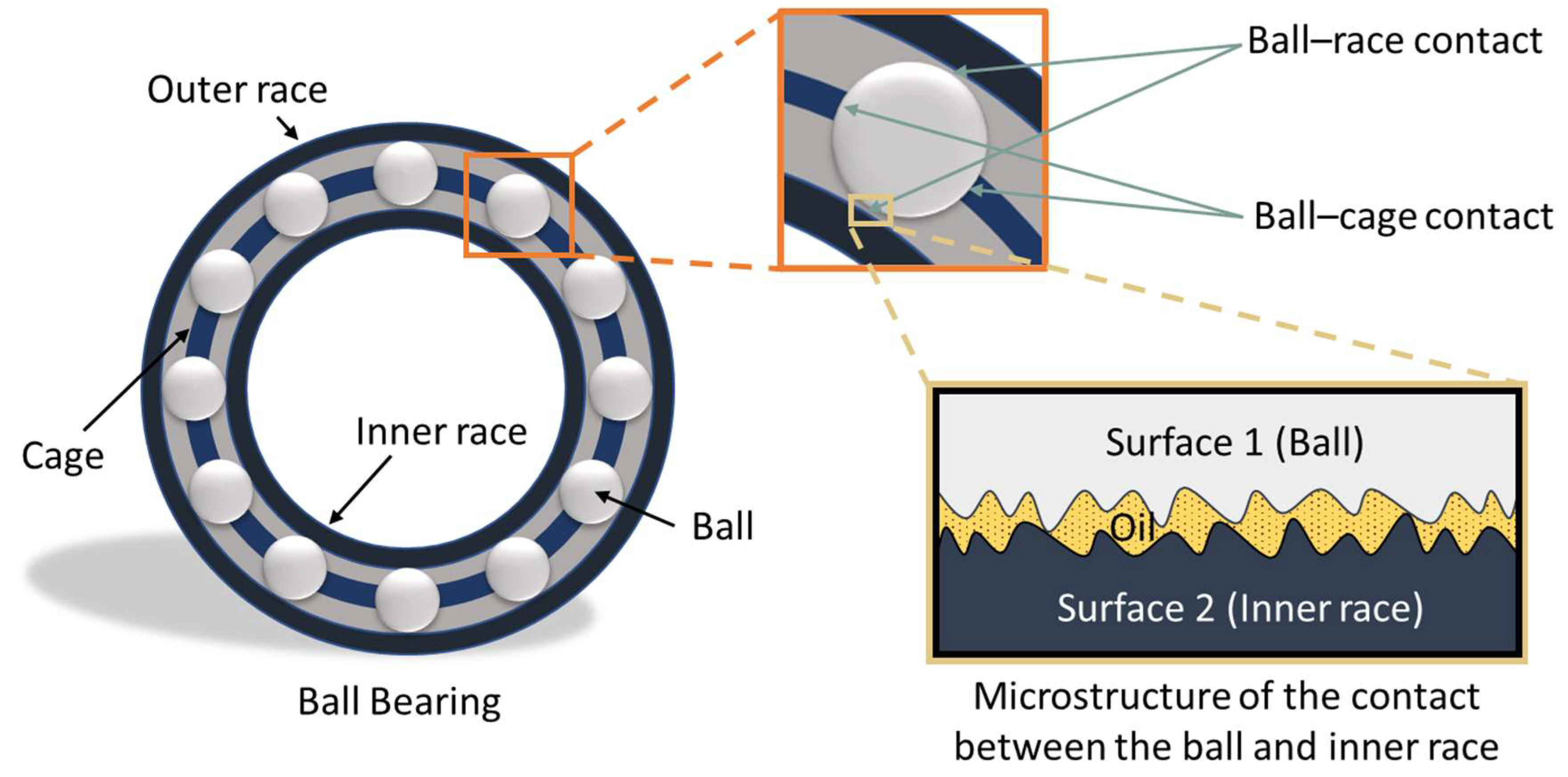
1. Introduction
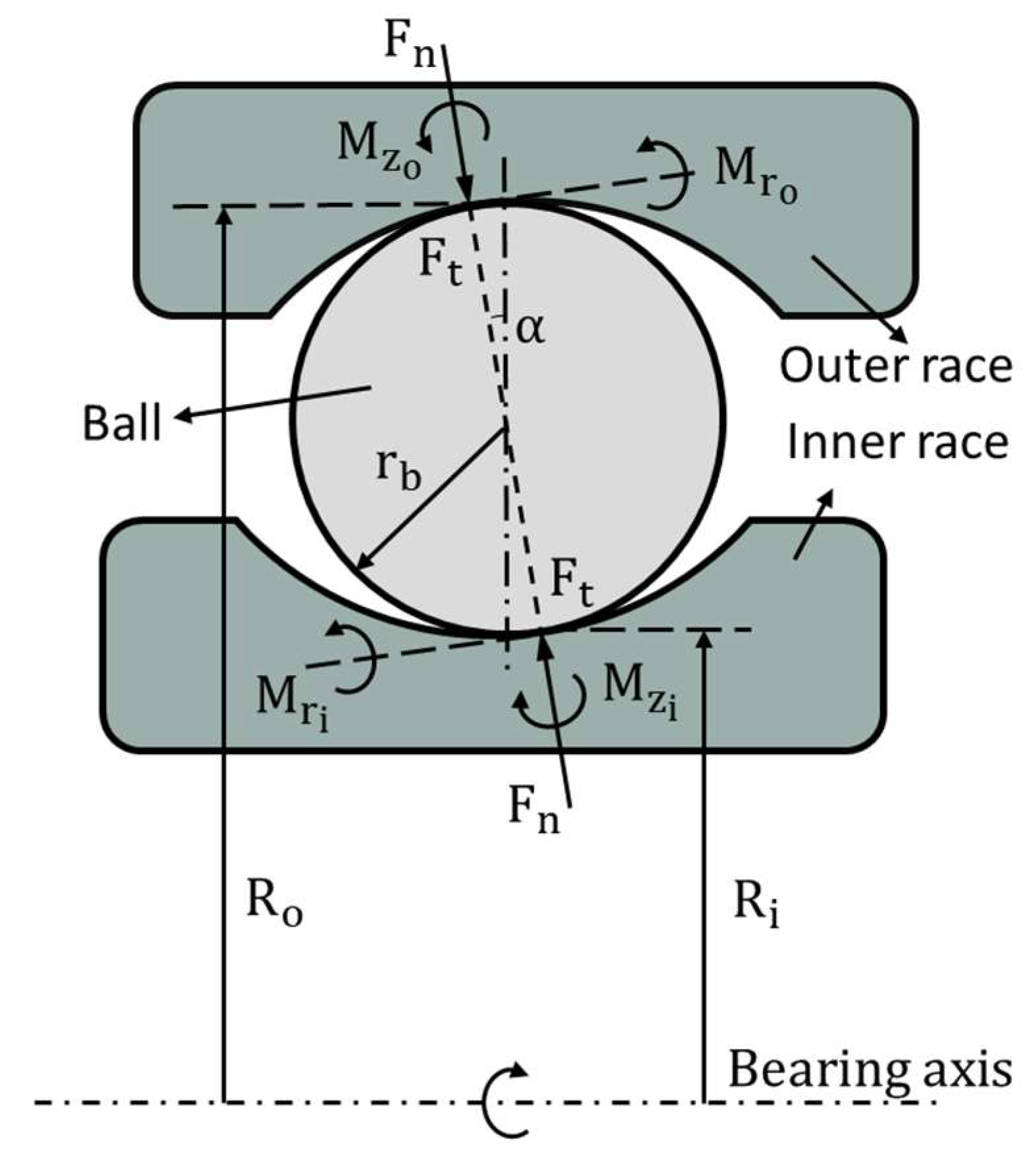
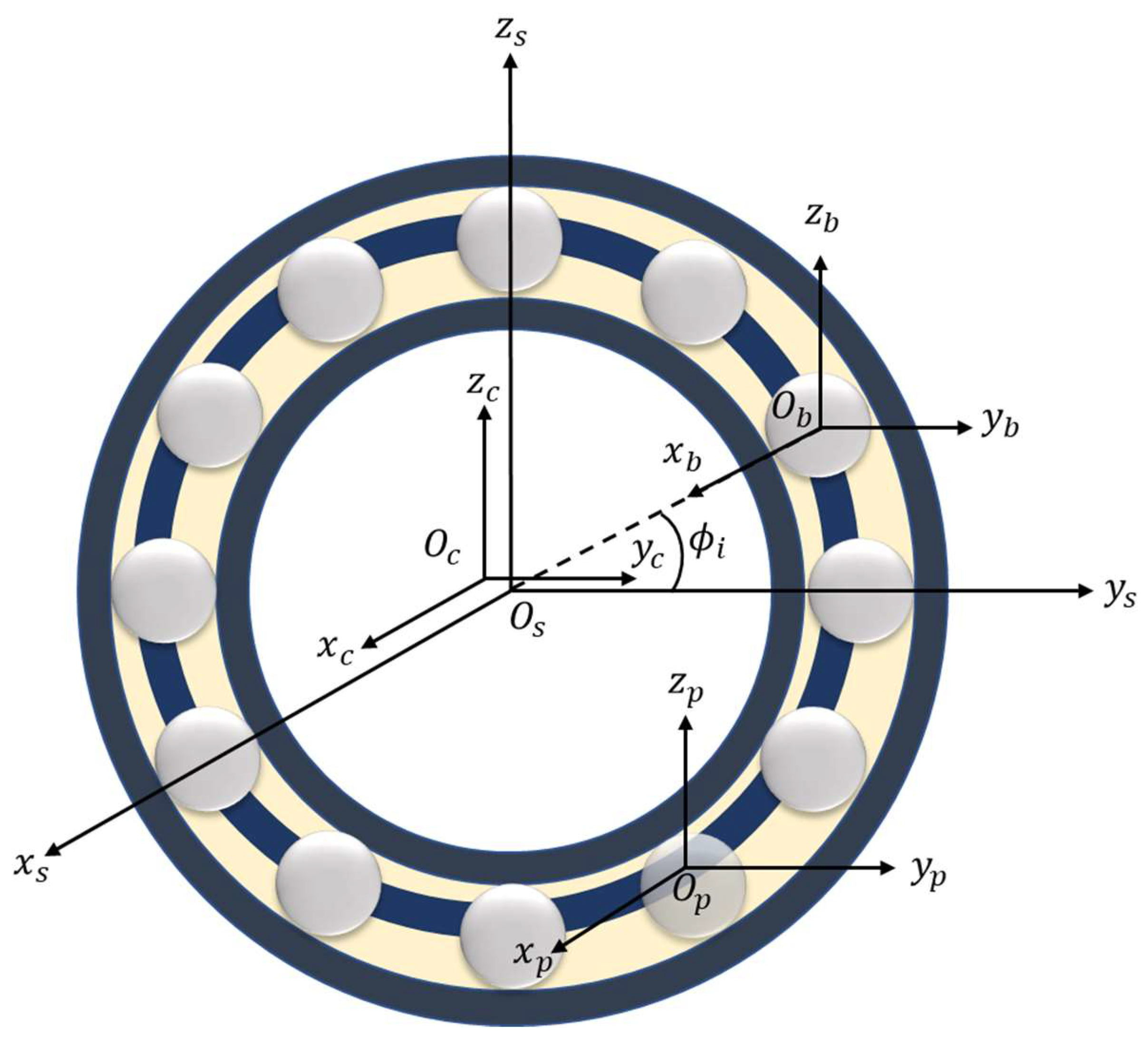
2. Theoretical Model
- The model is designed for open bearings, so the friction moments from seals and dust covers are not considered;
- The frictional moments from lubricant drag losses, churning, and splashing are ignored;
- The contact patch at the point of contact is assumed to have a Hertzian elliptical shape and the bodies are assumed to deform elastically at a local level.
2.1. Ball and Race Contact Friction Model
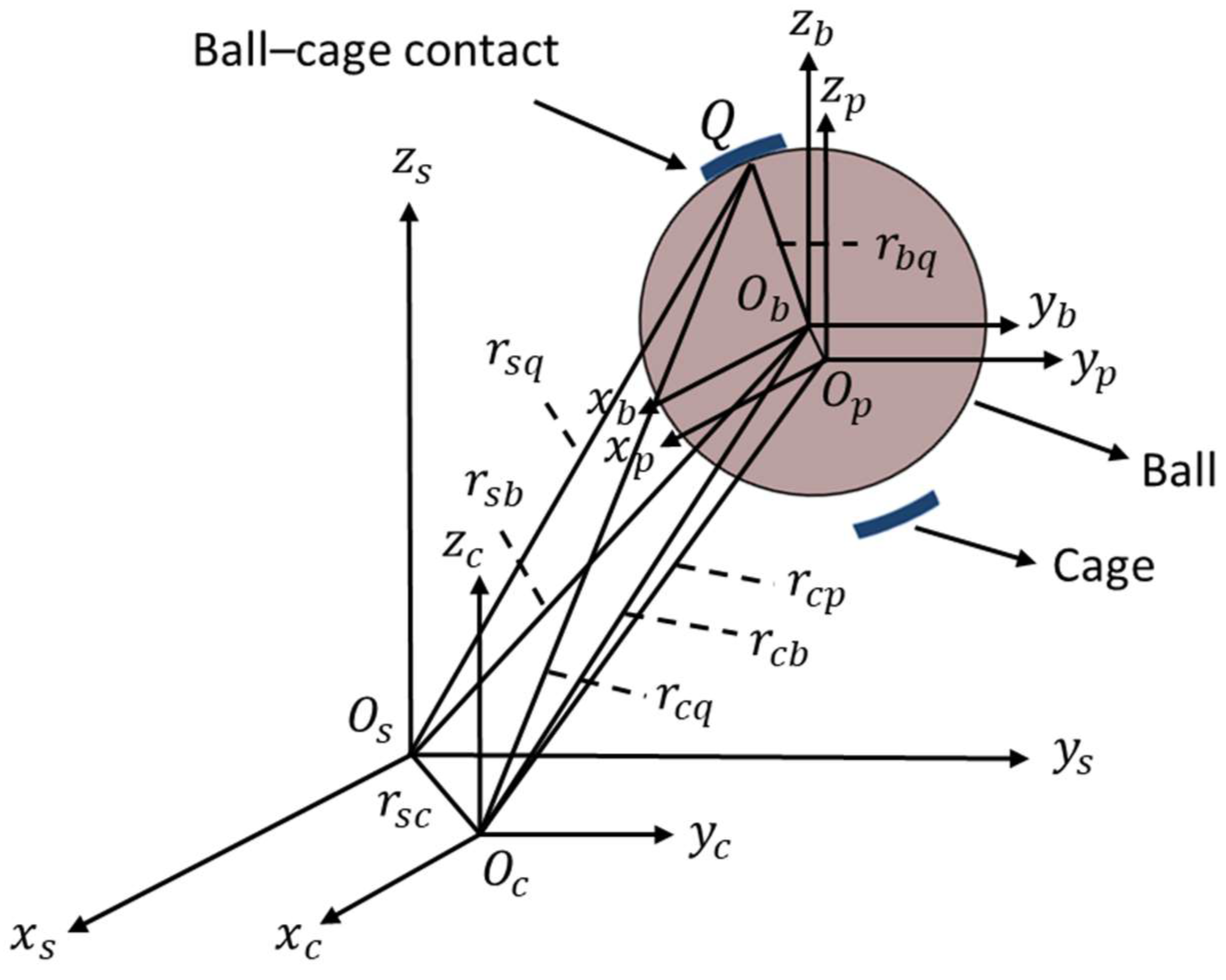
2.2. Ball and Cage Contact Friction Model
2.3. Mixed Elastohydrodynamic Lubrication Model
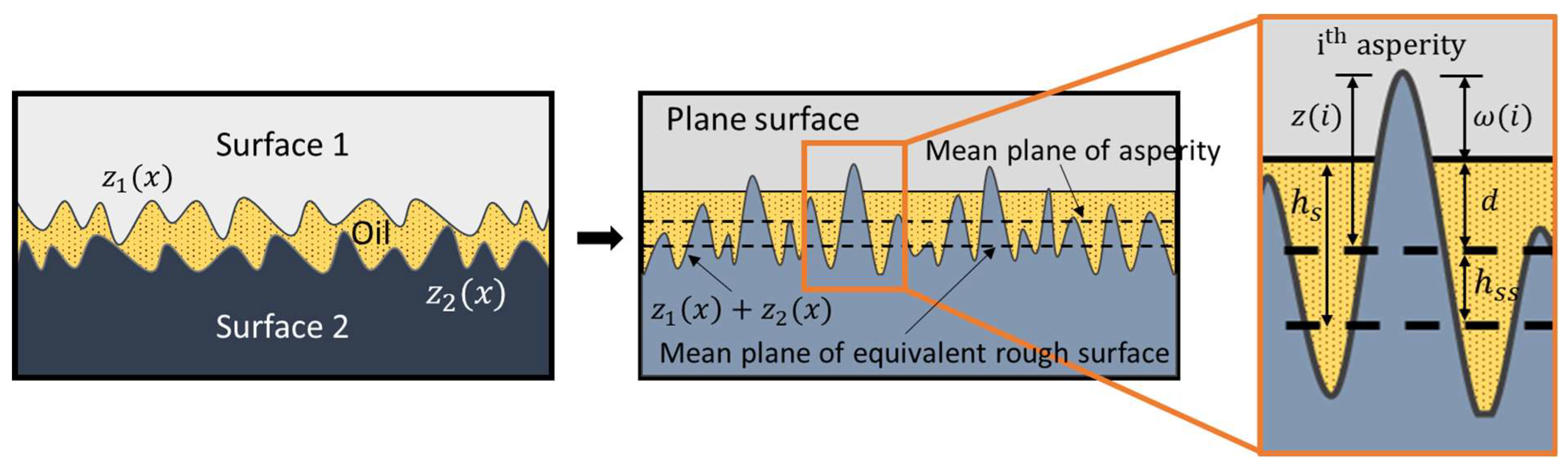
2.3.1. Asperity Contact Model
2.3.2. Lubrication Model
3. Methodology
4. Results and Discussion
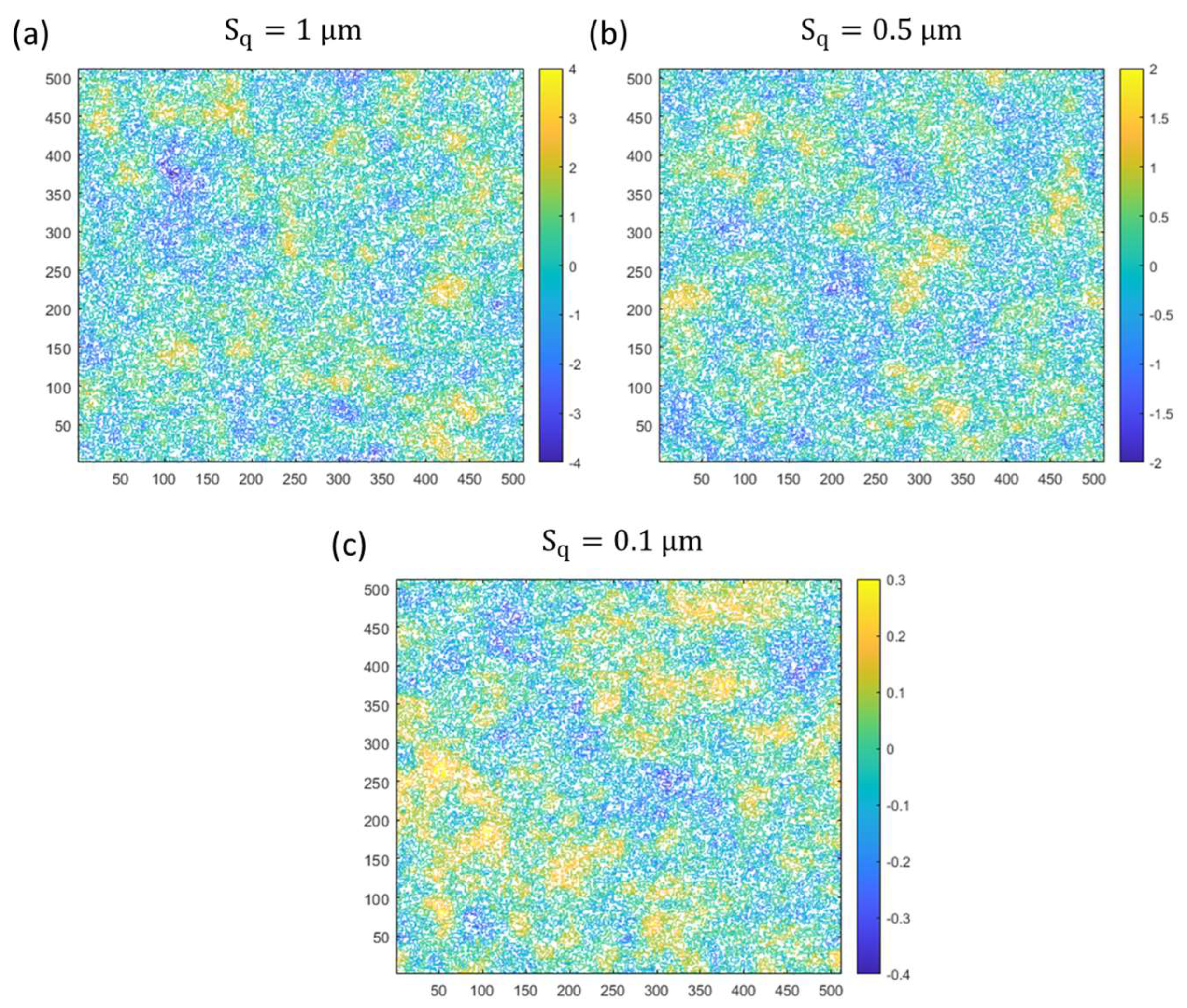
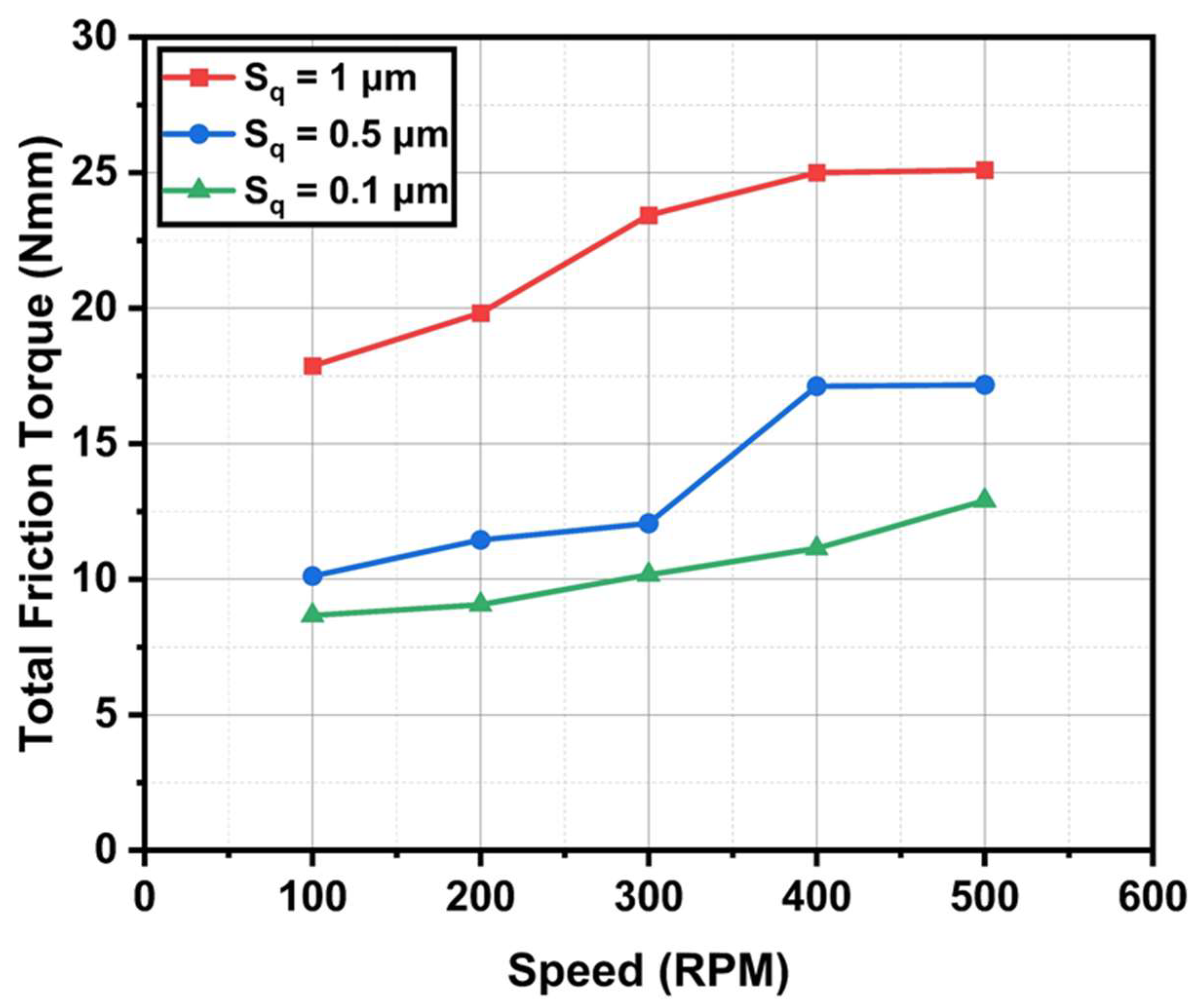
4.1. Effect of Surface Roughness on the Total Friction Torque
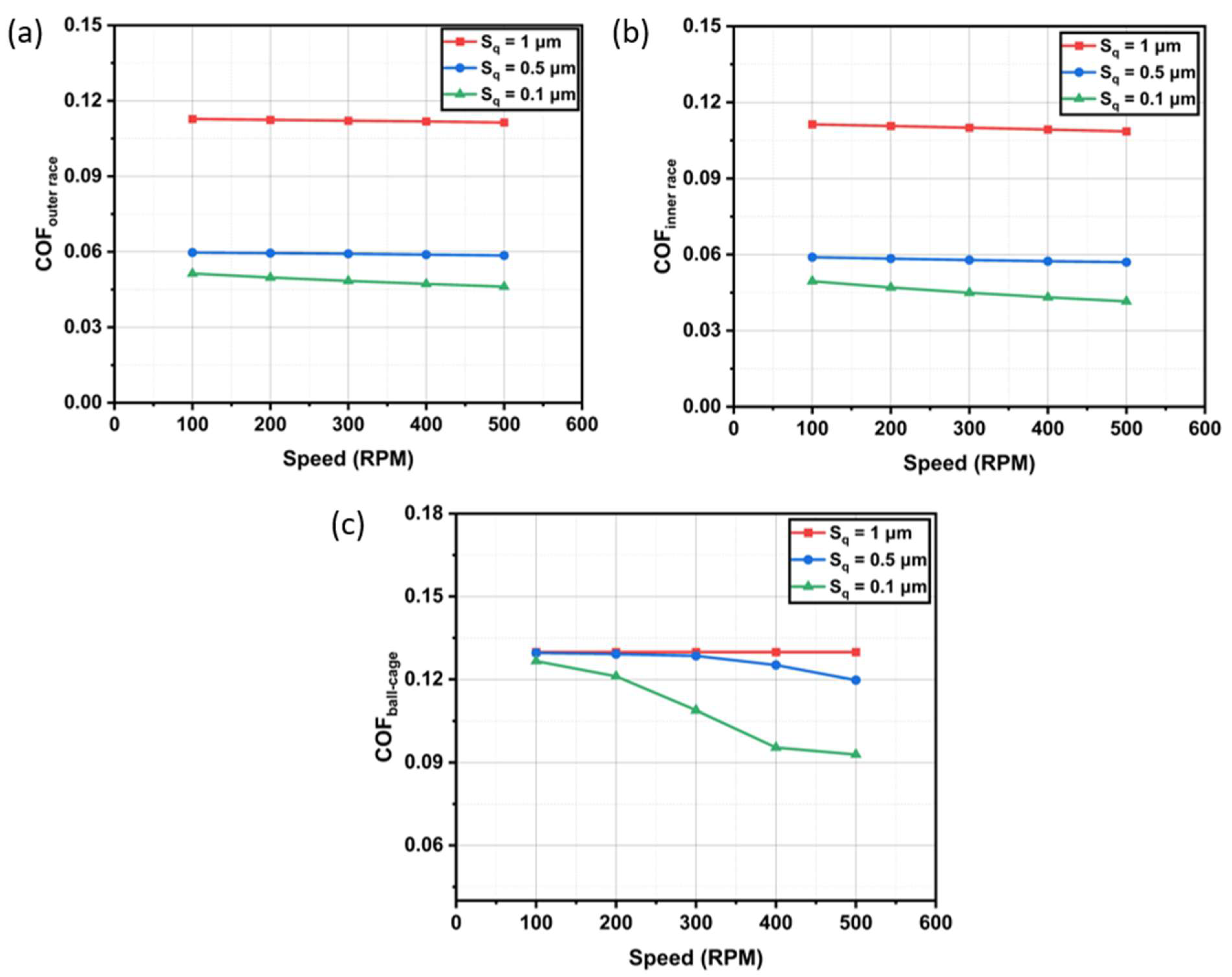
4.2. Effect of Surface Roughness and Speed on Friction Coefficient at Ball–Race and Ball–Cage Contacts
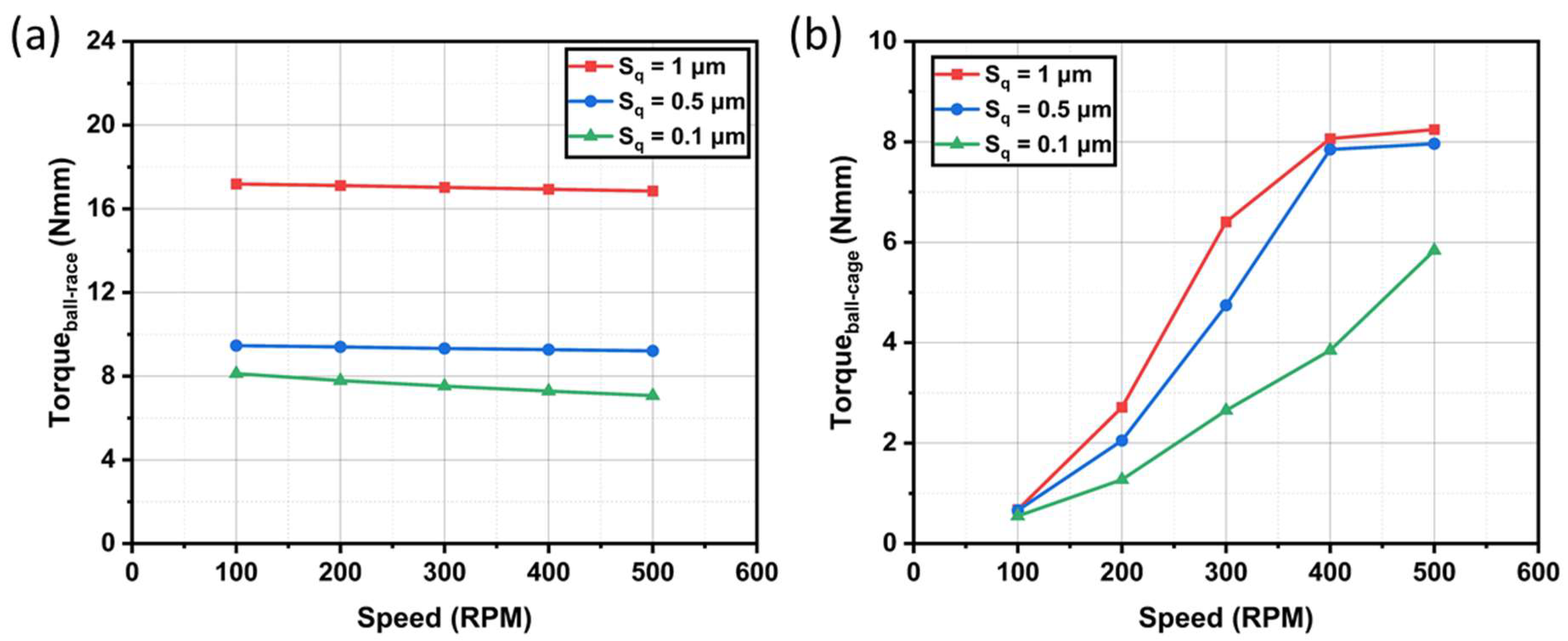
4.3. Effect of Surface Roughness and Speed on Friction Torque at Ball–Race and Ball–Cage Contacts
- (a)
- Ball–Race Friction Torque ():
- At Sq = 1 μm, the torque remained almost constant at around 17 N·mm across all the speeds from 100 RPM to 500 RPM;
- For Sq = 0.5 μm, the torque was lower, starting at around 9.5 N·mm at 100 RPM and remaining constant at approximately the same value as the speed increased to 500 RPM;
- At Sq = 0.1 μm, the lowest roughness, the torque started at about 8 N·mm and slowly decreased over the speed range to 7 N·mm;
- The torque values remained relatively constant across the speed range for each roughness level.
- (b)
- Ball–Cage Friction Torque ():
- At Sq = 1 μm, the torque started at around 0.6 N·mm at 100 RPM but rapidly increased to approximately 8.2 N·mm at 500 RPM;
- For Sq = 0.5 μm, the initial torque at 100 RPM was close to 0.6 N·mm, but it increased more slowly compared to the rougher surface, reaching around 8 N·mm at 500 RPM;
- At Sq = 0.1 μm, the torque at 100 RPM was about 0.5 N·mm and increased to 6 N·mm at 500 RPM;
- The rougher surfaces produced higher torque values at all the speeds.
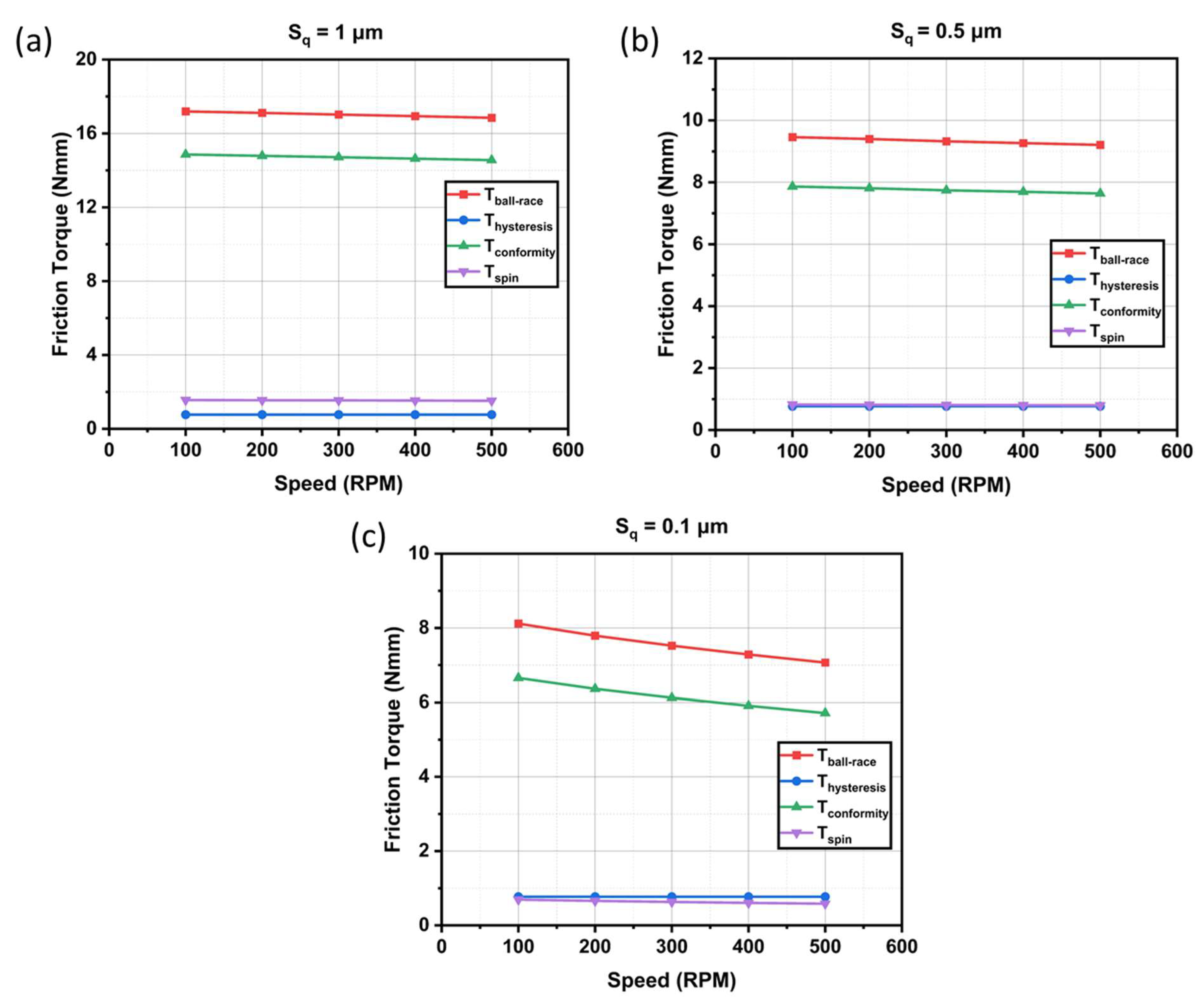
4.4. Effect of Surface Roughness on Different Factors Contributing to the Ball–Race Friction Torque
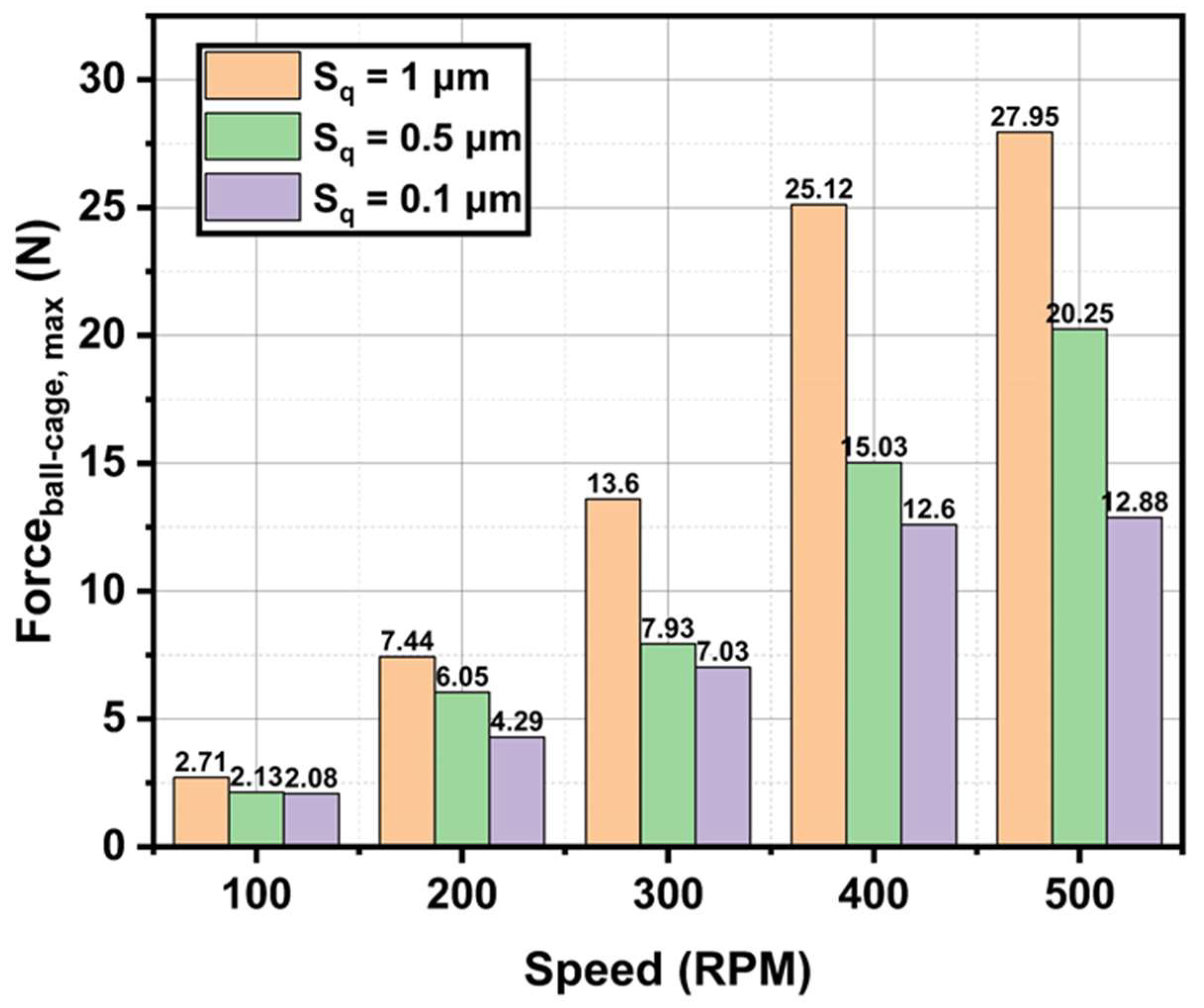
4.5. Effect of Surface Roughness on the Ball–Cage Contact Force
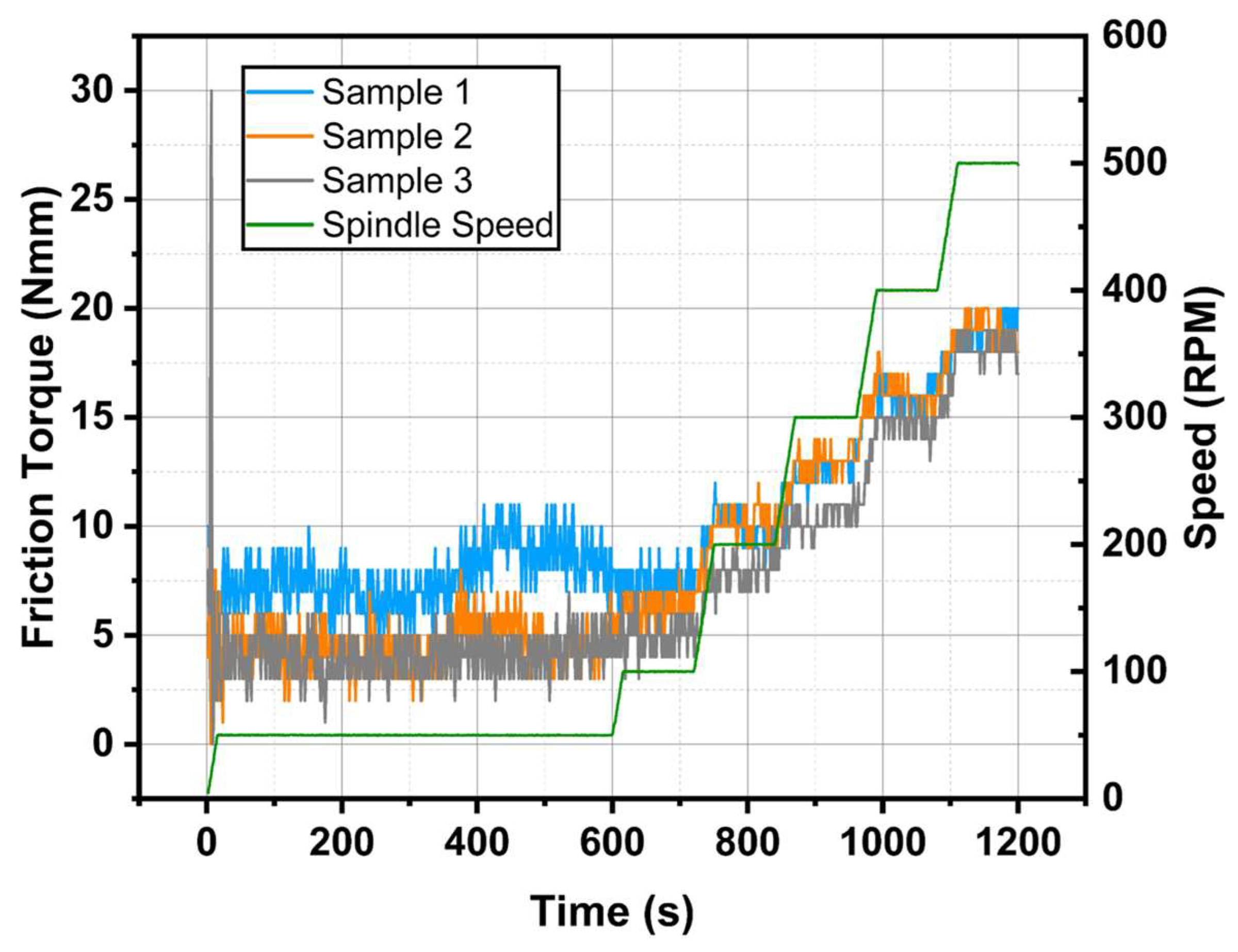
4.6. Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Semi minor axis of elliptical contact (m) | |
| Semi major axis of elliptical contact (m) | |
| Pitch circle diameter (m) | |
| Diameter of the ball (m) | |
| Equivalent Young’s Modulus (Pa) | |
| Hertzian contact stiffness | |
| Spin moment (N·m) | |
| Rolling moment due to conformity (N·m) | |
| Rolling moment due to hysteresis (N·m) | |
| Normal load at point of contact (N) | |
| Tangential load at point of contact (N) | |
| Radius of the ball (m) | |
| Distance of inner and outer contacts from the bearing axis (m) | |
| Radius of curvature at contact point (m) | |
| Friction moment at ball–race contact (N·m) | |
| Friction moment at ball–cage contact (N·m) | |
| Total friction moment (N·m) | |
| Number of balls | |
| Contact angle of bearing (rad) | |
| Hysteresis loss factor | |
| Angular position of the ball (rad) | |
| Complete elliptic integral of second kind | |
| Spin-to-roll ratio | |
| Ratio of major and minor axis length | |
| Half width of the cage pocket (m) | |
| Friction coefficient at ball–race and ball–cage contact | |
| Angular velocity of inner race and outer race (rad/s) | |
| Total load at contact (N) | |
| Load carried by asperity (N) | |
| Load carried by lubricant film (N) | |
| Friction force at contact (N) | |
| Friction force due to asperity (N) | |
| Friction force due to lubricant film (N) | |
| Lubricant film separation (m) | |
| Gap between mean plane of equivalent rough surface and asperity (m) | |
| Total actual contact area of asperity (m2) | |
| Boundary friction coefficient | |
| Dimensionless central film thickness | |
| Central film thickness (m) | |
| Reduced radius of curvature in x direction ( (m) | |
| Radius of curvature of surface 1 and surface 2 in contact in x direction (m) | |
| Reduced radius of curvature in y direction ( (m) | |
| Radius of curvature of surface 1 and surface 2 in contact in y direction (m) | |
| Sum of the velocity of surface 1 and surface 2 at the contact (m/s) | |
| Dynamic viscosity of oil at ambient pressure and temperature (Pa·s) | |
| Equivalent Young’s Modulus () (Pa) | |
| Young’s Modulus of surface 1 and surface 2 in contact (Pa) | |
| Poisson’s ratio of surface 1 and surface 2 in contact |
Appendix A
References
- Gouda, B.; Tandon, N.; Pandey, R.K.; Babu, C.K. Effects of positioning of inner race micro-textures on the tribodynamic performances of radial ball bearings. Mech. Syst. Signal Process 2025, 223, 111908. [Google Scholar] [CrossRef]
- Jin, C.; Wu, B.; Hu, Y. Heat generation modeling of ball bearing based on internal load distribution. Tribol. Int. 2012, 45, 8–15. [Google Scholar] [CrossRef]
- Wang, Y.S.; Liu, Z.; Zhu, H.F. Heat generation of bearing. In Key Engineering Materials; Trans Tech Publications Ltd.: Bäch, Switzerland, 2011; pp. 962–967. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Mindlin, R.D. Compliance of elastic bodies in contact. J. Appl. Mech. 1949, 259–268. [Google Scholar] [CrossRef]
- Dahl, P.R. A Solid Friction Model; The Aerospace Corporation: Chantilly, VA, USA, 1968; Volume 18, pp. 1–24. [Google Scholar]
- Todd, M.J.; Johnson, K.L. A model for coulomb torque hysteresis in ball bearings. Int. J. Mech. Sci. 1987, 29, 339–354. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, X.; Gu, J.; Shen, X. Friction moment analysis of space gyroscope bearing with ribbon cage under ultra-low oscillatory motion. Chin. J. Aeronaut. 2014, 27, 1301–1311. [Google Scholar] [CrossRef]
- Jones, A.B. A General Theory for Elastically Constrained Ball and Radial Roller Bearings Under Arbitrary Load and Speed Conditions. J. Basic Eng. 1960, 82, 309–320. [Google Scholar] [CrossRef]
- Harris, T.A.; Mindel, M.H. Rolling Element Bearing Dynamics; Elsevier Sequoia S.A: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Wang, W.Z.; Hu, L.; Zhang, S.G.; Zhao, Z.Q.; Ai, S. Modeling angular contact ball bearing without raceway control hypothesis. Mech. Mach. Theory 2014, 82, 154–172. [Google Scholar] [CrossRef]
- Popescu, A.; Houpert, L.; Olaru, D.N. Four approaches for calculating power losses in an angular contact ball bearing. Mech. Mach. Theory 2020, 144, 103669. [Google Scholar] [CrossRef]
- Rivera, G.; Tong, V.-C.; Hong, S.-W. Improved Formulation for Sliding Friction Torque of Deep Groove Ball Bearings. J. Korean Soc. Precis. Eng. 2022, 39, 779–789. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, Z.; Zi, Y. Skidding and spinning investigation for dry-lubricated angular contact ball bearing under combined loads. Friction 2023, 11, 1987–2007. [Google Scholar] [CrossRef]
- Li, J.H.; Deng, S.E.; Ma, C.M. Analysis on influence factors of friction torque of sensitive bearing of gyro frame. Bearing 2006, 1, 4–7. [Google Scholar]
- Xi, Y.; Ruan, W.; Li, H. Development of low friction torque of bearings. Bearing 2002, 10, 13–27. [Google Scholar]
- Gupta, P.K. Some dynamic effects in high-speed solid-lubricated ball bearings. ASLE Trans. 1983, 26, 393–400. [Google Scholar] [CrossRef]
- Meeks, C.R.; Ng, K.O. The dynamics of ball separators in ball bearings—Part I: Analysis. ASLE Trans. 1985, 28, 277–287. [Google Scholar] [CrossRef]
- Meeks, C.R. The dynamics of ball separators in ball bearings—Part II: Results of optimization study. ASLE Trans. 1985, 28, 288–295. [Google Scholar] [CrossRef]
- Houpert, L. CAGEDYN: A contribution to roller bearing dynamic calculations part I: Basic tribology concepts. Tribol. Trans. 2010, 53, 1–9. [Google Scholar] [CrossRef]
- Houpert, L. CAGEDYN: A Contribution to roller bearing dynamic calculations Part II: Description of the numerical tool and its outputs. Tribol. Trans. 2009, 53, 10–21. [Google Scholar] [CrossRef]
- Houpert, L.U.C. CAGEDYN: A contribution to roller bearing dynamic calculations. Part III: Experimental validation. Tribol. Trans. 2010, 53, 848–859. [Google Scholar] [CrossRef]
- Olaru, D.N.; Rodica, M.; Bălan, D.; Tufescu, A.; Cârlescu, V.; Prisacaru, G. Influence of the cage on the friction torque in low loaded thrust ball bearings operating in lubricated conditions. Tribol. Int. 2016, 107, 294–305. [Google Scholar] [CrossRef]
- Zhou, C.-G.; Wang, L.-D.; Shen, J.-W.; Chen, C.-H.; Ou, Y.; Feng, H.-T. Wear characterization of raceway surface profiles of ball screws. J. Tribol. 2022, 144, 111701. [Google Scholar] [CrossRef]
- Bachchhav, B.; Bagchi, H. Effect of surface roughness on friction and lubrication regimes. Mater. Today Proc. 2021, 38, 169–173. [Google Scholar] [CrossRef]
- Deng, L.; Su, J.; Jin, Z. Effect of composite textured rough surfaces on the lubrication performance of cylindrical roller bearings. Ind. Lubr. Tribol. 2024, 76, 852–863. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Huang, J.; Sang, D.; Yang, K.; Ling, J. Influence of surface texture on pocket pairs lubrication performance of cylindrical roller bearings. Ind. Lubr. Tribol. 2024, 76, 1085–1097. [Google Scholar] [CrossRef]
- Li, S.; Huang, S.; Wei, C.; Sun, J.; Wang, Y.; Wang, K. Effect of raceway surface topography based on solid lubrication on temperature rise characteristics of HIPSN full ceramic ball bearings. Ind. Lubr. Tribol. 2024, 76, 1036–1047. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, C.; Feng, H. A meticulous friction torque model for a lubricated ball screw considering the surface roughness. Tribol. Int. 2023, 190, 109014. [Google Scholar] [CrossRef]
- Bălan, M.R.D.; Houpert, L.; Tufescu, A.; Olaru, D.N. Rolling friction torque in ball-race contacts operating in mixed lubrication conditions. Lubricants 2015, 3, 222–243. [Google Scholar] [CrossRef]
- Shi, X.; Wu, J.; Zhao, B.; Ma, X.; Lu, X. Mixed thermal elastohydrodynamic lubrication analysis with dynamic performance of aero ball bearing during start-up and shut-down. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 873–886. [Google Scholar] [CrossRef]
- Cao, R.; Bai, H.; Cao, H.; Zhang, Y.; Meng, Y. Mixed lubrication analysis of tapered roller bearings and crowning profile optimization based on numerical running-in method. Lubricants 2023, 11, 97. [Google Scholar] [CrossRef]
- Harris, T.A. Rolling Bearing Analysis; Wiley: Hoboken, NJ, USA, 1966. [Google Scholar]
- Akbarzadeh, S.; Khonsari, M.M. Effect of surface pattern on Stribeck curve. Tribol. Lett. 2010, 37, 477–486. [Google Scholar] [CrossRef]
- Akbarzadeh, S.; Khonsari, M.M. Experimental and theoretical investigation of running-in. Tribol. Int. 2011, 44, 92–100. [Google Scholar] [CrossRef]
- Akchurin, A.; Bosman, R.; Lugt, P.M.; van Drogen, M. On a model for the prediction of the friction coefficient in mixed lubrication based on a load-sharing concept with measured surface roughness. Tribol. Lett. 2015, 59, 19. [Google Scholar] [CrossRef]
- Prajapati, D.K. Prediction of coefficient of friction for different surface topography in mixed-EHL regime. Surf. Topogr. 2021, 9, 015008. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A.; Poon, S.Y. A simple theory of asperity contact in elastohydro-dynamic lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar]
- Nijenbanning, G.; Venner, C.H.; Moes, H. Film thickness in elastohydrodynamically lubricated elliptic contacts. Wear 1994, 176, 217–229. [Google Scholar] [CrossRef]
- He, Y.F.; Tang, J.Y.; Zhou, W.; Liao, D.R. Research on the obtainment of topography parameters by rough surface simulation with fast fourier transform. J. Tribol. 2015, 137, 031401. [Google Scholar]
- Zhao, Y.; Maietta, D.M.; Chang, L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow. J. Trib. 2000, 122, 86–93. [Google Scholar] [CrossRef]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. 1966. Available online: http://resolver.tudelft.nl/uuid:1fb56839-9589-4ffb-98aa-4a20968d1f90 (accessed on 12 March 2024).







| Parameters | Value |
|---|---|
| 9 | |
| (gm) | 2.04 |
| (gm) | 6.58 |
| (mm) | 7.94 |
| Mass of inner race (gm) | 38.63 |
| Mass of outer race (gm) | 54.21 |
| Radius of inner race (mm) | 15.53 |
| Radius of outer race (mm) | 23.48 |
| Groove radius of inner race (mm) | 4.13 |
| Groove radius of outer race (mm) | 4.21 |
| Pocket diameter (mm) | 13.9 |
| Pocket depth (mm) | 6.81 |
| Parameters | Value |
|---|---|
| Young’s modulus (GPa) | 230 |
| Poisson’s ratio | 0.3 |
| Hysteresis loss factor (%) | 0.5 |
| (rad) | 0.18 |
| Boundary friction coefficient | 0.13 |
| Axial load (N) | 1000, 3000 |
| Speed (RPM) | 100, 200, 300, 400, 500 |
| Parameters | Value |
|---|---|
| Viscosity at 40 °C (mPa·s) | 20 |
| Pressure viscosity index | 0.65 |
| Eyring Shear Stress | 2.5 |
| Pressure viscosity coefficient (Pa−1) | 2.0 × 10−8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, H.; Gupta, V.; Bharath, V.; Tiwari, M.; Paul, S.K.; Agrawal, L.; Singh, A.P.; Jain, A. Effect of Surface Roughness on the Friction Moment in a Lubricated Deep Groove Ball Bearing. Lubricants 2024, 12, 443. https://doi.org/10.3390/lubricants12120443
Kumar H, Gupta V, Bharath V, Tiwari M, Paul SK, Agrawal L, Singh AP, Jain A. Effect of Surface Roughness on the Friction Moment in a Lubricated Deep Groove Ball Bearing. Lubricants. 2024; 12(12):443. https://doi.org/10.3390/lubricants12120443
Chicago/Turabian StyleKumar, Harsh, Vaibhav Gupta, Velamala Bharath, Mayank Tiwari, Surajit Kumar Paul, Lokesh Agrawal, Arendra Pal Singh, and Ayush Jain. 2024. "Effect of Surface Roughness on the Friction Moment in a Lubricated Deep Groove Ball Bearing" Lubricants 12, no. 12: 443. https://doi.org/10.3390/lubricants12120443
APA StyleKumar, H., Gupta, V., Bharath, V., Tiwari, M., Paul, S. K., Agrawal, L., Singh, A. P., & Jain, A. (2024). Effect of Surface Roughness on the Friction Moment in a Lubricated Deep Groove Ball Bearing. Lubricants, 12(12), 443. https://doi.org/10.3390/lubricants12120443







