The Temperature Dependence of Divergence Pressure
Abstract
:1. Introduction
2. The Hybrid Model
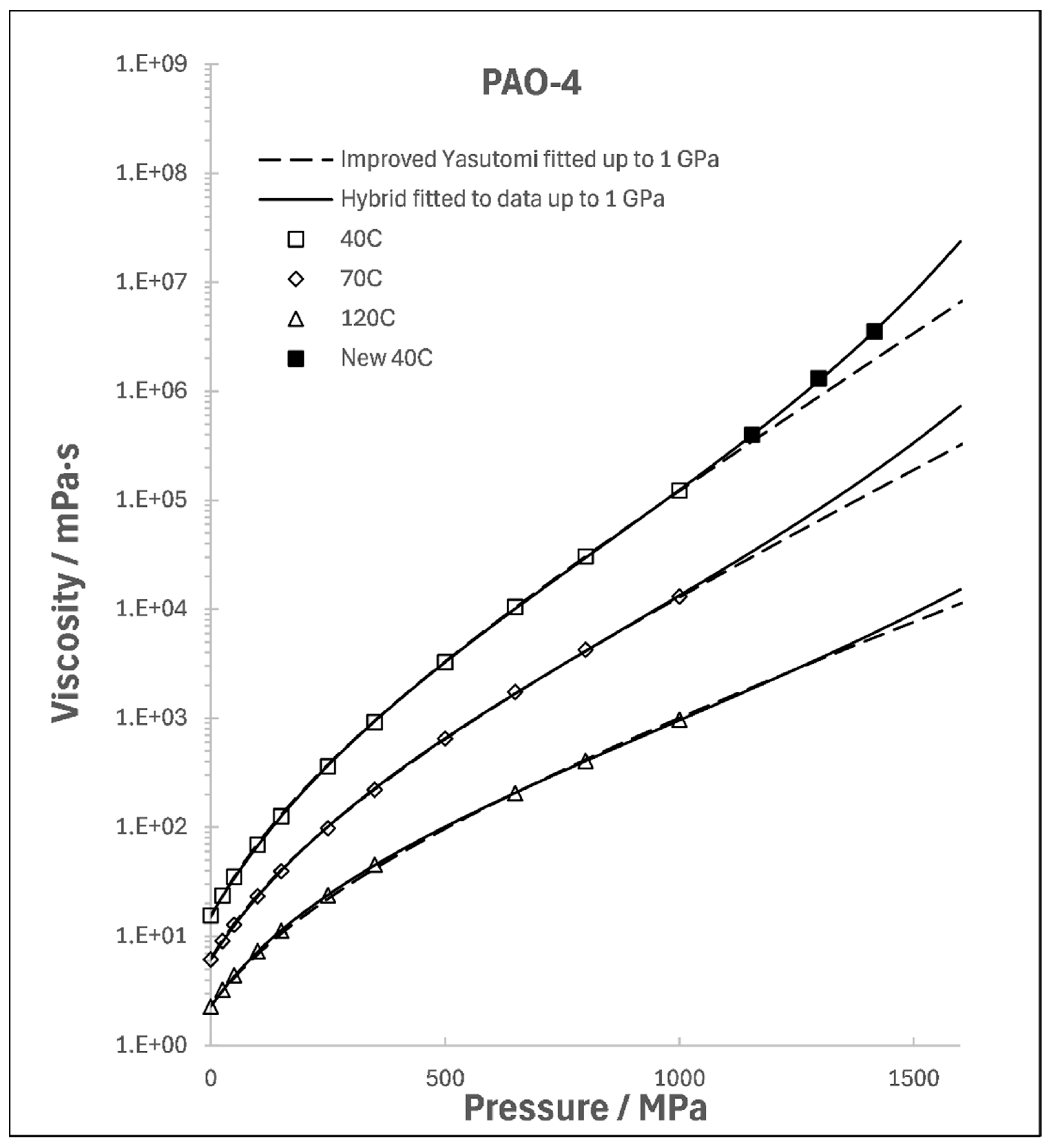
3. Temperature Dependence of Divergence Pressure
- Squalane;
- Diisodecyl phthalate (DIDP);
- Dipentaerythritol hexaisononanoate (DiPEiC9);
- Tri(2-ethylhexyl) trimellitate (TOTM);
- Gear Research Center, FZG, reference gear oil (FVA3).
4. Examples of Special Importance
5. An Application to High-Pressure Physics
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| pressure fragility parameter | |
| temperature fragility parameter | |
| p | pressure, Pa |
| divergence pressure, Pa | |
| McEwen exponent | |
| s | fraction in the Stokes Einstein Debye relation |
| T | temperature, K |
| divergence temperature, K | |
| parameter in the McEwen equation, Pa−1 | |
| μ | limiting low-shear viscosity, Pa·s |
| low-shear viscosity at , | |
| low-shear viscosity for unbounded temperature, | |
| DC electrical conductivity, Ω−1·m−1 |
References
- Bair, S. Roelands’ missing data. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2004, 218, 57–60. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Roland, C.M.; Imre, A.R. On the pressure evolution of dynamic properties of supercooled liquids. J. Phys. Condens. Matter 2008, 20, 244103. [Google Scholar] [CrossRef]
- Spikes, H. Basics of EHL for practical application. Lubr. Sci. 2015, 27, 45–67. [Google Scholar] [CrossRef]
- Bair, S. A critical evaluation of film thickness-derived pressure–viscosity coefficients. Lubr. Sci. 2015, 27, 337–346. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Pressure-related universal previtreous behavior of the structural relaxation time and apparent fragility. Front. Mater. 2019, 6, 103. [Google Scholar] [CrossRef]
- Johari, G.P.; Whalley, E. Dielectric properties of glycerol in the range 0.1–10 5 Hz, 218–357 K, 0–53 kb. Faraday Symp. Chem. Soc. 1972, 6, 23–41. [Google Scholar] [CrossRef]
- Houpert, L. New results of traction force calculations in elastohydrodynamic contacts. J. Lubr. Technol. 1985, 107, 241–248. [Google Scholar] [CrossRef]
- Bair, S. A discussion of Arana, A., Larrañaga, J., & Ulacia, I. (2019). Partial EHL friction coefficient model to predict power losses in cylindrical gears. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, Vol. 233 (2) 303–316. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 1168–1170. [Google Scholar]
- Bair, S. Choosing pressure-viscosity relations. High Temp.-High Press. 2015, 44, 415–428. [Google Scholar]
- Bair, S. Application of the Hybrid Model to EHL Reference Liquids for Pressure Extrapolation. Tribol. Trans. 2024, 67, 1–10. [Google Scholar] [CrossRef]
- American Society of Mechanical Engineers; Research Committee on Lubrication. Viscosity and Density of Over 40 Lubricating Fluids of Known Composition at Pressures to 150,000 Psi and Temperatures to 425 F; American Society of Mechanical Engineers: New York, NY, USA, 1953. [Google Scholar]
- Roelands, C.J.A. Correlational Aspects of the Viscosity-Temperature-Pressure Relationship of Lubricating Oils. Ph.D. Thesis, Technische Hogeschool Delft, Delft, The Netherlands, 1966. [Google Scholar]
- Paluch, M.; Dendzik, Z.; Rzoska, S.J. Scaling of high-pressure viscosity data in low-molecular-weight glass-forming liquids. Phys. Rev. B 1999, 60, 2979. [Google Scholar] [CrossRef]
- Bair, S.; Flores-Torres, S. The viscosity of polyalphaolefins mixtures at high pressure and stress. J. Tribol. 2019, 141, 021802. [Google Scholar] [CrossRef]
- Bair, S. Pressure-viscosity behavior of lubricants to 1.4 GPa and its relation to EHD traction. Tribol. Trans. 2000, 43, 91–99. [Google Scholar] [CrossRef]
- James, F.; Murphy, C.M.; O’Rear, J.G. Diester-Base Jet Engine Oils. Ind. Eng. Chem. 1959, 51, 673–674. [Google Scholar] [CrossRef]
- Bielowka, S.H.; Psurek, T.; Ziolo, J.; Paluch, M. Test of the fractional Debye-Stokes-Einstein equation in low-molecular-weight glass-forming liquids under condition of high compression. Phys. Rev. E 2001, 63, 062301. [Google Scholar] [CrossRef] [PubMed]
- Thoms, E.; Grzybowski, A.; Pawlus, S.; Paluch, M. Breakdown of the simple Arrhenius law in the normal liquid state. J. Phys. Chem. Lett. 2018, 9, 1783–1787. [Google Scholar] [CrossRef] [PubMed]
- Casalini, R.; Bair, S. The inflection point in the pressure dependence of viscosity under high pressure: A comprehensive study of the temperature and pressure dependence of the viscosity of propylene carbonate. J. Chem. Phys. 2008, 128. [Google Scholar] [CrossRef] [PubMed]
- Bair, S.; Habchi, W. Quantitative Elastohydrodynamic Lubrication—Seventeen Years In. J. Tribol. 2024, 146, 080801. [Google Scholar] [CrossRef]
- Habchi, W.; Sperka, P.; Bair, S. The role of the glass transition for EHL minimum film thickness. Tribol. Int. 2023, 190, 109061. [Google Scholar] [CrossRef]






| Equation (3) | Equation (4) | |
| mPa·s | 2.082 | 1.558 |
| K | 141.2 | 129.5 |
| GPa−1 | 31.8 | 40.0 |
| K/GPa | 266 | 303 |
| K2/GPa | −1.543 × 106 | −2.126 × 106 |
| −4.33 | −0.8887 | |
| K | 2101 | 709 |
| 4.23 | 5.31 | |
| GPa | 3.92 | −1.712 |
| K·GPa | −862 | - |
| GPa/K | - | 0.00923 |
| AARD | 5.1% | 3.3% |
| Sample | Squalane | DIDP | DiPEiC9 | TOTM | FVA3 | PAO-4 | PC |
|---|---|---|---|---|---|---|---|
| Temperature/°C | 20 to 65 | 40 to 100 | 50 to 90 | 40 to 100 | 40 to 120 | 40 to 120 | 25 to 105 |
| Max Measured Pressure/GPa | 1.35 | 1.00 | 0.70 | 1.10 | 1.20 | 1.00 | 1.00 |
| Max Measured Viscosity/Pa·s | 3.5 × 105 | 2.4 × 104 | 9 × 103 | 1.13 × 104 | 2 × 103 | 1.22 × 102 | 2.345 |
| mPa·s | 0.0337 | 0.0396 | 0.01580 | 0.01194 | 0.0477 | 0.0779 | 0.0396 |
| K | 150.8 | 176.0 | 156.3 | 140.6 | 176.8 | 171.4 | 96.4 |
| GPa−1 | −23.3 | −1.209 | 7.235 | 0.486 | 7.40 | 21.7 | −21.9 |
| K/GPa | −17,200 | 717 | −114.8 | −4038 | 319.2 | 9218 | −18,760 |
| K2/GPa | −1.31 × 106 | 2.145 × 106 | 1.339 × 106 | 0.312 × 106 | 1.153 × 106 | 2.26 × 106 | −3.34 × 106 |
| −4.246 | −2.828 | 1.194 | −1.368 | −8.319 | −5.231 | 0.7706 | |
| K | 2863 | 3395 | 1019 | 1520 | 4952 | 2964 | −87.60 |
| 6.581 | 5.35 | 10.12 | 10.90 | 5.794 | 4.374 | 8.639 | |
| GPa | −2.819 | −3.480 | −4.501 | −4.878 | −3.709 | −0.632 | −6.235 |
| GPa/K | 0.0175 | 0.0164 | 0.0171 | 0.0225 | 0.0164 | 0.0108 | 0.0292 |
| AARD | 2.5% | 3.0% | 3.6% | 2.2% | 3.2% | 2.0% | 1.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bair, S. The Temperature Dependence of Divergence Pressure. Lubricants 2024, 12, 434. https://doi.org/10.3390/lubricants12120434
Bair S. The Temperature Dependence of Divergence Pressure. Lubricants. 2024; 12(12):434. https://doi.org/10.3390/lubricants12120434
Chicago/Turabian StyleBair, Scott. 2024. "The Temperature Dependence of Divergence Pressure" Lubricants 12, no. 12: 434. https://doi.org/10.3390/lubricants12120434
APA StyleBair, S. (2024). The Temperature Dependence of Divergence Pressure. Lubricants, 12(12), 434. https://doi.org/10.3390/lubricants12120434





