Analysis of Water-Lubricated Journal Bearings Assisted by a Small Quantity of Secondary Lubricating Medium with Navier–Stokes Equation and VOF Model
Abstract
1. Introduction
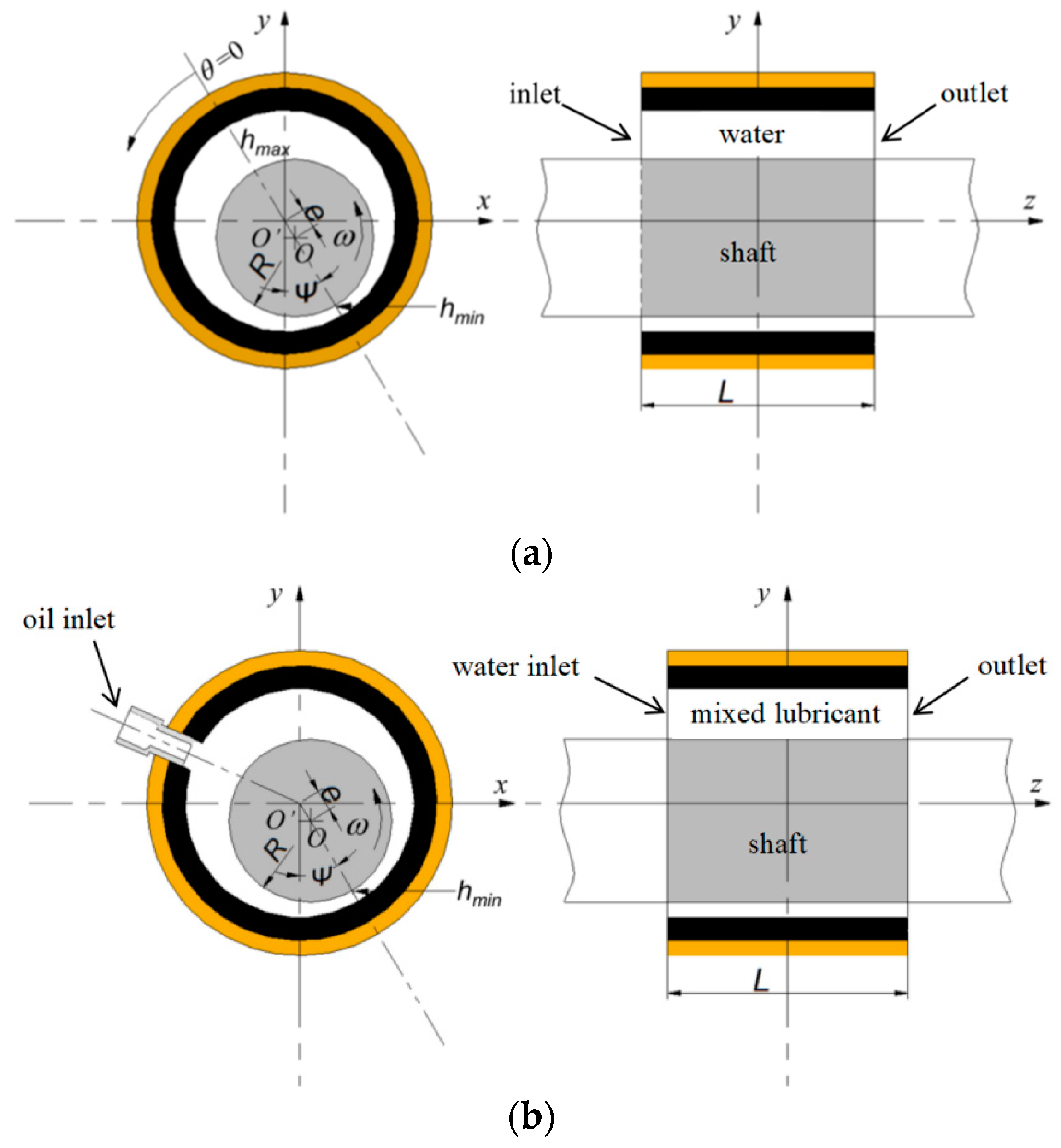
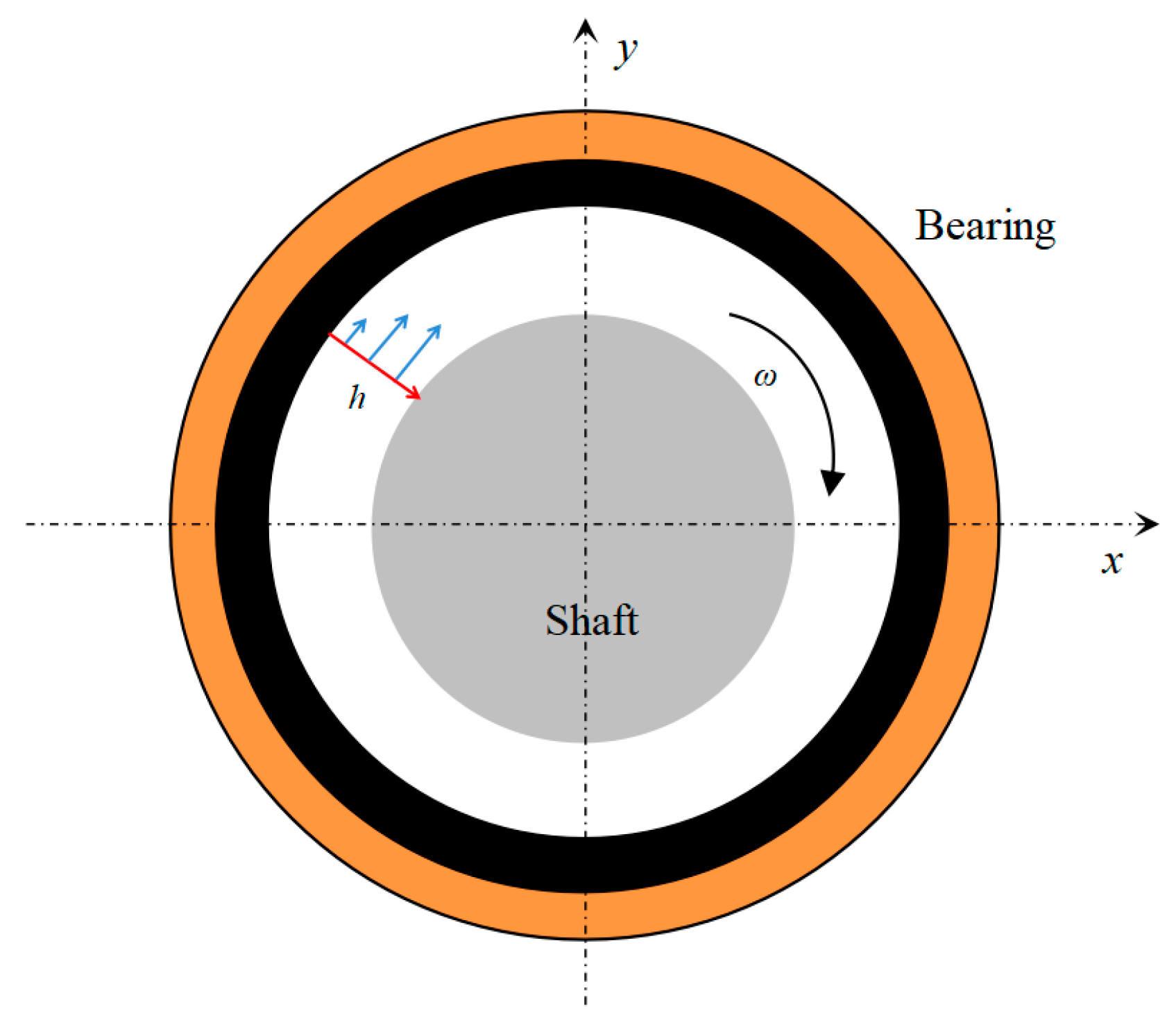
2. Geometry Description
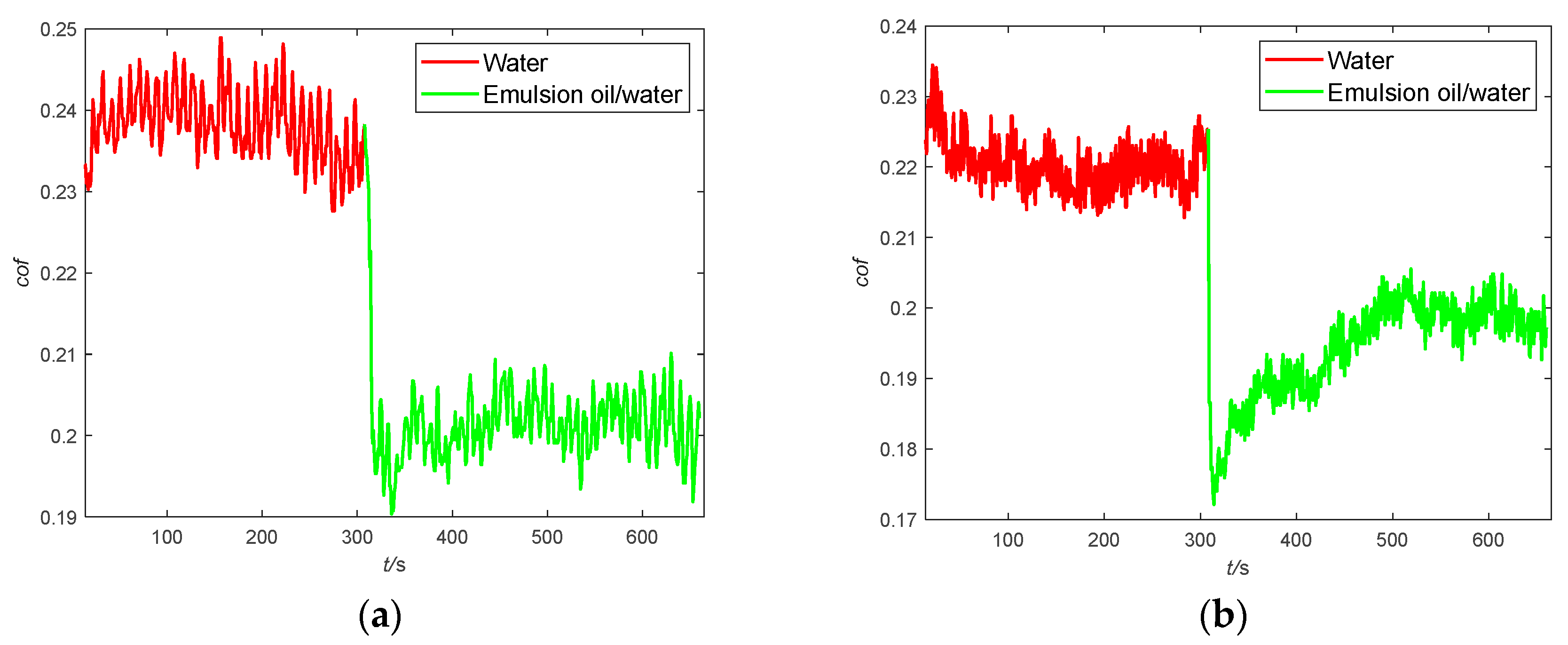
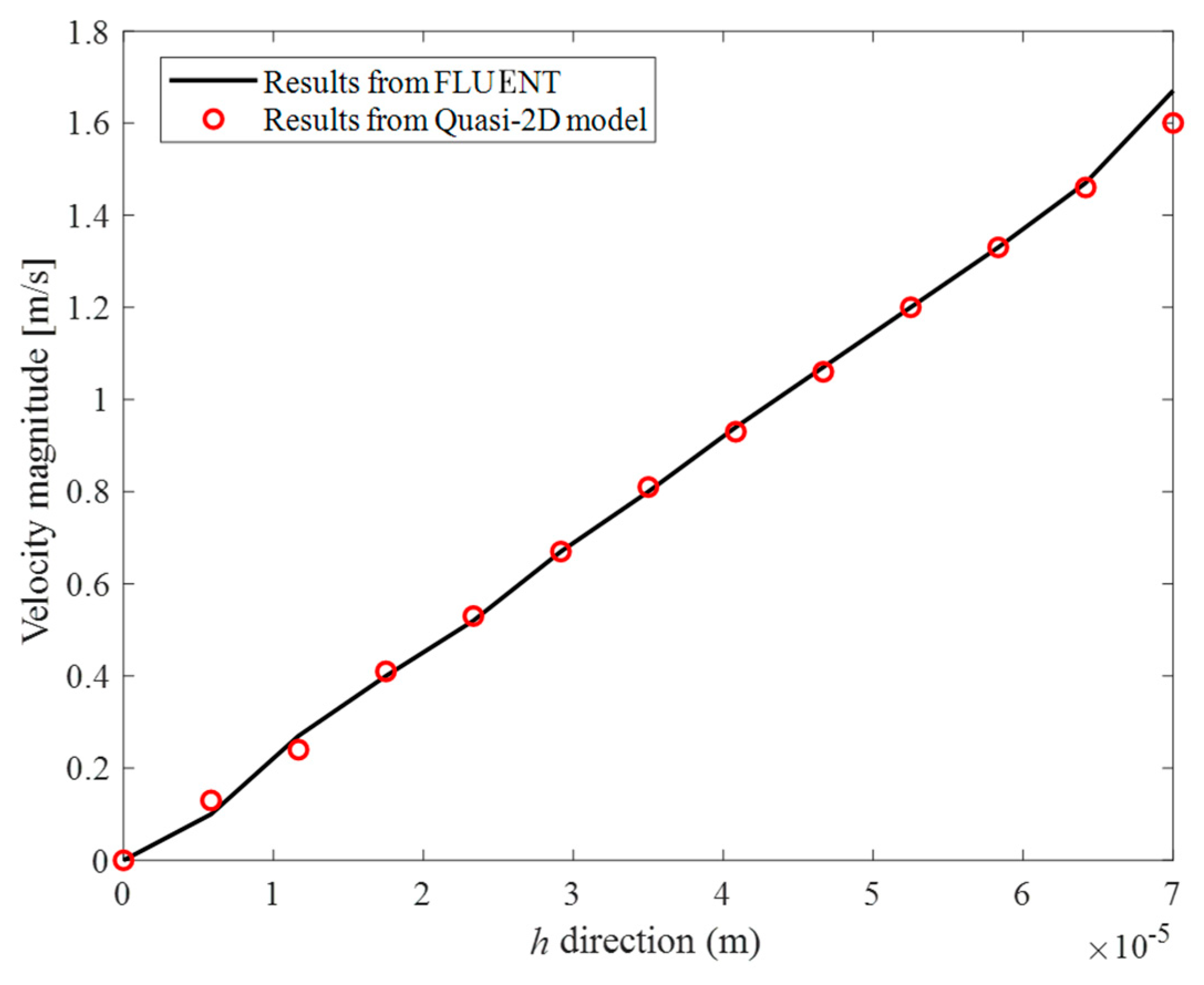
3. Experimental Verification
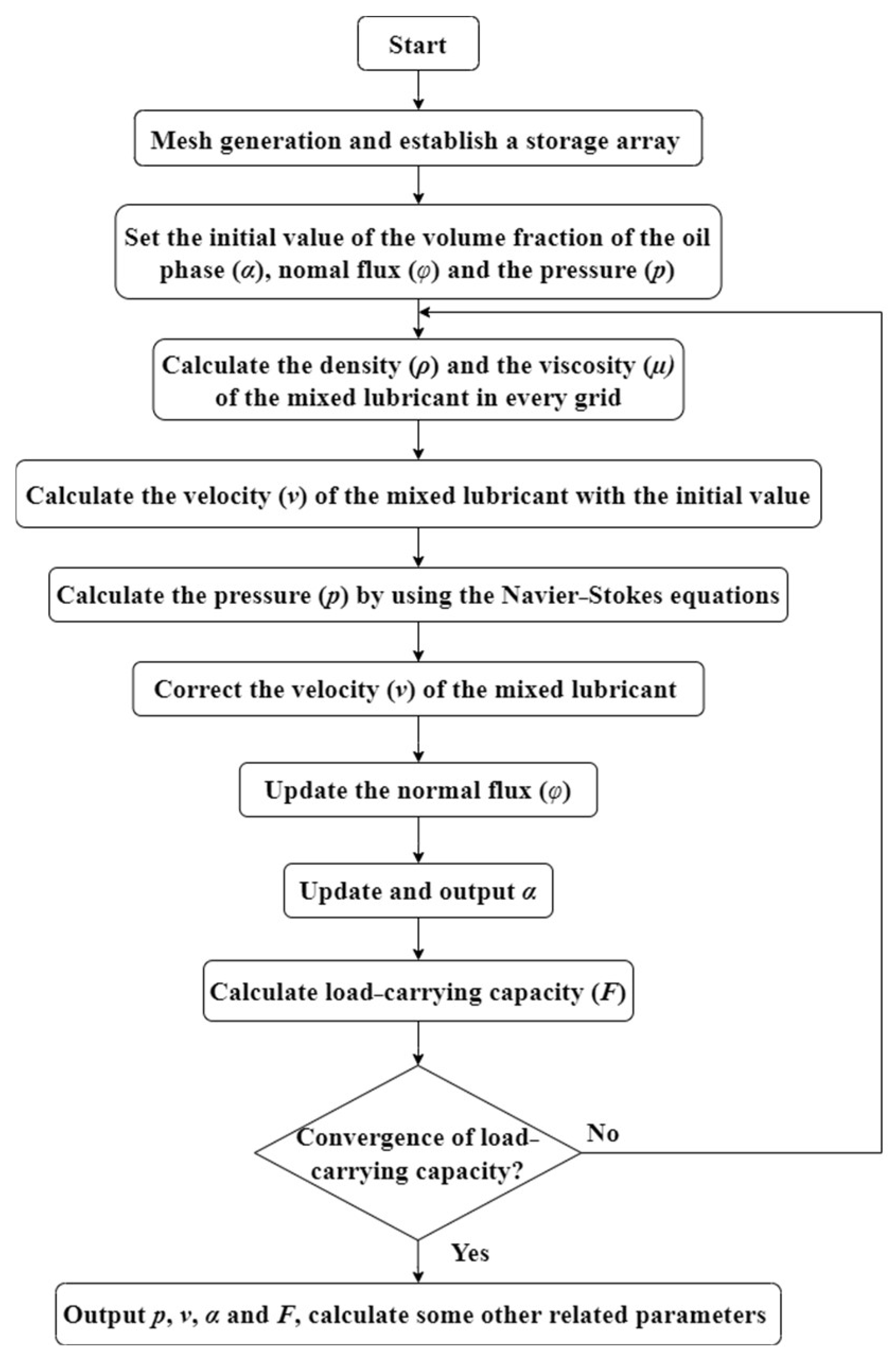
4. Methodology
4.1. Governing Equations
4.1.1. Navier–Stokes (N–S) Equation
4.1.2. Volume of Fluid (VOF) Method
4.1.3. Load-Carrying Capacity
4.2. Boundary Conditions
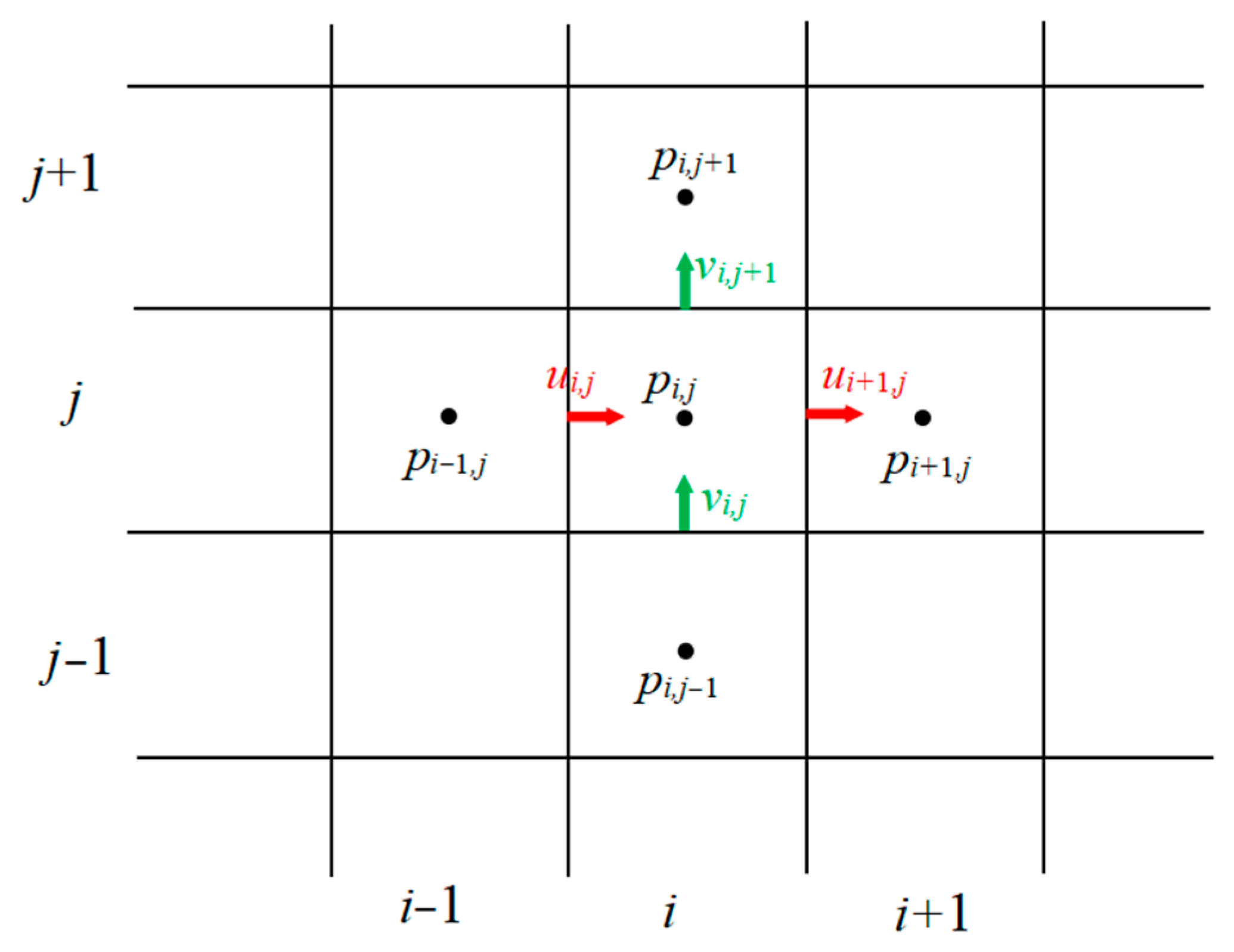
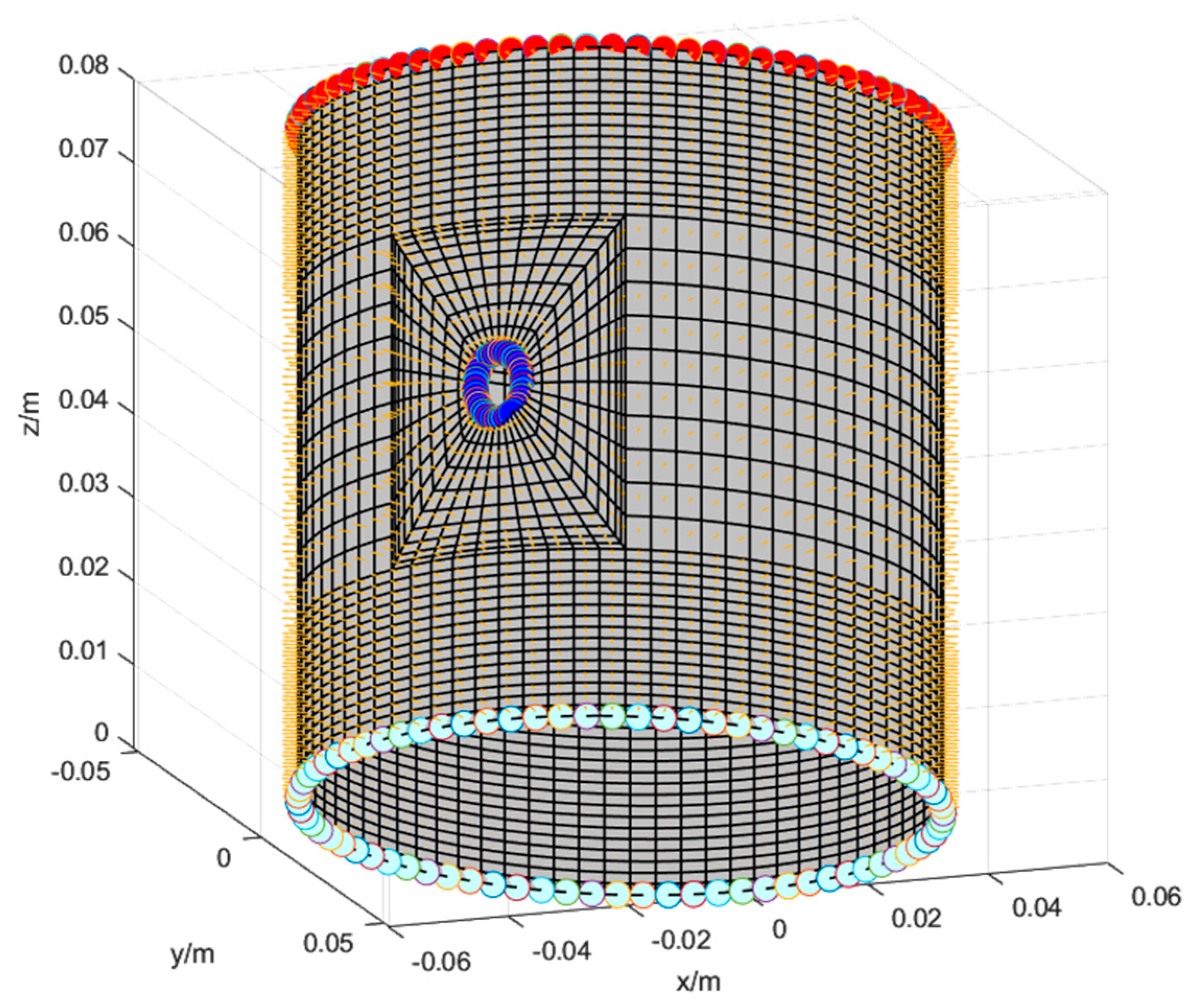
4.3. Mesh Generation
5. Model Verification
6. Results and Discussion
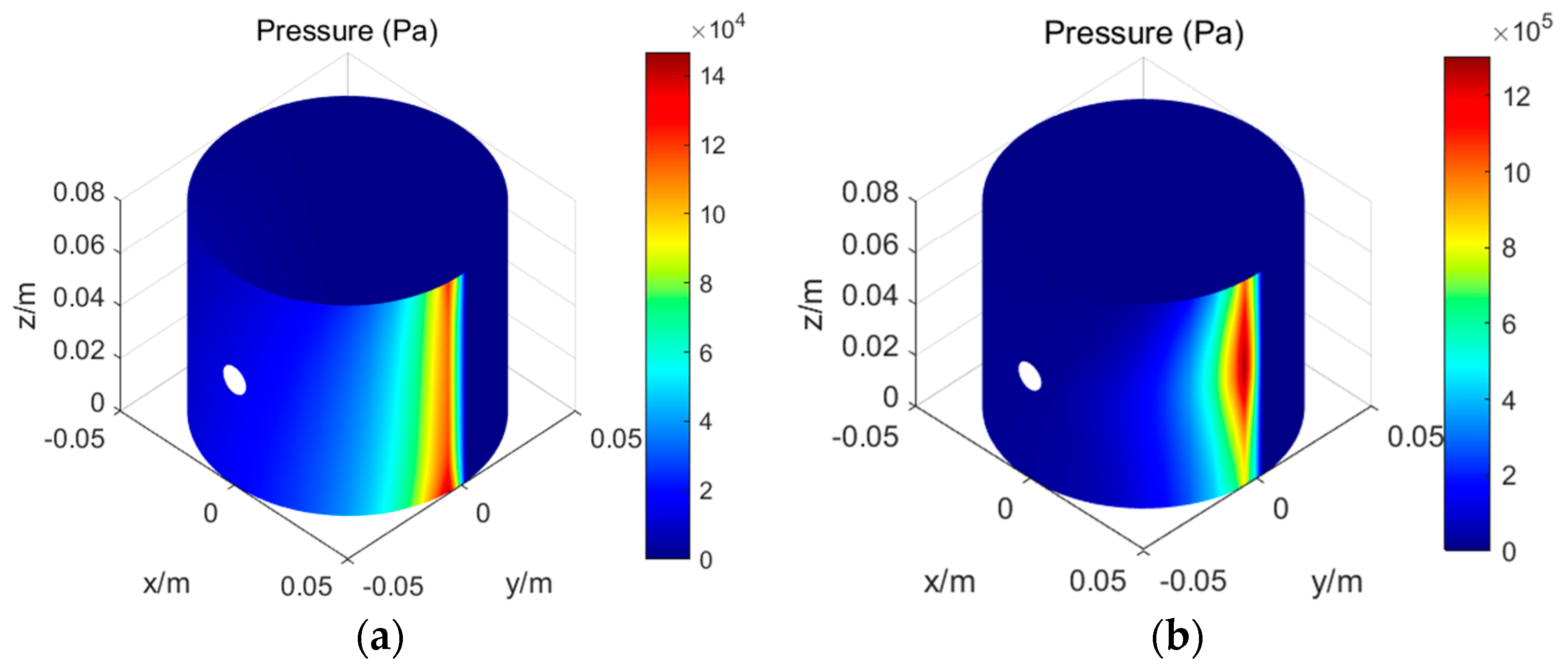
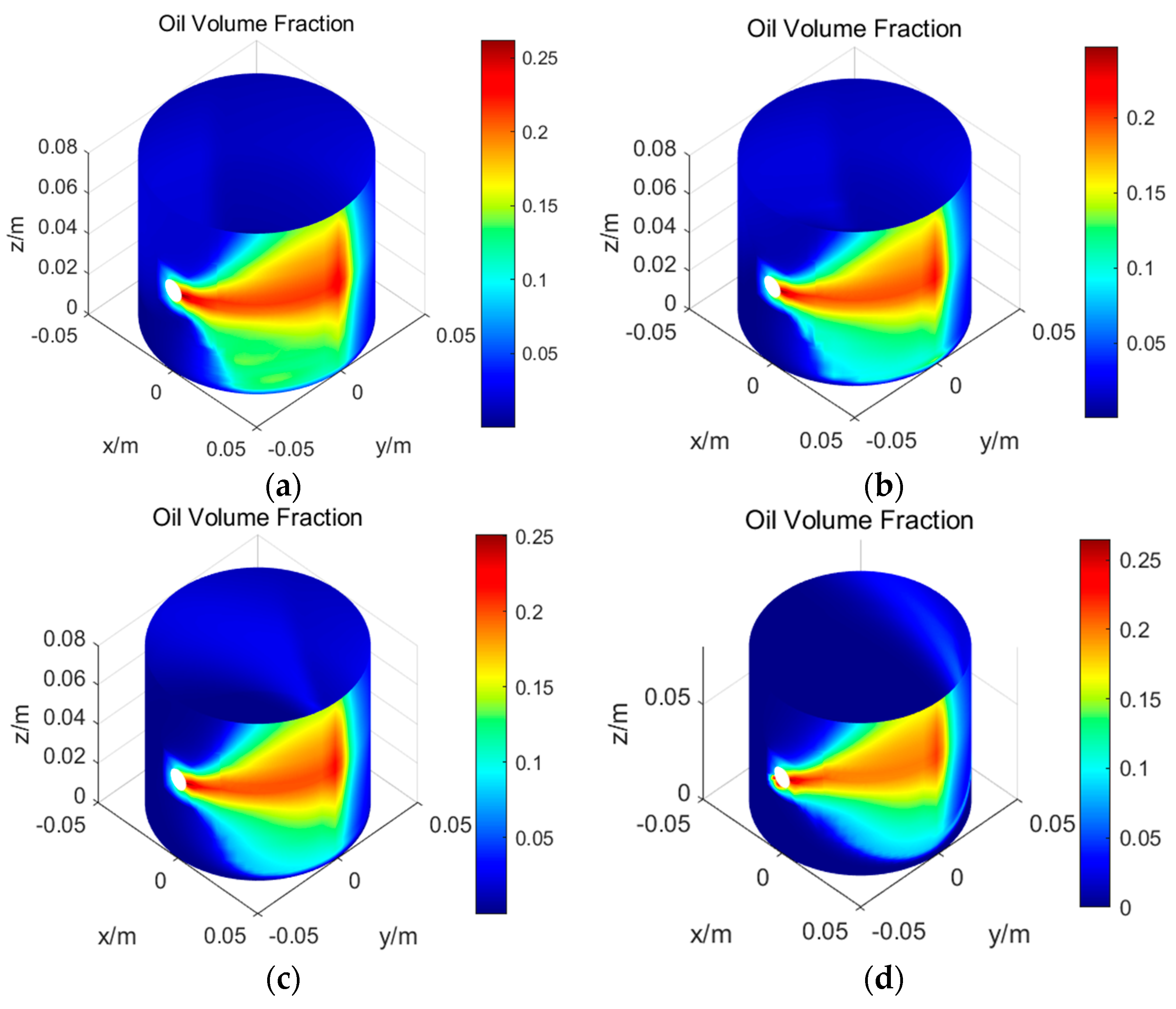
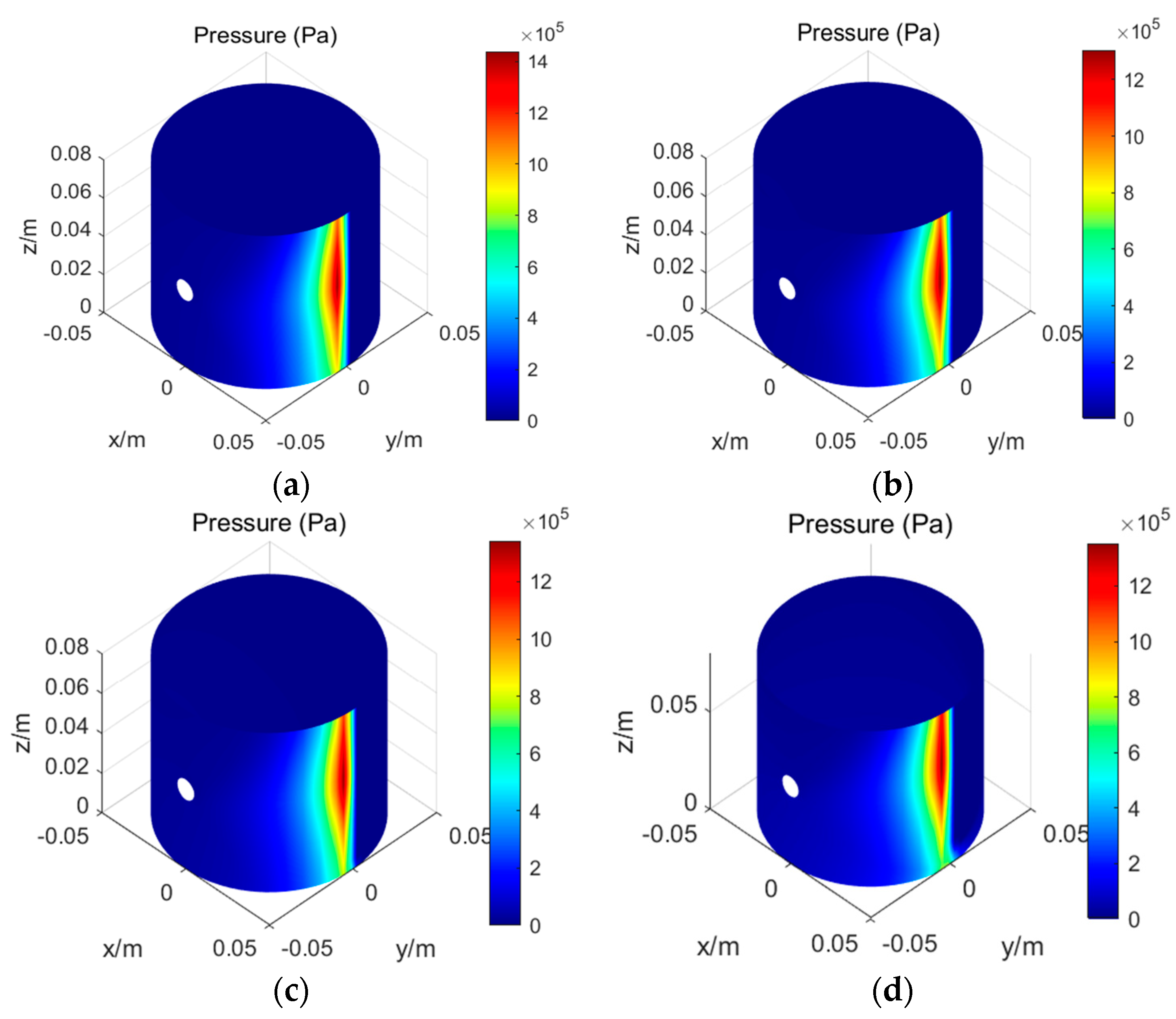
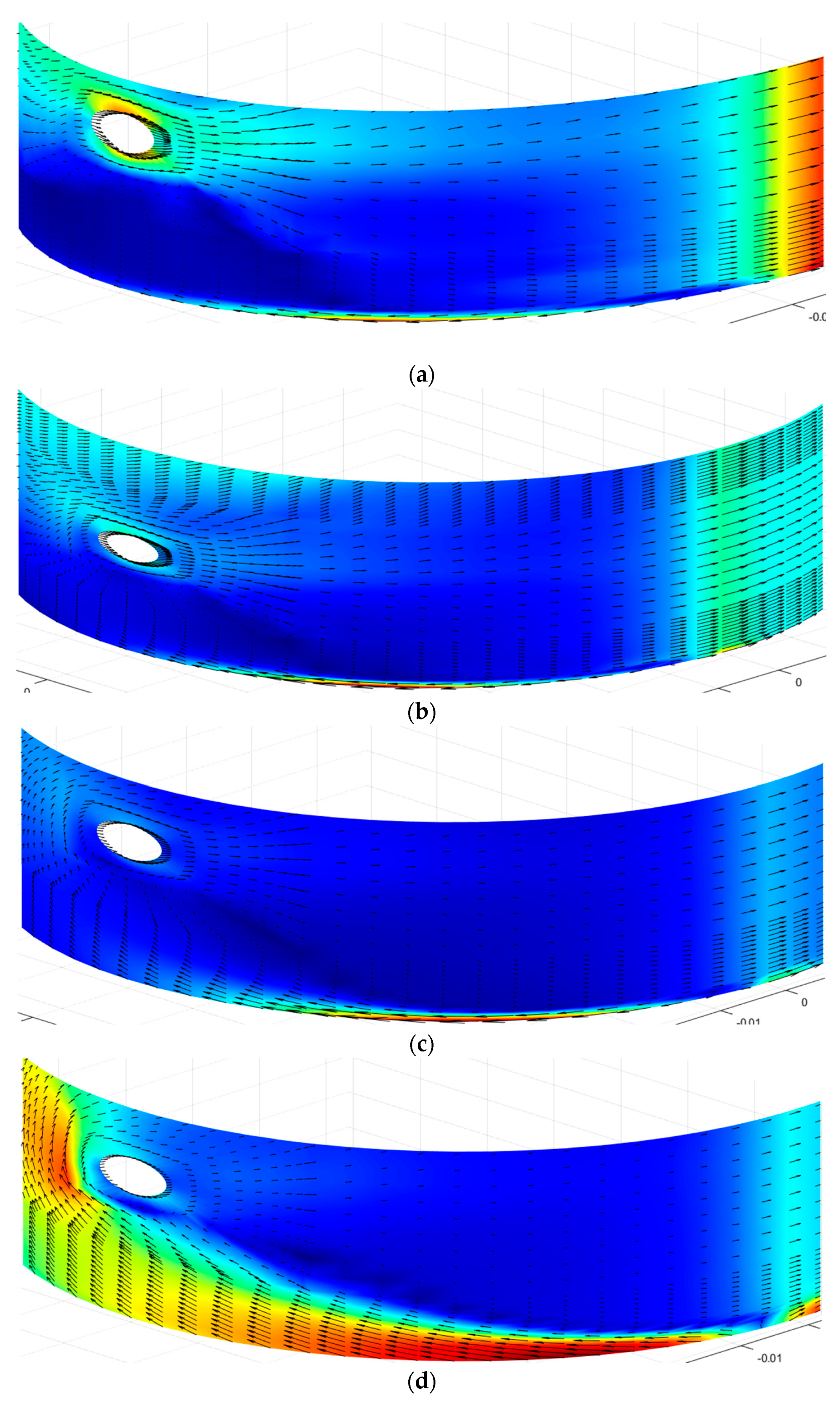
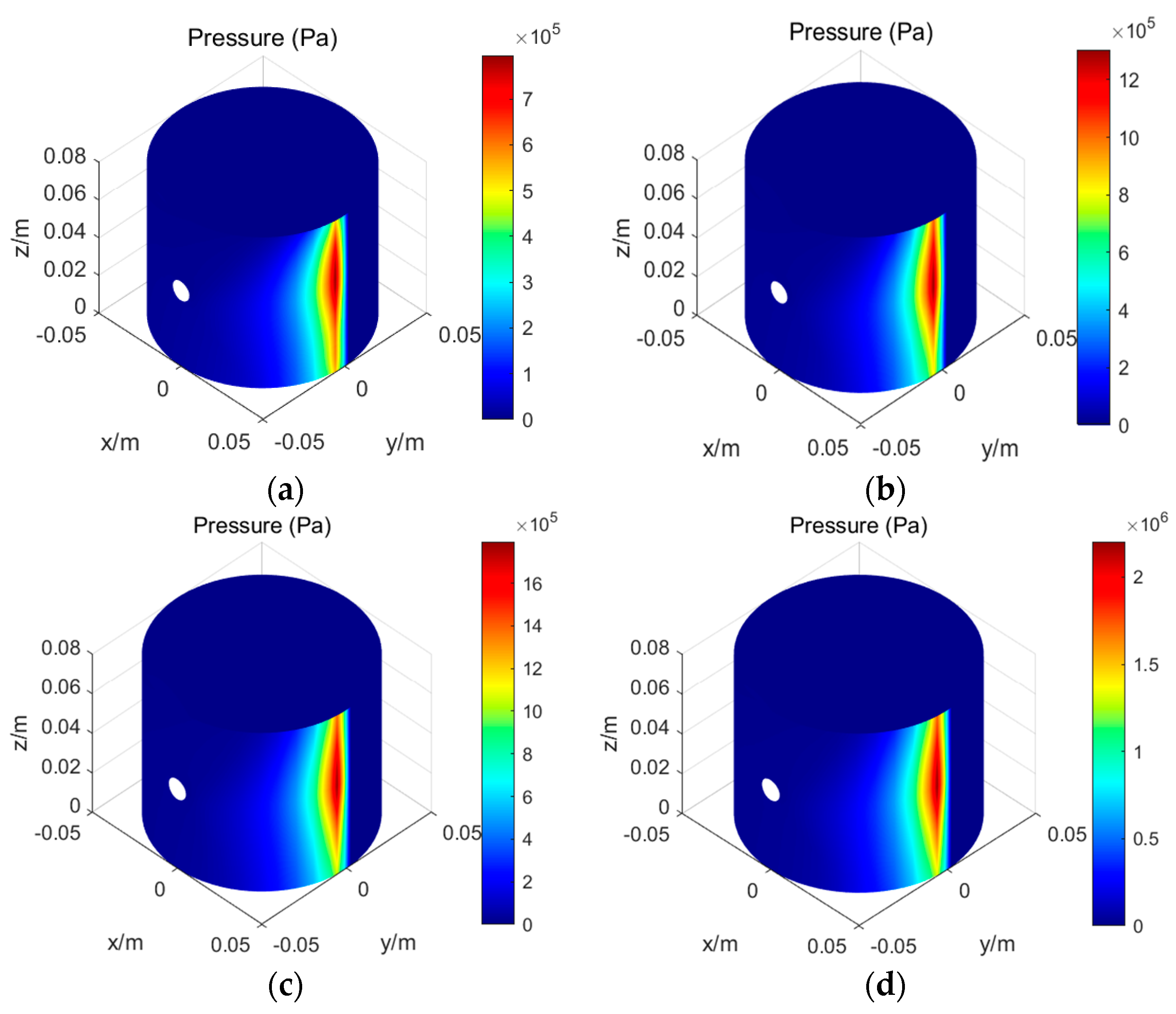
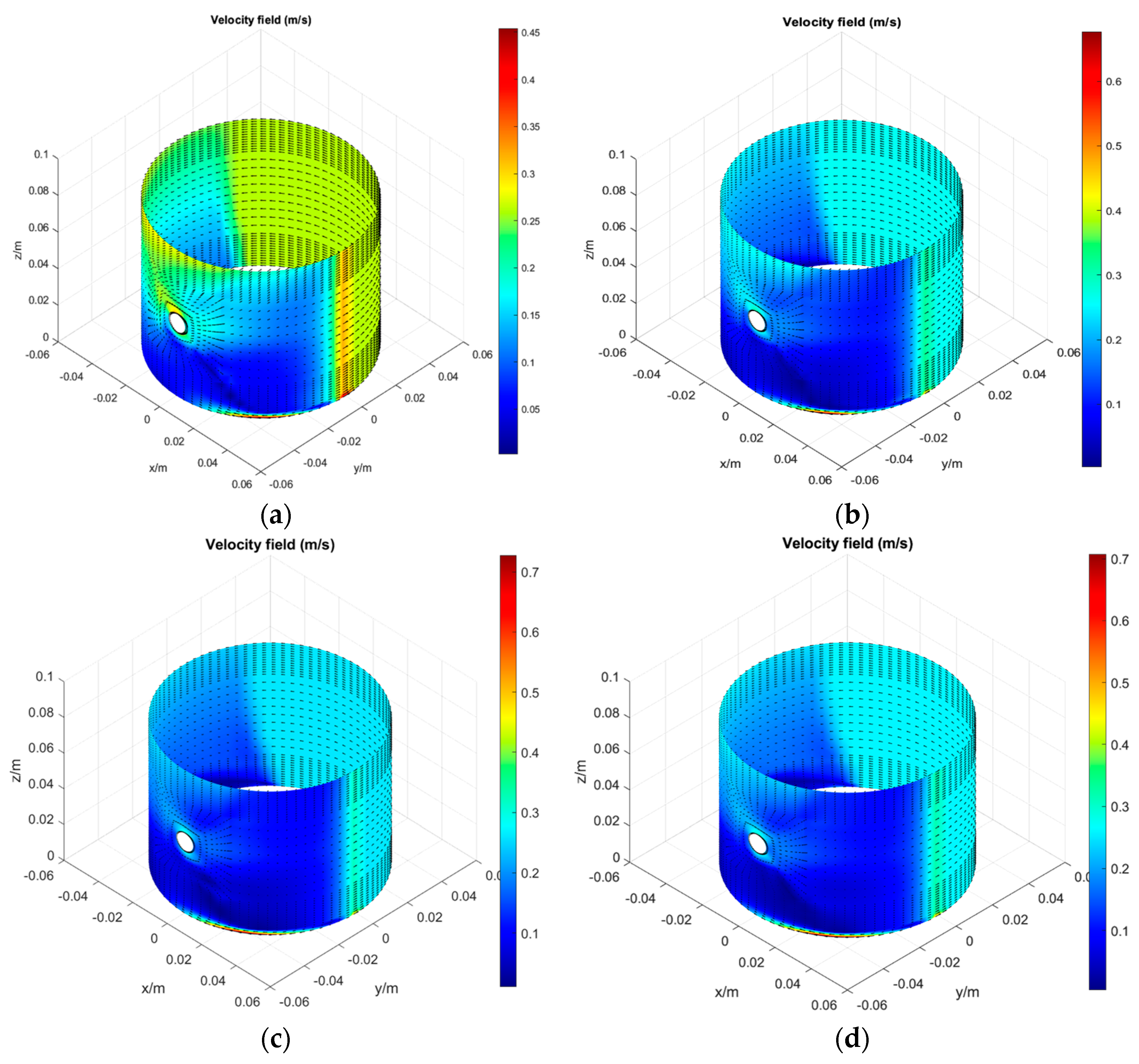
6.1. Different Lubrication Conditions (ω = 100 r/min, vw = 0.03 m/s, Oil Flow Rate = 125 μL/s)
6.2. Different Water Flow Velocity (ω = 100 r/min, Oil Flow Rate = 125 μL/s)
6.3. Different Oil Flow Rate (ω = 100 rpm, vw = 0.03 m/s)
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| C | radial clearance |
| E | eccentric distance |
| F | load-carrying capacity |
| K | number on the edge of the grid |
| L | bearing length |
| P | pressure |
| I | number on the grid |
| U | velocity of the flow |
| vo | velocity of the oil injection |
| vw | velocity of the water flow |
| z | axial direction |
| ω | shaft rotational speed |
| μ | viscosity |
| θ | circumferential direction |
| θ0 | film rupture position in the circumferential direction |
| ρ | density |
| φ | normal flux |
| α | volume fraction of the phase |
| attitude angle |
References
- Gong, J.; Jin, Y.; Liu, Z.; Jiang, H.; Xiao, M. Study on influencing factors of lubrication performance of water-lubricated micro-groove bearing. Tribol. Int. 2019, 129, 390–397. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; de Lacalle, L.N.L. Seals based on magnetic fluids for high precision spindles of machine tools. Int. J. Precis. Eng. Manuf. 2018, 19, 495–503. [Google Scholar] [CrossRef]
- Urreta, H.; Aguirre, G.; Kuzhir, P.; de Lacalle, L.N.L. Actively lubricated hybrid journal bearings based on magnetic fluids for high-precision spindles of machine tools. J. Intell. Mater. Syst. Struct. 2019, 30, 2257–2271. [Google Scholar] [CrossRef]
- Xie, Z.; Shen, N.; Zhu, W.; Tian, W.; Hao, L. Theoretical and experimental investigation on the influences of misalignment on the lubrication performances and lubrication regimes transition of water-lubricated bearing. Mech. Syst. Signal. Process. 2020, 149, 107211. [Google Scholar] [CrossRef]
- Mallya, R.; Shenoy, S.B.; Pai, R. Static characteristics of misaligned multiple axial groove water-lubricated bearing in the turbulent regime. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 385–398. [Google Scholar] [CrossRef]
- Wang, J.; Han, Y.; Geng, Z.; Xiang, G.; Wang, J.; Zhao, R. A profile design method to improve the wear performance of misaligned water-lubricated bearing. Lubr. Sci. 2021, 33, 215–228. [Google Scholar] [CrossRef]
- Xu, B.; Guo, H.; Wu, X.; He, Y.; Wang, X.; Bai, J. Static and dynamic characteristics and stability analysis of high-velocity water-lubricated hydrodynamic journal bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 236, 1994–1996. [Google Scholar]
- Fedorynenko, D.; Kirigaya, R.; Nakao, Y. Dynamic characteristics of spindle with water-lubricated hydrostatic bearings for ultra-precision machine tools. Precis. Eng. 2020, 63, 187–196. [Google Scholar] [CrossRef]
- Sayed, H.; El-Sayed, T.A. Nonlinear dynamics and bifurcation analysis of journal bearings based on second order stiffness and damping coefficients. Int. J. Non-Linear Mech. 2022, 142, 103972. [Google Scholar] [CrossRef]
- Brunetière, N.; Rouillon, M. Fluid flow regime transition in water lubricated spiral grooved face seals. Tribol. Int. 2021, 153, 106605. [Google Scholar] [CrossRef]
- Wu, Z.; Yuan, C.; Guo, Z.; Huang, Q. Effect of the groove parameters on the lubricating performance of the water-lubricated bearing under low speed. Wear 2023, 522, 204708. [Google Scholar] [CrossRef]
- Shinde, A.B.; Chavan, S.P. Parametric investigation of surface texturing on performance characteristics of water-lubricated journal bearing using, FSI approach. SN Appl. Sci. 2019, 2, 36. [Google Scholar] [CrossRef]
- Pai, R.; Hargreaves, D.J. Water-lubricated, Bearings. In Green Tribology; Green Energy and Technology; Nosonovsky, M., Bhushan, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhou, G.; Mi, X.; Wang, J.; Hu, R. Experimental comparison between the Stribeck curves of water-lubricated rubber bearing with straight and spiral grooves. Ind. Lubric. Tribol. 2018, 70, 1326–1330. [Google Scholar] [CrossRef]
- Feng, W.; Han, Y.; Xiang, G.; Wang, J. Hydrodynamic lubrication analysis of water-lubricated bearings with partial microgroove considering wall slip. Surf. Topogr. Metrol. Prop. 2021, 9, 015019. [Google Scholar] [CrossRef]
- Dong, C.; Yuan, C.; Xu, A.; Bai, X.; Tian, Y. Rippled polymer surface generated by stick-slip friction. Langmuir 2019, 35, 2878–2884. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, S.A. The Development of Computer Programme to Calculate the Hydrodynamic Lubrication Performance of a Ship Journal Bearing; UniKL MIMET: Lumut, Malaysia, 2020. [Google Scholar]
- Yang, Z.; Guo, Z.; Yuan, C. Effects of, MoS2 microencapsulation on the tribological properties of a composite material in a water-lubricated condition. Wear 2019, 432–433, 102919. [Google Scholar] [CrossRef]
- Liang, X.; Guo, Z.; Tian, J.; Yuan, C. Development of modified polyacrylonitrile fibers for improving tribological performance characteristics of thermoplastic polyurethane material in water-lubricated sliding bearings. Polym. Adv. Technol. 2020, 31, 3258–3271. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, S.; Ji, A. Investigations of the static and dynamic characteristics of water-lubricated hydrodynamic journal bearing considering turbulent, thermohydrodynamic and misaligned effects. Tribol. Int. 2019, 130, 245–260. [Google Scholar] [CrossRef]
- Narwat, K.; Kumar, V.; Singh, S.J.; Kumar, A.; Sharma, S.C. Performance of rough surface hydrodynamic circular and multi-lobe journal bearings in turbulent regimes. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2023, 237, 860–880. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Guo, F.; Liang, P. Analysis of the Influence of Small Quantity secondary lubricant on Water Lubrication. Tribol. Int. 2021, 159, 106998. [Google Scholar] [CrossRef]
- Yu, T.; Guo, F.; Zhang, X.; Ji, H.; Duan, W.; Liang, P. Water Lubrication Assisted by Small-quantity Silicone Oil. Tribol. Int. 2022, 173, 107619. [Google Scholar] [CrossRef]
- Katopodes, N. Volume of fluid method. In Free-Surface Flow; Katopodes, N., Ed.; Butterworth-Heinemann: Oxford, UK, 2019; pp. 766–802. [Google Scholar]
- Wu, Y.; Sun, T.; He, Z.; Zeng, X.; Ren, T.; de Vries, E.; van der Heide, E. Study on the relationship between the tribological properties and oxidation degree of graphene derivatives in O/W emulsion. Tribol. Int. 2021, 157, 106875. [Google Scholar] [CrossRef]
- Kumar, D.; Rajabi, H. Effect of lubrication on a surface parameter of strip in cold rolling with oil in water emulsion. Int. J. Appl. Eng. Res. 2019, 14, 3261–3267. [Google Scholar]
- Yu, T.; Zhang, X.; Guo, F.; Jin, W.; Liang, P. Enhancing water lubrication by secondary assistant lubricant in small quantity. Tribology 2022, 42, 358–365. (In Chinese) [Google Scholar]
- Xie, Z.; Jiao, J.; Wrona, S. The fluid-structure interaction lubrication performances of a novel bearing: Experimental and numerical study. Tribol. Int. 2023, 179, 108151. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Zhao, B.; Zhang, J.; Xu, F. Theoretical and experimental research on the effect of bi-directional misalignment on the static and dynamic characteristics of a novel bearing. Mech. Syst. Signal. Process. 2024, 208, 111041. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Yang, K. Experimental and numerical study on the mixed lubricant performances of a new bearing. Tribol. Int. 2023, 182, 108334. [Google Scholar] [CrossRef]





| Parameters | Values/Comments |
|---|---|
| Shaft material | 316 stainless steels |
| Bushing material | 3606 NBR |
| Bushing length | 80 mm |
| Bearing inner diameter | 100 mm |
| Radial clearance | 0.07 mm |
| Oil inlet diameter | 10 mm |
| Parameters | Values/Comments |
|---|---|
| Shaft rotational speed | 100 r/min |
| Water density | 1000 kg/m3 |
| Water dynamic viscosity | 1 mPa·s |
| Emulsifying oil density | 698 kg/m3 |
| Emulsifying oil viscosity(@ 21 °C) | 63.79 mPa·s |
| Eccentricity ratio | 0.9 |
| Radial clearance | 0.07 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Yu, T.; Ji, H.; Guo, F.; Duan, W.; Liang, P.; Ma, L. Analysis of Water-Lubricated Journal Bearings Assisted by a Small Quantity of Secondary Lubricating Medium with Navier–Stokes Equation and VOF Model. Lubricants 2024, 12, 16. https://doi.org/10.3390/lubricants12010016
Zhang X, Yu T, Ji H, Guo F, Duan W, Liang P, Ma L. Analysis of Water-Lubricated Journal Bearings Assisted by a Small Quantity of Secondary Lubricating Medium with Navier–Stokes Equation and VOF Model. Lubricants. 2024; 12(1):16. https://doi.org/10.3390/lubricants12010016
Chicago/Turabian StyleZhang, Xiaohan, Tao Yu, Hao Ji, Feng Guo, Wenbin Duan, Peng Liang, and Ling Ma. 2024. "Analysis of Water-Lubricated Journal Bearings Assisted by a Small Quantity of Secondary Lubricating Medium with Navier–Stokes Equation and VOF Model" Lubricants 12, no. 1: 16. https://doi.org/10.3390/lubricants12010016
APA StyleZhang, X., Yu, T., Ji, H., Guo, F., Duan, W., Liang, P., & Ma, L. (2024). Analysis of Water-Lubricated Journal Bearings Assisted by a Small Quantity of Secondary Lubricating Medium with Navier–Stokes Equation and VOF Model. Lubricants, 12(1), 16. https://doi.org/10.3390/lubricants12010016






