Enhancing Quality Control of Chip Seal Construction through Machine Learning-Based Analysis of Surface Macrotexture Metrics
Abstract
:1. Introduction
2. Literature Review
2.1. Surface Friction Metrics
2.2. Chip Seal Quality Acceptance
3. Data Collection and Preparation
3.1. Chip Seal Projects
3.2. Data Collection
3.3. Data Preparation and Processing
3.3.1. MSD Dataset
3.3.2. MPD Dataset
3.3.3. One-Mile Wheel Track Outlier Percentage Dataset
3.3.4. Unqualified One-Mile Wheel Track Percentage Dataset
4. Methodology
4.1. DBSCAN-Isolation Forest Model
4.1.1. Density-Based Spatial Clustering of Applications with Noise
4.1.2. Isolation Forest Algorithm
- when a node contains only a single data instance, rendering further splits redundant;
- when the tree reaches a predetermined maximum height, a measure employed to prevent overfitting.
4.1.3. DBSCAN-Isolation Forest Model
4.2. Statistical Methods for Quality Control
4.2.1. Analysis of Variance
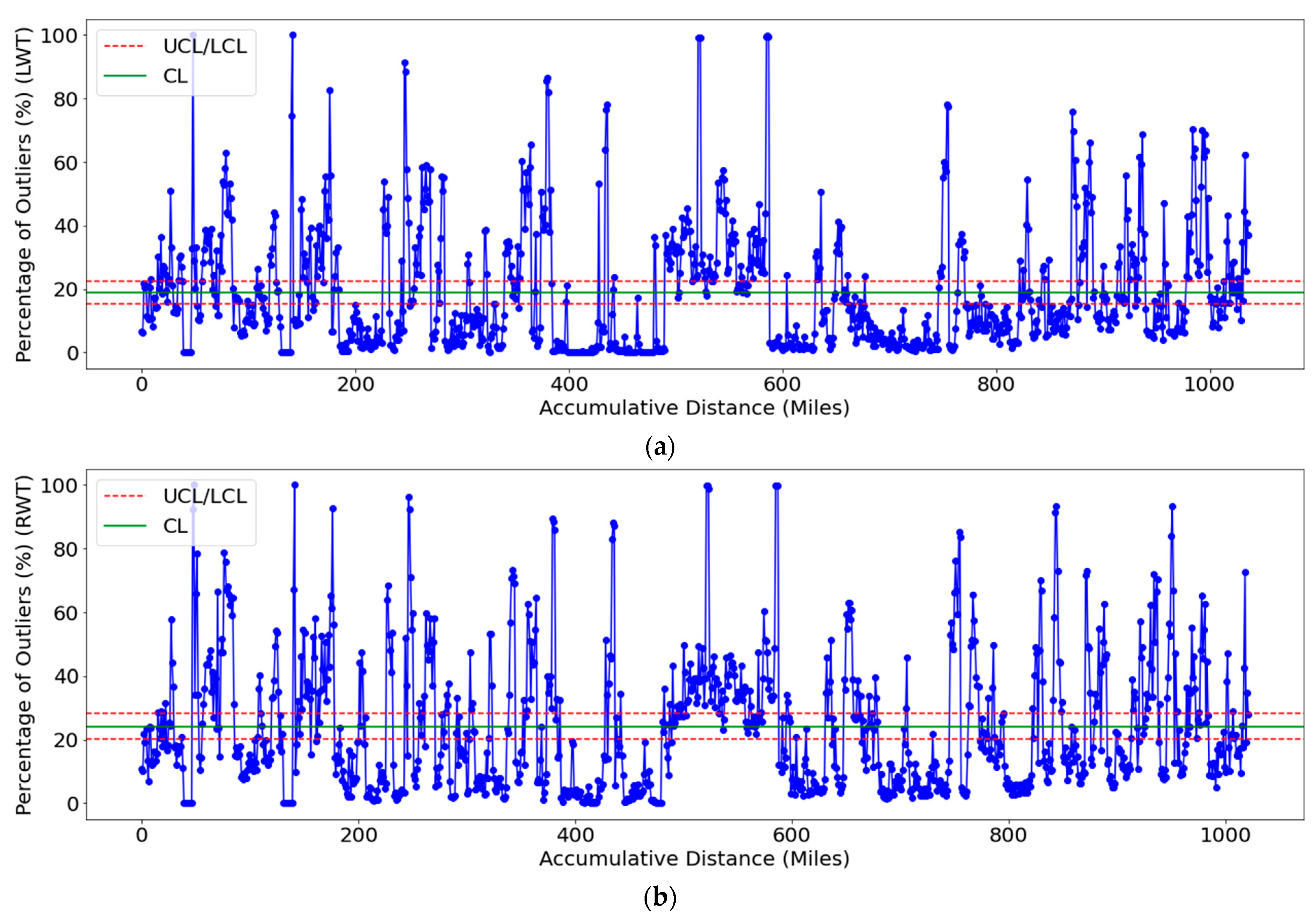
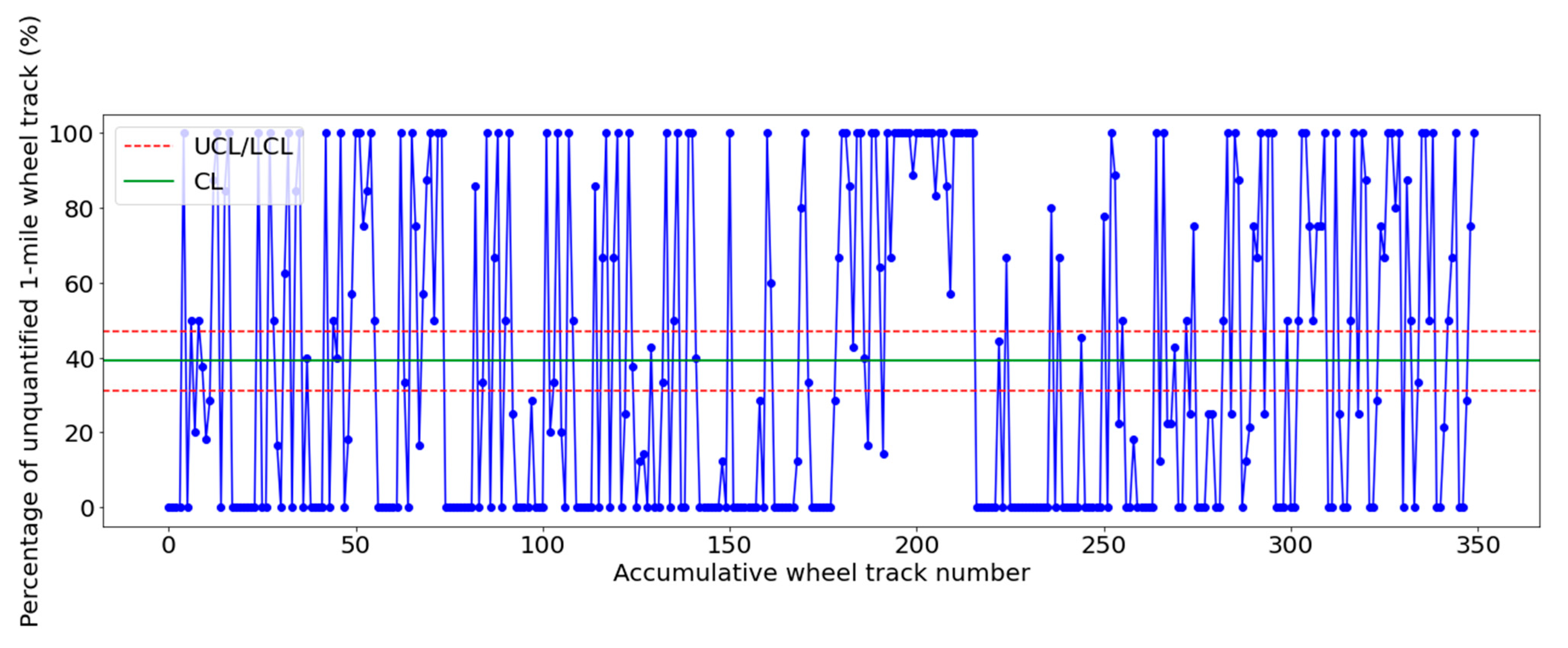
4.2.2. Proportion Control Chart
5. Results and Analysis
5.1. Anomaly Detection
5.2. Quality Control
5.3. Validation
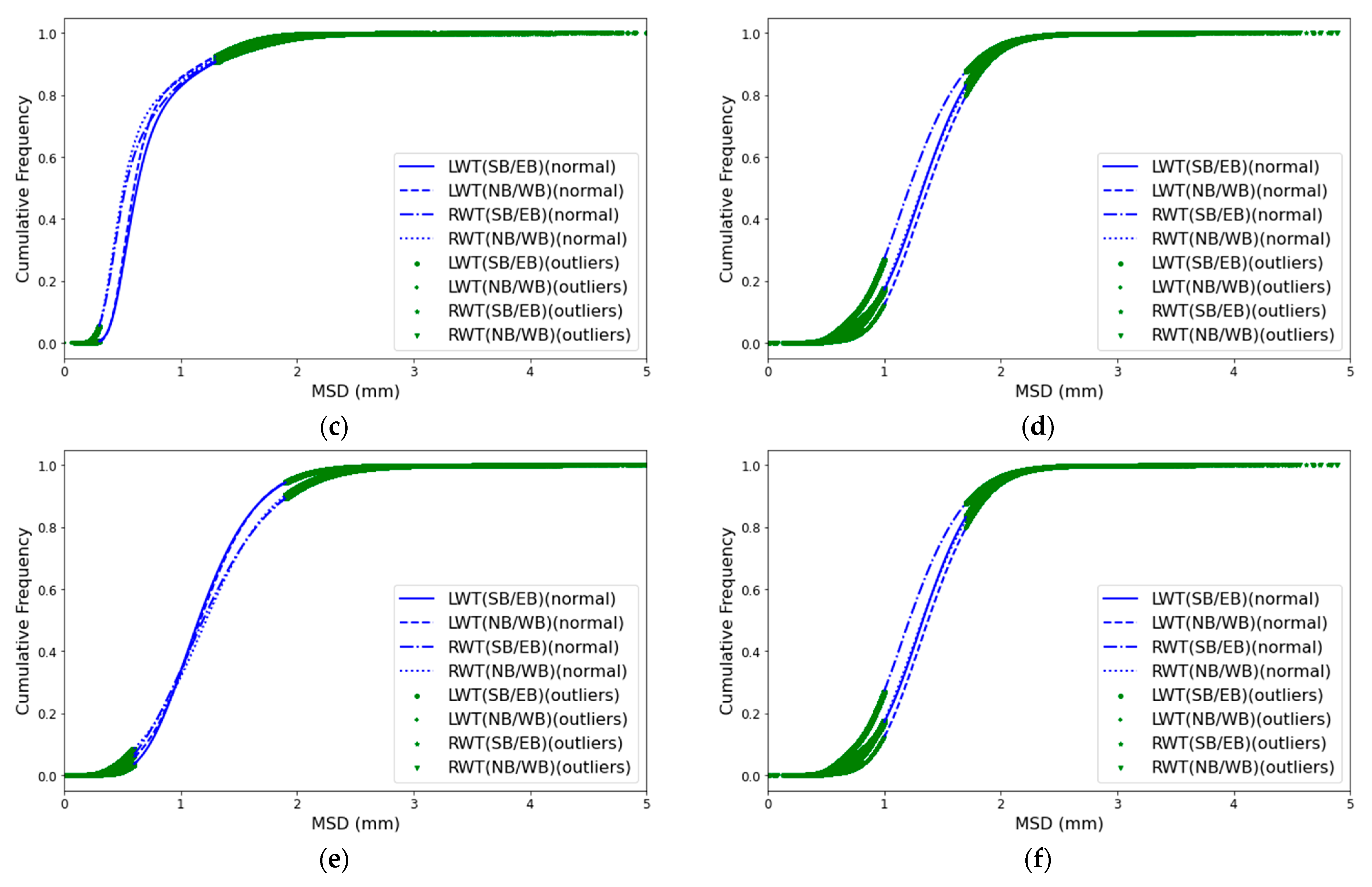
- In Section 1, a predominant portion of MSD outliers exceeded Fort Wayne’s 2.1 mm threshold. Notably, 97.5% of outliers in the northbound lane surpassed this limit across all wheel tracks. In the southbound lane, approximately 97.5% of outliers in the left wheel track and 95% in the right wheel track exceeded the 2.1 mm threshold. The above suggested that the surface texture may be very rough.
- In Section 2, over 95% of MSD outliers fell below the 0.6 mm threshold, encompassing all directions and tracks, which indicated a possible slippery surface.
- In Section 3, the 97.5th percentile of outliers for each wheel track fell below Seymour’s 0.6 mm mark, implying a potentially slippery surface.
- In Section 4, the 2.5th percentile of MSD outliers for each wheel track exceeded 2.3 mm, indicating a surface with a rough texture.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shuler, S.; Lord, A.; Epps-Martin, A.; Hoyt, D. Manual for Emulsion-Based Chip Seals for Pavement Preservation. In NCHRP Report 680; Transportation Research Board: Washington, DC, USA, 2011. [Google Scholar] [CrossRef]
- Wasiuddin, N.; Marshall, A.; Saltibus, N.; Saber, A.; Abadie, C.; Mohammad, L. Use of Sweep Test for Emulsion and Hot Asphalt Chip Seals: Laboratory and Field Evaluation. J. Test. Eval. 2013, 41, 289–298. Available online: https://www.astm.org/jte20120051.html (accessed on 5 September 2023). [CrossRef]
- INDOT. Chip Sealing; Indiana Department of Transportation: Indianapolis, IN, USA. Available online: https://www.in.gov/indot/maintenance-operations/ (accessed on 9 August 2023).
- Im, J.K.; Kim, Y.R. Performance Evaluation of Fog Seals on Chip Seals and Verification of Fog Seal Field Tests. Can. J. Civ. Eng. 2015, 42, 872–880. [Google Scholar] [CrossRef]
- Gransberg, D.; Musharraf, Z. Analysis of Emulsion and Hot Asphalt Cement Chip Seal Performance. J. Transp. Eng. 2005, 131, 229–238. [Google Scholar] [CrossRef]
- Buss, A.; Guirguis, M.; Gransberg, D. Chip Seal Aggregate Evaluation and Successful Roads Preservation. Constr. Build. Mater. 2018, 180, 394–404. [Google Scholar] [CrossRef]
- Lawson, W.D.; Senadheera, S. Chip Seal Maintenance: Solutions for Bleeding and Flushed Pavement Surfaces. Transp. Res. Rec. J. Transp. Res. Board 2009, 2108, 61–68. [Google Scholar] [CrossRef]
- Khattack, M.J.; Bhuyan, M.R. Performance Evaluation of Chip Seal Treatment on Flexible Pavements. Int. J. Pavement Res. Technol. 2023. [Google Scholar] [CrossRef]
- Gransberg, D.; James, D. Chip Seal Best Practices. In NCHRP Synthesis 342; Transportation Research Board: Washington, DC, USA, 2005. [Google Scholar] [CrossRef]
- Chipsealing in New Zealand; Transit New Zealand: Wellington, New Zealand, 2005.
- Pavement Preservation Checklist Series 2: Chip Seal; Publication No. FHWA-HIF-19-02; Federal Highway Administration: Washington, DC, USA, 2019.
- Li, S.; Shields, T.; Noureldin, S.; Jiang, Y. Field Evaluation of Surface Friction Performance of Chip Seals in Indiana. Transp. Res. Rec. 2012, 2295, 11–18. [Google Scholar] [CrossRef]
- Notes for the Specification of Bituminous Reseal, TNZ P17; Transit New Zealand: Wellington, New Zealand, 2002.
- Gransberg, D. Using a New Zealand Performance Specification to Evaluate U.S. Chip Seal Performance. J. Transp. Eng. 2007, 133, 688–695. [Google Scholar] [CrossRef]
- Montoya, M.A.; Haddock, J.E.; Weiss, W.J. Quality Control Tool for Asphalt Emulsion-Based Chip Seal Curing Times. In Bearing Capacity of Roads, Railways and Airfields; CRC Press: Boca Raton, FL, USA, 2017; pp. 603–608. [Google Scholar]
- Guirguis, M.; Buss, A. Chip Sealing Macro Texture Performance Evaluation Using Split-plot Repeated Measures. Road Mater. Pavement Des. 2021, 22, 185–199. [Google Scholar] [CrossRef]
- Vijaykumar, A.; Martin, A.; Arambula, E. Revision and Further Validation of Surface Performance-Graded Specification for Chip Seal Binders. Transp. Res. Rec. J. Transp. Res. Board 2013, 2370, 44–52. [Google Scholar] [CrossRef]
- Gransberg, D.D. Correlating Chip Seal Performance and Construction Methods. Transp. Res. Rec. J. Transp. Res. Board 2006, 1958, 54–58. [Google Scholar] [CrossRef]
- Rahman, M.D.; Sarkar, M.T.A.; Elseifi, M.A.; Mayeux, G.; Cooper, S.B., III; Free, K. Short-Term Field Performance and Cost-Effectiveness of Crumb-Rubber Modified Asphalt Emulsion in Chip Seal Applications. Transp. Res. Rec. 2021, 2675, 1049–1062. [Google Scholar] [CrossRef]
- Mamlouk, M.S.; Dosa, M. Verification of Effectiveness of Chip Seal as a Pavement Preventive Maintenance Treatment Using LTPP Data. Int. J. Pavement Eng. 2014, 15, 879–888. [Google Scholar] [CrossRef]
- Zhao, G.; Li, S.; Jiang, Y.; Lee, J. Quality Assurance Procedures for Chip Seal Operations Using Macrotexture Metrics (Joint Transportation Research Program Publication No. FHWA/IN/JTRP2018/12); Purdue University: West Lafayette, IN, USA, 2018. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine Learning: Trends, Perspectives, and Prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. Available online: https://www.nature.com/articles/nature14539 (accessed on 5 September 2023). [CrossRef] [PubMed]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Doshi-Velez, F.; Kim, B. Towards a Rigorous Science of Interpretable Machine Learning. arXiv 2017, arXiv:1702.08608. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Seitllari, A.; Kutay, M.E. Soft Computing Tools to Predict Progression of Percent Embedment of Aggregates in Chip Seals. Transp. Res. Rec. 2018, 2672, 32–39. [Google Scholar] [CrossRef]
- Amarasiri, S.; Muhunthan, B. Evaluating Cracking Deterioration of Prevent Maintenance-Treated Pavements Using Machine Learning. J. Transp. Eng. Part B Pavements 2022, 148, 04022014. [Google Scholar] [CrossRef]
- Gurganus, C.F.; Chang, S.; Ravipati, D.; Goehl, D.; Gharaibeh, N.G. Improving Chip Seal Construction Using Laser Intensity Data. J. Transp. Eng. Part B Pavements 2020, 146, 04020044. [Google Scholar] [CrossRef]
- Henry, J.J. Evaluation of Pavement Friction Characteristics. In NCHRP Synthesis 291; Transportation Research Board: Washington, DC, USA, 2000. [Google Scholar]
- Tobias, P.; de León Izeppi, E.; Flintsch, G.; Katicha, S.; McCarthy, R. Pavement Friction for Road Safety: Primer on Friction Measurement and Management Methods; FHWA-SA-23-007; Federal Highway Administration, Office of Safety: Washington, DC, USA, 2023. [Google Scholar]
- ASTM E274/E274M-15; Standard Test Method for Skid Resistance of Paved Surfaces Using a Full-Scale Tire. ASTM: West Conshohocken, PA, USA, 2020.
- ASTM E303; Standard Test Method for Measuring Surface Frictional Properties Using the British Pendulum Tester. ASTM: West Conshohocken, PA, USA, 2022.
- ASTM E1911; Standard Test Method for Measuring Surface Frictional Properties Using the Dynamic Friction Tester. ASTM: West Conshohocken, PA, USA, 2019.
- Kummer, H.W.; Meyer, W.E. Tentative Skid-resistance Requirements for Main Rural Highways. In NCHRP Report 37; Highway Research Board: Washington, DC, USA, 1967. [Google Scholar]
- Li, S.; Zhu, K.Q.; Noureldin, S.; Kim, D. Pavement surface friction test using standard smooth tire: The Indiana experience. In Transportation Research Board 83rd Annual Meeting Compendium of Papers (CD-ROM); Transportation Research Board: Washington, DC, USA, 2004. [Google Scholar]
- Li, S.; Noureldin, S.; Zhu, K.Q. Characterization of Microtexture on Typical Pavement Surfaces: A Pilot Study. In Proceedings of the Presented at 90th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 23–27 January 2011. [Google Scholar]
- ASTM E965-15; Standard Test Method for Measuring Pavement Macrotexture Depth Using a Volumetric Technique. ASTM: West Conshohocken, PA, USA, 2019.
- ASTM E2157-15; Standard Test Method for Measuring Pavement Macrotexture Properties Using the Circular Track Meter. ASTM: West Conshohocken, PA, USA, 2019.
- Adams, J.; Castorena, C.; Kim, Y.R. Construction quality acceptance performance-related specifications for chip seals. J. Traffic Transp. Eng. 2019, 6, 337–348. [Google Scholar] [CrossRef]
- INDOT. Standard Specifications; Indiana Department of Transportation: Indianapolis, IN, USA, 2020.
- Li, S.; Zhu, K.; Noureldin, S. Evaluation of friction performance of coarse aggregates and hot-mix asphalt pavements. J. Test. Eval. 2007, 35, 571–577. [Google Scholar] [CrossRef]
- Li, S.; Noureldin, S.; Zhu, Z. Upgrading the INDOT Pavement Friction Testing Program; Publication FHWA/IN/JTRP-2003/23; Joint Transportation Research Program, Indiana Department of Transportation and Purdue University: West Lafayette, IN, USA, 2004. [Google Scholar] [CrossRef]
- ASTM E1845-01; Standard Practice for Calculating Pavement Macrotexture Mean Profile Depth. ASTM: West Conshohocken, PA, USA, 2017.
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning on Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bao, J.; Jiang, J.; Li, S. Determination of Safety-Oriented Pavement-Friction Performance Ratings at Network Level Using a Hybrid Clustering Algorithm. Lubricants 2023, 11, 275. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw Hill Education Private Limited: New York, NY, USA, 2013. [Google Scholar]
- Montgomery, D.C. Introduction to Statistical Quality Control, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]




| District | No. of Projects | Total Length (km) | Asphalt Emulsion | Aggregate | ||
|---|---|---|---|---|---|---|
| Type | Class | Grade | ||||
| Crawfordsville | 23 | 186 | AE-90S | Crushed gravel | A or B | SC16 |
| Fort Wayne | 16 | 186 | RS-2 | Crushed stone | A or B | SC11 |
| Greenfield | 10 | 110 | AE-90S | Crushed stone | A or B | SC11 |
| LaPorte | 8 | 89 | AE-90S | Crushed stone | A or B | SC16 |
| Seymour | 14 | 206 | CRS-2P | Crushed stone | A or B | SC11 |
| Vincennes | 21 | 212 | AE-90S | Crushed stone | A or B | SC11 |
| Grade | Percent Passing | ||||||
|---|---|---|---|---|---|---|---|
| 12.5 mm | 9.5 mm | 4.75 mm | 2.36 mm | 1.18 mm | 0.6 mm | 75 μm | |
| SC 11 | 100 | 75–95 | 10–30 | 0–10 | - | - | 0–1.5 |
| SC 12 | 100 | 95–100 | 50–80 | 0–35 | - | 0–4 | 0–1.5 |
| SC 16 | 100 | 94–100 | 15–45 | - | 0–4 | - | 0–1.5 |
| District | MSD Quantity | MPD20 Quantity |
|---|---|---|
| Crawfordsville | 6,274,362 | 37,259 |
| Fort Wayne | 6,750,670 | 33,752 |
| Greenfield | 3,838,720 | 19,186 |
| LaPorte | 3,407,900 | 17,040 |
| Seymour | 7,950,646 | 39,754 |
| Vincennes | 7,359,219 | 36,803 |
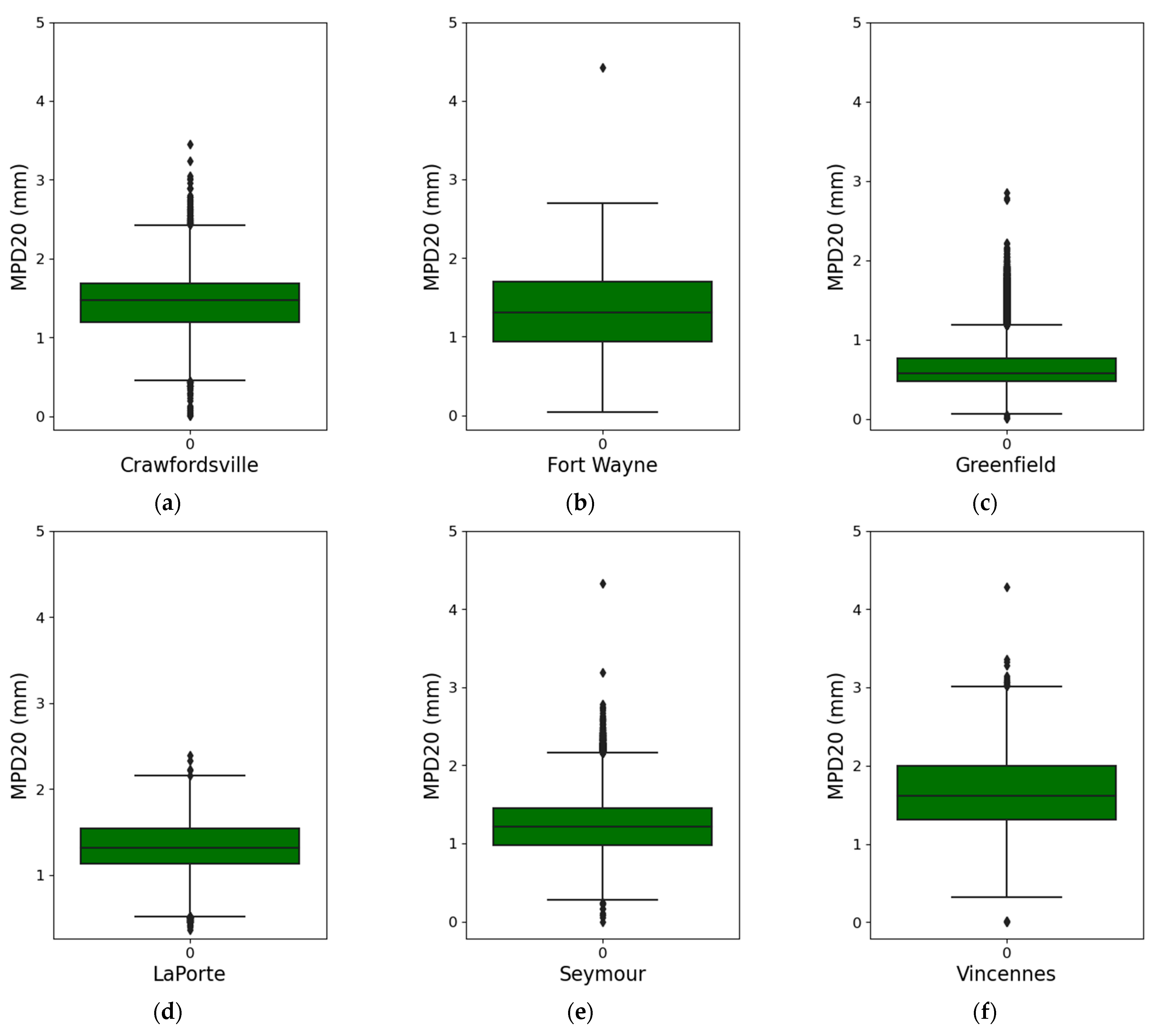
| District | Min. MPD20 Value (mm) | Max. MPD20 Value (mm) |
|---|---|---|
| Crawfordsville | 0.9 | 1.9 |
| Fort Wayne | 0.6 | 2.1 |
| Greenfield | 0.3 | 1.3 |
| LaPorte | 1.0 | 1.7 |
| Seymour | 0.6 | 1.9 |
| Vincennes | 1.0 | 2.3 |
| District | Validation Section | % of MSD < the Min. MPD20 Threshold | % of MSD > the Max. MPD20 Threshold | Overall MPD (mm) | Friction Number * |
|---|---|---|---|---|---|
| Fort Wayne | Section 1 | 0.4% | 41.3% | 2.14 | 59.0/61.0 |
| Fort Wayne | Section 2 | 25.4% | 0.3% | 0.57 | 12.3/19.1 |
| Seymour | Section 3 | 41.8% | 0.1% | 0.66 | 12.8/11.0 |
| Vincennes | Section 4 | 1.4% | 46.3% | 2.25 | 60.3/58.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, J.; Adcock, J.; Li, S.; Jiang, Y. Enhancing Quality Control of Chip Seal Construction through Machine Learning-Based Analysis of Surface Macrotexture Metrics. Lubricants 2023, 11, 409. https://doi.org/10.3390/lubricants11090409
Bao J, Adcock J, Li S, Jiang Y. Enhancing Quality Control of Chip Seal Construction through Machine Learning-Based Analysis of Surface Macrotexture Metrics. Lubricants. 2023; 11(9):409. https://doi.org/10.3390/lubricants11090409
Chicago/Turabian StyleBao, Jieyi, Joseph Adcock, Shuo Li, and Yi Jiang. 2023. "Enhancing Quality Control of Chip Seal Construction through Machine Learning-Based Analysis of Surface Macrotexture Metrics" Lubricants 11, no. 9: 409. https://doi.org/10.3390/lubricants11090409
APA StyleBao, J., Adcock, J., Li, S., & Jiang, Y. (2023). Enhancing Quality Control of Chip Seal Construction through Machine Learning-Based Analysis of Surface Macrotexture Metrics. Lubricants, 11(9), 409. https://doi.org/10.3390/lubricants11090409






