Multiscale Structural Mechanics of Rotary Shaft Seals: Numerical Studies and Visual Experiments
Abstract
1. Introduction
2. Materials and Methods
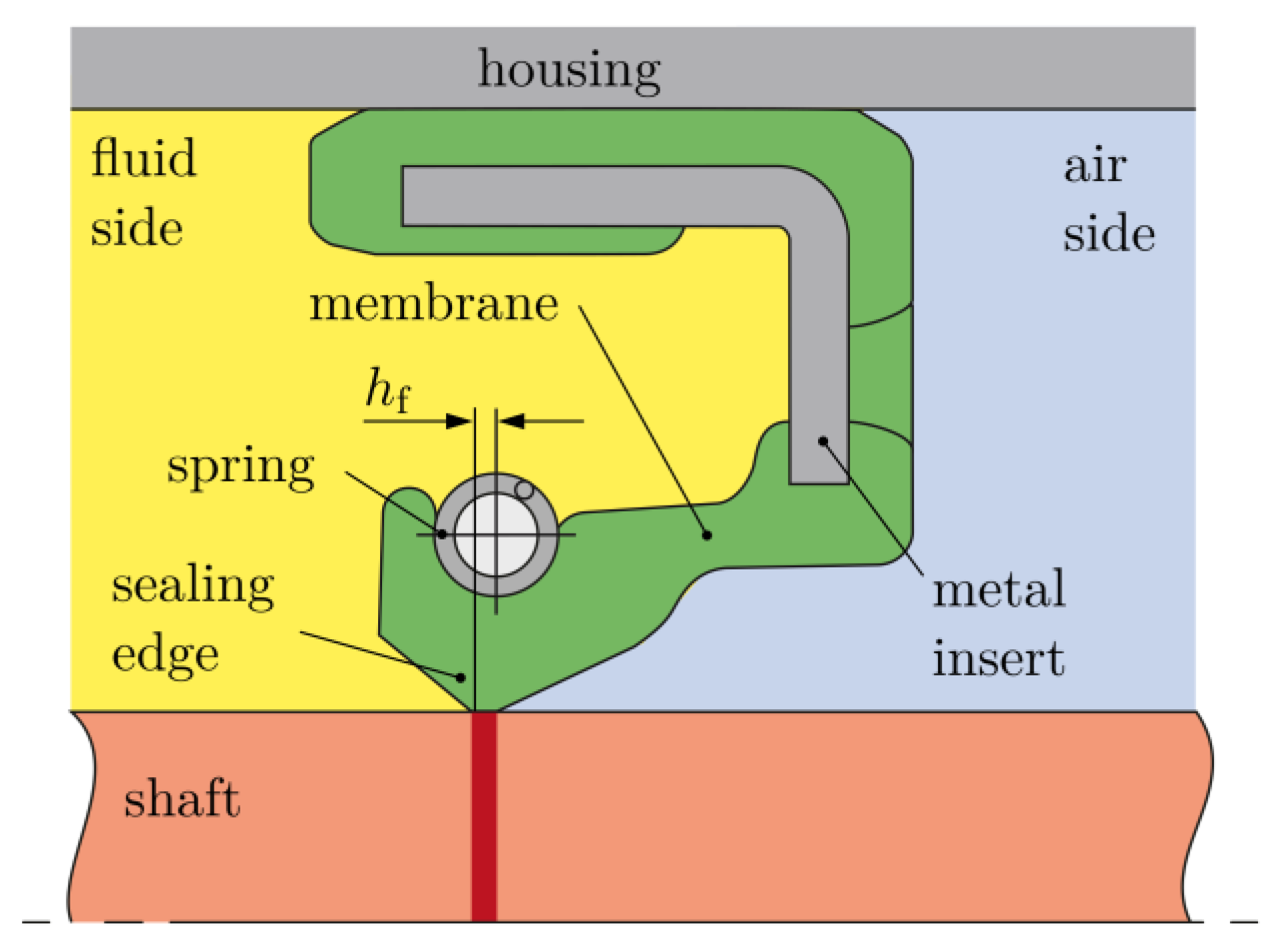
2.1. Materials
2.2. Radial Load Measurements
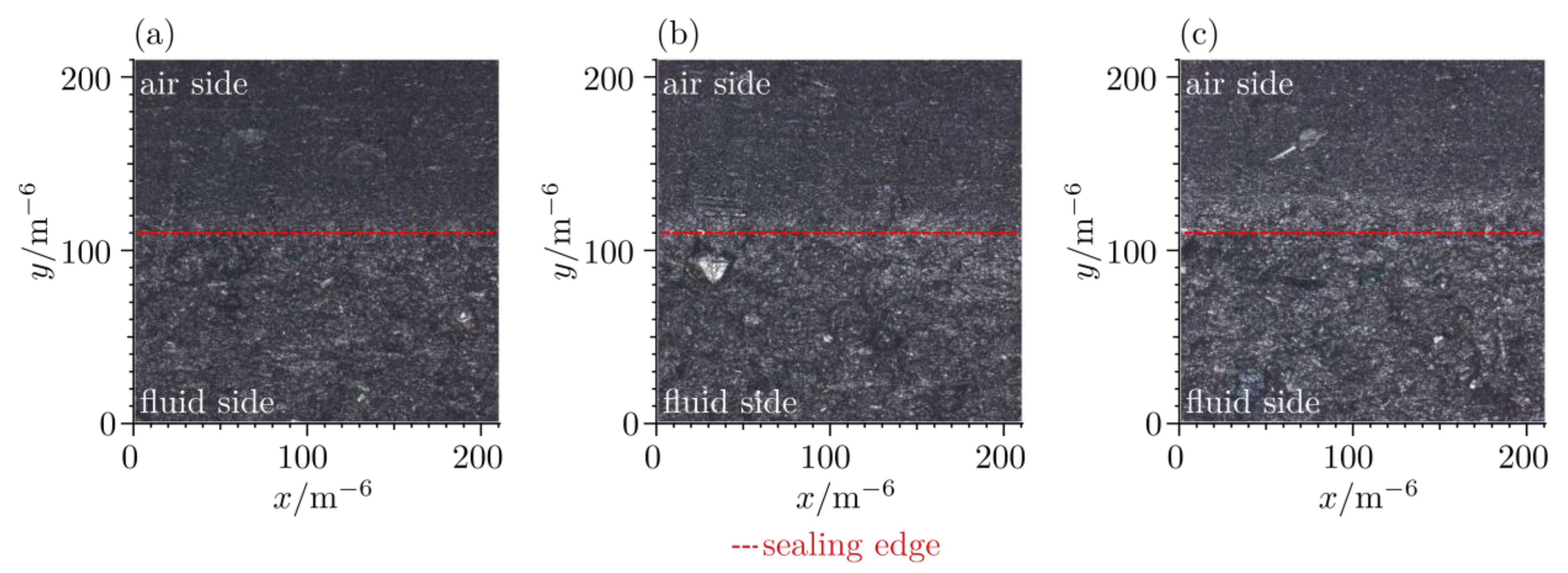
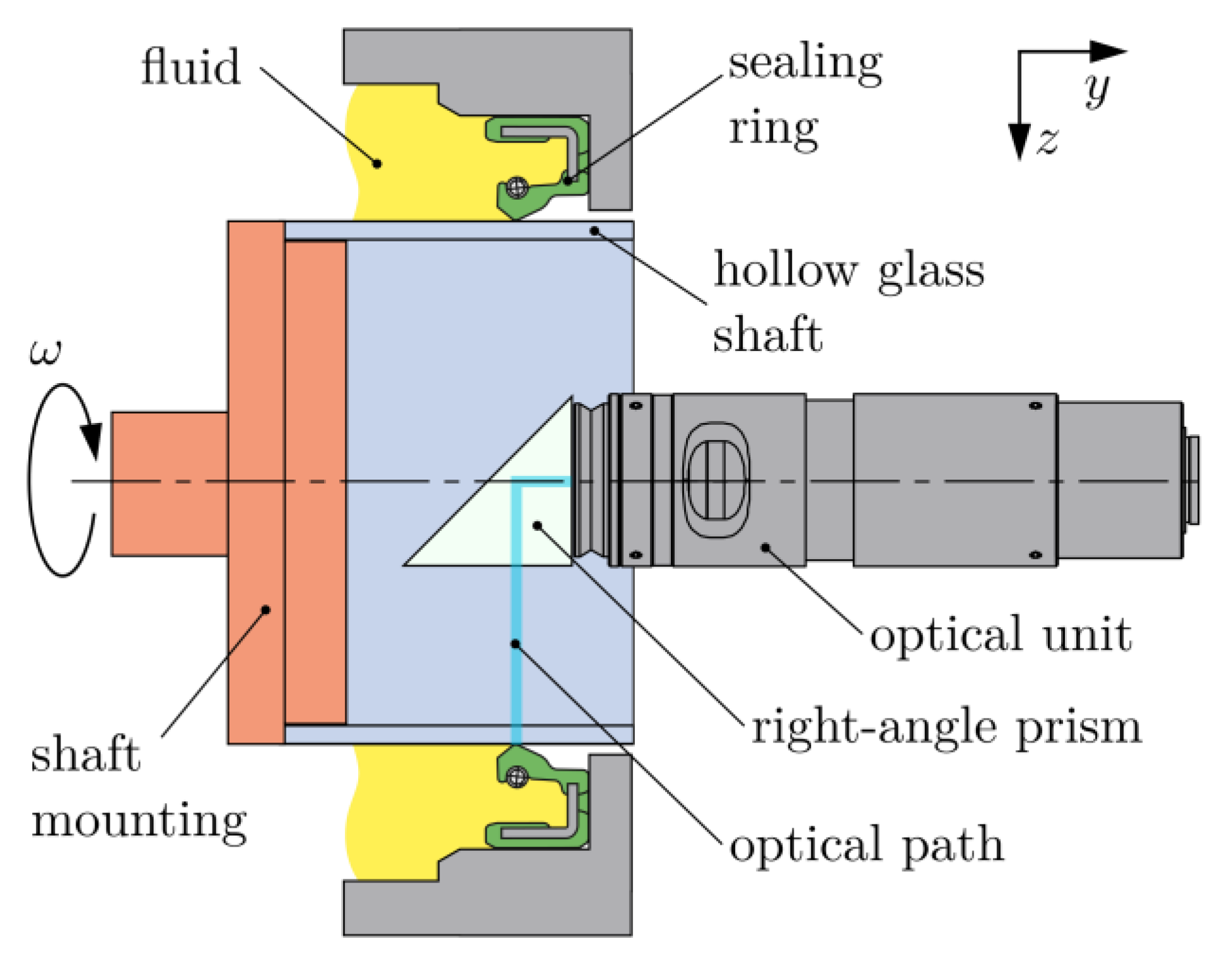
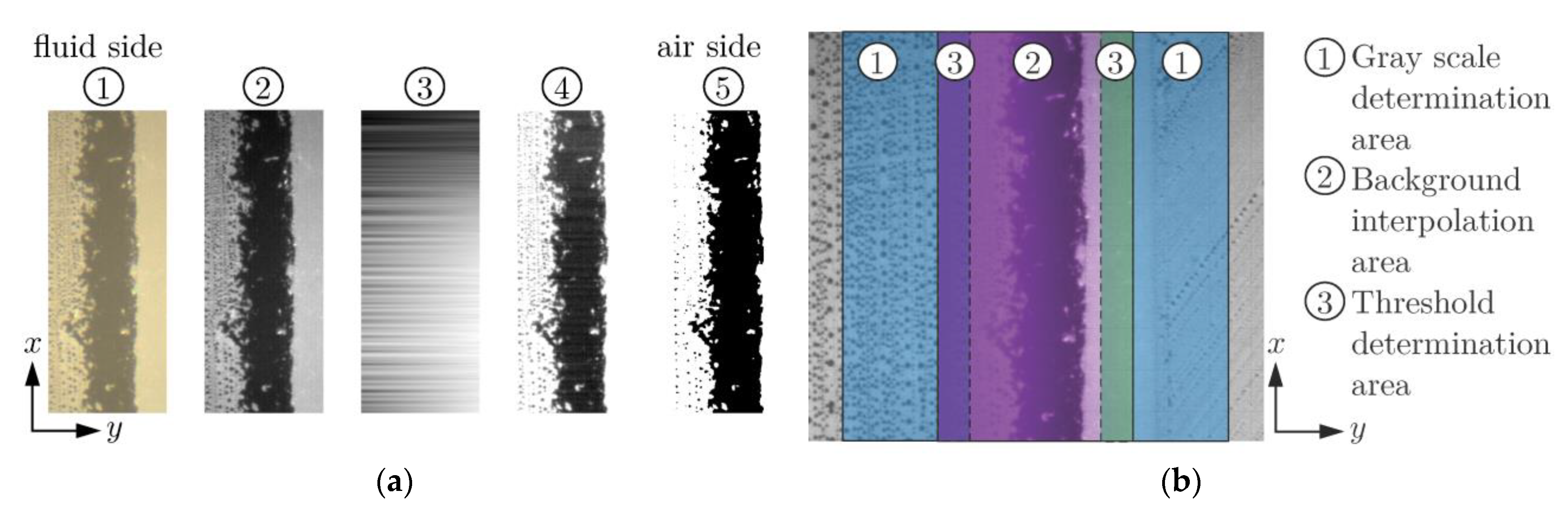
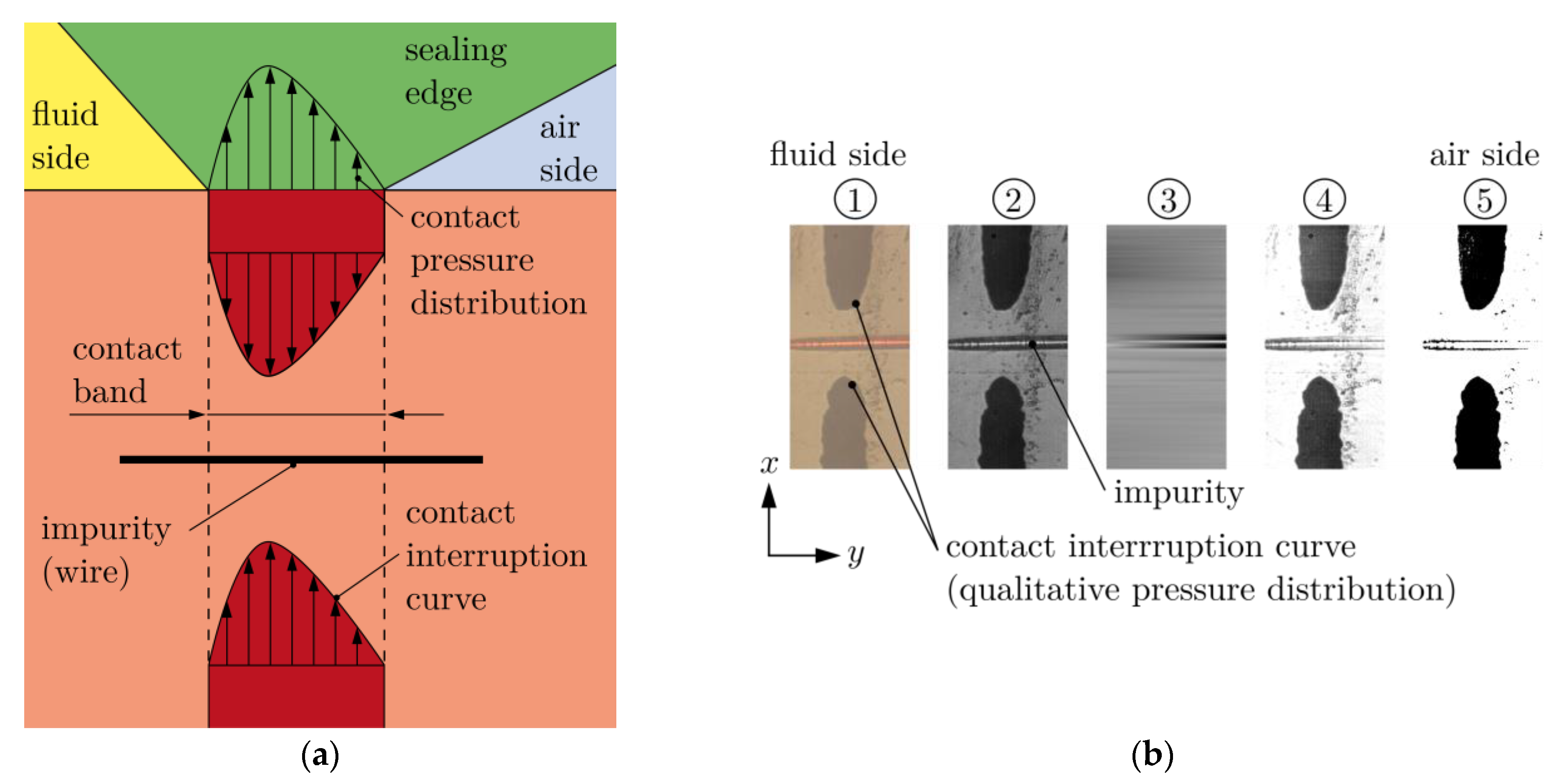
2.3. Visual Experiments
2.4. Friction Torque Measurements
2.5. FE Modeling
3. Results
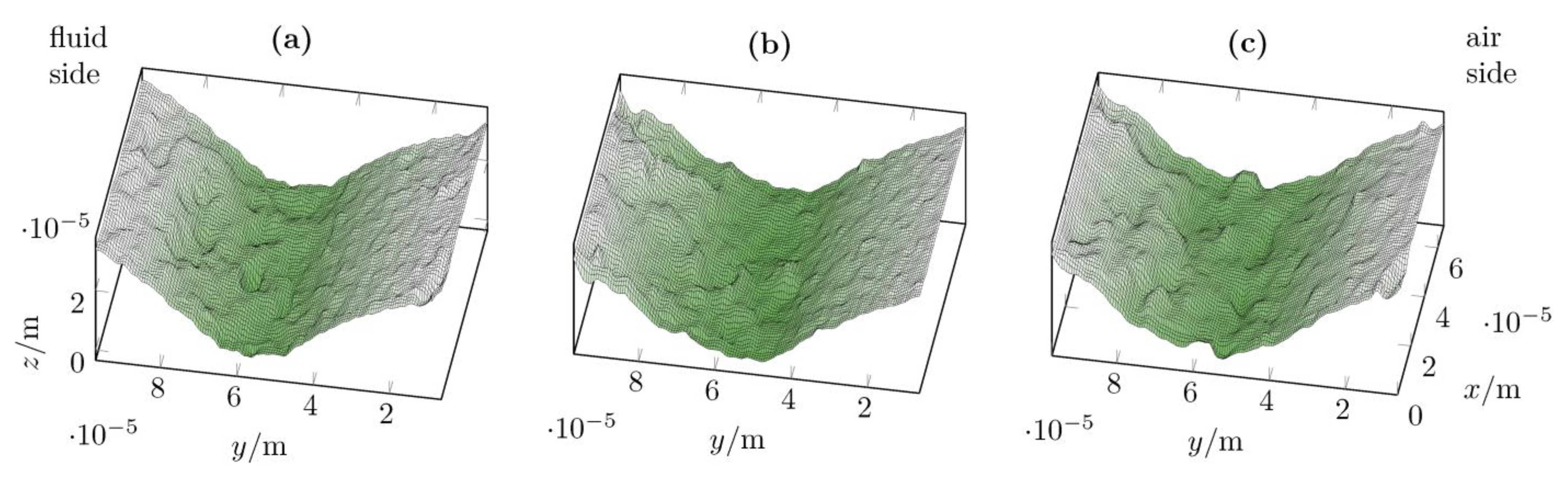
3.1. FE Analysis
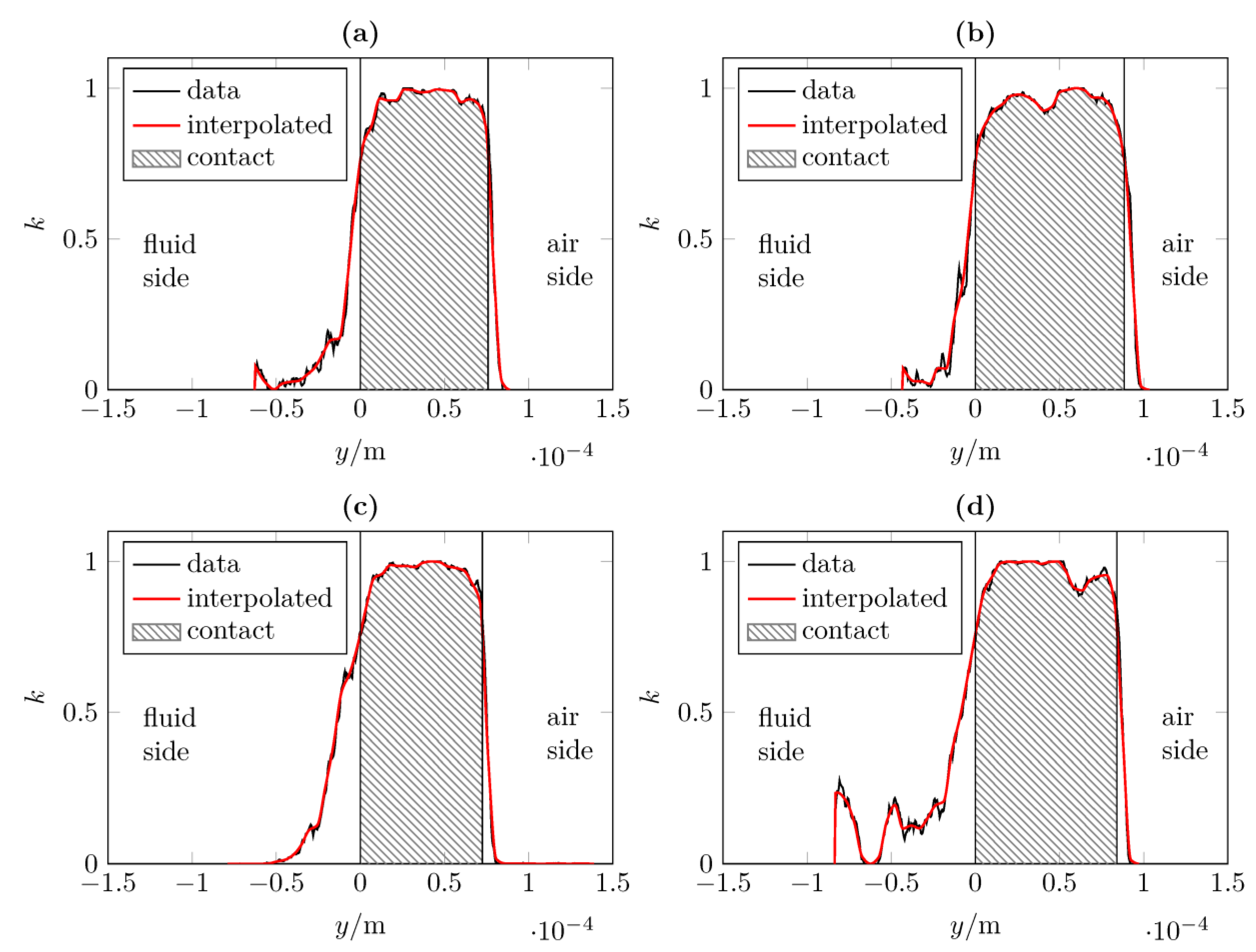
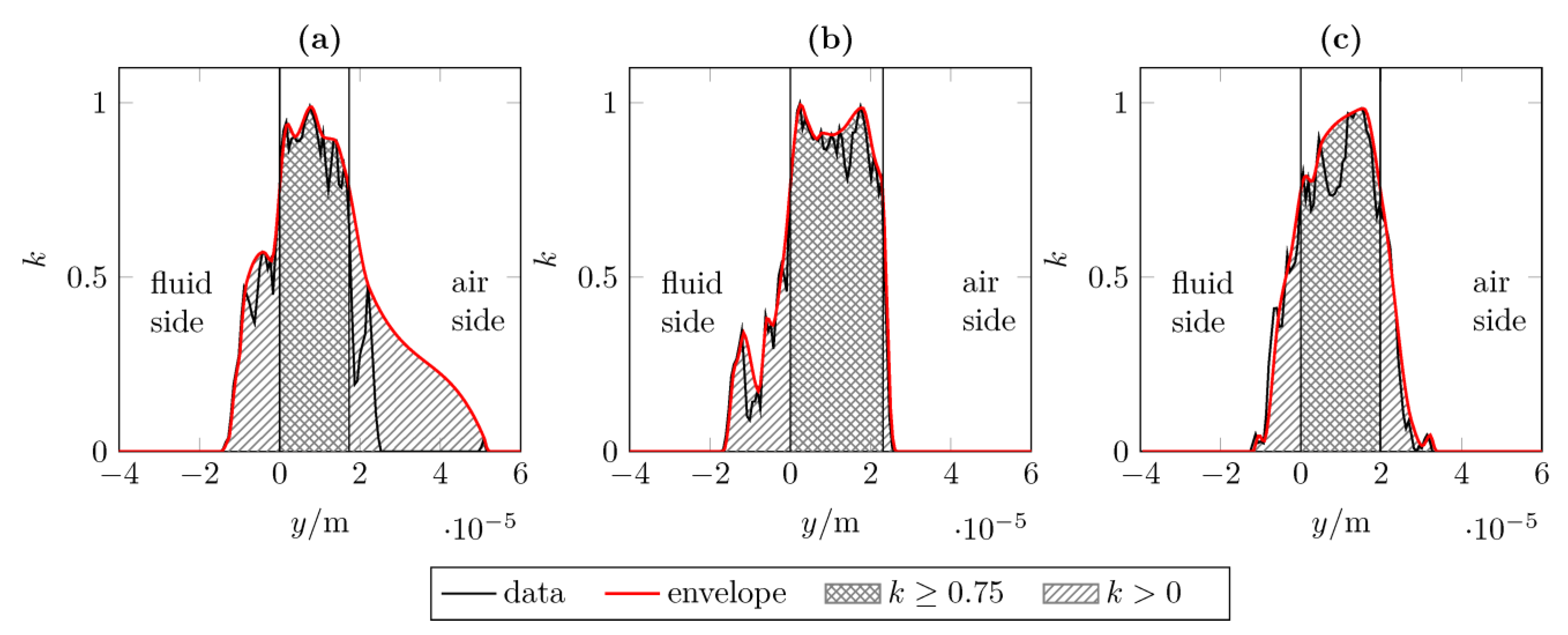
3.2. Contact Analysis
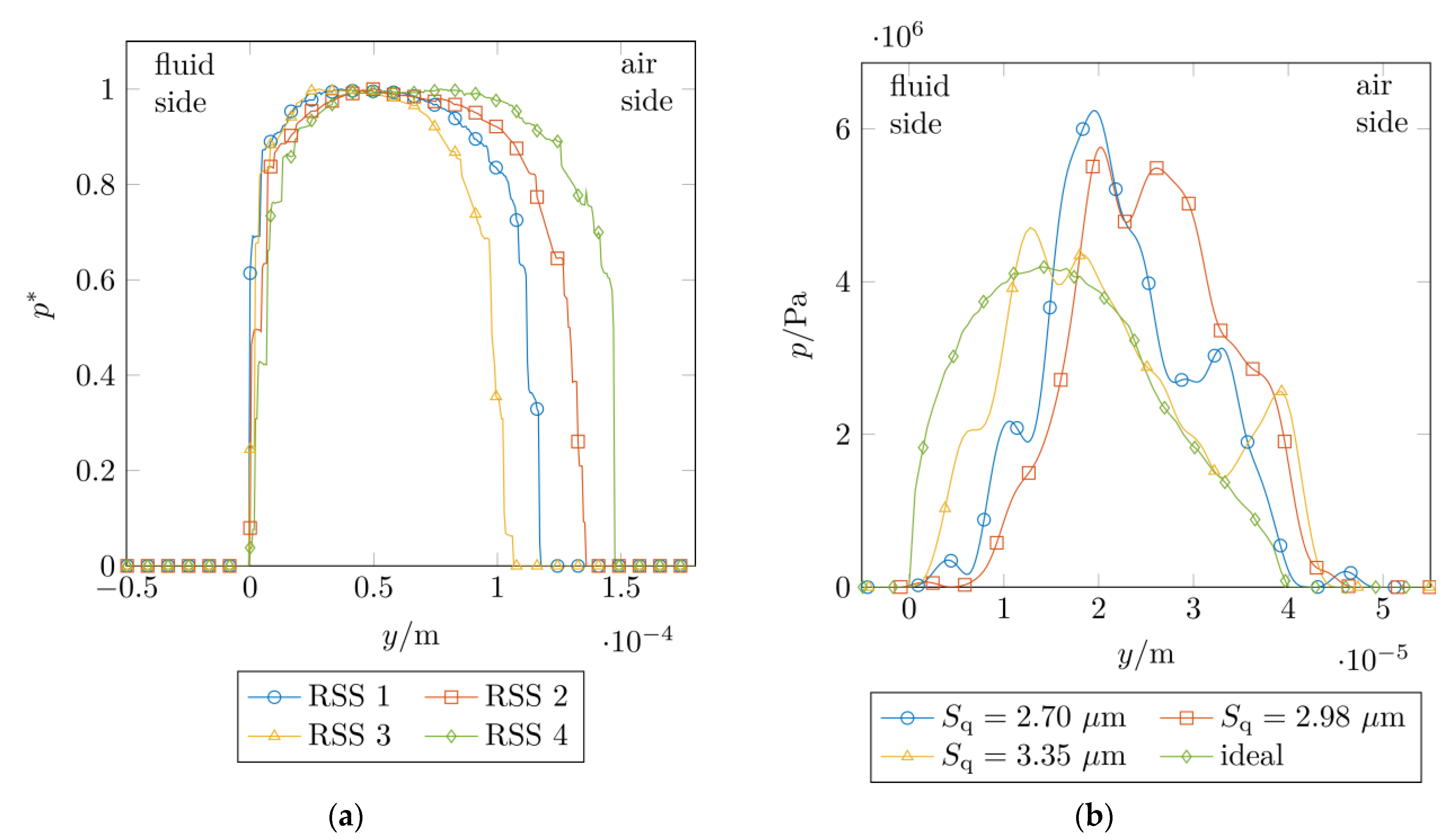
3.3. Contact Pressure
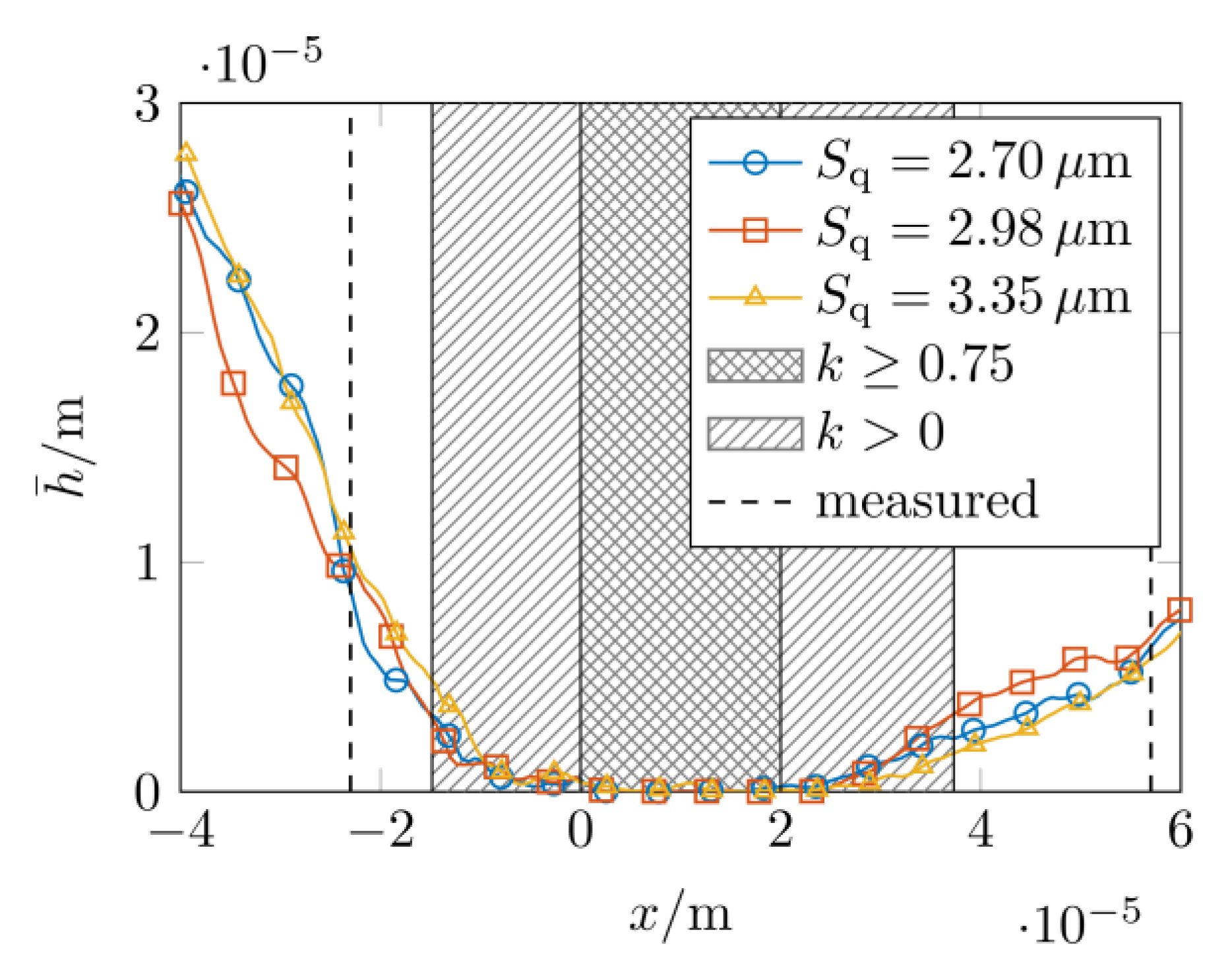
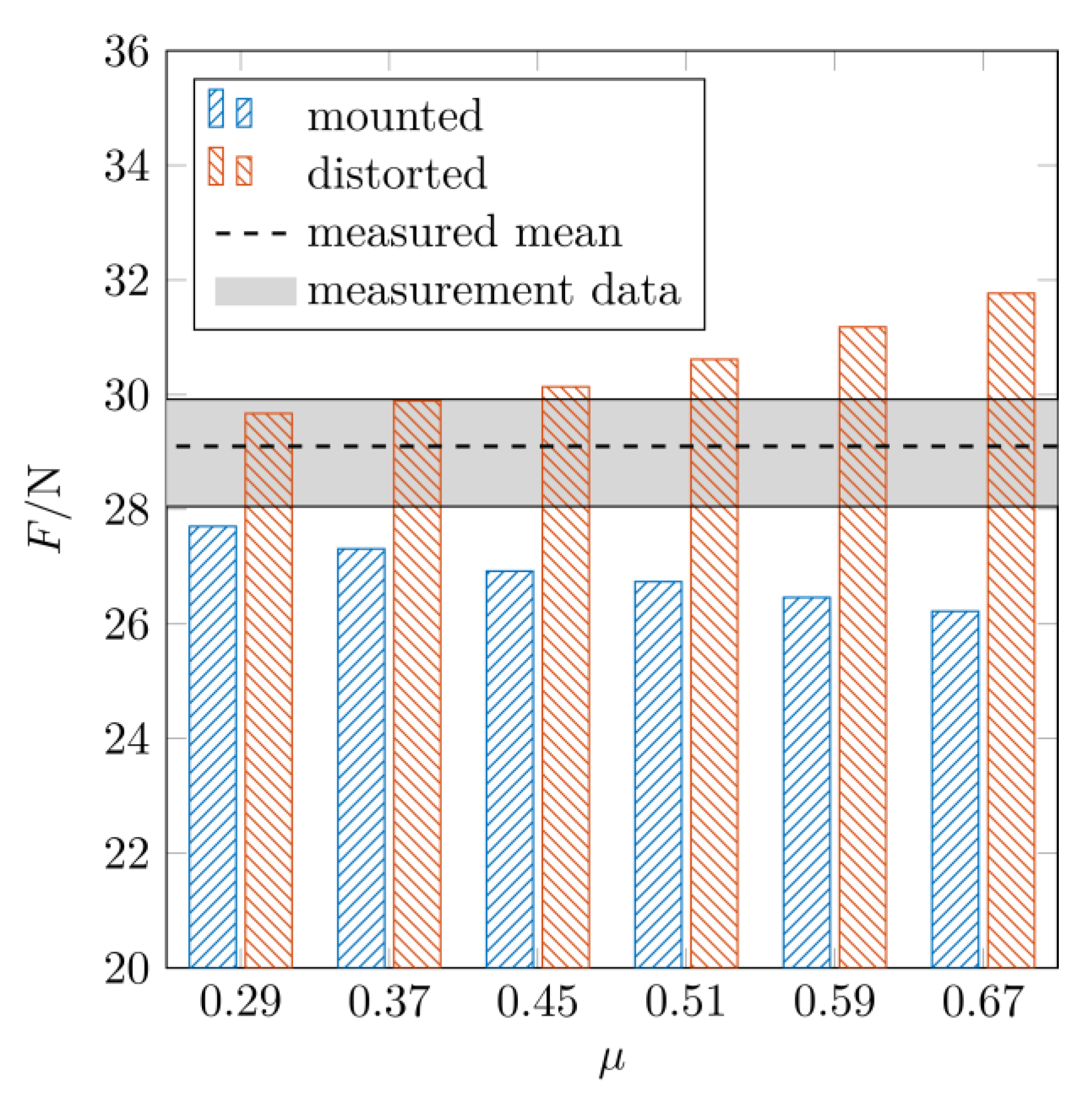
3.4. Radial Load
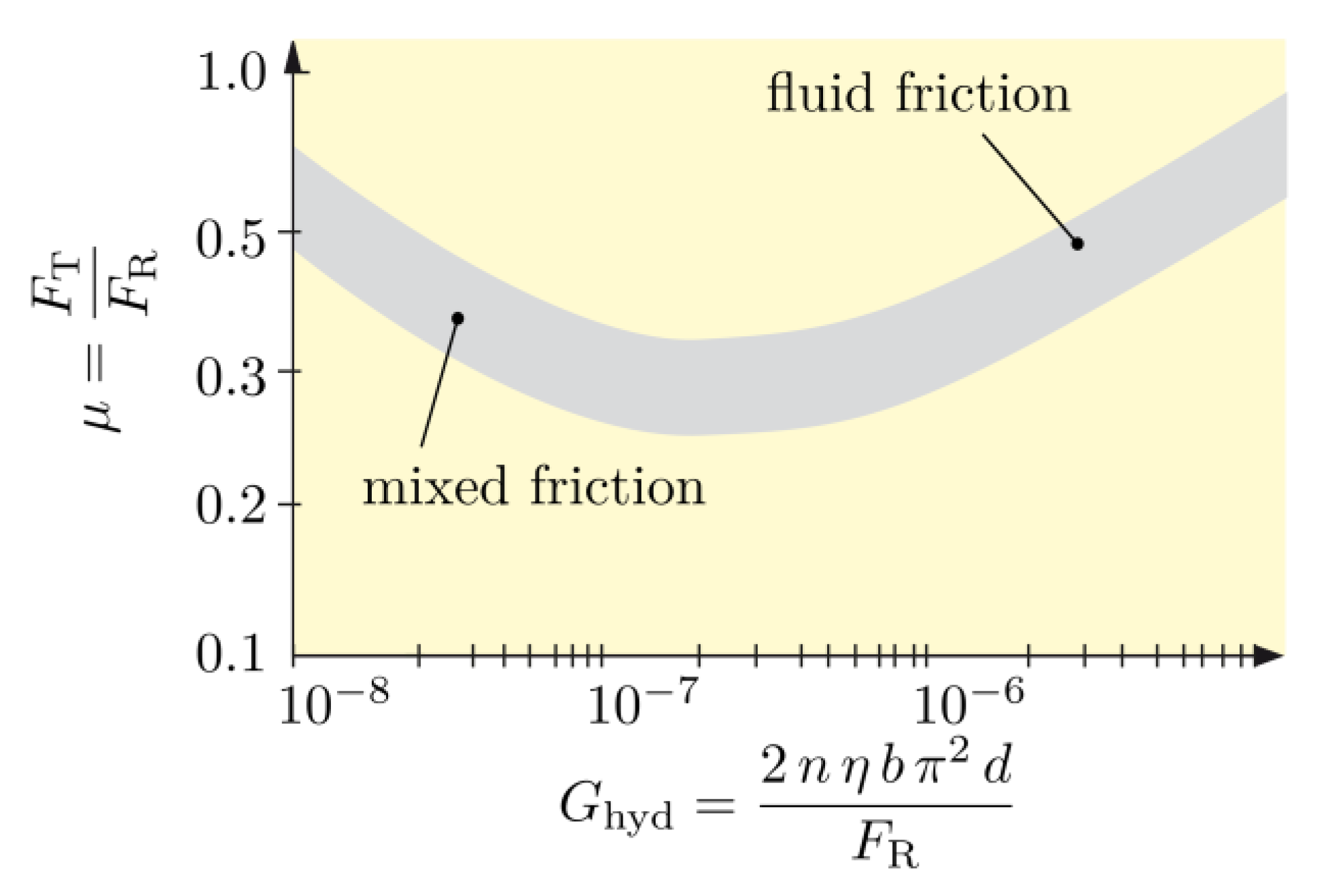
3.5. Friction Torque
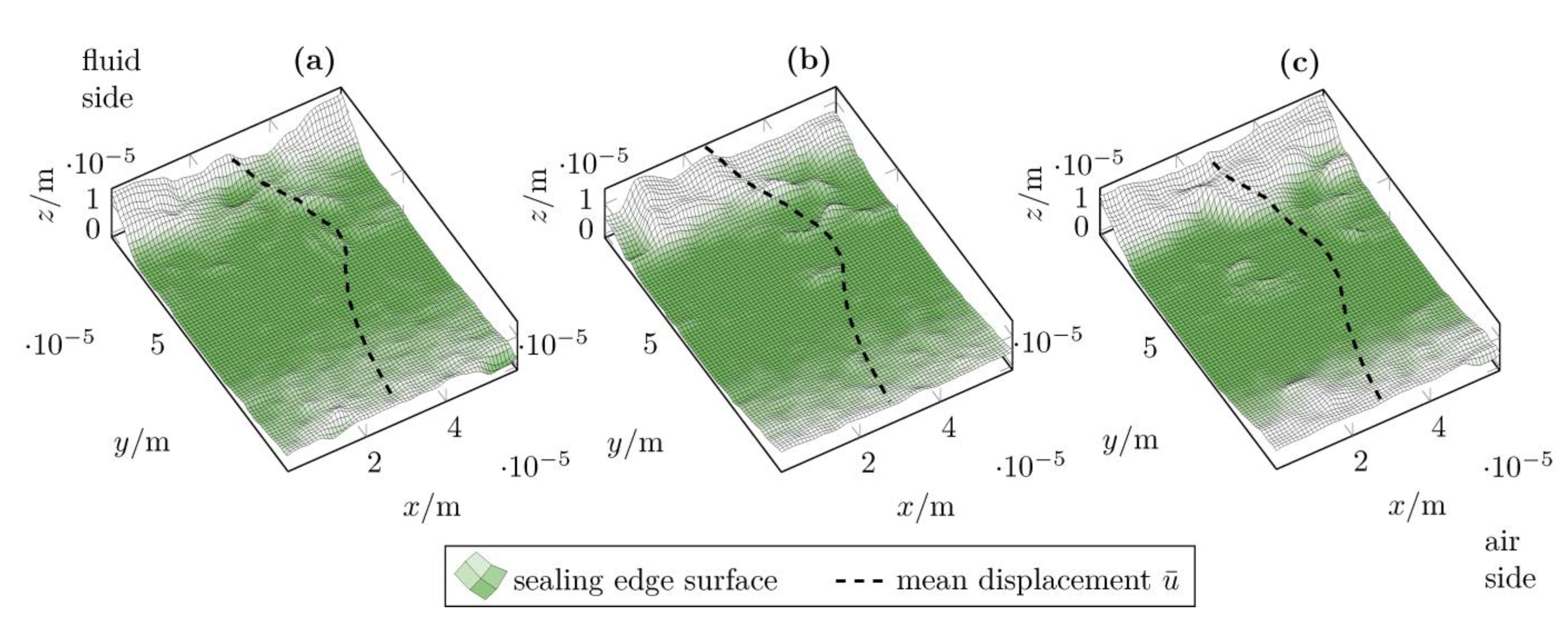
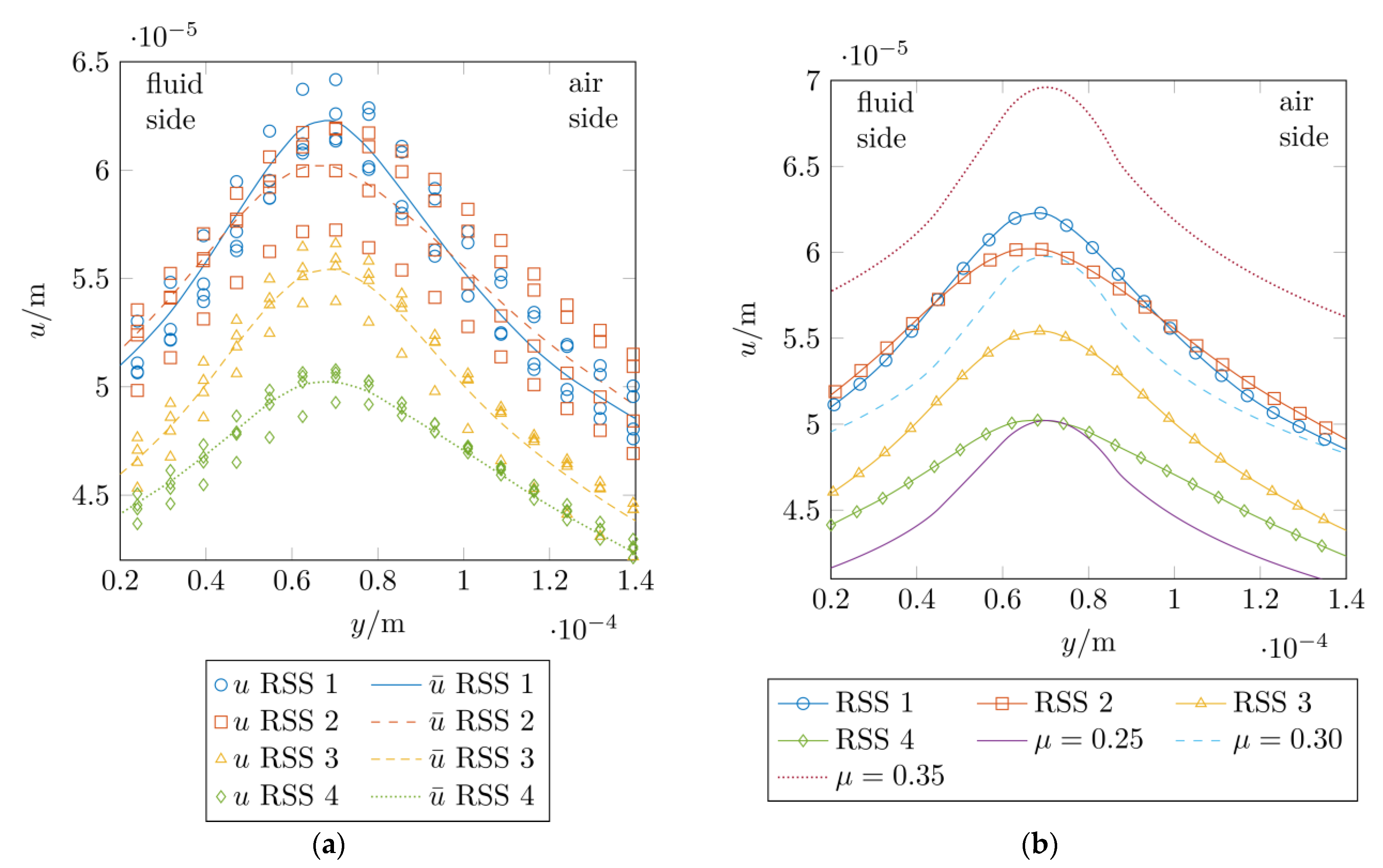
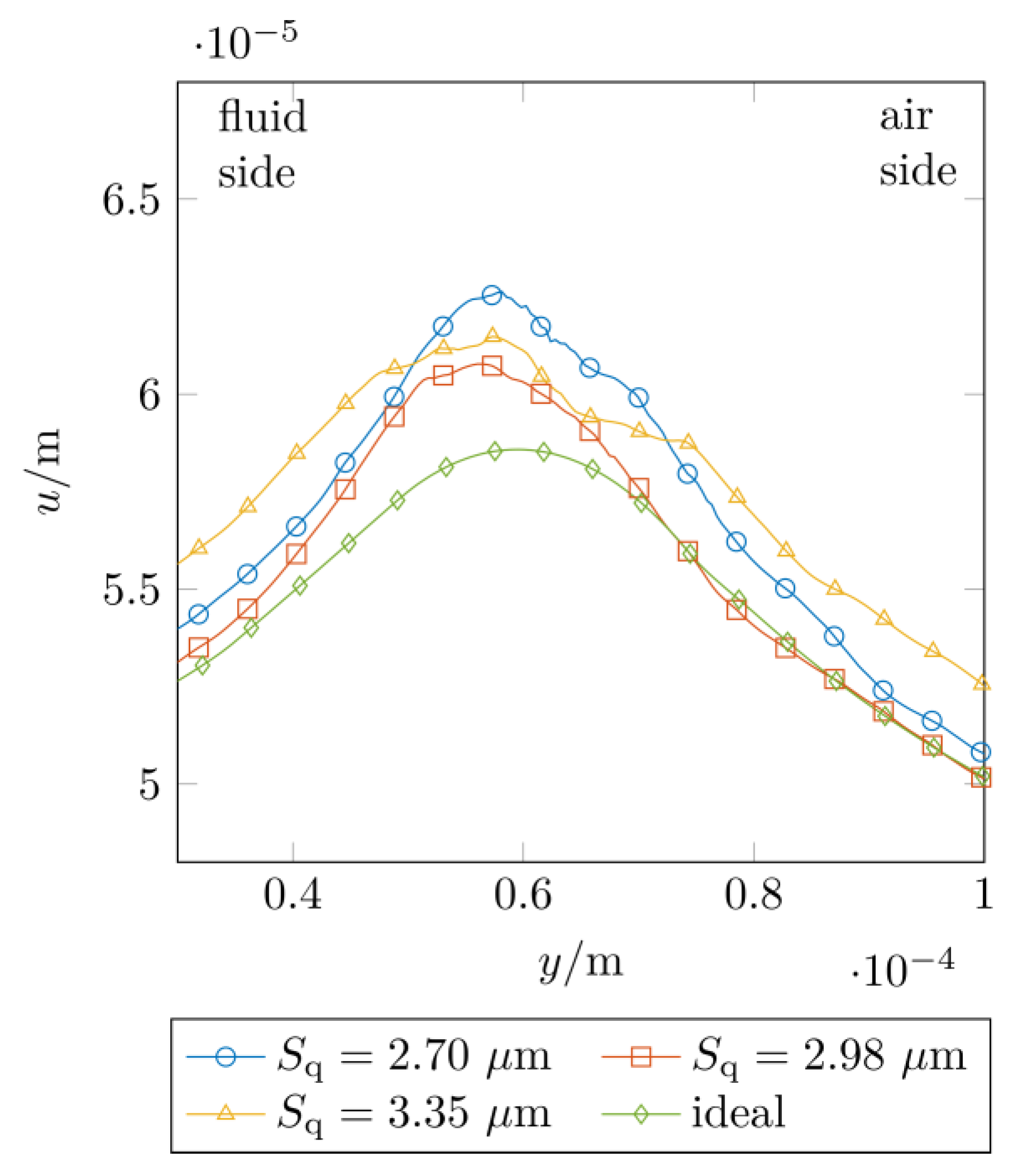
3.6. Tangential Displacement
4. Conclusions
- FE analyses are suitable for both macroscopic and microscopic investigations of the structural mechanics of rotary shaft seals. Real measured surface data can be directly integrated into the numerical model.
- Frustrated total internal reflection provided a qualitative analysis of the contact pressure distribution based on the contact interruption curve. This offers possible improvements with regard to a higher resolution of the contact interruption curve for the experimental detection of the microscopic effects in the contact pressure distribution.
- Particle image velocimetry (PIV) offers a possibility to quantify the tangential distortion of the sealing edge surfaces.
- Depending on the contact definition (threshold ), there were average differences of to between the measured and computed contact widths. This difference was also evident in the study of the contact pressure distribution. Possible reasons for this are tolerance deviations of the used materials and test rigs. There is potential for improvement here with regard to a completely user-independent contact analysis without the specification of a threshold .
- The measured and computed radial loads were in the same range. Furthermore, numerical analyses showed that the radial load in operation (with distorted sealing edge surface) was higher than in mounted condition (with a compressed seal edge).
- The measured and computed tangential displacements of the sealing edges showed a high agreement for coefficients of friction in a range of . There were no major differences between the ideally smooth sealing edge surface and the real surface measurement data.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Contact width | |
| Neo-Hookean material parameter | |
| Nominal diameter | |
| Outer shaft diameter | |
| Measured load | |
| Radial load | |
| Segment load | |
| Tangential friction load | |
| Gray values | |
| Threshold gray value | |
| Dimensionless number [23] | |
| Dimensionless (Gümbel/Hersey) number [24,25] | |
| Threshold for contact analysis | |
| Shaft rotation speed | |
| Refractive index | |
| Line load | |
| Maximum height of the roughness profile | |
| Root-mean-square roughness height | |
| Roundness deviation | |
| Measured friction torque | |
| Tangential displacement | |
| Circumferential direction | |
| Circumferential sliding velocity | |
| Axial direction | |
| Radial direction | |
| Dynamic viscosity | |
| Temperature | |
| Wavelength of the light | |
| Coefficient of friction | |
| Friction parameter [21,22] | |
| Angular velocity | |
| Abbreviations | |
| DIN | German Institute for Standardization (ger.: Deutsche Institut für Normung e.V.) |
| FEA | Finite element analysis |
| FKM | Fluororubber |
| FVA | Research Association for Drive Technology (ger.: Forschungsvereinigung Antriebstechnik e.V.) |
| ISO | International standards organization |
| PIV | Particle image velocimetry |
| PMMA | Polymethyl methacrylate |
| RSS | Rotary shaft seal |
| VG | Viscosity grade |
References
- Bauer, F. Tribologie; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021; ISBN 978-3-658-32919-8. [Google Scholar]
- Bauer, F. Federvorgespannte-Elastomer-Radial-Wellendichtungen; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2021; ISBN 978-3-658-32921-1. [Google Scholar]
- Jagger, E.T. Rotary Shaft Seals: The Sealing Mechanism of Synthetic Rubber Seals Running at Atmospheric Pressure. Inst. Mech. Eng. 1957, 171, 597–616. [Google Scholar] [CrossRef]
- Müller, H.K. Concepts of Sealing Mechanism of Rubber Lip Type Rotary Shaft Seals. In Proceedings of the 11th International Conference on Fluid Sealing, Cannes, France, 1 April 1987; pp. 698–709. [Google Scholar]
- Gawlinski, M.J. Lip Motion and Its Consequences in Oil Lip Seal Operation. In Proceedings of the Papers Presented at the Ninth International Conference on Fluid Sealing; Stephens, H.S., Stapleton, C.A., Eds.; BHRA Fluid Engineering: Noordwijkerhout, The Netherlands, 1981; pp. 111–124. [Google Scholar]
- Borras, F.X.; de Rooij, M.B.; Schipper, D.J. Misalignment-Induced Macro-Elastohydrodynamic Lubrication in Rotary Lip Seals. Tribol. Int. 2020, 151, 106479. [Google Scholar] [CrossRef]
- Bekgulyan, S.; Feldmeth, S.; Bauer, F. Influence of Static and Dynamic Eccentricity on the Pumping Rate of Radial Lip Seals. In Proceedings of the Papers Presented at: 25th International Conference on FLUID SEALING; Rackov, M., Mitrović, R., Čavić, M., Eds.; Springer: Cham, Switzerland; Manchester, UK, 2020; pp. 79–91. [Google Scholar]
- Kawahara, Y.; Abe, M.; Hirabayashi, H. An Analysis of Sealing Characteristics of Oil Seals. ASLE Trans. 1980, 23, 93–102. [Google Scholar] [CrossRef]
- Kammüller, M. Zur Abdichtwirkung von Radial-Wellendichtringen. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 1986. [Google Scholar]
- van Leeuwen, H.; Wolfert, M. The Sealing and Lubrication Principles of Plain Radial Lip Seals: An Experimental Study of Local Tangential Deformations and Film Thickness. Tribol. Ser. 1997, 32, 219–232. [Google Scholar] [CrossRef]
- Schulz, M.; Hagmayer, M.; Baumann, M.; Bauer, F. Analysis of Fluid Flow in the Sealing Gap of Radial Shaft Seals and Elastic Deformation of the Sealing Surface. J. Tribol. 2021, 143, 122301. [Google Scholar] [CrossRef]
- Grün, J.; Feldmeth, S.; Bauer, F. The Sealing Mechanism of Radial Lip Seals: A Numerical Study of the Tangential Distortion of the Sealing Edge. Tribol. Mater. 2022, 1, 1–10. [Google Scholar] [CrossRef]
- Grün, J.; Feldmeth, S.; Bauer, F. Wear on Radial Lip Seals: A Numerical Study of the Influence on the Sealing Mechanism. Wear 2021, 476, 203674. [Google Scholar] [CrossRef]
- Tønder, K.; Salant, R.F. Non-Leaking Lip Seals: A Roughness Effect Study. J. Tribol. 1992, 114, 595–599. [Google Scholar] [CrossRef]
- Salant, R.F.; Flaherty, A.L. Elastohydrodynamic Analysis of Reverse Pumping in Rotary Lip Seals with Microundulations. J. Tribol. 1994, 116, 56–62. [Google Scholar] [CrossRef]
- Salant, R.F.; Flaherty, A.L. Elastohydrodynamic Analysis of Reverse Pumping in Rotary Lip Seals with Microasperities. J. Tribol. 1995, 117, 53–59. [Google Scholar] [CrossRef]
- Wenk, J.F.; Stephens, L.S.; Lattime, S.B.; Weatherly, D. A Multi-Scale Finite Element Contact Model Using Measured Surface Roughness for a Radial Lip Seal. Tribol. Int. 2016, 97, 288–301. [Google Scholar] [CrossRef]
- Flitney, R. Seals and Sealing Handbook; Elsevier: Oxford, UK, 1995; ISBN 978-0-08-099416-1. [Google Scholar]
- Lein, J. Mechanische Untersuchungen an Dichtungsringen Für Rotierende Wellen; Springer: Berlin/Heidelberg, Germany, 1954; ISBN 978-3-662-23302-3. [Google Scholar]
- Lines, D.J.; O’Donoghue, J.P. Under-Lip Temperatures in Rotary Shaft Seals. In Proceedings of the Fifth International Conference on Fluid Sealing; The British Hydromechanics Research Association: Coventry, UK, 1971; pp. D1-1–D1-20. [Google Scholar]
- Hirano, F.; Ishiwata, H. Paper 15: The Lubricating Condition of a Lip Seal. Proc. Inst. Mech. Eng. Conf. Proc. 1965, 180, 187–196. [Google Scholar] [CrossRef]
- Hirano, F.; Ishiwata, H.; Kambayashi, H. Friction and Sealing Characteristics of Oil Seals. In Proceedings of the International Conference on Fluid Sealing; British Hydromechanics Research Association: Harlow, UK, 1961; pp. 1–17. [Google Scholar]
- Brink, R.V. Oil Seal Life—Good Loading or Good Luck. SAE Tech. Pap. 1965, 209–216. [Google Scholar] [CrossRef]
- Gümbel, L.K.F. Das Problem Der Lagerreibung. Mon. Des Berl. Bez. Dtsch. Ing. 1914, 5,6, 87–104, 109–120. [Google Scholar]
- Hersey, M.D. The Laws of Lubrication of Horizontal Journal Bearings. J. Wash. Acad. Sci. 1914, 4, 542–552. [Google Scholar]
- Schulz, M.; Baumann, M.; Bauer, F.; Haas, W. Influence of Different Shaft Surface Finishes on the Tribological and Functional Behaviour of Radial Shaft Seals. In Proceedings of the 7th International Conference Integrity-Reliability-Failure, Funchal, Portugal, 6–10 September 2018; Silva Gomes, J.F., Meguid, S.A., Eds.; pp. 351–368. [Google Scholar]
- Sommer, M.; Haas, W. A New Approach on Grease Tribology in Sealing Technology: Influence of the Thickener Particles. Tribol. Int. 2016, 103, 574–583. [Google Scholar] [CrossRef]
- Schulz, M.; Baumann, M.; Bauer, F. Influence of Belt Ground and Superfinished Shaft Counterfaces on the Tribological and Functional Behaviour of Elastomeric Lip Seals. In Proceedings of the 24th International Conference on Fluid Sealing, Manchester, UK, 7–8 March 2018; pp. 143–159. [Google Scholar]
- Feuchtmüller, O.; Hörl, L.; Bauer, F. An Empirical Study on the Friction of Reciprocating Rod Seals at Predefined Lubrication Conditions and Shear Rates. Lubricants 2022, 10, 56. [Google Scholar] [CrossRef]
- DIN 3760:1996-09; Radial-Wellendichtringe. 1996.
- DIN 3761-1:1984-01; Radial-Wellendichtringe Für Kraftfahrzeuge. Begriffe, Maßbuchstaben, Zulässige Abweichungen, Radialkraft. 1984.
- Freudenberg Sealing Technologies: Material 75 FKM 585. Available online: https://ecatalog.fst.com/ (accessed on 24 March 2022).
- Feldmeth, S.; Bauer, F.; Haas, W. Component-Based Parameter Identification for the Contact Simulation of Elastomeric Radial Lip Seals. In Proceedings of the Deutsche Kautschuk-Tagung DKT 2015/International Rubber Conference IRC 2015, Nürnberg, Germany, 29 June–2 July 2015; p. 194. [Google Scholar]
- DIN EN ISO 25178-2:2020-02; Geometrische Produktspezifikation (GPS)—Oberflächenbeschaffenheit: Flächenhaft—Teil 2: Begriffe, Definitionen Und Oberflächen-Kenngrößen (ISO/DIS 25178-2:2019). 2020.
- DIN 3761-2:1983-11; Radial-Wellendichtringe Für Kraftfahrzeuge. Anwendungshinweise. 1983.
- Feldmeth, S.; Stoll, M.; Bauer, F. How to Measure the Radial Load of Radial Lip Seals. Tribol. Und Schmier. 2021, 68, 5–12. [Google Scholar] [CrossRef]
- Stakenborg, M.J.L. On the Sealing Mechanism of Radial Lip Seals. Tribol. Int. 1988, 21, 335–340. [Google Scholar] [CrossRef]
- Sinzara, W.; Sherrington, I.; Smith, E.H.; Brooks, H.; Onsy, A. Effects of Eccentric Loading on Lip Seal Performance. In Proceedings of the 6th European Conference on Lubrication Management and Technology (Lubmat 2018), San Sebastian, Spain, 4–6 June 2018. [Google Scholar]
- Frölich, D.; Magyar, B.; Sauer, B. A Comprehensive Model of Wear, Friction and Contact Temperature in Radial Shaft Seals. Wear 2014, 311, 71–80. [Google Scholar] [CrossRef]
- Borras, F.X.; Bazrafshan, M.; De Rooij, M.B.; Schipper, D.J. Stern Tube Seals under Static Condition: A Multi-Scale Contact Modeling Approach. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 181–195. [Google Scholar] [CrossRef]
- Hermann, W.; Seffler, H.-W. Neue Erkenntnisse Für Den Abdichtmechanismus von Radial-Wellendichtringen. ATZ Automob. Z. 1985, 87, 475–484. [Google Scholar]
- Zhu, S.; Yu, A.W.; Hawley, D.; Roy, R. Frustrated Total Internal Reflection: A Demonstration and Review. Am. J. Phys. 1986, 54, 601–607. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-68851-0. [Google Scholar]
- Thielicke, W.; Sonntag, R. Particle Image Velocimetry for MATLAB: Accuracy and Enhanced Algorithms in PIVlab. J. Open Res. Softw. 2021, 9, 12. [Google Scholar] [CrossRef]
- Johnston, D.E.; Vogt, R. Rotary Shaft Seal Friction, the Influence of Design, Material, Oil and Shaft Surface. J. Passeng. Cars 1995, 104, 1453–1466. [Google Scholar]
- Plath, S.; Meyer, S.; Wollesen, V.M. Friction Torque of a Rotary Shaft Lip Type Seal—A Comparison between Test Results and Finite Element Simulation. Mechanika 2005, 54, 55–59. [Google Scholar]
- Engelke, T. Einfluss Der Elastomer-Schmierstoff-Kombination Auf Das Betriebsverhalten von Radialwellendichtringen. Ph.D. Thesis, Leibniz University Hannover, Hannover, Germany, 2011. [Google Scholar]
- Wennehorst, B.; Engelke, T.; Poll, G. Modelling Radial Lip Seal Friction—A Multi-Scale Mixed Lubrication Approach. In Proceedings of the 21st International Conference on Fluid Sealing, Milton Keynes, UK, 30 November–1 December 2011; pp. 207–226. [Google Scholar]
- Garcia, D. Robust Smoothing of Gridded Data in One and Higher Dimensions with Missing Values. Comput. Stat. Data Anal. 2010, 54, 1167–1178. [Google Scholar] [CrossRef]
- Garcia, D. A Fast All-in-One Method for Automated Post-Processing of PIV Data. Exp. Fluids 2011, 50, 1247–1259. [Google Scholar] [CrossRef]
- Schuler, P. Einfluss von Grenzflächeneffekten Auf Den Dichtmechanismus Der Radial-Wellendichtung. Ph.D. Thesis, Universität Stuttgart, Süßen, Germany, 2014. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grün, J.; Gohs, M.; Bauer, F. Multiscale Structural Mechanics of Rotary Shaft Seals: Numerical Studies and Visual Experiments. Lubricants 2023, 11, 234. https://doi.org/10.3390/lubricants11060234
Grün J, Gohs M, Bauer F. Multiscale Structural Mechanics of Rotary Shaft Seals: Numerical Studies and Visual Experiments. Lubricants. 2023; 11(6):234. https://doi.org/10.3390/lubricants11060234
Chicago/Turabian StyleGrün, Jeremias, Marco Gohs, and Frank Bauer. 2023. "Multiscale Structural Mechanics of Rotary Shaft Seals: Numerical Studies and Visual Experiments" Lubricants 11, no. 6: 234. https://doi.org/10.3390/lubricants11060234
APA StyleGrün, J., Gohs, M., & Bauer, F. (2023). Multiscale Structural Mechanics of Rotary Shaft Seals: Numerical Studies and Visual Experiments. Lubricants, 11(6), 234. https://doi.org/10.3390/lubricants11060234





