Abstract
The present study aims to establish a mixed lubrication model for staved stern tube bearings lubricated with water, in which the average Reynolds equation and a KE elastic–plastic contact model are introduced to calculate the hydrodynamic pressure and contact pressure, respectively. The difference in the mixed lubrication behaviors between circular- and flat-staved bearings is compared; moreover, the effects of the number of staves on the mixed-lubrication performance of these two kinds of staved bearing are investigated. The mechanism of action of the number of staves in staved bearings on the mixed-lubrication performance is revealed. The numerical results show that the number of staves has a significant effect on the mixed-lubrication performance in circular- and flat-staved bearings. Furthermore, there is an optimal value for the number of staves, shown to be 30 in the current simulation, for improving the mixed-lubrication performance of flat-staved stern tube bearings lubricated with water.
1. Introduction
In recent years, with people’s increasing awareness of environmental protection, researchers have paid water-lubricated bearings more attention, especially in the case of stern bearings used in marine ships. As is well known, the water-lubricated bearings typically operate under mixed-lubrication conditions, especially during the start and shut-down stage or under severe load, because of the low viscosity of water [1,2]. Moreover, in the case of mixed lubrication, the contact behavior can lead to increased friction and wear, which may exacerbate the vibration as well as the noise emitted by the propulsion system. Therefore, it is of great significance to investigate the mixed-lubrication performance of water-lubricated stern tube bearings.
He et al. [3] developed a mixed lubrication model to study the lubrication performance of marine stern tube bearings in consideration of the bending deformation of the stern shaft and cavitation. Lv et al. [4] presented a mixed lubrication model considering two-dimensional wall slip and journal misalignment to study the tribological properties of stern bearings. Both of the above studies employed the average Reynolds equation proposed by Patir and Cheng [5] to calculated the hydrodynamic pressure of the journal bearing. Deepak et al. [2] modified the average Reynolds equation to investigate the effect of non-Gaussian surface topography on the mixed-lubrication performance of water-lubricated journal bearings. Yang et al. [6] numerically investigated the performance of aft stern tube bearings during ship turning maneuvers using the Computation Fluid Dynamics (CFD) method. Huang et al. [7] proposed a numerical model to study the lubrication performance with misalignment of the shaft, and the effect of parameters including misalignment angle, eccentricity ratio, rotation speed, lubricant viscosity and center-line eccentricity angle on lubrication performance were investigated. Georgios et al. [8] compared two bearing modification designs, and determined the optimal geometric parameters of a double slope aft stern tube bearing necessary to maximize the effective pressure area while also minimizing the maximum local pressure. Xie et al. [9] theoretically and experimentally investigated the micro asperity contact load ratios and lubrication states of water-lubricated stern tube bearings. Liu et al. [10] experimentally demonstrated the phenomenon of pressure bias and bidirectional shaft inclination; furthermore, they numerically investigated the effects of eccentricity ratio, shaft inclination angle and bearing structure parameters on lubrication, as well as the dynamic characteristics of water-lubricated stern bearings. He et al. [11] established a mixed lubrication model for marine stern bearings in consideration of cavitation and the bending deformation of the shaft; moreover, they conducted a theoretical investigation on the effect of bending deformation on the dynamic characteristics. Zhu et al. [12] built a coupling model of shaft longitudinal vibration and bearing lubrication, in which the shaft axial shock and misalignment were considered, in order to investigate the effect of explosion shock on bearing lubrication performance. Wodtke et al. [13] conducted an investigation on the thermal effects of water-lubricated stern tube bearings with both experimental and theoretical methods. Zhang et al. [14] studied the effect of operating conditions on bearing temperature under hydrodynamic lubrication. In order to improve the lubrication performance as well as wear resistance of the water-lubricated stern bearings, Zhou et al. [15] studied the effects of different nano-fillers on friction, wear, mechanical and vulcanization properties of hydrogenated nitrile rubber used on ship stern shaft.
In addition to the research described above, many studies [16,17,18,19,20,21,22,23,24,25,26,27,28] on wear, dynamic characteristics, friction-induced vibration and noise of water-lubricated stern tube bearings have also been conducted by scholars. Han et al. [16] experimentally studied the mechanism of action of stick–slip nonlinear friction-induced vibration of water-lubricated stern rube bearing. To investigate the mechanism of friction-induced vibration and noise of marine stern tube bearings, a three-degree-of-freedom model considering perturbations of a stochastic rough surface was proposed by Lin et al. [17], whose results showed that the friction coefficient and the contact stiffness significantly influenced the stability of the system. Qin et al. [18] conducted an experimental investigation, in which a high-speed camera was used to track the vibration motion and a machine vision technique was employed to extract the friction-induced vibration of the bearing. Their analysis results showed that bearing vibration was mainly induced by the stick–slip phenomenon. A coupled vibration model, in which the lateral vibration response of the shaft journal under normal load was applied to the dynamic friction force, was proposed by Jin et al. [19] to investigate the interaction of the lateral vibration and friction vibration of a marine water-lubricated bearing. Subsequently, they updated the model to consider the movement of the stern shaft journal [20]. Lin et al. [21] pointed out that different parameters, including the rotation speed of the shaft, contact pressure, friction coefficient, system damping and stiffness, all have an important influence on the nonlinear friction-induced vibration characteristics of water-lubricated stern bearings. Ning et al. [22] proposed a wear monitoring method based on the amplitude spectrum of the ultrasonic reflection coefficient, and used this method to analyze the effects of bearing parameters, objective function and algorithm parameters on the identification results. A full-sized test rig of a water-lubricated stern bearing with an elevation adjustment device was built by Ouyang et al. [23], in which the eddy current sensor and high-precision wireless telemetry were used to collect the axis orbit signal and circumferential film pressure, respectively. In addition, the effect of bias load, rotational speed, and hull deformation on bearing lubrication characteristics were experimentally studied. Cai et al. [24] numerically explored the effects of wear and shaft shape error defects on the tribo-dynamic responses of water-lubricated bearings under non-linear propeller disturbance, and the results showed that the nonlinear disturbance had a significant influence on the dynamic behavior, and the use of reasonable wear parameters can improve the lubrication performance. Subsequently, they updated the tribo-dynamic model in order to consider mass conservation cavitation, and conducted an investigation on micro-groove water-lubricated bearings [25]. Recently, they proposed a new mathematical modeling technique to investigate the nonlinear dynamic mixed friction behaviors of journal-thrust-coupled bearings lubricated with water [26]. In order to improve the transient wear and asperity contact performance of the water-lubricated bearing, Xiang et al. [27] proposed a surface profile modification method under fluid–solid–thermal coupling conditions. Chen et al. [28] numerically investigated the effect of an imperfect journal, including journal error with respect to the amplitude as well as the waviness, on the tribo-dynamic behaviors of water-lubricated bearings during start-up. The studies on stern tube water-lubricated bearings described above all adopted a continuous circular bush, which is usually difficult to replace and maintain, while staved stern tube bearings lubricated with water can adapt to this situation better, with their convenient maintenance, because failed staves can be changed separately, instead of needing to replace the whole bearing. Recently, Anatoliy et al. [29] estimated the hydrodynamic pressure of water-lubricated staved bearings with circular and flat staves using an asymptotic technique, the results of which were compared with those obtained using Finite Element Method (FEM). However, to the best of authors’ knowledge, studies on staved stern tube water-lubricated bearings are still few in number. Therefore, it is necessary to conduct research on this topic.
The purpose of the present study is to establish a mixed lubrication model for staved stern tube bearings lubricated with water in order to investigate their mixed lubrication behaviors. Additionally, the effect of the number of staves on the mixed-lubrication performance of circular-staved and flat-staved bearings are analyzed comparatively in order to reveal the mechanism of effect of the number of staves. Furthermore, an optimization of the number of staves with respect to the mixed-lubrication performance of a flat-staved bearing is conducted, the results of which can serve as a reference for designers.
2. Methods and Material
2.1. Governing Equation
2.1.1. Hydrodynamic Pressure Model
In the present study, to investigate the mixed-lubrication performance of staved stern tube water-lubricated bearings, the average Reynolds equation developed by Patir et al. [5], which has been widely employed by researchers, was used to calculate the hydrodynamic pressure using the Finite Difference Method (FDM), which can be described as follows:
where θ and z are the circumferential and axial directions, respectively; RJ1 is the radius of the journal bearing, and are the flow factors in the circumferential and axial directions, respectively; and are the contact factor and the shear factor, respectively; η and ρ are the viscosity and density of the water, respectively; and are the lubrication gap and the hydrodynamic pressure of the journal bearing, respectively; ω is the angular velocity of the journal; and σs is the composite roughness of journal and bearing.
2.1.2. Geometrical Model of a Staved Bearing
Staved bearings with circular and flat staves were investigated in the present simulation, the respective structures of which are shown in Figure 1. The staves are installed in dovetail grooves on the inner surface of the bearing; moreover, there are grooves between two adjacent staves to allow any silt in the water to pass through, thus reducing abrasive wear on the bearing surface resulting from hard particles in water.
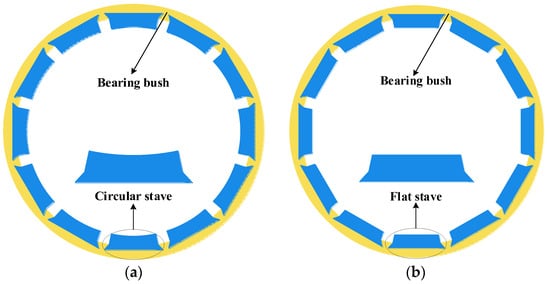
Figure 1.
Bearings with (a) circular staves and (b) flat staves.
As shown in Figure 2, AC is the lubrication gap, denoted by ; AB is the geometrical lubrication gap of a bearing with radius of RJ1, which can be calculated by ; and BC can be calculated by OC−OB, denoted by ; furthermore, the elastic deformation is also used in the present study; therefore, the lubrication gap can be written as follows:
where C and ε are the radius clearance and the eccentricity ratio, respectively, based on the center of the flat; and θ and ψ are the circumferential angle and the attitude angle, respectively.
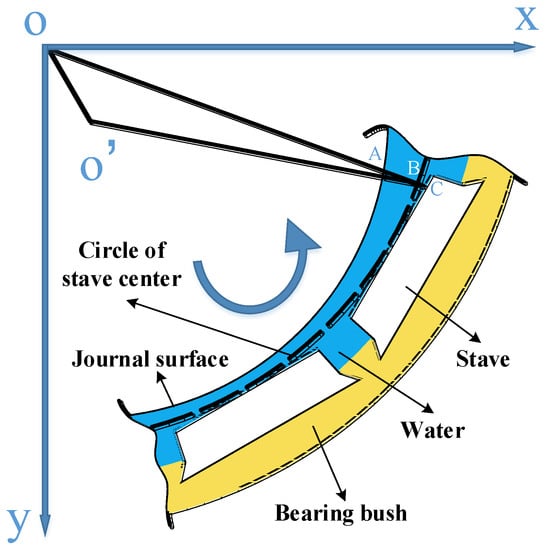
Figure 2.
Geometry model for calculating the lubrication gap of the staved bearing.
2.1.3. Asperity Contact Model
The widely accepted elastic–plastic contact model for Gaussian surfaces (KE model) proposed by Kogut and Etsion [30,31] was used in the present study to calculate the contact pressure, which can be written as follows:
where D and β are the density and composite curvature radius of asperity, respectively; K is a dimensionless parameter, which can be calculated by K = 0.454 + 0.41vB; HB is the hardness of the bearing; and * denotes a dimensionless parameter, where all dimensionless parameters are normalized to σ, which corresponds to the surface height. According to Beheshti and Khonsari [32], the value of σβD was reasonably set to 0.04 in the present study. h* is the dimensionless lubrication gap, where the critical interference marks the transition from elastic to elastic–plastic deformation, which can be written as follows:
where Ec is the composite elastic modulus of the journal and bearing. Furthermore, in Equation (3), is an integral operation, which can be written as follows:
where is the dimensionless asperity probability density function, which can be described as follows:
where is set to 1, in line with the recommendation of Kogut and Etsion [30].
2.2. Boundary Conditions
Considering the cavitation effect generated in the divergent area along the rotational direction, the Reynolds boundary condition is applied in the present study, which can be written as follows:
where θJ0 indicates the positions at which the cavitation effect occurs along the circumferential direction of the bearing. Furthermore, the hydrodynamic pressures at the entrance and exit edges of the bearing are set to zero.
2.3. Numerical Procedure
As shown in Figure 3, it can be observed that the flow chart includes four calculation steps and three convergence judgments. The first calculation step is performed to calculate the discontinuous lubrication gap of the staved stern tube bearing. In the second calculation step, the hydrodynamic pressure is obtained by solving the average Reynolds equation using the Finite Difference Method (FDM). In the third calculation step, the contact pressure is obtained using the KE model. After obtaining the hydrodynamic and contact pressure, a fourth step is performed in which the deformation of the bearing is calculated. Then, the calculation steps are subjected to the process of convergence judgment, and the calculation ends only when the fluid pressure, contact pressure and attitude angle all converge; otherwise, the fluid pressure or lubrication gap are recalculated. The parameters used for analysis in the present study are listed in Table 1.
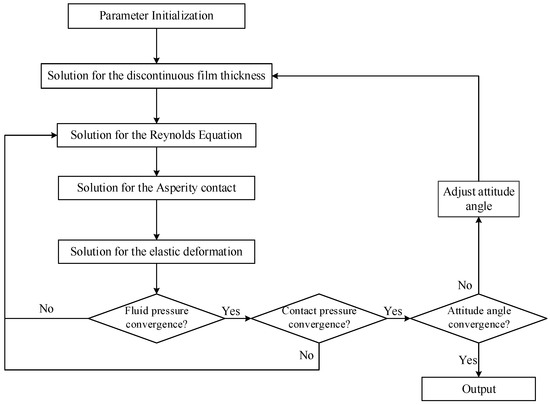
Figure 3.
Flow chart for calculation.

Table 1.
Parameters for calculation.
3. Results and Discussion
3.1. Verification
To verify the appropriateness as well as the accuracy of the model used in the present study, a comparison between the fluid pressure obtained using the present model and that obtained using the model of Anatoliy et al. [29] was performed. The parameters of the staved bearing for the purposes of verification are as follows: journal diameter RJ1 = 0.25 m, radius clearance C = 1 mm, rotation velocity ω = 100 rpm, bearing width L = 1 m, number of circular staves Nst = 12. It can be seen in Figure 4 that the results calculated using the present model are in good agreement with those calculated using the model of Anatoliy et al.
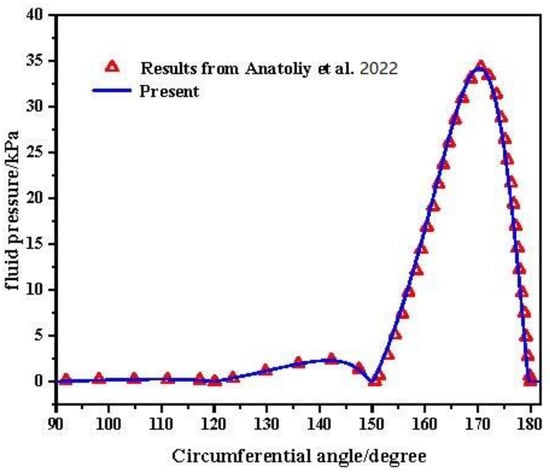
Figure 4.
Verification of the fluid pressure [29].
3.2. Performance Comparison between Bearings with Circular and Flat Staves
3.2.1. Load Capacity of the Staved Bearings
In Section 3.2, to compare the mixed-lubrication performance between circular- and flat-staved bearings, the numbers of staves are all set to be 12, and the rotation speed is set to 400rpm. As illustrated in Figure 5a, the load capacity of the circular-staved bearing is significantly stronger than that of the flat-staved bearing. In the hydrodynamic lubrication stage, the flat-staved bearing generates lower load capacity than the circular one. In fact, compared with the circular-staved bearing, the hydrodynamic effect generated by the flat-staved bearing is weak. Meanwhile, after moving into the mixed lubrication stage, the contact load of the flat-staved bearing is greater than that of the circular one, as shown in Figure 5b.
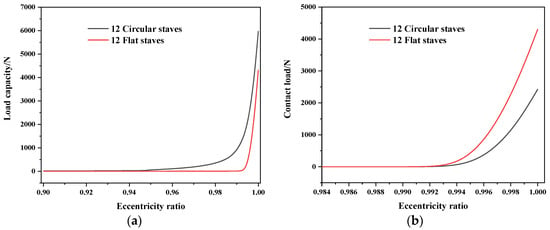
Figure 5.
Comparison of the (a) load capacity and (b) contact load between circular- and flat-staved bearings with variation of eccentricity ratio at ω = 400 rpm.
3.2.2. Mixed Lubrication Distributions of Staved Bearings
In order to further investigate the difference in performance between circular- and flat-staved bearings under mixed-lubrication conditions, the fluid distributions and contact pressures under an eccentricity ratio of 0.995 and a rotation velocity of 400rpm were calculated, and the results are shown in Figure 6. It can be seen in Figure 6a,b that the circular-staved bearing is superior to the flat-staved one, regardless of whether in terms of the peak value or the distribution area of the fluid pressure. Furthermore, as shown in Figure 6c,d, although the peak values of contact pressure are equal, the contact pressure distribution area is much smaller for the circular-staved bearing than for the flat-staved bearing. Therefore, it can be summarized that, in the mixed-lubrication stage, the load capacity of the circular-staved bearing is mainly caused by fluid pressure, while in the flat-staved bearing, contact pressure plays a dominant role. In conclusion, under the current operating conditions, the mixed-lubrication performance of the flat-staved bearing is worse than that of the circular-staved one.
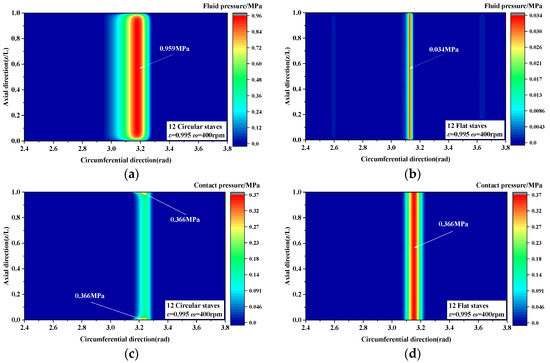
Figure 6.
Mixed lubrication distributions of circular- and flat-staved bearings: (a,b) fluid pressure and (c,d) contact pressure.
3.3. Effect of the Number of Staves on Mixed-Lubrication Performance
3.3.1. Under Different Eccentricity Ratios
In this section, in order to investigate the effect of different numbers of staves on the mixed-lubrication performance of the circular- and flat-staved bearings and to reveal the influence mechanism, different numbers of staves from 8 to 30 were employed. As can be observed from Figure 7, with increasing numbers of staves, the load capacity of the circular-staved bearing decreases, while the contact load increases. This is because the grooves between adjacent staves break the continuity of the water film, and more staves means more grooves, thus causing a greater amount of destruction to the water film. Therefore, circular-staved bearings with smaller numbers of staves present a higher load capacity and a lower contact load.
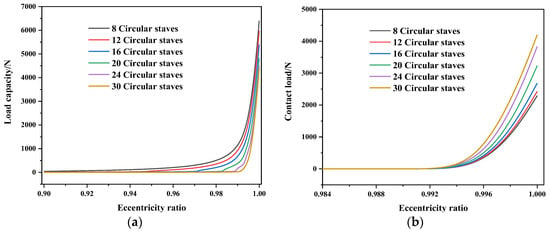
Figure 7.
Variations in (a) load capacity and (b) contact load of circular-staved bearings with eccentricity ratio at ω = 400 rpm.
Figure 8 shows the variation in load capacity and contact load for flat-staved bearings with eccentricity ratio under different numbers of staves, where it can be seen that in macro terms, for load capacity and contact load, different numbers of staves make little differences for flat-staved bearings, but on a small scale, differences are still evident. As illustrated in Figure 8a, the load capacity of a bearing with 30 flat staves is lower than the other five cases at first, but with increasing eccentricity ratio, this gradually surpasses the other five cases, becoming the highest among the cases in the present study at high eccentricity ratios. As has been mentioned above, the presence of grooves breaks the continuity of the water film; this phenomenon also occurs in flat-staved bearing, similar to the case of circular-staved bearings. However, it is different from the circular-staved bearing in that every flat stave along the circumferential direction provides a wedge gap that generates fluid pressure. There is a greater number of grooves with a greater number of staves, as well as more wedge gaps, which makes the fluid pressure a trade-off between water film damage from multiple grooves and the hydrodynamic effect of multiple wedge gaps, which provides the possibility of optimizing the number of staves in order to obtain better mixed-lubrication performance of flat-staved bearings.
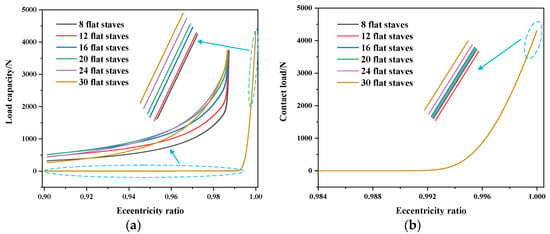
Figure 8.
Variations in (a) load capacity and (b) contact load of flat-staved bearings with eccentricity ratio at ω = 400 rpm.
3.3.2. Under Different Rotation Speeds
As shown in Figure 9 and Figure 10, with the increase in rotation speed, the load capacity rises, while the contact load decreases, for both the circular- and the flat-staved bearings. It can be seen in Figure 9 that under mixed-lubrication conditions, the bearing with fewer circular staves provides greater load capacity, and generates a lower contact load at ε = 0.995, indicating that it is able to achieve better mixed-lubrication performance, because of the presence of damage to the water film caused by the grooves.
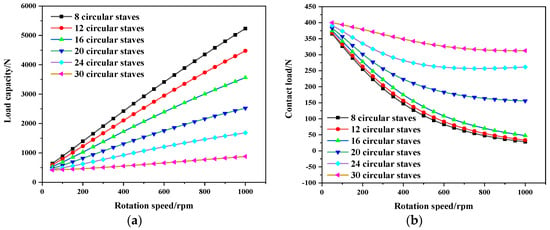
Figure 9.
Variations in (a) load capacity and (b) contact load of circular-staved bearings with rotation speed at ε = 0.995.
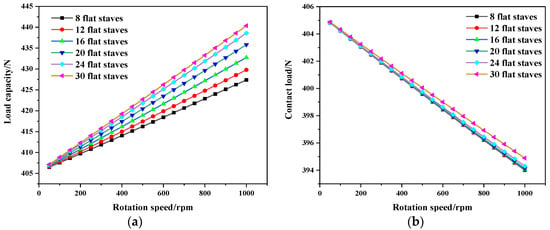
Figure 10.
Variations in (a) load capacity and (b) contact load of flat-staved bearings with rotation speed at ε = 0.995.
As can be observed in Figure 10, under mixed-lubrication conditions, among the investigated numbers of staves, bearings with a greater number of flat staves generate greater load capacity and contact load at ε = 0.995. As shown in Figure 10a,b, under mixed-lubrication conditions, the load capacity of the flat-staved bearing is mainly provided by the contact load, but with increasing rotation speed, the hydrodynamic effect improves, causing the contact load ratio in the load capacity to gradually decrease. Moreover, the higher the rotation speed, the better the load capacity performance presented by the bearing with 30 flat staves.
3.3.3. Mechanism of Action of the Number of Staves on Lubrication Performance
In this section, to explain the mechanism of action by which the number of staves affects the mixed-lubrication performance of staved bearings, the eccentricity ratio and rotation speed were set to 0.995 and 400 rpm, respectively. As shown in Figure 11, the number of staves has a significant effect on the fluid pressure distribution, with this effect mainly being a result of the grooves between adjacent staves, as well as the structure of the staves. The grooves divide the continuous bearing surface into multiple discontinuous parts, making the water film discontinuous, as shown in Figure 2; thus, the fluid pressure distribution becomes discontinuous. Additionally, as illustrated in Figure 11a, with the increase in the number of staves, the width and peak value of the fluid pressure decrease. This is because a greater number of staves means a greater number of grooves, greater discontinuity in the parts, and a narrower width of individual staves. Greater numbers of grooves result in more serious breaking of the water film, and narrower staves provide a smaller wedge gap, both of which weaken the hydrodynamics. This phenomenon also occurs in flat-staved bearings, but as shown in Figure 11b, every single stave in the flat-staved bearing provides an additional fluid pressure peak, with more fluid pressure peaks counteracting the lower main fluid pressure peak value and providing a greater hydrodynamic effect. In fact, these two kinds of stave are both able to generate extra fluid pressure peaks in the convergence region of the bearing, while in the divergence region, due to the difference between the structure of circular and flat staves, only flat staves are able to generate extra fluid pressure peaks. Meanwhile, the extra fluid pressure peaks generated by circular staves are very low compared to the main pressure peak, and thus have little effect on the fluid load, while that generated by the flat staves are obvious, and have a significant effect on the fluid load of the bearing. This causes flat-staved bearings with a greater number of staves to generate higher load capacities in the current cases, as shown by the results in Figure 8a and Figure 10a.
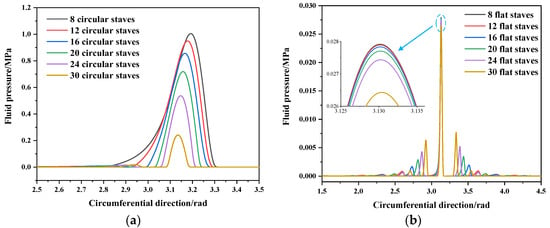
Figure 11.
Central fluid pressure distribution of (a) circular-staved bearing and (b) flat-staved bearing under different number of staves.
3.4. Optimization of Number of Staves in Flat-Staved Bearings
According to the mechanism analysis results above, there may be an optimal value for the number of staves to use in order to improve the lubrication performance of flat-staved bearings. To determine the optimal number of staves, the load capacity as well as the fluid load of flat-staved bearings with an additional set of different numbers of staves were compared under different eccentricity and rotation speeds. As can be observed from Figure 12a, the flat-staved bearing with 30 staves shows better carrying capacity than the other bearings at ε = 0.995. This is a result of the trade-off between the pressure breakdown caused by multiple grooves and the extra pressure peaks generated by the use of multiple flat staves. As shown in Figure 12b, the fluid load significantly decreases when the number of staves exceeds 30, and when the number of staves reaches 48, almost no fluid load is generated. Meanwhile, it is noteworthy that there is a crossing point between the curve with 24 flat staves and that with 30 flat staves, indicating that the optimal number of staves is highly dependent on the operation conditions. In addition, as can be observed from Figure 13, the flat-staved bearing with 30 flat staves presents better lubrication performance than the others at different rotation speeds, in particular at high rotation speeds. Moreover, consistent with Figure 12b, there is almost no fluid load generated with 48 flat staves at rotation speeds from 50 rpm to 1000 rpm compared with the other bearings. Hence, in the present case, 30 flat staves is the optimal number for maximizing the lubrication performance of flat-staved stern tube bearings lubricated with water.
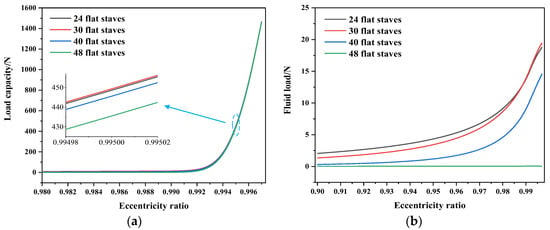
Figure 12.
Variations in (a) load capacity and (b) fluid load of flat-staved bearings with eccentricity ratio at ω = 400 rpm.
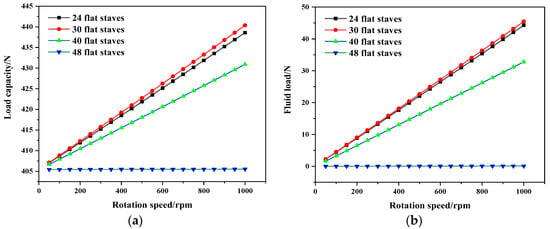
Figure 13.
Variations of (a) load capacity and (b) fluid load of flat-staved bearings with rotation speed at ε = 0.995.
4. Conclusions
In this paper, a numerical model was developed to investigate the mixed-lubrication performance of staved stern tube bearings lubricated with water, and the mixed-lubrication and asperity contact behaviors were obtained by solving the average Reynolds equation and the KE model. Compared with general bearings, the particularity of staved bearings lies in their discontinuous lubrication gap. The appropriateness and the accuracy of the established model were verified by comparing the results obtained with data from the published literature. Subsequently, the effect of the number of staves was compared for circular- and flat-staved bearings using the established model. The comparative results showed that the number of staves has a significant influence on the mixed-lubrication performance of staved bearings. In addition, the mechanism of action by which number of staves affects the lubrication performance of circular- and flat-staved bearings was revealed, and the optimal number of staves in order to maximize the lubrication performance of flat-staved bearings was obtained. The conclusions are listed as follows.
(1) For circular-staved bearings, a smaller number of staves provides a better hydrodynamic effect as well as improved load capacity.
(2) Additionally, there is an optimal value, which highly depends on the operation conditions, for the number of staves in order to improve the mixed-lubrication performance of flat-staved stern tube bearings lubricated with water. In the current simulation, the optimal value was 30.
Author Contributions
D.T.: conceptualization, methodology, validation, investigation, formal analysis, writing—original draft. Y.H.: conceptualization, methodology, investigation. L.Y.: investigation, formal analysis, modification, check. Y.C.: language, modification, checking. All authors have read and agreed to the published version of the manuscript.
Funding
The author(s) disclose receipt of the following financial support for the research, authorship, and/or publication of this article: National Natural Science Foundation of China (Nos. 51975064 and 52105052).
Data Availability Statement
The data that support the results of this study are available from the authors, upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| C | bearing clearance, mm |
| ε | eccentricity ratio |
| θ | circumferential direction |
| z | axial direction |
| ψ | attitude angle, rad |
| RJ1 | inner radius of the journal bearing, mm |
| L | journal bearing width, mm |
| hJ | lubrication gap of the journal bearing, μm |
| Nst | number of staves |
| hp | geometry clearance, mm |
| δJ | journal bearing elastic deform, μm |
| phJ | hydrodynamic pressure of the Journal bearing, MPa |
| ρ | density of the water, kg/m3 |
| η | viscosity of the water, Pa·s |
| σ | composite roughness, μm |
| ϕθ | flow factor in the circumferential direction |
| ϕr | flow factor in the radial direction |
| ϕs | shear factor |
| ϕc | contact factor |
| ω | rotational speed, rad/s |
| pc | contact pressure, MPa |
| β | asperity curvature |
| D | asperity density |
| EJ | elastic modulus of the journal bearing, GPa |
| Es | elastic modulus of the shaft, GPa |
| νJ | Poisson ratio of the journal bearing |
| νs | Poisson ratio of the shaft |
| γ | surface orientation |
References
- Xiang, G.; Han, Y.; He, T.; Wang, J.; Xiao, K. A Dynamic Wear Model for Micro-Grooved Water-Lubricated Bearings Under Transient Mixed Lubrication Condition. J. Tribol. 2020, 142, 7101. [Google Scholar] [CrossRef]
- Prajapati, D.K.; Ramkumar, P. Surface topography effect on tribological performance of water-lubricated journal bearing under mixed-EHL regime. Surf. Topogr. Metrol. Prop. 2022, 10, 45022. [Google Scholar] [CrossRef]
- He, T.; Zou, D.; Lu, X.; Guo, Y.; Wang, Z.; Li, W. Mixed-lubrication analysis of marine stern tube bearing considering bending deformation of stern shaft and cavitation. Tribol. Int. 2014, 73, 108–116. [Google Scholar] [CrossRef]
- Lv, F.; Rao, Z.; Ta, N.; Jiao, C. Mixed-lubrication analysis of thin polymer film overplayed metallic marine stern bearing considering wall slip and journal misalignment. Tribol. Int. 2017, 109, 390–397. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, h.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Tribol. Trans. ASME 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Yang, H.; Zhang, Y.; Lu, L. Numerical investigation of after stern tube bearing during ship turning maneuver. J. Mar. Sci. Technol. 2019, 25, 707–717. [Google Scholar] [CrossRef]
- Huang, Q.; Yan, X. Impact factors on lubricant performance of stern bearing with misalignment angle induced by transverse vibration of shaft. Ocean Eng. 2020, 216, 108051. [Google Scholar] [CrossRef]
- Rossopoulos, G.N.; Papadopoulos, C.I.; Leontopoulos, C. Tribological comparison of an optimum single and double slope design of the stern tube bearing, case study for a marine vessel. Tribol. Int. 2020, 150, 106343. [Google Scholar] [CrossRef]
- Xie, Z.; Zhu, W. Theoretical and experimental exploration on the micro asperity contact load ratios and lubrication regimes transition for water-lubricated stern tube bearing. Tribol. Int. 2021, 164, 107105. [Google Scholar] [CrossRef]
- Liu, Q.; Ouyang, W.; Cheng, Q.; Li, J.; Cheng, Q.; Li, R. Influences of bidirectional shaft inclination on lubrication and dynamic characteristics of the water-lubricated stern bearing. Mech. Syst. Signal Process. 2021, 169, 108623. [Google Scholar] [CrossRef]
- He, T.; Xie, Z.; Ke, Z.; Dai, L.; Liu, Y.; Ma, C.; Jiao, J. Theoretical Study on the Dynamic Characteristics of Marine Stern Bearing Considering Cavitation and Bending Deformation Effects of the Shaft. Lubricants 2022, 10, 242. [Google Scholar] [CrossRef]
- Zhu, J.; Wei, G.; Peng, Z.; Xia, Z.; Zheng, L.; Zhu., h. Analysis of underwater explosion shock on ship shaft stern bearing lubrication characteristics under different bearing working conditions. Int. J. Nav. Arch. Ocean Eng. 2022, 14, 100444. [Google Scholar] [CrossRef]
- Wodtke, M.; Litwin, W. Water-lubricated stern tube bearing - experimental and theoretical investigations of thermal effects. Tribol. Int. 2020, 153, 106608. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, C.; Tan, Z. A novel approach to investigate temperature field evolution of water lubricated stern bearings (WLSBs) under hydrodynamic lubrication. Adv. Mech. Eng. 2021, 13, 1–15. [Google Scholar] [CrossRef]
- Zhou, G.; Wu, K.; Pu, W.; Li, P.; Han, Y. Tribological modification of hydrogenated nitrile rubber nanocomposites for water-lubricated bearing of ship stern shaft. Wear 2022, 504, 204432. [Google Scholar] [CrossRef]
- Han, H.S.; Lee, K.H. Experimental verification of the mechanism on stick-slip nonlinear friction induced vibration and its evaluation method in water-lubricated stern tube bearing. Ocean Eng. 2019, 182, 147–161. [Google Scholar] [CrossRef]
- Lin, C.-G.; Zou, M.-S.; Sima, C.; Liu, S.-X.; Jiang, L.-W. Friction-induced vibration and noise of marine stern tube bearings considering perturbations of the stochastic rough surface. Tribol. Int. 2018, 131, 661–671. [Google Scholar] [CrossRef]
- Hongling, Q.; Chang, Y.; Hefa, Z.; Xufei, L.; Zhixiong, L.; Xiang, X. Experimental analysis on friction-induced vibration of water-lubricated bearings in a submarine propulsion system. Ocean Eng. 2020, 203, 107239. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, Z.; Zhou, X. Theoretical, numerical, and experimental studies on friction vibration of marine water-lubricated bearing coupled with lateral vibration. J. Mar. Sci. Technol. 2019, 25, 298–311. [Google Scholar] [CrossRef]
- Jin, Y.; Deng, T.; Liu, Z.; Zhou, J. Research on the influence of the normal vibration on the friction-induced vibration of the water-lubricated stern bearing. J. Vibroengineering 2020, 22, 762–772. [Google Scholar] [CrossRef]
- Lin, C.-G.; Zou, M.-S.; Zhang, H.C.; Qi, L.-B.; Liu, S.-X. Influence of different parameters on nonlinear friction-induced vibration characteristics of water lubricated stern bearings. Int. J. Nav. Arch. Ocean Eng. 2021, 13, 746–757. [Google Scholar] [CrossRef]
- Ning, C.; Hu, F.; Ouyang, W.; Yan, X.; Xu, D. Wear monitoring method of water-lubricated polymer thrust bearing based on ultrasonic reflection coefficient amplitude spectrum. Friction 2022, 11, 685–703. [Google Scholar] [CrossRef]
- Ouyang, W.; Liu, Q.; Xiao, J.; Huang, J.; Zhang, Z.; Wang, L. Experimental study on the distributed lubrication characteristics of full-size water-lubricated stern bearings under hull deformation. Ocean Eng. 2023, 267, 113226. [Google Scholar] [CrossRef]
- Cai, J.; Han, Y.; Xiang, G.; Wang, J.; Wang, L. Effects of wear and shaft-shape error defects on the tribo-dynamic response of water-lubricated bearings under propeller disturbance. Phys. Fluids 2022, 34, 077118. [Google Scholar] [CrossRef]
- Cai, J.; Han, Y.; Xiang, G.; Wang, C.; Wang, L.; Chen, S. Influence of the mass conservation cavitation boundary on the tribo-dynamic responses of the micro-groove water-lubricated bearing. Surf. Topogr. Metrol. Prop. 2022, 10, 045011. [Google Scholar] [CrossRef]
- Cai, J.; Xiang, G.; Li, S.; Guo, J.; Wang, J.; Chen, S.; Yang, T. Mathematical modeling for nonlinear dynamic mixed friction behaviors of novel coupled bearing lubricated with low-viscosity fluid. Phys. Fluids 2022, 34, 093612. [Google Scholar] [CrossRef]
- Xiang, G.; Yang, T.; Guo, J.; Wang, J.; Liu, B.; Chen, S. Optimization transient wear and contact performances of water-lubricated bearings under fluid-solid-thermal coupling condition using profile modification. Wear 2022, 502–503, 204379. [Google Scholar] [CrossRef]
- Chen, S.; Xiang, G.; Fillon, M.; Guo, J.; Wang, J.; Cai, J. On the tribo-dynamic behaviors during start-up of water lubricated bearing considering imperfect journal. Tribol. Int. 2022, 174, 107685. [Google Scholar] [CrossRef]
- Serdjuchenko, A.; Ursolov, A.; Batrak, Y. Asymptotic estimation of the fluid film pressure in non-metallic water-lubricated staved stern tube bearings. Tribol. Int. 2022, 175, 107798. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Finite Element Based Elastic-Plastic Model for the Contact of Rough Surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A Static Friction Model for Elastic-Plastic Contacting Rough Surfaces. J. Tribol. 2004, 126, 34–40. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M. An engineering approach for the prediction of wear in mixed lubricated contacts. Wear 2013, 308, 121–131. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).