Study on the Effect of Oil Supply on the Sound Field Characteristics of Full Ceramic Ball Bearings under Oil Lubrication

Abstract

To study the full sound field distribution characteristics of full ceramic ball bearings, reduce the radiation noise of the bearings, and improve their service performance. In this paper, the sound field distribution characteristics of 6206 silicon nitride ceramic deep groove ball bearings are studied under different oil supplies. A mathematical model of the sound field distribution of full ceramic ball bearings under oil lubrication is established, and the validity of the model is verified by experimental data. The bearing cavity simulation model of the full ceramic ball bearing is established, and the influence of oil supply on the operation characteristics of the full ceramic ball bearing is studied. Through theoretical and experimental research, the circular distribution law of the noise signal of ceramic ball bearings under different oil supplies is revealed. It is found that there is an optimal fuel supply when the speed and load are constant. Under optimal oil supply lubrication conditions, the full ceramic ball bearing has the minimum radiation noise, and the bearing exhibits optimal lubrication state, vibration and temperature rise characteristics. The new contribution of this paper: with the increase in oil supply, the sound pressure level of radiation noise of full ceramic ball bearings decreases and then increases. The research results reveal the radiation noise mechanism of full ceramic ball bearings, which is of great significance for enriching its theory and method.

1. Introduction

To study the influence of oil supply on the sound field distribution characteristics of full ceramic ball bearings under different working conditions. The oil supply required for the full ceramic ball bearing to generate the minimum radiation noise is obtained, which reduces the radiation noise and improves its service performance. With the progress of science and technology, the use environment and conditions of ball bearings are more and more demanding, such as high speed, high temperature, corrosion resistance, strong magnetism, oil-free lubrication, etc. [1,2]. As a new high-end product, full ceramic ball bearings have the advantages of large stiffness, good thermal stability, corrosion and wear resistance, high operation accuracy and long service life [3,4,5]. With the increasingly harsh operating conditions of bearings, the friction and impact between internal components of full ceramic ball bearings intensify, and the problem of radiated noise is gradually highlighted. Radiated noise has a large impact on the sound quality of bearings, limiting the development of equipment in the high speed and quiet direction [6]. Bearing lubrication effect has an important impact on the running performance and service life of bearings. Good lubrication can reduce friction and improve bearing performance. Different lubrication states will also produce different sound field characteristics of bearings [7,8]. Among them, the oil supply for bearings directly determines the lubrication state of the bearing, thus affecting the bearing acoustic characteristics. Therefore, it is of great significance to study the influence of oil supply on the sound field characteristics of full ceramic ball bearings and to explore the oil supply required to produce minimum radiated noise [9,10].

In recent years, experts and scholars at home and abroad have conducted a lot of research on the sound field and radiated noise characteristics of ball bearings. Yan Haipeng studied the radiated noise characteristics of a high-speed ceramic ball bearing motorized spindle. Through grinding tests on the spindle, it was found that speed is one of the main factors affecting the radiated noise of full ceramic ball bearings [11,12]. From the perspective of fault analysis of double-row tapered roller bearings, Li Defa conducted a mechanism study between the bearing state and acoustic emission signal through theoretical analysis and test comparison, which provided theoretical support for the application of acoustic emission perception in bearing state detection [13]. Xiong Shi analyzed the relationship between the sound pressure and acoustic power of the shaft-hull coupling structure under different bearing stiffness [14]. Zhang Qitao established a mathematical model for calculating the center motion trajectory of the rolling body of deep groove ball bearings and analyzed the influence of rotation speed and radial load on the noise size at a fixed point, as well as the change law of noise along the axis direction of the rolling bearing, combined with the acoustic theory and specific examples [15]. Under the condition of low speed and heavy load, Wang Jiaxu studied the influence of different friction coefficients, loads and rotation speeds on the transient characteristics of water-lubricated bearings using a finite element model, determined the vibration frequency and effective value of vibration acceleration of the bearings, and carried out experimental verification. This provides a theoretical basis for studying the vibration and noise mechanism of water-lubricated bearings [16]. Peng Liqiang considered the oil supply at the lubricating oil inlet as a variable parameter and solved the mathematical model with the finite difference method to analyze the influence of the oil supply on the static lubrication characteristics of the inner and outer oil film of floating ring bearings [17]. Nam Jaehyeon measured the vibration and sound pressure of the contact surfaces under two lubrication conditions, the change in friction coefficients, and analyzed the frictional noise mechanism of the lubricant under clean or polluted surfaces [18]. Zhang Qitao established a noise calculation model for deep groove ball bearings. The effect of the number of ripples, the ripple amplitude, the bearing speed, the bearing load, and the ball size error on the noise of the fixed measuring point bearings was studied through numerical calculations [19]. Jahagirdar studied the effect of noise on the statistical moment of a bearing vibration signal. The distribution function of the inner, outer, and sphere defects was tested using K-S tests. The change in noise level and its effect on the statistical moment were verified [20]. Botha established a sound radiation model for bearing related research objects, analyzed the characteristics of noise sources, and determined the location and mechanism of the main noise sources for fault detection [21].

The mechanism of bearing vibration is very complex, and the vibration characteristics of ball bearings directly affect the accuracy and radiation noise. P. K. Gupta [22] studied the vibration characteristics in rolling bearings, defining two characteristic intrinsic frequencies. They are the elastic boundary contact frequency and the bearing motion frequency, and their existence is verified by computer analysis simulations and available experimental data. Lynagh N. [23] presented a detailed model of bearing vibration, including the effect of contact spring non-linearity in balls-to-raceways contacts. This model was successfully employed for the recognition of complex real-time vibration spectra of a precision routing spindle obtained by accurate non-contact sensors. Based on the hydrodynamic lubrication model, contact force model, and wear prediction model, R.B. Randall [24] simulated the vibration signal generated by the relative motion between the journal and the bearing. D. Abbound [25] compared the application of the the minimum entropy deconvolution (MED)and the spectral kurtosis (SK) method and the cyclostationary method in actual rolling bearing vibration signal fault detection. It is found that, in most cases, both methods can detect bearing faults.

As can be seen from the research results in recent years, most studies on the radiated noise of ball bearings take the noise as the judgment basis for bearing fault analysis [26,27,28] or consider it as a whole sound source and calculate it based on experimental and finite element methods. The sound field model of ball bearings and the mechanism of sound field distribution are not established. However, there is little research on the influence of full ceramic ball bearing lubrication on sound field characteristics.

Therefore, this paper takes the silicon nitride full ceramic ball bearing as the research object, aiming at the problems of radiated noise generated by bearings when running at high speed. Based on the radiation noise mechanism, the full sound field distribution characteristics of full ceramic ball bearings are discussed. The influence of oil supply on the sound field distribution characteristics of full ceramic ball bearings under different working conditions is investigated. By establishing the simulation model of the bearing cavity of the full ceramic ball bearing, the influence of different oil supplies on the oil phase distribution in the bearing cavity, temperature rise, and vibration acceleration of the bearing is obtained. Based on the mathematical model of sound field characteristics, the influence of oil supply on the sound field characteristics of full ceramic ball bearings is analyzed by combining the simulation results and test data. The research results can provide theoretical support and experimental reference for the analysis of the sound field characteristics and noise signal transmission mechanism of full ceramic ball bearings.

2. Mathematical Model of Sound Field Characteristics of Full Ceramic Ball Bearings

2.1. Contact Analysis between Ceramic Balls and Bearing Rings

In general, the bearing inner ring rotates with the shaft. The outer ring is assembled on the bearing housing and does not rotate with the rotation of the inner ring, but it can still produce vibration. The noise mainly comes from the friction and impact vibration caused by interaction between components during its operation. In order to study the contact vibration characteristics of the ceramic ball and ring, the contact between the ball and the inner ring and the outer ring of the ball bearing can be regarded as a point-to-surface contact. In addition, the lubrication problem of the ball/outer ring tribology system can be regarded as a point contact elastohydrodynamic lubrication problem plane when the ball bearing’s contact with the micro area is taken as the research object.

The Hertz point contact elasticity theory studies the local stress and strain distribution of two smooth ellipsoids after contact under pressure [29].

According to the Hertz point contact elasticity theory, the contact force Q is:

$$Q=K{\delta }^{3/2}$$

(1)

where δ is the contact deformation, K is the contact stiffness, and the calculation formula is as follows:

$$\begin{array}{l}K=\frac{1}{3}{E}^{\prime }{\left(\Sigma \rho \right)}^{\frac{1}{2}}{\left(\frac{2}{{\delta }^{\ast }}\right)}^{\frac{3}{2}}\\ {\delta }^{\ast }=\frac{2F}{\pi }{\left(\frac{\pi }{2{\kappa }^{2}E}\right)}^{\frac{1}{3}}\end{array}$$

(2)

where E′ represents the elastic modulus parameter, κ represents the eccentricity parameter of the ellipse, and E and F are the first and second types of complete ellipse integral, respectively. Therefore, the contact force and the length of the long radius and short radius of the ellipse in the contact area can be found by calculating the contact deformation.

When analyzing the contact deformation between the ceramic balls and rings, the surface elastic deformation should be considered. According to the elastic theory, the elastic displacement of each point in the vertical direction can be deduced as [30]:

$$\begin{array}{l}v(x)=-\frac{2}{\pi E}{\displaystyle {\int }_{s_1}^{s_2}p(s)\ln {(s-x)}^2}ds+c\\ \frac{1}{E}=\frac{1}{2}(\frac{1-v_e{}^2}{E_e}+\frac{1-v_r{}^2}{E_r})\end{array}$$

(3)

where v(x) is the elastic displacement in the vertical direction. For the elastohydrodynamic lubrication (EHL) problem, p(s) is the fluid pressure distribution; s is the additional coordinate on the x-axis, representing the distance between p(s) and the origin of the coordinate; s₁ and s₂ are the starting point and ending point of the load, respectively; c is an undetermined constant, which can usually be incorporated into h₀; E is the equivalent elastic modulus; E_e is the elastic modulus of the outer raceway; E_r is the elastic modulus of ball bearings; v_e is the Poisson’s ratio of the outer raceway; and v_r is the Poisson’s ratio of ball bearings.

2.2. Vibration Differential Equations of Ceramic Balls

As the key component of a full ceramic ball bearing, the ceramic ball has contact force with the cage, inner ring and outer ring, so the stress of ceramic balls is complicated. Especially when considering the influence of the ceramic ball’s diameter error on the operating state of the bearings, the interaction between ceramic balls and rings with larger ball diameters and smaller ball diameters is more complicated [31].

In this paper, it is assumed that the cage pocket holes are uniformly distributed along the circumference of the cage, and there is no other dimensional error.

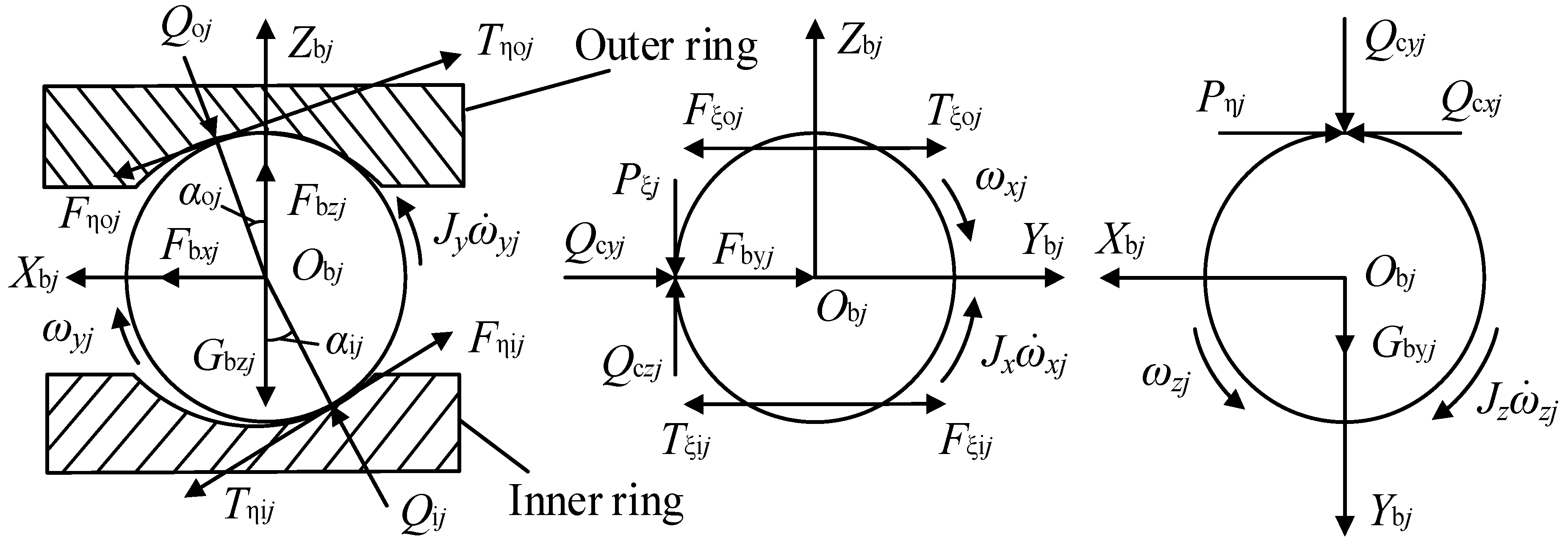
Figure 1 shows the acting force on the ceramic ball when the full ceramic ball bearing runs at high speed. α_ij and α_oj represent the contact angle between the ceramic ball and the inner and outer orbits, respectively. Q_ij and Q_oj represent the normal contact force between the ceramic ball and the inner and outer orbit, respectively. T_ηij, T_ηoj, T_ξij and T_ξoj represent the traction force between the ceramic ball and the contact surface of the inner and outer orbit. Q_cxj and Q_cyj represent the components of the impact force occurring between the ceramic ball and the cage along the coordinate direction. G_byj and G_bzj represent the gravity component of the ceramic ball along the coordinate direction. P_ηj and P_ξj indicate the friction force acting on the surface of the ceramic ball, including rolling friction force and sliding friction force. F_bxj, F_byj and F_bzj represent the hydrodynamic viscous resistance component acting on the ceramic ball. F_ηij, F_ηoj, F_ξij and F_ξoj represent the rolling friction force between the ceramic ball and the inner and outer raceway. J_x, J_y and J_z represent the component of inertia of the ceramic ball rotating about its own center. ω_xj, ω_yj and ω_zj represent the angular velocity of the ceramic ball in its coordinate system along the respective coordinate direction and represent the angular acceleration of the ceramic ball in its coordinate system along their respective coordinate directions [32].

Where D_W is the diameter of the ceramic ball; m_b is the mass of the ceramic ball; ${\ddot{x}}_{\mathrm{b}j}$, ${\ddot{y}}_{\mathrm{b}j}$ and ${\ddot{z}}_{\mathrm{b}j}$ represent the Jth ceramic ball in the coordinate system {O, X, Y, Z}; ω_bxj, ω_byj and ω_bzj represent the angular velocity of the ceramic ball in the coordinate system {O, X, Y, Z}; ${\dot{\omega }}_{\mathrm{b}xj}$, ${\dot{\omega }}_{\mathrm{b}yj}$ and ${\dot{\omega }}_{\mathrm{b}zj}$ represent the angular acceleration of the ceramic ball in the coordinate system {O, X, Y, Z}; ${\dot{\theta }}_{\mathrm{b}j}$ represents the orbital velocity of the ceramic ball in the coordinate system {O, X, Y, Z}; and I_b is the moment of inertia of the ball in the coordinate system {O, X, Y, Z}.

The vibration differential equation of the ceramic ball can be described as:

$$\begin{array}{l}{F}_{\mathrm{b}yj}-F_{\xi \mathrm{o}j}+T_{\xi \mathrm{o}j}+G_{\mathrm{b}yj}+Q_{\mathrm{c}yj}-F_{Dj}=m_{\mathrm{b}}{\ddot{y}}_{\mathrm{b}j}\\ F_{\mathrm{b}zj}-F_{\eta \mathrm{o}j}\sin {\alpha }_{\mathrm{o}j}+T_{\mathsf{\eta }\mathrm{o}j}\sin {\alpha }_{\mathrm{o}j}-Q_{\mathrm{o}j}\cos {\alpha }_{\mathrm{o}j}-G_{\mathrm{b}zj}+Q\\ (T_{\eta \mathrm{o}j}-F_{\eta \mathrm{o}j})\frac{D_{\mathrm{W}}}{2}-M_{gyj}-J_y{\dot{\omega }}_{yj}=I_{\mathrm{b}}{\dot{\omega }}_{\mathrm{b}yj}+I_{\mathrm{b}}{\omega }_{\mathrm{b}zj}{\dot{\theta }}_{\mathrm{b}j}\\ [(T_{\xi \mathrm{o}j}-F_{\xi \mathrm{o}j})\sin {\alpha }_{\mathrm{o}j}-P_{\eta j}]\frac{D_{\mathrm{W}}}{2}+M_{gzj}-J_z{\dot{\omega }}_{zj}=I_{\mathrm{b}}{\dot{\omega }}_{\mathrm{b}zj}+I_{\mathrm{b}}{\omega }_{\mathrm{b}yj}{\dot{\theta }}_{\mathrm{b}j}\end{array}$$

(4)

2.3. Properties of Lubricating Oil Properties

Good lubrication plays a crucial role in the operating condition of the bearing. If there is not enough lubrication, dry friction or boundary friction will occur between the ceramic balls and the raceway, causing friction and wear and producing more noise and even various failures. The total amount of oil supplied for full ceramic ball bearings during operation is:

$$q_m={\displaystyle \sum _{j=1}^N{q}_{\mathrm{i}j}}+{\displaystyle \sum _{j=1}^N{q}_{\mathrm{o}j}}$$

(5)

where N represents the number of ceramic balls, and q_ij and q_oj represent the oil supply required by the ceramic ball in the contact area with the inner and outer ring, respectively. If q_j represents the oil supply required for the ceramic ball in the contact area with the inner or outer ring, then:

$$q_j={\rho }_m{h}_c{\mu }_m$$

(6)

where ρ_m represents the lubricating oil density in the contact area; μ_m represents the average speed of the contact surface, that is, the equivalent speed; and h_c represents the thickness of the oil film in the contact area. Based on the results of Hamrock–Dowson [33], the lubricating oil film thickness can be calculated by the following formula:

$$h_c=2.69R_x{U}^{0.67}{G}^{0.53}{W}^{-0.067}\left(1-0.61e^{-0.73}\right)$$

(7)

where $U={\eta }_0{\mu }_m/E^{\prime }{R}_x$ represents the dimensionless velocity; η₀ represents the lubricant viscosity at 20 °C under the standard atmospheric pressure; $R_x=D_{\mathrm{W}}\left(1\mp {\gamma }_{\mathrm{b}}\right)/2$ represents the equivalent radius of curvature, where the negative sign is used to calculate the equivalent radius of curvature of the inner ring and the positive sign is used to calculate the equivalent radius of curvature of the outer ring; $G=E^{\prime }{c}_{\eta }$ represents the dimensionless elastic modulus; c_η represents the viscosity pressure coefficient; $W=Q/E^{\prime }{R}_x^2$ represents the dimensionless load; and Q represents the contact load.

The most important factors affecting the viscosity of the lubricating oil are the pressure and temperature of the lubricating oil. The relationship between the lubricating oil viscosity and the lubricating oil temperature and pressure is [34]:

$$\eta ={\eta }_0\exp \left\{(\ln {\eta }_0+9.67)\times \left[{(1+5.1\times {10}^{-9}p)}^{0.68}{\left(\frac{T_1-138}{T_0-138}\right)}^{-1.1}-1\right]\right\}$$

(8)

where η₀ is the initial viscosity of the lubricating oil, T₀ is the ambient temperature, and T₁ is the actual temperature of the oil film.

2.4. Establishment of Sound Field Points of the Full Ceramic Ball Bearing

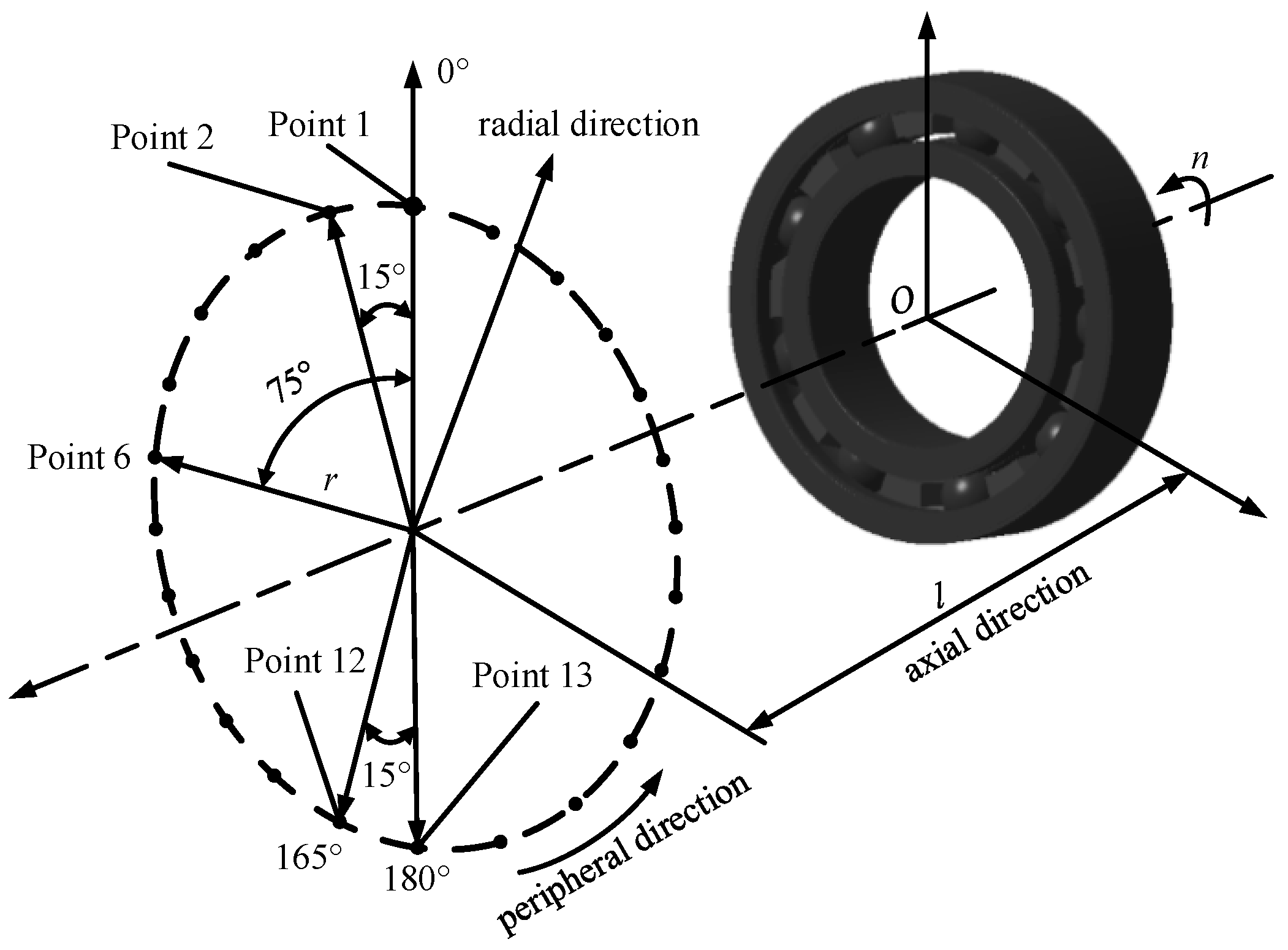
In order to facilitate the analysis of the sound field distribution characteristics of the full ceramic ball bearing, 24 field points are selected in the circumferential direction to calculate the radiated noise, as shown in Figure 2. All field points are evenly distributed in the same plane, the distance from the plane to the bearing plane is 50 mm, and the distance from each field point to the bearing axis is 210 mm. Therefore, the radial distance of each field point is 210 mm, the axial distance is 50 mm, and the angle between two adjacent field points is 15°. Here, the first field point is placed in the 12 o’clock direction and defined as 0° position angle or field point 1. The remaining field points are numbered counterclockwise.

2.5. Characterization of the Sound Field

2.5.1. Sound Pressure Level of the Sound Field

In general, the sound pressure level is the main index used to evaluate and analyze sound radiation. When analyzing the radiated noise of a certain point in the sound field of full ceramic ball bearings, the effective value of sound pressure is generally used for analysis. The effective sound pressure level can be calculated by:

$$p_e=\sqrt{\frac{1}{T}{\displaystyle {\int }_0^T{p}^{2}dt}}$$

(9)

where p_e represents the effective sound pressure level value, T represents sampling time, and p represents instantaneous sound pressure.

Therefore, the effective SPL at the analyzed field point can be obtained by Equation (2):

$$L=20\lg \frac{p_e}{p_{ref}}$$

(10)

where p_ref refers to the reference sound pressure. In this paper, the reference sound pressure value is 2 × 10⁻⁵ Pa.

2.5.2. Directivity of the Sound Field

The sound field directivity of radiated noise is also an important index for evaluating the sound field performance and noise environment. In order to further analyze the sound field distribution characteristics of full ceramic ball bearings, the directivity of the sound field is used to characterize the distribution law of the sound field. At different positions of the sound field, there will be different SPLs (sound pressure levels). Even if the field point is the same distance from the sound source, SPLs of different field points will still be different, which indicates that the sound source has directivity and can also be expressed by the directivity of the sound field. Directional angle and directional level can be used to describe the directivity of the sound field [35]. Directional angle and directional level are called directivity parameters of the sound field, and they can be defined as:

$$DA={\theta }_{\mathrm{SPL}}(n,r,l)$$

(11)

$$DL=\frac{SP{L}_{\max }(n,r,l)}{SP{L}_{\mathrm{ave}}(n,r,l)}$$

(12)

where SPL_max represents the maximum pressure level in the whole circumferential direction of a given radial distance r or represents the maximum pressure level in the angle range of a certain position at a given bearing speed n, radial distance r, and axial distance l. SPL_ave represents the average sound pressure level over the entire circumference of a given radial distance r. θ_SPL represents the angle of position where the maximum sound pressure level occurs. In the circumferential direction, the field point with the greatest radiated noise is also called the sensitive field point. Therefore, the direction of the position angle where the sensitive field point is located is the directional direction of the sound field.

2.6. Calculation Process

The numerical calculation process of this paper is shown in Figure 3.

3. Simulation Analysis of the Influence of Oil Supply on Radiated Noise of the Full Ceramic Ball Bearing

3.1. Simulation Analysis of the Influence of Oil Supply on the Circumferential Sound Field Distribution of the Full Ceramic Ball Bearing

In order to analyze the influence of the lubrication state on the radiated noise of full ceramic ball bearings, taking the oil supply as the lubrication index, the influence of different oil supplies on the radiated noise distribution of full ceramic ball bearings is discussed. In the circumferential direction with a radius of 210 mm, 24 uniformly distributed field points are selected for analysis. The included angle between two adjacent field points is 15°, and the distance between each field point and the bearing plane is 50 mm. The bearing speed is set at 18,000 r/min and 24,000 r/min for calculation. The preload is set as 350 N, and the radiated noise of the full ceramic ball bearing is calculated when the oil supply is 0.010 mL/min, 0.015 mL/min, 0.020 mL/min, 0.025 mL/min, 0.030 mL/min and 0.035 mL/min respectively [36,37]. After calculation, the radial noise distribution in the circumferential direction of the full ceramic ball bearing with different oil supplies is shown in Figure 4.

It can be found that under different oil supplies, the radiated noise of the full ceramic ball bearing presents uneven distribution in the circumferential direction and shows an obvious direction of the sound field. With the increase in oil supply, the radiated noise decreases first and then increases. It can also be seen from the figure that at different speeds, the amount of oil supply required for small radiated noise is different. When the speed is 18,000 r/min, there is a relatively small SPL at the oil supply of 0.020 mL/min, while when the speed is 24,000 r/min, there is a relatively small SPL at the oil supply of 0.030 mL/min.

3.2. Simulation Analysis of the Influence of Oil Supply on the Characterization of Different Regions of the Sound Field of Full Ceramic Ball Bearings

In the range of 15~75° of the upper left semicircle, because of the small contact force between the ceramic balls and the ring, the impact effect of the bearing ceramic balls, the ring and the cage will produce a large impact noise, so this area will produce a large radiated noise and is called the impact load zone. In the range of 195~255° of the lower right semicircle, due to the large contact force between the ceramic balls and the ring, the violent interaction between the ceramic balls and the bearing inner and outer ring produces a large friction noise [38,39], so this area will also produce a relatively large radiation noise and is called the friction load zone. Other regions are called stationary load zone because of the relatively small friction and impact and relatively stable radiation noise changes.

It can be seen from Figure 5 that the radiated noise in the friction load zone is higher than that in the impact load zone, and their variation trends are similar to the increase in oil supply. When the rotational speed is 18,000 r/min, the variation trend first decreases and then increases. When the rotational speed is 24,000 r/min, the SPL decreases with the increase in oil supply. Furthermore, when the oil supply is large, the amplitude of SPL increase tends to decrease.

In order to improve the analysis of how oil supply affects the directivity of the sound field, the variation trend of the directional level of the sound field in the impact load zone and friction load zone with the oil supply at different rotational speeds is simulated and calculated.

As can be seen from Figure 6, when the rotational speed is 18,000 r/min, the directional level of the impact load zone gradually decreases with the increase in the oil supply, while the directional level of the friction load zone firstly decreases and then increases. When the rotational speed is 24,000 r/min, it is the opposite. With the increase in oil supply, it can be found that the radiated noise of the full ceramic ball bearing has different directional levels in different zones.

Based on the above analysis, under the preload of 350 N applied to the bearing, when the rotational speed is 18,000 r/min, the oil supply required for the bearing to produce the minimum radiation noise is 0.020 mL/min. When the rotational speed is 24,000 r/min, the oil supply required for the bearing to produce the minimum radiation noise is 0.030 mL/min. With the increase in rotational speed, the oil supply of the full ceramic ball bearing when the minimum radiation noise is generated also increases.

4. Simulation Analysis of the Influence of Oil Supply on the Operation Characteristics of the Full Ceramic Ball Bearing

4.1. Geometric Modeling and Meshing

In this paper, the 6206 silicon nitride ceramic ball bearing is taken as the research object. The solid model of the 6206 deep groove ball bearing is drawn using three-dimensional modeling software, including the rolling element, bearing inner and outer ring, and cage, and then the patrs are assembled. Figure 7 shows the bearing model.

The bearing model is imported into the pre-processing software, and the fluid domain of the bearing is extracted. The research focus of this paper is the fluid domain part of the bearing, so the solid domain part of the bearing is suppressed, only the fluid domain part of the bearing is retained, and two inlets are added. The inlets are located above and below the end face of the model, the diameter is 2 mm, and the outlet is located at the other end face of the model. The bearing cavity model is meshed. Figure 8 is the bearing cavity grid. The number of elements in the overall calculation domain is 1,300,381, the number of nodes is 260,735, and the minimum mass of the grid is greater than 0.2, which meets the calculation requirements.

4.2. Boundary Condition Setting

The bearing cavity grid model is imported into Fluent for simulation analysis. The simulation parameters are set as follows:

(1) The lubricating inlet is set to speed inlet, and the inlet speed is set. The outlet is set to the pressure outlet, and the value is standard atmospheric pressure.

(2) The outer ring of the bearing is set as a stationary wall surface, and the surfaces in contact with the inlet and outlet areas are also set as stationary wall surfaces. Considering the revolution motion of the rolling element and the cage, the inner ring, the rolling element and the cage are set as the rotating wall surface, ignoring the spin motion of the rolling element, and the cage speed is the same as the rolling element.

(3) The heat flux at the corresponding speed is loaded on the inner and outer rings and balls.

(4) The VOF model [40] is used to solve the flow state of the oil and gas phases. Air is the main phase, and lubricating oil is the secondary phase. In the VOF method, the volume fraction α is used to mark the volume fraction of the oil phase. Then, α = 0 represents an oil-free unit, and α = 1 represents an oil-filled unit. If 0 < α < 1, it represents the interface between the oil phase and the gas phase.

4.3. Simulation Analysis of the Influence of Oil Supply on the Lubrication Characteristics of Full Ceramic Ball Bearings

When the bearing runs at high speed, the lubricant distribution and content of the key lubrication areas near the contact area, cage pocket hole, and rolling element surface are vital to the overall lubrication of the bearing and its operational reliability.

Figure 9 shows the distribution of oil volume fraction on the circumference under different oil supplies when the rotational speed is 24,000 r/min. In the bearing cavity, the lubricating oil is subjected to centrifugal force for radial movement and also circumferential movement by the influence of the cage and inner ring. The high-speed spin balls make the lubricating oil distribute in the contact area near the ball. The distributing oil is not uniformly distributed in the circumferential direction, and the content varies with the azimuth angle.

The average oil volume fraction inside the bearing under different oil supplies is shown in Figure 10. Figure 11a,b, respectively, show the oil volume fraction distribution inside the full ceramic ball bearing under the conditions of a rotation speed of 18,000 r/min and oil supply of 0.020 mL/min, and a rotation speed of 24,000 r/min and oil supply of 0.030 mL/min. The results show that with the increase in oil supply, the average oil volume fraction increases first and then decreases. When the bearing oil supply is small, the bearing cavity is in a starved state, and the oil film thickness of the two-phase flow is thin and incomplete, which is not conducive to bearing lubrication and heat transfer. When the oil supply increases, the oil film thickness of the two-phase flow increases and becomes more complete, enhancing the lubrication performance and decreasing the bearing temperature. When the oil supply increases to a certain amount, the oil film thickness of the two-phase flow reaches the maximum, and the bearing is in the best lubrication state. As the oil supply continues to increase, the oil film thickness decreases and gradually becomes incomplete. This is because the excess lubricating oil inside the bearing will cause churning and heat generation, resulting in a sharp rise in the bearing temperature and a decrease in the lubricating oil viscosity, thus thinning the oil film.

Figure 12 shows the influence of different oil supplies on the temperature rise of the outer ring of the full ceramic ball bearing at the rotational speed (18,000 r/min and 24,000 r/min). Figure 13a,b, respectively, show the oil phase distribution in the full ceramic ball bearing under the conditions of a rotation speed of 18,000 r/min and oil supply of 0.020 mL/min, and a rotation speed of 24,000 r/min and oil supply of 0.030 mL/min. With the increase in oil supply, the temperature rise decreases first and then increases. Each speed has a minimum oil supply, and the temperature rise increases with the increase in speed.

Figure 14 shows the influence of different oil supplies on the vibration acceleration of the outer ring of the full ceramic ball bearing at the rotational speed of 18,000 r/min and 24,000 r/min. The vibration acceleration decreases as the oil supply increases, and there is an optimum oil supply that minimizes the vibration acceleration. In addition, the vibration acceleration increases with the increase in speed. When the oil supply is low and the oil film thickness is low, little oil is introduced into the contact area of the rollers and raceways, which leads to oil pressure fluctuations and high bearing vibration. As the oil supply increases, the amount of oil in the bearing cavity increases, creating a thick oil film that helps reduce vibration.

5. Experimental Analysis of the Influence of Oil Supply on the Sound Field Distribution of the Full Ceramic Ball Bearing

5.1. Experimental Scheme and Method

According to the analysis of the simulation results, we set the working conditions in the experiment as the preload adjusted to 350 N and two set rotational speeds. Six groups of radiated noise tests with different oil supplies are carried out. During the test, the settings of other parameters are the same as during the simulation calculation.

The influence of the oil supply on the vibration and noise characteristics of the full ceramic ball bearing under oil lubrication conditions is tested by using the upgraded rolling bearing lubrication vibration test platform. The test device and the test process are shown in Figure 15.

The full ceramic ball bearing in this test is a P4 ultra-precision ball bearing. The type is a 6206 deep groove ball bearing. The material of the bearing inner and outer ring and balls is silicon nitride ceramic. The material of the cage is PVX. Its structural parameters are shown in

Table 1. Structural parameters of the test bearing.

Parameter Name/Unit	Bearing Data
Bearing bore diameter/mm	30
Bearing outside diameter/mm	62
Bearing width/mm	16
Amount of balls	9
Elastic modulus of silicon nitride material/GPa	300
Poisson’s ratio of silicon nitride material	0.27

.

5.2. Analysis of Test Results of the Influence of Oil Supply on the Circumferential Sound Field Distribution of Full Ceramic Ball Bearings

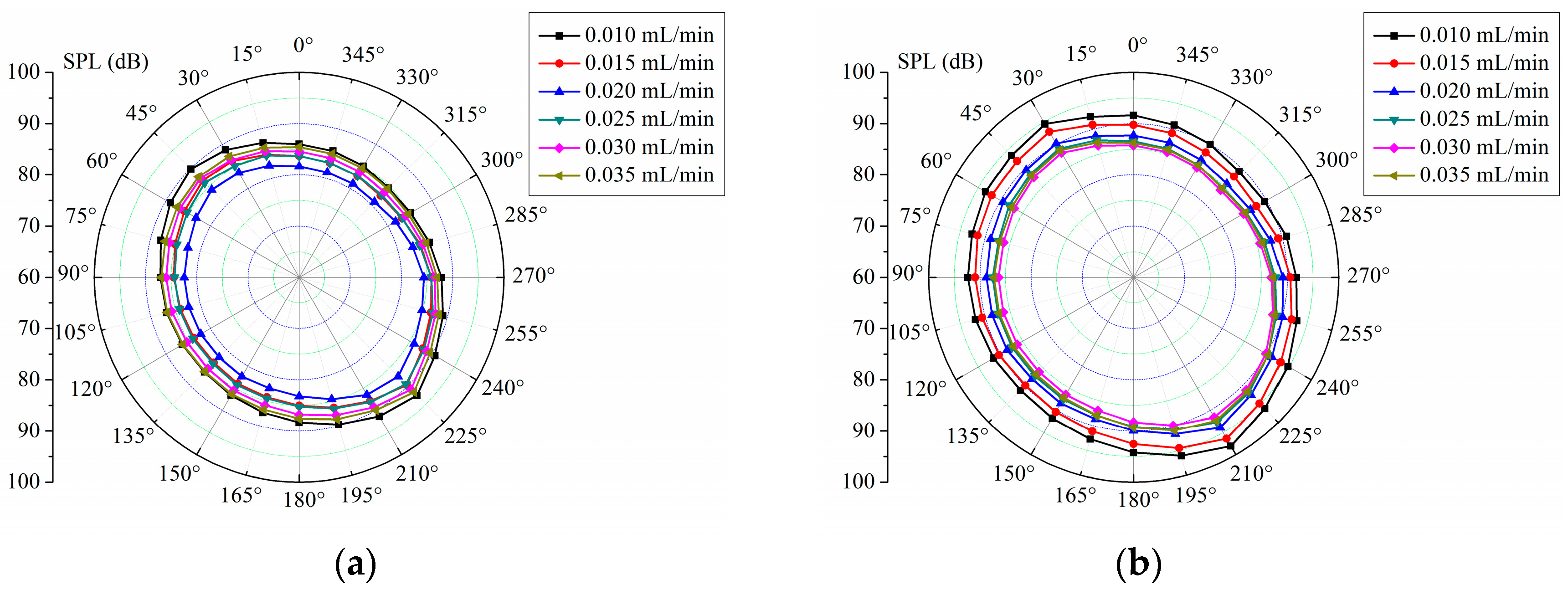
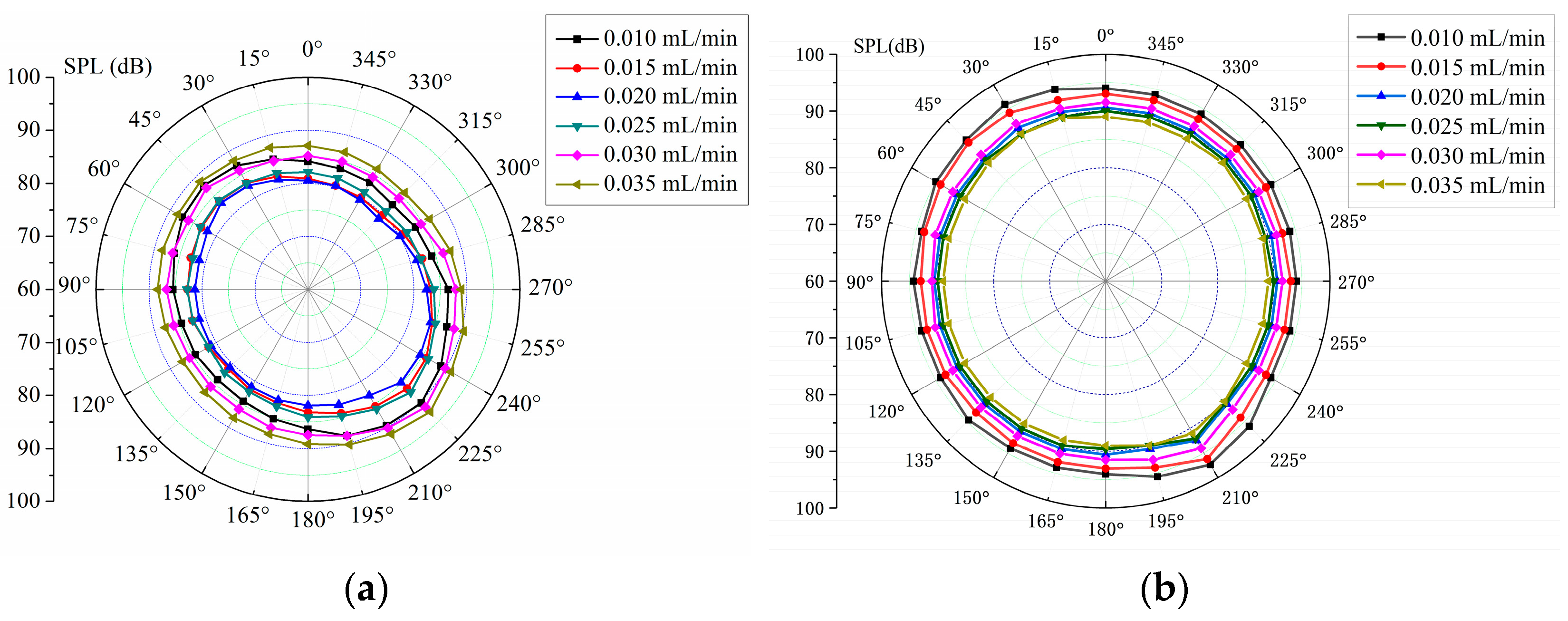
Figure 16 shows the circumferential distribution of the radiated noise of the full ceramic ball bearing with different oil supplies. With the increase in oil supply, the change in bearing radiation noise is more complicated, and the radiation noise varies greatly in the impact load area and the friction load area. When the oil supply increases from 0.010 mL/min to 0.035 mL/min, the change in radiated noise is first large, then small, and finally gentle. In addition, it can be seen from the figure that the overall variation trend of radiated noise with oil supply is consistent with the simulation results.

5.3. Influence of Oil Supply on the Characterization of Different Sound Field Regions of the Full Ceramic Ball Bearing

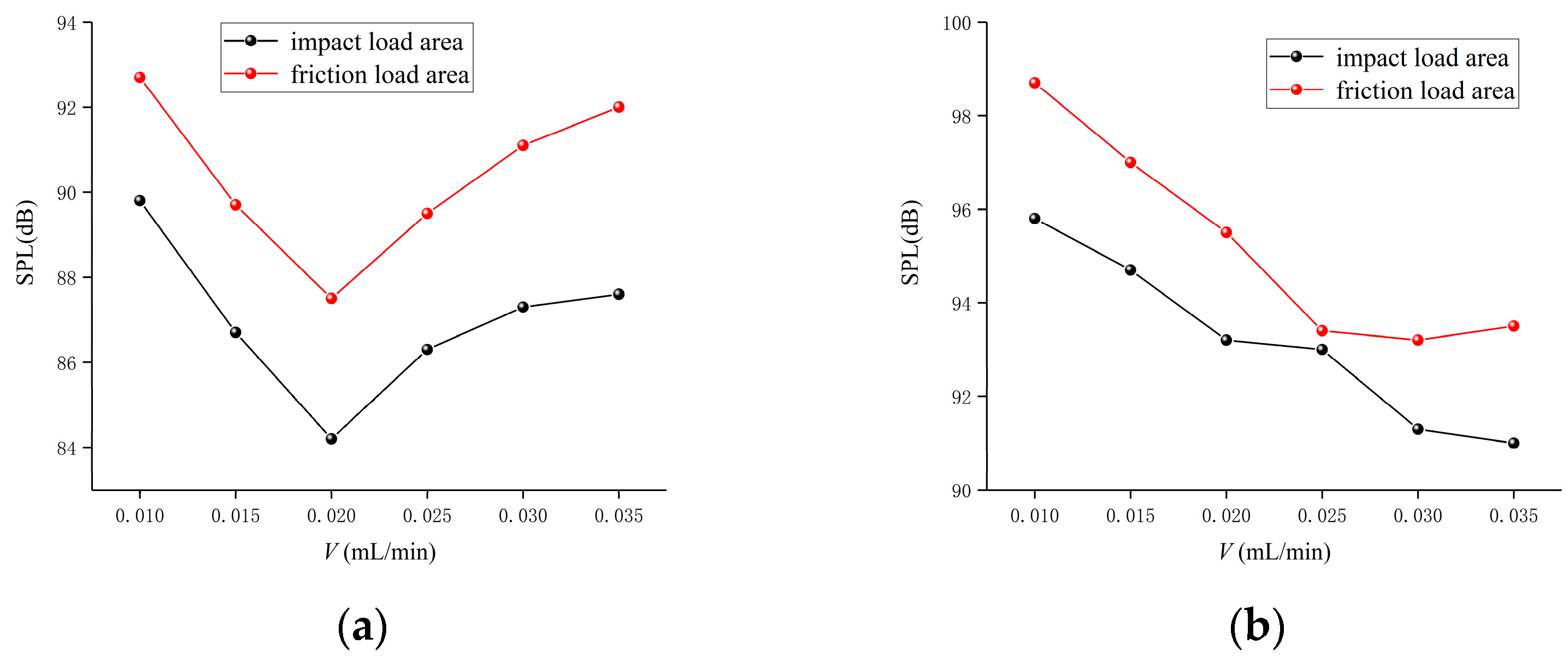
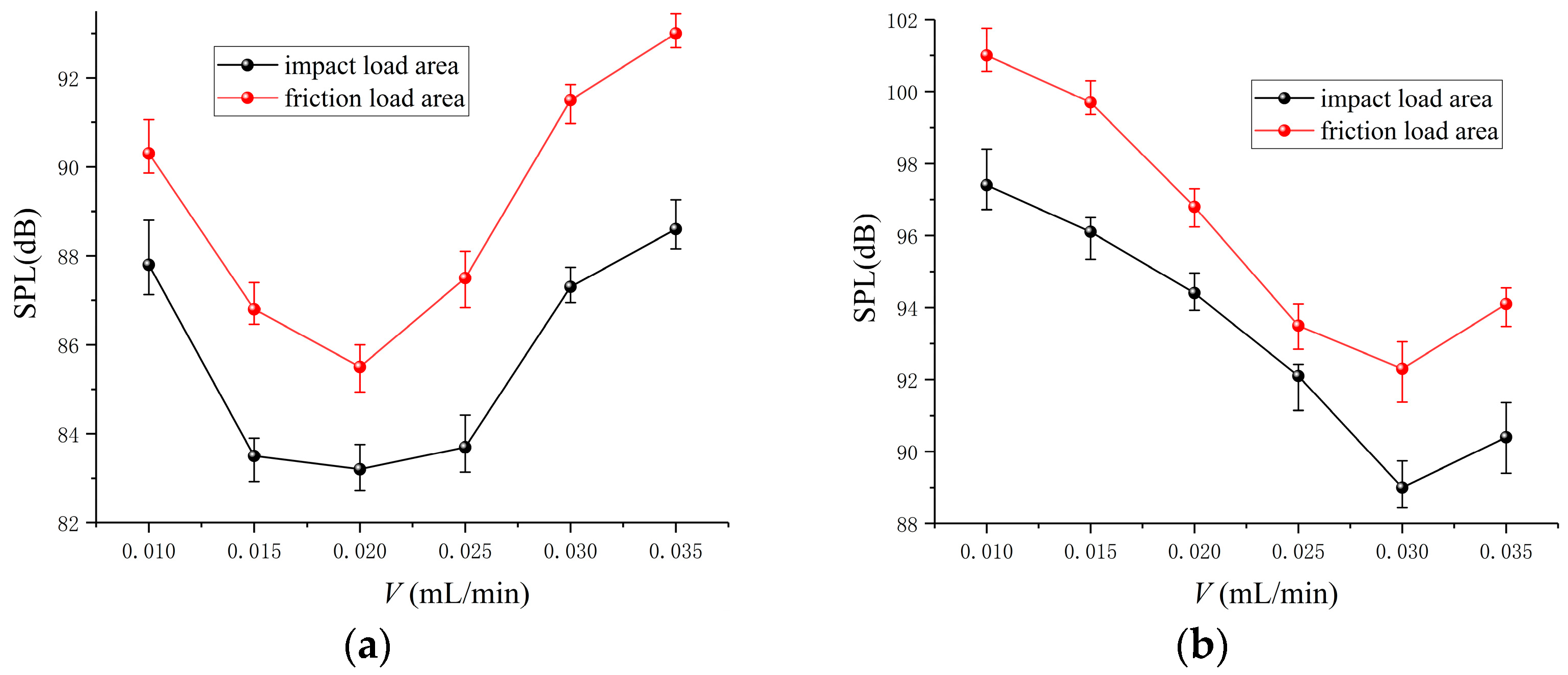
Figure 17 shows the curves of the sound pressure level of bearing radiated noise in the direction of the impact load and friction load with the change in oil supply. It can be seen from the figure that the radiation noise in the impact load area is weaker than that in the friction load area. When the rotational speed is 18,000 r/min, the maximum sound pressure level decreases first and then increases with the increase in oil supply in the impact load zone and friction load zone. The minimum sound pressure level is 83.15 dB and 84.83 dB when the oil supply is 0.020 mL/min. When the speed is 24,000 r/min, the change curves of the impact load and friction load area are consistent, and both reach the minimum sound pressure level when the oil supply is 0.030 mL/min.

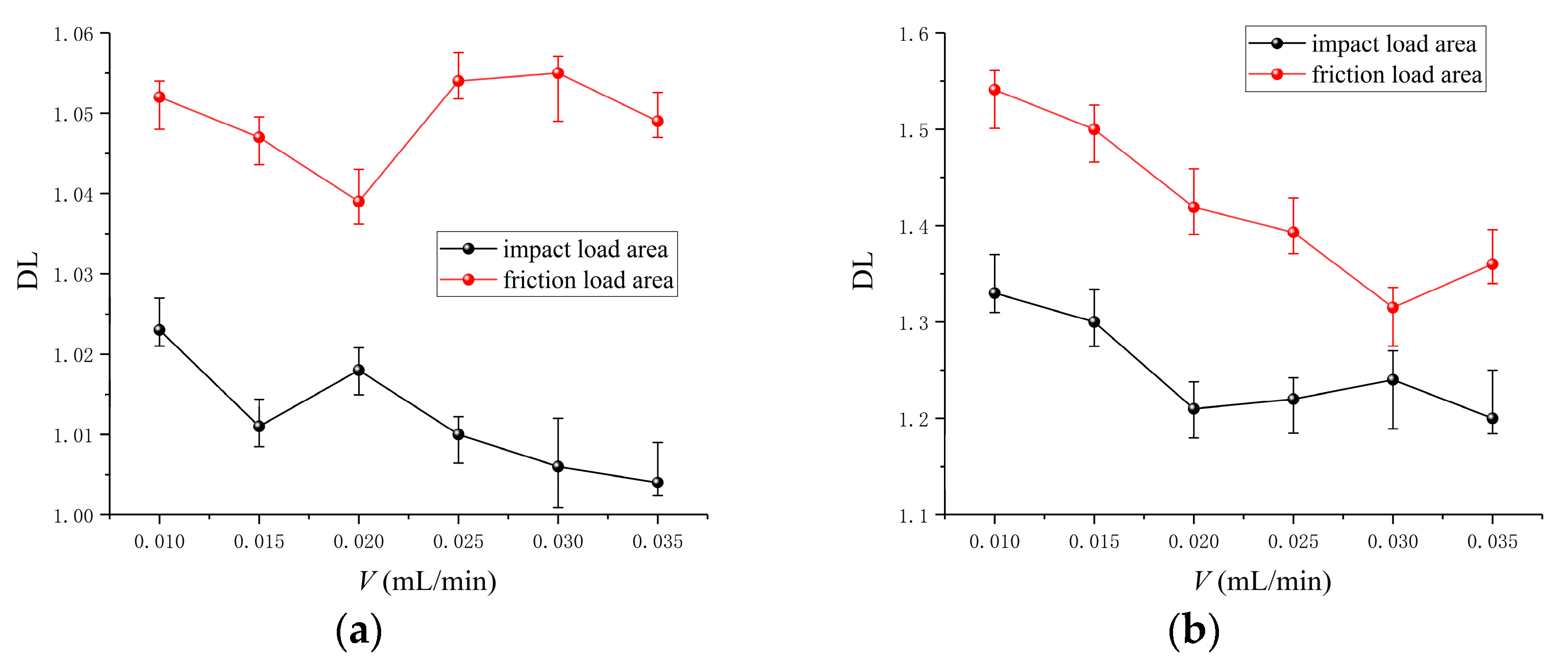
Figure 18 is the curve of the directional level of the sound field of bearing radiated noise in the impact load zone and friction load zone with the change in oil supply. It can be seen from the figure that, compared with the friction load zone, the sound field directivity of the impact load area is relatively weak. With the increase in oil supply, the directional level of the sound field in the impact load zone tends to weaken at different rotational speeds. In the friction load zone, more complex changes in the directivity of the sound field When the oil supply is small (0.010 mL/min), the directivity of the sound field tends to weaken with the increase in the oil supply, but when the oil supply reaches a certain value, the directivity of the sound field is enhanced.

The increase in lubricating oil reduces the impact and has a certain absorption effect on the radiated noise. Due to the increase in lubricating oil, the contact friction between the ceramic balls and the ring decreases, which leads to the above changes in the sound field directivity of the friction load area. Moreover, the oil film absorbs the noise to some extent, which results in a decrease in the radiated noise in this area, and the radiated noise in the circumferential direction also becomes more uniform, so the directivity of the sound field is weakened. However, when there is more lubricating oil, it will not only increase the friction resistance between bearing assemblies and the lubricating oil film but also make the temperature rise greatly, reducing the gap between the ceramic balls and the ring and increasing the friction radiation noise. Too much lubricating oil will also destroy the lubrication state so that the radiated noise in the whole circumferential direction increases and tends to be uniform, resulting in a slight weakening of the sound field directivity.

In conclusion, although the ceramic material has a small thermal expansion coefficient, it still has a certain amount of deformation at a higher temperature. When the lubricating oil is too much, the temperature of the full ceramic ball bearing will rise faster, and the temperature of the inner ring is higher than that of the outer ring so that the clearance between ceramic balls and the ring decreases slightly, which leads to the increase in the radiated noise of the full ceramic ball bearing. In addition, the cage has a large thermal expansion coefficient, which is prone to produce large deformation at high temperatures, leading to the increase in the clearance and the gap between the pocket hole and the ceramic ball, which reduces the stability of the cage and intensifies the impact between the pocket hole and the ceramic ball.

5.4. Analysis of the Influence of Oil Supply on the Sound Field Characteristics of the Full Ceramic Ball Bearing

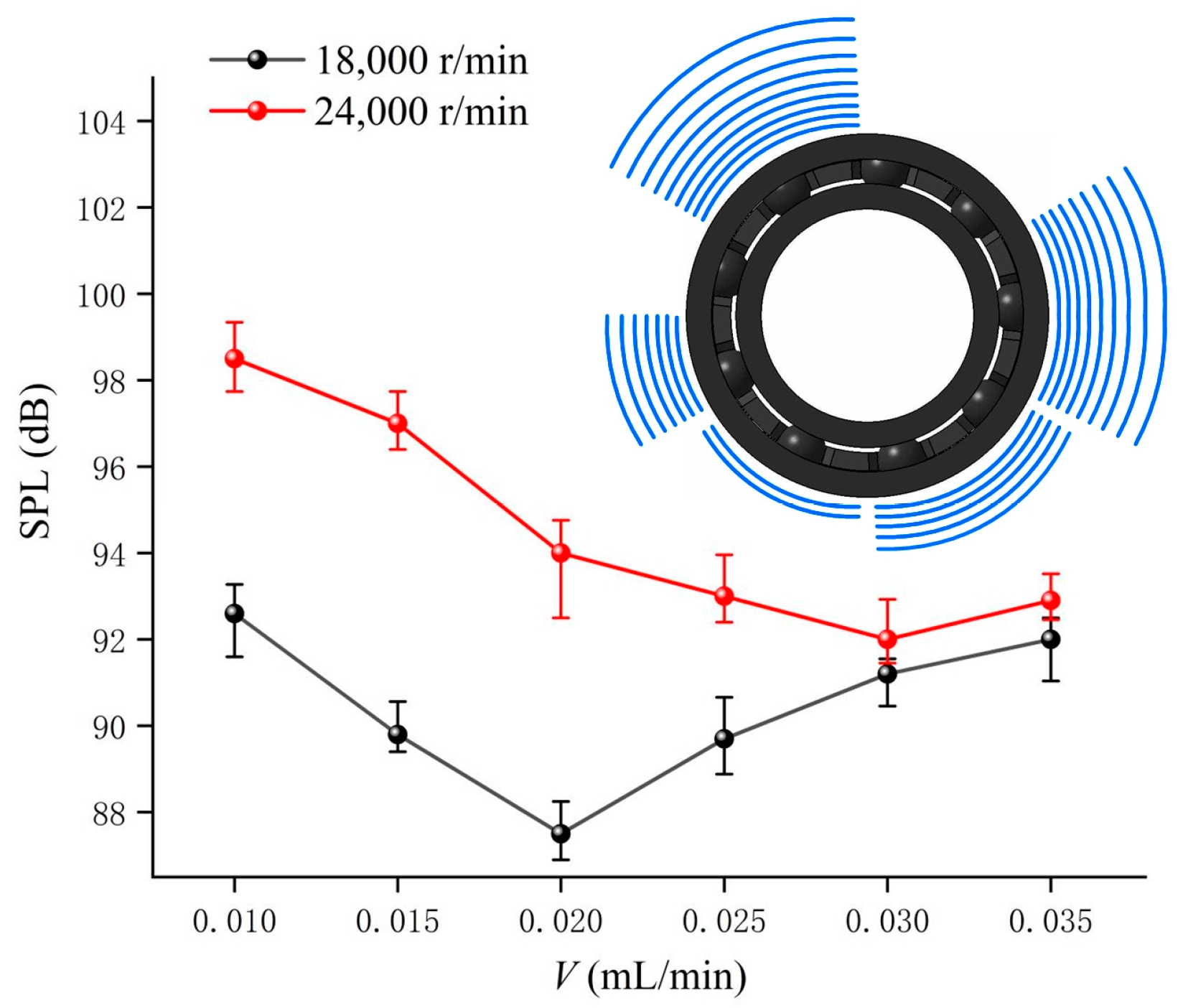
Figure 19 shows the variation curve of the SPL of the sound field directivity with the increase in oil supply for the full ceramic ball bearing. It can be seen from the figure that at different speeds, the maximum sound pressure level of the radiated noise of the full ceramic ball bearing decreases first and then increases with the increase in the oil supply, and there is a relatively large radiated noise at higher speeds. In the process of increasing the oil supply from 0.020 mL/min to 0.035 mL/min, the radiation noise at the speed of 18,000 r/min showed a gradually increasing trend. This indicates that when the fuel supply is greater than a certain amount, increasing the oil supply still leads to an increase in radiation noise, but the degree of increase is weaker and weaker.

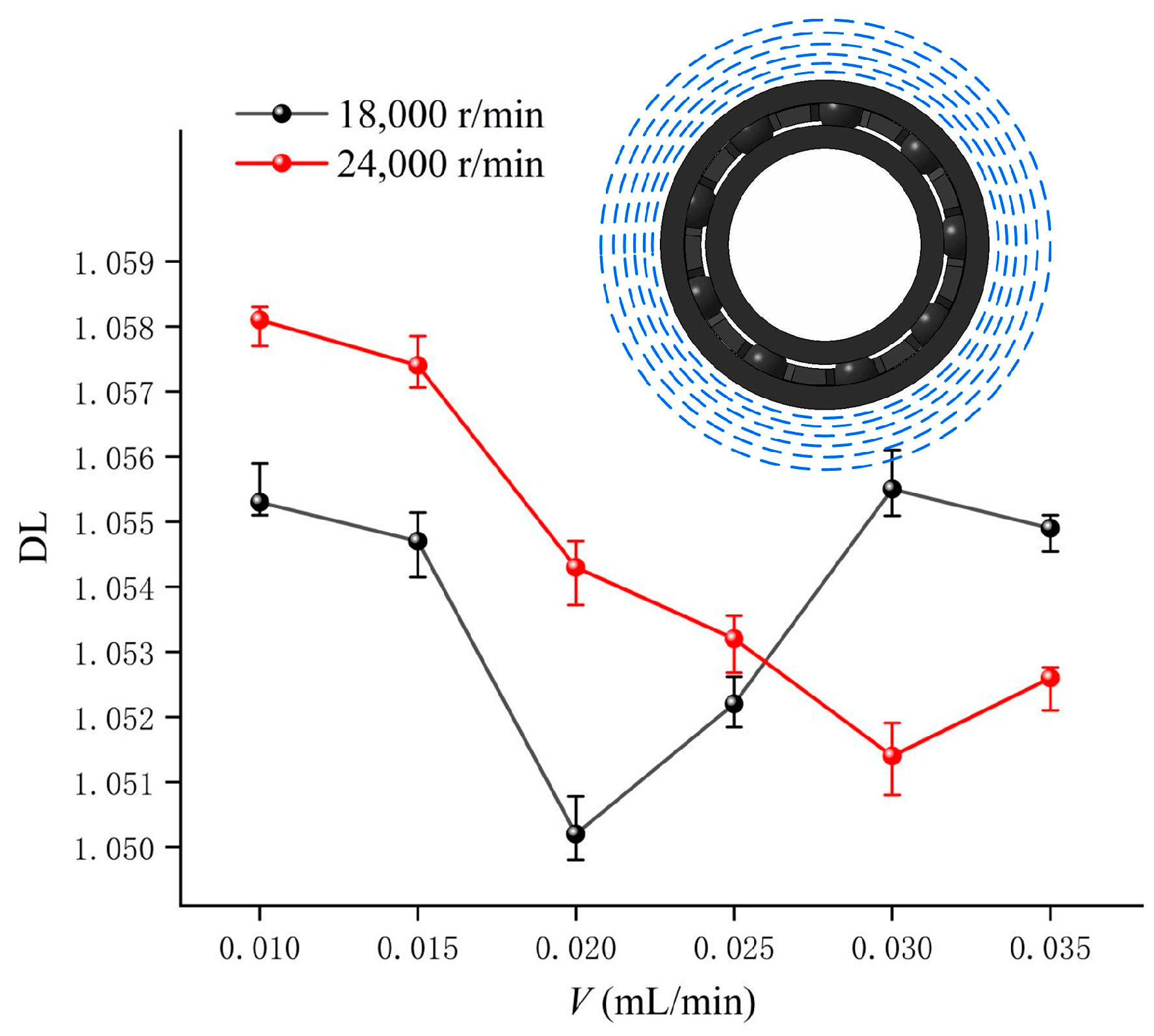
Figure 20 shows the variation of radiated noise sound pressure levels in the circumferential direction with different oil supplies. Combined with Figure 19 and Figure 20, when the rotational speed is 24,000 r/min, with the increase in oil supply, the changing trend of the sound pressure level in the circumferential direction of radiated noise is consistent with the changing trend of the maximum sound pressure level. When the oil supply is 0.030 mL/min, the radiation noise of the full ceramic ball bearing is evenly distributed in the circumferential direction. When the speed is 18,000 r/min, and the oil supply is 0.020 mL/min, the change in sound pressure level in the circumferential direction is small. This shows that the distribution of the radiated noise of the full ceramic ball bearing is uniform in the circumferential direction.

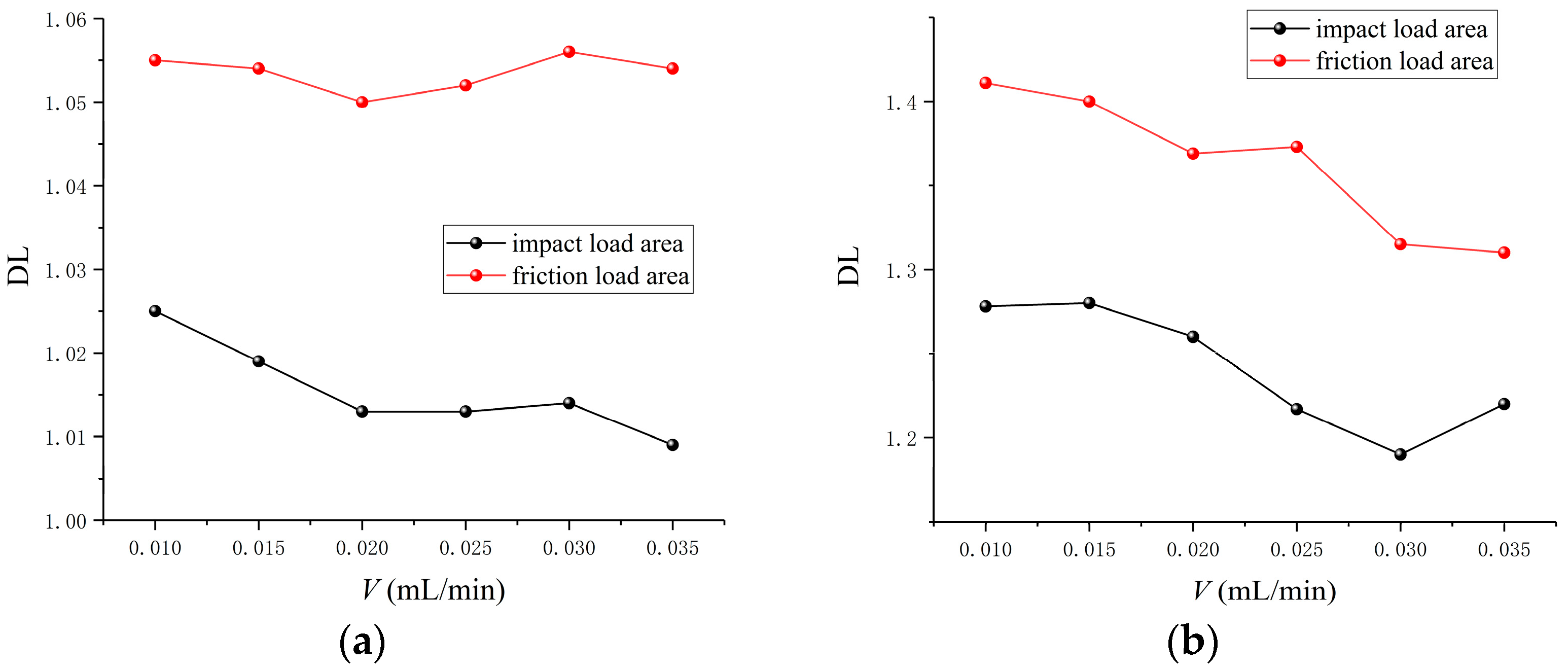
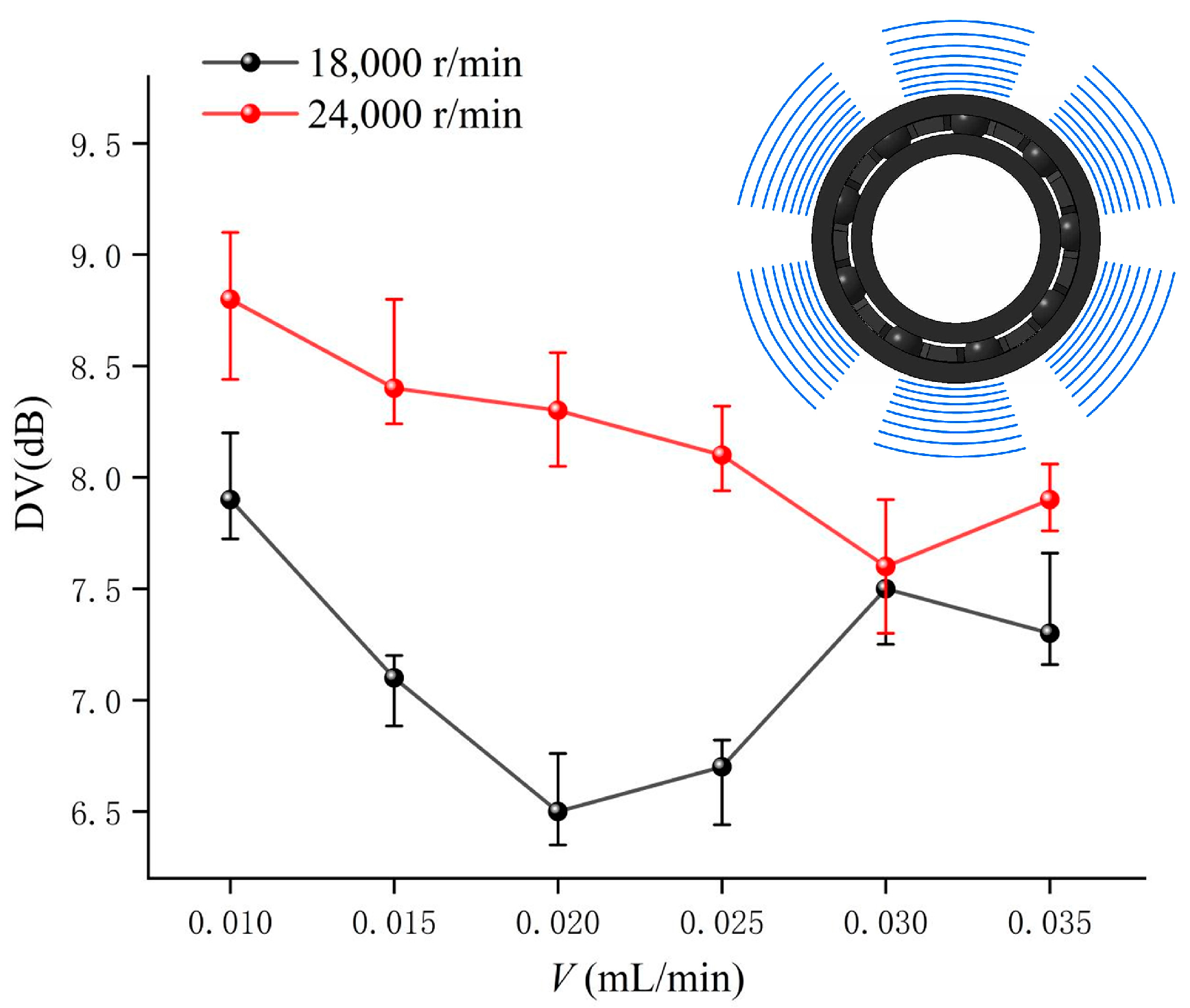
Figure 21 shows the variation curve of the DL of the sound field directivity with the oil supply. Combined with Figure 19 and Figure 21, it can be seen that in the range of oil supply from 0.010 mL/min to 0.025 mL/min, the directional level of the sound field at 24,000 r/min is larger relative to the sound pressure level than that at the speed of 18,000 r/min. However, when the oil supply is greater than 0.025 mL/min, the directivity of the sound field at 18,000 r/min is increasing, while that at 24,000 r/min is still decreasing, resulting in the directivity of the sound field at 24,000 r/min being gradually lower than that at 18,000 r/min, but the sound pressure level at high speed is still relatively high.

5.5. Comparative Analysis of the Test Results and Simulation Results

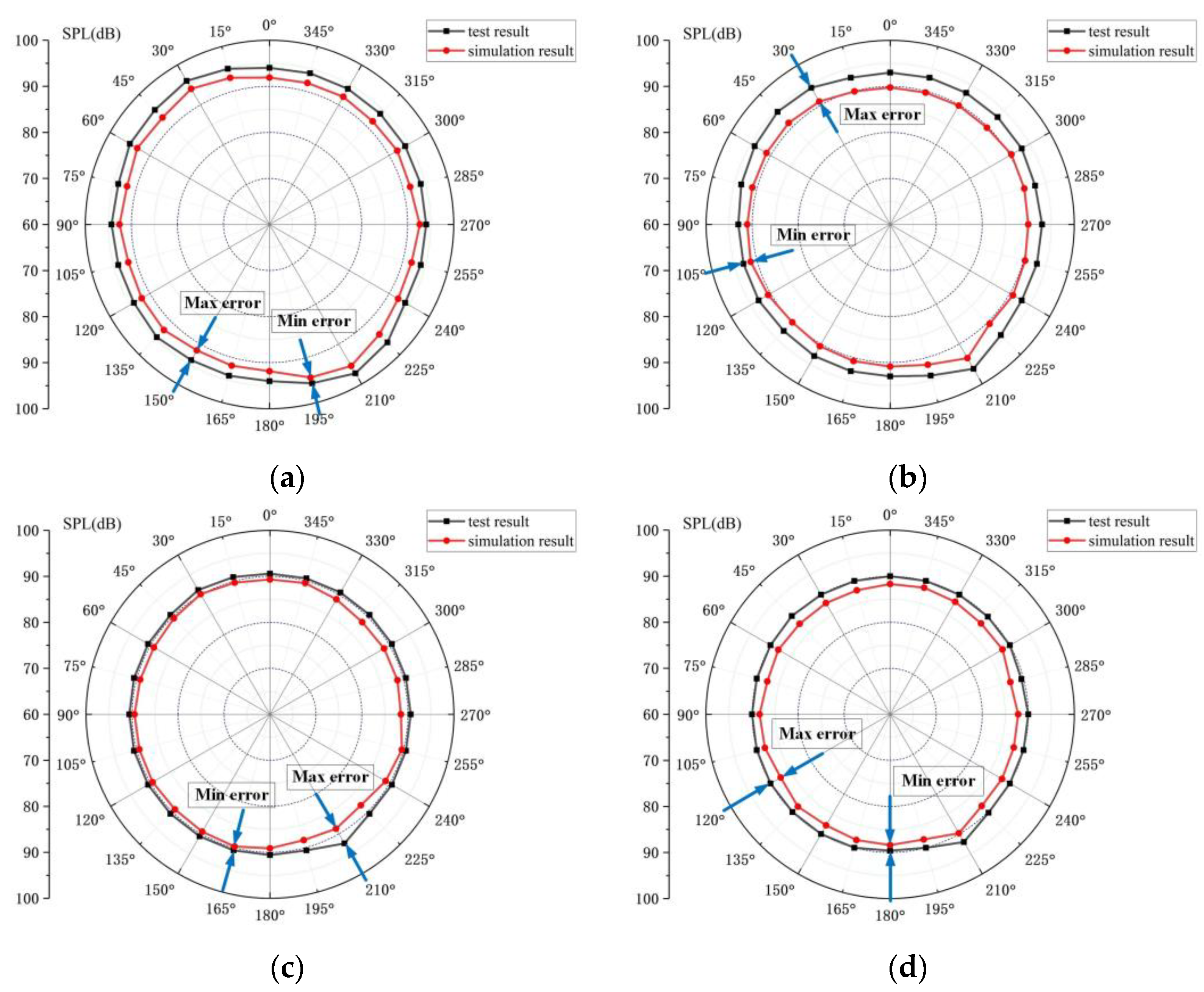
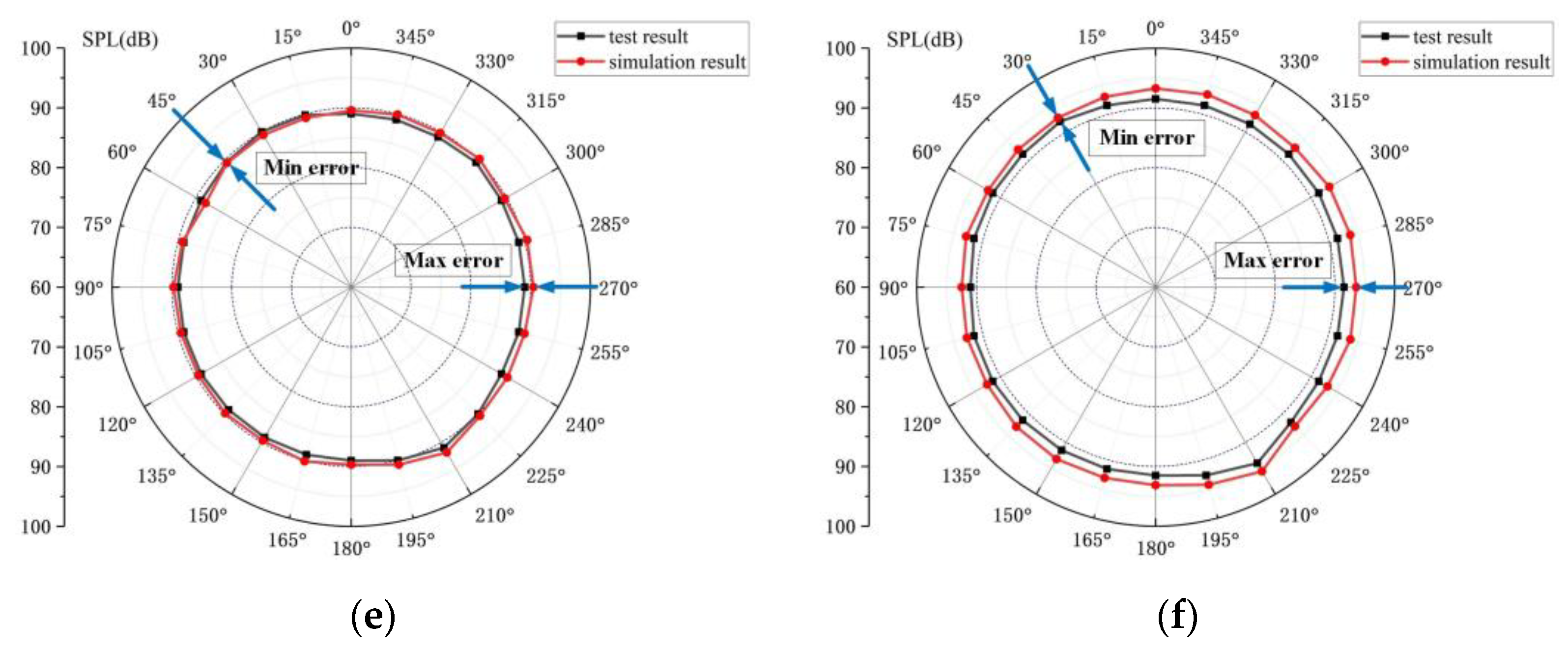
Figure 22 shows the simulation results and experimental results at different oil supplies. It is calculated that the relative error of radiation noise in the circumferential direction is less than 4.0% under different fuel supplies. When the oil supply is 0.030 mL/min and 0.035 mL/min, the test results are higher than the experimental results. According to the absolute value of the calculated relative error, when the oil supply is 0.020 mL/min, the relative error in the direction of 210° is the largest, which is 3.98%. When the oil supply is 0.030 mL/min, the relative error of the position angle of 45° is the smallest, which is 0.16%. It can be seen that the error at this time is very small.

Because the working equipment of bearings (such as the spindle and bearing housing) has a certain barrier and absorption effect on the transmission of the bearing sound signal, the general simulation results are greater than the test results, but in the case of large oil supply, the test results are greater than the simulation results. This is because in the test process, the full ceramic angular contact ball bearing is installed in the spindle, and the heat generated in its operation is not easy to dissipate, leading to a higher temperature rise in the bearing so that deviation appears in the results. In addition, the outer ring is in contact with the bearing housing, and the bearing housing is in contact with the outside air. The temperature is generally lower than the inner ring, the expansion of the inner ring is larger, the thermal expansion coefficient of the silicon nitride ceramic ball is smaller than the ring, and the deformation of the ball is very small so that the bearing clearance is reduced leading to a large friction noise. Additionally, the increase in temperature also makes the gap between the outer ring and the bearing housing larger, resulting in larger vibration noise, so that when the oil supply is larger, the test results are greater than the calculation results. Comparing the simulation calculation results with the test results, the error is within the acceptable range, and with the increase in the oil supply, the simulation results are consistent with the changing trend of the test results, so the accuracy and validity of the simulation results of the radiated noise of the full ceramic ball bearing with the oil supply are verified.

6. Conclusions

In this paper, the influence of lubricating oil supply on the sound field distribution characteristics of full ceramic ball bearings is studied. Some of the conclusions are as follows:

(1) Under different oil supplies, the sound pressure signal of the full ceramic ball bearing shows an uneven distribution in the circumferential direction. With the increase in oil supply, it shows a trend of decreasing and then increasing. With the increase in rotational speed, the amount of oil supply when the bearing produces the minimum radiation noise also increases. At a given speed and preload, there is an optimal amount of oil supply to minimize the radiation noise of full ceramic ball bearings.

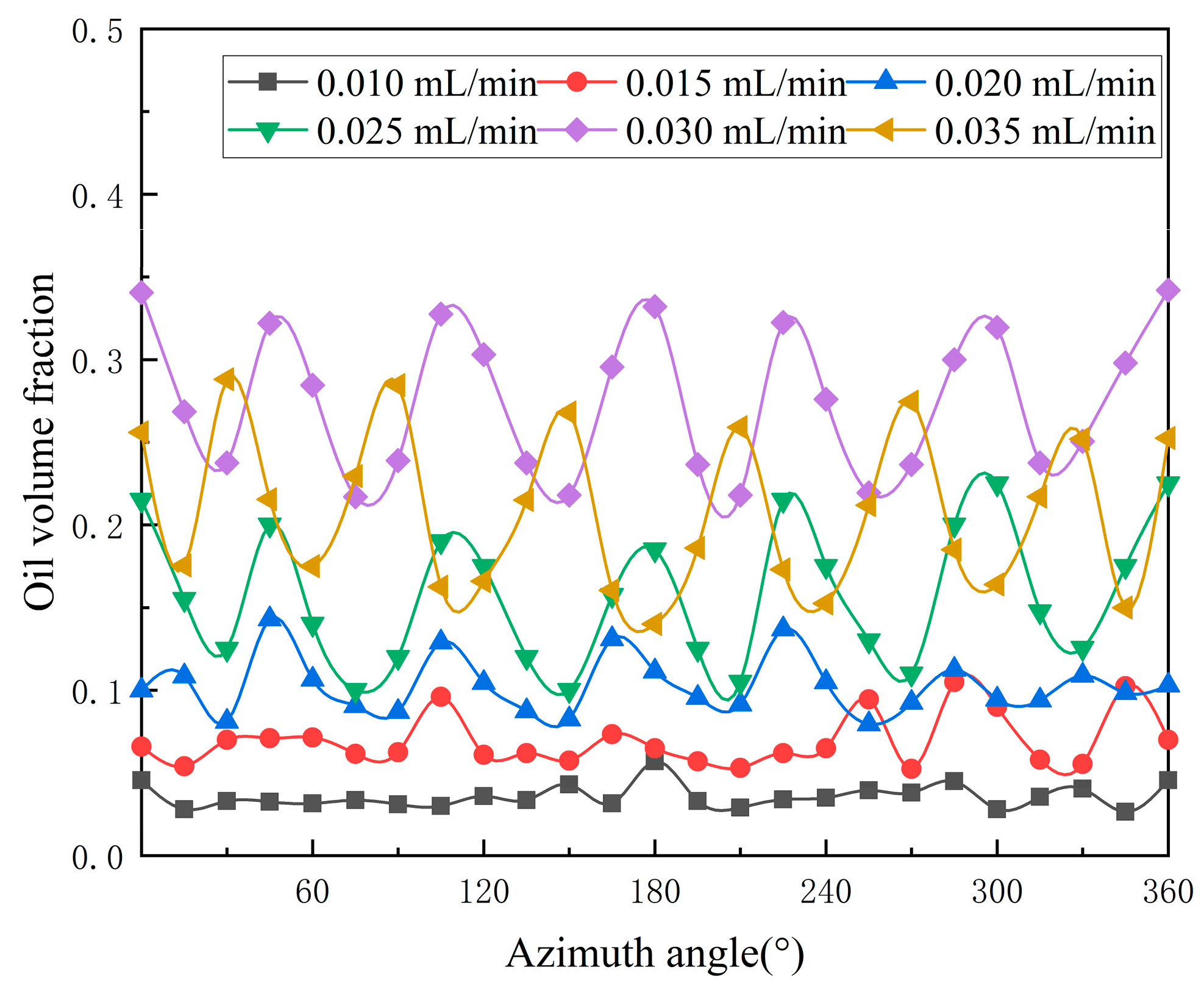
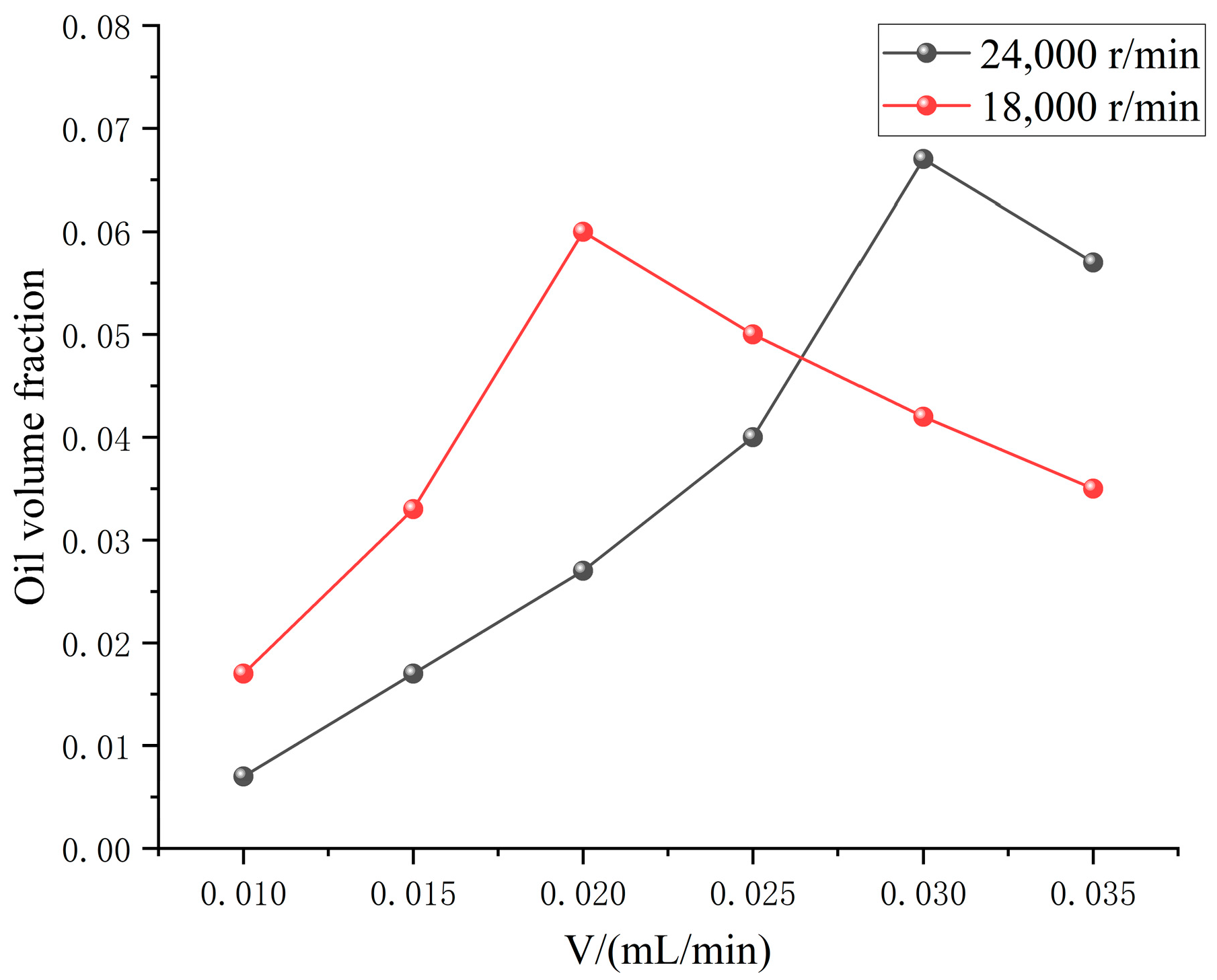
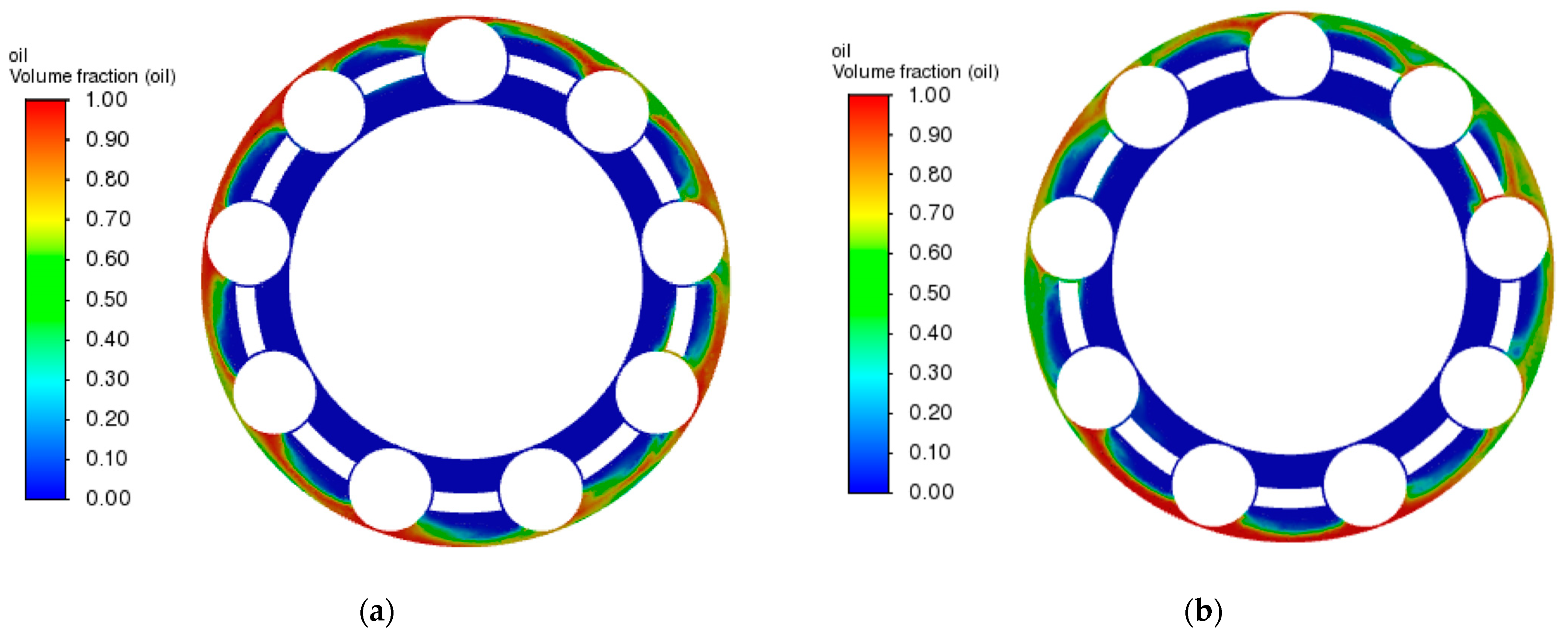
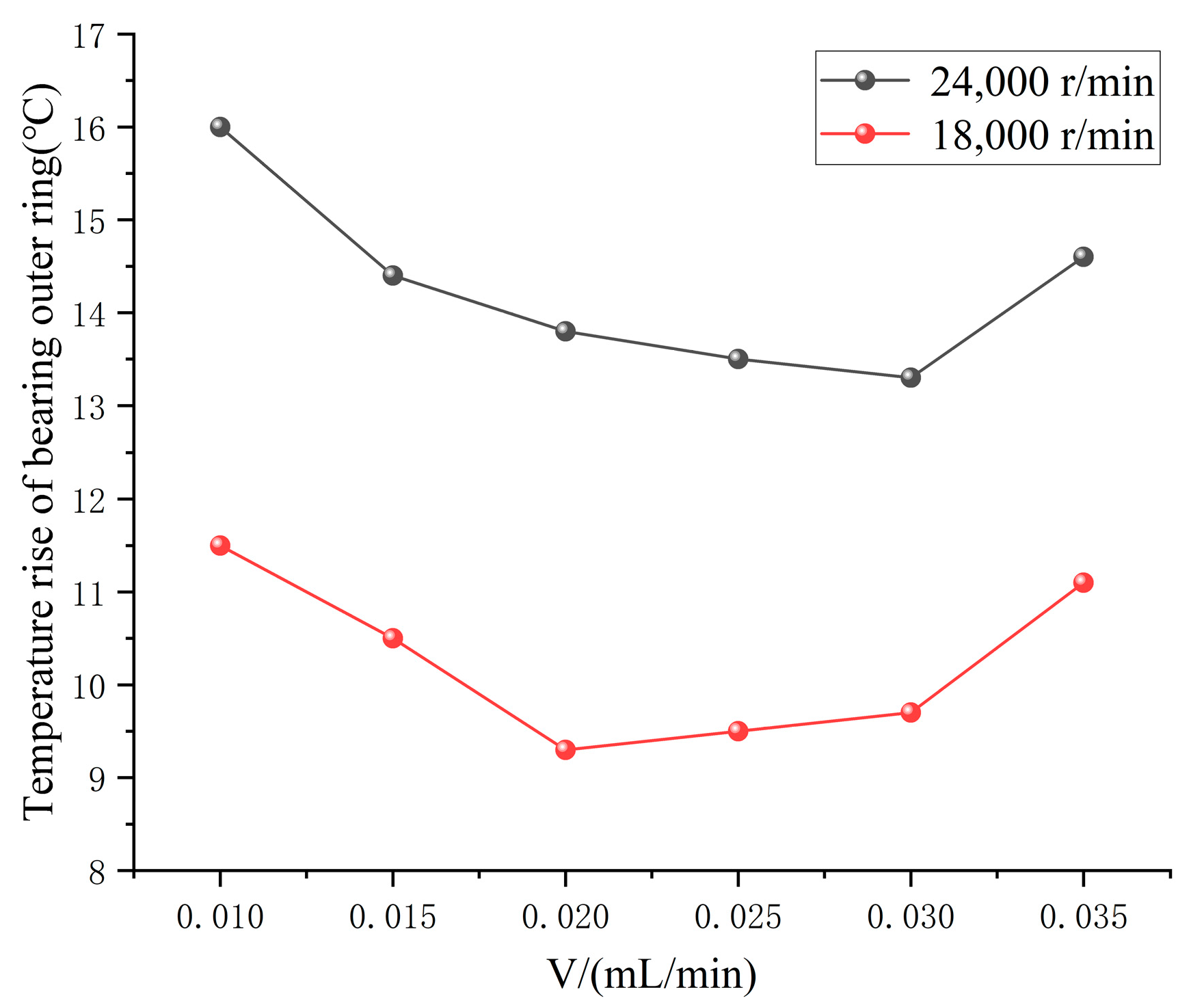
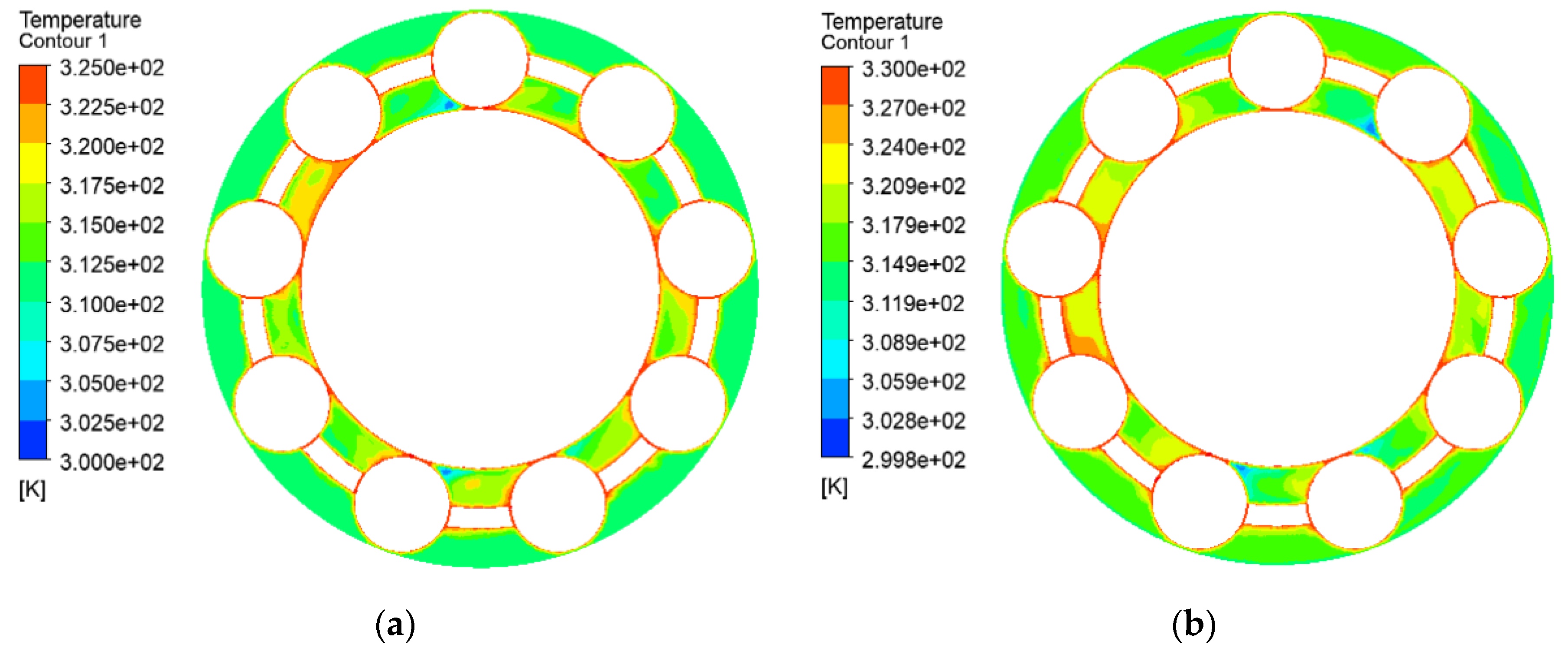
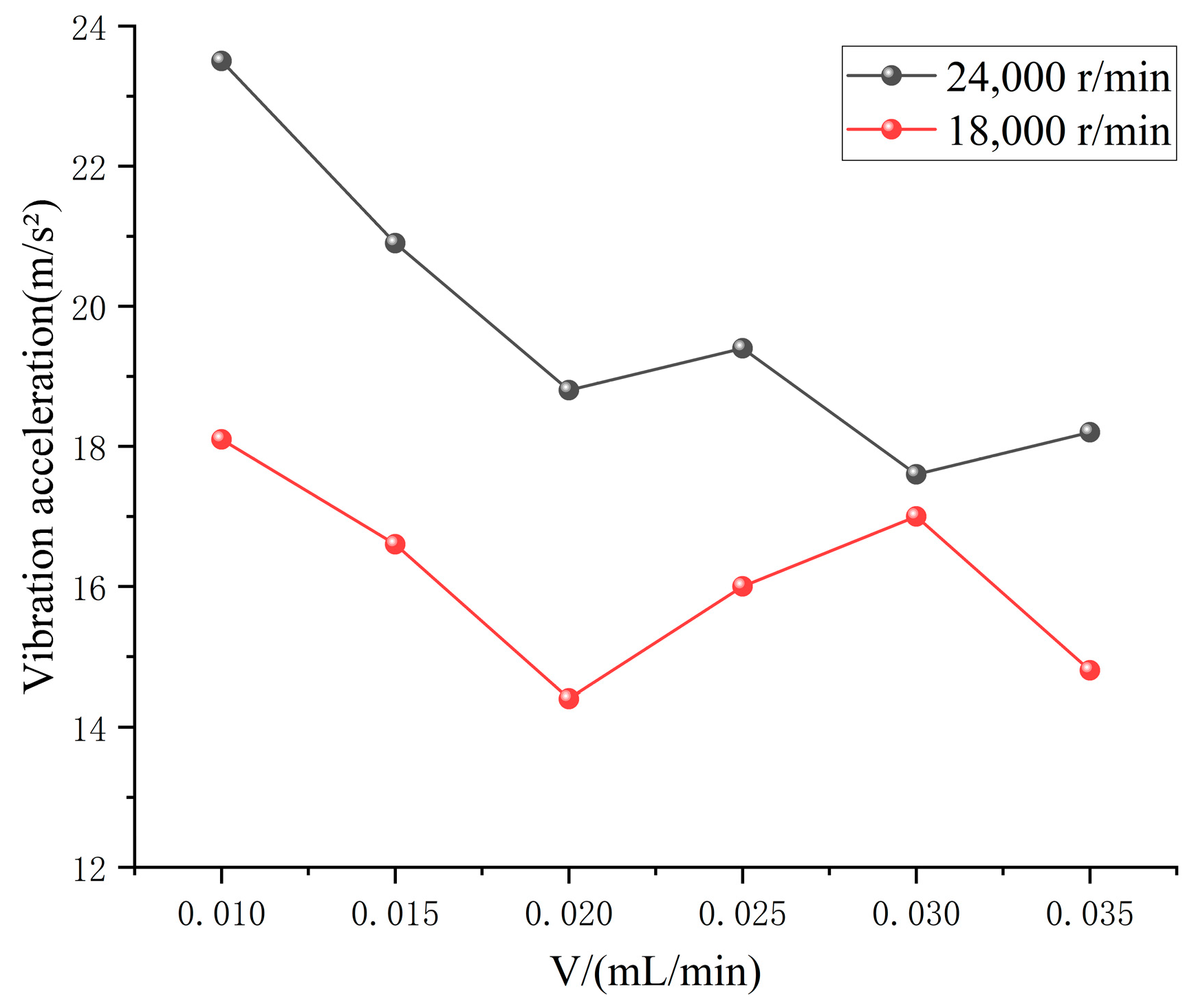
(2) Under different oil supplies, the oil phase distribution in the circumferential direction is not uniform in the full ceramic ball bearing cavity. With the increase in oil supply, the oil volume fraction increases first and then decreases, while the temperature rise and vibration acceleration of the bearing outer ring decreases first and then increases. There is an optimal oil supply to ensure the lubrication performance of the bearing reaches the optimal state.

(3) At different rotational speeds, the maximum sound pressure level and sound pressure level variation of the full ceramic ball bearing shows a trend of decreasing and then increasing with the increase in oil supply and are relatively larger at higher rotational speeds. The relative error between the simulation results and the test results of the radiated noise in the circumferential direction at different oil supply amounts does not exceed 4%.