Analysis of Nonlinear Time-Domain Lubrication Characteristics of the Hydrodynamic Journal Bearing System
Abstract
:1. Introduction
2. Numerical Procedures
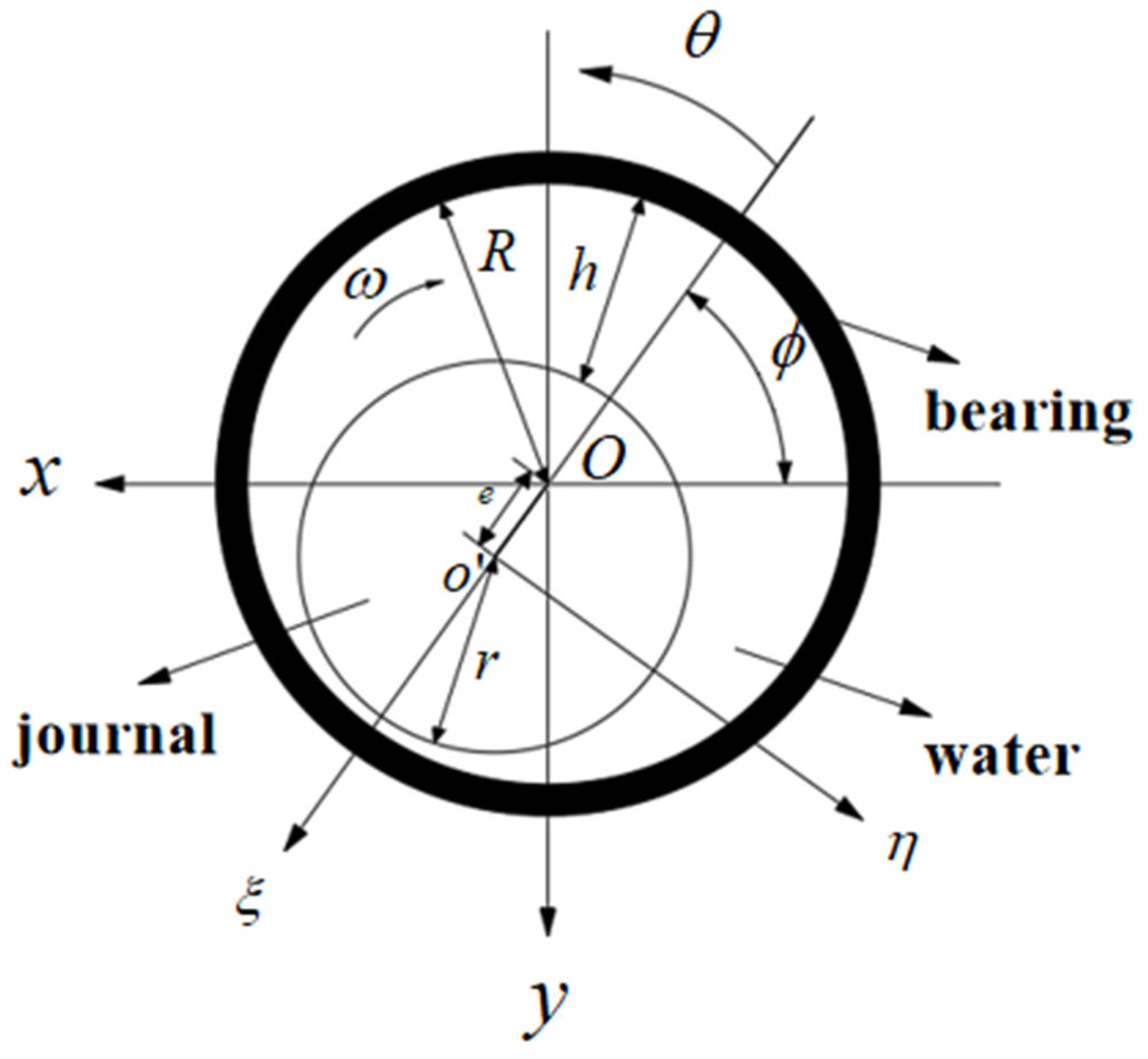
2.1. Governing Equation and Boundary Conditions
- (1)
- The film thickness is far smaller than the radius of curvature of the adjacent solid surface;
- (2)
- The water film pressure in the thickness direction is constant;
- (3)
- Only the velocity gradient in the film thickness direction is considered;
- (4)
- The lubricant is in an isothermal and incompressible state.
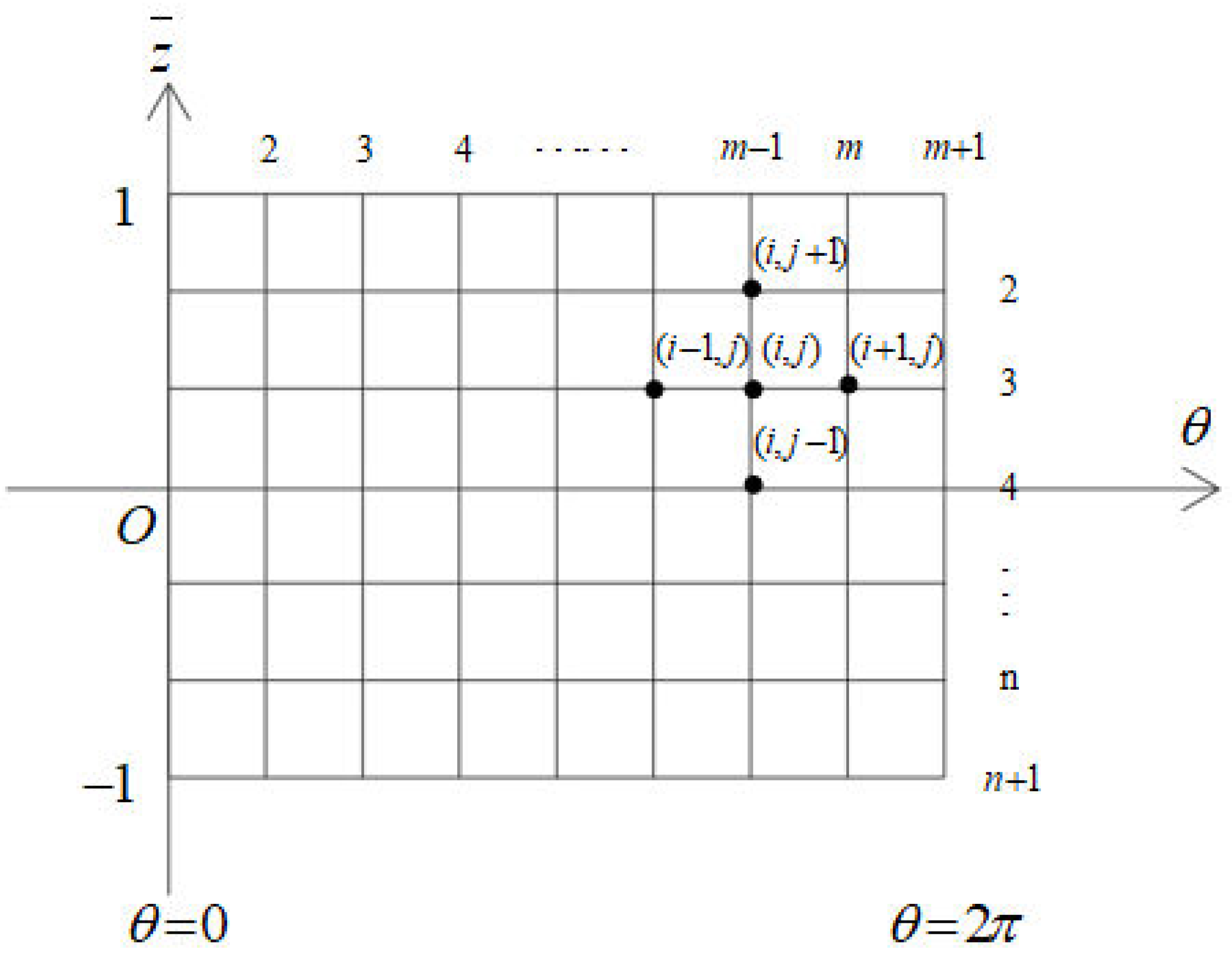
2.2. Discretisation of the Governing Equation
2.3. Solution Procedure with Translational Inertial Force and Centripetal Force
2.4. Iterative Method
3. Analysis of Water Film Dynamic Characteristics Considering Journal Inertial Force
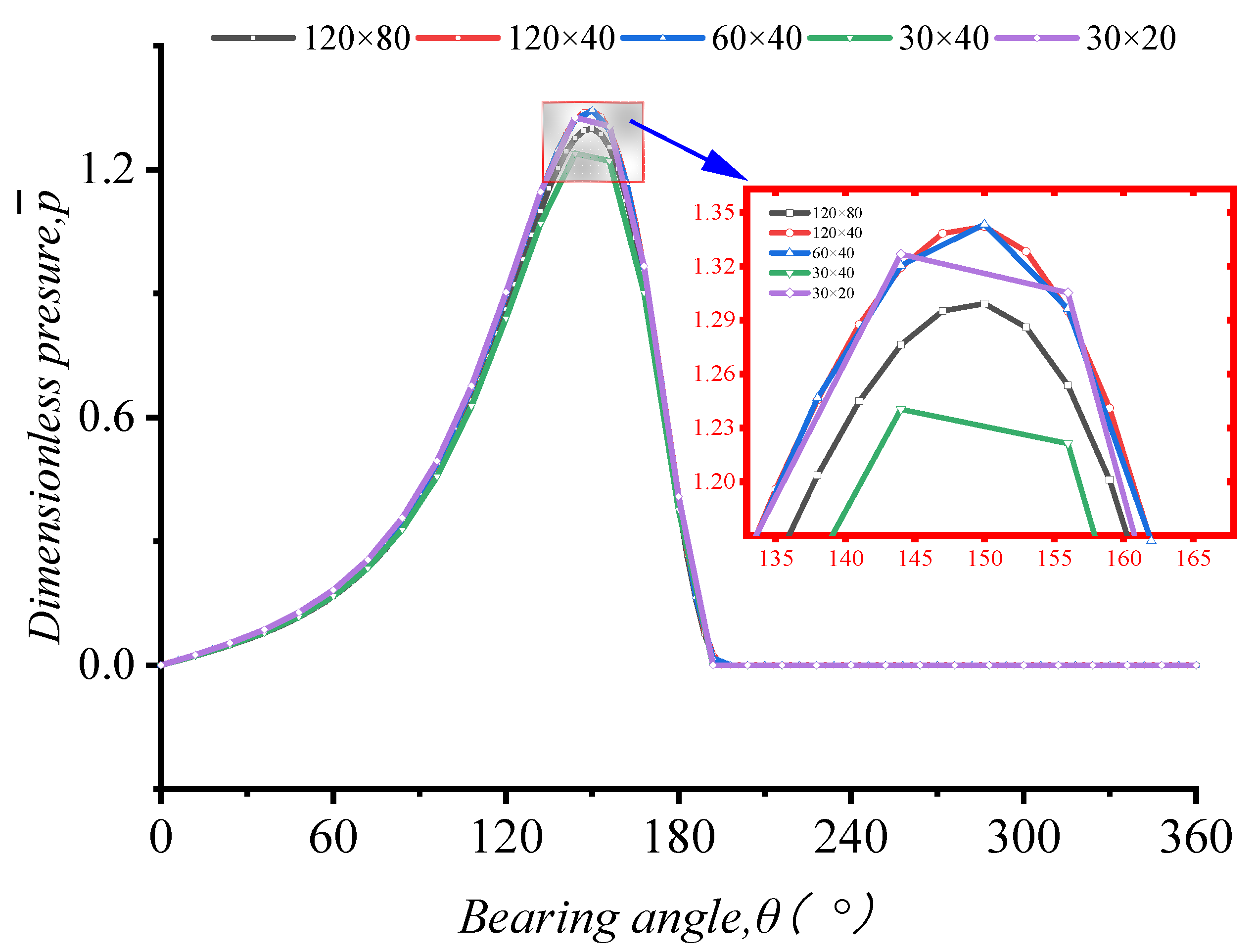
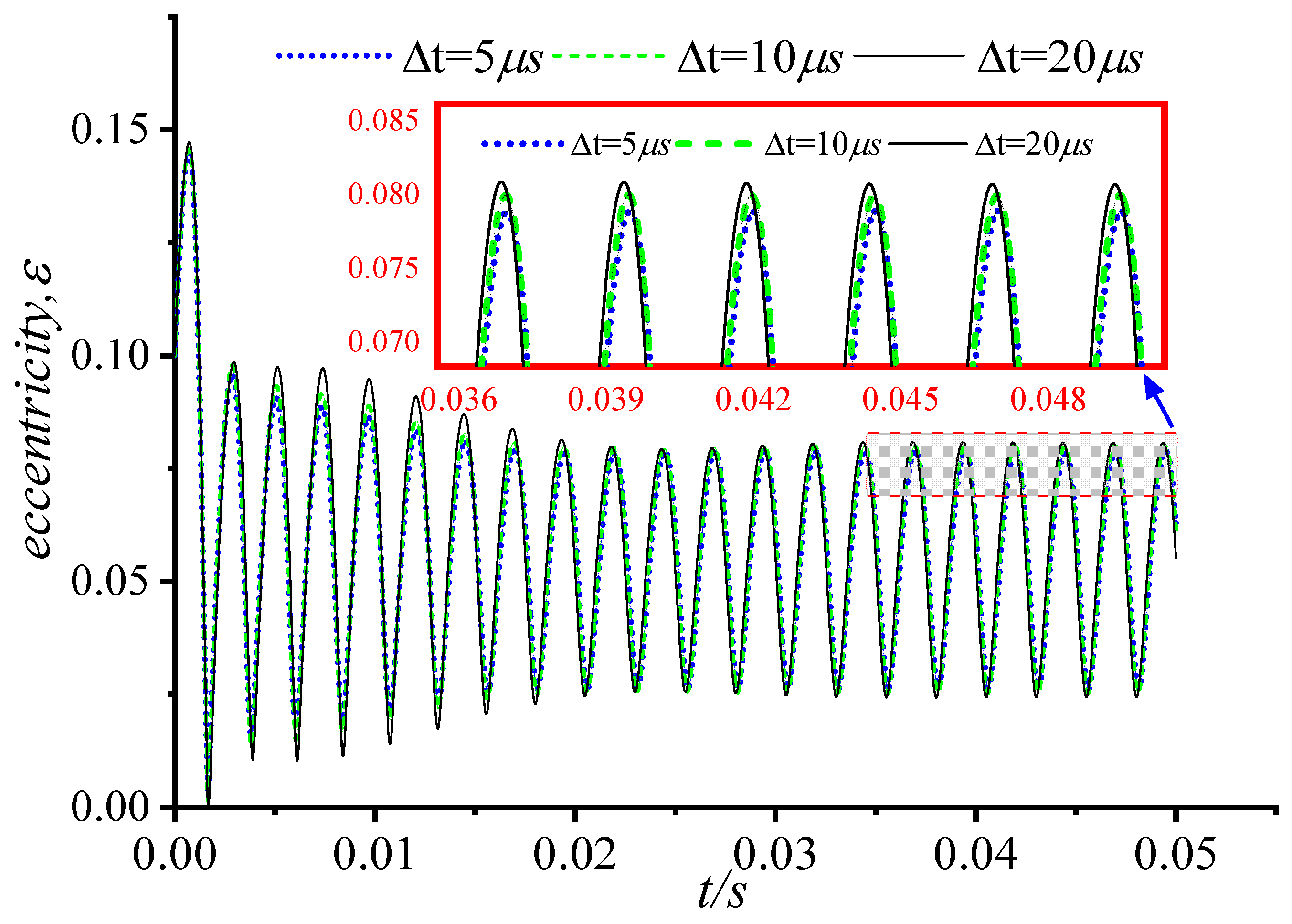
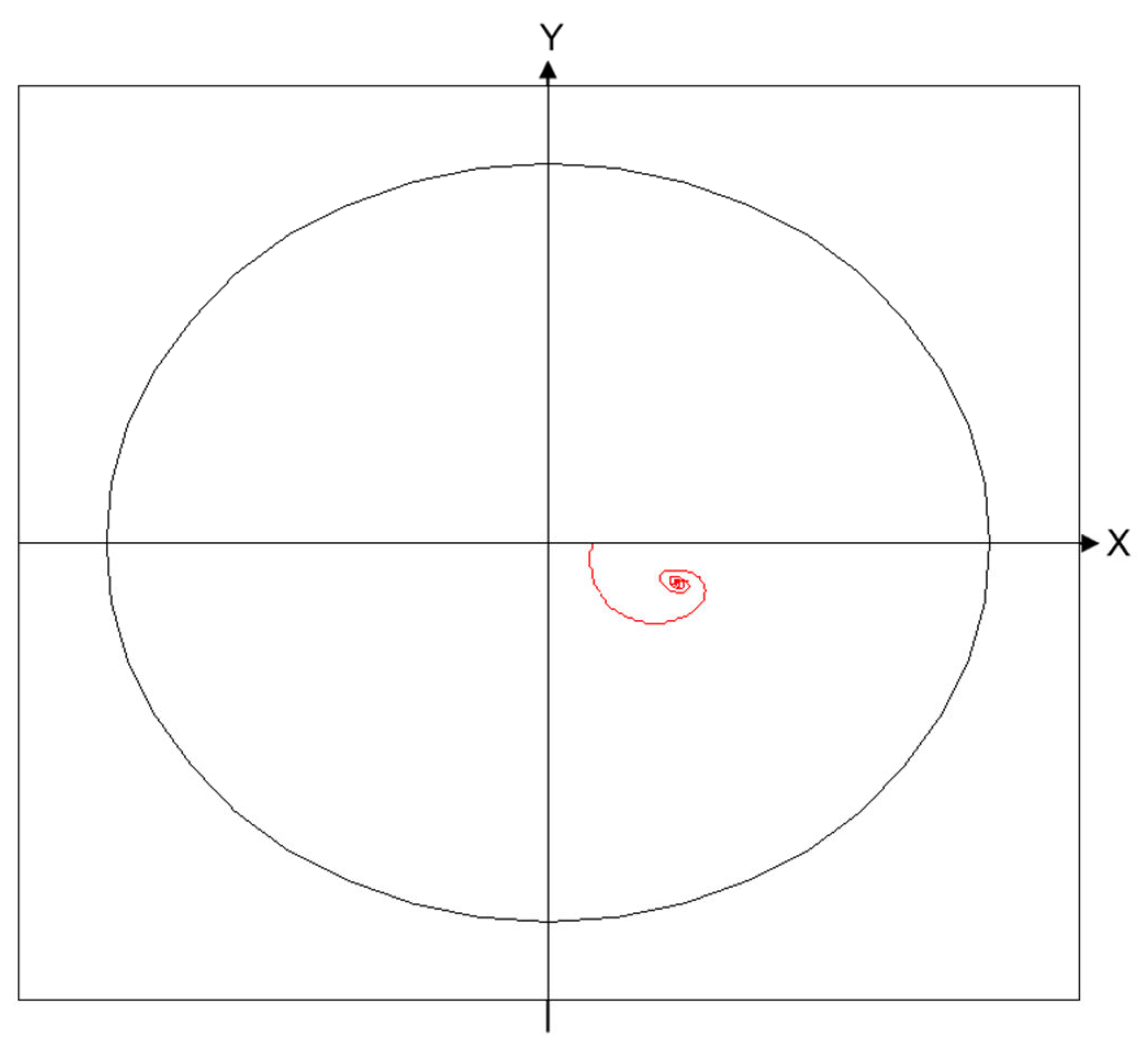
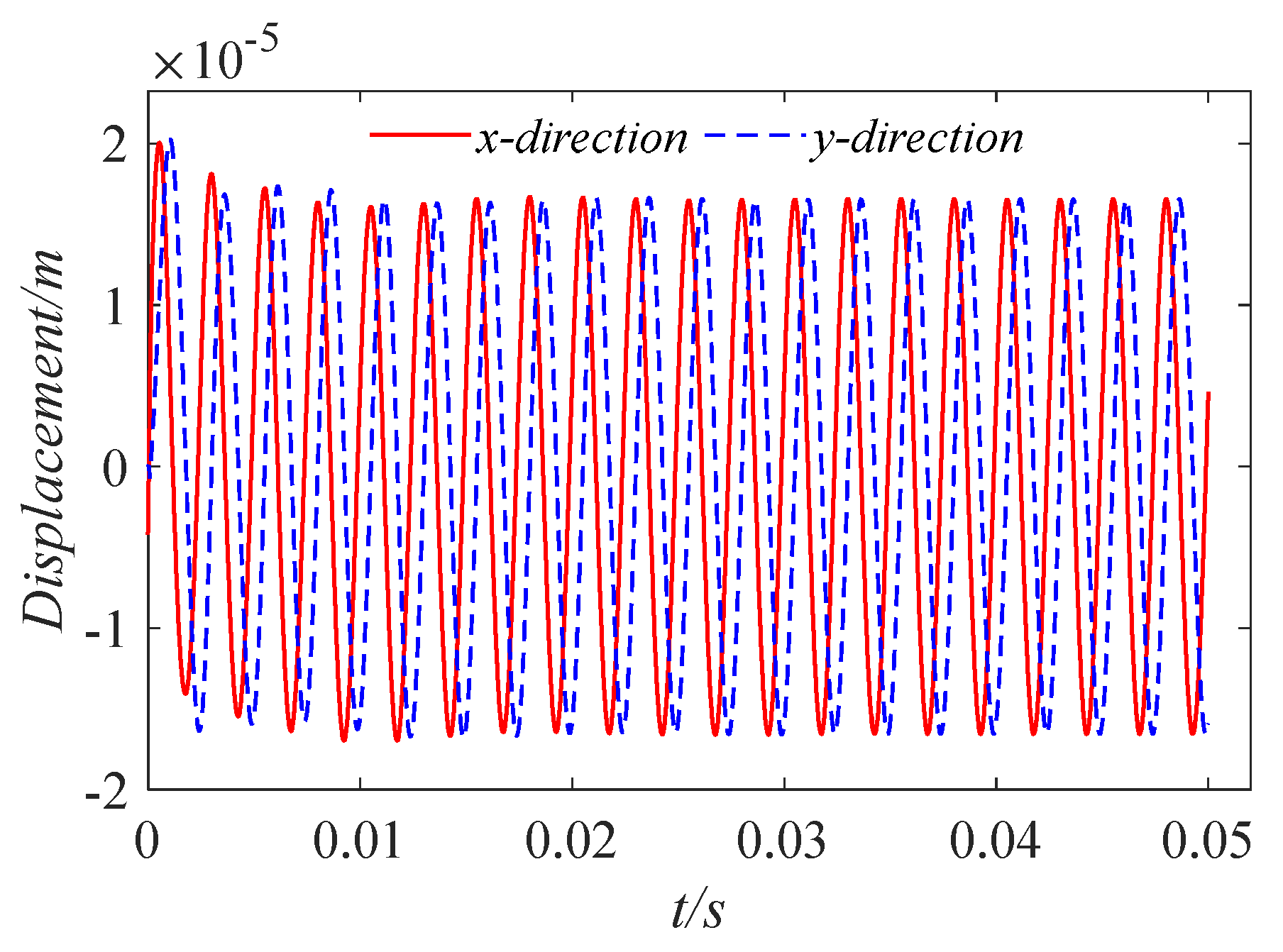
3.1. Validation
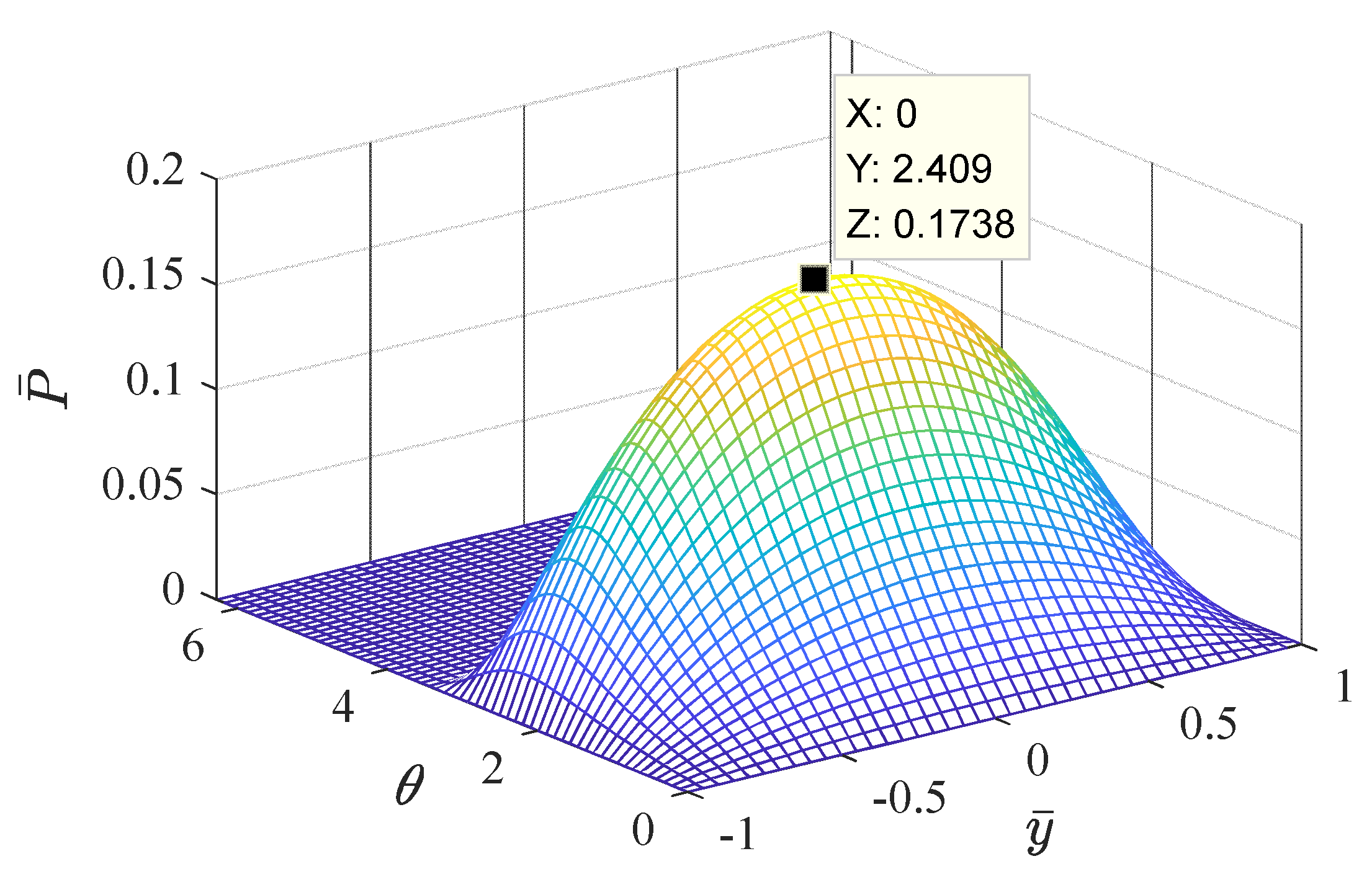
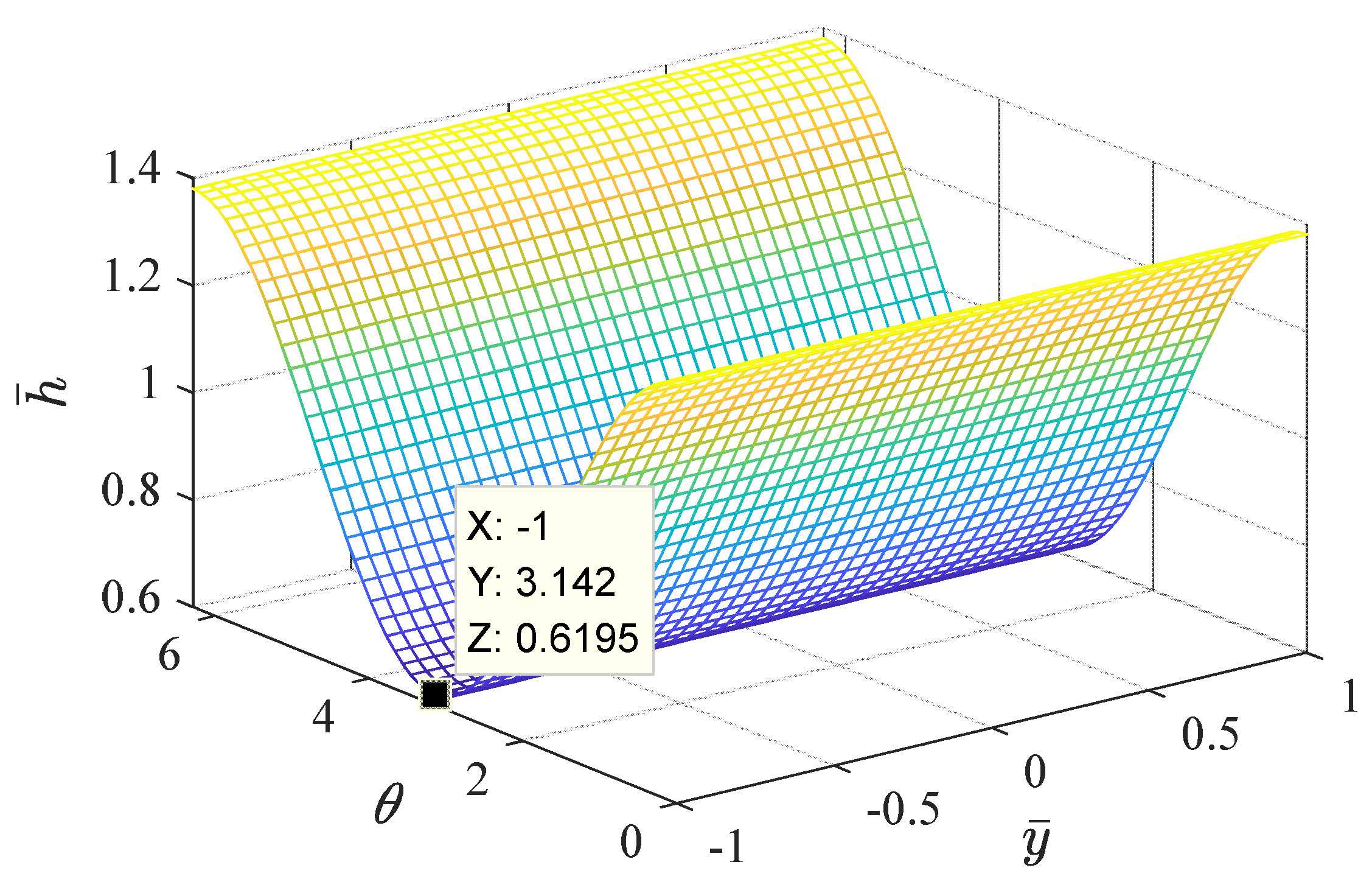
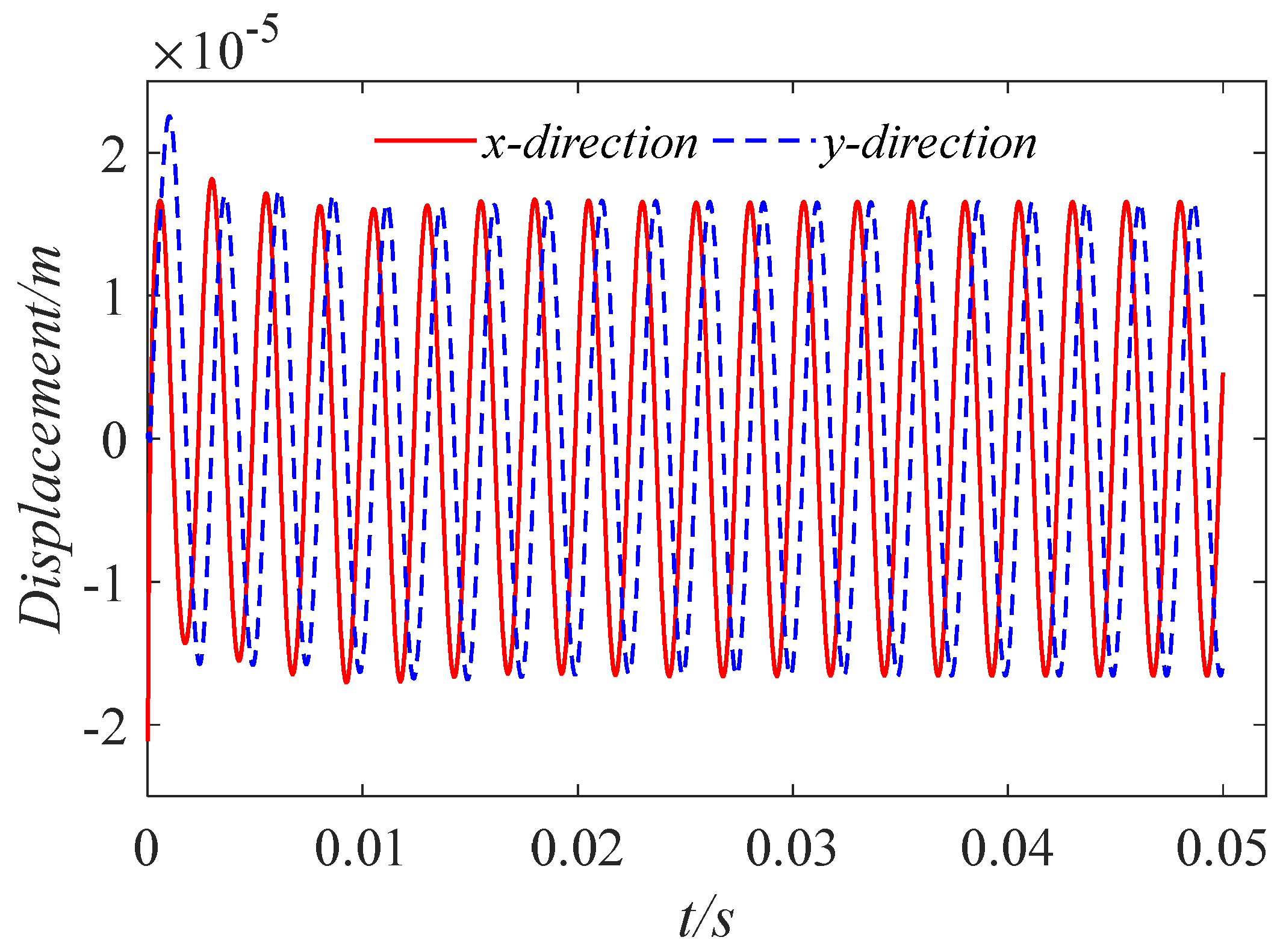
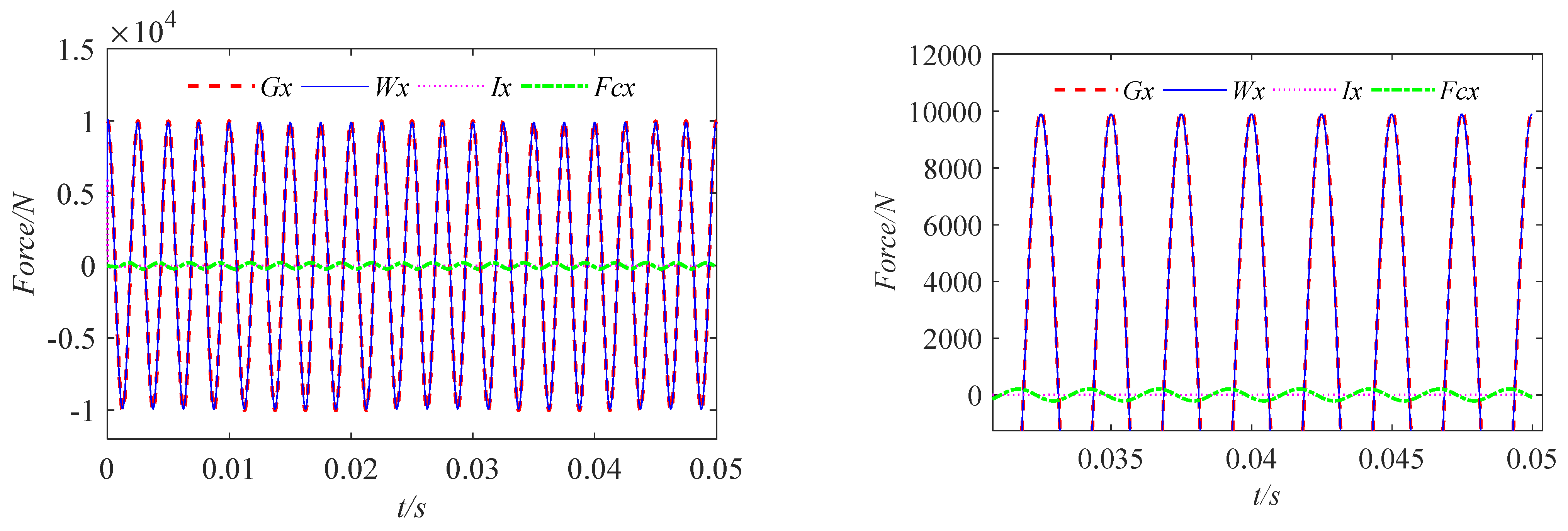
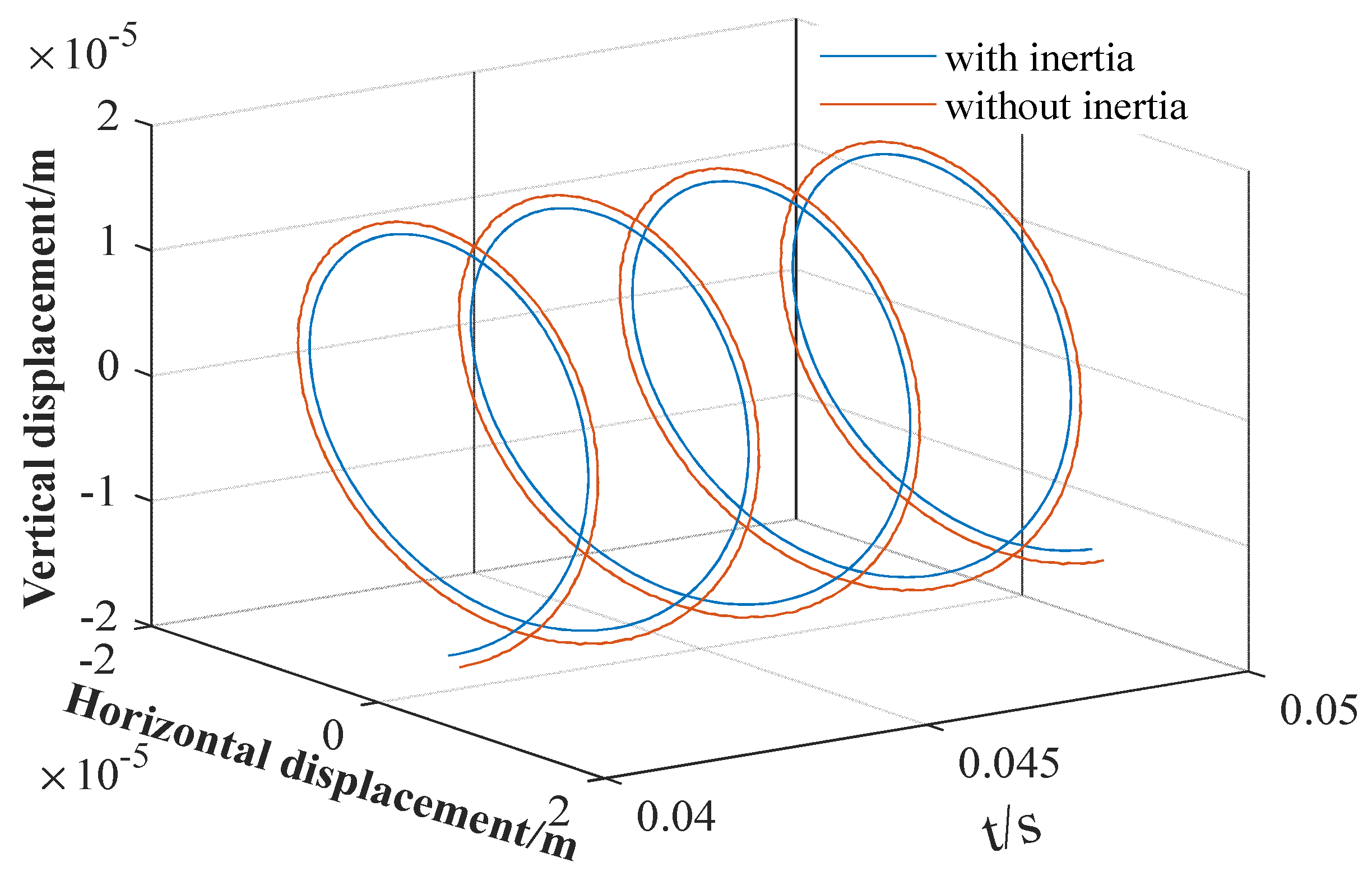
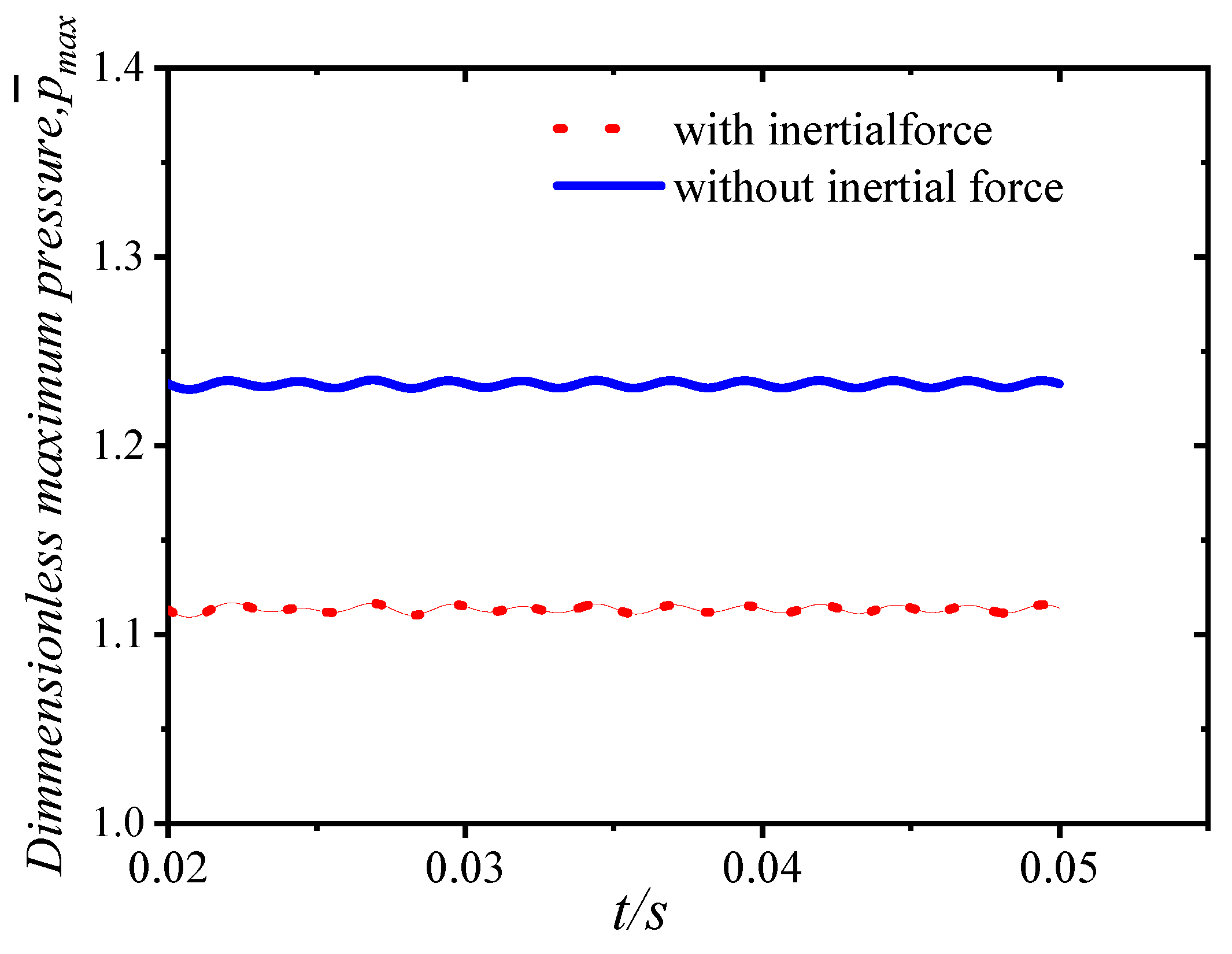
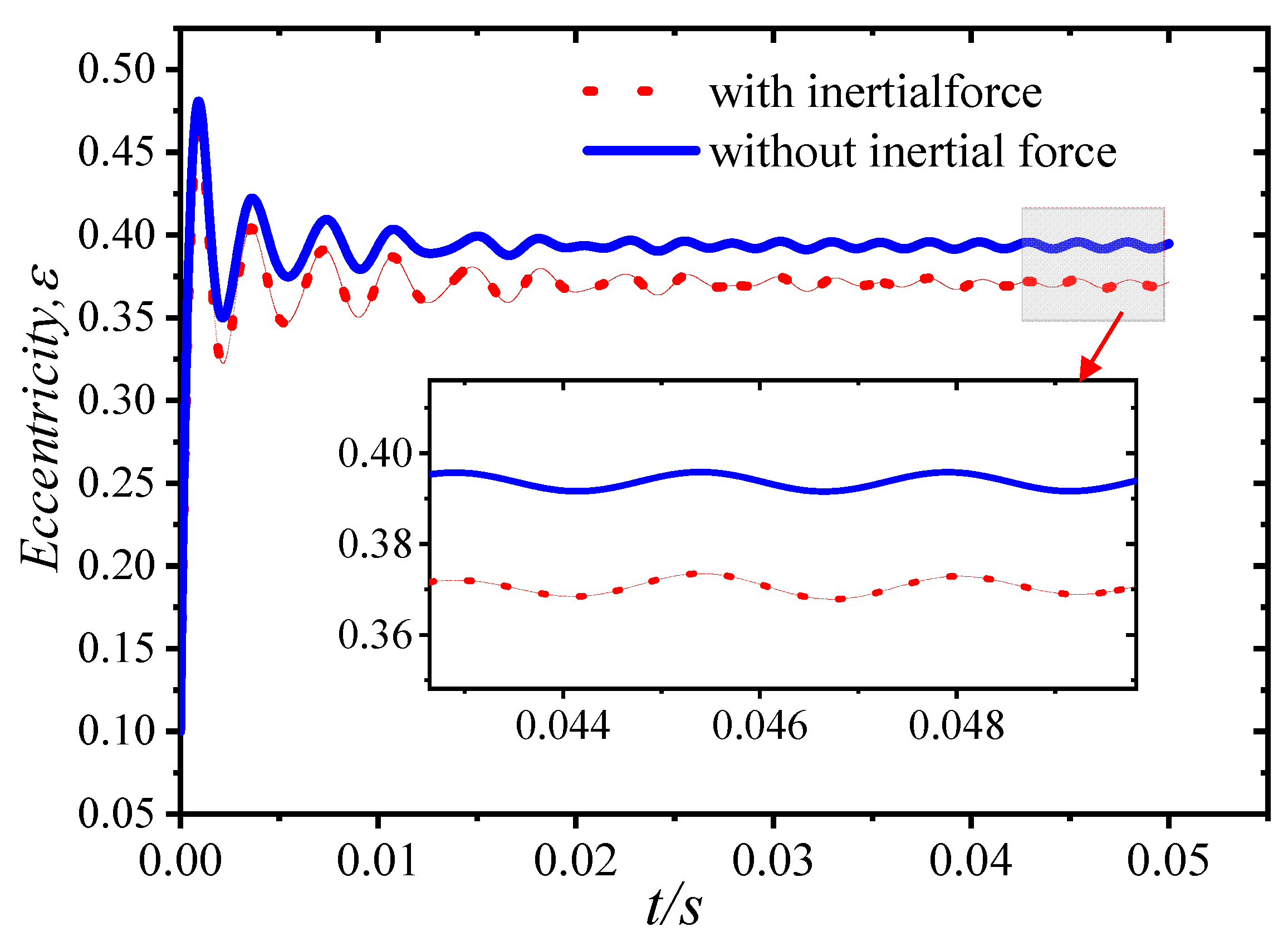
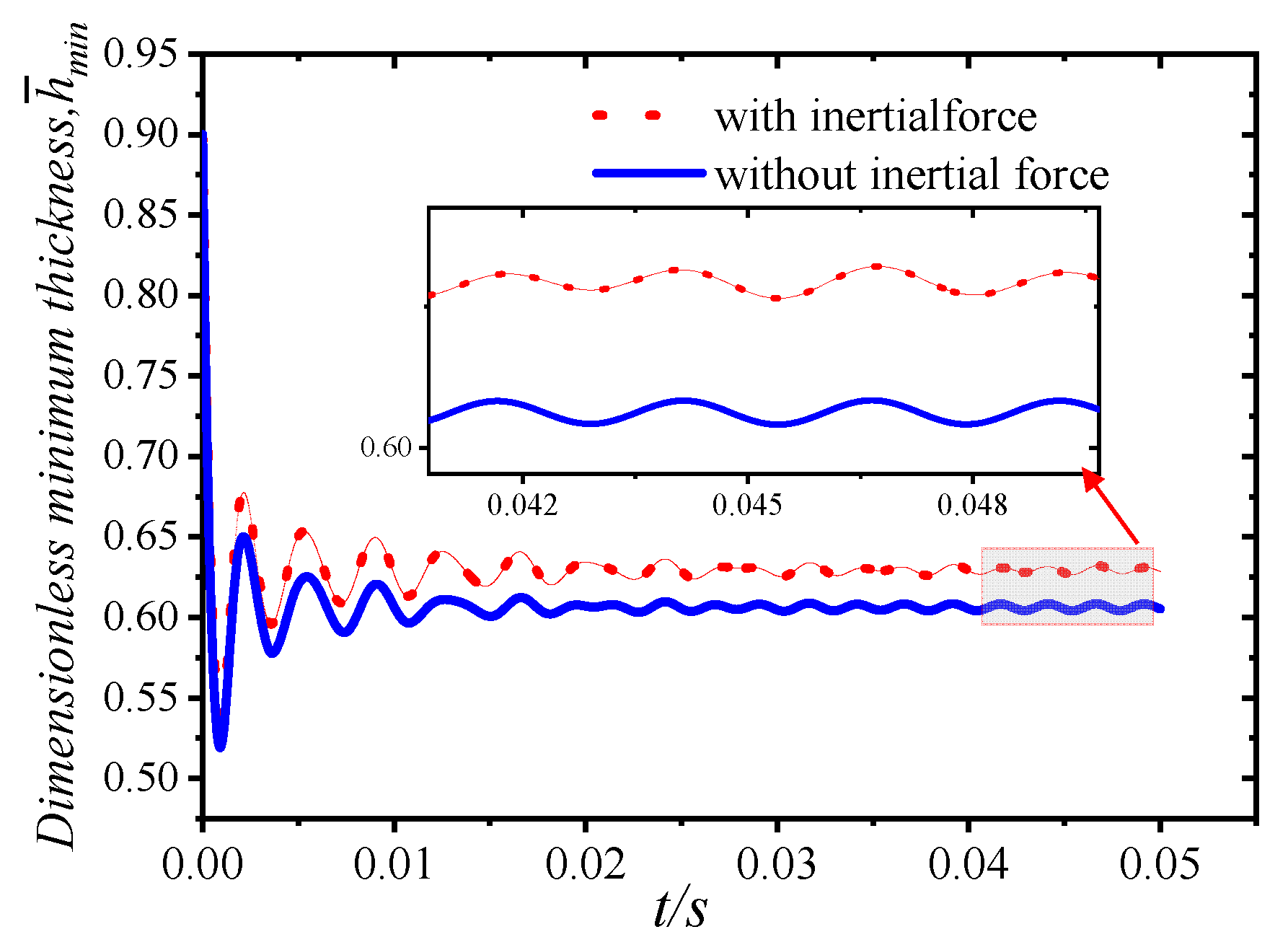
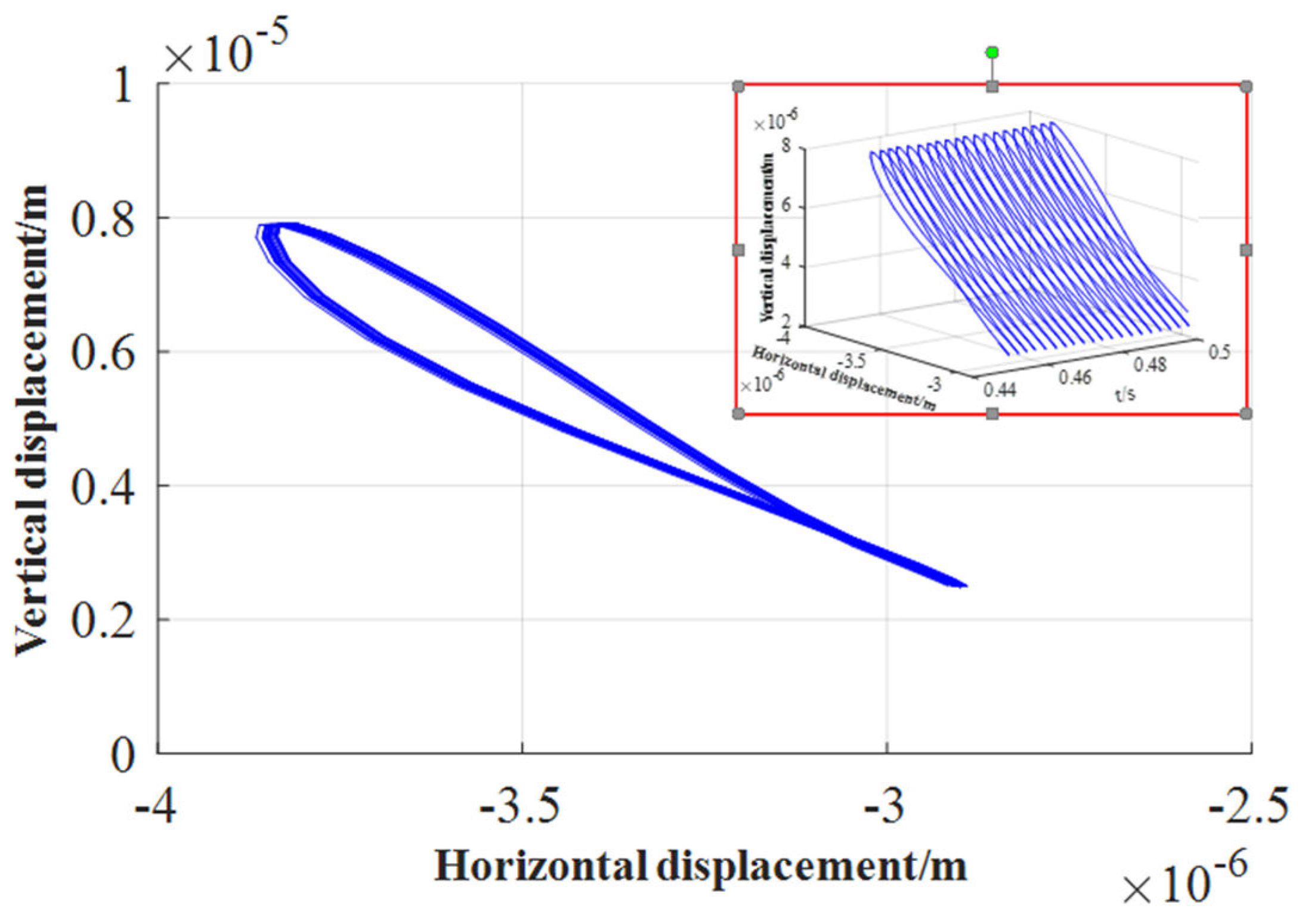
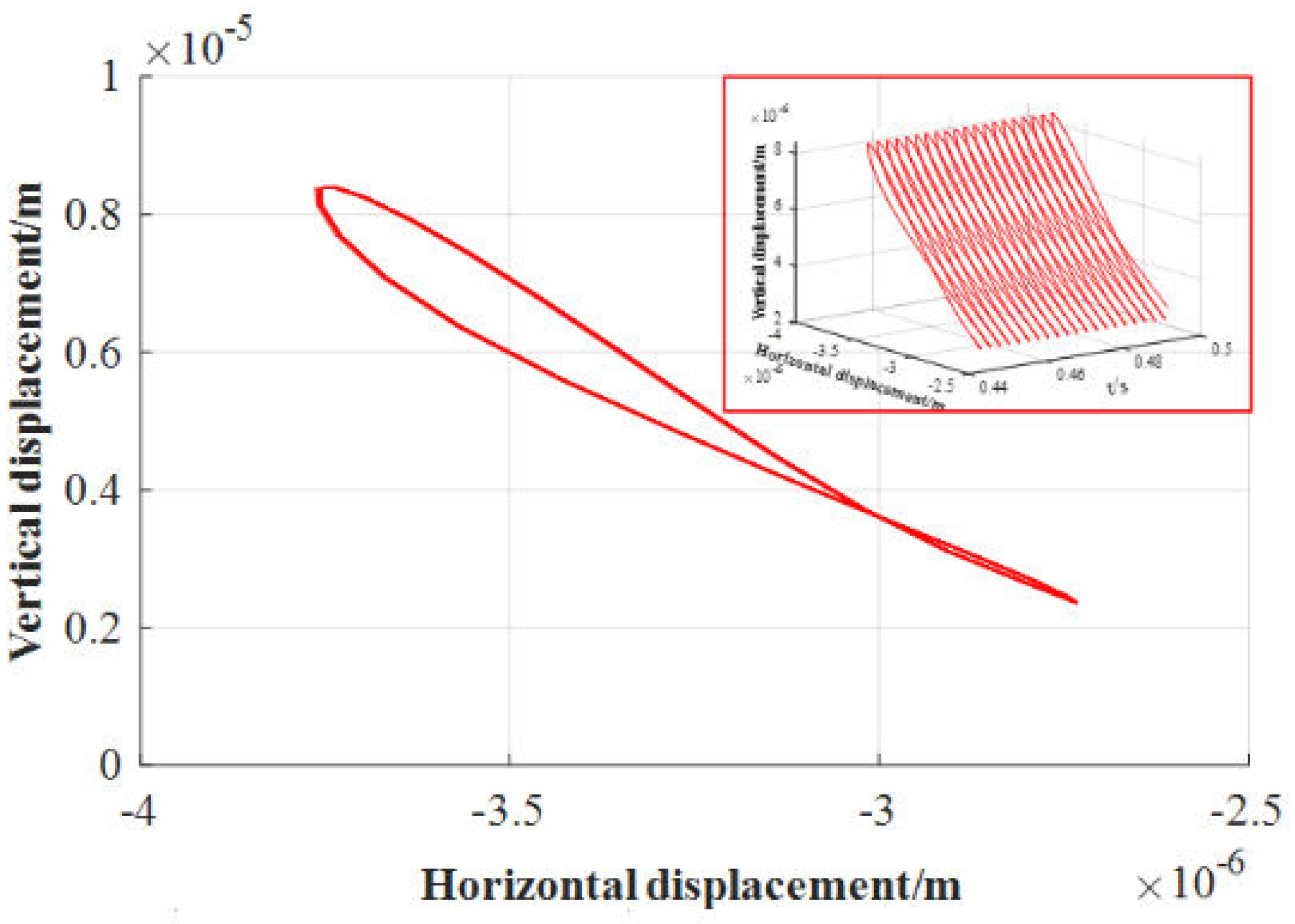
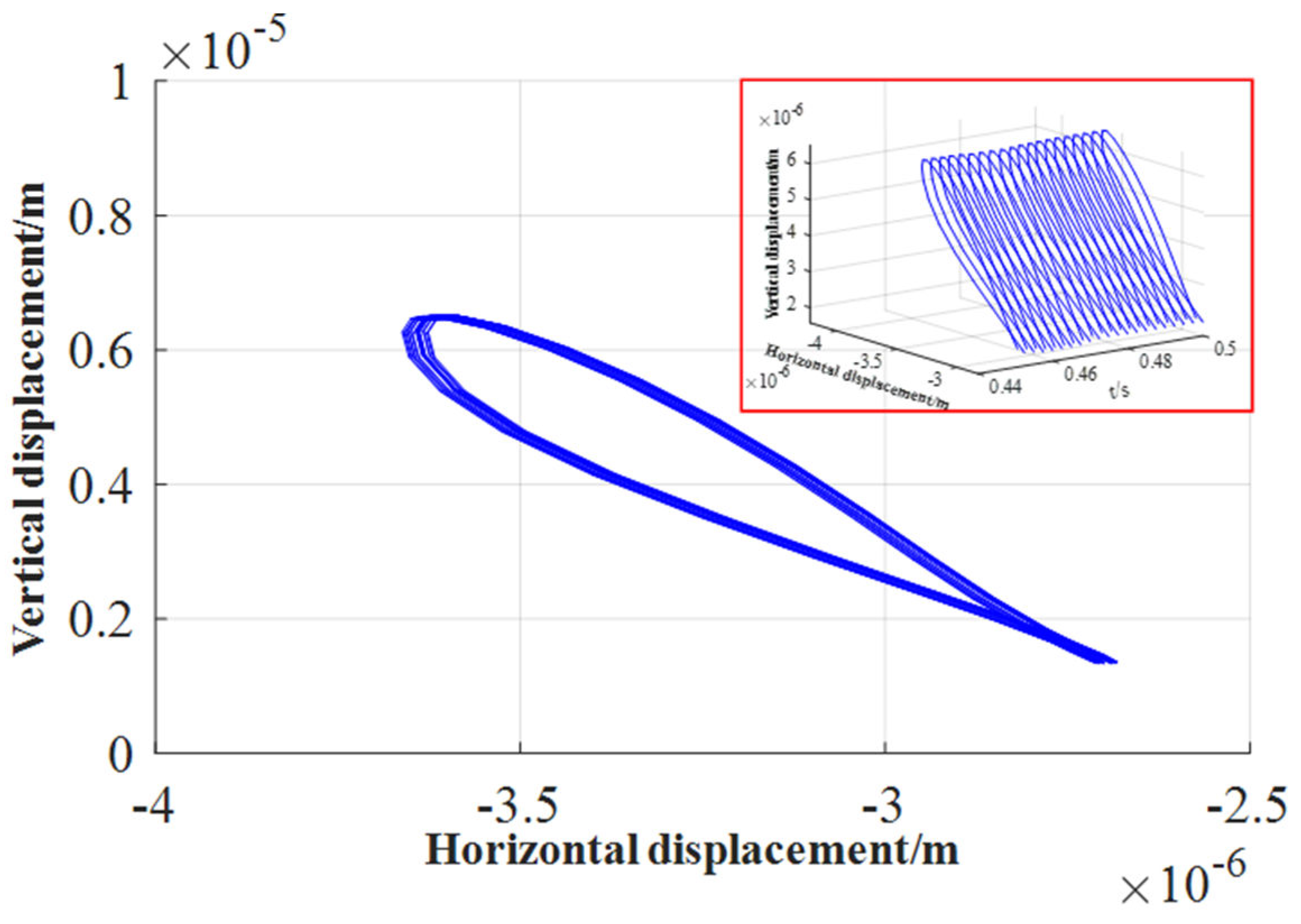
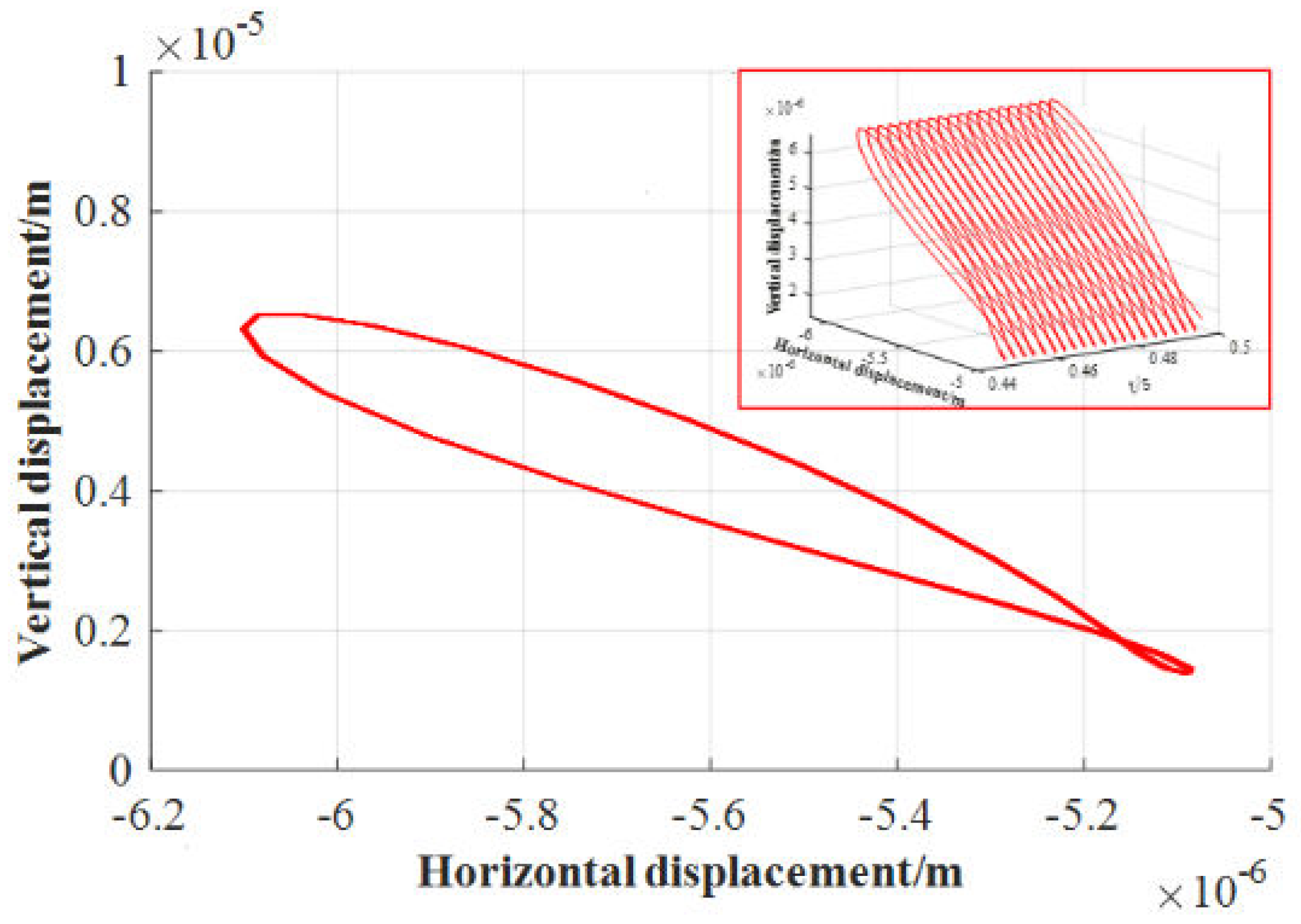
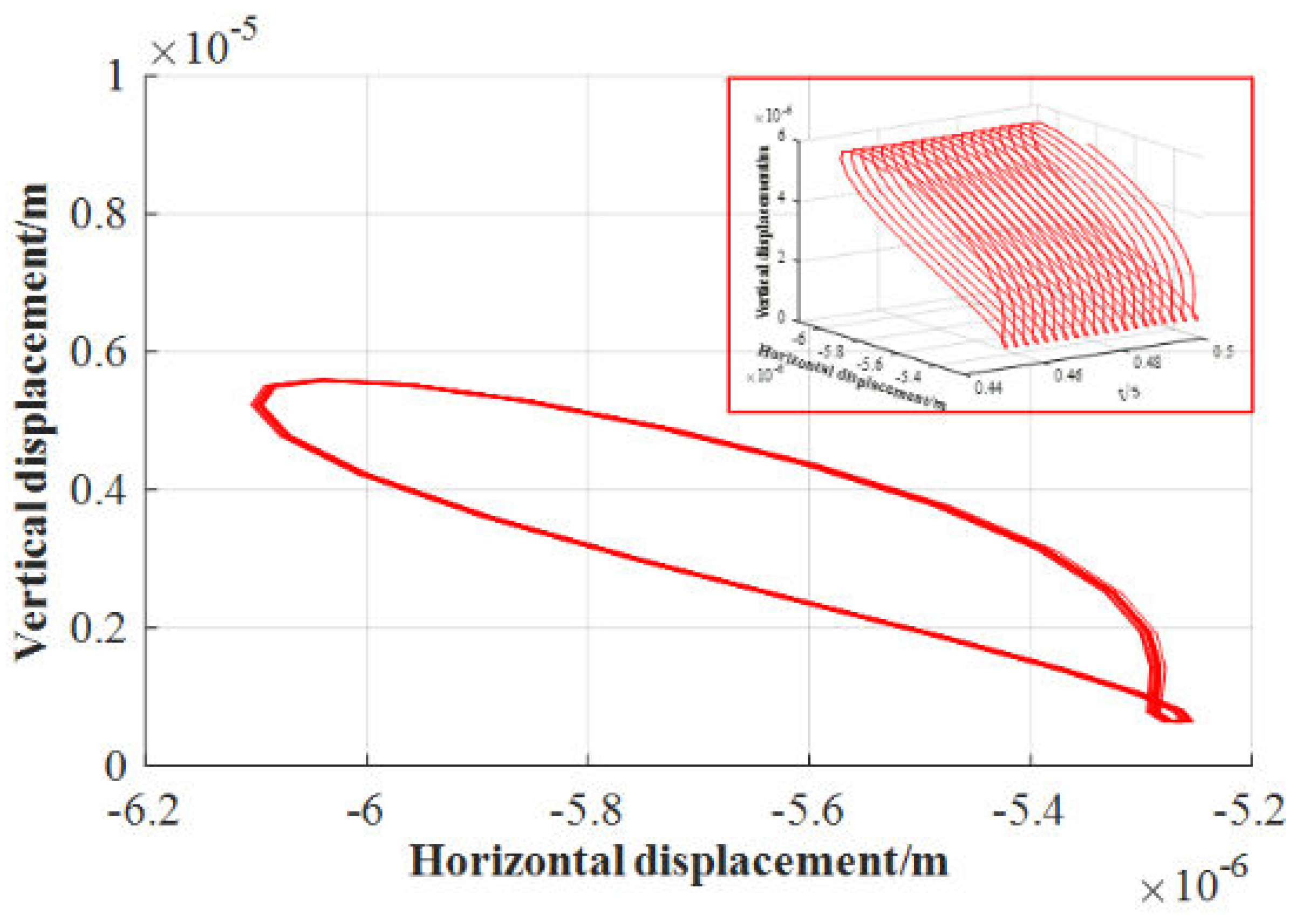
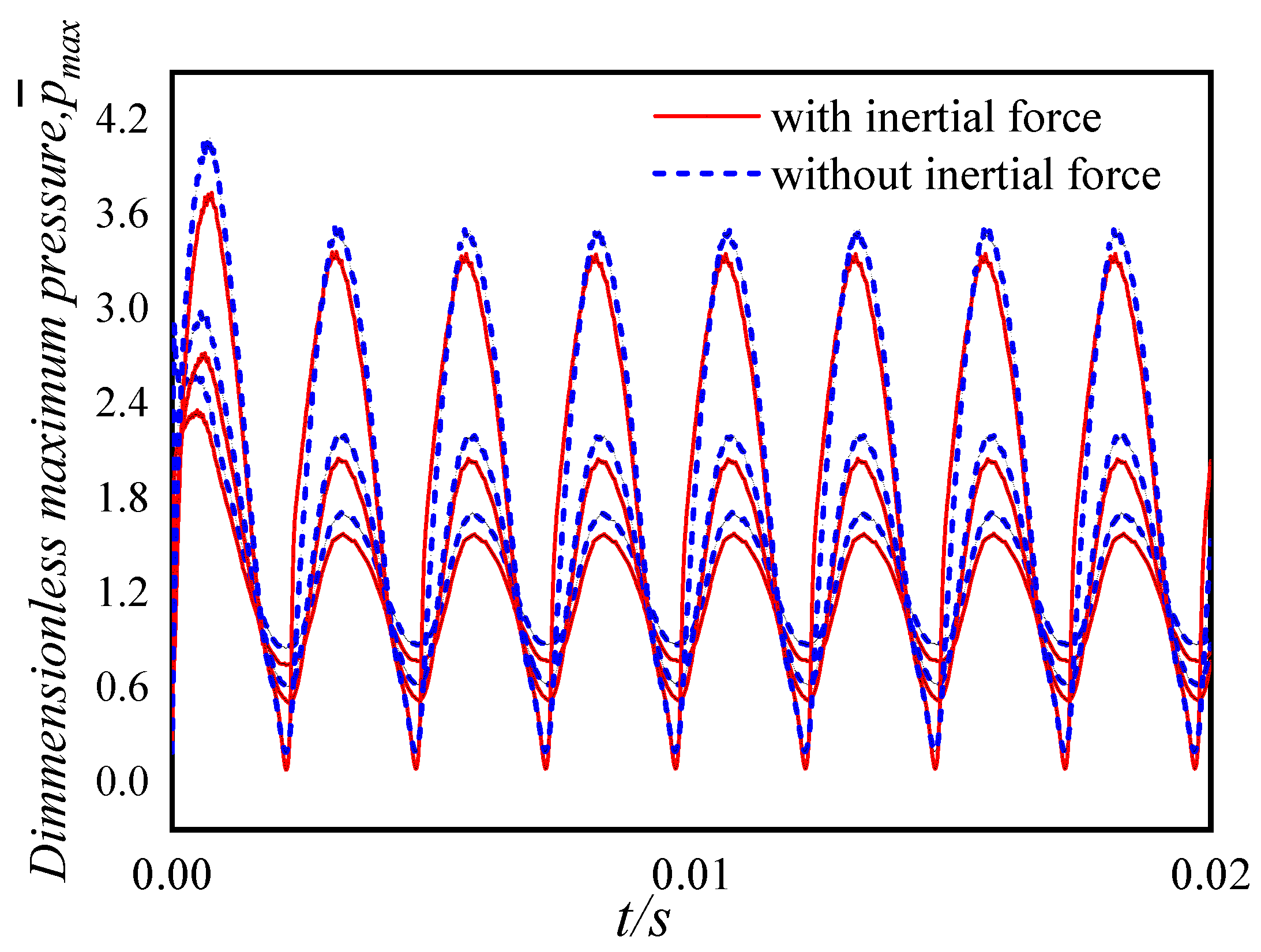
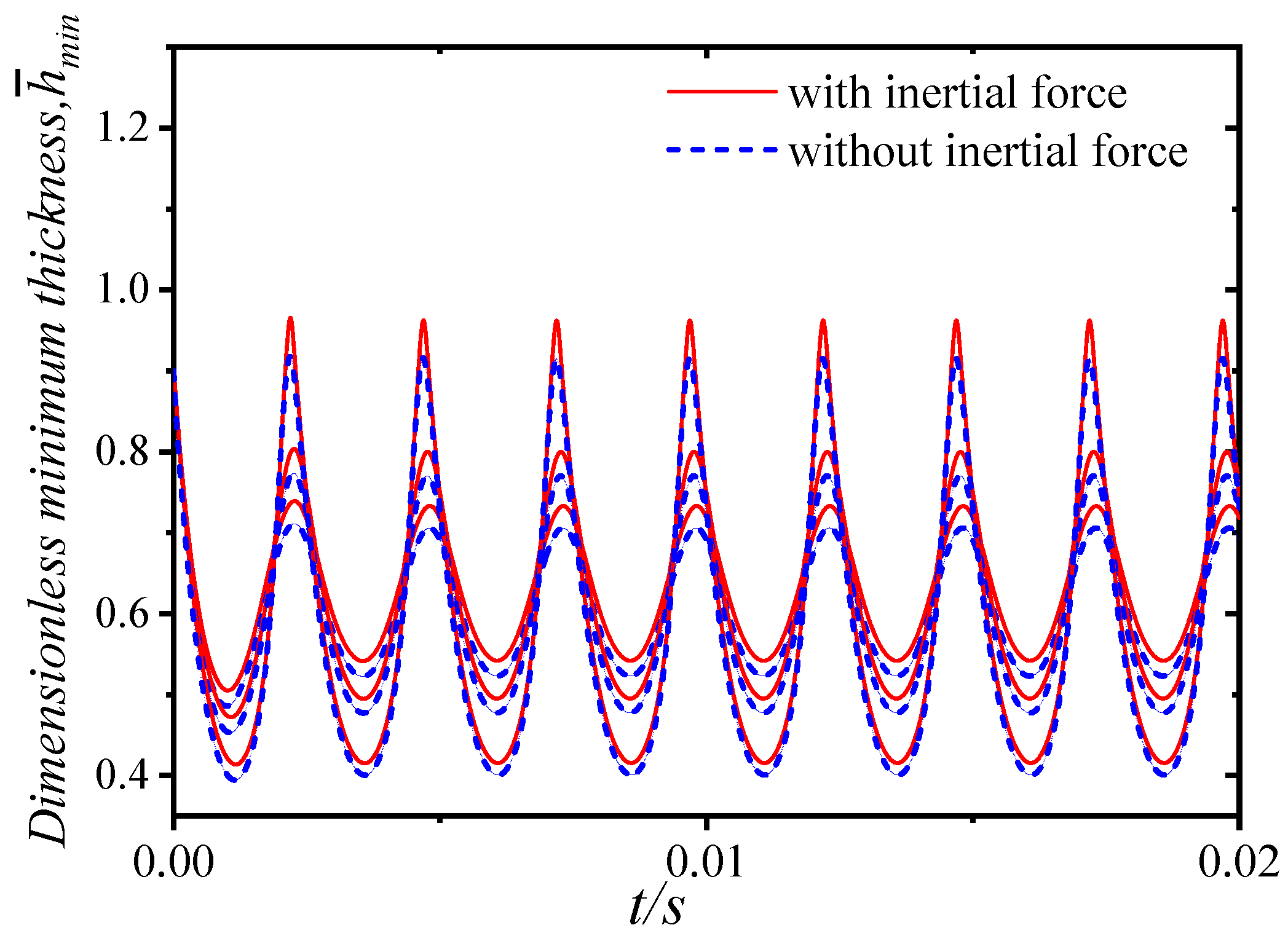
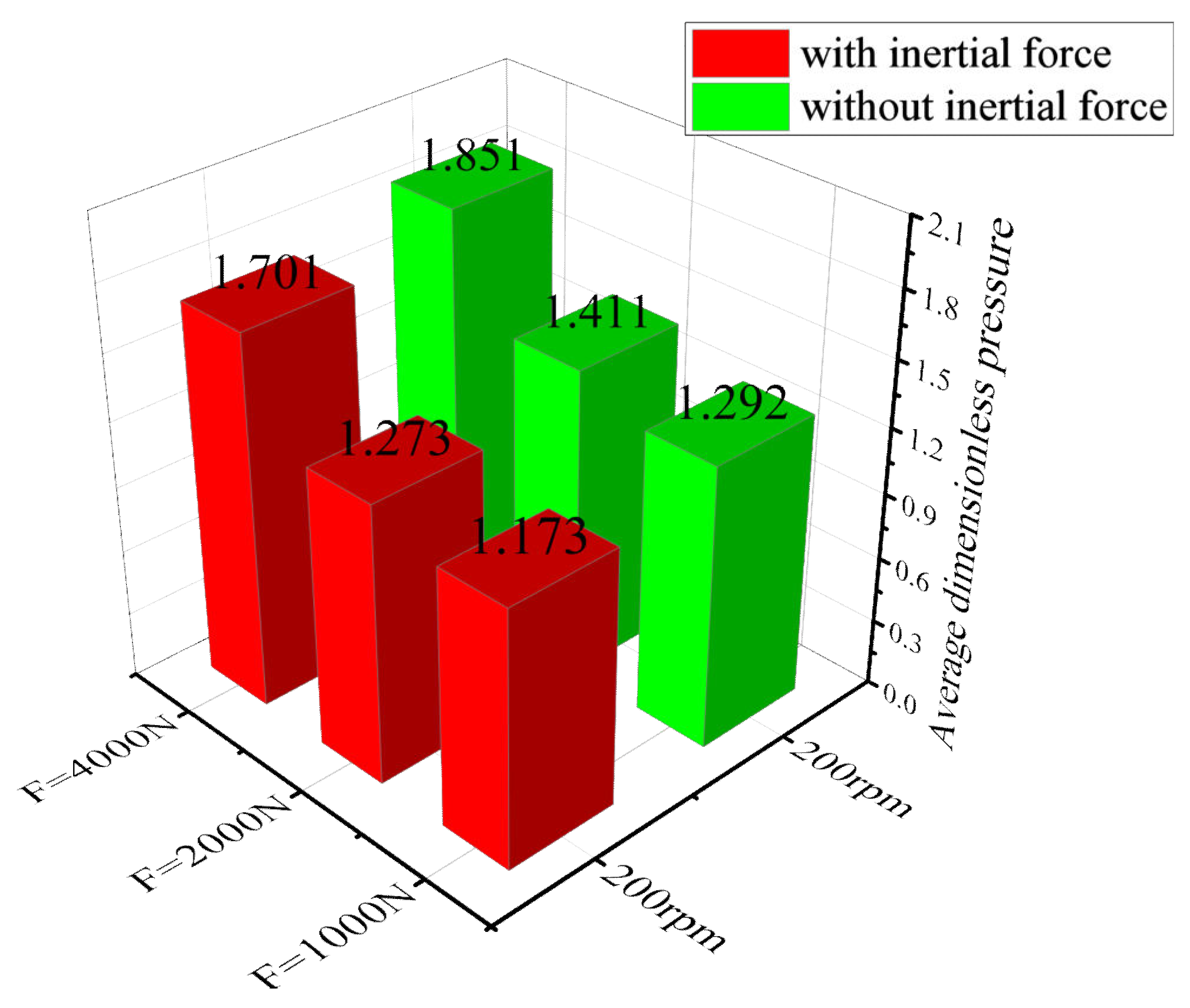
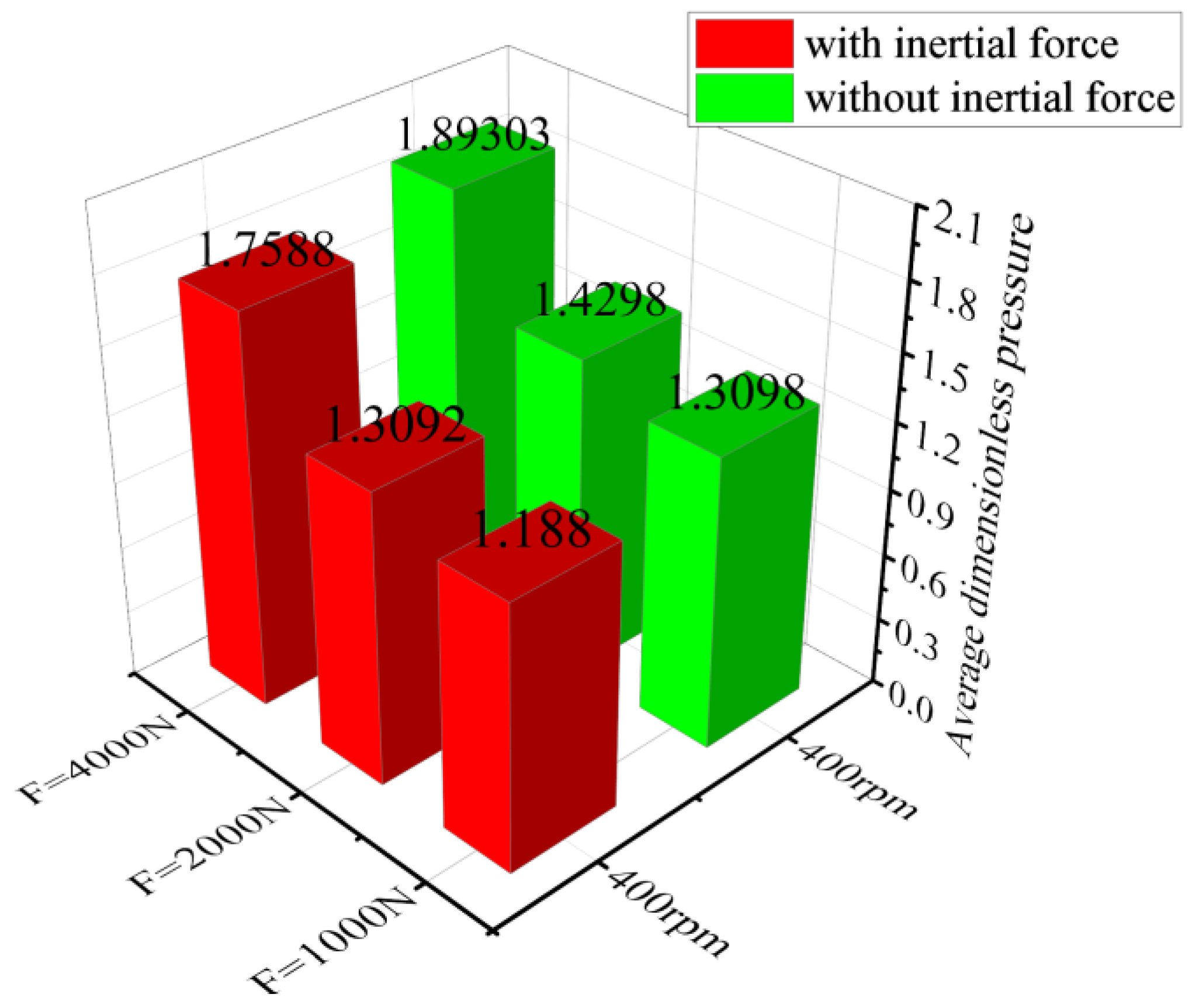
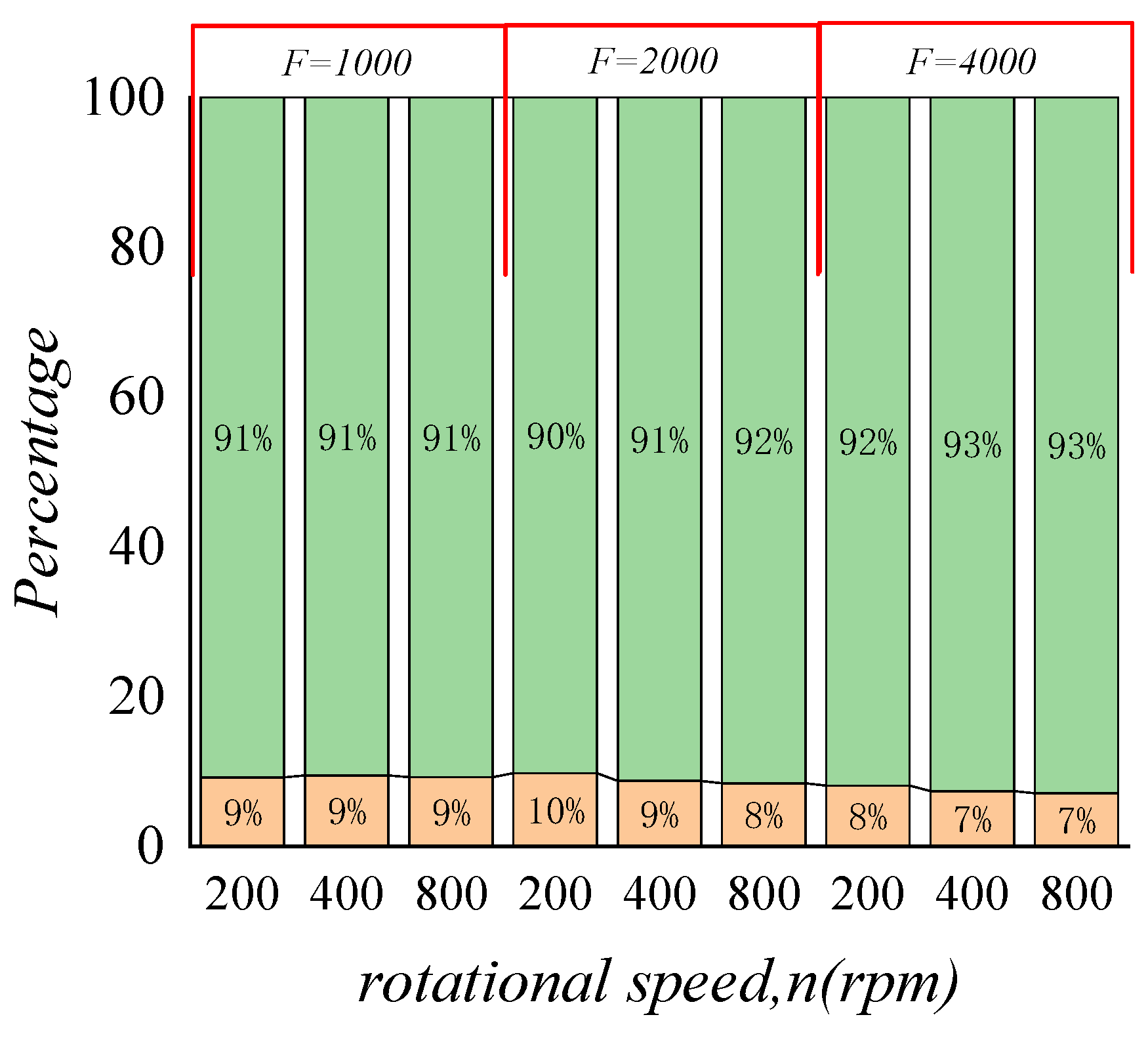
3.2. Effect of Inertial Force on Lubrication Characteristics
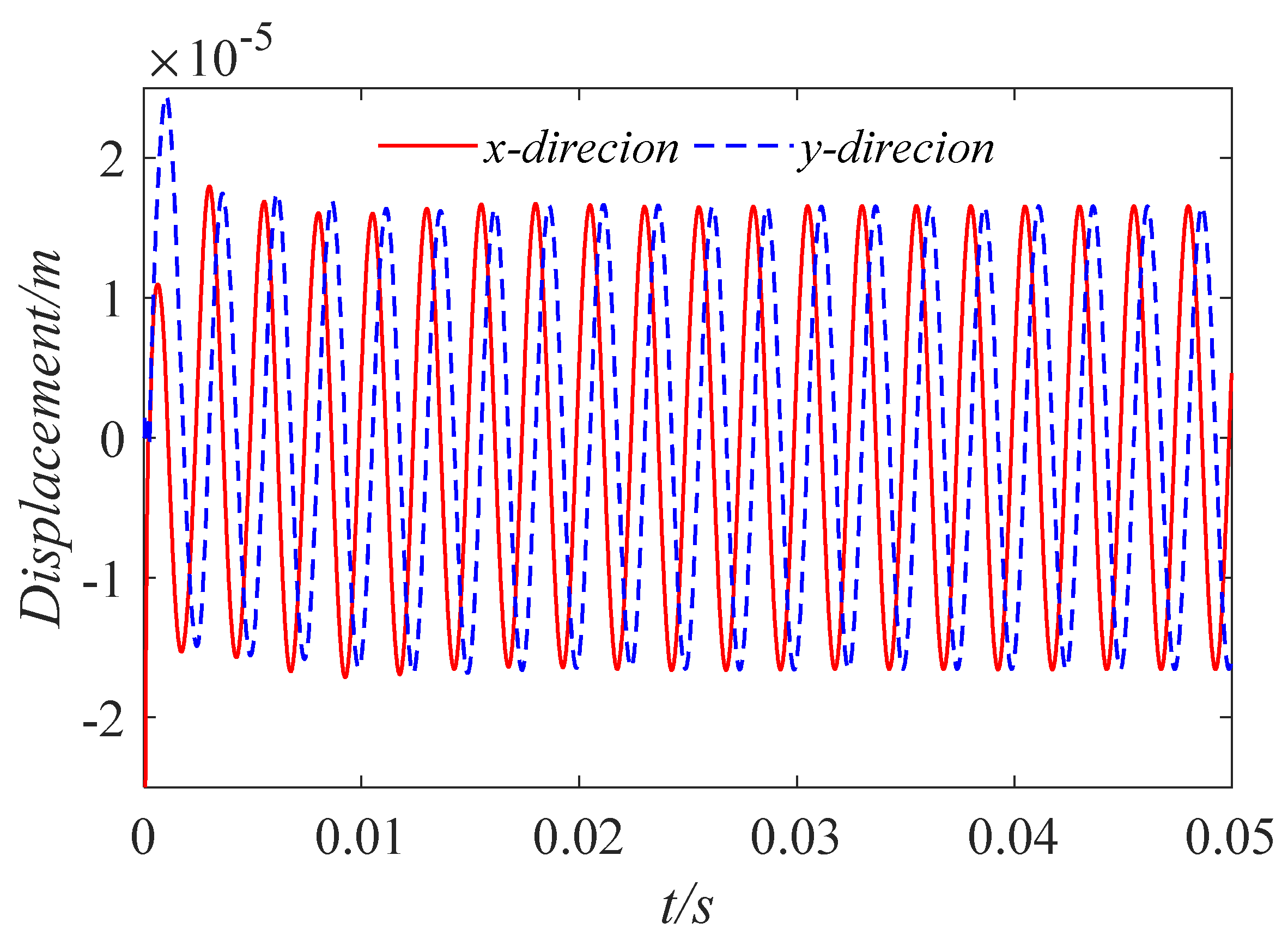
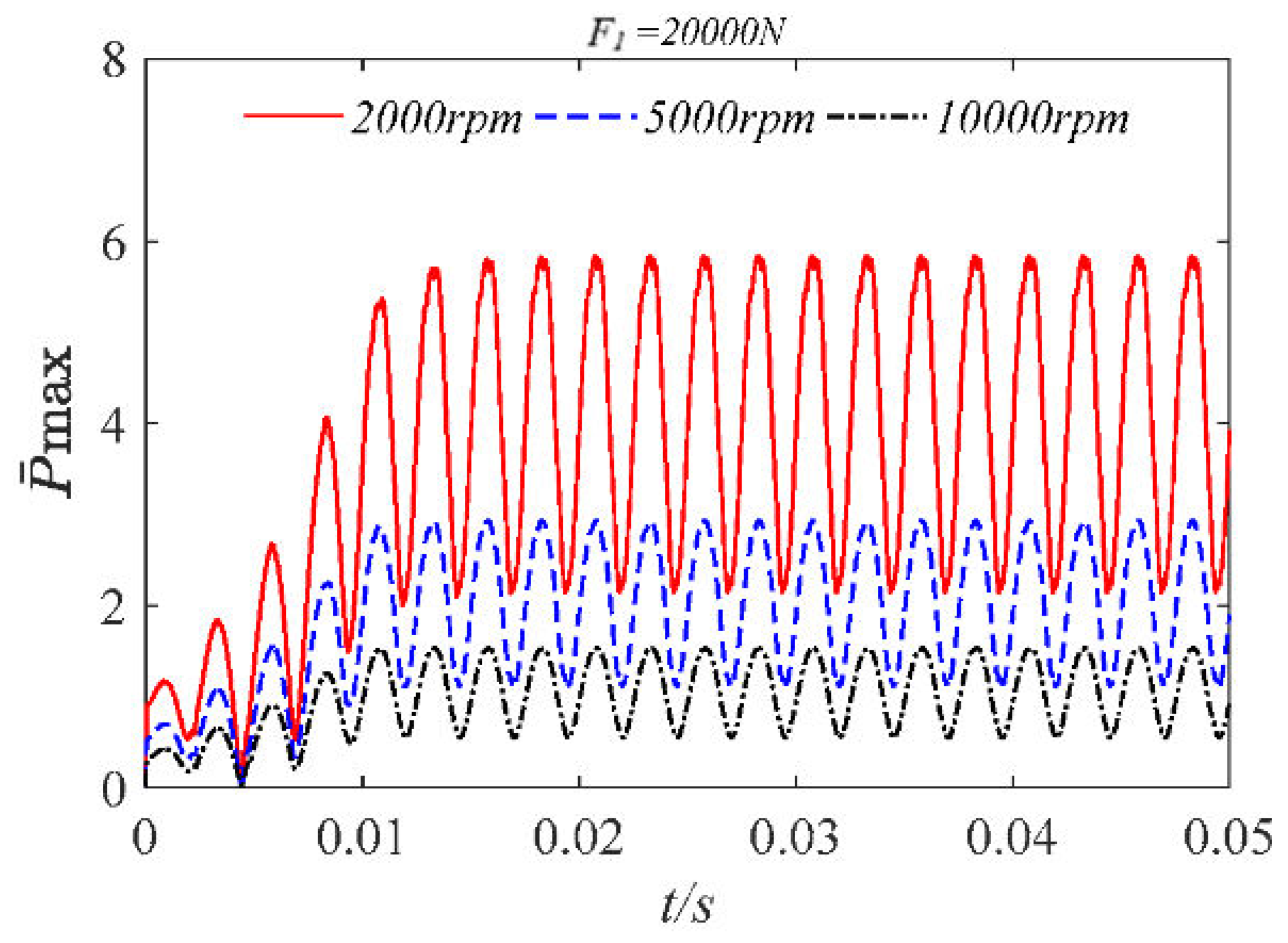
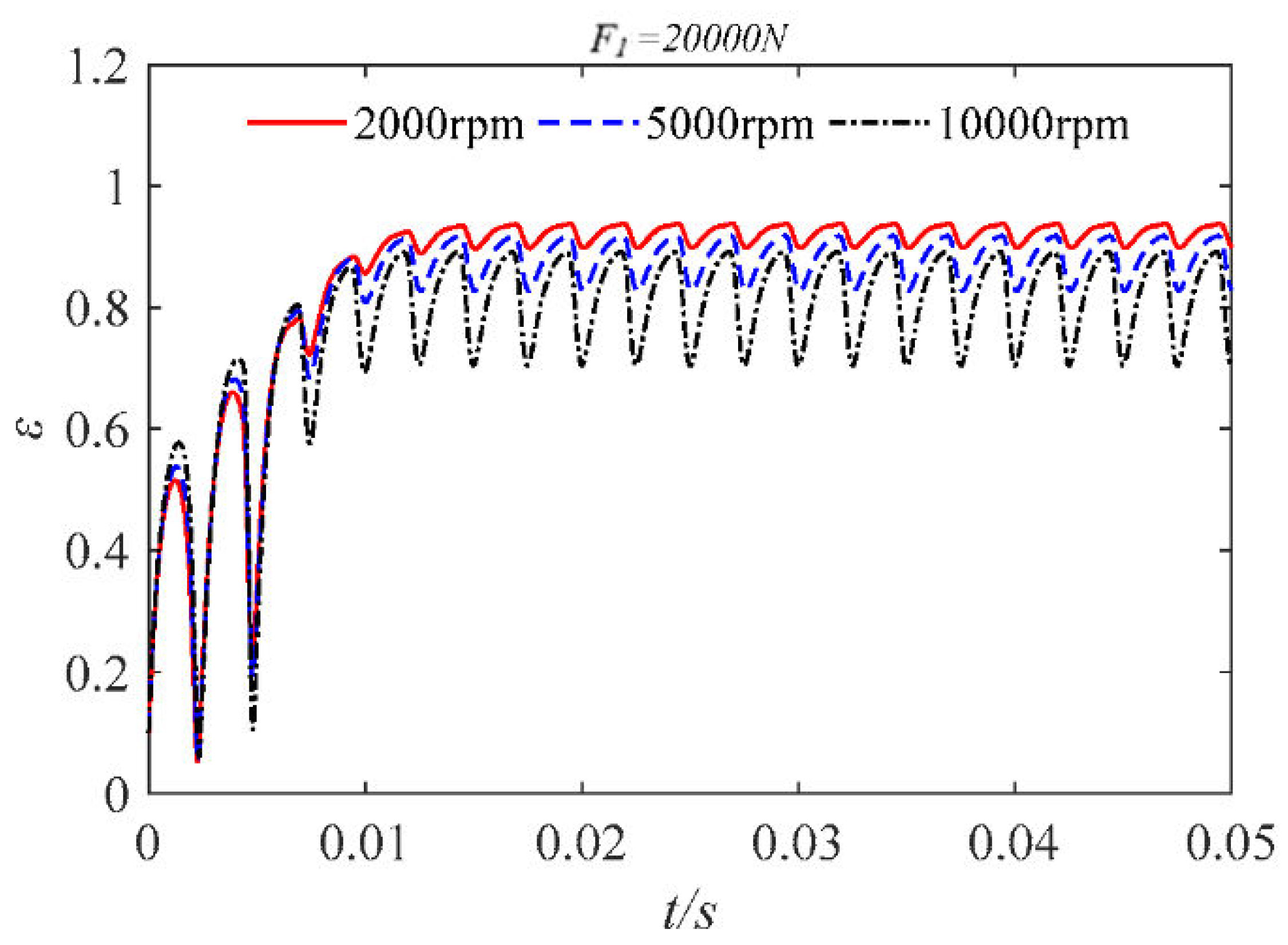
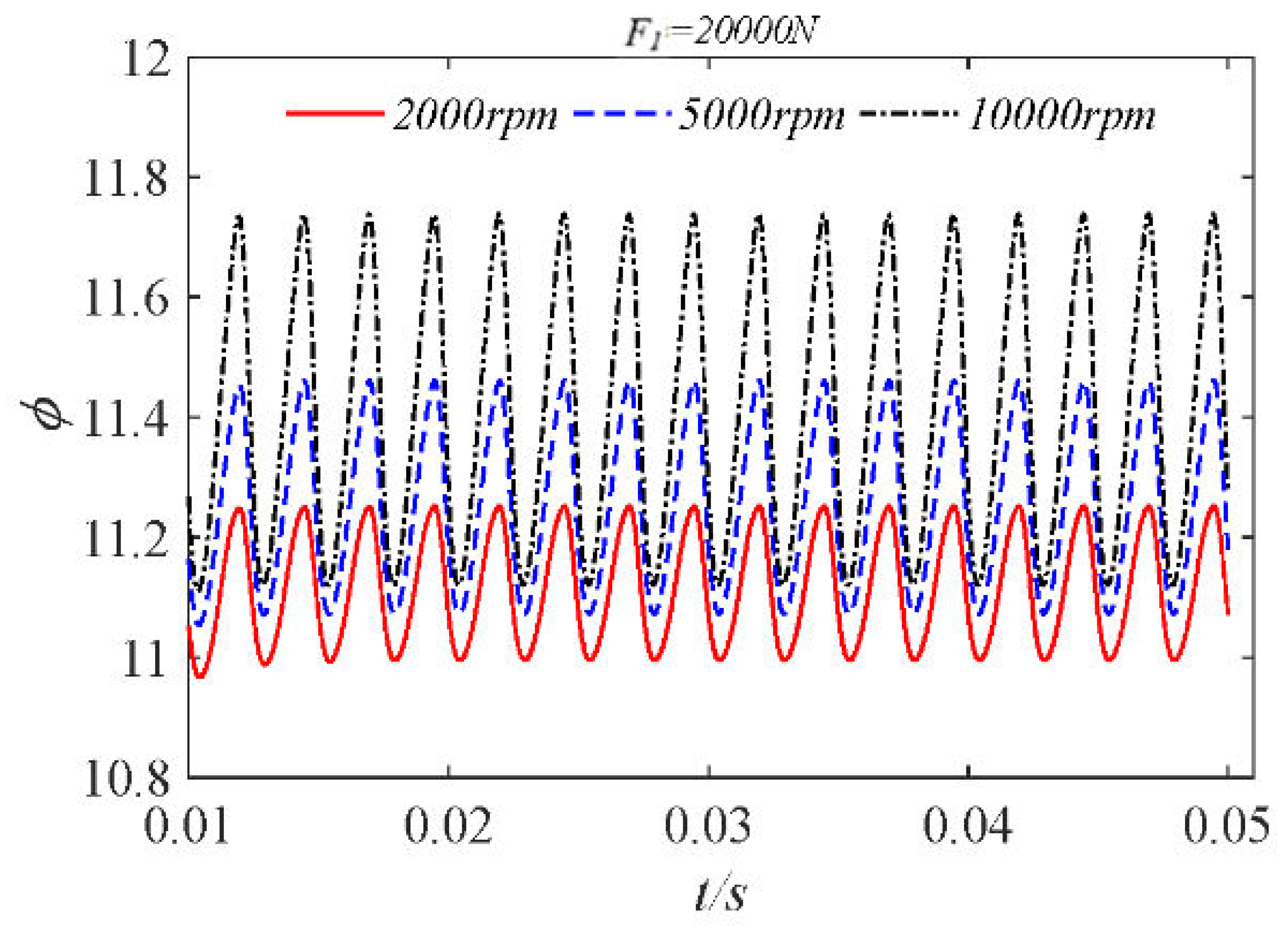
4. Analysis of Water Film Dynamic Characteristics under Low Speed and Heavy Load
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ε | Eccentricity ratio |
| D | Bearing diameter, m D = 2R |
| d | Journal diameter, m d = 2r |
| L | Bearing width, m |
| Attitude angle | |
| Angular velocity, rad | |
| c | Radial clearance, m |
| h | Water film thickness, m |
| ρ | Density of liquid phase. |
| e | Eccentricity, m |
| η0 | Viscosity of water, Pa·s |
| u, v | x, y direction displacement, m |
| n | Rotate speed, rpm |
| x, y direction external load, N | |
| M | Mass of the journal, kg |
| p | Pressure, Pa |
| v | Poisson’s ratio |
| Stiffness factor | |
| Damping factor | |
| Inertial forces, N | |
| Centripetal force, N | |
| Reynolds number | |
| Circumference, axial direction | |
| Radial, tangential direction | |
| Circumference, axial node |
References
- Xie, Z.L.; Jiao, J.; Yang, K. A state-of-art review on the water-lubricated bearing. Tribol. Int. 2023, 180, 108276. [Google Scholar] [CrossRef]
- Mallya, R.; Shenoy, S.B.; Pai, R. Steady state characteristics of misaligned multiple axial groove water-lubricated journal bearing. J. Eng. Tribol. 2015, 229, 712–722. [Google Scholar] [CrossRef]
- Lin, C.G.; Yang, Y.N.; Chu, J.L.; Sima, C.; Liu, P.; Qi, L.B.; Zou, M.S. Study on nonlinear dynamic characteristics of propulsion shafting under friction contact of stern bearings. Tribol. Int. 2023, 183, 108391. [Google Scholar] [CrossRef]
- Cai, J.L.; Xiang, G.; Li, S. Mathematical modeling for nonlinear dynamic mixed friction behaviors of novel coupled bearing lubricated with low viscosity fluid. Phys. Fluids 2022, 34, 093612. [Google Scholar] [CrossRef]
- Lin, C.G.; Zou, M.S.; Sima, C.; Liu, S.X.; Jiang, L.W. Friction-induced vibration and noise of marine stern tube bearings considering perturbations of the stochastic rough surface. Tribol. Int. 2019, 131, 661–671. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.R.; Niu, G.L.; Zhang, L.J. The Research Actuality and Development Trends of Water Lubricated Bearings. Equip. Manuf. Technol. 2008, 1, 101–102. [Google Scholar]
- Xie, Z.L.; Jiao, J.; Yang, K. Theoretical and experimental study on the fluid-structure-acoustic coupling dynamics of a new water lubricated bearing. Tribol. Int. 2023, 177, 107982. [Google Scholar] [CrossRef]
- Zou, M.S.; Tang, H.C.; Liu, S.X. Modeling and calculation of acoustic radiation of underwater stiffened cylindrical shells treated with local damping. Mar. Struct. 2023, 88, 103366. [Google Scholar] [CrossRef]
- Xie, Z.L.; Jiao, J.; Wrona, S. The fluid-structure interaction lubrication performances of a novel bearing: Experimental and numerical study. Tribol. Int. 2023, 179, 108151. [Google Scholar] [CrossRef]
- Wang, J.G.; Zhou, J.Z.; Dong, D.W.; Yan, B.; Huang, C.R. Nonlinear dynamic analysis of a rub-impact rotor supported by oil film bearings. Arch. Appl. Mech. 2012, 83, 413–430. [Google Scholar] [CrossRef]
- Brown, R.D.; Addison, P.; Chan, A.H.C. Chaos in the unbalance response of journal bearings. Nonlinear Dyn. 1994, 5, 421–432. [Google Scholar] [CrossRef]
- Jing, J.P.; Meng, G.; Sun, Y.; Xia, S.B. On the non-linear dynamic behavior of a rotor-bearing system. J. Sound Vib. 2004, 274, 1031–1044. [Google Scholar] [CrossRef]
- Brancati, R.; Rocca, E.; Russo, M.; Russo, R. Journal orbits and their stability for rigid unbalanced rotors. J. Tribol. 1995, 117, 709–716. [Google Scholar] [CrossRef]
- Brancati, R.; Russo, M.; Russo, R. On the stability of periodic motions of an unbalanced rigid rotor on lubricated journal bearings. Nonlinear Dyn. 1996, 10, 175–185. [Google Scholar] [CrossRef]
- Li, D.X.; Xu, J.X. A method to determine the periodic solution of the non-linear dynamics system. J. Sound Vib. 2004, 275, 1–16. [Google Scholar] [CrossRef]
- Lin, C.G.; Zou, M.S.; Sima, C.; Qi, L.B.; Yu, Y. Non-Linear coupled dynamics of a flexible propeller-shaft system supported by water film bearings. J. Vib. Acoust. 2020, 142, 031008. [Google Scholar] [CrossRef]
- Sun, W.P.; Yan, Z.M.; Tan, T.; Zhao, D.L.; Luo, X.Q. Nonlinear characterization of the rotor-bearing system with the oil-film and unbalance forces considering the effect of the oil-film temperature. Nonlinear Dyn. 2018, 92, 1119–1145. [Google Scholar] [CrossRef]
- Cai, J.L.; Han, Y.F.; Xiang, G.; Wang, J.X.; Wang, L.W. Effects of wear and shaft-shape error defects on the tribo-dynamic response of water-lubricated bearings under propeller disturbance. Phys. Fluids 2022, 34, 077118. [Google Scholar] [CrossRef]
- Singh, U.; Roy, L.; Sahu, M. Steady-state thermo-hydrodynamic analysis of cylindrical fluid film journal bearing with an axial groove. Tribol. Int. 2008, 13, 1135–1144. [Google Scholar] [CrossRef]
- Kornaeva, E.; Kornaev, A.; Savin, L.; Galichev, A.; Babin, A. Theoretical premises of a vibro-inertial method of viscosity measurement. Vibroengineering Procedia 2016, 8, 440–445. [Google Scholar]
- Xie, Z.L.; Ta, N.; Rao, Z.S. The lubrication performance of water lubricated bearing with consideration of wall slip and inertial force. J. Hydrodyn. 2017, 29, 52–60. [Google Scholar] [CrossRef]
- Gao, G.Y.; Yin, Z.W.; Jiang, D.X.; Zhang, X.L. Numerical analysis of plain journal bearing under hydrodynamic lubrication by water. Tribol. Int. 2014, 75, 31–38. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Yin, Z.W.; Jiang, D.; Gao, G.Y.; Zhang, X.L. Study of the lubrication performance of water-lubricated journal bearings with CFD and FSI method. Ind. Lubr. Tribol. 2016, 68, 341–348. [Google Scholar] [CrossRef]
- Wojciech, L. Influence of local bush wear on water lubricated sliding bearing load carrying capacity. Tribol. Int. 2016, 103, 352–358. [Google Scholar]
- Xiang, G.; Yang, T.Y.; Guo, J.; Wang, J.X. Optimization transient wear and contact performances of water-lubricated bearings under fluid-solid-thermal coupling condition using profile modification. Wear 2022, 502–503, 204379. [Google Scholar] [CrossRef]
- Sun, F.X.; Zhang, X.B.; Wei, Y.S.; Wang, X.; Wang, D. Stability analysis of rubber-supported thrust bearing in a rotor-bearing system used in marine thrusters under disturbing moments. Tribol. Int. 2020, 151, 106356. [Google Scholar] [CrossRef]
- Jakobsson, B. The finite journal bearing, considering vaporization. Trans. Chalmers Univ. Technol. 1957, 190, 1–116. [Google Scholar]
- Zhang, Z.M. Theory of Hydrodynamic Lubrication of Sliding Bearings; Higher Education Press: Beijing, China, 1986. [Google Scholar]
- Zhang, X.L.; Yin, Z.W.; Gao, G.Y.; Li, Z. Determination of stiffness coefficients of hydrodynamic water-lubricated plain journal bearings. Tribol. Int. 2015, 85, 37–47. [Google Scholar] [CrossRef]
- Booker, J.F. Mobility/impedance methods: A guide for application. J. Tribol. 2014, 136, 024501. [Google Scholar] [CrossRef]
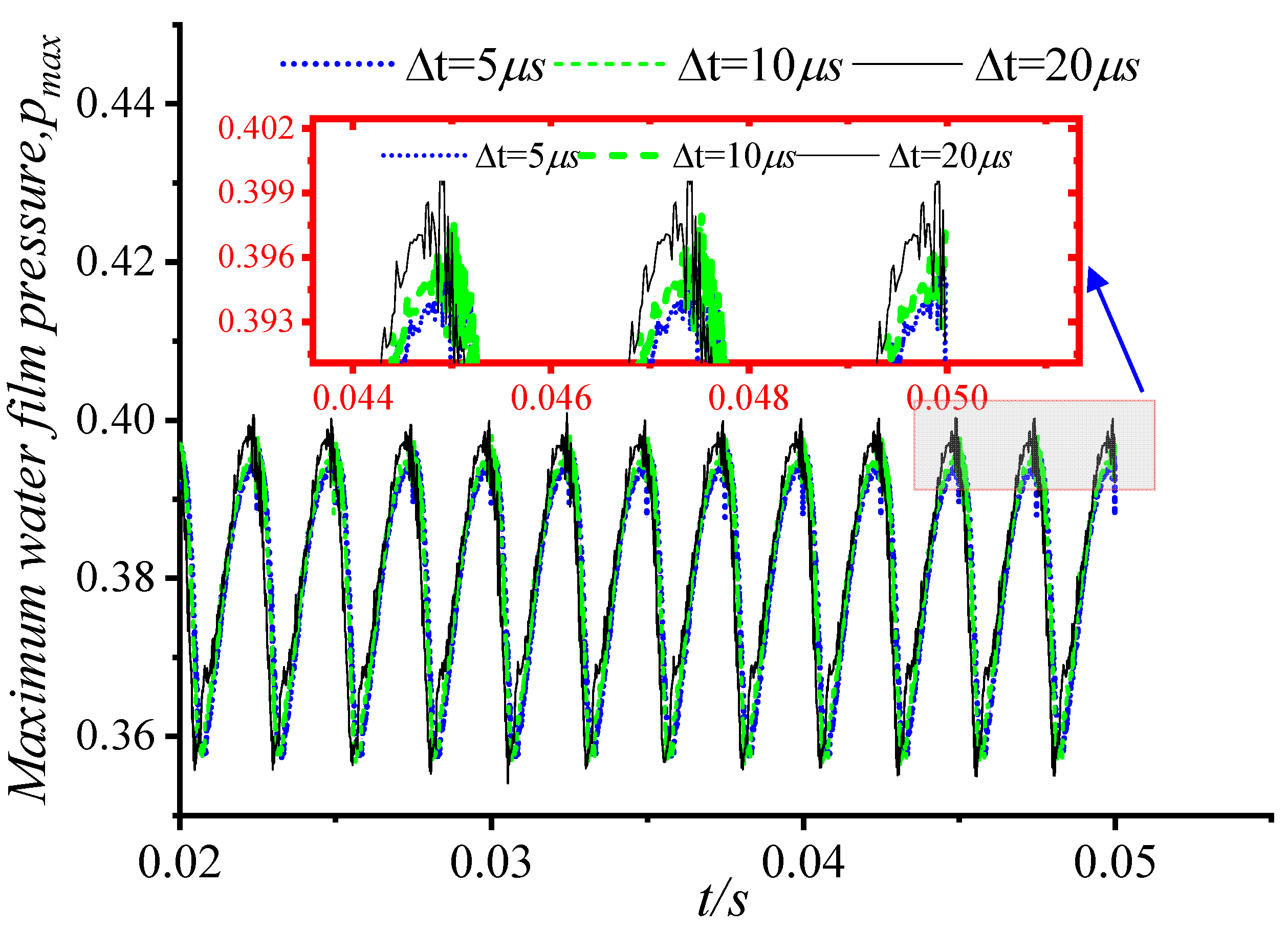
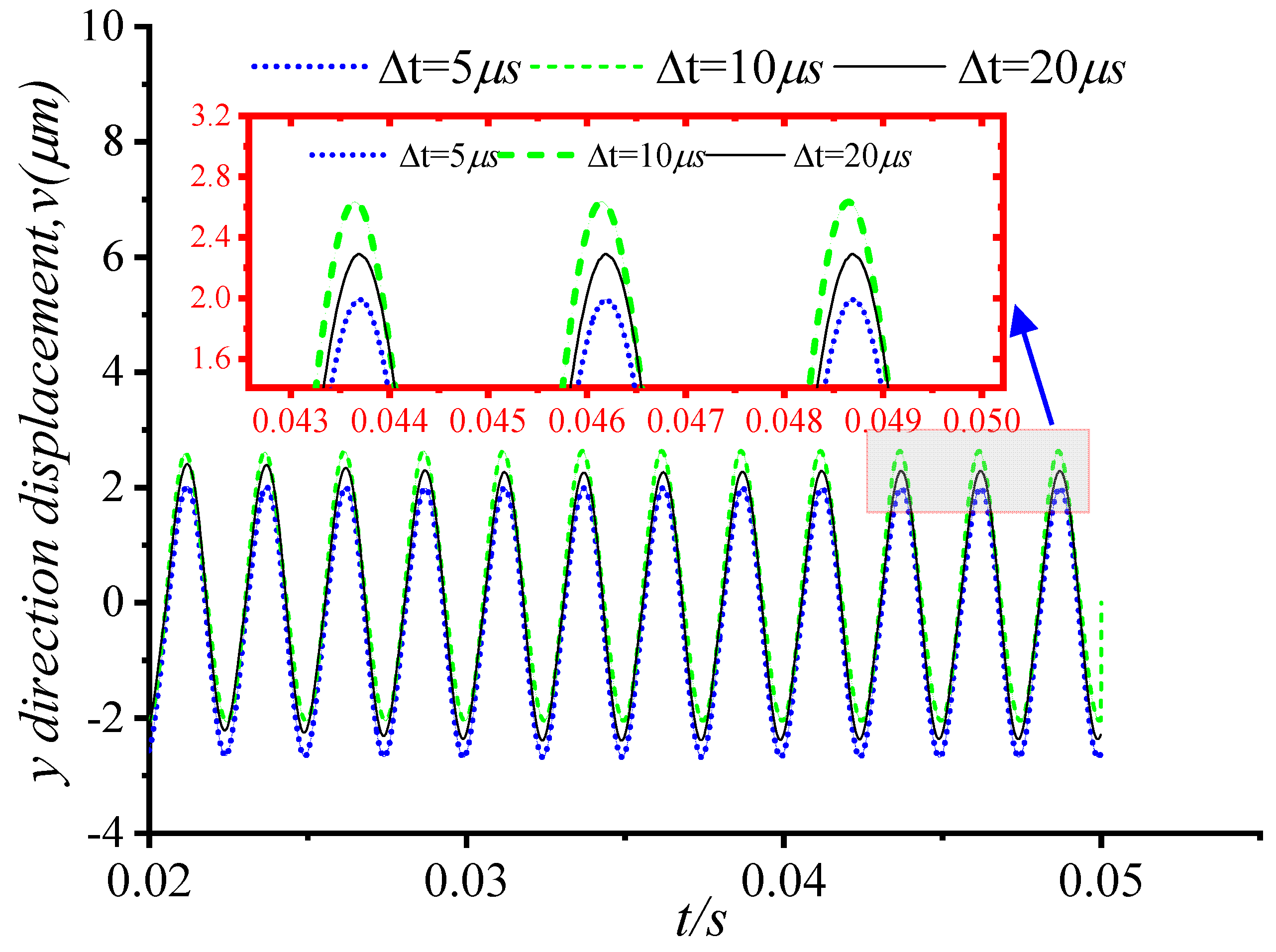
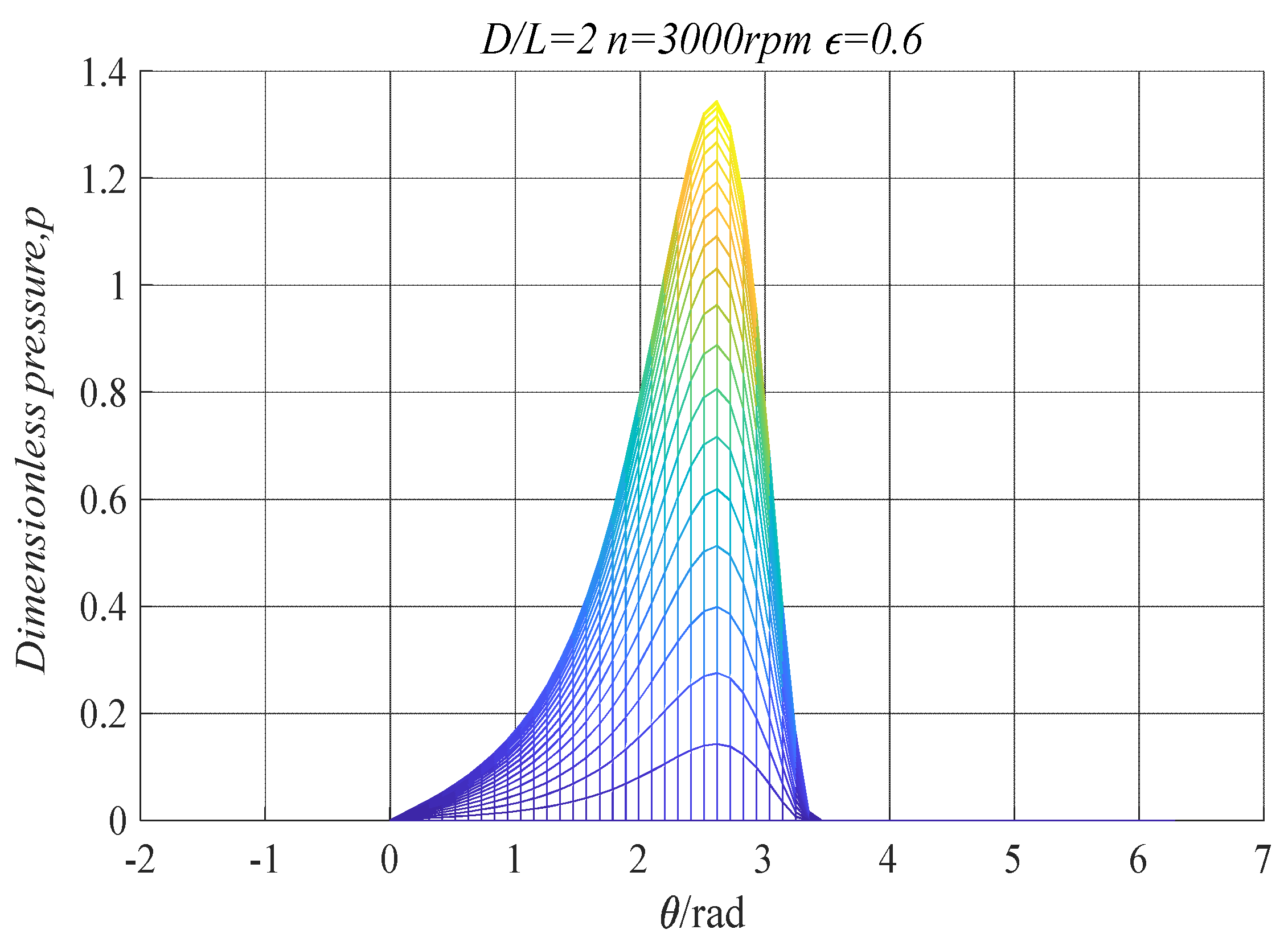
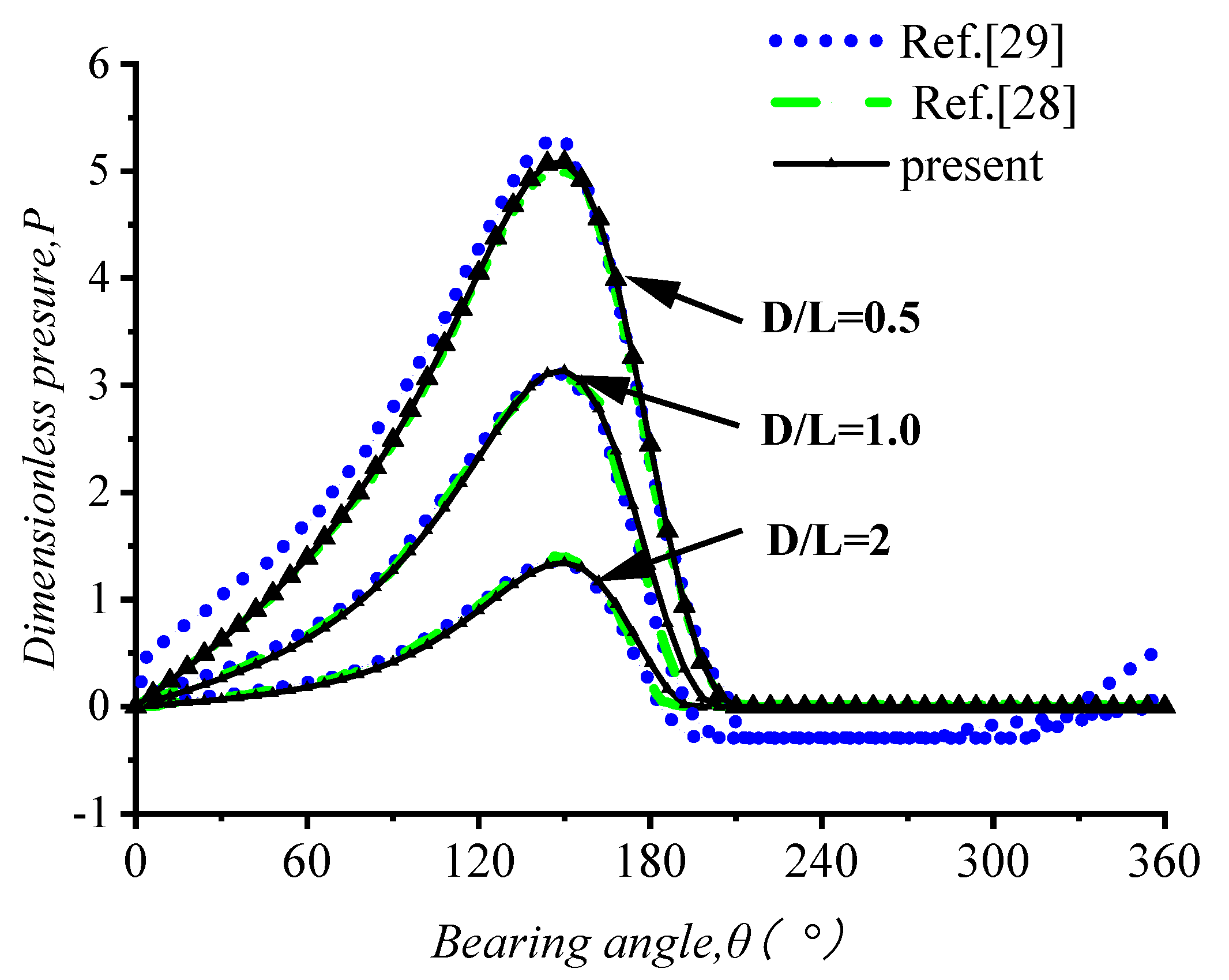
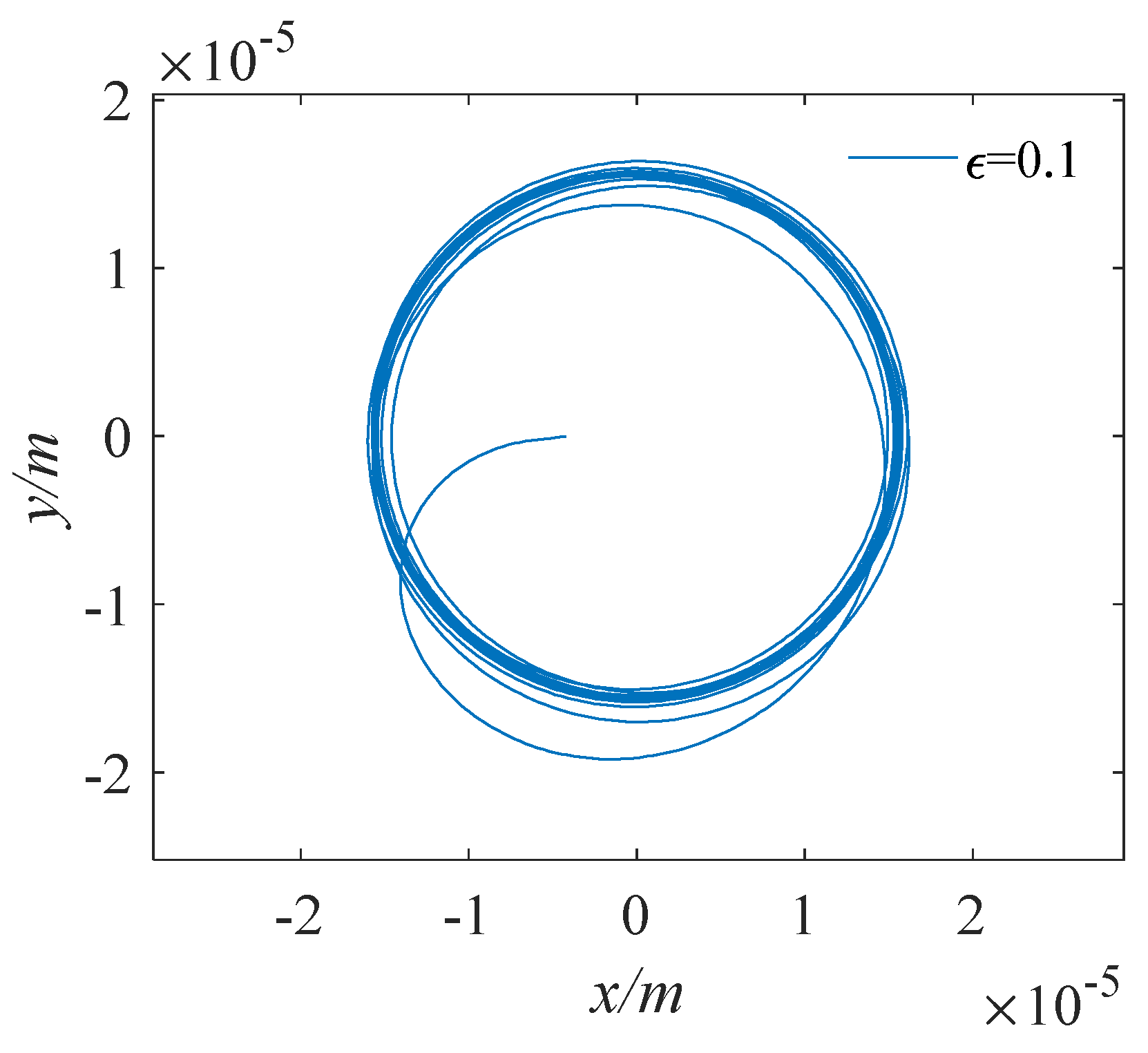

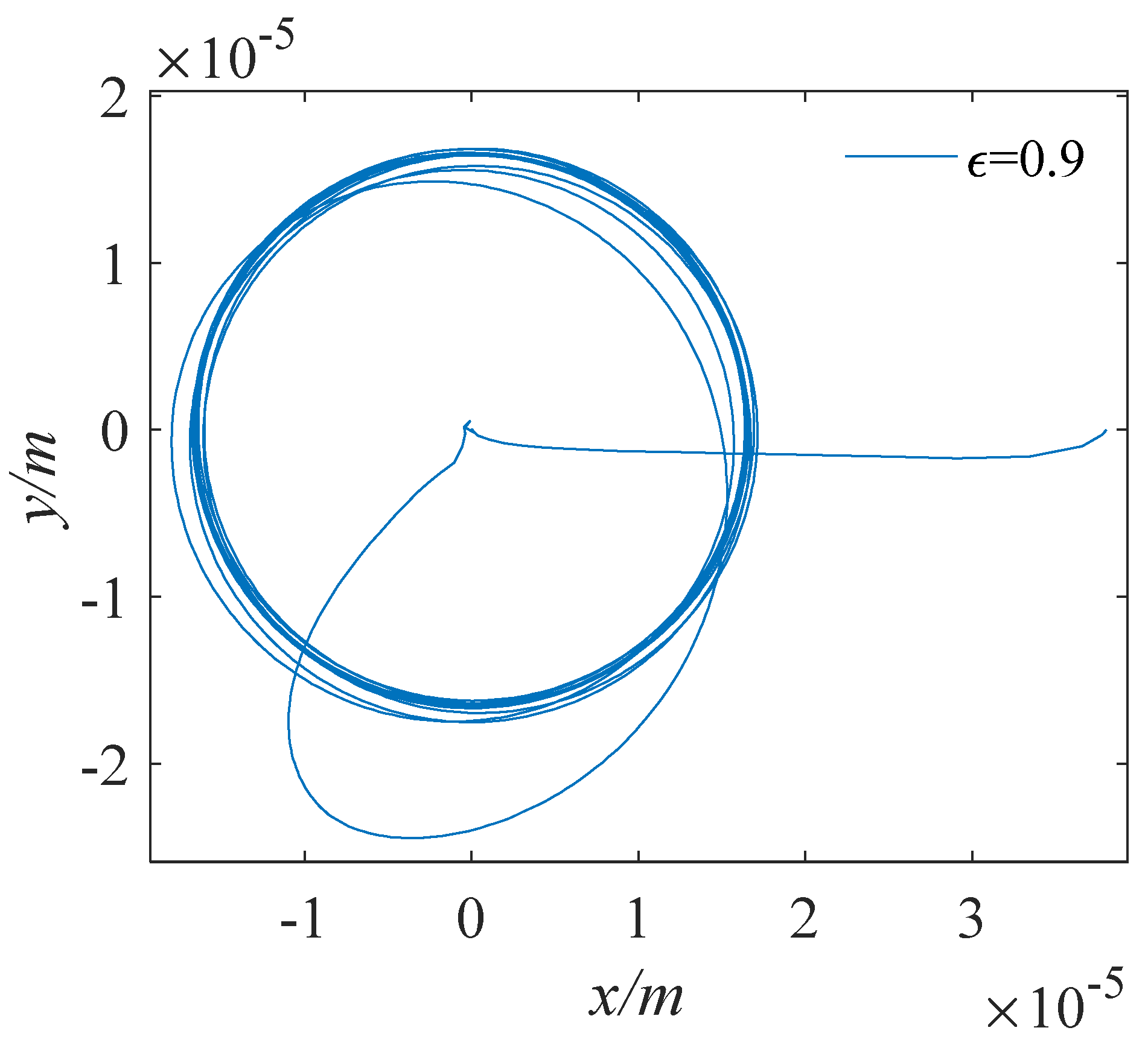





| Parameters | Value |
|---|---|
| Bearing radius, R | 40 mm |
| Bearing width | 80 mm |
| Bearing clearance, c | 0.04 mm |
| Rotate speed, r/min, | 3000 |
| Parameters | Value |
|---|---|
| Bearing radius, R | 35.05 mm |
| Bearing width, L | 70.09 mm |
| Bearing clearance, c | 0.0845 mm |
| Rotate speed, n | 545.6 r/min |
| Viscosity of water, η0 | 0.001103 Pa·s |
| The density of water, ρ | 1000 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Jian, F.; Sun, S.; Sima, C.; Qi, L.; Zou, M. Analysis of Nonlinear Time-Domain Lubrication Characteristics of the Hydrodynamic Journal Bearing System. Lubricants 2023, 11, 145. https://doi.org/10.3390/lubricants11030145
Lin C, Jian F, Sun S, Sima C, Qi L, Zou M. Analysis of Nonlinear Time-Domain Lubrication Characteristics of the Hydrodynamic Journal Bearing System. Lubricants. 2023; 11(3):145. https://doi.org/10.3390/lubricants11030145
Chicago/Turabian StyleLin, Changgang, Fan Jian, Shili Sun, Can Sima, Libo Qi, and Mingsong Zou. 2023. "Analysis of Nonlinear Time-Domain Lubrication Characteristics of the Hydrodynamic Journal Bearing System" Lubricants 11, no. 3: 145. https://doi.org/10.3390/lubricants11030145
APA StyleLin, C., Jian, F., Sun, S., Sima, C., Qi, L., & Zou, M. (2023). Analysis of Nonlinear Time-Domain Lubrication Characteristics of the Hydrodynamic Journal Bearing System. Lubricants, 11(3), 145. https://doi.org/10.3390/lubricants11030145




