Effects of Wear on Lubrication Performance and Vibration Signatures of Rotor System Supported by Hydrodynamic Bearings
Abstract
1. Introduction
2. Theory
2.1. Modeling of Rotor-Bearing System
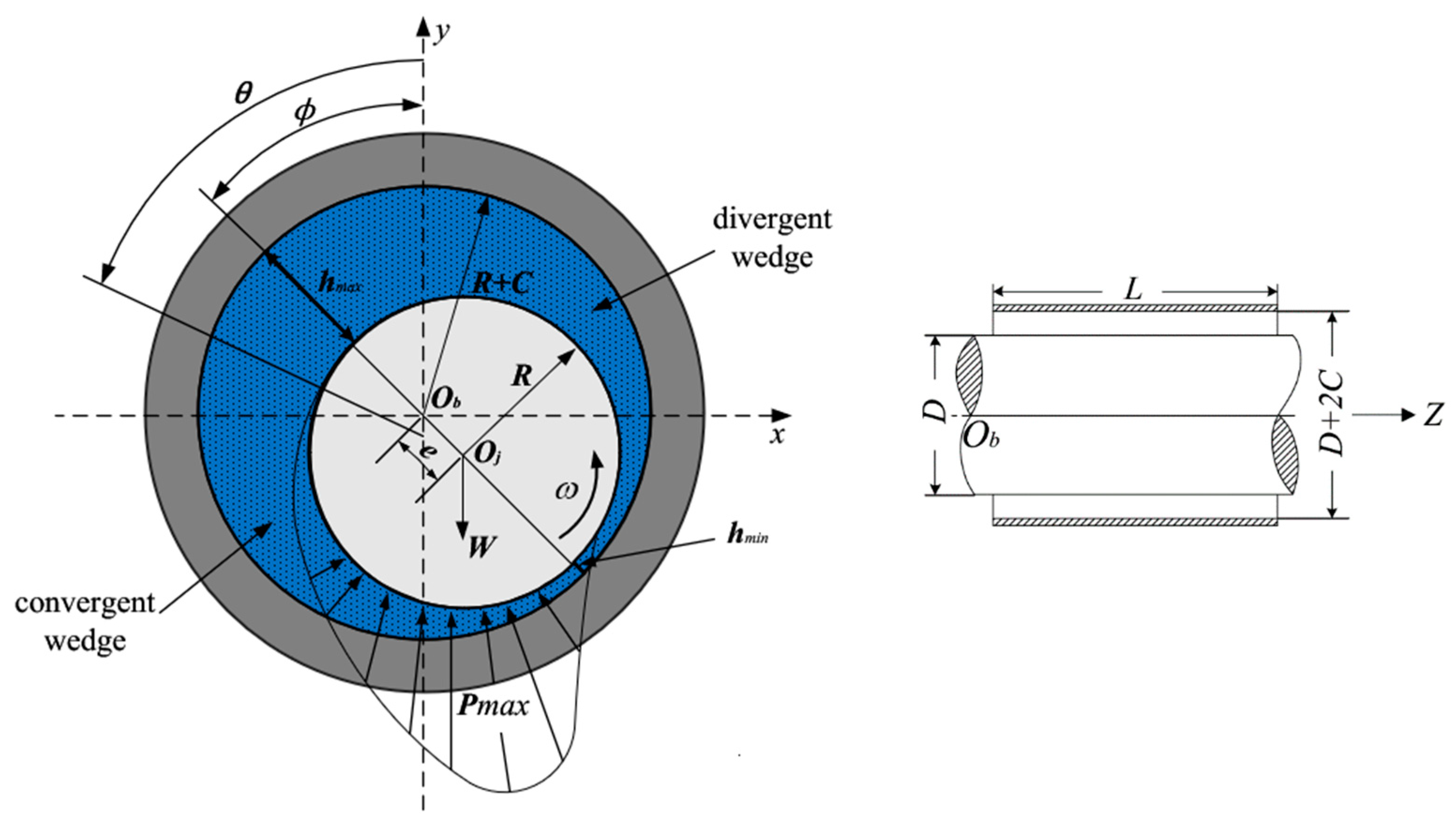
2.2. Modeling of Oil Film Force
2.2.1. Linear Oil Film Force Model
2.2.2. Nonlinear Oil Film Force Model
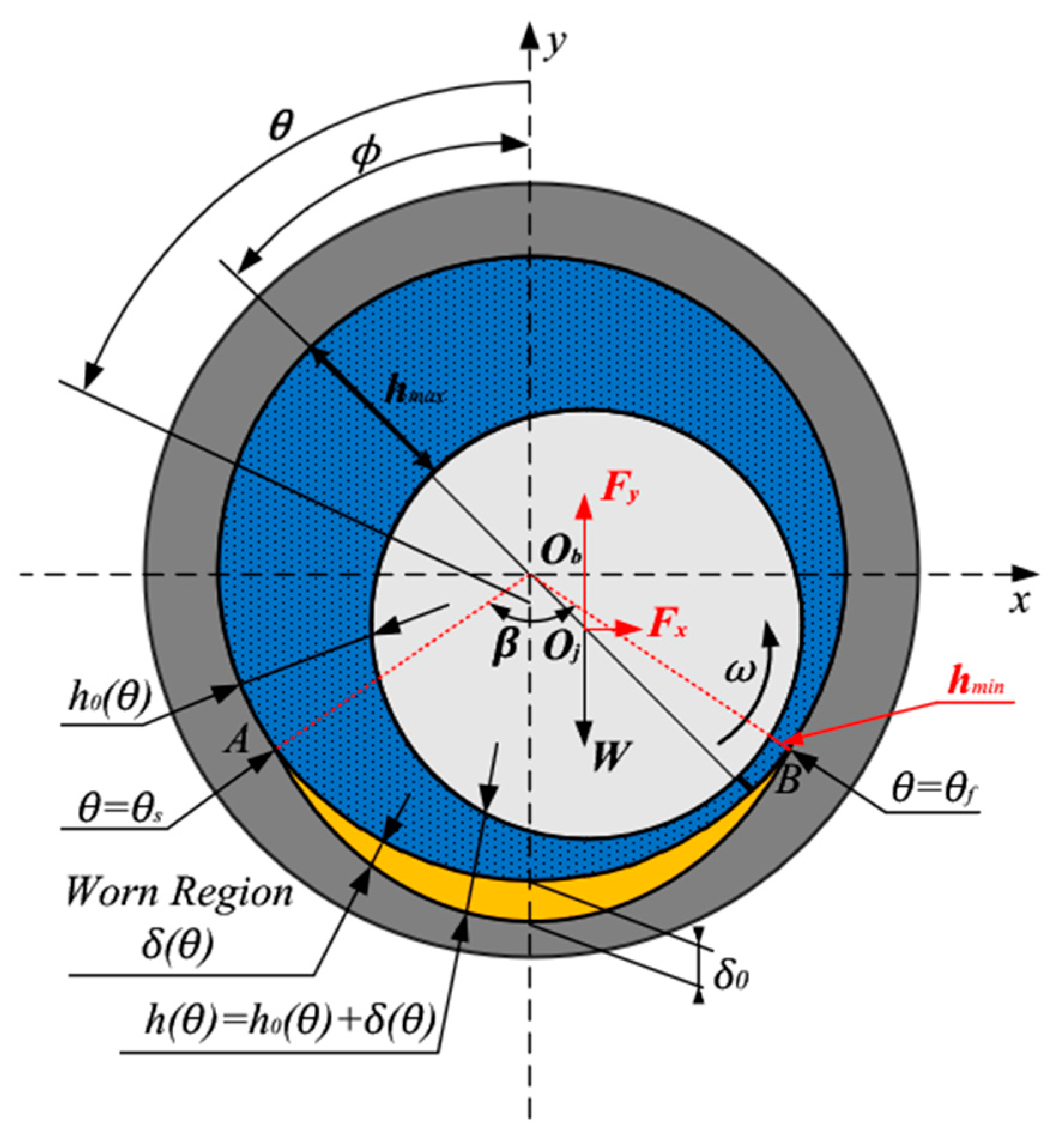
2.3. Modeling of Worn Bearing
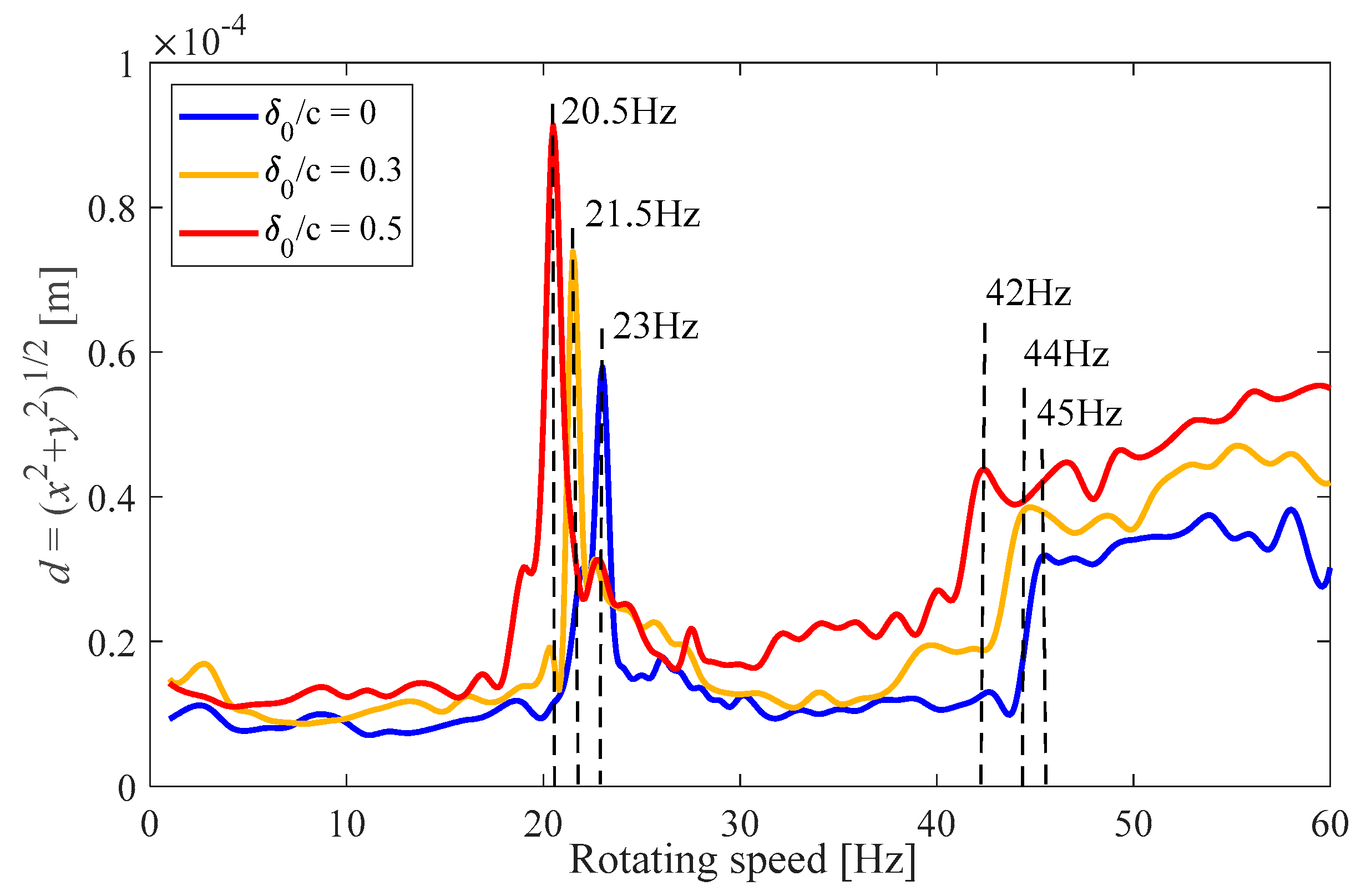
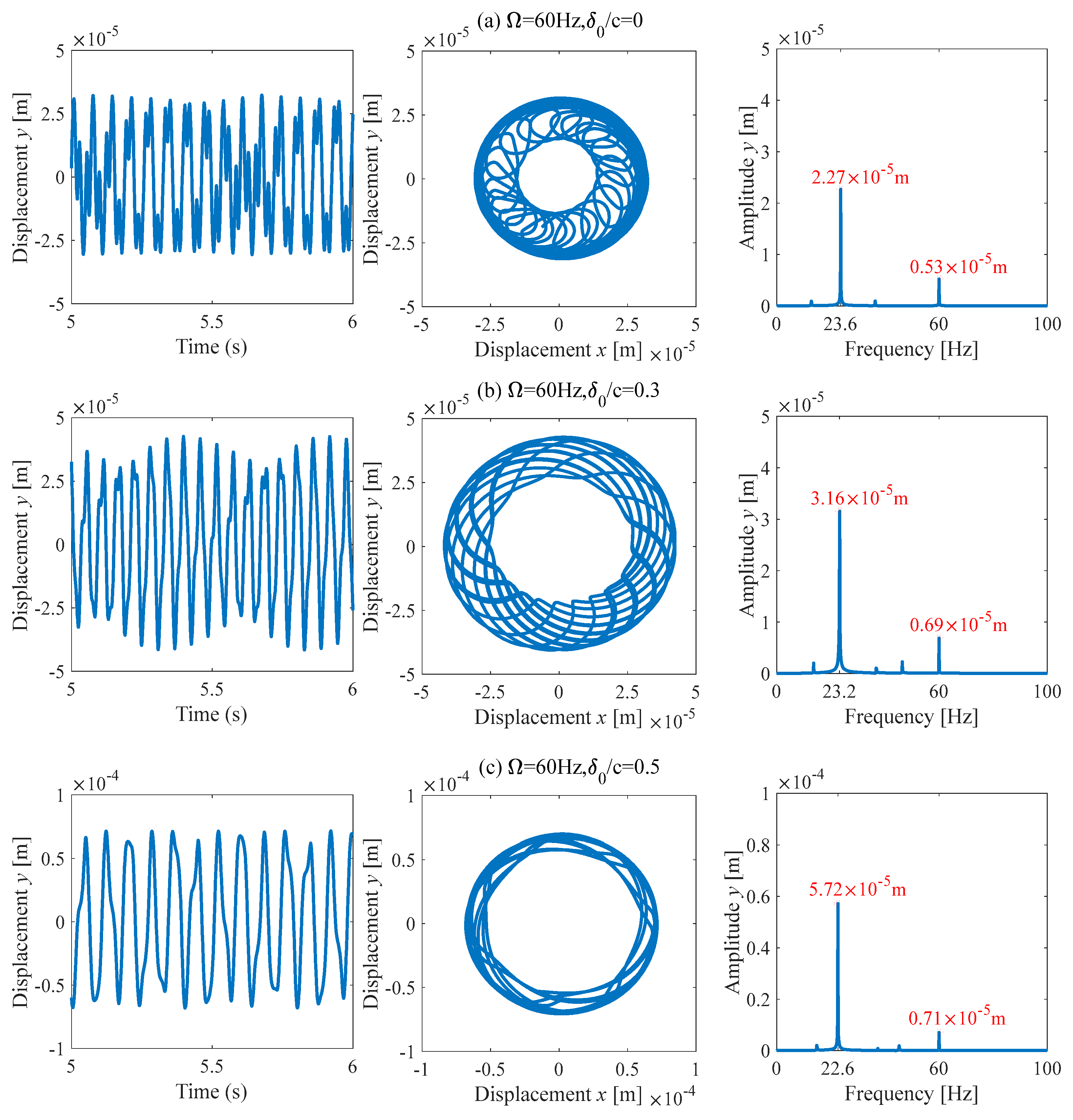
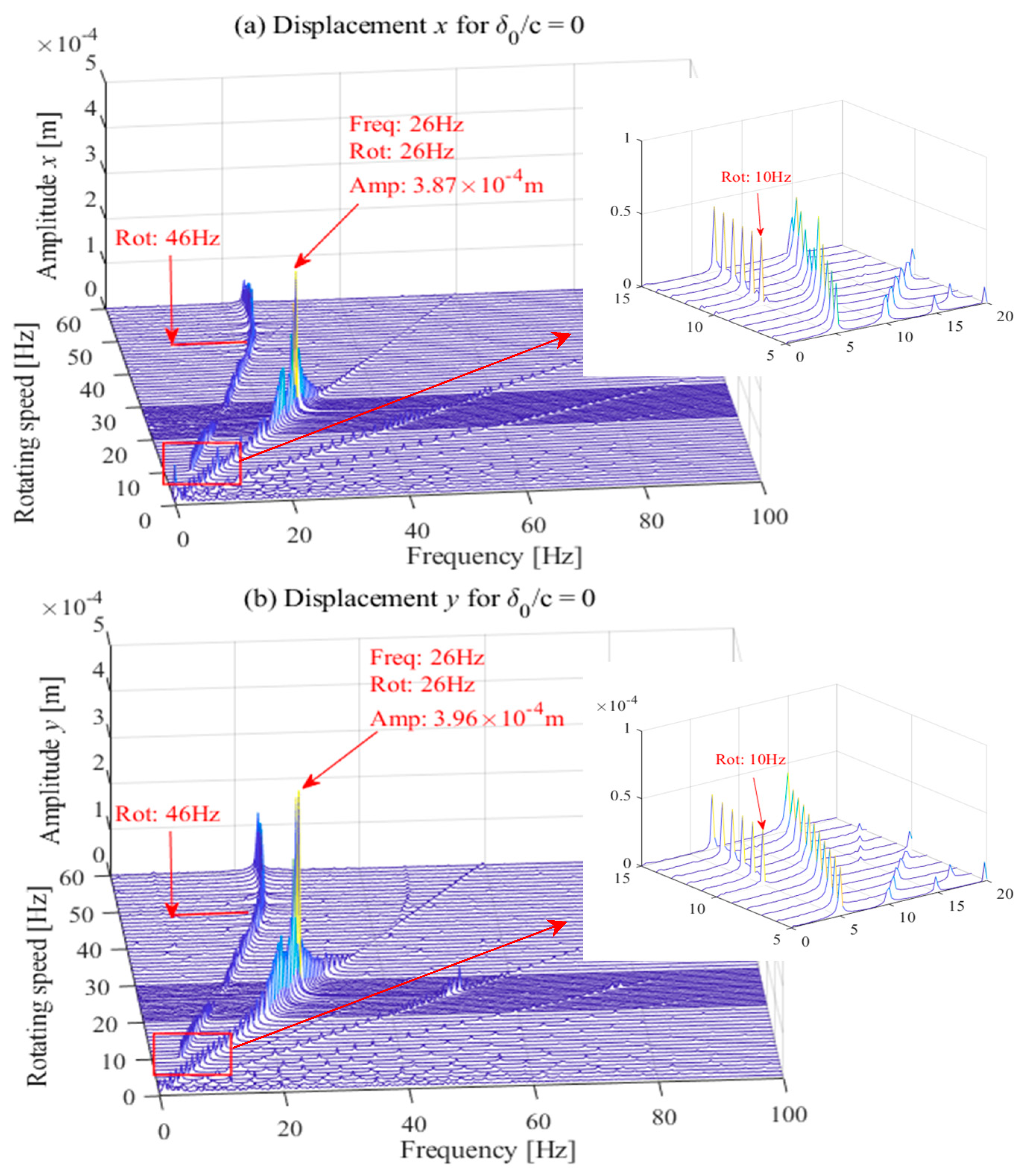
3. Simulation Results and Discussion
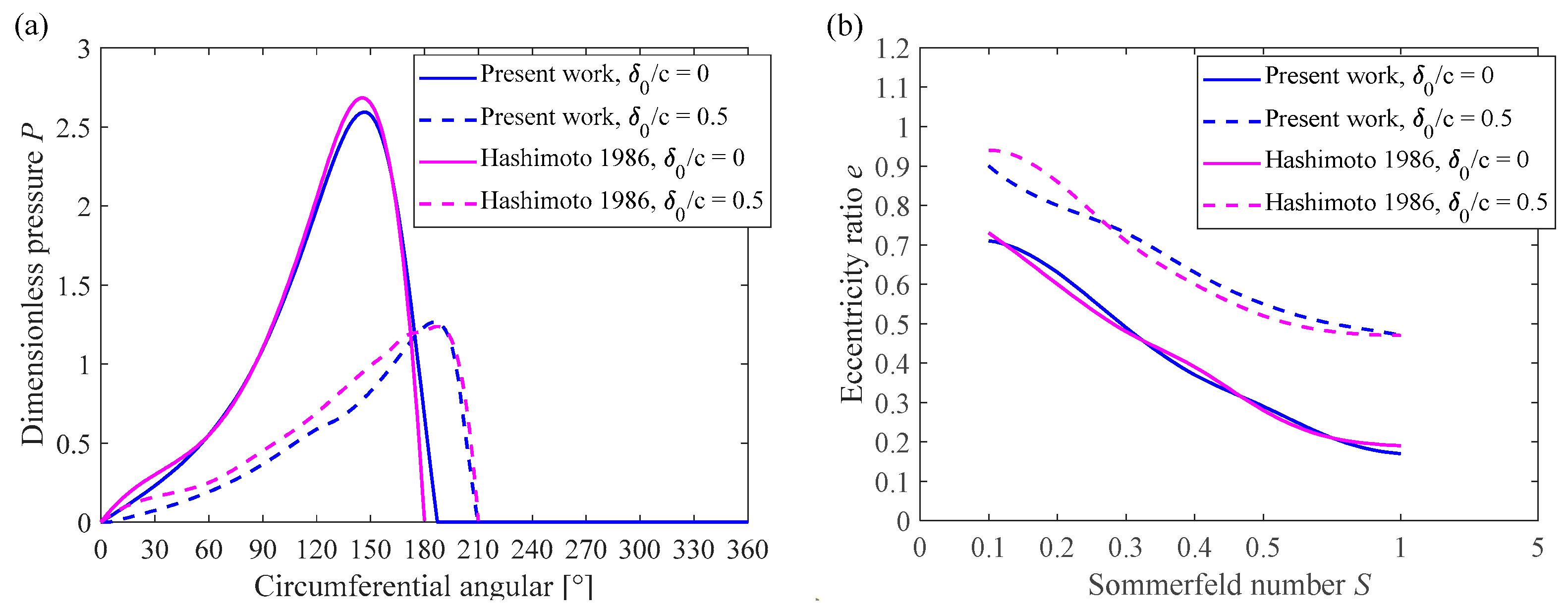
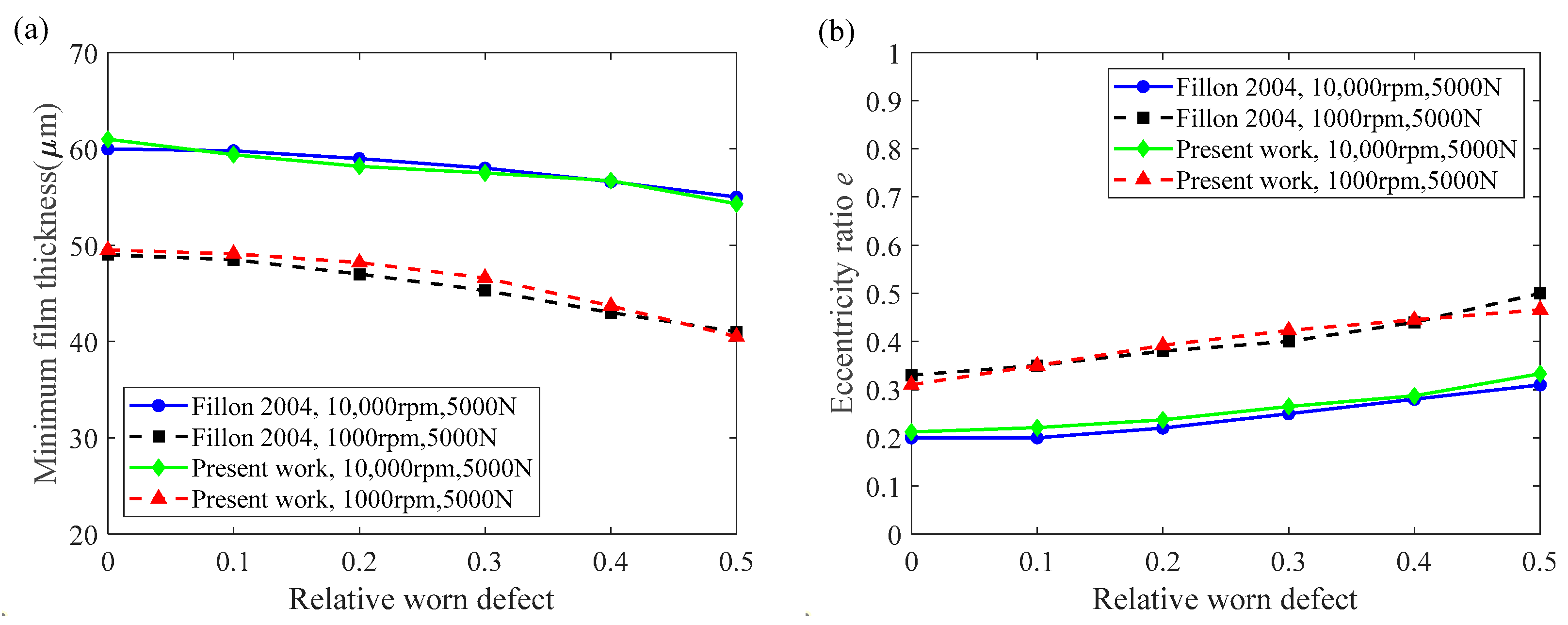
3.1. Algorithm Validation
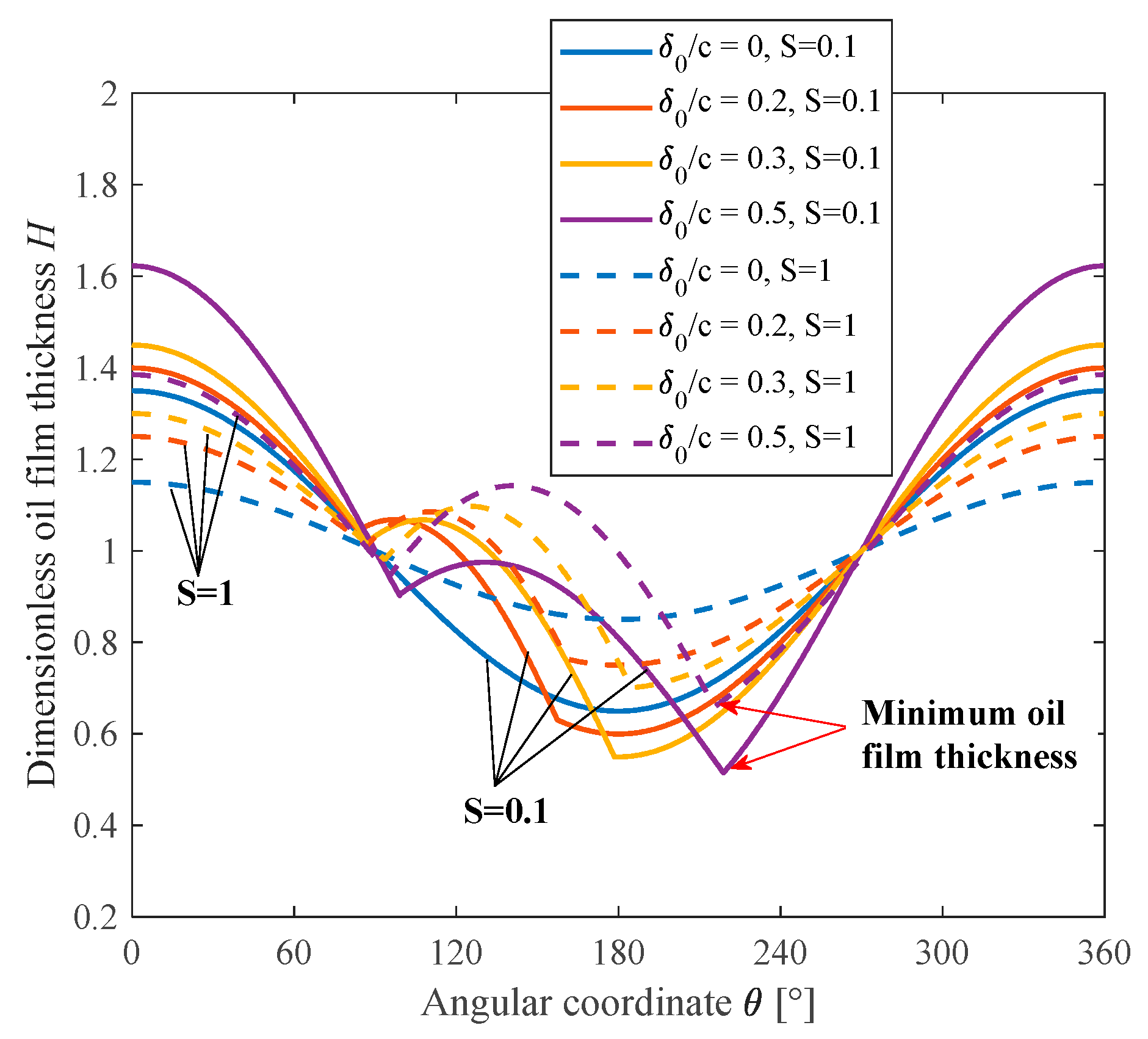
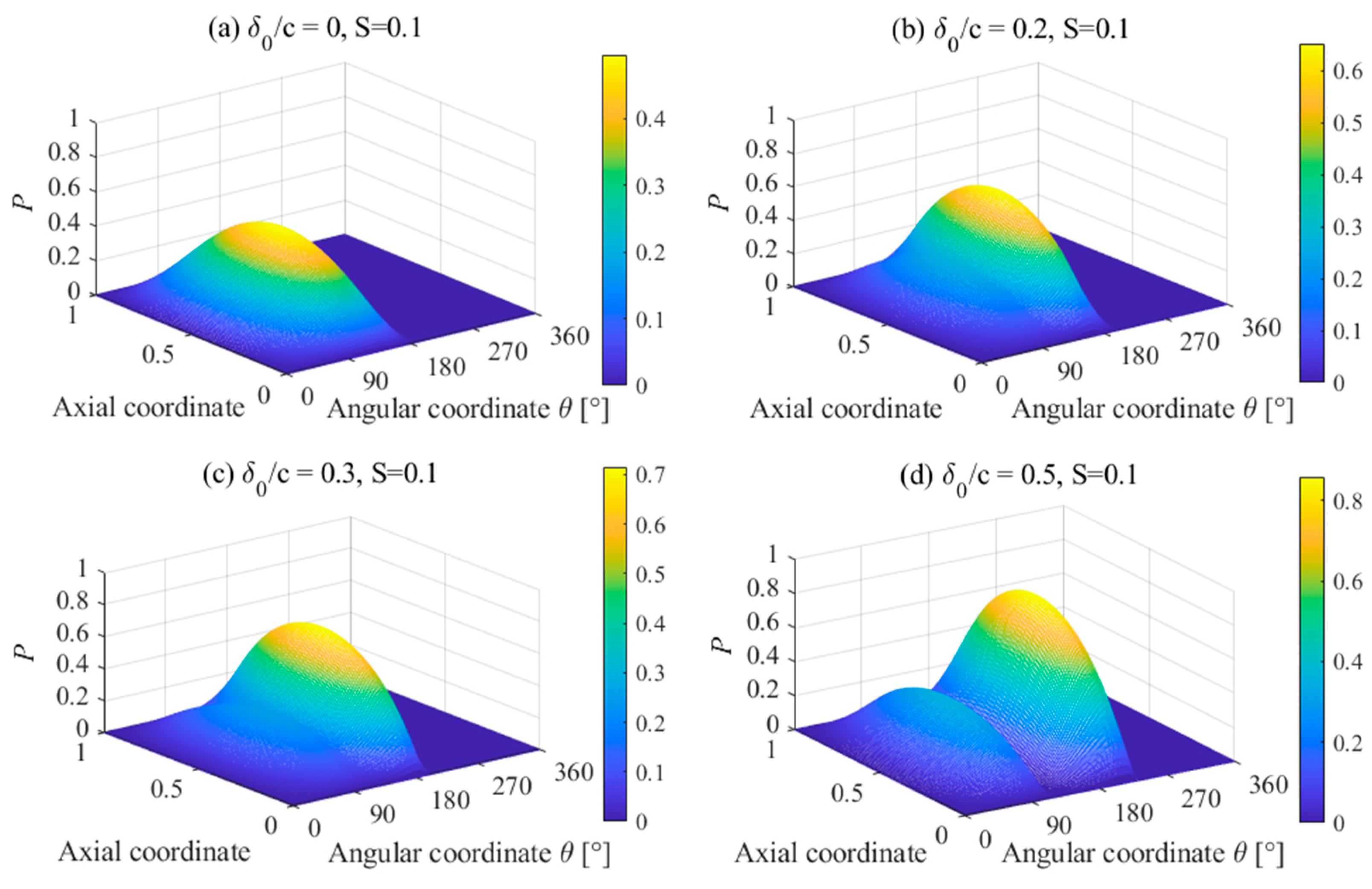
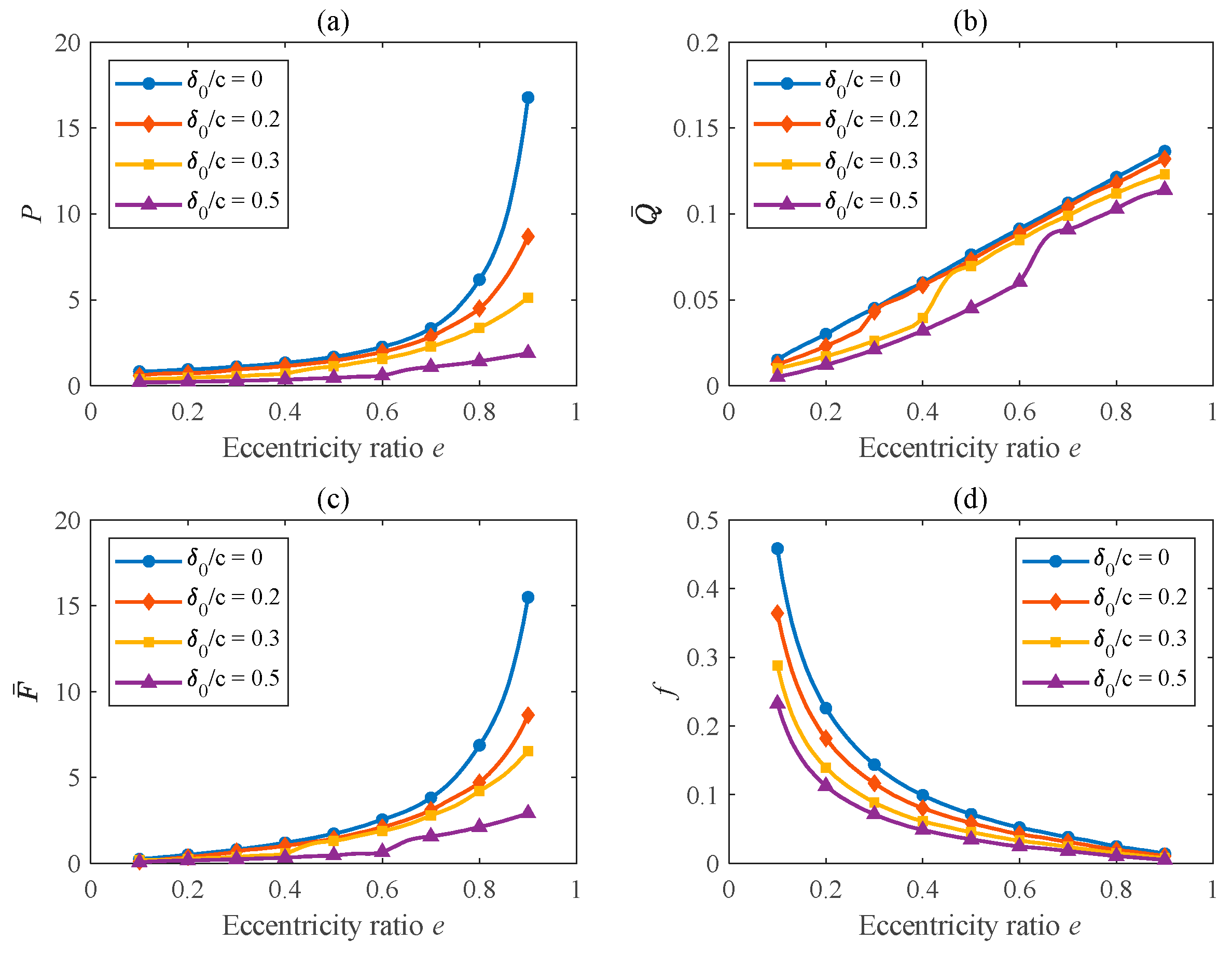
3.2. Static Characteristics
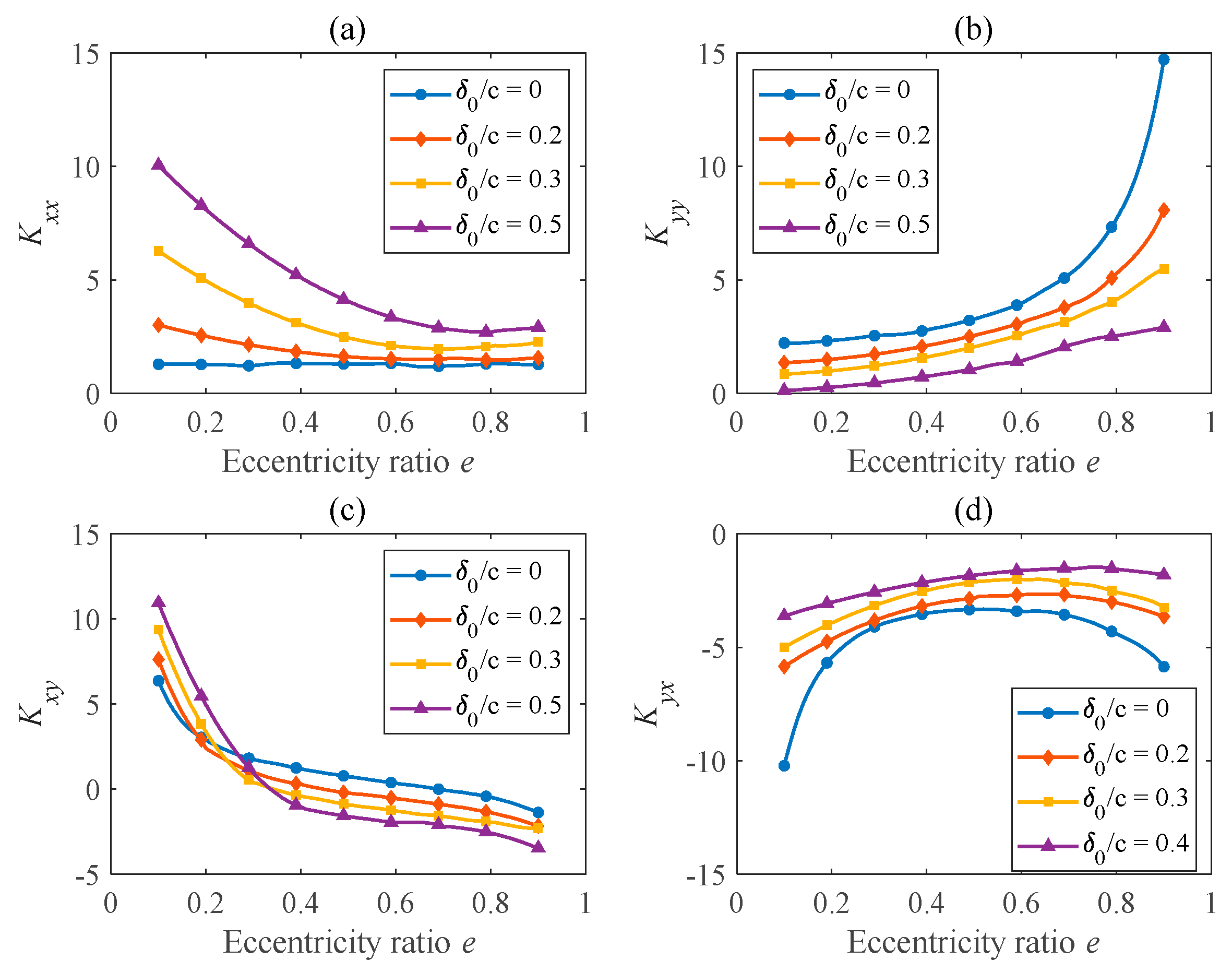
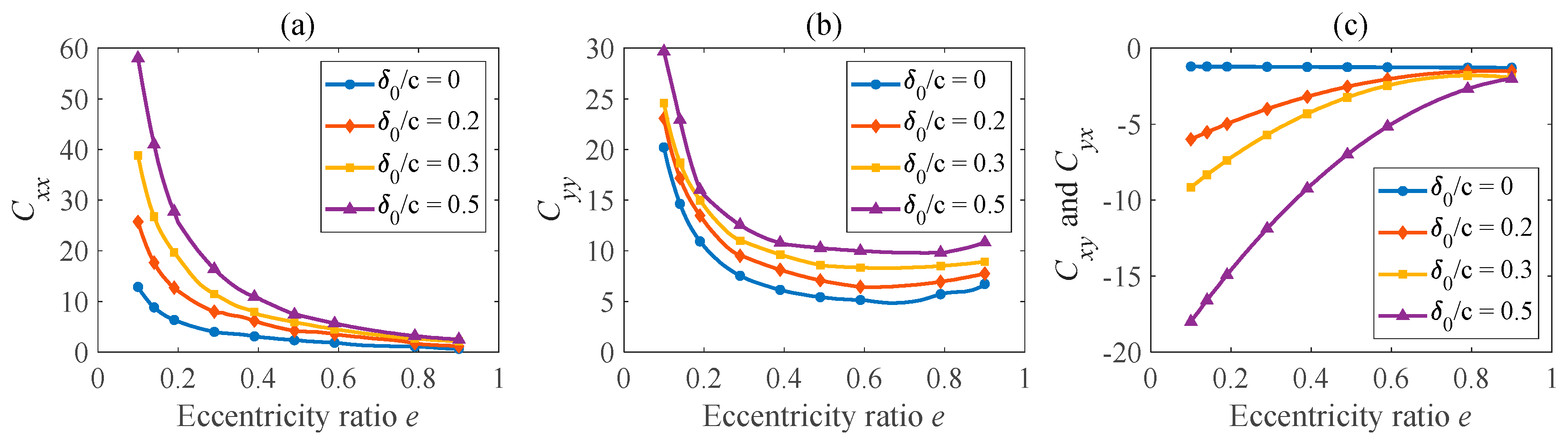
3.3. Stiffness and Damping Coefficients
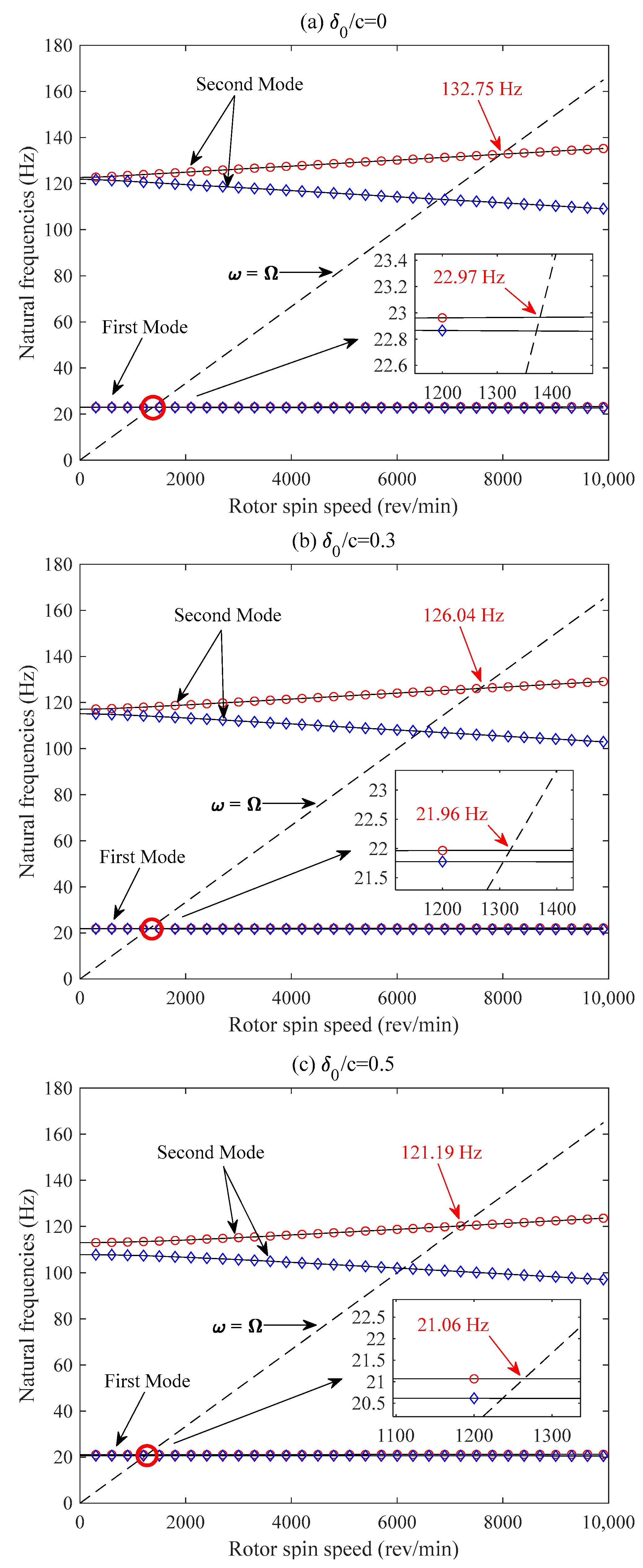
3.4. Critical Speeds and Mode Shapes
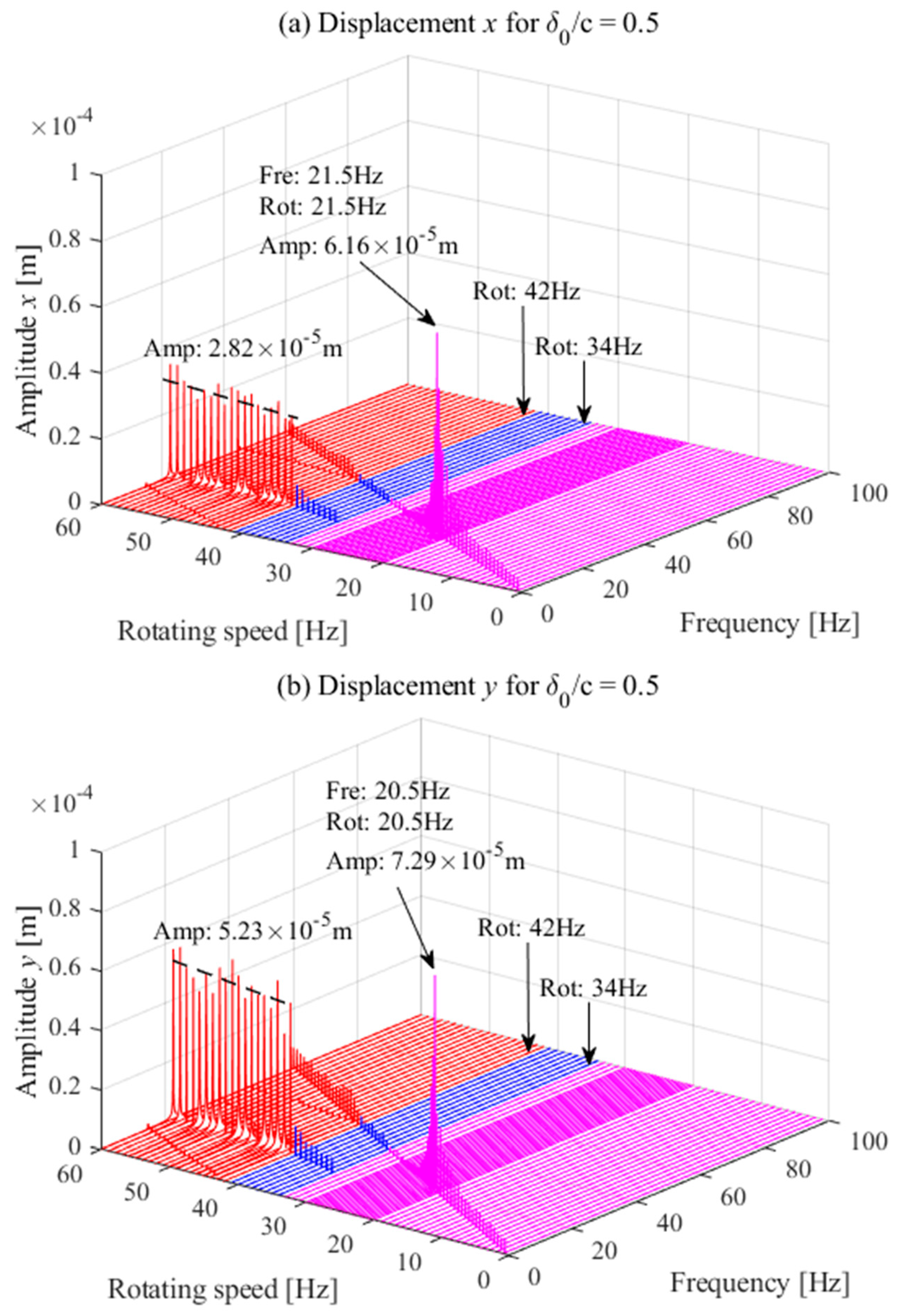
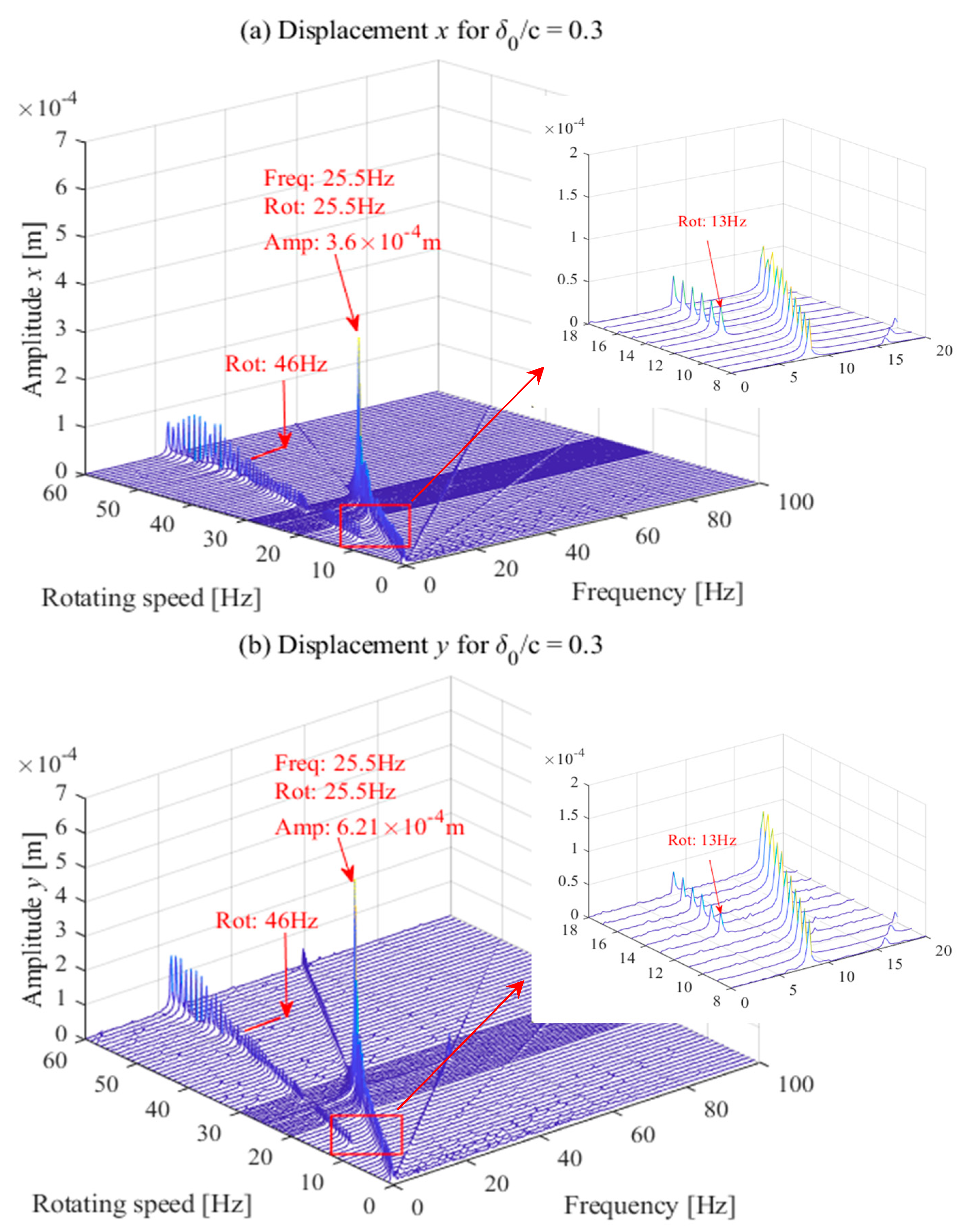
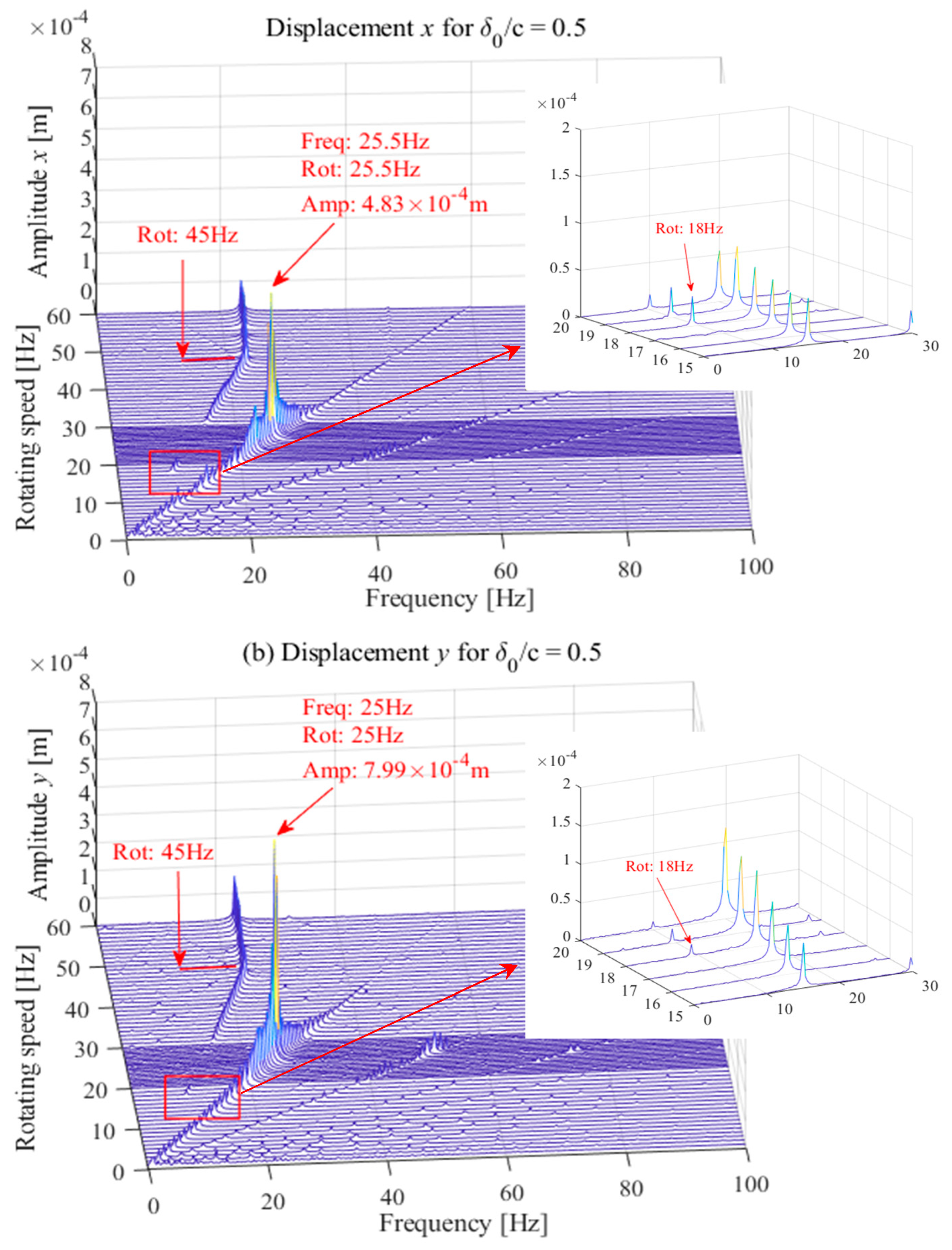
3.5. Vibrational Behavior of the Rotor-Bearing System
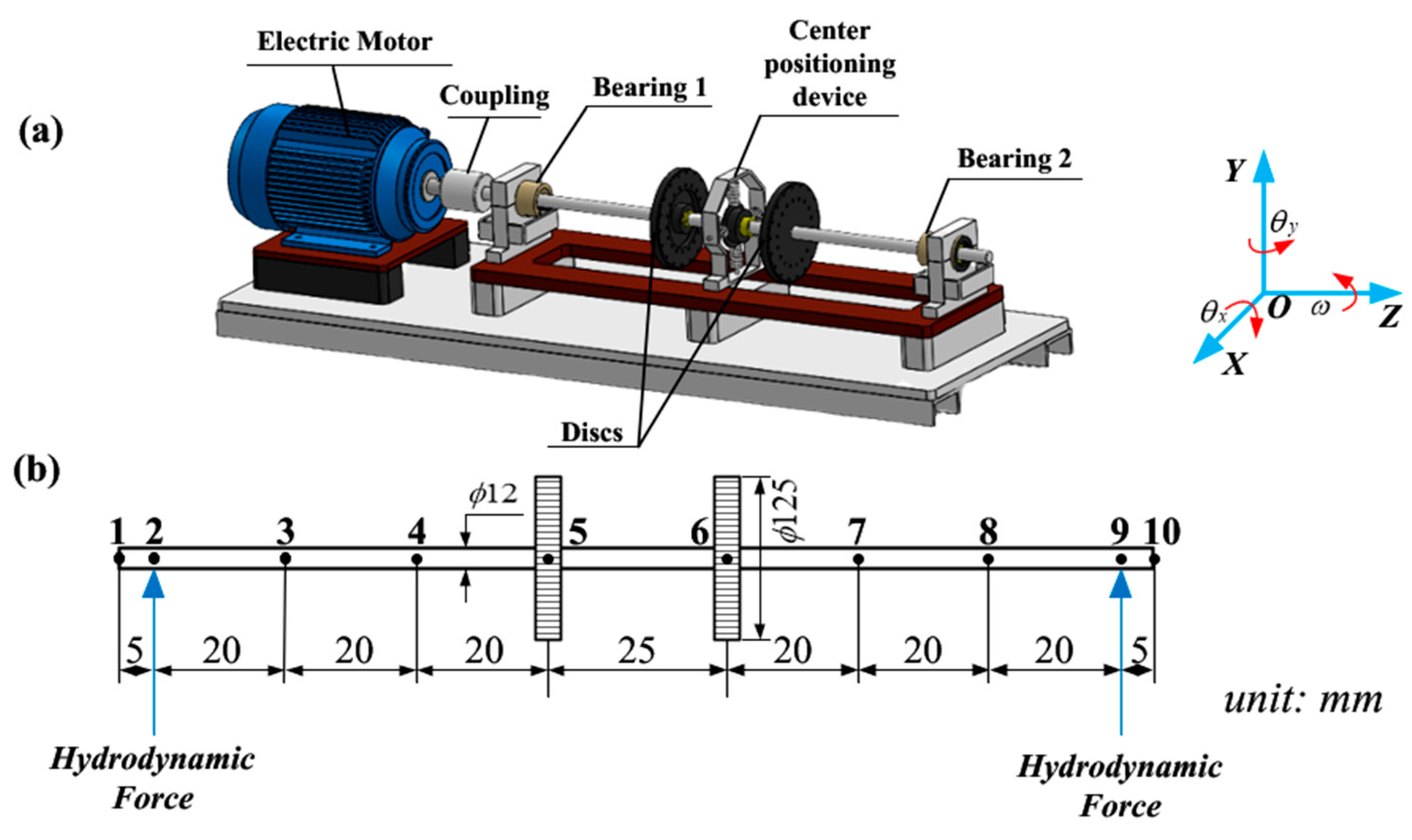
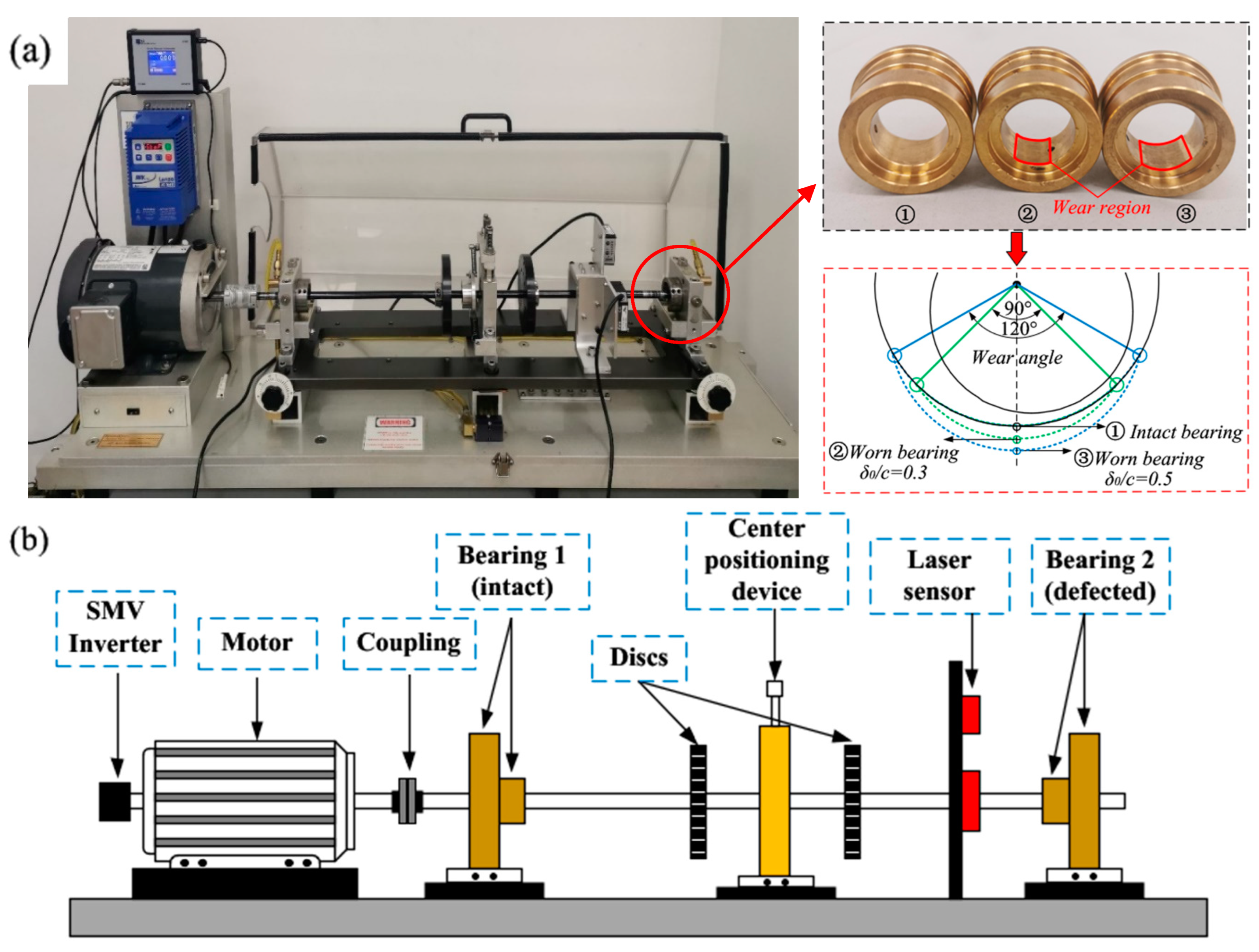
4. Experimental Validation
4.1. Test Rig Description
4.2. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Notation | Matrices | ||
| c | bearing radial clearance (m) | [M] | global mass matrix |
| R | bearing radius (m) | [K] | global stiffness matrix |
| D | bearing diameter (m) | [C] | global damping matrix |
| L | bearing length (m) | [G] | global gyroscopic matrix |
| h | oil film thickness (m) | [MS] | element mass matrix of shaft |
| ƞ | oil viscosity (Pa.s) | [GS] | element gyroscopic matrix of shaft |
| oil film pressure (Pa) | [KS] | element stiffness matrix of shaft | |
| x, y | displacement in x- and y-directions (m) | [CS] | element damping matrix of shaft |
| velocity in x- and y-directions (m/s) | [Gd] | element gyroscopic matrix of disc | |
| E | elastic modulus (GPa) | [Md] | element mass matrix of disc |
| I | second moment of area (m4) | [KB] | bearing stiffness matrix |
| A | area of the axial cross-section (m2) | [CB] | bearing damping matrix |
| l | length of the shaft element (m) | {Fu} | unbalanced force vector |
| mass of disk (kg) | {Fh} | nonlinear oil film force vector | |
| moment of inertia of disk (kg.m2) | {Wi} | gravity vector | |
| polar moment of inertia of the disk (kg.m2) | Greek symbols | ||
| nonlinear oil film force (N) | first and second natural frequencies (rad/s) | ||
| initial phase angle (rad) | first and second modal damping ratios | ||
| Dimensionless parameters | Rayleigh parameters | ||
| P | dimensionless oil film pressure | wear depth at any angle (m) | |
| dimensionless load capacity | rotation angle from y-axis (rad) | ||
| dimensionless friction force | attitude angle (rad) | ||
| dimensionless end leakage | angular speed (rad/s) | ||
| Kij | dimensionless stiffness coefficients | ρ | material density (kg/m3) |
| Cij | dimensionless stiffness coefficients | angles around the x-axis and y-axis (rad) | |
| dimensionless displacement vector | starting and end position of wear region (rad) | ||
| dimensionless time | dimensionless oil film thickness | ||
| e | eccentricity ratio | dimensionless bearing length | |
References
- Mokhtar, M.O.A.; Howarth, R.B.; Davies, P.B. Wear characteristics of plain hydrodynamic journal bearings during repeated starting and stopping. ASLE Trans. 1977, 20, 191–194. [Google Scholar] [CrossRef]
- Dufrane, K.F.; Kannel, J.W.; McCloskey, T.H. Wear of steam turbine journal bearings at low operating speeds. J. Lubr. Tech. 1983, 105, 313–317. [Google Scholar] [CrossRef]
- Hashimoto, H.; Wada, S.; Nojima, K. Performance characteristics of worn journal bearings in both laminar and turbulent regimes, Part I: Steady-state characteristics. ASLE Trans. 1986, 29, 565–571. [Google Scholar] [CrossRef]
- Kumar, A.; Mishra, S. Stability of a rigid rotor in turbulent hydrodynamic worn journal bearings. Wear 1996, 193, 25–30. [Google Scholar] [CrossRef]
- Kumar, A.; Mishra, S. Steady state analysis of noncircular worn journal bearings in nonlaminar lubrication regimes. Tribol. Int. 1996, 29, 493–498. [Google Scholar] [CrossRef]
- Fillon, M.; Bouyer, J. Thermohydrodynamic analysis of a worn plain journal bearing. Tribol. Int. 2004, 37, 129–136. [Google Scholar] [CrossRef]
- Lee, D.; Sun, K.H.; Kim, B.; Kang, D. Thermal behavior of a worn tilting pad journal bearing: Thermohydrodynamic analysis and pad temperature measurement. Tribol. Trans. 2018, 61, 1074–1083. [Google Scholar] [CrossRef]
- Awasthi, R.K.; Sharma, S.C.; Jain, S.C. Performance of worn non-recessed hole-entry hybrid journal bearings. Tribol. Int. 2007, 40, 717–734. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.G.; Papadopoulos, C.A. A study of friction in worn misaligned journal bearings under severe hydrodynamic lubrication. Tribol. Int. 2008, 41, 461–472. [Google Scholar] [CrossRef]
- Sander, D.E.; Allmaier, H. Starting and stopping behavior of worn journal bearings. Tribol. Int. 2018, 127, 478–488. [Google Scholar] [CrossRef]
- Jia, H.; Li, J.; Wang, J.; Xiao, K.; Han, Y. A lubricated wear model for determining wear surface geometry on journal-bearing surfaces. Surf. Topogr. Metrol. Prop. 2020, 8, 035002. [Google Scholar] [CrossRef]
- König, F.; Chaib, A.O.; Jacobs, G.; Sous, C. A multiscale-approach for wear prediction in journal bearing systems—From wearing-in towards steady-state wear. Wear 2019, 426, 1203–1211. [Google Scholar] [CrossRef]
- Liu, G.; Li, M. Lubrication Characteristics of Water-Lubricated Rubber Bearings with Partial Wear. J. Fluids Eng. 2020, 142, 021209. [Google Scholar] [CrossRef]
- Winkler, A.; Bartz, M.; Wartzack, S. Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime. Lubricants 2022, 10, 334. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.; Wang, J.; Ni, X. Coupling transient mixed lubrication and wear for journal bearing modeling. Tribol. Int. 2019, 138, 1–15. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, C.; Wang, Y.J.; Han, Y.F.; Wang, J.X.; Lv, J.L. Dynamic Mixed Lubrication Investigation of Water-Lubricated Bearing with Unbalanced Rotor during Start-Up. Tribol. Trans. 2021, 64, 764–776. [Google Scholar] [CrossRef]
- Papadopoulos, C.A.; Nikolakopoulos, P.G.; Gounaris, G.D. Identification of clearances and stability analysis for a rotor-journal bearing system. Mech. Mach. Theory 2008, 43, 411–426. [Google Scholar] [CrossRef]
- Chasalevris, A.C.; Nikolakopoulos, P.G.; Papadopoulos, C.A. Dynamic effect of bearing wear on rotor-bearing system response. J. Vib. Acoust. 2013, 135, 011008. [Google Scholar] [CrossRef]
- Chasalevris, A.; Dohnal, F.; Chatzisavvas, I. Experimental detection of additional harmonics due to wear in journal bearings using excitation from a magnetic bearing. Tribol. Int. 2014, 71, 158–167. [Google Scholar] [CrossRef]
- Machado, T.H.; Cavalca, K.L. Modeling of hydrodynamic bearing wear in rotor-bearing systems. Mech. Res. Commun. 2015, 69, 15–23. [Google Scholar] [CrossRef]
- Machado, T.H.; Cavalca, K.L. Investigation on an experimental approach to evaluate a wear model for hydrodynamic cylindrical bearings. Appl. Math. Model. 2016, 40, 9546–9564. [Google Scholar] [CrossRef]
- Mendes, R.U.; Machado, T.H.; Cavalca, K.L. Experimental wear parameters identification in hydrodynamic bearings via model based methodology. Wear 2017, 372, 116–129. [Google Scholar] [CrossRef]
- Machado, T.H.; Alves, D.S.; Cavalca, K.L. Investigation about journal bearing wear effect on rotating system dynamic response in time domain. Tribol. Int. 2019, 129, 124–136. [Google Scholar] [CrossRef]
- Alves, D.S.; Fieux, G.; Machado, T.H.; Keogh, P.S.; Cavalca, K.L. A parametric model to identify hydrodynamic bearing wear at a single rotating speed. Tribol. Int. 2021, 153, 106640. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Zou, L.; Yang, J. Influence of both friction and wear on the vibration of marine water lubricated rubber bearing. Wear 2017, 376, 920–930. [Google Scholar] [CrossRef]
- Visnadi, L.B.; De Castro, H.F. Influence of bearing clearance and oil temperature uncertainties on the stability threshold of cylindrical journal bearings. Mech. Mach. Theory 2019, 134, 57–73. [Google Scholar] [CrossRef]
- Dyk, Š.; Rendl, J.; Byrtus, M.; Smolík, L. Dynamic coefficients and stability analysis of finite-length journal bearings considering approximate analytical solutions of the Reynolds equation. Tribol. Int. 2019, 130, 229–244. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, J.; Li, X.; Xiao, S.; Gu, F.; Ball, A.D. Fluid-asperity interaction induced random vibration of hydrodynamic journal bearings towards early fault diagnosis of abrasive wear. Tribol. Int. 2021, 160, 107028. [Google Scholar] [CrossRef]
- Ma, J.; Fu, C.; Zheng, Z.; Lu, K.; Yang, Y. The Effects of Interval Uncertainties on Dynamic Characteristics of a Rotor System Supported by Oil-Film Bearings. Lubricants 2022, 10, 354. [Google Scholar] [CrossRef]
- Yan, X.; Xu, X.; Sheng, C.; Yuan, C.; Li, Z. Intelligent wear mode identification system for marine diesel engines based on multi-level belief rule base methodology. Meas. Sci. Technol. 2017, 29, 015110. [Google Scholar] [CrossRef]
- Nissilä, J.; Laurila, J. Diagnosing simultaneous faults using the local regularity of vibration signals. Meas. Sci. Technol. 2019, 30, 045102. [Google Scholar] [CrossRef]
- De Castro, H.F.; Cavalca, K.L.; Nordmann, R. Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model. J. Sound Vib. 2008, 317, 273–293. [Google Scholar] [CrossRef]
- Safizadeh, M.S.; Golmohammadi, A. Prediction of oil whirl initiation in journal bearings using multi-sensors data fusion. Measurement 2020, 151, 107241. [Google Scholar] [CrossRef]
- Ma, H.; Li, H.; Zhao, X.; Niu, H.; Wen, B. Effects of eccentric phase difference between two discs on oil-film instability in a rotor–bearing system. Mech. Syst. Signal Process. 2013, 41, 526–545. [Google Scholar] [CrossRef]
- Ma, H.; Wang, X.; Niu, H.; Wen, B. Oil-film instability simulation in an overhung rotor system with flexible coupling misalignment. Arch. Appl. Mech. 2015, 85, 893–907. [Google Scholar] [CrossRef]
- Machado, T.H.; Alves, D.S.; Cavalca, K.L. Discussion about nonlinear boundaries for hydrodynamic forces in journal bearing. Nonlinear Dynam. 2018, 92, 2005–2022. [Google Scholar] [CrossRef]
- Nelson, H.D.; McVaugh, J.M. The dynamics of rotor-bearing system using finite elements. J. Eng. Ind. 1976, 98, 593–600. [Google Scholar] [CrossRef]
- Bathe, K.; Wilson, E. Numerical Methods in Finite Element Analysis; Prentice-Hall Inc.: Hoboken, NJ, USA, 1976. [Google Scholar]
- Ebrat, O.; Mourelatos, Z.P.; Vlahopoulos, N.; Vaidyanathan, K. Calculation of journal bearing dynamic characteristics including journal misalignment and bearing structural deformation. Tribol. Trans. 2004, 47, 94–102. [Google Scholar] [CrossRef]








| Bearing Parameter | Specification | Rotor Parameter | Specification |
|---|---|---|---|
| Bearing length L (mm) | 20 | Shaft radius R1 (mm) | 10 |
| Bearing diameter D (mm) | 20 | Shaft length l (mm) | 850 |
| Radial clearance c (μm) | 100 | Disk radius R2 (mm) | 125 |
| Maximum wear depth (μm) | 20, 30, 50 | Disk thickness h2 (m) | 10 |
| Viscosity η (Pa.s) | 0.0135 | Density ρ (kg/m^3) | 7850 |
| Load W (N) | 100 | Elastic modulus E (GPa) | 211 |
| Sommerfeld number S | 0.01~1 | Unbalanced moment me (kg.m) | 2 × 10−5 |
| Parameter | Hashimoto [3] | Fillon and Bouyer [6] |
|---|---|---|
| Bearing diameter (mm) | 70 | 100 |
| Bearing length (mm) | 70 | 100 |
| Radial clearance (μm) | 287 | 75 |
| Viscosity (Pa.s) | 14 × 10−3 | 0.03 |
| Rotational speed (rpm) | 615 | 1000 and 10,000 |
| Load (N) | 5000 | |
| Maximum wear depth (μm) | 142 | |
| Relative worn defect | 0.5 | 0~0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhang, H.; Li, X.; Xiao, S.; Gu, F.; Shi, Z. Effects of Wear on Lubrication Performance and Vibration Signatures of Rotor System Supported by Hydrodynamic Bearings. Lubricants 2023, 11, 107. https://doi.org/10.3390/lubricants11030107
Chen Y, Zhang H, Li X, Xiao S, Gu F, Shi Z. Effects of Wear on Lubrication Performance and Vibration Signatures of Rotor System Supported by Hydrodynamic Bearings. Lubricants. 2023; 11(3):107. https://doi.org/10.3390/lubricants11030107
Chicago/Turabian StyleChen, Yang, Hao Zhang, Xin Li, Sen Xiao, Fengshou Gu, and Zhanqun Shi. 2023. "Effects of Wear on Lubrication Performance and Vibration Signatures of Rotor System Supported by Hydrodynamic Bearings" Lubricants 11, no. 3: 107. https://doi.org/10.3390/lubricants11030107
APA StyleChen, Y., Zhang, H., Li, X., Xiao, S., Gu, F., & Shi, Z. (2023). Effects of Wear on Lubrication Performance and Vibration Signatures of Rotor System Supported by Hydrodynamic Bearings. Lubricants, 11(3), 107. https://doi.org/10.3390/lubricants11030107






