Static and Dynamic Performances of Novel Aerostatic Bearings with Primary and Secondary Orifice Restrictors
Abstract
:1. Introduction
2. Aerostatic Bearings with Primary and Secondary Orifice Restrictors
3. Numerical Calculation Method
3.1. Large Eddy Simulation
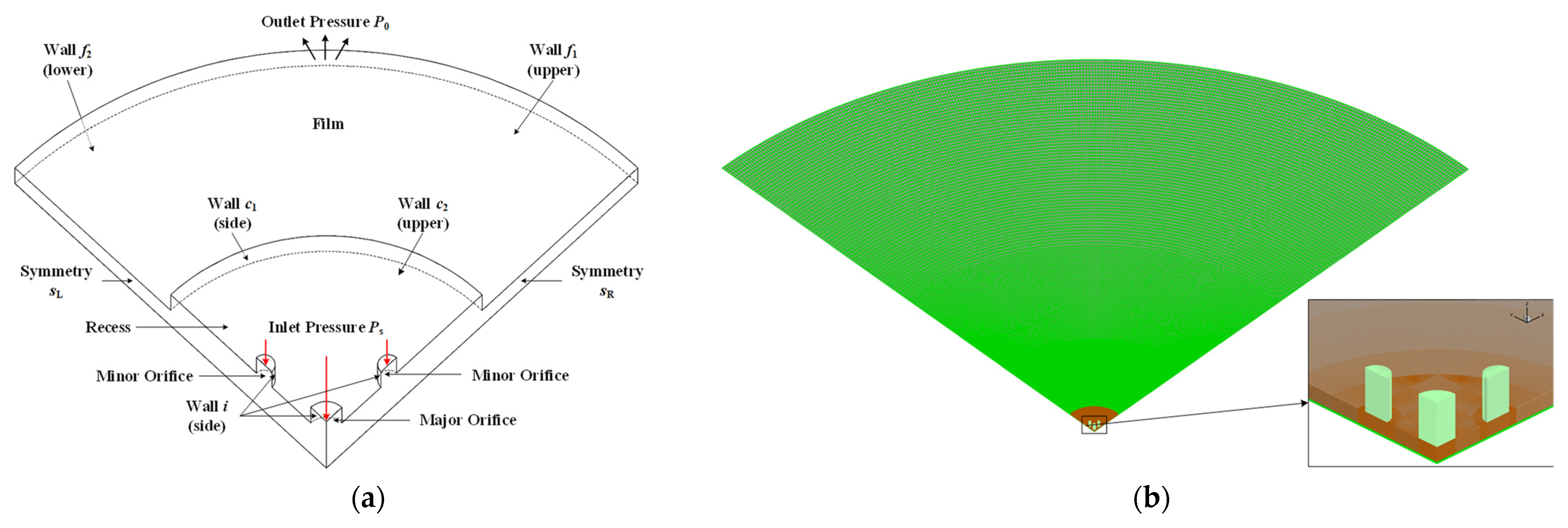
3.2. Grid Generation and Boundary Conditions
3.3. Mesh Grid Independent Analysis
4. Simulation Results and Discussion
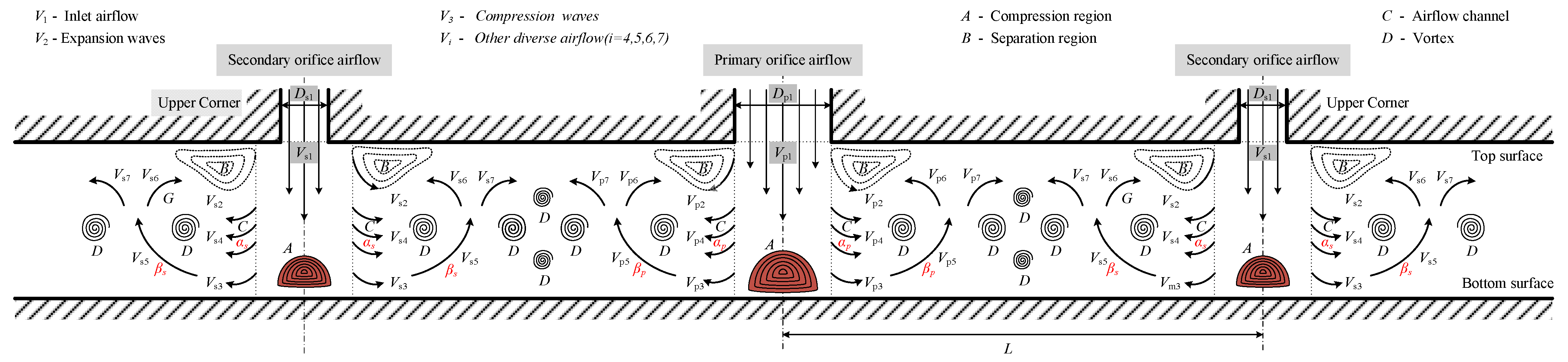
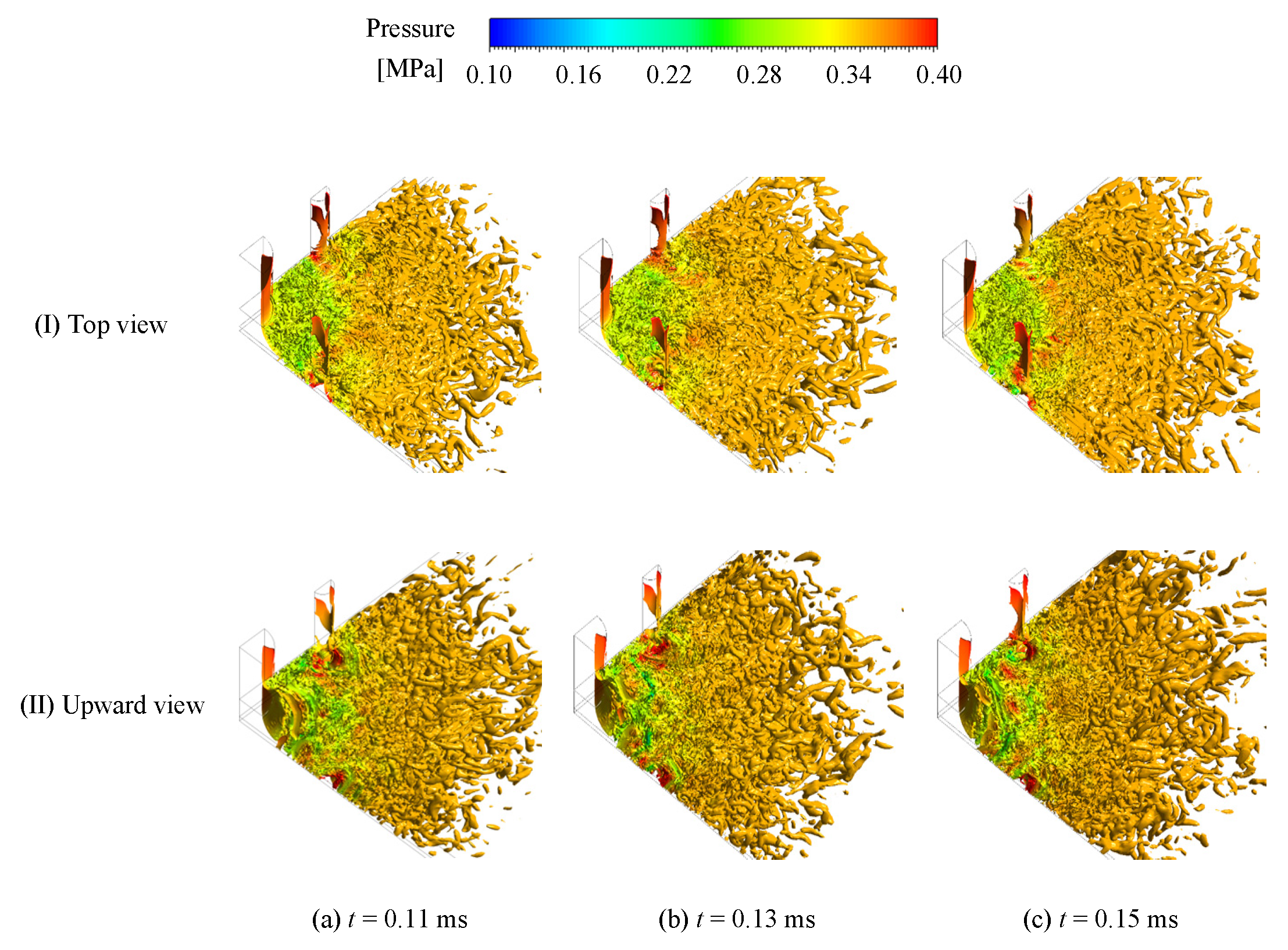
4.1. Turbulent Vortex Formation Mechanism
4.2. Transient Flow Behaviors
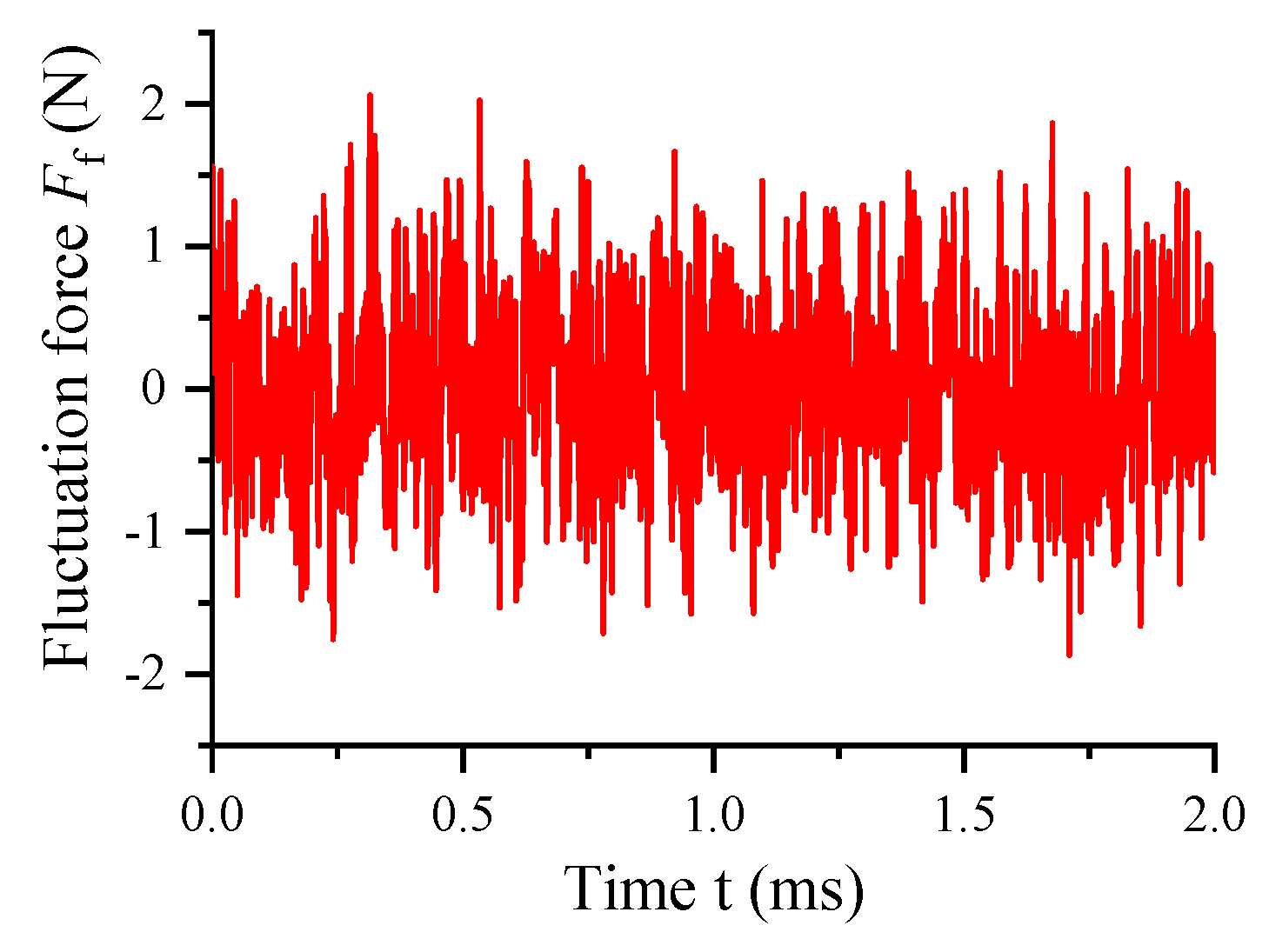
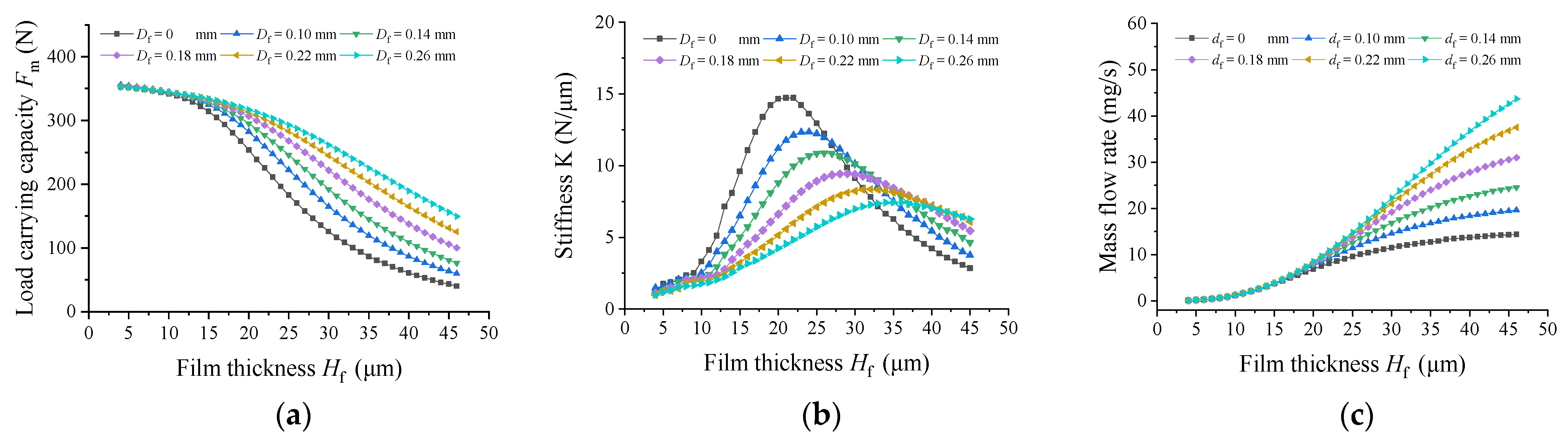
4.3. Effects of the Varying Diameter of Secondary Orifices on Nano−Vibration Characteristics
5. Experiment Results
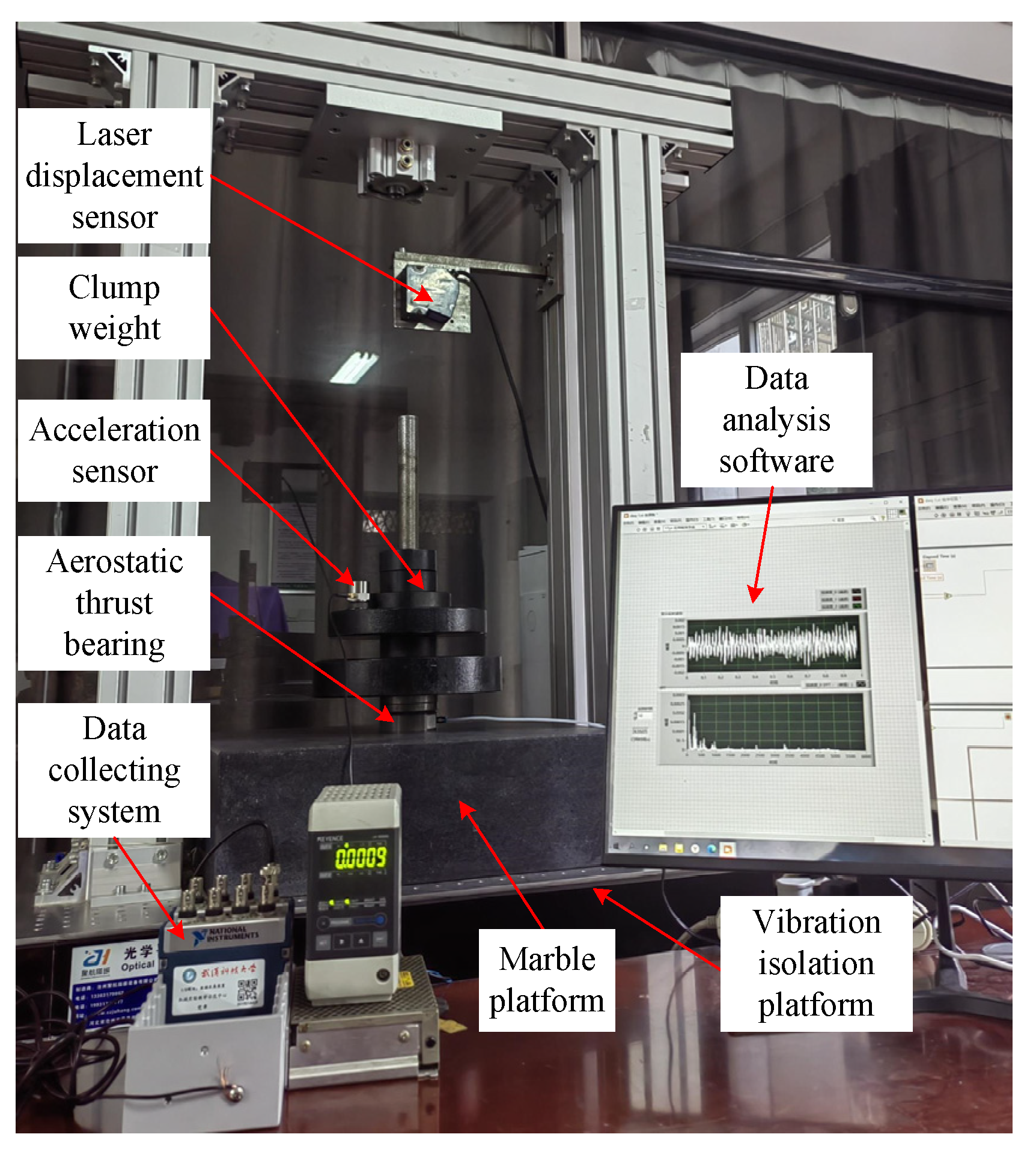
5.1. Tested Aerostatic Bearings
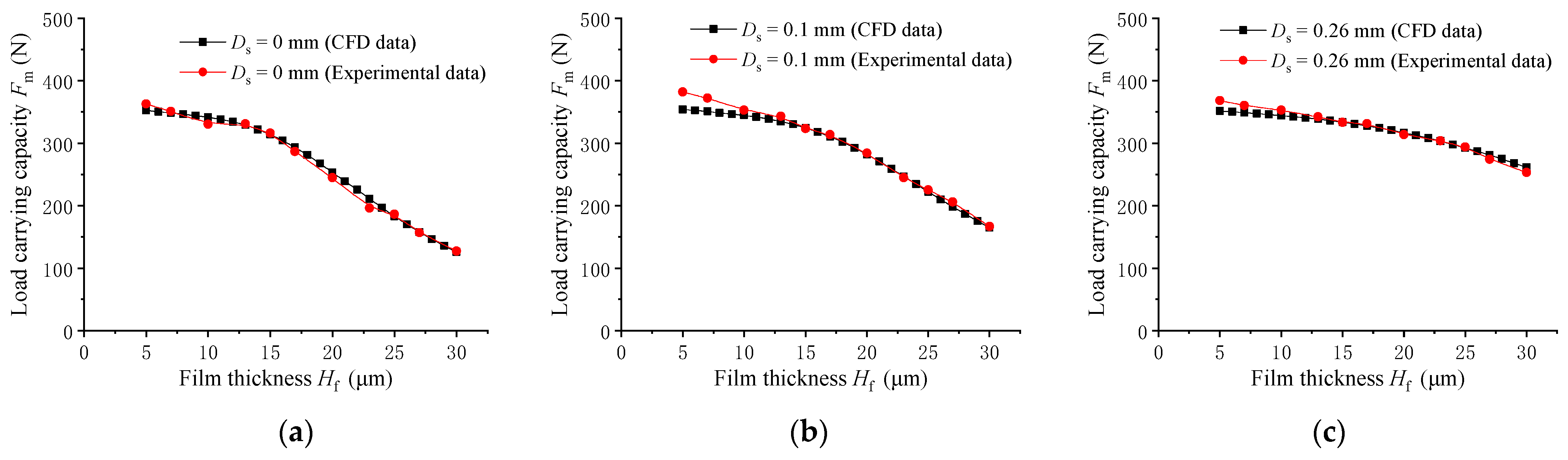
5.2. Load−Carrying Capacity Testing and Analyzing
5.3. Nano−Vibration Testing and Analyzing
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| D | aerostatic bearing outer diameter | Vi | airflows velocity (i = 1, 2, 3, 4, 5, 6, 7) |
| Dp | primary orifice diameter | τw | wall shear stress |
| Ds | secondary orifice diameter | Δ | gird element volume |
| Dc | chamber diameter | σij | viscous stress tensor |
| Hc | height of compression area | τij | subgrid−scale (SGS) stress |
| Hr | restrictor height | m | mass flow rate |
| Hf | air film thickness | t | time |
| Ps | air supply pressure | xi, xj, xk | coordinates in various directions |
| P0 | atmosphere pressure | ui, uj, uk | flow velocities in various directions |
| Hc | cylindrical chamber height | Re | Reynolds number |
| K | stiffness | T | temperature |
| L | spacing between the primary orifice and the secondary orifice | μ | air viscosity |
| ρ | air density | Δx | size of the control volume |
| p | dynamic pressure | R | ideal gas constant |
| α | angle of the flow V3 | Δt | time step size |
| β | angle of the flow V4 | pd | dynamic pressure |
| Rij | SGS Reynolds stresses | Fd | dynamic load−carrying capacity (DLCC) |
| Cij | cross stresses | Fm | mean force |
| Lij | subgrid−scale Leonard stresses | Ff | fluctuation force of the DLCC |
| δij | Kronecker delta function | σf | standard deviation of the DLCC |
References
- Lian, H.; Rong, C.; Li, Y. Influence of Operating Temperature on the Static Characteristics of an Externally Pressurized Thrust Bearing Lubricated with Refrigerant Gas. Tribol. Lett. 2021, 69, 123. [Google Scholar] [CrossRef]
- Ise, T.; Arita, N.; Asami, T.; Kawashima, I.; Maeda, T.; Nakajima, T. Experimental study of small−size air turbo blower supported by externally pressurized conical gas bearings. Mech. Mach. Theory 2015, 84, 57–66. [Google Scholar] [CrossRef]
- Lu, Z.W.; Zhang, J.A.; Liu, B. Study on the Gas Film Flow Field and its Influencing Factors at the Outlet of the Orifice of the Aerostatic Bearing. Shock Vib. 2020, 2020, 8891382. [Google Scholar] [CrossRef]
- Chang, S.H.; Chan, C.W.; Jeng, Y.R. Numerical analysis of discharge coefficients in aerostatic bearings with orifice−type restrictors. Tribol. Int. 2015, 90, 157–163. [Google Scholar] [CrossRef]
- Majumdar, B.C. Zero−load stability of a rigid rotor supported on pressurized porous gas bearings. Mech. Mach. Theory 1977, 12, 303–310. [Google Scholar] [CrossRef]
- Lohiya, S.H.; Pande, S.S. Analysis of tapered land aerostatic thrust bearing operating under nonsteady loads. Mech. Mach. Theory 1989, 24, 515–521. [Google Scholar] [CrossRef]
- Chen, M.F.; Lin, Y.T. Static behavior and dynamic stability analysis of grooved rectangular aerostatic thrust bearings by modified resistance network method. Tribol. Int. 2002, 35, 329–338. [Google Scholar] [CrossRef]
- Sahto, M.P.; Wang, W.; Imran, M.; He, L.; Li, H.; Weiwei, G. Modelling and Simulation of Aerostatic Thrust Bearings. IEEE Access 2020, 8, 121299–121310. [Google Scholar] [CrossRef]
- Colombo, F.; Lentini, L.; Raparelli, T.; Trivella, A.; Viktorov, V. Dynamic characterisation of rectangular aerostatic pads with multiple inherent orifices. Tribol. Lett. 2018, 66, 133. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Trivella, A.; Viktorov, V.; Visconte, C. CFD analysis of a simple orifice−type feeding system for aerostatic bearings. Tribol. Lett. 2015, 58, 25. [Google Scholar] [CrossRef]
- Kassab, S.Z. Empirical correlations for the pressure depression in externally pressurized gas bearings. Tribol. Int. 1997, 30, 59–67. [Google Scholar] [CrossRef]
- Kassab, S.Z.; Noureldeen, E.M.; Shawky, M.A. Effects of operating conditions and supply hole diameter on the performance of a rectangular aerostatic bearing. Tribol. Int. 1997, 30, 533–545. [Google Scholar] [CrossRef]
- Nishio, U.; Somaya, K.; Yoshimoto, S. Numerical calculation and experimental verification of static and dynamic characteristics of aerostatic thrust bearings with small feedholes. Tribol. Int. 2011, 44, 1790–1795. [Google Scholar] [CrossRef]
- Boffey, D.A.; Duncan, A.E.; Dearden, J.K. An experimental investigation of the effect of orifice restrictor size on the stiffness of an industrial air lubricated thrust bearing. Tribol. Int. 1981, 14, 287–291. [Google Scholar] [CrossRef]
- Boffey, D.; Barrow, A.A.; Dearden, J.K. Experimental investigation into the performance of an aerostatic industrial thrust bearing. Tribol. Int. 1985, 18, 165–168. [Google Scholar] [CrossRef]
- Chen, Y.S.; Chiu, C.C.; Cheng, Y.D. Influences of operational conditions and geometric parameters on the stiffness of aerostatic journal bearings. Precis. Eng. 2010, 34, 722–734. [Google Scholar] [CrossRef]
- Chen, X.D.; He, X.M. The effect of the recess shape on performance analysis of the gas−lubricated bearing in optical lithography. Tribol. Int. 2006, 39, 1336–1341. [Google Scholar] [CrossRef]
- Li, Y.; Han, D. Influences of the geometrical parameters of aerostatic thrust bearing with pocketed orifice −type restrictor on its performance. Tribol. Int. 2007, 40, 1120–1126. [Google Scholar] [CrossRef]
- Salem, E.; Kamal, W. Effect of recess geometry on shock wave formation in circular gas bearings. Wear 1978, 46, 351–366. [Google Scholar] [CrossRef]
- Talukder, H.M.; Stowell, T.B. Pneumatic hammer in an externally pressurized orifice−compensated air journal bearing. Tribol. Int. 2003, 36, 585–591. [Google Scholar] [CrossRef]
- Fourka, M.; Tian, Y.; Bonis, M. Prediction of the stability of air thrust bearings by numerical, analytical and experimental methods. Wear 1996, 198, 1–6. [Google Scholar] [CrossRef]
- Kawai, T.; Ebihara, K.; Takeuchi, Y. Improvement of machining accuracy of 5−axis control ultraprecision machining by means of laminarization and mirror surface finishing. CIRP Ann. 2005, 54, 329–332. [Google Scholar] [CrossRef]
- Yoshimura, T.; Hanafusa, T.; Kitagawa, T.; Hirayama, T.; Matsuoka, T.; Yabe, H. Clarifications of the mechanism of nano−fluctuation of aerostatic thrust bearing with surface restriction. Tribol. Int. 2012, 48, 29–34. [Google Scholar] [CrossRef]
- Chen, X.; Han, C.; Xin, L.; Ye, Y.; Hu, Y.; Xu, J. Air Vortices and Nano−Vibration of Aerostatic Bearings. Tribol. Lett. 2011, 42, 179–183. [Google Scholar] [CrossRef]
- Eleshaky, M.E. CFD investigation of pressure depressions in aerostatic circular thrust bearings. Tribol. Int. 2009, 42, 1108–1117. [Google Scholar] [CrossRef]
- Otsu, Y.; Somaya, K.; Yoshimoto, S. High−speed stability of a rigid rotor supported by aerostatic journal bearings with compound restrictors. Tribol. Int. 2011, 44, 9–17. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y.; Feng, L.; Hou, W.; Wang, J.; Li, W.; Feng, K. Study on the pneumatic hammer phenomenon of aerostatic bearings based on the empirical mode method: Numerical and experimental analysis. Tribol. Int. 2023, 181, 108305. [Google Scholar] [CrossRef]
- Aoyama, T.; Kakinuma, Y.; Kobayashi, Y. Numerical and Experimental Analysis for the Small Vibration of Aerostatic Guideways. CIRP Ann.—Manuf. Technol. 2006, 55, 419–422. [Google Scholar] [CrossRef]
- Ma, W.; Cui, J.; Liu, Y.; Tan, J. Improving the pneumatic hammer stability of aerostatic thrust bearing with recess using damping orifices. Tribol. Int. 2016, 103, 281–288. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, H.; Chen, X. Large eddy simulation of vortex shedding and pressure fluctuation in aerostatic bearings. J. Fluids Struct. 2013, 40, 42–51. [Google Scholar] [CrossRef]
- Yifei, L.; Yihui, Y.; Hong, Y.; Xinen, L.; Jun, M.; Hailong, C. Modeling for optimization of circular flat pad aerostatic bearing with a single central orifice−type restrictor based on CFD simulation. Tribol. Int. 2017, 109, 206–216. [Google Scholar] [CrossRef]
- Chen, X.; Chen, H.; Zhu, J.; Jiang, W. Vortex suppression and nano−vibration reduction of aerostatic bearings by arrayed microhole restrictors. J. Vib. Control 2017, 23, 842–852. [Google Scholar] [CrossRef]
- Feng, K.; Wang, P.; Zhang, Y.; Hou, W.; Cui, H. Novel 3−D printed aerostatic bearings for the improvement of stability: Theoretical predictions and experimental measurements. Tribol. Int. 2021, 163, 107149. [Google Scholar] [CrossRef]
- Yu, P.; Lu, J.; Luo, Q.; Li, G.; Yin, X. Optimization Design of Aerostatic Bearings with Square Micro−Hole Arrayed Restrictor for the Improvement of Stability: Theoretical Predictions and Experimental Measurements. Lubricants 2022, 10, 295. [Google Scholar] [CrossRef]
- Li, L.; Lou, J.; Nishikawa, H.; Luo, H. Reconstructed Discontinuous Galerkin Methods for Compressible Flows Based on a New Hyperbolic Navier−Stokes system. J. Comput. Phys. 2020, 427, 110058. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Zhu, H.; Lin, Y. Numerical analysis and experimental study on the microvibration of an aerostatic thrust bearing with a pocketed orifice−type restrictor. ARCHIVE Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 1994−1996 (Vols 208–210) 2014, 229, 609–623. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid−Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator−splitting. J. Comput. Phys. 1991, 62, 40–65. [Google Scholar] [CrossRef]
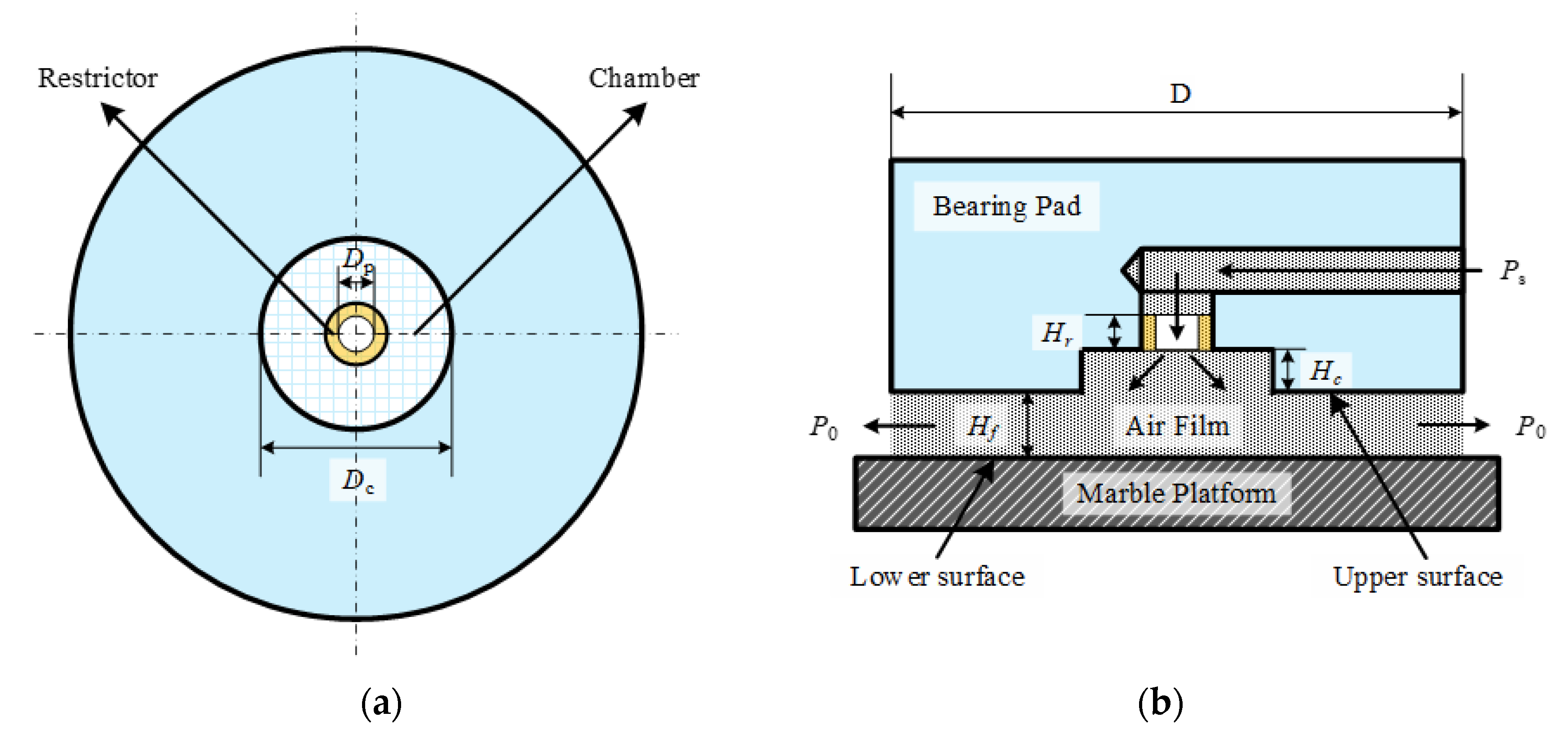

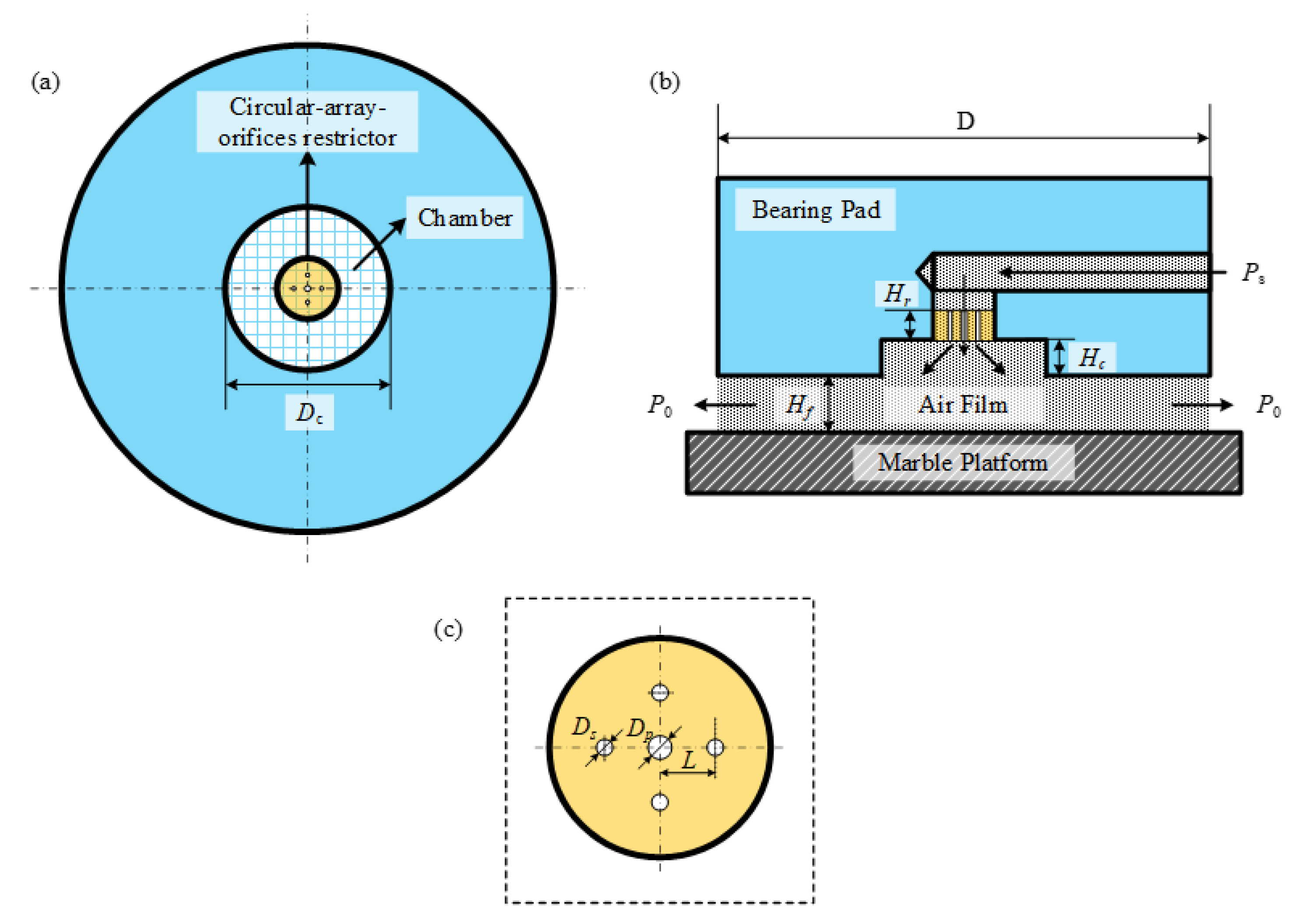







| Type | Restrictor | Primary Orifice Diameter Dp (mm) | Secondary Orifice Diameter Ds (mm) | Spacing L (mm) | Chamber Height Hc (mm) | Chamber Diameter Dc (mm) | Bearing Diameter D (mm) | Orifice Height Hr (mm) |
|---|---|---|---|---|---|---|---|---|
| A | 1 Po + 4 So | 0.3 | 0.10~0.26 | 0.5 | 0.1 | 5 | 80 | 0.3 |
| B | 1 Po | 0.3 | 0 | 0 | 0.1 | 5 | 80 | 0.3 |
| Air Temperature | Density | Specific Heat | Heat Conductivity | Viscosity | Molecular Weight |
|---|---|---|---|---|---|
| 293.15 K | 1.202 kg/m3 | 1006.43 J/(kg·K) | 0.0242 W/(m·K) | 1.7894 × 10−5 kg/(m·s) | 28.966 × 10−3 kg/mol |
| Type | Chamber | Orifice | Air Film | y+max | Total Number | Mean Force Fm/N | Standard Deviation σf | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Δmin | Δmax | Δmin | Δmax | Δmin | Δmax | |||||
| 1 | 1.51 | 1714 | 21.66 | 81.27 | 894 | 6260 | 1.84 | 1,418,400 | 320.22 | 0.530 |
| 2 | 1.10 | 1203 | 21.66 | 81.27 | 1375 | 9630 | 1.51 | 2,181,621 | 324.72 | 0.525 |
| 3 | 0.55 | 469 | 21.66 | 81.27 | 1375 | 9630 | 0.65 | 3,278,216 | 325.16 | 0.527 |
| 4 | 0.03 | 281 | 21.66 | 81.27 | 1103 | 5643 | 0.46 | 4,134,320 | 325.06 | 0.522 |
| Type | Restrictor | Primary Orifice Diameter Dp (mm) | Secondary Orifice Diameter Ds (mm) | Spacing L (mm) | Chamber Height Hc (mm) | Chamber Diameter Dc (mm) | Orifice Height Hr (mm) |
|---|---|---|---|---|---|---|---|
| A1 | 1 Po + 4 So | 0.3 | 0.10 | 0.5 | 0.1 | 5 | 0.3 |
| A2 | 1 Po + 4 So | 0.3 | 0.26 | 0.5 | 0.1 | 5 | 0.3 |
| B | 1 Po | 0.3 | 0 | 0 | 0.1 | 5 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, P.; Zuo, T.; Lu, J.; Zhong, M.; Zhang, L. Static and Dynamic Performances of Novel Aerostatic Bearings with Primary and Secondary Orifice Restrictors. Lubricants 2023, 11, 518. https://doi.org/10.3390/lubricants11120518
Yu P, Zuo T, Lu J, Zhong M, Zhang L. Static and Dynamic Performances of Novel Aerostatic Bearings with Primary and Secondary Orifice Restrictors. Lubricants. 2023; 11(12):518. https://doi.org/10.3390/lubricants11120518
Chicago/Turabian StyleYu, Puliang, Te Zuo, Jiong Lu, Min Zhong, and Liping Zhang. 2023. "Static and Dynamic Performances of Novel Aerostatic Bearings with Primary and Secondary Orifice Restrictors" Lubricants 11, no. 12: 518. https://doi.org/10.3390/lubricants11120518
APA StyleYu, P., Zuo, T., Lu, J., Zhong, M., & Zhang, L. (2023). Static and Dynamic Performances of Novel Aerostatic Bearings with Primary and Secondary Orifice Restrictors. Lubricants, 11(12), 518. https://doi.org/10.3390/lubricants11120518




