1. Introduction
Increasing the rotational speed of rotating machinery can significantly improve energy density and efficiency. Gas foil bearings (GFBs) are oil-free bearings that meet the high-speed requirement due to their low friction and high DN (shaft diameter in millimeters multiplied by shaft rotational speed in rev/min) limit [
1,
2,
3]. In contrast with traditional oil-lubricated bearings, GFBs eliminate the need for an oil-lubrication system, resulting in a compact structure and reduced energy loss [
4,
5]. These advantageous characteristics have greatly facilitated the successful application of GFBs in high-speed turbomachinery systems, including cryogenic turboexpanders, Brayton air refrigerator systems, high-speed machining centers, and micro-power generator systems [
6,
7,
8,
9].
However, GFB-rotor systems often experience severe subsynchronous vibrations at high rotating speeds, limiting the range of their applications [
10]. As a result, numerous studies have focused on investigating the dynamic responses of GFB-rotor systems. Several researchers have used a perturbation method to calculate the dynamic stiffness and damping coefficients for analyzing the dynamic responses of GFB-rotor systems. Ku et al. [
11] introduced this method to predict the structural stiffness and damping of foil when a rotor is in its static equilibrium position. Lee et al. [
12] compared the dynamic responses of a super-critical rotor supported by conventional bump foil bearings and viscoelastic bearings using experimental and theoretical results. The theoretical orbit calculations, based on dynamic stiffness and damping coefficients, showed a good agreement with the experimental results when the vibration amplitude of the rotating speed remained below the bending critical speed. The theoretical findings indicated that enhancing the structural damping of the foil structure reduced vibration. Vleugels et al. [
13] conducted a stability analysis of the GFB-rotor system using dynamic stiffness and damping coefficients. They assumed the foil structure acted as a uniform elastic foundation to calculate the dynamic stiffness and damping properties. Numerical results indicated that bearing compliance significantly influenced the dynamic stiffness, and increasing the bearing load and reducing the ratio of the nominal bearing clearance to the rotor radius enhanced stability. Kim et al. [
14] performed theoretical and experimental research on the effects of mechanical preload. Metal shims were inserted beneath the bump-strip layers of shimmed GFBs to introduce mechanical preload. Compared with the original GFBs, the shimmed GFBs exhibited a noticeable increase in dynamic direct stiffness and direct damping. The multiple lobe film clearance profile created by the metal shims reduced the amplitude of subsynchronous whirl motions and increased the natural frequency of the GFB-rotor system, as confirmed by experimental results. Theoretical and experimental results also indicated that rotor unbalance and the gas film had a significant influence on nonlinear dynamic responses, although the foil structure was simplified as a uniform elastic foundation with a given value. Xu et al. [
15] developed a more comprehensive GFB model that considered nonlinearity in the foil structure to predict dynamic responses in GFB-rotor systems. They calculated dynamic stiffness and damping coefficients based on a quadratic bump stiffness model derived from experimental bearing stiffness data. The simulation results of the quadratic bump stiffness model differed significantly from those of the linear bump stiffness model, indicating the significant impact of foil structure nonlinearity on the dynamic responses of GFB-rotor systems. Hoffmann et al. [
16] used a link-spring model incorporating frictional contacts and bump interactions to investigate the nonlinear vibrations of GFB-rotor systems. Using experimental and numerical testing of two contrasting cases with different balanced rotors, they identified the source of subsynchronous vibrations. The simulation results showed good agreement with the measurements, indicating that interaction between the gas film and the rotor caused subsynchronous vibrations when unbalance was significant. When unbalance was minor, the subsynchronous vibrations originated from the self-excitation of the gas film.
However, the dynamic stiffness and damping coefficients were perturbation results calculated using linearized Reynolds equations when the rotor displacements were small relative to its static equilibrium position. Subsynchronous vibrations with large amplitudes were common in many tests, highlighting the limitations of the linear perturbation approach. Kim [
17] investigated the dynamic responses of GFB-rotor systems using both linear and nonlinear approaches. It was found that the rotor–bearing natural frequencies predicted using the two approaches were similar. However, the onset speeds of instability differed significantly between the time domain nonlinear orbit simulations and the linear stability simulations based on the dynamic stiffness and damping coefficients. Bou et al. [
18] conducted a comparison between a nonlinear time-dependent approach and the classical linear approach using dynamic stiffness and damping coefficients. The classical linear approach was found to have a valid range of relative eccentricity lower than 0.65. For high values of eccentricity, the accuracy of the results required the use of the nonlinear approach. Larsen et al. [
19] also compared the two approaches for predicting the onset speed of instability. It was observed that the classical linear approach was only suitable when the uniform foil stiffness was high and the load was small. When the uniform foil stiffness was reduced or the load level was increased, there were significant discrepancies in the prediction of the onset speed of instability. The nonlinear time domain approach, however, could accurately predict the actual rotor response, which the classical linear approach was unable to achieve. Consequently, many researchers have adopted nonlinear analysis approaches. Bhore et al. [
20] proposed a nonlinear time domain orbit simulation that coupled the equations of the unsteady Reynolds equation, foil deformation, and rotor motion. They conducted parametric studies on rotating speed, unbalance eccentricity, compliance, and the loss factor, revealing highly nonlinear behaviors of the disc and journal center motion. However, the foil structure was simplified as a uniform elastic foundation. Larsen et al. [
21] studied the effect of unbalance and rotational speed using theoretical modeling and experimental testing. The theoretical results, solved with a mathematical approach in the time domain, showed good agreement with the experimental results. Both the theoretical and experimental results indicated that subsynchronous vibrations were primarily influenced by unbalance and rotational speed. Additionally, the correct estimation of the foil stiffness and loss factor significantly affected the accuracy of the predictions. Osmanski et al. [
22] proposed a new foil model based on truss representation, considering foil mass and frictional energy dissipation at foil interfaces. They presented a nonlinear time domain model to calculate the dynamic responses of GFB-rotor systems using this foil model. The simulation results showed good agreement with the experimental results, suggesting that the natural frequencies and mode shapes were accurately captured. Bonello et al. [
23] introduced a modal-based bump foil model that considered the dynamic interaction between bumps and their inertia. They used a simultaneous solution technique to integrate the rotor, gas film, and foil domains into a coupled dynamical system model. This approach accurately predicted the nonlinear behaviors of GFB-rotor systems. The imposition of pressure constraints on the gas film delayed the onset speed of instability, aligning well with experimental results. Moreover, the significant influence of gas film nonlinearity on the non-linear behaviors of GFB-rotor systems was verified with measured and predicted nonlinear phenomena. The aforementioned studies demonstrate that nonlinear analysis approaches yield more accurate dynamic responses of GFB-rotor systems.
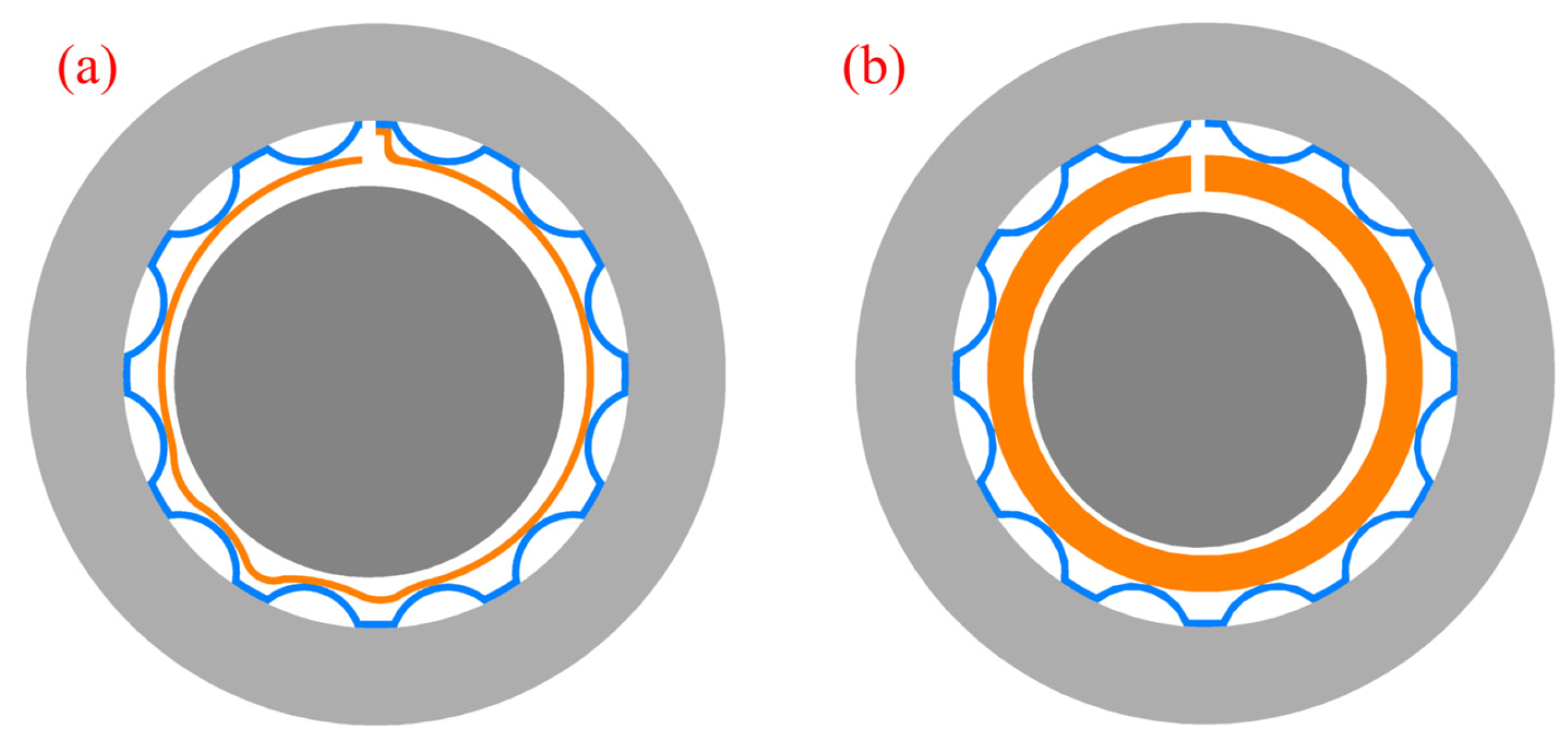
Most recently, a type of bump-type foil bearing with a thick top foil was introduced to handle heavy load conditions [
24,
25]. In comparison with traditional gas foil bearings (GFBs) with thin top foils, TTFBs showed significant improvements in load capacity by reducing the sagging of the top foil, as depicted in
Figure 1. Wang et al. [
24] developed a theoretical model for a TTFB and predicted its load capacity and dynamic force coefficients. The numerical results indicated a 23% increase in load capacity compared with a GFB, along with different dynamic force coefficients. However, the numerical results were not experimentally validated. Li et al. [
25] developed a three-dimensional finite element model based on contact mechanics to investigate the load capacity of TTFBs. The numerical results, which agreed well with experimental findings, demonstrated a 100% improvement in load capacity compared with GFBs with thin top foils. The thickness of the top foil was found to have a significant impact on the degree of sagging and bearing stiffness. However, the study primarily focused on load capacity, and there is currently a lack of research on the dynamic responses of TTFB-rotor systems. This knowledge gap severely hinders the application and wider adoption of TTFBs, despite their high load capacity.
This paper presents an integrated nonlinear dynamic model for investigating the dynamic responses of TTFB-rotor systems, where a rigid rotor is supported by TTFBs. The model consists of a time-domain orbit simulation that couples unsteady Reynolds equations, foil deformation equations, thick top foil motion equations, and rotor motion equations. To validate the simulation results, various bump foil stiffness scenarios are tested against data obtained from a symmetrical test rig. The analysis of dynamic responses uses fast Fourier transform (FFT), waterfall plots, orbit simulations, and Poincaré maps. The simulation considers the impact of parameters such as nominal clearance, static load, and unbalance on the nonlinear responses of the TTFB-rotor system. By carefully selecting these parameters, a deeper understanding of the TTFB-rotor system is obtained. Furthermore, the obtained results and discussions are of importance to promote the application of TTFBs in high-speed and high-performance rotating machinery systems.
2. Nonlinear Numerical Prediction Method
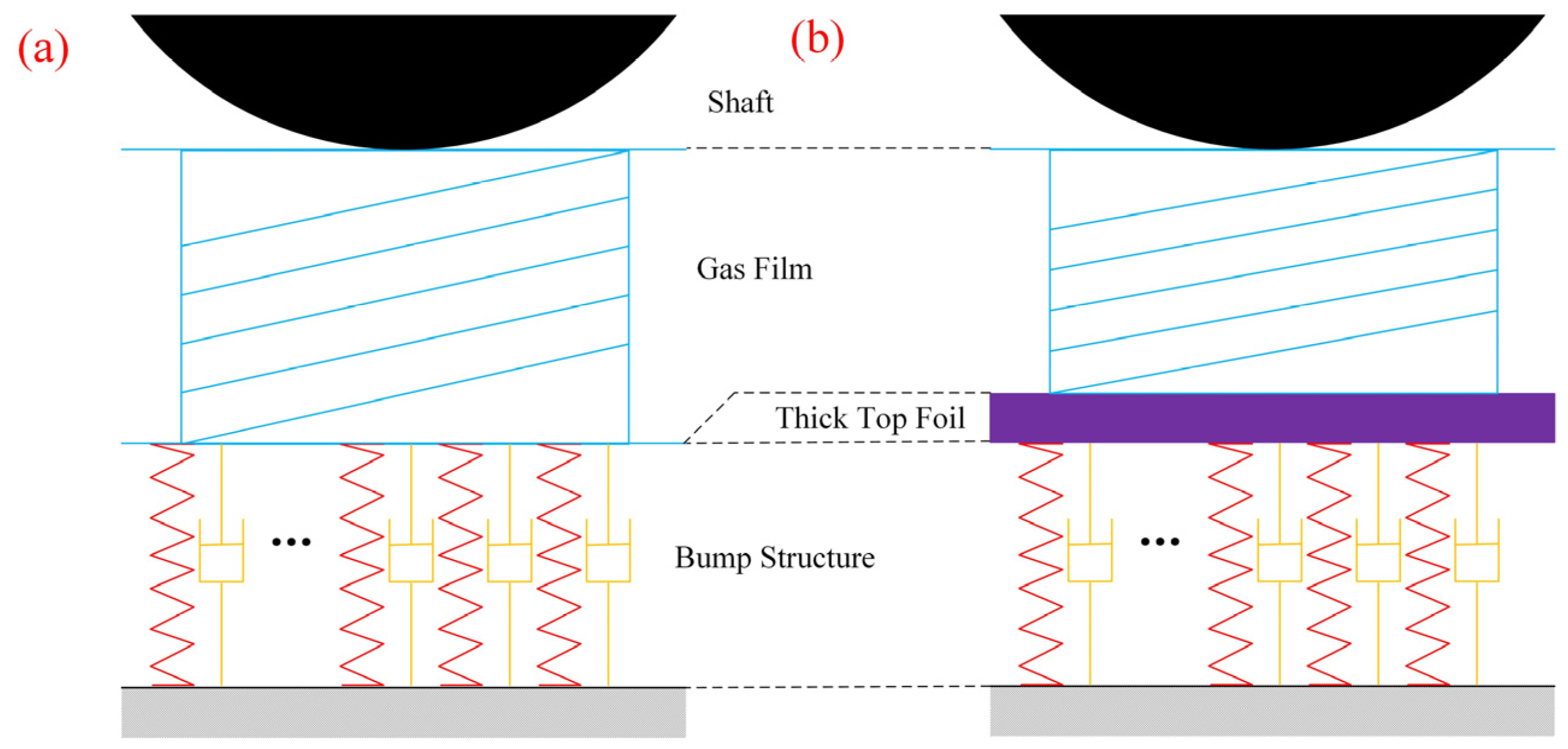
The nonlinear model of the GFB-rotor system is typically divided into three components: the shaft part, which is based on rotor motion equations; the gas film part, which is based on unsteady Reynolds equations; and the bump structure part, which is based on foil deformation equations, as depicted in
Figure 2a [
26]. However, in the case of the TTFB-rotor system, the weight of the thick top foil needs to be considered. The thick top foil has a thickness of 1.5~2.0 mm, which is significantly thicker than the thin top foil’s 0.1~0.2 mm. As a result, the thick top foil part should be added as the fourth component to the TTFB-rotor system, as shown in
Figure 2b. A time-domain orbit simulation is conducted, integrating these four components, to accurately simulate the performance of the TTFB-rotor system.
2.1. Theoretical Model for TTFB
As shown in
Figure 3, the theoretical model of a TTFB is composed of a gas film part based on unsteady Reynolds equations, a bump structure part based on foil deformation equations, and a thick top foil part based on motion equations of the thick top foil. The dimensionless transient compressible Reynolds equation that calculates the dynamic pressure and film thickness distribution of a TTFB is written as
The dimensionless bearing axial width
, pressure
, gas film thickness
, bearing number
, excitation frequency ratio
, and time
in Equation (1) are written in Equation (2) as
where the bearing radius
ambient pressure
, nominal clearance
, viscosity of gas
, rotational frequency
, excitation frequency
, and time
are used in the dimensionless representation of the above-mentioned parameters.
Based on the structural characteristics of TTFBs, both the displacement of the rotor and the movement of the thick top foil dominate the eccentricity of a TTFB. Therefore, the eccentricity vector of a TTFB is the relative eccentricity vector
obtained by subtracting the eccentricity vector of the rotor and the eccentricity vector of the thick top foil. The unsteady gas film thickness is written as
where
and
are the modulus and angle of the relative eccentricity vector
, respectively. In Equation (3), the term of the bump deflection is not included for the thick top foil is assumed as the rigid body [
24].
The dimensionless transient compressible Reynolds equation is solved using the alternating-direction implicit method. When the transient gas film pressure field meets the condition of convergence, the pressure field is integrated using Simpson’s one-third rule to calculate transient TTFB hydrodynamic film force in the x- and y-directions. The force is written as
The weight of the thick top foil is no longer small compared with that of the rotor; thus, it should be taken into account. The motion equation of the thick top foil is written as
where
and
,
and
, and
and
are the displacement, stiffness, damping of the thick top foil in the x- and y-directions, respectively.
and
are the combined stiffness of the deformed bumps in the x- and y-directions, they can be written as
where
is the stiffness of the JTH deformed bump and
is the angle of the JTH deformed bump. In this paper,
is derived on the basis of the model with linear stiffness distribution [
27].
and
are the combined damping of the deformed bumps in the x- and y-directions, they can be written as
where
is foil structural loss factor [
20].
2.2. Theoretical Model for the Rigid Rotor
The structure of the TTFB-rotor system, as depicted in
Figure 4, was investigated in this study. Unbalance was added symmetrically to the shaft, and the eddy current probe was positioned symmetrically for measurement. The shaft was divided into 20 beam elements with 80 degrees of freedom, utilizing a beam model based on the finite element method (FEM). The thrust disks and turbines mounted on the shaft were treated as beam elements and the Timoshenko beam theory was used to account for the shear effect. The nonlinear bearing forces were represented as concentrated forces at the centers of each thick top foil.
When adopting the assumptions described above, the motion equation of the shaft is written as
where
is the displacement of each node at the shaft,
,
and
,
are the lateral and rotational displacements, respectively.
,
,
, and
are the mass, damping, gyroscopic, and stiffness matrixes. The damping effect of the system is considered to be related only to the nonlinear bearing force; therefore, the damping matrix
is set to zero [
26].
is the nonlinear TTFB force vector, and
is the gravity force vector.
is the force vector induced by the unbalance, and
of each node at the shaft is written as
where
and
are the unbalance force in the horizontal and vertical directions, whereas the unbalance moments
and
are set to zero [
26].
is the unbalance mass of the shaft, and
is the radius of the unbalance mass.
2.3. Orbit Simulation
A time-domain orbit simulation coupling unsteady Reynolds equations, foil deformation equations, thick top foil motion equations, and rotor motion equations is conducted to analyze the nonlinear dynamic responses.
Equations (6), (7) and (10) are nonlinear equations. Two kinds of numerical calculation methods, one being the explicit time history method and the other being the implicit time history method, can be adopted to solve them [
28]. The Newmark method selected in this paper is an implicit time history method. The Newmark method is a method for modifying linear acceleration. By introducing two parameters
and
into the velocity and displacement expressions at time
, two basic equations of the Newmark method can be written as
In the Newmark method, the control parameters
and
affect the accuracy and stability of the whole algorithm. Only when
and
, the Newmark method has second-order accuracy and unconditional stability. Therefore, the control parameters
and
are assigned as 0.5 and 0.25, respectively, in research and engineering applications. The Newmark method is called the constant mean acceleration method. Equations (12) and (13) are transformed into
Accordingly, the constant average acceleration method is used in this paper to calculate the trajectory of the rigid rotor and the thick top foil.
For the shaft, the dynamic response at time
is calculated using
For the thick top foil, the dynamic response at time
is calculated using
In the TTFB-rotor system, the compressible transient Reynolds equation used to solve the gas film transient pressure distribution is a second-order partial differential equation, and the dynamic equation used to solve the rotor and thick top foil trajectory is a second-order ordinary differential equation. In the process of solving the rotor trajectory, in each time step, these two equations need to be solved simultaneously. However, in the process of solving these two equations, the results of the other side are required as the initial conditions, so the synchronous coupling solution is difficult to carry out. In order to predict the nonlinear dynamic characteristics of the TTFB-rotor system, a linear displacement prediction method is used to solve the synchronous coupling problem [
28]. The linear displacement prediction method assumes that the displacement of the thick top foil and rotor changes linearly at step
, step
, and step
, and can be written as
According to Equations (23) and (24), based on the thick top foil and axial diameter displacement of step
and step
, the gas film thickness of step
can be predicted as
To provide a referable analysis, 50 time steps are calculated per revolution to solve the rotor orbit. The steady-state solutions for each rotational speed are carried out to simulate the entire TTFB-rotor system speed-up test because unsteady-state solutions are very time-consuming.
3. Model Verification
To validate the method for predicting subsynchronous responses in the TTFB-rotor system, an experimental setup is designed and conducted. The TTFB used in the test is illustrated in
Figure 5 and consists of a thick top foil, bump foil, bearing housing, and snap ring. The displacement of the thick top foil in the circumferential direction is restricted by inserting lugs into the grooves of the snap ring and bearing housing. In the axial direction, the displacement of the thick top foil is limited by the snap ring and the internal end face of the bearing housing. The configuration of the test rig is shown in
Figure 6. A symmetric design is used for the rotor, which comprises two identical impulse turbines to ensure that both TTFBs bear the same load. A pair of gas foil thrust bearings is utilized to limit axial movement of the rotor. Four eddy current sensors are used to measure the radial displacement of the TTFBs, while a laser speed sensor tracks the rotor’s speed and phase. The dimensions of the two test TTFBs are as follows: a radius of 17.56 mm and a width of 30 mm. The impulse turbine tip clearance is set at 0.3 mm, ensuring that the rotor has sufficient torque to lift off and reach a maximum speed of 60 krpm under an inlet compressed air pressure of 0.7 Mpa. All data are acquired using a dynamic signal acquisition system developed by Donghua. The shaft weight is 4 kg, resulting in a static load of 2 kg on each bearing. Both TTFBs undergo the same manufacturing process, heat treatment, and assembly. The inner diameter of the TTFBs is measured with a micrometer gauge as shown in
Figure 7, and the diameter of the shaft is measured with an outside micrometer. The value of the nominal clearance is obtained by subtracting the radius of the TTFBs from the radius of the shaft. In this paper, a nominal clearance of 60 μm was tested. The thick top foil has a thickness of 1.5 mm and is coated with a 20 μm thickness of PTFE to prevent potential wear on both the TTFBs and the shaft. The rotor unbalance is reduced to a G1.0 level using a commercial dynamic balancer. Scribed lines are marked to ensure that the unbalance amount of the rotor remains unchanged after disassembly and reassembly.
Table 1 provides a detailed overview of the physical and geometric parameters of the TTFB-rotor system.
The maximum stable speed is achieved by accelerating the rotational speed using two symmetrically identical impulse turbines. During orbit simulations, a stable limit cycle cannot form beyond the maximum stable speed. In the experiment, when the maximum stable speed is exceeded, there is a noticeable sound of abnormal collision between the shaft and the thick top foil. To mitigate the impact of additional vibrations near the critical speed, a modal analysis of the rotor is performed, and the resulting Campbell diagram plot is presented in
Figure 8. The first-order forward and backward whirling frequencies are 2247 Hz and 1999 Hz, respectively. Due to the symmetrical structure of the test rig, the vibrations on the left and right sides are similar. For research convenience, the vibration signals in the vertical direction at the right end are uniformly analyzed.
Figure 9 illustrates that synchronous vibrations, marked as 1X and characterized by a frequency equal to the rotational frequency, are present. The amplitude of synchronous vibrations remains stable as the rotational speed changes, with simulation and experimental steady values of 0.88 μm and 1.21 μm, respectively. Subsynchronous vibrations, on the other hand, maintain a frequency that does not vary with the rotational speed. As the rotational speed increases, the simulation amplitude of subsynchronous vibrations also increases, and the increase becomes more pronounced as the rotational speed approaches the maximum stable speed. The experimental results exhibit a similar trend. Using ten-order zero-phase digital band pass filters [
29],
Figure 10 also illustrates that as the rotational speed increases, the simulation results and experimental results exhibit more pronounced subsynchronous vibrations. The predicted frequency and peak amplitude of the subsynchronous vibrations are 99 Hz and 9.12 μm, respectively, closely matching the corresponding experimental results of 102 Hz and 10.30 μm. The predicted and experimental maximum stable speeds are also close, with values of 36 krpm and 35.58 krpm, respectively. Comparing the simulation results with the experimental results, it is evident that both synchronous and subsynchronous vibrations are well-matched between the two.
To further validate the method, two additional cases were conducted with different bump foil stiffnesses. The first case involved a lower stiffness configuration, using a 0.1 mm C17200 bump foil material with a Young’s modulus of 130 Gpa, resulting in 0.7 times the original stiffness as per the above model [
27]. The second case utilized a higher stiffness configuration, using a 0.2 mm 3J1 alloy as the bump foil material with 8 times the original stiffness.
Figure 11 illustrates waterfall plots depicting the simulation and experimental vertical vibrations at the right end. Upon comparing these plots, it is evident that even with variations in bump foil stiffness, the simulation results for synchronous and subsynchronous vibrations align well with the experimental results. The simulation’s maximum stable speed and subsynchronous frequency also exhibit good agreement with the experimental findings. Thus, we can conclude that the time-domain orbit simulation accurately predicts the dynamic responses of TTFB-rotor systems.
The impact of bump foil stiffness on the dynamic responses of the TTFB-rotor system can also be inferred from these cases. It is observed that increasing the bump foil stiffness leads to a higher subsynchronous frequency. However, this observation contradicts the results of previous studies on GFB-rotor systems, which suggested a positive correlation between the subsynchronous frequency and the square root of bump foil stiffness [
26]. This discrepancy implies that the thick top foil also plays a role in influencing the nonlinear responses of the TTFB-rotor system. Regarding the maximum stable speed, the simulation indicates that the maximum stable rotor speed for the lower bump stiffness bearing is 34.2 krpm, while the experimental result is 33.42 krpm. Similarly, for the original bearing, the simulation and experimental results correspond to 36 krpm and 35.58 krpm, respectively. Finally, for the higher bump stiffness bearing, the simulation and experimental results show 39 krpm and 39.12 krpm. These findings clearly demonstrate that as the bump foil stiffness increases, the stable speed of the TTFB-rotor system also increases. Consequently, a TTFB-rotor system with a higher bump foil stiffness exhibits enhanced stability.
5. Conclusions
In this study, we developed a nonlinear dynamic model for TTFB-rotor systems by combining unsteady Reynolds equations, foil deformation equations, thick top foil motion equations, and rotor motion equations. This comprehensive model enables us to predict the dynamic responses of the TTFB-rotor system using time-domain orbit simulations, which accurately determine the rotor’s orbital path.
To validate the accuracy of our model, we constructed a symmetrical test rig that effectively minimizes errors caused by varying bearing loads. We conducted calculations and tests using three different types of TTFBs with varying bump foil stiffness. The resulting waterfall plots of vibrations, both calculated and tested, indicated that higher bump foil stiffness effectively suppresses subsynchronous vibrations. Furthermore, by comparing these simulation results with the corresponding experimental results, we observed a strong correlation in vibration patterns, validating the reliability of our model.
Based on our new model, we conducted separate studies on the effects of nominal clearance, static load, and unbalance on the TTFB-rotor system. It was found that increasing the nominal clearance or the static load, both of which reduce the bearing attitude angle, enhances the maximum stable speed of the TTFB-rotor system. As a result, for TTFB-rotor systems, other related parameters reducing the bearing attitude angle contribute to improved stability. In terms of unbalance, it was observed that an increase in unbalance has a strong positive correlation with the amplitude of synchronous vibration. However, unbalance has minimal impact on subsynchronous vibrations, and all TTFB-rotor systems exhibit the same maximum stable speed. This study not only demonstrates an advanced tool for predicting the dynamic responses of TTFB-rotor systems but also paves the way for future developments of TTFB in high-speed rotating machinery systems.