Characterisation of the Contact between Cross-Country Skis and Snow: On the Multi-Scale Interaction between Ski Geometry and Ski-Base Texture

Abstract

In elite endurance sports, marginal differences in finishing times drive ongoing equipment improvement to enhance athlete performance. In cross-country skiing, researchers, since the 1930s, have faced the challenge of minimising the resistance caused by friction in the contact between skis and snow. This study was designed to evaluate the multi-scale interaction between the macro-scale ski-camber profile and the micro-scale ski-base texture. Considerations included real contact area, average interfacial separation, and total reciprocal interfacial separation between the ski and snow, which are properties that are intimately coupled to ski–snow friction. We found that both the profile of the ski camber and the texture of the ski base play decisive roles in determining viscous friction. At the same time, the texture of the ski base exerts a greater impact on the average real contact pressure, real contact area, and minimal average interfacial separation between the ski and snow than the ski-camber profile.

1. Introduction

At the top level of endurance sports, race times are long, but the differences among finishing times can be small. Therefore, in most endurance sports, the equipment is constantly improved, e.g., minimised in weight to increase the athlete’s performance. Reduced equipment weight helps the athlete overcome gravitational forces, which is one of the resistive forces present in many sports. In some sports, other resistive forces are present; e.g., in cross-country skiing, friction is one of the dominant resistive forces [1]. In cross-country skiing, friction has even been correlated with winning time [2]. Friction in contact involving snow has interested researchers for quite some time. Already in 1939, Bowden [3] published a paper on this topic. In the years thereafter, several papers discussing this topic were published, e.g., [4,5], and even now, researchers are still trying to fully understand the physics and phenomena [6] associated with snow contact.

In the literature, several friction mechanisms occurring in ski–snow contact are considered, for example, compaction, micro-ploughing, adhesion, viscous contact, and water bridging, which are mentioned in Almqvist et al. [1]. The ones considered most commonly are the adhesive and viscous contributions to friction; see, e.g., [7,8,9,10,11,12,13]. Lever et al. [14] showed that abrasive friction in the form of micro-ploughing is dominant in the absence of meltwater at sub-zero temperatures. Friction originating from compaction, micro-ploughing, and water bridges in ski–snow contact is, however, not yet understood well enough.

When trying to estimate friction in cross-country skiing, it is crucial to consider the entire ski. The macro-scale geometry of the ski, under a given loading condition, can be measured using profilometry; see, e.g., [15]. The resulting ski-camber profile features the front and the rear contact zones, as well as the camber between them, and it is often used to determine how well suited a ski is for a particular condition. Breitschadel et al. [16] did, for instance, conclude that skis that were determined by the Norwegian Ski Team to work under a given condition had similar ski-camber profiles. In another paper, Breitschadel et al. [17], also investigated how different attributes of ski-camber profiles change when subjected to temperatures at which skiing often occurs compared with room temperature, at which the ski-camber profile is usually characterised. They observed an increase in stiffness and shorter contact zones as the temperature decreased. Recently, Kalliorinne et al. [15] showed how skiers’ pose during tucking influences the length of the rear and front contact zones, as well as the load partitioning between them.

A lot of information can be extracted from the ski-camber profile, e.g., the apparent length (thus area) of the rear and front contact zones and the topology of the kick–wax zone under a given loading condition. The profile does not, however, provide information on how the nominal load, i.e., the meso-scale pressure defined in [18], is distributed over the contact zones. Neither does it tell us what contact could look like at the micro scale in terms of real contact area and the corresponding real contact pressure distribution.

Measuring the pressure between the ski and a rigid counter-surface, at a given magnification, gives some information about the contact interface. Accordingly, both Bäckström et al. [19] and Schindelwig et al. [20] developed techniques for measuring the contact pressure between a ski and a counter-body that can be considered rigid in comparison to snow. The advantage of this method is that the apparent area and contact pressure distribution can be estimated, with the drawback being that it is not the same as for ski–snow contact. The counter-body can, however, be replaced; Mössner et al. [21] recently developed a system for measuring the “penetration depth of the cross-country ski in an elastomer pad”, used to simulate a ski in contact with snow. They then obtained the contact pressure using Euler–Bernoulli beam theory, as previously described in [22]. Another way of obtaining the contact pressure is to use a Boundary Element Method (BEM) to simulate the contact between a ski-camber profile and counter-surface representing snow, as in Kalliorinne et al. [18]. This method enables a variety of counter-surface material properties, as well as non-flat counter-surfaces.

Both ski-camber profile and contact pressure measurements consider the ski in a stationary setting, but while skiing, it is loaded dynamically and vibrates at the ends. Already in the 1980s, Lehtovaara et al. [23] found that vibrations could decrease the friction between a polymer sample and ice. Afterwards, Koptyug et al. [24,25,26] continued this work, and it was concluded that a beam model of the entire ski is necessary to fully understand the ski vibrations in the interaction between ski and snow. Another related work is the one by Nam et al. [27], who developed a numerical model for jumping-ski vibration and concluded that the relation between friction and mode/amplitude is more complex than what was reported in Lehtovaara et al. [23], since full-sized skis behave differently from a small-sized polymer sample.

There is no question of the structural mechanics of the ski being a key determinant when it comes to ski–snow friction, but perhaps equally important is the snow counter-surface. Gold [28] studied the compression strength of snow while considering density, temperature, and snow crystal size and presented a relation between these parameters and the hardness of snow. It was also noted that the compression strength could differ by several orders of magnitude for the same parameter values. Bader [29] conducted thorough work on the properties of snow in which 14 properties that characterise snow were listed. It was stated that at least five of these, i.e., density, hardness, grain size, grain shape, and temperature, which were viewed as the most important for characterising snow, should always be used. Lintzén and Edeskär studied uni-axial compression of snow and observed that there are both an elastic region and a plastic region in the stress–strain curve. They also found that there exists a critical compression rate at which snow becomes brittle and, in connection to this, that old machine-made snow is more brittle than new machine-made snow. However, as discussed in [30,31], it should be taken into consideration that the behaviour due to the small deformations that occur in a ski track may be different from the behaviour of the bulk of snow during compression.

Apart from the macro-scale properties of skis, their micro-scale properties have also been studied to a large extent. Moldestad et al. [32] developed a methodology for measuring ski-base textures in 3Ds, which nowadays is a standard procedure used for the characterisation of the topography of ski-base surfaces. Jordan et al. [33] found that fractal analysis is a better tool than the standard roughness parameters and Fast Fourier Transform (FFT) techniques for differentiating ski-base textures. Ski-base textures are most commonly fabricated with a stone-grinding procedure; see, e.g., Breitschädel et al. [34,35], where different techniques for changing/obtaining new ski-base textures, such as manual texturing with an embossing tool and texturing the ski base with a milling machine, are discussed.

Giesbrecht et al. [36] tested ski-base materials, surface roughness, and texture orientation using miniature skis; they found that there was optimal roughness in the range of $R_a=0.5-$ $1.0$ $\mathrm{\mu }$$\mathrm{m}$, and they also observed that texture orientation had less of an impact on surfaces with lower $R_a$ values. Rohm et al. [37] performed friction tests with two different surface textures with completely different bearing ratios. They found that the surface with the highest core roughness value, i.e., “the bearing surface”, exhibited lower friction at lower temperatures ( $-19$ ${}^{\circ }\mathrm{C}$) and that the other surface, i.e., “the non-bearing surface”, exhibited lower friction at higher temperatures ( $-2.6$ ${}^{\circ }\mathrm{C}$). Recently, Scherge et al. [38] studied five different ski-base textures and found that the sliding time increased with the increase in contact area. Along with the contact area being highlighted as one of the important parameters in ski–snow friction, different methods for evaluating the contact area have been presented, e.g., [39,40]. The latter of the two, which was developed by the same group presenting this work, employs a BEM-based method for evaluating the contact mechanical response for different ski-base textures in contact with a counter-surface representing snow.

There are many length scales to be considered in most tribological applications, and specific numerical models have been and are still being developed for each one of the length scales; see [41]. When a model considers two or more scales, it is denoted as multi-scale, and when using a multi-scale model, the interaction among different scales can be studied. In many tribological applications, there are several topographical scales present, and these have been readily assessed and may be found in the literature. Tribology research does, in general, show that multi-scale interaction among different topographical scales has a considerable influence on friction [42]. Ski–snow contact is no exception, with at least three clearly distinguishable geometrical scales being present at the same time.

The interaction between the ski’s macro-scale mechanics and geometry, and its micro-scale, encompassing the ski-base texture, and how the interplay between them is connected to frictional performance have, however, not yet been thoroughly studied. Accordingly, the objective of the present work is to combine the methods developed for macro- [18] and micro-scale [40] ski–snow contact simulations to present metrics that describe multi-scale contact.

By employing the novel multi-scale method presented herein, we study ski–snow contact in four combinations of two pairs of skis (with significantly different ski-camber profiles) and two different ski-base textures. The results are presented in terms of four functional parameters, namely, the real area of contact, the corresponding average real contact pressure, the minimum average interfacial separation, and the total average reciprocal interfacial separation. The analysis shows that different macro- and micro-scale properties of the ski are related to different friction mechanisms and that both the ski-camber profile and the texture of the ski base play decisive roles in determining the viscous contribution to friction.

2. Theory

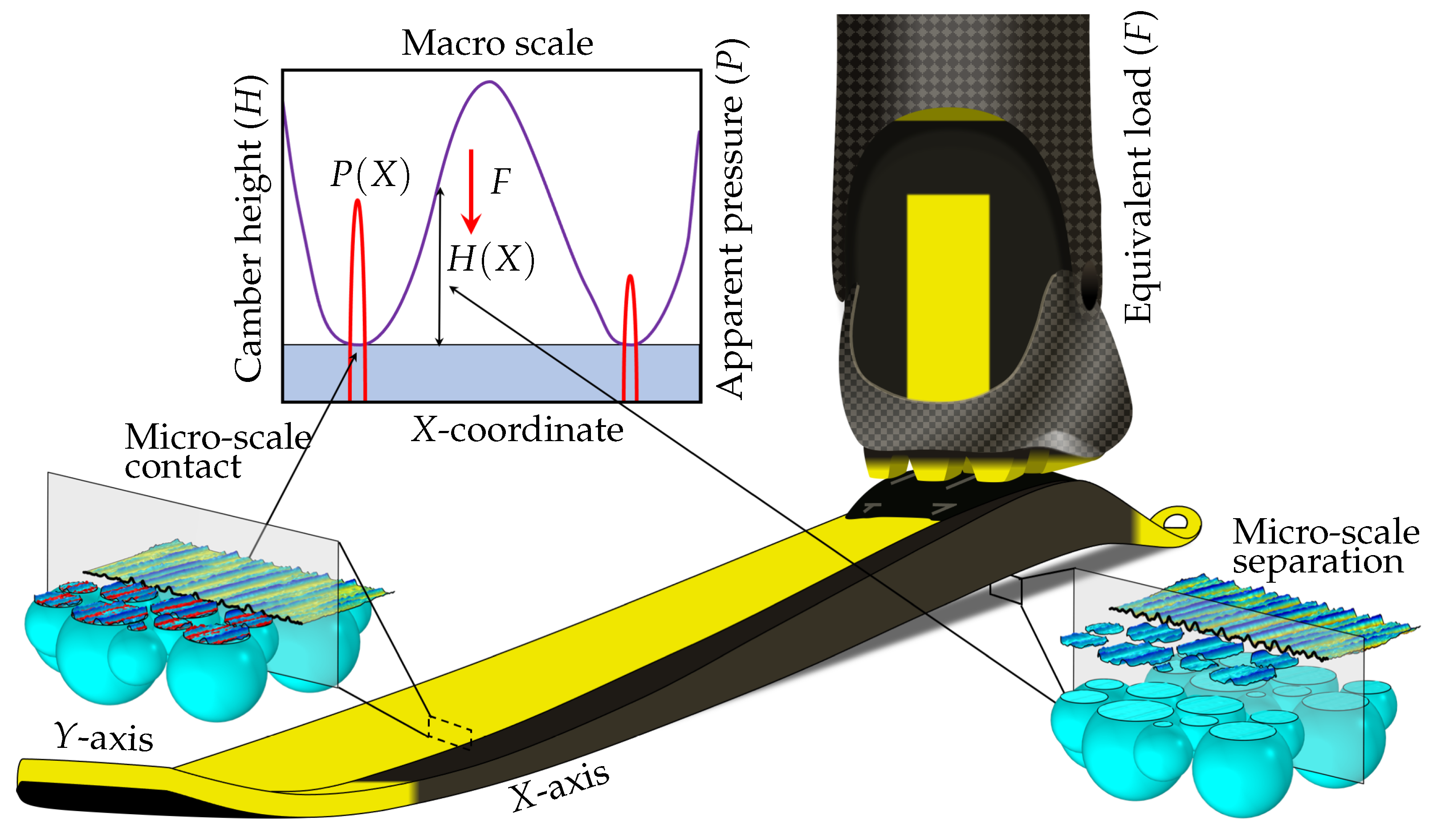
In this section, we will present a novel multi-scale approach that combines the methods developed for macro- [18] and micro-scale [40] ski–snow contact simulations. Figure 1 presents an effort to graphically illustrate the present method, in which the geometry of the selected ski is measured using a ski-camber profile measurement device according to the principles presented in [18]. These macro-scale ski-camber profile data, which can be viewed in the upper-left insert, together with the corresponding apparent pressure distribution, are used to train an Artificial Neural Network (ANN) with a carefully designed architecture (also described in [18]). The lower-left insert of Figure 1 presents a micro-scale perspective of a situation where the ski-base texture is in contact with virtual snow, explained below, under apparent pressure acting over the rear contact zone. Similarly, the lower-right insert shows the same ski-base texture at a location where it is separated from the virtual snow.

The concept of virtual snow is introduced since the counter-surface is treated as a perfectly linear elastic surface; real snow, on the other hand, may behave elastically in the initial loading regimes, but at a certain load, it plastically deforms. Lintzén and Edeskär [43] conducted compression measurements of new machine-made snow, and the resulting stress–strain curves they presented exhibited an approximately bilinear behaviour. For strain rates below the critical value of approximately 0.003 s⁻¹ they found the Young’s modulus of the snow, $E_{snow}$, to be scattered between 100 $\mathrm{M}$$\mathrm{Pa}$ and 250 $\mathrm{M}$$\mathrm{Pa}$, and residual strength to be linearly increasing (from 2 $\mathrm{M}$$\mathrm{Pa}$ to 8 $\mathrm{M}$$\mathrm{Pa}$) with the strain rate.

Given an equivalent load (magnitude and position), corresponding to the plantar pressure exerted by the athlete, that, during, e.g., tucking downhill, represents half the skier’s body weight applied 16 $\mathrm{c}$$\mathrm{m}$ behind the balance point [15], an ANN can be employed to predict the geometry of the ski-camber profile as a function of the coordinate along the ski. Hence, the predicted ski-camber profile may be used as input in the BEM-based model presented in [18] to simulate the macro-scale contact between the ski-camber profile and virtual snow.

The main output from a numerical simulation, based on this macro-scale method, is the contact mechanical response in terms of the apparent contact area and pressure between ski and virtual snow. In the present multi-scale method, the apparent pressure represents a coupling variable between the macro- and micro-scales, at which it defines the nominal load that the ski-base texture should be pressed against the virtual snow with.

More precisely, for a given loading condition, a prediction of the ski-camber profile ($H^{*}$) as a function of the macro-scaleX-coordinate ($H^{*}=H^{*}\left(X\right)$) along the entire ski, which constitutes macro-scale computational domain $\Omega$, can be obtained with an ANN. In turn, ski-camber profile $H^{*}$ (which represents the undeformed geometry of the rigid half space), the loading condition, and the effective Young’s modulus ($E^{\prime }$). This is composed by the Young’s modulus of the ski base ($E_{base}$), the viritual snow ($E_{snow}$) and the Poisson’s ratio $\nu$ (which describes the effective material properties of the deformable half space) defined as

$${\displaystyle \frac{2}{E^{\prime }}}={\displaystyle \frac{1-{\nu }^2}{E_{snow}}}+{\displaystyle \frac{1-{\nu }^2}{E_{base}}}$$

(1)

are input into the macro-scale BEM model [18]. The Young’s modulus of the ski base is here specified as 900 $\mathrm{M}$$\mathrm{Pa}$ and the Poisson ratio for both the ski base and the viritual snow is taken as $\nu =0.3$ although it may vary substationally depending on the type of the snow. This method is adapted from [44], which can be used to determine the apparent pressure (P) as a function of the X-coordinate ($P=P\left(X\right)$), as well as the apparent clearance ($H\left(X\right)$) between the ski and the deformed counter-body, made of virtual snow, for which the classical complementarity $P·H=0$ holds. An important feature of this macro-scale model of ski–snow contact, which conventional variational principle-based methods such as [44,45,46] lack, is that it requires moment balance. This is because the equivalent load (F), i.e., the load representing the skier’s plantar pressure distribution, is often located at an offset, $X_m$, from the ski’s balance point. Also, note that it is assumed that the ski maintains a consistent ski-camber profile ($H^{*}$) across its entire width b. This simplifies the analysis to a 1D BEM-based model, corresponding to a 2D, plain -strain contact mechanics problem. Hence, the present 1D model (for the 2D contact mechanics problem) may be formulated as

$$\begin{array}{cc}\hfill & \underset{P\ge 0}{min}\left(\frac{1}{2}\int {\int }_{\mathrm{\Omega }}P\left(X\right)U_e\left(X\right)dX+\int {\int }_{\mathrm{\Omega }}P\left(X\right)H^{*}\left(X\right)dX-\mathrm{\Delta }F\right),\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill & H=U_e+H^{*}-\mathrm{\Delta },\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill & U_e=-{\displaystyle \frac{4}{E^{\prime }}}{\int }_{\mathrm{\Omega }}ln\left|X-X^{\prime }\right|P\left(X^{\prime }\right)d{X}^{\prime },\hfill \end{array}$$

(2c)

$$\begin{array}{cc}\hfill & {\int }_{\mathrm{\Omega }}P\left(X\right)dX={\displaystyle \frac{F}{b}},\hfill \end{array}$$

(2d)

$$\begin{array}{cc}\hfill & {\int }_{\mathrm{\Omega }}(X+X_m)P\left(X\right)dX=0,\hfill \end{array}$$

(2e)

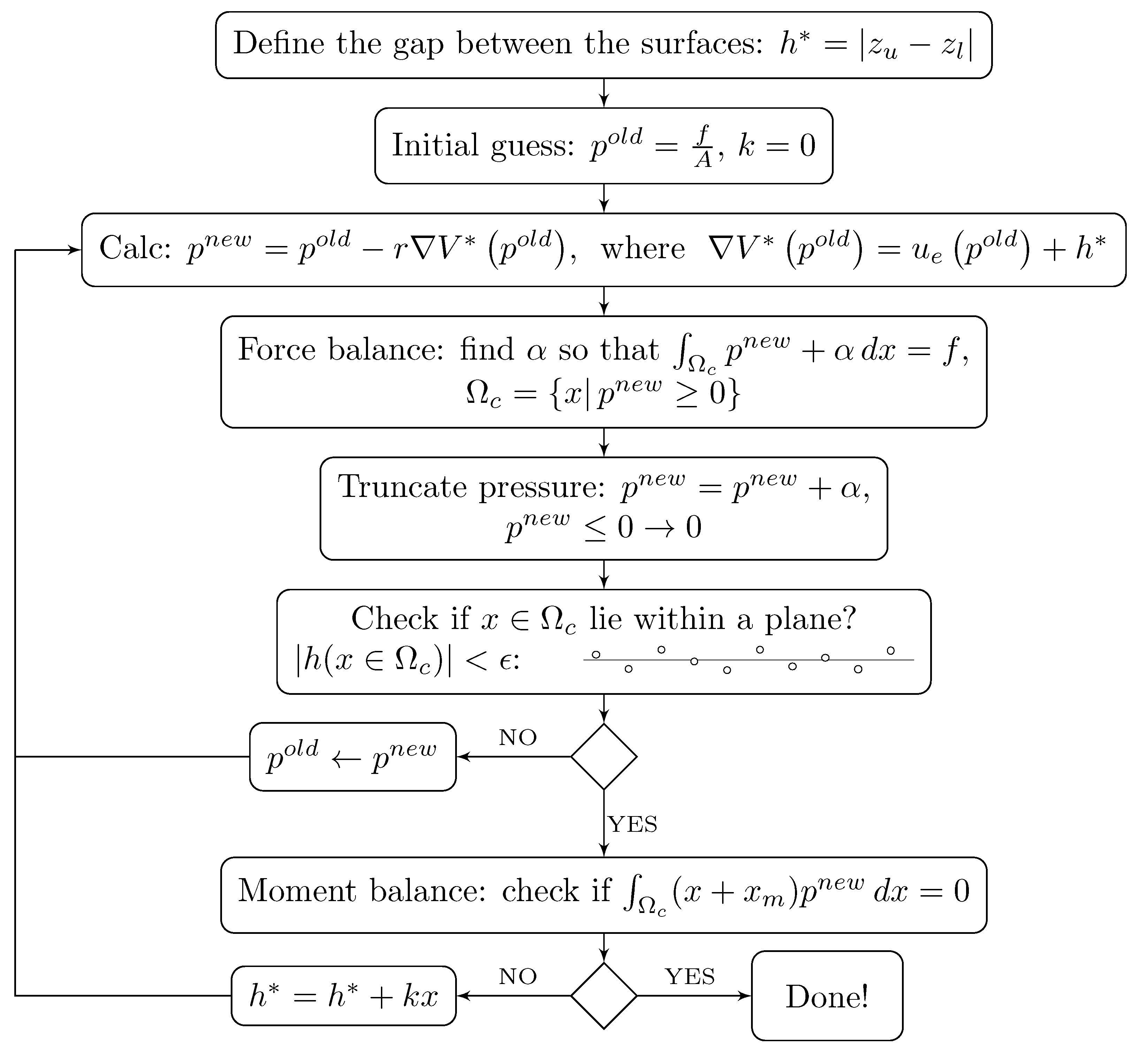
where $U_e$ is the elastic deformation; $\mathrm{\Delta }$, the rigid-body separation; F, the load; b, the width of the ski; and $X_m$, the position where the load is applied, measured from the balance point of the ski. A flow chart of the solution procedure may be found in Appendix A.

The inputs to the micro-scale BEM model [40,44], which is defined on computational domain $\omega$, can be specified in terms of the load ($f=PA$, where P is the apparent pressure and A is the nominal area, i.e., $A=\left|\omega \right|\ll |\mathrm{\Omega }|$), a surface topography with height function $h^{*}$ and an effective Young’s modulus defined as

$${\displaystyle \frac{2}{E^{\prime }}}={\displaystyle \frac{1-{\nu }^2}{E_{ice}}}+{\displaystyle \frac{1-{\nu }^2}{E_{base}}},$$

(3)

expressed in terms of the Young’s modulus of the ice ($E_{ice}=$ 7 $\mathrm{G}$$\mathrm{Pa}$), the ski base ($E_{base}=$ 7 $\mathrm{M}$$\mathrm{Pa}$) and the Poisson’s ratio ($\nu =0.3$). Hence, the micro-scale BEM model, presented in lowercase letters, may be stated as

$$\begin{array}{cc}\hfill & \underset{p\ge 0}{min}\left(\frac{1}{2}\int {\int }_{\omega }p(x,y)u_e(x,y)dxdy+\int {\int }_{\omega }p(x,y)h^{*}(x,y)dxdy-\delta f\right),\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill & h=u_e+h^{*}-\delta ,\hfill \end{array}$$

(4b)

$$\begin{array}{cc}\hfill & u_e={\displaystyle \frac{2}{E^{\prime }}}{\int }_{\omega }{\displaystyle \frac{p\left(x^{\prime },y^{\prime }\right)d{x}^{\prime }d{y}^{\prime }}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2}}},\hfill \end{array}$$

(4c)

$$\begin{array}{cc}\hfill & {\int }_{\omega }p\left(x,y\right)dxdy=f.\hfill \end{array}$$

(4d)

When snow porosity is introduced as the ratio between the pore surface area and nominal area A, i.e., $0\le n\le 1$, the apparent pressure at the macro-scale (P) and nominal area A are related to the effective pressure ($P_n$) and the effective area ($A_n=A(1-n)$) via load f at the micro-scale, as $PA=f=P_n{A}_n$. Hence, the relation between apparent pressure and effective pressure becomes

$$P_n\left(X\right)=P\left(X\right)/(1-n).$$

(5)

The output of the micro-scale BEM model can, therefore, be expressed as the clearance ($h_n$) and the corresponding pressure ($p_n$), for which $p_n·h_n=0$ holds. Note that subscript n denotes both the dependence of the X-coordinate and porosity n.

With f, $E^{\prime }$, and the ski-base texture ($h^{*}=h^{*}(x,y)$, where $(x,y)\in \omega$ are the micro-scale coordinates) as input to the micro-scale BEM model, the real contact area, interfacial separation, and the corresponding contact pressure can be determined as functions of $(x,y)$ for each X-coordinate along the ski and snow porosity n. This means that the real contact area may be considered a function of the X-coordinate, parameterised using n, or a function of the effective pressure ($P_n\left(X\right)$), i.e.,

$$A_{r,n}\left(X\right):=A_r\left(P_n\left(X\right)\right)=A_r(P\left(X\right)/(1-n)).$$

(6)

We may now also define the average interfacial separation as a function of X as

$${\overline{h}}_n\left(X\right)={\displaystyle \frac{1}{\left|\omega \right|}}{\int }_{\omega }{h}_n(x,y)+H\left(X\right)dxdy={\displaystyle \frac{1}{\left|\omega \right|}}{\int }_{\omega }{h}_n(x,y)dxdy+H\left(X\right),$$

(7)

where the nominal area ($\left|\omega \right|=A$) is the area of $\omega$. The average reciprocal interfacial separation may now be described in the same way, i.e.,

$${\overline{1/h}}_n\left(X\right)={\displaystyle \frac{1-n}{|{\omega }_g|}}{\int }_{{\omega }_g}{\displaystyle \frac{dxdy}{h_n(x,y)+H\left(X\right)}}.$$

(8)

where ${\omega }_g=\omega \setminus {\omega }_c$ is the part of the domain at the micro-scale where there is a gap (and possibly solid–liquid contact) between the surfaces and ${\omega }_c$ is the part of the domain where there is solid–solid contact.

The multi-scale metrics considered in the present work are functional parameters deduced from the definitions of the real area of contact, the average interfacial separation, and the average reciprocal interfacial separation presented above. These functional parameters are total contact area

$$A_{tot}={\int }_{\mathrm{\Omega }}{A}_{r,n}\left(X\right)dX,$$

(9)

the corresponding average real contact pressure

$$F/A_{tot},$$

(10)

the minimum average interfacial separation

$$\underset{\mathrm{\Omega }}{min}\left({\overline{h}}_n\left(X\right)\right),$$

(11)

and the total average reciprocal interfacial separation

$${\int }_{\mathrm{\Omega }}{\overline{1/h}}_n\left(X\right)dX.$$

(12)

3. Method

To show how the present multi-scale method can be used to analyse the contact mechanical response, we present a study in which two different ski-base textures are applied to two pairs of skis with significantly different ski-camber profiles, leading to four combinations in total.

The macro-scale contact mechanical responses of two pairs of classical skis, named “Ski A” and “Ski B”, both with the width of 44 $\mathrm{m}$$\mathrm{m}$, considered in the present work were simulated under a load equivalent to 40 $\mathrm{k}$$\mathrm{g}$ placed $1.6$ $\mathrm{d}$$\mathrm{m}$ behind the balance point. The reason for choosing this loading condition is that it was found, in [15], to be the equivalent load corresponding to the neutral G7 position for a skier of 80 $\mathrm{k}$$\mathrm{g}$ in body weight. 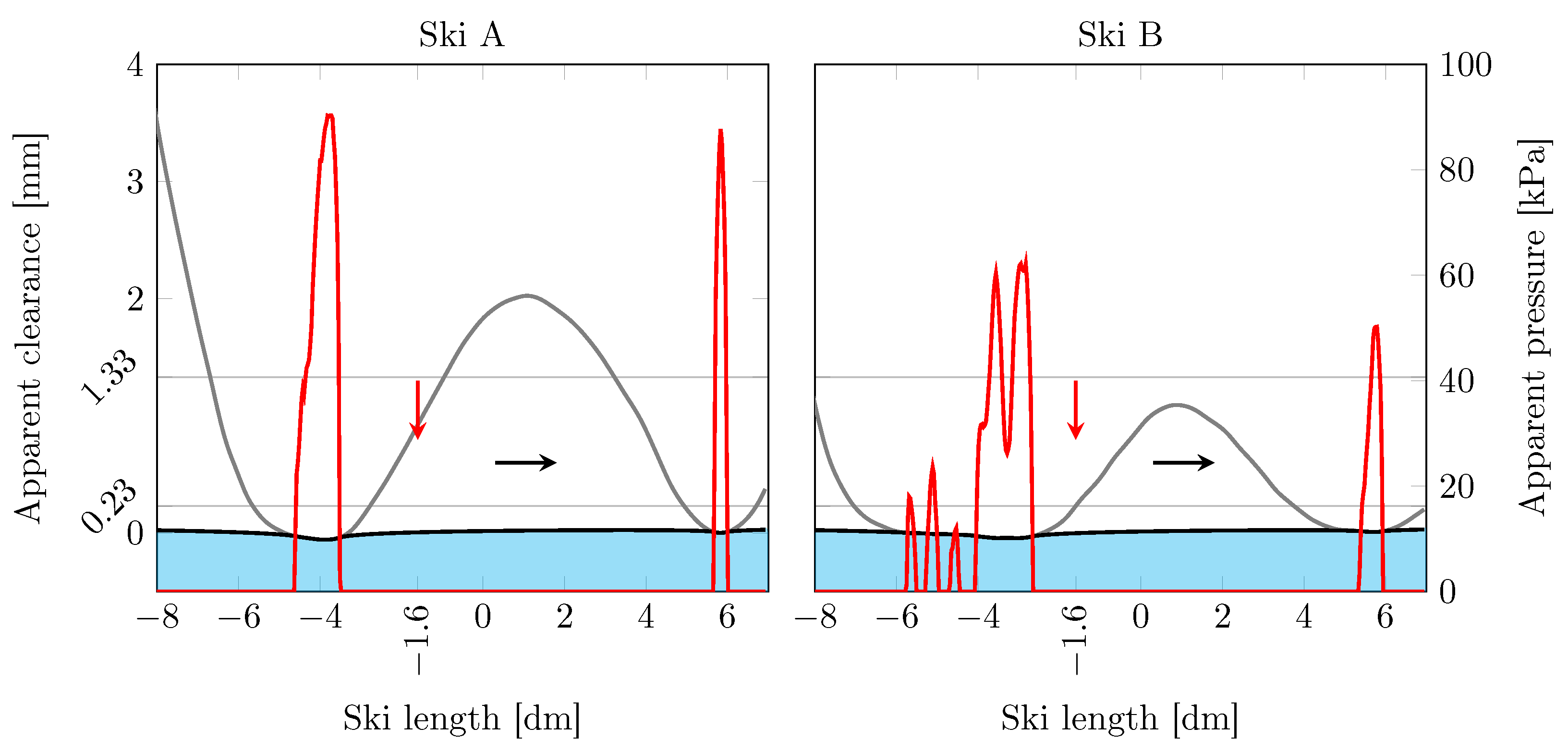The results, in terms of H and P, are depicted in Figure 2. It is clear that the two pairs render completely different contact mechanical responses under the same load. That is, Ski A exhibits higher mean apparent pressure, $61.40$ $\mathrm{k}$$\mathrm{Pa}$, over a smaller apparent contact area, $63.98$ $\mathrm{c}$$\mathrm{m}$${}^2$, than Ski B, which presents lower mean apparent pressure, $32.24$ $\mathrm{k}$$\mathrm{Pa}$, over a larger apparent contact area, $121.84$ $\mathrm{c}$$\mathrm{m}$${}^2$. The Young’s modulus of virtual snow is specified as $E_{snow}=$ 200 $\mathrm{M}$$\mathrm{Pa}$, which is in the range of Young’s moduli of snow that Lintzén and Edeskär presented in [43].

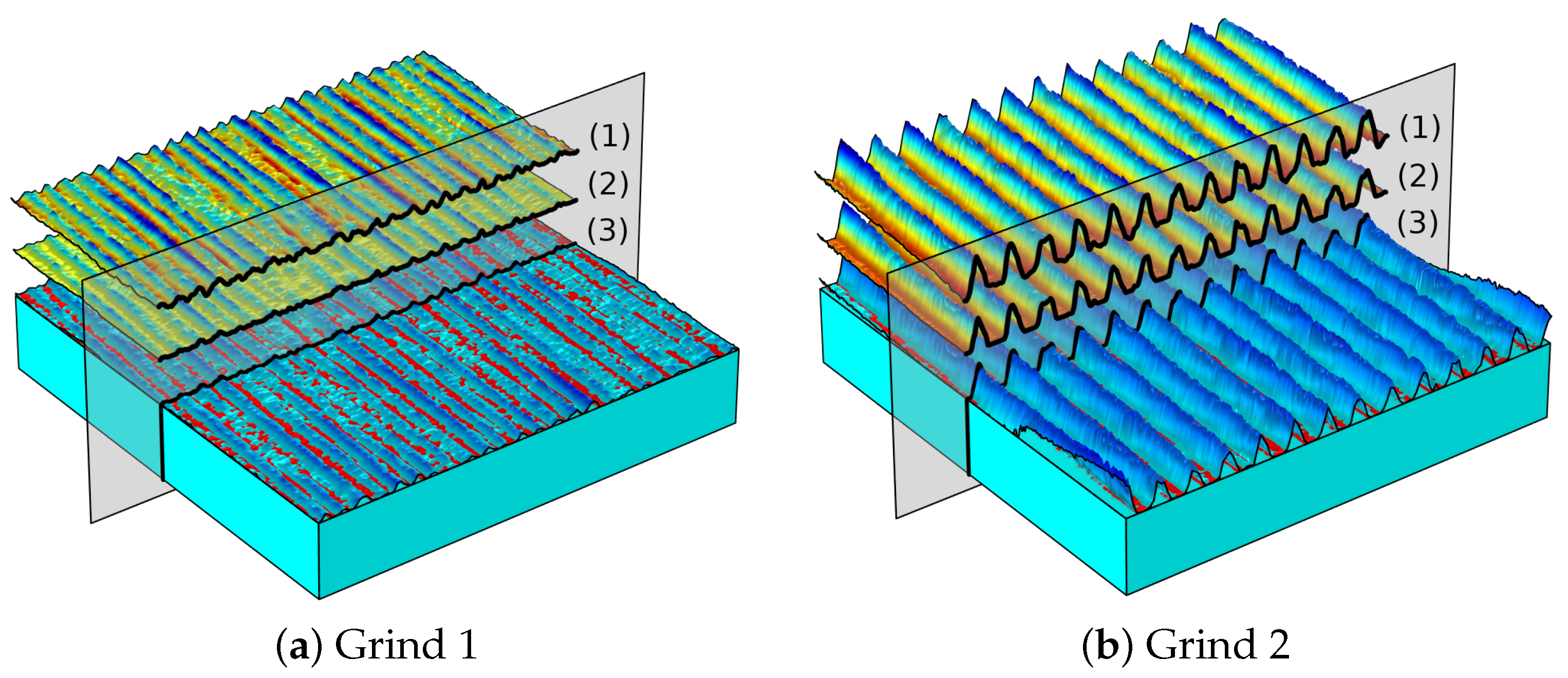
Two different ski-base textures, herein named Grind 1 and Grind 2, are considered, and their micro-scale topography can be seen in Figure 3. These have previously been used in the work by Kalliorinne et al. [40], where they were named “Linear 1” and “Linear 3”. Both these topographies were produced on the skis by running a single pass through a stone-grinding machine, where the dressing speed of the diamond was varied to obtain linear textures with varying pitches.

Table 1. Surface roughness parameters for the ski-base textures shown in Figure 3.

Texture	${\mathit{S}}_{\mathit{a}}$ ($\mathsf{\mu }$m)	${\mathit{S}}_{\mathit{q}}$ ($\mathsf{\mu }$m)	${\mathit{S}}_{\mathbf{sk}}$ (-)	${\mathit{S}}_{\mathbf{ku}}$ (-)	${\mathit{S}}_{\mathbf{dq}}$ ($\mathsf{\mu }$m/mm)	${\mathit{S}}_{\mathbf{pk}}$ ($\mathsf{\mu }$m)	${\mathit{S}}_{\mathit{k}}$ ($\mathsf{\mu }$m)	${\mathit{S}}_{\mathbf{vk}}$ ($\mathsf{\mu }$m)
Grind 1	1.77	2.16	−0.16	2.58	65.79	1.44	6.01	1.92
Grind 2	8.77	9.62	−0.43	1.63	185.77	2.16	11.65	20.02

presents a group of common surface roughness parameters for these two surfaces.

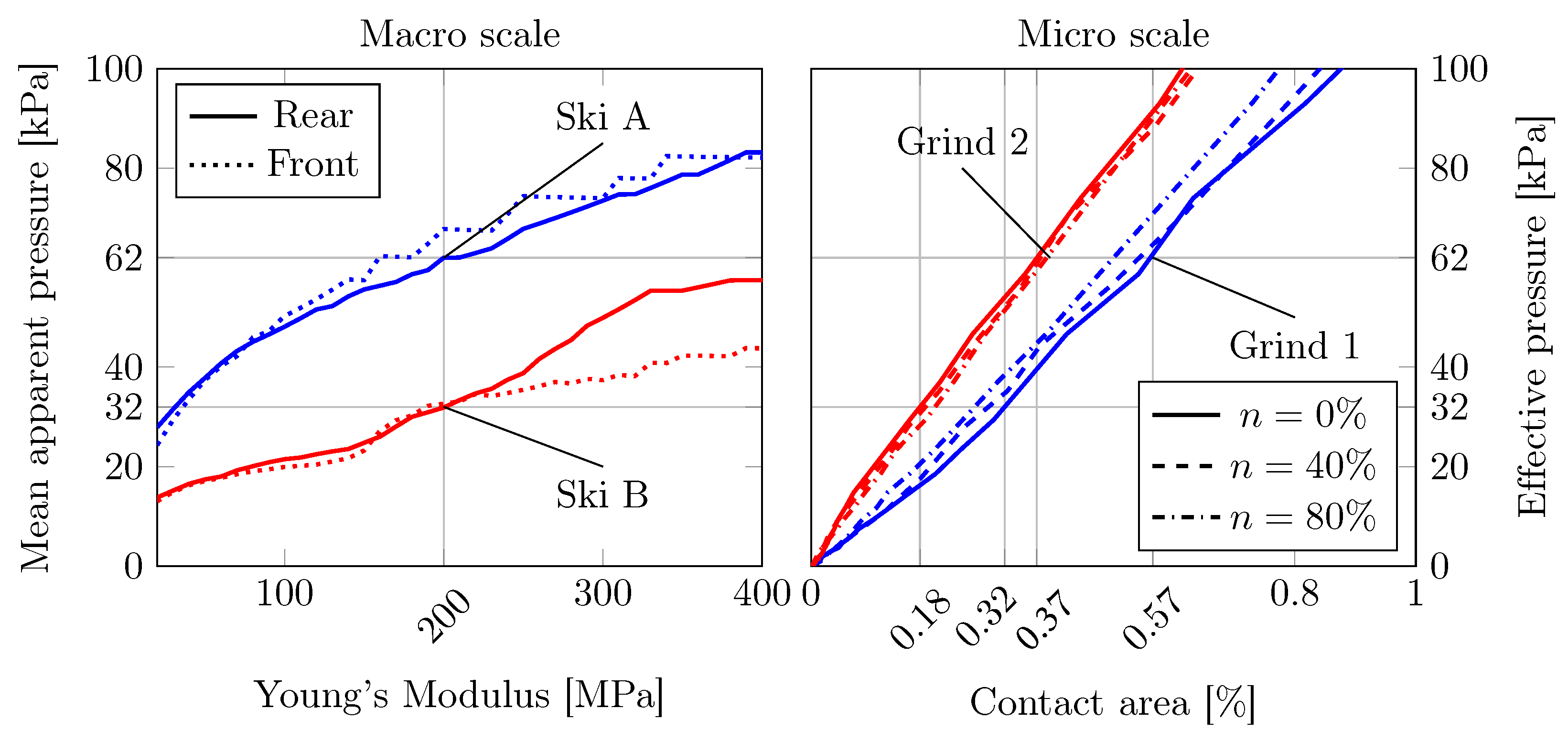
Depicted in Figure 4 (left) are the mean apparent pressure values for the rear and front friction interfaces in contact with a range of differently stiff virtual snow with elastic moduli ranging from 20 to 400 $\mathrm{M}$$\mathrm{Pa}$. It is clear that the ski-camber profile of Ski A yields higher mean apparent pressure over the whole range of counter-surface stiffness. Figure 4 (right) shows the relation between micro-scale contact area $A_{r,n}$ and effective pressure $P_n$ for the two ski-base textures, and the relation is shown for 3 different snow porosity values. Grind 1 develops the contact area faster than Grind 2 when subjected to a load, e.g., 54 more contact area under 62 $\mathrm{k}$$\mathrm{Pa}$ apparent pressure. It is also clear that Grind 1 exhibits higher variability with porosity and that Grind 2 yields a lower real area of contact.

4. Results and Discussion

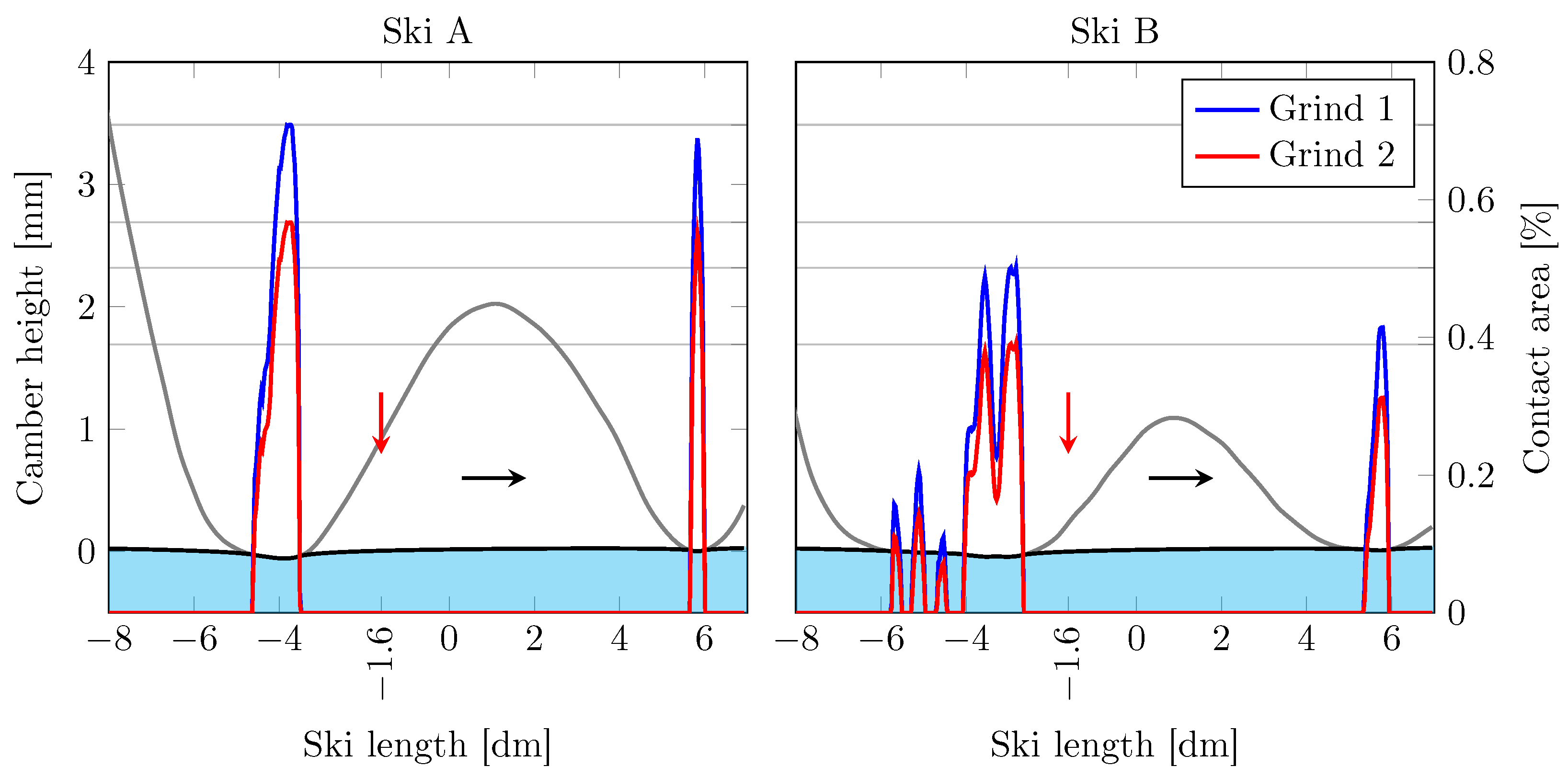
In this section, the multi-scale results obtained by combining macro- and micro-scale contact mechanics are presented. Depicted in Figure 5 are the distributions of the real area of contact for the four combinations of skis and ski-base textures along the apparent contact area of the skis. As already shown in Figure 4, Grind 1 clearly yields a larger contact area than Grind 2. The micro-scale contact areas’ almost linear dependency on the load shown in Figure 4 is also visible here, as the distributions closely follow the shape of the apparent pressure distributions.

By integrating the distributions of the real area of contact (6), along the entire ski, the total contact area ($A_{tot}$) of the contact that the ski makes with the snow can be obtained, i.e., (9). The results are presented in

Table 2. The total real area of contact for the 4 combinations of skis and grinds.

${\mathit{A}}_{\mathbf{tot}}$	Grind 1	Grind 2
Ski A	31.52 mm2	24.62 mm2
Ski B	32.89 mm2	24.52 mm2

, and they show that the total area of contact is, in principle, solely determined by the grind, with a rather large difference between Grind 1 and Grind 2 for both Skis A and B, i.e., ≈28% and ≈34%, respectively. However, when comparing the variability in $A_{tot}$ with the different ski-base textures, the differences for Ski A and Ski B are only ≈4% and ≈0.4%, respectively. Most of the available adhesive friction models [7,8,9,10,11,12,13] take the total real area of contact as the main input, and in all of them, a lower contact area renders less friction. Hence, the present results suggest that the ski-base texture might be the denominator of the adhesive friction contribution to ski–snow contact.

Likewise, as shown in

Table 3. The average real contact pressure for the 4 combinations of skis and grinds.

$\mathit{F}/{\mathit{A}}_{\mathbf{tot}}$	Grind 1	Grind 2
Ski A	12.46 MPa	15.95 MPa
Ski B	11.94 MPa	16.02 MPa

, the average real contact pressure, defined in (10), corresponds to the total real area of contact and depends on the ski-base texture to a larger degree than on the ski-camber profile. In fact, according to Table 3, both skis show similar average real contact pressure for the same grind, but the differences between Grind 1 and Grind 2 on Ski A and on Ski B are ≈28% and ≈34%, respectively. The average real contact pressure can be viewed as a measurement of the abrasive part of friction, acting as a counterpart to the contact area. At a certain limit, the snow yields, and abrasion, in terms of snow compaction and/or micro-ploughing, results in higher friction. In turn, this limits the minimisation of the contact area (globally and locally), which means that there is an optimum. This was highlighted by Lever et al. [14] as one of the dominant factors in snow friction and is perhaps connected to the second phase of snow contact described by Theile et al. [30].

The average real contact pressure indicates that abrasion is a friction mechanism predominantly generated at the micro-scale, i.e., by the ski-base texture. On the other hand, the apparent contact pressure is directly related to the ski-camber profile, which is a macro-scale feature of the ski, and Figure 2 shows that the ski-camber profile of Ski A results in higher apparent pressure values than that of Ski B, suggesting that Ski A causes more abrasive friction in the form of snow compaction than Ski B. This is important information, augmenting the information that can be extracted from the average real contact pressure (Table 3).

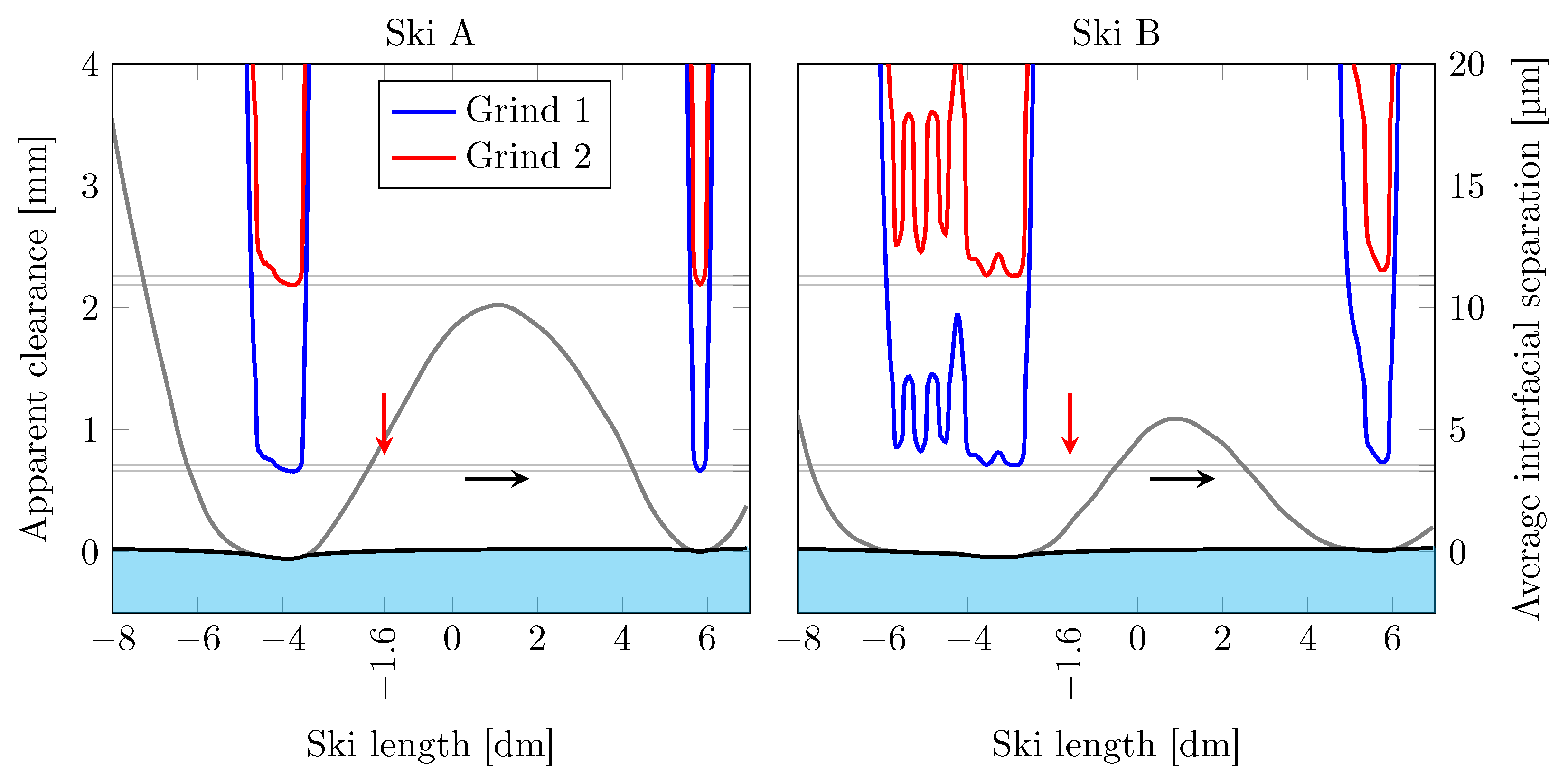
Figure 6 depicts the distributions of the average interfacial separation for the different combinations of skis and ski-base textures. The figure also indicates its minimum value for Grinds 1 and 2 applied to both Skis A and B, and it is clear that the ski-camber profile gives a very small contribution and that the ski-base texture highly influences the resulting minimum average interfacial separation. This was also shown in Kalliorinne et al. [40], where only a minute variation in the average interfacial separation with load was found as soon as the load increased above 10 $\mathrm{k}$$\mathrm{Pa}$. The ski-camber profile does, however, determine the number of local minimum interfacial separation points.

Table 4. The minimum average interfacial separation along the ski for the 4 combinations of skis and grinds.

$min\left({\overline{\mathit{h}}}_{\mathit{n}}\right)$	Grind 1	Grind 2
Ski A	3.31 μm	10.94 μm
Ski B	3.55 μm	11.32 μm

presents the minimum average interfacial separation along the entire ski, defined in (7), for the four combinations of skis and ski-base textures. The differences between Ski A and Ski B with Grind 1 and Grind 2 are ≈7 and ≈3, respectively. The differences between Grind 1 and Grind 2 on Ski A and Ski B are, however, 331% and 319% , for Skis A and B, respectively. In a situation where the counter-surface is smooth and non-porous, a too-small average interfacial separation could result in a restriction in water transportation, and the consequence could be going from a boundary-lubricated regime to full-film lubricated contact, which does not necessarily favour the glide. The present analysis suggests that the ski-base texture has a larger impact than the ski-camber profile with respect to water transport. The number of local minima and/or the total area of low interfacial separation are probably also very important, as they might increase the likelihood that a restriction will occur.

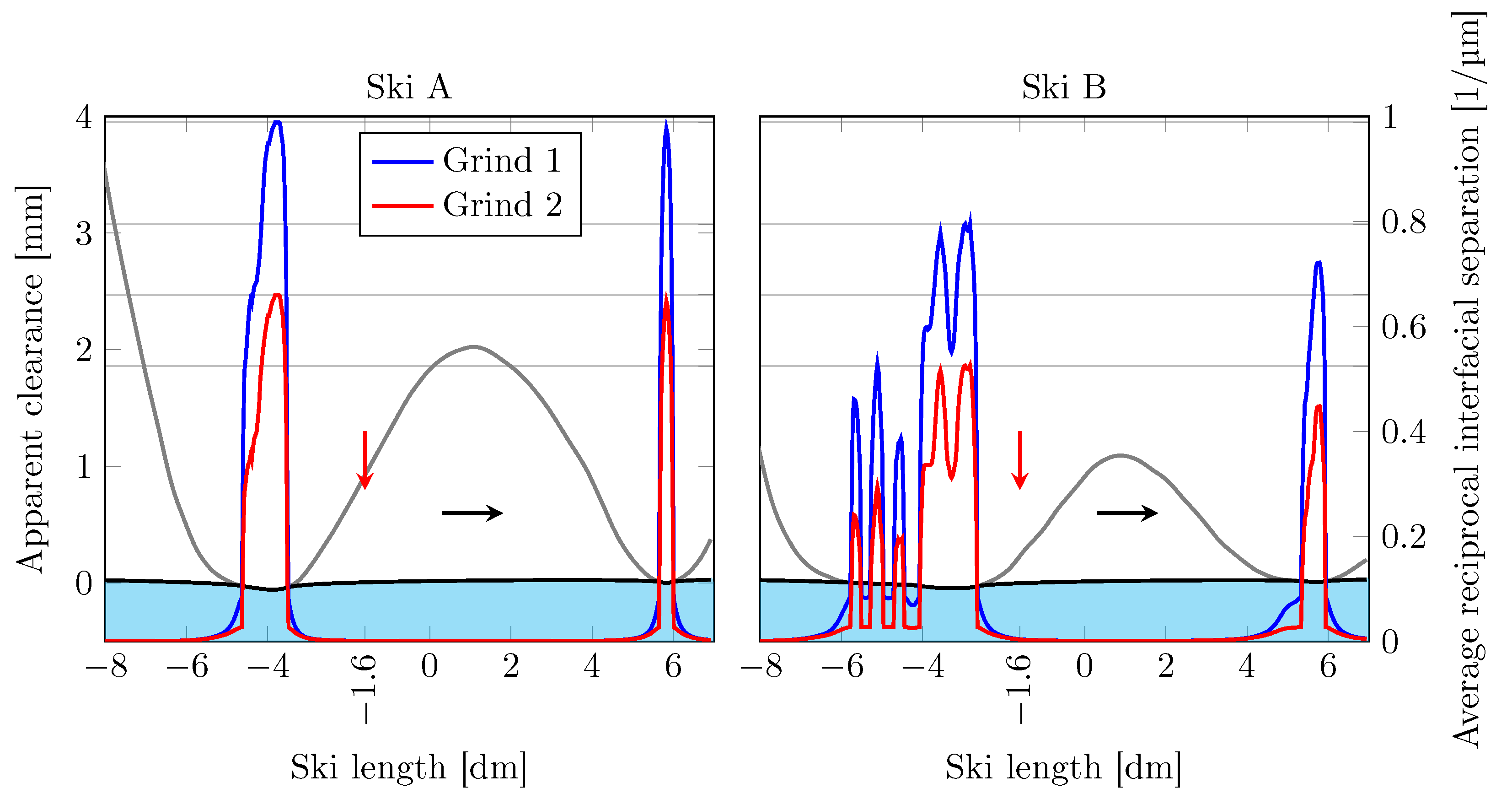
Depicted in Figure 7 is the average reciprocal interfacial separation for the different combinations of skis and ski-base textures. One of the things worth noting here is that all maximum values are different in each case. It should also be noted that the average reciprocal interfacial separation takes values outside the regions where there is contact (where the surfaces are separated), and in these regions, it is clear that Grind 1 yields a larger value than Grind 2.

Table 5. The total average reciprocal interfacial separation for the 4 combinations of skis and grinds.

${\int }_{\mathbf{\Omega }}{\overline{1/\mathit{h}}}_{\mathit{n}}\left(\mathit{X}\right)\mathit{dX}$	Grind 1	Grind 2
Ski A	5.47 km	3.44 km
Ski B	7.97 km	4.51 km

shows the total average reciprocal interfacial separation, defined in (8). Contrary to the results for the other functional parameters, the total average reciprocal interfacial separation exhibits a distinct value for each of the four combinations of skis and ski-base textures. More precisely, there are decreases when changing from Grind 1 to Grind 2 for Skis A and B, ≈59% and ≈77%, respectively, and there are increases when changing from Ski A to Ski B for Grinds 1 and 2, ≈46% and ≈31%, respectively. The reciprocal interfacial separation is linked to the viscous friction induced by shearing the water film (Couette flow); hence, the results may be interpreted as indicating that both the ski camber and the ski-base texture play important roles in reducing viscous friction.

5. Conclusions

To conclude the present paper, two methods for determining the multi-scale contact mechanical response in ski–snow contact were combined. One considers the macro-scale response of the entire ski, and the other one, the micro-scale response of the ski-base structure. The analysis based on the functional parameters considered in this work suggests that the ski-base texture has a larger impact on ski–snow friction than the ski-camber profile itself. The ski-camber profile has the largest impact on the integrated average reciprocal interfacial separation, but the impact of the ski-base texture on all four of the function parameters considered is larger. On the other hand, the apparent contact pressure is directly related to the ski-camber profile, and the results presented herein show that there were significant differences between the skis tested. This suggests that there might be conditions where macro-scale snow compaction supersedes the other friction mechanisms involved.

Related to ski–snow friction, these are the specific findings of the present work:

• Adhesive friction: The difference in real contact area between the two ski-base textures was larger than ≈28%, while the difference between the skis was less than ≈4% (merely ≈0.4% for Grind 2). Hence, the ski-base texture seems to have a larger impact on the adhesive part of friction.
• Abrasive friction: Because of the coupling between the real contact area and the average contact pressure, the same can be said about the influence of the ski-base texture and the ski camber for the abrasive part of friction as for the adhesive part.
• Friction regime: The minimum average interfacial separation was strongly influenced by the ski-base texture, showing values larger than ≈318%, while the difference between the two ski-camber profiles was less than ≈8%. Though the minimum average interfacial separation is meaningful, a larger area with lower separation could potentially affect the transition between boundary and full-film lubrication. This might be avoided by reducing the apparent contact area.
• Viscous friction: The difference between the two ski-base textures, in terms of total average reciprocal interfacial separation, was larger than ≈59%, while the maximum difference between the skis was less than ≈46%. The differences for all combinations were, however, of comparable sizes, suggesting that the ski-base texture and the ski-camber profile have a similar impact on the viscous part of friction.

According to the conclusions stated above, the ski-base texture and the ski-camber profile both significantly influence the ski’s performance under wet conditions, i.e., where the risk of full-film lubrication, causing viscous friction, is likely. Under cold and dry conditions, friction originates predominately from abrasion and adhesion, and under these conditions, the ski-base texture has the largest influence on the ski’s performance. It should be noted that according to the general consensus, the ski is the most important aspect of ski–snow friction; thereby, there are probably other aspects of ski–snow contact that have to be considered for a full understanding of friction in this particular system.