Rheological and Tribological Study of Polyethylsiloxane with SiO2 Nanoparticles Additive
Abstract
1. Introduction
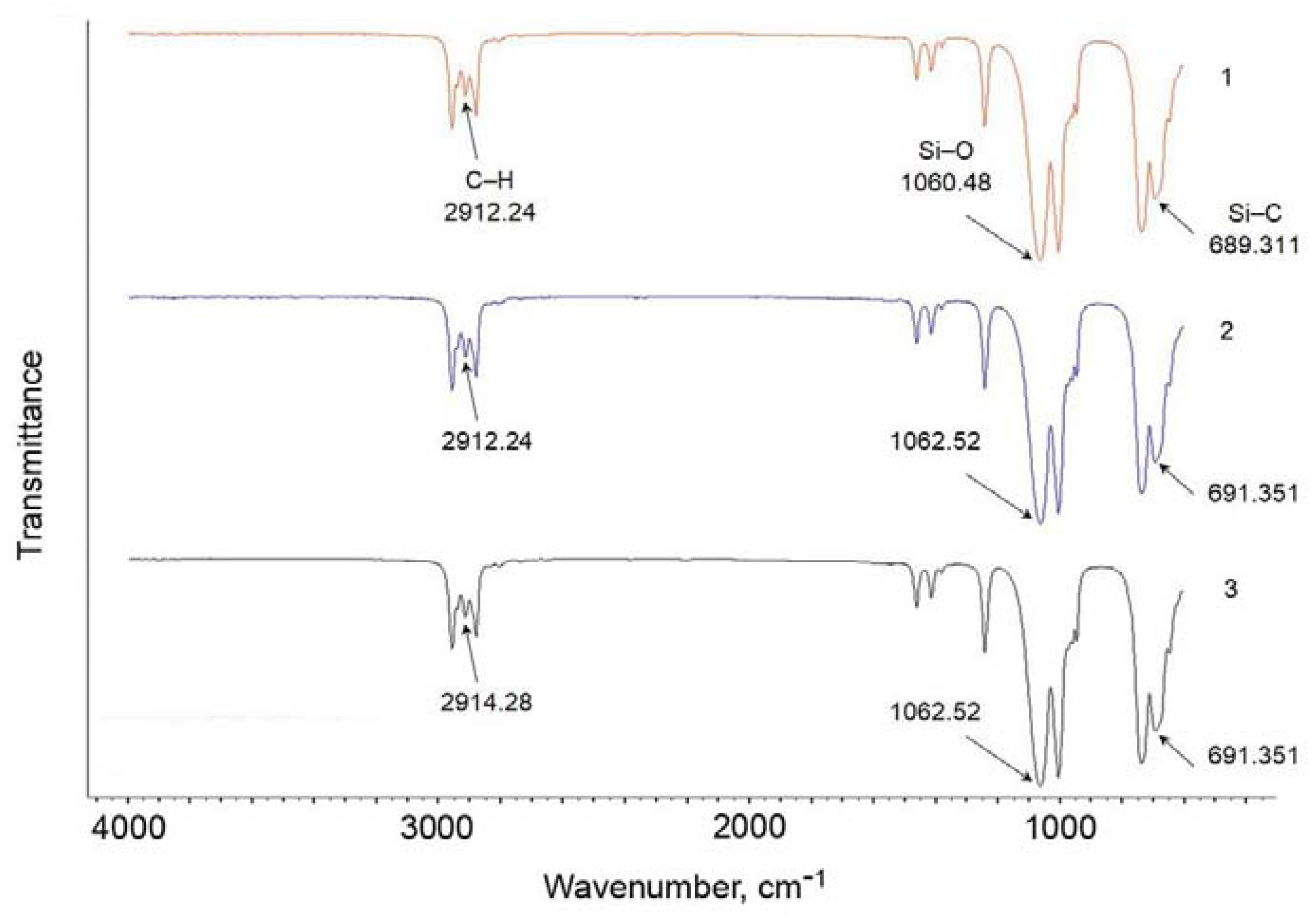
2. Materials
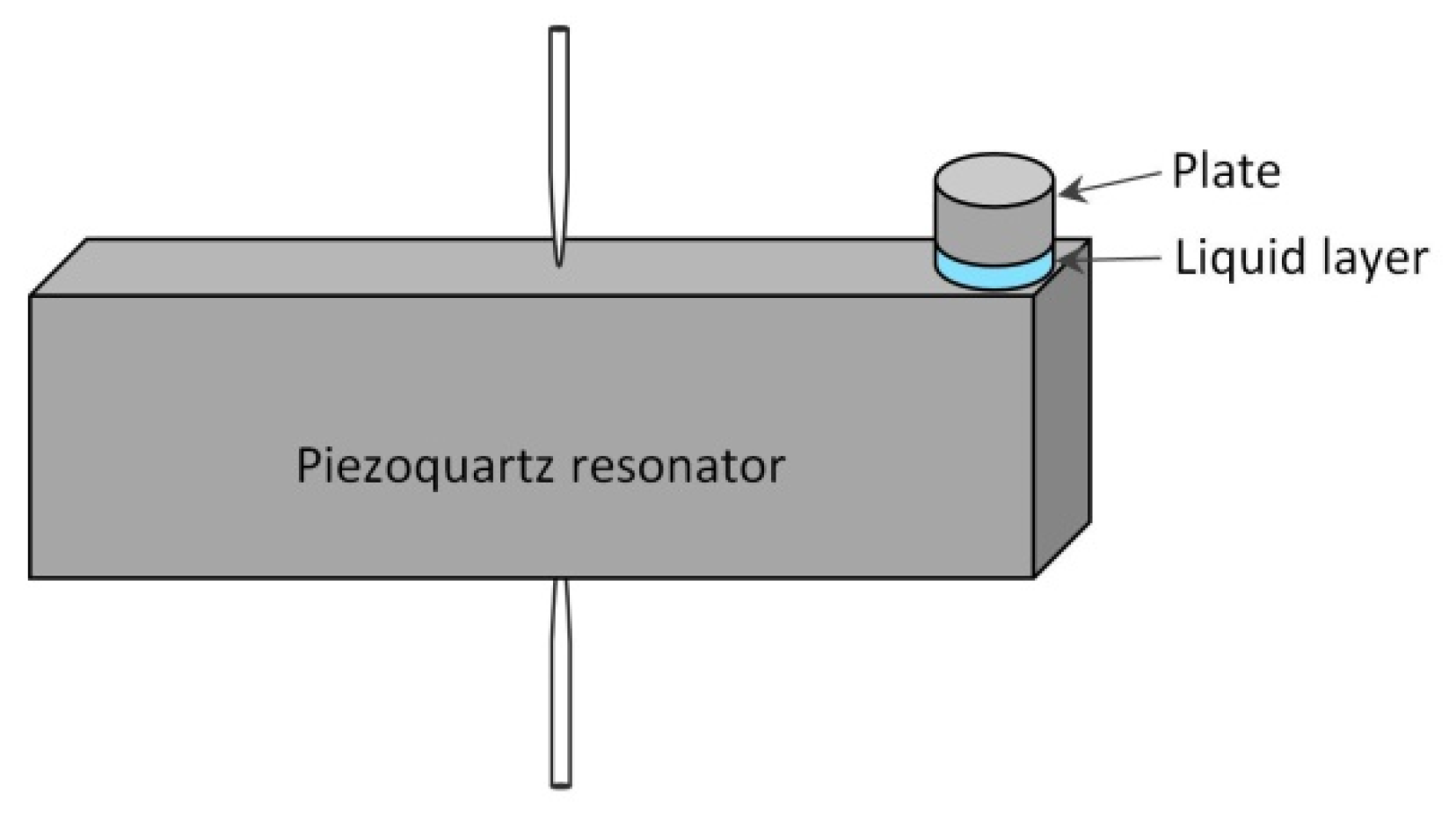
3. Methods
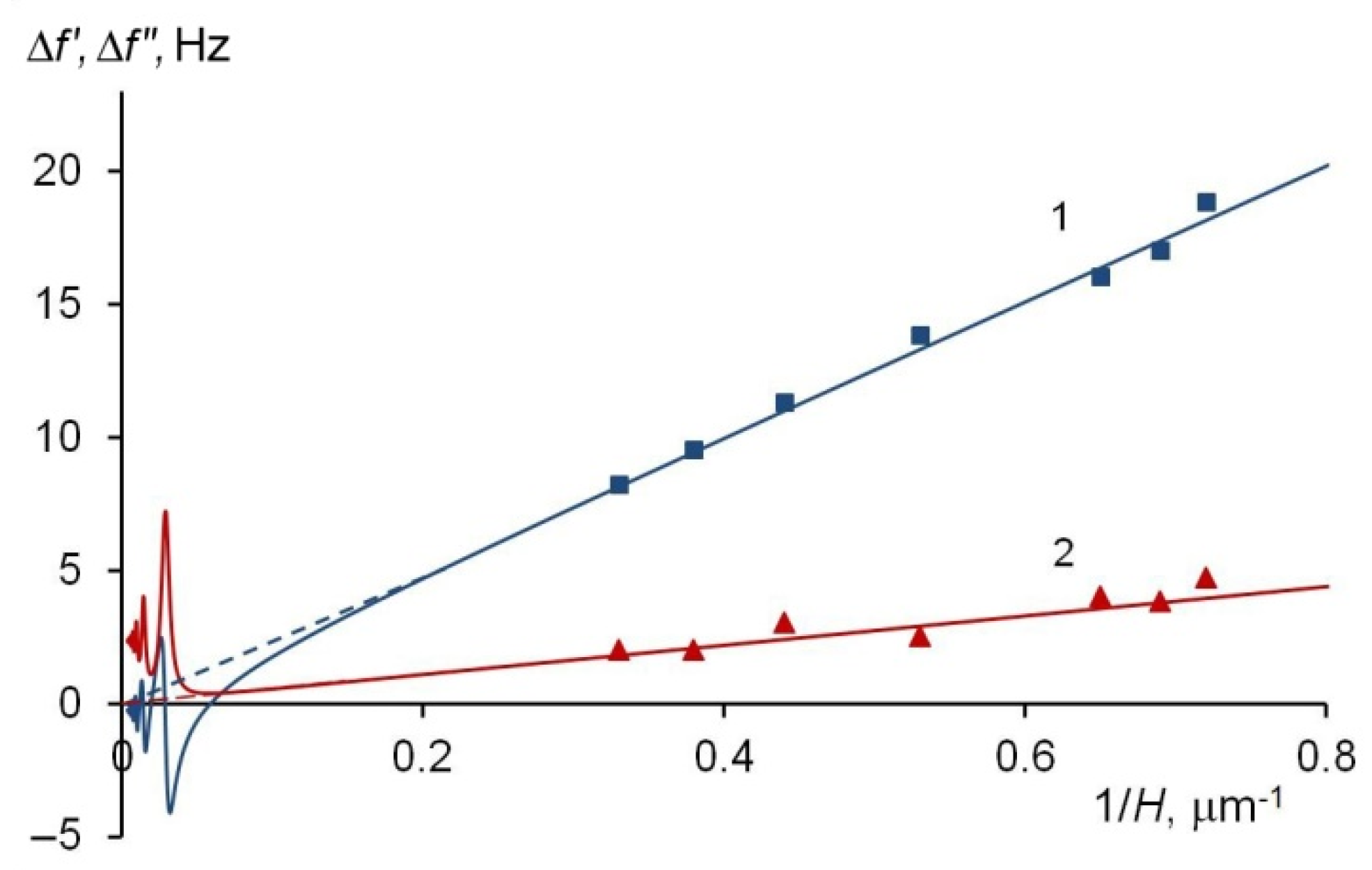
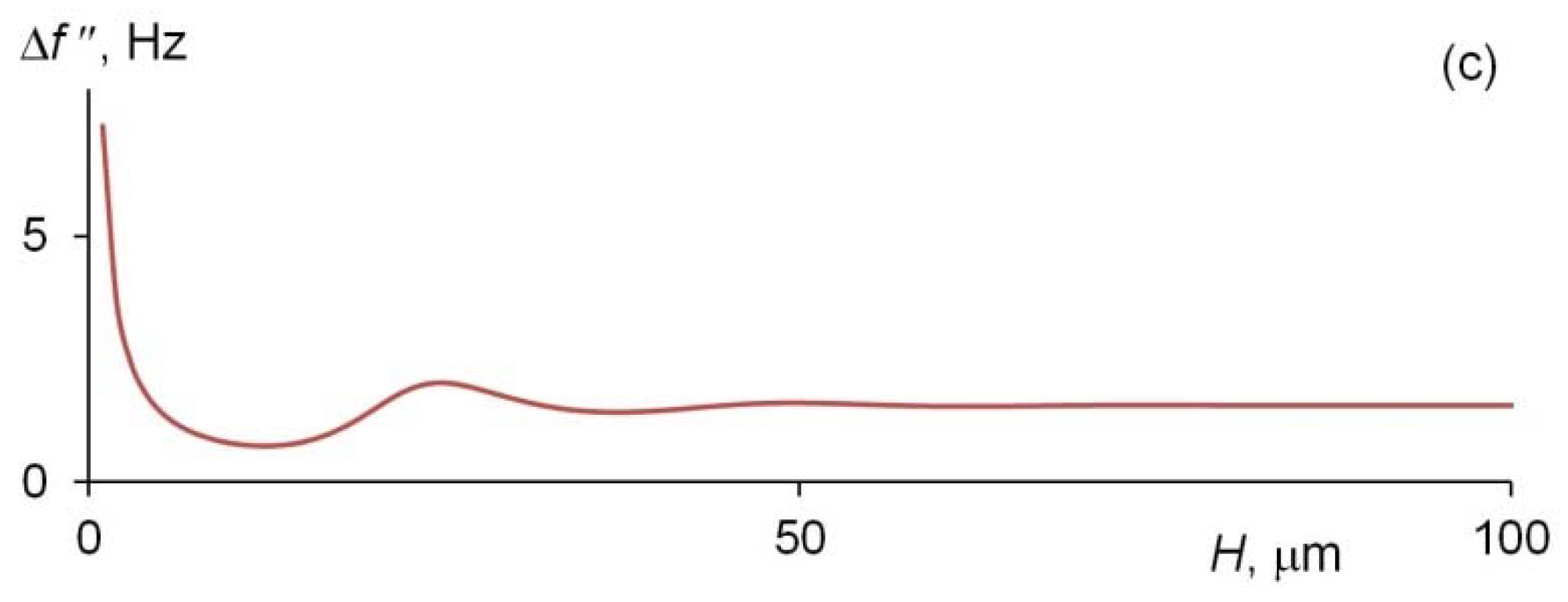
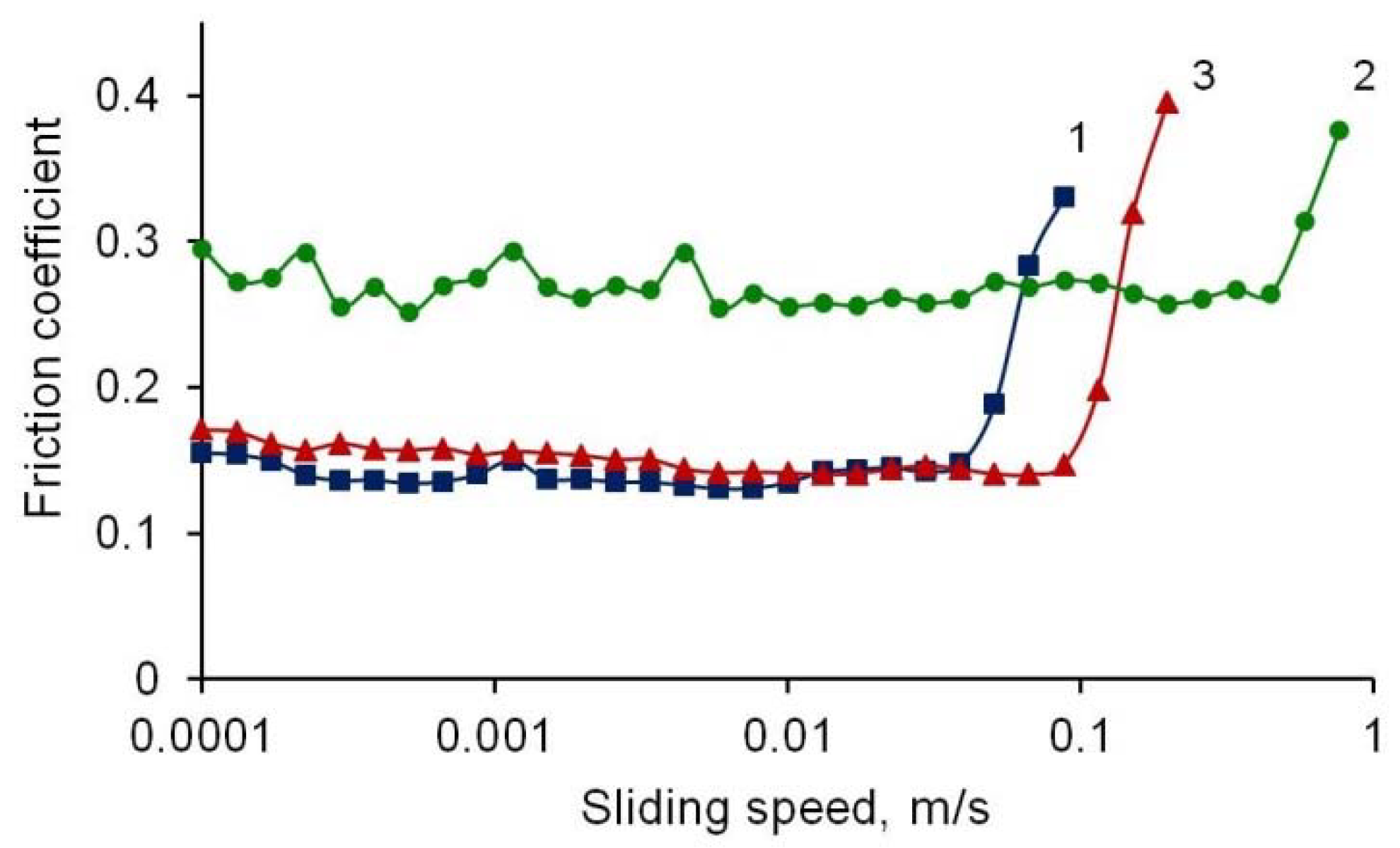
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oganesova, E.Y.; Lyadov, A.S.; Parenago, O.P. Nanosized Additives to Lubricating Materials. Russ. J. Appl. Chem. 2018, 91, 1559–1573. [Google Scholar] [CrossRef]
- Dai, W.; Kheireddin, B.; Gao, H.; Liang, H. Roles of nanoparticles in oil lubrication. Tribol. Int. 2016, 102, 88–98. [Google Scholar] [CrossRef]
- Gulzar, M.; Masjuki, H.H.; Kalam, M.A.; Varman, M.; Zulkifli, N.W.M.; Mufti, R.A.; Zahid, R. Tribological performance of nanoparticles as lubricating oil additives. J. Nanopart. Res. 2016, 18, 223. [Google Scholar] [CrossRef]
- Luo, T.; Wei, X.; Huang, X.; Huang, L.; Yang, F. Tribological properties of Al2O3 nanoparticles as lubricating oil additives. Ceram. Int. 2014, 40, 7143–7149. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Liu, A.; Wu, C.; Li, W. Tribological performance of silicone oil based Al2O3 nano lubricant for an Mg alloy subjected to sliding at elevated temperatures. Tribol. Int. 2022, 175, 107779. [Google Scholar] [CrossRef]
- Rawat, S.S.; Harsha, A.P.; Deepak, A.P. Tribological performance of paraffin grease with silica nanoparticles as an additive. Appl. Nanosci. 2018, 9, 305–315. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, L.; Li, M.; Xie, G. Synthesis of Core–Shell Micro/Nanoparticles and Their Tribological Application: A Review. Materials 2020, 13, 4590. [Google Scholar] [CrossRef]
- Qu, M.; Yao, Y.; He, J.; Ma, X.; Feng, J.; Liu, S.; Hou, L.; Liu, X. Tribological study of polytetrafluoroethylene lubricant additives filled with Cu microparticles or SiO2 nanoparticles. Tribol. Int. 2017, 110, 57–65. [Google Scholar] [CrossRef]
- Peng, D.; Kang, Y.; Hwang, R.; Shyr, S.; Chang, Y. Tribological properties of diamond and SiO2 nanoparticles added in paraffin. Tribol. Int. 2009, 42, 911–917. [Google Scholar] [CrossRef]
- Ur’ev, N.B.; Emel’yanov, S.V.; Titov, K.A. Structure-rheological properties of oil suspensions based on technical carbon and nanoscale fillers. Prot. Met. Phys. Chem. Surfaces 2015, 51, 226–229. [Google Scholar] [CrossRef]
- Minakov, A.; Rudyak, V.; Pryazhnikov, M. Rheological behavior of water and ethylene glycol based nanofluids containing oxide nanoparticles. Colloids Surfaces A Physicochem. Eng. Asp. 2018, 554, 279–285. [Google Scholar] [CrossRef]
- Koppula, S.B.; Sudheer, N.V.V.S. A review on effect of adding additives and nano additives on thermal properties of gear box lubricants. Int. J. Appl. Eng. Res. 2016, 11, 3509–3526. [Google Scholar] [CrossRef]
- Rudyak, V.Y.; Dimov, S.V.; Kuznetsov, V.V. On the dependence of the viscosity coefficient of nanofluids on particle size and temperature. Tech. Phys. Lett. 2013, 39, 779–782. [Google Scholar] [CrossRef]
- Zolper, T.J.; Seyam, A.M.; Chen, C.; Jungk, M.; Stammer, A.; Stoegbauer, H.; Marks, T.J.; Chung, Y.-W.; Wang, Q. Energy Efficient Siloxane Lubricants Utilizing Temporary Shear-Thinning. Tribol. Lett. 2013, 49, 525–538. [Google Scholar] [CrossRef]
- Sobolevsky, M.V.; Muzovskaya, O.A.; Popeleva, G.S. Properties and Applications of Organosilicone Products; Khimiya: Moscow, Russia, 1975; pp. 88–110. [Google Scholar]
- Anisimov, A.A.; Visochinskaya, Y.S.; Buzin, M.I.; Vasil’ev, V.G.; Nikiforova, G.G.; Peregudov, A.S.; Dubovik, A.S.; Orlov, V.N.; Shchegolikhina, O.I.; Muzafarov, A.M. New polydimethylsiloxanes with bulky end groups: Synthesis and properties. Bull. Acad. Sci. USSR Div. Chem. Sci. 2019, 68, 1275–1281. [Google Scholar] [CrossRef]
- Zolper, T.; Li, Z.; Chen, C.; Jungk, M.; Marks, T.; Chung, Y.-W.; Wang, Q. Lubrication Properties of Polyalphaolefin and Polysiloxane Lubricants: Molecular Structure–Tribology Relationships. Tribol. Lett. 2012, 48, 355–365. [Google Scholar] [CrossRef]
- Zhiheng, W.; Dehua, T.; Xuejin, S.; Xiaoyang, C. Study on a new type of lubricating oil for miniature bearing operating at ultra-low temperature. China Pet. Process. Petrochem. Technol. 2018, 20, 93–100. Available online: http://www.chinarefining.com/EN/Y2018/V20/I1/93 (accessed on 21 November 2022).
- Chichester, C.W.; Nevskaya, A. Modeling Molecular Structure to Tribological Performance. 2016. Available online: https://saemobilus.sae.org/content/2016-01-0291/ (accessed on 21 November 2022).
- Chichester, C.W. Development of High Service Temperature Fluids. 2016. Available online: https://saemobilus.sae.org/content/2016-01-0484/ (accessed on 21 November 2022).
- Wu, W.; Li, P.; Wang, X.; Zhang, B. Grafting of thermotropic fluorinated mesogens on polysiloxane to improve the processability of linear low-density polyethylene. RSC Adv. 2022, 12, 12463–12470. [Google Scholar] [CrossRef]
- Guan, X.; Cao, B.; Cai, J.; Ye, Z.; Lu, X.; Huang, H.; Liu, S.; Zhao, J. Design and Synthesis of Polysiloxane Based Side Chain Liquid Crystal Polymer for Improving the Processability and Toughness of Magnesium Hydrate/Linear Low-Density Polyethylene Composites. Polymers 2020, 12, 911. [Google Scholar] [CrossRef]
- STAR. Available online: https://star-pro.ru/gost/13004-77 (accessed on 28 November 2022).
- Bardakhanov, S.P.; Vikulina, L.S.; Lysenko, V.I.; Nomoev, A.V.; Poluyanov, S.A.; Tuzikov, F.V. Analysis of Nanopowders by Small-Angle X-Ray Scattering Method’s. Sib. J. Phys. 2012, 7, 107–116. [Google Scholar] [CrossRef]
- Dembelova, T.S.; Balzhinov, S.A.; Makarova, D.N.; Vershinina, Y.D.; Bazarova, S.B.; Badmaev, B.B. Dynamic viscosity of dispersion of silica dioxide nanoparticles. IOP Conf. Series Mater. Sci. Eng. 2020, 1000, 012005. [Google Scholar] [CrossRef]
- Badmaev, B.B.; Dembelova, T.S.; Damdinov, B.B. Viscoelastic Properties of Polymer Liquids; Buryat Scientific Center, SB RAS: Ulan-Ude, Russia, 2013; pp. 56–136. [Google Scholar]
- Badmaev, B.B.; Dembelova, T.S.; Makarova, D.N.; Gulgenov, C.Z. Ultrasonic Interferometer on Shear Waves in Liquids. Sov. Phys. J. 2020, 62, 1708–1715. [Google Scholar] [CrossRef]
- Badmaev, B.; Bazaron, U.; Derjaguin, B.; Budaev, O. Measurement of the shear elasticity of polymethylsiloxane liquids. Phys. B+C 1983, 122, 241–245. [Google Scholar] [CrossRef]
- Badmaev, B.; Dembelova, T.; Damdinov, B.; Makarova, D.; Budaev, O. Influence of surface wettability on the accuracy of measurement of fluid shear modulus. Colloids Surfaces A Physicochem. Eng. Asp. 2011, 383, 90–94. [Google Scholar] [CrossRef]
- Badmaev, B.B.; Damdinov, B.B.; Dembelova, T.S. Viscoelastic relaxation in fluids. Bull. Russ. Acad. Sci. Phys. 2015, 79, 1301–1305. [Google Scholar] [CrossRef]
- Derjaguin, B.; Bazaron, U.; Zandanova, K.; Budaev, O. The complex shear modulus of polymeric and small-molecule liquids. Polymer 1989, 30, 97–103. [Google Scholar] [CrossRef]
- Frenkel, J.I. Kinetic Theory of Liquids; Academy of Sciences of USSR: Moscow/Leningrad, Russia, 1959; pp. 195–248. [Google Scholar]
- Collin, D.; Martinoty, P. Dynamic macroscopic heterogeneities in a flexible linear polymer melt. Phys. A Stat. Mech. Appl. 2003, 320, 235–248. [Google Scholar] [CrossRef]
- Noirez, L.; Baroni, P. Identification of a low-frequency elastic behaviour in liquid water. J. Phys. Condens. Matter 2012, 24, 372101. [Google Scholar] [CrossRef]
- Noirez, L.; Baroni, P. Identification of thermal shear bands in a low molecular weight polymer melt under oscillatory strain field. Colloid Polym. Sci. 2018, 296, 713–720. [Google Scholar] [CrossRef]
- Zaccone, A.; Trachenko, K. Explaining the low-frequency shear elasticity of confined liquids. Proc. Natl. Acad. Sci. USA 2020, 117, 19653–19655. [Google Scholar] [CrossRef]
- Makarova, D.N.; Dembelova, T.S.; Badmaev, B.B. Low-Frequency Shear Elasticity of a Colloid Nanosuspension. Acoust. Phys. 2020, 66, 613–615. [Google Scholar] [CrossRef]
- Philippoff, W. Relaxation in polymer solutions, polymer liquids and gels. In Physical Acoustics. Properties of Polymers and Nonlinear Acoustics; Part B.; Mason, W.P., Ed.; Mir: Moscow, Russia, 1969; Volume II, pp. 9–109. [Google Scholar]
- Badmaev, B.B.; Budaev, O.R.; Dembelova, T.S.; Damdinov, B.B. Shear elasticity of fluids at low-frequent shear influence. Ultrasonics 2006, 44, e1491–e1494. [Google Scholar] [CrossRef] [PubMed]
- Badmaev, B.B.; Dembelova, T.S.; Damdinov, B.B.; Gulgenov, C.Z. Impedance method for measuring shear elasticity of liquids. Acoust. Phys. 2017, 63, 642–644. [Google Scholar] [CrossRef]
- Dembelova, T.S.; Badmaev, B.B.; Makarova, D.N.; Vershinina, Y.D. Nonlinear viscoelastic properties of nanosuspensions. IOP Conf. Series Mater. Sci. Eng. 2019, 704, 012005. [Google Scholar] [CrossRef]
- Dembelova, T.S.; Badmaev, B.B.; Makarova, D.N. Investigation of physical-mechanical and tribological properties of suspensions of nanoparticles based on polyethylsiloxane liquid. J. Phys. Conf. Ser. 2019, 1281, 012009. [Google Scholar] [CrossRef]
- Yamada, Y.; Ichii, T.; Utsunomiya, T.; Sugimura, H. Visualizing polymeric liquid/solid interfaces by atomic force microscopy utilizing quartz tuning fork sensors. Jpn. J. Appl. Phys. 2020, 59, SN1009. [Google Scholar] [CrossRef]
- Su, B.; Zhou, Y.-G.; Wu, H.-H. Influence of mechanical properties of polypropylene/low-density polyethylene nanocomposites. Nanomater. Nanotechnol. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Shim, S.E.; Isayev, A.I. Rheology and structure of precipitated silica and poly(dimethyl siloxane) system. Rheol. Acta 2003, 43, 127–136. [Google Scholar] [CrossRef]
- Boonstra, B.B.; Cochrane, H.; Dánnenberg, E.M. Reinforcement of Silicone Rubber by Particulate Silica. Rubber Chem. Technol. 1975, 48, 558–576. [Google Scholar] [CrossRef]


| Molecular Weight | Density 20 °C, kg/m3 | Viscosity, mm2s−1 | Boiling Point, °C (133–400 Pa) | Pour Point, °C | ||
|---|---|---|---|---|---|---|
| −60 °C | 20 °C | 60 °C | ||||
| 341 | 940 | 312 | 9 | 4 | 110–150 | −110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dembelova, T.; Badmaev, B.; Makarova, D.; Mashanov, A.; Mishigdorzhiyn, U. Rheological and Tribological Study of Polyethylsiloxane with SiO2 Nanoparticles Additive. Lubricants 2023, 11, 9. https://doi.org/10.3390/lubricants11010009
Dembelova T, Badmaev B, Makarova D, Mashanov A, Mishigdorzhiyn U. Rheological and Tribological Study of Polyethylsiloxane with SiO2 Nanoparticles Additive. Lubricants. 2023; 11(1):9. https://doi.org/10.3390/lubricants11010009
Chicago/Turabian StyleDembelova, Tuyana, Badma Badmaev, Dagzama Makarova, Aleksandr Mashanov, and Undrakh Mishigdorzhiyn. 2023. "Rheological and Tribological Study of Polyethylsiloxane with SiO2 Nanoparticles Additive" Lubricants 11, no. 1: 9. https://doi.org/10.3390/lubricants11010009
APA StyleDembelova, T., Badmaev, B., Makarova, D., Mashanov, A., & Mishigdorzhiyn, U. (2023). Rheological and Tribological Study of Polyethylsiloxane with SiO2 Nanoparticles Additive. Lubricants, 11(1), 9. https://doi.org/10.3390/lubricants11010009






