Significance of Melting Heat Transfer and Brownian Motion on Flow of Powell–Eyring Fluid Conveying Nano-Sized Particles with Improved Energy Systems
Abstract
1. Introduction
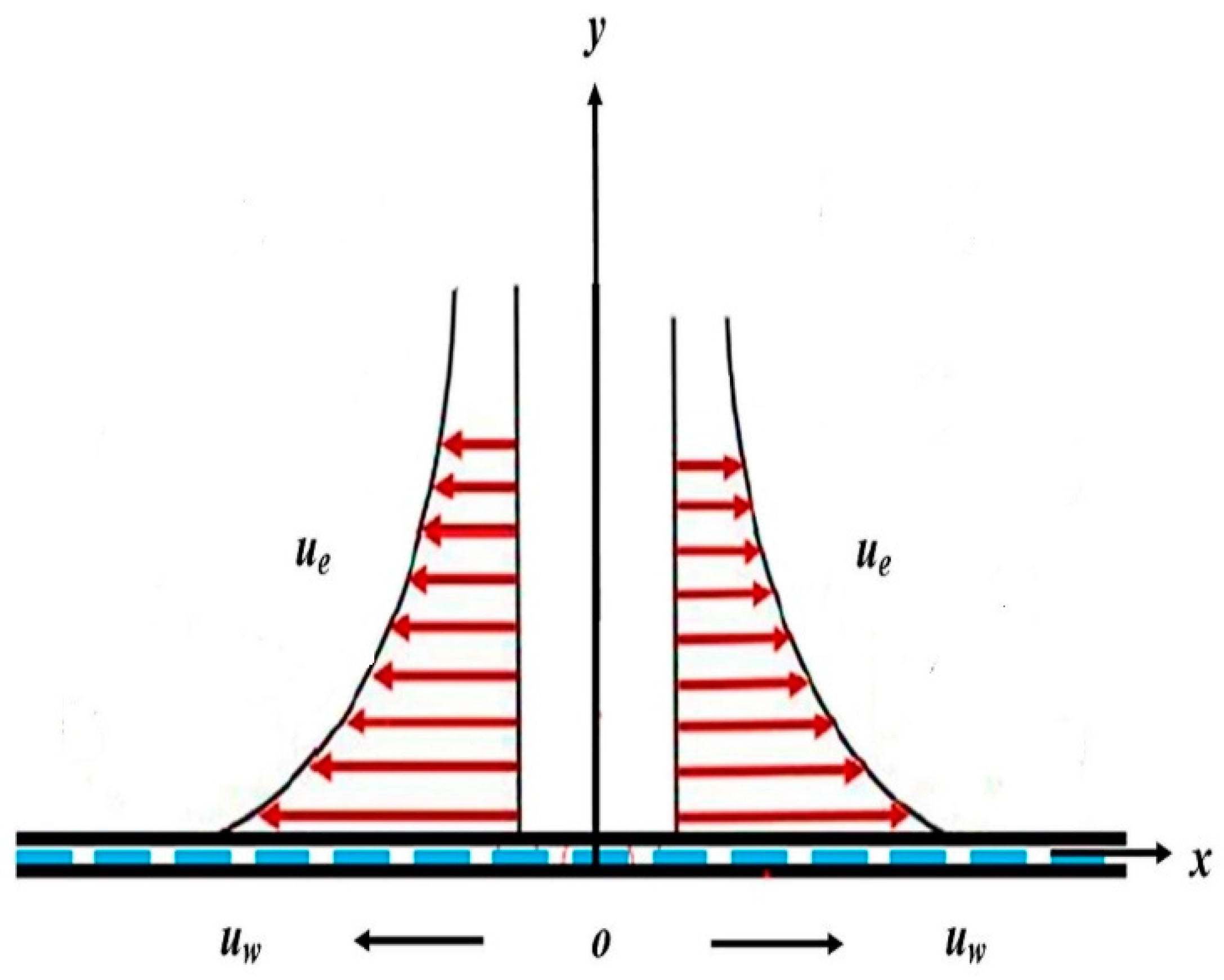
2. Mathematical Modelling
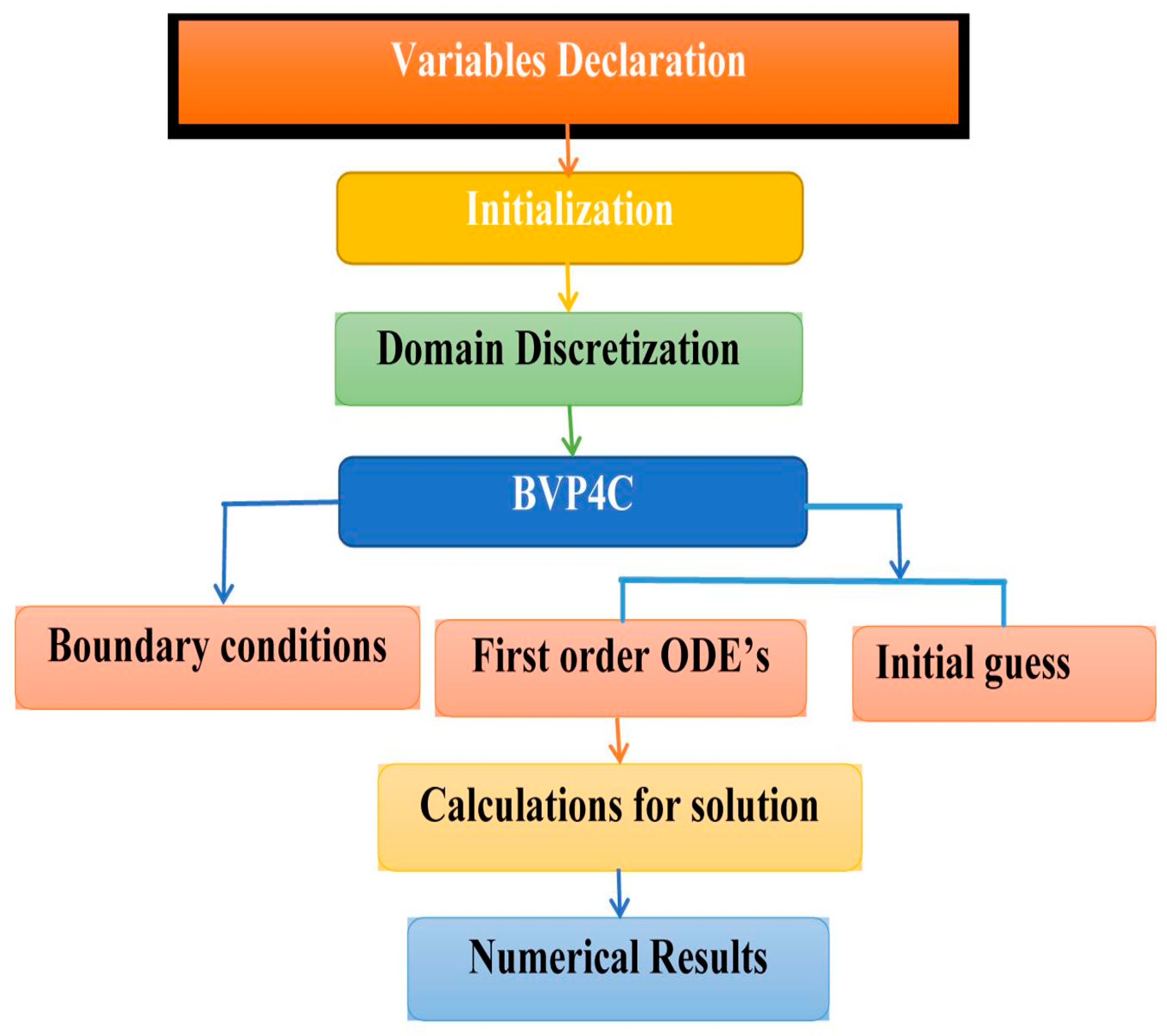
3. Numerical Scheme
4. Validation of Results
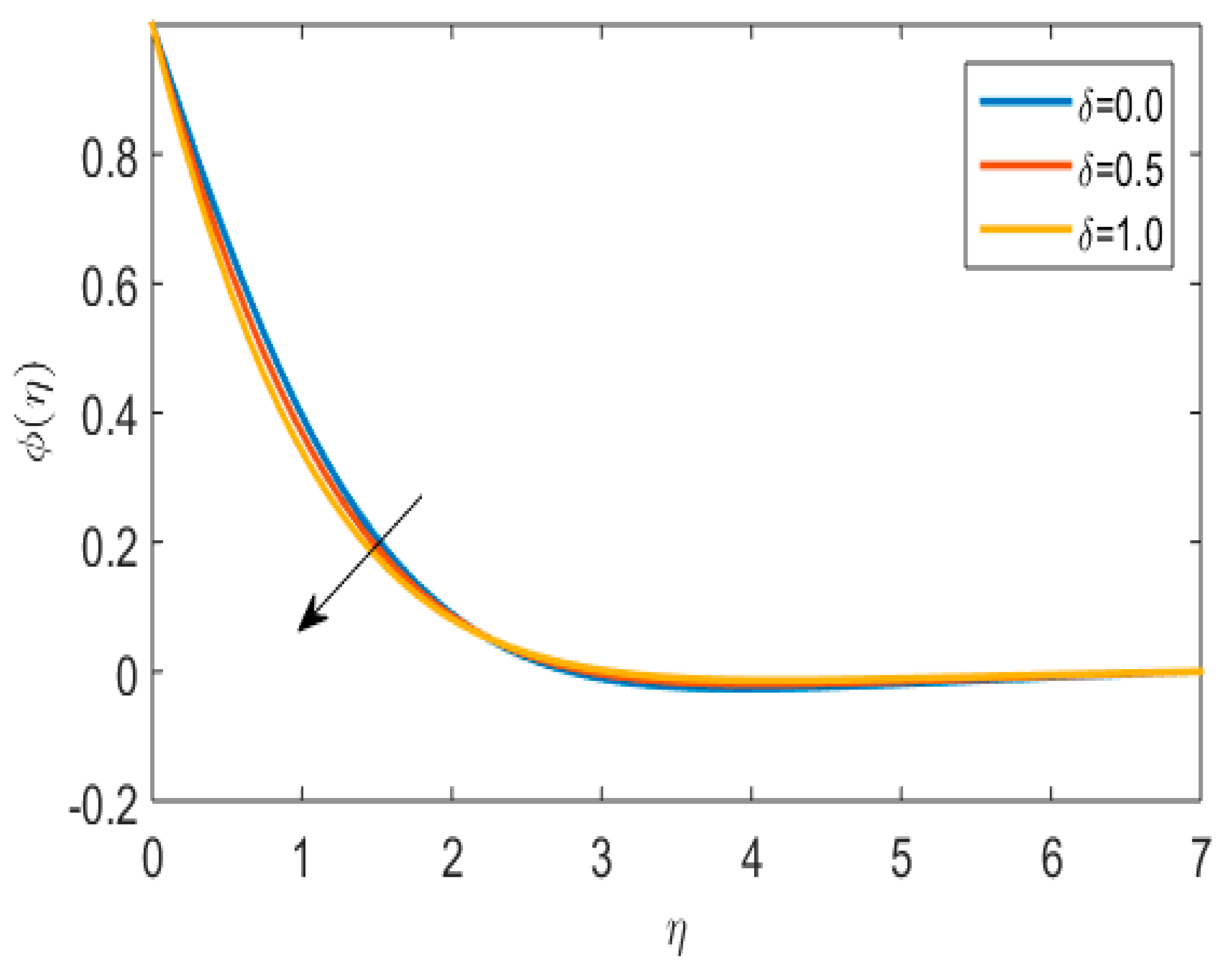
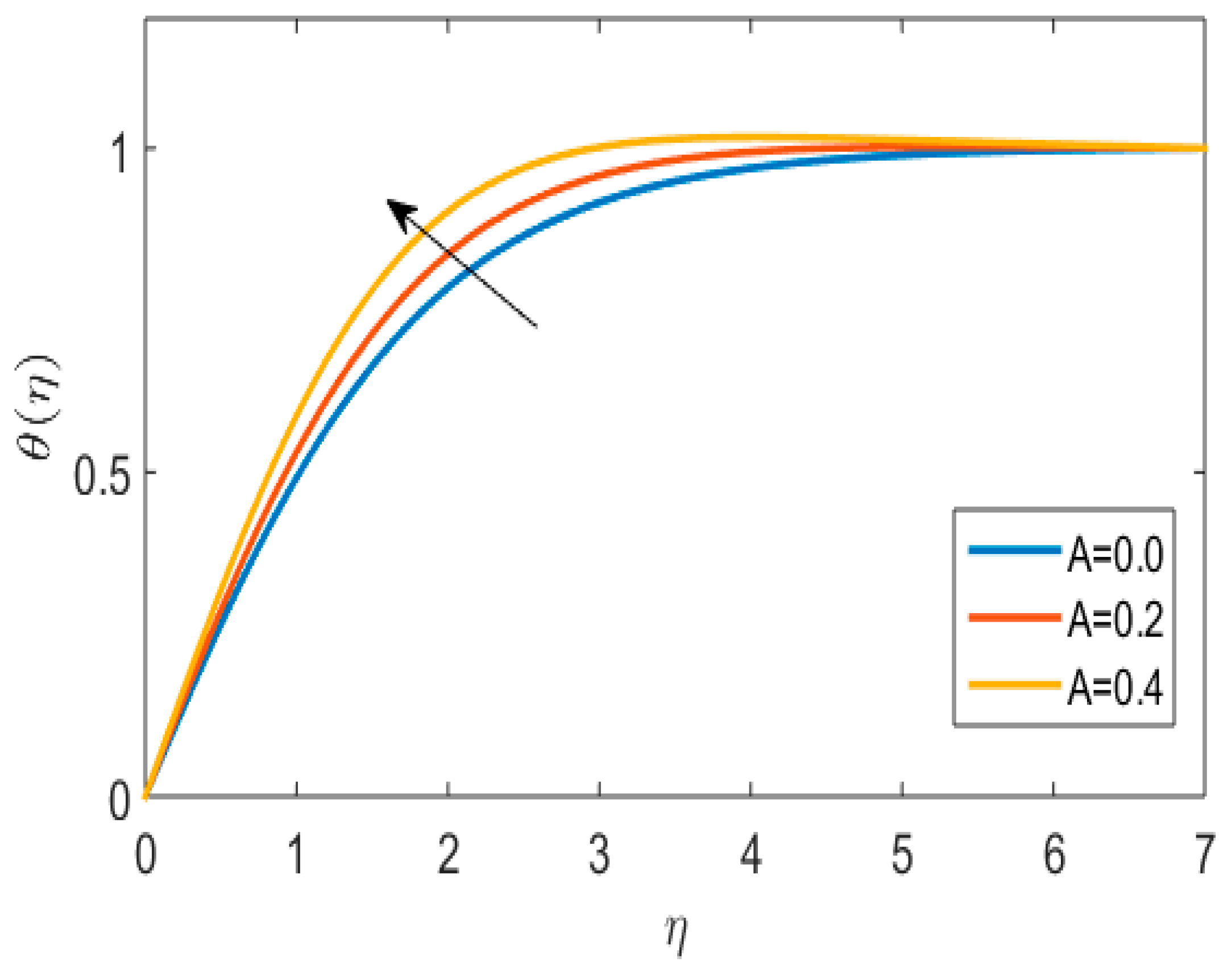
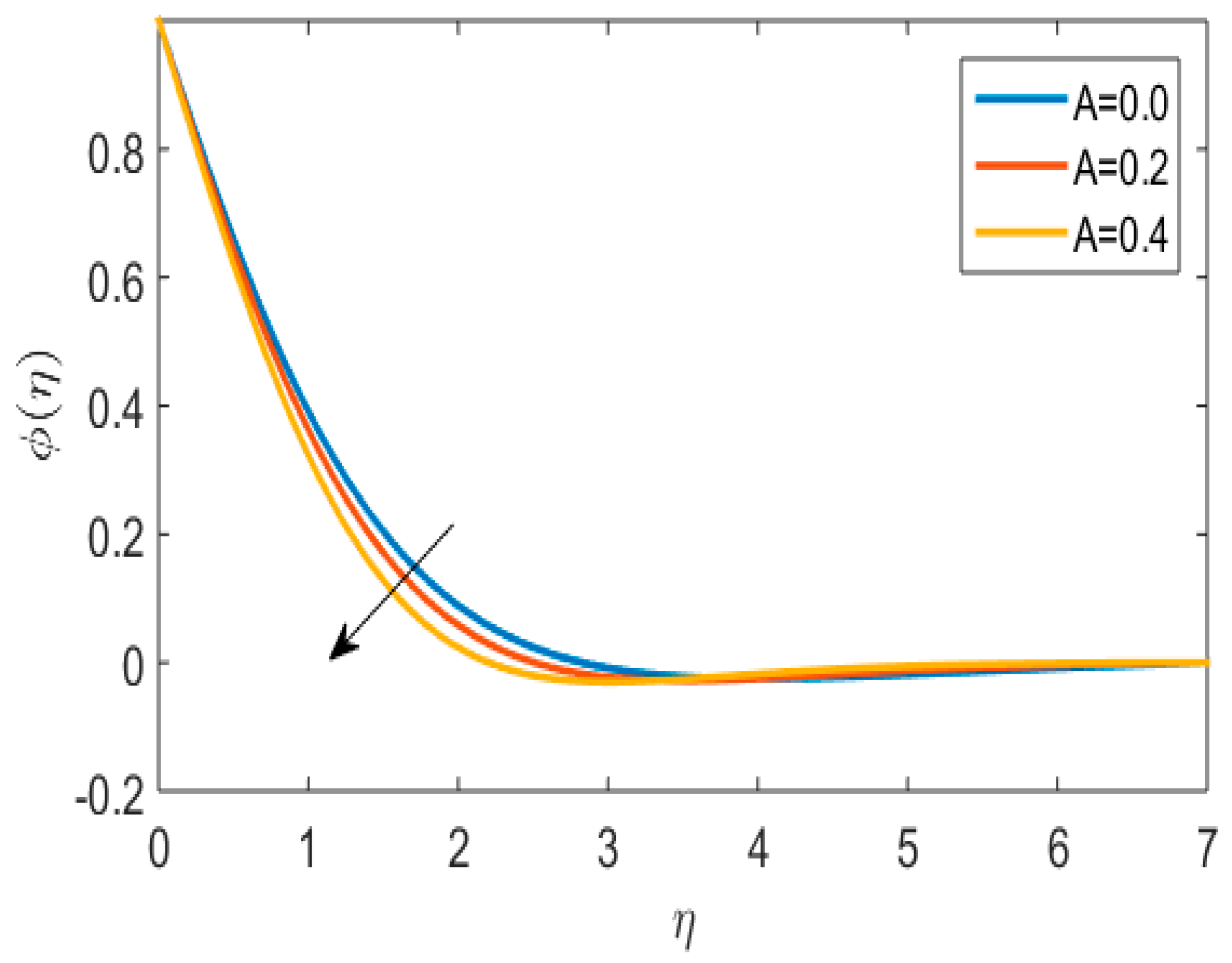
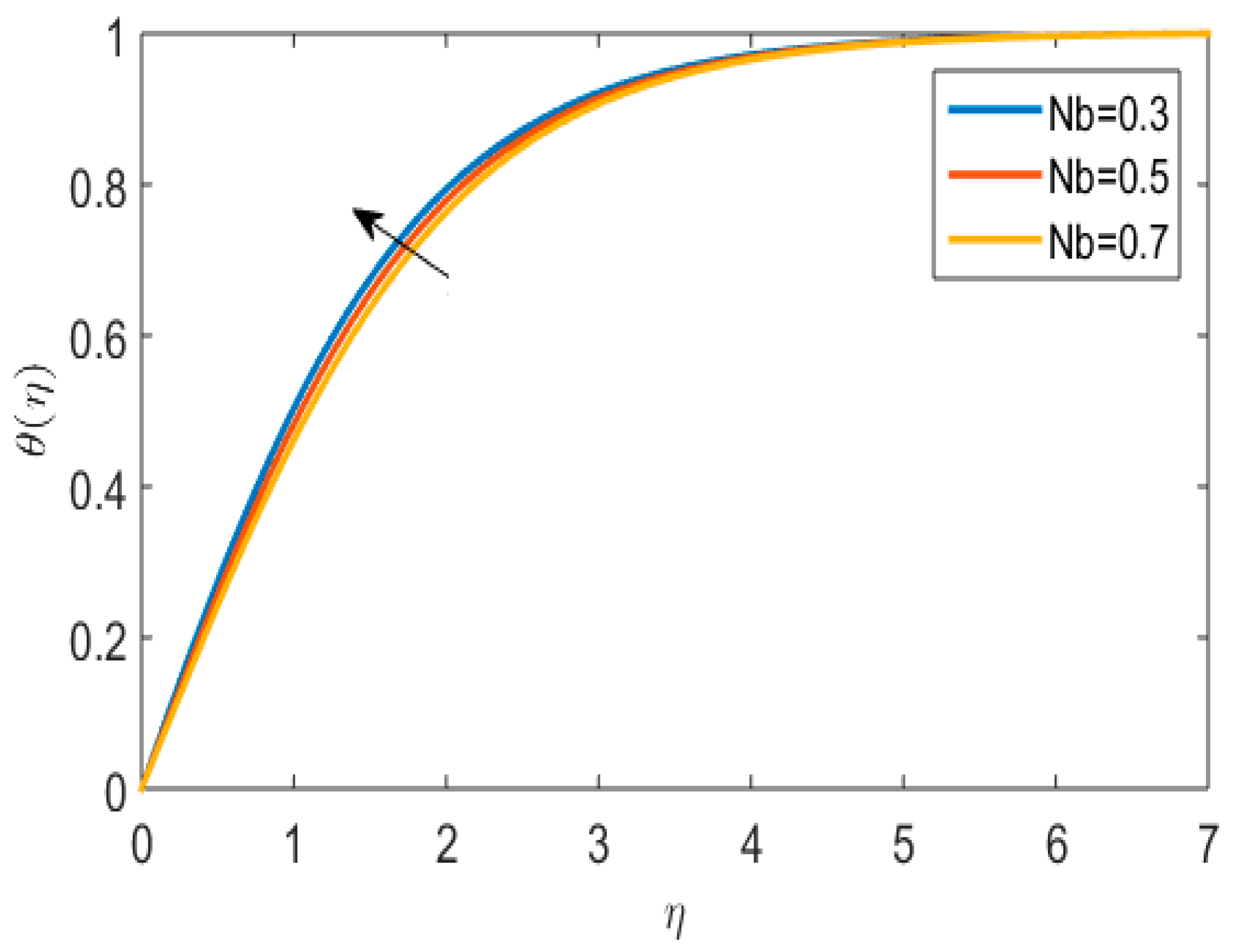
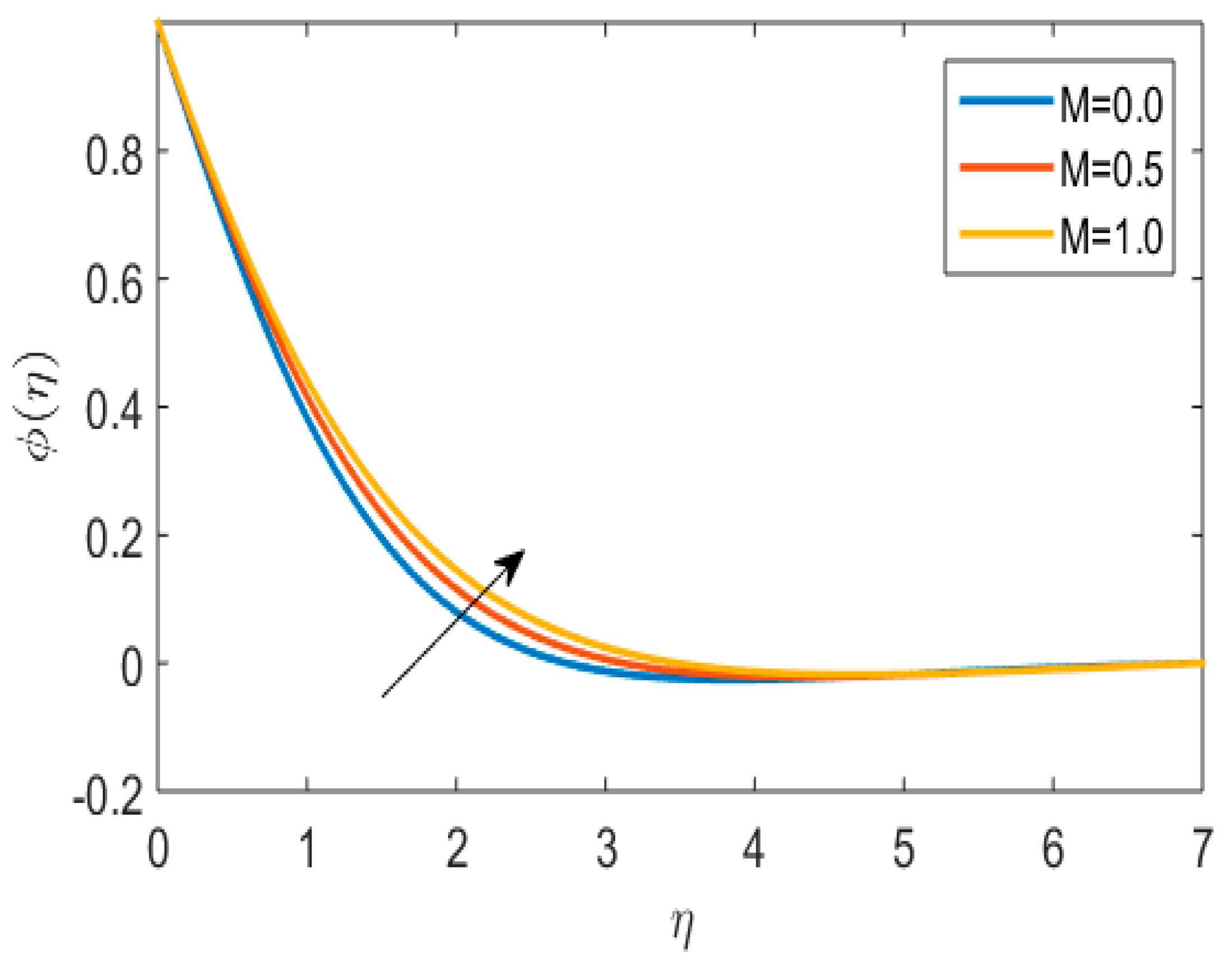
5. Results and Discussions
6. Conclusions
- ➢
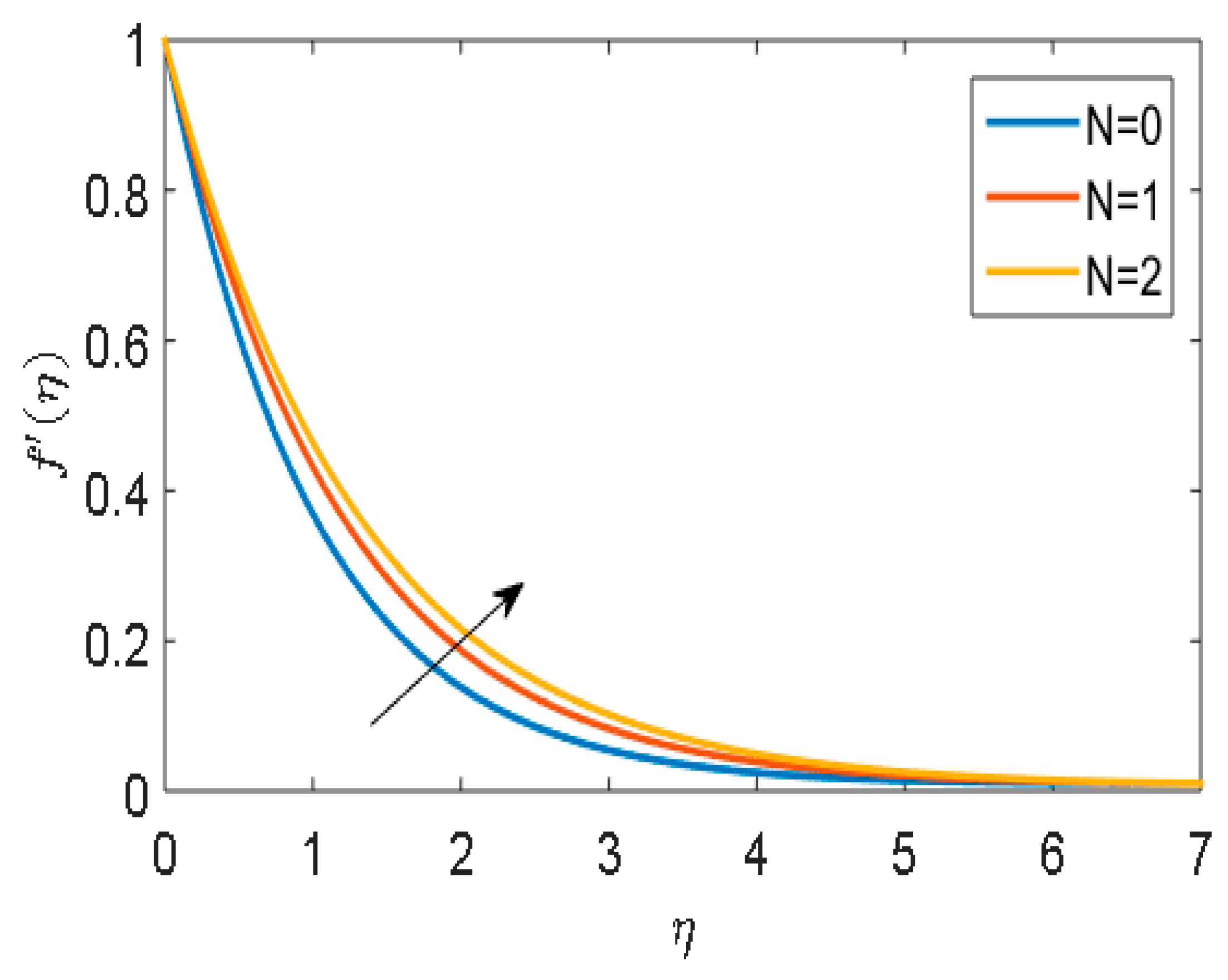
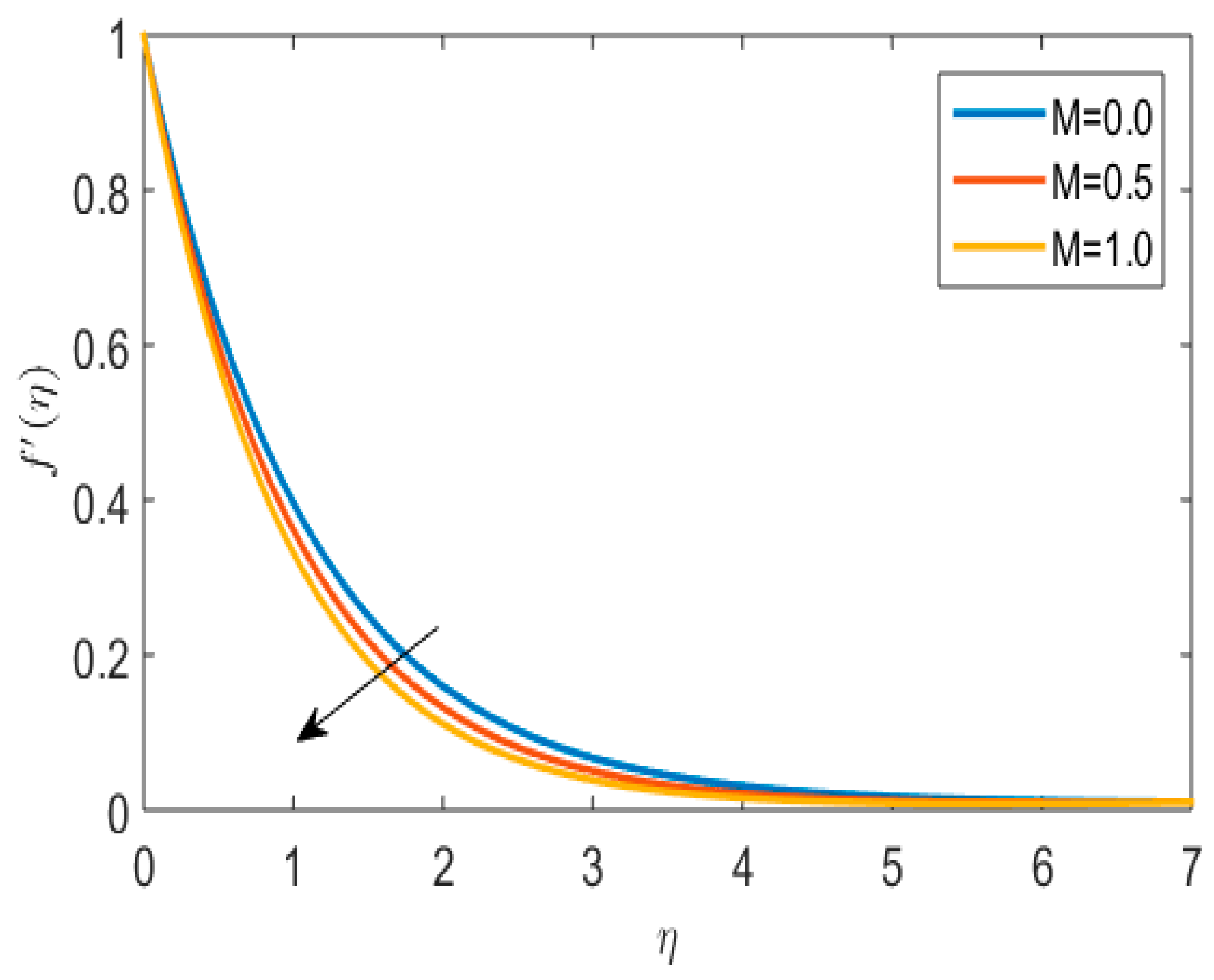
- An enhanced impact in velocity due to the melting heat transfer parameter has been observed.
- ➢
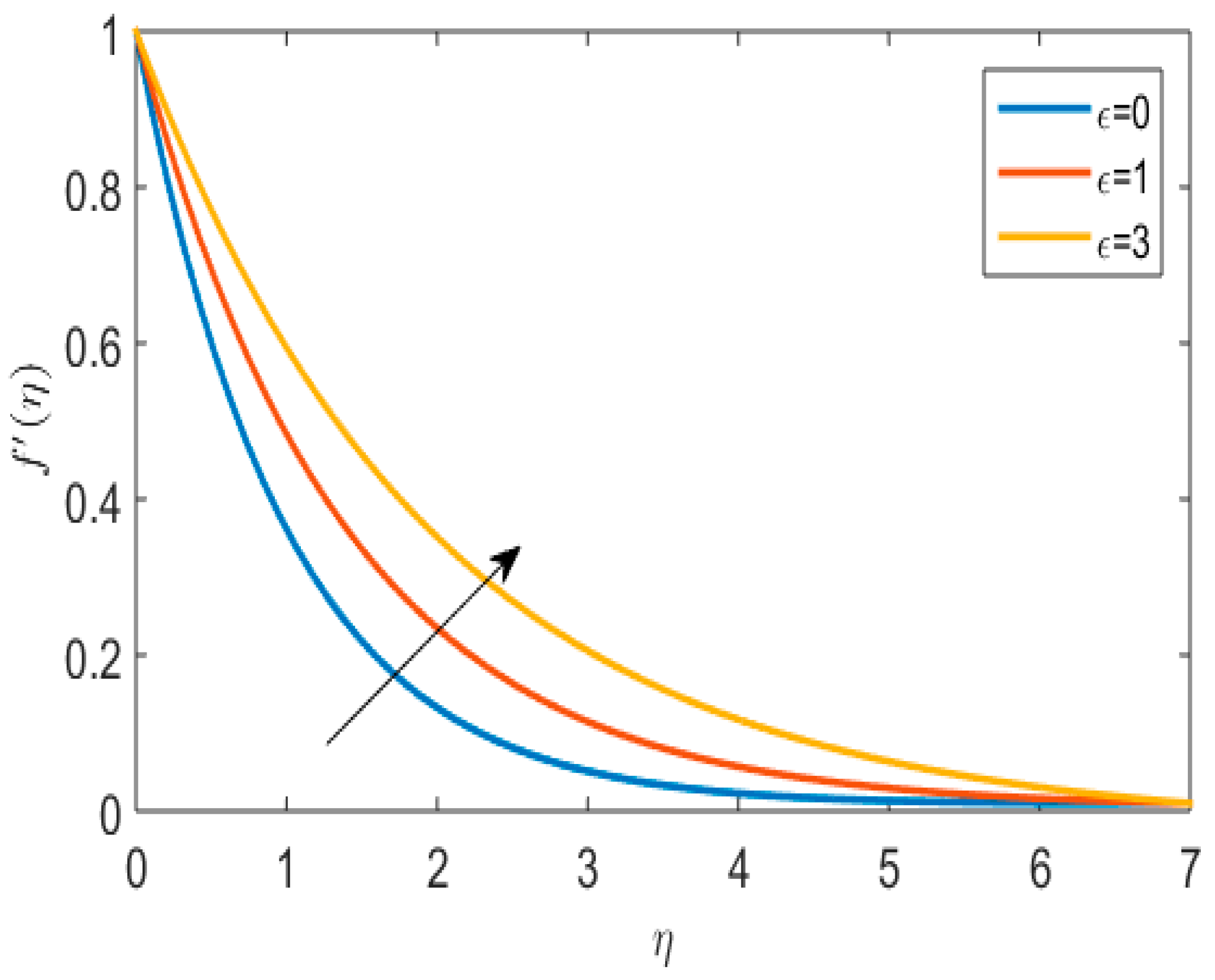
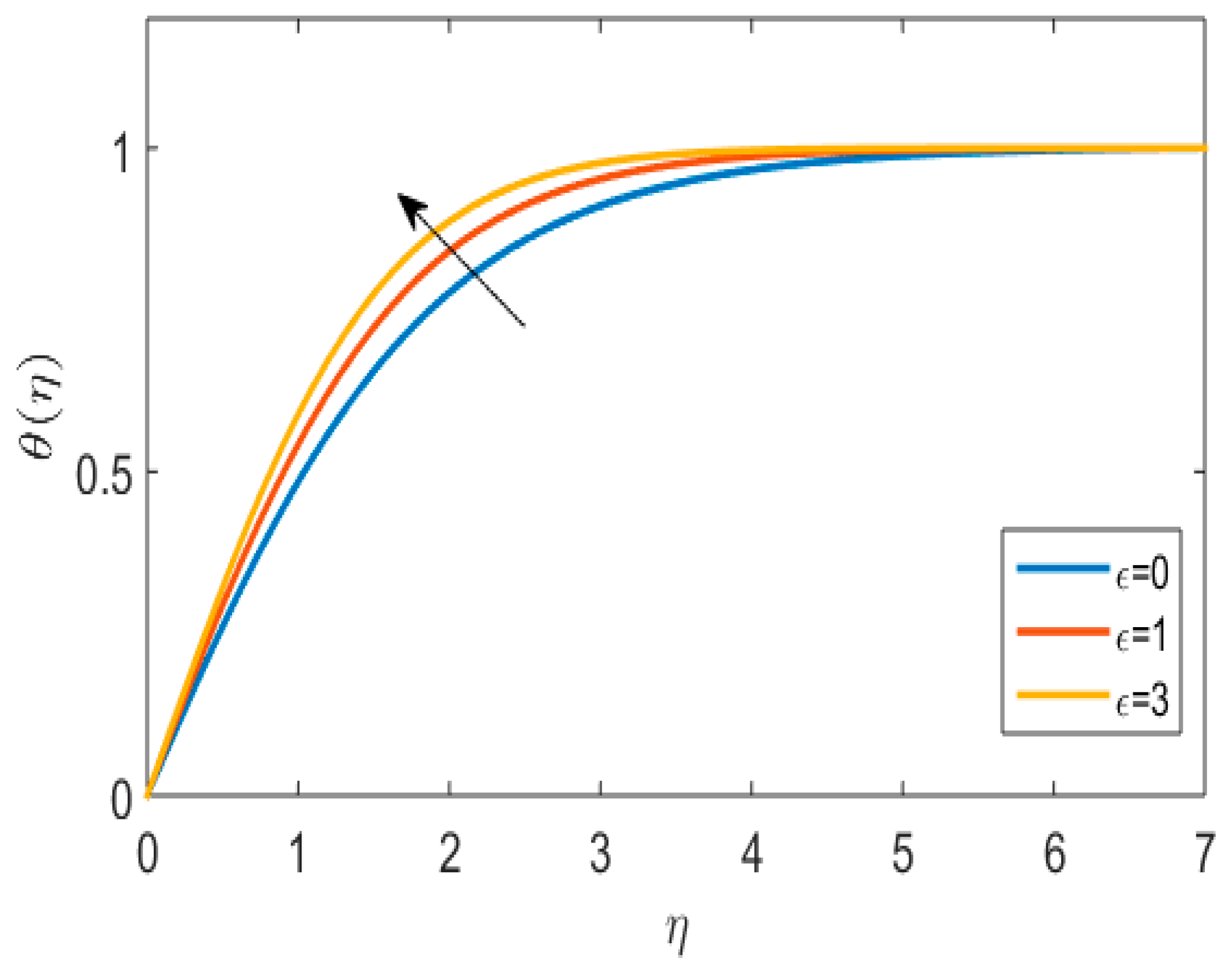
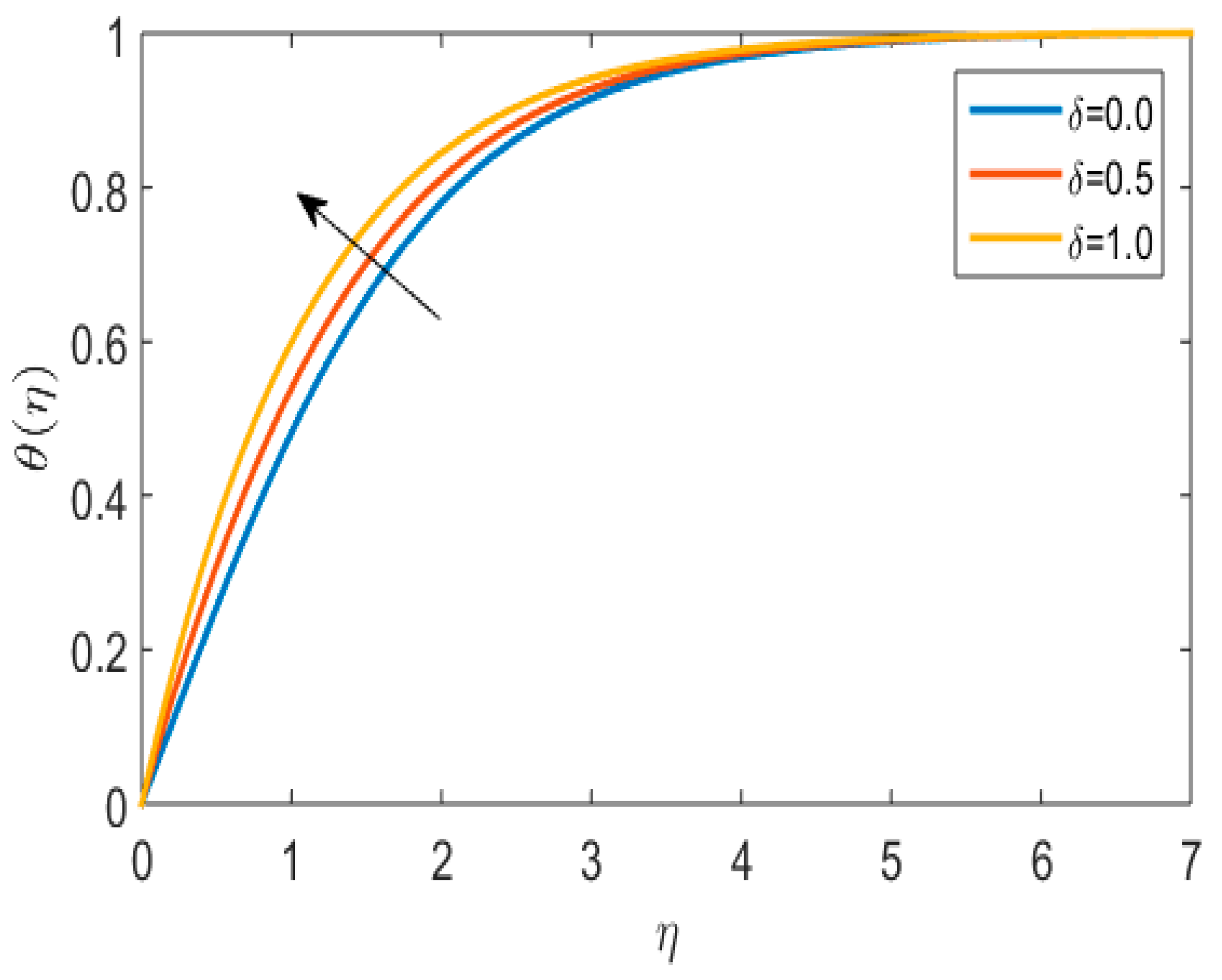
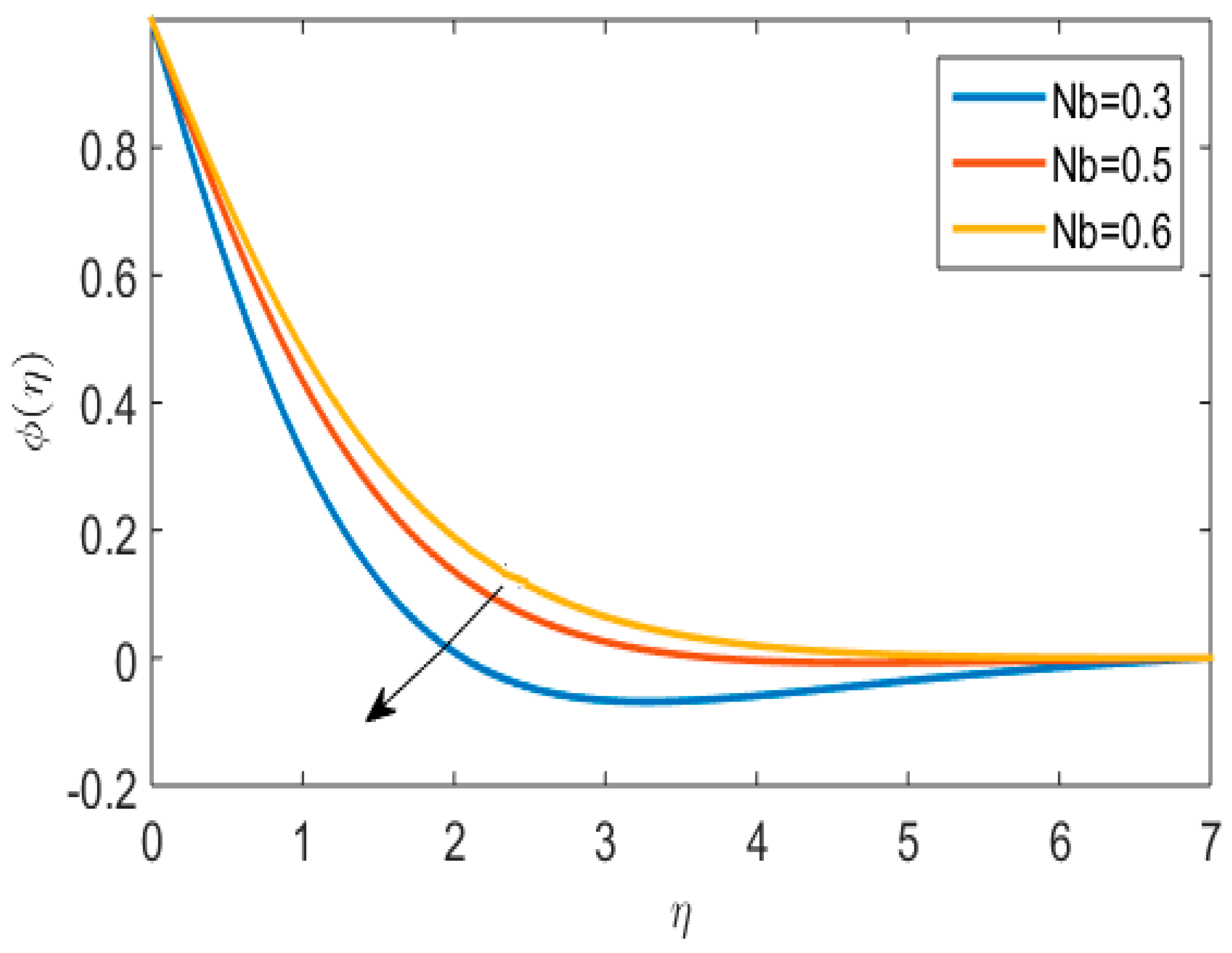
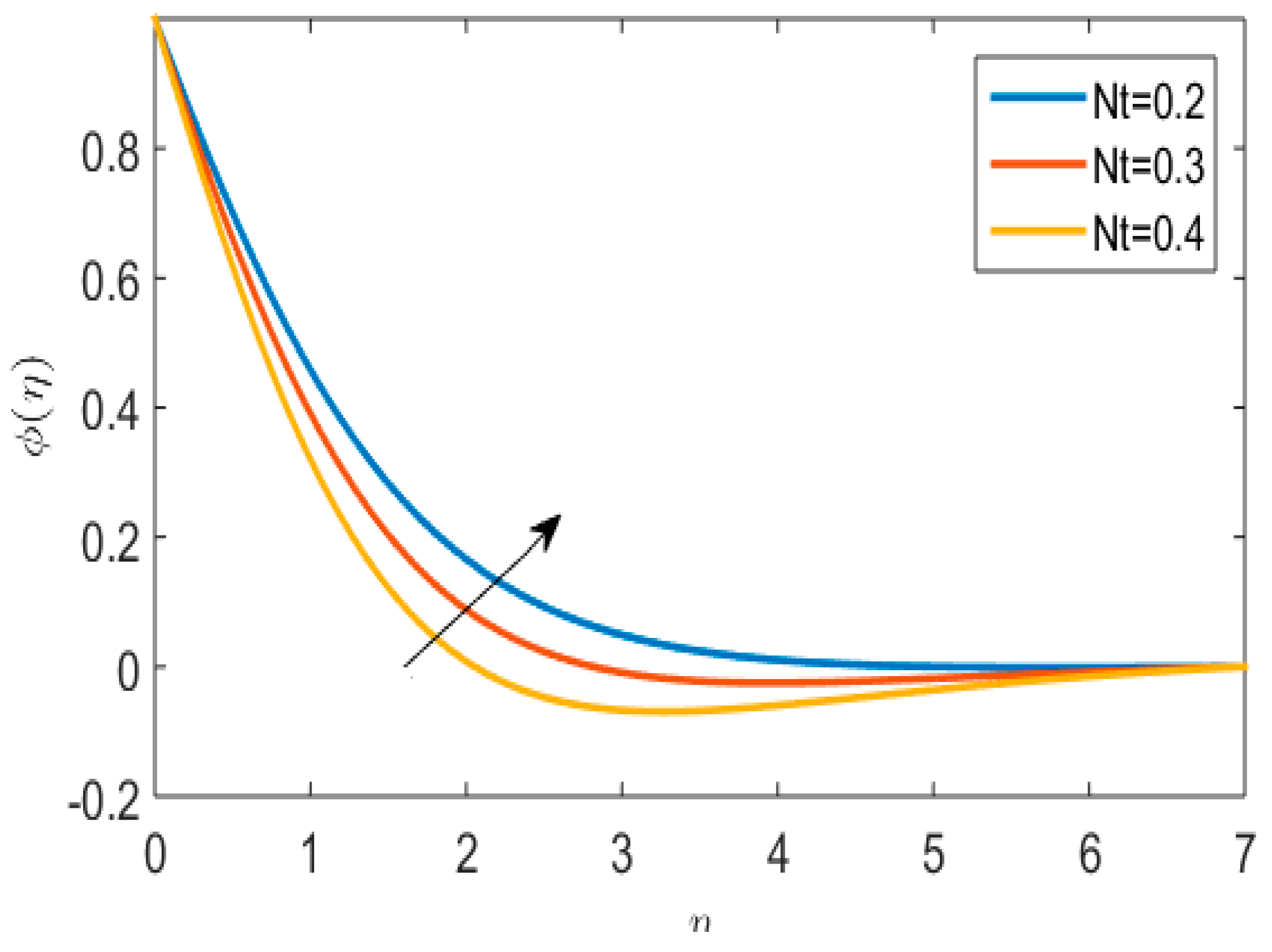
- An increase in the thermal profile is observed for melting heat transfer parameter and Powell–Eyring fluid parameter.
- ➢
- The temperature profile was enhanced due to Powell–Eyring fluid parameters.
- ➢
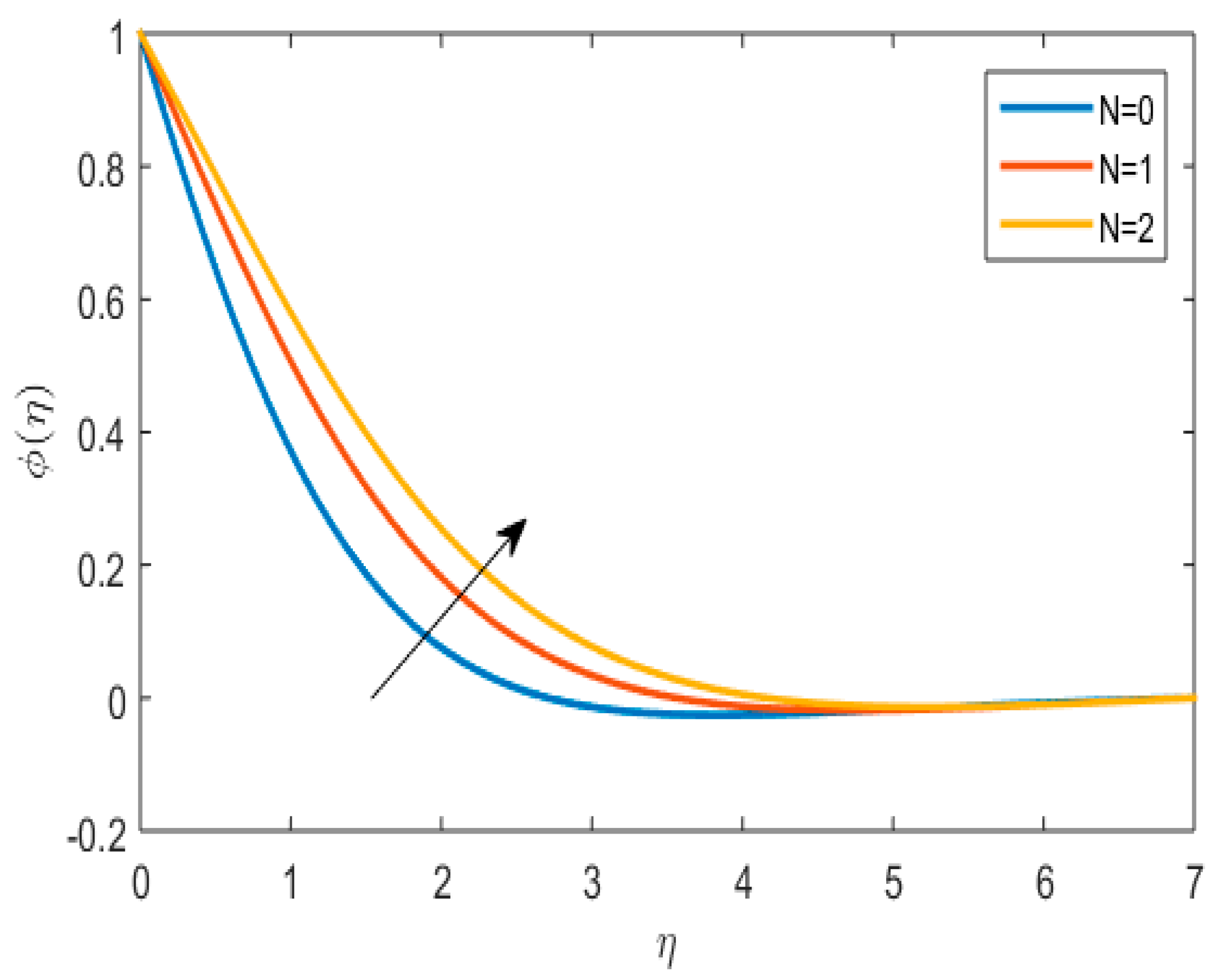
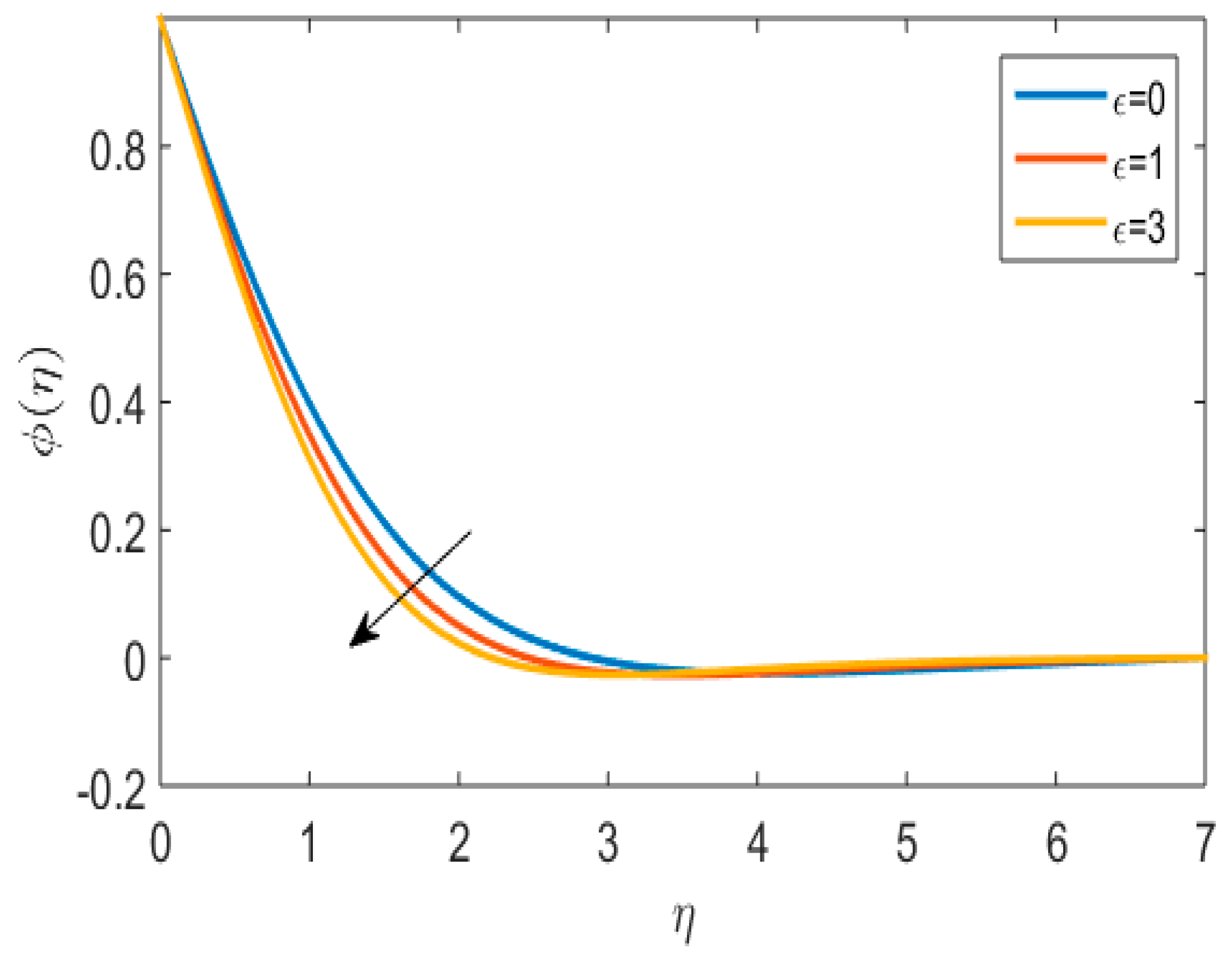
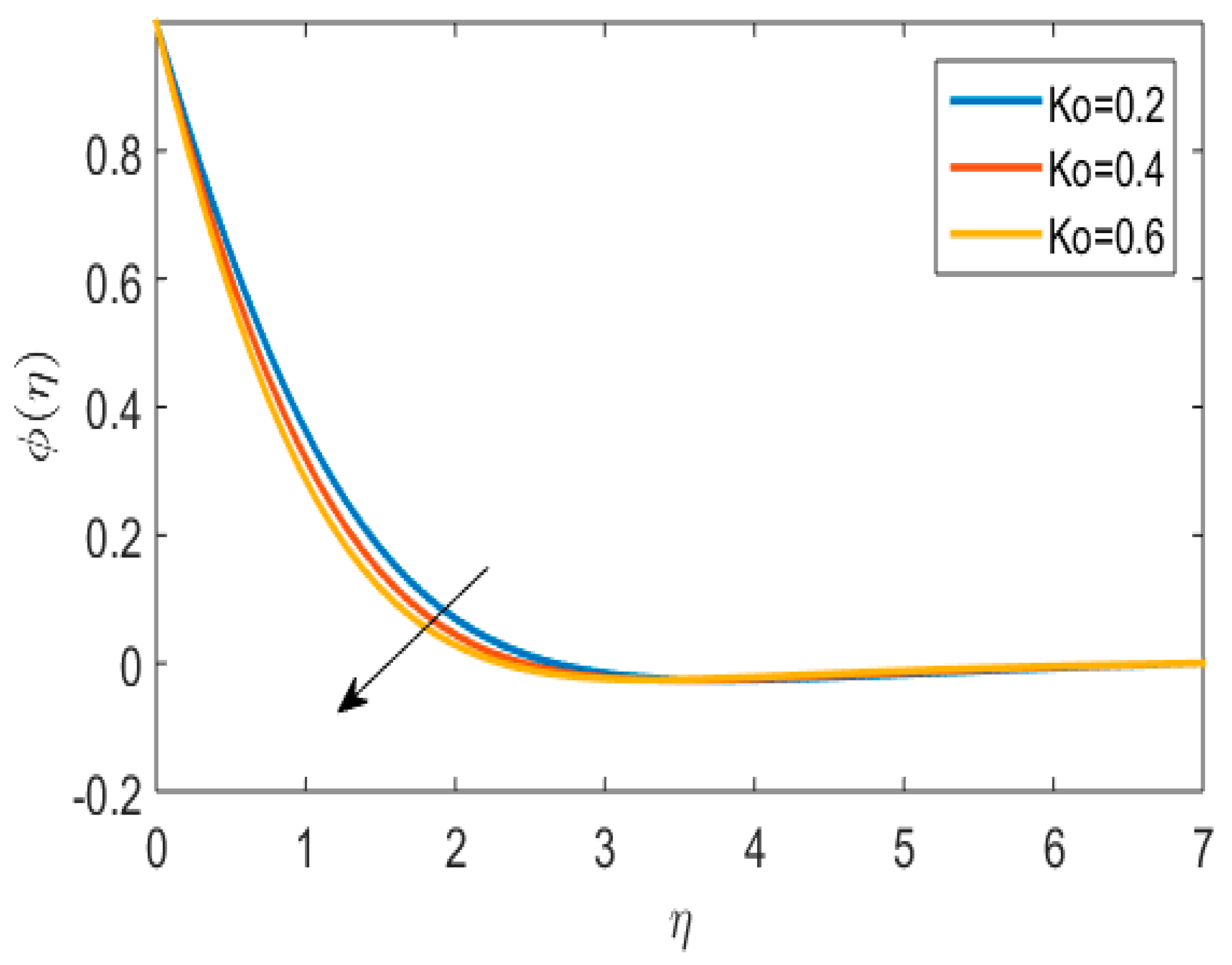
- With increasing velocity ratio and chemigation reaction constant, the concentration profile declined.
- ➢
- For larger Eckert numbers, increasing observations for temperature profile are claimed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| (u, v) | velocity components |
| ρ | fluid density |
| β | material parameter |
| T | fluid temperature |
| k | thermal conductivity |
| cp | specific heat |
| v | kinematic viscosity |
| λ | latent heat |
| cs | heat capacity |
| T0 | melting surface temperature. |
| ∊, δ | Eyring fluid parameters |
| A | velocity ratio of a free stream |
| N | melting heat transfer parameter |
| Nb | Brownian motion parameter |
| Nt | thermophoresis parameter |
| M | Hartmann number |
| Le | Lewis number |
| Ec | Eckert number |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME-Publications-Fed. 1995, 231, 99–106. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 18, 240–250. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Natural convective boundary-layer flow of a nanofluid past a vertical plate: A revised model. Int. J. Therm. Sci. 2014, 77, 126–129. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Prasad, K.V.; Setty, S.B.; Mebarek-Oudina, F.; Vaidya, H.; Choudhari, R.; Animasaun, I.L. Mixed convective Williamson nanofluid flow over a rotating disk with zero mass flux. Z. Angew. Math. Mech. 2022, 102, e202100117. [Google Scholar] [CrossRef]
- Hassan, M.; Mebarek-Oudina, F.; Faisal, A.; Ghafar, A.; Ismail, A.I. Thermal energy and mass transport of shear thinning fluid under effects of low to high shear rate viscosity. Int. J. Thermofluids 2022, 15, 100176. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. Appl. Nanosci. 2014, 4, 625–631. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Chamkha, A.J.; Gireesha, B.J. Magnetohydrodynamic flow of a non-Newtonian nanofluid over an impermeable surface with heat generation/absorption. J. Nanofluids 2014, 3, 78–84. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Mahanthesh, B.; Gorla, R.S.R. Suspended particle effect on nanofluid boundary layer flow past a stretching surface. J. Nanofluids 2014, 3, 267–277. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B.; Nandeppanavar, M.M. MHD stagnation point flow and heat transfer due to nanofluid towards a stretching sheet. Int. J. Heat Mass Transf. 2013, 56, 1–9. [Google Scholar] [CrossRef]
- Macha, M.; Kishan, N. Magnetohydrodynamic mixed convection stagnation-point flow of a power-law non-Newtonian nanofluid towards a stretching surface with radiation and heat source/sink. J. Fluids 2015, 2015, 634186. [Google Scholar]
- Mahesh, K.; Gorla, R.S.R. Effect of Melting on Natural Convective Boundary Layer Flow Over a Horizontal Plate Embedded in a Porous Medium Saturated with a Non-Newtonian Nanofluid. J. Nanofluids 2014, 3, 278–286. [Google Scholar]
- Leonard, R. On the melting of a semi-infinite body of ice placed in a hot stream of air. J. Fluid Mech. 1958, 4, 505–528. [Google Scholar]
- Hayat, T.; Farooq, M.; Alsaedi, A.; Iqbal, Z. Melting heat transfer in the stagnation point flow of Powell–Eyring fluid. J. Thermophys. Heat Transf. 2013, 27, 761–766. [Google Scholar] [CrossRef]
- Kalidas, D. Radiation and melting effects on MHD boundary layer flow over a moving surface. Ain Shams Eng. J. 2014, 5, 1207–1214. [Google Scholar]
- Epstein, M.; Cho, D.H. Melting heat transfer in steady laminar flow over a flat plate. J. Heat Transf. 1976, 98, 531–533. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Makinde, O.D.; Saleem, S. Mixed convection flow of Newtonian fluids over an upper horizontal thermally stratified melting surface of a paraboloid of revolution. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–14. [Google Scholar] [CrossRef]
- Gorla, R.R.S.; Mansour, M.A.; Hassanien, I.A.; Bakier, A.Y. Mixed convection effect on melting from a vertical plate in a porous medium. Transp. Porous Media 1999, 36, 245–254. [Google Scholar] [CrossRef]
- Bachock, N.; Ishak, A.; Pop, I. Melting heat transfer in boundary layer stagnation point flow towards a stretching/shrinking sheet. Phys. Lett. 2010, A374, 4075–4079. [Google Scholar] [CrossRef]
- Anuar, I.; Nazar, R.; Bachok, N.; Pop, I. Melting heat transfer in steady laminar flow over a moving surface. Heat Mass Transf. 2010, 46, 463–468. [Google Scholar]
- Gireesha, B.J.; Mahanthesh, B.; Shivakumara, I.S.; Eshwarappa, K.M. Melting heat transfer in boundary layer stagnation-point flow of nanofluid toward a stretching sheet with induced magnetic field. Eng. Sci. Technol. Int. J. 2016, 19, 313–321. [Google Scholar] [CrossRef]
- Kazmierczak, M.; Poulikakos, D.; Pop, I. Melting from a flat plate embedded in a porous medium in the presence of steady natural convection. Numer. Heat Transf. 1986, 10, 571–581. [Google Scholar] [CrossRef]
- Rahmat, E.; Riaz, A.; Abbasbandy, S.; Hayat, T.; Vafai, K. A study on the mixed convection boundary layer flow and heat transfer over a vertical slender cylinder. Therm. Sci. 2014, 18, 1247–1258. [Google Scholar]
- Riaz, A.; Ellahi, R.; Sait, S.M. Role of hybrid nanoparticles in thermal performance of peristaltic flow of Eyring–Powell fluid model. J. Therm. Anal. Calorim. 2021, 143, 1021–1035. [Google Scholar] [CrossRef]
- Aaqib, M.; Zubair, M.; Khan, A.; Muhammad, T.; Alqarni, M.S. Significance of Thermophoretic and Brownian Motion on MHD Nanofluids Flow towards a Circular Cylinder under the Inspiration of Multiple Slips: An Industrial Application. Math. Probl. Eng. 2021, 2021, 8634185. [Google Scholar]
- Tasawar, A.; Ahmad, B.; Majeed, A.; Muhammad, T.; Ismail, M. Numerical Investigations of Radiative Flow of Viscous Fluid Through Porous Medium. J. Magn. 2021, 26, 277–284. [Google Scholar]
- Majeed, A.; Zeeshan, A.; Xu, H.; Kashif, M.; Masud, U. Heat transfer analysis of magneto-Eyring–Powell fluid over a nonlinear stretching surface with multiple slip effects: Application of Roseland’s heat flux. Can. J. Phys. 2019, 97, 1253–1261. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Ibraheem, R.O.; Mahanthesh, B.; Babatunde, H.A. A meta-analysis on the effects of haphazard motion of tiny/nano-sized particles on the dynamics and other physical properties of some fluids. Chin. J. Phys. 2019, 60, 676–687. [Google Scholar] [CrossRef]
- Smith, S.R.; Rafati, R.; Haddad, A.S.; Cooper, A.; Hamidi, H. Application of aluminium oxide nanoparticles to enhance rheological and filtration properties of water based muds at HPHT conditions. Colloids Surf. A Physicochem. Eng. Asp. 2018, 537, 361–371. [Google Scholar] [CrossRef]
- Vleggaar, J. Laminar boundary-layer behaviour on continuous, accelerating surfaces. Chem. Eng. Sci. 1977, 32, 1517–1525. [Google Scholar] [CrossRef]
- Powell, R.E.; Eyring, H. Mechanisms for the relaxation theory of viscosity. Nature 1944, 154, 427–428. [Google Scholar] [CrossRef]
- Malik, M.Y.; Hussain, A.; Nadeem, S. Boundary layer flow of an Eyring–Powell model fluid due to a stretching cylinder with variable viscosity. Sci. Iran. 2013, 20, 313–321. [Google Scholar]
- Hayat, T.; Iqbal, Z.; Qasim, M.; Obaidat, S. Steady flow of an Eyring Powell fluid over a moving surface with convective boundary conditions. Int. J. Heat Mass Transf. 2012, 55, 1817–1822. [Google Scholar] [CrossRef]
- Islam, S.; Shah, A.; Zhou, C.Y.; Ali, I. Homotopy perturbation analysis of slider bearing with Powell–Eyring fluid. Z. Angew. Math. Phys. 2009, 60, 1178–1193. [Google Scholar] [CrossRef]
- Makinde, O.D.; Sandeep, N.; Ajayi, T.M.; Animasaun, I.L. Numerical exploration of heat transfer and Lorentz force effects on the flow of MHD Casson fluid over an upper horizontal surface of a thermally stratified melting surface of a paraboloid of revolution. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 93–106. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Gupta, A.S. Heat transfer in stagnation-point flow towards a stretching sheet. Heat Mass Transf. 2002, 38, 517–521. [Google Scholar] [CrossRef]
- Khan, S.U.; Ali, H.M. Swimming of gyrotactic microorganisms in unsteady flow of Eyring Powell nanofluid with variable thermal features: Some bio-technology applications. Int. J. Thermophys. 2020, 41, 159. [Google Scholar] [CrossRef]
- Song, Y.Q.; Obideyi, B.D.; Shah, N.A.; Animasaun, I.L.; Mahrous, Y.M.; Chung, J. Significance of haphazard motion and thermal migration of alumina and copper nanoparticles across the dynamics of water and ethylene glycol on a convectively heated surface. Case Stud. Therm. Eng. 2021, 26, 101050. [Google Scholar] [CrossRef]
- Jawad, M.; Mebarek-Oudina, F.; Vaidya, H.; Prashar, P. Influence of Bioconvection and Thermal Radiation on MHD Williamson Nano Casson Fluid Flow with the Swimming of Gyrotactic Microorganisms Due to Porous Stretching Sheet. J. Nanofluids 2022, 11, 500–509. [Google Scholar] [CrossRef]
- Sharma, K.; Kumar, S.; Narwal, A.; Mebarek-Oudina, F.; Animasaun, I.L. Convective MHD Fluid flow over Stretchable Rotating Disks with Dufour and Soret Effects. Int. J. Appl. Comput. Math 2022, 8, 159. [Google Scholar] [CrossRef]
- Anjum, N.; Khan, W.A.; Hobiny, A.; Azam, M.; Waqas, M.; Irfan, M. Numerical analysis for thermal performance of modified Eyring Powell nanofluid flow subject to activation energy and bioconvection dynamic. Case Stud. Therm. Eng. 2022, 39, 102427. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Kumar, R.; Bahadur, S.; Seth, G. Modeling and interpretation of peristaltic transport of Eyring–Powell fluid through uniform/non-uniform channel with Joule heating and wall flexibility. Chin. J. Phys. 2022, 80, 167–182. [Google Scholar] [CrossRef]
- Hussain, M.; Ranjha, Q.A.; Anwar, M.S.; Jahan, S.; Ali, A. Eyring-Powell model flow near a convectively heated porous wedge with chemical reaction effects. J. Taiwan Inst. Chem. Eng. 2022, 139, 104510. [Google Scholar] [CrossRef]



| A | Hayat [37] | Present Results |
|---|---|---|
| 0.10 | −0.96802 | −0.968021 |
| 0.20 | −0.91692 | −0.916920 |
| 0.50 | −0.66722 | −0.667222 |
| 2.00 | 2.0175 | 2.01762 |
| 3.00 | 4.7291 | 4.72925 |
| N | Pr | ϵ | A | ||
|---|---|---|---|---|---|
| 0.0 | 1.0 | 0.5 | 1.1162 | 0.7088 | |
| 0.3 | 0.7750 | 0.6910 | |||
| 0.5 | 0.5490 | 0.6953 | |||
| 0.8 | 0.2214 | 0.7116 | |||
| 0.8 | 0.5552 | 0.7540 | |||
| 1.0 | 0.5652 | 0.8629 | |||
| 1.2 | 0.5729 | 0.9630 | |||
| 0.0 | 0.4400 | 0.8444 | |||
| 0.5 | 0.5652 | 0.8629 | |||
| 1.0 | 0.6749 | 0.8766 | |||
| 1.2 | 0.7157 | 0.8813 | |||
| 0.0 | 0.7037 | 0.7496 | |||
| 0.2 | 0.5652 | 0.8629 | |||
| 0.5 | 0.2750 | 1.0463 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Majeed, A.; Al-Khaled, K.; Abbas, T.; Naeem, M.; Khan, S.U.; Saeed, M. Significance of Melting Heat Transfer and Brownian Motion on Flow of Powell–Eyring Fluid Conveying Nano-Sized Particles with Improved Energy Systems. Lubricants 2023, 11, 32. https://doi.org/10.3390/lubricants11010032
Yang H, Majeed A, Al-Khaled K, Abbas T, Naeem M, Khan SU, Saeed M. Significance of Melting Heat Transfer and Brownian Motion on Flow of Powell–Eyring Fluid Conveying Nano-Sized Particles with Improved Energy Systems. Lubricants. 2023; 11(1):32. https://doi.org/10.3390/lubricants11010032
Chicago/Turabian StyleYang, Hong, Aaqib Majeed, Kamel Al-Khaled, Tasawar Abbas, Muhammad Naeem, Sami Ullah Khan, and Munazza Saeed. 2023. "Significance of Melting Heat Transfer and Brownian Motion on Flow of Powell–Eyring Fluid Conveying Nano-Sized Particles with Improved Energy Systems" Lubricants 11, no. 1: 32. https://doi.org/10.3390/lubricants11010032
APA StyleYang, H., Majeed, A., Al-Khaled, K., Abbas, T., Naeem, M., Khan, S. U., & Saeed, M. (2023). Significance of Melting Heat Transfer and Brownian Motion on Flow of Powell–Eyring Fluid Conveying Nano-Sized Particles with Improved Energy Systems. Lubricants, 11(1), 32. https://doi.org/10.3390/lubricants11010032






