Abstract
Heat transfer technologies are experiencing rapid expansion as a result of the demand for efficient heating and cooling systems in the automotive, chemical, and aerospace industries. Therefore, the current study peruses an inspection of mixed convective radiative Williamson flow close to a stagnation point aggravated by a single nanoparticle (alumina) from a vertical flat plate with the impact of Hall. The convective heating of water conveying alumina (Al2O3) nanoparticles, as appropriate in engineering or industry, is investigated. Using pertinent similarity variables, the dominating equations are non-dimensionalized, and after that, via the bvp4c solver, they are numerically solved. We extensively explore the effects of many relevant parameters on axial velocity, transverse velocity, temperature profile, heat transfer, and drag force. In the opposing flow, there are two solutions seen; in the aiding flow, just one solution is found. In addition, the results designate that, due to nanofluid, the thickness of the velocity boundary layer decreases, and the thermal boundary layer width upsurges. The gradients for the branch of stable outcome escalate due to a higher Weissenberg parameter, while they decline for the branch of lower outcomes. Moreover, a magnetic field can be used to influence the flow and the properties of heat transfer.
1. Introduction
As research of subject, the mechanics of shear-thinning (pseudoplastic) fluids has grown in popularity because of its enormous significance in biosciences, engineering, and industrial sectors, such as in extruded polymer sheets, high melts of natural polymers, and sheets coated with emulsion-like photographic films. To examine the rheological characteristics of all varieties of pseudoplastic fluids, numerous models have been developed (paints, blood, honey, etc.). The Cross model, Power-law model, Carreau model, Ellis model, and Williamson model are a few of them. For further research, we have taken into account the model of Williamson fluid in this analysis. The advantage of this model is that it takes into account both minimum (shear stress goes to zero) and maximum (shear stress goes to infinity) viscosities. Williamson [1] considered a model for analyzing the behavior of pseudoplastic flows in 1929 and provided experimental support for it. He discussed the significance of shear-thinning flows and pointed out how they differ greatly from viscous flows. In their study of the Williamson fluid flow across a stretchy sheet, Nadeem et al. [2] found that the velocity distribution and friction factor degrade by increasing the Williamson parameter. Hayat et al. [3] explored the Williamson fluid passing via a stretchy sheet and looked at the degradation of wall shear stress for a greater amount of Williamson fluid when heat radiation and a magnetic field were present. The features of mass and heat transfer comprising Williamson fluid across a permeable stretchy sheet subject to a magnetic field were inspected by Shawky et al. [4]. The rate at which heat is transferred to the stretched surface increases as the Williamson and porosity parameters are increased. Significant studies regarding distinct aspects of Williamson fluid are found in references [5,6,7,8].
Nanofluids have been widely used in industry. Nanofluid, characterized by a substantial increase in molecular mobility compared to unadventurous engineered fluid [9], is found to serve in many practical applications, such as porous materials [10,11], and has drawn particular attention for encapsulation in the medical industry in recent years. The addition of nanoparticles or metal oxide is a renowned tactic for modifying the heat transfer, as well as the thermal conductivity, of fluids. Metals are the most valuable nanoparticles due to their greater thermal conductivity correlation than traditional fluids [12]. By suspending a specific kind of nanoparticle in working fluids, a persistent fluid, known as a nanofluid, is created. When it comes to heat transfer, nanofluids usually perform better than more common fluids such as water, oil, and ethylene glycol. Due to their superior heat transmission qualities, nanofluids have attracted a lot of attention. The inherent difficulty of heat transmission is the most well-known concern with heating systems. A better solvent that is less expensive and more widely available is water. As a result, water is frequently utilized in industry for the dispensation of nano-liquids due to its weak thermal conductivity (TCN), which requires perfection if employed as a heat exchanger by dispersion of nanomaterials [13]. Masuda et al. [14] demonstrated that the viscosity and TCN of common fluids can be altered by the addition of nanoparticles. Choi and Eastman [15] explored that the TCN of fluid substantially increases when the nanoparticles are detached in regular fluids. Beg et al. [16] utilized Soret and Dufour impacts to achieve a non-identical solution of buoyancy flow over an inclined surface. They observed that the fluid flow is increased due to the negative inclination of the plate, whilst the reverse trend is observed for the positive inclination. Anbuchezhian et al. [17] investigated the impact of temperature stratification on the flow of a nanofluid across a stretchy sheet when powered by solar radiation. It has been demonstrated that base liquids’ thermal conductivity and convective heat transfer abilities are improved by nanofluids. Nasrin and Alim [18] scrutinized free convective flow and heat transport-incorporated nanofluids in a wavy solar collector. According to Kandasamy et al. [19], solar radiation submerged in a non-Darcy porous medium caused an erratic magnetic flow of a nanofluid across a permeable wedge. They have shown that the copper nanoparticle plays a vital role in absorbing solar radiation. By using solar radiation, Khan et al. [20] calculated the numerical outcomes of a 3D flow via a bi-directional exponentially stretchy surface that was filled with nanofluid. The model for solar energy was created by Shehzad et al. [21] by taking into account a non-Newtonian nanofluid from a stretchy sheet. Zeeshan and Majeed [22] investigated the buoyancy flow in a non-Darcy porous media using a stretchy sheet and magnetic ferroparticles. They concluded that the frictional reluctance of a Lorentz force diminishes with a higher electric field, whereas the opposite behavior is seen for temperature. Madhukesh et al. [23] examined the flow with heat transfer stimulated through water-based AA7072/AA7075 hybrid nanofluids past a stretchable curved surface. The heat transfer is improved due to thermal relaxation and Newtonian heating parameters. The flow of hybrid nanofluid scattered ferrite particles through a contraction/expansion rotating disc was inspected by Gowda et al. [24]. More about the significance of nanofluids can be observed in references [25,26,27]. Recently, Animasaun et al. [28] considered the impact of the magnetic field inspired by three kinds of nanofluids through a heated convective surface with a source/sink. A rise in the wall’s convective heating is a factor that can improve the temperature distribution.
Magnetohydrodynamic (MHD) electrically conducting fluid is widely used in many engineering and industrial processes. Flow meters, MHD power plants, nuclear reactors, stirring, and MHD pumps are a few examples. This is also relevant to how the solar cycle and sunspots grow in terms of solar physics. The idea of the magnetic flow of an electrically conducting liquid from a flexible sheet was first discussed by Pavlov [29]. Many researchers have indeed discussed the electrically conducting fluid transient from a stretchy surface with a magnetic field [30,31,32]. On the other hand, in the rarefied medium, with a low density or a strong magnetic field, the fluid conductivity is anisotropic and the Hall current cannot be ignored. The Hall current plays a vital role in the Hall accelerator problem and flight MHD. Due to the low density of plasma in the magnetosphere and the solar wind, the Hall influence may be significant during the restoration of the magnetic field near the Earth’s magnetopause [33]. Su and Zheng [34] looked at how velocity slip affected the magneto flow of a nanofluid while transporting heat through a stretchy wedge using Joule heating. Zaib and Shafie [35] examined the mutual influences of MHD and Hall current on viscous, dissipative, time-dependent free convective flow via a stretchy sheet. Hall current and radiation absorption were used by Sreedevi et al. [36] to evaluate the magneto free convective flow from a stretchy surface. The magneto flow with heat transport of nanoparticles over a nonlinear stretchable/shrinking sheet was investigated by Pal and Mandal [37] using Hall current (HC). The HC impact on the radiative flow included by nanofluid across a revolving disc was prompted by Khan et al. [38]. In addition to using sensitivity analysis, Rana et al. [39] investigated the importance of Hall current, activation energy, and nanoparticles in enhancing the phenomenon of heat transfer through a nanofluid. A water-based hybrid nanofluid’s quadratic buoyancy convection flow was recently studied by Rana and Gupta [40] using the surface of a rotating cone with Hall current.
Numerous engineering and industrial processes use the thermal radiation impact with convective boundary conditions in die forging, storage of thermal energy, chemical reactions, and nuclear turbines. Aziz [41] inspected the viscous convective flow across a plate under convectively heated conditions. Makinde and Aziz [42] prompted the magnetic impact on buoyancy flow from a vertically heated plate saturated in a porous medium. Ishak [43] used numerical analysis to investigate the flow and heat transfer toward a stretchy, highly permeable, convectively heated sheet. The specific issue of viscous flow through a penetrable, convectively heated, elongating wall was resolved by Yao et al. [44]. Rahman et al. [45] provoked the convective heat transport phenomenon through a vertical plate. Maxwell fluid in a nanofluid was assessed by Mustafa et al. [46] using an exponentially stretchy sheet under convective conditions. Ibrahim and Haq [47] examined the magnetic flow of a nanofluid past a convectively heated stretched sheet as it travelled toward an SP. Recently, Makinde et al. [48] examined the effects of slip and irregular radiation on magneto flow-integrated nanoparticles near an SP toward a connective heated stretchy sheet.
The novelty of this work is to propose the mutual impacts of MHD and Hall current on the mixed convection Williamson flow induced by nanofluid over a heated vertical flat plate with a convective boundary condition and irregular radiation. Nanofluid is basically the combination of water-based and alumina nanoparticles which are also investigated in the current problem. The numerical, transmogrified, nonlinear ODEs are solved using the bvp4c solver. One of the goals of this challenge is to find multiple solutions for the scenario of opposing flow. According to the available information, no one has yet considered this particular problem.
2. Problem Formulation
The magneto-mixed convective Williamson fluid flow via a stagnation point stimulated by nanoparticles via a vertical flat plate with thermal radiation and Hall current effects is considered. The convective boundary condition is also examined. The problem of nanofluid flow is schematically shown in Figure 1, where the positive and coordinates deliberate along and normal to the flat plate in the trend of motion and toward the fluid, respectively, while the axis coordinate is transverse to the plane. There is a significant external magnetic impact in the corresponding direction. Due to the exceedingly low persuasive Reynolds number, the induced magnetic influence is also disregarded. The Hall impact cannot be disregarded because the strength of electron–atom collisions is assumed to be quite strong [49]. The flow becomes three-dimensional as the Hall current becomes stronger in the respective direction, causing a crossflow in that direction. To get around this issue, we presupposed that flow amounts in the direction had not changed. The flat plate must have infinite lengths in that direction for this to be true. It is also believed that the plate is electrically non-conducting and that is applied uniformly across the flow according to the generalized Ohms’ law [50]. The governing equations for controlling the flow, along with Boussinesq approximations, are provided as per these presumptions [35,37].
subject to the boundary conditions are
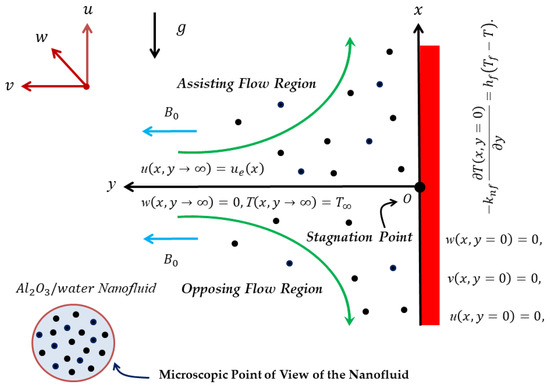
Figure 1.
The geometry of the physical flow problem along with the nanofluid.
Fourier’s law of heat conduction, which is expressed in differential form by Equation (5), asserts that the rate of heat transmission through a medium is inversely proportional to the negative gradient in the temperature per area. Further, in these above equations, are the components of velocity in the , and directions, respectively, is the Hall current parameter, is the time constant, is the viscosity of the nanofluid, is the density of the nanofluid (NF), and signify the temperature and the free-stream temperature, the radiative heat-flux, the coefficient of heat transfer, the nanofluid EC, is the NF thermal conductivity, the gravitational acceleration, and the NF heat capacity. These are demonstrated as [23,24,30,51]:
where signpost the thermal conductivity of the solid nanoparticles and the regular-based fluid (water), respectively. Additionally, signifies the solid nanoparticles volume fraction, which is here the sum of the single nanoparticles and the regular fluid (water). In addition, , designate the coefficient of thermal expansion of the nanoparticles and base fluid respectively, , signpost the electrical conductivity of the solid nanoparticles and the basic fluid, and and signify the density of the nanoparticle and base fluid, respectively. Moreover, the remaining subscripts in the above equations defined as and are called the based fluid and the nanofluid. The thermophysical data of the base fluid (water) and the (Al2O3/water) nanofluid are written in Table 1.

Table 1.
The thermophysical features of the base fluid and nanoparticles [52].
The radiative heat-flux is articulated as [26]:
where and indicate the absorption coefficient and the Stefan–Boltzmann constant, respectively. Utilizing Equation (12), Equation (4) can be written as
To ease the analysis of the given nanofluid problem, the following self-similarity variables are introduced [35,39]:
where presents the stream function and it is distinguished as and .
With the aid of Equation (14), the nonlinear Equations (2), (3), and (13) yield the following nonlinear ODEs:
and the transformed subjected boundary conditions are:
where denote differentiation with respect to the pseudo-similarity variable In addition, the aforementioned similarity equations comprised different influential controlling parameters which are symbolically and namely written as follows: and imply the magnetic parameter, the mixed convective parameter (which is the ratio of the Grash of number and the square of the local Reynolds number), the Prandtl number, the radiation parameter, the Weissenberg parameter, and the convective parameter, respectively.
The important physical quantities of interest are the skin frictions in axial and transverse directions and the local Nusselt Number, which is stated as [35]
where and are the shear stresses for the Williamson nanofluid flow in the axial and transverse directions, respectively. Meanwhile, is the heat flux, which is stated as:
Using (14), we get
where is called the local Reynolds number.
3. Results and Discussion
This section illustrates the analysis of the solutions both graphically and in the form of several numerical tables for the branches of unstable and stable solution. Thus, to understand the behavior of the dual results for a limiting case, we first discuss in detail the numerical scheme, as well as the code reliability and validations for the phenomenon of available results. The distorted system of nonlinear Equations (15)–(17) and (18) were eased numerically via an efficient bvp4c solver for dissimilar values of pertaining parameters that were apprehensive in the ensuing given the (Al2O3/water) nanofluid flow problem. According to Oztop and Abu-Nada [53], the value of the Prandtl number Pr = 6.2 is taken into account throughout the investigation and the volume fraction of nanoparticles ranges from 0 to 0.2, which correlates to the base fluid.
Table 2 depicts the assessment of the friction factor and heat transfer for the varied values with the available reported work (Ishak et al. [54]) for the limiting cases when , , , , , , , and . The results show that the upper branch’s current fallouts are in good arrangement with the published research of Ishak et al. [54]. Moreover, Table 3 is also constructed to compare the heat transfer numerical upper branch solution values with the published work of Grubka and Bobba [55], Ali [56], and Yih [57] for the several values of Pr when , , , , , , , and . We can be confident that the supplied code is adequately developed to identify the unknown results of the given problem because the solutions are in exceptional alignment in both tables.

Table 2.
Comparison of and for various values of .

Table 3.
Comparison of for various values of Pr.
To observe the impressions of different prominent constraints on the shear stress in the axial and transverse directions, the heat transfer and the streamline profiles of the alumina (Al2O3/water) nanoparticles for the unstable and stable branches of outcome are graphically presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14, and also in Table 4, Table 5 and Table 6, respectively. The given problem simulations were performed by varying one parameter at a time and fixing the rest of the comprised parameters. The default values of the fixed embraced parameters are the following: , , , , , and . In the whole study, the stable and unstable solutions are signified by the solid blue and dashed lines, respectively. Meanwhile, the small, solid black, red, pink, and blue balls symbolize the critical or bifurcation point, where the two solutions converge to one location.
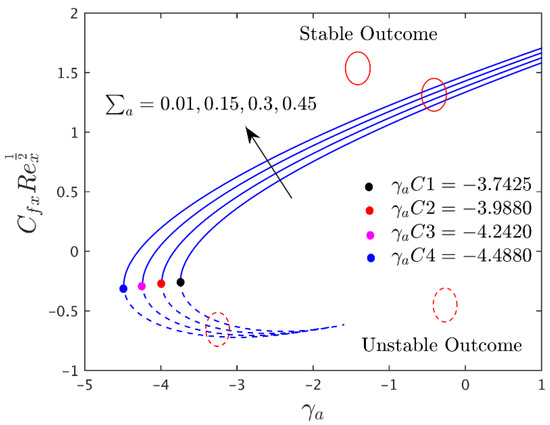
Figure 2.
Influence of on axial shear stress.
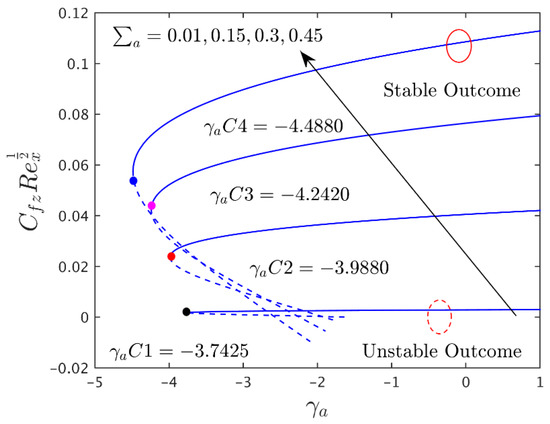
Figure 3.
Influence of on transverse shear stress.
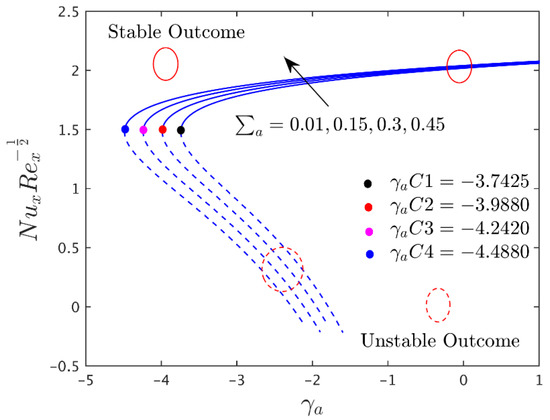
Figure 4.
Influence of on heat transfer.
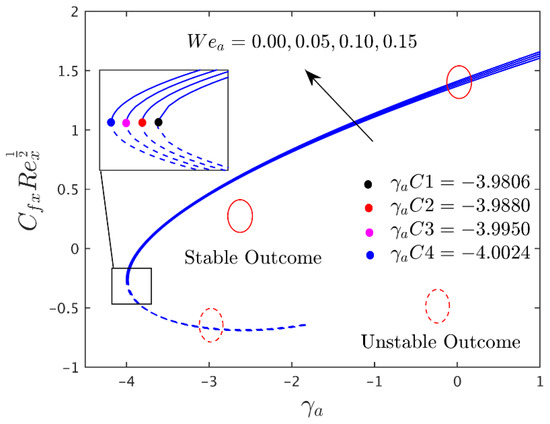
Figure 5.
Influence of on axial shear stress.
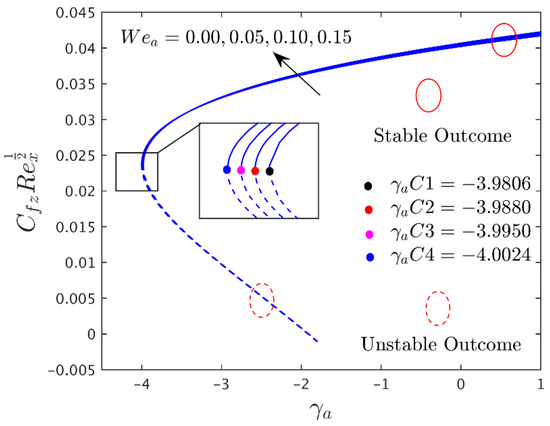
Figure 6.
Influence of on transverse shear stress.
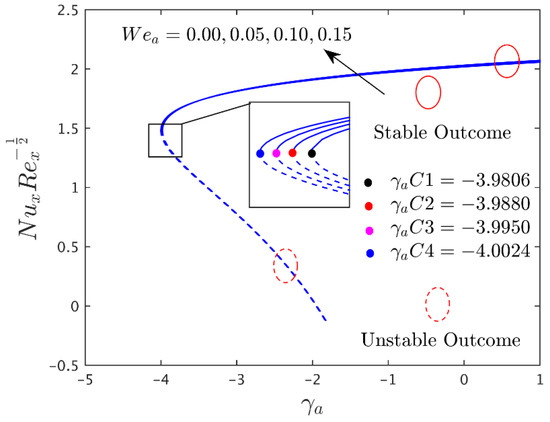
Figure 7.
Influence of on heat transfer.
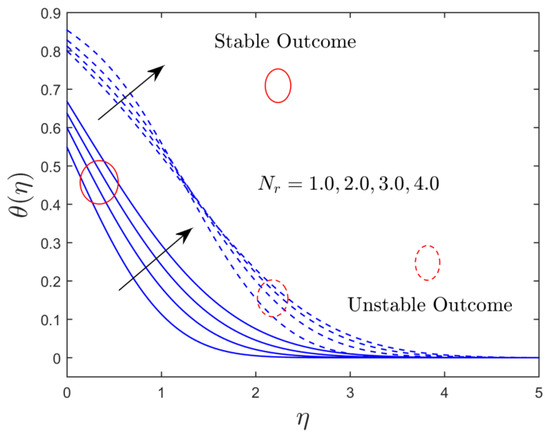
Figure 8.
Influence of on temperature.
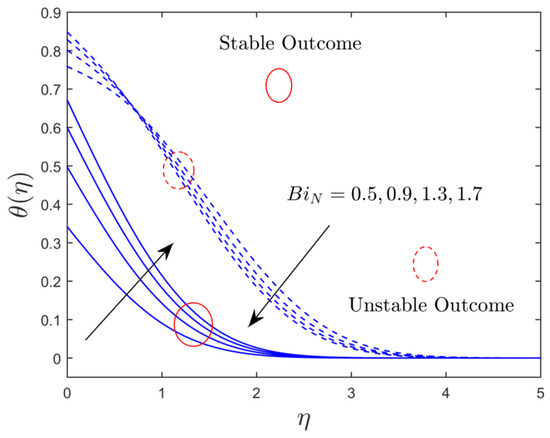
Figure 9.
Influence of on temperature.
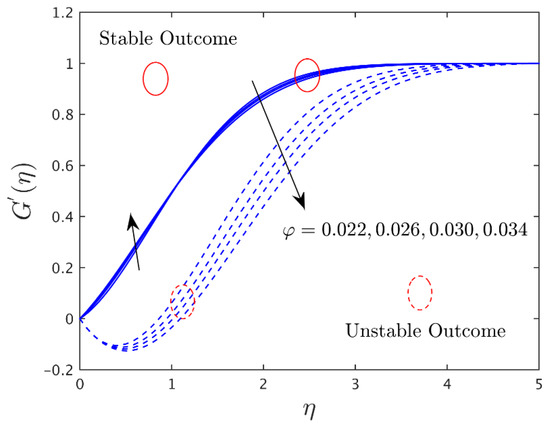
Figure 10.
Influence of on the axial velocity profile.
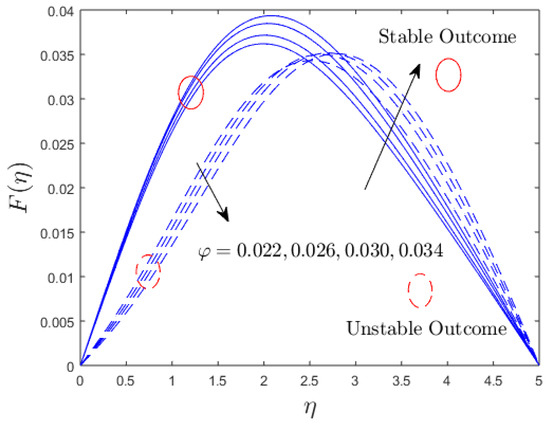
Figure 11.
Influence of on the transverse velocity profile.
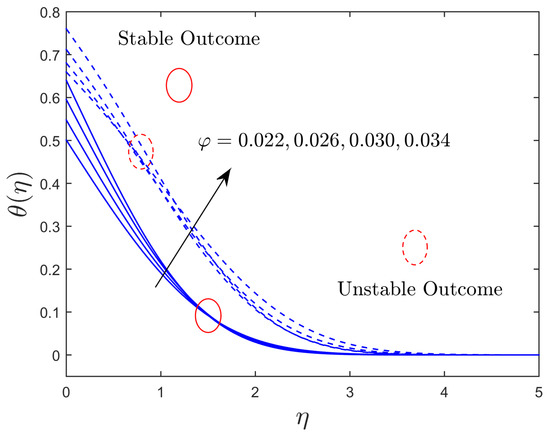
Figure 12.
Influence of on the temperature profile.
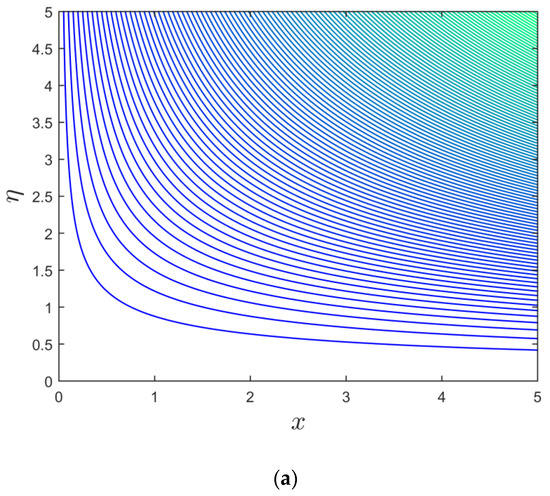
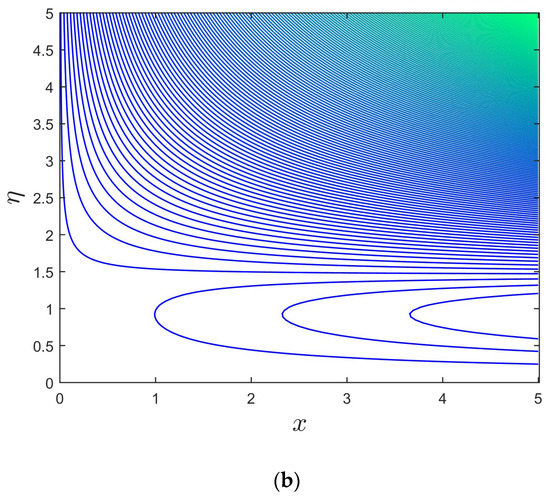
Figure 13.
(a,b): Streamline profile for the branch of upper and lower solutions when .
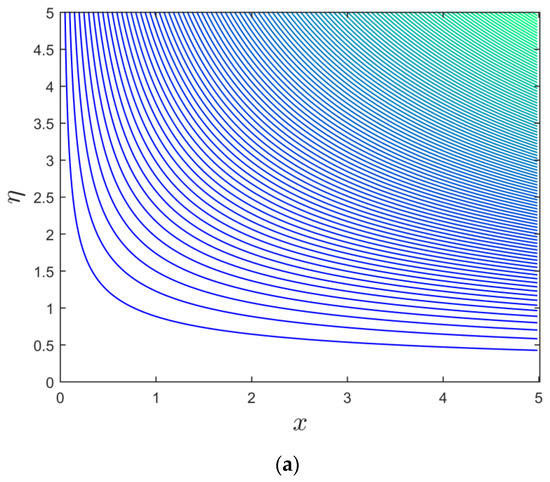
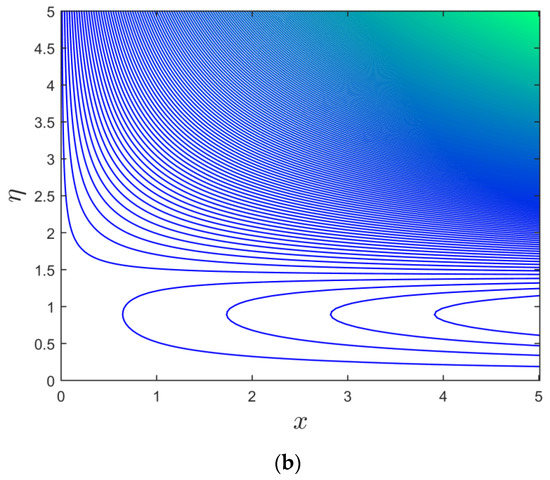
Figure 14.
(a,b): Streamline profile for the branch of upper and lower solutions when .

Table 4.
Numerical values of the skin friction coefficient along the axis direction for the several values of , , and when , , and .

Table 5.
Numerical values of the skin friction coefficient along the axis direction for the several values of , , and when , , and .

Table 6.
Numerical values of the heat transfer for the numerous values of , and when , , , .
Table 4 and Table 5 display the quantitative outcome of the shear stress in both the axial and transverse axes directions for the stable and unstable solutions, with variations in the solid nanoparticle volume fractions , the magnetic parameter , the Weissenberg parameter , and the Hall parameter . Since the output of the products signifies that the shear stress in both directions (axial and transverse) escalates for the branch of stable outcomes, with sophisticated values of and , the impact of the same constraints can reverse the alumina nanomaterials flow for the unstable branch solutions. However, the shear stress augments and declines in the corresponding transverse and axial directions with higher influences of the Hall parameter. Physically, the useful conductivity decreases due to the Hall parameter, which lessens the magnetic damping force on transverse and axial velocities. Consequently, the shear stress increases in the transverse direction. Conversely, the heat transfer values for the stable and unstable solution branches are quantitatively bounded in Table 6. Here, the heat transfer behaves magnificently for the stable branch solution, compared quantitatively to the unstable solution branch, with superior impacts of and . The Nusselt number is quantitatively augmented in both distinct solutions as we increase the implementation of the convective parameter. In addition, the heat transfer coefficient is directly proportional to the dimensionless convective parameter. According to basic physics, if we increase the values of the convective parameter, as a result, the heat transfer also increases; therefore, the Nusselt number is significantly boosted for both branches of the solution.
Figure 2, Figure 3 and Figure 4 illustrate the disparity of the magnetic parameter () versus buoyancy parameter on axial shear stress, transverse shear stress, and rate of heat transfer of the alumina (Al2O3/water) nanoparticles, respectively. Figure 2 and Figure 3 display that the axial and transverse shear stresses upsurge with increasing for the branch of stable solutions. For the branch of unstable solutions, however, the behavior of the results is the same in the directions of transverse shear stress and inverted in the axial shear stress. Physically, there is a drag-type force known as a Lorentz force that tends to impede the velocity of the flow, and, consequently, the thicknesses of the velocity boundary layer become depressed. Consequently, the velocity profiles behave inversely to the coefficient of shear stresses. Hence, the shear stress escalates due to the larger consequences of . As illustrated in Figure 4, the heat transmission decreases with for the branch of stable solutions, but it increases with for the branch of unstable solutions. Since there is a large resistance to the motion of fluid due to the Lorentz force, which in turn produces the heat, as an artefact, the thickness or width of the thermal boundary layer, as well as the Nusselt number profiles, increases. Further, the temperature of fluid disappears from the flat plate at some large distance. This is not surprising, since there is a magnetic field that exerts retarding force on the free convection flow. Several physical properties of such fluids can be adjusted by varying the magnetic field. The obtained solutions undoubtedly demonstrate that the flow and the characteristics of heat transfer can be controlled using the magnetic field. Moreover, the changing critical values are obtained for each selected default values of (see Figure 2, Figure 3 and Figure 4). With growing values of , the critical or bifurcation value elevates magnitude-wise. As a result, this pattern suggests that the flow separation decreases as the magnetic parameter’s effects increase. Moreover, for negative values of , there exists a critical value , with dual solutions for : a saddle node bifurcation at , and no outcome for . The separation of the boundary layer occurs at ; therefore, it is not possible to obtain the solution beyond this amount.
Figure 5, Figure 6 and Figure 7 demonstrate the impact of the Williamson parameter on the shear stresses and heat transfer rate for both branch solutions. These solutions describe that the shear stresses in both directions augment, along with the heat transfer, in both branch solutions. Furthermore, the critical values indicate that the Willaimson parameter delays the separation of boundary layers. In addition, it can be seen from these portraits that the heat transfer values are positive, suggesting that heat is transferring from a heated plate to a cool liquid.
The thermal radiation and convective parameter influences on the temperature distribution for both solution branches are illustrated in Figure 8 and Figure 9, respectively. Figure 8 discloses that the temperature distribution uplifts with growing values of in both solutions. This is because higher impressions of radiation indicate the supremacy of conduction and improve the thermal conductivity of the alumina nanoparticles, resulting in a rise in the thickness of the TBL, as well as an increase in the profile of temperature. Figure 9 discloses that the augmentation in the amount of comes with the stronger convective-type heating at the wall surface of the plate, which increases the temperature slope at the flat plate for the upper branch, and a slight transformation behavior is seen for the branch of the unstable solution. The thermal efficiency can now dive deeper into the static fluid. As a result, as increases, so does the temperature and thickness of the TBL. It is worth noting that, by using reasonably large influences of the convective restriction, the uniform wall temperature can be recovered. Furthermore, pertains to the insulated sheet case.
Figure 10, Figure 11 and Figure 12 display the impression of the solid nanoparticle volume fraction on the axial and transverse velocity profiles and the dimensionless temperature distribution profiles for the stable and unstable solution branches, respectively. Outcomes indicate that the axial velocity portrays an intensifying tendency for the upper branch solutions initially and then starts to decline continuously for both branches due to the augmentation in the values of the solid nanoparticle volume fraction. On the other hand, the transverse velocity profile curves are amplified for the branch of upper solutions due to the larger impacts of the nanoparticle volume fraction, while it is reduced for the branch of lower solutions owing to the superior impact of nanoparticles. In addition, the temperature profiles enlarged for both solution branches, with larger impacts of the solid nanoparticles’ volume fraction. Physically, it is worth mentioning that, due to the increasing impacts of the nanoparticles’ volume fraction, the thermal conductivity rises as a result, which produces a high improvement in the thermal boundary layer, as well as the temperature profiles.
4. Conclusions
This enquiry has looked at the cumulative effects of MHD and Hall current on the flow of a Williamson fluid incorporated by nanofluid through a vertical flat plate that has been convectively heated while being exposed to thermal radiation. The converted system of ODEs has been numerically solved using the bvp4c solver for various values of the pertinent parameters. From this study, the following findings can be made:
- For the stable branch solutions, the magnetic parameter causes an increase in the axial shear stress and the rate of heat transfer, while it has an entirely different effect on the branch of unstable solutions.
- Due to the higher values of the magnetic parameter, the transverse shear stress increases for upper and lower branches.
- Due to the bigger values of the magnetic parameter, the magnitude of the bifurcation values was increased.
- The radiation parameter is more significantly impacted by the escalating temperature distribution in both solution branches.
- Due to the greater Hall parameter, the axial shear stress falls, while the transverse shear stress increases.
- The heat transfer rate is increased by the nanoparticles for stable branch solutions, while it is decreased for unstable branch solutions.
- The Williamson constraint augments the shear stresses, as well as the heat transfer.
Author Contributions
Conceptualization, U.K. and A.Z.; methodology, U.K., A.Z. and I.W.; software, U.K.; validation, A.J., E.-S.M.S., U.K., A.I. and I.W.; formal analysis, A.J., E.-S.M.S. and A.I.; investigation, U.K.; resources, A.I. and I.P.; data curation, U.K.; writing—original draft preparation, N.B., A.Z. and A.I.; writing—review and editing, N.B., A.J., I.P., E.-S.M.S. and A.I.; visualization, E.-S.M.S. and U.K.; supervision, A.I. and I.P.; project administration, N.B. and A.J.; funding acquisition, A.J. and N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Researchers Supporting Project Number (RSP-2021/33), King Saud University, Riyadh, Saudi Arabia.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Did not report any data.
Acknowledgments
This research was supported by Researchers Supporting Project Number (RSP-2021/33), King Saud University, Riyadh, Saudi Arabia. In addition, this research received support from Rajamangala University of Technology Suvarnabhumi and Phuket Rajabhat University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Williamson, R.V. The flow of pseudoplastic materials. Ind. Eng. Chem. 1929, 21, 1108–1111. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, S.T.; Lee, C. Flow of a Williamson fluid over a stretching sheet. Braz. J. Chem. Eng. 2013, 30, 619–625. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A. Hydromagnetic boundary layer flow of Williamson fluid in the presence of thermal radiation and Ohmic dissipation. Alex. Eng. J. 2016, 55, 2229–2240. [Google Scholar] [CrossRef]
- Shawky, H.M.; Eldabe, N.T.; Kamel, K.A.; Abd-Aziz, E.A. MHD flow with heat and mass transfer of Williamson nanofluid over stretching sheet through porous medium. Microsyst. Technol. 2018, 25, 1155–1169. [Google Scholar] [CrossRef]
- Kho, Y.B.; Hussanan, A.; Mohamed, M.K.A.; Salleh, M.Z. Heat and mass transfer analysis on flow of Williamson nanofluid with thermal and velocity slips: Buongiorno model. Propuls. Power Res. 2019, 8, 243–252. [Google Scholar] [CrossRef]
- Qureshi, M.A. Numerical simulation of heat transfer flow subject to MHD of Williamson nanofluid with thermal radiation. Symmetry 2020, 13, 10. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Cattaneo-Christov Double diffusion (CCDD) and magnetized stagnation point flow of non-Newtonian fluid with internal resistance of particles. Phys. Scr. 2020, 95, 125002. [Google Scholar] [CrossRef]
- Chandel, S.; Sood, S. Unsteady flow of Williamson fluid under the impact of prescribed surface temperature (PST) and prescribed heat flux (PHF) heating conditions over a stretching surface in a porous enclosure. Z. Angew. Math. Mech. 2022, 102, e202100128. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Ekiciler, R. Effects of novel hybrid nanofluid (TiO2–Cu/EG) and geometrical parameters of triangular rib mounted in a duct on heat transfer and flow characteristics. J. Therm. Anal. Calorim. 2021, 143, 1371–1387. [Google Scholar] [CrossRef]
- Sundar, L.S.; Ramana, E.V.; Said, Z.; Pereira, A.M.B.; Sousa, A.C.M. Heat transfer of rGO/Co3O4 hybrid nanomaterials-based nanofluids and twisted tape configuration in a tube. J. Therm. Sci. Eng. Appl. 2021, 13, 031004. [Google Scholar] [CrossRef]
- Masuda, H.; Ebata, A.; Teramae, K.; Hishinuma, N. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Netsu Bussei 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In ASME International Mechanical Engineering Congress & Exposition, San Francisco, CA, USA, 12–17 November 1995; Argonne National Lab: Argonne, IL, USA, 1995. [Google Scholar]
- Bég, O.A.; Bakier, A.Y.; Prasad, V.R. Numerical modelling of non-similar mixed convection heat and species transfer along an inclined solar energy collector surface with cross diffusion effects. World J. Mech. 2011, 4, 185–196. [Google Scholar] [CrossRef]
- Anbuchezhian, N.; Srinivasan, K.; Chandrasekaran, K.; Kandasamy, R. Thermophoresis and Brownian motion effects on boundary layer flow of nanofluid in presence of thermal stratification due to solar energy. Appl. Math. Mech. English Ed. 2012, 33, 765–780. [Google Scholar] [CrossRef]
- Nasrin, R.; Alim, M.A. Performance of nanofluids on heat transfer in a wavy solar collector. Int. J. Eng. Sci. Technol. 2013, 5, 58–77. [Google Scholar] [CrossRef][Green Version]
- Kandasamy, R.; Muhaimin, I.; Rosmila, A.K. The performance evaluation of unsteady MHD non-Darcy nanofluid flow over a porous wedge due to renewable (solar) energy. Renew. Energy 2014, 64, 1–9. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Alsaedi, A. Numerical study of Cattaneo-Christov heat flux model for viscoelastic flow due to an exponentially stretching surface. PLoS ONE 2015, 10, e0137363. [Google Scholar]
- Shehzad, S.A.; Hayat, T.; Alsaedi, A.; Chen, B. A useful model for solar radiation. Energy Ecol. Environ. 2016, 1, 30–38. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A. Non Darcy mixed convection flow of magnetic fluid over a permeable stretching sheet with ohmic dissipation. J. Magn. 2016, 21, 153–158. [Google Scholar] [CrossRef]
- Madhukesh, J.K.; Kumar, R.N.; Punith Gowda, R.J.; Prasannakumara, B.C.; Ramesh, G.K.; Khan, M.I.; Khan, S.U.; Chu, Y.-M. Numerical simulation of AA7072-AA7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: A non-Fourier heat flux model approach. J. Mol. Liq. 2021, 335, 116103. [Google Scholar] [CrossRef]
- Gowda, R.J.P.; Kumar, R.N.; Aldalbahi, A.; Prasannakumara, B.C.; Rahimi-Gorji, M.; Rahaman, M. Thermophoretic particle deposition in time-dependent flow of hybrid nanofluid over rotating and vertically upward/downward moving disk. J. Mol. Liq. 2021, 22, 100864. [Google Scholar]
- Hamid, M.; Usman, M.; Haq, R.U.; Tian, Z. A Galerkin approach to analyze MHD flow of nanofluid along converging/diverging channels. Arch. Appl. Mech. 2021, 91, 1907–1924. [Google Scholar] [CrossRef]
- Waqas, H.; Yasmin, S.; Muhammad, T.; Imran, M. Flow and heat transfer of nanofluid over a permeable cylinder with nonlinear thermal radiation. J. Mater. Res. Technol. 2021, 14, 2579–2585. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Ishak, A.; Raizah, Z.; Galal, A.M. Analytical approach for a heat transfer process through nanofluid over an irregular porous radially moving sheet by employing KKL correlation with magnetic and radiation effects: Applications to thermal system. Micromachines 2022, 13, 1109. [Google Scholar] [CrossRef]
- Animasaun, I.L.; Yook, S.-J.; Muhammad, T.; Mathew, A. Dynamics of ternary-hybrid nanofluid subject to magnetic flux density and heat source or sink on a convectively heated surface. Surf. Interfaces 2022, 28, 101654. [Google Scholar] [CrossRef]
- Pavlov, K.B. Magnetohydrodynamic flow of an incompressible viscous fluid caused by deformation of a plane surface. Magnetohydrodynamics 1974, 10, 507–510. [Google Scholar]
- Salem, A.M.; El-Aziz, M.A. MHD-mixed convection and mass transfer from a vertical stretching sheet with diffusion of chemically reactive species and space- or temperature-dependent heat source. Can. J. Phys. 2007, 85, 359–373. [Google Scholar]
- Akbar, N.S.; Ebai, A.; Khan, Z.H. Numerical analysis of magnetic field effects on Eyring Powell fluid flow towards a stretching sheet. J. Magn. Magn. Mater. 2015, 382, 355–358. [Google Scholar] [CrossRef]
- Khan, M.; Hussain, M.; Azam, M.; Hashim. Magnetohydrodynamic flow of Carreau fluid over a convectively heated surface in the presence of non-linear radiation. J. Magn. Magn. Mater. 2016, 412, 63–68. [Google Scholar] [CrossRef]
- Moralesa, L.F.; Dasso, S.; Gomez, D.O.; Mininni, P. Hall effect on magnetic reconnection at the Earth's magnetopause. J. Atmosp. Solar-Terr. Phys. 2005, 67, 1821–1826. [Google Scholar] [CrossRef]
- Su, X.; Zheng, L. Hall effect on MHD flow and heat transfer of nanofluids over a stretching wedge in the presence of velocity slip and Joule heating. Central Euro. J. Phys. 2013, 11, 1694–1703. [Google Scholar] [CrossRef]
- Zaib, A.; Shafie, S. Thermal diffusion and diffusion thermo effects on unsteady MHD free convection flow over a stretching surface considering Joule heating and viscous dissipation with thermal stratification, chemical reaction and hall current. J. Frank. Inst. 2014, 351, 1268–1287. [Google Scholar] [CrossRef]
- Sreedevi, G.; Rao, R.R.; Prasada Rao, D.R.V.; Chamkha, A.J. Combined influence of radiation absorption and Hall current effects on MHD double-diffusive free convective flow past a stretching sheet. Ain Shams Eng. J. 2016, 7, 383–397. [Google Scholar] [CrossRef]
- Pal, D.; Mandal, G. Influence of Lorentz force and thermal radiation on heat transfer of nanofluids over a stretching sheet with velocity–thermal slip. Int. J. Appl. Comput. Math. 2017, 3, 3001–3020. [Google Scholar] [CrossRef]
- Khan, M.; Ali, W.; Ahmed, J. A hybrid approach to study the influence of Hall current in radiative nanofluid flow over a rotating disk. Appl. Nanosci. 2017, 10, 5167–5177. [Google Scholar] [CrossRef]
- Rana, P.; Mahanthesh, B.; Thriveni, K.; Muhammad, T. Significance of aggregation of nanoparticles, activation energy, and Hall current to enhance the heat transfer phenomena in a nanofluid: A sensitivity analysis. Waves Rand. Complex Media 2022, 1–23. [Google Scholar] [CrossRef]
- Rana, P.; Gupta, G. FEM solution to quadratic convective and radiative flow of Ag-MgO/H2O hybrid nanofluid over a rotating cone with Hall current: Optimization using response surface methodology. Math. Comp. Simul. 2022, 201, 121–140. [Google Scholar] [CrossRef]
- Aziz, A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1064–1068. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Thermal Sci. 2010, 49, 1813–1820. [Google Scholar] [CrossRef]
- Ishak, A. Similarity solutions for flow and heat transfer over a permeable surface with a convective boundary condition. Appl. Math. Comp. 2010, 217, 837–842. [Google Scholar] [CrossRef]
- Yao, S.; Fang, T.; Zhong, Y. Heat transfer of a generalized stretching/shrinking wall problem with convective boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 752–760. [Google Scholar] [CrossRef]
- Rahman, M.M.; Merkin, J.H.; Pop, I. Mixed convection boundary-layer flow past a vertical flat plate with a convective boundary condition. Acta Mech. 2015, 226, 2441–2460. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. Simulations for Maxwell fluid flow past a convectively heated exponentially stretching sheet with nanoparticles. AIP Adv. 2015, 5, 037133. [Google Scholar] [CrossRef]
- Ibrahim, W.; Haq, R.U. Magnetohydrodynamic (MHD) stagnation point flow of nanofluid past a stretching sheet with convective boundary condition. J. Braz. Soc. Mech. Sci. Eng. 2015, 38, 1155–1164. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Stagnation point flow of MHD chemically reacting nanofluid over a stretching convective surface with slip and radiative heat. Proc. Inst. Mech E Part E J. Process Mech. Eng. 2017, 231, 695–703. [Google Scholar] [CrossRef]
- Abo-Eldahab, E.M.; El Aziz, M.A. Hall and Ion-Slip effects on MHD free convective heat generating flow past a semi-infinite vertical flat plate. Phys. Scr. A 2000, 61, 344. [Google Scholar] [CrossRef]
- Sutton, G.W.; Sherman, A. Engineering Magnetohydrodynamics; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 2014, 147059. [Google Scholar] [CrossRef]
- Arifuzzaman, M.; Uddin, M.J. Convective flow of alumina–water nanofluid in a square vessel in presence of the exothermic chemical reaction and hydromagnetic field. Res. Eng. 2021, 10, 100226. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat Mass Transf. 2008, 44, 921. [Google Scholar] [CrossRef]
- Grubka, L.J.; Bobba, K.M. Heat transfer characteristics of a continuous, stretching surface with variable temperature. ASME J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Ali, M.E. On thermal boundary layer on a power-law stretched surface with suction or injection. Int. J. Heat Fluid Flow 1995, 16, 280–290. [Google Scholar] [CrossRef]
- Yih, K.A. Free convection effect on MHD coupled heat and mass transfer of a moving permeable vertical surface. Int. Commun. Heat Mass Transf. 1999, 26, 95–104. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).