Design and Performance Analysis of Dual Membrane Restrictor for Hydrostatic Bearing

Abstract

In this paper, a dual membrane restrictor design was proposed to improve the stiffness performance of the compensated hydrostatic bearing. Theoretical models for the proposed dual membrane restrictors were derived. Analysis of these models showed that a high stiffness region could be achieved at the desired loading region through the proper selection of the design parameters. A series of simulations were conducted to study the variations in the design parameters on the stiffness and clearance variations. It was found that the dimensionless membrane stiffness in the inlet restrictor, $K_{mi}^{*}$, was the most dominant parameter for the performance of the compensated bearing system. The main advantages of the proposed dual membrane restrictor are the increase in flexibility by providing high stiffness at the desired loading region; and improving the stiffness performance of the bearing system especially at the desired loading region.

1. Introduction

Compared with typical rolling element bearings, hydrostatic bearings have several advantages such as low straightness ripple, good damping characteristics, low friction, and low wear. With these advantages, hydrostatic bearings were frequently used in high-precision grinding machines to produce high quality components. In the hydrostatic bearing, lubricant pressured by a pumping system was forced into the recess and flowed through the paired surfaces such that the conjugated pair surface could be separated. There are two types of pumping system frequently used in this application, namely, constant pressure type and constant flow type. A constant flow pump was needed for each recess in the constant flow type system, while a constant pressure pump may be used for several recesses in the constant pressure system. This is the reason why the constant pressure-type system is a much more popular one.

For the constant pressure system, restrictors are used to regulate the pressures of the recesses. Related research has been conducted to study and to optimize the performance of hydrostatic system. In general, a hydrostatic bearing with high stiffness is desired, such that the variation of the deflection due to load variation is limited. There are approaches to increase the stiffness of the system such as reducing the nominal bearing clearance, using the opposed-pad design, etc. [1]. Morsi [2] found that with the use of a membrane-type restrictor, the stiffness of the compensated bearing can be improved. Similar conclusions were confirmed by DeGast [3], Cusano [4] and Gohara et al. [5].

Kotilainen [6] indicated that the flow in the membrane-type restrictor is controlled by the deflections of a diaphragm caused by the feedback bearing pressure instead of a spool valve used in many other variable restrictors. A change in the bearing load results in a change in the bearing pressure and a displacement of the diaphragm, thus changing the clearance of the restricted plant and, accordingly, its flow resistance.

Singh [7] and Phalle [8] showed that the static characteristics of multirecess hybrid journal bearings using membrane-type restrictors were affected by the shapes of the recess and bearing. Kang [9,10,11] proposed ways to identify the design parameters of membrane-type restrictors of hydrostatic bearings and proposed a modified prediction model for a membrane restrictor. Bassani [12], Chang [13] and Pan [14] also worked on the parameter design and performance analysis off membrane-type restrictor. Chen et al. [15] performed a fluid–structure interaction analysis of the diaphragm to more acurrately model the behavior of membrane restrictors.

In previous studies [16,17], it was shown that a high-static stiffness bearing system could be achieved if membrane restrictors were properly designed. The dimensionless stiffness of the membrane $K_r^{*}$ and the design restriction ratio $\lambda$ are the two key parameters for membrane-restrictor design. When $K_r^{*}=4/3, \lambda =0.25$, one can theoretically obtain infinite bearing stiffness under some specific loading conditions (i.e., $\mathrm{W}/(A_e{p}_s)=1/3$). It was found theoretically that high bearing stiffness could be achieved within some loading regions (i.e., $\mathrm{W}/(A_e{p}_s)=0.2-0.5$). However, it was also found that the system performance was very sensitive to the change of $K_r^{*}$, and the clearance and clearance variation of the bearing was relatively high and such that the stiffness of the bearing was very low when a small load was applied.

A chance for further improvement of the single membrane restrictor design is to add an outlet restrictor between the recess and tank. The outlet restrictor is opened to leak lubricant to the tank to reduce clearance as well as clearance variation in terms of increasing bearing stiffness when the loading is small and closed when the loading is large.

In this paper, the design of the proposed dual membrane restrictor and the model of the bearing system compensated with the proposed dual membrane restrictor was derived first. The analysis for the design parameters to show ways for designing the proposed dual membrane restrictor were then conducted. A series of simulations were conducted to study how variations in the design parameters might affect the performance of the bearing compensated by the proposed dual membrane restrictor. Finally, conclusions are drawn based on the observations of these simulation results.

2. Modelling of the Proposed Dual Membrane Restrictor

The bearing system with a single membrane restrictor and those with the proposed dual membrane restrictor are depicted in Figure 1. The flow resistance of the restrictor was varied due to the deflections of the membrane caused by the pressure difference between the upper surface of the membrane and the lower surface of the membrane. The restricting plane is the inner surface of the protruding portion surrounding the outlet of the restrictor, where the inner radius of the restricting plane is $r_1$ and the outer radius of the restricting plane is $r_2$ as shown in Figure 1a.

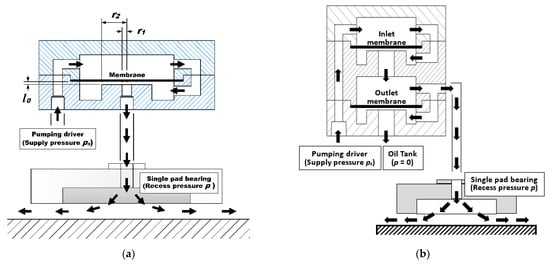
Figure 1. (a) Bearing compensated with single membrane restrictor. (b) Bearing compensated with proposed dual membrane restrictor. Sketch plots for bearing systems with single membrane restrictor and the proposed dual membrane restrictor.

Some major differences between these two restrictors should be noted. For the dual membrane restrictor, the supplied lubricant is regulated by an inlet membrane first then flows into the bearing recess; at the same time, the recess pressure is also regulated by an outlet membrane which controls the drainage bypassing a partial lubricant to the tank. Therefore, the proposed system has two outlets: one is to the recess of the bearing, another one is going through the outlet membrane then directly draining to the tank.

With the proposed dual restrictor, the lubricant flow rate, $q$, is determined by the supply pressure, $p_s$, the flow resistance of the inlet membrane restrictor (i.e., the flow resistance of the inlet restricting plane), $R_{mi}$, the flow resistance of the outlet membrane restrictor (i.e., the flow resistance of the outlet restricting plane), $R_{mo}$, and the flow resistance of the pad, $R$. The flow rate to the bearing through the inlet membrane restrictor is equivalent to the sum of that flow out of the recess and that flow through the outlet membrane restrictor to the tank, and the following equation could be derived:

$$q=\frac{p_s-p}{R_{mi}}=\frac{p}{R}+\frac{p}{R_{mo}} \mathrm{and} \frac{p_s-p}{R_{mi}}>\frac{p}{R_{mo}},$$

(1)

where $p$ is the recess pressure. The recess’ pressure can also be expressed as

$$p=\frac{R R_{mo}}{R R_{mo}+R R_{mi}+R_{mi}{R}_{mo}}{p}_s \mathrm{with} \frac{p_s-p}{R_{mi}}>\frac{p}{R_{mo}}.$$

(2)

For simplicity, α is defined as the resistance ratio of bearing pad, R/R_r; α_i is defined as inlet membrane resistance ratio, R_mi/R_r; and α_o is defined as outlet membrane resistance ratio, R_mo/R_r outlet membrane resistance ratio $R_{mo}/R_r$, respectively, where R_r is a constant reference for the flow resistance of the bearing R with a corresponding clearance of h_r (the subscript “r” refers to the reference configuration). Then Equation (2) can also be expressed in a dimensionless form as the following.

$$\beta =\frac{p}{p_s}=\frac{ \alpha {\alpha }_{mo}}{\alpha {\alpha }_{mo}+\alpha {\alpha }_{mi}+{\alpha }_{mi}{\alpha }_{mo}} \mathrm{and} \frac{\left(1-\beta \right)}{\beta }>\frac{{\alpha }_{mi}}{{\alpha }_{mo}}.$$

(3)

Based on the cubic law of the flow resistance [12], the flow resistances of the membrane restrictor, R_m, can be expressed as

$$R_m=\frac{\eta }{{\left(l_0-x\right)}^3}\frac{6}{\pi }ln\frac{r_2}{r_1}=\frac{R_{ma}}{{\left(1-\xi \right)}^3},$$

(4)

where $\eta$ is dynamic viscosity of lubricant; as depicted in Figure 1, l_o is the assembly clearance between membrane and the restricting plane; x is the membrane deformation; $r_1$ and $r_2$ are the inner and outer radius of the restricting plane in the restrictor; R_ma are the restrictor flow resistance when there is no membrane deflection; and $\xi =x/l_0$ is the membrane deformation ratio.

From Equations (3) and (4), the dimensionless deformation–pressure relationship can be derived as:

$$\begin{array}{c}\beta =\frac{\alpha {\alpha }_{moa} {\left(1-{\xi }_o\right)}^{-3}}{\alpha {\alpha }_{moa} {\left(1-{\xi }_o\right)}^{-3}+\alpha {\alpha }_{mia} {\left(1-{\xi }_i\right)}^{-3}+{\alpha }_{mia}{\alpha }_{moa} {\left(1-{\xi }_i\right)}^{-3} {\left(1-{\xi }_o\right)}^{-3}}\\ \mathrm{with} {\alpha }_{moa} {\left(1-{\xi }_i\right)}^{-3}\frac{\left(1-\beta \right)}{\beta }>{\alpha }_{mia} {\left(1-{\xi }_o\right)}^{-3}\end{array}$$

(5)

where the corresponding flow resistance ratio for inlet membrane restrictor ${\alpha }_{mia}=R_{mia}/R_r=R_{mi}{\left(1-{\xi }_i\right)}^3/R_r$ and that for outlet membrane restrictor ${\alpha }_{moa}=R_{moa}/R_r=R_{mo}{\left(1-{\xi }_o\right)}^3/R_r$; R_mia and R_moa are R_ma values for the inlet and outlet membrane restrictor; ξ_i and ξ_o are the membrane deformation ratios in the inlet and outlet membrane restrictors, respectively.

The stiffness of the inlet membrane, K_m, can be described as

$$K_m=\frac{d}{dx}{A}_m\left(p_s-p\right)=-\frac{A_m}{l_0}\frac{d}{d\xi }p.$$

(6)

In previous studies [16,17], the dimensionless stiffness of the membrane, $K_m^{*}$, is defined as

$$K_m^{*}=\frac{K_m{l}_0}{A_m{p}_s},$$

(7)

where A_m is the effective area of the restricting plane in the membrane restrictor [12]:

$$A_m=\frac{1}{2}\pi r_2^2\frac{1-{\left(r_1/r_2\right)}^2}{\ln \left(r_2/r_1\right)}.$$

(8)

The pressure ratio, $\beta$, is mainly determined by the load applied, effective area of the bearing, A_b, and supplied pressure.

$$\beta =p/p_s=W/\left(A_b{p}_s\right).$$

(9)

For the membrane restrictors in the proposed dual membrane restrictor as shown in Figure 1b, an increased applied load will increase recess pressure and then the inlet membrane deflection will be decreased while the deflection of the outlet membrane will be increased. With constant stiffness, $K_{mi}$ and $K_{mo}$ for the inlet membrane and outlet membrane, the membrane deflection ratio can be described as a function of dimensionless stiffness of the inlet membrane and outlet membrane, $K_{mi}^{*} \mathrm{and} K_{mo}^{*}$:

$$\begin{array}{c}{\xi }_i= \frac{1-\beta }{K_{mi}^{*}} \mathrm{and} 0\le \beta \le 1; 0\le {\xi }_i\le 1.\\ {\xi }_o= \frac{\beta }{K_{mo}^{*}} \mathrm{and} 0\le \beta \le 1; 0\le {\xi }_o\le 1.\end{array}$$

(10)

Then, the dimensionless deformation–pressure relationship shown in Equation (4) can be derived as

$$\begin{array}{c}\beta =\frac{\alpha {\alpha }_{moa} {\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^{-3}}{\alpha {\alpha }_{moa} {\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^{-3}+\alpha {\alpha }_{mia} {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-3}+{\alpha }_{mia}{\alpha }_{moa} {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-3} {\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^{-3}}\\ \mathrm{and} {\alpha }_{moa}{K}_{mo}^{*}{}^3 {\left(K_{mi}^{*}-1+\beta \right)}^3\left(1-\beta \right)>{\alpha }_{mia} K_{mi}^{*}{}^3{\left(K_{mo}^{*}-\beta \right)}^3\beta .\end{array}$$

(11)

However, if the recess pressure ratio is larger than the dimensionless membrane stiffness for the outlet restrictor, $\beta \ge K_{mo}^{*}$, then the exit of the outlet membrane restrictor was closed, the pressure ratio can then be derived as

$$\beta =\frac{\alpha }{\alpha +{\alpha }_{mia} {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-3}}$$

(12)

The relationships between clearance ratio, $\epsilon$, and recess pressure ratio (loading) can be derived as:

$$\begin{array}{c}\mathrm{For} \beta <K_{mo}^{*},\\ \alpha =\frac{R}{R_r}={\left(\frac{h_r}{h}\right)}^3=\frac{\beta {\alpha }_{mia}{\alpha }_{moa} {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-3}{\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^{-3}}{{\alpha }_{moa} {\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^{-3}-\beta {\alpha }_{moa} {\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^{-3}-\beta {\alpha }_{mia} {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-3},}\\ \mathrm{and}\\ \epsilon =\frac{h}{h_r}=\sqrt[3]{\frac{{\alpha }_{moa}\left({\beta }^{-1}-1\right){\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^3-{\alpha }_{mia}{\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^3}{{\alpha }_{mia}{\alpha }_{moa}}}\end{array}$$

(13)

$$\begin{array}{c}\mathrm{For} \beta \ge K_{mo}^{*},\\ \alpha =\frac{R}{R_r}={\left(\frac{h_r}{h}\right)}^3=\frac{\beta {\alpha }_{mia} {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-3}}{1-\beta },\\ \mathrm{and}\\ \epsilon =\frac{h}{h_r}=\sqrt[3]{\frac{1-\beta }{\beta {\alpha }_{mia}}}\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right).\end{array}$$

(14)

The dimensionless stiffness of the bearing can then be derived from Equation (13):

$$\begin{array}{c}\mathrm{For} \beta <K_{mo}^{*},\\ K_b^{*}=K_b\frac{h_r}{P_s{A}_b}=-\frac{dW}{dh}\frac{h_r}{P_s{A}_b}=-\frac{d\beta }{d\epsilon }=\\ 3{\left[\frac{{\alpha }_{moa}\left({\beta }^{-1}-1\right) {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^3-{\alpha }_{mia}{\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^3}{{\alpha }_{mia}{\alpha }_{moa}}\right]}^{2/3}\frac{{\alpha }_{mia}{\alpha }_{moa}}{{\alpha }_{moa}{\beta }^{-2}{\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^3-\frac{3}{K_{mi}^{*}}{\alpha }_{moa}\left({\beta }^{-1}-1\right){\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^2-\frac{3}{K_{mo}^{*}}{\alpha }_{mia}{\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^2}\end{array}$$

(15)

$$\begin{array}{c}\mathrm{For} \beta \ge K_{mo}^{*},\\ K_b^{*}=K_b^{*}=3{\left[\frac{\left({\beta }^{-1}-1\right) {\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^3}{{\alpha }_{mia}}\right]}^{2/3}\frac{{\alpha }_{mia}}{{\beta }^{-2}{\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^3-\frac{3}{K_{mi}^{*}}\left({\beta }^{-1}-1\right){\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^2}\end{array}$$

(16)

The performance of the hydrostatic bearing is highly dependent on the design of the restrictor used. With the derived equations, the effects of the design parameters on these bearing performance measures can be estimated for further analysis.

3. Analysis for Parameters Designs

Theoretically, infinite stiffness for bearings can be achieved by letting the denominator of Equation (15) or (16) be zero. In other words, infinite stiffness for the bearing can be achieved when the following equations are satisfied:

$$\begin{array}{c}\mathrm{For} \beta <K_{mo}^{*},\\ \frac{{\alpha }_{moa}}{{\alpha }_{mia}}=\frac{3}{K_{mo}^{*}}{\left(\frac{\left(K_{mi}^{*}-1\right){\beta }^{-2}-2{\beta }^{-1}+3}{K_{mi}^{*}}\right)}^{-1}{\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-2}{\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^2\end{array}$$

(17)

$$\begin{array}{c}\mathrm{For} \beta \ge K_{mo}^{*},\\ K_{mi}^{*}=1+2\beta -3{\beta }^2\end{array}$$

(18)

It was indicated that for any recess pressure ratio, $\beta$, we can find a proper value for the design theoretically such that the bearing system can reach an unlimited stiffness at that $\beta$ value. However, there are several constraints that should also be followed for practical applications.

1.

To maintain the load capacity of the system, the outlet membrane resistor should be closed when the load is high. Therefore, the dimensionless stiffness of the outlet membrane should be restricted by the following equation:

$$K_{mo}^{*}\le 1.$$

(19)

2.

Flow through the inlet membrane restrictor to the recess should be no less than the flow out of the recess through the outlet membrane restrictor.

$$\frac{{\alpha }_{moa}}{{\alpha }_{mia}}\ge \left(\frac{\beta }{1-\beta }\right){\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-3}{\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^3$$

(20)

3.

The bearing stiffness should not be negative to prevent system instability. Therefore,

$$\begin{array}{c}\mathrm{For} \beta <K_{mo}^{*}, \\ \frac{{\alpha }_{moa}}{{\alpha }_{mia}}\ge \frac{3}{K_{mo}^{*}}{\left(\frac{(K_{mi}^{*}-1){\beta }^{-2}-2{\beta }^{-1}+3}{K_{mi}^{*}}\right)}^{-1}{\left(\frac{K_{mi}^{*}-1+\beta }{K_{mi}^{*}}\right)}^{-2}{\left(\frac{K_{mo}^{*}-\beta }{K_{mo}^{*}}\right)}^2,\\ \mathrm{for} \mathrm{any} \beta \mathrm{that} 0<\beta <K_{mo}^{*}.\end{array}$$

(21)

$$\begin{array}{c}\mathrm{For} \beta \ge K_{mo}^{*},\\ K_{mi}^{*}\ge 1+2\beta -3{\beta }^2 \mathrm{for} \mathrm{any} \beta \mathrm{that} 0<\beta <1, \mathrm{therefore}, K_{mi}^{*}\ge \frac{4}{3}.\end{array}$$

(22)

It should be noted that the term at the left-hand side of Equation (21) is the same as that of Equation (17). It was indicated that the ratio of $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$ should be equal to the maximum value of the term at the left-hand side and the corresponding value ${\beta }_c$ for the pressure ratio $\beta$ is the loading condition where infinite stiffness for the system appears. In other words, for known dimensionless membrane stiffness of $K_{mi}^{*}$ and $K_{mo}^{*}$, a set of corresponding $\beta$ and $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$ can be found such that the bearing system can maintain positive stiffness over the entire load region and reach infinite stiffness at ${\beta }_c$.

A series of calculations were conducted to study the effects of membrane stiffness of $K_{mi}^{*}$ and $K_{mo}^{*}$ on corresponding $\beta$ and $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$. These results provided information for us on how to select these design parameters properly such that a high stiffness hydrostatic system could be designed for some specific loading regions.

Figure 2 shows the effects of dimensionless stiffness of membranes, $K_{mi}^{*}$ and $K_{mo}^{*}$, on the corresponding pressure ratio ${\beta }_c$. Examining these results, the following observations can be made:

1.

The corresponding pressure ratio β_c where theoretical infinite stiffness can be reached mainly depends on the value chosen of dimensionless outlet membrane $K_{mo}^{*}$. The larger the $K_{mo}^{*}$, the larger the ${\beta }_c$. However, the ${\beta }_c$ is always smaller than 0.5.

2.

With a dimensionless membrane stiffness for the inlet restrictor, $K_{mi}^{*}$, of 4/3 and a $K_{mo}^{*}$ larger than 1/3, the ${\beta }_c$ is maintained at the constant level of 1/3.

3.

The effects of $K_{mi}^{*}$ on ${\beta }_c$ are less significant. Based on these observations, we found that if high stiffness for a specific loading region is desired, we can identify the corresponding pressure ${\beta }_c$, then the proper $K_{mo}^{*}$ and the selection of $K_{mi}^{*}$ is less critical.

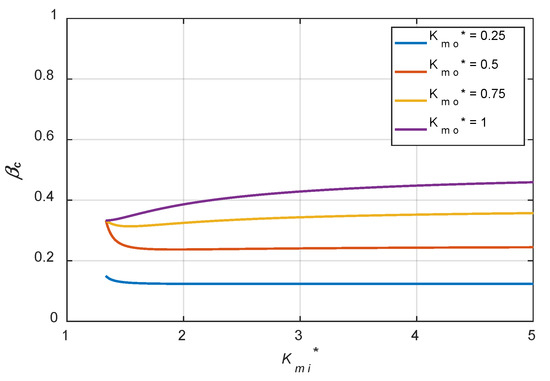
Figure 2. Effects of membrane stiffness of $K_{mi}^{*}$ and $K_{mo}^{*}$ on corresponding ${\beta }_c$.

Figure 3 shows the effects of the dimensionless stiffness of membranes, $K_{mi}^{*}$ and $K_{mo}^{*}$, on the corresponding $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$. Examining these results, the following observations can be made:

1.

Much larger $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$ is preferred when $K_{mi}^{*}$ is small and it drastically increases when $K_{mi}^{*} \mathrm{is} \mathrm{smaller} \mathrm{than} 2$. When $K_{mi}^{*}$ is smaller than 1.5, most of the corresponding ratio is larger than 1. It is indicated that the flow resistance of the outlet membrane without membrane deformation should be larger than that of the inlet membrane without membrane deformation. However, when $K_{mi}^{*} \mathrm{is} \mathrm{larger} \mathrm{than} 2$, the flow resistance of the outlet membrane without membrane deformation should be smaller than that of the inlet membrane without membrane deformation. This indicated that the flow rate of the inlet membrane restrictor should be much larger.

2.

The larger $K_{mo}^{*}$, a larger $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$ is preferred. It indicated that if a stiffer membrane was used in the outlet membrane restrictor, the flow resistance of the outlet membrane without membrane deformation should be larger. Based on these observations, it was shown that if a smaller $K_{mi}^{*}$ is adopted, the $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$ is very sensitive to the selection of $K_{mo}^{*}$. This might increase the difficulty in manufacturing and assembly of these restrictors.

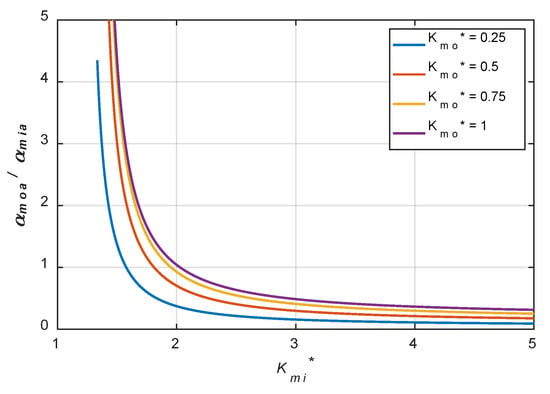
Figure 3. Effects of membrane stiffness of $K_{mi}^{*}$ and $K_{mo}^{*}$ on corresponding $\frac{{\alpha }_{moa}}{{\alpha }_{mia}}$.

4. Simulations and Discussions

In previous sections, the ways to select the design parameters for the proposed dual membrane restrictors was discussed. It is known that due to manufacturing variations, there are always variations occurring, such that the performance of the system is not what had been designed. Furthermore, the simplifications in modelling would also increase the differences in the performance of the designed systems. However, simulation studies still provide some design guidelines for product design. In this section, a series of simulations were conducted to study how variations in design parameters affect the performance of the system.

$\underset{\_}{K_{mi}^{*}>1.33}$

Figure 4 is another way to show the relationship between ${\beta }_c$, $K_{mi}^{*}$ and $K_{mo}^{*}$. The first set of cases ($K_{mi}^{*}$ > 1.33) studied are also indicated in the figures and parameters for these cases listed in Table 1. For each case, a 10% variation in each design parameter was also simulated.

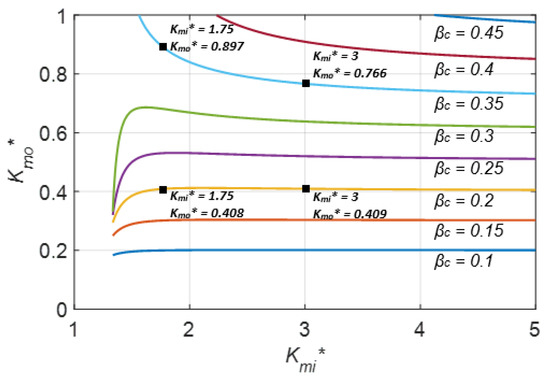
Figure 4. The relationship between ${\beta }_c$, $K_{mi}^{*}$ and $K_{mo}^{*}$.

Table 1. Design parameters for cases studied ($K_{mi }^{*}$ > 4/3).

Case	${\mathit{\beta }}_{\mathit{c}}$	${\mathit{K}}_{\mathit{m}\mathit{i}}^{*}$	${\mathit{K}}_{\mathit{m}\mathit{o}}^{*}$	${\mathit{\alpha }}_{\mathit{m}\mathit{i}\mathit{a}}$	${\mathit{\alpha }}_{\mathit{m}\mathit{o}\mathit{a}}$
1	0.2	1.75	0.408	0.502	0.486
2	0.2	3	0.409	1.040	0.259
3	0.35	1.75	0.897	0.321	0.519
4	0.35	3	0.766	0.506	0.210

Figure 5, Figure 6, Figure 7 and Figure 8 show the effects of parameter variations on the variation of clearance for Case 1 (${\beta }_c$ = 0.20, $K_{mi}^{*}$ = 1.75). After examining all simulation results, the following observations can be made:

1.

Decrease in $K_{mi}^{*}$, or increase in $K_{mo}^{*}$, or increase in α_mia, or decrease in α_moa will induce negative stiffness, which might result in system instability.

2.

$K_{mi}^{*}$ is the most dominant factor for the performance of the system.

3.

Compared with $K_{mi}^{*}$ and ${\alpha }_{mia}$, the effects of $K_{mo}^{*}$ and α_moa on system performance are more localized and appear around the loading condition corresponding to ${\beta }_c$.

4.

Compared with the bearing system compensated with a single membrane, the proposed dual membrane system with the same $K_{mi}^{*}$ and ${\alpha }_{mia}$ and the optimized $K_{mo}^{*}$ and ${\alpha }_{moa}$ do improve the bearing stiffness.

5.

Even with variation in design parameters, improvement is possible for the bearing system especially when the loading is around the desired ${\beta }_c$.

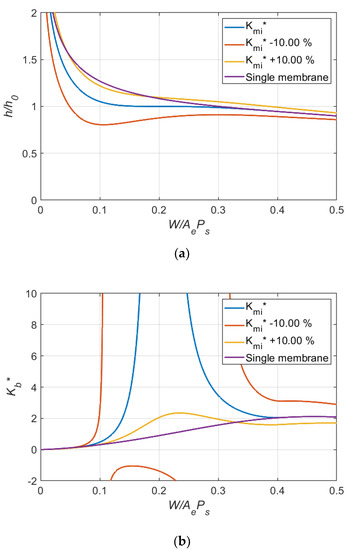
Figure 5. Effects of variation in dimensionless stiffness of inlet membrane on (a) bearing clearance ratio and (b) dimensionless bearing stiffness. (Case 1:${\beta }_c$ = 0.20, $K_{mi}^{*}$ = 1.75).

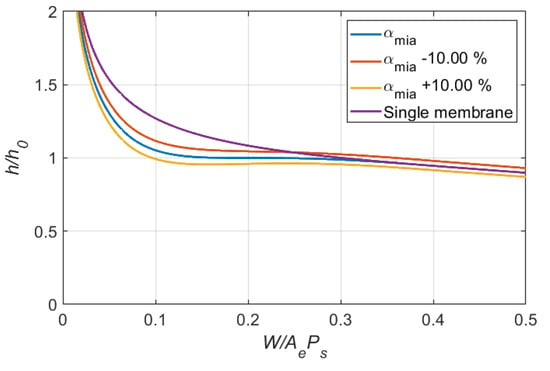
Figure 6. Effects of variation in dimensionless inlet flow resistance ratio on bearing clearance ratio (Case 1:${\beta }_c$= 0.20, $K_{mi}^{*}$ = 1.75).

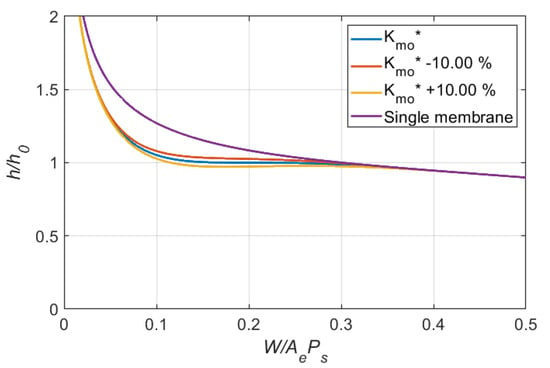
Figure 7. Effects of variation in dimensionless outlet membrane stiffness on clearance ratio (Case 1:${\beta }_c$= 0.20,$K_{mi}^{*}$ = 1.75).

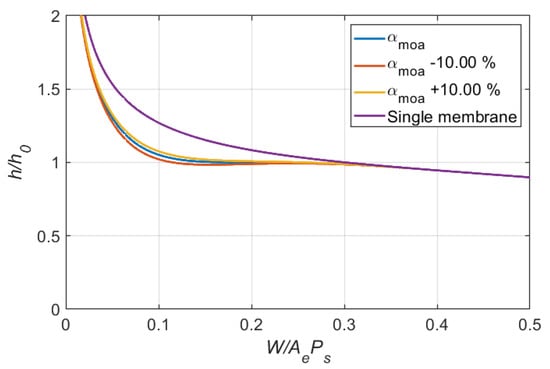
Figure 8. Effects of variation in dimensionless outlet flow resistance ratio on clearance ratio (Case 1:${\beta }_c$ = 0.20, $K_{mi}^{*}$ = 1.75).

Figure 9, Figure 10 and Figure 11 show the effects of variation in $K_{mi}^{*}$ on the variation of clearance for the other cases. After examining all simulation results, the following observations can be made:

1.

For a single membrane restrictor, a smaller $K_{mi}^{*}$, a smaller variation in clearance over the loading region ($\beta$ = 0.2 to 0.8) can be observed.

2.

The working region improved by the optimal design of the dual membrane restrictor is increased as a larger ${\beta }_c$ is used.

3.

The effects of variation in dimensionless inlet membrane stiffness, $K_{mi}^{*}$, on the variation of clearance decreased as $K_{mi}^{*}$ increased. It is indicated that a larger tolerance is allowable when a larger $K_{mi}^{*}$ is used.

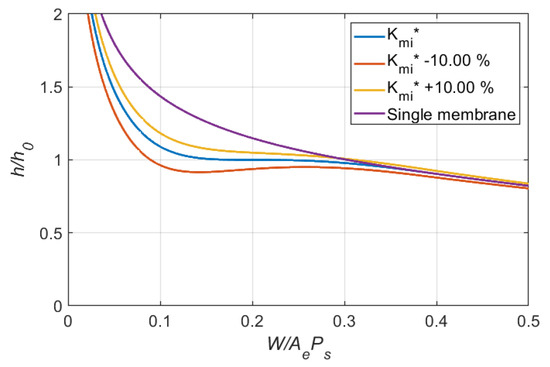
Figure 9. Effects of variation in dimensionless inlet membrane stiffness on clearance ratio (Case 2:${\beta }_c$ = 0.2, $K_{mi}^{*}$ = 3).

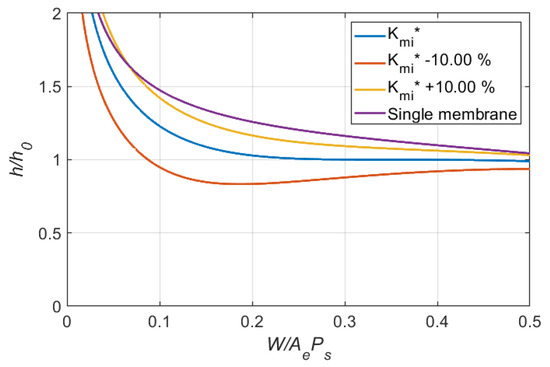
Figure 10. Effects of variation in dimensionless inlet membrane stiffness on clearance ratio (Case 3:${\beta }_c$ = 0.35, $K_{mi}^{*}$ = 1.75).

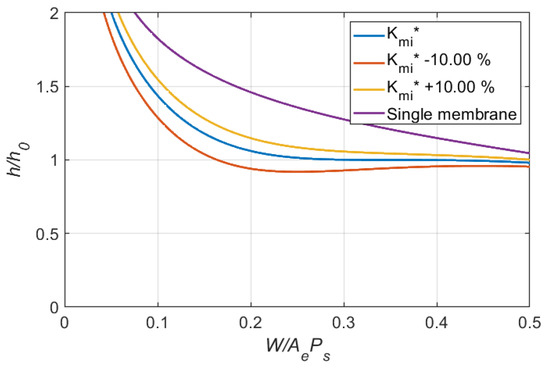
Figure 11. Effects of variation in dimensionless inlet membrane stiffness on clearance ratio (Case 4:${\beta }_c$ = 0.35, $K_{mi}^{*}$ = 3).

$\underset{\_}{K_{mi}^{*}>1.33}$

Theoretically, infinite stiffness for the single pad hydrostatic bearing can be achieved by using a membrane restrictor with a $K_{mi}^{*}$ of 4/3 and ${\alpha }_{mia}$ of 1/4 when loading appeared at the ${\beta }_c$ of 1/3 [15]. However, it was also found that the stiffness of the system was very low when the loading was small. The concept of the dual membrane restrictor was originated to improve the performance of the single membrane restrictor at the low loading region. The parameters for the second set of cases ($K_{mi}^{*}$ = 1.33) studied are listed in Table 2.

Table 2. Design parameters for cases studied ($K_{mi}^{*}$ = 4/3).

Case	${\mathit{\beta }}_{\mathit{c}}$	${\mathit{K}}_{\mathit{m}\mathit{i}}^{*}$	${\mathit{K}}_{\mathit{m}\mathit{o}}^{*}$	${\mathit{\alpha }}_{\mathit{m}\mathit{i}\mathit{a}}$	${\mathit{\alpha }}_{\mathit{m}\mathit{o}\mathit{a}}$
5	0.1	1.33	0.183	0.273	0.714
6	0.2	1.33	0.294	0.251	1.639

Figure 12 and Figure 13 show the effects of variation in $K_{mi}^{*}$ on the variation of clearance and the stiffness for the bearing system for these cases. After examining all simulation results, the following observations can be made:

1.

Two infinite stiffness regions appeared at the loading corresponding to $\beta$ = ${\beta }_c$ and $\beta$= 1/3.

2.

The dual membrane restrictor can provide better performance than a single membrane. However, the clearance levels for these two infinite stiffness loading regions are different and the difference increases as the difference between ${\beta }_c$ and 1/3 increases.

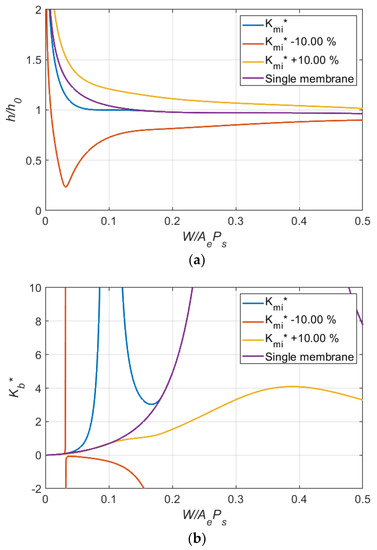
Figure 12. Effects of variation in dimensionless stiffness of inlet membrane on (a) clearance ratio and (b) dimensionless bearing stiffness (Case 6:${\beta }_c$ = 0.10, $K_{mi}^{*}$ = 1.33).

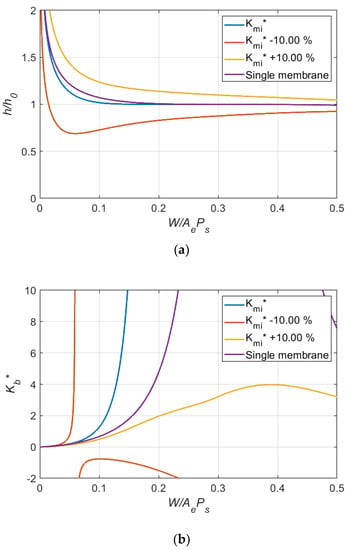
Figure 13. Effects of variation in dimensionless stiffness of inlet membrane on (a) clearance ratio and (b) dimensionless bearing stiffness (Case 6:${\beta }_c$ = 0.20, $K_{mi}^{*}$ = 1.33).

5. Feasibility Tests to Prove the Proposed Concept

In order to prove the concept of the proposed design, feasibility tests were conducted. Figure 14 and Figure 15 show the photo and schematic sketch of the test set-up. In order to prevent the movement of the bearing in the lateral direction, an air bearing was used to hold the horizontal position of the single pad bearing while it provided almost no friction in the vertical direction. The dimensions of all key components are summarized in Table 3. The dimensions were designed such that the dimensionless parameters of the test system were close to the simulated conditions of Case 1.

Figure 14. Photo of the test set-up.

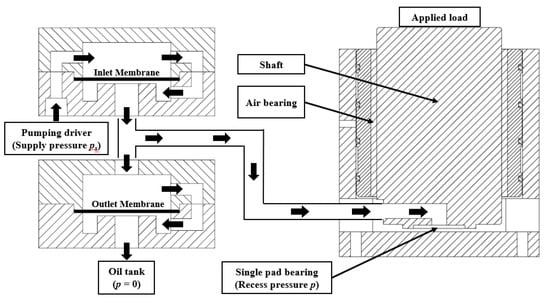
Figure 15. The schematic sketch of the test set-up.

Table 3. Parameters used in experiment for case 1: ${\beta }_c$ = 0.20, $K_{mi}^{*}$ = 1.75.

Supply Pressure ps	1.4 MPa
Corresponding pressure ratio βc	0.2
Lubricant viscosity η	0.02 Pa·s
Young’s modulus of membrane E	210 GPa
Poisson’s ratio of membrane υ	0.3
Radius of restricting plane of inlet membrane r1, r2, r3	4.5, 7.5, 15 mm
Assembly clearance of inlet membrane restrictor li	47 μm
Thickness of inlet membrane t	0.9 mm
Radius of restricting plane of outlet membrane r1, r2, r3	2.5, 9, 15 mm
Assembly clearance of outlet membrane restrictor lo	50 μm
Thickness of outlet membrane t	0.5 mm
Radius of restricting plane of circular bearing r1, r2	15.5, 22 mm
Reference clearance of bearing pad hr	33 μm

In these tests, 10 kg iron blocks were added on the top of the bearing one by one to increase the loading on the bearing. The supply pressure, recess pressure, flowing rate of the lubricant measured and the estimated flow resistance of the recess are listed in Table 4. The temperature of the lubricant measured and the estimated viscosity of the lubricant, and hence the film thickness of the bearing under different loading conditions were estimated and are listed in Table 5.

Table 4. The supply pressure, recess pressure, flow rate of the lubricant measured and the estimated flow resistance of the recess.

	Single Membrane				Dual Membrane
Loading (N)	ps (bar)	p (bar)	Flow Rate (mL/min)	Flow Resistance (Pa-s/mm3)	ps (bar)	p (bar)	Flow Rate (mL/min)	Flow Resistance (Pa·s/mm3)
41	14	0.37	22	201	14.11	0.38	23.4	218
139	13.95	1.28	26	412	14.04	1.29	23.4	412
237	13.92	2.15	30	563	13.97	2.16	23.4	565
335	13.87	3.05	35	652	13.88	3.05	23.4	634
433	13.84	3.91	39	715	13.88	3.91	23.4	715
531	13.8	4.78	43	761	13.86	4.75	23.4	794
629	13.77	5.6	46	807	13.83	5.52	23.4	817
728	13.75	6.32	49	897	13.8	6.23	23.4	899
825	13.75	6.74	50	863	13.75	6.74	23.4	857
923	13.75	7.37	52	886	13.72	7.27	23.4	985
1021	13.75	7.9	52	988	13.73	7.9	23.4	1010
1119	13.76	8.46	52	1100	13.73	8.46	23.4	1090
1217	13.77	8.96	52	1300	14.11	0.38	23.4	1230

Table 5. The temperature of the lubricant measured, the estimated viscosity of the lubricant and the estimated film thickness of the bearing.

	Single Membrane			Dual Membrane
Loading (N)	Temp. (°C)	Viscosity (Pa·s)	Film Thickness h(μm)	Temp. (°C)	Viscosity (Pa·s)	Film Thickness h (μm)
41	23.9	0.016	37.61	23.4	0.0178	37.45
139	23.8	0.016	29.62	23.4	0.0177	30.21
237	23.7	0.0162	26.80	23.4	0.0177	27.18
335	23.7	0.0162	25.52	23.4	0.0175	26.07
433	23.6	0.0163	24.80	23.4	0.0175	25.04
531	23.6	0.0164	24.34	23.4	0.0174	24.14
629	23.6	0.0164	23.87	23.4	0.0174	23.91
728	23.6	0.0165	23.08	23.4	0.0173	23.11
825	23.6	0.0166	23.43	23.4	0.0172	23.44
923	23.5	0.0166	23.23	23.4	0.0172	22.38
1021	23.5	0.0168	22.49	23.4	0.0172	22.21
1119	23.4	0.0169	21.73	23.4	0.0172	21.62
1217	23.4	0.0169	20.58	23.4	0.0172	20.78

Figure 16 shows the comparison of the simulation and test results for both the single membrane restrictor and the proposed dual membrane restrictor. It was shown that the test results were quite close to the simulation results for bearing compensation with both single membrane and dual membrane restrictors. As expected, the proposed dual membrane restrictor can improve the performance of the bearing in the light loading region.

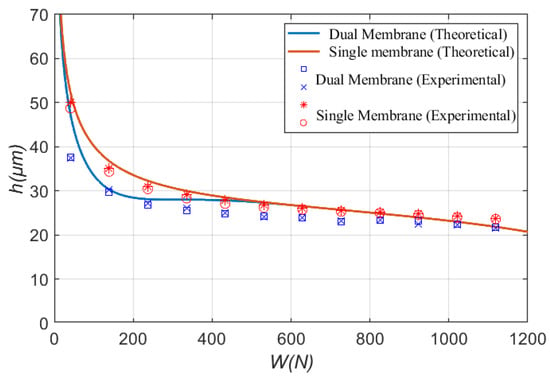
Figure 16. Experimental results of dual-membrane restrictor comparing with single membrane restrictor (Case 1:${\beta }_c$ = 0.20, $K_{mi}^{*}$ = 1.75).

6. Conclusions

In this paper, a dual membrane restrictor design was proposed to improve the stiffness performance of the compensated single pad bearing. The design concept was initiated to improve the performance of a single membrane restrictor in the light loading region. Theoretical models for the proposed dual membrane restrictors were derived. Analysis of these models provided a way to select parameters such that a high stiffness region could be achieved at the desired loading region. A series of simulations were conducted to study the variations in the design parameters on the stiffness and clearance variations. It was found that the dimensionless stiffness of the inlet membrane, $K_{mi}^{*}$, was the most dominant parameter for the performance of the compensated bearing system.

The main advantages of the proposed dual membrane restrictor are the increase in flexibility in providing high stiffness at the desired loading region; and the improvement of the stiffness performance of the bearing system, especially at the desired loading region. In order to prove the concept of the proposed design, a set of experiments were conducted. It was shown that the test results were quite close to the simulation results for bearing compensation with both single membrane and dual membrane restrictors. As expected, the proposed dual membrane restrictor could improve the performance of the bearing in the light loading region.