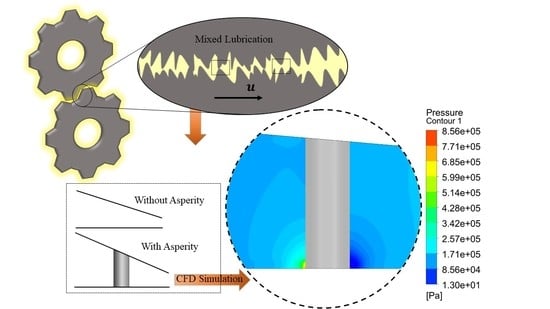
CFD Investigation of Reynolds Flow around a Solid Obstacle
Abstract
:1. Introduction
2. Methodology
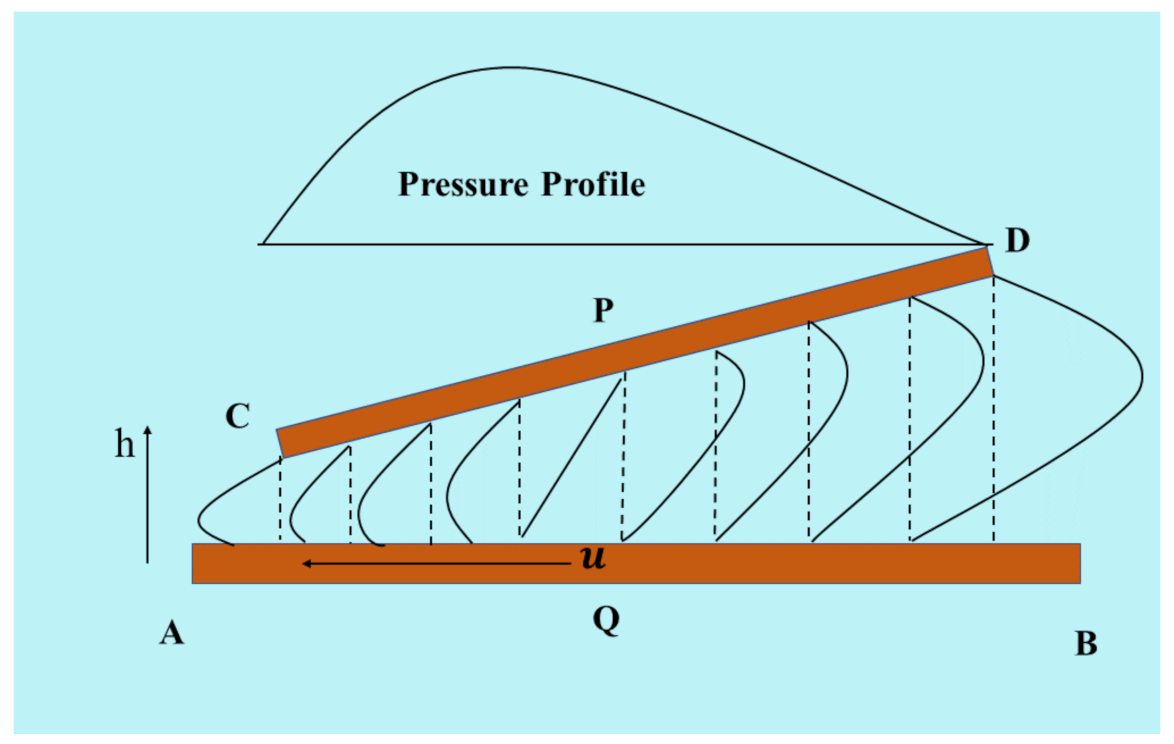
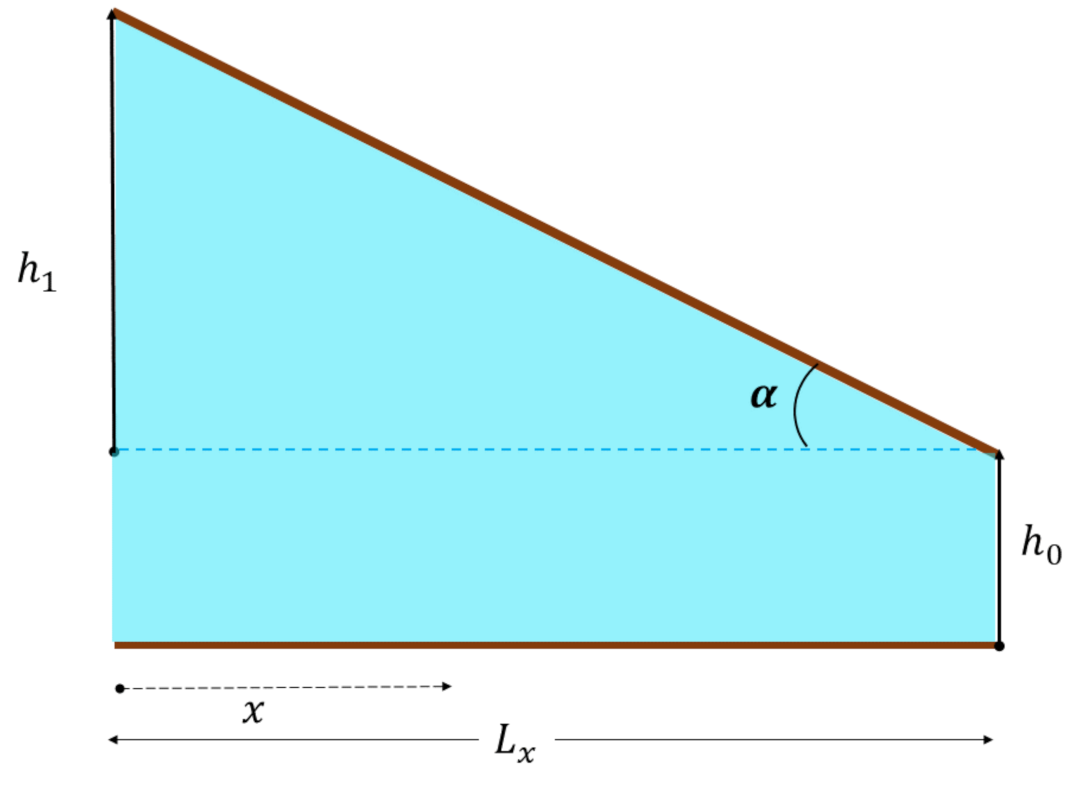
3. Simple Wedge (Without-Asperity Contact Model)
3.1. Analytical Method
3.2. Numerical Method
3.3. CFD Model
Model Setup
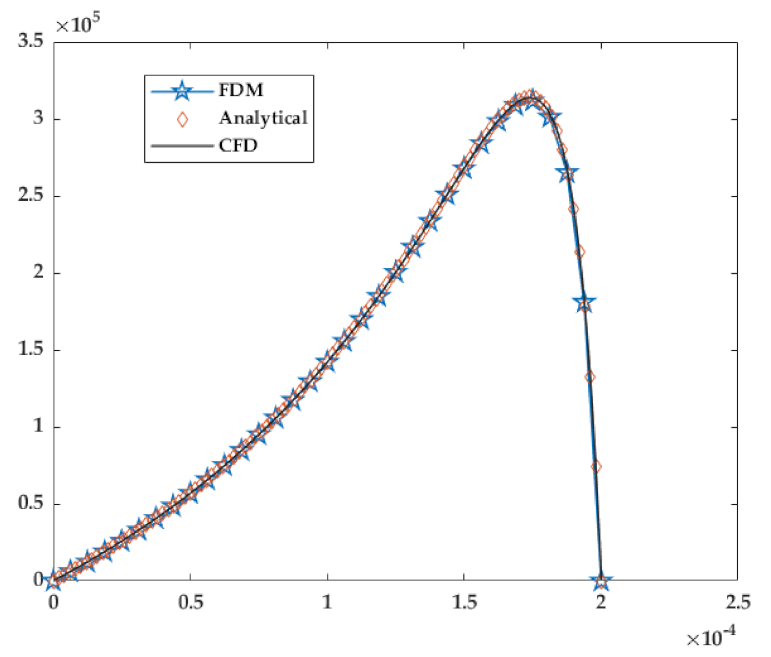
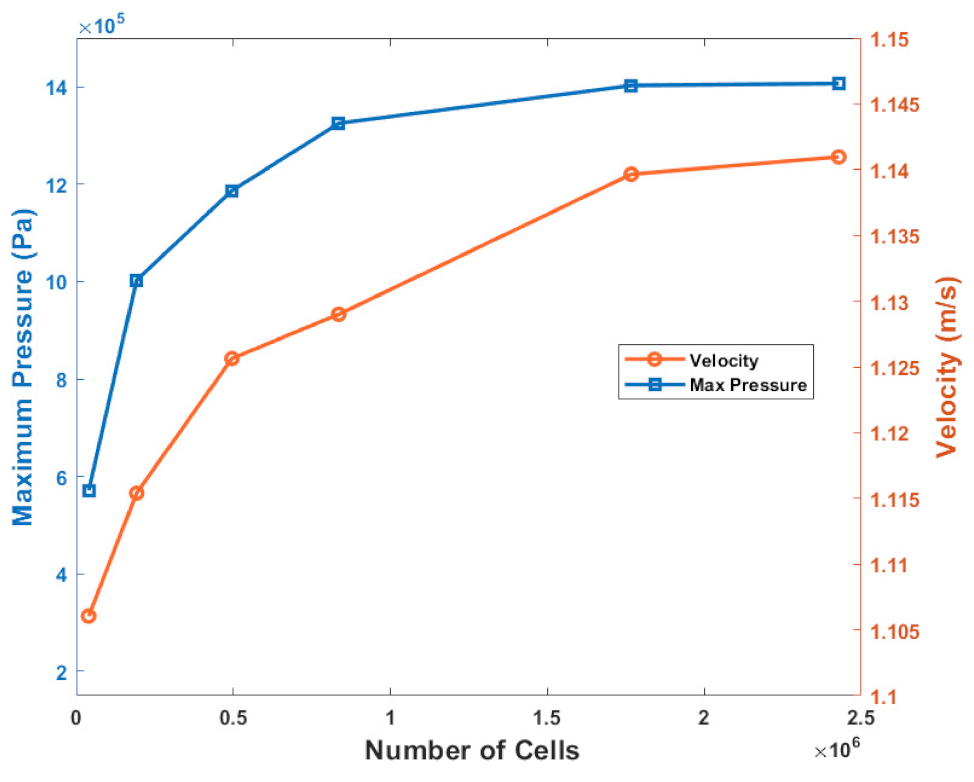
3.4. Model Verification
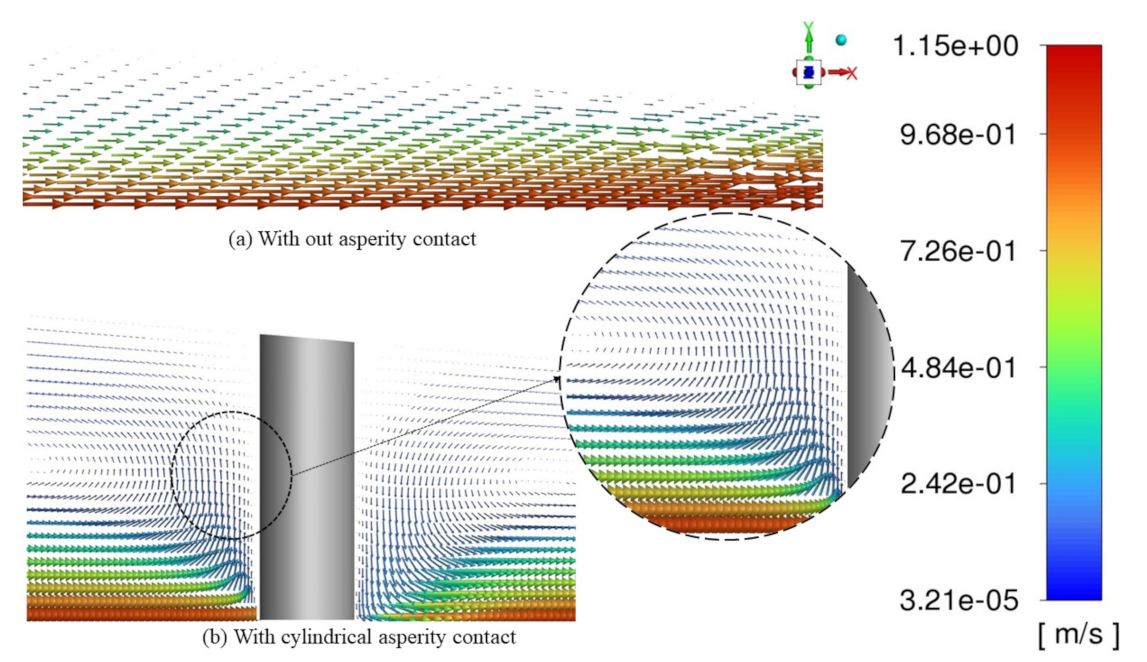
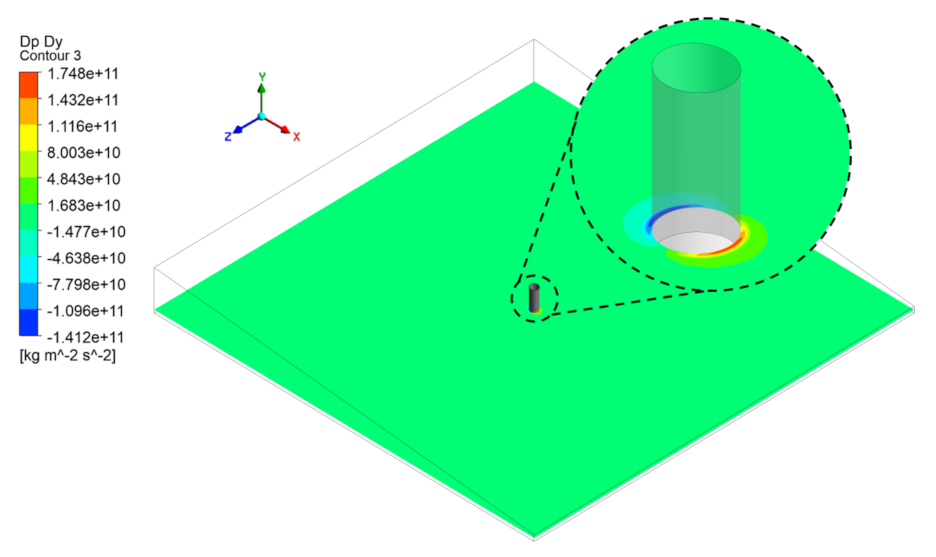
4. Cylindrical Asperity Contact (With Asperity Contact Model)
5. Results and Discussion
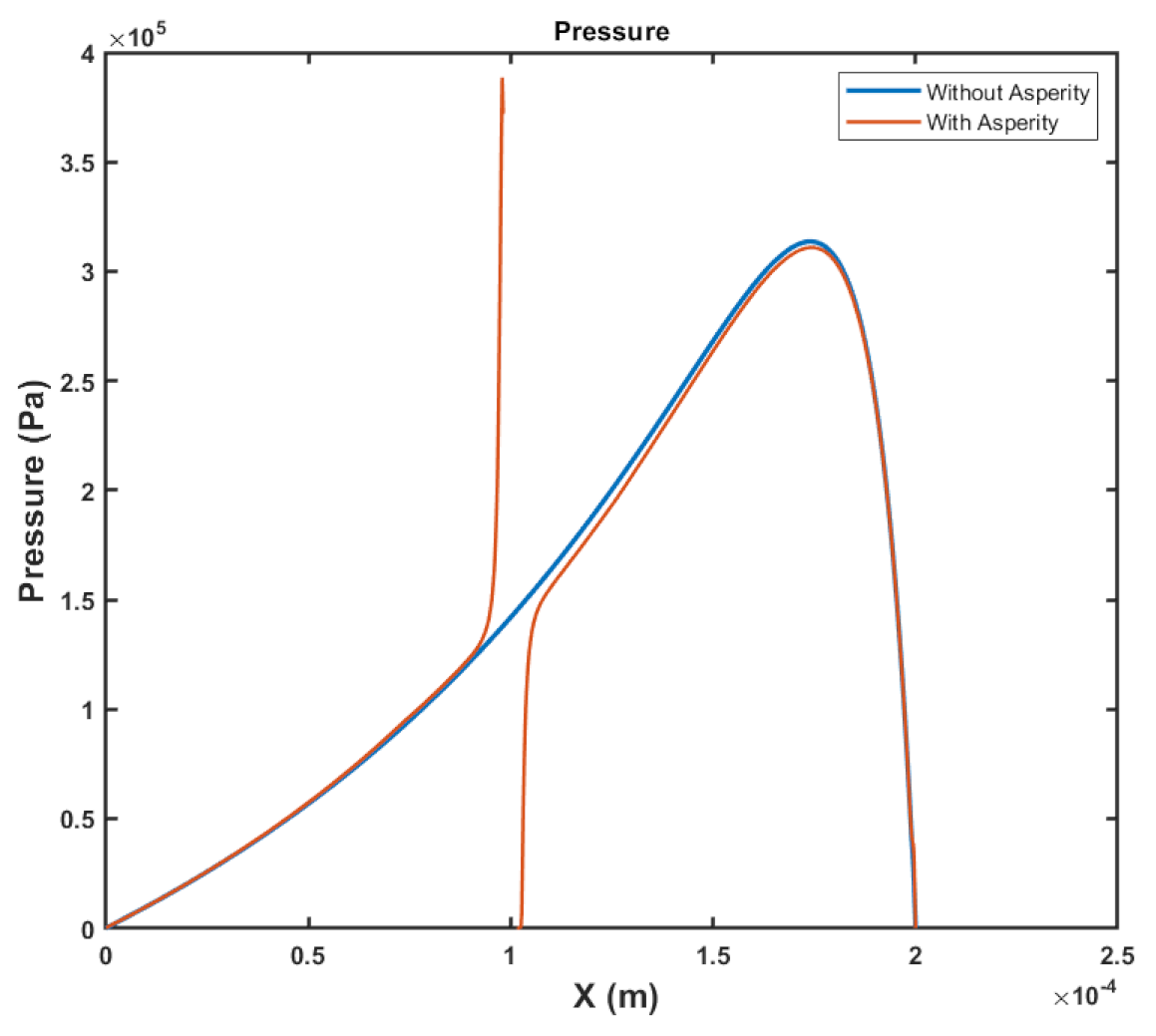
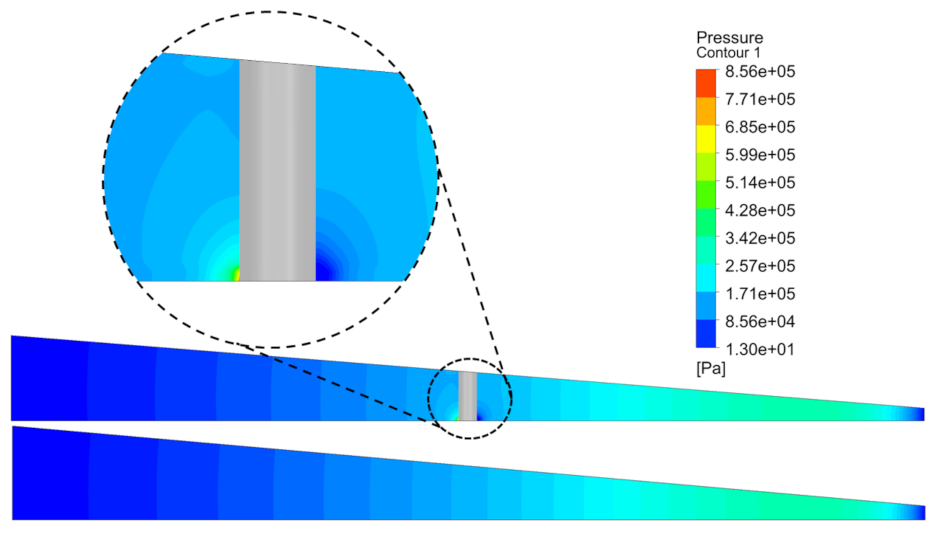
5.1. Pressure Comparison
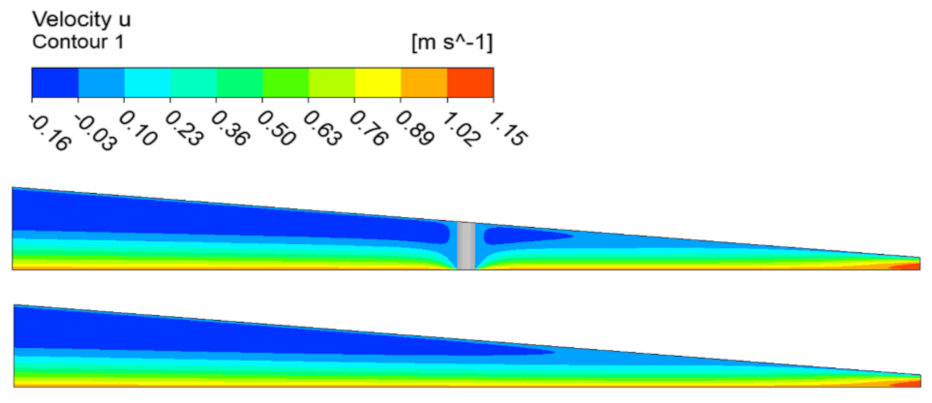
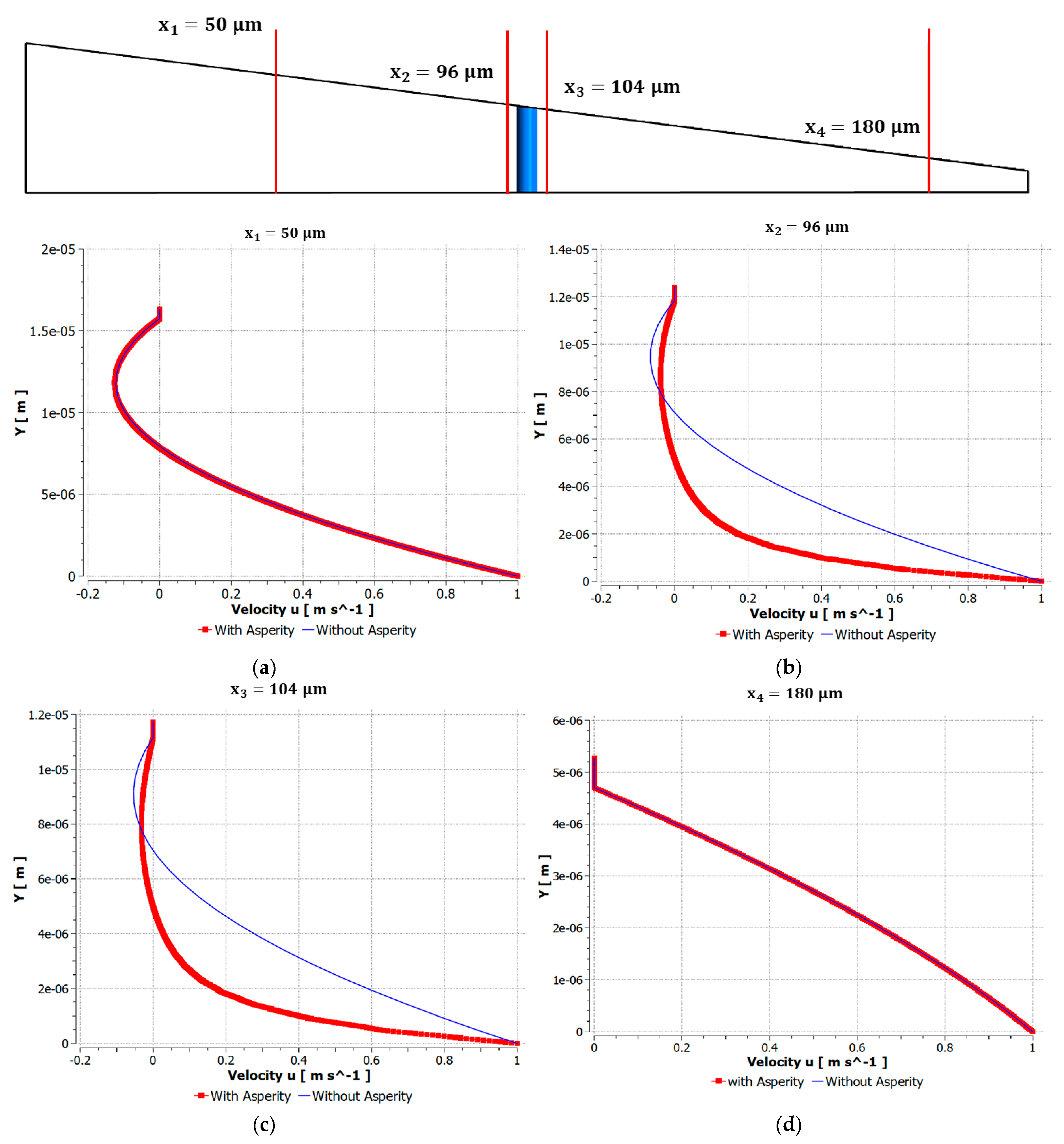
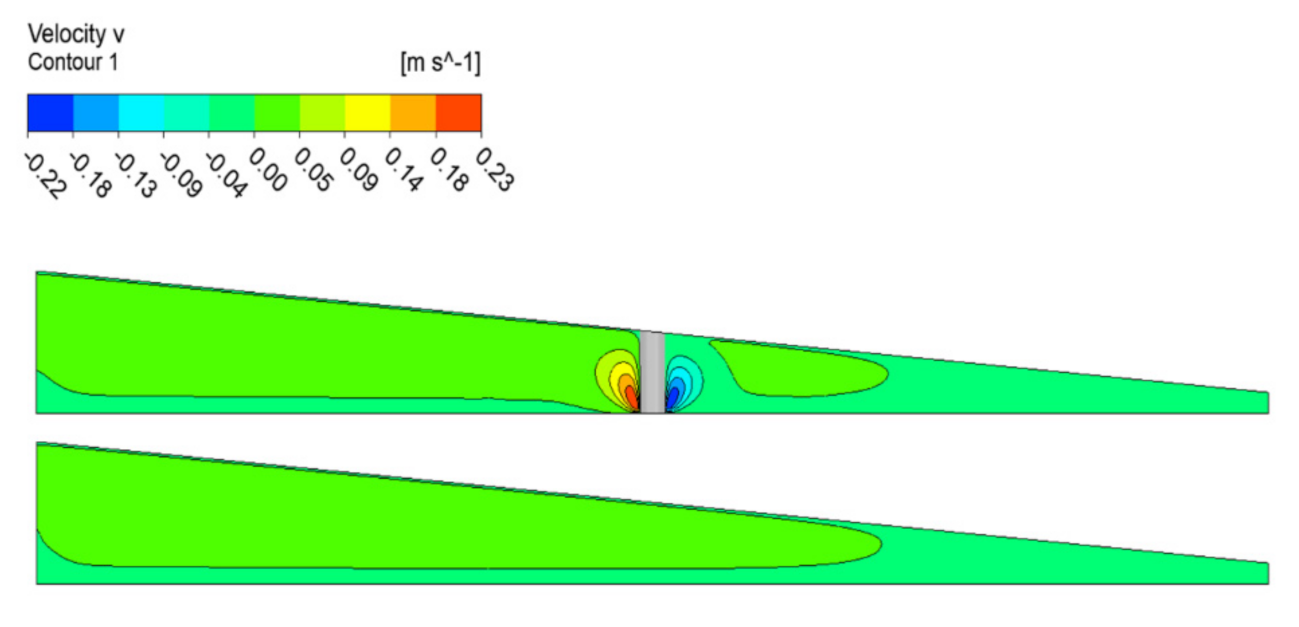
5.2. Velocity Comparison
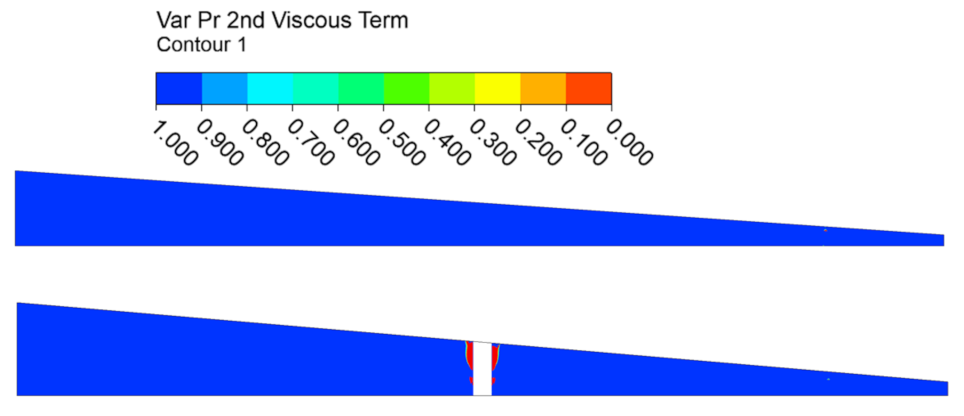
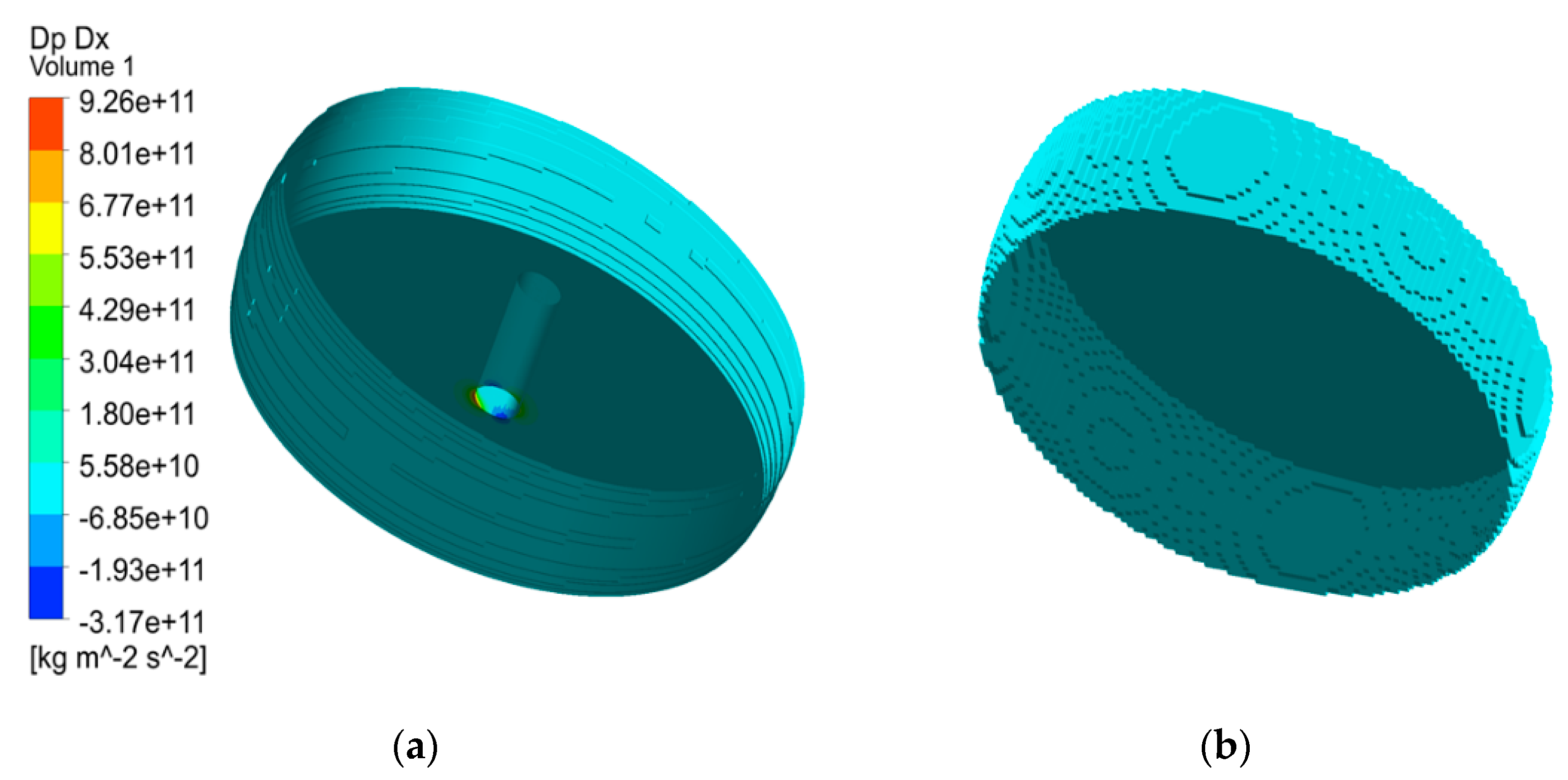
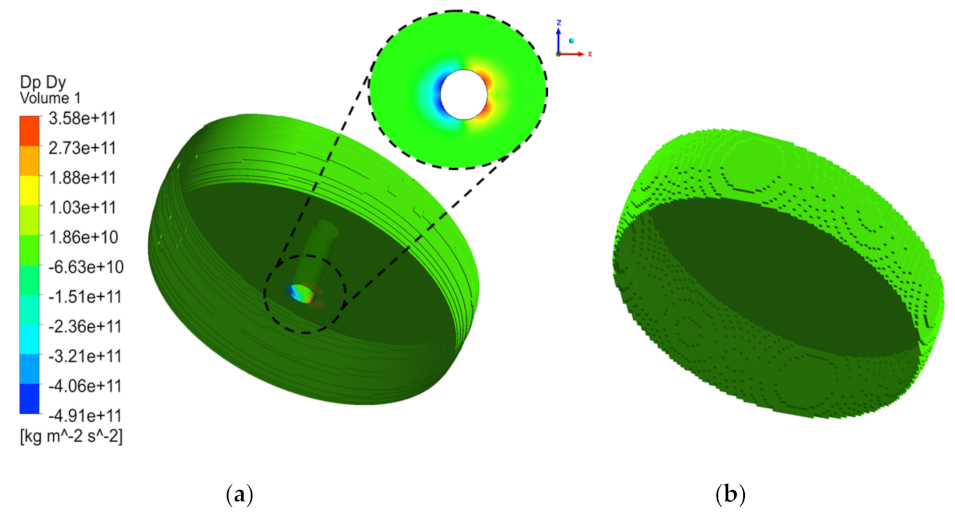
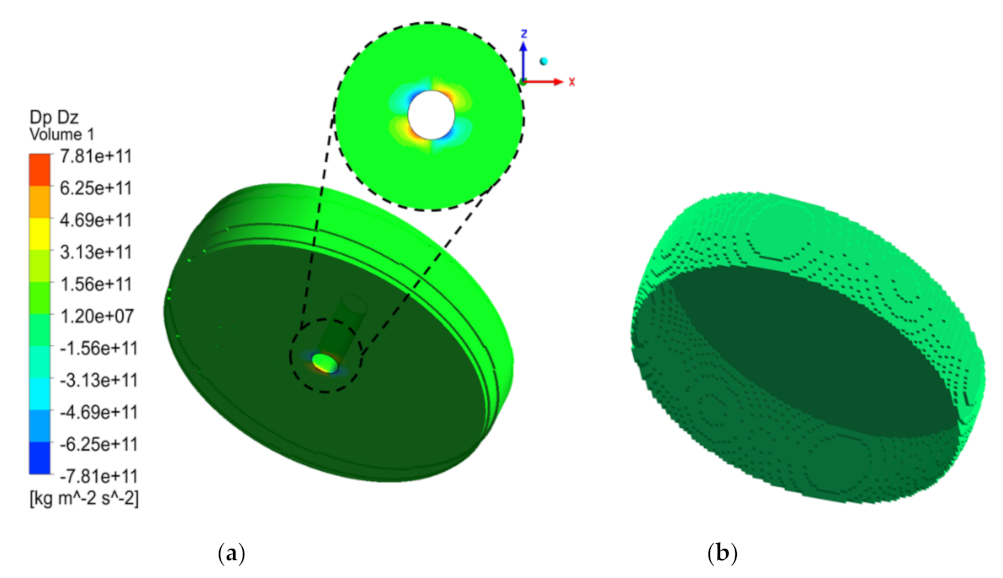
5.3. Comparison of Each Term of the Navier–Stokes (NS) Equation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Coordinate | |
| Length of the wedge horizontal direction | |
| Film thickness | |
| Velocity component | |
| Velocity of upper plate | |
| Velocity of lower plate | |
| Density | |
| Dynamic viscosity | |
| Pressure and dimensionless pressure | |
| Angle of inclination | |
| Film thickness and dimensionless film thickness at the outlet | |
| Film thickness at max pressure | |
| Poisson’s ratio | |
| Length in lateral direction | |
| Dimensionless grid size | |
| Indices for nodes | |
| Epsilon ratio = dh/dL |
References
- Deolalikar, N.; Sadeghi, F.; Marble, S. Numerical Modeling of Mixed Lubrication and Flash Temperature in EHL Elliptical Contacts. J. Tribol. 2007, 130, 011004. [Google Scholar] [CrossRef]
- Holmberg, K.; Erdemir, A. Influence of tribology on global energy consumption, costs and emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Rajput, H.; Atulkar, A.; Porwal, R. Optimization of the surface texture on piston ring in four-stroke IC engine. Mater. Today Proc. 2021, 44, 428–433. [Google Scholar] [CrossRef]
- Reynolds, O. IV. On the theory of lubrication and its application to Mr. Beauchamp tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Dowson, D. A generalized Reynolds equation for fluid-film lubrication. Int. J. Mech. Sci. 1962, 4, 159–170. [Google Scholar] [CrossRef]
- Hamrock, B.J. Fundamentals of Fluid Film Lubrications; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Liu, S.; Qiu, L.; Wang, Z.; Chen, X. Influences of Iteration Details on Flow Continuities of Numerical Solutions to Isothermal Elastohydrodynamic Lubrication With Micro-Cavitations. J. Tribol. 2021, 143, 101601. [Google Scholar] [CrossRef]
- Zhu, D. On some aspects of numerical solutions of thin-film and mixed elastohydrodynamic lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 561–579. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, Q.J. Elastohydrodynamic Lubrication: A Gateway to Interfacial Mechanics—Review and Prospect. J. Tribol. 2011, 133, 041001. [Google Scholar] [CrossRef]
- Lubrecht, A.A. The Numerical Solution of Elastohydrodynamic Lubricated Line and Point Contact Problems Using Multigrid Techniques. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1987. [Google Scholar]
- Venner, C.H.; Lubrecht, A.A. Multilevel Methods in Lubrication; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Ai, X. Numerical Analyses of Elastohydrodynamically Lubricated Line and Point Contacts with Rough Surfaces by Using Semi-System and Multigrid Methods. (Volumes I and II). Ph.D. Thesis, Northwestern University, Evanston, IL, USA, 1993. [Google Scholar]
- Wang, W.-Z.; Liu, Y.-C.; Wang, H.; Hu, Y.-Z. A Computer Thermal Model of Mixed Lubrication in Point Contacts. J. Tribol. 2004, 126, 162–170. [Google Scholar] [CrossRef]
- Venner, C. Multilevel Solution of the EHL Line and Point Contact Problems. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1991. [Google Scholar]
- Morales-Espejel, G.E.; Dumont, M.L.; Lugt, P.M.; Olver, A.V. A Limiting Solution for the Dependence of Film Thickness on Velocity in EHL Contacts with Very Thin Films. Tribol. Trans. 2005, 48, 317–327. [Google Scholar] [CrossRef]
- Zhu, D.; Hu, Y. The study of transition from full film elastohydrodynamic to mixed and boundary lubrication. In The Advancing Frontier of Engineering Tribology, Proceedings of the 1999 STLE/ASME HS Cheng Tribology Surveillance; ASME: New York, NY, USA, 1999; pp. 150–156. [Google Scholar]
- Morales-Espejel, G.E. Surface roughness effects in elastohydrodynamic lubrication: A review with contributions. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 1217–1242. [Google Scholar] [CrossRef]
- Cheng, H.S. Analytical Modeling of Mixed Lubrication Performance; Tribology Series; Elsevier: Amsterdam, The Netherlands, 2002; pp. 19–33. [Google Scholar] [CrossRef]
- Patel, R.; Khan, Z.A.; Saeed, A.; Bakolas, V. A Review of Mixed Lubrication Modelling and Simulation. Tribol. Ind. 2021, 44, 150–168. [Google Scholar] [CrossRef]
- Dobrica, M.B.; Fillon, M.; Maspeyrot, P. Influence of Mixed-Lubrication and Rough Elastic-Plastic Contact on the Performance of Small Fluid Film Bearings. Tribol. Trans. 2008, 51, 699–717. [Google Scholar] [CrossRef]
- Cui, S.; Gu, L.; Fillon, M.; Wang, L.; Zhang, C. The effects of surface roughness on the transient characteristics of hydrodynamic cylindrical bearings during startup. Tribol. Int. 2018, 128, 421–428. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1966, 295, 300–319. [Google Scholar] [CrossRef]
- Wu, C.; Zheng, L. An Average Reynolds Equation for Partial Film Lubrication With a Contact Factor. J. Tribol. 1989, 111, 188–191. [Google Scholar] [CrossRef]
- Xu, W.; Tian, Y.; Li, K.; Zhang, M.; Yang, J. Reynolds boundary condition realization in journal bearings: Location of oil film rupture boundary with layering-sliding mesh method. Tribol. Int. 2022, 165, 107330. [Google Scholar] [CrossRef]
- Peterson, W.; Russell, T.; Sadeghi, F.; Berhan, M.T.; Stacke, L.-E.; Ståhl, J. A CFD investigation of lubricant flow in deep groove ball bearings. Tribol. Int. 2021, 154, 106735. [Google Scholar] [CrossRef]
- Vilhena, L.; Sedlaček, M.; Podgornik, B.; Rek, Z.; Žun, I. CFD Modeling of the Effect of Different Surface Texturing Geometries on the Frictional Behavior. Lubricants 2018, 6, 15. [Google Scholar] [CrossRef] [Green Version]
- Dhande, D.Y.; Pande, D.W. Multiphase flow analysis of hydrodynamic journal bearing using CFD coupled Fluid Structure Interaction considering cavitation. J. King Saud Univ.—Eng. Sci. 2018, 30, 345–354. [Google Scholar] [CrossRef] [Green Version]
- Hajishafiee, A.; Kadiric, A.; Ioannides, S.; Dini, D. A coupled finite-volume CFD solver for two-dimensional elasto-hydrodynamic lubrication problems with particular application to rolling element bearings. Tribol. Int. 2017, 109, 258–273. [Google Scholar] [CrossRef] [Green Version]
- Dobrica, M.; Fillon, M.; Maspeyrot, P. Deterministic EHD Analysis of Fluid Film Bearings in Mixed Lubrication—Model Validation and Application to Measured Rough Surfaces. In Proceedings of the AUSRIB06 Conference 2006, Brisbane, Australia, 29 September–2 October 2006. paper 111. [Google Scholar]
- Almqvist, T.; Almqvist, A.; Larsson, R. A comparison between computational fluid dynamic and Reynolds approaches for simulating transient EHL line contacts. Tribol. Int. 2004, 37, 61–69. [Google Scholar] [CrossRef]
- Johnston, G.J.; Wayte, R.; Spikes, H.A. The Measurement and Study of Very Thin Lubricant Films in Concentrated Contacts. Tribol. Trans. 1991, 34, 187–194. [Google Scholar] [CrossRef]
- Dou, P.; Jia, Y.; Zheng, P.; Wu, T.; Yu, M.; Reddyhoff, T.; Peng, Z. Review of ultrasonic-based technology for oil film thickness measurement in lubrication. Tribol. Int. 2022, 165, 107290. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Q.J.; Chung, Y.-W.; Berkebile, S. Lubrication–Contact Interface Conditions and Novel Mixed/Boundary Lubrication Modeling Methodology. Tribol. Lett. 2021, 69, 164. [Google Scholar] [CrossRef]
- Zhu, D. Elastohydrodynamic Lubrication in Extended Parameter Ranges—Part II: Load Effect. Tribol. Trans. 2002, 45, 549–555. [Google Scholar] [CrossRef]
- Krupka, I.; Hartl, M.; Liska, M. Thin lubricating films behaviour at very high contact pressure. Tribol. Int. 2006, 39, 1726–1731. [Google Scholar] [CrossRef]
- Chang, L. A deterministic model for line-contact partial elastohydrodynamic lubrication. Tribol. Int. 1995, 28, 75–84. [Google Scholar] [CrossRef]
- Jiang, X.; Hua, D.Y.; Cheng, H.S.; Ai, X.; Lee, S.C. A Mixed Elastohydrodynamic Lubrication Model With Asperity Contact. J. Tribol. 1999, 121, 481–491. [Google Scholar] [CrossRef]
- Zhao, J.; Sadeghi, F.; Hoeprich, M.H. Analysis of EHL Circular Contact Start Up: Part I—Mixed Contact Model With Pressure and Film Thickness Results. J. Tribol. 2001, 123, 67–74. [Google Scholar] [CrossRef]
- Hu, Y.-Z.; Zhu, D. A Full Numerical Solution to the Mixed Lubrication in Point Contacts. J. Tribol. 1999, 122, 1–9. [Google Scholar] [CrossRef]
- Wang, W.-Z.; Li, S.S.; Shen, D.; Zhang, S.G.; Hu, Y.-Z. A mixed lubrication model with consideration of starvation and interasperity cavitations. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 1023–1038. [Google Scholar] [CrossRef]
- Azam, A.; Dorgham, A.; Morina, A.; Neville, A.; Wilson, M.C. A simple deterministic plastoelastohydrodynamic lubrication (PEHL) model in mixed lubrication. Tribol. Int. 2019, 131, 520–529. [Google Scholar] [CrossRef] [Green Version]
- Patir, N.; Cheng, H.S. An Average Flow Model for Determining Effects of Three-Dimensional Roughness on Partial Hydrodynamic Lubrication. J. Lubr. Technol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Morales-Espejel, G.E. Flow factors for non-Gaussian roughness in hydrodynamic lubrication: An analytical interpolation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 1433–1441. [Google Scholar] [CrossRef]
- Sahlin, F.; Larsson, R.; Almqvist, A.; Lugt, P.; Marklund, P. A mixed lubrication model incorporating measured surface topography. Part 1: Theory of flow factors. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 335–351. [Google Scholar] [CrossRef] [Green Version]
- Sahlin, F.; Larsson, R.; Marklund, P.; Almqvist, A.; Lugt, P.M. A mixed lubrication model incorporating measured surface topography. Part 2: Roughness treatment, model validation, and simulation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2010, 224, 353–365. [Google Scholar] [CrossRef]
- Babu, P.V.; Ismail, S.; Ben, B.S. Experimental and numerical studies of positive texture effect on friction reduction of sliding contact under mixed lubrication. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 360–375. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.J.; Wang, W.; Hu, Y.; Zhu, D. Effects of Differential Scheme and Mesh Density on EHL Film Thickness in Point Contacts. J. Tribol. 2006, 128, 641–653. [Google Scholar] [CrossRef]
- Zhu, D.; Liu, Y.; Wang, Q. On the Numerical Accuracy of Rough Surface EHL Solution. Tribol. Trans. 2014, 57, 570–580. [Google Scholar] [CrossRef]
- Bakolas, V.; Mihailidis, A. Analysis of rough line contacts operating under mixed elastohydrodynamic lubrication conditions. Lubr. Sci. 2004, 16, 153–168. [Google Scholar] [CrossRef]
- Jiang, M.; Gao, L.; Yang, P.; Jin, Z.M.; Dowson, D. Numerical analysis of the thermal micro-EHL problem of point contact with a single surface bump. Tribol. Interface Eng. Ser. 2005, 48, 627–635. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Szeri, A.Z. On an inconsistency in the derivation of the equations of elastohydrodynamic lubrication. Proc. R. Soc. A Math. Phys. Eng. Sci. 2003, 459, 2771–2786. [Google Scholar] [CrossRef]
- Wang, Q.J.; Zhu, N.; Cheng, H.S.; Yu, T.H.; Jiang, X.F.; Liu, S.B. Mixed Lubrication Analyses by a Macro-Micro Approach and a Full-Scale Mixed EHL Model. J. Tribol. 2004, 126, 81–91. [Google Scholar] [CrossRef]
- Jiang, X.; Cheng, H.S.; Hua, D.Y. A Theoretical Analysis of Mixed Lubrication by Macro Micro Approach: Part I—Results in a Gear Surface Contact. Tribol. Trans. 2000, 43, 689–699. [Google Scholar] [CrossRef]




| Parameters | Value | Unit |
|---|---|---|
| Velocity | 1 | m/s |
| Wedge inlet | 0.02 | 10−3 m |
| Wedge outlet | 0.003 | 10−3 m |
| Solid Properties | ||
| Solid Elastic Modulus, E | 210 | G Pa |
| Solid Poisson’s ratio, | 0.3 | - |
| Solid Density, | 7850 | kg/m3 |
| Lubricant Properties | ||
| Inlet viscosity of the lubricant, | 0.085 | Pa·s |
| Kinematic viscosity, | 100 | mm2/s |
| Reynolds Number, Re | 0.1 | - |
| Oil Density | 850 | kg/m3 |
| Vapor density | 0.0288 | kg/m3 |
| Vapor viscosity | 8.97 × 10−6 | Pa·s |
| S. N | Parameter Compared | Without Asperity | With Asperity | |
|---|---|---|---|---|
| Max Value (m/s2) | Max Value (m/s2) | |||
| 1. | X-Dir first inertia | 2.481 × 101 | 2.358 × 105 | |
| 2. | X-Dir second inertia | 1.933 × 102 | 4.303 × 104 | |
| 3. | X-Dir third inertia | 3.153 × 10−2 | 2.572 × 105 | |
| 4. | X-Dir first viscous | 1.798 × 10 3 | 6.598 × 108 * | |
| 5. | X-Dir second viscous | 3.232 × 106 * | 2.243 × 108 * | |
| 6. | X-Dir third viscous | 1.226 × 102 | 8.812 × 107 * | |
| 7. | X-Dir pressure term | −1.988 × 106 * | 3.886 × 108 * | |
| 8. | Y-Dir first inertia | 2.043 × 101 | 4.074 × 104 | |
| 9. | Y-Dir second inertia | 1.211 × 101 | 4.303 × 104 | |
| 10. | Y-Dir third inertia | 4.247 × 10−6 | 3.343 × 104 | |
| 11. | Y-Dir Pressure Term | 2.538 × 105 | 1.365 × 109 * | |
| 12. | Y-Dir first viscous | 1.798 × 103 | 6.598 × 108 * | |
| 13. | Y-Dir second viscous term | 6.836 × 104 | 3.732 × 107 * | |
| 14. | Y-Dir third viscous term | 1.235 × 10−1 | 2.079 × 108 * | |
| 15. | Z-Dir first inertia | 6.200 × 100 | 1.952 × 105 | |
| 16. | Z-Dir second inertia | 1.635 × 100 | 4.776 × 104 | |
| 17. | Z-Dir third inertia | 5.430 × 10−2 | 1.526 × 105 | |
| 18. | Z-Dir pressure term | 7.909 × 103 * | 1.088 × 109 * | |
| 19. | Z-Dir first viscous term | 1.459 × 102 | 7.682 × 108 * | |
| 20. | Z-Dir second viscous term | 8.408 × 103 * | 7.231 × 107 * | |
| 21. | Z-Dir third viscous term | 2.293 × 101 | 5.876 × 108 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patel, R.; Khan, Z.A.; Saeed, A.; Bakolas, V. CFD Investigation of Reynolds Flow around a Solid Obstacle. Lubricants 2022, 10, 150. https://doi.org/10.3390/lubricants10070150
Patel R, Khan ZA, Saeed A, Bakolas V. CFD Investigation of Reynolds Flow around a Solid Obstacle. Lubricants. 2022; 10(7):150. https://doi.org/10.3390/lubricants10070150
Chicago/Turabian StylePatel, Ruchita, Zulfiqar Ahmad Khan, Adil Saeed, and Vasilios Bakolas. 2022. "CFD Investigation of Reynolds Flow around a Solid Obstacle" Lubricants 10, no. 7: 150. https://doi.org/10.3390/lubricants10070150
APA StylePatel, R., Khan, Z. A., Saeed, A., & Bakolas, V. (2022). CFD Investigation of Reynolds Flow around a Solid Obstacle. Lubricants, 10(7), 150. https://doi.org/10.3390/lubricants10070150